| Issue |
A&A
Volume 575, March 2015
|
|
|---|---|---|
| Article Number | A7 | |
| Number of page(s) | 14 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201425005 | |
| Published online | 11 February 2015 | |
How can double-barred galaxies be long-lived?
Observatoire astronomique de Strasbourg, Université de Strasbourg – CNRS
UMR 7550, 11 rue de l’Université,
67000
Strasbourg,
France
e-mail:
herve.wozniak@astro.unistra.fr
Received: 16 September 2014
Accepted: 18 November 2014
Context. Double-barred galaxies account for almost one third of all barred galaxies, suggesting that secondary stellar bars, which are embedded in large-scale primary bars, are long-lived structures. However, up to now it has been hard to self-consistently simulate a disc galaxy that sustains two nested stellar bars for longer than a few rotation periods.
Aims. The dynamical and physical requirements for long-lived triaxiality in the central region of galaxies still need to be clarified.
Methods. N-body/hydrodynamical simulations including star formation recipes have been performed. Their properties (bar lengths, pattern speeds, age of stellar population, and gas content) have been compared with the most recent observational data in order to prove that they are representative of double-barred galaxies, even SB0. Overlaps in dynamical resonances and bar modes have been looked for using Fourier spectrograms.
Results. Double-barred galaxies have been successfully simulated with lifetimes as long as 7 Gyr. The stellar and gaseous distributions in the central regions are time dependent and display many observed morphological features (circumnuclear rings, pseudo-bulges, triaxial bulges, ovals, etc.) typical of barred galaxies, even early-type. The stellar population of the secondary bar is younger on average than for the primary large-scale bar. An important feature of these simulations is the absence of any resonance overlap for several Gyr. In particular, there is no overlap between the primary bar inner Lindblad resonance and the secondary bar corotation. Therefore, mode coupling cannot sustain the secondary bar mode. Star formation is identified here as possibly being responsible for bringing energy to the nuclear mode. Star formation is also responsible for limiting the amount of gas in the central region which prevents the orbits sustaining the secondary bar from being destroyed. Therefore, the secondary bar can dissolve but reappear after ≈1 Gyr as the associated wave is persistent as long as central star formation is active. When star formation is switched off the dynamical perturbation associated with the secondary bar needs several Gyr to fully vanish, although the central morphological signature is almost undetectable after 2 Gyr.
Conclusions. Double-bars can be long-lived in numerical simulations with a gaseous component, even in the absence of overlap of resonances or mode coupling, provided that star formation remains active, even moderately, in the central region where the nuclear bar lies.
Key words: galaxies: bulges / galaxies: evolution / galaxies: kinematics and dynamics / galaxies: spiral / galaxies: nuclei
© ESO, 2015
1. Introduction
The early idea that any central triaxial massive component embedded in a stellar disc could be efficient enough to bring gas close to the nucleus (e.g. Kormendy 1982) has for a long time turned the attention of both observers and theoreticians to the fruitful framework of “bars within bars” (Shlosman et al. 1989) preceded by a few works dealing with triaxial bulges (e.g. Louis & Gerhard 1988). At that time, the bars within bars scenario was sustained by a few crucial observations (e.g. de Vaucouleurs 1974; Buta 1986). Since then, the observation of small samples of double-barred galaxies (e.g. Buta & Crocker 1993; Wozniak et al. 1995) laid the groundwork for larger samples, less biased, that has refined the global picture by removing from the list of prototypes a few false detections made in the optical and adding a lot of new examples mainly detected in the near infrared (Erwin 2011, for a comprehensive review).
Main initial parameters.
However, the formation of nuclear bars has remained puzzling in spite of the efforts made by several groups to perform realistic modelling of these complex systems. Our difficulty in creating a standard scenario for the evolution of the central kpc is certainly not due to the lack of models that show how the stellar material can be assembled to form the inner bar, but rather is due to the coexistence of several credible physical mechanisms. Most of these mechanisms have been studied mainly through numerical simulations (N-body and/or hydrodynamical simulations) although orbit analysis (Maciejewski & Sparke 1997, 2000; Maciejewski & Small 2010) has helped a lot to understand the foundation of double-bar dynamics.
The double-bar formation scenarios can first be divided into two major classes: either the large-scale bar forms first, i.e. before the inner one, or the contrary. The first case is sustained by early theoretical works (Shlosman et al. 1989), simulations with a gaseous component present (Friedli & Martinet 1993; Combes 1994; Friedli et al. 1996), but also pure collisionless simulations (Rautiainen & Salo 1999; Curir et al. 2006) making the need for a gaseous component questionable if the initial stellar disc is dynamically hot and embedded in a massive halo. The second case was considered hypothetical until Debattista & Shen (2007) created such examples by fine tuning the initial conditions of their collisionless simulations. One can argue that a third case should exist, that is the two bars growing simultaneously (Saha & Maciejewski 2013). It seems in all cases that the outer bar forms slightly before the inner bar.
Whatever the formation scenario is, the main concern with inner bars formed in N-body/hydrodynamical simulations is that they are short-lived because the central gas concentration naturally tends to destroy the bar. However, the lifetime of any nuclear bar must be long enough to be compatible with the high frequency of double-bars: 30% of barred galaxies or 20% of all galaxies (Erwin 2011). Past simulations that were able to produce long-lived double-barred models (e.g. Rautiainen et al. 2002; Debattista & Shen 2007) are either 2D or purely collisionless.
We show here that 3D N-body/hydrodynamical simulations, implementing classical star formation recipes, are able to create long-lived double-barred galaxies. We identify the dynamical and physical processes whereby a double-barred system can survive on several Gyr.
This paper is focused on the long-term evolution of double-barred galaxies. In Sect. 2 we describe our simulations and introduce postprocessing techniques. The evolution of the central region is addressed in detail in Sect. 3. As forthcoming papers dealing with other aspects of double-barred galaxies will be based on this topic, we give a detailed description there. We compare the properties of simulations with observational constraints in Sect. 4. Finally, we discuss our results in Sect. 5 and conclude in the last section.
2. Description of the numerical simulations
We performed several simulations of disc galaxies varying mainly the initial disc scale lengths and the gas contents. For each simulation, the conditions for the initial stellar and gaseous populations were computed as follows. The initial stellar population was set up to reproduce a typical disc galaxy. The positions and velocities for Ns particles were drawn from a superposition of two axisymmetrical Miyamoto & Nagai (1975) discs of mass respectively M1 and M2 (cf. Table 1). The shape of Miyamoto & Nagai density distribution depends on the choice of two parameters, traditionally called a and b. The Plummer (1911) sphere (a = 0) and the Kuzmin (1956) flat disc (b = 0) are the two extreme possible distributions. The use of Miyamoto & Nagai distributions enabled us to create initial conditions very close to typical disc galaxies. The real radial scale lengths are respectively l1 = a1 + b and l2 = a2 + b. We chose a scale height of b = 0.5 kpc common to all simulations. Thus, with our choice of parameters (cf. Table 1), the first component can be viewed as representing a bulge, the second one a disc, with the main advantage that there is no discontinuity in either the mass density distribution or the gravitational forces. The initial velocity dispersions were computed by solving numerically the Jeans equations. The gaseous component is represented by Ng particles for a total mass of Mg distributed in a lg scalelength Miyamoto-Nagai disc.
Some differences in the initial conditions should be noted. The disc scalelength of SimL (l2 = 6.5 kpc, hence the “L” for “long”) is almost twice that of SimS (3.5 kpc, “S” for “short”) for the same scaleheight (b = 0.5 kpc). The dynamical timescales of the stellar bar development should thus be longer for SimL than for SimS.
The dynamical evolution was computed with a particle-mesh N-body code that includes stars, gas, and recipes to simulate star formation. The broad outlines of the code are the following. The gravitational forces are computed with a particle-mesh method using a 3D polar grid with (NR,Nφ,NZ) = (60,64,312) active cells, leading to a vertical sampling of 50 pc. The smallest radial cell in the central region is 36 pc large. The hydrodynamics equations are solved using the smoothed particle hydrodynamics (SPH) technique, following closely the implementation suggested by Benz (1990). Since we used a log-polar grid, we improved the pre-computation of self-forces by subdividing each cell in (nr,nφ,nz) = (32,6,6) subcells. Self-forces were then linearly interpolated before being subtracted from gravitational forces. The spatial and forces resolutions are thus much higher than in our previous studies based on the same code (e.g. Michel-Dansac & Wozniak 2006; Wozniak & Champavert 2006).
The star formation and feedback modelling is based on the instantaneous star formation approximation (see Michel-Dansac & Wozniak 2004, and reference therein, for details). The major steps are 1) the identification of the regions where star formation can be ignited; 2) the conversion of a fraction of gas into stars; and 3) the computation of the amount of energy and metals injected in the interstellar medium (i.e. the energy and chemical feedback from type II supernovae – SNII). Because the last step leads to gas heating, a simple treatment of radiative cooling is implemented in the energy equation.
The first task is to identify the gaseous particles that will form stars. Friedli & Benz (1993) examined some possible criteria. Not surprisingly, they found that the standard Jeans instability criterion can be applied to spherical non-rotating gaseous systems, but for rotating flat discs that Toomre’s instability criterion (Toomre 1964) is a better indicator. Observational evidence also appears to support the use of this criterion as a good indicator for locating star formation at intermediate scalelengths (Kennicutt 1998, and references therein). In all cases, a particle i will be assumed to undergo a star formation episode if the following condition is verified,
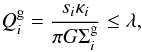 where
where 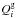 is Toomre’s parameter, si is the local sound speed, κi is the generalized epicyclic frequency, and
is Toomre’s parameter, si is the local sound speed, κi is the generalized epicyclic frequency, and 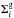 is the gas surface density. The constant λ equals unity in the case of an axisymmetric gaseous disc subject to radial instabilities (cf. Toomre 1964). However, a value of λ ≈ 1.4 (with s = 6 km s-1) has been derived from observations (Kennicutt 1990). Since we intend to reproduce realistic conditions for star formation, we adopted the same value for λ.
is the gas surface density. The constant λ equals unity in the case of an axisymmetric gaseous disc subject to radial instabilities (cf. Toomre 1964). However, a value of λ ≈ 1.4 (with s = 6 km s-1) has been derived from observations (Kennicutt 1990). Since we intend to reproduce realistic conditions for star formation, we adopted the same value for λ.
The pattern speed Ωp of the large-scale bar is easily determined using its position-angle measured every 10 Myr during the simulation run. Any post-processing technique applied on snapshots (spaced by 50 Myr) or on movies (timestep of 1 Myr) gives the same results. For the nuclear or inner bar, the determination of Ωs is more difficult. The initial size of the nuclear bar is unpredictable, and so it is difficult to catch its position-angle in real time during the simulation run. The snapshot sampling (every 50 Myr) is too long to make a proper measurement as the rotation period of the nuclear bar can be much shorter. Therefore, the nuclear position-angle was determined directly from the movies using the inertia moment technique confirmed by eye measurements. However, the errors can be large (typically ≈2 Myr on rotation period measurements), especially when the nuclear bar rotation period Ts is of the order of a few tens of Myr. A Fourier transform technique (as used by Quillen et al. 2011) is unapplicable here because of the frequency cutoff. Therefore, for a few periods of interest, simulations have been partly recomputed using a smaller output timestep (1 Myr) in order to apply this technique (see Sect. 5). For these particular periods, this technique confirms our manual measurements well within our conservative error bars.
The terminology used in the case of double-barred galaxies is wide and thus confusing. We thus clarify hereby what terms will be used throughout this paper. The simulations will represent double-barred galaxies, which means two stellar bars will coexist. A primary bar is the main bar with respect to its size. It is a large-scale structure. It is often named large-scale bar. This does not imply that it appears first, even if this is the case for our simulations. A secondary bar is a smaller stellar structure embedded in the primary bar. However, it is often called the inner or nuclear bar. Hereafter, in the context of this paper, we use the word “nuclear” for a rapidly rotating secondary bar extending less than 500 pc across, and reserve the term “inner” for larger secondary bars.
3. Evolution of the central regions
In Figs. 3 and 5 we show the face-on projections of the central region (2 × 2 kpc) for the two runs used throughout this paper. Figure 2 focuses on the 1 × 1 kpc of SimS during the formation of the nuclear bar. The stellar mass distribution has been photometrically calibrated using the technique of Michel-Dansac & Wozniak (2004). A blue photometric band (B Cousins) has been chosen to emphasize the regions with the youngest stellar population. For this purpose, the age of the initial stellar population has been kept fixed at 10 Gyr for all snapshots. This implies that a direct photometric comparison of snapshots has no sense since the initial stellar population is not getting old and thus its luminosity is not dimming. Because it is a post-processing technique, this obviously has no impact on the self-consistent chemodynamical evolution of the simulation.
The two simulations show different histories of star formation (Fig. 1). Their dynamical history is obviously different, the main driver being the dynamical timescale that is roughly doubled for SimL with respect to SimS.
 |
Fig. 1 Star formation rate (SFR) averaged in a sliding window of 10 Myr for runs SimS (red) and SimL (black). |
 |
Fig. 2 Run SimS: gas mass surface density (left) and B-Cousins surface brightness (right) in the central ±1 kpc for t< 0.7 Gyr. Isocontours are spaced by 0.15 mag in log M⊙ pc-2 for the gas and 0.5 Bmag pc-2 for the stars. The map resolution is 10 pc. Gas particles have been convolved by the SPH kernel to obtain the real distribution. Gas surface densities below 1 M⊙ pc-2 are contoured with dashed lines. The straight dotted line is the primary bar position-angle. |
3.1. Run SimS
3.1.1. The nuclear bar formation
The initial disc quickly develops a typical strong bar and a spiral structure both in the stellar and the gaseous components. The gravity torques due to the bar and spiral structure drive the gas inwards and reorganize the mass distribution even for the old stellar population; this gas inflow occurs in a rather short timescale since the star formation rate peaks at t = 0.45 Gyr (cf. Fig. 1). As expected, star formation also occurs along gaseous spiral arms that are not shown in Figs. 2 and 3.
 |
Fig. 3 As in Fig. 2, but for t> 0.7 Gyr in the central ±2 kpc. The map resolution is now 20 pc. Gas isocontours are spaced by 0.25 mag in log M⊙ pc-2. The radius of ILRp is indicated by dashed white circles. |
From t ≈ 0.36 Gyr, the gas distribution in the central 400 pc (Fig. 3) starts to twist by an increasing angle that amounts to ≈45° at t = 0.4 Gyr. This twist is also visible in the distribution of the new stellar population. At the beginning of the twisting process, the new stellar population is aligned with the gas distribution. Afterwards, the gas twist angle still increases, quickly reaching 90° at t ≈ 0.42 Gyr, but not the stellar angle since the collisionless component is less reactive to the torque induced by the local gravitational potential twist. Moreover, the stellar mass trapped in that region also increases as a result of the on-going star formation, thus making the decoupling of the stellar component easier. When the gas twist angle continues to increase so that the central gas distribution eventually realigns with the larger scale flows, the new stellar population is rather axisymmetric.
At t ≈ 0.5 Gyr there is, however, as much mass in the new stellar component as in the gas component. A second episode of twisting then begins. At t ≈ 0.51 Gyr, the angular motion of the new stellar population distribution becomes elongated and definitively decouples from the gas distribution. For t ≈ 0.52 Gyr, the central gas twist is again almost perpendicular to the major-axis large-scale stellar bar. At that point, one can clearly identify a so-called nuclear secondary bar whose rotating motion seems independent from the gas motion.
During this formation phase, the pattern speed of the nuclear bar is very high, leading to a low rotation period of Ts ≈ 10 Myr (Fig. 4). This value is the dynamical signature of the gas from which the new stellar population has been created. The radius of the nuclear bar is then ls ≈ 250 pc, whereas lp ≈ 4.55 kpc, which leads to ls/lp ≈ 0.056.
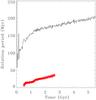 |
Fig. 4 Period of rotation for the primary bar (in black) and the nuclear bar (in red) for SimS. |
3.1.2. The nuclear bar evolution
Once the nuclear bar has been formed and rotates independently of the gas (what was called “decoupling” in some studies from the 1990s), the central gas concentration quickly gets aligned with the stellar component. For t ≳ 0.63 Gyr the gas dynamics can be considered fully driven by the nuclear bar evolution (orientation, velocity) since the gas no longer represents the most massive component in that part of the galaxy. The morphology is modified consequently. Indeed, the gas distribution is more ring-like around the nuclear bar or sometimes disc-like, especially when the energy feedback from SNII temporarily dissolves a part of the gaseous ring.
After 1 Gyr, the total mass inside the central kpc has increased by a factor of 1.5. Indeed, a nuclear gas disc is formed from the accumulation of gas in the centre, and new stars are actively formed there. The first cause of this mass inflow is the overall reorganization of the mass distribution under the influence of the stellar bar, even the old population. Owing to gravitational torques exerted on the gas by the stellar bar, the extra mass in the form of gas and new stars amounts to 1.97 × 109M⊙ at t = 1 Gyr, which is only 31% of the whole additional mass. The redistribution of the old stellar population contributes to the other 69%.
The length of the nuclear bar slowly increases as it slows down. The large-scale bar also increases, but at a lower rate. Therefore, at t = 2 Gyr ls ≈ 1 kpc, lp ≈ 5 kpc so that ls/lp ≈ 0.2.
3.1.3. The nuclear bar dissolution. Formation of the nuclear disc
While the nuclear stellar bar continuously grows, the gaseous ring radius increases. For t ≳ 2 Gyr the nuclear bar gets also thicker, looking sometimes like an oval surrounded by a ring of gas. The ring itself gets broader as the nuclear bar thickens. The nuclear bar is sometimes slightly off-centred, in particular around t ≈ 1.6 Gyr, but this is a transient effect.
It is impossible to precisely date the moment when the nuclear bar can be considered as dissolved because the dissolution process is smooth and has a long timescale. Except for t ≳ 2.7−3.0 Gyr, one can consider that the nuclear bar has been replaced by a nuclear disc. This stellar nuclear disc has a clear signature in the edge-on mass distribution. It also drives the shape of the gaseous nuclear ring. Any slight temporary ovalization of the stellar nuclear disc leads to an alignment of the major-axis of the gaseous ring.
Since the gas accumulation in the central region continues, whereas the star formation rate is very low in the ring, the gas mass increases in the ring and the nucleus. For t> 4 Gyr the gaseous ring becomes unstable. It starts to twist and collapse. This permits the gas flows to reach the nucleus and leads the star formation rate to briefly increase (Fig. 1). As a result, the nice broad gaseous ring is replaced by a gaseous disc of the same size as the nuclear disc for t> 4.3 Gyr until the end of the simulation.
3.2. Run SimL
3.2.1. The nuclear bar formation: the first secondary bar
As for SimS, the initial disc of SimL develops a typical large-scale strong bar and spiral structure. However, because the disc scalelength of SimL is roughly twice that of SimS, the dynamical timescale for the development of the main stellar bar is significantly greater. It is only after t ≈ 0.8 Gyr that the new stellar population created in the central gas concentration forms a nuclear bar-like structure (Fig. 5). This nuclear structure is very small, ls ≈ 250 pc, whereas lp ≈ 5 kpc, which leads to ls/lp = 0.05. It is also transient, lasting less than ≈0.6 Gyr, and is often asymmetric and/or off-centred. It then dissolves into a stellar nuclear spiral structure surrounded by a circumnuclear gaseous ring. It must be also mentioned that the large-scale bar growth is not completed yet. However, even if the length of both bars increases during this phase, the ratio ls/lp remains approximately constant. For instance, at t ≈ 1.3 Gyr, ls/lp ≈ 0.3/6.0 = 0.05.
Because of its time dependent morphology, the pattern speed of this nuclear structure is difficult to measure precisely. The pattern rotation period of the large-scale bar and the nuclear structure are shown in Fig. 6. It was not possible to determine properly the nuclear rotation period for the whole lifetime because of the quick changes in morphology. However, the nuclear structure has a very short rotation period (between 10 and 30 Myr) that strongly contrasts with the primary bar rotation period; it is at least ten times longer. During the lifetime of the nuclear structure, the large-scale bar temporarily slows down, the rotation period increasing from 200 Myr to 300 Myr (Fig. 6).
 |
Fig. 5 As in Fig. 3, but for SimL. From t = 6535 Myr the dashed white circle represents ILRs instead of ILRp which is outside the field of view. |
When the nuclear structure dissolves, both a gaseous disc and a stellar disc (mainly made of new stellar population), surrounded by a ring-like structure, survive. These discs form the remnant of the nuclear bar. The size of both gaseous and stellar discs increases to ≈1.8 kpc in diameter, which leads to ls/lp ≈ 0.9/8 = 0.11. However, because the remnant stellar disc is no longer barred, ls/lp has another meaning here. Transient gaseous and/or stellar spiral arms often appear inside and outside the ring-like structure until t ≈ 2.6 Gyr.
3.2.2. The inner bar formation: the second secondary bar
After t ≈ 2.6 Gyr, the inner region returns to a bar-like shape. The pattern speed can be determined much more precisely now than for the first nuclear bar. The gaseous and stellar components both display the same features. The inner bar ends in a broad circumnuclear ring. In the centre, the remnant of the first nuclear bar settles in the centre as a flattened small bulge. As the stellar inner bar begins to turn into an oval, the gaseous counterpart progressively dissolves. Only a gaseous circumnuclear ring survives, that gradually gets broader (up to roughly 500 pc across the torus).
For t ≳ 4 Gyr, it becomes difficult to unambiguously determine a nuclear bar structure. The central kpc region looks like the triaxial pseudobulges described by Kormendy & Kennicutt (2004). However, even if the contrast between the inner structure and the old stellar population background is too low to permit a proper pattern speed determination, the inner region is not devoid of non-axisymmetries. Therefore, for t ≳ 4.5 Gyr, the whole inner stellar structure, including the now vanishing circumnuclear ring, turns into a strong oval that looks like a ls = 2.2 kpc long bar (ls/lp ≈ 0.275). The shape of this second (in the time sequence) inner bar depends strongly on its relative orientation with respect to the large-scale bar. The higher axis ratio is obtained when the angle between the two bars reaches 90°. When the two bars are aligned, the axis ratio is roughly halved.
For t ≳ 4.5 Gyr, the responsive gaseous ring also starts to turn into an oval, meaning that the gas ring shrinks and expands depending on the relative orientation of the inner bar with respect to the large-scale bar. The ring progressively dissolves into a disc that closely follows the same changes in morphology as the stellar nuclear bar and thus shares the same orientation.
Because star formation, which mainly occurs in the central region, consumes the gas, the nuclear disc size significantly decreases for t ≳ 6 Gyr and becomes dynamically unstable. For 6 <t< 7 Gyr, the star formation rate temporarily increases (Fig. 1) because of the collapse of the gaseous nuclear ring. This is the last episode of star formation in that region. At t ≈ 7 Gyr, the gaseous nuclear disc has almost fully disappeared, whereas the stellar counterpart is made of an inner bar with ls ≈ 1.3 kpc embedded in a slightly larger stellar disc. The large-scale bar has lp = 8.5 kpc leading to ls/lp ≈ 0.15.
As the stellar inner bar (oval-like) still exists for t> 7 Gyr, the gas inflow continues in such a way that a gaseous circumnuclear ring forms again. The gas mass surface density in the ring, and in the region encircled by the ring, is higher than 1 M⊙ pc-2, but never reaches the same high values as during the first 2 Gyr. In particular, the gas distribution is smoother.
These structures, the inner stellar bar or oval and gaseous circumnuclear ring, last until the end of the simulation at t ≈ 9.5 Gyr without any significant morphological change. The only noticeable fact is the permanent slow down of both bars due to the classical angular momentum exchange with the large-scale disc.
At the end of the simulation, ls/lp ≈ 1.5/9 = 0.17, quite close to the value at t = 7 Gyr. Indeed, the two bars slow down, but at different rates.
4. Comparison with observations
4.1. Gas mass in the central kpc
It has been argued in the past (Petitpas & Wilson 2004, and references therein) that large amounts of gas are not required to form and sustain a double-bar. However, if the nuclear bar is long-lived, and we can imagine that the galaxy has been gas rich in the past, then its gas has been consumed and possibly redistributed thus explaining the current low content. Alternatively, if the nuclear bar is a short-lived phenomenon, one has to define the lower gas mass limit to initiate the formation process. This means that the expressions “gas rich” or “gas poor” used in the literature must be clarified.
The last development stage (i.e. after 7 Gyr) of SimL is morphologically close to SB0 galaxies, and so it is morphologically comparable to the Petitpas & Wilson (2004) observations. We can thus determine the amount of gas in a region of similar surface limited by the beam size. For ten objects, the radius encircling the mass that has been measured ranges from 0.3 kpc to 2.6 kpc, but for their SB0 subsample (NGC 2859, NGC 2950, NGC 3081, NGC 4340, and NGC 4371) r< 1 kpc and r< 2.3 kpc are more representative. For r< 1 kpc, observational gas mass upper limits range from 1.5 × 107 to 8.1 × 107M⊙, whereas it amounts to 4.4 × 107M⊙ for SimL. For r< 2.3 kpc it increases to 2.8 × 108M⊙ for our simulation, whereas for NGC 3081 the gas mass amounts to 6.2 or 6.5 × 108M⊙. Since our simulation is not fine tuned to fit any particular galaxy, we can conclude that SimL is well within the observational constraints. A value of 4.4 × 107M⊙ is low enough to explain why Petitpas & Wilson (2004) were unable to detect molecular gas in NGC 2859, NGC 4340, and NGC 4371, but obviously one cannot conclude that the gas component do not play a role in the formation of nuclear bars.
4.2. Stellar population in nuclear bars
Studying the stellar populations of double-barred galaxies NGC 2859, NGC 3941, NGC 4725, and NGC 5850, de Lorenzo-Cáceres et al. (2013) have recently concluded that the inner bars are younger and more metal rich than the large-scale primary bars. It has been argued (Wozniak 2007) that the stellar age distribution in bars has to be interpreted with a dynamical approach. For instance, two regions of apparent low age at the end of the large-scale bars (Pérez et al. 2007) are due to the accumulation of a composite stellar population, younger in average and trapped in orbits shaped like an ellipse in average, aligned with the bar.
To make a comparison with de Lorenzo-Cáceres et al. (2013), a mean age profile has been computed as the average of individual particle age in annuli 100 pc wide and ±100 pc thick centred on the nucleus. Being an azimuthal average approach, each annulus mixes the population inside and outside the structures (inner and outer bars, circumnuclear ring). Moreover, all particles of the initial population arbitrarily have the same age (0 at the beginning of the simulation) so that snapshot time is also the age of the initial population.
 |
Fig. 7 Radial profile of the age difference with the time of the snapshot (t = 9.486 Gyr) for SimL. The mean age has been computed in concentric annuli of 100 pc wide. For the sake of comparison, the radius of the NGC 5850 inner bar and the limit of age measurement (de Lorenzo-Cáceres et al. 2013) have been scaled to SimL and overplotted as dashed and dot-dashed lines, respectively. |
In Fig. 7 we show the relative mean age of the particle population at t = 9.486 Gyr. The region inside the nuclear bar is 2.5−3.0 Gyr younger than the large-scale bar. Because of the mixing with older regions outside the inner bar, and the rough assumption that all initial particles have an age of 9.486 Gyr, this value is certainly a lower limit. The outermost region of the large-scale bar is also younger. This effect is obviouly that discovered by Pérez et al. (2007) and explained by Wozniak (2007).
Even if a direct and quantitative comparison with de Lorenzo-Cáceres et al. (2013) is not possible because the averaging technique is different (they measured ages along ellipses fitted on the isochrone maps), the results are in good qualitative agreement. In particular, the age difference for NGC 5850 amounts to ≈4 Gyr between the nuclear bar and the outermost measurements. To help the comparison, the large-scale bar radius of NGC 5850 (using the de Lorenzo-Cáceres et al. 2013 value, i.e. 63′′) has been scaled to SimL (lp ≈ 9 kpc). The large-scale bar radius was used as its determination is much more accurate than the nuclear radius. In Fig. 7 the outermost limit of age measurement by de Lorenzo-Cáceres et al. (2013) is also plotted showing that their age measurements might be well inside the large-scale bar.
4.3. Pattern speeds
The ratio of pattern speeds (Ωp/Ωs or equivalently Ts/Tp, cf. Fig. 8) is not constant over time. For the two simulations, both Ωp and Ωs decrease as a function of time (Figs. 4 and 6) but are not locked into a particular ratio. The slopes seem different between SimS and SimL, but are in fact consistent with a factor of roughly two in dynamical timescales. This means that the ratio is the same for SimL after twice the time needed by SimS. Because on average Ωs decreases much faster than Ωp, the ratio Ωp/Ωs monotonically increases up to ≈0.21−0.25. Only a change in the slope and a lower dispersion between 6 and 8 Gyr are notable for SimL, mainly due to Ωs variations during the circumnuclear ring collapse (cf. Sect. 3.2). The fluctuations of the ratio is due to oscillations of Ωs and Ωp (Figs. 4 and 6) that depend on the relative phase of the two bars, a fact already observed by Englmaier & Shlosman (2004) and Debattista & Shen (2007).
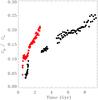 |
Fig. 8 Ratio of the primary to secondary bar pattern speed. Black dots are for SimL, red dots for SimS. |
The best model of Friedli & Martinet (1993) has Ωp/Ωs ≈ 0.32, and 0.3 for Englmaier & Shlosman (2004), values that our simulations never reach. Our values of Ωp and Ωs are comparable, however, to the few measurements in double-barred galaxies. Most observational methods to directly estimate Ωp cannot be easily applied to Ωs and, more generally, are not suited when multiple patterns are present (Maciejewski 2006; Shen & Debattista 2009). However, keeping in mind the questionable viability of Ωs measurement, we must rely on available attempts.
Therefore, if we assume two bars in NGC 5248 (cf. discussion in van der Laan et al. 2013), Ωp = 30 kms-1 kpc-1 (Jogee et al. 2002) and Ωs ≳ 135 kms-1 kpc-1 leading to a ratio Ωp/Ωs≲ 0.23. Corsini et al. (2003) found a value as low as 0.13 for NGC 2950 using the Tremaine-Weinberg method (but see Maciejewski 2006; Shen & Debattista 2009). Hernandez et al. (2005) and Fathi et al. (2009) applied the same technique to Hα velocity fields to determine pattern speeds and found 0.3 < Ωp/Ωs< 0.55, but with large error bars on Ωs. An in-depth analysis of NGC 1068, based both on multiwavelength observations and numerical simulations, led Emsellem et al. (2006) to conclude that 0.19 ≲ Ωp/Ωs ≲ 0.26.
Zhang & Buta (2007) introduced a potential-density phase-shift method that is able to determine the position of multiple corotations in a galaxy without any kinematical information. This method is thus particularly well suited to double-barred galaxies. Moreover, it is based on the properties of quasi-stationary density wave modes. Zhang & Buta (2007) did not publish values for Ωp and Ωs, but only radii for CRs and CRp. However, the ratio of corotation radii CRs/CRp can be used as it evolves like Ωp/Ωs. For their small sample (seven objects), they found ratios between 0.086 (NGC 1530) and 0.3 (NGC 936) and a mean of ≈0.17. For SimS and SimL, CRs/CRp starts at ≈0.03 when a nuclear bar is just detected for the first time and then increases to respectively ≈0.24 and 0.30. Our values are thus comparable even for SB0 galaxies.
The most recent survey (Font et al. 2014b) of pattern speeds in double-barred galaxies, using a phase reversal technique in Hα kinematical maps (Font et al. 2014a) found a narrow range of ratios 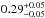 , a bit higher than our end values. However, Font et al. (2014b) have introduced an important assumption: the nuclear bar ends near its corotation (CRs) which in turn overlaps (or is close to) the primary bar ILR (ILRp). If this new technique could be useful to determine the location of resonances (although a firm physical foundation must be found), it gives no information on the type of these resonances, especially the main ones, ILR, ultraharmonic (UHR, also called 4:1), CR, and OLR. Therefore, the identification of the resonance needs to assume that any bar ends inside and close to its corotation. Whereas this is reasonable true for the primary bars (although it has been argued by Michel-Dansac & Wozniak 2006 that typical observational bar length measurement techniques are more correlated with the UHR resonance than with the CR), this assumption is questionable for nuclear bars. Indeed, if CRs is determined in SimL as being the end of the nuclear bar, and moreover identical to ILRp, this leads to a large underestimation of Ωs. For the sake of illustration, we consider the moment t = 7.5 Gyr. At this time, RILRp ≈ 4.84 kpc and Ωp ≈ 15 kms-1 kpc-1. If we assume that this radius is identical to the corotation radius of the nuclear bar, this leads to Ωs ≈ 45 kms-1 kpc-1 instead of ≈73 kms-1 kpc-1 (see also Fig. 10 in the next section). Therefore, the ratio Ωp/Ωs might be spuriously estimated to be 0.33, a value which appears to be in good agreement with Font et al. (2014b), instead of ≈0.2, its real value.
, a bit higher than our end values. However, Font et al. (2014b) have introduced an important assumption: the nuclear bar ends near its corotation (CRs) which in turn overlaps (or is close to) the primary bar ILR (ILRp). If this new technique could be useful to determine the location of resonances (although a firm physical foundation must be found), it gives no information on the type of these resonances, especially the main ones, ILR, ultraharmonic (UHR, also called 4:1), CR, and OLR. Therefore, the identification of the resonance needs to assume that any bar ends inside and close to its corotation. Whereas this is reasonable true for the primary bars (although it has been argued by Michel-Dansac & Wozniak 2006 that typical observational bar length measurement techniques are more correlated with the UHR resonance than with the CR), this assumption is questionable for nuclear bars. Indeed, if CRs is determined in SimL as being the end of the nuclear bar, and moreover identical to ILRp, this leads to a large underestimation of Ωs. For the sake of illustration, we consider the moment t = 7.5 Gyr. At this time, RILRp ≈ 4.84 kpc and Ωp ≈ 15 kms-1 kpc-1. If we assume that this radius is identical to the corotation radius of the nuclear bar, this leads to Ωs ≈ 45 kms-1 kpc-1 instead of ≈73 kms-1 kpc-1 (see also Fig. 10 in the next section). Therefore, the ratio Ωp/Ωs might be spuriously estimated to be 0.33, a value which appears to be in good agreement with Font et al. (2014b), instead of ≈0.2, its real value.
4.4. Bar lengths
The absolute sizes of simulated secondary bars fit quite well with the values given by Erwin (2011). Erwin showed that ls/lp, the secondary over primary bar lengths, ranges from 0.025 to 0.25 with a median of ≈0.12. For the first nuclear bar of SimL, ls/lp remains roughly constant at 0.05. It is only when the nuclear bar has been fully dissolved that this ratio reaches 0.11 (this is then the size of the remnant nuclear disc relative to the large-scale bar). The inner bar restarts with a rather high ratio (0.275 at t ≈ 4.5 Gyr), but then decreases to 0.15−0.19. However, the observational relative size distribution does not show any strong evidence of two different kinds of secondary bars that could help to distinguish the first generation from the subsequent ones. Our simulations should also show some similarities with that of Friedli & Martinet (1993) since our recipes are quite similar, although our initial conditions are different. Indeed, the basic process leading to the formation of a nuclear bar is the same. However, their best model has a bar length ratio of 0.26.
Although it is incorrect to base an argument on absolute sizes, it is also noteworthy that, all other factors being equal, if primary bars have low Ωp (as for SimL), they are longer than bars with high Ωp (as for SimS), assuming here that they systematically fill the region inside their corotation radius. Erwin (2011) emphasizes that the sizes of large-scale bars are longer in double-barred galaxies than in single-barred ones whereas all the other properties are similar.
5. Discussion
SimS and SimL having morphological, kinematical and stellar population properties similar to real galaxies, we can now discuss their dynamical structure and long-term evolution.
5.1. Resonance overlap or not?
In the framework of the epicyclic approximation, we solved the equations Ω − κ/n = Ωp,s for the resonance radii (ILRp and ILRs for n = 2, UHRp and UHRs for n = 4, CRp and CRs for n = ∞, OLRp and OLRs for n = −2). Athanassoula (1992) and Michel-Dansac & Wozniak (2006) have shown that, even in the case of strong bars for which the epicyclic approximation breaks down, the errors on the resonance positions remain within 10%, especially in the case of the ILR and the CR. In Fig. 9 we show the evolution of ILR, UHR, CR, and OLR as a function of time. Since most of the time two ILRs exist, hereafter we only deal with the outermost one (named oILR by most authors). Moreover, because it is very close to the centre in the case of SimS, the position of ILRs is not always reliable for t ≲ 2 Gyr.
 |
Fig. 9 Radius of the linear resonances (ILR, UHR, CR, OLR) for the secondary bar (subscript “s”, red triangles) and the primary bar (“p”, black dots) in the simulations SimS (top) and SimL (bottom). OLRp is not shown. |
The immediate observation is that the whole resonance system of the inner bar, up to OLRs, remains well inside the ILRp for a long time (roughly 2 Gyr for SimS and 8 Gyr for SimL). Therefore, there is no CRs–ILRp overlap, unlike Friedli & Martinet (1993) and many other similar studies that followed.
However, such a situation is not new as a few examples have been already reported by Rautiainen & Salo (1999) and Rautiainen & Salo (2000), but with different experimental setups (either 2D simulations or an analytical bulge component). Moreover, Moellenhoff et al. (1995) reported evidence of an OLRs–ILRp coupling in the case of NGC 4736, before the paradigm of CRs–ILRp coupling was firmly established. They claimed this configuration could weaken the interaction and increase the lifetime of the nuclear bar.
To further investigate the dynamical impact of possible resonance overlaps, we have built spectrograms, as introduced by Sellwood & Athanassoula (1986) and widely used (see e.g. Quillen et al. 2011, and references therein). We note m the azimuthal wavenumber of a wave of frequency ω. Spectrograms can be used to determine the pattern speed Ω of any wave as being Ω = ω/m and helps to identify any potential non-linear mode coupling when resonances overlap. As discussed by Rautiainen & Salo (1999) and Quillen et al. (2011), spectrograms show many small features, often transient, probably linked to the main modes. Some of these features with a well-defined pattern speed can be beat modes triggered by the non-linear couplings of other waves at the location of resonance overlaps. Rautiainen & Salo (1999) found many kinds of resonance overlaps in addition to the classical CRs–ILRp, although they were not always able to determine whether these couplings were stationary or accidental.
Figure 10 shows spectrograms for m = 2, centred at t = 3 and 7.5 Gyr for SimL and computed in a window of 269 Myr corresponding to 256 outputs. To compute the spectra we included only the stellar component to extract the information on stellar modes. Similar spectrograms have been obtained for SimS. Spectra with greater wavenumbers (m ≥ 4) confirm what can be inferred from m = 2, in particular the presence of harmonics of the large-scale bar mode. They are not shown here. For the two moments shown in Fig. 10 representative of the rest of the simulations, the two dominant modes correspond to the secondary and primary bars, with pattern speed values in good agreement with all other measurements (cf. Sect. 2). The features are not as thin as for Masset & Tagger (1997). This is due in part to our narrower time window. This also shows that these features do not correspond to quasi-stationary structures.
 |
Fig. 10 m = 2 power spectra for SimL in log scale. The time window spans 269 Myr centred at t = 3.3 and t = 7.5 Gyr. The left vertical scale gives values of ω, the wave frequency in Myr-1, whereas the right vertical scale is for the pattern speed Ω = ω/2 in kms-1 kpc-1. The horizontal white lines represent Ωs and Ωp, respectively, at the beginning of the time window (full line) and the end (dot-dashed one). Ωs decreases from 146 to 139 at t = 3.3 Gyr and from 81 to 71 kms-1 kpc-1 at t = 7.5 Gyr, whereas Ωp decreases by less than 1 kms-1 kpc-1 so that the two lines cannot be distinguished. The averaged curves 2Ω − κ (which allows the ILR to be identified) and 2Ω + κ (for the OLR) are drawn as white short dashed lines, 2Ω − κ/2 (for the UHR) as long dashed line, and 2Ω as a solid line (for the CR). A logarithmic scale has been chosen for the radius to emphasize the central kpc. |
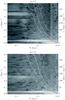 |
Fig. 11 m = 2 power spectra for SimL centred at t = 2 (top panel) and t = 4.275 Gyr (bottom) in a window of 538 Myr, whereas the inner bar cannot be detected on density maps. Consequently, Ωs cannot be measured because the position-angle of the central structure cannot be properly determined. |
Figure 10 clearly shows that most of the power of the nuclear bar mode remains inside the UHRs. For the large-scale primary bar, it has been argued that the most appropriate orbits to sustain a bar are those existing inside the UHR (see e.g. Sect. 6.1 of Michel-Dansac & Wozniak 2006,and reference therein). This also seems to be true for the secondary bars of SimL and SimS. This additionally supports our previous claim (Sect. 4.3) that one cannot systematically assume that the morphological end of a nuclear bar coincides with CRs.
Finally, whatever the approach, the linear resonance analysis or the mode analysis both lead to the same conclusion: there is no resonance overlap or mode coupling in SimL and SimS.
5.2. Double-bar lifetime
Rautiainen et al. (2002) reported the case of a long-lived double-barred system (their model I) which could be very similar to SimL, although SimL is 3D and fully self-consistent whereas their model I is 2D and the bulge is represented by an analytical Plummer sphere. However, the fact that long-lived systems can exist is important in order to explain the high frequency of double-barred galaxies. In our case, the nuclear bar lifetime is clearly linked to the lifetime of the central bar mode. The fact that we are not able to determine a proper pattern speed during roughly 1 Gyr centred on t ≈ 2 and 4 Gyr (cf. Fig. 5) does not mean that dynamically the nuclear mode has disappeared. Indeed, the mode still exists (Fig. 11) at a pattern speed of respectively ≈215 and 125 kms-1 kpc-1. This means that even if, on photometrical grounds, it can be stated that the nuclear bar has been dissolved into a triaxial bulge or pseudobulge (Kormendy & Kennicutt 2004), or even a weaker structure like nuclear spirals (cf. Sect. 3), the bar mode does survive, which in turn facilitates the morphological revival of the nuclear bar later on.
Debattista & Shen (2007) also reported long-lived double-barred systems in purely collisionless simulations. A direct comparison is not possible since the initial conditions of their simulations, especially the bulge part, were fine-tuned to produce such gas-free double-barred galaxies. However, their enforced rotating bulge mimics perfectly the effect of a dissolved or weak first nuclear bar.
Another crucial dynamical feature of our models that could play an important role in the lifetime of the secondary bar, is the absence of any overlap of resonances for a long time. Indeed, the whole nuclear dynamical system evolves as if embedded in a quasi-stationary gravitational background due to the rest of the galaxy. The mass (both gas and stars) encircled by the OLRs is so large that the two dynamical systems are unable to couple together through their resonances. For SimL, almost 38 % of the total mass of the galaxy lie inside R ≲ 5 kpc at t = 7 Gyr.
All previous works that have looked for mode coupling in 3D self-consistent N-body/hydrodynamical simulations have found an CRs–ILRp overlap whereas their double-barred systems were short-lived (e.g. Friedli & Martinet 1993). One noticeable exception is Rautiainen et al. (2002) who argue that this mode coupling is not necessary for the coexistence of bars and show examples of other kinds of coupling. Rautiainen & Salo (2000), using 2D N-body simulations and inelastically colliding massless gas particles, exhibit an example very close to SimL with OLRs well inside ILRp (their model A2.5). This is the situation of SimS for t ≲ 2 Gyr and SimL for t ≲ 8 Gyr. However, their model develops a very weak primary bar (more oval than SimL) and the m = 2 of the nuclear mode remains close to the maximum of Ω − κ/2 all through the simulation, which is not the case of our simulations.
Can we infer a strong dynamical perturbation when OLRs position comes close to ILRp and eventually overlaps with ILRp? For SimS, less than 1 Gyr after OLRs intersects ILRp, the nuclear bar is transformed into a disc with a very time-dependent shape. It is also remarkable that the nuclear bar then starts to dissolve in the case of SimS whereas it continues to evolve as a large oval for SimL, showing larger fluctuations in Ωs. Three spectrograms centred at t = 2,3.4, and 5.47 Gyr for SimS (Fig. 12) show that the nuclear bar mode progressively vanishes whereas the large-scale bar mode (with a lower pattern speed) expands toward the centre. However, the OLRs-ILRp overlap seems to play no role. Indeed, the primary bar mode is at a maximum just inside ILRs, but we have not found a mode associated with the nuclear bar that might be present near the OLRs to explain the energy and angular momentum exchanges. The overlap thus seems neutral and the nuclear bar mode extinction could simply be due to classical Landau damping at ILRs.
 |
Fig. 12 m = 2 power spectra for SimS centred at t = 2 (top panel), when OLRs intersects ILRp, t = 3.4 (middle), and t = 5.47 Gyr (bottom) where the nuclear bar is dissolved. For t = 2 Gyr the time window has been halved (269 Myr) because Ωs evolves rapidly. |
In the case of SimL, the shape of the inner bar is oval for t ≳ 7 Gyr. Looking at the spectrograms (Fig. 13) for t = 7.6 and 9.2 Gyr, it appears that the power of the inner bar mode is concentrated just outside ILRs whereas the maximum power of the primary bar is just inside ILRp, as it is for SimS. Again, it is hard to find any mode between CRs and OLRs. Unlike SimS, several modes can be detected at low level with Ωp< Ω < Ωs or Ω > Ωs, but only inside a region limited by Ω(r). As we do for SimS, we can suspect Landau damping at ILRs to be responsible for the inner bar mode decrease.
 |
Fig. 13 m = 2 power spectra for SimL centred at t = 7.6 (top panel) just before OLRs intersects ILRp, t = 9.2 Gyr (bottom) whereas the nuclear bar has been replaced by a large rotation oval. The time windows is 568 Myr wide. |
5.3. What makes double-bars long-lived?
The lack of mode coupling is a major difference with previous simulations. For pure N-body simulations, but also for models with massless gas particles, this situation would prevent the nuclear bar from being long-lived. Indeed, apart form the swing amplification at corotation that does not operate here, there is no mechanism to bring energy to the inner bar wave. Therefore, this wave should vanish by Landau damping at ILRs.
In our simulations, the first difference is the presence of a self-gravitating gas component. This component behaves differently from the stellar component because of its dissipative nature. However, as shown for example by Friedli & Martinet (1993), the gas does not help to sustain a long-lived nuclear bar because the mass accumulation close to the centre reinforces ILRp, which in turn destabilizes the nuclear bar orbits.
Another major difference is the star formation process that creates a stellar population with initial dynamical properties inherited from their parent gas elements (SPH particles). During the first Gyrs, when the secondary bar grows, gas inflow and star formation are responsible for bringing energy to the inner waves. When the central star formation fades out as the mass of gas inflowing in the central region decreases, the energy dissipation at ILRs prevails. This is basically the scenario of SimS for t ≳ 2 Gyr. What delays the inner bar extinction in SimL is a sustained local star formation rate for several Gyr (cf. Fig. 1). In the same way as for sustaining the σ-drop phenomenon (Wozniak & Champavert 2006), the regular feeding of the central region with recent stellar populations enables secondary bars to be long-lived. Simulations by Friedli & Martinet (1993) did not take star formation into account, leading to the extinction of the secondary bar in roughly 5 turns. This is also the case of other past simulations with a gaseous component that have been discussed before. A noticeable exception is Friedli et al. (1996) who ran a simulation with star formation, but only on a short timescale (less than 2 Gyr).
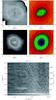 |
Fig. 14 Top and middle panels: as for Fig. 5 at t = 7.6 Gyr, with (SimL, top) and without (SimLnosf, middle) star formation. The surface brightness ranges from 22.8 to 17 Bmag pc-2 for SimL and 22.8 to 19.1 Bmag pc-2 for SimLnosf. Bottom: m = 2 power spectra for SimLnosf, centred at t = 7.6 (top panel). This figure can be directly compared with Fig. 13. |
To firmly establish the role of star formation, we recomputed SimL from t = 5.25 Gyr until t = 7.6 Gyr switching off the star formation process in the simulation code (SimLnosf in short). Wozniak & Champavert (2006) used this method for σ-drops. Figure 14 shows the gas and stellar mass distributions at t = 7.6 Gyr. They are significantly different from SimL. The gas distribution is more concentrated in SimLnosf than in SimL since the gas is no longer consumed by the formation of new stars. This has two immediate consequences. First, this predictably makes dissolving the inner bar easier as the gas can now reach the centre, increasing there the mass that in turn axisymmetrizes the gravitational potential. Second, no more gas is turned into stars so that the mass of the inner stellar bar cannot increase. After roughly 2 Gyr, the inner bar is indeed barely detectable in the stellar distribution of SimLnosf. The spectrogram centred at t = 7.6 Gyr, as in Fig. 13, confirms that, although it has not yet fully disappeared, the amplitude of the m = 2 mode has strongly decreased with respect to SimL.
The role of star formation in sustaining the nuclear bar over several Gyr is thus demonstrated for the first time.
6. Conclusions
Unlike the outcome of most numerical simulations with both stellar and gaseous components, we have successfully simulated a long-lived inner bar embedded in a large-scale primary bar.
The ratio of the two bar lengths, the ratio of pattern speeds, as well as the age of the inner stellar bar population and the central gas mass fit well with observations published in the literature. Moreover, throughout the simulation, our models go through various morphological phases representative of the diversity of observations, including SB0.
The most important difference with past simulations leading to short-lived double-barred galaxies is the lack of overlap between the primary bar inner Lindblad resonance (ILRp) and the nuclear bar corotation (CRs) and, more generally, the lack of any kind of resonance overlap. The absence of mode coupling, confirmed by a Fourier analysis, implies that to sustain a permanent nuclear bar mode another physical or dynamical mechanism must feed the central waves.
Star formation in the central region is identified as possibly being responsible for bringing energy to the nuclear mode. Star formation is also responsible for regulating the gas mass accumulation close to the centre, in the sense that it prevents a strong increase in mass density that can destabilize the inner bar orbits.
As a direct consequence (whereas the inner bar can be temporarily undetectable, leading the pattern speed to be barely measurable or unmeasurable), the corresponding perturbation modes survive and allow the revival of the nuclear structure less than 1 Gyr after it disappears, provided that star formation continues.
A side result of our study is that an overlap between the ILR of the main bar and the CR of the nuclear bar cannot be systematically assumed as it is not a necessary condition for the existence of double-barred galaxies. Another direct consequence of our simulations is the evidence that several morphological features in barred galaxies that have been identified by various names (double-bars, pseudo-bulges, triaxial bulges, etc.) originate dynamically from an unique inner mode. SimL displays all these features at various stages of its evolution. This speaks for a global analysis of triaxiality in the central regions of barred galaxies as being a unique dynamical phenomenon due to persistent modes in the central region.
Acknowledgments
I warmly thank Witold Maciejewski for fruitful discussions during the meeting “The Role of Bars in Galaxy Evolution” in Granada, which revived my long-lived interest in double-barred galaxies, and Isabel Pérez for organizing this productive meeting. I am grateful to the anonymous referee for his/her suggestions that have improved the legibility of the paper. I would also like to acknowledge the Pôle HPC (High Performance Computing department) of the University of Strasbourg for supporting this work by providing technical support and access to computing resources. Part of the computing resources were funded by the Equipex Equip@Meso project. Local post-processing resources have been funded by the INSU Programme National Cosmologie & Galaxies.
References
- Athanassoula, E. 1992, MNRAS, 259, 328 [NASA ADS] [CrossRef] [Google Scholar]
- Benz, W. 1990, in Numerical Modelling of Nonlinear Stellar Pulsations Problems and Prospects, ed. J. R. Buchler, 269 [Google Scholar]
- Buta, R. 1986, ApJS, 61, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Buta, R., & Crocker, D. A. 1993, AJ, 105, 1344 [NASA ADS] [CrossRef] [Google Scholar]
- Combes, F. 1994, in Mass-Transfer Induced Activity in Galaxies, ed. I. Shlosman, 170 [Google Scholar]
- Corsini, E. M., Debattista, V. P., & Aguerri, J. A. L. 2003, ApJ, 599, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Curir, A., Mazzei, P., & Murante, G. 2006, A&A, 447, 453 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Lorenzo-Cáceres, A., Falcón-Barroso, J., & Vazdekis, A. 2013, MNRAS, 431, 2397 [NASA ADS] [CrossRef] [Google Scholar]
- de Vaucouleurs, G. 1974, in The Formation and Dynamics of Galaxies, ed. J. R. Shakeshaft, IAU Symp., 58, 335 [Google Scholar]
- Debattista, V. P., & Shen, J. 2007, ApJ, 654, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Emsellem, E., Fathi, K., Wozniak, H., et al. 2006, MNRAS, 365, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Englmaier, P., & Shlosman, I. 2004, ApJ, 617, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Erwin, P. 2011, Mem. Soc. Astron. It. Supp., 18, 145 [Google Scholar]
- Fathi, K., Beckman, J. E., Piñol-Ferrer, N., et al. 2009, ApJ, 704, 1657 [NASA ADS] [CrossRef] [Google Scholar]
- Font, J., Beckman, J. E., Querejeta, M., et al. 2014a, ApJS, 210, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Font, J., Beckman, J. E., Zaragoza-Cardiel, J., et al. 2014b, MNRAS, 444, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Friedli, D., & Benz, W. 1993, A&A, 268, 65 [NASA ADS] [Google Scholar]
- Friedli, D., & Martinet, L. 1993, A&A, 277, 27 [NASA ADS] [Google Scholar]
- Friedli, D., Wozniak, H., Rieke, M., Martinet, L., & Bratschi, P. 1996, A&AS, 118, 461 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hernandez, O., Wozniak, H., Carignan, C., et al. 2005, ApJ, 632, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Jogee, S., Shlosman, I., Laine, S., et al. 2002, ApJ, 575, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, Jr., R. C. 1990, in The Interstellar Medium in Galaxies, eds. H. A. Thronson, Jr., & J. M. Shull, Astrophys. Space Sci. Lib., 161, 405 [Google Scholar]
- Kennicutt, Jr., R. C. 1998, ARA&A, 36, 189 [Google Scholar]
- Kormendy, J. 1982, in Saas-Fee Advanced Course 12: Morphology and Dynamics of Galaxies, eds. L. Martinet, & M. Mayor, 113 [Google Scholar]
- Kormendy, J., & Kennicutt, Jr., R. C. 2004, ARA&A, 42, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Kuzmin, B. 1956, Astron. Zh., 33, 27 [Google Scholar]
- Louis, P. D., & Gerhard, O. E. 1988, MNRAS, 233, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Maciejewski, W. 2006, MNRAS, 371, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Maciejewski, W., & Small, E. E. 2010, ApJ, 719, 622 [NASA ADS] [CrossRef] [Google Scholar]
- Maciejewski, W., & Sparke, L. S. 1997, ApJ, 484, L117 [NASA ADS] [CrossRef] [Google Scholar]
- Maciejewski, W., & Sparke, L. S. 2000, MNRAS, 313, 745 [NASA ADS] [CrossRef] [Google Scholar]
- Masset, F., & Tagger, M. 1997, A&A, 322, 442 [NASA ADS] [Google Scholar]
- Michel-Dansac, L., & Wozniak, H. 2004, A&A, 421, 863 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Michel-Dansac, L., & Wozniak, H. 2006, A&A, 452, 97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miyamoto, M., & Nagai, R. 1975, PASJ, 27, 533 [NASA ADS] [Google Scholar]
- Moellenhoff, C., Matthias, M., & Gerhard, O. E. 1995, A&A, 301, 359 [NASA ADS] [Google Scholar]
- Pérez, I., Sánchez-Blázquez, P., & Zurita, A. 2007, A&A, 465, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petitpas, G. R., & Wilson, C. D. 2004, ApJ, 603, 495 [NASA ADS] [CrossRef] [Google Scholar]
- Plummer, H. C. 1911, MNRAS, 71, 460 [CrossRef] [Google Scholar]
- Quillen, A. C., Dougherty, J., Bagley, M. B., Minchev, I., & Comparetta, J. 2011, MNRAS, 417, 762 [NASA ADS] [CrossRef] [Google Scholar]
- Rautiainen, P., & Salo, H. 1999, A&A, 348, 737 [NASA ADS] [Google Scholar]
- Rautiainen, P., & Salo, H. 2000, A&A, 362, 465 [NASA ADS] [Google Scholar]
- Rautiainen, P., Salo, H., & Laurikainen, E. 2002, MNRAS, 337, 1233 [NASA ADS] [CrossRef] [Google Scholar]
- Saha, K., & Maciejewski, W. 2013, MNRAS, 433, L44 [NASA ADS] [CrossRef] [Google Scholar]
- Sellwood, J. A., & Athanassoula, E. 1986, MNRAS, 221, 195 [NASA ADS] [Google Scholar]
- Shen, J., & Debattista, V. P. 2009, ApJ, 690, 758 [NASA ADS] [CrossRef] [Google Scholar]
- Shlosman, I., Frank, J., & Begelman, M. C. 1989, Nature, 338, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Toomre, A. 1964, ApJ, 139, 1217 [NASA ADS] [CrossRef] [Google Scholar]
- van der Laan, T. P. R., Schinnerer, E., Emsellem, E., et al. 2013, A&A, 556, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wozniak, H. 2007, A&A, 465, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wozniak, H., & Champavert, N. 2006, MNRAS, 369, 853 [NASA ADS] [CrossRef] [Google Scholar]
- Wozniak, H., Friedli, D., Martinet, L., Martin, P., & Bratschi, P. 1995, A&AS, 111, 115 [NASA ADS] [Google Scholar]
- Zhang, X., & Buta, R. J. 2007, AJ, 133, 2584 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Star formation rate (SFR) averaged in a sliding window of 10 Myr for runs SimS (red) and SimL (black). |
| In the text | |
 |
Fig. 2 Run SimS: gas mass surface density (left) and B-Cousins surface brightness (right) in the central ±1 kpc for t< 0.7 Gyr. Isocontours are spaced by 0.15 mag in log M⊙ pc-2 for the gas and 0.5 Bmag pc-2 for the stars. The map resolution is 10 pc. Gas particles have been convolved by the SPH kernel to obtain the real distribution. Gas surface densities below 1 M⊙ pc-2 are contoured with dashed lines. The straight dotted line is the primary bar position-angle. |
| In the text | |
 |
Fig. 3 As in Fig. 2, but for t> 0.7 Gyr in the central ±2 kpc. The map resolution is now 20 pc. Gas isocontours are spaced by 0.25 mag in log M⊙ pc-2. The radius of ILRp is indicated by dashed white circles. |
| In the text | |
 |
Fig. 4 Period of rotation for the primary bar (in black) and the nuclear bar (in red) for SimS. |
| In the text | |
 |
Fig. 5 As in Fig. 3, but for SimL. From t = 6535 Myr the dashed white circle represents ILRs instead of ILRp which is outside the field of view. |
| In the text | |
 |
Fig. 6 As in Fig. 4 for SimL. |
| In the text | |
 |
Fig. 7 Radial profile of the age difference with the time of the snapshot (t = 9.486 Gyr) for SimL. The mean age has been computed in concentric annuli of 100 pc wide. For the sake of comparison, the radius of the NGC 5850 inner bar and the limit of age measurement (de Lorenzo-Cáceres et al. 2013) have been scaled to SimL and overplotted as dashed and dot-dashed lines, respectively. |
| In the text | |
 |
Fig. 8 Ratio of the primary to secondary bar pattern speed. Black dots are for SimL, red dots for SimS. |
| In the text | |
 |
Fig. 9 Radius of the linear resonances (ILR, UHR, CR, OLR) for the secondary bar (subscript “s”, red triangles) and the primary bar (“p”, black dots) in the simulations SimS (top) and SimL (bottom). OLRp is not shown. |
| In the text | |
 |
Fig. 10 m = 2 power spectra for SimL in log scale. The time window spans 269 Myr centred at t = 3.3 and t = 7.5 Gyr. The left vertical scale gives values of ω, the wave frequency in Myr-1, whereas the right vertical scale is for the pattern speed Ω = ω/2 in kms-1 kpc-1. The horizontal white lines represent Ωs and Ωp, respectively, at the beginning of the time window (full line) and the end (dot-dashed one). Ωs decreases from 146 to 139 at t = 3.3 Gyr and from 81 to 71 kms-1 kpc-1 at t = 7.5 Gyr, whereas Ωp decreases by less than 1 kms-1 kpc-1 so that the two lines cannot be distinguished. The averaged curves 2Ω − κ (which allows the ILR to be identified) and 2Ω + κ (for the OLR) are drawn as white short dashed lines, 2Ω − κ/2 (for the UHR) as long dashed line, and 2Ω as a solid line (for the CR). A logarithmic scale has been chosen for the radius to emphasize the central kpc. |
| In the text | |
 |
Fig. 11 m = 2 power spectra for SimL centred at t = 2 (top panel) and t = 4.275 Gyr (bottom) in a window of 538 Myr, whereas the inner bar cannot be detected on density maps. Consequently, Ωs cannot be measured because the position-angle of the central structure cannot be properly determined. |
| In the text | |
 |
Fig. 12 m = 2 power spectra for SimS centred at t = 2 (top panel), when OLRs intersects ILRp, t = 3.4 (middle), and t = 5.47 Gyr (bottom) where the nuclear bar is dissolved. For t = 2 Gyr the time window has been halved (269 Myr) because Ωs evolves rapidly. |
| In the text | |
 |
Fig. 13 m = 2 power spectra for SimL centred at t = 7.6 (top panel) just before OLRs intersects ILRp, t = 9.2 Gyr (bottom) whereas the nuclear bar has been replaced by a large rotation oval. The time windows is 568 Myr wide. |
| In the text | |
 |
Fig. 14 Top and middle panels: as for Fig. 5 at t = 7.6 Gyr, with (SimL, top) and without (SimLnosf, middle) star formation. The surface brightness ranges from 22.8 to 17 Bmag pc-2 for SimL and 22.8 to 19.1 Bmag pc-2 for SimLnosf. Bottom: m = 2 power spectra for SimLnosf, centred at t = 7.6 (top panel). This figure can be directly compared with Fig. 13. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


