| Issue |
A&A
Volume 575, March 2015
|
|
|---|---|---|
| Article Number | L10 | |
| Number of page(s) | 5 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201424925 | |
| Published online | 27 February 2015 | |
Extended supernova shock breakout signals from inflated stellar envelopes
Argelander Institute for Astronomy, University of Bonn,
Auf dem Hügel 71,
53121
Bonn,
Germany
e-mail:
moriyatk@astro.uni-bonn.de
Received: 5 September 2014
Accepted: 11 February 2015
Stars close to the Eddington luminosity can have large low-density inflated envelopes. We show that the rise times of shock breakout signals from supernovae can be extended significantly if supernova progenitors have an inflated stellar envelope. If the shock breakout occurs in inflated envelopes, the shock breakout signals diffuse in them, and their rise time can be significantly extended. Then, the rise times of the shock breakout signals are dominated by the diffusion time in the inflated envelope rather than the light-crossing time of the progenitors. We show that our inflated Wolf-Rayet star models whose radii are on the order of the solar radius can have shock breakout signals that are longer than ~100 s. The existence of inflated envelopes in Wolf-Rayet supernova progenitors may be related to the mysterious long shock breakout signal observed in Type Ib SN 2008D. Extended shock breakout signals may provide evidence for the existence of inflated stellar envelopes and can be used to constrain the physical properties of these enigmatic structures.
Key words: stars: evolution / stars: massive / supernovae: general / supernovae: individual: SN 2008D
© ESO, 2015
1. Introduction
The first electromagnetic signals from a supernova (SN) are emitted when the shock wave that travels through the stellar interior reaches the stellar surface (e.g., Colgate, 1974; Klein & Chevalier, 1978; Ensman & Burrows, 1992; Matzner & McKee, 1999; Tominaga et al., 2011; Tolstov et al., 2013). Photons trapped in the shock wave are suddenly released near the surface and start to be observed at this moment. This sudden release of photons in the shock wave near the stellar surface is called shock breakout.
The shock breakout signals are strongly affected by the properties of the SN progenitor and can be used to estimate them. Especially the duration of the shock breakout signals is assumed to approximately correspond to the light-crossing time tlc of the progenitor, that is, tlc ≃ R⋆/c, where R⋆ is the progenitor radius and c is the speed of light. If a Wolf-Rayet (WR) star explodes, its shock breakout signal is expected to have a duration of about 1−10 s because typical radii of WR stars are on the order of 1−10R⊙ (e.g., Crowther, 2007; Yoon et al., 2010).
The shock breakout durations are, however, suggested to be extended for several reasons. For example, if the circumstellar medium (CSM) density is high enough to be optically thick, shock breakout durations can be extended as a result of photon diffusion in the dense CSM (e.g., Balberg & Loeb, 2011; Svirski & Nakar, 2014a,b). Aspherical photospheres may also cause an extension of the shock breakout durations (Suzuki & Shigeyama, 2010; Couch et al., 2011). In addition, the duration of the shock breakout signals from Type Ib SN 2008D was observed to last for ~ 300 s with a rise time of ~ 60 s (Soderberg et al., 2008; Modjaz et al., 2009), indicating a progenitor radius of R⋆ ≃ tlcc ~ 130 R⊙. The indicated progenitor radius is too large to correspond to a WR star, but its SN spectral type and the early light curve modeling point to a WR progenitor with a radius smaller than 10 R⊙ (e.g., Chevalier & Fransson 2008; Rabinak & Waxman 2011, see also Dessart et al. 2011; Bersten et al. 2013). The observed long shock breakout duration may also indicate the existence of mechanisms to extend shock breakout signals.
In this Letter, we argue that shock breakout rise times can be extended significantly if SN progenitors have inflated envelopes. In that case, the shock breakout signals diffuse in the inflated envelope, resulting in the extension of the shock breakout rise times. The diffusion times td of canonical WR SN progenitors are shorter than the light-crossing time tlc (Table 1). However, we show that the diffusion time can be much longer than the light-crossing time in inflated WR SN progenitors even if their radii are on the order of the solar radius.
We first explain the inflation of stellar envelopes and our inflated stellar evolution models in Sect. 2. We show the effect of the inflated envelopes on the SN shock breakout signals in Sect. 3. Our conclusions and their implications are summarized in Sect. 4.
2. Inflation of stellar envelopes
We first discuss the inflation of stellar envelopes. Inflation refers to the extended low-density envelopes in stellar models that reach Eddington luminosity in their outer layers (Ishii et al., 1999; Petrovic et al., 2006; Gräfener et al., 2012). The phenomenon was first discussed by Kato (1985, 1986) in the context of supermassive stars, considering electron-scattering as the only opacity source. The envelope inflation in the models discussed below is, however, caused by the Fe-group opacity bump at T ~ 200 kK (Ishii et al., 1999; Petrovic et al., 2006; Gräfener et al., 2012). When the stellar envelope approaches the Eddington luminosity, it will become convectively unstable (Langer, 1997). The convective luminosity would need to carry any super-Eddington flux so that the radiative luminosity does not exceed the Eddington luminosity. However, if the envelope density is too low, convection cannot become efficient enough to transport sufficient energy inside the envelope. Then, the star expands its envelope in order to find a structure with a lower opacity so that the Eddington luminosity is not exceeded.
To discuss the actual structure of inflated envelopes in WR SN progenitors, we performed stellar evolution calculations by using an advanced one-dimensional hydrodynamic binary stellar evolution code (BEC; see Heger et al. 2000; Yoon et al. 2006, 2010; Brott et al. 2011) to model WR stars as nonrotating hydrogen-free helium stars. The code solves the Lagrangian version of the equations for mass, energy, and momentum conservation together with convective and radiative energy transport and is explicitly coupled to a diffusive mixing scheme and a nucleosynthesis network (see Kozyreva et al. 2014, for details). BEC incorporates the latest input physics (Heger et al., 2000; Yoon et al., 2006, 2010; Brott et al., 2011; Köhler et al., 2015) and is well-suited to investigate stars evolving close to the Eddington limit with inflated envelopes (Köhler et al. 2015; Sanyal et al., in prep.).
In particular, the opacities used to compute the models were interpolated from the OPAL tables (Iglesias & Rogers, 1996), which contain an opacity enhancement around T ~ 200 kK due to Fe-group elements. Convection was treated within the framework of the standard mixing-length theory (Böhm-Vitense, 1958) with the mixing length set to 1.5 times the local pressure scale height. The WR mass-loss recipe proposed by Nugis & Lamers (2000) was used for our computations. The stellar surface was set at the photosphere where the optical depth is 2/3. We investigate the evolution of helium stars with initial masses of 10 and 12 M⊙ in this Letter. We explored two sets of models, one with solar metallicity and the other with half-solar metallicity. The half-solar metallicity models were computed until the oxygen-burning stage, while solar metallicity models were only computed until carbon ignition because we encountered numerical problems to iteratively converge models with large inflated envelopes that are larger at higher metallicity (Ishii et al., 1999). The inflation in these models at the time of the SN explosion could thus be somewhat stronger than we assume here. The evolutionary tracks of the models in the Hertzsprung-Russell (HR) diagram are presented in Fig. 1. The final stellar properties are summarized in Table 1.
The helium zero-age main-sequence models of both 10 and 12 M⊙ stars are marginally inflated. As a consequence of the applied mass loss, they lose mass and decrease in luminosity during the core helium-burning phase. After helium is exhausted in the core, the stars begin to contract and become hotter and brighter. The models are hardly inflated during this phase because the Fe-group opacity bump is only partially contained inside the stars. When the helium-shell ignites, the evolutionary tracks eventually move toward cooler temperatures because of the mirror principle (e.g., Kippenhahn et al., 2013). As the models become cooler, they become significantly inflated and exhibit a pronounced core-halo structure, as shown in Fig. 2. The electron-scattering Eddington factors of our models are shown in Table 1. When the full opacity is counted into the Eddington factor, all models reach the critical value of one. The envelope inflation is stronger for the solar metallicity models because the prominence of the Fe-group opacity bump increases with metallicity, as found in the studies by Ishii et al. (1999) and Petrovic et al. (2006). For comparison, we also show a polytropic star with M⋆ = 7 M⊙ and R⋆ = 2.4 R⊙ obtained with the polytropic index of 3 which does not have an inflated envelope. Figure 2 shows that our stellar models have extended low-density layers on top of the core structure. This type of the envelope inflation is also found in the previously reported models with similar final core masses (Yoon et al., 2012). The evolution and final position of our stars in the HR diagram are consistent with their models.
 |
Fig. 1 Evolutionary tracks of the helium star models in the HR diagram. The initial metallicity, initial mass, and final mass of the models are shown. The locations of helium-shell ignition (circles), core carbon ignition (squares), and core oxygen ignition (triangles) are marked. Lines of the constant radii of 0.5, 1, and 2 R⊙ are also shown. |
 |
Fig. 2 Final density structure of our stellar models. We also show the structure of a star without the envelope inflation, which is a polytiropic star of 7 M⊙ and 2.4 R⊙ with the polytropic index of 3. The inflated stellar models have the extended low-density regions on top of the core structure. |
 |
Fig. 3 Optical depth τ in our models. The optical depth in the polytropic star is obtained with the constant opacity of 0.2 cm2 g-1. |
Stellar properties and corresponding timescales.
3. Shock breakout in inflated stellar envelopes
The shock breakout in a SN occurs when photons start to leak from the shock wave, that is, when the dynamical timescale tdy of the shock propagation in the remaining unshocked stellar envelope with radius ΔR (tdy ≃ ΔR/vsh) becomes similar to the diffusion timescale td ≃ τΔR/c, where vsh is the shock velocity and τ is the optical depth in the remaining unshocked stellar envelope (e.g., Weaver, 1976). The shock breakout condition can be simply expressed as τ ≃ c/vsh. For a shock breakout at the stellar surface without the inflated envelope, ΔR is so small that td is smaller than the light-crossing time tlc ≃ R⋆/c, making the shock breakout duration tlc ≃ R⋆/c. For example, in the case of the 2.4 R⊙ polytropic star we show in Fig. 2, the light-crossing time is tlc ≃ 5.60 s and the diffusion time is td ≃ 1.31 s, assuming vsh = 10 000km s-1 (Table 1).
The inflated stellar models are characterized by extended low-density envelopes (Fig. 2). As a result, ΔR can be much larger than the corresponding values for the uninflated stellar models. In Fig. 3, we show the optical depth in our stellar models. In Table 1, we summarize the light-crossing time tlc and the diffusion time td for several shock velocities. In the uninflated polytropic model, the shock breakout occurs at the edge of the stellar surface (ΔR = 0.0187 R⊙ for τ = 30), making the diffusion time shorter than the light-crossing time. If the progenitor has an inflated envelope, however, the shock breakout can occur at the bottom of the inflated envelope, keeping ΔR large when the shock breakout occurs. For example, our solar-metallicity 10 M⊙ model has ΔR = 1.73 R⊙ for τ = 30 because of the envelope inflation. The large ΔR makes the diffusion time (td ≃ 121 s) much longer than the light-crossing time (tlc ≃ 5.67 s). Thus, the timescale of the shock breakout signals within the inflated envelopes can be dominated by the diffusion time, and their rise time is determined by the diffusion time. The subsequent light curve is expected to decline exponentially with an e-folding timescale of the diffusion time due to the photon diffusion in the shocked envelope. Overall, the total shock breakout duration becomes significantly longer than the light-crossing time. The dynamical timescales of our inflated envelopes at the time of their explosions are ~ 2000 s, and the inflated envelopes can be sustained until the shock passes through.
We have computed the diffusion times for several shock velocities between 10 000 and 30 000 km s-1. If the shock velocity at the shock breakout is too high, the diffusion time becomes shorter than the light-crossing time. In our models, the diffusion time starts to be shorter than the light-crossing time when the shock velocity is higher than ~ 30 000km s-1 (Table 1). The shock velocity is suggested to reach above 30 000 km s-1 at the shock breakout in WR stars (e.g., Nakar & Sari, 2010). However, previous studies assume that WR stars only have a steeply declining envelope as in our polytropic model. A flat inflated envelope exists on top of the steeply declining core in the density structure of our models. The flat density structure decelerates the shock significantly, and the shock velocity at the shock breakout in inflated envelopes can be lower than 30 000 km s-1. Because the shock propagation in inflated stellar structure has not yet been investigated, hydrodynamical modeling in inflated envelopes is required to estimate the shock velocity at breakout in this case.
The sizes of the inflated envelopes in the half-solar-metallicity models are smaller than those in the solar-metallicity models because the Fe-group opacity bump is weaker with decreasing metallicity. However, the diffusion time can still be longer than the light-crossing time, and the shock breakout rise times can be longer than 10 s in these WR stars.
Although higher metallicity models are preferred to have large ΔR and thus long td in terms of opacity, the inflated envelope can disappear because of higher mass-loss rates. Petrovic et al. (2006) showed that the inflated envelope disappears when the mass-loss rate of the star is higher than the critical mass-loss rate defined as 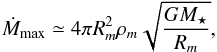 (1)where ρm is the lowest density in the inflated envelope and Rm is the radius at the lowest density (see also Gräfener et al., 2012). We show the ratio of the mass-loss rate in our models to the critical mass-loss rate in Table 1. Our solar-metallicity models are close to the critical mass-loss rates. Higher-metallicity stars are likely to exceed the critical mass-loss rate.
(1)where ρm is the lowest density in the inflated envelope and Rm is the radius at the lowest density (see also Gräfener et al., 2012). We show the ratio of the mass-loss rate in our models to the critical mass-loss rate in Table 1. Our solar-metallicity models are close to the critical mass-loss rates. Higher-metallicity stars are likely to exceed the critical mass-loss rate.
Although we have focused on WR SN progenitors in this Letter, stars do not need to be WR stars to have inflated envelopes. When stars are near the Eddington luminosity, they can have inflated envelopes even if they are hydrogen-rich. For example, luminous blue variables are hydrogen-rich stars that are close to the Eddington luminosity, and they have recently been suggested to be SN progenitors (e.g., Gal-Yam & Leonard, 2009). They can also have inflated envelopes when they explode.
To confirm that some SN progenitors are actually inflated stars, observational consequences of the inflated envelopes in SN observational properties other than the shock breakout rise times are required to be investigated. Because the inflated envelopes in our models only have ~ 10-8M⊙, they are not likely to strongly affect later SN observables such as its light curve. However, the shock breakout spectra or very early SN spectra such as that recently obtained by Gal-Yam et al. (2014) may be affected by an inflated envelope. It is especially important to distinguish the shock breakout extension caused by an inflated envelope from that produced by a dense stellar wind because the shock breakout signals can be extended by the photon diffusion in both cases. Estimates of the progenitor mass-loss rate, for instance from multiwavelength SN observations, may constrain the wind density near the stellar photosphere and thereby confirm or rule out a shock break-out extension caused by winds (see Sect. 3.1 for the case of SN 2008D). Maeda (2013) also discusses possible observational consequences of the inflated envelopes.
3.1. SN 2008D
The extension of shock breakout signals by an inflated envelope may explain the long duration of the shock breakout signal observed in SN 2008D. Even if the progenitor of SN 2008D is a WR star with R⋆ ~ R⊙, our result show that the rise time of the shock breakout signals can be ~ 60 s because of the long diffusion time in the inflated envelope below which the shock breakout occurs. The shock-breakout luminosity decline after the luminosity peak is found to be similar to an exponential decay for a while (Soderberg et al., 2008), which is consistent with the diffusion interpretation.
The observed high temperature of the shock breakout signals in SN 2008D (~ 0.1−1 keV, e.g., Modjaz et al. 2009; Li 2008) is suggested to indicate the shock velocity above ~ 20 000km s-1 (e.g., Katz et al., 2010; Balberg & Loeb, 2011). The longest diffusion time for vsh = 20 000km s-1 among our models is 19 s from the solar 12 M⊙ model. Although it is shorter than observed, ~ 60 s, the diffusion time is still much longer than the light-crossing time. The observed e-folding timescale in the declining phase (~ 130 s, Soderberg et al. 2008) is also longer than the diffusion time in our models, but our models do predict the overall extension of the shock breakout signals. The shock temperature becomes ~ 0.1 keV using vsh = 20 000km s-1 and our inflated envelope density (Katz et al., 2010), which corresponds to the observational constraints (e.g., Modjaz et al., 2009) and can explain the observed thermal X-ray luminosities (~ 1043erg s-1) with a radius of ~ R⊙. More investigations are required to see whether the X-ray spectra can be explained by our model.
The later shock velocity is observed to be 0.25c (Soderberg et al., 2008). However, the shock can have accelerated after the shock breakout because of the steep density decline between the stellar surface and the low density wind (cf. Tolstov et al. 2013). Thus, the observed velocity may not correspond to the actual shock velocity at the shock breakout.
The estimated SN ejecta mass of SN 2008D is 3−7 M⊙ (Soderberg et al., 2008; Mazzali et al., 2008; Tanaka et al., 2009; Bersten et al., 2013). Our pre-SN stellar models (Table 1) have 6.3−7.8 M⊙. Subtracting a remnant mass of about 1.4 M⊙, the expected ejecta masses from our inflated stellar models are consistent with those of SN 2008D. The mass-loss rates of our models are also consistent with that estimated from radio observations (7 × 10-6 M⊙ yr-1, Soderberg et al. 2008).
The metallicity at the location where SN 2008D appeared is estimated to be 0.5 Z⊙ based on the metallicity gradient in the host galaxy (Soderberg et al., 2008). Our 0.5 Z⊙ stars do not inflate enough to explain the long shock breakout rise time of ~ 60 s. However, Galactic metallicity gradients have large dispersions (e.g., Pedicelli et al., 2009). Since our Z⊙ stars have much longer diffusion times, it is possible that the progenitor metallicity of SN 2008D is around Z⊙ or higher, and the progenitor had a sufficiently inflated envelope to show the long shock breakout rise time with the estimated shock velocity. Recent metallicity measurements at the location of SN 2008D support our arguments (Modjaz et al., 2011; Thöne et al., 2009).
4. Conclusions
We have shown that the rise times of supernova shock breakout signals can be extended because of inflated stellar envelopes. The shock breakout can occur within the low-density inflated envelopes in which the shock breakout signals are diffused and extended. The long diffusion time in the inflated envelopes makes the shock breakout rise times long. The shock breakout timescale is then dominated by the diffusion time instead of by the light-crossing time. Even if a SN progenitor has a radius on the order of the solar radius whose light-crossing time is a few seconds, the rise time of the shock breakout signals can be more than 100 s because of the inflated envelope. The extension of the shock breakout signals by the inflated envelope may explain the mysterious long shock breakout rise time observed in Type Ib SN 2008D, although more investigations are required to confirm this.
The actual existence of inflated stellar envelopes is still widely debated. While we find the envelope inflation in our stellar evolution models, the envelope inflation is not as prominent in other models (e.g., Ekström et al., 2012). If inflated envelopes exist, they are also pulsationally unstable (e.g., Glatzel et al., 1993) with unknown consequences. If we can confirm that SN shock breakout signals from WR SN progenitors have signatures of inflated envelopes, for example, extended shock breakout signals from SN progenitors with low mass-loss rates, it may indicate the common existence of inflated stellar envelopes in nature. The shock breakout signals can be a viable probe of unsolved problems in stellar structure as well as a touchstone of the stellar evolution theory, which predicts the final status of the massive stars.
Acknowledgments
T.J.M. is supported by Japan Society for the Promotion of Science Postdoctoral Fellowships for Research Abroad (26·51).
References
- Balberg, S., & Loeb, A. 2011, MNRAS, 414, 1715 [NASA ADS] [CrossRef] [Google Scholar]
- Bersten, M. C., Tanaka, M., Tominaga, N., Benvenuto, O. G., & Nomoto, K. 2013, ApJ, 767, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Böhm-Vitense, E. 1958, Z. Astrophys., 46, 108 [Google Scholar]
- Brott, I., de Mink, S. E., Cantiello, M., et al. 2011, A&A, 530, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chevalier, R. A., & Fransson, C. 2008, ApJ, 683, L135 [NASA ADS] [CrossRef] [Google Scholar]
- Colgate, S. A. 1974, ApJ, 187, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Couch, S. M., Pooley, D., Wheeler, J. C., & Milosavljević, M. 2011, ApJ, 727, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Crowther, P. A. 2007, ARA&A, 45, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Dessart, L., Hillier, D. J., Livne, E., et al. 2011, MNRAS, 414, 2985 [NASA ADS] [CrossRef] [Google Scholar]
- Ekström, S., Georgy, C., Eggenberger, P., et al. 2012, A&A, 537, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ensman, L., & Burrows, A. 1992, ApJ, 393, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Gal-Yam, A., & Leonard, D. C. 2009, Nature, 458, 865 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gal-Yam, A., Arcavi, I., Ofek, E. O., et al. 2014, Nature, 509, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Glatzel, W., Kiriakidis, M., & Fricke, K. J. 1993, MNRAS, 262, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Gräfener, G., Owocki, S. P., & Vink, J. S. 2012, A&A, 538, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heger, A., Langer, N., & Woosley, S. E. 2000, ApJ, 528, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Ishii, M., Ueno, M., & Kato, M. 1999, PASJ, 51, 417 [NASA ADS] [Google Scholar]
- Kato, M. 1985, PASJ, 37, 311 [NASA ADS] [Google Scholar]
- Kato, M. 1986, Ap&SS, 119, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Katz, B., Budnik, R., & Waxman, E. 2010, ApJ, 716, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Kippenhahn, R., Weigert, A., & Weiss, A. 2013, Stellar Structure and Evolution, Astronomy and Astrophysics Library (Berlin, Heidelberg: Springer-Verlag) [Google Scholar]
- Klein, R. I., & Chevalier, R. A. 1978, ApJ, 223, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Köhler, K., Langer, N., de Koter, A., et al. 2015, A&A, 573, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kozyreva, A., Yoon, S.-C., & Langer, N. 2014, A&A, 566, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Langer, N. 1997, in Luminous Blue Variables: Massive Stars in Transition, ASP Conf. Ser., 120, 83 [Google Scholar]
- Li, L.-X. 2008, MNRAS, 388, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Maeda, K. 2013, ApJ, 762, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Matzner, C. D., & McKee, C. F. 1999, ApJ, 510, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Mazzali, P. A., Valenti, S., Della Valle, M., et al. 2008, Science, 321, 1185 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Modjaz, M., Li, W., Butler, N., et al. 2009, ApJ, 702, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Modjaz, M., Kewley, L., Bloom, J. S., et al. 2011, ApJ, 731, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Nakar, E., & Sari, R. 2010, ApJ, 725, 904 [NASA ADS] [CrossRef] [Google Scholar]
- Nugis, T., & Lamers, H. J. G. L. M. 2000, A&A, 360, 227 [NASA ADS] [Google Scholar]
- Pedicelli, S., Bono, G., Lemasle, B., et al. 2009, A&A, 504, 81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petrovic, J., Pols, O., & Langer, N. 2006, A&A, 450, 219 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rabinak, I., & Waxman, E. 2011, ApJ, 728, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Soderberg, A. M., Berger, E., Page, K. L., et al. 2008, Nature, 453, 469 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Suzuki, A., & Shigeyama, T. 2010, ApJ, 717, L154 [NASA ADS] [CrossRef] [Google Scholar]
- Svirski, G., & Nakar, E. 2014a, ApJ, 788, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Svirski, G., & Nakar, E. 2014b, ApJ, 788, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, M., Tominaga, N., Nomoto, K., et al. 2009, ApJ, 692, 1131 [NASA ADS] [CrossRef] [Google Scholar]
- Thöne, C. C., Michałowski, M. J., Leloudas, G., et al. 2009, ApJ, 698, 1307 [NASA ADS] [CrossRef] [Google Scholar]
- Tolstov, A. G., Blinnikov, S. I., & Nadyozhin, D. K. 2013, MNRAS, 429, 3181 [NASA ADS] [CrossRef] [Google Scholar]
- Tominaga, N., Morokuma, T., Blinnikov, S. I., et al. 2011, ApJS, 193, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Weaver, T. A. 1976, ApJS, 32, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Yoon, S.-C., Langer, N., & Norman, C. 2006, A&A, 460, 199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yoon, S.-C., Woosley, S. E., & Langer, N. 2010, ApJ, 725, 940 [NASA ADS] [CrossRef] [Google Scholar]
- Yoon, S.-C., Gräfener, G., Vink, J. S., Kozyreva, A., & Izzard, R. G. 2012, A&A, 544, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Evolutionary tracks of the helium star models in the HR diagram. The initial metallicity, initial mass, and final mass of the models are shown. The locations of helium-shell ignition (circles), core carbon ignition (squares), and core oxygen ignition (triangles) are marked. Lines of the constant radii of 0.5, 1, and 2 R⊙ are also shown. |
| In the text | |
 |
Fig. 2 Final density structure of our stellar models. We also show the structure of a star without the envelope inflation, which is a polytiropic star of 7 M⊙ and 2.4 R⊙ with the polytropic index of 3. The inflated stellar models have the extended low-density regions on top of the core structure. |
| In the text | |
 |
Fig. 3 Optical depth τ in our models. The optical depth in the polytropic star is obtained with the constant opacity of 0.2 cm2 g-1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


