| Issue |
A&A
Volume 575, March 2015
|
|
|---|---|---|
| Article Number | A129 | |
| Number of page(s) | 11 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201424806 | |
| Published online | 11 March 2015 | |
Polarimetric modeling of corotating interaction regions threading massive-star winds⋆
1 Department of Physics & Astronomy, East Tennessee State University, Johnson City, TN 37614, USA
e-mail: ignace@etsu.edu
2 Département de Physique, Pavillon Roger Gaudry, Université Montréal, CP 6128, Succ. Centre-Ville, Montréal, H3C 3J7 Quebec, Canada
Received: 14 August 2014
Accepted: 13 January 2015
Context. Massive star winds are complex radiation-hydrodynamic (sometimes magnetohydrodynamic) outflows that are propelled by their enormously strong luminosities. The winds are often found to be structured and variable, but can also display periodic or quasi-periodic behavior in a variety of wind diagnostics.
Aims. The regular variations observed in putatively single stars, especially in UV wind lines, have often been attributed to corotating interaction regions (CIRs) like those seen in the solar wind. We present light curves for variable polarization from winds with CIR structures.
Methods. We develop a model for a time-independent CIR based on a kinematical description. Assuming optically thin electron scattering, we explore the range of polarimetric light curves that result as the curvature, latitude, and number of CIRs are varied.
Results. We find that a diverse array of variable polarizations result from an exploration of cases. The net polarization from an unresolved source is weighted more toward the inner radii of the wind. Given that most massive stars have relatively fast winds compared to their rotation speeds, CIRs tend to be conical at inner radii, transitioning to a spiral shape at a few to several stellar radii in the wind.
Conclusions. Winds with a single CIR structure lead to easily identifiable polarization signatures. By contrast allowing for multiple CIRs, all emerging from a range of azimuth and latitude positions at the star, can yield complex polarimetric behavior. Although our model is based on some simplifying assumptions, it produces qualitative behavior that we expect to be robust, and this has allowed us to explore a wide range of CIR configurations that will prove useful for interpreting polarimetric data.
Key words: polarization / stars: early-type / stars: massive / stars: rotation / stars: winds, outflows / stars: Wolf-Rayet
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
A corotating interaction region (CIR) arises from the interaction of wind flows that have different speeds: rotation of the star ultimately leads to a collision between the different speed flows to produce a spiral pattern in the wind. CIRs have been well-studied in the solar wind (e.g., Rouillard et al., 2008; Burlaga et al., 1983, 1997; Gosling & Pizzo, 1999). They have also been invoked to explain a variety of phenomena observed in massive star winds. Evidence of large-scale structure in the winds of massive stars is manifold. For example, the ubiquitousness of discrete absorption components (DACs) in the ultraviolet (UV) spectra of OB stars (Howarth & Prinja, 1989; Fullerton et al., 1997), some shown to have a recurrence timescale related to the rotation rate (Kaper et al., 1999), are thought to be a consequence of the presence in the wind of CIRs. Cranmer & Owocki (1996) predicted that such regions should develop following a perturbation, such as a bright or dark spot, on the stellar photosphere that propagates in the wind, thus generating a complex spiral-like structure of low and high density and velocity regions as the star rotates. CIRs have also been associated with the periodic spectroscopic, photometric, and polarimetric variability observed in some Wolf-Rayet (WR) stars (St-Louis et al., 1995; Morel et al., 1997, 1999; Chené & St-Louis, 2010).
Nevertheless, the origin of the perturbations generating the departure from spherical symmetry in massive-star winds remains unclear. Possible physical processes include non-radial pulsations and magnetic fields. The latter is particularly promising. Large-scale, organized magnetic fields have been found in only 7% of O stars (Wade et al., 2014), and these are thought to have a fossil origin. However, it has been suggested that smaller scale, localized magnetic structures could be responsible for the onset of DACs (Kaper & Henrichs, 1994). More recently, Cantiello & Braithwaite (2011) have presented a model that suggests that such structures could be widespread for stars that harbor a subsurface convection zone. Such zones have been predicted to exist in hot massive stars by Cantiello et al. (2009) owing to an opacity peak caused by the partial ionization of iron-group elements. Detecting such small-scale magnetic structures at the surface of massive stars is an extremely difficult task when dealing with O stars (Kochukhov & Sudnik, 2013) and even more difficult for WR stars where the photosphere is hidden by the optically thick wind.
Studying the wind structures themselves can provide useful constraints that will shed new light on their origin. Polarimatry is a powerful means of studying asymmetries in stellar winds. Indeed, in view of their high temperatures, massive-star outflows contain a copious number of free electrons that scatter light, thereby generating linear polarization. For unresolved and spherically symmetric envelopes, there is total cancellation of the polarization as integrated across the source. Consequently, a net polarization intrinsic to the source demonstrates deviation by the source geometry from the spherical. Brown & McLean (1977) showed that for optically thin scattering and an axisymmetric envelope, the net polarization depends on three factors1: the viewing inclination, an average optical depth for the scattering envelope, and the shape of the envelope.
Since electron scattering is gray, broadband continuum polarization measurements can be used to characterize the asymmetry at any given time. If time-dependent measurements are available, more accurate constraints can be obtained because the structure will then be observed from different viewing angles. Spectropolarimetry can also be used to study the structure in the line-forming region and to obtain kinematic information. In the case of CIRs, this is particularly important because they are thought to originate in the photosphere and propagate throughout the line-forming region of the wind.
To understand the phenomena of CIR and use their occurrence as a diagnostic of wind and atmospheric structure, models are needed to interpret observations. Mullan (1986) was an early proponent of CIRs observed in the solar wind as a viable explanation for certain types of variability (noted above) observed in massive star winds. An important breakthrough in the field came with 2D hydrodynamic simulations by Cranmer & Owocki (1996), who modeled an equatorial CIR for a steady-state, line-driven wind. Following on this, Dessart (2004) developed 3D simulations for CIRs off the equator. Both of those works explore the consequences for wind line-profile effects, such as DACs and other periodic signatures. Brown et al. (2004) considered inverse techniques for extracting kinematic information about CIRs from wind emission lines.
Pertinent to this contribution, there has also been work on the polarization that can arise from CIR structures. Harries (2000) explored a number of effects that give rise to variable polarization for rotating stars, including a model for an equatorial CIR structure. Harries explored these effects using Monte Carlo radiative transfer simulations. In contrast, Ignace et al. (2009) adopted a similar kinematic prescription for the structure of an equatorial CIR in an application for the variable linear polarization seen in the blue supergiant star HD 92207. In this paper we extend these initial results in a parameter study of variable polarization from a wind with CIRs. Neither of the preceding papers allowed for multiple CIRs, and both were restricted to a CIR in the equatorial plane. Here results are presented that allow for multiple CIRs and at arbitrary latitudes.
The structure of the paper is as follows. Section 2 presents the base model for the CIR structure and the resulting variable polarization, following but expanding on Ignace et al. (2009). The results of our parameter study are presented in Sect. 3. Concluding remarks are given in Sect. 4, with particular consideration of applications for observations. Our results are presented for a wind model that is set by a commonly used velocity structure. An Appendix provides a solution for a different velocity structure as a comparison example.
2. Polarization from a simple CIR
In the next section, the approach of Brown & McLean (1977), modified by Cassinelli et al. (1987), for optically thin electron scattering (i.e., single scattering) in an axisymmetric geometry is reviewed. Then, an application is considered for a cone structure in an otherwise spherical wind. Then we show how to use the cone as a basis for computing variable polarization from an equatorial CIR for a rotating star, and finally the polarization for CIRs is explored at arbitrary latitudes.
2.1. Polarization from optically thin electron scattering
For optically thin scattering, the amount of scattered light from a circumstellar envelope is determined by integrating the volume emissivity over the extent of the envelope. The volume emissivity j for electron scattering depends on the electron number density ne, the Thomson scattering cross-section σT, and the amount of incident radiation, as well as geometrical factors relating to dipole scattering toward the observer. It is assumed that the star is the sole source of illumination for circumstellar electrons, meaning that the circumstellar envelope is sufficiently optically thin so that the amount of scattered light is small compared to the starlight.
We consider a coordinate system with the Earth along the z-axis. The star has an axis z∗ that is its rotation axis. The angle of inclination between these axes is signified by ẑ·ẑ∗ = cosi0. It is further assumed that y = y∗, and therefore 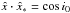 as well. Following Brown & McLean (1977) for a point source of illumination, the scattering angle between a ray of starlight and the observer is χ. A scatterer is oriented about the observer’s axis with azimuth ψ from the x-axis.
as well. Following Brown & McLean (1977) for a point source of illumination, the scattering angle between a ray of starlight and the observer is χ. A scatterer is oriented about the observer’s axis with azimuth ψ from the x-axis.
In the Stokes vector prescription, the polarization properties of intensity are described in terms of I, Q, U, and V (e.g., Chandrasekhar, 1960). The latter is for circular polarization, which will not be considered further. Stokes I is a measure of the total intensity. Stokes-Q and U describe the linear polarization of the light. For example, the relative linear polarization is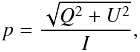 (1)and the polarization position angle is
(1)and the polarization position angle is 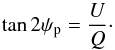 (2)Again, we assume that the total flux of light will be dominated by direct starlight, meaning (a) that the amount of scattered starlight is small and (b) that the amount of absorbed starlight by the circumstellar envelope is miniscule. Consequently, the emissivity for the Stokes-I component is not a concern here. The emissivities for Stokes-Q and U are given by
(2)Again, we assume that the total flux of light will be dominated by direct starlight, meaning (a) that the amount of scattered starlight is small and (b) that the amount of absorbed starlight by the circumstellar envelope is miniscule. Consequently, the emissivity for the Stokes-I component is not a concern here. The emissivities for Stokes-Q and U are given by 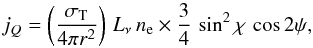 (3)and
(3)and 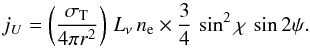 (4)Here r is the radius for a scattering electron from the center of the star, and Lν is the monochromatic stellar luminosity at frequency ν. As previously noted, the angle χ and ψ pertain to the geometry of the scattering.
(4)Here r is the radius for a scattering electron from the center of the star, and Lν is the monochromatic stellar luminosity at frequency ν. As previously noted, the angle χ and ψ pertain to the geometry of the scattering.
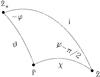 |
Fig. 1 Scattering geometry for Thomson scattering. Here ẑ∗, ẑ, and |
The star has spherical coordinates (r,ϑ,ϕ). The observer is located at ϕ = 0° and ϑ = i0 (see Fig. 1). Using μ = cosϑ, Brown & McLean (1977) showed that for an axisymmetric distribution of electron scatterers, integration about ψ gives 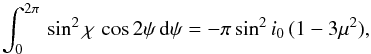 (5)and
(5)and 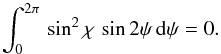 (6)These imply that only the U-polarization vanishes upon integration about the scattering volume for an unresolved source, and only the Q-polarization survives. The total polarization p is then given by
(6)These imply that only the U-polarization vanishes upon integration about the scattering volume for an unresolved source, and only the Q-polarization survives. The total polarization p is then given by ![\begin{equation} q = \frac{L_{\rm P}}{L_\nu}=\frac{3}{16}\,\tau_0\,\sin^2 i_0\, \int\int\,\left[\frac{n_{\rm e}(\tilde{r},\mu)}{n_0}\right]\,(1-3\mu^2)\,{\rm d}\tilde{r}\,{\rm d}\mu, \label{eq:BM} \end{equation}](/articles/aa/full_html/2015/03/aa24806-14/aa24806-14-eq39.png) (7)where LQ is the luminosity of polarized light, n0 some reference number density of scatterers,
(7)where LQ is the luminosity of polarized light, n0 some reference number density of scatterers, 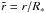 the radius in the wind as normalized to the stellar radius, and τ0 an optical depth parameter. The factor τ0 is given by
the radius in the wind as normalized to the stellar radius, and τ0 an optical depth parameter. The factor τ0 is given by 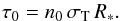 (8)Cassinelli et al. (1987) introduced a correction term to relax the assumption of a point source star. The correction is known as the finite depolarization factor, D(r). The factor assumes a star of uniform brightness (i.e., no limb darkening). Although Brown & McLean (1977) considered more general representations for this correction, we assume a star of uniform brightness.
(8)Cassinelli et al. (1987) introduced a correction term to relax the assumption of a point source star. The correction is known as the finite depolarization factor, D(r). The factor assumes a star of uniform brightness (i.e., no limb darkening). Although Brown & McLean (1977) considered more general representations for this correction, we assume a star of uniform brightness.
The factor D accounts for the varying degree of anisotropy of the radiation field as perceived by a scattering electron at different distances from the star. The factor is given by 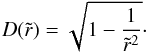 (9)This corrective modifies the polarization by being inserted as a “weighting” factor in the integrand of Eq. (7):
(9)This corrective modifies the polarization by being inserted as a “weighting” factor in the integrand of Eq. (7): 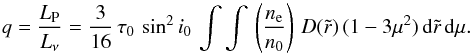 (10)The net relative polarization is determined by q with u = 0, owing to the axisymmetry of the envelope. We note that q can be positive or negative, signifying the orientation of the net polarization against the sky. The projected symmetry axis of the envelope is taken lie along as the north-south direction in the sky. Consequently, a structure like a bipolar jet would have q< 0, whereas one like an equatorial disk would have q> 0. The result shows that the polarization scales in relation to viewing inclination as sin2i. Additionally, the polarization is linear in the optical depth scaling parameter for the envelope with q ∝ τ0. The ratio q/τ0 is thus a function purely from the envelope geometry.
(10)The net relative polarization is determined by q with u = 0, owing to the axisymmetry of the envelope. We note that q can be positive or negative, signifying the orientation of the net polarization against the sky. The projected symmetry axis of the envelope is taken lie along as the north-south direction in the sky. Consequently, a structure like a bipolar jet would have q< 0, whereas one like an equatorial disk would have q> 0. The result shows that the polarization scales in relation to viewing inclination as sin2i. Additionally, the polarization is linear in the optical depth scaling parameter for the envelope with q ∝ τ0. The ratio q/τ0 is thus a function purely from the envelope geometry.
2.2. The case of a simple cone
Our treatment for CIRs is in terms of segments of a cone that are phase-lagged from each other in a radially dependent way. It therefore is useful to first review the treatment of the polarization from a simple cone.
We consider a cone with z∗ the symmetry axis of the cone: the cone lies directly over the stellar rotation axis with opening angle β0. The star has a spherically symmetric wind, and the cone represents an axisymmetric sector of the wind that has either higher or lower density, thereby breaking the spherical symmetry of the system and leading to a net polarization from electron scattering of starlight as described in the previous section. In relation to the results presented in that section, the main considerations here are (a) to relate the polarization to the properties of the wind and (b) to use the result as a basis for our construction of a CIR.
The stellar wind is taken to have mass-loss rate Ṁ and wind terminal speed v∞. The gas is ionized with a mean molecular weight per free electron μe. The number density of electrons in the spherical wind is given by ![\begin{equation} n_{w} = \frac{\dot{M}/\mu_{\rm e}m_{\rm H}}{4\pi\,R_\ast^2\vinf}\,\left[\frac{1} {\tilde{r}^2\,w(\tilde{r})}\right]\equiv n_0\,\tilde{r}^{-2}\,w^{-1}, \end{equation}](/articles/aa/full_html/2015/03/aa24806-14/aa24806-14-eq58.png) (11)where n0 is a parameter for the scale of the number density that is given by the factors for wind and star parameters at the beginning of the equation, and
(11)where n0 is a parameter for the scale of the number density that is given by the factors for wind and star parameters at the beginning of the equation, and 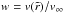 is the normalized wind velocity. We use a standard wind velocity law given by
is the normalized wind velocity. We use a standard wind velocity law given by 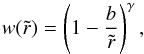 (12)with γ ≥ 0 the velocity law exponent, and b a dimensionless parameter that sets the initial wind speed at the wind base, with w0 = (1 − b)γ. Examples used in this paper adopt γ = 1 (although the Appendix presents a solution with γ = 2).
(12)with γ ≥ 0 the velocity law exponent, and b a dimensionless parameter that sets the initial wind speed at the wind base, with w0 = (1 − b)γ. Examples used in this paper adopt γ = 1 (although the Appendix presents a solution with γ = 2).
The electron density in the cone is parametrized by 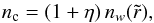 (13)where η is a dimensionless parameter taking values in the interval η ∈ [ − 1,∞). In effect, η represents an excess or decrement of density in the cone relative to the otherwise spherical wind. The cone has zero density if η = −1. If η = 0, the cone has the same density as the wind, in which case sphericity is preserved, and one expects zero net polarization. In this form we are taking the run of density with radius in the cone to have the same functional form as in the wind. This need not be the case, and certainly a different radial dependence for the density in the cone as compared to the wind could be treated (e.g., perhaps γ is different for the flow in the cone as compared to the wind flow).
(13)where η is a dimensionless parameter taking values in the interval η ∈ [ − 1,∞). In effect, η represents an excess or decrement of density in the cone relative to the otherwise spherical wind. The cone has zero density if η = −1. If η = 0, the cone has the same density as the wind, in which case sphericity is preserved, and one expects zero net polarization. In this form we are taking the run of density with radius in the cone to have the same functional form as in the wind. This need not be the case, and certainly a different radial dependence for the density in the cone as compared to the wind could be treated (e.g., perhaps γ is different for the flow in the cone as compared to the wind flow).
The results of Brown & McLean and Cassinelli et al. are general to any axisymmetric distribution of scatterers. However, a cone is an example of a special class of axisymmetric envelopes in which the density is mathematically separable in terms of radial and angular functions. With μ = cosθ, we define the functions f and g as 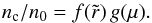 (14)In the application here,
(14)In the application here, 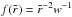 is the same both in the cone and in the wind. For a cone the function g = 1 for μ ≥ cosβ0 and g = 0 for μ< cos(β0).
is the same both in the cone and in the wind. For a cone the function g = 1 for μ ≥ cosβ0 and g = 0 for μ< cos(β0).
Consider now the polarization from the cone. It is determined by a volume integral over the entire envelope, in both the cone and the non-cone regions. The polarization is given by 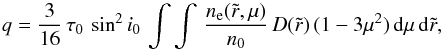 (15)where ne is the electron density, which is either nw or nc. Since the cone density scales with the wind density, the integration can be recast as
(15)where ne is the electron density, which is either nw or nc. Since the cone density scales with the wind density, the integration can be recast as ![\begin{eqnarray} q & = & \frac{3}{16}\,\tau_0\,\sin^2 i_0 \times \left[\int_1^\infty\int_{-1}^{+1} \,\frac{n_{\rm e}}{n_0}\, D(\tilde{r})\,(1-3\mu^2)\,{\rm d}\mu\,{\rm d}\tilde{r} \right. \nonumber\\ & & \left. +~\eta\,\int_1^\infty\int_{\mu_0}^{+1} \,\frac{n_{\rm e}}{n_0}\, D(\tilde{r})\,(1-3\mu^2)\,{\rm d}\mu\,{\rm d}\tilde{r}\right], \end{eqnarray}](/articles/aa/full_html/2015/03/aa24806-14/aa24806-14-eq84.png) (16)where μ0 = cosβ0. The first integral is an integration over the spherical wind, which of course vanishes. The second integral is over the cone, which scales with the factor η.
(16)where μ0 = cosβ0. The first integral is an integration over the spherical wind, which of course vanishes. The second integral is over the cone, which scales with the factor η.
The separability means that the integration and radius and in angle can be written as a product of factors, with 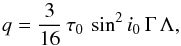 (17)where
(17)where 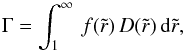 (18)and
(18)and 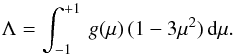 (19)For the problem at hand, and using a change of variable with
(19)For the problem at hand, and using a change of variable with 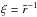 , these functions become
, these functions become 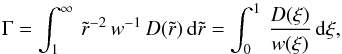 (20)and
(20)and 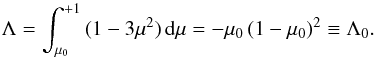 (21)In relation to the radial integral factor, Γ, it is useful to consider the sensitivity of the polarization to structure at different radii in the wind. Figure 2 shows the value of Γ as integrated from ξ to 1. In this form the plot displays Γ as the cumulative polarization from the stellar surface out to the radius
(21)In relation to the radial integral factor, Γ, it is useful to consider the sensitivity of the polarization to structure at different radii in the wind. Figure 2 shows the value of Γ as integrated from ξ to 1. In this form the plot displays Γ as the cumulative polarization from the stellar surface out to the radius 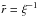 (for a given value of Λ), hence the label for the vertical axis. The plot is normalized to have a unit value when the integral is carried out to infinite distance. The reference lines show the locations where 50% and 90% of the polarization are obtained. In terms of the radial weighting, half of the polarization is set between 1.0 and about 1.5 stellar radii; 90% is set between 1.0 and about 5.6 stellar radii. The remaining 10% arises between 5.6R∗ and beyond. As a result, when discussing the polarization due to a curved CIR, the bulk of the polarization will be determined by the structure of the CIR at the inner few stellar radii.
(for a given value of Λ), hence the label for the vertical axis. The plot is normalized to have a unit value when the integral is carried out to infinite distance. The reference lines show the locations where 50% and 90% of the polarization are obtained. In terms of the radial weighting, half of the polarization is set between 1.0 and about 1.5 stellar radii; 90% is set between 1.0 and about 5.6 stellar radii. The remaining 10% arises between 5.6R∗ and beyond. As a result, when discussing the polarization due to a curved CIR, the bulk of the polarization will be determined by the structure of the CIR at the inner few stellar radii.
 |
Fig. 2 Normalized cumulative polarization in terms of distance from the star. The figure applies when the polarization calculation is seperable (see text). In the case γ = 1, references lines show that half of the polarization will be determined within half a stellar radius above the atmosphere; 90% will be determined between one and 5.6 stellar radii. |
A word about convention is useful to mention at this point. The observer system being used assumes the orientation of the cone as projected in the sky lies along a north-south direction (i.e., along a meridian). For a cone with η> 0, and noting that Λ0< 0, the net polarization would be negative. This simply indicates that the electric vector of the net polarization is parallel to the east-west line, which is orthogonal to the orientation of the cone projected onto the sky. If η< 0, then q> 0 because the polarization is dominated by scatterers lying outside the cone, and the polarization position angle lies parallel to the cone.
Finally, that the cone orientation is north-south corresponds to an orientation of the projected axis of symmetry on the sky as ψ = 90° as measured from west through north. Obviously, an arbitrary source could have an orientation on the sky, and the net polarization would not change. It is straightforward to represent this polarization and position angle as follows. Let p0 = | q(ψ = 90°) |. Then for arbitrary orientation as perceived by an observer, the normalized Stokes q and u parameters become  In developing a simplified model for the polarization from CIRs, we use these constructions in what follows.
In developing a simplified model for the polarization from CIRs, we use these constructions in what follows.
2.3. CIRs in the equatorial plane
A CIR amounts to a spiral-shaped zone of flow that threads a stellar wind. Its structure can indeed be complicated, as seen in the hydrodynamic simulations of Cranmer & Owocki (1996) and Dessart (2004). Our goal is to construct an approximation for the structure of a CIR to rapidly explore model parameter space and trends in the variable polarization with rotation phase. To this end, we approximate a cross-section of a CIR with a sphere as a “spherical cap”. This cap has circular cross-section and is identical to the intersection of a sphere of radius r with a cone. Our construction for a CIR is simply these cap segments for a cone, but where each successive segments in radius are azimuthally phase-lagged. In fact we require an equation of motion for the centers of the segments.
Initially, we consider a CIR that is spiral in shape where the center of the spiral lies in the equatorial plane. The calculation for the polarization can take an arbitrary function of density into account with radius inside the cone and even a varying solid angle of the segments with radius. As long as the CIR segments are individually axisymmetric and scattering is optically thin, the approach described in preceding sections can be employed. However, to reduce the number of free parameters, we assume that all segments of the CIR have a constant solid angle, and we adopt the same parameterization for the CIR density as for the cone of the preceding section: the scaling with η such that η is a constant throughout the CIR, and the γ velocity exponent is also the same in both the cone and the wind.
The question now is what to use for the equation of motion of the segment centers. What is the geometric form for the spiral? A physically motivated approach could be based on wind-compression theory (Bjorkman & Cassinelli, 1993; Ignace et al., 1996). That model is for a rotating wind in which streamline flow is solved via kinematic relations, namely a velocity law and conservation of angular momentum. This model for rotating winds leads to density enhancements toward equatorial latitudes at the expense of polar latitudes. However, wind-compression theory assumes a central force for the wind driving. Owocki et al. (1996) have shown that this does not hold for line-driven winds for massive stars. Indeed, Owocki et al. find that including non-radial forces leads to density-enhanced polar flows.
For our purposes we adopt purely radial streamlines for wind flow in the observer’s frame. This means that a parcel of fluid injected into the wind from the star travels along a radial line, but since the star rotates, subsequent parcels of gas also follow a radial trajectory, but are successively displaced in azimuth. Consequently, the CIR amounts to a spiral pattern of flow that spins as a whole with the rotation period of the star. It is basically the same problem as for perceiving a spiral pattern of water flow from a rotating hose. The shape is found from the streamline flow for a CIR in the rotating frame of the star and recognizing that the shape is equivalent to the spiral pattern as seen by an observer. (A similar approach was used by Ignace et al. 1998 to model the magnetic field topology in the context of wind-compression theory.)
In the rotating frame of the star, we imagine a generalized “spot” of opening angle β0 and solid angle Ω0 at the equator of a star that rotates with period P and angular velocity ω. This spot is the source of a density perturbation on the wind (i.e., the cause of η ≠ 0). In the rotating frame, the spot is fixed. If we assume that the flow from the spot only has a radial component, then in the rotating frame, a fluid element emerging from the spot will progressively displace the spot azimuthally in proportion to ωt, where t is the interval of time after the fluid parcel was injected into the flow.
Generally, the fluid element should of course emerge from the spot with an azimuthal speed of ωR∗. However, with the complexity of non-radial force considerations, we simply ignore the details of the azimuthal component of speed vϕ that a fluid element would have. Certainly, a parametrization for vϕ could be included. In fact, for vϕ the radius-dependent azimuthal velocity in the frame of the star, the equation of motion for the center of the fluid element in the rotating frame of the star would be ![\begin{equation} \frac{{\rm d}\varphi '}{{\rm d}r} = \frac{1}{r}\,\left[\frac{v_\varphi(r) - \omega r}{v_r}\right], \end{equation}](/articles/aa/full_html/2015/03/aa24806-14/aa24806-14-eq112.png) (24)where ϕ′ is the azimuth about the star in the rotating frame as measured from the spot (i.e., ϕ′ = 0° is the location of the spot). Our model for the spiral CIR assumes vϕ(r) = 0.
(24)where ϕ′ is the azimuth about the star in the rotating frame as measured from the spot (i.e., ϕ′ = 0° is the location of the spot). Our model for the spiral CIR assumes vϕ(r) = 0.
The solution to the preceding equation then becomes 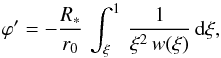 (25)where r0 = v∞/ω is a convenient parameterization representing the “winding radius” of the CIR spiral. Fast radial flow means that the spiral is mostly a linear cone at radii close to the star because the rotation is relatively slow, and so r0/R∗ is large, yielding ϕ′ is roughly constant for r<r0. In contrast, fast rotation relative to the radial flow speed indicates a rapid winding up of the spiral, which is represented by a relatively low value of r0.
(25)where r0 = v∞/ω is a convenient parameterization representing the “winding radius” of the CIR spiral. Fast radial flow means that the spiral is mostly a linear cone at radii close to the star because the rotation is relatively slow, and so r0/R∗ is large, yielding ϕ′ is roughly constant for r<r0. In contrast, fast rotation relative to the radial flow speed indicates a rapid winding up of the spiral, which is represented by a relatively low value of r0.
In the observer’s frame, the equation for the center of the spiral is 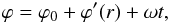 (26)where ϕ0 allows for the azimuthal location of the spot to be defined in terms of an arbitrary reference.
(26)where ϕ0 allows for the azimuthal location of the spot to be defined in terms of an arbitrary reference.
For γ = 1, the integral equation in ξ is analytic. The solution is ![\begin{equation} \varphi '(r=\xi^{-1}) = -\frac{R_\ast}{r_0}\,\left[\frac{1-\xi}{\xi} + b\,\ln\,\left(\frac{w}{u\,w_0}\right) \right] \cdot \label{eq:eqmotion} \end{equation}](/articles/aa/full_html/2015/03/aa24806-14/aa24806-14-eq123.png) (27)Analytic solutions can also be found for other integer values of γ (see the Appendix). For our case of γ = 1, the influence of the winding radius, r0/R∗, for the shape of the CIR spiral is shown in Fig. 3. Two reference circles are shown for radii of 2R∗ and 4R∗. The four curves are for the solution to ϕ′ for different values of r0/R∗ = 2,4,6, and 8, as labeled. Lower values of r0 indicate relatively high equatorial rotation speeds as compared to the wind terminal speed. Curves with lower r0 have higher values of ϕ′ at a given radius.
(27)Analytic solutions can also be found for other integer values of γ (see the Appendix). For our case of γ = 1, the influence of the winding radius, r0/R∗, for the shape of the CIR spiral is shown in Fig. 3. Two reference circles are shown for radii of 2R∗ and 4R∗. The four curves are for the solution to ϕ′ for different values of r0/R∗ = 2,4,6, and 8, as labeled. Lower values of r0 indicate relatively high equatorial rotation speeds as compared to the wind terminal speed. Curves with lower r0 have higher values of ϕ′ at a given radius.
 |
Fig. 3 Examples of the spiral shape for the CIRs as a function of the winding radius, r0. The figure displays the centroid of four different CIRs with distance from the star. The star is the shaded magenta circle. The CIRs are in the equatorial plane, shown here as seen from above. The two larger dotted circles are reference circles at 2R∗ and 4R∗. The different spirals are distinguished by different winding radii as labeled. Lower values of r0 place the transition from a cone-shaped CIR to a spiral one closer to the star; higher values of r0 indicate that the CIR has small curvature until achieving large distances from the star. |
To evaluate the polarization, a key result is to recognize the separability of the spatial integrations for our adopted model. Our assumption is that the cross-section for the CIR is the same as for a cone; therefore, Λ0 for the cone holds for the CIR. The polarization for a CIR reduces to evaluating Γ. However, the solution for Γ, which is an integration in radius, must take account of the radius-dependent phase-lagging of segments as given by the solution of Eq. (27).
The phase-lagging must be related to the observer system of coordinates. The result from Brown & McLean reveals that the polarization from a given conical segment scales with sin2i. For a CIR, each segment is essentially at a different inclination and position angle. In effect, each segment has i = i(ϕ(r,t)) and ψ = ψ(ϕ(r,t)). Using spherical trigonometry, one can show that 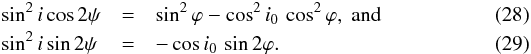 Then the polarization for a CIR at a given a time in terms of the normalized Stokes parameters q and u is given by
Then the polarization for a CIR at a given a time in terms of the normalized Stokes parameters q and u is given by  where
where 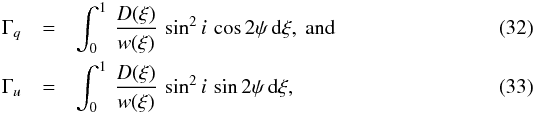 with
with 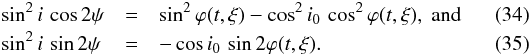 The total polarization and the polarization position angle become
The total polarization and the polarization position angle become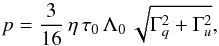 (36)and
(36)and 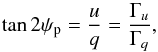 (37)where the last equality is specifically true for the many assumptions that we have adopted, such as every cross-sectional segment of the CIR having the same solid angle. In the optically thin limit, the polarization position angle is independent of the wind optical depth, the value of η, and even the CIR cross-section as encapsulated in Λ0. The only relevant factor is the shape of the spiral as a function of radius as weighted by the geometrical factors associated with Thomson scattering.
(37)where the last equality is specifically true for the many assumptions that we have adopted, such as every cross-sectional segment of the CIR having the same solid angle. In the optically thin limit, the polarization position angle is independent of the wind optical depth, the value of η, and even the CIR cross-section as encapsulated in Λ0. The only relevant factor is the shape of the spiral as a function of radius as weighted by the geometrical factors associated with Thomson scattering.
It is straightforward to include multiple CIR structures by computing the q and u values for each one separately. This holds as long as each one is optically thin. For N CIRs at the equator, each one having its own value of ηi, ϕ0,i, and βi for the ith CIR, the Stokes q and u parameters are linear combinations with  However, it is useful to formulate the total mass loss of the flow. The angle-averaged electron optical depth of the entire envelope becomes
However, it is useful to formulate the total mass loss of the flow. The angle-averaged electron optical depth of the entire envelope becomes ![\begin{equation} \bar{\tau}_{\rm e} = \tau_{w} \, \left[1 + \sum_{i\,=\,1}^N \, \eta_{i}\,\frac{\Omega_{i}}{4\pi} \right]\cdot \label{eqsumm} \end{equation}](/articles/aa/full_html/2015/03/aa24806-14/aa24806-14-eq142.png) (40)If one associates a certain Ṁ with the wind component, then a total mass-loss rate can be determined from the preceding equation after inclusion of CIRs.
(40)If one associates a certain Ṁ with the wind component, then a total mass-loss rate can be determined from the preceding equation after inclusion of CIRs.
It is worth mentioning that CIRs arise from redistribution of wind flow, as contrasted to a model of sectors with enhanced or diminished mass loss relative to an average spherical wind. In redistribution one envisions CIRs as perturbations of the wind density, and the summation term in Eq. (40) must vanish. In this framework a “CIR” would actually consist of two CIR structures, one with positive η and the other with negative η so as to conserve the mass-loss rate. In other words redistribution of density implies that 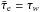 , and our model would then suggest pairs of CIRs with high (ηh) and low (ηl) densities, such that
, and our model would then suggest pairs of CIRs with high (ηh) and low (ηl) densities, such that 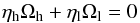 (41)for every pair. Model results to be presented in Sect. 3 adopt a framework of high and low density streams instead of a consideration of redistribution. The point is that redistributive approach could be modeled in a crude way with pairs of CIRs as just described.
(41)for every pair. Model results to be presented in Sect. 3 adopt a framework of high and low density streams instead of a consideration of redistribution. The point is that redistributive approach could be modeled in a crude way with pairs of CIRs as just described.
2.4. CIRs from arbitrary latitudes
Off the equator, the processes for formulating the CIR geometry and the polarization is largely the same. At the equator the CIR remains centered in the equatorial plane. At other latitudes the center of a CIR moves along a conical surface under our scheme (since the flow is radial). The equation of motion for ϕ(t,r,θ0) for a stream originating at latitude θ0 is almost unchanged from the equatorial case. With ϖ = rsinθ0, the differential equation for the centers of CIR segments is 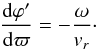 (42)Given that for our approximation, θ = θ0 is fixed at all radii for a CIR originating at θ0, the solution for ϕ becomes
(42)Given that for our approximation, θ = θ0 is fixed at all radii for a CIR originating at θ0, the solution for ϕ becomes 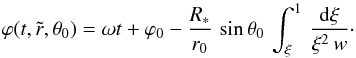 (43)The main difference is the appearance of the factor sinθ0. The interpretation is that there is now an “effective winding radius” with reff = r0/ sinθ0, and this becomes larger for latitudes closer to the pole. At the pole, reff → ∞, and a CIR emerging from the pole would be a conical stream.
(43)The main difference is the appearance of the factor sinθ0. The interpretation is that there is now an “effective winding radius” with reff = r0/ sinθ0, and this becomes larger for latitudes closer to the pole. At the pole, reff → ∞, and a CIR emerging from the pole would be a conical stream.
A major difference from the equatorial case comes in the form of the more complex spherical trigonometric relations that transform between the star coordinate system and that of the observer. The expressions needed for Γq and Γu become ![\begin{eqnarray} \sin^2 i \, \cos 2\psi & = & \sin^2\theta_0\,\sin^2\varphi - \left(\cos\theta_0\,\sin i_0 \right. \nonumber \\[0.5mm] & & \left. -\cos i_0\,\sin\theta_0\,\cos\varphi \right)^2,~{\rm and} \\[0.5mm] \sin^2 i \, \sin 2\psi\, & = & \sin i_0\,\sin 2\theta_0\,\sin\varphi \nonumber \\[0.5mm] & & - \cos i_0\,\sin^2\theta_0\,\sin 2\varphi . \end{eqnarray}](/articles/aa/full_html/2015/03/aa24806-14/aa24806-14-eq159.png) With these relations in hand, polarization light curves can be computed for a CIR emerging from an arbitrary location on the star. Indeed, using the approach of the preceding section, a model with multiple CIRs can also be calculated.
With these relations in hand, polarization light curves can be computed for a CIR emerging from an arbitrary location on the star. Indeed, using the approach of the preceding section, a model with multiple CIRs can also be calculated.
The next section details an exploration of parameters as a sampling of the kinds of variable polarizations that can result for a number of select scenarios.
3. Results
We have conducted a broad parameter study for the variable polarization resulting from our model of CIRs. Before discussing these results, we wish to emphasize two points. First, these models represent the intrinsic source polarization. Real measurements are contaminated by an additional component arising from interstellar polarization. An unresolved star that is spherically symmetric will generally have a measurable polarization of the polarizing influence of the interstellar gas and dust through which the starlight must travel to reach Earth. This influence depends on wavelength. The effect is frequently modeled or removed using a Serkowski law (Serkowski et al., 1975). Suppose the star has an intrinsic normalized polarization given by [q∗(λ),u∗(λ)] at the Earth. The interstellar contribution can be modeled as adding an additional [qISM(λ),uISM(λ)]. The measured polarization will then become (q∗ + qISM,u∗ + uISM). The ISM contribution essentially produces a wavelength-dependent translation of the intrinsic stellar polarization in the q − u diagram.
Second, and most important for our purposes, the interstellar contribution is constant. Any variable polarization is therefore necessarily intrinsic to the stellar source. One cannot generally say that the interstellar polarization is given by the observed minimum q and u values. In other words, even if the star did not display variable polarization, it may still have a non-zero intrinsic polarization. Nonetheless, variable polarization is taken as evidence for intrinsic polarization. If the amplitude of that polarization is larger than the minimum value, then one may certainly conclude that the stellar polarization is large compared to the interstellar component.
With these points in mind, what follows presents idealized model results for q∗(t) and u∗(t) that ignore the ISM component, as well as considerations of sources of random or systematic (e.g., instrumental) errors present in the data. Our assumption is that our models would be applied to processed data after interstellar and systematic effects have been corrected.
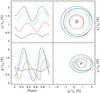 |
Fig. 4 Periodic variations of polarization with stellar rotational phase for CIRs with different winding radius values. Left panels: polarization light curves with phase; right panels: variations in the q-u plane. Top panels: viewing inclination of i = 30° and lower: i = 60°. Different curves are for different winding radii, with values r0/R∗ = 1 (black), 3 (red), 9 (green), and 27 (blue). |
The parameter space for CIR simulations is large owing to our rather general model. Our model for the structure of CIRs is admittedly parameteric. We have strived to minimize the number of free parameters in our approach. Nonetheless, simulation variables include opening angle β, viewing inclination i, latitude of the CIR ϑ, azimuthal location ϕ, the winding radius r0/R∗, and the density enhancement factor η. In addition, simulations allow for an arbitrary number of CIR structures N.
As a sampling of this enormous range of possible models, we focus on four basic sets: the effect of changing the winding radius for one equatorial CIR, the effect of multiple CIRs all emerging from the equator of the star, the effect of CIRs from different latitudes as seen from different viewing inclinations, and the effect of different numbers of randomly distributed CIRs as seen from a typical viewing perspective. Except for the first set of models, the winding radius will be fixed at r0/R∗ = 5. This amounts to an equatorial rotation speed that is 20% of the wind terminal speed. In addition, the opening angle β = 15° is fixed. Thus at a given radius, the CIR covers a solid angle of just under 2% of the “sky” as seen from the star. Since our model is for optically thin scattering, the polarization parameters q, u, and p all scale linearly with the optical depth τ0, so results will be presented as normalized to τ0 as percentage values.
3.1. Changing the winding radius
Figure 4 shows model results for a single equatorial CIR as the wind radius r0/R∗ is varied. Left panels are polarization light curves; right are q-u planes. The top panels are for a viewing inclination of i = 30°, whereas the bottom panels are for i = 90°. The curves are for r0/R∗ = 1,3,9, and 27. Higher values for the winding radius imply that CIRs start to curve at larger radii.
Not surprisingly, small winding radii tend to have low relative polarization (i.e., p/τ0) amplitudes. This is because material is more spread out in azimuth about the star, and so a greater range of scattering angles are sampled, leading to polarimetric cancellation. Higher values of r0/R∗ lead to higher relative polarization amplitudes. In all cases, two peaks separated by half a rotational phase are seen in the polarization light curve because there is a single CIR structure. In the q-u plane, these lead to a double loop. The two troughs of the light curves (and the two loops in the q-u plane) are not identical because of stellar occultation in conjunction with the CIR being asymmetric.
 |
Fig. 5 Periodic variable polarization for two equatorial CIRs. The format is the same as in Fig. 4 with light curves to the left, q-u plane variations to the right, a viewing perspective of i = 30° at the top, and i = 60° along the bottom. The two CIRs are shifted from each other by an angle Δϕ of 0° (black), 30° (red), 60° (green), 90° (dark blue), 120° (light blue), 150° (magenta), and 180° (orange). |
3.2. Equatorial CIRs
We consider a model with two equatorial CIRs. The first CIR has η = 1 and emerges from an azimuth of ϕ = 0°. A second also has η = 1 but emerges from ϕ = 0° to 180° in 30° increments. (Models from 180° to 360° are degenerate with our set, within a phase shift.) The two are co-added with q = q1 + q2 and u = u1 + u2.
Figure 5 displays polarimetric light curves for this set of models. The display is the same as in Fig. 4. The different colors for the different azimuthal offsets between the pair of CIRs is indicated in the caption. All of the light curves are double peaked, but (a) the shape of the peaks; (b) the interval between the peaks in phase; and (c) the amplitude of the peaks depend on the relative positioning of the two CIRs in azimuth. Of particular interest is that for the parameters shown, the two peaks are closest when the CIRs emerge at 90° from one another around the equator.
 |
Fig. 6 Periodic variations in polarization are shown here for CIRs that emerge from different latitudes of the star. The layout of the figure is the same as in Fig. 5. Here the colors are for CIRs at latitudes of ϑ = 20° (black), 40° (red), 60° (green), and 80° (blue). |
3.3. CIRs at different latitudes
In this set of models, a single CIR structure threads the wind, but with the CIR emerging from different latitudes and viewed from different inclinations. Figure 6 shows results in a format similar to Fig. 4. Like that figure, the upper panels are for i = 30° and the lower for i = 60°: left is for polarization light curves and right for the q-u plane. The different curves are for CIRs from different latitudes, with ϑ = 20°, 40°, 60°, and 80°.
Changing the latitude has distinctive effects on the variable polarization as compared to the previous two sections that considered only equatorial CIRs. Changing the latitude, all else being equal, has consequences for whether the light curve is single or double peaked. In the q-u plane, the effects are either a single or a double loop. The reason is that a CIR that is more closely located near the pole tends to be more nearly stationary in projection on the sky, despite the rotation of the star. The limiting case is a CIR at the pole, which is just a conical flow that maintains a fixed projected position angle.
Model parameters for randomly distributed CIRs.
3.4. Random distributions of CIRs
The case that may perhaps most closely represent real stars is one with multiple CIR structures emerging from different azimuth and latitude locations. In this example seven models have been calculated with individual CIRs. A random number generator was used to place the individual CIRs around the star. Values of η were randomly assigned in the range of − 1 to + 4. Table 1 summarizes the assigned parameters for the seven cases.
Figures 7 and 8 show polarization light curves and q-u planes using the following construction. The viewing perspective is fixed at i = 60°. All the CIRs have r0/R∗ = 5. Then the results are superimposed and normalized according to 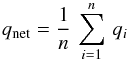 (46)and
(46)and 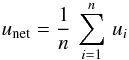 (47)where n runs from 1 to 7. Figures 7 and 8 thus show results for one CIR, two CIRs, three CIRs, and so on, up to all seven CIRs together. This is an incremental approach for seeing what happens as additional randomly placed CIR structures are added to the model.
(47)where n runs from 1 to 7. Figures 7 and 8 thus show results for one CIR, two CIRs, three CIRs, and so on, up to all seven CIRs together. This is an incremental approach for seeing what happens as additional randomly placed CIR structures are added to the model.
 |
Fig. 7 Periodic polarization light curves for a randomized distribution of CIRs across the star. Each curve represents the addition of one more randomly placed CIR. The curves correspond to a number of CIRs of 1 (black), 2 (red), 3 (green), 4 (dark blue), 5 (light blue), 6 (magenta), and 7 (orange). Table 1 lists model parameters of the individual CIRs. |
 |
Fig. 8 Polarization model results from Fig. 7 displayed in the q-u plane. The colors correspond to the identifications indicated in Fig. 7. |
The normalization ensures that the curves are comparing the same things. For example, if we were to co-add seven models of exactly the same CIR, the resulting polarization would simply be the same curve as one CIR, only with a polarization that is seven times greater. Normalization ensures that as more curves are added, the curves are being compared on the same basis.
The result is a diverse set of possible outcomes. The black curve shows the case of just one CIR. Adding additional CIRs moves through the curves in color in the order of red, green, dark blue, light blue, magenta, and finally orange. A variety of shapes with more or fewer peaks result. Add to this the fact that for this example, all CIRs have the same opening angle and that only one viewing inclination case is being shown, it seems clear that a wide variety of variable polarizations could result.
4. Conclusion
In this paper we have described a parametric representation of a corotating interaction region (CIR) that threads an otherwise spherical wind. There is no denying that we took some liberties in presenting a simplified structure for a CIR: circular cross-section, constant solid angle, uniform density within the CIR, and a simple prescription for its spiral curvature. However, the advantages of the approach allow, for the first time, a broad exploration of consequences for variable polarization signals. The goals were to adopt a flexible, semi-analytic description of a CIR structure, basically motivated by hydrodynamic simulations, in which to explore the range of polarimetric behavior easily and rapidly. These results may then be used in conjunction with other methods, such as UV line variability (for a recent example, see Prinja et al., 2012), optical variability (e.g., Chené & St-Louis, 2010), and perhaps X-ray variability (Ignace et al., 2013; Massa et al., 2014).
An important result of our study is allowance for CIRs from latitudes other than the equator. The majority of previous works have focused on equatorial CIRs (one exception being Dessart, 2004). The motivation is often one of simplicity. Frequently, CIRs are considered in relation to variable blueshifted absoprtion for UV line data involving the intersection of the CIR with the absorption column between the observer and the star. Consideration of an equatorial CIR makes the modeling easier. In contrast, polarization is sensitive to the fully three-dimensional structure of the asymmetric distribution of density about the star. (The trade-off in relation to line-profile studies is the loss of velocity shift information.) A major consequence of having CIRs from different latitudes rather than just the equator is a far more diverse range of polarimetric light curves and of behavior in the q-u plane. The potential-added complexity can be a strength when used in conjunction with other diagnostics, such as line variability.
This contribution focused on the theoretical aspects of CIRs and variable polarization. There are several data sets to which these results could be applied. In a follow-up paper, our model will be employed to interpret variable polarization for the Wolf-Rayet (WR) star EZ CMa (Drissen et al., 1989). WR stars are known to form pseudo-photospheres, where optical depth unity occurs in the wind itself (e.g., Hillier, 1987). Although our model is for optically thin scattering, useful results can still be obtained through adoption of the last scattering approximation (e.g., Stenflo, 1982). The merit for such an approach is empirically suggested by Schulte-Ladbeck et al. (1992) for EZ CMa. However, the approach will require modifications to the prescription for CIR curvature, which will be explained in the follow-up paper.
Online material
Appendix A: CIRs for the case γ = 2
Our results have focused exclusively on the case of γ = 1 for the wind velocity law. Of course, other values of γ may be considered. In general, the solution for the spiral shape of the spiral will not be analytic but must be evaluated numerically. However, analytic solutions for ϕ(ξ) can be found for integer values of γ. Expected values of γ for early-type star winds range from γ = 0.5 from the original Castor et al. (1975) paper for line-driven winds to γ ≈ 0.8 from Pauldrach et al. (1986) that augmented the initial results of Castor et al. to the γ = 1 that is typically used for the inner wind of WR stars (e.g., Schmutz et al., 1989) and then to γ ≈ 3, which has been suggested for some supergiant winds (e.g., Prinja et al., 1995).
As an example, the case of γ = 2 is provided here as a comparison case to γ = 1. In general, higher values of γ tend to increase the radial width over which the bulk of wind acceleration takes place. For example, with 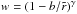 , the radius in the wind where the flow achieves half its terminal speed, w = 0.5, occurs at
, the radius in the wind where the flow achieves half its terminal speed, w = 0.5, occurs at 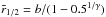 , which increases as γ becomes larger. As a case in point,
, which increases as γ becomes larger. As a case in point, 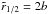 for γ = 1, but for γ = 2, the value of
for γ = 1, but for γ = 2, the value of 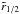 increases to 3.4b. The net effect of this is that for our construction of the CIR spiral shape, at a given value of ω, a CIR tends to wind up at smaller radius with increasing γ, so the effective winding radius decreases with larger γ.
increases to 3.4b. The net effect of this is that for our construction of the CIR spiral shape, at a given value of ω, a CIR tends to wind up at smaller radius with increasing γ, so the effective winding radius decreases with larger γ.
We need to evaluate ϕ′ for γ = 2. We start with Eq. (25) for a CIR in the equatorial plane, reproduced here: 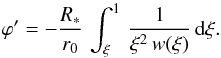 (A.1)The wind velocity is w = (1 − bξ)2. Inserting w into the above expression gives
(A.1)The wind velocity is w = (1 − bξ)2. Inserting w into the above expression gives 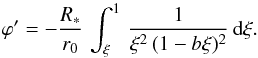 (A.2)The solution for this expression is
(A.2)The solution for this expression is ![\appendix \setcounter{section}{1} \begin{equation} \varphi ' = -\frac{R_\ast}{r_0}\,\left[\left(\frac{2b-1}{1-b}\right) + \left(\frac{1-2b\xi}{\xi\,(1-b\xi)}\right) + 2b\,\ln \left(\frac{1-b\xi}{\xi\,(1-b)}\right) \right]\cdot \end{equation}](/articles/aa/full_html/2015/03/aa24806-14/aa24806-14-eq216.png) (A.3)Figure A.1 shows a comparison between these functions. There a value of r0/R∗ = 10 is used. At most radii the value of ϕ′ is about 50% to 100% higher for γ = 2 than for γ = 1. As compared to γ = 1, the effective value of r0 is about half as large when γ = 2.
(A.3)Figure A.1 shows a comparison between these functions. There a value of r0/R∗ = 10 is used. At most radii the value of ϕ′ is about 50% to 100% higher for γ = 2 than for γ = 1. As compared to γ = 1, the effective value of r0 is about half as large when γ = 2.
For the polarization one should also note that for a given optical depth of the envelope, larger γ essentially implies a relatively higher density of scatterers at small radii as compared to winds with lower γ values. Figure A.2 compares the polarization light curves for the solutions displayed in Fig. A.1: equatorial CIRs, r0/R∗ = 10, w0 = 0.03, same opening angle, with η = 1, and i0 = 60° for both cases. The polarization is plotted as the ratio p/τ, where τ is the optical depth of the wind. As can be seen, for the selected parameters that are relevant to fast winds, the polarization per unit optical depth is similar for the two cases, but there is a slight phase shift owing to the different degrees of CIR winding. This result does not assume the same base density n0 for the two cases, but rather the same wind optical depth.
(For the same n0, the optical depth of a γ = 2 wind is 1.6 times greater than for γ = 1.)
 |
Fig. A.1 Comparison of the azimuth location of the CIR centroid with radius from the star. Here blue is for γ = 1, and red is for γ = 2. This example uses a wind radius of r0 = 10R∗. The value of φ′ is generally between 50% to 100% larger for γ = 2 than for γ = 1 indicating that a spiral CIR is considerably more curved at a given radius for the higher γ case. |
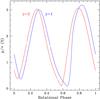 |
Fig. A.2 Comparison of polarization light curves for the γ = 1 and γ = 2 cases shown in the previous figure. The polarization is plotted as normalized to the wind optical depth along a radial. The case of γ = 1 produces a relatively stronger polarization signal (per unit optical depth) than in the case of γ = 2. The polarization extrema are slightly shifted in phase between the two cases. |
The analysis of Brown & McLean (1977) does not include limb darkening. Brown et al. (1989) considered limb darkening, which can introduce chromatic effects.
Acknowledgments
The authors gratefully acknowledge helpful comments from an anonymous referee. R.I. wishes to acknowledge support for this research through a grant from the National Science Foundation (AST-0807664). N.S.L. acknowledges financial support from the Natural Sciences and Engineering Research (NSERC) of Canada.
References
- Bjorkman, J. E., & Cassinelli, J. P. 1993, ApJ, 409, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. C., & McLean, I. S. 1977, A&A, 57, 141 [NASA ADS] [Google Scholar]
- Brown, J. C., Carlaw, V. A., & Cassinelli, J. P. 1989, ApJ, 344, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. C., Barrett, R. K., Oskinova, L. M., et al. 2004, A&A, 413, 959 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burlaga, L. F., Schwenn, R., & Rosenbauer, H. 1983, Geophys. Res. Lett., 10, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Burlaga, L. F., Ness, N. F., & Belcher, J. W. 1997, J. Geophys. Res., 102, 4661 [NASA ADS] [CrossRef] [Google Scholar]
- Cantiello, M., & Braithwaite, J. 2011, A&A, 534, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cantiello, M., Langer, N., Brott, I., et al. 2009, A&A, 499, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cassinelli, J. P., Nordsieck, K. H., & Murison, M. A. 1987, ApJ, 317, 290 [NASA ADS] [CrossRef] [Google Scholar]
- Castor, J. I., Abbott, D. C., & Klein, R. I. 1975, ApJ, 195, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Chandrasekhar, S. 1960, Radiative transfer (New York: Dover) [Google Scholar]
- Chené, A.-N., & St-Louis, N. 2010, ApJ, 716, 929 [NASA ADS] [CrossRef] [Google Scholar]
- Cranmer, S. R., & Owocki, S. P. 1996, ApJ, 462, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Dessart, L. 2004, A&A, 423, 693 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drissen, L., Robert, C., Lamontagne, R., et al. 1989, ApJ, 343, 426 [NASA ADS] [CrossRef] [Google Scholar]
- Fullerton, A. W., Massa, D. L., Prinja, R. K., Owocki, S. P., & Cranmer, S. R. 1997, A&A, 327, 699 [NASA ADS] [Google Scholar]
- Gosling, J. T., & Pizzo, V. J. 1999, Space Sci. Rev., 89, 21 [Google Scholar]
- Harries, T. J. 2000, MNRAS, 315, 722 [NASA ADS] [CrossRef] [Google Scholar]
- Hillier, D. J. 1987, ApJS, 63, 947 [NASA ADS] [CrossRef] [Google Scholar]
- Howarth, I. D., & Prinja, R. K. 1989, ApJS, 69, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Ignace, R., Cassinelli, J. P., & Bjorkman, J. E. 1996, ApJ, 459, 671 [NASA ADS] [CrossRef] [Google Scholar]
- Ignace, R., Cassinelli, J. P., & Bjorkman, J. E. 1998, ApJ, 505, 910 [NASA ADS] [CrossRef] [Google Scholar]
- Ignace, R., Hubrig, S., & Schöller, M. 2009, AJ, 137, 3339 [NASA ADS] [CrossRef] [Google Scholar]
- Ignace, R., Gayley, K. G., Hamann, W.-R., et al. 2013, ApJ, 775, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Kaper, L., & Henrichs, H. F. 1994, Ap&SS, 221, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Kaper, L., Henrichs, H. F., Nichols, J. S., & Telting, J. H. 1999, A&A, 344, 231 [NASA ADS] [Google Scholar]
- Kochukhov, O., & Sudnik, N. 2013, in Massive Stars: From alpha to Omega [Google Scholar]
- Massa, D., Oskinova, L., Fullerton, A. W., et al. 2014, MNRAS, 441, 2173 [NASA ADS] [CrossRef] [Google Scholar]
- Morel, T., St-Louis, N., & Marchenko, S. V. 1997, ApJ, 482, 470 [NASA ADS] [CrossRef] [Google Scholar]
- Morel, T., Marchenko, S. V., Eenens, P. R. J., et al. 1999, ApJ, 518, 428 [NASA ADS] [CrossRef] [Google Scholar]
- Mullan, D. J. 1986, A&A, 165, 157 [NASA ADS] [Google Scholar]
- Owocki, S. P., Cranmer, S. R., & Gayley, K. G. 1996, ApJ, 472, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Pauldrach, A., Puls, J., & Kudritzki, R. P. 1986, A&A, 164, 86 [NASA ADS] [Google Scholar]
- Prinja, R. K., Massa, D., & Fullerton, A. W. 1995, ApJ, 452, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Prinja, R. K., Massa, D. L., & Cantiello, M. 2012, ApJ, 759, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Rouillard, A. P., Davies, J. A., Forsyth, R. J., et al. 2008, Geophys. Res. Lett., 35, 10110 [Google Scholar]
- Schmutz, W., Hamann, W.-R., & Wessolowski, U. 1989, A&A, 210, 236 [NASA ADS] [Google Scholar]
- Schulte-Ladbeck, R. F., Nordsieck, K. H., Taylor, M., et al. 1992, ApJ, 387, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Serkowski, K., Mathewson, D. S., & Ford, V. L. 1975, ApJ, 196, 261 [NASA ADS] [CrossRef] [Google Scholar]
- St-Louis, N., Dalton, M. J., Marchenko, S. V., Moffat, A. F. J., & Willis, A. J. 1995, ApJ, 452, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Stenflo, J. O. 1982, Sol. Phys., 80, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Wade, G. A., Grunhut, J., Alecian, E., et al. 2014, IAU Symp., 302, 265 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Scattering geometry for Thomson scattering. Here ẑ∗, ẑ, and |
| In the text | |
 |
Fig. 2 Normalized cumulative polarization in terms of distance from the star. The figure applies when the polarization calculation is seperable (see text). In the case γ = 1, references lines show that half of the polarization will be determined within half a stellar radius above the atmosphere; 90% will be determined between one and 5.6 stellar radii. |
| In the text | |
 |
Fig. 3 Examples of the spiral shape for the CIRs as a function of the winding radius, r0. The figure displays the centroid of four different CIRs with distance from the star. The star is the shaded magenta circle. The CIRs are in the equatorial plane, shown here as seen from above. The two larger dotted circles are reference circles at 2R∗ and 4R∗. The different spirals are distinguished by different winding radii as labeled. Lower values of r0 place the transition from a cone-shaped CIR to a spiral one closer to the star; higher values of r0 indicate that the CIR has small curvature until achieving large distances from the star. |
| In the text | |
 |
Fig. 4 Periodic variations of polarization with stellar rotational phase for CIRs with different winding radius values. Left panels: polarization light curves with phase; right panels: variations in the q-u plane. Top panels: viewing inclination of i = 30° and lower: i = 60°. Different curves are for different winding radii, with values r0/R∗ = 1 (black), 3 (red), 9 (green), and 27 (blue). |
| In the text | |
 |
Fig. 5 Periodic variable polarization for two equatorial CIRs. The format is the same as in Fig. 4 with light curves to the left, q-u plane variations to the right, a viewing perspective of i = 30° at the top, and i = 60° along the bottom. The two CIRs are shifted from each other by an angle Δϕ of 0° (black), 30° (red), 60° (green), 90° (dark blue), 120° (light blue), 150° (magenta), and 180° (orange). |
| In the text | |
 |
Fig. 6 Periodic variations in polarization are shown here for CIRs that emerge from different latitudes of the star. The layout of the figure is the same as in Fig. 5. Here the colors are for CIRs at latitudes of ϑ = 20° (black), 40° (red), 60° (green), and 80° (blue). |
| In the text | |
 |
Fig. 7 Periodic polarization light curves for a randomized distribution of CIRs across the star. Each curve represents the addition of one more randomly placed CIR. The curves correspond to a number of CIRs of 1 (black), 2 (red), 3 (green), 4 (dark blue), 5 (light blue), 6 (magenta), and 7 (orange). Table 1 lists model parameters of the individual CIRs. |
| In the text | |
 |
Fig. 8 Polarization model results from Fig. 7 displayed in the q-u plane. The colors correspond to the identifications indicated in Fig. 7. |
| In the text | |
 |
Fig. A.1 Comparison of the azimuth location of the CIR centroid with radius from the star. Here blue is for γ = 1, and red is for γ = 2. This example uses a wind radius of r0 = 10R∗. The value of φ′ is generally between 50% to 100% larger for γ = 2 than for γ = 1 indicating that a spiral CIR is considerably more curved at a given radius for the higher γ case. |
| In the text | |
 |
Fig. A.2 Comparison of polarization light curves for the γ = 1 and γ = 2 cases shown in the previous figure. The polarization is plotted as normalized to the wind optical depth along a radial. The case of γ = 1 produces a relatively stronger polarization signal (per unit optical depth) than in the case of γ = 2. The polarization extrema are slightly shifted in phase between the two cases. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



