| Issue |
A&A
Volume 575, March 2015
|
|
|---|---|---|
| Article Number | A93 | |
| Number of page(s) | 10 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201323113 | |
| Published online | 03 March 2015 | |
The effect of supernova rate on the magnetic field evolution in barred galaxies
1 Astronomical Observatory, Jagiellonian University, ul. Orla 171, 30-244 Kraków, Poland
e-mail: nala@oa.uj.edu.pl
2 Centre for Astronomy, Nicolaus Copernicus University, Faculty Physics, Astronomy and Informatics, Grudziadzka 5, 87100 Toruń, Poland
3 AGH University of Science and Technology, ACC Cyfronet AGH, ul. Nawojki 11, PO Box 386, 30-950 Kraków 23, Poland
Received: 22 November 2013
Accepted: 5 November 2014
Context. For the first time, our magnetohydrodynamical numerical calculations provide results for a three-dimensional model of barred galaxies involving a cosmic-ray driven dynamo process that depends on star formation rates. Furthermore, we argue that the cosmic-ray driven dynamo can account for a number of magnetic features in barred galaxies, such as magnetic arms observed along the gaseous arms, magnetic arms in the inter-arm regions, polarized emission that is at the strongest in the central part of the galaxy, where the bar is situated, polarized emission that forms ridges coinciding with the dust lanes along the leading edges of the bar, as well as their very strong total radio intensity.
Aims. Our numerical model probes what kind of physical processes could be responsible for the magnetic field topology observed in barred galaxies (modes, etc.). We compare our modelled results directly with observations, constructing models of high-frequency (Faraday rotation-free) polarized radio emission maps out of the simulated magnetic field and cosmic ray pattern in our modeled galaxy. We also take the effects of projection into account as well as the limited resolution.
Methods. We applied global 3D numerical calculations of a cosmic-ray driven dynamo in barred galaxies with different physical input parameters such as the supernova (SN) rate.
Results. Our simulation results lead to the modelled magnetic field structure similar to the one observed on the radio maps of barred galaxies. Moreover, they cast new light on a number of properties in barred and spiral galaxies, such as fast exponential growth of the total magnetic energy to the present values. The quadrupole modes of magnetic field are often identified in barred galaxies, but the dipole modes (e.g., in NGC 4631) are found very seldom. In our simulations the quadrupole configuration dominates and the dipole configuration only appears once in the case of model S100, apparently as a consequence of the choice of the random number seed. Synthetic radio maps of our models display X-type structure similar to what is observed in real galaxies.
Conclusions. We conclude that a cosmic-ray driven dynamo process in barred galaxies can amplify magnetic fields efficiently. The fastest rate of magnetic field increase is 195 yr for a SN frequency of 1/50 yr-1.The obtained strength of magnetic field corresponds to the observational values (a few in spiral arms). The polarization and rotation measure maps also agree with observations. We found the effect of shifting magnetic arms in 4 models (out of the sample of 5).
Key words: dynamo / magnetohydrodynamics (MHD) / methods: numerical / galaxies: magnetic fields
© ESO, 2015
1. Introduction
Radio observations indicate that magnetic fields are important agents in the interstellar medium (ISM) within both spiral and barred galaxies (Beck 2012). The large-scale structure of magnetic field in such galaxies is generally represented by a superposition of modes with different azimuthal and vertical field directions and symmetries. In the galactic disks, the axisymmetric spiral (ASS) mode is the strongest one (Ruzmaikin et al. 1988); however, the bi-symmetric spiral mode (BSS) or a mixture of both with a preponderance of either pattern is also observed (Beck et al. 1996; Krause 2004; Beck 2012). The vertical symmetry can be even (quadrupole) or odd (bipolar). Rotation measure observations show that the ASS magnetic field is present in several galaxies, for example, in M31 (Sofue & Takano 1981), IC 342 (Sokoloff et al. 1992), or the Large Magellanic Cloud (Gaensler et al. 2005). The BSS mode was unequivocally observed just in one galaxy, M81 (Sokoloff et al. 1992). Many other observations indicate that the BSS mode can occur in the ASS mode, e.g., in M33 or NGC 2276 (Hummel & Beck 1995) or NGC 4631 (Hummel et al. 1991). According to the magnetohydrodynamical (MHD) dynamo theory, the galactic magnetic fields should have the even symmetry rather than the odd one, and the global magnetic fields of spherical objects (including stars and planets) are mostly dipolar, while those of flattened objects (spiral galaxies) are quadrupolar (Beck et al. 1996; Krause 2004). Although a distinct ASS or BSS mode was detected in several galaxies, most of magnetic field structures seem to be a superposition of the different dynamo modes (Beck 2012). This could be due to the many processes occurring in disks of galaxies, which may be correlated with the MHD dynamo process, for example, “cosmic-ray” driven one (see below for explanation).
The main theoretical model of the dynamo process is the mean-field dynamo theory (Ruzmaikin et al. 1988), which can explain magnetic fields in various environments, terrestrial, solar, or stellar. The theory describes the generation of regular large-scale magnetic field in galaxies as an effect of the combined action of differential rotation Ω and helical turbulent motions of interstellar gas (the so-called α-effect). However, the classic kinematic dynamo gives a rather long timescale of magnetic field amplification for galaxies, about , which is too long to account for strong magnetic fields in high-redshift galaxies beyond z = 1 (Berezinski et al. 1990). A faster amplification is possible when the cosmic-ray (CR) driven dynamo (Parker 1992; Hanasz & Lesch 2003; Hanasz et al. 2006, 2009a,b; Kulpa-Dybeł et al. 2011) is applied, involving three principal effects: first, the CR energy is continuously supplied by supernovae (SNe) remnants to the galactic disk, which became turbulent through buoyancy of magnetic field due to CRs; second, the fast turbulent magnetic reconnection (Lazarian & Vishniac 1999; Kowal et al. 2009, 2012; Hanasz et al. 2004) allows small-scale loops of magnetic field to merge into large-scale coherent structures in the limit of vanishing resistivity; and third, the differential rotation leads to generating a toroidal magnetic field component from the poloidal one.
However, every dynamo requires a seed field. The origin of first magnetic fields in the Universe is still one of the most challenging problems in modern astrophysics (e.g., Kulesza-Żydzik et al. 2010). Two different views of the generation of seed fields are presently considered: one, the seed fields can be essentially of cosmological (primordial) origin, and second, the seed fields are generated in astrophysical processes at work in the ISM. A variety of cosmological processes occurring in the early Universe were proposed (magnetic fields could be generated in various phase transitions, such as the electroweak transition (Quashnock et al. 1989), and the quark-hadron phase transition (Quashnock et al. 1989), or during the inflation era (Turner & Widrow 1988)). These processes lead to creating very tiny magnetic fields of about (Widrow 2002; Subramanian 2010).
Another possibility is generation of seed fields in astrophysical processes, such as the Biermann battery (Syrovatskii 1970; Xu et al. 2008). In this scenario, even if magnetic fields are initially absent in a star, a weak field is produced via the Biermann mechanism owing to the different inertia of electrons and ions. The newly created tiny magnetic fields are then amplified by a stellar dynamo. Next, a star can explode as an SN, releasing magnetized material that spreads into the ISM. Rees (1987) suggested that Crab-type SNe remnants have fields of the order of 10-4 G. He also estimated that at an early stage in galactic evolution there could have been as much as 106 randomly oriented SNe remnants similar to the Crab Nebula, giving rise to quite substantial seed fields of the order of 10-9 G. The recent simulations by Hanasz et al. (2009b) and Kulpa-Dybeł et al. (2011) have shown that small-scale magnetic fields of stellar origin can be amplified exponentially by the CR driven dynamo up to the observed values, which means that SNe explosions can produce a sufficiently strong seed field for the CR dynamo action.
Dubois & Teyssier (2010) did 3D MHD calculations of an isolated dwarf galaxy that had been formed self-consistently inside a cooling halo. Their simulations took the influence of supernova explosions onto ISM and the galactic magnetic field into account. They found a linear growth of the total magnetic energy caused by differential rotation, as well as a strong magnetic wind into the halo contributing to the intergalactic magnetic field (see also Siejkowski et al. 2010, 2011). The recent radio observations of magnetic fields in dwarf irregulars (Chyży et al. 2011) do not indicate that such galaxies could effectively provide magnetic field to the intergalactic medium, but dwarf galaxies with high starburst can provide such a field to the intergalactic medium. The paper showing 2D numerical MHD simulations of a barred galaxy was published by Kim & Stone (2012), who considered the effect of gaseous flow to the galactic central black hole and find that the gas streams down much faster after including the magnetic field in the calculations. They also confirm our process of shifting magnetic arms into the inter-arm region.
Another model of fast galactic dynamo, the so-called supernova-driven dynamo, has been proposed by Gressel et al. (2008). They assumed that the thermal energy is injected into the galactic disk during a SN explosion, neglecting the CR component. This contrasts to the CR driven dynamo model, where the CR energy is introduced to the galactic disk during a SN explosion, while the thermal energy is not taken into account. In the supernova-driven dynamo, the authors also applied the cooling and heating functions to reflect the multi-phase nature of the ISM. Numerical simulations in the shearing-box approximation have shown that the supernova driven-dynamo causes an exponential amplification of magnetic field and can explain a number of observational features of magnetic fields in galaxies.
Booth et al. (2013) made a numerical model of CR driven gas motions for two galaxies, the Milky Way and the Small Magellanic Cloud, including only gas and CR with no magnetic field, so their model involved just the isotropic diffusion of CR gas in the disk of modelled galaxies. The model yielded a reasonable velocity of winds of CR and gas in both the galaxies.
The aim of the paper is to address the question of what physical processes could be responsible for magnetic field configurations observed in barred galaxies. To answer the question we apply global 3D numerical simulations of a CR driven dynamo with different values of SN rate, while the other parameters are fixed. We constructed polarized radio-emission maps and compare our results with observations.
The description of our model is provided in Sect. 2, the results in Sect. 3, the discussion in Sect. 4, and the conclusions in Sect. 5.
2. Model
2.1. Basic equations
Parameters adopted for the barred galaxy model.
The computations of evolution of a barred galaxy are done by solving the isothermal non-ideal MHD equations of the form 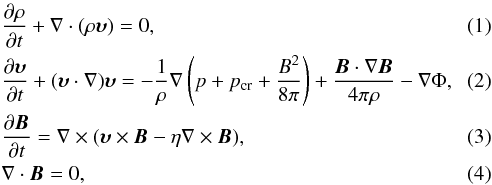
where υ is the large-scale velocity of gas, ρ is the gas density distribution, p is the gas pressure, pcr is the CR pressure, Φ is the gravitational potential, B is the magnetic induction, e is the thermal energy density and η is the turbulent magnetic diffusivity. An isothermal equation of state was assumed, that is 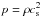 , where cs is the isothermal speed of sound. We investigated the problem of propagation of CR transport (Schlickeiser & Lerche 1985) in the ISM by solving the following diffusion-advection equation:
, where cs is the isothermal speed of sound. We investigated the problem of propagation of CR transport (Schlickeiser & Lerche 1985) in the ISM by solving the following diffusion-advection equation: 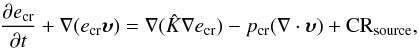 (5)where ecr is the CR energy density, pcr = (γcr − 1)ecr is the CR pressure,
(5)where ecr is the CR energy density, pcr = (γcr − 1)ecr is the CR pressure, 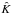 the diffusion tensor, υ the gas velocity and CRsource the source term for the CR energy. Moreover, we assume that 10% of of the SNe kinetic energy from their outburst is transformed into the CR energy and leave out the thermal energy, we also applying the value of adiabatic index for the CR gas as γcr = 14/9 and adding the CRs pressure to the total pressure in the ISM gas motion equation as ∇pcr (Berezinski et al. 1990). It is also assumed that the CR gas diffuses anisotropically (Ryu et al. 2003). The CR diffusion tensor K is defined as
the diffusion tensor, υ the gas velocity and CRsource the source term for the CR energy. Moreover, we assume that 10% of of the SNe kinetic energy from their outburst is transformed into the CR energy and leave out the thermal energy, we also applying the value of adiabatic index for the CR gas as γcr = 14/9 and adding the CRs pressure to the total pressure in the ISM gas motion equation as ∇pcr (Berezinski et al. 1990). It is also assumed that the CR gas diffuses anisotropically (Ryu et al. 2003). The CR diffusion tensor K is defined as 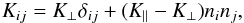 (6)where K⊥ and K∥ are the parallel and perpendicular (with respect to the local magnetic field direction) CR diffusion coefficients and ni = Bi/B are components of unit vectors tangent to the magnetic field lines.
(6)where K⊥ and K∥ are the parallel and perpendicular (with respect to the local magnetic field direction) CR diffusion coefficients and ni = Bi/B are components of unit vectors tangent to the magnetic field lines.
2.2. Galactic disk model
We made similar kinematical and dynamical assumptions to those in Kulpa-Dybeł et al. (2011). The CR-driven dynamo models of a barred galaxy were solved numerically in a 3D computational box with the size of Lx = Ly = 30 kpc and Lz = 7 kpc. The domain resolution is 300 × 300 × 75 grid zones in the x, y, and z directions, respectively. We introduced the following units: time was given in , the mass, length, velocity, and magnetic field are measured in 106M⊙, , , and , respectively. The initial state of the modelled galactic disk was that of hydrostatic equilibrium. In our simulations, we assumed that the barred galaxy contains four components of gravitational potentials: a large and massive dark matter halo, a central bulge, a rotating stellar disk, and a bar. The halo and bulge components were represented by two Plummer spheres, the disk of stars was represented by an isochrone gravitational potential, and the bar was given as a prolate spheroid (see Table 1). We started our calculations without a bar potential, introducing it from the time t = 0.1 Gyr to t = 0.4 Gyr, until it reached the mass Mbar assumed for the respective model. To keep the total mass of our model galaxy constant, we reduced the mass of the bulge, keeping Mbar(t) + Mb(t) = const. throughout the simulation. It was further assumed that the angular velocity of the bar’ rotation Ωbar = 30 km s-1 kpc-1, which determines the values of RILR = 0.4 kpc, RCR = 6 kpc, and ROLR = 8.5 kpc. (see Kulpa-Dybeł et al. 2011), as well as the speed of sound as cs = 5.12 km s-1 and gas density at the galactic disk centre ρ0 is equal to 1.0 H cm-3. At each time step, we added a small amount of mass in the galactic plane to compensate for the gas escaped through the outer domain boundaries. We also applied (e.g., Strong et al. 2007), the following values of the cosmic ray diffusion: and , and set the diffusion coefficient η as s, assuming that initially the CR pressure is equal to the gas pressure, 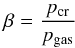 (7)and that β is constant and equal to 1. Furthermore, we applied the outflow boundary conditions in the x, y, and z directions.
(7)and that β is constant and equal to 1. Furthermore, we applied the outflow boundary conditions in the x, y, and z directions.
We performed five different simulations of the barred galaxy and analysed its evolution for a set of different SN frequencies of fSN. As the SNe probability distribution and its rate, we use the (Schmid 1959) law in the form 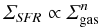 (8)where ΣSFR is the surface density of the star formation, Σgas is the surface density of gas, and n = 1 (Kennicutt 1998). The probability distribution of SN explosion in xy plane is computed according to the Schmidt-Kennicutt law. The probability distribution in z coordinate is described by the Gaussian distribution with the width of 40′′ corresponding to 1.14 kpc. Each SN remnant is represented by aspherically symmetric Gaussian profile with the radius . In all models we assume that 10% of of the SN kinetic energy output is converted into the CR energy, while the thermal energy from SNe explosions was neglected. In some of the models weak and randomly oriented magnetic vector potentials were also injected during SNe explosions. Following Jackson (1999) (see also Hanasz et al. 2009b), the magnetic vector potential A of dipolar magnetic field produced by an individual SN explosion can be expressed as
(8)where ΣSFR is the surface density of the star formation, Σgas is the surface density of gas, and n = 1 (Kennicutt 1998). The probability distribution of SN explosion in xy plane is computed according to the Schmidt-Kennicutt law. The probability distribution in z coordinate is described by the Gaussian distribution with the width of 40′′ corresponding to 1.14 kpc. Each SN remnant is represented by aspherically symmetric Gaussian profile with the radius . In all models we assume that 10% of of the SN kinetic energy output is converted into the CR energy, while the thermal energy from SNe explosions was neglected. In some of the models weak and randomly oriented magnetic vector potentials were also injected during SNe explosions. Following Jackson (1999) (see also Hanasz et al. 2009b), the magnetic vector potential A of dipolar magnetic field produced by an individual SN explosion can be expressed as 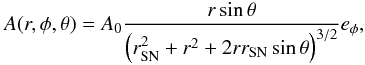 (9)where rSN is the radius of the SN remnant; r, θ, and φ are spherical coordinates; and A0 is the amplitude. Parameter rSN denotes the half-width of the Gaussian profile describing the distribution of injected CR energy. To obtain a model that is fully reproducible, a random distribution of SNe explosions is initialized using the same “seed”1.
(9)where rSN is the radius of the SN remnant; r, θ, and φ are spherical coordinates; and A0 is the amplitude. Parameter rSN denotes the half-width of the Gaussian profile describing the distribution of injected CR energy. To obtain a model that is fully reproducible, a random distribution of SNe explosions is initialized using the same “seed”1.
Following Ferrière (1998) the observed SN frequency for the Galaxy is 1/445 yr-1 for Type I and 1/52 yr-1 for Type II SNe. Taking both types of SNe into account, one explosion occurs every 47 years. In our simulations, we denoted the frequency of SN explosion fSN as equal to 25 when there is one SN in every 25 years. All parameters of our model are summarized in Table 1.
3. Results
3.1. General evolution for the reference model RM (S200)
To show the essential dynamical and magnetic features of the simulated barred galaxy, we present below a short description of the time evolution of the reference model RM (S200, fSN = 1/200 yr-1), which was published in Kulpa et al. (2011). We chose this model because, in our opinion, it is the representative example that we are going to refer to (see Table 1).
3.1.1. Polarization maps
In Fig. 1, we present the magnetic field evolution in time as seen in the polarized synchrotron emission for the reference model RM using the following time steps: t = 0.5, 1.5, 2.5, 3.75, 4.75, 6.0 Gyr. The polarization maps show the distribution of polarization angle and polarized intensity superimposed onto the gas column density during 6.0 Gyr of galactic evolution. All face-on and edge-on polarization maps have been smoothed down to the resolution of 40 pc. At first, the magnetic field maxima correspond to the gas density enhancements, where SN explosions are located, which can be easily seen at t = 0.5 Gyr (Fig. 1). At this time, there is a magnetic field in the gaseous arms, as well as in the central part of the galaxy. Figure 1 shows that prominent spiral arms appear in early stages of the simulation. A plausible explanation of the magnetic arms growing towards in inter-arm regions is a local dynamo action. However at polarization maps (Fig. 1) magnetic arms start to detach from the gaseous spirals and drift into the inter-arm region. For instance, at the time steps t = 2.5 Gyr or 4.75 Gyr (Fig. 1), the magnetic spiral is located in the inter-arm region, while at t = 6.0 Gyr (Fig. 1), it is less visible, because it merges with the inner edge of the adjacent arm.
 |
Fig. 1 Face-on and edge-on polarization maps at λ = 6.2 cm for selected times steps for the reference model RM (S200). Polarized intensity (contours) and polarization angles (dashes) are superimposed onto the column density plots. |
3.2. Dependence on the SN frequency
In Fig. 2 we present magnetic field structures of the following models (from left to right): S25, S50, and S100, and in Fig. 3 for the S200 and S500 models. In the top panel we present the distribution of toroidal magnetic field in vertical (top) and horizontal (bottom) slices and the face-on (bottom) and edge-on (top) polarization maps of the presented models, in the bottom panels.
In four experiments, S25, S50, S200, and S500, the magnetic field in vicinity of the disk and the halo of the barred galaxy was of even (quadrupole-like) symmetry. An odd (dipole-type) configuration of magnetic field with respect to the galactic plane appeared in all the models at an early stage of evolution. However, only in the S100 model (fSN = 1/100 yr-1) was such a configuration observed during the entire simulation time. The variable polarity of magnetic field apparent in the horizontal slice showing model S100 is caused by the corrugated surface dividing the regions of positive and negative azimuthal magnetic fields.
Forming magnetic arms could be observed in the case of S200 and S500 (see Fig. 3, left and right panels), as well as S50 and S100 (see Fig. 2, middle and right panels). The polarization vectors in the edge-on maps revealed the so-called X-shaped structure in all the experiments (see Figs. 2 and 3).
In the S25 model, with the highest SN activity (fSN = 1/25 yr-1), the initial random toroidal magnetic field component evolved towards well-ordered structures only in the bar region. At the time t = 4.5 Gyr (Fig. 2, the left top panel), the large-scale magnetic field was of even (quadrupole like) parity with respect to the disk mid-plane. Model S25 has weaker field strength, which is presumably due to the high star formation rate applied in this model. The high SN rate increases the efficiency of the dynamo, but only up to a certain maximum value. Above this value the losses caused by galactic winds are greater than the rate of generation in the dynamo process. In fact, the amplification of magnetic field only occurs in the bar region. The lack of magnetic arms is also apparent in the polarization maps (Fig. 2 bottom right). Characteristic for this model is strong concentration of gas in the galactic centre. Therefore star formation, CR energy density, and magnetic field strongly contrast with the remaining parts of the disk.
In Fig. 4 we show the face-on (bottom panel) and edge-on maps (top panel) of Faraday rotation measures RM for all the experiments S25, S50 , S100 , S200, and S500, at the time 4 Gyr. The Faraday rotation measure RM is proportional to the product of the thermal electron density ne and the line-of-sight component B|| of a regular magnetic field, integrated over the path length L: 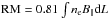 . Negative RM (face-on maps) in bar can be observed in two models S25 (about –680 rad m-2) and S200 (about –440 rad m-2). In the S200 model, we can also see a positive RM about 30 rad m-2 in spiral arms. A negative RM means that the line-of-sight component of magnetic field points away from us. In the models S50 (about 860 rad m-2), S100 (about 160 rad m-2), and S500 (about 35 rad m-2), we find a positive RM in the bar and a negative RM in the spiral arms. However, a different sequence of random numbers used second time in model S100 leads to quadrupole magnetic field configurations (see Fig. 4; Model S100 NEW). This showed that observed magnetic configurations in our simulations depend on the pseudo random number sequence of SN coordinates and the orientation of magnetic dipoles.
. Negative RM (face-on maps) in bar can be observed in two models S25 (about –680 rad m-2) and S200 (about –440 rad m-2). In the S200 model, we can also see a positive RM about 30 rad m-2 in spiral arms. A negative RM means that the line-of-sight component of magnetic field points away from us. In the models S50 (about 860 rad m-2), S100 (about 160 rad m-2), and S500 (about 35 rad m-2), we find a positive RM in the bar and a negative RM in the spiral arms. However, a different sequence of random numbers used second time in model S100 leads to quadrupole magnetic field configurations (see Fig. 4; Model S100 NEW). This showed that observed magnetic configurations in our simulations depend on the pseudo random number sequence of SN coordinates and the orientation of magnetic dipoles.
 |
Fig. 2 Top panels: distribution of toroidal magnetic field in vertical and horizontal slices through the disk centre for three models: S25 (left panel), S50 (middle panel), and S100 (right panel). Red represents regions with positive toroidal magnetic field, blue with negative, while unmagnetized regions are white. To enhance weaker magnetic field structures in the outer galactic disk (e.g., magnetic arms), the colour scale in the magnetic field maps is saturated. Bottom panels: face-on and edge-on polarization maps for selected time steps for three models: S25 (left panel), S50 (middle panel), and S100 (right panel). Polarized intensity (contours) and polarization angles (dashes) are superimposed onto the column density plots. |
 |
Fig. 3 Top panels: distribution of toroidal magnetic field in vertical and horizontal slices through the disk centre for models: S200 (left panel) and S500 (right panel). Red represents regions with positive toroidal magnetic field, blue with negative, while unmagnetized regions are white. To enhance weaker magnetic field structures in the outer galactic disk (e.g., magnetic arms), the colour scale in the magnetic field maps is saturated. Bottom panels: face-on and edge-on polarization maps for the selected time steps for two models: S200 and S500. Polarized intensity (contours) and polarization angles (dashes) are superimposed onto the column density plots. |
 |
Fig. 4 Faraday rotation maps for selected times steps for five models: S25 (top left panel), S50 (top middle panel), S100 (top right panel), S200 (bottom left panel), S500 (bottom middle panel), and S100 NEW (bottom right panel) at the time 4.5 Gyr. The red area denotes the positive RM and blue area denotes the negative RM. |
 |
Fig. 5 Evolution of total magnetic energy EB (top panel) and of mean azimuthal flux Bφ (bottom panel) for different values of SN frequency fSN. Both quantities are normalized with respect to the saturation value. |
 |
Fig. 6 Distribution of polarized intensity and B-vector orientations for the reference model RM (S200) superimposed onto the gas density at λ = 6.2 cm in the frame of azimuthal angle in the disk and ln(r). The map has been smoothed down to the resolution of 40′′. |
In Fig. 5, the evolutions of the total flux (bottom panel) of azimuthal magnetic field component and of the total magnetic field energy (top panel) for all the models are shown. The time evolution of magnetic energy and magnetic flux are shown in Fig. 5. Magnetic energy is summed over the whole computational volume. Magnetic flux is calculated through to the vertical plane extending from the disk axis to the vertical edge of the domain. Both are normalized with respect to the values achieved at the end of the simulations. It is apparent that a very similar exponential growth takes place for all of them. The fastest amplification of total magnetic field is observed for the model with an intermediate supernova rate, S50. For the S25 model, we got a bit longer amplification time. In both cases, the magnetic field reaches its saturation state approximately at the time t ~ 3.1 − 3.3 Gyr. The equipartition in the S100 and S200 models is achieved approximately 1 Gyr later than in the S25 and S50 models. For the S500 model, with the lowest SN rate, the magnetic field energy attains its saturation value at time t ~ 5.5 Gyr. The ultimate saturation levels of magnetic flux are lower than in the case of total magnetic energy. The e-folding times of magnetic flux growth deduced from the righthand panel of Fig. 5 are respectively for model S25, 194 Myr for model S50 (the fastest amplification), for model S100, 300 Myr for model S200, and 360 Myr for model S500 (see Table 2). It can be noticed that by varying the frequency of SNe explosions, one does not get any significantly different results, so we found that after 1 Gyr, the supplied dipole magnetic field from the supernova remnants was negligible in comparison with the field generated by the dynamo. This fact could account for the narrow interval of the observed values of magnetic field intensity in morphologically different galaxies. In fact, in all the simulations, two phases of increasing magnetic flux can be distinguished. The first one starts at the beginning of calculations and lasts until time t ~ 2.0 Gyr (bottom panel in Fig. 5). During that period, the magnetic flux reverses its sign, and its absolute value varies randomly around the exponential curve. These variations are associated with transformation of magnetic field structures, that is in all the models during this time, the initial random toroidal magnetic field component evolves, forming large-scale magnetic structures with odd symmetry. On the other hand, after time t ~ 2.0 Gyr the total azimuthal flux stops to reverse. Then the toroidal magnetic field becomes almost regular and reversals, if any, are very weak (see top right and middle panels in Fig. 2). The only exception is the S100 model, for which variations in magnetic flux, as well as reversals of toroidal magnetic field component, are visible throughout the entire simulation time. These results show that the magnetic field amplification in barred galaxies is relatively insensitive to the value of SN rate, which means that the CR-driven dynamo process is efficient for a wide range of SN activity.
In Table 2, the maximum magnetic field strengths in the magnetic arms (taken at the coordinate points belonging to the magnetic arm regions) for all the models are presented. The highest values of magnetic field were reached for the models with weak SN activity. The maximum magnetic field in magnetic arms (9.5 μG) was obtained in the S200 model. Similar values were observed for the models S100 () and S500 (). For the models with strong SN activity, the maximum field in magnetic arms was weaker, about in model S50 or almost none () in the case of model S25.
For model S25, with the strongest magnetic field within the bar, the lowest value of mean magnetic field became averaged over all coordinate points belonging to the bar region was obtained (see Table 2). This is quite possible for a very low magnetic field (of the order of ) in the outer part of the disk, located outside the corotation radius. On the other hand, for the S200 model, the mean magnetic field had the highest value . In the S200 model the value of the magnetic field in the spiral structure area averaged in all coordinate points belonging to the spiral arms (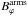 ) was about 9.5 . For models S50, S100, and S500, the values of mean magnetic field were very similar ~. The averaged mass outflow rate grew with increasing SN frequency (Table 2). The mass outflow through the upper and lower boundaries was calculated at each time step of calculations, and then the mass flux fz = ρvz was integrated over the surface area at the upper and lower domain boundaries for all the steps. Actually, in the S25 model with the highest SN rate, the overall rate of the mass outflow was , while for the S500 model with the lowest SN activity, the overall rate of mass outflows was just .
) was about 9.5 . For models S50, S100, and S500, the values of mean magnetic field were very similar ~. The averaged mass outflow rate grew with increasing SN frequency (Table 2). The mass outflow through the upper and lower boundaries was calculated at each time step of calculations, and then the mass flux fz = ρvz was integrated over the surface area at the upper and lower domain boundaries for all the steps. Actually, in the S25 model with the highest SN rate, the overall rate of the mass outflow was , while for the S500 model with the lowest SN activity, the overall rate of mass outflows was just .
3.2.1. Pitch angles
To compare pitch angles of magnetic and gaseous arms, the results are shown in the coordinate system of azimuthal angle and ln(r) (r being the galactocentric distance). In this case, the logarithmic spiral is represented by a straight line inclined by a relevant pitch angle. In Fig. 6, the gas density (integrated along the line of sight) with overlaid contours of polarized intensity and B-vectors for four time steps () are shown. At the beginning at , we can see that polarized structures form along the inner edges of spiral arms observed in actual galaxies that typically correspond to dust lanes. Later on, we observe an obvious drift of magnetic field arms into the inter-arm region (between and r = 9.5 kpc). Initially we find that (t = 0.75 Gyr, Fig. 6) magnetic and gaseous arms possess similar pitch angles of ~−13°. However, at later times magnetic structures move to the inter-arm region and significantly decrease their pitch angles. Moreover, the estimated mean pitch angle (averaged over azimuthal angle and radius in the galaxy’s plane) changes only slightly during the evolution of the galaxy, ranging between −7° and −8° of the slope arms.
4. Discussion
We present a series of simulations of CR-driven dynamo in barred galaxies for a wide range of SN rates. In most of our models, the regular magnetic field is axisymmetric (ASS topology, quadrupole topology). A distinct ASS mode is also observed in the actual galaxies, M31 (Sofue & Takano 1981) and IC 342 (Krause et al. 1989). The ASS symmetry in the presented numerical models is not surprising, since the axisymmetric mode can be excited most readily by a mean-field dynamo process (Krause 2003). This shows that observed magnetic configurations in our simulations depend on the pseudo-random number sequence determining SN coordinates and orientation of magnetic dipoles.
In the S25, S50, S200, and S500 models, the toroidal magnetic field component has the same direction above and below the galactic disk. This configuration corresponds to the even (quadrupole-type) symmetry of magnetic fields in galaxies. This picture is supported by theoretical studies (e.g., Ruzmaikin et al. 1988), by observational evidence (e.g., Beck 2009; Heesen et al. 2009), as well as by a number of numerical investigations (e.g., Brandenburg et al. 1993). The quadrupole-like symmetry was also obtained by Hanasz et al. (2009b), who studied CR driven dynamos in the case of axisymmetric galactic gravitational potential.
The results presented in this work confirm that a CR-driven dynamo can produce odd dipolar symmetries of magnetic fields in barred galaxies. In the case of S100 model, the toroidal magnetic field component has a different direction above and below the disk plane, which indicates an odd (dipole-type) configuration of magnetic field with respect to the galactic plane. The odd symmetry of the magnetic field is not the preferred configuration in the disk geometry (Moss et al. 2010), while it has been found in some galaxies (e.g., in NGC 4631, Krause 2003).
Magnetic arms between the gaseous spiral and the bar have been observed in most of the barred galaxy simulations. The drift of magnetic arms is caused by the same mechanism as proposed by Otmianowska-Mazur et al. (2002), Kulesza-Żydzik et al. (2009); Kulpa-Dybeł et al. (2010, 2011), and Kim & Stone (2012). It could be explained as follows initially the gravitational potential of the bar rotates faster than the gas outside the corotation radius, generating spiral arms. The magnetic field present in the galactic disk is advected with the gas velocity. In particular, the magnetic field produced by disturbances within the arms drifts with the gas velocity and, after some time runs into the next arm (see Kulesza-Zydzik et al. 2010, and references therein). Only in one model, S25, can no magnetic arms be discerned either in the gaseous arms or in the inter-arm area (right top and bottom panels in Fig. 2). The lack of magnetic arms can be traced back to the very high star formation rate (fSN = 1/25 yr-1) applied in this model. If SNe explosions generate a random magnetic field in a continuous and violent manner, the outflow of the random field component into the z direction advects the magnetic field in the outer part of the galaxy, so it cannot be transformed into a regular field. In that case the polarized magnetic field only appears in the bar region. The results obtained for the S25 model resemble the radio polarization structure observed in barred galaxies, for example in NGC 986 (Beck et al. 2002). In this barred galaxy, the polarized emission was only found in the inner bar.
Overview of the obtained parameters for the barred galaxy models.
The mass outflow rate by galactic winds in the barred galaxy simulations ranged from 0.6 to 4.7. The overall rate of mass outflow grew with increasing SN activity in the galactic disk. The galactic-scale outflows (galactic winds) from galactic disks are common phenomena that can be observed both in the nearby galaxies (Tüllmann et al. 2006) and in the high-redshift Universe (Tapken et al. 2007). From observations, one of the main sources of galactic winds are SNe explosions (e.g., Matsubayashi et al. 2009). According to the review of galactic winds by Bland-Hawthorn et al. (2007), the mass outflow rate in other observed spiral galaxies ranges between 0.1 and 10 . The authors find that the outflow rate increased with increasing star formation rate. The results presented in this paper support this statement and fit the observed values perfectly.
In the barred galaxy simulations, there is apparent dependence of the magnetic field growth rate on the SN rate (Beck 2012). The overall e-folding times presented in this work are comparable to the values obtained in other numerical experiments of CR driven dynamo. Hanasz et al. (2006, 2009a) performed shearing-box simulations of a CR driven dynamo and find that the e-folding timescale in normal spiral galaxies is about 150 − 250 Myr. Very similar results are presented by Gressel et al. (2008) who made galactic dynamo simulations in the box model, taking the turbulent ISM driven by multiple clustered SNe explosions into account.
In the absence of CRs, only a 15-fold growth of the magnetic energy and a few times increase in azimuthal flux was observed (Kulesza-Żydzik et al. 2009, Fig. 2)
5. Conclusions
The following conclusions can be drawn from our investigations:
-
1.
The polarized radio emission found in the face-on syntheticpolarization maps indicates that the CR driven dynamo can beresponsible for various magnetic structures discerned in actualobservations of barred galaxies, such as the polarized emissionthat is at its strongest in the central part of the galaxy where the bar ispresent, and the polarized emission from the ridges marks the dustlanes along the leading edges of the bar.
-
2.
In the case of simulated barred galaxies, a drift of magnetic arms can be observed during the entire simulation time in most of the experiments.
-
3.
The synthetic edge-on radio maps of polarized emission show that the CR driven dynamo can reproduce the vertical magnetic field structures observed in edge-on galaxies (so-called X-type).
-
4.
In barred galaxies, the large-scale magnetic field grows exponentially on a timescale comparable to what is obtained for normal spirals. The fastest amplification of magnetic fields was obtained for the S50 model with a SN frequency of 1/50 yr-1 and with the corresponding e-folding time of 194 Myr.
-
5.
For simulated barred galaxies, there is no significant dependence on the SN rate. We found that after about 1 Gyr from the beginning of evolution of the modelled galaxies, the total magnetic energy did not depend on how much of magnetic field energy from the supernovae remnants we had introduced.
-
6.
According to theoretical studies, the quadrupole-like symmetry of magnetic field is preferred in numerical studies of the galactic dynamo. The even symmetry of magnetic field with respect to the mid-plane was found in most of barred galaxy simulations. Just one model involved the odd symmetry of magnetic field.
Our simulations of barred galaxies showed that the CR driven dynamo is able to efficiently amplify magnetic energy, as well as magnetic flux. Furthermore, we demonstrated that the CR driven dynamo can account for a number of observational magnetic features, such as magnetic arms in the inter-arm regions and magnetic arms observed sometimes along the gaseous arms in barred galaxies.
Acknowledgments
This work was supported by Polish grant NCN UMO-2011/03/B/ST9/01859, UMO-2012/07/B/ST9/04404 and N203511038. The project has been (partially) supported by the grant of the Polish Ministry of Science and Higher Education number 7150/E-338/M/2013. The computations were performed on the GALERA in TASKn Academic Computer Centre in Gdansk and on the Zeus in Academic Computer Centre CYFRONET AGH in Kraków.
References
- Beck, R. 2009, Astrophys. Space Sci. Trans., 5, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, R. 2012, Space Sci. Rev., 166, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, R., Shoutenkov, V., Ehle, M., et al. 2002, A&A, 391, 83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, R., Brandenburg, A., Moss, D., Shukurov, A., & Sokoloff, D. D. 1996, ARA&A, 34, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Berezinski, V. S., Bulanov, S. V., Dogiel, V. A., Ginzburg, V. L., & Ptuskin, V. S. 1990, Astrophysics of cosmic rays (Amsterdam: North-Holland) [Google Scholar]
- Bland-Hawthorn, J., Veilleux, S., & Cecil, G. 2007, Ap&SS, 311, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Booth, C. M., Agertz, O., Kravtsov, A. V., & Gnedin, N. Y. 2013, ApJ, 777, L162 [CrossRef] [Google Scholar]
- Brandenburg, A., Donner, K. J., Moss, D., et al. 1993, A&A, 271, 36 [NASA ADS] [Google Scholar]
- Chyży, K. T., Weżgowiec, M., Beck, R., & Bomans, D. J. 2011, A&A, 529, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dubois, Y., & Teyssier, R. 2010, A&A, 523, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferriére, K. 1998, ApJ, 497, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Gaensler, B. M., Haverkorn, M., Staveley-Smith, L., et al. 2005, Science, 307, 1610 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gressel, O., Elstner, D., Ziegler, U., & Rüdiger, G. 2008, A&A, 486, 35 [Google Scholar]
- Hanasz, M., & Lesch, H. 2003, A&A, 412, 331 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hanasz, M., Kowal, G., Otmianowska-Mazur, K., & Lesch, H. 2004, ApJ, 605, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Hanasz, M., Kowal, G., Otmianowska-Mazur, K., & Lesch, H. 2006, Astron. Nachr., 327, 469 [Google Scholar]
- Hanasz, M., Otmianowska-Mazur, K., Kowal, G., & Lesch, H. 2009a, A&A, 498, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hanasz, M., Wóltański, D., & Kowalik, K. 2009b, ApJ, 706, 155 [Google Scholar]
- Heesen, V., Krause, M., Beck, R., & Dettmar, R. 2009, A&A, 506, 1123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hummel, E., & Beck, R. 1995, A&A, 303, 691 [NASA ADS] [Google Scholar]
- Hummel, E., Beck, R., & Dahlem, M. 1991, A&A, 248, 23 [NASA ADS] [Google Scholar]
- Jackson, J. D. 1999, Classical Electrodynamics, 3rd edn. (New York: Wiley) [Google Scholar]
- Kennicutt, R. J. 1998, ApJ, 498, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, W.-T., & Stone, J. 2012, ApJ, 751, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Kowal, G., Lazarian, A., Vishniac, E. T., & Otmianowska-Mazur, K. 2009, ApJ, 700, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Kowal, G., Lazarian, A., Vishniac, E. T., & Otmianowska-Mazur, K. 2012, Nonlinear Processes Geophys., 19, 297 [Google Scholar]
- Kowalik, K., & Hanasz, M. 2007, YSC’14 Proc. of Contributed Papers, eds. G. Ivashchenko, & A. Golovin, 49 [Google Scholar]
- Krause, M. 2004, in The Magnetized Interstellar Medium, eds. B. Uyaniker, W. Reich, & R. Wielebinski, Conf. Proc., Antalya [Google Scholar]
- Krause, M. 2003, in Radio Studies of Galactic Objects, Galaxies and AGNs, eds. J. L. Han, X. H. Sun, J. Yang, & R. Wielebinski, Acta Astron. Sin., 44, 123 [Google Scholar]
- Krause, M., Hummel, E., & Beck, R. 1989, A&A, 217, 4 [NASA ADS] [Google Scholar]
- Kulesza-Żydzik, B., Kulpa-Dybeł, K., Otmianowska-Mazur, K., Kowal, G., & Soida, M. 2009, A&A, 498, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kulesza-Żydzik, B., Kulpa-Dybeł, K., Otmianowska-Mazur, K., Soida, M., & Urbanik, M. 2010, A&A, 522, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kulpa-Dybeł, K., Kowal, G., Otmianowska-Mazur, K., Lazarian, A., & Vishniac, E. T. 2010, A&A, 514, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kulpa-Dybeł, K., Otmianowska-Mazur, K., Kulesza-Żydzik, B., et al. 2011, ApJ, 733, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Lazarian, A., & Vishniac, E. T. 1999, ApJ, 517, 700 [NASA ADS] [CrossRef] [Google Scholar]
- Matsubayashi, K., Sugai, H., Hattori, T., et al. 2009, ApJ, 701, 1636 [NASA ADS] [CrossRef] [Google Scholar]
- Moss, D., Sokoloff, D., Beck, R., & Krause, M. 2010, A&A, 512, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Otmianowska-Mazur, K., Elstner, D., Soida, M., & Urbanik, M. 2002, A&A, 384, 48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parker, E. N. 1992, ApJ, 401, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Quashnock, J. M., Loeb, A., & Spergel, D. N. 1989, ApJ, 344, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Rees, M. J. 1987, Roy. Astron. Soc. Quant. J., 28, 197 [Google Scholar]
- Ruzmaikin, A. A., Shukurov, A. M., & Sokoloff, D. D. 1988, Magnetic Fields of Galaxies (Dordrecht: Kluwer) [Google Scholar]
- Ryu, D., Kim, J., Hong, S. S., & Jones, T. W. 2003, ApJ, 589, 338 [NASA ADS] [CrossRef] [Google Scholar]
- Schlickeiser, R., & Lerche, I. 1985, A&A, 151, 151 [NASA ADS] [Google Scholar]
- Schmidt, M. 1959, ApJ, 129, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Siejkowski, H., Soida, M., Otmianowska-Mazur, K., Hanasz, M., & Bomans, D. J. 2010, A&A, 510, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Siejkowski, H., Soida, M., Otmianowska-Mazur, K., Hanasz, M., & Bomans, D. J. 2011, IAU Symp., 274, 389 [NASA ADS] [Google Scholar]
- Sofue, Y., & Takano, T. 1981., PASJ, 33, 47 [Google Scholar]
- Sokoloff, D., Shukurov, A., & Krause, M. 1992, A&A, 264, 396 [NASA ADS] [Google Scholar]
- Strong, A. W., Moskalenko, I. V., & Ptuskin, V. S. 2007, Annu. Rev. Nucl. Part. Sci., 57, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Subramanian, K. 2010, Astron. Nachr., 331, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Syrovatskii, S. 1970, in Interstellar Gas Dynamics, ed. H. Habing (Dordrecht, D. Reidel Pub. Co.), IAU Symp., 39, 192 [Google Scholar]
- Tapken, C., Appenzeller, I., Noll, S., et al. 2007, A&A, 467, 63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tüllmann, R., Pietsch, W., Rossa, J., Breitschwerdt, D., & Dettmar, R.-J. 2006, A&A, 448, 43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Turner, M. S., & Widrow, L. M. 1988, Phys. Rev. D, 37, 2743 [NASA ADS] [CrossRef] [Google Scholar]
- Widrow, L. M. 2002, Rev. Mod. Phys., 74, 775 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, H., O’Shea, B. W., Collins, D. C., et al. 2008, ApJ, 688, L57 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Face-on and edge-on polarization maps at λ = 6.2 cm for selected times steps for the reference model RM (S200). Polarized intensity (contours) and polarization angles (dashes) are superimposed onto the column density plots. |
| In the text | |
 |
Fig. 2 Top panels: distribution of toroidal magnetic field in vertical and horizontal slices through the disk centre for three models: S25 (left panel), S50 (middle panel), and S100 (right panel). Red represents regions with positive toroidal magnetic field, blue with negative, while unmagnetized regions are white. To enhance weaker magnetic field structures in the outer galactic disk (e.g., magnetic arms), the colour scale in the magnetic field maps is saturated. Bottom panels: face-on and edge-on polarization maps for selected time steps for three models: S25 (left panel), S50 (middle panel), and S100 (right panel). Polarized intensity (contours) and polarization angles (dashes) are superimposed onto the column density plots. |
| In the text | |
 |
Fig. 3 Top panels: distribution of toroidal magnetic field in vertical and horizontal slices through the disk centre for models: S200 (left panel) and S500 (right panel). Red represents regions with positive toroidal magnetic field, blue with negative, while unmagnetized regions are white. To enhance weaker magnetic field structures in the outer galactic disk (e.g., magnetic arms), the colour scale in the magnetic field maps is saturated. Bottom panels: face-on and edge-on polarization maps for the selected time steps for two models: S200 and S500. Polarized intensity (contours) and polarization angles (dashes) are superimposed onto the column density plots. |
| In the text | |
 |
Fig. 4 Faraday rotation maps for selected times steps for five models: S25 (top left panel), S50 (top middle panel), S100 (top right panel), S200 (bottom left panel), S500 (bottom middle panel), and S100 NEW (bottom right panel) at the time 4.5 Gyr. The red area denotes the positive RM and blue area denotes the negative RM. |
| In the text | |
 |
Fig. 5 Evolution of total magnetic energy EB (top panel) and of mean azimuthal flux Bφ (bottom panel) for different values of SN frequency fSN. Both quantities are normalized with respect to the saturation value. |
| In the text | |
 |
Fig. 6 Distribution of polarized intensity and B-vector orientations for the reference model RM (S200) superimposed onto the gas density at λ = 6.2 cm in the frame of azimuthal angle in the disk and ln(r). The map has been smoothed down to the resolution of 40′′. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


