| Issue |
A&A
Volume 574, February 2015
|
|
|---|---|---|
| Article Number | A38 | |
| Number of page(s) | 17 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201424582 | |
| Published online | 21 January 2015 | |
TRAPPIST monitoring of comet C/2012 F6 (Lemmon)⋆
Institut d’Astrophysique et Géophysique, Université de Liège,
allée du 6 Août 17,
4000
Liège,
Belgium
e-mail:
cyrielle.opitom@ulg.ac.be
Received: 10 July 2014
Accepted: 8 October 2014
We report the results of the long-term narrowband photometry and imaging monitoring of comet C/2012 F6 (Lemmon) with the robotic TRAPPIST telescope (La Silla Observatory). Observations covered 52 nights pre- and post-perihelion between December 11, 2012, and June 11, 2013 (perihelion: 24 March, 2013). We followed the evolution of the OH, NH, CN, C3, and C2 production rates computed with the Haser model as well as the evolution of the A(θ)fρ parameter as a proxy for the dust production. All five gas species display similar slopes for the heliocentric dependence. An asymmetry about perihelion is observed, the rate of brightening being steeper than the rate of fading. The chemical composition of the comet’s coma changes slightly along the orbit: the relative abundance of C2 to CN increases with the heliocentric distance (r) below −1.4 au and decreases with r beyond 1.4 au while the C3-to-CN ratio is constant during our observations. The behavior of the dust is different from that of the gas, the slope of the heliocentric dependence becoming steeper in early February, correlated to a change in the visual lightcurve slope. However, the dust color does not vary during the observations. The application of several enhancement techniques on the images revealed structures in the CN, C3, and C2 images. These features imply the existence of one or several active zone(s) on the comet nucleus. The shape of the structures is similar in these three filters and changes from a roughly hourglass shape in December and January to a corkscrew shape in February and March. The structures in the continuum filters (sampling the dust) are not correlated to those observed for the gas. During several full nights in February, we observed changes in the CN and C2 structures that repeated periodically because of the nucleus rotation, our derived rotational period being of 9.52 ± 0.05 h.
Key words: comets: individual: C/2012 F6 (Lemmon) / techniques: photometric
Full Tables 2, 4, 6 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/574/A38
© ESO, 2015
1. Introduction
Comets are among the most pristine bodies in the solar system. Their ices contain information about the conditions prevailing at the time of the formation of the solar system and the accretion of planetesimals. Dynamical models suggest that comets formed in a range of environments in the protoplanetary disk and were then ejected into two main reservoirs, the Kuiper belt and the Oort Cloud, where they are currently stored (Gomes et al. 2005). Surveys at different wavelengths, in the radio domain (Crovisier et al. 2009), in the infrared (Bockelée-Morvan et al. 2004), and in the optical (A’Hearn et al. 1995; Fink 2009) revealed chemical diversity among comets. At this time the larger optical database contains about 150 comets and reveals as many as ten compositional groupings, some of them possibly related with the comets’ place of formation (Schleicher et al. 2007). However, extensive data sets on a single comet over a wide range of heliocentric distances and on both sides of perihelion are still scarce, especially for Oort Cloud comets. These data sets could bring important information about the homogeneity of ice and dust mixing in cometary nuclei and a better understanding of the pristine or evolutionary origin of chemical diversity among comets. The purpose of this paper is to present one of the most extended sets of homogeneous observations of a comet – C/2012 F6 (Lemmon), a dynamically old comet.
TRAPPIST (TRAnsiting Planets and Planetesimals Small Telescope) is a 60 cm robotic telescope installed at ESO La Silla Observatory (Jehin et al. 2011). It is almost exclusively devoted to the detection and characterization of exoplanets and to the study of comets and other small bodies of the solar system. The amount of observing time on this telescope and the set of narrowband cometary filters permanently mounted make it a perfect instrument for the study of comets activity and chemical composition evolution. Since its installation during the year 2010, TRAPPIST already observed more than 20 comets with narrowband filters, and we expect it to observe ten more comets every year. Our goal is to gather a sample of at least 30 Jupiter family and Oort Cloud comets observed with the same instrument and reduced with a standard procedure, allowing us to investigate chemical composition differences among comets and their origin. When possible we perform long-term monitoring of bright comets along an important part of their orbit. This allows us to study how their activity – its amount, its morphology, and its composition – evolve with the heliocentric distance.
Comet C/2012 F6 (Lemmon) was discovered by A. R. Gibbs on March 23, 2012 at the Mount Lemmon Observatory, when it was at approximately 5 au from the Sun. It remained weak until it was lost because of Sun conjunction in June 2012. When the comet was recovered in October it had brightened by −4 mag, reaching mag 15. In January and February 2013, the comet was observable several hours per night from the southern hemisphere. Comet Lemmon follows a highly eccentric and inclined orbit with a perihelion distance of 0.73 au (March 24, 2013). It is a long-period comet (around 10000 years) originating from the Oort Cloud that has already entered the inner solar system many times. In December 2012, the comet was unexpectedly bright, allowing us to start an intensive monitoring of its activity through narrowband filters.
In Sect. 2 we describe our data set and the detailed reduction procedures. The next sections present the results of the evolution of comet Lemmon gas and dust activity with the heliocentric distance. The chemical composition is studied in Sect. 3.3 and the determination of the nucleus rotation period from morphological study is explained at Sect. 3.4. The results are summarized and discussed in the last section.
2. Observations and data reduction
We used the TRAPPIST telescope at ESO-La Silla Observatory (Jehin et al. 2011) to perform a long-term monitoring of comet Lemmon. The detector mounted on the telescope is a thermoelectrically-cooled 2K × 2K FLI Proline CCD camera with a field of view of 22′ × 22′. The high sensitivity of the Fairchild 3041 detector in the blue part of the spectrum and the fused silica camera window allow us to observe most of the emission bands in the coma of comets including OH at 310 nm.
Cometary OH, NH, CN, C3, and C2 emission bands and four emission free regions were isolated using a set of HB narrowband filters (see Table 1 and Farnham et al. 2000 for filters characteristics). These filters were lent by David Schleicher from Lowell Observatory. A complete filter characterization was made in 2009 at La Silla Observatory with a monochromator to ensure their quality. The resulting measurements, presented in Table 1, are in good agreement with the nominal filters characteristics given in Farnham et al. (2000). Broadband B, V, R, and Ic Johnson-Cousins (Bessel 1990) filters have also been used regularly.
Narrowband filters characteristics: central wavelength (CWL), full width at half maximum (FWHM), and peak transmission (T%).
One thousand three hundred and fifty-eight images of comet Lemmon were collected on 52 nights spanning over 6 months both pre- and post-perihelion. We started the observations as soon as the comet was bright enough on December 11, 2012, at about 2 au from the Sun, and we observed two to three times a week until January 13, 2013. A technical problem suspended the observations between January 13 and February 7. We were able to follow the comet pre-perihelion until it was too close to the Sun on March 4. We then recovered it on April 29 and observed it until June 11 at a heliocentric distance of 1.6 au, after which the comet was too far north to be observed from La Silla. Exposure times ranged from 15 to 90 s for broadband filters and from 60 to 480 s for narrowband filters. Most observing nights were photometric and cloudy nights were discarded from the final data set. Observational circumstances and number of exposures for each filter are given in Table 2.
Calibration followed standard procedures using frequently updated master bias, flat and dark frames. The frequent observations of the narrowband photometric standard stars listed by Farnham et al. gave the extinction coefficients and the zero points of the system. Those authors provide the additional coefficients necessary to transform the count rates into spectral radiance and molecular band radiance. These coefficients are proper to the standard system, but the characteristics of our filters are sufficiently close to allow their use without correction.
The next step was the removal of the sky contribution which is always problematic for extended objects. In this case the TRAPPIST field of view was always wide enough to determine the sky contribution from parts of the image that do not contain a cometary contribution. We determined the closest distance from the coma optocenter where each image was free of cometary emission, and measured the median sky level at this nucleocentric distance. The standard deviation of the measured sky values was used to estimate the error on sky subtraction.
The main uncertainties in the molecular production rates and their dust equivalent (the so-called Afrho) presented in Sect. 3 come from the absolute flux calibration and the sky background subtraction. A long-term analysis of our standard stars observations showed that the scatter in extinction coefficient determined from different nights is around 5%. This is almost negligible compared to the sky level uncertainty when the target is observed at low airmass, even though the effect of extinction coefficients uncertainty becomes significant at high airmasses. We estimated the 3σ level uncertainty on the sky background value and used it to compute the error on production rates due to the sky subtraction. As a result, errors given in the following sections are a quadratical combination of sky background and extinction coefficient uncertainties.
All TRAPPIST images are reduced following the same procedure, providing highly homogeneous data sets for the study of the evolution of comets’ activity along their orbits as well as for comparison of chemical composition differences among comets. Tests on the reproducibility of our measurements in the case of comet Lemmon showed that the agreement between identical consecutive measurements is within a few percents.
Observational circumstances of comet C/2012 F6 (Lemmon).
3. Data analysis and results
In this section we present the results of comet Lemmon monitoring. We show the evolution of both gas and dust activity as well as the evolution of the comet’s chemical composition and morphology.
3.1. Gas production rate computation and evolution
We compute the gas production rates by adjusting a radial coma brightness model on the observed radial profile for each individual image from each filter. After determining the comet’s optocenter (by using the Iraf task imcntr), we derive median radial brightness profiles from gas and dust images. The use of a median profile eliminates the contribution of background stars. Even though OH, NH, CN, C3, and C2 narrowband filters have been carefully designed to isolate specific molecular emissions, they are contaminated by the underlying sunlight reflected by the dust, especially in the case of C3 and C2 filters. The dust subtraction is thus a very important step prior to computing reliable gas production rates. We use images of the comet in the BC filter to obtain the dust radial profile, because it is less contaminated by cometary gas emission than GC or UC filters and has a more central wavelength than RC (see Farnham et al. 2000). We scale the dust radial profile depending on the contamination in each gas filter and subtract it from the gas profile. Continuum frames used for the dust subtraction are usually taken during the same hour as the associated frame to avoid changes in the observing conditions or in the rotational state of the comet. If no BC image is available we use a GC image, but comparison of these two continuum filters for dust contamination removal showed that the error in the computed production rates is well within the error bars.
We analyzed the azimuthal distribution of intensity of OH, NH, CN, C3, and C2 in the coma. Even though features could be detected in some CN, C3, and C2 images (see Sect. 3.4), the radial profiles were not strongly dependent on the azimuthal direction, even when the structures were the most contrasted. The median radial profile used to compute the production rates is then representative of the entire coma radial intensity distribution.
The parent (LP) and daughter (LD) scalelengths used for the computation of OH, NH, CN, C3, and C2 production rates with the Haser model.
The gas production rates were computed by adjusting a Haser model to each brightness profile (Haser 1957). The Haser model considers the photodissociation of parent species into daughter and then grand-daughter species in a spherically symmetric coma. Even though some of its assumptions such as the existence of only one possible parent for each daughter species or the dissociation in a single step process are not physically realistic, the model reproduces quite well the observed brightness profiles in most cases. More realistic models such as vectorial model (Festou 1981) exist, but the Haser model allows an easy comparison between data sets from different observing conditions and instruments. This model has only two free parameters: the parent and daughter scalelengths, or lifetimes. Despite several studies aiming to determine Haser scalelengths, such as Newburn & Spinrad (1989), Cochran et al. (1992), Randall et al. (1992), or A’Hearn et al. (1995), these parameters remain the main source of uncertainty when determining production rates. The scaling at large heliocentric distances is especially problematic and the influence of solar activity on the lifetime of mother and daughter species is also poorly known. The most widely used Haser scalelengths are those from A’Hearn et al. (1995) (Table 3) and we chose to use it for this work in order to facilitate the comparison of comet Lemmon activity and composition with those from comets studied by A’Hearn et al. (1995) and others. As the comet Lemmon heliocentric distance (r) in our data set is smaller than 2 au, we scale scalelengths as r2, as is usually done. We use a constant velocity of 1 km s-1 for both parent and daughter species as considered in A’Hearn et al. (1995). Given that fluorescence efficiencies (g) depend on both heliocentric distance and velocity for some species, they must be calculated individually for each image. We obtained fluorescence efficiencies from Schleicher’s website1. These g values account for the Swings effect (Swings 1941).
 |
Fig. 1 Original images of comet C/2012 F6 (Lemmon) and the corresponding radial profiles for OH, NH, CN, C3, and C2. These images were taken on January 7, 2013, while the comet was 1.57 au from the Sun. We plotted the original radial profile (dark triangles), the radial profile obtained after dust subtraction (red circles), and the adjusted Haser model (black line). As comet Lemmon is relatively gaseous, the original radial profile and the dust-subtracted profile are mostly overlapping. The images are oriented north up and east left. The field of view is 22′ × 22′. |
We adjusted the Haser model to the observed radial profile at a physical distance of about 10 000 km in the coma. At this distance, the signal-to-noise ratio is usually still high and the influence of the dust contamination is lower. By adjusting the model directly on the radial profile instead of measuring the flux in a single aperture, we reduce aperture trends (variation of the production rates with the size of the aperture) often observed while computing production rates with the Haser model. Since the effect of the seeing and the instrumental PSF is limited to a few pixels around the nucleus and we adjust the profile at much larger distance, these effects are negligible. The adjustment of the radial profiles is illustrated in Fig. 1 for images taken on January 7, 2013. For OH, NH, and CN the original profile and the dust subtracted profile are almost overlapping since these filters are less contaminated by the dust than the C3 and C2 filters. For C3 and C2, even though the contamination is stronger, it is well corrected by the dust subtraction method, as can be seen in Fig. 1. Except for NH, the agreement between the observed radial profiles and the Haser model fitting shown in Fig. 1 is satisfactory. As the comet approached the Sun, the discrepancy between observed and modeled profile increased, probably because of the uncertainty in Haser scalelengths values, and affected the computed production rates. The largest discrepancy is observed for the NH radical because the scalelengths are poorly known. A sharp feature oriented in the direction opposite to the Sun is observed in the NH images. We identify this contamination as the 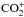 tail.
tail. 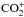 has a transition at 337.8 nm (O’dell et al. 1991) which is within the bandpass of the NH filter, but the contamination is in general faint.
has a transition at 337.8 nm (O’dell et al. 1991) which is within the bandpass of the NH filter, but the contamination is in general faint.
Nightly averages of gas production rates for comet C/2012 F6 (Lemmon).
The gas production rates have been computed from each frame taken in the gas filters and nightly means are given in Table 4. The evolution of comet Lemmon gas activity vs. heliocentric distance is summarized in Fig. 2. The comet activity rises as it approaches perihelion and then decreases after perihelion. As shown in Fig. 3, there is some dispersion in the production rates computed during the same night (at the same heliocentric distance). These variations larger than the error bars are observed for all the species and are attributed to the nucleus rotation (see Sect. 3.4). The detection in the images of jets whose position and orientation vary with the nucleus rotation further confirmed that the nightly variation was due to the nucleus rotation (see Sect. 3.4).
 |
Fig. 2 Logarithm of the OH, NH, CN, C3, and C2 production rates as a function of the heliocentric distance r (au). The x-axis is interrupted at perihelion (0.73 au). |
Each species’ evolution as a function of the heliocentric distance is represented on a log-log scale in Fig. 3. Pre-perihelion data are represented with full symbols and post-perihelion data with empty symbols. A least square linear fit has been performed for each radical to study the evolution of the production rates with the heliocentric distance. We made two separated fits for pre- (solid lines) and post-perihelion (dotted lines) data to point out asymmetries about perihelion. Even though the heliocentric range covered post-perihelion is shorter than pre-perihelion, it is sufficient to derive a slope for the heliocentric dependence of the post-perihelion production rates. The best pre- and post-perihelion slopes are overplotted on the data in Fig. 3.
Pre- and post-perihelion fitted power-law slopes for OH, NH, CN, C3, and C2 the heliocentric dependences of the production rates.
Examination of the power-law slopes given in Table 5 shows that the heliocentric dependence of the gas production rates is similar for all the species. There is an asymmetry about perihelion, the slope being steeper before than after perihelion and the production rates being in general higher after perihelion over the same distance, except for OH. A’Hearn et al. (1995) showed that the heliocentric dependence of the gas production rates strongly varies from comet to comet. The average trend for their comet sample is Q(gas) ∝ r-2.7. Pre-perihelion slope values for comet Lemmon from Table 5 are in good agreement with this average trend.
 |
Fig. 3 Logarithm of OH, NH, CN, C3, and C2 production rates of C/2012 F6 (Lemmon) as a function of the logarithm of the heliocentric distance (r). Pre-perihelion data points are represented with filled symbols and post-perihelion data points are represented with open symbols. The origin of the x-axis is perihelion. Solid lines are linear fits of the production rates variation with the pre-perihelion heliocentric distance. Dotted lines are the same for post-perihelion values. |
3.2. Dust: A(θ)fρ, spatial profiles and dust color
The use of narrowband continuum filters at four wavelengths allows us to make a study of the evolution of both dust production and properties along the orbit of the comet. We use the parameter A(θ)fρ first introduced in 1984 (A’Hearn et al. 1984) as a proxy for dust production: A is Bond albedo of the dust grains, θ is the phase angle, f the filling factor in the aperture, and ρ is the projected distance from the nucleus. The A(θ)fρ parameter presents the advantage of allowing easy comparison of dust production from comet to comet. This parameter is often relatively independent of the aperture size used for the observation as long as the dust production is in a steady state. We decided to systematically compute A(θ)fρ values at a distance of about 10 000 km from the nucleus because significant aperture trends were present in the A(θ)fρ data. These aperture trends will be addressed later while studying the slope of the dust radial profiles.
We did not apply any phase angle correction on A(θ)fρ values presented below. Comet Lemmon phase angle varies only from 29° to 58° during the entire observing run and phase function effects are strong only at smaller phase angles. If we apply the phase function derived for comet Halley by Schleicher et al. (1998a) (A(θ)fρ = 0.01807θ + 0.000177θ2) to the data presented here, the maximum effect of the phase angle variation is on the order of 25%.
A(θ)fρ nightly averages of comet C/2012 F6 (Lemmon).
Nightly averaged A(θ)fρ values are given in Table 6 for each filter. The complete data set with the corresponding error bars is represented in Fig. 4 in a logarithmic scale. Few data are available in the near-UV (UC) filter at heliocentric distances larger than 1.5 au because the comet was too faint.
In the same way as the gas production rates in Sect. 3.1, we studied the slope of the A(θ)fρ heliocentric dependence. We separated pre- and post-perihelion data and fitted a slope. Post-perihelion data fitting was satisfactory but we were unable to represent the pre-perihelion A(θ)fρ heliocentric dependence with a single slope. We then split the pre-perihelion data into two data sets. The first set (pre-perihelion-1) contains A(θ)fρ values obtained while the comet was beyond 1.4 au and the second set contains the pre-perihelion data below 1.4 au (pre-perihelion-2). This resulted in a much better representation of the A(θ)fρ trend with the heliocentric distance as shown in Fig. 4. The best-fit slope values for the split data set are given in Table 7. Since only four images of the comet were taken during the first period with the UC filter, no slope of the A(θ)fρ heliocentric dependence is given for the first data set. The same asymmetry about perihelion as for most gas species is observed, with A(θ)fρ values being higher after perihelion.
 |
Fig. 4 Logarithm of comet C/2012 F6 (Lemmon) A(θ)fρ computed from UC, BC, GC, and RC narrowband continuum filters as a function of the logarithm of the heliocentric distance r (au). Pre-perihelion data are represented with filled symbols and post-perihelion data with open symbols. The origin of the x-axis is perihelion. Solid lines represent linear fits of the A(θ)fρ variation with the pre-perihelion heliocentric distance. Dotted lines are the same for post-perihelion values. |
These results do not show a wavelength dependence of the slope derived for any of our data sets. The slopes are consistent with those measured by A’Hearn et al. (1995) for their large comets sample even though there are strong changes of dust behavior with time and heliocentric distance. The slope of the A(θ)fρ heliocentric dependence rises significantly between January 13 and February 7, 2013. The gap in the data makes it difficult to determine precisely when the change took place. Trends in visual magnitude lightcurves from Seiichi2 also show a change of slope taking place around February 2, 2013: mv = 4.5 + 5log (Δ) + 18.0log (r) before February 2, mv = 5.2 + 5 log (Δ) + 10.0log (r) between February 2 and March 4, and mv = 5.2 + 5log (Δ) + 9.5 log (r) after that. The agreement between dust production and the comet visual magnitude is not surprising as most of the light we observe visually is the solar light reflected by the coma dust continuum. The change in A(θ)fρ evolution cannot be caused by a phase angle effect as we know that the maximum amplitude of this effect (around 25% in this case) is smaller than the observed changes.
 |
Fig. 5 Dust brightness radial profiles of comet C/2012 F6 (Lemmon) at 6 epochs are represented: 2012-Dec.-22 (104 km = 22.5′′), 2013-Jan-07 (104 km = 17.5′′), 2013-Feb-07 (104 km = 13.2′′), 2013-Mar-04 (104 km = 16.1′′), 2013-May-14 (104 km = 22.9′′), 2013-Jun-05 (104 km = 23.3′′). The profile extraction was made for 20° wide wedges in the tail direction, i.e., the anti-sunward direction (black crosses), the sunward direction (dark blue triangles), and the ambient coma perpendicular to the sunward direction. A 1 /ρ profile is overlaid on each plot. |
As mentioned above, we observe significant aperture effects in A(θ)fρ which can be easily understood by looking at the dust radial brightness profiles in Fig. 5. The logarithm of the measured flux is plotted against the logarithm of the nucleocentric distance (ρ) expressed in kilometers. We performed profile extraction for a 20° wide wedge in three directions: the sunward direction (dark blue triangles), the anti-sunward direction (the tail, black crosses), and the ambient coma at 90° of the tail (light blue points). The profile inner cutoff is 3.3′′ to avoid PSF and seeing effects. For a coma with constant dust production in steady state and no radiation pressure effects or grain fading, the radial brightness profile follows a canonical 1 /ρ decay (Jewitt et al. 1982). The canonical 1 /ρ law (corresponding to a −1 slope in a log-log representation) is overlaid on the radial profiles presented in Fig. 5.
At all epochs we find that the profile aspect and slope strongly depend on the azimuthal direction. For the first two profiles we observe a significant deviation from 1 /ρ whatever the direction. The deviation is clearly seen even at small nucleocentric distances. The fitted slope in the anti-sunward direction for observations between December 11 and January 13 is about −1.25 and even steeper in the sunward and perpendicular directions. The slopes become progressively closer to −1 as the comet approaches the Sun. For observations after February 6, the slope in the tail direction is always very close to −1. In the other two directions the radial profile close to the nucleus follows a 1 /ρ law and then progressively deviates from it at larger nucleocentric distances.
In February and March 2013, we observe that the dust radial profile in the sunward direction is significantly brighter close to the nucleus than in the perpendicular direction. If we examine the original images and we apply a Larson-Sekanina filter we see a strong jet almost coinciding with the sunward direction (see Sect. 3.4). As the jet is brighter than the ambient coma, this explains the excessive brightness in the sunward direction compared to the perpendicular direction. In May and June 2013, no strong jets are seen in our images, in agreement with the radial profile aspect. In December and January, we detect a small jet in the direction perpendicular to the Sun-comet line. Since this jet is weaker than the one observed in February and its extension is only a few pixels from the nucleus, it has almost no influence on the radial profiles.
We use A(θ)fρ computed at four wavelengths to derive the dust normalized reflectivity gradients, also called color of the dust, and study their evolution with the comet heliocentric distance (Jewitt & Meech 1987). The normalized gradient of A(θ)fρ computed from two continuum filters is expressed as: ![\begin{equation} \text{color} [\lambda _{1},\lambda _{2}]=\frac{A(\theta) f\rho _{1}-A(\theta) f\rho _{2}}{\lambda _{1}-\lambda _{2}}\frac{2000}{A(\theta) f\rho _{1}+A(\theta) f\rho _{2}}\cdot \end{equation}](/articles/aa/full_html/2015/02/aa24582-14/aa24582-14-eq100.png) (1)The normalized reflectivity gradient is expressed as the percentage of reddening by 1000 Å. In Fig. 6 we show the dust colors computed from the gradient between RC (713 nm) and UC (334 nm), BC (445 nm), and GC (526 nm). The dust color is also computed at 10 000 km from the nucleus, in the same way as the A(θ)fρ.
(1)The normalized reflectivity gradient is expressed as the percentage of reddening by 1000 Å. In Fig. 6 we show the dust colors computed from the gradient between RC (713 nm) and UC (334 nm), BC (445 nm), and GC (526 nm). The dust color is also computed at 10 000 km from the nucleus, in the same way as the A(θ)fρ.
C/2012 F6 (Lemmon) pre- and post-perihelion fitted power-law slopes for A(θ)fρ computed from the UC, BC, GC, and RC filters.
 |
Fig. 6 Evolution of the dust normalized reflectivity gradient of comet C/2012 F6 (Lemmon) computed from A(θ)fρ values as a function of the heliocentric distance. The origin of the x-axis is the perihelion. Pre-perihelion values are represented with full symbols and post-perihelion values with empty symbols. The dust color is computed from RC and UC filters (top), RC and BC filters (middle), and RC and GC filters (bottom). |
 |
Fig. 7 Dust normalized reflectivity gradient as a function of nucleocentric distance (ρ) for the RG-GC continuum pair. The evolution of dust color with cometocentric distance is plotted for five dates sampling our observing run. |
For RC-BC and RC-GC continuum pairs, the dust is clearly reddened by approximately the same amount with a mean value of 7.02 ± 0.19% / 1000 Å for the RC-BC pair and 9.57 ± 0.16% / 1000 Å for the RC-GC pair. These values are close to those observed for other comets. A reddening between 5 and 12%/1000 Å was found by Lin et al. (2013) for comet Hartley 2. Lin et al. (2012) found that comet 81P/Wild 2 was redenned by approximately 8.2–8.6%/1000 Å. Dust reddening for comet C/2000 WM1 was also around the same value (Lara et al. 2004). There is no strong trend in dust color with heliocentric distance. This is not surprising, as a study performed by Solontoi et al. (2012) on 35 comets did not show any correlation between the colors of active comets and the heliocentric distance.
For the RC-UC continuum pair, the reddening is significantly lower than for the other two pairs and even sometimes negative. However, we do not think that the comet is really bluer in the near-UV. As comet Lemmon is quite gaseous, this is probably due to the contamination of the UC filter by some molecular emission artificially raising the A(θ)fρ. For gaseous comets emission lines from OH (0–1) and from 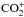 to a lesser extent are detected within the bandpass of the UC filter (Leach et al. 1978; Schleicher & A’Hearn 1988 and Valk et al. 1992). The main contamination in the UC filter is usually considered to be C3 (Farnham et al. 2000). However, we examined VLT-UVES spectra of more than ten comets gathered by our team and OH (0–1) is clearly the brightest emission in that wavelength range, while C3 and
to a lesser extent are detected within the bandpass of the UC filter (Leach et al. 1978; Schleicher & A’Hearn 1988 and Valk et al. 1992). The main contamination in the UC filter is usually considered to be C3 (Farnham et al. 2000). However, we examined VLT-UVES spectra of more than ten comets gathered by our team and OH (0–1) is clearly the brightest emission in that wavelength range, while C3 and 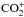 are very weak. We see that the reddening from these filters is higher at larger heliocentric distances. Around 1.6 au it comes close to the reddening computed from the RC-BC and the RC-GC pairs. Indeed, at this distance, the comet was less active and the contamination of UC filter by molecular emissions was lower. Knowing this effect we discarded the UC-BC and the UC-GC continuum pairs.
are very weak. We see that the reddening from these filters is higher at larger heliocentric distances. Around 1.6 au it comes close to the reddening computed from the RC-BC and the RC-GC pairs. Indeed, at this distance, the comet was less active and the contamination of UC filter by molecular emissions was lower. Knowing this effect we discarded the UC-BC and the UC-GC continuum pairs.
In Fig. 7 we analyze the effect of aperture size on the dust color. For December and January observations, the reddening rises with the nucleocentric distance, while for observations made after February the percentage of reddening by 1000 Åslowly decreases with the aperture size. This confirms that dust grains properties change around February 2, as already seen for the radial profiles. Aperture effects are quite small though, i.e., on the order of 5%, but they could explain the dispersion in dust color observed in Fig. 6.
3.3. Composition
We can compare the production rates measured in this paper with those derived from other observations of the comet. Paganini et al. (2014) obtained near-infrared spectra of comet Lemmon pre- and post-perihelion at three heliocentric distances: 1.2 au (February 2 and 4), 0.75 au (March 31 and April 1), and 1.74 au (June 20). February and June observations are sufficiently close to TRAPPIST observations to allow comparison between production rates of mother species detected in the infrared domain and production rates of daughter species observed by TRAPPIST in the optical domain. Combi et al. (2014) also derived water production rates for comet Lemmon from observations of the hydrogen Lyα emission with the SWAN camera onboard the SOHO spacecraft. Their observations cover the period from November 29, 2012, to June 31, 2013. Paganini et al. derived a water production rate of Q(H2O) = 1.9 ± 0.1 × 1029 mol/s for both February 2 and 4 and Q(H2O) = 1.1 ± 0.1 × 1029 mol/s for June 20. On February 6 and June 5 Combi et al. respectively measured Q(H2O) = 2.07 ± 0.01 × 1029 mol/s and Q(H2O) = 2.03 ± 0.02 × 1029 mol/s. We measured a mean value of Q(OH) = 1.09 ± 0.21 × 1029 mol/s on February 7 and Q(OH) = 0.72 ± 0.17 × 1029 mol/s on June 5 with TRAPPIST. From OH production rates we can compute vectorial-equivalent water production rates using the relation given in Cochran & Schleicher (1993) which takes into account the heliocentric dependence of the water velocity and the branching ratio for photodissociation of water into OH: Q(H2O) = 1.361r-0.5Q(OH). This gives Q(H2O) = 1.39 ± 0.26 × 1029 mol/s for February 7 and Q(H2O) = 0.79 ± 0.19 × 1029 mol/s for June 5. Our production rates are lower than those obtained by Paganini et al. (2014) and Combi et al. (2014). When comparing the water production rates in comets computed from different sources there is usually a discrepancy between the values computed from observations of H, OH, or H2O directly at different wavelengths. The scatter can be as large as a factor of two. This could be explained by the differences in the aperture sizes (30 or 40′′ in the infrared vs. 22′ in the optical), the type of model and the value of parameters used to compute production rates and the effect of the nucleus rotation.
Paganini et al. (2014) detected HCN emission in the near-infrared on February 2 and June 20. The origin of the CN radical in cometary coma has not been yet firmly determined. HCN photodissociation seems to be the process responsible for most of the CN production but other mother molecules or other processes are necessary to explain the discrepancies observed between HCN and CN production rates in some comets (Fray et al. 2005). A’Hearn et al. (1986) first proposed that CN radical could also be produced from grains to explain the existence of CN jets in comet Halley. Evidences for extended sources in jets and correlation between CN and dust production (Newburn & Spinrad 1989 and A’Hearn et al. 1995) further reinforced the hypothesis of CN production from grains. In this context, comparison between infrared and optical data is of great importance to study the origin of the CN radical in the coma. Paganini et al. (2014) obtained Q(HCN) = 2.1 ± 0.08 × 1026 mol/s on February 2 and Q(HCN) = 2.3 ± 0.2 × 1026 mol/s on June 20. We can compare it to TRAPPIST measurements: Q(CN) = 3.18 ± 0.14 × 1026 mol/s on February 7 and Q(CN) = 2.01 ± 0.13 × 1026 mol/s on June 11. If we take into account the rapid rise of production rates from one day to another in February and the rotational variability, there is no strong discrepancy between our values and those from Paganini et al. (2014). Biver et al. (2014) also derived comet Lemmon HCN production rate on April 06.4 to 08.6, 2013 from observations with the 30 m telescope of the Institut de radioastronomie millimétrique (IRAM). They measured Q(HCN) = 1.27 ± 0.09 × 1027 mol/s. We only have measurements of the CN production rate a month before on March 4: Q(CN) = 0.89 ± 0.31 × 1026 mol/s. Within the error bars and taking into account the rapid evolution of the comet activity and the nucleus rotation, the HCN and CN productions rates are consistent with each other, indicating that HCN could be the main source of CN radicals in the coma of comet Lemmon and that only a small fraction of CN could be released from grains.
 |
Fig. 8 Ratio of C2 to CN (top) and C3 to CN (bottom) production rates as a function of the heliocentric distance. The x-axis origin is the perihelion. Pre-perihelion values are represented with filled symbols and post-perihelion values with open symbols. |
 |
Fig. 9 Logarithm of the ratio of C2 (top) and C3 to OH production against logarithm of the ratio of CN to OH and their error bars. Pre-perihelion values are represented with filled symbols and post-perihelion values with open symbols. The solid red line indicates the evolution of comet Lemmon between December 11 and January 13 and the dashed line between February 7 and March 4. |
A’Hearn et al. (1995) distinguished two main compositional classes among comets: typical and carbon-chain depleted comets. These classes are defined by the ratio of the CN production rate to the carbon-chain species C2 and C3. They obtained a mean Q(C2) /Q(CN) value of 1.15 for typical comets with limits around 0.7 and 2 while depleted comets are defined as those having log (Q(C2) /Q(CN)) < −0.18. About half of the Jupiter family comets are carbon-chain depleted and almost no long-period comets are depleted. From the production ratios of C2, C3, and CN shown in Fig. 8, we conclude that comet Lemmon is a typical comet, as expected for a new comet. The C2-to-CN ratio varies between 1.2 and 2, well within the range defined by A’Hearn et al. (1995) for typical comets.
In Fig. 8 we observe a variation of the C2-to-CN ratio with the heliocentric distance. The ratio does not vary significantly near the perihelion, but Q(C2) /Q(CN) starts decreasing when the heliocentric distance is larger than 1.4 au (both pre- and post-perihelion), showing that the apparent chemical composition of a comet can evolve with the heliocentric distance. Since the amplitude of the variation remains small, with a maximum variation smaller than a factor of 2 between the most extreme values, the chemical classification of comet Lemmon as a typical comet does not change. The C3-to-CN ratio remains constant within the error bars during the whole observing run.
In the upper part of Fig. 9, the ratio of C2 to OH production rates is plotted against the ratio of CN to OH. We can distinguish two groups of points: a diagonal band across the graph and a group of points below the diagonal. The full line indicates temporal evolution of the comet between December 11 and January 13. The comet moves upwards in the diagram during this period of time, indicating an increase of the C2-to-CN production rates ratio when the comet is beyond 1.4 au. This effect has already been pointed out in Fig. 8. Between February 7 and March 4, the data points move on a diagonal band from the lower left towards the upper right. This indicates a decrease in the OH production rate compared to the CN and C2 production rates for heliocentric distances smaller than 1.4 au. If we plot the C2-to-OH and CN-to-OH ratios as a function of the heliocentric distance we clearly see they rise while the comet approaches the Sun for heliocentric distances smaller than 1.4 au. A’Hearn et al. (1995) also found a peak of Q(OH)/Q(CN) between 1 and 2 au for their global analysis of a large sample of comets. The variation observed in Q(OH)/Q(CN) and Q(OH)/Q(C2) is less than a factor of 2. The number of post-perihelion observations is not sufficient to detect any significant trend.
The lower part of Fig. 9 shows the C3-to-OH ratio against the CN-to-OH ratio. Both pre- and post-perihelion data points lie on a diagonal band indicating that there is no strong variation of Q(C3)/Q(CN) with the heliocentric distance. This is in complete agreement with what we deduced from Fig. 8. No clear trend within the diagonal band could be found because of the large dispersion of the data points. However the study of the C3-to-OH ratio shows the same trend as for C2 and CN.
 |
Fig. 10 Ratio of A(θ)fρ to CN (top) and OH (bottom) production rates as a function of the heliocentric distance. The x-axis origin is the perihelion. Pre-perihelion values are represented with filled symbols and post-perihelion values with empty symbols. A(θ)fρ values have not been corrected for the phase angle effect. |
The dust-to-gas ratio is usually defined as the ratio of A(θ)fρ to the OH production rate or the ratio of A(θ)fρ to the CN production rate. We derive both ratios and we show their evolution with the heliocentric distance in Fig. 10. The logarithm of A(θ)fρ/Q(OH) is between −25.9 and −25.4. There is an asymmetry about perihelion. The dust-to-gas ratio is higher after perihelion. In Sects. 3.1 and 3.2 we found higher gas production rates and A(θ)fρ values post-perihelion. The asymmetry is stronger for the dust than for gas species, explaining the lower value of dust-to-gas ratio before perihelion.
3.4. Coma morphology and rotation period
This section focuses on the study of comet Lemmon dust and gas coma morphology. We first applied image enhancement techniques to improve the contrast between the jets and other features and the bulk coma brightness. We tested several techniques: subtraction and division of an azimuthal median profile, rotational filter, and Larson-Sekanina filter (see Schleicher & Farnham 2004; Larson & Sekanina 1984). As can be seen in Fig. 11 for a representative CN narrowband image, the Larson-Sekanina (bottom right) and rotational filters (bottom left) reveal essentially the same features even though their orientation is slightly different. These two techniques use rotations of the original image around its center by a certain angle combined in different ways. Several rotation angles were tested, always revealing the same features and we finally chose to use a 30° angle, which provides the higher contrast images. The removal of an azimuthal median profile is illustrated at the upper right panel of Fig. 11. Features close to the nucleus are not as contrasted and sharp as when using rotational and Larson-Sekanina filters but this technique reveals fainter large-scale features. The techniques presented here are very sensitive to the centering of the nucleus. However, because the images are centered with an accuracy of better than 1 pixel, this should not produce deviations in the observed features. Given that the subtraction of an azimuthal median profile generally does not introduce artifacts and that we observe essentially the same features using the three different techniques we are confident that the structures described below are real. Images from December 2012 and January 2013 and post-perihelion images (after April 2013) have a lower signal-to-noise ratio. For these images we used preferentially Larson-Sekanina filtering to enhance faint features. We only used the azimuthal median removal on CN images from February and March 2013.
 |
Fig. 11 Representative CN image from February 12, 2013, and three different enhancement techniques. The original image of the comet is shown at the upper left of the panel. At the upper right, the removal of an azimuthal median profile is shown. The results of the rotational and Larson-Sekanina filters are shown respectively at the bottom left and right of the figure. The images are oriented north up and east left. The field of view is 4.3′ × 4.3′. The arrow indicates the direction of the Sun. |
 |
Fig. 12 C/2012 F6 (Lemmon) enhanced OH, NH, CN, C3, C2, and RC images from January 13 (top panel), February 25 (middle panel), and May 14 (bottom panel). Each image is enhanced by Larson-Sekanina filtering. The field of view is 4.3′ × 4.3′ and images are oriented with north up and east left. The arrow indicates the direction of the Sun. |
Features are detected mainly in CN, C3, C2, and in the dust filters, suggesting the existence of at least one active zone on the nucleus. As expected, the features aspect is strongly dependent on the viewing geometry of the comet at the time of the observations. If the Earth is oriented inside the cone described by the rotation of the active region around the spin axis, features appear as spirals or arcs. When the Earth is outside the cone, we mainly see radial features. Three main configurations are seen during the whole period. We chose one representative night from each of these configurations; the result of the Larson-Sekanina filtering on OH, NH, CN, C3, C2, and RC images is shown in Fig. 12. We only show the enhanced result for the RC filter as the features are similar in all dust filters.
In December and January the features are difficult to detect because of the low signal-to-noise of the images (Fig. 12, top panel). No clear structure are found in OH and NH filters. Both Larson-Sekanina filtering and azimuthal median profile removal revealed a roughly hourglass shaped morphology in the CN filter. The features are oriented respectively to the sunward and anti-sunward directions. Both C3 and C2 display the same morphology even if very weak and less extended in C3 because of the poor signal-to-noise and shorter C3 lifetime. The dust morphology is quite different from the hourglass shape observed for the gas coma. We clearly see the dust tail in the anti-sunward direction. A second feature is detected perpendicular to the anti-sunward direction, towards the northeast. Both gas and dust morphologies are almost identical from night to night. The two long series of observations from January 7 and 13 do not show variations in gas and dust morphologies due to the nucleus rotation.
When we recovered the comet in early February, we observed significant changes in the coma morphology. As in December and January, no feature is detected in the OH filter because of the rather poor signal-to-noise ratio, but other gas filters display a more complex morphology. The broad structure in the anti-sunward direction in the NH filter clearly reveals the contamination by the ionic tail (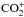 ion). Corkscrew-like shaped features are identified in the CN, C3, and C2 filters. Close to the nucleus, two sharp features are observed. The remnants of these features after one nucleus rotation period are detected as a broad structure at larger nucleocentric distances, see Figs. 12 and 13. The gas coma is enhanced in the anti-sunward direction in CN, C3, and C2. Given that contamination by the dust in the CN filter is very weak, we do not think that the gas coma enhancement in the anti-sunward direction is only due to contamination by the dust tail. A strong dust tail is detected in the RC filter in the anti-sunward direction. However, no corkscrew-like shaped structures similar to the gas are observed in the RC filter. Instead, we see a strong jet in the sunward direction and a weaker one oriented to the west. In February, comet Lemmon has been observed during several almost entire nights. We found variations of the gas morphology during these nights caused by the nucleus rotation. No morphological change is observed for the dust. The detailed description of the morphology evolution with the nucleus rotation as well as the determination of the rotation period are given below. The features described here remained observable as the comet was approaching the Sun until March 4, when the observations were interrupted.
ion). Corkscrew-like shaped features are identified in the CN, C3, and C2 filters. Close to the nucleus, two sharp features are observed. The remnants of these features after one nucleus rotation period are detected as a broad structure at larger nucleocentric distances, see Figs. 12 and 13. The gas coma is enhanced in the anti-sunward direction in CN, C3, and C2. Given that contamination by the dust in the CN filter is very weak, we do not think that the gas coma enhancement in the anti-sunward direction is only due to contamination by the dust tail. A strong dust tail is detected in the RC filter in the anti-sunward direction. However, no corkscrew-like shaped structures similar to the gas are observed in the RC filter. Instead, we see a strong jet in the sunward direction and a weaker one oriented to the west. In February, comet Lemmon has been observed during several almost entire nights. We found variations of the gas morphology during these nights caused by the nucleus rotation. No morphological change is observed for the dust. The detailed description of the morphology evolution with the nucleus rotation as well as the determination of the rotation period are given below. The features described here remained observable as the comet was approaching the Sun until March 4, when the observations were interrupted.
We observed comet Lemmon again after perihelion, from April 28 to June 11, 2013. The comet was weaker, making structures in the coma very difficult to identify. A feature in the anti-sunward direction is detected in all filters except OH. No other feature could be identified in NH and C3 filters. Only weak CN and C2 features could be distinguished close to the nucleus. In the dust processed images we observe a second feature oriented to the south.
Structures observed in the coma suggest that the comet Lemmon nucleus has at least one discrete active zone. The similarity of the CN, C3, and C2 features strongly suggests that these species originate from the same areas. No conclusion can be drawn about OH and NH. Dust morphology is different from that of the gas, in agreement with the differences observed between gas and dust production evolution in the previous sections of this paper.
 |
Fig. 13 C/2012 F6 (Lemmon) CN images processed with Larson-Sekanina filtering (left) and azimuthal median profile subtraction (right) acquired between February 7 and February 12, 2013. The images have been sorted out by rotational phase assuming a rotation period of 9.52 h and a zero point on February 7.16. All images are oriented with north up and east left. The field of view is 4.3′ × 4.3′. |
We mentioned earlier that the gas morphology, especially in the CN filter, was evolving during the long observing runs performed in February. In Fig. 13, examples of CN images processed with Larson-Sekanina filtering (left) and azimuthal median profile subtraction (right) are shown. We selected images taken between February 7 and February 12. We assumed a rotation period of 9.52 h and sorted the images according to their rotational phase. Two small spiral-like features appear close to the nucleus. Then they progressively extend and rotate clockwise as the gas expands. At the end of the rotation cycle, structures are broad and extend farther away from the nucleus. As a new rotational cycle begins, new spiral-like shaped features appear. Features from the previous rotation cycles can be distinguished at larger nucleocentric distances.
The periodic repetition of similar coma morphology in CN and C2 filters allowed us to determine the nucleus rotation period. Images taken between February 9 and 25 were selected, as this epoch has the best temporal coverage. We first searched for pairs of matching images and recorded the time interval between matching pairs. Tens of pairs were found and the only possible rotation period was around 9 h. We then refined the period determination. We decided to work on CN images as these were the ones with the highest signal-to-noise ratio and were less contaminated by the dust. All the original CN images from February 9 to February 25 were normalized and divided between each other. We computed the RMS of the images resulting from each division. The division of two images displaying the same morphology gives a minimum RMS, so that minima in the RMS should repeat with the nucleus rotation period. We studied the value of the RMS as a function of the time interval between the images and the result is shown in Fig. 14. We eliminated all possible aliases and determined the rotation period by dividing the time interval between matching pairs by the number of cycles between them. We measured a period of 9.52 ± 0.05 h from 13 matching pairs between February 9 and February 25. The uncertainty in the rotation period is given by the standard deviation of the period measurements. We do not detect any increase or decrease of the comet rotation period during this time. We performed a similar study on C2 images. The average rotation period derived from C2 images is 9.50 ± 0.18 h. This is in agreement within the error bars with the measurement made from CN images even though the uncertainty is bigger, probably as a result of the contamination by the dust in C2 filter. The signal-to-noise ratio in the other filters is not sufficient to perform this kind of analysis. The morphological evolution of CN during a complete rotation cycle is shown in Fig. 13. Nucleus rotation periods have only been determined for approximately two dozen comets. The measured values vary from a few hours for comets like Hyakutake (1996 B2) (Schleicher et al. 1998b; Schleicher & Woodney 2003) or 10P/Tempel 2 (A’Hearn et al. 1989; Jewitt & Luu 1989; Sekanina 1991) to more than a day for comet 9P/Tempel 1 (Belton et al. 2005) or comet Halley (Belton et al. 1991), for example. The rotation period measured for comet Lemmon lies within the range of values usually observed for comets.
 |
Fig. 14 Result of C/2012 F6 (Lemmon) rotation analysis. CN images from February 9 to February 25 have been normalized and divided between each other. We plot the RMS resulting from each division as a function of the time difference between the images. Minima in the RMS repeat with the nucleus rotation period. We measured a period of 9.52 ± 0.05 h from 13 matching pairs between February 9 and February 25. |
4. Discussion
We have presented the analysis of comet Lemmon long-term photometry and imaging monitoring with the robotic telescope TRAPPIST. We observed the comet during several months both pre- and post-perihelion. We have studied the evolution of the activity and the coma chemical composition along a part of the orbit from 1.95 au pre-perihelion to 1.61 au post-perihelion. We also performed an analysis of the variation of the coma structures that allowed us to determine the nucleus rotation period.
The heliocentric dependence of OH, NH, CN, C3, and C2 production rates displays similar slopes. Morphological study of the coma also showed that identical features are observed for CN, C3, and C2, ranging from a roughly hourglass shape in December and January to a corkscrew-like shape in February and March. The agreement between evolution and morphology for all gas species suggests that they have the same origin. All five gas species exhibit an asymmetry about perihelion, the rate of brightening being steeper than the rate of fading and the production rates of all radicals except OH being higher after perihelion. Such asymmetries are not unusual for comets (see, e.g., A’Hearn et al. 1995; Knight & Schleicher 2013; Schleicher et al. 1998a) but their origin is still difficult to understand because of the lack of comets observed over a sufficient range of heliocentric distances both pre- and post-perihelion. However, in some cases, such as comet Halley, the increased brightness after perihelion was probably linked to seasonal effects (Weissman 1987). For comets on highly eccentric orbits with one or several active zones on their nuclei, rapid changes of insolation and active zone illumination can occur near perihelion. Since the orientation of the rotation axis is assumed to be random, different kinds of asymmetries should be observed among comets: higher activity pre-perihelion, post-perihelion, or almost no asymmetry. The monitoring of a large number of comets both pre- and post-perihelion is then critical in order to study the impact of seasonal effects on comet activity. In the case of comet Lemmon, we observed features in the coma indicating one or several active region(s) on the nucleus and a possible seasonal effect that could explain the asymmetry about perihelion. In order to confirm this hypothesis, modeling of the nucleus and determining of the comet pole orientation would be needed.
Even though all gas species display similar behavior, small variations of the production rate ratios are observed. The C2-to-CN ratio is almost constant for heliocentric distances smaller than 1.4 au and decreases at larger distances. Both pre- and post-perihelion data exhibit the same trend. This behavior seems thus only linked to the comet heliocentric distance. However, the C3-to-CN ratio does not vary with the heliocentric distance. We also found that for heliocentric distances smaller than 1.4 au, the OH production rate rises at a slower pace than carbonaceous species. The coma chemical composition then evolves with the comet heliocentric distance confirming the importance of studying the composition of comets along their orbits and not only at a specific moment. Evolution of the production rate ratios has already been found for other comets, such as for comet Halley which displayed temporal variation of the carbon species relative to OH (Schleicher et al. 1998a). A’Hearn et al. (1995) also noticed a slight but systematic decrease of Q(C2)/Q(CN) with increasing heliocentric distance for several comets in their data set.
In Sect. 3.1 we explain that in some cases there are discrepancies between the observed gas radial profiles and the fitted Haser model. This indicates that the Haser scalelengths used for modeling did not perfectly correspond to the observed profiles. Scalelengths determinations are usually performed only on small ranges of heliocentric distances and from profiles with poor spatial resolution. We scaled scalelengths as r2 for all gas species, as is usually done. However, Rauer et al. (2003) showed in the case of comet Hale-Bopp at large heliocentric distances, that the scalelength variation with heliocentric distance could be more complex than assumed here, and could also depend on the radical under study. Even though the use of radial profiles allows us to sample the entire coma, the effect of model parameters that do not exactly match the spatial distribution of the species has to be considered. This could of course affect the C2 and CN production rates computed with these scalelengths and their ratio with the heliocentric distance for example. The C2 abundance is particularly affected since its profile is often less steep in the inner coma than can be reproduced with the Haser model (Schulz et al. 1994). A re-determination of Haser scalelengths for comet Lemmon and other comets and a study of their dependence on the heliocentric distance would be necessary. We plan to address Haser scalelengths determination in a forthcoming paper. However, some tests performed for comet Lemmon showed that the effect of the Haser scalelengths on the CN and C2 production rates becomes really significant only when the comet is close to the Sun and then should not strongly affect the trend in the C2-to-CN ratio we observed here.
The study of the dust radial profiles showed some peculiarities. For a simple steady-state coma, the radial brightness profile should decrease as 1 /ρ with the nucleocentric distance ρ (i.e. follow a −1 slope in a log-log representation). However, significant deviations of the dust radial brightness profile from the expected canonical distribution were noted. In most cases, the slope of the profile was steeper than expected for a steady-state dust coma and variations of the slope with the azimuthal direction were observed. In February, early March, and after perihelion, the slope was close to −1 in the tail direction. In the other directions, it was close to −1 at small nucleocentric distances and then progressively deviated at larger nucleocentric distances. However, in December and January, the dust profile slope was about−1.25 in the tailward direction and even steeper in the sunward and perpendicular directions. Radial profiles steeper than 1 /ρ have already been observed for a number of comets see, e.g., Baum & Kreidl (1986), Jewitt & Luu (1989), Baum et al. (1992) and Schleicher et al. (2003). This behavior is partially explained by the radiation pressure effect. Radiation pressure accelerates grains in the anti-sunward direction. Baum et al. (1992) modeled the effect of radiation pressure on a dust coma. In the tailward direction, their modeled profile follows a 1 /ρ law. In the sunward direction, the modeled profile follows a 1 /ρ law at small nucleocentric distances and is steeper farther away from the nucleus. This is exactly what we observe for the dust radial profiles in February, early March, and after perihelion. The effect is particularly strong for March 4 when the comet was only at 0.73 au from the Sun. This was the observation where the comet was the closest to the Sun and was thus undergoing the strongest radiation pressure effects. The dust behavior is quite different in December and January. At that time, the dust brightness profile is steeper than 1 /ρ even at small nucleocentric distances and, more importantly, even in the tailward direction. This indicates that another phenomenon is taking place in the dust coma. Baum et al. (1992) proposed different possible explanations for this departure of the 1 /ρ law. The first one is grain fading, already invoked by Jewitt & Luu (1989) to explain profiles observed for comet Tempel 2. They also considered the issue of large old grains that could have a brightness profile different than 1 /ρ. Because comet Lemmon was visiting the inner solar system for the first time, a halo of large old grains could have dominated the dust coma brightness profile at large heliocentric distances pre-perihelion. When the comet comes closer to the Sun new dust ejecta would then account for most of the dust coma brightness and produce a nearly canonical profile in the tail direction. This could also explain the change in the profile aspect observed before and after February; the large old grains being progressively outnumbered by smaller grains more sensitive to radiation pressure.
We found significant differences between dust and gas behavior. First, the heliocentric dependence of A(θ)fρ values differs from that of the gas production rates. In December and January, the slope of the A(θ)fρ heliocentric dependence was shallower than that of the gas. Between January 14 and February 7, the slope became much steeper, and steeper than that of the gas. After perihelion, the slope was similar to that observed in December and January. The evolution of the dust activity thus does not seem to be correlated to the evolution of the gas activity. A second piece of evidence of the decoupling between dust and gas is given by the study of the coma morphology. The features observed in the RC filter do not correspond to the structures observed in the CN, C3, and C2 filters. Changes due to the nucleus rotation were observed in the CN, C3, and C2 morphology during the night but no morphological changes were observed for the dust jet. This is quite surprising given that according to almost all models, the dust is lifted by the gas. Hence, the absence of morphological changes for the dust seems to indicate that the structures that control the dust lifting could be much larger than those involved in the radicals outgassing. Such large-scale structures could remain undetected using our images enhancement techniques. Alternatively, if the dust jet is located around the pole of the nucleus rotation axis, little or no changes in morphology are expected over one rotation. Other volatiles could also drive the dust activity and lift dust grains from the surface; CO and CO2 are good candidates, as we detected a relatively strong 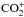 ion tail contaminating the NH filter in the dust tail direction. These species have already been found by A’Hearn et al. (2011) to drive comet Hartley 2 dust ejection, for example. In the case of Hartley 2, most of the water comes from icy grains lifted by CO2. If this is also the case for comet Lemmon, we would expect to see an enhancement of OH in the anti-sunward direction, the icy grains being pushed away in the direction opposite to the Sun by the radiation pressure before releasing water. We do not see such enhancement at any time in the images presented in Fig. 12. These images were obtained by applying a Larson-Sekanina filtering to the original OH images. However, as presented in Fig. 11, this technique better enhances sharp small-scale features while the subtraction of the azimuthal median profile detects fainter large-scale features more efficiently. We then reprocessed the OH and dust images by subtracting an azimuthal median profile and the result is shown in Fig. 15. With this technique we could see a slight enhancement in OH in a given direction. Since this feature did not vary between images taken on the same night, we added three OH images to increase the signal-to-noise ratio. In the resulting image we clearly see that OH is enhanced in a region around PA 20°. In the dust image we see the dust tail around PA 300° and the dust jet. From this image we can see that the OH feature is not centered in the tail direction, but is 80° from the anti-sunward direction and then we do not have any observational evidence of the effect of radiation pressure on the icy grains. Another interesting point is that in the case of Hartley 2 an onset of the CO and CO2 activity around 1.4 au pre-perihelion is required to model the lightcurve (Meech et al. 2011). If we assume that the dust grains are lifted by CO2 in comet Lemmon, the change in slope of the dust production around 1.4 au could be explained by the CO2 activity turning on at that time. However, we could also expect a change in slope of the water production due to the lifting of icy grains by CO2. No such change in the slope of the OH production with the heliocentric distance is detected, but the dispersion of the OH production rates is much higher than for the dust and this prevents us from drawing a clear conclusion.
ion tail contaminating the NH filter in the dust tail direction. These species have already been found by A’Hearn et al. (2011) to drive comet Hartley 2 dust ejection, for example. In the case of Hartley 2, most of the water comes from icy grains lifted by CO2. If this is also the case for comet Lemmon, we would expect to see an enhancement of OH in the anti-sunward direction, the icy grains being pushed away in the direction opposite to the Sun by the radiation pressure before releasing water. We do not see such enhancement at any time in the images presented in Fig. 12. These images were obtained by applying a Larson-Sekanina filtering to the original OH images. However, as presented in Fig. 11, this technique better enhances sharp small-scale features while the subtraction of the azimuthal median profile detects fainter large-scale features more efficiently. We then reprocessed the OH and dust images by subtracting an azimuthal median profile and the result is shown in Fig. 15. With this technique we could see a slight enhancement in OH in a given direction. Since this feature did not vary between images taken on the same night, we added three OH images to increase the signal-to-noise ratio. In the resulting image we clearly see that OH is enhanced in a region around PA 20°. In the dust image we see the dust tail around PA 300° and the dust jet. From this image we can see that the OH feature is not centered in the tail direction, but is 80° from the anti-sunward direction and then we do not have any observational evidence of the effect of radiation pressure on the icy grains. Another interesting point is that in the case of Hartley 2 an onset of the CO and CO2 activity around 1.4 au pre-perihelion is required to model the lightcurve (Meech et al. 2011). If we assume that the dust grains are lifted by CO2 in comet Lemmon, the change in slope of the dust production around 1.4 au could be explained by the CO2 activity turning on at that time. However, we could also expect a change in slope of the water production due to the lifting of icy grains by CO2. No such change in the slope of the OH production with the heliocentric distance is detected, but the dispersion of the OH production rates is much higher than for the dust and this prevents us from drawing a clear conclusion.
 |
Fig. 15 Representative OH (left) and RC (right) images from January 12, 2013, processed by removing the azimuthal median profile. Since the signal-to-noise ratio in the OH images is low and since we could not see any variation between images from the same night, we added three processed OH images from January 13 to obtain the result presented here. The images are oriented north up and east left. The field of view is 4.3′ × 4.3′. The arrow indicates the direction of the Sun. |
Evidence suggest that the dust properties changed in February. The slope of the heliocentric dependence and the slope of the dust radial brightness profile both change in early February, and are correlated with a change in visual magnitudes lightcurves. Moreover, the trend of the dust normalized reflectivity gradient with the nucleocentric distance is completely reversed at the same time: it increased with nucleocentric distance in December and January whereas decreased with nucleocentric distance after February. It is then clear that the properties of the grains changed at that time. However, no trend or sudden variation of the dust color with the heliocentric distance could be detected. Seasonal effects could be invoked to explain the sudden change in the dust behavior: different dominant source regions having different grain properties. However, with only optical observations it is difficult to determine if the change occurred in the physical properties of the grains or in their size distribution, and what caused it.
5. Summary
The monitoring of the comet Lemmon during several months with the robotic TRAPPIST telescope permitted us to obtain several interesting results. The coma morphology indicates the existence of one or several active region(s) on the nucleus. The active region(s) are probably the cause of the seasonal effect observed for the gas species. Indeed, the evolution of the OH, NH, CN, C3, and C2 production rates with heliocentric distance is similar and shows an asymmetry about perihelion, the rate of brightening being steeper than the rate of fading. The abundance ratios in the coma vary: the C2-to-CN ratio inceases with the heliocentric distance (r) below −1.4 au and decreases with r beyond 1.4 au while the C3-to-CN ratio does not vary. Both the morphology and the activity evolution indicate that the dust and the gas are not coupled. Several pieces of evidence also point to a sudden change in the dust properties in early February. Last but not least, thanks to several large sets of continuous data acquired during several hours on a few nights, we could follow gas coma features of CN and C2 and determine a nucleus rotation period of 9.52 ± 0.05 h.
Acknowledgments
TRAPPIST is a project funded by the Belgian Fund for Scientific Research (Fonds National de la Recherche Scientifique, F.R.S.-FNRS) under grant FRFC 2.5.594.09.F, with the participation of the Swiss National Science Fundation (SNF). C. Opitom acknowledges the support of the FNRS. E. Jehin and M. Gillon are FNRS Research Associates, D. Hutsemékers is FNRS Senior Research Associate and Jean Manfroid is Honorary Research Director of the FNRS. We thank Claude Arpigny for helpful discussions. We are grateful to David Schleicher and the Lowell Observatory for the loan of a set of NASA HB comet filters.
References
- A’Hearn, M. F., Schleicher, D. G., Millis, R. L., Feldman, P. D., & Thompson, D. T. 1984, AJ, 89, 579 [NASA ADS] [CrossRef] [Google Scholar]
- A’Hearn, M. F., Hoban, S., Birch, P. V., et al. 1986, Nature, 324, 649 [NASA ADS] [CrossRef] [Google Scholar]
- A’Hearn, M. F., Campins, H., Schleicher, D. G., & Millis, R. L. 1989, ApJ, 347, 1155 [NASA ADS] [CrossRef] [Google Scholar]
- A’Hearn, M. F., Millis, R. C., Schleicher, D. O., Osip, D. J., & Birch, P. V. 1995, Icarus, 118, 223 [NASA ADS] [CrossRef] [Google Scholar]
- A’Hearn, M. F., Belton, M. J. S., Delamere, W. A., et al. 2011, Science, 332, 1396 [NASA ADS] [CrossRef] [Google Scholar]
- Baum, W. A., & Kreidl, T. J. 1986, in Asteroids, Comets, Meteors II, Proc. Int. Meet., eds. C.-I. Lagerkvist, H. Rickman, B. A. Lindblad, & H. Lundstedt, 397 [Google Scholar]
- Baum, W. A., Kreidl, T. J., & Schleicher, D. G. 1992, AJ, 104, 1216 [NASA ADS] [CrossRef] [Google Scholar]
- Belton, M. J. S., Julian, W. H., Anderson, A. J., & Mueller, B. E. A. 1991, Icarus, 93, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Belton, M. J. S., Samarasinha, N. H., Fernández, Y. R., & Meech, K. J. 2005, Icarus, 175, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Bessel, M. S. 1990, PASP, 102, 1181 [NASA ADS] [CrossRef] [Google Scholar]
- Biver, N., Bockelée-Morvan, D., Debout, V., et al. 2014, A&A, 566, L5 [Google Scholar]
- Bockelée-Morvan, D., Crovisier, J., Mumma, M. J., & Weaver, H. A. 2004, in The composition of cometary volatiles, ed. G. W. Kronk (Tucson: University of Arizona Press), 391 [Google Scholar]
- Cochran, A. L., & Schleicher, D. G. 1993, Icarus, 105, 235 [Google Scholar]
- Cochran, A. L., Barker, E. S., Ramseyer, T. F., & Storrs, A. D. 1992, Icarus, 98, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Combi, M. R., Bertaux, J.-L., Quémerais, E., et al. 2014, AJ, 147, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Crovisier, J., Biver, N., Bockelée-Morvan, D., & Colom, P. 2009, Planet. Space Sci., 57, 1162 [NASA ADS] [CrossRef] [Google Scholar]
- Farnham, T., Schleicher, D., & A’Hearn, M. 2000, Icarus, 147, 180 [NASA ADS] [CrossRef] [Google Scholar]
- Festou, M. C. 1981, A&A, 95, 69 [NASA ADS] [Google Scholar]
- Fink, U. 2009, Icarus, 201, 311 [Google Scholar]
- Fray, N., Bénilan, Y., Cottin, H., Gazeau, M.-C., & Crovisier, J. 2005, Planet. Space Sci., 53, 1243 [NASA ADS] [CrossRef] [Google Scholar]
- Gomes, R., Levison, H. F., Tsiganis, K., & Morbidelli, A. 2005, Nature, 435, 466 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Haser, L. 1957, Bulletin de l’Académie Royale des Sciences de Belgique, 63, 739 [Google Scholar]
- Jehin, E., Gillon, M., Queloz, D., et al. 2011, The Messenger, 145, 2 [NASA ADS] [Google Scholar]
- Jewitt, D., & Luu, J. 1989, AJ, 97, 1766 [NASA ADS] [CrossRef] [Google Scholar]
- Jewitt, D. C., & Meech, K. J. 1987, ApJ, 317, 992 [NASA ADS] [CrossRef] [Google Scholar]
- Jewitt, D. C., Soifer, B. T., Neugebauer, G., Matthews, K., & Danielson, G. E. 1982, AJ, 87, 1854 [NASA ADS] [CrossRef] [Google Scholar]
- Knight, M. M., & Schleicher, D. G. 2013, Icarus, 222, 691 [NASA ADS] [CrossRef] [Google Scholar]
- Lara, L.-M., Tozzi, G. P., Boehnhardt, H., DiMartino, M., & Schulz, R. 2004, A&A, 422, 717 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Larson, S. M., & Sekanina, Z. 1984, AJ, 89, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Leach, S., Stannard, P. R., & Gelbart, W. M. 1978, Mol. Phys., 36, 1119 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, Z.-Y., Lara, L. M., Vincent, J. B., & Ip, W.-H. 2012, A&A, 537, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lin, Z.-Y., Lara, L. M., & Ip, W.-H. 2013, AJ, 146, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Meech, K. J., A’Hearn, M. F., Adams, J. A., et al. 2011, ApJ, 734, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Newburn, R. L., & Spinrad, H. 1989, AJ, 97, 552 [NASA ADS] [CrossRef] [Google Scholar]
- O’dell, C. R., Miller, C. O., Cochran, A. L., et al. 1991, ApJ, 368, 616 [NASA ADS] [CrossRef] [Google Scholar]
- Paganini, L., DiSanti, M. A., Mumma, M. J., et al. 2014, AJ, 147, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Randall, C. E., Schleicher, D. G., Ballou, R. G., & Osip, D. J. 1992, BAAS, 24, 1002 [NASA ADS] [Google Scholar]
- Rauer, H., Helbert, J., Arpigny, C., et al. 2003, A&A, 397, 1109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schleicher, D. G., & A’Hearn, M. F. 1988, ApJ, 331, 1058 [Google Scholar]
- Schleicher, D. G., & Farnham, T. L. 2004, in Photometry and imaging of the coma with narrowband filters, eds. M. C. Festou, H. U. Keller, & H. A. Weaver (Tucson: University of Arizona Press), 449 [Google Scholar]
- Schleicher, D. G., & Woodney, L. M. 2003, Icarus, 162, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Schleicher, D. G., Millis, R. L., & Birch, P. V. 1998a, Icarus, 132, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Schleicher, D. G., Millis, R. L., Osip, D. J., & Lederer, S. M. 1998b, Icarus, 131, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Schleicher, D. G., Woodney, L. M., & Millis, R. L. 2003, Icarus, 162, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Schleicher, D. G., Farnham, T. L., & Bair, A. N. 2007, in Planetary Atmospheres, LPI contribution, 1376, 103 [Google Scholar]
- Schulz, R., McFadden, L. A., Chamberlin, A. B., A’Hearn, M. F., & Schleicher, D. G. 1994, Icarus, 109, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Sekanina, Z. 1991, AJ, 102, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Solontoi, M., Ivezić, Ž., Jurić, M., et al. 2012, Icarus, 218, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Swings, P. 1941, Lick Observatory Bulletin, 19, 131 [Google Scholar]
- Valk, J. H., O’dell, C. R., Cochran, A. L., et al. 1992, ApJ, 388, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Weissman, P. R. 1987, A&A, 187, 873 [NASA ADS] [Google Scholar]
All Tables
Narrowband filters characteristics: central wavelength (CWL), full width at half maximum (FWHM), and peak transmission (T%).
The parent (LP) and daughter (LD) scalelengths used for the computation of OH, NH, CN, C3, and C2 production rates with the Haser model.
Pre- and post-perihelion fitted power-law slopes for OH, NH, CN, C3, and C2 the heliocentric dependences of the production rates.
C/2012 F6 (Lemmon) pre- and post-perihelion fitted power-law slopes for A(θ)fρ computed from the UC, BC, GC, and RC filters.
All Figures
 |
Fig. 1 Original images of comet C/2012 F6 (Lemmon) and the corresponding radial profiles for OH, NH, CN, C3, and C2. These images were taken on January 7, 2013, while the comet was 1.57 au from the Sun. We plotted the original radial profile (dark triangles), the radial profile obtained after dust subtraction (red circles), and the adjusted Haser model (black line). As comet Lemmon is relatively gaseous, the original radial profile and the dust-subtracted profile are mostly overlapping. The images are oriented north up and east left. The field of view is 22′ × 22′. |
| In the text | |
 |
Fig. 2 Logarithm of the OH, NH, CN, C3, and C2 production rates as a function of the heliocentric distance r (au). The x-axis is interrupted at perihelion (0.73 au). |
| In the text | |
 |
Fig. 3 Logarithm of OH, NH, CN, C3, and C2 production rates of C/2012 F6 (Lemmon) as a function of the logarithm of the heliocentric distance (r). Pre-perihelion data points are represented with filled symbols and post-perihelion data points are represented with open symbols. The origin of the x-axis is perihelion. Solid lines are linear fits of the production rates variation with the pre-perihelion heliocentric distance. Dotted lines are the same for post-perihelion values. |
| In the text | |
 |
Fig. 4 Logarithm of comet C/2012 F6 (Lemmon) A(θ)fρ computed from UC, BC, GC, and RC narrowband continuum filters as a function of the logarithm of the heliocentric distance r (au). Pre-perihelion data are represented with filled symbols and post-perihelion data with open symbols. The origin of the x-axis is perihelion. Solid lines represent linear fits of the A(θ)fρ variation with the pre-perihelion heliocentric distance. Dotted lines are the same for post-perihelion values. |
| In the text | |
 |
Fig. 5 Dust brightness radial profiles of comet C/2012 F6 (Lemmon) at 6 epochs are represented: 2012-Dec.-22 (104 km = 22.5′′), 2013-Jan-07 (104 km = 17.5′′), 2013-Feb-07 (104 km = 13.2′′), 2013-Mar-04 (104 km = 16.1′′), 2013-May-14 (104 km = 22.9′′), 2013-Jun-05 (104 km = 23.3′′). The profile extraction was made for 20° wide wedges in the tail direction, i.e., the anti-sunward direction (black crosses), the sunward direction (dark blue triangles), and the ambient coma perpendicular to the sunward direction. A 1 /ρ profile is overlaid on each plot. |
| In the text | |
 |
Fig. 6 Evolution of the dust normalized reflectivity gradient of comet C/2012 F6 (Lemmon) computed from A(θ)fρ values as a function of the heliocentric distance. The origin of the x-axis is the perihelion. Pre-perihelion values are represented with full symbols and post-perihelion values with empty symbols. The dust color is computed from RC and UC filters (top), RC and BC filters (middle), and RC and GC filters (bottom). |
| In the text | |
 |
Fig. 7 Dust normalized reflectivity gradient as a function of nucleocentric distance (ρ) for the RG-GC continuum pair. The evolution of dust color with cometocentric distance is plotted for five dates sampling our observing run. |
| In the text | |
 |
Fig. 8 Ratio of C2 to CN (top) and C3 to CN (bottom) production rates as a function of the heliocentric distance. The x-axis origin is the perihelion. Pre-perihelion values are represented with filled symbols and post-perihelion values with open symbols. |
| In the text | |
 |
Fig. 9 Logarithm of the ratio of C2 (top) and C3 to OH production against logarithm of the ratio of CN to OH and their error bars. Pre-perihelion values are represented with filled symbols and post-perihelion values with open symbols. The solid red line indicates the evolution of comet Lemmon between December 11 and January 13 and the dashed line between February 7 and March 4. |
| In the text | |
 |
Fig. 10 Ratio of A(θ)fρ to CN (top) and OH (bottom) production rates as a function of the heliocentric distance. The x-axis origin is the perihelion. Pre-perihelion values are represented with filled symbols and post-perihelion values with empty symbols. A(θ)fρ values have not been corrected for the phase angle effect. |
| In the text | |
 |
Fig. 11 Representative CN image from February 12, 2013, and three different enhancement techniques. The original image of the comet is shown at the upper left of the panel. At the upper right, the removal of an azimuthal median profile is shown. The results of the rotational and Larson-Sekanina filters are shown respectively at the bottom left and right of the figure. The images are oriented north up and east left. The field of view is 4.3′ × 4.3′. The arrow indicates the direction of the Sun. |
| In the text | |
 |
Fig. 12 C/2012 F6 (Lemmon) enhanced OH, NH, CN, C3, C2, and RC images from January 13 (top panel), February 25 (middle panel), and May 14 (bottom panel). Each image is enhanced by Larson-Sekanina filtering. The field of view is 4.3′ × 4.3′ and images are oriented with north up and east left. The arrow indicates the direction of the Sun. |
| In the text | |
 |
Fig. 13 C/2012 F6 (Lemmon) CN images processed with Larson-Sekanina filtering (left) and azimuthal median profile subtraction (right) acquired between February 7 and February 12, 2013. The images have been sorted out by rotational phase assuming a rotation period of 9.52 h and a zero point on February 7.16. All images are oriented with north up and east left. The field of view is 4.3′ × 4.3′. |
| In the text | |
 |
Fig. 14 Result of C/2012 F6 (Lemmon) rotation analysis. CN images from February 9 to February 25 have been normalized and divided between each other. We plot the RMS resulting from each division as a function of the time difference between the images. Minima in the RMS repeat with the nucleus rotation period. We measured a period of 9.52 ± 0.05 h from 13 matching pairs between February 9 and February 25. |
| In the text | |
 |
Fig. 15 Representative OH (left) and RC (right) images from January 12, 2013, processed by removing the azimuthal median profile. Since the signal-to-noise ratio in the OH images is low and since we could not see any variation between images from the same night, we added three processed OH images from January 13 to obtain the result presented here. The images are oriented north up and east left. The field of view is 4.3′ × 4.3′. The arrow indicates the direction of the Sun. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


