| Issue |
A&A
Volume 573, January 2015
|
|
|---|---|---|
| Article Number | L7 | |
| Number of page(s) | 4 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201425264 | |
| Published online | 23 December 2014 | |
Gamma-ray burst engines may have no memory
Department of Physics and Earth Sciences, University of Ferrara, via Saragat 1, 44122 Ferrara, Italy
e-mail: adriano.baldeschi@student.unife.it, guidorzi@fe.infn.it
Received: 3 November 2014
Accepted: 25 November 2014
Context. A sizeable fraction of gamma-ray burst (GRB) time profiles consist of a temporal sequence of pulses. The nature of this stochastic process carries information on how GRB inner engines work. The so-called interpulse time defines the interval between adjacent pulses, excluding the long quiescence periods during which the signal drops to the background level. It was found by many authors in the past that interpulse times are lognormally distributed, at variance with the exponential case that is expected for a memoryless process.
Aims. We investigated whether the simple hypothesis of a temporally uncorrelated sequence of pulses is really to be rejected, as a lognormal distribution necessarily implies.
Methods. We selected and analysed a number of multi-peaked CGRO/BATSE GRBs and simulated similar time profiles, with the crucial difference that we assumed exponentially distributed interpulse times, as is expected for a memoryless stationary Poisson process. We then identified peaks in both data sets using a novel peak search algorithm, which is more efficient than others used in the past.
Results. We independently confirmed that the observed interpulse time distribution is approximately lognormal. However, we found the same results on the simulated profiles, in spite of the intrinsic exponential distribution. Although intrinsic lognormality cannot be ruled out, this shows that intrinsic interpulse time distribution in real data could still be exponential, while the observed lognormal could be ascribed to the low efficiency of peak search algorithms at short values combined with the limitations of a bin-integrated profile.
Conclusions. Our result suggests that GRB engines may emit pulses after the fashion of nuclear radioactive decay, that is, as a memoryless process.
Key words: gamma-ray burst: general / methods: statistical
© ESO, 2014
1. Introduction
Decades after their discovery, the prompt emission of gamma-ray bursts (GRBs) is still one of the least understood aspects of the GRB phenomenon. While it is established today that most (if not all) long-duration GRBs are connected with the final collapse of some kind of massive stars, the nature of the inner engine and the process(es) through which γ-rays are released are unclear (see Kumar & Zhang 2014 for a recent comprehensive review). GRB prompt emission time-profiles consist of one or several pulses without compelling evidence for periodic patterns despite occasional claims (Beskin et al. 2010; Cenko et al. 2010; de Luca et al. 2010). The information connected with the time interval between two adjacent pulses, the so-called interpulse time (IT), and its possible correlations with properties of the same pulses can shed light on the process at work (Ramirez-Ruiz & Merloni 2001; Ramirez-Ruiz et al. 2001). Within the context of internal shocks, the IT distribution (ITD) is tightly connected with the emission-time history of the inner engine (Kobayashi et al. 1997). Specifically, it can reveal the nature of the stochastic process ruling the production of elementary energy releases in the form of pulses, which is likely driven by the way accretion works in GRB engines (e.g., Tchekhovskoy & Giannios 2014; Bernardini et al. 2013).
The importance of ITDs cannot be overstated, as is the case for other different astrophysical sources, such as the Sun (e.g., Wheatland 2000; Aschwanden & McTiernan 2010), and outbursting magnetars (Göǧüşet al. 1999, 2000; Gavriil et al. 2004). In the case of GRBs a number of papers have investigated this property (McBreen et al. 1994; Norris et al. 1996). The different peak detection algorithms (Li & Fenimore 1996; Nakar & Piran 2002; Drago & Pagliara 2007; Bhat et al. 2012) or techniques (Quilligan et al. 2002) yielded as the main result that the GRB ITD is generally well described by a lognormal with mean values ≲1 s, with evidence for a power-law excess at relatively long (Δt> 5–10 s) ITs. These long, rare ITs during which the GRB signal drops to background are often referred to as quiescent times (QTs) and are interpreted as caused by something different from what rules the shorter and more frequent ITs (e.g., Drago et al. 2008; Tchekhovskoy & Giannios 2014). The identification of QTs in individual time profiles was made by different authors in different ways through different operative, loose definitions, similarly to what was done for emission precursors (e.g., Burlon et al. 2008), even though a recent time-frequency algorithm adapted from gravitational wave data analysis seems to provide an interestingly less subjective alternative (Charisi et al. 2014).
So far, most efforts were focused on identifying and interpreting QTs as opposed to ITs, especially when extremely long-duration (~102–103 s) GRBs with comparably long QTs are occasionally observed. This has led part of the GRB community to think in terms of a class of their own, known as ultra-long GRBs (Gendre et al. 2013; Levan et al. 2014; Evans et al. 2014; see however Virgili et al. 2013; Zhang et al. 2014). However, the other side of the ITD, the short IT tail, did not raise much speculation, although the nature of lognormal, that is, the departure from a pure exponential distribution, would imply some kind of memory in the GRB engine. In other words, a pure memoryless engine, when one neglects QTs, gives an exponential ITD that deviates from lognormality. This means that one observes fewer short ITs than expected for a memoryless engine. Before trying to interpret the physical as well as statistical origin of the lognormal ITD (Ioka & Nakamura 2002), it is therefore crucial to establish to what extent the dearth of short interpulse-times is due to the low efficiency of algorithm(s). In other words, it is key for understanding whether the lognormal distribution, particularly at short values, is intrinsic.
Our aim is to test whether the pure memoryless case is to be rejected when the effects of the peak detection algorithms are carefully taken into account by means of synthetic light curves. More specifically, we simulate time profiles assuming exponentially distributed ITs that otherwise resemble real GRB profiles as closely as possible, and compare the corresponding ITDs with that of real data. In Sect. 2 we describe the real data sample selection and how simulations were carried out. Results and implications are then reported and discussed in Sects. 3 and 4.
2. Data analysis
2.1. Real data selection
We started from the light curves of the BATSE catalogue made available by the team as concatenated burst data with 64 ms temporal resolution in four energy channels1. We took the summed light curve of the four energy channels and preliminarily subtracted the background by fitting it with polynomials of up to fourth degree, as suggested by the BATSE team (e.g., Guidorzi 2005), and then applied MEPSA (Guidorzi 2014b,a), a novel peak search algorithm. By selecting the GRBs with at least 20 peaks each we formed a final sample of 85 GRB light curves, which we hereafter refer to as the real sample. The choice of 20 peaks is somewhat arbitrary, and it was aimed at ensuring statistical significance. The choice of the BATSE catalogue was driven by the unrivalled wealth of multi-peaked GRBs. In principle, if there were many pulses narrower than 64 ms, the peak search would not be optimally set up. However, most GRBs have minimum variability timescales above tens of milliseconds (Golkhou & Butler 2014), and autocorrelation (Fenimore et al. 1995) and pulse-fitting (Norris et al. 1996) studies find typical pulse widths of ≳0.2 s in the BATSE energy ranges.
That we used MEPSA instead of other algorithms, such as the popular one proposed by (Li & Fenimore 1996, hereafter LF), was motivated by its much lower false-positive probability (FP; 1–2 × 10-5 to be compared with 3–5 × 10-3 FP bin-1), particularly when the signal drops to background, and by its capability to detect slowly varying, dim peaks. Essentially, MEPSA simultaneously compares various moving intervals (with different lengths) with adjacent bins against a number of thresholds (in units of statistical noise) that must be fulfilled simultaneously to trigger at least one out of 39 different criteria. This search was carried out over increasingly longer timescales (Guidorzi 2014a). The basic principle is very similar to that of LF, but, in addition, MEPSA has a lower FP rate because multiple conditions are to be fulfilled, while its sensitivity to dim and long-lasting peaks is ensured by its multiple-timescale monitoring.
2.2. Simulated data set
The light curves were simulated assuming exponentially distributed interpulse times. To this aim, much effort was put so as to ensure that the simulated time-profiles were as alike to observed GRB profiles as possible. We assumed the shape by Norris et al. (1996) for a single shot, which well reproduces a so-called fast-rise exponential decay (FRED), ![\begin{eqnarray} f(t) & = & A\, \exp{[-(|t-t_{\rm p}|/\tau_{\rm r})^\nu]}, \quad (t<t_{\rm p})\nonumber\\ & = & A\, \exp{[-(|t-t_{\rm p}|/\tau_{\rm d})^\nu]}, \quad (t>t_{\rm p})\;, \label{eq:shot} \end{eqnarray}](/articles/aa/full_html/2015/01/aa25264-14/aa25264-14-eq12.png) (1)where A is the peak counts, tp is the peak time, τr,d are the rise and decay times, and ν is the so-called peakedness, which determines the pulse sharpness. Except for tp, these parameters were found to be approximately lognormally distributed (Norris et al. 1996; Quilligan et al. 2002), so we assumed corresponding distributions to reproduce the variety of observed time profiles. We verified that the uncertainties on these distribution parameters had a negligible impact on the results. We generated random light curves for each GRB of the real sample to mimic the average temporal features of the real curve as closely as possible.
(1)where A is the peak counts, tp is the peak time, τr,d are the rise and decay times, and ν is the so-called peakedness, which determines the pulse sharpness. Except for tp, these parameters were found to be approximately lognormally distributed (Norris et al. 1996; Quilligan et al. 2002), so we assumed corresponding distributions to reproduce the variety of observed time profiles. We verified that the uncertainties on these distribution parameters had a negligible impact on the results. We generated random light curves for each GRB of the real sample to mimic the average temporal features of the real curve as closely as possible.
The more two adjacent pulses overlap, the more difficult for any peak search algorithm to identify them as separate pulses. The so-called separability, which describes how easily a given pulse can be separated from the adjacent ones, depends on both the pulse duration and the ITs next to it, and affects the chance MEPSA has to identify it. In this context, using algorithms such as LF instead of MEPSA exacerbates the situation (Guidorzi 2014a). In addition, the signal-to-noise ratio of the pulse itself affects its detectability. We therefore ensured that both properties, pulse duration and peak counts, were as similar as possible to what is observed in the corresponding real GRB curve. We summarise in the following steps the procedure we adopted:
-
1.
Simulate an exponential ITD whose expected value equals themean value of the real ITD of a given profile from the real sample.The mean value is computed by excluding possible QTs from thelight curve. In Sect. 2.3 we describe how wedefined QTs. The intrinsic expected value of the real curve isprobably shorter (by about a factor F) than the observed value, because very close peaks cannot be resolved. This turns into a loss of true, short ITs. Starting from 1, we determined F by assuming progressively decreasing values, until the overall real and simulated ITDs (as obtained by applying MEPSA) were compatible according to a Kolmogorov-Smirnov (KS) test. F was found only once for all GRBs together and was 0.67.
-
2.
Simulate lognormally distributed peak counts whose expected value and variance were preliminarily estimated from the data of the corresponding real light curve.
-
3.
Simulate lognormally distributed values for τr and τd, with expected values equal to the corresponding observed real values. The full width at half maximum (FWHM) of one pulse is (τr + τd)(ln2)1 /ν.
-
4.
Finally, we added the background observed in the real curve and added Poisson statistical noise.
The peakedness is not a crucial parameter to our aim, so we fixed it to ν = 1.5, as is typically observed in real data (Norris et al. 1996). The corresponding typical FWHM is therefore 0.78 (τr + τd).
2.3. Quiescent times
For both the real and the simulated ITDs we preliminarily removed the so-called quiescent times, that is, ITs during which the GRB signal drops to the background level for a relatively long time (Nakar & Piran 2002; Quilligan et al. 2002; Drago & Pagliara 2007). There is no rigorous definition of QT, since the evidence for them as a separate class comes from a power-law tail in the ITD in excess of the lognormal distribution tail (Nakar & Piran 2002; Quilligan et al. 2002; Drago & Pagliara 2007).
Hence we adopted the following operative procedure to identify QTs: Let tp,i and tp,i + 1 be the times of two adjacent peaks. The interpulse time Δti = tp,i + 1 − tp,i is said to be a QT when it fulfils the following requirements:
-
1.
Δti ≥ 5 s;
-
2.
there exists at least one time bin tk (tp,i<tk<tp,i + 1) such that ck ≤ 3 σk, that is, the signal drops to background within 3σ (σk is the error on the background-subtracted counts ck);
-
3.
let ti,1 = min(tk) and ti,2 = max(tk), calculated over the tk that fulfil 2.; let cM,i = median(cj) and σM,i = median(σj) (ti,1 ≤ tj ≤ ti,2). The condition to be fulfilled is cM,i ≤ σM,i.
While condition 1 demands that the QT candidate is long enough, conditions 2 and 3 ensure that the median signal is compatible with background. The lowest value of 5 s was estimated from the time at which the power-law excess becomes visible with respect to the lognormal tail in the ITD (see also Quilligan et al. 2002; Drago & Pagliara 2007).
3. Results
Following the procedure described in Sect. 2, we obtained three different ITDs for each event of our real sample: that on the real curve (real detected, RD), the true one based on the peak times as they were generated in the simulated curve (simulated true, ST), and the one obtained by applying MEPSA to the simulated curve (simulated detected, SD). We detected 2220 ITs in the real sample in total. In the ST sample we generated 3548 ITs, 2298 of which were measured with MEPSA. Thus, RD, ST, and SD ITDs collect 2220, 3548, and 2298 ITs, respectively. For each simulated curve the peak search was carried out over a time interval with the same duration as that of the interval considered for the corresponding real curve. The different size of the RD and SD samples is 78, which is compatible with expectations from Poisson statistics, 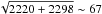 .
.
Since each real GRB has its own average peak rate, we had to rescale based on each individual mean rate before merging the corresponding ITD. Following Li & Fenimore (1996), we rescaled the RD and SD ITDs of each GRB by subtracting the logarithmic mean and rescaling by the sample variance. This way, each individual ITD has null mean and unitary variance. We finally merged the entire sample into RD and SD total ITDs for all GRBs together, which we refer to as rescaled ITDs; they are displayed in Fig. 1. The rescaled (non-rescaled) RD and SD are indistinguishable according to a KS test, whose p-value is 9.2% (30%), and both appear to be lognormally distributed. Given the large number of ITs in each distribution, the KS test is correspondingly sensitive. Therefore, one cannot reject the hypothesis that the corresponding exponential ST ITD may also well be the intrinsic distribution of real data. Figure 1 shows that the rescaled SD and RD ITDs look broadly compatible with a lognormal, although a rigorous χ2 test for lognormality yields <1% p-values in both cases.
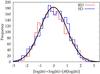 |
Fig. 1 Rescaled RD (thin solid) and SD (dashed) ITDs, including 2220 and 2298 interpulse times, respectively. The thick solid line is N(0,1) and is normalised to the SD sample. |
 |
Fig. 2 ITDs of real detected (thin solid), simulated true (thick solid), and simulated detected (dashed). A close-up in the short interpulse-time region is shown in the inset. |
The effect of the peak detection algorithm efficiency on the observed distribution is shown by the comparison between ST and SD in Fig. 2. At Δt< 0.8 s (that is, 12 times the temporal bin size of 64 ms) the SD significantly deviates from the ST ITD: the dearth of short ITs is due to the low efficiency of MEPSA when nearby pulses become hardly separable (Guidorzi 2014a).
We also explored the compatibility of an intrinsic lognormal ITD with real data. We carried out the same simulations and found that the best match between rescaled (non-rescaled) SD and RD yielded a KS p-value of 32% (4.2%).
Taken at face value, these results indicate that the lognormal ITD observed in real data, in particular the dearth of short values compared with what is expected for a (memoryless) stationary Poisson process, might be intrinsic, but it might also be an artefact of the low efficiency of the peak detection algorithms, even at relatively long ITs compared with the binning time of the profile (Δt ≲ 10 × 64 ms). Thus, lognormality is not necessarily an intrinsic property of the real ITD.
 |
Fig. 3 Example of a real curve (bottom) and of its corresponding simulated one (top) assuming an exponential ITD. |
Figure 3 illustrates an example of real and corresponding simulated curves. In the real curve there is a slowly varying component superposed on peaks that have no counterpart in the simulations. This kind of low pedestal is strongest in the softest energy channels and almost absent from the hardest channels, as was first pointed out in the hard X-ray (2–28 keV) prompt emission of BeppoSAX GRBs (Vetere et al. 2006). For our purposes, its absence in simulated curves is not a problem since ITs are given by the spikier activity in the real and simulated data.
4. Discussion and conclusions
Using a novel peak search algorithm, we confirmed previous results that ITDs in multi-peaked GRBs are approximately lognormal when the long-tail of QTs is not considered. Surprisingly, it had not been investigated before whether the lack of short ITs, even at Δt a factor of a few longer than the temporal binning size, might entirely be an artefact of the low efficiency of peak searches. We amended this lack through simulated profiles that share common properties with the observed real profiles in terms of peak counts, pulse durations, and measured ITs, as proved by KS tests. What is more, we proved that assuming an intrinsic memoryless process in which GRB engines emit pulses according to a stationary Poisson process on timescales Δt< 5–10 s (that is, neglecting QTs), the true exponential ITD still cannot be recovered because of the low efficiency of peak detection algorithms in the short IT tail. In particular, we were able to reproduce a measured ITD that is compatible with the real one and approaches lognormality, in spite of its intrinsic exponential nature.
While lognormality is reminiscent of central limit theorem and probably is the result of the multiplicative combination of independent variables (Ioka & Nakamura 2002), our results show that the simplest hypothesis one can make about the way GRB engines work, that is, an uncorrelated process on relatively short time intervals, cannot be rejected.
The immediate implication is that GRB engines possibly do not retain any memory after they have just emitted a pulse and do not, on average, wait for some more time before emitting the next one. We therefore conclude that the lognormality of
the observed ITDs in real GRBs may not be intrinsic, since it can entirely be explained as an artefact of peak-finding algorithms. In terms of accretion process, our results suggest that the individual accretion episodes that shape the GRB prompt emission profiles in terms of pulses may on average be uncorrelated, as long as long quiescent periods are not considered. This can help constrain the way magnetic flux repeatedly induces and halts accretion, if it is verified (Bernardini et al. 2013; Tchekhovskoy & Giannios 2014). Another possibility is that current-driven instabilities in strongly magnetised jets can lead to non-axisymmetric jet structures which, combined with beaming effects and even small changes in the Lorentz factor, are responsible for the observed short timescale variability (Levinson & Begelman 2013). Alternatively, short timescale variability could result from magnetic reconnection episodes triggered by collisions between magnetised shells (Zhang & Yan 2011), which do not necessarily require temporal correlation, in the same way that internal shocks do not, either.
Acknowledgments
We are grateful to the referee for very useful comments that helped improve the paper. We also thank S. Dichiara, F. Frontera, P. Rosati, L. Amati, A. Drago for useful discussions. PRIN MIUR project on “Gamma Ray Bursts: from progenitors to physics of the prompt emission process”, P. I. F. Frontera (Prot. 2009 ERC3HT) is acknowledged.
References
- Aschwanden, M. J., & McTiernan, J. M. 2010, ApJ, 717, 683 [NASA ADS] [CrossRef] [Google Scholar]
- Bernardini, M. G., Campana, S., Ghisellini, G., et al. 2013, ApJ, 775, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Beskin, G., Karpov, S., Bondar, S., et al. 2010, ApJ, 719, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Bhat, P. N., Briggs, M. S., Connaughton, V., et al. 2012, ApJ, 744, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Burlon, D., Ghirlanda, G., Ghisellini, G., et al. 2008, ApJ, 685, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Cenko, S. B., Butler, N. R., Ofek, E. O., et al. 2010, AJ, 140, 224 [NASA ADS] [CrossRef] [Google Scholar]
- Charisi, M., Márka, S., & Bartos, I. 2014 [arXiv:1409.2491] [Google Scholar]
- de Luca, A., Esposito, P., Israel, G. L., et al. 2010, MNRAS, 402, 1870 [NASA ADS] [CrossRef] [Google Scholar]
- Drago, A., & Pagliara, G. 2007, ApJ, 665, 1227 [Google Scholar]
- Drago, A., Pagliara, G., & Schaffner-Bielich, J. 2008, J. Phys. G Nucl. Phys., 35, 014052 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, P. A., Willingale, R., Osborne, J. P., et al. 2014, MNRAS, 444, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Fenimore, E. E., in ’t Zand, J. J. M., Norris, J. P., Bonnell, J. T., & Nemiroff, R. J. 1995, ApJ, 448, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Gavriil, F. P., Kaspi, V. M., & Woods, P. M. 2004, ApJ, 607, 959 [NASA ADS] [CrossRef] [Google Scholar]
- Gendre, B., Stratta, G., Atteia, J. L., et al. 2013, ApJ, 766, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Golkhou, V. Z., & Butler, N. R. 2014, ApJ, 787, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Göǧüş, E., Woods, P. M., Kouveliotou, C., et al. 1999, ApJ, 526, L93 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Göǧüş, E., Woods, P. M., Kouveliotou, C., et al. 2000, ApJ, 532, L121 [NASA ADS] [CrossRef] [Google Scholar]
- Guidorzi, C. 2005, MNRAS, 364, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Guidorzi, C. 2014a, Astron. Comput., submitted [Google Scholar]
- Guidorzi, C. 2014b, Astrophys. Source Code Lib. [record ascl:1410.002] [Google Scholar]
- Ioka, K., & Nakamura, T. 2002, ApJ, 570, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Kobayashi, S., Piran, T., & Sari, R. 1997, ApJ, 490, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Kumar, P., & Zhang, B. 2014, Phys. Rep., in press [arXiv:1410.0679] [Google Scholar]
- Levan, A. J., Tanvir, N. R., Starling, R. L. C., et al. 2014, ApJ, 781, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Levinson, A., & Begelman, M. C. 2013, ApJ, 764, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Li, H., & Fenimore, E. E. 1996, ApJ, 469, L115 [NASA ADS] [CrossRef] [Google Scholar]
- McBreen, B., Hurley, K. J., Long, R., & Metcalfe, L. 1994, MNRAS, 271, 662 [NASA ADS] [CrossRef] [Google Scholar]
- Nakar, E., & Piran, T. 2002, MNRAS, 331, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, J. P., Nemiroff, R. J., Bonnell, J. T., et al. 1996, ApJ, 459, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Quilligan, F., McBreen, B., Hanlon, L., et al. 2002, A&A, 385, 377 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramirez-Ruiz, E., & Merloni, A. 2001, MNRAS, 320, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Ramirez-Ruiz, E., Merloni, A., & Rees, M. J. 2001, MNRAS, 324, 1147 [NASA ADS] [CrossRef] [Google Scholar]
- Tchekhovskoy, A., & Giannios, D. 2014, MNRAS, submitted [arXiv:1409.4414] [Google Scholar]
- Vetere, L., Massaro, E., Costa, E., Soffitta, P., & Ventura, G. 2006, A&A, 447, 499 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Virgili, F. J., Mundell, C. G., Pal’shin, V., et al. 2013, ApJ, 778, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Wheatland, M. S. 2000, ApJ, 536, L109 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Zhang, B., & Yan, H. 2011, ApJ, 726, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, B.-B., Zhang, B., Murase, K., Connaughton, V., & Briggs, M. S. 2014, ApJ, 787, 66 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Rescaled RD (thin solid) and SD (dashed) ITDs, including 2220 and 2298 interpulse times, respectively. The thick solid line is N(0,1) and is normalised to the SD sample. |
| In the text | |
 |
Fig. 2 ITDs of real detected (thin solid), simulated true (thick solid), and simulated detected (dashed). A close-up in the short interpulse-time region is shown in the inset. |
| In the text | |
 |
Fig. 3 Example of a real curve (bottom) and of its corresponding simulated one (top) assuming an exponential ITD. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


