| Issue |
A&A
Volume 573, January 2015
|
|
|---|---|---|
| Article Number | A37 | |
| Number of page(s) | 6 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201424667 | |
| Published online | 12 December 2014 | |
The structure of TeV-bright shell-type supernova remnants
1 Yunnan Observatories, Chinese Academy of Sciences, 650011 Kunming, PR China
e-mail: chyy@ynao.ac.cn
2 Key Laboratory for the Structure and Evolution of Celestial Objects, Chinese Academy of Sciences, 650011 Kunming, PR China
3 Key Laboratory of Dark Matter and Space Astronomy, Purple Mountain Observatory, Chinese Academy of Science, 210008 Nanjing, PR China
e-mail: liusm@pmo.ac.cn
4 Department of Astronomy, Yunnan University, 650091 Kunming, PR China
e-mail: fangjun@ynu.edu.cn
5 Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA
Received: 24 July 2014
Accepted: 26 September 2014
Aims. Two-dimensional magnetohydrodynamic (MHD) simulations are used to model the emission properties of TeV-bright shell-type supernova remnants (SNRs) and to explore their nature.
Methods. In the leptonic scenario for the TeV emission, the γ-ray emission is produced via inverse Compton scattering of background soft photons by high-energy electrons accelerated by the shocks of the SNRs. In a previous paper, we showed that since the energy densities of the cosmic microwave background radiation and that of the IR/optical background photons are much higher than that of the photons produced by the same high-energy electrons via the synchrotron process, the observed correlation between X-ray and TeV brightness of SNR RX J1713.7-3946 can be readily explained with the assumption that the energy density of relativistic electrons is proportional to that of the magnetic field. The TeV emissivity is therefore proportional to the magnetic field energy density and MHD simulations can be used to model the TeV structure of such remnants directly. Two-dimensional MHD simulations for SNRs are then performed under the assumption that the ambient interstellar medium is turbulent with the magnetic field and density fluctuations, following a Kolmogorov-like power-law spectrum.
Results. (1) As expected, these simulations confirm early 1D and 2D modelings of these sources, namely the hydrodynamical evolution of the shock waves and amplification of magnetic field by Rayleigh-Taylor convective flows and by shocks propagating in a turbulent medium; (2) we reproduce rather complex morphological structure for γ-rays, for example, the bright thin rim and significant asymmetry, suggesting intrinsic variations of the source morphology not related to the structure of the progenitor and environment; and (3) the observed radial profile of several remnants are well reproduced with an ambient medium density of 0.1−1 cm-3. An even lower ambient density leads to a sharper drop of the TeV brightness with radius than what is observed near the outer edge of these remnants.
Conclusions. In a turbulent background medium, we can reproduce the observed characteristics of several shell-type TeV SNRs with reasonable parameters except for a higher ambient density than that inferred from X-ray observations.
Key words: turbulence / shock waves / radiation mechanisms: non-thermal
© ESO, 2014
1. Introduction
It is generally believed that supernova remnants (SNRs) are the main acceleration sites of Galactic cosmic rays. Since charged cosmic ray particles escaping from SNRs are mixed in the Galactic magnetic fields and cannot be used to image their sources of origin directly, detection of high-energy γ-rays from SNRs is very useful for testing whether SNRs are responsible for the origin of the bulk of the cosmic rays observed at the Earth. However, an open question is whether the observed high-energy γ-ray emission from an SNR has a hadronic or a leptonic origin (e.g., Katz & Waxman 2008; Yuan et al. 2012).
Nonthermal photons from SNRs in the radio to X-ray bands are produced by the synchrotron radiation of relativistic electrons. The detection of synchrotron X-rays in some SNRs shows that electrons can be accelerated efficiently to TeV energies by shocks in SNRs (e.g., Koyama et al. 1995). Although several young SNRs have been detected to emit GeV to TeV γ-rays (e.g., Abdo et al. 2011; Abramowski et al. 2011), it is not clear whether these SNRs produce high-energy protons or not. High-energy γ-ray photons can be produced by either the inverse-Compton(IC) process or π0-decay, corresponding to the leptonic or hadronic origin, respectively. For example, γ-ray emission from SNR RX J1713.7-3946 is likely produced by very energetic electrons radiating through IC scattering against a photon background (Abdo et al. 2011). Objects like the Tycho SNR likely emit GeV γ-rays via the decay of neutral pions produced in nuclear collisions between shock accelerated relativistic nuclei and those in the background plasma (Morlino & Caprioli 2012; Ackermann et al. 2013).
Recent X-ray and γ-TeV observations have revealed a group of TeV-bright shell-type SNRs with SNR RX J1713.7-3946 as a prototype. Similar to SNR RX J1713.7-3946, no thermal emission has been detected from SNRs RX J0852.0-4622 and HESS J1731-347; the γ-ray luminosity is only a factor of a few lower than the X-ray luminosity; and they have very hard spectra in the ~GeV energy range, which favor the leptonic origin for the GeV−TeV emission with a low mean magnetic field of ~ 10 μGauss (Li et al. 2011; Ellison et al. 2012; Yuan et al. 2012; Yang et al. 2014). Rapid variations of X-ray filaments with a width of about 0.1 light year on a timescale of ~ 1 year have been interpreted as due to radiative energy loss of TeV electrons in strong (~ 1 mG) fields (Uchiyama et al. 2007). The strong field may only exist in these filaments with a very small volume filling factor, and alternative explanations for this variability with a weak mean field have been proposed as well (Bykov et al. 2008; Liu et al. 2008). Although thermal emission has been detected from SNR RCW 86 (Williams et al. 2011), the characteristics of nonthermal emission from this remnant is very similar to other TeV-bright shell-type SNRs (Lemoine-Goumard et al. 2012; Yuan et al. 2014). These results imply a universal mechanism of particle acceleration by shocks in SNRs (Yuan et al. 2012).
The nonthermal emission of these remnants has a well-defined shell structure and there is evidence that the relative mean thickness of the emitting shell varies from remnant to remnant (Aharonian et al. 2006, 2007). Previously 1D modeling of particle acceleration in SNRs has been used to study the radial brightness profile in the hadronic scenario (Berezhko & Völk 2010). A detailed study of the source structure with magnetohydrodynamic (MHD) simulations has not been carried out. Although these remnants have a complicated appearance in X-rays and γ-rays with significant fluctuations in both the radial and azimuthal directions, there is a good correlation between the X-ray and γ-ray brightness (Acero et al. 2009). Magnetic fields play an important role in collisionless astrophysical shocks and in the acceleration of charged particles. They can be amplified by cosmic ray induced streaming instability in the presence of efficient particle acceleration (e.g., Bell 2004; Riquelme & Spitkovsky 2009). In a turbulent medium, they can also be amplified by turbulent motion in the shock downstream (Giacalone & Jokipii 2007). This has been explored recently by Guo et al. (2012) who performed extensive 2D numerical simulations for an SNR blast wave interacting with a turbulent plasma background and found that the magnetic field can also be amplified by Rayleigh-Taylor convective flows induced at the contact discontinuity of the shock flows. In our previous paper (Yang & Liu 2013), we have shown that the observed correlation between X-ray and γ-ray brightness for SNR RXJ 1713.7-3946 suggests that the energy density of the accelerated electrons is proportional to that of the magnetic field in the leptonic scenario for the γ-ray emission. In this paper, we study the structure of these remnants and the effect of magnetic inhomogeneity on the TeV profile and morphology by using 2D MHD simulations.
Our 2D MHD simulations are based on the PLUTO code (Mignone et al. 2007). In Sect. 2, we describe the MHD model and show the magnetic field structure. In Sect. 3, an algorithm is proposed to convert the 2D magnetic field structure into a γ-ray image of the remnant and several simulations are done to fit the azimuthal averaged radial profile of the TeV brightness of the remnants mentioned above. Our discussion and conclusions are given in Sect. 4.
2. Model description
The numerical model has been described in Yang & Liu (2013). For the sake of completeness, we briefly summarize the key issues here. The dynamical evolution of an SNR shock propagating into a turbulent ambient medium is simulated with the time-dependent ideal MHD equations of mass, momentum, and energy conservation: ![\begin{eqnarray} &&\partial_t \rho+\nabla\cdot(\rho\vec{u} ) =0, \\ &&\partial_t \rho\vec{u}+\nabla\cdot\left(\rho{\vec{uu}-{\vec{BB}\over 4\pi}}\right)+ \nabla P^\prime =0 , \\[-0.5mm] &&\partial E +\nabla\cdot\left[(E+P^\prime){\vec{u}-{\vec{B}(\vec{u}\cdot \vec{B})\over 4\pi}}\right]=0, \end{eqnarray}](/articles/aa/full_html/2015/01/aa24667-14/aa24667-14-eq8.png) and the induction equation:
and the induction equation: 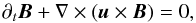 (4)where P′ = P + B2/ 8π is the total pressure with thermal pressure P and magnetic pressure B2/ 8π, E is the total energy density:
(4)where P′ = P + B2/ 8π is the total pressure with thermal pressure P and magnetic pressure B2/ 8π, E is the total energy density: 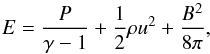 (5)and ρ, u, B, and γ = 5/3 are the plasma mass density, fluid velocity, magnetic field, and the adiabatic index, respectively. The cgs units have been adopted in this paper.
(5)and ρ, u, B, and γ = 5/3 are the plasma mass density, fluid velocity, magnetic field, and the adiabatic index, respectively. The cgs units have been adopted in this paper.
The numerical scheme to solve the ideal MHD equations was presented by Mignone et al. (2007) in detail. We model the simulation in a two-dimensional Cartensian coordinate (x,y) with uniform grids. The size of simulation domain is chosen to be 40 pc × 40 pc to cover the extension of young SNRs. The supernova blast wave is driven by the injection of internal energy and ram pressure in a small circular region at the center of simulation box, in which the density is assumed to be constant corresponding to a plateau volume (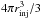 ) with rinj = 0.5 pc. The initial magnetic field and the density in the background plasma include an average component and a turbulent component. We assume a constant average magnetic field B0 along the x direction and a constant average gas density n0 (Guo et al. 2012).
) with rinj = 0.5 pc. The initial magnetic field and the density in the background plasma include an average component and a turbulent component. We assume a constant average magnetic field B0 along the x direction and a constant average gas density n0 (Guo et al. 2012).
Both density and magnetic fluctuations are generated by the assumption of a Kolmogorov-like power-law spectrum of the form 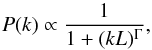 (6)where the spectral index Γ depends on the dimensionality and equals 8/3 for 2D system, k is the magnitude of the wave vector and L = 3 pc is the turbulence coherence length. The turbulence is generated by summing a large number of discrete wave modes with random phases (Giacalone & Jokipii 1999). The random component of magnetic field is given by
(6)where the spectral index Γ depends on the dimensionality and equals 8/3 for 2D system, k is the magnitude of the wave vector and L = 3 pc is the turbulence coherence length. The turbulence is generated by summing a large number of discrete wave modes with random phases (Giacalone & Jokipii 1999). The random component of magnetic field is given by 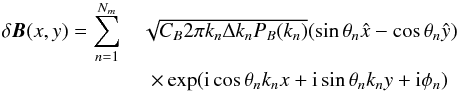 (7)where PB(kn) represents the power of the wave mode n with wavenumber kn, CB is a normalization constant determined by
(7)where PB(kn) represents the power of the wave mode n with wavenumber kn, CB is a normalization constant determined by 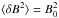 , where ⟨⟩ represents averaging in space. The turbulence distributes randomly in propagation direction −1 < cosθn< 1 and with a random phase 0 <φn< 2π.
, where ⟨⟩ represents averaging in space. The turbulence distributes randomly in propagation direction −1 < cosθn< 1 and with a random phase 0 <φn< 2π.
 |
Fig. 1 Left: structure of the magnetic field B in units of μG at 1600 years of a test run with n0 = 0.04 cm-3. The rest of the model parameters are shown in the text. Middle: TeV image derived from the 2D MHD simulation. The image has been normalized to its peak value. Right: comparison of the observed radial profile averaged along the azimuthal direction with results (solid line) derived from the 2D MHD simulation. The dotted line is obtained by averaging the radial brightness profiles obtained in the position angle range of 0.7π to 0.95π in the middle panel. |
The density fluctuations satisfy the following probability distribution (Giacalone & Jokipii 2007; Burlaga & Lazarus 2000): 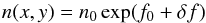 (8)where f0 is a constant chosen to yield the average density n0 and the description of δf is similar to the turbulent part of the magnetic field:
(8)where f0 is a constant chosen to yield the average density n0 and the description of δf is similar to the turbulent part of the magnetic field: 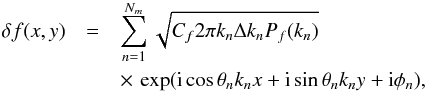 (9)with the normalization constant Cf determined by
(9)with the normalization constant Cf determined by 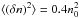 .
.
Guo et al. (2012) carried out an extensive study of 2D MHD simulations of SNRs in a turbulent medium. We first carried out a test run with n0 = 0.04 cm-3, B0 = 0.8 μG, the total injected internal energy ESN = 2 × 1051 erg, and the total mass of the ejector Mej = 2 M⊙. The left panel of Fig. 1 shows the magnetic field structure at 1600 years. The units of the coordinates are pc and the color scale is the logarithmic of the magnetic field in units of μG with the peak magnetic field reaching about 100 μG. The magnetic field near the shock front is mostly amplified by turbulent motion in the downstream (Giacalone & Jokipii 2007). The strongest magnetic field, however, is produced by Rayleigh-Taylor convective flows near the contact discontinuity. Since the ejector is uniform, the magnetic field is very weak in the downstream of the reverse shock.
In order to construct the profile of ~TeV emission, we adopt the leptonic scenario where the γ-ray is produced via the IC of background soft photons off high-energy electrons accelerated by the shocks. Besides the cosmic microwave background (CMB) radiation, we also include an IR background photon component with a temperature of T = 30 K and an energy density of 1.2 eV cm-3 (Yang & Liu 2013). The energy density of radio to X-ray band synchrotron component of the SNRs is much lower than the energy density of the CMB radiation, the synchrotron self-Comptonization process therefore can be ignored. Since the background photon field is approximately uniform, the γ-ray emission characteristics are then determined by the properties of energetic electrons. Yang & Liu (2013) showed that the observed correlation between the X-ray and γ-ray brightness of these SNRs implies that the electron energy density is proportional to the magnetic field energy density, we then can describe the electron spatial distribution simply as the following: 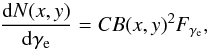 (10)where
(10)where 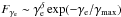 is a power-law energy distribution with an exponential cutoff and γe is the electron Lorentz factor. From the overall γ-ray spectrum of SNR RX J1713.7-3946, we find δ = −2 and γmax = 1.3 × 107 (Li et al. 2011; Yang & Liu 2013). The proportionality of the magnetic field and high-energy electron energy densities then implies that the electron distribution only depends on the magnetic field energy density and the structure of TeV emission is determined by B2. A recent study of TeV bright shell-type SNRs by Yang et al. (2014) showed that the energy partition between energetic electrons above 1 GeV and the magnetic field may be different for different SNRs with a tendency that the total magnetic field energy within the volume enclosed by the front shock of SNRs increases faster than that of energetic electrons as the SNRs evolve. But the proportionality of these energy densities is inferred from the correlation between the X-ray and γ-ray brightness in the leptonic scenario. We therefore expect our treatment be valid for sources with a good correlation between the X-ray and γ-ray brightness as far as the spatial structure of the γ-ray emission is concerned.
is a power-law energy distribution with an exponential cutoff and γe is the electron Lorentz factor. From the overall γ-ray spectrum of SNR RX J1713.7-3946, we find δ = −2 and γmax = 1.3 × 107 (Li et al. 2011; Yang & Liu 2013). The proportionality of the magnetic field and high-energy electron energy densities then implies that the electron distribution only depends on the magnetic field energy density and the structure of TeV emission is determined by B2. A recent study of TeV bright shell-type SNRs by Yang et al. (2014) showed that the energy partition between energetic electrons above 1 GeV and the magnetic field may be different for different SNRs with a tendency that the total magnetic field energy within the volume enclosed by the front shock of SNRs increases faster than that of energetic electrons as the SNRs evolve. But the proportionality of these energy densities is inferred from the correlation between the X-ray and γ-ray brightness in the leptonic scenario. We therefore expect our treatment be valid for sources with a good correlation between the X-ray and γ-ray brightness as far as the spatial structure of the γ-ray emission is concerned.
3. Results
In the following, we use SNR RX J1713.7-3946 as a prototype to describe the modeling. The remnant was first discovered in X-rays with the ROSAT all-sky survey in 1996 (Pfeffermann & Aschenbach 1996). It is close to the Galactic plane and its distance and ages are about 1 kpc and 1600 yrs, respectively (e.g., Fukui et al. 2003; Cassam-Chenaï et al. 2004), and the radius of the remnant is about 10 pc (Acero et al. 2009). The gamma-ray image of SNR RX J1713.7-3946 is consistent with a thick emitting shell with a thickness close to half of the radius, and with the emissivity of southeast part is a factor of two lower than the rest (Aharonian et al. 2006).
3.1. Structure and radial profile of TeV emission
To model the observed morphology of the TeV emission, we also need to construct a pseudo 3D structure with 2D simulations. One can integrate B2, which is proportional to the TeV emissivity, along a direction (presumably corresponding to the line-of-sight) in the 2D simulation domain to obtain a brightness profile in the radial direction of the SNR. Such a radial profile can be obtained for all angular directions in the 2D domain1. To mimic the observed TeV image, we stack the radial profile obtained above continuously in a polar coordinate and smooth the resultant 2D structure with the point spread function of the H.E.S.S. The middle panel of Fig. 1 shows such an image derived from the structure of the magnetic field shown in the left panel for an assumed distance of 1 kpc. The arcs connecting the center and the outer rim are artifacts of the algorithm proposed above. Although this image does not recover all of the details of the TeV image obtained with the H.E.S.S. (Aharonian et al. 2006), the strong variation of the brightness in the azimuthal directions and the shell structure is well reproduced. The one-sided structure of the simulated TeV image is closely related to the asymmetry of the magnetic field structure. Because of the presence of a large scale magnetic field in the horizontal direction, the magnetic field at the bottom and top segments of the SNR shown in the left panel is preferentially amplified with the bottom segment amplified the most. Since the TeV emissivity is proportional to B2, the asymmetry in the magnetic field structure is further amplified in the TeV image giving rise to the bright southern rim in the TeV image shown in the middle panel.
The right panel of Fig. 1 compares the model predicted azimuthal averaged radial profile with the observed profile. The radial profiles have been normalized to their peak value. It can be seen that the solid line of the model result is much narrower than the observed profile. This is not surprising since the left panel of Fig. 1 shows that the emission comes from a shell with a thickness less than one-third of the radius, while the observed profile is consistent with an emitting shell with a thickness about half of the radius (Aharonian et al. 2006). In the 1D model proposed by Berezhko & Völk (2010), it is claimed that a broad radial profile can be produced by considering the angular resolution of the observations. This 1D model predicts a very bright rim at the shock front. The smoothing effect caused by the angular resolution of the observations can reduce the brightness of this rim dramatically and therefore suppress the brightness contrast between the center and the shock front regions. In our 2D model, we do n0t have a very bright rim and the azimuthal variance also reduces the intrinsic brightness contrast of the averaged radial profile. The angular resolution of the observations does not drastically change the brightness contrast between the center and the shock front regions.
Considering the complex structure of the magnetic field in the left panel of Fig. 1 and its dependence on the large scale magnetic field, the projection effect may play a role in the brightness profile. Instead of averaging the whole 2π angle, the dotted line shows the profile averaged from 0.7π to 0.95π. The model prediction is more consistent with observations than the solid line, however, the brightness profile of the model still falls faster than the observed profile near the edge of the remnant. Three-dimensional simulations are needed to clarify this issue.
Model parameters.
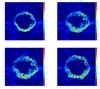 |
Fig. 2 Structure of magnetic energy density B2 for four SNRs investigated in this paper. The parameters of model are described in Table 1. |
3.2. Application to TeV images of SNRs
Besides SNR RX J1713.7-3946, SNR RX J0852.0-4622 is another very important Galactic SNR. The X-ray and gamma-ray images of this remnant are consistent with a very thin shell of 1° in radius and ~ 0.2° in thickness. The radius of SNR RX J0852.0-4622 is 5−10 pc (Aharonian et al. 2005, 2007) for a distance of 0.26−0.50 kpc, and its age is about 420−1400 yrs (Bamba et al. 2005). The young shell-type SNR RCW 86 (also known as G315.4-2.3 and MSH 14-63) has been observed in radio (Kesteven & Caswell 1987), optical (Smith 1997), X-ray (Pisarskietal et al. 1984), and gamma-ray (Yuan et al. 2014; Aharonian et al. 2009) with a nearly circular shape of 40′ in diameter. Rosado, et al. (1996) deduced a distance of 2.8 kpc and an age of ~ 10 000 years by using optical observations, whereas recent observations of the northeast part of the remnant with the Chandra and XMM-Newton satellites strengthen the case that the event recorded by the Chinese in 185 AD was a supernova and RCW 86 is likely its remnant (Vink et al. 2006). Tian, et al. (2008) reported the discovery of a faint radio and X-ray shell with a distance of 3.2 ± 0.8 kpc closely matching the extended TeV source HESS J1731-347 (Aharonian et al. 2008). Deeper γ-ray observations of the source have revealed a large shell-type structure with similar position and extension (r ~ 0.25°) as the radio SNR, confirming their association (Abramowski et al. 2011). These authors suggested that its distance is not much larger than the derived low limit of 3.2 kpc, and a physical size of ≤15 pc is also reasonable.
To improve the fitting to the azimuthal averaged radial profile of the TeV brightness, one may adjust the mean density n0 of the ambient medium. In the following, we will adjust n0 as the major free parameter to fit the radial brightness profile of these SNRs. Considering the ambiguity of the progenitor, we picked the mass and total energy of the ejector in a reasonable region to reproduce the physical size of these SNRs. A fit to the observed radial TeV brightness profile is then used to constrain the density n0. The model parameters are shown in Table 1 including the output parameters, such as the shock velocity Vs and age.
 |
Fig. 4 Same as the right panel of Fig. 1 except for the four SNRs in Fig. 2. The data of RX J0852.0-4622, RX J1713.7-3946, RCW86, and HESS J1731-347 are from H.E.S.S. observations (Aharonian et al. 2006, 2007, 2009; Abramowski et al. 2011). |
Figure 2 shows the magnetic field intensity B. It is evident that the shell thickness increases with the increase of the mean density of the background. The results for RX J1713.7-3946 and RCW 86 have thicker shells than the other two sources. Figures 3 and 4 show that the TeV morphology and radial profile of these sources can be approximately reproduced with our model. To improve this model, one may consider more realistic 3D simulations with the structure of the progenitor wind and environment of these sources taken into account properly. We note that the background density derived from our model is higher than the upper limit inferred from the X-ray observations, which poses the most serious challenge to our model. The thermal X-ray emission must be suppressed in the shock downstream to be consistent with the absence or weakness of thermal X-ray emission from these sources. Alternatively, in a 3D simulation, a lower background density may be derived from the TeV radial brightness profiles.
4. Discussion and conclusions
Based on 2D MHD simulations of shell-type supernova remnants evolving in a turbulent background, the evolution of the magnetic field for these remnants can be obtained. In the leptonic scenario for the γ-ray emission, the observed correlation between the X-ray and γ-ray brightnesses implies that the energy density of high-energy electrons is proportional to that of the magnetic field. One can then model the multiband, nonthermal emission with the MHD simulations with the energy partition between energetic electrons and the magnetic field as a free parameter. It is shown that the radial profile of the TeV emission is very sensitive to the density of the background plasma. With reasonable parameters for four TeV bright shell-type SNRs, we reproduce the azimuthal averaged radial brightness profile of the TeV emission obtained with the H.E.S.S. observations.
Using multidimensional hydrodynamic simulations, Obergaulinger et al. (2014) interpreted the inhomogeneities of the emission from the SNR RX J0852.0-4622 by assuming the blast wave evolved in a cloudy environment. To reproduce the morphology of two opposite lobes for the SNR Kepler, Tsebrenko & Soker (2013) proposed that jets existed before the explosion, which can produce the axisymmetric structure with lobes. Our simulations are intrinsically 2D, and a 3D model, including the details of both the ejecta and the background medium around the TeV remnants, is needed to reproduce the detailed structure of nonthermal emission of the four remnants studied here.
Acknowledgments
We thank Dr. Fan Guo for providing a code to generate turbulent ISM. This work is partially support by the Strategic Priority Research Program, the Emergence of Cosmological Structures, of the Chinese Academy of Sciences, Grant No. XDB09000000, NSFC grants: 11163006, 11173064, 11233001, and 11233008. Fang is supported by the NSFC grant (11103016), and by the Key Project of Chinese Ministry of Education (212160). H.L. is supported by the LDRD program at LANL.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2011, ApJ, 734, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Acero, F., Ballet, J., Decourchelle, A., et al. 2009, A&A, 505, 157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ackermann, M., Ajello, M., Allafort, A., et al. 2013, Science, 339, 807 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2005, A&A, 437, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2006, A&A, 449, 223 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2007, ApJ, 661, 236 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Barres de Almeida, U., et al. 2008, A&A, 477, 353 [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., de Almeida, U. B., et al. 2009, ApJ, 692, 1500 [NASA ADS] [CrossRef] [Google Scholar]
- Abramowski, A., Acero, F., Aharonian, F., et al. 2011, A&A, 531, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bamba, A., Yamazaki, R., & Junko S., Hiraga, 2005, ApJ, 632, 294 [NASA ADS] [CrossRef] [Google Scholar]
- Bamba, A., Pühlhofer, G., Acero, F., et al. 2012, ApJ, 756, 149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bell, A. R. 2004, MNRAS, 353, 550 [Google Scholar]
- Berezhko, E., & Völk 2010, A&A, 511, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bocchino, F., Vink, J., Favata, F., Maggio, A., & Sciortino, S. 2000, A&A, 360, 671 [NASA ADS] [Google Scholar]
- Burlaga, L. F., & Lazarus, A. J. 2000, J. Geophys. Res., 105, 2357 [Google Scholar]
- Bykov, A. M., Uvarov, Y. A., & Ellison, D. C. 2008, ApJ, 689, L133 [Google Scholar]
- Cassam-Chenaï, G., Decourchelle, A., Ballet, J., et al. 2004, A&A, 427, 199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ellison, D. C., Patnaude, D. J., Slane, P., & Raymond, J. 2010, ApJ, 712, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Ellison, D. C., Slane, P., Patnaude, D. J., & Bykov, A. M. 2012, ApJ, 744, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, Z. H., Liu, S. M., & Fryer, C. L. 2010, MNRAS, 406, 1337 [NASA ADS] [Google Scholar]
- Fukui, Y., Moriguchi, Y., Tamura, K., et al. 2003, PASJ, 55, L61 [NASA ADS] [Google Scholar]
- Giacalone, J., & Jokipii, J. R. 1999, ApJ, 520, 204 [Google Scholar]
- Giacalone, J., & Jokipii, J. R. 2007, ApJ, 663, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, F., Li, S., Li, H., et al. 2012, ApJ, 747, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Inoue, T., Yamazaki, R., & Inutsuka, S. 2009, ApJ, 695, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Katz, B., & Waxman, E. 2008, JCAP, 01, 018 [NASA ADS] [CrossRef] [Google Scholar]
- Kesteven, M. J., & Caswell, J. L. 1987, A&A, 183, 118 [NASA ADS] [Google Scholar]
- Koyama, K., Petre, R., Gotthelf, E. V., et al. 1995, Nature, 378, 225 [Google Scholar]
- Lemoine-Goumard, M., Renaud, M., Vink, J., et al. 2012, A&A, 545, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, H., Liu, S., & Chen, Y. 2011, ApJ, 742, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, S., Fan, Z., Fryer, C. L., Wang, J. M., & Li, H. 2008, ApJ, 683, L163 [NASA ADS] [CrossRef] [Google Scholar]
- Mignone, A., Bodo, G., Massaglia, S., et al. 2007, ApJS, 170, 228 [Google Scholar]
- Moriguchi, Y., Tamura, K., & Tawara, Y., et al. 2005, ApJ, 631, 947 [NASA ADS] [CrossRef] [Google Scholar]
- Morlino, G., & Caprioli, D. 2012, A&A, 538, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morlino, G., Amato, E., & Blasi, P. 2009, MNRAS, 392, 240 [NASA ADS] [CrossRef] [Google Scholar]
- Obergaulinger, M., Iyudin, A. F., Müller, E., & Smoot, G. F. 2014, MNRAS, 437, 976 [NASA ADS] [CrossRef] [Google Scholar]
- Pacholczyk, A. G. 1970, Radio Astrophysics (San Francisco: Freeman) [Google Scholar]
- Pfeffermann, E., & Aschenbach, B. 1996, in Roentgenstrahlung from the Universe, eds. H. U. Zimmermann, J. Trmper, & H. Yorke, 267 [Google Scholar]
- Pisarski, P. L., Helfand, D. J., & Kahn, S. M. 1984, ApJ, 277, 710 [NASA ADS] [CrossRef] [Google Scholar]
- Porter, T. A., Moskalenko, I. V., & Strong, A. W. 2006, ApJ, 648, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Riquelme, M. A., & Spitkovsky, A. 2009, ApJ, 694, 626 [Google Scholar]
- Rosado, M., Ambrocio-Cruz, P., Le Coarer, E., & Marcelin, M. 1996, A&A, 315, 243 [NASA ADS] [Google Scholar]
- Sano, H., Sato, J., Horachi, H., et al. 2010, ApJ, 724, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. C. 1997, AJ, 114, 2664 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, T., Uchiyama, Y., Aharonian, F. A., et al. 2008, ApJ, 685, 988 [NASA ADS] [CrossRef] [Google Scholar]
- Tian, W. W., Leahy, D. A., Haverkorn, M., & Jiang, B. 2008, ApJ, 679, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Tsebrenko, D., & Soker, N. 2013, MNRAS, 435, 320 [NASA ADS] [CrossRef] [Google Scholar]
- Uchiyama, Y., Aharonian, F. A., Tanaka, T., Takahashi, T., & Maeda, Y. 2007, Nature, 449, 576 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Williams, B. J., Blair, W. P., Blondin, J. M., et al. 2011, ApJ, 741, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Vink, J., Bleeker, J., Van Der Heyden, K., et al. 2006, ApJ, 648, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Yamazaki, R., Kohri, K., & Katagiri, H. 2009, A&A, 495, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yang, C., & Liu, S. M. 2013, ApJ, 773, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, R. Z., Zhang, X., Yuan, Q., & Liu, S. M. 2014, A&A, 567, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yuan, Q., Liu, S. M., Fan, Z. H., Bi, X. J., & Fryer, C. L. 2011, ApJ, 735, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, Q., Liu, S. M., & Bi, X. J. 2012, ApJ, 761, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, Q., Huang, X. Y., Liu, S. M., & Zhang, B. 2014, ApJ, 785, L22 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Left: structure of the magnetic field B in units of μG at 1600 years of a test run with n0 = 0.04 cm-3. The rest of the model parameters are shown in the text. Middle: TeV image derived from the 2D MHD simulation. The image has been normalized to its peak value. Right: comparison of the observed radial profile averaged along the azimuthal direction with results (solid line) derived from the 2D MHD simulation. The dotted line is obtained by averaging the radial brightness profiles obtained in the position angle range of 0.7π to 0.95π in the middle panel. |
| In the text | |
 |
Fig. 2 Structure of magnetic energy density B2 for four SNRs investigated in this paper. The parameters of model are described in Table 1. |
| In the text | |
 |
Fig. 3 Same as the middle panel of Fig. 1 except for the four SNRs in Fig. 2. |
| In the text | |
 |
Fig. 4 Same as the right panel of Fig. 1 except for the four SNRs in Fig. 2. The data of RX J0852.0-4622, RX J1713.7-3946, RCW86, and HESS J1731-347 are from H.E.S.S. observations (Aharonian et al. 2006, 2007, 2009; Abramowski et al. 2011). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


