| Issue |
A&A
Volume 573, January 2015
|
|
|---|---|---|
| Article Number | A57 | |
| Number of page(s) | 10 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201424562 | |
| Published online | 17 December 2014 | |
A pair of CO + He white dwarfs as the progenitor of 2005E-like supernovae?
1
Yunnan Observatories, Chinese Academy of Sciences,
650216
Kunming,
PR China
e-mail: xiangcunmeng@ynao.ac.cn;
zhanwenhan@ynao.ac.cn
2
Key Laboratory for the Structure and Evolution of Celestial
Objects, Chinese Academy of Sciences, 650216
Kunming, PR
China
Received: 9 July 2014
Accepted: 28 October 2014
Context. Ca-rich transients (CRTs, 2005E-like supernovae) exhibit unusually strong Ca features during their nebular phase, and their distribution in their host galaxies indicates that they belong to a metal-poor old population. A pair of low-mass CO + He white dwarfs (WD) has been suggested to be the progenitor of CRTs. A helium shell is accumulated onto the CO WD by accretion, and then a helium-shell detonation is ignited when the helium shell reaches a critical mass, which could lead to the second detonation in the center of the CO WD.
Aims. Taking the birth rate of CRTs into consideration, we examine whether and if yes, which type of low-mass CO + He WD pairs fulfill the constraints of being of an old population and of the birth rate derived from observations.
Methods. We carried out a series of binary population syntheses and present four different channels in which CO + He WD pairs can be formed. We selected the systems that fulfill the constraints of being of an old population and of the birth rate from all the CO + He WD pairs by constraining the component mass of the WD pairs.
Results. For the four channels, the stable Roche lobe overflow (RLOF) could significantly influence the formation of the WD pairs. Based on their position on the MCO-MHe plane, the mass-transfer between the components for most of the CO + He WD pairs is neither always unstable nor always stable. We found that it is necessary that the CO WDs are less massive than 0.6 M⊙ and the He WDs are less massive than 0.25 M⊙ if CO + He WD pairs are to fulfill the constraints of being of an old population and of the birth rate of CRTs. However, the He WD mass is lower than the ejecta mass of the CRTs derived from observations, while the total mass of the low-mass WD pairs is higher than this.
Conclusions. Our results imply that the CO WDs participate in CRT explosions and at the same time, a bound remnant could be left after the CRT explosion if the low-mass WD pairs are the progenitors of CRTs. Therefore, it needs to be examined whether or not the helium detonation on a low-mass CO WD may lead to the second detonation in the center of the CO WDs, and whether or not the bound remnant is left after the thermonuclear explosion.
Key words: white dwarfs / supernovae: general / binaries: close
© ESO, 2014
1. Introduction
Supernovae (SNe) are one of the possible evolutionary end stages of stars and are divided into several observational subclasses according to the line features of different chemical elements in their spectrum. Type Ia supernovae (SNe Ia) generally result from the thermonuclear explosion of a white dwarf (WD) in a binary system (Hillebrandt & Niemeyer 2000; Leibundgut 2000), while Type Ib/c supernovae (SNe Ib/c) and Type II supernovae (SNe II) result from the gravitational core-collapse of a star of ≥8 M⊙ (Smartt 2009). However, the discovery of SN 2005E appears to contradict this understanding, because this supernova was classified as a SN Ib while it seems impossible for it to have arisen from a massive star. This means that it probably belongs to a new type of stellar explosion (Perets et al. 2010). The SNe belonging to this new subclass share many common properties: 1) a low peak luminosity with a magnitude between that of regular novae and supernovae (MR = −16 ± 0.5 mag); 2) a relatively fast rise and decay time (~12–15 days); 3) a photospheric velocity similar to normal SNe Ia; 4) a quick spectral transition into the nebular phase (~1–3 months); 5) peculiar nebular spectra dominated by calcium lines; 6) they are located in border regions of host galaxies and then belong to a metal-poor old population (even older than 10 Gyr); and they have 7) fewer ejecta in terms of mass (0.4–0.7 M⊙) (Kasliwal et al. 2012; Yuan et al. 2013; Lyman et al. 2013). As a result of the dominant calcium lines in the nebular phase, these SNe are called Ca-rich transients (CRTs), and the sample size of this subclass is still increasing (Valenti et al. 2014). Perets et al. (2010) estimated that the birth rate of CRTs is 7% ± 5% relative to the total SNe Ia rate (see also Kasliwal et al. 2012). At present, the identity of CRT progenitors is still unclear (Kawabata et al. 2010; Perets et al. 2011). Considering that the CRTs originate from a metal-poor old population and that some CRTs exhibit helium lines in their spectra, a binary with a carbon-oxygen white dwarf (CO WD) primary and a helium-rich secondary was proposed (Perets et al. 2010), and the helium-rich secondary is more likely to be a helium (He) WD since a helium star usually belongs to a young population (Kasliwal et al. 2012; Yuan et al. 2013; Lyman et al. 2013). Observationally, there are indeed such WD pairs, and the mass-transfer between the components of some WD pairs may be dynamically stable, which could mean that the accreted helium may be gradually accumulated onto the CO WD, eventually leading to a helium-shell detonation (Kilic et al. 2012; 2014). In theory, a helium-shell detonation on a low-mass CO WD, where the helium-rich material is accreted from a low-mass He WD, may reproduce the properties of the prototype of the CRTs (SN 2005E), while for a massive CO WD, the detonation mainly leaves 56Ni and unburnt helium, and the predicted spectrum is unlikely to fit the unique features of CRTs (Shen et al. 2010; Waldman et al. 2011). Although observations and numerical simulations support CO + He WD pairs as the progenitor of CRTs, it is still unclear which type of CO + He WD pairs may contribute to the CRTs and whether the CO + He WD pairs can account for the delay time and birth rate of CRTs. It is especially unclear whether the CO + He WD pairs can account for other properties of CRTs such as the ejecta mass. Judging from observational constraints, the WD pairs producing CRTs should belong to metal-poor old populations, and their merging rate should be consistent with the birth rate of CRTs. In this paper, we try to discuss these problems based on a detailed binary population synthesis (BPS) study.
In Sect. 2, we describe our BPS method, and we present the results in Sect. 3. We provide our discussions in Sect. 4 and our conclusions in Sect. 5.
2. Binary population synthesis method
A very complex process is required to form a CO + He WD pair, and different primordial systems will experience different evolution channels, in which they will undergo one or two common-envelope (CE) phases. We first introduce the different evolution channels in which the CO + He WD pairs can form, and the methods with which we treat the CE evolution in this chapter.
2.1. Evolution channel
From a primordial main-sequence (MS) binary, a CO + He WD pair may form on an evolutionary timescale tE after one or two CE phases (Han 1998; Nelemans et al. 2005; Ruiter et al. 2009). tE is mainly determined by the evolutionary timescale of the secondary. Following the CO + He WD pair, orbital angular momentum loss by gravitational-wave (GW) radiation dominates the evolution of the system, and finally, the system merges within a timescale tGW (Landau & Lifshitz 1962), 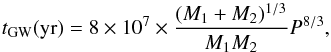 (1)where P is the orbital period of the pair in hours, and M1 and M2 are the masses of the CO WD and the He WD in solar mass, respectively. Thus, the delay time elapsed from the birth of a primordial binary system to the occurrence of the merger, ttot, is equal to the sum of tE and tGW. We assume that if ttot is shorter than 15 Gyr, the merger is a potential candidate to be the progenitor of the CRTs. The delay time ttot can also be used to determine whether the progenitor of the CRTs belongs to a young or old population. We identify the progenitors from these potential candidates, based on the constraints of the old population and birth rate of the CRTs derived from observations.
(1)where P is the orbital period of the pair in hours, and M1 and M2 are the masses of the CO WD and the He WD in solar mass, respectively. Thus, the delay time elapsed from the birth of a primordial binary system to the occurrence of the merger, ttot, is equal to the sum of tE and tGW. We assume that if ttot is shorter than 15 Gyr, the merger is a potential candidate to be the progenitor of the CRTs. The delay time ttot can also be used to determine whether the progenitor of the CRTs belongs to a young or old population. We identify the progenitors from these potential candidates, based on the constraints of the old population and birth rate of the CRTs derived from observations.
Based on the number of the CEs that the WD pairs experienced and the time that the primordial primary fills its Roche lobe, there are four channels in which the CO + He WD pairs can form from primordial binaries, as shown in Fig. 1. Below, we briefly outline the four channels: Cases A–D.
Case A (2RLOF+1/2CE): the primordial zero-age main-sequence (ZAMS) mass of primaries is relatively massive: 2.5–4.5 M⊙, while that of the secondary is between 0.9–2.5 M⊙, and the primordial orbital separation is short, 10–140 R⊙. Case A is divided into two subchannels, Cases Aa and Ab. The main difference between the two subcategories lies in different primordial orbital separations, which determine the time of the first Roche-lobe overflow (RLOF) and whether a CE forms following the first RLOF. For Case Aa, the first RLOF occurs when the primary is at the end of the Hertzprung gap (HG). After a short period of stable RLOF, the primary becomes a first giant branch (FGB) star, and then the RLOF becomes dynamically unstable, leading to the formation of a CE. After the CE ejection, the primary becomes a helium star and continues to evolve. The helium star fills its Roche lobe (RL) again after exhausting the central helium, and the second stable RLOF begins at a relatively low mass ratio, which leads to the formation of a CO WD + MS system. Following this, the secondary evolves to the FGB and the RLOF is also unstable, resulting in the second CE. After ejecting the CE, a CO + He WD pair forms. For Case Ab, the first RLOF may always be stable if the primary fills its RL when it is crossing the HG. Thus, instability may be avoidable for the first CE, and the system becomes a He star + MS system directly after the first RLOF (Han et al. 2002). The following evolution is similar to Case Aa. After the merging of the WD pairs, Case A mainly contributes to the young and medium-age population.
Case B (2CE+1/2RLOF): this channel is also divided into two subchannels, Cases Ba and Bb. The primordial mass ratio (m2/m1) is between 0.4 and 0.9, and the primordial separation is mainly from 100 R⊙ to 400 R⊙ for both subchannels. For Case Ba, the primordial ZAMS primary is relatively massive, 3–4.5 M⊙, while it is smaller, 1.6–3.3 M⊙, for Case Bb. The primary fills its RL when it is an early asymptotic giant branch (EAGB) star. The following RLOF is dynamically unstable for a deep convective envelope, which results in a CE. After the CE ejection, the primary becomes a helium red giant (RG) star. Soon, the helium RG star fills its RL again, and the following RLOF is dynamically stable for a low mass ratio. Then, a CO WD + MS forms after the RLOF. When the secondary becomes an FGB star, it fills its RL and the RLOF is dynamically unstable, leading to a CE. The surviving systems resulting from cases Ba and Bb are different. For Case Bb, a CO + He WD pair forms directly after the CE ejection, while for Case Ba it is a CO WD + He star system because of the relative high mass of the secondary. For the CO WD +He star system, the orbital separation is so small for the two CE evolution that the He star fills its RL during the helium-burning phase of its main sequence. When the mass of the helium star is lower than the lowest value required to maintain helium burning, the helium burning is quenched in the center of the helium star, and the helium star becomes a He WD (Han et al. 2002). A CO + He WD pair forms as a result. After the merging of the system, Case Ba mainly contributes to merger formation in young populations, while Case Bb contributes to that of the medium-age and old populations.
Case C (2CE+0/1RLOF): this channel is divided into two sub-channels, Cases Ca and Cb. The primordial mass ratio (m2/m1) is between 0.5 and 0.6, and the primordial separation ranges from 450 R⊙ to 850 R⊙ for both subchannels. For Case Cb, the mass of the primordial ZAMS primary is from 2 M⊙ to 4 M⊙, while it is usually more massive than 4 M⊙ for Case Ca. The primary fills its RL when it is a thermal pulsing asymptotic giant branch (TPAGB) star. The RLOF is then dynamically unstable for a deep convective envelope, leading to a CE. After CE ejection, a CO WD + MS system forms. The secondary fills its RL when it is climbing the FGB, and then the following RLOF also becomes dynamically unstable, resulting in a second CE. After the ejection of the second CE, the surviving system directly becomes a CO + He WD pair for Case Cb and a CO WD + He star for Case Ca. The following evolution of Case Ca is similar to Case Ba. After the merging of the WD pairs, Case Ca mainly contributes to merger formation in young populations, while Case Cb contributes to that of the medium-age and old populations.
Case D (1CE+0/1RLOF): this channel is also divided into two sub-channels, Cases Da and Db. The primordial mass ratio (m2/m1) is higher than 0.9, even close to 1 in some cases, and the primordial separation is from 500 R⊙ to 1000 R⊙ for Case Db, while it can be larger than 1000 R⊙ for Case Da. The mass of the primordial primary is from 1 M⊙ to 2.5 M⊙. As a result of the high mass ratio and the large primordial orbital separation, the secondary is an FGB star when the primary fills its RL at the TPAGB stage. The following RLOF results in a CE, where the CE also includes the envelope of the FGB star, and the binary embedded in the CE consists of the dense cores of the TPAGB and the FGB stars. After the CE ejection, the surviving system is a CO + He WD pair for Case Db, while a CO WD + He star results from Case Da. The following evolution of Case Da is similar to that of Cases Ba and Ca. After the merging of the WD pairs, Case Da mainly contributes to merger formation in medium-age populations, while Case Db contributes to that of old populations.
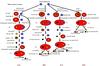 |
Fig. 1 Schematic for the evolution channels that can form the CO + He WD pairs, where q = M2/M1 is the primordial mass ratio and a is the primordial orbital separation (see text for details). |
2.2. Common envelope
As mentioned above, the CE phase is very important for the formation of the CO + He WD pairs. The mass ratio (q = Mdonor/Maccretor) is crucial during binary evolution. If the mass ratio is higher than a critical value, qc, mass transfer between the two components is dynamically unstable, and a CE will form (Paczyński 1976). The critical ratio qc varies with the evolutionary state of the donor star at the onset of the RLOF (Hjellming & Webbink1987; Webbink 1988; Han et al. 2002; Podsiadlowski et al. 2002; Chen & Han 2008). We adopted qc = 4.0 when the donor star is a MS star or is in the HG, following previous detailed binary evolution studies (Han et al. 2000; Chen & Han 2002; 2003). If the primordial primary is on the FGB or the AGB, we adopted ![\begin{eqnarray} q_{\rm c}=\left[1.67-x+2\left(\frac{M_{\rm c}}{M}\right)^{\rm 5}\right]\Big/2.13, \label{eq:qc} \end{eqnarray}](/articles/aa/full_html/2015/01/aa24562-14/aa24562-14-eq24.png) (2)where Mc is the core mass of the donor star and x = dlnR1/ dlnM is the mass–radius exponent of the donor star and varies with composition. If the mass donors (primaries) are naked helium giants, qc = 0.748, as calculated from Eq. (2) (see Hurley et al. 2002 for details).
(2)where Mc is the core mass of the donor star and x = dlnR1/ dlnM is the mass–radius exponent of the donor star and varies with composition. If the mass donors (primaries) are naked helium giants, qc = 0.748, as calculated from Eq. (2) (see Hurley et al. 2002 for details).
The binary embedded in the CE consists of the dense core of the donor star and the secondary. The orbit of the embedded binary gradually shrinks owing to frictional drag introduced by the envelope, and a large part of the orbital energy released during the spiral-in process is injected into the CE (Livio & Soker 1988). Here, we assumed that the CE is ejected if 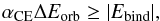 (3)where ΔEorb is the orbital energy released during the spiral-in process, and Ebind is the binding energy of the CE. It is very sensitive to the value of the CE ejection efficiency, αCE, which represents the fraction of the released orbital energy used to eject the CE. Since the thermal energy in the envelope is not incorporated into the binding energy here, it is possible for αCE to be greater than 1 (see Han et al. 1995 for details about the thermal energy). At present, the value of αCE is very uncertain (Zorotovic et al. 2010; Camacho et al. 2014; Zuo & Li 2014). We here set αCE = 3.0 as our standard value and αCE = 1.0 to test the influence of αCE on the final results.
(3)where ΔEorb is the orbital energy released during the spiral-in process, and Ebind is the binding energy of the CE. It is very sensitive to the value of the CE ejection efficiency, αCE, which represents the fraction of the released orbital energy used to eject the CE. Since the thermal energy in the envelope is not incorporated into the binding energy here, it is possible for αCE to be greater than 1 (see Han et al. 1995 for details about the thermal energy). At present, the value of αCE is very uncertain (Zorotovic et al. 2010; Camacho et al. 2014; Zuo & Li 2014). We here set αCE = 3.0 as our standard value and αCE = 1.0 to test the influence of αCE on the final results.
After the CE evolution, the initial orbital separation at the onset of the CE phase, ai, becomes af, which is determined by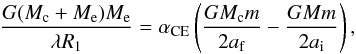 (4)where λ is a structural parameter depending on the evolutionary stage of the donor. M, Mc, and Me are the masses of the donor, the donor core, and the envelope, respectively. R1 is the radius of the donor, and m is the mass of the secondary. We assumed a constant structural parameter and set λ = 0.25, 0.5 and 1.0 to test its effect on the final results (de Kool et al. 1987), since a variable λ may not significantly affect the final results compared with a constant value of λ, such as λ = 1.0 (Claeys et al. 2014), although an exact calculation should take into account that λ depends on the stellar structure1. Thus, the final orbital separation of a surviving binary system after the CE phase, af, is determined by
(4)where λ is a structural parameter depending on the evolutionary stage of the donor. M, Mc, and Me are the masses of the donor, the donor core, and the envelope, respectively. R1 is the radius of the donor, and m is the mass of the secondary. We assumed a constant structural parameter and set λ = 0.25, 0.5 and 1.0 to test its effect on the final results (de Kool et al. 1987), since a variable λ may not significantly affect the final results compared with a constant value of λ, such as λ = 1.0 (Claeys et al. 2014), although an exact calculation should take into account that λ depends on the stellar structure1. Thus, the final orbital separation of a surviving binary system after the CE phase, af, is determined by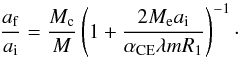 (5)Here, we may combine αCE and λ into one free parameter αCEλ, and then its value is 0.25, 0.5, 1.0, or 1.5 based on the selected value of αCE and λ (e.g., Lü et al. 2006). From Eq. (5), we can see that the results from simulations with αCE = 1.0 and λ = 0.25 or 0.5 are exactly the same as those with αCE = 0.5 and λ = 0.5 or 1.0.
(5)Here, we may combine αCE and λ into one free parameter αCEλ, and then its value is 0.25, 0.5, 1.0, or 1.5 based on the selected value of αCE and λ (e.g., Lü et al. 2006). From Eq. (5), we can see that the results from simulations with αCE = 1.0 and λ = 0.25 or 0.5 are exactly the same as those with αCE = 0.5 and λ = 0.5 or 1.0.
Nelemans et al. (2000) and Nelemans & Tout (2005) argued that it may be difficult for this prescription to produce a close pair of white dwarfs and suggested an alternative algorithm that conserves angular momentum. However, the feasibility of this suggestion is itself open to debate (see the reviews by Webbink 2008; Ivanova 2011; Woods et al. 2011). Especially when one tries to constrain the CE mechanism by WD + WD pairs observed, it is commonly assumed that the WD + WD pairs only experienced two CE phases (Case Cb here) and the influence of RLOF is neglected (Woods et al. 2011). However, as described above, there are four channels by which CO + He WD pairs can be formed, and subchannel Cb is not dominant. As a result of these considerations, the impact of RLOFs on the formation of WD + WD pairs warrants further attention, and we did not implement the suggestion of Nelemans et al. (2000) and Nelemans & Tout (2005) here.
2.3. Basic parameters for Monte Carlo simulations
To investigate the birth rate of CRTs from CO + He WD pairs, we carried out a series of detailed Monte Carlo simulations with the Hurley rapid binary evolution code (Hurley et al. 2000; 2002). We followed the evolution of 107 sample binaries until a CO + He WD pair formed. The 107 sample binaries were generated by a Monte Carlo algorithm based on the following assumptions: (1) all the stars form in a single starburst (where 1011M⊙ of stars are formed at the same instant); (2) the mass distribution of the newly formed stars follows the initial mass function (IMF) of Miller & Scalo (1979); (3) the binaries either follow a constant mass-ratio distribution, that is, n(q) = 1, a rising distribution, that is, n(q) = 2q, or both binary components are chosen randomly and independently from the same IMF (uncorrelated); (4) the binary separation distribution is constant in log a for wide binaries, where a is the orbital separation; (5) binary orbits are either circular or follow a rising distribution, that is, n(e) = 2e; (6) all stars have a metallicity of Z = 0.001 (see Table 1 for details). We also simulated a case with solar metallicity to test its effects, even though CRTs typically favor a low-metallicity environment (Yuan et al. 2013).
Based on these simulations, we calculated the evolution of the birth rate of the merger under various conditions. For a merger to produce a CRT, it should satisfy two terms: 1) the merger must have a long delay time; 2) the birth rate of the merger should match the birth rate of observed CRTs within error margins at a delay time longer than 10 Gyr. We arbitrarily chose 1 Gyr and 3 Gyr to be loose and strict age boundaries, respectively, for the purpose of judging whether a population is old. Most mergers probably have a delay time longer than this boundary, since, statistically, the ratio of the number of young CRTs to that of all CRTs must be very low. In addition, according to the estimation of Perets et al. (2010), the birth rate of CRTs at a delay time of longer than 10 Gyr is normalized to the birth rate of the SNe Ia in S0/E galaxies (Mannucci et al. 2005)2.
Parameters used to produce the binary sample.
 |
Fig. 2 Distribution of CO WD and He WD masses for different BPS sets. The mass transfer between the CO WD and the He WD is always unstable for the systems above the dashed line (q = MHe/MCO> 2/3), while it is always stable below the dot-dashed line (Marsh et al. 2004). The systems located at the right side of the triple-dot-dashed line have a mass of ≥1.378 M⊙. Three extremely low-mass (ELM) WD systems (J0751, J1741 and J1257+5428), whose component masses were accurately measured, are clearly located in the region allowing stable mass transfer (Kulkarni & van Kerkwijk 2010; Marsh et al. 2011; Kilic et al. 2014). The filled triangles represent the systems from the ELM survey that may merge within 10 Gyr, where i = 60° is assumed for systems with unknown inclinations (Kilic et al. 2012). |
3. Results
If a CO + He WD pair is the progenitor of a CRT, its merger should belong to an old population, and the merging rate should also match the birth rate of the CRTs derived from observations. The delay time of the mergers is a function of the masses of the components, as well as the orbital period, which is itself a function of the masses of the components during CE evolution, as is the mass ratio of the components. Therefore we identified possible progenitors of the CRTs by the masses of its components. An additional criterion was that, in theory, the CRTs have a tendency to result from low-mass WD pairs (Shen et al. 2010; Waldman et al. 2011), which was also considered when identifying possible progenitors.
3.1. Mass ratio?
Figure 2 shows the distributions of MHe and MCO of the systems that are potential candidates for CRT progenitors, and Fig. 3 presents the evolution of the merging rate of the potential progenitors for different mass-ratio constraints. At first glance, the distributions in Fig. 2 are all similar, that is, most of the systems have a CO WD of 0.55–0.85 M⊙ and a He WD of 0.2–0.35 M⊙. Notably, in every set, there is a concentration of He WDs at ~0.35 M⊙ (~0.32 M⊙ for the case of Z = 0.02), which result from quenched helium stars, meaning that the mass-transfer between a CO WD and a low-mass helium star begins when the helium star is still a helium main-sequence star on a short orbital period, and then the helium burning is quenched when the mass of the helium star reaches its minimum mass for helium burning (see Han et al. 2002), which leads to the formation of a He WD of ~0.35 M⊙ (~0.32 M⊙ for the case of Z = 0.02). See also Fig. 1 for subchannels for Cases Ba, Ca, and Da.
 |
Fig. 3 Evolution of the birth rate of potential candidates of CRT progenitors. The red solid line is for all the potential systems, while the green dashed and light-blue dotted lines are for those with always unstable and stable mass transfer, respectively. The blue dot-dashed line represents the systems whose mass transfer is neither always stable nor always unstable (see also Fig. 1). The vertical bar indicates the range of the birth rate of CRTs, normalized to the birth rate of SNe Ia in S0/E galaxies (Mannucci et al. 2005). The two vertical dotted lines mark the positions of delay times of 1 Gyr and 3 Gyr. |
From Fig. 2, we can see that most of the systems are located between the dashed and dot-dashed lines. The systems where q = MHe/MCO> 2/3, whose mass transfer is always dynamically unstable, are rare and typically have a delay time shorter than 1 Gyr (see the dashed line in Fig. 3). In addition, the birth rate of mergers of such a high mass ratio is also much lower than the birth rate of CRTs. Thus, it can be said at the very least that not all WD pairs undergoing unstable mass transfer contribute to the total number of CRTs, and that the number of CRTs they produce is negligible, if they produce CRTs at all. For systems below the dot-dashed line, the mass-transfer is always stable. Such systems usually have a CO WD with a mass higher than 0.7 M⊙. Although the birth rate of mergers from such systems matches those of CRTs with a delay time longer than 10 Gyr (the dotted line in Fig. 3), there should be many CRTs from young populations if these systems are indeed CRT progenitors. Moreover, in theory, a detonation at the bottom of a helium shell surrounding a relatively massive CO WD can result in a second detonation, the expected result of which would be a SN Ia (Shen & Bildsten 2014; Kilic et al. 2014). Furthermore, the material produced by the thermonuclear explosion is mainly 56Ni, the spectra of which cannot match the unique features of CRTs. From these perspectives, it seems impossible for such systems to be the progenitors of CRTs.
It can be seen from both Figs. 2 and 3 that the systems whose mass transfer processes are neither always stable nor always unstable dominate the population of CO + He WD pairs. Whether the mass transfer is dynamically stable or not depends on the synchronization timescale τs of the accretor, that is, dynamically unstable mass transfer is more likely for a long τs (Marsh et al. 2004). Here, τs may be the manifestation of a torque resulting from dissipative coupling, tidal or magnetic, which may be different between different CO + He WD pairs. However, the merging rate of these system is much higher than the birth rate of CRTs, and too many mergers are young, which cannot account for the trend of CRTs appearing among old populations (Fig. 3). In addition, most of the systems have a CO WD of larger than 0.6 M⊙, on which the helium detonation leaves mainly 56Ni and unburnt helium, and the predicted spectrum from such explosion is unlikely to fit the unique features of CRTs (Waldman et al. 2011).
In Fig. 2, we also plot some WD pairs from the ELM survey, which may merge within 10 Gyr (assuming i = 60° for the systems with unknown inclinations, Kilic et al. 2012). The distribution of the sample seems to favor low-mass WDs compared with our calculation, which is very likely due to an observational selection effect, since the effect of cooling during evolution on the brightness of the WDs is not considered here, and the aim of the project is to search extremely low-mass WDs (Kilic et al. 2011). However, in Fig. 2, we can see that many systems with an extremely low-mass WD from the ELM survey are located in the region where mass transfer is always stable, notably J0751, J1257+5428 and J1741. These systems are suspected to be progenitors of subluminous SNe Ia via double detonation (Branch et al. 1995; Solheim & Yungelson 2005; Hillebrandt et al. 2013). If these systems produce SNe Ia, they should contribute several percent of all SNe Ia based on the calculation above, which is higher than the estimate of 1% by Solheim & Yungelson (2005). Three main reasons contribute to this difference. Generally, the CO WD should be more massive than 0.8 M⊙ if the second detonation is expected in the center of the CO WD (Shen et al. 2010), but there is no such constraint in this paper. Secondly, we did not consider the effect of cooling on the brightness of the WDs, which means that early-formed high-mass WDs may be too dim to be discovered (Fontaine et al. 2001). Finally, the CO WD may receive the angular momentum of the accreted material and spin up. The effect of rapid rotation reduces the violence of helium flashes on the surface of the CO WD (Yoon & Langer 2004), and a helium nova is expected instead of a helium detonation. At present, there are clearly too many uncertainties about the double-detonation model leading to subluminous SNe Ia, and we do not discuss it further.
In Fig. 2, we also plot a triple-dot-dashed line, at which the total mass of a CO + He WD pair is equal to 1.378 M⊙ (close to the Chandrasekhar mass limit, Nomoto et al. 1984). The systems located at the right side of the line could produce normal SNe Ia if helium is stably burned into carbon and oxygen to increase the mass of the CO WD. However, according to the study of Shen et al. (2012), one may expect that after the destruction of the less massive He WD, a giant-like structure can be formed during the accretion stage. As a result of the relatively long time during which the giant-like structure is maintained, one could expect to lose about half a solar mass from the system, and thus it should be very difficult for the CO WD to increase its mass to 1.378 M⊙. Regardless of the exact mass, these systems are still interesting candidates as possible progenitors of SNe Ia, and numerical simulations of the merging of such systems should be studied. Irrespective of the uncertainties during the merging stage, these systems cannot be the progenitors of CRTs for the relatively massive CO WDs (see Fig. 2).
Based on this discussion, it seems impossible to distinguish progenitors of CRTs from other CO + He WD pairs by constraining the mass ratio alone.
 |
Fig. 4 Evolution of the birth rate of the merger of CO + He WD pairs for different CO WD mass constraints. The red solid line is for all WD pairs and the green dashed, blue dot-dashed and light-blue dotted lines are for the pairs with a CO WD of ≤0.8 M⊙, ≤0.6 M⊙, and ≤0.55 M⊙, respectively. Two vertical dotted lines mark the delay times of 1 Gyr and 3 Gyr. |
3.2. CO WD mass?
In Fig. 4, we plot the evolution of the merging rate of CO + He WD pairs for different CO WD mass constraints. From the figure, we can see a significant trend that the shortest delay time increases with decreasing CO WD mass constraint, which is expected because the shortest delay time is determined by the evolutionary timescale of the primordial secondary. A lower CO WD mass means a less massive primordial primary and a less massive primordial secondary, which in turn results in a long evolutionary timescale of the secondary. From the figure, we can see that the mergers with long delay times are dominated by the pairs with CO WDs of larger than 0.6 M⊙ due to a relatively longer tGW. In addition, for MCO ≤ 0.6 M⊙, the mergers seem to be divided into two age groups, one that is mainly younger than 1 Gyr, the other older than 1 Gyr. The reason they form these two groups is that they are derived from different evolutional channels: the young group mainly from the 2RLOF + 2CE channel, the old group mainly from the 2CE + 1RLOF channel. For the second group (MCO ≤ 0.55 M⊙), both the delay time and the merging rate seem to be consistent with the constraints from CRT observations. However, for the set in which Z = 0.02, even under the constraint of MCO ≤ 0.55, the merging rate at an age older than 10 Gyr is still much higher than the birth rate of CRTs. This is mainly due to the effect of metallicity on the initial-to-final mass relation (IFMR), which stipulates that a higher metallicity leads to a lower WD mass for a star with a given initial mass (Han et al. 1994; Umeda & Nomoto 1999; Meng et al. 2008). So, relative to the low-metallicity sample, the percentage of low-mass WDs from the high-metallicity sample is higher. In any case, it also seems impossible to distinguish the progenitor of CRTs from other CO + He WD pairs by constraining the CO WD mass alone.
3.3. Low-mass CO WD and low-mass He WD?
 |
Fig. 5 Evolution of the merging rate for systems with MCO ≤ 0.6 M⊙ (0.55 M⊙ for set 8) and MHe ≤ 0.4M⊙ (red solid line), MHe ≤ 0.3M⊙ (green dashed line), MHe ≤ 0.25M⊙ (blue dot-dashed line), and MHe ≤ 0.2M⊙ (light-blue dotted line). The two vertical dotted lines indicate the delay times of 1 Gyr and 3 Gyr. |
Shen et al. (2010) and Waldman et al. (2011) indicated that if the CO WD mass is higher than 0.6 M⊙, helium detonation leaves mainly 56Ni and unburnt He, and the predicted spectrum from this type of detonation is unlikely to match the unique features of CRTs. We also found that a significant proportion of the systems with a CO WD more massive than 0.6 M⊙ will merge within a delay time shorter than 3 Gyr, and the merging rate at a delay time of more than 10 Gyr is much higher than that of CRTs. In addition, although the mass ratio could be a very important factor in deciding the final result of the merger, the mass ratios of CRT progenitors are statistically indistinguishable from those of the general CO + He WD binary population, as discussed in Sect. 3.1. In this section, we therefore only consider systems with a CO WD of less mass than 0.6 M⊙, and identify the progenitors of CRTs by constraining the He WD mass. In Fig. 5, we plot the evolution of the merging rate for the systems with MCO ≤ 0.6 and various He WD mass constraints. We again see the trend that the shortest delay time increases with decreasing He WD mass constraints, which is because the delay time is determined by the evolutionary timescale of the primordial secondary: a low He WD mass means a less massive primordial secondary, and, consequently, a longer evolutionary timescale. The figure shows that the merging rate at a delay time of longer than 10 Gyr mainly arises from the systems with a He WD of MHe> 0.25 M⊙. For the sets with Z = 0.001, all the systems with a He WD of MHe ≤ 0.25 fulfill the loose delay-time criterion, while almost all the systems with a He WD of MHe ≤ 0.2 fulfill the strict delay-time criterion. However, although the systems with a He WD of MHe ≤ 0.2 from sets 3–7 match the birth rate of CRTs at a delay time longer than 10 Gyr, there is not a single system with a He WD less massive than 0.2 M⊙ for set 2 and for set 1, even the systems with the He WDs of MHe ≤ 0.25 are rare (see also Fig. 2). The reason for this phenomenon is that for a low αCEλ, a system is more likely to merge during the CE evolution, especially for systems with low-mass components (see also Eq. (5)). However, the birth rate of mergers with MHe ≤ 0.25 at a delay time longer than 10 Gyr is still higher than the observed birth rate of CRTs for set 2 and MHe ≤ 0.3 for set 1. Considering that the results from a variable λ are similar to that from a constant value of λ = 1.0 (Claeys et al. 2014), we assume that αCEλ ≥ 0.5, that is, αCE ≥ 0.5, is reasonable since the thermal energy is not included in our simulations. In conclusion, based on the results in this figure and the numerical simulations from Shen et al. (2010) and Waldman et al. (2011), it is necessary that the CO WD is less massive than 0.6 M⊙ and the He WD is less massive than 0.25 M⊙ for WD pairs to fulfill the constraints from both the host population age and the birth rate of CRTs. These systems could be the progenitors of CRTs. This is also consistent with the numerical simulation by Waldman et al. (2011). However, these constraints could be MCO ≤ 0.55 and MHe ≤ 0.2 M⊙ for a population with a metallicity of Z = 0.02 as a result of the influence of metallicity on the IFMR (Meng et al. 2008).
4. Discussion
We identified the progenitors of CRTs from a general binary population by constraining their component masses to fulfill the age and birth rate constraints of CRTs. However, many questions still remian open, such as the age of CRTs, the ejecta mass of the explosion, and the explosion mechanism itself. We discuss these problems below.
4.1. Uncertainties
As shown in Figs. 2, 4, and 5, among all the input parameters in the BPS simulations, αCEλ, that is, αCE and λ, is the most important parameter to affect the BPS results. The low-mass systems become rarer with the decrease of αCEλ because of the merging of the low-mass systems during the CE evolution for a low value of αCEλ (see sets 1–3, and 5 in Figs 2, 4, and 5). However, at present, the values of αCE and λ are quite uncertain (Han 1998; Politano & Weiler 2007; Xu & Li 2010; Zorotovic et al. 2010; Zuo & Li 2014; Claeys et al. 2014). Our results are based on the assumption that αCEλ ≥ 0.5. At present, we cannot exclude the possibility of αCEλ< 0.5, although such a low value seems to be unreasonable since the thermal energy is not included for CE evolution in our BPS simulation. If αCEλ were lower than 0.5, e.g. 0.25, the progenitors of CRTs could be the systems with MCO ≤ 0.6 and MHe ≤ 0.3M⊙ (set 1 in Fig. 5). Our other conclusions are not significantly affected by the value of αCEλ (see the following discussions).
4.2. Age
Although the observations made to constrain the progenitor population of the CRTs favored an old population (Kasliwal et al. 2012; Yuan et al. 2013; Lyman et al. 2013), the possibility is still not completely excluded that a small part of CRTs might be hosted by a relatively young population, such as SN 2001co (Lyman et al. 2013). In addition, quantitatively, the association of CRTs with the regions of ongoing star formation in their host galaxies matches that of SNe Ia (Lyman et al. 2013), which implies that some CRTs may originate from relatively young populations. There might be an observational selection effect because a subluminous supernova is more easily discovered in the border region than in the inner region of a host galaxy. From Fig. 5, we know that some pairs with low-mass CO WDs and low-mass He WDs have a medium delay time (between 1 Gyr and 3 Gyr), although there are relatively few of them. At present, the sample of CRTs is still small, and the statistical uncertainties about the population of the progenitors of CRTs are very large. This means that additional observations are necessary to confirm whether all the CRTs are hosted by old populations.
 |
Fig. 6 Distribution for different sets of the total mass of the WD pairs that qualify under the constraints that both are hosted by an old population and match the birth rate of CRTs. |
4.3. Ejecta mass
The ejecta mass of CRTs is concentrated at 0.4–0.7 M⊙ (Kasliwal et al. 2012), while that of a small minority of CRTs is beyond this range (Perets et al. 2010; Valenti et al. 2014). The scatter of the peak luminosity of the CRTs is small, 0.5 mag. These results could indicate that the distribution of the parameter determining the peak luminosity have a narrow peak with a wing, and the parameter could be relevant with one of the masses related to the low-mass CO + He WD pairs. Clearly, for the systems satisfying both the old population and the birth rate constraints, neither the CO WD mass nor the He WD mass fulfills the constraints of the ejecta mass. An ideal candidate for the parameter is the total mass of the merger. In Fig. 6, we present a histogram of the total mass of the WD pairs qualifying for the above constraints. The figure shows that the distribution of the total mass of the mergers has a narrow peak with a wing, although the position of the peak is dependent of the initial conditions of BPS set. However, the total mass is significantly higher than the ejecta mass of CRTs. This implies that if the low-mass CO + He WD pairs are the progenitors of CRTs, the merger probably is not completely destroyed, and a remnant survive after the explosion.
In theory, it is generally believed that a He-shell detonation is followed by a second detonation in the core of the CO WD, although it is still not clear whether and where the second detonation will occur (see Fink et al. 2007; Kromer et al. 2010). Shen et al. (2010) investigated He-shell detonations for three different CO WD masses (0.6, 1.0 and 1.2 M⊙) with different He-shell masses (0.02, 0.05, 0.1, 0.2, and 0.3 M⊙), and Waldman et al. (2011) extended the work of Shen et al. (2010) to low-mass CO WDs (0.45–0.6 M⊙) with a 0.2 M⊙ He shell. Similar to Waldman et al. (2011), Sim et al. (2012) also studied the He-shell detonation on a low-mass CO WD, but extended the simulation to the cases where a second detonation occurs. Based on these studies, if the second detonation occurs, the models show a brighter light curve than those from observations (Sim et al. 2012). If the second detonation does not occur, the peak luminosity is similar to, but the evolution of the light curve is much faster and the ejecta mass is less massive than, those from observations (Waldman et al. 2011). Notably, even the best-fit model to the data of SN 2005E in Waldman et al. (2011) is still somewhat fainter at peak, and clearly fades more rapidly after maximum light than, the observed light curve of SN 2005E. The observed ejecta mass is also too high for a shell detonation, which suggests that the CO core also participated in the explosion. At the same time, as indicated by the distribution of the total mass of CO + He WD pairs in Fig. 6, to account for the ejecta mass of CRTs, a remnant should survive the thermonuclear explosion if low-mass CO + He WD pairs are progenitors of CRTs. This seems to require a certain level of fine-tuning if the properties of CRTs are to be matched by exploding mergers. Even though many theoretical works have addressed the CRT model, more efforts may still be necessary to obtain a conclusive result on this, especially regarding whether the second detonation is triggered, and how a remnant is left. Since the second detonation in the center of the CO WD usually destroys the whole merger, an off-center detonation might be an alternative (Shen & Bildsten 2014).
4.4. Other mechanisms
Kasliwal et al. (2012) argued that CRTs cannot be the standard result of a thermonuclear explosion of a CO WD, which SNe Ia are, and presented two main differences from SNe Ia to support their argument. One is that no CRT conforms to the Philips relation (Philips 1993), and the other is that Fe-group elements seen in all SNe Ia are absent from the nebular spectra of CRTs. Kasliwal et al. (2012) examined the predictions from several theoretical models such as the deflagration of a sub-Chandrashekar-mass WD (Woosley & Weaver 1994) and the accretion-induced collapse of a rapidly rotating ONeMg WD into a neutron star (Metzger et al. 2009). They found that none of their predictions is consistent with the properties of CRTs. Yuan et al. (2013) suggested that one possible interpretation of the unusual subluminous CRTs is that it might be the result of a violent merger of two equal-mass CO WDs (Pakmor et al. 2010). However, such a violent merger has either a very short delay time or a very low birth rate (see Fig. 1 in Meng et al. 2011), and the ejecta mass resulting from such a violent merger is too massive compared with the observed ejecta masses. In addition, it could be difficult for the merger of two equal-mass WDs to reproduce the helium line in the spectra of some CRTs (Kasliwal et al. 2012). Another possible mechanism is a variation of the violent merger model, that is, a violent merger from a CO + He WD pair, which was suggested to explain the existence of subluminous SNe Ia (Pakmor et al. 2013). However, this model also fails to explain the observed CRT ejecta masses. Moreover, observationally, it could be difficult to distinguish the difference between the classical double-detonation model and the violent merger model from the CO + He WD pairs, especially for the delay time and the birth rate.
One of the CRTs (PTF 09dav) in the sample of Kasliwal et al. (2012) exhibited a hydrogen line in its nebular spectra, and Kasliwal et al. (2012) suggested that there might have been a series of nova eruptions prior to this particular CRT to account for this feature (see also Shen et al. 2013). In fact, there is another possible explanation for the hydrogen line, which is that the CRT with the hydrogen line in its nebular spectra evolved from the Case Db subchannel, which is similar to the proposition of Livio & Riess (2003) when explaining the properties of SN 2002ic. If this CRT results from this subchannel, one would expect a fairly thin shell of hydrogen ejecta, similar to what is seen in planetary nebulae with close binary cores. Judging from the estimation in Kasliwal et al. (2012), and given the velocity of 10 km s-1 for the ejecta shell, the CE ejection should cease 7800 yr before the supernova if the shell is photoionized, and 260 yr before the supernova if the shell is collision-ionized when the shock front reaches the shell.
5. Conclusions
In summary, we tried to investigate whether and which types of low-mass CO + He WD pairs can result in CRTs by examining whether the results of their evolution matches the host population ages and birth rates of CRTs in general. We presented four channels that produce CO + He WD pairs and showed that the classical channel to produce WD + WD pairs, in which a WD + WD pair only experiences two CE phases and does not undergo a stable RLOF, is not the dominant channel. This means that future attention should be paid to the stable RLOF when studying the formation of WD pairs. We found that the CO + He WD pairs with CO WDs less massive than 0.6 M⊙ and He WDs less massive than 0.25 M⊙ may qualify as CRT progenitors under the constraints of both host population ages and birth rates if αCEλ ≥ 0.5. If αCEλ were lower than 0.5, for example 0.25, the upper limit for the mass of the He WDs could be relaxed to 0.3 M⊙. However, the helium WD mass is lower than, while the total mass of the CO + He WD pairs is higher than, the ejecta mass of CRTs. If these low-mass WD pairs are the progenitors of CRTs, the CO WD should participate in the explosion, and a bound remnant could remain after the explosion. Clearly, many problems regarding CRTs need to be addressed both in theory and observation, especially to determine whether the second detonation is ignited at the center of a CO WD following a helium detonation at the surface of the CO WD, and whether there is a bound remnant after the CRT explosion, and whether all CRTs are from an old population. Finally, we suggest that the CRT with a hydrogen line in its nebular spectra might have evolved from the Case Db channel.
Different authors showed different formulae for λ, which means that there are many uncertainties in calculating the value of λ, such as the definition of the core of an AGB star and the stellar chemical composition (Xu & Li 2010; Claeys et al. 2014). In addition, our code is an old version and the subroutine for calculating the variable λ is not included.
Acknowledgments
We are grateful to the anonymous referee for his/her comments that improved this manuscript. This work was partly supported by NSFC (11473063,11390374) and Key Laboratory for the Structure and Evolution of Celestial Objects, Chinese Academy of Sciences. Z.H. thanks the support by the Strategic Priority Research Program “The Emergence of Cosmological Structures” of the Chinese Academy of Sciences, Grant No. XDB09010202.
References
- Branch, D., Livio, M., Yungelson, L. R., et al. 1995, PASP, 107, 1019 [NASA ADS] [CrossRef] [Google Scholar]
- Camacho, J., Torres, S., García-Berro, E., et al. 2014, 566, A86 [Google Scholar]
- Chen, X., & Han, Z. 2002, MNRAS, 335, 948 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, X., & Han, Z. 2003, MNRAS, 341, 662 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, X., & Han, Z. 2008, MNRAS, 387, 1416 [NASA ADS] [CrossRef] [Google Scholar]
- Claeys, Pols, O., Izzard, R., et al. 2014, A&A, 563, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Kool, M., van den Heuvel, E. P. J., & Pylyser, E. 1987, A&A, 183, 47 [NASA ADS] [Google Scholar]
- Fink, M., Hillebrandt, W., & Röpke, F. K. 2007, A&A, 476, 1133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fontaine, G., Brassard, P., & Bergeron, P. 2001, PASP, 113, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z. 1998, MNRAS, 296, 1019 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z., Podsiadlowski, P., & Eggleton, P. P. 1994, MNRAS, 270, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z., Podsiadlowski, P., & Eggleton, P. P. 1995, MNRAS, 272, 800 [NASA ADS] [Google Scholar]
- Han, Z., Tout, C. A., & Eggleton, P. P. 2000, MNRAS, 319, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z., Podsiadlowski, Ph., Maxted, P. F. L., Marsh, T. R., & Ivanova, N. 2002, MNRAS, 336, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Hillebrandt, W., & Niemeyer, J. C. 2000, ARA&A, 38, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Hillebrandt, W., Kromer, M., Röpke, F. K., & Ruiter, A. J. 2013, Frontiers of Physics, 8, 116 [Google Scholar]
- Hurley, J. R., Pols, O. R., & Tout, C. A. 2000, MNRAS, 315, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley, J. R., Tout, C. A., & Pols, O. R. 2002, MNRAS, 329, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Hjellming, M. S., & Webbink, R. F. 1987, ApJ, 318, 794 [NASA ADS] [CrossRef] [Google Scholar]
- Ivanova, N. 2011, ASPC, 441, 91 [NASA ADS] [Google Scholar]
- Kasliwal, M. M., Kulkarni, S. R., Gal-Yam, A., et al. 2012, ApJ, 755, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Kawabata, K. S., Maeda, K., Nomoto, K., et al. 2010, Nature, 465, 326 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kilic, M., Brown, W. R., Allen de Prieto, C., et al. 2011, ApJ, 727, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Kilic, M., Brown, W. R., Allen de Prieto, C., et al. 2012, ApJ, 751, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Kilic, M., Hermes, J. J., Gianninas, A., et al. 2014, MNRAS, 438, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Kulkarni, S. R., & van Kerkwijk, M. H. 2010, ApJ, 719, 1123 [NASA ADS] [CrossRef] [Google Scholar]
- Kromer, M., Sim, S. A., Fink, M., et al. 2010, A&A, 514, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Landau, L. D., & Lifshitz, E. M. 1962, The Classical Theory of Fields (Oxford: Pergamon) [Google Scholar]
- Leibundgut, B. 2000, A&ARv, 10, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Li, W. D., Chornock, R., Leaman, J., et al. 2011, MNRAS, 412, 1473 [NASA ADS] [CrossRef] [Google Scholar]
- Livio, M., & Riess, A. 2003, ApJ, 594, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Livio, M., & Soker, N. 1988, ApJ, 329, 764 [NASA ADS] [CrossRef] [Google Scholar]
- Lü, G., Yungelson, L., & Han, Z. 2006, MNRAS, 372, 1389 [NASA ADS] [CrossRef] [Google Scholar]
- Lyman, J. D., James, P. A., Perets, H. B., et al. 2013, MNRAS, 434, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Mannucci, F., Della Valle, M., Panagia, N., et al. 2005, A&A, 433, 807 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marsh, T. R., Nelemans, G., & Steeghs, D. 2004, MNRAS, 350, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Marsh, T. R., Gänsicke, B. T., Steeghs, D., et al. 2011, ApJ, 736, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Meng, X., Chen, X., & Han, Z. 2008, A&A, 487, 625 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meng, X., Chen, W., Yang, W., & Li, Z. 2011, A&A, 525, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miller, G. E., & Scalo, J. M. 1979, ApJSS, 41, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Metzger, B. D., Piro, A. L., Quataert, E., & Thompson, T. A. 2009 [arXiv:0908.1127] [Google Scholar]
- Nelemans, G., Verbunt, F., Yungelson, L. R., et al. 2000, A&A, 360, 1011 [NASA ADS] [Google Scholar]
- Nelemans, G., Napiwotzki, R., Karl, C., et al. 2005, A&A, 440, 1087 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nomoto, K., Thielemann, F.-K., & Yokoi, K. 1984, ApJ, 286, 644 [Google Scholar]
- Paczyński, B. 1976, in Structure and Evolution of Close Binaries, eds. P. P. Eggleton, S. Mitton, & J. Whelan (Dordrecht: Kluwer), 75 [Google Scholar]
- Pakmor, R., Kromer, M., Röopke, F. K., et al. 2010, Nature, 463, 61 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Pakmor, R., Kromer, M., Taubenberger, S., & Springel, V. 2013, ApJ, 770, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Politano, M., & Weiler, K. P. 2007, ApJ, 665, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Perets, H. B., Gal-Yam, A., Mazzali, P. A., et al. 2010, Nature, 465, 322 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Perets, H. B., Gal-yam, A., Crockett, R. M., et al. 2011, 728, L36 [Google Scholar]
- Phillips, M. M. 1993, ApJ, 413, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Podsiadlowski, P., Rappaport, S., & Pfahl, E. D. 2002, ApJ, 565, 1107 [NASA ADS] [CrossRef] [Google Scholar]
- Ruiter, A., Belczynski, K., & Fryer, C. 2009, ApJ, 699, 2026 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, K. J., & Bildsten, L. 2014, ApJ, 785, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, K. J., Kasen, D., Weinberg, N. N., et al. 2010, ApJ, 715, 767 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, K. J., Bildsten, L., Kasen, D., et al. 2012, ApJ, 748, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, K. J., Guillochon, J., & Foley, R. J. 2013, ApJ, 770, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Sim, S. A., Fink, M., Kromer, M., et al. 2012, MNRAS, 420, 3003 [NASA ADS] [CrossRef] [Google Scholar]
- Smartt, S. J. 2009, ARA&A, 47, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Solheim, J. E., & Yungelson, L. R. 2005, ASP Conf. Ser., 334, 387 [NASA ADS] [Google Scholar]
- Umeda, H., & Nomoto, K. 1999, ApJ, 513, 861 [NASA ADS] [CrossRef] [Google Scholar]
- Valenti, S., Yuan, F., Taubenberger, S., et al. 2014, MNRAS, 437, 1519 [NASA ADS] [CrossRef] [Google Scholar]
- Waldman, R., Sauer, D., Livne, E., et al. 2011, ApJ, 738, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Webbink, R. F. 1988, in The Symbiotic Phenomenon, eds. J. Mikolajewska, M. Friedjung, S. J. Kenyon, & R. Viotti (Dordrecht: Kluwer), 311 [Google Scholar]
- Webbink, R. F. 2008, ASSL, 352, 233 [NASA ADS] [Google Scholar]
- Woods, T. E., Ivanova, N., van der Sluys, M., & Chaichenets, S. 2011, ASP Conf. Ser., 447, 127 [NASA ADS] [Google Scholar]
- Woosley, S. E., & Weaver, T. A. 1994, ApJ, 423, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, X., & Li, X. 2010, ApJ, 716, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, F., Kobayashi, C., Schmidt, B. P., et al. 2013, MNRAS, 432, 1680 [NASA ADS] [CrossRef] [Google Scholar]
- Yoon, S.-C., & Langer, N. 2004, A&A, 419, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zorotovic, M., Schreiber, M., & Gäsiche, B. 2010, A&A, 520, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zuo, Z., & Li, X. 2014, MNRAS, 442, 1980 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Schematic for the evolution channels that can form the CO + He WD pairs, where q = M2/M1 is the primordial mass ratio and a is the primordial orbital separation (see text for details). |
| In the text | |
 |
Fig. 2 Distribution of CO WD and He WD masses for different BPS sets. The mass transfer between the CO WD and the He WD is always unstable for the systems above the dashed line (q = MHe/MCO> 2/3), while it is always stable below the dot-dashed line (Marsh et al. 2004). The systems located at the right side of the triple-dot-dashed line have a mass of ≥1.378 M⊙. Three extremely low-mass (ELM) WD systems (J0751, J1741 and J1257+5428), whose component masses were accurately measured, are clearly located in the region allowing stable mass transfer (Kulkarni & van Kerkwijk 2010; Marsh et al. 2011; Kilic et al. 2014). The filled triangles represent the systems from the ELM survey that may merge within 10 Gyr, where i = 60° is assumed for systems with unknown inclinations (Kilic et al. 2012). |
| In the text | |
 |
Fig. 3 Evolution of the birth rate of potential candidates of CRT progenitors. The red solid line is for all the potential systems, while the green dashed and light-blue dotted lines are for those with always unstable and stable mass transfer, respectively. The blue dot-dashed line represents the systems whose mass transfer is neither always stable nor always unstable (see also Fig. 1). The vertical bar indicates the range of the birth rate of CRTs, normalized to the birth rate of SNe Ia in S0/E galaxies (Mannucci et al. 2005). The two vertical dotted lines mark the positions of delay times of 1 Gyr and 3 Gyr. |
| In the text | |
 |
Fig. 4 Evolution of the birth rate of the merger of CO + He WD pairs for different CO WD mass constraints. The red solid line is for all WD pairs and the green dashed, blue dot-dashed and light-blue dotted lines are for the pairs with a CO WD of ≤0.8 M⊙, ≤0.6 M⊙, and ≤0.55 M⊙, respectively. Two vertical dotted lines mark the delay times of 1 Gyr and 3 Gyr. |
| In the text | |
 |
Fig. 5 Evolution of the merging rate for systems with MCO ≤ 0.6 M⊙ (0.55 M⊙ for set 8) and MHe ≤ 0.4M⊙ (red solid line), MHe ≤ 0.3M⊙ (green dashed line), MHe ≤ 0.25M⊙ (blue dot-dashed line), and MHe ≤ 0.2M⊙ (light-blue dotted line). The two vertical dotted lines indicate the delay times of 1 Gyr and 3 Gyr. |
| In the text | |
 |
Fig. 6 Distribution for different sets of the total mass of the WD pairs that qualify under the constraints that both are hosted by an old population and match the birth rate of CRTs. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


