| Issue |
A&A
Volume 573, January 2015
|
|
|---|---|---|
| Article Number | A86 | |
| Number of page(s) | 4 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201424531 | |
| Published online | 23 December 2014 | |
Research Note
A method to deconvolve mass ratio distribution of binary stars
1 Instituto de Física y Astronomía, Universidad de Valparaíso,
Chile
e-mail:
michel.cure@uv.cl
2
Departamento de Matemáticas, Facultad de Ciencias Exactas y
Naturales, Universidad de Buenos Aires and Instituto de Matemática Luis
Santalo, IMAS–CONICET, Argentina
e-mail:
drial@mate.uba.ar
3
Universidad Nacional de General Sarmiento,
Buenos Aires,
Argentina
e-mail:
jcassett@ungs.edu.ar
4 Instituto de Estadística, Pontificia Universidad Católica de
Valparaíso, Chile
e-mail:
alejandra.christen@ucv.cl
5
ESO, Vitacura, Santiago, Chile
e-mail:
hboffin@eso.org
Received: 4 July 2014
Accepted: 30 November 2014
Aims. It is important to know the binary mass-ratio distribution to better understand the evolution of stars in binary systems and to constrain their formation. However, in most cases, that is, for single-lined spectroscopic binaries, the mass ratio cannot be measured directly, but can only be derived as the convolution of a function that depends on the mass ratio and on the unknown inclination angle of the orbit on the plane of the sky.
Methods. We extend our previous method for deconvolving this inverse problem by obtaining the cumulative distribution function (CDF) for the mass-ratio distribution as an integral.
Results. After a suitable transformation of variables, this problem becomes the same as the problem of rotational velocities vsini, allowing a close analytic formulation for the CDF. We here apply our method to two real datasets: a sample of Am star binary systems, and a sample of massive spectroscopic binaries in the Cyg OB2 association.
Conclusions. We are able to reproduce previous results for the sample of Am stars. In addition, the mass-ratio distribution of massive stars shows an excess of systems with a low mass ratio, in contrast to what was claimed elsewhere. Our method proves to be very reliable and deconvolves the distribution from a sample in one single step.
Key words: methods: analytical / methods: data analysis / methods: numerical / methods: statistical / binaries: general / stars: fundamental parameters
© ESO, 2014
1. Introduction
Knowing the mass-ratio distribution of binary systems is crucial for understanding how stars form and for distinguishing between the various proposed scenarios. Different ranges of mass ratios and separations have been obtained depending on the formation process (e.g., Halbwachs 1987; Mazeh & Goldberg 1992; Clarke 2007; Kouwenhoven et al. 2009; Bate 2012). Similarly, the mass-ratio distribution can provide useful information on the formation channels of various classes of binary stars because it affects the evolution of a binary system (e.g., Boffin et al. 1992; Halbwachs et al. 2003). In most cases, it is unfortunately impossible to directly measure the mass ratio because we only have access to the projected quantity qsin3i, where i is the inclination angle of the orbit on the plane of the sky and q a function of the mass ratio (see below).
To deconvolve the mass-ratio distribution function, it is assumed that the rotational axes are uniformly distributed over the sphere. Based on this assumption, Heacox (1995) discussed different algorithms to distinguish them. Among these algorithms, we find i) the analytic inverse that corresponds to the pioneer work of Chandrasekhar & Münch (1950), giving a formal solution proportional to a derivative of an Abel integral; and ii) the iterative inverse that corresponds to the work of Cerf & Boffin (1994; see Boffin 2010, 2012, for more recent applications of this method), using a Bayesian iterative method proposed by Lucy (1974). This method has the disadvantage that it possesses no convergence criteria (Bi & Boerner 1994), and the requested number of iterations has to be estimated carefully based on the signal-to-noise ratio of the data to ensure that no spurious peaks are obtained (Brown 2011; Boffin 2012). Despite these facts, Lucy’s method is widely used in the astronomical community to deconvolve distribution functions from different observation samples (Lucy 1994).
For the similar problem of rotational velocities, where the observed quantity is vsini, Curé et al. (2014, hereafter Paper I) enhanced the work of Chandrasekhar & Münch (1950) by integrating the probability distribution function (PDF) and obtain the cumulative distribution function (CDF) for the velocity distribution as a smooth function and in only one step, without iteration.
Following Paper I, we here apply this methodology to deconvolve the mass-ratio distribution from a sample of qsin3i under the common assumption of uniform distribution of rotational axes. This article is structured as follows: in Sect. 2 we present a short summary of Paper I and present the mathematical description of this binary mass-ratio distribution problem. Section 3 is devoted to calculating the deconvolution of the distribution and to discussing the robustness of this method. In Sect. 4 we calculate the CDF for two real samples of spectroscopic binaries. In the last section we present our conclusions and future work.
2. Method
In Paper I we obtained the CDF of the rotational velocities of stars. We started from the integral representation of the problem, 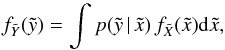 (1)here
(1)here 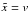 (rotational speed),
(rotational speed), 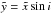 , where i is the inclination angle. This integral corresponds to a Fredholm integral of the first kind (Lucy 1994). Here
, where i is the inclination angle. This integral corresponds to a Fredholm integral of the first kind (Lucy 1994). Here 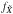 is the function of interest (PDF), and the kernel p of this integral is calculated assuming that the rotational axes are uniformly (randomly) distributed over the sphere. Replacing the kernel p (see Paper I), the Fredholm integral reads
is the function of interest (PDF), and the kernel p of this integral is calculated assuming that the rotational axes are uniformly (randomly) distributed over the sphere. Replacing the kernel p (see Paper I), the Fredholm integral reads 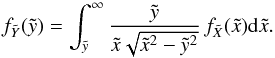 (2)Chandrasekhar & Münch (1950) deconvolved this equation to obtain the PDF,
(2)Chandrasekhar & Münch (1950) deconvolved this equation to obtain the PDF, 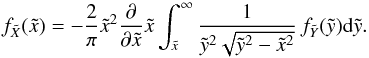 (3)After integrating the PDF, the corresponding CDF reads
(3)After integrating the PDF, the corresponding CDF reads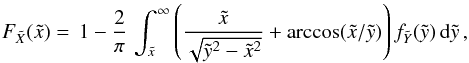 (4)see Paper I for details.
(4)see Paper I for details.
We here focus on a similar problem in astrophysics: the mass-ratio distribution of binary stars (see, e.g., Heacox 1995). For single-lined spectroscopic binaries, we have only access to the spectroscopic mass function, given by 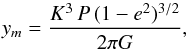 (5)where K, P, and e are the semi-amplitude of the radial velocity, orbital period, and eccentricity. This mass function can be rewritten as
(5)where K, P, and e are the semi-amplitude of the radial velocity, orbital period, and eccentricity. This mass function can be rewritten as 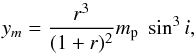 (6)where mp is the mass of the primary, mc the mass of the companion, r = mc/mp is the mass ratio, and i corresponds to the inclination angle between the orbital plane and the plane of the sky. Thus, the observed reduced spectroscopic mass function is
(6)where mp is the mass of the primary, mc the mass of the companion, r = mc/mp is the mass ratio, and i corresponds to the inclination angle between the orbital plane and the plane of the sky. Thus, the observed reduced spectroscopic mass function is 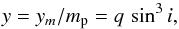 (7)where q ≡ r3/ (1 + r)2.
(7)where q ≡ r3/ (1 + r)2.
For this case, the kernel p, following Boffin et al. (1992) and Cerf & Boffin (1994), reads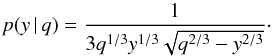 (8)Cerf & Boffin (1994) found that the Friedholm integral Eq. (1) can the be written as
(8)Cerf & Boffin (1994) found that the Friedholm integral Eq. (1) can the be written as 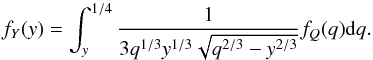 (9)Now we have to solve this inverse problem, that is, obtain fQ(q) from Eq. (9).
(9)Now we have to solve this inverse problem, that is, obtain fQ(q) from Eq. (9).
3. Deconvolving the mass-ratio distribution
Defining Y = x3, then fX(x) = 3x2fY(x3), Eq. (9) becomes 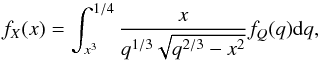 and applying the following transformation of variables q = p3, Eq. (9) now reads
and applying the following transformation of variables q = p3, Eq. (9) now reads 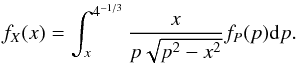 (10)This last expression is the same as Eq. (2), which has the following solution:
(10)This last expression is the same as Eq. (2), which has the following solution: 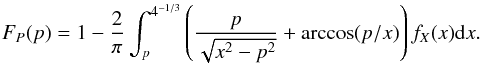 (11)To avoid numerical instabilities in the integration process of Eq. (11), we propose to use the following variable,
(11)To avoid numerical instabilities in the integration process of Eq. (11), we propose to use the following variable, 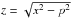 , or equivalently
, or equivalently 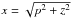 and
and 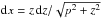 . Therefore, Eq. (11) transforms to
. Therefore, Eq. (11) transforms to 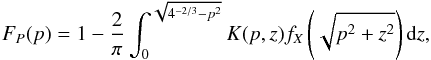 (12)where the function K is defined as
(12)where the function K is defined as 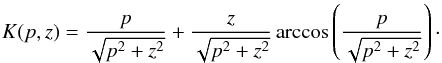 (13)Finally, the CDF as function of the original variable (r), reads
(13)Finally, the CDF as function of the original variable (r), reads 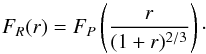 (14)
(14)
3.1. Logarithmic variables
Boffin (2010) has shown that when dealing with spectroscopic mass function distributions, which span a wide range of values, it is often necessary to use logarithmic variables. We therefore define z = e−s, such that the previous expression (Eq. (12)) is written as 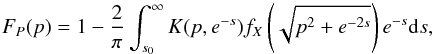 (15)where
(15)where 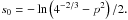
4. CDF application to real datasets
In this section we apply the proposed method to two samples of real astronomical data to obtain the CDF distribution as function of the mass ratio r. In addition, we compare our results with the method of Lucy (1974).
4.1. Real dataset 1: Am binaries
Boffin (2010) derived the mass-ratio distribution for a sample of 134 Am binaries using the method of Lucy (1974) as implemented by Boffin et al. (1993). He found that this distribution can be approximated by a uniform distribution.
Smalley et al. (2014) reported the discovery of 70 eclipsing Am systems using light curves from the SuperWASP project. Based on these light curves, they estimated the mass-ratio distribution of Am stars. When taking into account the fact that low-mass companions to Am stars may be too small and too faint to be detected as eclipsing, they found a mass-ratio distribution consistent with that of Boffin (2010).
 |
Fig. 1 Estimated CDF using our method plotted as a solid line. The short-dashed lines show the 95% confidence interval. The CDF using the method of Lucy (1974) as adopted by Boffin (2010) is shown as the long-dashed line, while the theoretical CDF from a uniform distribution is plotted as a dot-dashed line. See text for details. |
To constrain the range of y = qsin3i as function of r, we have to take in account the following: sini is smaller than one, then we are left with q = r3/ (1 + r)2. Similarly, for physical reasons, the mass ratio has to be lower than or equal to 1 (r ≤ 1), otherwise, if the companion is more massive because they are main-sequence stars, it would be more luminous, and the system would not appear as it is. Thus q has to be smaller than 1/4.
The reason why some values of y appear higher than 0.25 are most likely observational errors on the spectroscopic mass functions or an incorrect estimate of the primary mass. As such cases are very rare, we preferred to remove them from the sample to have a more homogeneous sample.
For these reasons, our method was developed in the range: 0 <y< 1/4.
We filtered the dataset of Boffin (2010) for values of y (Eq. (7)) in that range, which yielded 119 data values. Then we calculated the CDF as function of r, shown as solid line in Fig. 1.
To calculate the error of our method, we used the bootstrap method (Efrom 1993). The bootstrap method attempts to determine the probability distribution from the data themselves, without recourse to central limit theorem. This method is a way to estimate the error of the sample. The basic idea of bootstrapping in our case is to compute the CDF from a sample, create an artificial sample by randomly drawing elements from the original sample (some elements will be picked more than once), then to compute the new CDF and repeat this procedure 100–1000 times to determine the distribution of these CDFs.
Thus, we created 500 bootstrap samples from the original sample from Boffin (2010) and calculated the corresponding CDF for each of these bootstrap samples. To obtain a 95% confidence interval, we used the same procedure as in Curé et al. (2014): we calculated the confidence interval with the normal standard percentile Zα/ 2: 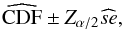 (16)where
(16)where 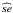 is the standard deviation of all bootstrap samples, and Zα/ 2 is the value for which the standard normal distribution accumulate 97.5% of the area under its PDF, and α = 0.05( = 1−0.95) is the complement of the confidence.
is the standard deviation of all bootstrap samples, and Zα/ 2 is the value for which the standard normal distribution accumulate 97.5% of the area under its PDF, and α = 0.05( = 1−0.95) is the complement of the confidence.
Our method for the CDF completely agrees with that of Lucy, that is, we arrive at the same conclusion that the sample is compatible with a uniform distribution. In addition to the advantage that our method does not need any iteration criteria and it deconvolves the mass-ratio CDF in one step, it can also provide (using the bootstrap method) confidence intervals for this CDF.
 |
Fig. 2 Estimated CDF for the Cyg OB2 association using the sample from Kobulnicky et al. (2014). Our method is plotted as solid lines with the confidence intervals as short-dashed lines. The method of Lucy is plotted as a long-dashed line. The theoretical CDF from a uniform distribution is shown as a dot-dashed line. |
4.2. Real dataset 2: binaries in the Cyg OB2 association
Based on a previous work spanning several years, Kobulnicky et al. (2014) presented a sample of 48 massive multiple-star systems known in the Cygnus OB2 association and analyzed their orbital properties. Using a Monte Carlo method, they conclude in particular that the observed distribution of mass ratios is consistent with a uniform distribution, even though they estimated that as a result of incompleteness, the bins at r< 0.2 are probably underestimated. We used their spectroscopic mass function sample and adopted primary mass, assuming that all systems are single-lined spectroscopic binaries. After filtering in the range 0 <y< 1/4, the sample consisted of 47 data points. Then we computed the mass-ratio distribution with the confidence intervals based on our methodology and on the method of Lucy as implemented by Boffin (2010). The results are shown in Fig. 2.
It is clear that instead of finding a uniform distribution over the full range of mass ratios, we find an excess of systems in the whole interval 0 <r< 1 as compared with a uniform distribution. A comparison between the two methods shows a similar behavior in almost the entire r-interval, but this does not correspond to a uniform distribution. The CDF derived with the method of Lucy lies inside the confidence interval of our CDF, therefore we conclude that statistically, they are the same CDF. On the other hand, Fig. 3 shows the CDF vs. log (r), and it seems that the CDF is linear in log (r) from r ≳ 0.2. This indicates that instead of a uniform distribution, the sample of massive stars is more consistent with an excess of low-mass companions.
As mentioned above, the interval r< 0.2 suffers from incompleteness, therefore the real contribution of these low-mass companions may be even larger than found here. This may have important consequences for the final binary fraction of massive stars and should be taken into account in further observational campaigns to aim at discovering companions to massive stars.
 |
Fig. 3 Estimated CDF plotted as function of log (r) as solid line with the confidence intervals as short-dashed lines. The theoretical CDF from a uniform distribution is plotted as a dot-dashed line. This estimated CDF seems to be linear in log (r) from r ≳ 0.2. |
5. Conclusion
We have obtained the cumulative distribution function of deprojected mass ratios from binary systems. After a suitable change of variables, we showed that this problem is the same as the problem of the distribution of rotational velocities from stars, therefore its solution is known (Paper I).
This method allowed us to obtain the CDF without the numerical instabilities caused by the use of derivative (Chandrasekar & Münch 1950) in only one step without needing any convergence criteria as needed by the widely used iterative method of Lucy (1974). In addition, confidence intervals can be attained using a bootstrap algorithm.
We applied our method to two real binary samples. While we find the same result as Boffin (2010) for the sample of Am spectroscopic binaries, we find that the mass-ratio distribution of massive binaries in the Cyg2 OB association presents an excess of systems with mass ratios r< 0.2, and it is highly probable that this sample does not come from a uniform distribution, which contradicts the analysis of Kobulnicky et al. (2014).
In the future, we plan to extend the applicability of our model to a general function describing an arbitrary orientation of inclination angles (see, e.g., Boffin 2012, for reasons why this might be needed) and study these distributions (rotational velocities or mass-ratio distributions) in a more precise formulation.
Acknowledgments
M.C. thanks for the support of FONDECYT project 1130173 and Centro de Astrofísica de Valparaíso. J.C. thanks for the financial support from the project “Ecuaciones Diferenciales y Análisis Numérico” – Instituto de Ciencias, Instituto de Desarrollo Humano e Instituto de Industria – Universidad Nacional de General Sarmiento. D.R. acknowledges the support of project PIP11420090100165, CONICET. A.C. thanks for the support from PUCVs projects 126.711/2014 and 37.375/2014.
References
- Bate, M. R. 2012, MNRAS, 419, 3115 [NASA ADS] [CrossRef] [Google Scholar]
- Bi, H., & Boerner, G. 1994, A&AS, 108, 409 [NASA ADS] [Google Scholar]
- Boffin, H. M. J. 2010, A&A, 524, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boffin, H. M. J. 2012, Proc. of the workshop Orbital Couples: Pas de Deux in the Solar System and the Milky Way, Held at the Observatoire de Paris, eds. F. Arenou, & D. Hestroffer, 41 [Google Scholar]
- Boffin, H. M. J., Paulus, G., & Cerf, N. 1992, in Binaries as Tracers of Star Formation, 26 [Google Scholar]
- Boffin, H. M. J., Cerf, N., & Paulus, G. 1993, A&A, 271, 125 [NASA ADS] [Google Scholar]
- Brown, R. A. 2011, ApJ, 733, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Cerf, N., & Boffin, H. M. J. 1994, Inverse Problems, 10, 533 [Google Scholar]
- Chandrasekhar, S., & Münch, G. 1950, ApJ, 111, 142 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Clarke, C. J. 2007, in Binary Stars as Critical Tools & Tests in Contemporary Astrophysics, eds. W. I. Hartkopf, E. F. Guinan, & P. Harmanec (Cambridge University Press), Proc. IAU Symp., 240, 337 [Google Scholar]
- Curé, M., Rial, D. F., Christen, A., & Cassetti, J. 2014, A&A, 565, A85 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Efrom, B., & Tibshirani, R. J. 1993, An Introduction to the Bootstrap (London: Chapman and Hall) [Google Scholar]
- Halbwachs, J. L. 1987, A&A, 183, 234 [NASA ADS] [Google Scholar]
- Halbwachs, J. L., Mayor, M., Udry, S., & Arenou, F. 2003, A&A, 397, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heacox, W. D. 2005, AJ, 109, 2670 [Google Scholar]
- Knowles, I., & Remka, R. J. 2014, in Variational and Topological Methods: Theory, Applications, Numerical Simulations, and Open Problems. Electron. J. Diff. Eqns., Conference 21, 235 [Google Scholar]
- Kouwenhoven, M. B. N., Brown, A. G. A., Goodwin, S. P., et al. 2009, A&A, 493, 979 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kobulnicky, H. A., Kiminki, D. C., Lundquist, M. J., et al. 2014, ApJS, 213, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Lucy, L. B. 1974, AJ, 79, 745 [NASA ADS] [CrossRef] [Google Scholar]
- Lucy, L. B. 1994, Rev. Mod. Astron., 7, 31 [NASA ADS] [Google Scholar]
- Mazeh, T., & Goldberg, D. 1992, ApJ, 394, 592 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., et al. 1993, The Observatory, 113, 214 [NASA ADS] [Google Scholar]
- Smalley, B., Southworth, J., Pintado, O. I., et al. 2014, A&A, 564, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tikhonov, A. N., & V. Y. Arsenin 1977, Solution of Ill-posed Problems (Washington: Winston & Sons) [Google Scholar]
- Tikhonov, A. N., Goncharsky, A. V., Stepanov, V. V., et al. 1995, Numerical Methods for the Solution of Ill-Posed Problems (Kluwer Academic Publishers) [Google Scholar]
- Watkins, S. J.,Boffin, H. M. J., Francis, N., & Whitworth, A. P. 1998, in Star Formation with the Infrared Space Observatory, ASP Conf. Ser., 132, 430 [Google Scholar]
All Figures
 |
Fig. 1 Estimated CDF using our method plotted as a solid line. The short-dashed lines show the 95% confidence interval. The CDF using the method of Lucy (1974) as adopted by Boffin (2010) is shown as the long-dashed line, while the theoretical CDF from a uniform distribution is plotted as a dot-dashed line. See text for details. |
| In the text | |
 |
Fig. 2 Estimated CDF for the Cyg OB2 association using the sample from Kobulnicky et al. (2014). Our method is plotted as solid lines with the confidence intervals as short-dashed lines. The method of Lucy is plotted as a long-dashed line. The theoretical CDF from a uniform distribution is shown as a dot-dashed line. |
| In the text | |
 |
Fig. 3 Estimated CDF plotted as function of log (r) as solid line with the confidence intervals as short-dashed lines. The theoretical CDF from a uniform distribution is plotted as a dot-dashed line. This estimated CDF seems to be linear in log (r) from r ≳ 0.2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


