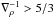| Issue |
A&A
Volume 573, January 2015
|
|
|---|---|---|
| Article Number | A89 | |
| Number of page(s) | 17 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201423760 | |
| Published online | 23 December 2014 | |
The Stagger-grid: A grid of 3D stellar atmosphere models
III. The relation to mixing length convection theory⋆,⋆⋆
1 Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 85741 Garching, Germany
e-mail: magic@mpa-garching.mpg.de
2 Research School of Astronomy & Astrophysics, Cotter Road, ACT 2611 Weston, Australia
Received: 5 March 2014
Accepted: 19 August 2014
Aims. We investigate the relation between 1D atmosphere models that rely on the mixing length theory and models based on full 3D radiative hydrodynamic (RHD) calculations to describe convection in the envelopes of late-type stars.
Methods. The adiabatic entropy value of the deep convection zone, sbot, and the entropy jump, Δs, determined from the 3D RHD models, were matched with the mixing length parameter, αMLT, from 1D hydrostatic atmosphere models with identical microphysics (opacities and equation-of-state). We also derived the mass mixing length parameter, αm, and the vertical correlation length of the vertical velocity, C[vz,vz], directly from the 3D hydrodynamical simulations of stellar subsurface convection.
Results. The calibrated mixing length parameter for the Sun is α๏MLT (Sbot) = 1.98. . For different stellar parameters, αMLT varies systematically in the range of 1.7 − 2.4. In particular, αMLT decreases towards higher effective temperature, lower surface gravity and higher metallicity. We find equivalent results for α๏MLT (ΔS). In addition, we find a tight correlation between the mixing length parameter and the inverse entropy jump. We derive an analytical expression from the hydrodynamic mean-field equations that motivates the relation to the mass mixing length parameter, αm, and find that it qualitatively shows a similar variation with stellar parameter (between 1.6 and 2.4) with the solar value of α๏m = 1.83.. The vertical correlation length scaled with the pressure scale height yields 1.71 for the Sun, but only displays a small systematic variation with stellar parameters, the correlation length slightly increases with Teff.
Conclusions. We derive mixing length parameters for various stellar parameters that can be used to replace a constant value. Within any convective envelope, αm and related quantities vary strongly. Our results will help to replace a constant αMLT.
Key words: convection / hydrodynamics / stars: atmospheres / stars: evolution / stars: late-type / stars: solar-type
Appendices are available in electronic form at http://www.aanda.org
Full Table A.1 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/573/A89 as well as at http://www.stagger-stars.net
© ESO, 2014
1. Introduction
In the past century, insights in various fields of physics led to a substantially more accurate interpretation and understanding of the processes taking place in the interior of celestial bodies. Astronomers can parameterize the conditions on the surface of stars with theoretical stellar atmosphere models, and with the theory of stellar structure and evolution, they are additionally capable to predict the complex development of stars.
The radiated energy of cool stars, originating from the deeper interior because of nuclear burning in the center, is advected to the surface by convective motions in the envelope that are driven by negative buoyancy acceleration. At the thin photospheric transition region the large mean free path of photons allows them to escape into space, and the convective energy flux is abruptly released. To theoretically model this superadiabatic boundary domain of stars is challenging because of the nonlinear and nonlocal nature of turbulent subsurface convection and radiative transfer, and an analytical solution is a long-standing unresolved problem.
To account for the convective energy transport, Böhm-Vitense (1958) formulated the mixing length theory (MLT), which was initially proposed by Prandtl (1925) in analogy to the concept of the mean free path in the kinetic gas theory. In the framework of MLT, it is assumed that the heat flux is carried by convective elements for a typical distance before they dissolve instantaneously into the background. This distance is the so-called mixing length, l, usually expressed in units of the pressure scale height, αMLT = l/HP. The mixing length parameter αMLT is a priori unknown, hence it has to be calibrated, usually by matching the current radius and luminosity of the Sun by a standard solar model with a single depth-independent 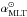 . This calibrated value for the Sun is then used for all stellar parameters. We recall that
. This calibrated value for the Sun is then used for all stellar parameters. We recall that 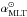 , in fact, corrects for all other shortcomings of the solar model, deficits in the equation-of-state (EOS), the opacities, or the solar composition. It therefore is no wonder that its numerical value (typically around 1.7 to 1.9; e.g., see Magic et al. 2010) varies with progress in these aspects and from code to code. In addition, MLT is a local and time-independent theory that effectively contains three additional, free parameters, and assumes symmetry in the up- and downflows, hence also in the vertical and horizontal direction. The actual formulation of MLT can also vary slightly (e.g., see Henyey et al. 1965; Mihalas 1970; Ludwig et al. 1999).
, in fact, corrects for all other shortcomings of the solar model, deficits in the equation-of-state (EOS), the opacities, or the solar composition. It therefore is no wonder that its numerical value (typically around 1.7 to 1.9; e.g., see Magic et al. 2010) varies with progress in these aspects and from code to code. In addition, MLT is a local and time-independent theory that effectively contains three additional, free parameters, and assumes symmetry in the up- and downflows, hence also in the vertical and horizontal direction. The actual formulation of MLT can also vary slightly (e.g., see Henyey et al. 1965; Mihalas 1970; Ludwig et al. 1999).
Many attempts have been made to improve MLT, a substantial one being the derivation of a nonlocal mixing length theory (Gough 1977; Unno et al. 1985; Deng et al. 2006; Grossman et al. 1993). The standard MLT is a local theory, meaning that the convective energy flux is derived purely from local thermodynamical properties, ignoring thus any nonlocal properties (e.g., overshooting) of the flow. Nonlocal models are typically derived from the hydrodynamic equations, which are a set of nonlinear moment equations including higher order moments. To solve them, closure approximations are considered (e.g., diffusion approximation, anelatistic approximations, or introducing a diffusion length). Other aspects have also been studied: the asymmetry of the flow by a two-stream MLT model (Nordlund 1976), the anisotropy of the eddies (Canuto 1989), the time-dependence (Xiong et al. 1997), and the depth-dependence of αMLT (Schlattl et al. 1997). While standard MLT accounts for only a single eddy size (which is l), Canuto & Mazzitelli (1991) extended this to a larger spectrum of eddy sizes by including the nonlocal second-order moment (Canuto et al. 1996). The original Canuto-Mazzitelli theory – also known as the full spectrum turbulence model – used the distance to the convective region border as a proxy for the mixing length; a later version (Canuto & Mazzitelli 1992) re-introduced a free parameter resembling αMLT.
These approaches are often complex, but so far, the standard MLT is still widely in use, and a breakthrough has not been achieved, despite all the attempts for improvements. In 1D atmosphere modeling, the current procedure is to assume a universal value of 1.5 for the mixing length parameter αMLT (see Gustafsson et al. 2008; Castelli & Kurucz 2004). For full stellar evolution models, the solar “calibration” yields values around ~1.7–1.9 (see, e.g. Magic et al. 2010). Since the value of the mixing length parameter sets the convective efficiency and therefore changes the superadiabatic structure of stellar models, an accurate knowledge of αMLT for different stellar parameters would be a first step in improving models in that respect. However, apart from the Sun, other calibrating objects are rare and data are much less accurate (see Sect. 3.7 for an example), such as binary stars with well-determined stellar parameters.
The mixing length parameter can be deduced from multidimensional radiative hydrodynamic (RHD) simulations, where convection emerges from first principles (e.g., see Ludwig et al. 1999). Over the past decades, the computational power has increased and the steady development of 3D RHD simulations of stellar atmospheres has established their undoubted reliability by manifold successful comparisons with observations (Nordlund 1982; Steffen et al. 1989; Ludwig et al. 1994; Freytag et al. 1996; Stein & Nordlund 1998; Nordlund & Dravins 1990; Nordlund et al. 2009). The 3D RHD models have demonstrated that the basic picture of MLT is incorrect: there are no convective bubbles, but highly asymmetric convective motions. Nonetheless, an equivalent mixing length parameter has been calibrated by Ludwig et al. (1999) based on 2D hydrodynamic models by matching the resulting adiabats with 1D MLT models (see Freytag et al. 1999, for the metal-poor cases). The authors showed that αMLT varies significantly with the stellar parameters (from 1.3 to 1.8), and also studied the impact of a variable αMLT on a globular cluster (Freytag & Salaris 1999). In addition, Trampedach (2007) applied a grid of 3D atmosphere models with solar metallicity to calibrate the mixing length parameter (from 1.6 to 2.0), and the so-called mass mixing length (Trampedach & Stein 2011).
In the present work we calibrate the mixing length parameter with a 1D atmosphere code that consistently employs the identical EOS and opacity as used in the 3D RHD simulations (Sect. 2). We present the resulting mixing length parameter in Sect. 3. We also determine the mass mixing length – the inverse of the logarithmic derivative of the unidirectional mass flux – in Sect. 4, and the vertical correlation length of the vertical velocity (Sect. 5) directly from the 3D atmosphere models. For the former quantity, we derive a relation from the hydrodynamic mean-field equations that demonstrates the relation to αMLT, which is further substantiated by our numerical results. Finally, we conclude in Sect. 6.
2. Theoretical models
 |
Fig. 1 Mean ⟨3D⟩z entropy (black solid line) vs. depth, and 1D models for different mixing length parameters, αMLT = 1.5 − 2.5 (blue lines), for the solar model (left panel) and a metal-poor dwarf with [Fe/H] − 2.0,Teff = 4500 K, and log g = 4.5 (right panel). We indicate the constant entropy value of the deep adiabatic convection zone, sbot, in both figures by the horizontal dotted line. In the deeper layers, we extended the 1D models (dashed lines) with the aid of the entropy gradient from the ⟨3D⟩ models. The calibration of the mixing length parameter αMLT for the solar model is illustrated by the smaller insets, which depict the relative differences between the 1D and 3D models (δs = s1D/s3D − 1) for sbot (solid) and the entropy jump Δs (dashed). For the solar model the two approaches result in αMLT = 1.98 and 2.09. |
2.1. 3D atmosphere models
We computed the Stagger-grid, a large grid of 3D RHD atmosphere models that covers a wide range in stellar parameter space (see Magic et al. 2013a, hereafter Paper I). The 3D atmosphere models were computed with the Stagger-code, which solves the 3D hydrodynamic equations for conservation of mass, momentum and energy, coupled with a realistic treatment of the radiative transfer. We employed the EOS by Mihalas et al. (1988), and up-to-date continuum and line opacities (Gustafsson et al. 2008). For the solar chemical abundances, we used the values by Asplund et al. (2009, hereafter AGS09). Our simulations are of the so-called box-in-a-star type, that is we compute only a small, statistically representative volume that includes typically ten granules. Our (shallow) simulations only cover a small fraction of the total depth of the convective envelope. Because of the adiabaticity of the gas in the lower parts of the simulation box, the asymptotic entropy value of the convective zone, sad, is matched by the fixed entropy at the bottom of the simulation domain, sbot, which is one of the simulation parameters. The effective temperature is therefore a result in our 3D simulations, and is actually a temporally averaged quantity. In 1D models Teff is an actual fixed input value in addition without fluctuations.
We determine the entropy jump, Δs, as the difference between the entropy minimum and the constant entropy value of the adiabatic convection zone with Δs = sbot − smin. In Magic et al. (2013b, hereafter Paper II), we studied in detail the differences between mean ⟨3D⟩ models resulting from different reference depth scales. In the present work, we show and discuss only averages on constant geometrical height ⟨3D⟩z, since these fulfill the hydrodynamic equilibrium and extend over the entire vertical depth of the simulations. The Stagger-grid encompasses ~220 models ranging in effective temperature, Teff, from 4000 to 7000 K in steps of approximately 500 K (we recall that Teff is the result of the input quantity sad, and the intended Teff grid point values are adjusted within a margin below 100 K). The surface gravity, log g, ranges from 1.5 to 5.0 in steps of 0.5 dex, and metallicity, [Fe/H], from − 4.0 to + 0.5 in steps of 0.5 and 1.0 dex. We refer to Paper I for detailed information on the actual methods for computing the grid models, their global properties, and mean stratifications.
2.2. 1D atmosphere models
For the Stagger-grid, a 1D MLT atmosphere was developed that uses exactly the same opacities and EOS as the 3D models (Paper I). Therefore, the chemical compositions are identical. The code uses the MLT formulation by Henyey et al. (1965, see Appendix C.1 for details), similar to the MARCS code (Gustafsson et al. 2008). Furthermore, for consistency, the 1D models were computed with exactly the same Teff as the 3D models.
The actual implementation of MLT differs slightly depending on the considered code (e.g., Ludwig et al. 1999). In the standard MLT formulation there are four parameters in total. The mixing length parameter, αMLT = l/Hp, sets the convective efficiency, while y = 3/(4π2) ≃ 0.076 is assumed for the temperature distribution, and ν = 8 for the turbulent viscosity (see Appendix C.2 for a discussion). We only considered the mixing length parameter αMLT for the calibration, while the additional parameters were kept fixed to their default values, and the turbulent pressure was entirely neglected.
3. Mixing length parameter
 |
Fig. 2 Kiel-diagram (Teff − log g diagram) with the mixing length parameter calibrated with the constant entropy value of the adiabatic convection zone, |
3.1. Matching the mixing length parameter
We calibrated αMLT by matching either the asymptotic entropy value of the deep convection zone, sbot, or the entropy jump, Δs, from the 1D and 3D models. We refer to these throughout as 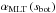 and αMLT(Δs). The value of sbot is an input parameter in our 3D simulations and represents the adiabatic entropy of the incoming upflows at the bottom of the box that are replenishing the outflows. The horizontally and temporally averaged entropy at the bottom, ⟨s⟩bot, in contrast, considers both the up- and downflow, and is thus slightly lower than sbot because of the entropy-deficient downflows. However, in our simulations the deeper layers have almost adiabatic conditions. The contrast of the thermodynamic variables at the bottom is extremely low with ⟨X⟩bot − Xbot ≪ 1 %.
and αMLT(Δs). The value of sbot is an input parameter in our 3D simulations and represents the adiabatic entropy of the incoming upflows at the bottom of the box that are replenishing the outflows. The horizontally and temporally averaged entropy at the bottom, ⟨s⟩bot, in contrast, considers both the up- and downflow, and is thus slightly lower than sbot because of the entropy-deficient downflows. However, in our simulations the deeper layers have almost adiabatic conditions. The contrast of the thermodynamic variables at the bottom is extremely low with ⟨X⟩bot − Xbot ≪ 1 %.
For the calibration, we computed 1D models with αMLT from 1.0 to 2.5 in steps of 0.1 and determined αMLT by minimizing the difference 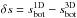 or the difference in the entropy jumps δs = Δs1D − Δs3D. We remark that some 1D atmosphere models had convergence problems, when they were extended to the same depth as the 3D models. Therefore, we had to calculate slightly shallower 1D models. However, we extended the 1D entropy stratifications with the entropy gradients of the ⟨3D⟩ model (see Fig. 1). We performed tests by truncating ⟨3D⟩ models and extending them with our method, which led to the same stratification. Therefore, we assume that the missing depth in the 1D entropy run leads to only minor uncertainties in the resulting αMLT. We fitted the differences, δs, with a second-order polynom to derive the value of αMLT. We emphasize that the calibration of αMLT is more meaningful for identical EOS, and the entropy is consistently computed. For the calibration, we neglected the turbulent pressure in the 1D models entirely (i.e., β = 0). Including turbulent pressure would clearly influence the calibration of αMLT, but, to account properly for pturb, one would need to employ an improved description of convection that accounts for nonlocal effects (private communication with D. Gough, and see also Ludwig et al. 2008). Because of the local nature of the standard MLT, the impact of the turbulent pressure is confined to the convective region and the turbulent leviation is rendered poorly. We note that the influence of the turbulent pressure is included in the calibrated αMLT values.
or the difference in the entropy jumps δs = Δs1D − Δs3D. We remark that some 1D atmosphere models had convergence problems, when they were extended to the same depth as the 3D models. Therefore, we had to calculate slightly shallower 1D models. However, we extended the 1D entropy stratifications with the entropy gradients of the ⟨3D⟩ model (see Fig. 1). We performed tests by truncating ⟨3D⟩ models and extending them with our method, which led to the same stratification. Therefore, we assume that the missing depth in the 1D entropy run leads to only minor uncertainties in the resulting αMLT. We fitted the differences, δs, with a second-order polynom to derive the value of αMLT. We emphasize that the calibration of αMLT is more meaningful for identical EOS, and the entropy is consistently computed. For the calibration, we neglected the turbulent pressure in the 1D models entirely (i.e., β = 0). Including turbulent pressure would clearly influence the calibration of αMLT, but, to account properly for pturb, one would need to employ an improved description of convection that accounts for nonlocal effects (private communication with D. Gough, and see also Ludwig et al. 2008). Because of the local nature of the standard MLT, the impact of the turbulent pressure is confined to the convective region and the turbulent leviation is rendered poorly. We note that the influence of the turbulent pressure is included in the calibrated αMLT values.
In Fig. 1, we illustrate the calibration for the solar model and for a cool metal-poor dwarf with the mean entropy, s, in the convection zone. For the solar simulation, we determined a mixing length parameter of αMLT = 1.98 and 2.09 from matching either the adiabatic entropy value or the entropy jump. Note how s converges asymptotically against sbot. Furthermore, it is also evident from Fig. 1 that for a higher αMLT the adiabat (sbot) of the 1D models is decreasing in the convection zone. The entropy minimum of the ⟨3D⟩z on geometrical height is slightly mismatched by the 1D models, which is reflected by slightly different calibrated αMLT(Δs) values. In the 1D models smin varies only little for different αMLT, and the differences, ΔαMLT, are between ~10-4 and 10-3 (cf. also the right panel). Since the entropy jumps are in general much larger than the variation of smin, their influence is very weak, and only for very cool metal-poor models with very small entropy jumps, differences in smin influence the calibration (see right panel in Fig. 1).
We find in general very similar results for αMLT by employing a 1D envelope code, which solves the stellar structure equations down to the radiative interior by including the same EOS and opacities (Christensen-Dalsgaard 2008). This is in particular true for solar metallicity. The 1D envelope code relies on an assumed T(τ) relation in the (Eddington gray) atmosphere, which obviously influences the thermal stratification at the outer boundary of the convective envelope. In particular, metal-poor 1D convective interior models with a fixed T(τ) relation are affected by this, and will return different mixing length parameters. The 1D atmosphere code works without the need for any T(τ) relation, since it solves the radiative transfer by itself. We therefore present and discuss only the mixing length parameters matched by the 1D atmosphere code.
Furthermore, we have performed functional fits for the calibrated mixing length parameters, that is αMLT = f(Teff,log g,[Fe/H]), with the same functional basis as used by Ludwig et al. (1999). For more details see Appendix B, and the resulting coefficients are provided in Table B.1. In Table B.1 we also listed the uncertainties of the fits estimated with the root-mean-square and highest deviation, which are increasing for lower metallicities.
 |
Fig. 3 As Fig. 2, but here we show the mixing length parameter calibrated with the entropy jump αMLT(Δs). |
 |
Fig. 4 Dependence of the mixing length parameters on the different stellar parameters ( |
3.2. Calibrations with the adiabatic entropy value
In Fig. 2, we show an overview of the variation of the αMLT values calibrated with sbot for different stellar parameters in the Kiel-diagram, in particular, for two illustrating metallicities ([Fe/H] = 0 and − 2). The mixing length parameter varies rather systematically in the range between ~1.7 and ~2.3: αMLT increases for lower Teff and [Fe/H] and higher log g (see also Fig. 4). Towards lower metallicity, models with cooler Teff deviate from a linear run, which can be attributed to the differences in the outer boundary condition of the 1D models. A larger αMLT relates to a higher convective efficiency, which implies that a smaller entropy jump is necessary to carry the same convective energy flux. Indeed, we find the entropy jump to increase for higher Teff, lower log g, and higher [Fe/H] (see Paper I); we find that αMLT varies qualitatively inversely to the entropy jump. The mixing length parameter is inversely proportional to the variation of the logarithmic values of the entropy jump, the peak in the entropy contrast, and vertical rms-velocity (see Sect. 3.4). This agrees with the fact that both the entropy jump and the mixing length parameter are related to the convective efficiency (see Sect. 3.4).
3.3. Calibrations with the entropy jump
We also calibrated the mixing length parameter with the 1D MLT atmosphere code by matching the entropy jump Δs. The resulting values are summarized for two metallicities in Fig. 3, showing a similar behavior as the results of the previous section (see also Fig. 4). We find that the αMLT values based on Δs are systematically higher by ~0.1 (between ~1.8 and ~2.4) than the values based on sbot (Fig. 5), but the range in αMLT(Δs) is with ΔαMLT ≈ 0.6 very similar to that for 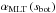 . The differences arise from the minimum of the entropy smin around the optical surface, which is lower for the 1D models than for the ⟨3D⟩ model (see Fig. 1), and therefore leads to larger mixing length parameters. The metal-poor simulations deviate more strongly between αMLT(Δs) and
. The differences arise from the minimum of the entropy smin around the optical surface, which is lower for the 1D models than for the ⟨3D⟩ model (see Fig. 1), and therefore leads to larger mixing length parameters. The metal-poor simulations deviate more strongly between αMLT(Δs) and 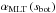 , since the boundary effect, induced by the differences in Δs, increases for lower [Fe/H]. We note that the entropy jump is a relative value, and consequently, the matching is less sensitive to outer boundary effects.
, since the boundary effect, induced by the differences in Δs, increases for lower [Fe/H]. We note that the entropy jump is a relative value, and consequently, the matching is less sensitive to outer boundary effects.
3.4. Comparison with global properties
We searched for systematic correlations between the mixing length parameter and mean thermodynamic properties. The inverse of the entropy jump correlates well with αMLT. In Fig. 6 we demonstrate this by comparing the mixing length parameter αMLT(Δs) with the logarithm of the inverse of the entropy jump. Convection is driven by radiative cooling in the surface layers. The entropy jump results from the radiative losses at the optical surface, therefore, the correlation of αMLT originates in the interplay of the opacity, κλ, radiative cooling rates, qrad, and vertical velocity, vz,rms. The vertical velocity results from buoyancy forces, fb = gΔρ, that act on the overturning, overdense flows at the optical surface. Hence, a larger entropy jump will entail higher contrast in the entropy and density (δsrms and δρrms), which will induce a stronger downward acceleration. We illustrate this in Fig. 7, where the peak values for δsrms and δρrms in the superadiabatic region are plotted against the peak vertical rms-velocity. Evidently, the entropy and density contrast correlate well with the vertical velocity, and this is the underlying reason for the tight (inverse) correlation between mixing length parameter and entropy jump. In Paper I we have already discussed the correlation of the entropy jump with the peak vertical velocity and the density at the same location, and we deduced the reason for this in the convective energy flux, which essentially contains these quantities.
3.5. Comparison with 2D calibrations
We compared the differences between our inferred mixing length parameters with those of Ludwig et al. (1999) based on similar, but 2D hydrodynamical surface convection simulations. These authors also matched the resulting 2D-based sbot by varying αMLT of a 1D envelope code that uses the same EOS and opacity. However, the EOS and opacity are not identical to those used by us, and there are other differences in the models, such as, most importantly, the solar composition. This needs to be kept in mind when interpreting the comparison.
We also remark that Ludwig et al. (1999) derived T(τ)-relations from the 2D models, and used them for the 1D models as boundary conditions to render the entropy minimum of the 2D simulations more correctly. In Paper I we noticed that sbot resulting from the Stagger-grid is very similar to values from the 2D grid, while the entropy jump Δs differs slightly.
In Fig. 8 we compare the calibrated mixing length parameter from both studies. The results of Ludwig et al. (1999) also show a clear Teff-dependence, while surface gravity has only very little influence on αMLT. While the 3D-calibrated mixing length parameter decreases with lower surface gravity, its 2D equivalent increases moderately. Their solar mixing length parameter is αMLT = 1.59, which is lower by 0.39 (~20%) than our mixing length parameter, but similar to the solar model value of that time, as is ours for the present generation of solar models. The αMLT values for dwarf models (log g = 4.5) are in general around 20% lower than in our case. Towards giants the difference decreases, since the 3D values decrease with log g. For 3D convection simulations it is known that convection is more efficient than for the 2D case. Therefore, the mixing length parameters derived from the 3D models are in general systematically larger. Taking into account the model generation effect, the comparison is quite satisfactory with the exception of the discrepant log g-dependence.
3.6. Impact on stellar evolutionary tracks
 |
Fig. 5 Comparison of the mixing length parameter calibrated with the entropy jump, αMLT(Δs), and the constant entropy value of the adiabatic convection zone, |
 |
Fig. 6 Comparison between the mixing length parameter calibrated with the entropy jump, αMLT(Δs), and the logarithm of the inverse of the entropy jump, − ln(Δs), for different stellar parameters. |
 |
Fig. 7 Highest contrast of the entropy and density compared with the highest vertical rms-velocity (top and bottom panel, respectively) for different stellar parameters. |
 |
Fig. 8 Top panel: calibration of αMLT with 2D (Ludwig et al. 1999) and 3D simulations in comparison (solid and dashed lines, respectively). The surface gravity is indicated and color-coded. The solar values are indicated. Bottom panel: relative differences (δ = 2D/3D − 1). |
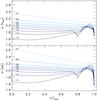 |
Fig. 9 Mixing length parameter along stellar evolutionary tracks with solar metallicity against the normalized age for the masses from 0.7 to 1.5 M⊙ (indicated). The tracks are derived from the functional fits f(Teff,log g) of αMLT-calibrations with sbot and Δs (top and bottom panel, respectively) and all tracks end on the RGB when log g = 1. |
The variation of αMLT along typical stellar evolutionary tracks ranges from 1.6 to 2.4 from higher to lower mass (see Fig. 9), and deviates by up to ±20% from the solar value (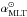 ). Note that in Fig. 9 we show αMLT along tracks calculated with a constant value of the mixing length parameter (1.78) obtained from the usual solar model calibration (see Magic et al. 2010). The figure therefore does not show the actual, self-consistent changes in αMLT along the evolution, but, significant differences are hardly to be expected. During the main-sequence evolution αMLT varies only little and is almost constant, in particular for the lower masses without a convective core. The variable mixing length parameter has a stronger influence during later evolutionary stages, the TO and the RGB ascent; αMLT increases first towards values around ~1.9–2.1, and then drops sharply to values of ~1.7 for all masses, which is the consequence of the narrow range in red giant temperature and surface gravity.
). Note that in Fig. 9 we show αMLT along tracks calculated with a constant value of the mixing length parameter (1.78) obtained from the usual solar model calibration (see Magic et al. 2010). The figure therefore does not show the actual, self-consistent changes in αMLT along the evolution, but, significant differences are hardly to be expected. During the main-sequence evolution αMLT varies only little and is almost constant, in particular for the lower masses without a convective core. The variable mixing length parameter has a stronger influence during later evolutionary stages, the TO and the RGB ascent; αMLT increases first towards values around ~1.9–2.1, and then drops sharply to values of ~1.7 for all masses, which is the consequence of the narrow range in red giant temperature and surface gravity.
The mixing length parameter not only determines Teff of the stellar models, but also influences the adiabatic stratification of the 1D models in the deeper convection zone. In particular, for a larger αMLT the lower boundary of the convection zone is located deeper in the interior. Therefore, for stars with lower (higher) masses, a variable mixing length parameter with stellar parameter will increase (decrease) the depth of the convection zone. As a consequence, one can expect that the convective mixing will be enhanced (reduced) for less (more) massive stars in stellar evolutionary calculations. This may influence, for example, the depletion and burning of Li in low-mass stars.
3.7. Comparison with observations
 |
Fig. 10 Relative differences between the the mixing length parameter derived from observations and our 3D RHD models for different stellar parameters. |
Observations provide an opportunity to constrain free parameters in theoretical models. Bonaca et al. (2012) attempted to calibrate the mixing length parameter from Kepler-observations of dwarfs and subgiants (90 stars). Employing the usual scaling relations for the frequency of the maximal oscillation mode power, νmax, and the large frequency separation, Δν (see, for example, Huber et al. 2011), in connection with Teff and [Fe/H] from spectroscopic observations, they estimated mass and radius of the observed objects. From a grid of stellar evolutionary tracks computed with different αMLT values, they then selected the value that matched the inferred stellar parameters. The stellar evolutionary tracks were computed with the Yale stellar evolution code by employing the EOS and opacities from OPAL (see Demarque et al. 2008). For the outer boundary conditions they used the Eddington T(τ) relation and the standard MLT formulation by Böhm-Vitense (1958). These differences need to be considered in the comparison of the resulting αMLT values.
Bonaca et al. (2012) derived an average mixing length parameter of 1.60 from the observations, which is in general lower than their solar-calibrated value with 1.69, which resulted from the 1D models without the comparison with observations. We compare the (linear) functional fit of αMLT derived in Bonaca et al. (2012), with stellar parameters to our own results in Fig. 10. We compare the calibration resulting from their complete data set. They also derived a fit for a subset of dwarfs, which is quite restricted in the range of stellar parameters and quite different from the fit for the full sample, however, they determined the solar mixing length parameter with 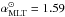 , which is 20% lower than our result of 1.98. However, we remark that because of differences in the input physics and methods, the comparison between absolute values of αMLT is limited. Interestingly, the variation with Teff for a given log g and [Fe/H] is rather similar apart from an almost constant offset. For different log g and [Fe/H], we find significant systematical differences (see Fig. 10). The values for dwarfs are in general lower by up to ~20–40% depending on gravity and metallicity, while the values for giants are greater by the similar amount. The comparison is made more difficult because even the full sample of Bonaca et al. (2012) is rather limited in log g, and biased towards dwarfs. Additionally, the input physics (EOS and opacity) of their models deviates from ours. The authors themselves mention the absence of strong correlations with log g, their restricted range in [Fe/H], the discrepancies to the results by Ludwig et al. (1999) and Trampedach (2007), and the fact that αMLT effectively compensates for everything else that influences Teff.
, which is 20% lower than our result of 1.98. However, we remark that because of differences in the input physics and methods, the comparison between absolute values of αMLT is limited. Interestingly, the variation with Teff for a given log g and [Fe/H] is rather similar apart from an almost constant offset. For different log g and [Fe/H], we find significant systematical differences (see Fig. 10). The values for dwarfs are in general lower by up to ~20–40% depending on gravity and metallicity, while the values for giants are greater by the similar amount. The comparison is made more difficult because even the full sample of Bonaca et al. (2012) is rather limited in log g, and biased towards dwarfs. Additionally, the input physics (EOS and opacity) of their models deviates from ours. The authors themselves mention the absence of strong correlations with log g, their restricted range in [Fe/H], the discrepancies to the results by Ludwig et al. (1999) and Trampedach (2007), and the fact that αMLT effectively compensates for everything else that influences Teff.
Our mixing length parameters also differ significantly from the spectroscopical findings by Fuhrmann et al. (1993), who concluded that one would need an αMLT with very low values with ~0.5, to properly fit hydrogen lines for various stars with the resulting temperature stratifications. This, however, can be explained completely by the fact that here only the outermost convective layers are traced, which are not tested with our method for inferring αMLT from the adiabatic structure at the bottom of the convection zone, and that the mixing length parameter is indeed depth-dependent (see Sect. 4.2). This was already verified by Schlattl et al. (1997).
4. Mass mixing length parameter
4.1. Deriving the mass mixing length parameter
In the following, we denote the temporal and spatial averaged thermodynamic quantities with ⟨... ⟩, which depict only the z-dependence. Then, the momentum equation for a stationary system yields 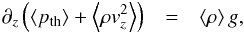 where the divergence of the viscosity stress tensor vanishes on average. This equation states that a given mass stratification (ρg) has to be supported by the joint thermodynamic (pth) and turbulent pressure (
where the divergence of the viscosity stress tensor vanishes on average. This equation states that a given mass stratification (ρg) has to be supported by the joint thermodynamic (pth) and turbulent pressure (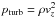 ) forces to sustain equilibrium. Since the vertical velocity, vz, appears here, we solve for the latter and obtain
) forces to sustain equilibrium. Since the vertical velocity, vz, appears here, we solve for the latter and obtain 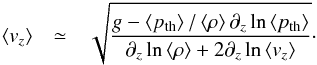 Here, we assume that
Here, we assume that 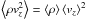 , but, we validated this equation with comparisons of averaged models. Then, similar to the temperature gradient, ∇ = dln⟨T⟩/dln⟨ptot⟩, we introduce the notation for the gradient for a value X, but, instead of the total pressure it is scaled by the thermodynamic pressure scale height,
, but, we validated this equation with comparisons of averaged models. Then, similar to the temperature gradient, ∇ = dln⟨T⟩/dln⟨ptot⟩, we introduce the notation for the gradient for a value X, but, instead of the total pressure it is scaled by the thermodynamic pressure scale height, 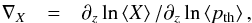 and we can rewrite the vertical velocity to
and we can rewrite the vertical velocity to 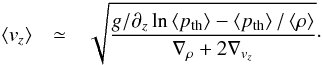 (1)This equation depicts the correlation of the vertical velocity with the gravity and pressure stratification, as well as the gradient of the density and the gradient of the vertical velocity itself in the hydrodynamic equilibrium. Now, we consider the gradient of the absolute vertical mass flux, ⟨jz⟩ = ⟨ρvz⟩, for the up- or downflows (because of conservation of mass, the mass flux of the upflows,
(1)This equation depicts the correlation of the vertical velocity with the gravity and pressure stratification, as well as the gradient of the density and the gradient of the vertical velocity itself in the hydrodynamic equilibrium. Now, we consider the gradient of the absolute vertical mass flux, ⟨jz⟩ = ⟨ρvz⟩, for the up- or downflows (because of conservation of mass, the mass flux of the upflows, 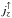 , equals the mass flux of the downflows,
, equals the mass flux of the downflows, 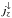 ) with
) with 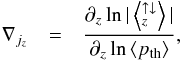 which indicates the length over which the up- or downflow has changed by the e-fold, where the length scale is expressed in pressure scale heights. Trampedach & Stein (2011) introduced the mass mixing length as the inverse vertical mass flux scale height, that is
which indicates the length over which the up- or downflow has changed by the e-fold, where the length scale is expressed in pressure scale heights. Trampedach & Stein (2011) introduced the mass mixing length as the inverse vertical mass flux scale height, that is 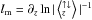 , which is in concordance with the gradient of the vertical mass flux with lm = HP/ ∇jz. Furthermore, we define the mass mixing length parameter as the inverse gradient of the vertical mass flux,
, which is in concordance with the gradient of the vertical mass flux with lm = HP/ ∇jz. Furthermore, we define the mass mixing length parameter as the inverse gradient of the vertical mass flux, 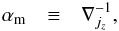 (2)and we can decompose the gradient of the vertical mass flux into its components and find
(2)and we can decompose the gradient of the vertical mass flux into its components and find 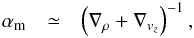 (3)which states that the mass mixing length parameter is the inverse sum of the changes in the density and vertical velocity gradients. The gradient of the filling factor also contributes, but, since it vanishes in the deeper adiabatic convection zone and contributes only very little confined to the photospheric transition region, we nelgect this in our discussions (see Trampedach & Stein 2011). We note that the definition in Eq. (2) is the same as introduced by Trampedach & Stein (2011). Finally, we can now identify the mass mixing length parameter in the denominator of the vertical velocity (Eq. (1)) and obtain the following expression:
(3)which states that the mass mixing length parameter is the inverse sum of the changes in the density and vertical velocity gradients. The gradient of the filling factor also contributes, but, since it vanishes in the deeper adiabatic convection zone and contributes only very little confined to the photospheric transition region, we nelgect this in our discussions (see Trampedach & Stein 2011). We note that the definition in Eq. (2) is the same as introduced by Trampedach & Stein (2011). Finally, we can now identify the mass mixing length parameter in the denominator of the vertical velocity (Eq. (1)) and obtain the following expression: 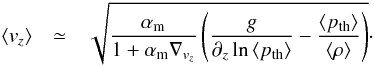 (4)This illustrates why the vertical velocity depends on the mass mixing length parameter, similarly to the MLT velocity vMLT, which depends on mixing length parameter with vMLT ∝ αMLT (see Eq. (C.2)).
(4)This illustrates why the vertical velocity depends on the mass mixing length parameter, similarly to the MLT velocity vMLT, which depends on mixing length parameter with vMLT ∝ αMLT (see Eq. (C.2)).
To complete the comparison of the mass mixing length parameter with the (MLT) mixing length parameter, we derive its dependence on the convective energy flux. We assume that the mean convective energy flux consists of the fluctuations of the total energy (εtot = ε + pth/ρ + v2/ 2), which we depicted with f, and is carried by the mean vertical mass flux, that is 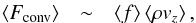 where we assume that vz is the hydrodynamic velocity given in Eq. (1) and also that ⟨ρvz⟩ = ⟨ρ⟩⟨vz⟩. We determine the divergence of the convective energy flux, ∂z⟨Fconv⟩, and solve for the total energy fluctuations, which yields
where we assume that vz is the hydrodynamic velocity given in Eq. (1) and also that ⟨ρvz⟩ = ⟨ρ⟩⟨vz⟩. We determine the divergence of the convective energy flux, ∂z⟨Fconv⟩, and solve for the total energy fluctuations, which yields 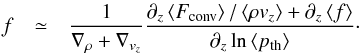 Then, we can substitute the convective energy losses, ∂z⟨Fconv⟩, by the radiative cooling rate, − ⟨qrad⟩, because of conservation of total energy, and we can identify the mass mixing length parameter in the convective energy flux as well and obtain
Then, we can substitute the convective energy losses, ∂z⟨Fconv⟩, by the radiative cooling rate, − ⟨qrad⟩, because of conservation of total energy, and we can identify the mass mixing length parameter in the convective energy flux as well and obtain 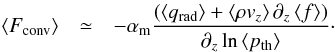 (5)This equation is basically the expression for the conservation of energy. These two equations for the velocity and the convective energy flux are just reformulated approximations of the hydrodynamic mean-field equations. To close this set of equations, one still would need information about the gradient of the velocity and total energy fluctuation, as well as the radiative cooling rates.
(5)This equation is basically the expression for the conservation of energy. These two equations for the velocity and the convective energy flux are just reformulated approximations of the hydrodynamic mean-field equations. To close this set of equations, one still would need information about the gradient of the velocity and total energy fluctuation, as well as the radiative cooling rates.
4.2. Depth-dependence of the mass mixing length parameter
 |
Fig. 11 Top panel: mass mixing length parameter αm from Eq. (3) (solid) and the inverse gradient of the density, |
Following Trampedach & Stein (2011), we tried to derive the mass mixing length parameter from the vertical mass flux of the downflows (Eq. (2)), but, we found that the fluctuations in the vertical velocity field are enhanced in our simulations, which is probably caused by the higher numerical vertical resolution (the simulations by Trampedach et al. (2013) have a thrice lower vertical resolution and therefore exhibit fewer turbulent and more laminar structures in the downflows). We found the rms vertical velocity to be less sensitive to the statistical fluctuations in the deeper convection zone, therefore, we derived the mass mixing length by using the gradient of the rms vertical velocity in Eq. (3), instead of deriving the mass mixing length from the vertical mass flux of the downflows (Eq. (2)). Therefore, a comparison with Trampedach & Stein (2011) is only qualitatively meaningful.
In Fig. 11, we illustrate the horizontally and temporally averaged, depth-dependent mass mixing length parameter for different stellar parameters, which we derived from our 3D RHD simulations. In the convection zone, the mass mixing length parameter has values around ~2, while above the optical surface, αm has lower values around ~0.5. Fuhrmann et al. (1993) found that similar low values for the mixing length parameter αMLT yield better fits for Balmer lines, but, they also used high values for the temperature distribution parameter with y = 0.5 (see also Appendix C.2), and moreover, the influence of αMLT becomes negligible towards the optical surface, where the Balmer lines form (see Fig. 1). Therefore, the agreement of the depth-dependent αm with their low values for αMLT might be just a coincidence. Furthermore, just below the optical surface (log ptot/psurf = 0) at the photospheric transition region, αm features a peak, which depends on the stellar parameters, in particular, for higher Teff, the peak in between increases, while in the convection zone it is the flatter. We remark that the peak in αm coincides with the location of the peak in the vz,rms. We also included the inverse gradient of density in the same figure with αm, demonstrating that the adiabatic value of αm in the convection zone is mainly contributed by the density gradient.
We also show the gradients of the density and vertical velocity in Fig. 11, which are the two main components of αm. The gradients of the filling factors also contribute to the variation of mass mixing length. However, similar to the findings by Trampedach & Stein (2011), we find that the fillings factors are constant in the convection zone, therefore, their contribution is negligible. The variation of αm in the convection zone arises mainly because of the different velocity gradients, since the density gradient converges always to very similar adiabatic values (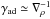 ). For a monoatomic ideal gas with radiation pressure the adiabatic exponent is given by γad = (1 − ∇ad)-1, and with ∇ad = 1/4 one obtains γad ~ 4/3 (see Kippenhahn et al. 2013).
). For a monoatomic ideal gas with radiation pressure the adiabatic exponent is given by γad = (1 − ∇ad)-1, and with ∇ad = 1/4 one obtains γad ~ 4/3 (see Kippenhahn et al. 2013). 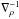 it is close to 1.2 (see Fig. 11). For a nonideal gas differences due to nonideal effects are to be expected. On the other hand, ∇ρ is close to ~0.8 therefore, similar to a value for an ideal gas with 3/4, while ∇vz is between − 0.4 and − 0.15 (see also Fig. 14).
it is close to 1.2 (see Fig. 11). For a nonideal gas differences due to nonideal effects are to be expected. On the other hand, ∇ρ is close to ~0.8 therefore, similar to a value for an ideal gas with 3/4, while ∇vz is between − 0.4 and − 0.15 (see also Fig. 14).
In the vicinity of the optical surface, the cooling rates are imprinted on the gradients for the density and velocity with a sharp transition. Towards the interior, the density increases because of the stratification and hydrostatic equilibrium, hence the gradient is ∇ρ> 0, while the velocity decreases, and therefore ∇vz< 0. The signs of ∇ρ and ∇vz are opposite because of the conservation of mass. In the interior, the stellar fluid is compressed and the velocity slows down, meaning that the convective energy is carried with a slower, thicker mass flux. For higher Teff, the (negative) velocity gradient has a lower amplitude and is therefore closer to zero, and a smaller amplitude of ∇vz implies a steeper drop of the vertical velocity towards the interior, which also entails a larger maximum of the vertical velocity (see Fig. 14). The velocity gradient reduces the density gradient, but, a lower sum of ∇ρ and ∇vz relates to a higher αm because of the inverse relation (see Fig. 12). Since the density gradient is very similar for different stellar parameters, the variation in αm arises mainly from the differences in the velocity gradient. Therefore, we can relate the variation of the entropy jump with the variation of the velocity gradient, that is Δs ~ e∇vz, which was also concluded by Trampedach & Stein (2011) for the mass mixing length parameter in an extended solar simulation.
 |
Fig. 14 Mean gradient of the density, ∇ρ, and the vertical velocity, ∇vz, in the convection zone for different stellar parameters. |
4.3. Mean mass mixing length parameter in the convection zone
We determined the mean mass mixing length parameter of the convection zone below the optical surface between the location of the peak in the density scale height, that is max(∂zlnρ)τ> 1, and the bottom, but, avoided bottom boundary effects on the vertical velocity. We performed linear fits of the density and vertical rms-velocity gradients by considering all snapshots, and from both gradients we determined the mean value of αm as given in Eq. (3). We note that our method of retrieving a mean value differs from that by Trampedach & Stein (2011). The convection zones in the 3D simulations have to be extended enough, so that lower boundary effects on the vertical velocities are minimized, which is the case for most models, except for some metal-poor giants that are slightly too shallow to properly match αm.
The results for αm are displayed in Fig. 12, while in Fig. 14 we depict the mean values of the density and velocity gradients. From the solar simulation we determined 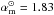 , which is close to the solar mass mixing length parameter by Trampedach & Stein (2011) with 1.76. Furthermore, the mass mixing length parameter depicts qualitatively very similar systematic variations with stellar parameter, as we found for αMLT above. In particular, it decreases for higher Teff and [Fe/H], and lower log g, and the range in αm between ~1.7 and ~2.3 is qualitatively similar to that of αMLT (see also Fig. 13). In general, we find values for αm that are qualitatively similar to those found by Trampedach & Stein (2011), in particular, the dwarf models (log g = 4.5) have a similar slope with Teff. As mentioned above, we consider the mass mixing length parameter from the gradients of the density and rms vertical velocity (see Eq. (3)) instead of the unidirectional mass flux, and we also used a different method for determining a mean value, therefore, differences in the results are to be expected.
, which is close to the solar mass mixing length parameter by Trampedach & Stein (2011) with 1.76. Furthermore, the mass mixing length parameter depicts qualitatively very similar systematic variations with stellar parameter, as we found for αMLT above. In particular, it decreases for higher Teff and [Fe/H], and lower log g, and the range in αm between ~1.7 and ~2.3 is qualitatively similar to that of αMLT (see also Fig. 13). In general, we find values for αm that are qualitatively similar to those found by Trampedach & Stein (2011), in particular, the dwarf models (log g = 4.5) have a similar slope with Teff. As mentioned above, we consider the mass mixing length parameter from the gradients of the density and rms vertical velocity (see Eq. (3)) instead of the unidirectional mass flux, and we also used a different method for determining a mean value, therefore, differences in the results are to be expected.
 |
Fig. 15 Correlation of the mass mixing length parameter, αm, with the logarithmic inverse of the entropy jump − ln(Δs) and the peak of the vertical rms-velocity (top and bottom panel, respectively). |
The variation of αm is also similar to the logarithmic inverse variation of the entropy jump. In Fig. 15 we compare αm with the logarithmic inverse entropy jump and find a similar tight correlation between the two as we found for the mixing length parameter αMLT(Δs) above (Sect. 3.3). The stronger deviations for the metal-poor giants originate from the fact that these models are slightly shallower, therefore, the match of the mass mixing length parameter is perturbed because of the lower boundary effects on the velocity. We also illustrate the tight anticorrelation of the peak vertical rms-velocity with the mass mixing length parameter in Fig. 15.
 |
Fig. 16 Comparison of the mass mixing length parameter, αm, with the mixing length parameter calibrated with sbot and Δs (top and bottom panel, respectively). |
A comparison of the mass mixing length parameter with the mixing length parameter calibrated with the entropy of the deep adiabatic convection zone and the entropy jump is shown in Fig. 16, and these also correlate well. The mixing length parameters are slightly higher than αm with a systematic offset around ~0.1 and ~0.2, which is smaller for 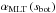 than for αMLT(Δs). This illustrates that the mixing length parameter in the framework of MLT has a physical background that originates in the mass mixing length parameter (or inverse vertical mass flux gradient). However, since the MLT is incomplete, a one-to-one correspondence between αMLT and αm is hardly expected; nonetheless, the good agreement between the two is an interesting result.
than for αMLT(Δs). This illustrates that the mixing length parameter in the framework of MLT has a physical background that originates in the mass mixing length parameter (or inverse vertical mass flux gradient). However, since the MLT is incomplete, a one-to-one correspondence between αMLT and αm is hardly expected; nonetheless, the good agreement between the two is an interesting result.
5. Velocity correlation length
The physical interpretation of the mixing length parameter is conceptually the mean free path of a convective eddy over which it can preserve its identity before it resolves into its environment. In a real stratified hydrodynamic fluid the spatial two-point (auto)correlation function of the vertical velocity can be regarded as the 3D analog of the mixing length parameter αMLT as proposed by Chan & Sofia (1987). The two-point correlation function for the values q1 and q2 is given by ![\begin{eqnarray} C\left[q_{1},q_{2}\right] & = & \frac{\left\langle q_{1}q_{2}\right\rangle -\left\langle q_{1}\right\rangle \left\langle q_{2}\right\rangle }{\sigma_{1}\sigma_{2}},\label{eq:correlation_function} \end{eqnarray}](/articles/aa/full_html/2015/01/aa23760-14/aa23760-14-eq138.png) (6)with σi being the the standard deviation of qi and ⟨... ⟩ is the spatial horizontal average. To derive the vertical correlation function of the convective velocity field, we considered the vertical component of the velocity field, vz, of a single fixed layer z0 and derived the correlation functions for all other layers zi, i.e. C[vz0,vzi], which was performed for twenty equidistant layers and covered the whole vertical depth scale of the simulation box.
(6)with σi being the the standard deviation of qi and ⟨... ⟩ is the spatial horizontal average. To derive the vertical correlation function of the convective velocity field, we considered the vertical component of the velocity field, vz, of a single fixed layer z0 and derived the correlation functions for all other layers zi, i.e. C[vz0,vzi], which was performed for twenty equidistant layers and covered the whole vertical depth scale of the simulation box.
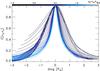 |
Fig. 17 Vertical two-point correlation function of the vertical velocity, C[vz,vz], vs. the difference in the thermodynamic pressure, Δlog Pth, for the solar simulation. The different heights are indicated with a blue color-coding. Note the convergence of the correlation width in the convection zone against an adiabatic value. |
 |
Fig. 18 Top panel: vertical correlation length of the vertical velocity (solid line with triangles) and pressure scale height (dotted-dashed line) shown against the depth for the solar model. We indicate the different heights with the same color-coding as used in Fig. 17. Bottom panel: vertical correlation length scaled by the pressure scale height, which yields an average of 1.71 (dashed line) in the considered region for averaging the correlation length (vertical dotted lines with filled circles) for the solar simulation. |
In Fig. 17 we show the two-point correlation function of the vertical velocity field, C[vz,vz], derived for the solar simulation for the individual snapshots and then temporally averaged. For convenience, the correlation function is shown in differences of logarithmic pressure to the considered layer, Δlog Pth = log Pth(z0) − log Pth(zi). Then, the correlation function always reaches unity for zi = z0 and has a Gaussian-like shape. Furthermore, it is broader above the optical surface (ptot/psurf = 1), which is due to the rapid decline of the pressure scale height; while below the latter the width seems to converge on a certain adiabatic value (see Fig. 18). When one considers the width of the correlation function in geometrical depth, instead of pressure, then W(vz) is constant around ~0.6 Mm from the top down to ~0.5 Mm and increases then with a fixed multiple (1.71) of the pressure scale height (see Fig. 18), which is the same as Robinson et al. (2003) found. The higher values for W(vz) /HP above 0.5 Mm result from the lower HP.
The full width at half maximum (FWHM) of the two-point correlation function of the vertical velocity, C[vz,vz], which we denote with W(vz), gives an estimate on the size or length scale of the coherent vertical structures. The characteristic local length scale for the turbulent convective eddies can be determined with W(vz). With the term vertical correlation length we refer to W(vz). Similar to the mixing length, it is preferable to scale the correlation length by the pressure scale height, that is W(vz) /HP, since the the latter increases towards deeper layers. Then, for the solar simulation (see Fig. 18) the converging value for the width is W(vz) /HP = 1.71. This means that the coherent vertical structures extend 1.71HP in the convection zone, and this value is similar to the mixing length parameter (αMLT = 1.94). Chan & Sofia (1987, 1989) also found a similar scaling of C[vz,vz] with pressure scale height in a 3D simulation for the Sun. For different stellar parameters we find a rather similar convergence of the correlation length of the vertical velocity in the convection zone (see Fig. 19). Ludwig et al. (2006) found similar values for the correlation length of the vertical velocity with W(vz) /HP ~ 2 in the vicinity of the lower boundary for a number of different simulations, while Viallet et al. (2013) recently found for a red-giant simulation that the vertical correlation length of the vertical velocity scales with approximately twice of the pressure scale height.
 |
Fig. 19 Correlation length of the vertical velocity vs. surface normalized pressure for different stellar parameters. |
 |
Fig. 20 Overview of mean vertical correlation length of the vertical velocity in the convection zone for different stellar parameters. |
We also determined the mean value of the correlation length in the convection zone below log ptot/ log psurf> 1. Close to the bottom boundary, the correlation function will increasingly overturn because we lack information in the deeper layers. Therefore, we applied for a mean correlation length a cut at the bottom, where W(vz) /HP begins to decrease (see Fig. 18).
The resulting mean values of W(vz) /HP for different stellar parameters are depicted in Fig. 20. They are distributed between ~1.5 and ~1.8. This is an interesting result, since it confirms, to a certain extent, the physical motivation for the mixing length parameter, αMLT: the vertical velocity field, hence the vertical mass flux, correlates similarly with the pressure scale heights in the convection zone. However, the variation of W(vz) /HP with stellar parameters (Fig. 20) is not as clear and systematical as we found above for αMLT and αm (see Sect. 4).
Furthermore, in contrast to the mixing length parameter (αMLT and αm), the correlation length seems to increase for higher Teff. The reason for this might be the horizontal granule size, which we found to decrease slightly for lower effective temperatures, since the pressure scale height decreases (see Paper I). Moreover, the granular cells, which can be highlighted with the temperature excess from the background, feature distinct regular flat cylindric or pillar-like topologies.
Finally, we considered the correlation length of other variables and found that the horizontal velocity is rather similar, but with slightly lower correlation length with ~1.4. In addition, the entropy, temperature, and pressure have values around ~1.3, while the value for the density is close to unity.
6. Conclusions
We have calibrated the mixing length parameter using realistic 3D RHD simulations of stellar surface convection by employing a 1D MLT stellar atmosphere code with identical microphysics. The calibration was achieved by varying the mixing length parameter and matching the adiabatic entropy value of the deeper convection zone, sbot, or alternatively, matching the entropy jump, Δs. In both ways we found the mixing length to decrease for higher Teff and [Fe/H], and lower log g. The mixing length varies in the range of 1.7 − 2.3 for 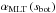 and ~1.8–2.4 for αMLT(Δs), and will lead to differences of up to ±20% in αMLT depending on the stellar mass. This changes the stellar interior structure by extending or shortening the depth of the convection zone and thus the stellar evolution; we intend to investigate in future studies how in detail a realistic αMLT will impact basic stellar evolution predictions.
and ~1.8–2.4 for αMLT(Δs), and will lead to differences of up to ±20% in αMLT depending on the stellar mass. This changes the stellar interior structure by extending or shortening the depth of the convection zone and thus the stellar evolution; we intend to investigate in future studies how in detail a realistic αMLT will impact basic stellar evolution predictions.
Furthermore, we derived from the hydrodynamic mean field equations (for the first-time) a physically motivated connection of the mass mixing length, which is the inverse of the vertical mass flux gradient, with the mixing length. We determined the mass mixing length parameter and found that it varies qualitatively similar to the mixing length parameter in the range of 1.6 − 2.3. The mass mixing length parameter is also depth-dependent and decreases above the surface to lower values around ~0.5, which agrees with previous findings from observations. The mass mixing length parameter and mixing length parameter strongly correlate with the logarithmic inverse of the entropy jump for different stellar parameters, that is αMLT ~ − lnΔs. Finally, we also derived the vertical velocity correlation length, which features values similar to that of the mixing length with approximately ~1.6–1.8 of pressure scale height, but, the dependence with Teff is inverted, meaning that the correlation length decreases with Teff.
To summarize the importance of our work: we can finally remove the free parameters inherent in MLT and also avoid having to use solar calibrations for other stars.
Online material
Appendix A: Tables
In Table A.1, we list results for the solar metallicity. The complete table is available at the CDS and also at http://www.stagger-stars.net
Stellar parameters: effective temperature, Teff, and surface gravity, log g (Cols. 1 and 2 in [K] and [dex]).
Appendix B: Functional fits
Similar to Ludwig et al. (1999), we performed functional fits of the mixing length parameters and the mass mixing length parameter with the Teff and log g for the different metallicities individually. We transformed the stellar parameters with x = (Teff − 5777)/1000 and y = log g − 4.44, and fitted the values with a least-squares minimization method for the functional basis 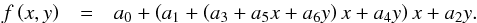 (B.1)The resulting coefficients, ai, are listed in Table B.1.
(B.1)The resulting coefficients, ai, are listed in Table B.1.
Appendix C: Addendum on MLT
Appendix C.1: Mixing length formulation
In the framework of MLT, the convective flux is determined by ![\appendix \setcounter{section}{3} \begin{eqnarray} F_{\mathrm{conv}} & = & \left[\amlt c_{P}T\Delta/2\right]\rho v_{\mathrm{MLT}},\label{eq:convective flux} \end{eqnarray}](/articles/aa/full_html/2015/01/aa23760-14/aa23760-14-eq191.png) (C.1)with cP being the heat capacity, Δ the superadiabatic energy excess, and αMLT the adjustable mixing length parameter, giving the mean free path of convective elements in units of pressure scale height. The convective velocity is determined by
(C.1)with cP being the heat capacity, Δ the superadiabatic energy excess, and αMLT the adjustable mixing length parameter, giving the mean free path of convective elements in units of pressure scale height. The convective velocity is determined by 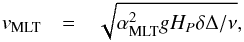 (C.2)where HP is the pressure scale height, δ = −(∂lnρ/∂lnT)p the thermal expansion coefficient, and ν the energy dissipation by turbulent viscosity. The superadiabatic excess is given by
(C.2)where HP is the pressure scale height, δ = −(∂lnρ/∂lnT)p the thermal expansion coefficient, and ν the energy dissipation by turbulent viscosity. The superadiabatic excess is given by 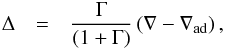 (C.3)and the convective efficiency factor by
(C.3)and the convective efficiency factor by 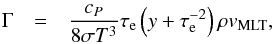 (C.4)with the optical thickness τe, and temperature distribution y of the convective element. The turbulent pressure
(C.4)with the optical thickness τe, and temperature distribution y of the convective element. The turbulent pressure 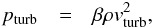 (C.5)can be included, but a depth-independent turbulent velocity, vturb is assumed, which is the common approach for atmospheric modeling. The resulting photospheric temperature stratifications are very similar to the MARCS (Gustafsson et al. 2008) and ATLAS models (Kurucz 1979; Castelli & Kurucz 2004). In Paper I, we showed that below the surface, where convective energy transport starts to dominate, the 1D models are systematically cooler than the ⟨3D⟩ stratifications because of the fixed αMLT with 1.5, in particular for hotter Teff.
(C.5)can be included, but a depth-independent turbulent velocity, vturb is assumed, which is the common approach for atmospheric modeling. The resulting photospheric temperature stratifications are very similar to the MARCS (Gustafsson et al. 2008) and ATLAS models (Kurucz 1979; Castelli & Kurucz 2004). In Paper I, we showed that below the surface, where convective energy transport starts to dominate, the 1D models are systematically cooler than the ⟨3D⟩ stratifications because of the fixed αMLT with 1.5, in particular for hotter Teff.
Appendix C.2: Influence of additional MLT parameters
 |
Fig. C.1 Entropy and superadiabatic gradient vs. depth (left and right panel, respectively) illustrating the influence of the additional MLT parameters ν, y, and β (top, middle, and bottom panel, respectively), the latter with the depth-independent vturb = 1 km s-1. The mixing length is kept fixed at αMLT = 1.5. We also included the standard values of β = 0, ν = 8 and y = 0.076 (dashed lines). Shown is the case for solar parameters. |
In the formulation of Henyey et al. (1965) of MLT, there are at least three additional free parameters apart from αMLT, which usually are not mentioned explicitly, but are compensated for by the value of αMLT. These are the scaling factor of the turbulent pressure, β, the energy dissipation by turbulent viscosity, ν, and the temperature distribution of a convective element, y. The default values are usually β = 1/2, ν = 8 and y = 3/4π2 = 0.076 (see Gustafsson et al. 2008). In many cases, the turbulent pressure is neglected (β = 0). In the notation of Ludwig et al. (1999), these parameters would yield f1 = ν-1 and f4 = y-1, f2 = 1/2 and f3 = 8 /y.
The turbulent pressure indirectly influences the T-stratification, gradients, and hydrostatic equilibrium by reducing the gas pressure. The parameter ν enters the convective velocity inverse proportionally, vMLT ∝ ν-1 (see Eq. (C.2)), and since 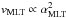 , an increase in ν would have the same effect as a reduction in αMLT, i.e. ν ∝ sbot. On the other
, an increase in ν would have the same effect as a reduction in αMLT, i.e. ν ∝ sbot. On the other
hand, y enters in the (nonlinear) convective efficiency factor, Γ, for the superadiabatic excess (see Eq. (C.4)), and therefore y is correlated with αMLT in a more complex way.
Considering a variation of the three additional parameters in the computation of the solar 1D model, we notice that the adiabatic entropy value of the deep convection zone is altered significantly (see Fig. C.1). Furthermore, the two parameters ν and y also change the entropy jump and the superadiabatic temperature gradient, ∇sad, and in particular, its maximum of ∇sad. The effect of the variation of y on the entropy stratification is similar to that by αMLT (see Fig. 1). However, the entropy of the deep convection zone exhibits a more nonlinear dependence with the y parameter. The increasing turbulent pressure with higher β changes the stratification only slightly, but shifts the location of the maximum of ∇sad to the deeper interior. Towards the optical surface the influence of the MLT parameters decreases, as expected because of decreasing convective flux. A fine-tuning of β, ν and y is only useful when these parameters introduce an independent influence on the mixing length, since otherwise its effects can be summarized in αMLT alone.
Acknowledgments
We thank Regner Trampedach, Åke Nordlund, and Bob Stein for helpful discussions. We acknowledge access to computing facilities at the Rechenzentrum Garching (RZG) of the Max Planck Society and at the Australian National Computational Infrastructure (NCI), where the 3D RHD simulations were carried out.
References
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Böhm-Vitense, E. 1958, Z. Astrophys., 46, 108 [Google Scholar]
- Bonaca, A., Tanner, J. D., Basu, S., et al. 2012, ApJ, 755, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Canuto, V. M. 1989, A&A, 217, 333 [NASA ADS] [Google Scholar]
- Canuto, V. M., & Mazzitelli, I. 1991, ApJ, 370, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Canuto, V. M., & Mazzitelli, I. 1992, ApJ, 389, 724 [NASA ADS] [CrossRef] [Google Scholar]
- Canuto, V. M., Goldman, I., & Mazzitelli, I. 1996, ApJ, 473, 550 [NASA ADS] [CrossRef] [Google Scholar]
- Castelli, F., & Kurucz, R. L. 2004 [arXiv:astro-ph/0405087] [Google Scholar]
- Chan, K. L., & Sofia, S. 1987, Science, 235, 465 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Chan, K. L., & Sofia, S. 1989, ApJ, 336, 1022 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen-Dalsgaard, J. 2008, Ap&SS, 316, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Demarque, P., Guenther, D. B., Li, L. H., Mazumdar, A., & Straka, C. W. 2008, Ap&SS, 316, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Deng, L., Xiong, D. R., & Chan, K. L. 2006, ApJ, 643, 426 [NASA ADS] [CrossRef] [Google Scholar]
- Freytag, B., & Salaris, M. 1999, ApJ, 513, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Freytag, B., Ludwig, H.-G., & Steffen, M. 1996, A&A, 313, 497 [Google Scholar]
- Freytag, B., Ludwig, H.-G., & Steffen, M. 1999, 173, 225 [Google Scholar]
- Fuhrmann, K., Axer, M., & Gehren, T. 1993, A&A, 271, 451 [NASA ADS] [Google Scholar]
- Gough, D. O. 1977, ApJ, 214, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Grossman, S. A., Narayan, R., & Arnett, D. 1993, ApJ, 407, 284 [NASA ADS] [CrossRef] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Henyey, L., Vardya, M. S., & Bodenheimer, P. 1965, ApJ, 142, 841 [NASA ADS] [CrossRef] [Google Scholar]
- Huber, D., Bedding, T. R., Stello, D., et al. 2011, ApJ, 743, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Kippenhahn, R., Weigert, A., & Weiss, A. 2013, Stellar Structure and Evolution (Berlin: Springer) [Google Scholar]
- Kurucz, R. L. 1979, ApJS, 40, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Ludwig, H.-G., Jordan, S., & Steffen, M. 1994, A&A, 284, 105 [NASA ADS] [Google Scholar]
- Ludwig, H.-G., Freytag, B., & Steffen, M. 1999, A&A, 346, 111 [NASA ADS] [Google Scholar]
- Ludwig, H.-G., Allard, F., & Hauschildt, P. H. 2006, A&A, 459, 599 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ludwig, H.-G., Caffau, E., & Kučinskas, A. 2008, in IAU Symp. 252, eds. L. Deng, & K. L. Chan, 75 [Google Scholar]
- Magic, Z., Serenelli, A., Weiss, A., & Chaboyer, B. 2010, ApJ, 718, 1378 [NASA ADS] [CrossRef] [Google Scholar]
- Magic, Z., Collet, R., Asplund, M., et al. 2013a, A&A, 557, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magic, Z., Collet, R., Hayek, W., & Asplund, M. 2013b, A&A, 560, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mihalas, D. 1970, Stellar atmospheres, Series of Books in Astronomy and Astrophysics (San Francisco: Freeman) [Google Scholar]
- Mihalas, D., Dappen, W., & Hummer, D. G. 1988, ApJ, 331, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Nordlund, A. 1976, A&A, 50, 23 [NASA ADS] [Google Scholar]
- Nordlund, A. 1982, A&A, 107, 1 [NASA ADS] [Google Scholar]
- Nordlund, A., & Dravins, D. 1990, A&A, 228, 155 [Google Scholar]
- Nordlund, Å., Stein, R. F., & Asplund, M. 2009, Liv. Rev. Sol. Phys., 6, 2 [Google Scholar]
- Prandtl, L. 1925, Z. Angew. Math. Mech., 5, 136 [Google Scholar]
- Robinson, F. J., Demarque, P., Li, L. H., et al. 2003, MNRAS, 340, 923 [NASA ADS] [CrossRef] [Google Scholar]
- Schlattl, H., Weiss, A., & Ludwig, H.-G. 1997, A&A, 322, 646 [NASA ADS] [Google Scholar]
- Steffen, M., Ludwig, H.-G., & Kruess, A. 1989, A&A, 213, 371 [NASA ADS] [Google Scholar]
- Stein, R. F., & Nordlund, A. 1998, ApJ, 499, 914 [Google Scholar]
- Trampedach, R. 2007, 948, 141 [Google Scholar]
- Trampedach, R., & Stein, R. F. 2011, ApJ, 731, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Trampedach, R., Asplund, M., Collet, R., Nordlund, Å., & Stein, R. F. 2013, ApJ, 769, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Unno, W., Kondo, M.-A., & Xiong, D.-R. 1985, PASJ, 37, 235 [NASA ADS] [Google Scholar]
- Viallet, M., Meakin, C., Arnett, D., & Mocák, M. 2013, ApJ, 769, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Xiong, D. R., Cheng, Q. L., & Deng, L. 1997, ApJS, 108, 529 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Stellar parameters: effective temperature, Teff, and surface gravity, log g (Cols. 1 and 2 in [K] and [dex]).
All Figures
 |
Fig. 1 Mean ⟨3D⟩z entropy (black solid line) vs. depth, and 1D models for different mixing length parameters, αMLT = 1.5 − 2.5 (blue lines), for the solar model (left panel) and a metal-poor dwarf with [Fe/H] − 2.0,Teff = 4500 K, and log g = 4.5 (right panel). We indicate the constant entropy value of the deep adiabatic convection zone, sbot, in both figures by the horizontal dotted line. In the deeper layers, we extended the 1D models (dashed lines) with the aid of the entropy gradient from the ⟨3D⟩ models. The calibration of the mixing length parameter αMLT for the solar model is illustrated by the smaller insets, which depict the relative differences between the 1D and 3D models (δs = s1D/s3D − 1) for sbot (solid) and the entropy jump Δs (dashed). For the solar model the two approaches result in αMLT = 1.98 and 2.09. |
| In the text | |
 |
Fig. 2 Kiel-diagram (Teff − log g diagram) with the mixing length parameter calibrated with the constant entropy value of the adiabatic convection zone, |
| In the text | |
 |
Fig. 3 As Fig. 2, but here we show the mixing length parameter calibrated with the entropy jump αMLT(Δs). |
| In the text | |
 |
Fig. 4 Dependence of the mixing length parameters on the different stellar parameters ( |
| In the text | |
 |
Fig. 5 Comparison of the mixing length parameter calibrated with the entropy jump, αMLT(Δs), and the constant entropy value of the adiabatic convection zone, |
| In the text | |
 |
Fig. 6 Comparison between the mixing length parameter calibrated with the entropy jump, αMLT(Δs), and the logarithm of the inverse of the entropy jump, − ln(Δs), for different stellar parameters. |
| In the text | |
 |
Fig. 7 Highest contrast of the entropy and density compared with the highest vertical rms-velocity (top and bottom panel, respectively) for different stellar parameters. |
| In the text | |
 |
Fig. 8 Top panel: calibration of αMLT with 2D (Ludwig et al. 1999) and 3D simulations in comparison (solid and dashed lines, respectively). The surface gravity is indicated and color-coded. The solar values are indicated. Bottom panel: relative differences (δ = 2D/3D − 1). |
| In the text | |
 |
Fig. 9 Mixing length parameter along stellar evolutionary tracks with solar metallicity against the normalized age for the masses from 0.7 to 1.5 M⊙ (indicated). The tracks are derived from the functional fits f(Teff,log g) of αMLT-calibrations with sbot and Δs (top and bottom panel, respectively) and all tracks end on the RGB when log g = 1. |
| In the text | |
 |
Fig. 10 Relative differences between the the mixing length parameter derived from observations and our 3D RHD models for different stellar parameters. |
| In the text | |
 |
Fig. 11 Top panel: mass mixing length parameter αm from Eq. (3) (solid) and the inverse gradient of the density, |
| In the text | |
 |
Fig. 12 As Fig. 2, but here the mass mixing length parameter αm is shown. |
| In the text | |
 |
Fig. 13 As Fig. 4, but here the mass mixing length parameter αm is shown. |
| In the text | |
 |
Fig. 14 Mean gradient of the density, ∇ρ, and the vertical velocity, ∇vz, in the convection zone for different stellar parameters. |
| In the text | |
 |
Fig. 15 Correlation of the mass mixing length parameter, αm, with the logarithmic inverse of the entropy jump − ln(Δs) and the peak of the vertical rms-velocity (top and bottom panel, respectively). |
| In the text | |
 |
Fig. 16 Comparison of the mass mixing length parameter, αm, with the mixing length parameter calibrated with sbot and Δs (top and bottom panel, respectively). |
| In the text | |
 |
Fig. 17 Vertical two-point correlation function of the vertical velocity, C[vz,vz], vs. the difference in the thermodynamic pressure, Δlog Pth, for the solar simulation. The different heights are indicated with a blue color-coding. Note the convergence of the correlation width in the convection zone against an adiabatic value. |
| In the text | |
 |
Fig. 18 Top panel: vertical correlation length of the vertical velocity (solid line with triangles) and pressure scale height (dotted-dashed line) shown against the depth for the solar model. We indicate the different heights with the same color-coding as used in Fig. 17. Bottom panel: vertical correlation length scaled by the pressure scale height, which yields an average of 1.71 (dashed line) in the considered region for averaging the correlation length (vertical dotted lines with filled circles) for the solar simulation. |
| In the text | |
 |
Fig. 19 Correlation length of the vertical velocity vs. surface normalized pressure for different stellar parameters. |
| In the text | |
 |
Fig. 20 Overview of mean vertical correlation length of the vertical velocity in the convection zone for different stellar parameters. |
| In the text | |
 |
Fig. C.1 Entropy and superadiabatic gradient vs. depth (left and right panel, respectively) illustrating the influence of the additional MLT parameters ν, y, and β (top, middle, and bottom panel, respectively), the latter with the depth-independent vturb = 1 km s-1. The mixing length is kept fixed at αMLT = 1.5. We also included the standard values of β = 0, ν = 8 and y = 0.076 (dashed lines). Shown is the case for solar parameters. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.