| Issue |
A&A
Volume 573, January 2015
|
|
|---|---|---|
| Article Number | A89 | |
| Number of page(s) | 17 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201423760 | |
| Published online | 23 December 2014 | |
Online material
Appendix A: Tables
In Table A.1, we list results for the solar metallicity. The complete table is available at the CDS and also at http://www.stagger-stars.net
Stellar parameters: effective temperature, Teff, and surface gravity, log g (Cols. 1 and 2 in [K] and [dex]).
Appendix B: Functional fits
Similar to Ludwig et al. (1999), we performed functional fits of the mixing length parameters and the mass mixing length parameter with the Teff and log g for the different metallicities individually. We transformed the stellar parameters with x = (Teff − 5777)/1000 and y = log g − 4.44, and fitted the values with a least-squares minimization method for the functional basis ![]() (B.1)The resulting coefficients, ai, are listed in Table B.1.
(B.1)The resulting coefficients, ai, are listed in Table B.1.
Appendix C: Addendum on MLT
Appendix C.1: Mixing length formulation
In the framework of MLT, the convective flux is determined by ![]() (C.1)with cP being the heat capacity, Δ the superadiabatic energy excess, and αMLT the adjustable mixing length parameter, giving the mean free path of convective elements in units of pressure scale height. The convective velocity is determined by
(C.1)with cP being the heat capacity, Δ the superadiabatic energy excess, and αMLT the adjustable mixing length parameter, giving the mean free path of convective elements in units of pressure scale height. The convective velocity is determined by ![]() (C.2)where HP is the pressure scale height, δ = −(∂lnρ/∂lnT)p the thermal expansion coefficient, and ν the energy dissipation by turbulent viscosity. The superadiabatic excess is given by
(C.2)where HP is the pressure scale height, δ = −(∂lnρ/∂lnT)p the thermal expansion coefficient, and ν the energy dissipation by turbulent viscosity. The superadiabatic excess is given by 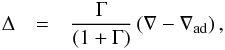 (C.3)and the convective efficiency factor by
(C.3)and the convective efficiency factor by ![]() (C.4)with the optical thickness τe, and temperature distribution y of the convective element. The turbulent pressure
(C.4)with the optical thickness τe, and temperature distribution y of the convective element. The turbulent pressure ![]() (C.5)can be included, but a depth-independent turbulent velocity, vturb is assumed, which is the common approach for atmospheric modeling. The resulting photospheric temperature stratifications are very similar to the MARCS (Gustafsson et al. 2008) and ATLAS models (Kurucz 1979; Castelli & Kurucz 2004). In Paper I, we showed that below the surface, where convective energy transport starts to dominate, the 1D models are systematically cooler than the ⟨3D⟩ stratifications because of the fixed αMLT with 1.5, in particular for hotter Teff.
(C.5)can be included, but a depth-independent turbulent velocity, vturb is assumed, which is the common approach for atmospheric modeling. The resulting photospheric temperature stratifications are very similar to the MARCS (Gustafsson et al. 2008) and ATLAS models (Kurucz 1979; Castelli & Kurucz 2004). In Paper I, we showed that below the surface, where convective energy transport starts to dominate, the 1D models are systematically cooler than the ⟨3D⟩ stratifications because of the fixed αMLT with 1.5, in particular for hotter Teff.
Appendix C.2: Influence of additional MLT parameters
 |
Fig. C.1
Entropy and superadiabatic gradient vs. depth (left and right panel, respectively) illustrating the influence of the additional MLT parameters ν, y, and β (top, middle, and bottom panel, respectively), the latter with the depth-independent vturb = 1 km s-1. The mixing length is kept fixed at αMLT = 1.5. We also included the standard values of β = 0, ν = 8 and y = 0.076 (dashed lines). Shown is the case for solar parameters. |
| Open with DEXTER | |
In the formulation of Henyey et al. (1965) of MLT, there are at least three additional free parameters apart from αMLT, which usually are not mentioned explicitly, but are compensated for by the value of αMLT. These are the scaling factor of the turbulent pressure, β, the energy dissipation by turbulent viscosity, ν, and the temperature distribution of a convective element, y. The default values are usually β = 1/2, ν = 8 and y = 3/4π2 = 0.076 (see Gustafsson et al. 2008). In many cases, the turbulent pressure is neglected (β = 0). In the notation of Ludwig et al. (1999), these parameters would yield f1 = ν-1 and f4 = y-1, f2 = 1/2 and f3 = 8 /y.
The turbulent pressure indirectly influences the T-stratification, gradients, and hydrostatic equilibrium by reducing the gas pressure. The parameter ν enters the convective velocity inverse proportionally, vMLT ∝ ν-1 (see Eq. (C.2)), and since ![]() , an increase in ν would have the same effect as a reduction in αMLT, i.e. ν ∝ sbot. On the other
, an increase in ν would have the same effect as a reduction in αMLT, i.e. ν ∝ sbot. On the other
hand, y enters in the (nonlinear) convective efficiency factor, Γ, for the superadiabatic excess (see Eq. (C.4)), and therefore y is correlated with αMLT in a more complex way.
Considering a variation of the three additional parameters in the computation of the solar 1D model, we notice that the adiabatic entropy value of the deep convection zone is altered significantly (see Fig. C.1). Furthermore, the two parameters ν and y also change the entropy jump and the superadiabatic temperature gradient, ∇sad, and in particular, its maximum of ∇sad. The effect of the variation of y on the entropy stratification is similar to that by αMLT (see Fig. 1). However, the entropy of the deep convection zone exhibits a more nonlinear dependence with the y parameter. The increasing turbulent pressure with higher β changes the stratification only slightly, but shifts the location of the maximum of ∇sad to the deeper interior. Towards the optical surface the influence of the MLT parameters decreases, as expected because of decreasing convective flux. A fine-tuning of β, ν and y is only useful when these parameters introduce an independent influence on the mixing length, since otherwise its effects can be summarized in αMLT alone.
© ESO, 2014
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


