| Issue |
A&A
Volume 572, December 2014
|
|
|---|---|---|
| Article Number | A110 | |
| Number of page(s) | 8 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201424345 | |
| Published online | 04 December 2014 | |
MY Camelopardalis, a very massive merger progenitor⋆,⋆⋆
1
Departamento de Física, Ingeniería de Sistemas y Teoría de la
SeñalUniversidad de Alicante,
Apdo. 99,
03080
Alicante,
Spain
e-mail:
fjle3@alu.ua.es
2
Departamento de Astrofísica, Centro de Astrobiología (CSIC–INTA), Ctra. de Torrejón a
Ajalvir, km 4, 28850 Torrejón de Ardoz, Madrid, Spain
3
Instituto de Astrofísica de Canarias, Vía Láctea s/n, 38200 La Laguna, Tenerife, Spain
4
Departamento de Astrofísica, Universidad de La Laguna, Facultad de
Física y Matemáticas, Universidad de La Laguna, Avda. Astrofísico Francisco Sánchez, s/n, 38205 La
Laguna, Tenerife,
Spain
5
Departamento de Lenguajes y Sistemas Informáticos, Universidad de
Alicante, Apdo. 99,
03080
Alicante,
Spain
6
Departamento de Ciencias, IES Arroyo Hondo, c/ Maestro Manuel Casal 2, 11520
Rota, Cádiz,
Spain
Received: 6 June 2014
Accepted: 28 September 2014
Context. The early-type binary MY Cam belongs to the young open cluster Alicante 1, embedded in Cam OB3.
Aims. MY Cam consists of two early-O type main-sequence stars and shows a photometric modulation suggesting an orbital period slightly above one day. We intend to confirm this orbital period and derive orbital and stellar parameters.
Methods. Timing analysis of a very exhaustive (4607 points) light curve indicates a period of 1.1754514 ± 0.0000015 d. High-resolution spectra and the cross-correlation technique implemented in the todcor program were used to derive radial velocities and obtain the corresponding radial velocity curves for MY Cam. Modelling with the stellar atmosphere code fastwind was used to obtain stellar parameters and create templates for cross-correlation. Stellar and orbital parameters were derived using the Wilson-Devinney code, such that a complete solution to the binary system could be described.
Results. The determined masses of the primary and secondary stars in MY Cam are 37.7 ± 1.6 and 31.6 ± 1.4M⊙, respectively. The corresponding temperatures, derived from the model atmosphere fit, are 42 000 and 39 000 K, with the more massive component being hotter. Both stars are overfilling their Roche lobes, sharing a common envelope.
Conclusions. MY Cam contains the most massive dwarf O-type stars found so far in an eclipsing binary. Both components are still on the main sequence, and probably not far from the zero-age main sequence. The system is a likely merger progenitor, owing to its very short period.
Key words: binaries: spectroscopic / binaries: eclipsing / stars: massive / stars: early-type
Tables 1 and 3 are available in electronic form at http://www.aanda.org
Photometric data (Table 2) are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/572/A110
© ESO, 2014
1. Introduction
Numerous studies show the importance of massive stars for the current properties of galaxies (e.g. Massey 2003). Among O-type stars, relatively unevolved massive stars, there is a very high fraction of binaries, where the initial orbital period determines their evolution and final fate. Sana et al. (2012) note that 60% of O-type binaries have a period shorter than ten days. In close to 90% of O-type binaries, at least one of the components will fill its Roche lobe during their lifetime. This leads to interaction with its companion, where mass transfer, followed by common envelope evolution, may lead to a merger. Some estimates put 25% as the fraction of binaries that will merge at some point (Langer 2012). In particular, when a binary system has an initial orbital period, Porb, shorter than two days and mass ratio q lower than 0.6, evolutionary models predict that both components will merge while on the main sequence. This fate is expected for half of the binary systems that evolve according to Case A, i.e. those in which mass transfer starts during core hydrogen burning (Wellstein et al. 2001; Langer 2012). For smaller Porb, systems with higher q will also come into contact during H core burning (Wellstein et al. 2001).
Sybesma (1985) notes that short-period binary systems with q> 0.8 form stable overcontact systems. These systems would be classified as Case A interacting binaries with slow evolution to contact (Eggleton 2000). Other theoretical studies have also shown that these types of binaries tend to become overcontact systems evolving through slow Case A (e.g. Qian et al. 2007).
Despite all these theoretical predictions, our observational constraints are limited. There are only two known binary systems with two main-sequence O-star components presenting Porb< 2 d whose orbits have been solved: V382 Cyg (Harries et al. 1997) and TU Mus (Terrell et al. 2003). Moreover, because the merger phase is so short compared to stellar lifetimes, only two systems have been proposed to have experienced an observed merger event, and neither of them is a massive system: V838 Mon could represent an intermediate-mass merger (Munari et al. 2002; Tylenda et al. 2011) and V1309 Sco may have been a low-mass merger (Mason et al. 2010; Tylenda et al. 2011).
Mergers are the consequence of angular momentum loss in tidally synchronised systems with short initial orbital periods (Andronov et al. 2006). The physics of mergers is poorly understood, but it is believed that they follow a common envelope phase. This phase, when both stars share the same envelope, is extremely important in close binary evolution, but is still not fully understood (Ivanova et al. 2013). The results of mergers are expected to have unusual properties, such as very high rotational velocities or unusual surface abundances (Langer 2012).
In recent years, the mergers of high-mass binaries have been proposed as an effective mechanism to form very massive stars. Using population synthesis models, de Mink et al. (2014) estimate that 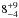 % of apparently single early-type stars are the products of a merger. A binary merger origin has been proposed as an explanation for the extremely fast rotation (vrot> 500km s-1) of the O-type star VFTS 102 (Jiang et al. 2013), though its peculiar radial velocity is strongly suggestive of other types of binary interaction (Dufton et al. 2011). Dynamically induced mergers of very massive binaries in the cores of dense clusters have been proposed as an explanation for the formation of very massive stars (M∗> 150 M⊙) in the core of R136 (Banerjee et al. 2012). Some of the energetic events known as supernova impostors could also be due to the merger of a massive binary (Soker & Kashi 2013). Somewhat less massive mergers have been proposed as the progenitors of peculiar O-type stars with high magnetic fields (see references in Langer 2012) or very massive runaway stars (Vanbeveren et al. 2009).
% of apparently single early-type stars are the products of a merger. A binary merger origin has been proposed as an explanation for the extremely fast rotation (vrot> 500km s-1) of the O-type star VFTS 102 (Jiang et al. 2013), though its peculiar radial velocity is strongly suggestive of other types of binary interaction (Dufton et al. 2011). Dynamically induced mergers of very massive binaries in the cores of dense clusters have been proposed as an explanation for the formation of very massive stars (M∗> 150 M⊙) in the core of R136 (Banerjee et al. 2012). Some of the energetic events known as supernova impostors could also be due to the merger of a massive binary (Soker & Kashi 2013). Somewhat less massive mergers have been proposed as the progenitors of peculiar O-type stars with high magnetic fields (see references in Langer 2012) or very massive runaway stars (Vanbeveren et al. 2009).
MY Cam (BD +56°864 = GSC 3725-0498) is the brightest star in the open cluster Alicante 1, a sparsely populated, very young open cluster embedded in the Cam OB3 association (Negueruela & Marco 2008). This association has a distance estimate of ≈4 kpc, which places it in the Cygnus arm. The Galactic coordinates of MY Cam are 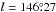 ,
, 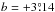 . MY Cam was classified as O6nn by Morgan et al. (1955). Higher quality spectroscopic observations later showed that it was a double-lined spectroscopic binary (Negueruela & Marco 2003). The two components seemed to have similar spectral types, close to O6 V, while the large separation in radial velocity suggested a very short orbital period (Negueruela & Marco 2003). Using data from the Northern Sky Variability Survey (Woźniak et al. 2004), Greaves & Wils (2004) noted a periodicity of ≈1.18 d in the light curve and suggested it was due to elliptical variations. If this periodicity is the orbital period of the binary, then MY Cam would represent an excellent candidate for a very massive merger progenitor. In this paper, we derive the properties of the two components of MY Cam and find that it fulfils all criteria to be considered as a very massive merger progenitor: it is a high-mass binary system with two early-O type components on the main sequence, a very short period, very high rotational velocity due to synchronisation and components already filling their Roche lobes.
. MY Cam was classified as O6nn by Morgan et al. (1955). Higher quality spectroscopic observations later showed that it was a double-lined spectroscopic binary (Negueruela & Marco 2003). The two components seemed to have similar spectral types, close to O6 V, while the large separation in radial velocity suggested a very short orbital period (Negueruela & Marco 2003). Using data from the Northern Sky Variability Survey (Woźniak et al. 2004), Greaves & Wils (2004) noted a periodicity of ≈1.18 d in the light curve and suggested it was due to elliptical variations. If this periodicity is the orbital period of the binary, then MY Cam would represent an excellent candidate for a very massive merger progenitor. In this paper, we derive the properties of the two components of MY Cam and find that it fulfils all criteria to be considered as a very massive merger progenitor: it is a high-mass binary system with two early-O type components on the main sequence, a very short period, very high rotational velocity due to synchronisation and components already filling their Roche lobes.
2. Observations
Spectroscopic observations of MY Cam were obtained between 23 and 31 December 2004, using the Fibre Optics Cassegrain Échelle Spectrograph (FOCES) mounted on the 2.2 m telescope of the Calar Alto Observatory (Spain). The observations were performed in service mode, and sky conditions were very variable. The log of observations is displayed in Table 1, where we have assigned a number to each spectrum, sorted by date in ascending order. Heliocentric corrections, calculated using the rv program included in the Starlink suite, are also listed in Table 1. A total of 63 spectra were obtained, with fixed exposure times of 1800 s. The signal-to-noise ratio (S/N) varies strongly between spectra, from ~20 to ~50 per pixel. The spectrograph covers a wide spectral range between 3780 and 10 864 Å. The resolution is slightly variable with wavelength, but always ≈40 000 for a 2-pixel resolution element. Given the faintness of the source and the spectral response, data for wavelengths shorter than ~4000 Å are not useful.
We reduced all spectra with two methods. Firstly, we used the IDL standard pipeline provided by the observatory. The extracted spectra showed a good blaze correction and order merging, but very poor S/N. The spectra were therefore processed (bias-subtracted, flat-fielded and wavelength-calibrated) using standard iraf tools for the reduction of échelle spectroscopy. The 99 échelle orders were blaze-corrected, combined and continuum-normalised to obtain a single spectrum using the pipeline-reduced spectra as a guide.
In addition, on 22 November 2002, we obtained one intermediate-resolution spectrum with the blue arm of the Intermediate dispersion Spectrograph and Imaging System (ISIS) double-beam spectrograph, mounted on the 4.2 m William Herschel Telescope (WHT) in La Palma (Spain). The instrument was fitted with the R1200B grating and the EEV12 CCD. This configuration covers a spectral range from ~4000 to 4700 Å in the unvignetted section of the CCD with a nominal dispersion of 0.25 Å/pixel. The CCD was unbinned in the spectral direction and a 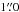 slit, was used. With this slit the resolution element is expected to be smaller than four pixels. The resolving power of our spectrum is thus R ≈ 5000.
slit, was used. With this slit the resolution element is expected to be smaller than four pixels. The resolving power of our spectrum is thus R ≈ 5000.
Photometric data (Table 2 avalaible at the CDS) were obtained with two 8-inch aperture telescopes, a Meade LX200 and a Vixen VISAC, with focal-ratios of f/6.3 and f/9, respectively. Observations were made through a Johnson R-filter with uniform 120 s exposures. We reduced the data with the standard commercial software packages AIP4Win and Mira Pro. We followed the standard procedures for bias and flat correction. A total of 4607 photometric points were registered, randomly distributed in nights between 4 March and 13 September 2008. Photometric values were derived differentially with respect to three reference stars with similar colours in the same frame: TYC 3725-797-1, TYC 3725-00486-1, and TYC 3725-00437-1. The latter is an B1.5 V star likely associated with the open cluster Alicante 1, to which MY Cam belongs. The photometric light-curve is displayed in Fig. 1. A photometric variability of approximately 0.3 mag is apparent.
 |
Fig. 1 Photometric light curve, showing the amplitude of the modulation. |
3. Spectroscopic analysis: radial velocity determination
The spectrum of MY Cam shows strong He ii 4686Å absorption, a characteristic of O-type main-sequence stars. The He ii 4542 and 5411 Å lines are also strongly in absorption. A very weak N iii 4634-40-42 Å emission complex may be guessed in the spectra with better S/N. According to the classical criteria for O-type spectral classification by Walborn & Fitzpatrick (1990), the ratio between the He ii 4542 Å and He i 4471 Å lines is larger than unity for spectral types earlier than O7. Both stars show this characteristic, with the ratio being larger for one of the stars that we will from now on identify as the primary. Because of blending and the possibility of the Struve-Sahade effect being present (cf. Linder et al. 2007), accurate spectral types cannot be given. However, we can confidently claim that the primary is at least as early as O5.5 V and the secondary is earlier than O7 V (see Fig. 2).
 |
Fig. 2 Some representative lines in the spectrum of MY Cam and some model line fits. Solid line: Teff1 = 42 000 K, log g1 = 3.9; Teff2 = 39 000 K, log g2 = 4.1. Dashed line: Teff1 = 40 000 K, log g1 = 3.7; Teff2 = 38 000 K, log g2 = 3.9. Dashed-dotted line: Teff1 = 44 000 K, log g1 = 4.1; Teff2 = 41 000 K, log g2 = 4.3. |
With the purpose of applying the technique of cross-correlation for the determination of radial velocities, we have synthesised two templates using the fastwind model atmosphere code (Puls et al. 2005; Santaloya-Rey et al. 1997). The WHT spectrum, which has a much better S/N than any of the FOCES spectra, was used to derive the best-fit parameters. The separation between the two components is sufficient to allow for two synthetic spectra to be fitted. For O-type stars, the effective temperature is determined from the ionisation balance of He i and He ii. There is a small degree of degeneracy between values of Teff and log g. We therefore used the grid of fastwind models of solar metallicity presented in Simón-Díaz & Herrero (2011), and obtained fits by eye. The best-fit model and two models that define the error bars are shown in Fig. 2. From this, we conclude that the best fitting parameters are: 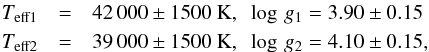 where the error bars indicate the range of parameters that provide acceptable fits (hereafter, we will use the subindex 1 for the primary star and the subindex 2 for the secondary star). These parameters are in good agreement with the derived spectral types. The rotational velocities were estimated simultaneously with the fitting, finding vrot1,2sin i = 280 ± 20km s-1.
where the error bars indicate the range of parameters that provide acceptable fits (hereafter, we will use the subindex 1 for the primary star and the subindex 2 for the secondary star). These parameters are in good agreement with the derived spectral types. The rotational velocities were estimated simultaneously with the fitting, finding vrot1,2sin i = 280 ± 20km s-1.
On the observational scale of Martins et al. (2005), the temperatures correspond to spectral types O4.5 V and O6 V. We must note that the stars on the scale of Martins et al. (2005) are assumed to have log g= 3.9. Our values of log g have not been corrected for the effect of the centrifugal force, which, at the rotational velocities observed, should be by about 0.05 dex in the direction of higher gravities. The model fit is better when the He abundance of the more massive component is increased from the usual YHe = 0.10 to YHe = 0.15. In any case, we must stress that fastwind assumes spherical symmetry, an approximation that, as we will see below, is not well justified in such a close binary.
To derive the radial velocities for both components of the binary system, we used the technique of cross-correlation in two dimensions developed by Zucker & Mazeh (1994) and implemented in the todcor program. We cross-correlated our observational spectra against the two previously synthesised templates. The spectral range of 4400–5585Å was chosen for the analysis, since it includes the main He ii lines (4542, 4686 and 5411 Å) as well as Hβ. These are the only lines clearly detectable in all the FOCES spectra, as all He i lines become too shallow as soon as the system moves out of eclipse. We rebinned all the spectra and the synthetic templates to 9000 bins. The apodization factor used in the process was 0.3, meaning that the spectra are smoothed with a cosine bell over the 15% of their length closer to the edges. All radial velocities measured were corrected to the heliocentric velocity system.
The determination of the uncertainties in the radial velocities is based on the width of the peak in the cross-correlation function. In the case of MY Cam, because of the very large rotational velocity, the lines are very wide, and therefore uncertainties around 100 kms-1 are expected. Given the size of the bin (around 8 kms-1), the uncertainties could be reduced using a larger number of lines for the two-dimensional correlation algorithm. Unfortunately, because of the poor S/N of many of the spectra, we could not work with more lines. In many spectra, for wavelengths shorter than 4300 Å, lines and continuum are practically indistinguishable. As mentioned previously, the He i lines are only visible when both stars are found at the systemic velocity and the lines of both components are super-imposed. The only other line that is clearly seen is Hα, but we preferred not to include it in the analysis because, even for stars on the main sequence, it can be significantly affected by stellar wind effects.
In spite of the paucity of spectral features used for the analysis, the results are reliable. We used the period program inside the Starlink suite to perform a search for periodicities in the radial velocities. The Lomb-Scargle algorithm (Lomb 1976; Scargle 1982) gives a spectroscopic period of 1.17 ± 0.04 d, which is in excellent agreement with the photometric period. This value is confirmed with the clean algorithm (Roberts et al. 1987), which removes periods caused by the window function (see Fig. 3).
4. Combined analysis: photometry and spectroscopy
A combined analysis of the photometric data and the radial velocities was made using the Wilson-Devinney code (Wilson & Devinney 1971; Wilson & Biermann 1976; Wilson 1990) in its 2010 version. Because of the low signal-to-noise ratio of the spectra and the very high quality of the photometric data (which cover the whole orbital period with excellent sampling), we chose to analyse the radial velocity curve and light curve separately, following the method described in Ribas et al. (2005). The radial velocity curve and light curve are analysed with an iterative procedure until convergence is reached for all free parameters. The criterion for convergence adopted is that for three consecutive iterations all adjustable parameters must be within two standard deviations. Once convergence is reached, five solutions are derived by varying the parameters within the standard deviation and fitting the observations again. We choose the fit with the smallest dispersion as a final solution. The initial parameters were derived from the spectroscopic analysis in the previous section and the stellar parameters obtained from the atmospheric model. The first steps of the procedure rely on finding the period and the zero time of ephemeris, using the photometric data. From the folded light curve, we classify MY Cam as a contact binary with a short period (around a day), so we can assume that the system is circularised and synchronised. The eccentricity can then be assumed to be zero. The location in orbital phase of the primary and secondary eclipses will be exactly 0.0 and 0.5, respectively. At phase 0.0, the primary component is being eclipsed by the secondary component, while at phase 0.5, the primary component eclipses the secondary component. This is barely perceivable in the light curve (Fig. 4), where the minimum at phase 0.0 is very slightly deeper than the minimum at phase 0.5. To quantify this difference, we average all photometric data points between φ = 0.99 and 0.01 (average R = 9.5743), and all points between φ = 0.49 and 0.51 (average R = 9.5683). The difference between the two minima is thus 0.0060 mag.
 |
Fig. 3 Results of the Lomb-Scargle periodogram for the radial velocities. The inset shows the result of applying the clean algorithm. |
The implementation of the Wilson-Devinney code requires some previous assumptions. Given the stellar parameters found from the fastwind analysis and the extremely short orbital period, we assume that MY Cam must be a contact system and therefore share a common equipotential surface. The effective temperatures of both components were fixed to the value found from the fastwind analysis for the hottest component, Teff = 42 000 K. Every component is considered to be divided in a 40 × 40 grid of surface elements. A reflection model is included in the code (Wilson 1990) as well. A square root limb-darkening law is applied, as it is more precise than the linear law (van Hamme 1993) and is the most adequate approximation for radiative stars (Diaz-Cordoves et al. 1995). Gravity darkening and ellipsoidal effects are evaluated because the components must be very close to each other. Finally, the bolometric albedos are taken to be equal to unity, considering that the stellar atmospheres are in radiative equilibrium (von Zeipel 1924). Other contraints applied are described in mode 1 of the Wilson-Devinney code.
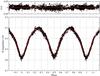 |
Fig. 4 Light curve model fitted to the observational data. Residuals are displayed in the top panel. |
The quadrature phases in a circular orbit happen at phases 0.25 and 0.75. At these phases, the stars are not eclipsed, and we receive the maximum flux from the binary system (see Fig. 4). In the phenomenological classification, the light curve of MY Cam corresponds to an eclipsing variable of the EW type. The curve displayed in Fig. 4 shows a continuous variation of brightness, with minimal difference between the two eclipse depths. The model curve fitted to the observational data is also shown in Fig. 4. The standard deviation of the fit is only 0.011 mag, and the residuals are always smaller than 0.05 mag, demonstrating an excellent fit.
From the period and the zero time of ephemeris, we can write the linear ephemeris equation,
where the epoch of successive times of primary-eclipse minima (phase zero), Tmin, is
calculated as:
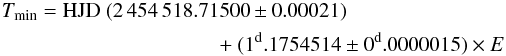 where E is the integer value of the number of orbital
cycles.
where E is the integer value of the number of orbital
cycles.
The radial velocity points are displayed in Fig. 5 together with the final fitted velocity curves. The standard deviations are 42kms-1 for the primary star (black curve) and 33kms-1 for the secondary star. The residuals, also shown in Fig. 5, reach a maximum value of 100kms-1, in agreement with the uncertainties in the radial velocities. The radial velocities sorted by orbital phase and their residuals are listed in Table 3. Residuals significantly larger than the standard deviation are found at phases around 0.5, owing to the blending of the spectral lines at these phases.
 |
Fig. 5 Radial velocity curves fitted to the observational data and displayed against orbital phase (black line: primary star; red line: secondary star) fitted to the observational data. The dashed line corresponds to the systemic velocity. The residuals are displayed in the top panel. |
Some radial velocities for the primary star around the second quadrature (φ ~ 0.75) reach values clearly above the fitted curve. These velocities correspond to the spectra numbered as 36, 37 (December 24) and 44, 45, and 47 (December 30; see Table 1). We assume that these deviant velocities can be due to the effects of the stellar wind, being more noticeable when the component is not eclipsed by the companion star.
5. Results
The combined analysis of the radial velocity curve and photometric light curve permits the determination of the stellar and orbital parameters for the MY Cam binary system. All the parameters are listed in Table 4. It is worth mentioning that the spectroscopic period is only 54 s shorter than the photometric period. The difference between the two periods is around 0.05%. This close agreement guarantees the quality of the results derived.
 |
Fig. 6 Representative drawing of MY Cam to scale at quadrature phase, created with the PHOEBE 2.0-alpha code via the Python interface. |
Stellar parameters derived from the combined analysis of the radial velocity and photometric light curve.
Close binaries suffer significant deformations in their shape, which is noticeable in the radii shown in Table 4. The point radius is defined as the equatorial radius in the direction to the centre of the other component. The solution provides a value for the point radius, indicating a separation between the two stars of 0.39R⊙, but this small distance is compatible with zero within the uncertainties derived (see Table 4). Therefore, the solution is consistent with the assumption that both stars are overfilling their Roche lobes. Thus, the solution found is compatible with mass transfer already taking place, as suggested by the shape of the light curve. A schematic drawing of MY Cam is displayed in Fig. 6, showing the shape of both components at quadrature phase.
In addition, since the mass ratio is still significantly different from unity, at q = 0.84, we can conclude that mass transfer has only started recently. The surface gravities are difficult to compare, because the fastwind model assumes spherical symmetry, while the Wilson-Devinney code takes into account that gravity is varying throughout the stellar surface. According to the Wilson-Devinney model, the maximum value for gravity is achieved in the pole of the star (log g = 4.25), with the minimum value occurring at the point of maximum stellar radius (log g = 4.03). Interestingly, in spite of the very different physics used in the atmosphere model and the binary solution, the values obtained for the rotational velocities are essentially the same, within their respective errors.
Examining the subclasses of Case A listed by Eggleton (2000), MY Cam would be included in subclass AS (slow evolution to contact), because both components have already reached contact well before leaving the main sequence. Unfortunately, evolutionary models presented by Nelson & Eggleton (2001) do not include binaries with massive components and very short periods, such as MY Cam.
The derived systemic velocity of −47 ± 4 km s-1 is fully consistent with the heliocentric velocities of several members of Cam OB3 measured by Rubin (1965), which cluster around −40km s-1. This is to be expected for such a massive system in a small-size cluster, where no other stars would have a comparable mass necessary for dynamical interactions to provide it with a peculiar velocity. The next most massive star in the cluster (and only other high-mass star) is LS I + 57°138, with spectral type O7 V (Negueruela & Marco 2008).
6. Discussion and conclusions
The masses found for the two components of MY Cam are very high, and, to the best of our knowledge, are the highest masses ever derived for main-sequence O-type stars in an eclipsing binary. The literature offers a few examples that can be used as comparison systems. For instance, Niemela et al. (2006) determined the mass of the primary star in V662 Car (Porb = 1.41 d) to be around 30M⊙. This star is spectroscopically catalogued as O5.5 V, which is a cooler (later) star than the primary of MY Cam, and thus less massive. The primary of V1182 Aql (Porb = 1.62 d; Mayer et al. 2005) is very similar to the primary in V662 Car, with a mass of 31M⊙ and of the same spectral type, O5.5 V .
The secondary of MY Cam can be compared to the primary in V3903 Sgr (O7 V). This system has an orbital period of 1.74 d, and the mass of the primary is 27M⊙ (Vaz et al. 1997). Similarly, the O7 V primary in V382 Cyg (Porb = 1.89 d) has a mass of 28 M⊙ (Yaşarsoy & Yakut 2013). Again, the secondary of MY Cam is hotter and heavier than both stars.
A system with more massive O-type components is DH Cep, although its orbital period is longer (2.11 days). The masses derived by Hilditch et al. (1996) are around 33M⊙ for the primary and 30M⊙ for the secondary. Again, the secondary of MY Cam is similar in mass to the primary in DH Cep, while the primary in MY Cam is even earlier and more massive. We note that DH Cep is not an eclipsing binary, and so the masses of its components were determined using other methods of analysis (Hilditch et al. 1996).
All the systems listed as comparisons are detached eclipsing binaries, while MY Cam is an early-type overcontact binary. In fact, the mean radii of both components in MY Cam are smaller than the radii derived for stars of similar (or even later) spectral types in these other binary systems. This difference is very likely due to proximity effects, such as ellipsoidal effects, high rotational velocity and tidal effects (Zahn 1977).
Based on the high effective gravities derived for both components, a second possible interpretation to the small radii of the two components could be that the stars are very close to the zero-age main sequence (ZAMS). The almost complete absence of N iii emission in their spectra could support this interpretation, though the high rotational velocity also contributes to making N iii emission undetectable. Moreover, the strength of He ii 4686 Å, which is deeper than both He ii 4542 Å and He i 4471 Å, implies that the two components of MY Cam are O Vz stars. Objects thus classified are generally close to the ZAMS, and they are believed to present weak stellar winds (Walborn 2009; Sabín-Sanjulián et al. 2014). A near-ZAMS nature for MY Cam would be in agreement with the models of Wellstein et al. (2001), who find that stars with period ≲1.2 d should be in contact at the ZAMS for mass ratios q ≳ 0.7.
The effective temperatures found for the components of MY Cam through model atmosphere fitting are hotter than expected for the observed spectral type. Morgan et al. (1955) found a combined spectral type of O6nn, while Negueruela & Marco (2008) estimated that one of the components was slightly earlier and the other slightly later than O6 V. The temperatures derived would imply approximate spectral types O4 V and O6 V, according to the calibration of Martins et al. (2005). Even though the Struve-Sahade effect (the strengthening of the secondary spectrum of the binary when it is approaching) may distort the spectral types in massive binaries (Gies et al. 1997; Bagnuolo et al. 1999), the high gravity of the stars may also contribute to their higher temperatures. It is also possible that reflection effects contribute to increasing the surface temperatures of both components.
Stars more massive than the primary of MY Cam have been found in binary systems, but these objects appear as either Of supergiants or WNha stars. The best known examples are the eclipsing binaries NGC 3603 A1 (Porb = 3.7724 d, M1 = 116 ± 31 M⊙, M2 = 89 ± 16 M⊙; Schnurr et al. 2008) and W20a (Porb = 3.69± 0.01 d, M1 = 83 ± 5 M⊙, M2 = 82± 5 M⊙; Bonanos et al. 2004), where all the components are WN6ha stars. When such massive objects start interacting, the physics of mass transfer is likely to be very complex. Conversely, MY Cam seems to simply be an extremely massive version of slow Case A binary evolution. Even though models describing the final fate of such a massive close binary do not exist, analogy with lower-mass binaries suggest that common envelope evolution will result in a stellar merger before any of the components finish H-core burning. Even if some material is lost from the system during such a process, the product of this merger will be a very massive star that will probably display unusual properties (Ivanova et al. 2013, and references therein).
Online material
Log of spectroscopic observations sorted by date.
Radial velocities and residuals for both components of MY Cam, sorted by orbital phase.
Acknowledgments
We thank Francesc Vilardell for many rewarding discussions on the use of the Wilson-Devinney code. We also thank the referee, Dirk Terrell, for many insightful comments. Based on observations collected at the Centro Astronómico Hispano Alemán (CAHA), operated jointly by the Max-Planck Institut für Astronomie and the Instituto de Astrofísica de Andalucía (CSIC). The WHT is operated on the island of La Palma by the Isaac Newton Group in the Spanish Observatorio del Roque de Los Muchachos of the Instituto de Astrofísica de Canarias. We thank Prof. Norbert Langer for comments on binary models of merger progenitors. This research is partially supported by the Spanish Ministerio de Econoía y Competitividad under grant AYA2012-39364-C02-01/02, and the European Union. This research has made use of the Simbad, Vizier and Aladin services developed at the Centre de Données Astronomiques de Strasbourg, France
References
- Andronov, N., Pinsonneault, M. H., & Terndrup, D. M. 2006, ApJ, 646, 1160 [NASA ADS] [CrossRef] [Google Scholar]
- Argelander, F. W. A. 1903, Bonner Durchmusterung des nordlichen Himmels, eds. Marcus & Weber’s Verlag, Bonn [Google Scholar]
- Bagnuolo, W. G, Gies, D. R., Riddle, R., & Penny, L. R. 1999, ApJ, 527, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Banerjee, S., Kroupa, P., & Oh, S. 2012, MNRAS, 426, 1416 [NASA ADS] [CrossRef] [Google Scholar]
- Bonanos, A. Z., Stanek, K. Z., Udalski, A., et al. 2004, ApJ, 611, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Diaz-Cordoves, J., Claret, A., & Gimenez, A. 1995, A&AS, 110, 329 [NASA ADS] [Google Scholar]
- Dufton, P. L., Dunstall, P. R., Evans, C. J., et al. 2011, ApJ, 743, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Eggleton, P. P. 2000, New Astron. Rev., 44, 111 [Google Scholar]
- Gies, D. R., Bagnuolo, W. G, & Penny, L. R. 1997, ApJ, 479, 408 [NASA ADS] [CrossRef] [Google Scholar]
- Greaves, J., & Wils, P. 2004, Inform. Bull. Variable Stars, 5517, 1 [NASA ADS] [Google Scholar]
- Harries, T. J., Hilditch, R. W., & Hill, G. 1997, MNRAS, 285, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Hilditch, R. W., Harries, T. J., & Bell, S. A. 1996, A&A, 314, 165 [NASA ADS] [Google Scholar]
- Ivanova, N., Justham, S., Chen, X., et al. 2013, A&ARv, 21, 59 [Google Scholar]
- Jiang, D., Han, Z., Yang, L., & Li, L. 2013, MNRAS, 428, 1218 [NASA ADS] [CrossRef] [Google Scholar]
- Mason, E., Diaz, M., Williams, R. E., Preston, G., & Bensby, T. 2010, A&A, 516, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massey, P. 2003, ARA&A, 41, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Mayer, P., Drechsel, H., & Lorenz, R. 2005, ApJS, 161, 171 [NASA ADS] [CrossRef] [Google Scholar]
- de Mink, S. E., Sana, H., Langer, N., Izzard, R. G., & Schneider, F. R. N. 2014, ApJ, 782, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, N. 2012, ARA&A, 50, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Linder, N., Rauw, G., Sana, H., De Becker, M., & Gosset, E. 2007, A&A, 474, 193 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lomb, N. R. 1976, Ap&SS, 39, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Martins, F., Schaerer, D., & Hillier, D. J. 2005, A&A, 436, 1049 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morgan, W. W., Code, A. D., & Whitford, A. E. 1955, ApJS, 2, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Munari, U., Henden, A., Kiyota, S., et al. 2002, A&A, 389, L51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Negueruela, I., & Marco, A. 2003, A&A, 406, 119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Negueruela, I., & Marco, A. 2008, A&A, 492, 441 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nelson, C. A., & Eggleton, P. P. 2001, ApJ, 552, 664 [NASA ADS] [CrossRef] [Google Scholar]
- Niemela, V. S., Morrell, N. I., Fernández Lajús, E., et al. 2006, MNRAS, 367, 1450 [NASA ADS] [CrossRef] [Google Scholar]
- Puls, J., Urbaneja, M. A., Venero, R., et al. 2005, A&A, 435, 669 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Qian, S.-B., Yuan, J.-Z., Liu, L., et al. 2007, MNRAS, 380, 1599 [NASA ADS] [CrossRef] [Google Scholar]
- Ribas, I., Jordi, C., Vilardell, F., et al. 2005, ApJ, 635, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, D. H., Lehar, J., & Dreher, J. W. 1987, AJ, 93, 968 [NASA ADS] [CrossRef] [Google Scholar]
- Rubin, V. C. 1965, ApJ, 142, 934 [NASA ADS] [CrossRef] [Google Scholar]
- Sana, H., de Mink, S. E., de Koter, A. et al. 2012, Science, 337, 444 [Google Scholar]
- Santolaya-Rey, A. E., Puls, J., & Herrero, A. 1997, A&A, 323, 488 [NASA ADS] [Google Scholar]
- Sabín-Sanjulián, C., Simón-Díaz, S., & Herrero, A., et al. 2014, A&A, 564, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scargle, J. D. 1982, ApJ, 263, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Schnurr, O., Casoli, J., Chené, A.-N., et al. 2008, MNRAS, 389, L38 [NASA ADS] [CrossRef] [Google Scholar]
- Simón-Díaz, S., Castro, N., Herrero, A., et al. 2011, J. Phys. Conf. Ser., 328, 012021 [NASA ADS] [CrossRef] [Google Scholar]
- Soker, N., & Kashi, A. 2013, ApJ, 764, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Sybesma, C. H. B. 1985, A&A, 142, 171 [NASA ADS] [Google Scholar]
- Terrell, D., Munari, U., Zwitter, T., & Nelson, R. H. 2003, AJ, 126, 2988 [NASA ADS] [CrossRef] [Google Scholar]
- Tylenda, R., Hajduk, M., Kamiński, T., et al. 2011, A&A, 528, A114 [Google Scholar]
- Tylenda, R., Kamiński, T., Schmidt, M., Kurtev, R., & Tomov, T. 2011, A&A, 532, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vanbeveren, D., Belkus, H., van Bever, J., & Mennekens, N. 2009, Ap&SS, 324, 271 [NASA ADS] [CrossRef] [Google Scholar]
- van Hamme, W. 1993, AJ, 106, 2096 [NASA ADS] [CrossRef] [Google Scholar]
- Vaz, L. P. R., Cunha, N. C. S., Vieira, E. F., & Myrrha, M. L. M. 1997, A&A, 327, 1094 [NASA ADS] [Google Scholar]
- von Zeipel, H. 1924, MNRAS, 84, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Walborn, N. R. 2009, in STScI Symp. Ser. 20, Massive Stars from Pop III and GRBs to the Milky Way, eds. M. Livio, & E. Villaver (Cambridge: Cambridge Univ. Press), 167 [Google Scholar]
- Walborn, N. R., & Fitzpatrick, E. L. 1990, PASP, 102, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Wellstein, S., Langer, N., & Braun, H. 2001, A&A, 369, 939 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilson, R. E. 1990, ApJ, 356, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, R. E., & Devinney, E. J. 1971, ApJ, 166, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, R. E., & Biermann, P. 1976, A&A, 48, 349 [NASA ADS] [Google Scholar]
- Woźniak, P. R., Vestrand, W. T., Akerlof, C. W., et al. 2004, AJ, 127, 2436 [NASA ADS] [CrossRef] [Google Scholar]
- Yaşarsoy, B., & Yakut, K. 2013, AJ, 145, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Zahn, J.-P. 1977, A&A, 57, 383 [NASA ADS] [Google Scholar]
- Zucker, S., & Mazeh, T. 1994, ApJ, 420, 806 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
All Tables
Stellar parameters derived from the combined analysis of the radial velocity and photometric light curve.
Radial velocities and residuals for both components of MY Cam, sorted by orbital phase.
All Figures
 |
Fig. 1 Photometric light curve, showing the amplitude of the modulation. |
| In the text | |
 |
Fig. 2 Some representative lines in the spectrum of MY Cam and some model line fits. Solid line: Teff1 = 42 000 K, log g1 = 3.9; Teff2 = 39 000 K, log g2 = 4.1. Dashed line: Teff1 = 40 000 K, log g1 = 3.7; Teff2 = 38 000 K, log g2 = 3.9. Dashed-dotted line: Teff1 = 44 000 K, log g1 = 4.1; Teff2 = 41 000 K, log g2 = 4.3. |
| In the text | |
 |
Fig. 3 Results of the Lomb-Scargle periodogram for the radial velocities. The inset shows the result of applying the clean algorithm. |
| In the text | |
 |
Fig. 4 Light curve model fitted to the observational data. Residuals are displayed in the top panel. |
| In the text | |
 |
Fig. 5 Radial velocity curves fitted to the observational data and displayed against orbital phase (black line: primary star; red line: secondary star) fitted to the observational data. The dashed line corresponds to the systemic velocity. The residuals are displayed in the top panel. |
| In the text | |
 |
Fig. 6 Representative drawing of MY Cam to scale at quadrature phase, created with the PHOEBE 2.0-alpha code via the Python interface. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


