| Issue |
A&A
Volume 571, November 2014
|
|
|---|---|---|
| Article Number | A64 | |
| Number of page(s) | 12 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201424331 | |
| Published online | 10 November 2014 | |
Dust environment and dynamical history of a sample of short-period comets
II. 81P/Wild 2 and 103P/Hartley 2
1 Instituto de Astrofísica de Andalucía (CSIC), Glorieta de la Astronomía s/n, 18008 Granada, Spain
e-mail: pozuelos@iaa.es
2 Amateur Association Cometas-Obs, Spain
3 Universidad de Granada-Phd Program in Physics and Mathematics (FisyMat), 18071 Granada, Spain
Received: 3 June 2014
Accepted: 5 August 2014
Aims. This paper is a continuation of the first paper in this series, where we presented an extended study of the dust environment of a sample of short-period comets and their dynamical history. On this occasion, we focus on comets 81P/Wild 2 and 103P/Hartley 2, which are of special interest as targets of the spacecraft missions Stardust and EPOXI.
Methods. As in the previous study, we used two sets of observational data: a set of images, acquired at Sierra Nevada and Lulin observatories, and the Afρ data as a function of the heliocentric distance provided by the amateur astronomical association Cometas-Obs. The dust environment of comets (dust loss rate, ejection velocities, and size distribution of the particles) was derived from our Monte Carlo dust tail code. To determine their dynamical history we used the numerical integrator Mercury 6.2 to ascertain the time spent by these objects in the Jupiter family Comet region.
Results. From the dust analysis, we conclude that both 81P/Wild 2 and 103P/Hartley 2 are dusty comets, with an annual dust production rate of 2.8 × 109 kg yr-1 and (0.4−1.5) × 109 kg yr-1, respectively. From the dynamical analysis, we determined their time spent in the Jupiter family Comet region as ~40 yr in the case of 81P/Wild 2 and ~1000 yr for comet 103P/Hartley 2. These results imply that 81P/Wild 2 is the youngest and the most active comet of the eleven short-period comets studied so far, which tends to favor the correlation between the time spent in JFCs region and the comet activity previously discussed.
Key words: methods: observational / methods: numerical / comets: individual: 81P/Wild 2 / comets: individual: 103P/Hartley 2 / comets: general
© ESO, 2014
1. Introduction
Cometary science has been revolutionized by in situ missions over the last several decades. It will continue to develop and transform with the arrival of Rosetta Spacecraft at Comet 67P/Churyumov-Gerasimenko. Unfortunately, only a few comets have been studied by spacecraft missions. In this paper we focus on comets 81P/Wild 2 and 103P/Hartley 2. Both comets have been the subject of extensive studies in past years and were the targets of the Stardust and EPOXI missions.
Comet nucleus 81P/Wild 2 (hereafter 81P) has been determined as a triaxial ellipsoid having radii of (1.65 × 2.00 × 2.75) ± 0.05 km by Duxbury et al. (2004). The surface shows an ancient terrain composed of cohesive porous materials, probably as a consequence of a mixture of fine dust and volatiles when the comet was formed. It also shows the presence of large-impact craters, implying that the cohesive nature of the surface is old, since it was present before the comet entered the inner part of the solar system (Brownlee et al. 2004). Sekanina (2003) established its current orbit as a consequence of a close encounter with Jupiter in 1974, when its perihelion and aphelion distances decreased from 5.0 to 1.5 AU and from 24.7 to 5.2 AU respectively. Comet 103P/Hartley 2 (hereafter 103P), has a small nucleus with a bilobed shape and a diameter in the range of 0.69 to 2.33 km (A’Hearn et al. 2011). It is considered to be a hyperactive comet, with large-grain production with velocities of several to tens of meters per second (Harmon et al. 2011; Kelley et al. 2013; Boissier et al. 2014). Its orbit period is 6.47 yr, with current perihelion and aphelion distances of q = 1.05 AU and Q = 5.88 AU.
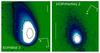 |
Fig. 1 Representative images of the observations obtained using a CCD camera at 1.52 m telescope at the Observatorio de Sierra Nevada in Granada, Spain. Right panel corresponds to 81P/Wild 2 on April 9, 2010. Isophote levels in solar disk units (SDU) are: 0.25 × 10-13, 0.77 × 10-13, 2.20 × 10-13. Left panel corresponds with comet 103P/Hartley 2 on August 4, 2010. Isophote levels are: 0.20 × 10-13, 0.40 × 10-13, 1.10 × 10-13. In both cases the directions of celestial north and east are given. The vertical bars correspond to 2 × 104 km in the sky. |
In this paper we study these comets in the same way as in Pozuelos et al. (2014, hereafter Paper I). Thus, we use our Monte Carlo dust tail code (e.g., Moreno 2009), which allows us to obtain the dust parameters: i.e., dust loss rate, ejection velocities and the size distribution of particles, and the emission pattern. For anisotropic emission, we introduce active area regions, along with the rotational parameters of the nucleus: rotation period and orientation of the spin axis defined by the angles I (obliquity) and φ (argument of the subsolar meridian at perihelion) (e.g., Sekanina 1981). In the second part of our study we analyze the dynamical history of these comets. To perform this task we use the numerical integrator developed by Chambers (1999), which has been used before by other authors, such as Hsieh et al. (2012a,b) and Lacerda (2013). From this analysis we studied the last 15 Myr of these comets, and we obtained the time spent by them in the region of the Jupiter family Comets (JFCs). Both dust environment and dynamical studies allowed us to determine how active these comets are as a function of the time spent as JFCs. We based our studies on two different kinds of observational data: direct imaging in Johnson R filter from ground-based telescopes, most of them obtained at the 1.52-m Sierra Nevada Observatory (Spain), and some of them at the 1-m telescope of Lulin Observatory (Taiwan) (Lin et al. 2012). The second block of observational data corresponds to Afρ measurements provided by the amateur astronomical association Cometas-Obs. These observations almost completely cover the orbital path when the comets are active.
The observations and the data reduction are explained in Sect. 2; the model is described in Sect. 3 ; the dust analysis, and comparison with others currently available are given in Sect. 4; the dynamical study appears in Sect. 5; and finally the summary and conclusions are given in Sect. 6.
2. Observations and data reduction
Log of the observations.
Most of the images of 81P and 103P were taken at the 1.52 m telescope at the Sierra Nevada Observatory (OSN) in Granada, Spain. We used a 1024 × 1024 pixel CCD camera with a R Johnson filter. For comet 81P, we also used observations acquired at the 1 m telescope at Lulin Observatory in Taiwan, using a 1340 × 1300 pixel CCD with an Ashi R broadband filter. Table 1 shows the log of the observations. Additional details for the observations at Lulin Observatory are given in Lin et al. (2012) and the references therein. Several images of the comets were taken in order to improve the signal-to-noise ratio. A median stack was obtained from available images. The individual images from each night were bias-subtracted and flat-fielded using standard techniques. To perform the flux calibration, we used the USNO-B1.0 star catalog (Monet et al. 2003), so that each image we acquired was calibrated to mag arcsec-2 and then converted to solar disk units (SDU). We rotated each image to the (N, M) system (Finson & Probstein 1968), where M is the projected Sun-comet radius vector, and N is perpendicular to M in the opposite half plane with respect to the nucleus velocity vector. The images were finally rebinned so that the physical dimensions were small enough to be analyzed with our Monte Carlo dust tail code. Representative reduced images of 81P and 103P are displayed in Fig. 1.
The second block of our observational data are the Afρ (A’Hearn et al. 1984) measurements carried out by the amateur astronomical association Cometas-Obs1. These observations cover most of the orbital arc where the comets are active. They are given as a function of the heliocentric distance and are always referred to as an aperture of ρ = 104 km projected on the sky at each observation date. The calibration was made using the star catalogs CMC-14 and USNO A2.0. To make a direct comparison, we computed the Afρ with ρ = 104 km from the OSN and Lulin image observations (see Table 1).
It is important to note that some of the observational data correspond to times where the phase angle is close to zero degree. We corrected for the backscattering enhancement (Kolokolova et al. 2004) by the expression:
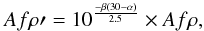 (1)where β is the linear phase coefficient, for which we assumed β = 0.03 mag deg-1, based on the studies by Meech & Jewitt (1987) for several comets. The correction is applied when α ≤ 30°. More details are given in Sect. 3 of Paper I. This backscattering effect becomes especially important for comet 81P. In Fig. 2 we observe a clear increase in Afρ for small phase angles and see how these data are corrected after application of Eq. (1). Despite this clear correlation between Afρ and α, there are authors who attributed this enhancement to an outburst experienced by the comet after perihelion passage. We discuss this in Sect. 4.
(1)where β is the linear phase coefficient, for which we assumed β = 0.03 mag deg-1, based on the studies by Meech & Jewitt (1987) for several comets. The correction is applied when α ≤ 30°. More details are given in Sect. 3 of Paper I. This backscattering effect becomes especially important for comet 81P. In Fig. 2 we observe a clear increase in Afρ for small phase angles and see how these data are corrected after application of Eq. (1). Despite this clear correlation between Afρ and α, there are authors who attributed this enhancement to an outburst experienced by the comet after perihelion passage. We discuss this in Sect. 4.
3. Monte Carlo dust tail model
As in Paper I, to fit the observational data described in the previous section, we used our Monte Carlo dust tail code (see e.g., Moreno 2009). This code allowed us to generate synthetic images that can be directly compared with the observations, from which we can derive the synthetic Afρ curves. This code was successfully used in previous works to determine the dust properties of some short-period comets such as 29P/Schwassmann-Wachmann 1 and 22P/Kopff (Moreno 2009; Moreno et al. 2012), as well as some Main-belt comets: P/2010 R2 (La Sagra), P/2012 T1 (PANSTARRS), and P/2013 P5 (PANSTARRS; Moreno et al. 2011, 2013, 2014). This code is also called the Granada model in Fulle et al. (2010) where the authors describe the dust environment of the Rosetta target 67P/Churyumov-Gerasimenko. The model computes the trajectory of a large number of particles when they are ejected from the nucleus surface and are submitted to the solar gravity and radiation pressure force, describing a Keplerian orbit around the Sun. Considered to be spherically shaped, the particles are characterized by the β parameter, which is the ratio of the radiation pressure force to the gravity force. For those particles β = CprQpr/ (ρdd), where Cpr = 1.19 × 10-3 kg m-2, Qpr is the radiation pressure coefficient, ρ the particle density, assumed as ρ = 1000 kg m-3, and d the particle diameter.
To compute the geometric albedo pv and Qpr, we used the Mie theory to describe the interaction of the electromagnetic field with spherical particles, assuming a refractive index of m = 1.88 + 0.71i that is typical of carbonaceous spheres at red wavelengths (Edoh 1983). This gives pv = 0.04 for r ≥ 1 μm at most of the phase angles, and Qpr ~ 1 (Burns et al. 1979).
In the model, the trajectories and positions of the particles in the N, M plane and their contribution to the tail brightness are computed. The free parameters dust loss rate, ejection velocities, size distribution of the particles, and the dust ejection pattern, which can be either isotropic or anisotropic. In cases where an anisotropic outgassing is obtained, the emission is parametrized by a rotating nucleus with active areas on the surface. The rotation state is parametrized by two angles: the obliquity I of the orbit plane to the equator and the argument φ of the subsolar meridian at perihelion (Sekanina 1981). The size distribution of the particles is defined by the maximum and minimum sizes rmax,rmin, and the index δ of the power law function n(r) ∝ rδ, which describes the size distribution. For simplicity rmin has been set to 1 μm in all calculations. For large sets of comets, δ has been concluded to be in the range of −4.2 and −3.0 (e.g., Jockers 1997). The terminal velocity is parametrized as v(t,β) = v1(t) × βγ where v1(t) is determined during the modeling process, and the index γ is a constant assumed as γ = 1/2, which is the value commonly accepted for hydrodynamical drag from sublimating ices (e.g., Moreno et al. 2011; Licandro et al. 2013). Owing to the large number of parameters that are used in the model, the solution is not unique and it is possible to find an alternative set of parameters to fit the observational data. However, the range of possible solutions is considerably reduced when the available observations cover most of the orbital arc of the comets. For this reason, we combined direct imaging observations and a large number of Afρ measurements given by different observers in different locations, such as those provided by the association Cometas-Obs.
 |
Fig. 2 81P/Wild 2 Afρ measurements by Cometas-Obs. Upper panel: original data and phase angle as a function of heliocentric distance. Lower panel: original Afρ data and corrected Afρ data by Eq. (1) (see text). |
4. Dust analysis
In Paper I, we determined three categories according to the amount of dust emitted: (i) weakly active: 115P, 157P and Rinner with an annual production rate of Td ≤ 1 × 108 kg yr-1; (ii) moderately active: 30P, 123P, and 185P where the annual production rate is Td = 1 − 3 × 108 kg yr-1; and (iii) highly active: 78P, 22P, and 118P with an annual production rate of Td ≥ 8 × 108 kg yr-1. For three of those targets, an anisotropic ejection pattern was obtained: 30P, 115P, and 157P. The general method used to fit the observations and obtain the dust parameters is a trial-and-error procedure, starting with the simplest scenario, where we consider an isotropic ejection outgassing model, with rmin = 1μm, rmax = 1 cm, δ = − 3.5, and both v1(t) and dM/ dt monotonically symmetric evolution with respect to perihelion. Once we reproduced the tail intensity in the optocenter, we started to vary the parameters and their dependence on the heliocentric distance to obtain the best possible fit. When the observations cannot be reproduced by isotropic emission, we set active areas on the surfaces, i.e., an anisotropic emission pattern, and repeat different combinations of the dust parameters until an acceptable result is obtained.
4.1. 81P/Wild 2
The comet 81P has an effective nucleus of RN = 2.00 km (Sekanina et al. 2004) and a bulk density of ρ = 600 kg m-3 reported by Davidsson & Gutierrez (2004). Our observational data for comet 81P are six direct images post-perihelion passage at OSN 1.52 m telescope and ~300Afρ measurements by Cometas-Obs, which cover from ~−2.15 to ~2.45 AU. In addition, we benefited from observations carried out in the 1 m Lulin telescope by Z.-Y. Lin. From these observations we selected one pre-perihelion image (January 16.81, 2010) and 5 Afρ measurements pre- and post-perihelion (see Table 1). The complete set of Afρ data as a function of the heliocentric distance is shown in Fig. 4, where all the data have been corrected from backscattering enhancement using Eq. (1).
We observed two enhancements in the measurements that were not related to low α values. We considered them as small outbursts suffered by the comet. The first one occurred on October 29 (2009), when the comet was at rh ~ 1.949 AU inbound, where the maximum value of Afρ was ~782 cm. To our knowledge, this outburst has not been reported previously. In our dust characterization we concluded that the event duration was ~40 h, and the comet emitted mob.I ~ 9.2 × 108 kg of dust, reaching a peak dust production rate of 1190 kg s-1, returning to normal activity on November 13. However we only have a limited number of sample observations for this period, so this result must be read with caution. The second outburst was first identified by Bertini et al. (2012). This second event took place post-perihelion, August 5 (2010), at ~2.215 AU outbound, with a maximum value of Afρ ~ 380 cm. Our dust analysis estimated this event as three times less intense than the first one, mob.II ~ 3.0 × 108 kg with a duration of ~55 h and a peak dust production rate of 450 kg s-1. During both outbursts, I and II, the maximum particle size was 3 cm.
Overall, without taking the outburst events into account, we concluded that the comet reached its maximum level of activity at rh ~ 1.64 AU inbound, that is ~40 days before perihelion, with a dust production rate of 900 kg s-1. The comet emission pattern is found to be anisotropic at 35%, with active areas located on the surface between +45° to −30°. From the anisotropic model we derived the rotational angles as I = (50 ± 5)° and φ = (300 ± 20)°. Figure 3 we display the evolution of the dust parameters as a function of heliocentric distance, and in Figs. 4 and 5 we present the comparison of the model with the observational data, which are remarkably similar. From the dust analysis, we determined that the total dust production rate of 81P was 1.1 × 1010 kg during the 3.8 yr covered by the study, that is, an annual dust production rate of Td = 2.8 × 109 kg yr-1 and an average dust mass lost rate of 87.5 kg s-1. The contribution to the annual interplanetary dust replacement, established by Grun et al. (1985) as 2.9 × 1011 kg yr-1, is ~0.96%.
4.2. 103P/Hartley 2
 |
Fig. 3 Best-fit modeled parameters to the dust environment of 81P/Wild 2 Afρ data and images (Figs. 4 and 5). All parameters are given as a function of the heliocentric distance. From top to bottom and left to right the panels are a) dust production rate [kg s-1]; b) ejection velocities of 1-cm particles [m s-1]; c) maximum size of particles [cm]; d) power index of the size distribution, δ. The solid red line corresponds to pre-perihelion and the dashed blue line to post-perihelion. |
 |
Fig. 4 Comparison of observed and modeled Afρ data as a function of heliocentric distance. Parameter Afρ versus heliocentric distance. The Afρ measurements have been corrected using Eq. (1). Black dots: Afρ data from Cometas-Obs. Green triangles: Afρ data derived from OSN images. Blue diamonds: Afρ data from Lulin observatory images. The observations labeled (a) to (g) correspond to the Afρ derived from images (a) to (g) in Fig. 5. The outbursts I (inbound) and II (outbound) described in the text are marked with arrows. All the Afρ values refer to ρ = 104 km. |
The observational data of comet 103P consist of four direct images obtained at the 1.52 m OSN telescope, three pre-perihelion and one post-perihelion (see Table 1), and ~430 Afρ measurements carried out by Cometas-Obs, covering pre- and post-perihelion branches in the orbit, from ~−2.00 to ~2.60 AU. The observations have been corrected by Eq. (1) for the data having α ≤ 30° as in the case of 81P, but in this case there is not a strong dependence between α and any enhancements in the measurements. This comet has been subjected to an extensive study as a consequence of its encounter with the Deep Impact spacecraft in the framework of the EPOXI mission (see e.g., A’Hearn et al. 2011; Meech et al. 2011). For most of those studies it was considered as a hyperactive comet with an emission of large particles (see e.g., Harmon et al. 2011; Kelley et al. 2013; Boissier et al. 2014).The mean radius (radius of a sphere of equivalent volume) is calculated by Thomas et al. (2013b) as 0.580 ± 0.018 km, but the bulk density is not determined well, since it is in the range of ρ = 140 − 520 kg m-3 (A’Hearn et al. 2011; Richardson & Bowling 2014; Thomas et al. 2013b). Consequently, the escape velocity of particles is in the range of vesc = 3.6 − 6.9 cm s-1. Thus, for our purposes, we assume the maximum value of the bulk density as ρ = 520 kg m-3, which corresponds to the upper limit of escape velocity. To perform the dust characterization we introduce two models, which agree with the observations. The first one is based on previous knowledge, i.e., large particle emission and high dust production rate (hyperactivity).The second one tries to reproduce the observations without the emission of large particles and with moderate dust production rate.
Model I or hyperactive model. In this case we consider the results derived from the EPOXI mission and other authors, such as Harmon et al. (2011), where a large size of particles were obtained, with sizes in the range of ~20 cm and larger. To try to reproduce these results, we fixed the maximum size of particles to r = 20 cm around perihelion, where the comet reaches its maximum dust production rate. This model has a gentle increase in the dust parameters toward perihelion, where a strong increase occurs, peaking at ~1.20 AU post-perihelion. This behavior is also seen in the Afρ measurements (Fig. 8). The maximum dust production rate is found to be 600 kg s-1, and the ejection velocity of 1-cm size particles reaches ~14 m s-1. The total dust mass ejected during the 3.79 yr span in this study is 5.9 × 109 kg, so the annual dust production rate is Td = 1.5 × 109 kg yr-1. This model represents an annual contribution of 0.51% to interplanetary dust. Figure 6 we show the evolution of the dust parameters as a function of the heliocentric distance, and in Figs. 8 and 9 we show the comparison between the available observations and the model.
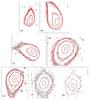 |
Fig. 5 Isophote field comparison between observations and model. The black contours correspond to the observations and the red ones to the model. The dates and the SDU levels are a) Jan. 16.81, 2010. Levels are 0.80 × 10-13, 2.00 × 10-13, and 5.00 × 10-13 SDU; b) Apr. 9.06, 2010. Levels are 0.25 × 10-13, 0.77 × 10-13, and 2.20 × 10-13 SDU; c) Apr. 21.06, 2010. Levels are 0.25 × 10-13, 0.77 × 10-13, and 2.20 × 10-13 SDU; d) May 15.96, 2010. Levels are 0.10 × 10-13, 0.25 × 10-13, 0.77 × 10-13, and 2.20 × 10-13 SDU; e) Jun. 3.93, 2010. Levels are 0.10 × 10-13, 0.25 × 10-13, 0.77 × 10-13, and 2.20 × 10-13 SDU; f) Jul. 6.89, 2010. Levels are 0.08 × 10-13, 0.25 × 10-13, and 0.77 × 10-13 SDU; g) Aug. 21.85, 2010. Levels are 0.25 × 10-13, 0.77 × 10-13, and 2.20 × 10-13 SDU. See log of the observations in Table 1. |
Model II or standard model. In this case, the maximum particle size was not forced to 20 cm, but is a free parameter that can have any possible value. It reaches 3 cm at perihelion. As in Model I the peak of the dust parameter occurs after perihelion at ~1.20 AU, where the dust production rate is 160 kg s-1, and the ejection velocity for 1 cm particles is ~7 m s-1. In this case the total dust emitted by the comet was 1.7 × 109 kg, and the annual dust production rate was Td = 4.5 × 108 kg yr-1. The contribution to the interplanetary dust per year represents 0.15% of the total. The evolution along the heliocentric distance of the dust parameters is displayed in Fig. 7, and the comparison of the observations to the model are shown in Figs. 8 and 10.
In both cases, Models I and II, the emissions have been found to be isotropic.
4.3. Discussion
The dust characterization of 81P shows the peak of activity around ~40 days pre-perihelion. In previous studies of this comet during the perihelion passages in 1990, 1997, and 2004, the comet showed the peak of activity a few weeks pre-perihelion due to a seasonal effect. Sekanina (2003) studied this behavior when the comet activity reached its maximum value three weeks before perihelion with a post-perihelion fading. To explain this behavior, the author proposed that the spin axis is not quite normal to the orbital plane. In addition, Farnham & Schleicher (2005) attribute this conduct to a strong seasonal effect with at least one source region moving from summer to winter speedily. Analogous results of this behavior have also been obtained in independent studies by other authors (e.g., Hanner & Hayward 2003; Hadamcik & Levasseur-Regourd 2009).
In the analysis carried out by Bertini et al. (2012), the authors identified an enhancement of Afρ measurements ~60 days post-perihelion. The authors also noticed that during that period there was a minimum phase angle, and they corrected the effect by reducing all A(α)fρ values to α = 0°, and using A(0)fρ as reference. After the authors applied the correction, the enhancement on Afρ measurements was still evident, which led them to consider it as an outburst event. In our case, Cometas-Obs also reported this enhancement in the Afρ measurements, but in contrast to Bertini et al. (2012), the enhancement completely disappeared after correction (using Eq. (1), see Fig. 2), so we concluded that the comet started to fade after the pre-perihelion peak.
During the Stardust flyby on 2 January 2004 (at rh = 1.855 AU post-perihelion), Green et al. (2004) used the Dust Flux Monitor Instrument (DFMI) to obtain a cumulative mass distribution index ξ (where the number of particles of mass m or larger is given by the power law N(m) ∝ m− ξ) in the coma ranges from 0.3 to 1.1, where ξ = 0.75 ± 0.05 was found to be the best fit for the data. From this cumulative mass distribution index we can conclude that the power index of the differential size distribution is δ = − 3ξ − 1. Thus, δ is in the range of −1.9 to −4.3, with the best match to the data being δ = − 3.25 ± 1.25. This value perfectly agrees with the one derived from our model at the same heliocentric distance.
The rotational parameters derived from the model agree with the ones proposed by Sekanina et al. (2004), who concluded that I = 55° and φ = 150°. The equivalent solution for φ is 180° + φ = 330, Sekanina (1981), which is close of our value. Belton et al. (2013a) established a relationship between mini-outbursts suffered by the comet 9P/Temple 1 and pits (large population of quasi-circular depression) on the surface of the comet, reported by the encounter of Stardust-NExT spacecraft and Deep Impact mission (see e.g., Veverka et al. 2013; A’Hearn et al. 2005; Thomas et al. 2013a). The authors argue that ~96% of these features were due to mini-outbursts, while ~4% had their origin in other processes, such as collisions with asteroidal material and cryo-volcanism. From this relationship, the authors propose that the pits observed on the surface of 81P are also due to outburst events. In our model, we have identified two outbursts, one inbound and the other outbound, both more intense than the mini-outbursts studied by Belton et al. (2013a), which were in the range of 6 − 30 × 104 kg. However, Brownlee et al. (2004), Kirk et al. (2005) and Basilevsky & Keller (2006, 2007) considered the origin of pits in the context of impact phenomena. Therefore, the relationship between outbursts and pits are not clear in the case of 81P, and more studies would be desirable to determine how often the outbursts occur in this comet, and if they are the cause of pits on the surface.
The comet 81P has been found to be the most active one in the whole sample of short-period comets studied in Paper I and in this paper, with an annual dust production rate of Td = 2.8 × 109 kg yr-1.
 |
Fig. 6 As Fig. 3 but for comet 103P/Hartley 2. Corresponding to Model I. This model fits the observations displayed in Figs. 9 and 8, where it is represented by the red line. |
 |
Fig. 7 As in Fig. 3 but for comet 103P/Hartley 2. Corresponding to Model II. This model fits the observations displayed in Figs. 10 and 8 where it is represented by the blue line. |
Our study of the 103P offers two solutions to fitting the observation: Model I, where the comet is found to be hyperactive, and Model II where we proposed a standard dust behavior. In Model I we imposed large size particles (up to rmax = 20 cm) and we concluded that the annual dust production rate is Td = 1.5 × 109 kg yr-1, with a dust production rate of 300−550 kg s-1 during perihelion and Deep Impact spacecraft closet approach. In contrast, in Model II our solution also agrees with the observations but with a maximum particle size of rmax = 3 cm, where the annual dust production rate is Td = 4.5 × 108 kg yr-1. During the perihelion and Deep Impact encounter, the dust mass loss rate was in the range of 120−140 kg s-1. Thus, the range of the dust production rate obtained by our study is 120−550 kg s-1 during perihelion passage and spacecraft encounter. Harmon et al. (2011) established a value of 300 kg s-1 roughly in the same period, while Boissier et al. (2014) inferred a much wider range of 830−2700 kg s-1 based on their two models under various assumptions, such as the dust composition, size distribution, and grain velocities. The authors attributed the uncertainty of their values to the uncertainties in the size distribution cut-off and kinematics. The total dust emitted by 103P for the whole orbit during 2010 perihelion passage, has been found to be in the range of 1 − 4 × 109 kg in previous studies (see e.g., Lisse et al. 2009; Bauer et al. 2011; Thomas et al. 2013b; Knight & Schleicher 2013). These values agree with the range of 1.7 − 5.9 × 109 kg derived from our models, which cover most of the time in which the comet is active.
The very complex rotational state of the nucleus was studied in detail in Belton et al. (2013b). In Belton (2013) the authors described the active areas migration over the lobes of the nucleus following the Sun; thus, the strong activity shown by this comet is correlated with the rotation of the nucleus. Two faint dust jets seem to have had their origin in those active areas (see e.g., Lara et al. 2011; Mueller et al. 2013; Tozzi et al. 2013). Thanks to this correlation between active areas and rotation of the nucleus, the comet has an isotropic pattern of time-averaged outgassing from its nuclear surface. This fact led Groussin et al. (2004), Lisse et al. (2009), and Knight & Schleicher (2013) to report the comet as a highly active nucleus with ~100% of the surface area active. These results agree with the isotropic dust emission pattern derived from our Models I and II.
 |
Fig. 8 Comparison between observational data and the models proposed for the comet 103P/Hartley 2. Afρ measurements have been corrected using Eq. (1). Black dots are the data from Cometas-Obs, and green triangles marked from (a) to (d) are the observations at OSN telescope. The red line corresponds to Model I or Hyperactive model, which fits the observations in Fig. 9. The blue line is the Model II or Standard model, and its fits with observations can be checked in Fig. 10. All the Afρ values are referred to ρ = 104 km. |
Another important point is the nature of the large chunks, observed during the EPOXI flyby and inferred from radar observations (see e.g., A’Hearn et al. 2011; Harmon et al. 2011), and the real size of them. Knight & Schleicher (2013) deduced that those chunks are large dust grains (up to 20 cm) because of the lack of interaction between the radiation pressure and the dust jets observed. However, Kelley et al. (2013) propose two models: (1) the icy case, where the particles have an albedo of 0.67, ρ = 0.1 g cm-3, and the size of particles are in the range of 1−20 cm; (2) the dusty case, with an albedo of 0.049, ρ = 0.3 g cm-3, and the particle sizes in the range of 10−210 cm. The authors concluded that the icy model is more likely. However, these models may not reflect the true nature of the particles, although they did produce useful information on the limits of particle size and the fact that a coma of both icy and dusty particles is possible.
To explain the relatively short life times of those large chunks, Tozzi et al. (2013) established that they need to have some impurities such as silicates embedded in them, and inferred the presence of grains which might have lot of organics. Finally, Boissier et al. (2014) present two models based on crystalline/amorphous (of ratio of 1) silicate particles with a grain density of ρ = 0.5 g cm-3, where the maximum size of the particles was obtained depending on the escaping gas: (1) amax = 1 m, to H2O; (2) amax = 2.4 m, to CO2. Therefore, the true nature and the size of the large chunks observed are not completely accurate and are still under study. The presence of the large particles in the coma of this comet was already inferred in Epifani et al. (2001) during the observations of 1 January 1998 using the ISOCAM. The authors deduced that the dust production rate at perihelion ranged from 10 kg s-1 to 100 kg s-1. The peak of the dust production rate and the ejection velocities of the particles occurred two weeks after perihelion, with a rapid decrease just before it. However, the authors attributed this behavior to the instability of the model outputs around perihelion, showing unrealistically large variations in the power index of the size distribution. The best fitting power law was found to be δ = − 3.2 ± 0.1 by the authors. In the 2010 perihelion passage, the power index of the size distribution derived from our models take values from −3.45 to −3.25, which are bit higher than the values assumed/derived by other authors, such as Bauer et al. (2011) of −4.0, Kelley et al. (2013) in the range of −6.6 to −4.7, and Boissier et al. (2014) of −3.5.
It is important to note that in general, when the power index is −3 <δ< − 4, the dust mass depends on the largest particles, while the brightness in the tail depends on the smallest grains, so that it is always difficult to determine the large particle population in the tail (Fulle 2004). For this reason, the mass found in the models should be considered as lower limits of the total dust emitted (see Paper I). In the case of 103P, Model I is closer to a real solution than Model II, which represents a lower limit in the dust production.
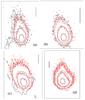 |
Fig. 9 Isophote field comparison between observations and Model I or Hyperactive model. The black contours correspond to the observations and the red ones to the model. The dates and the SDU levels are a) Jul. 12.14, 2010. Levels are 0.30 × 10-14, 0.55 × 10-14, and 1.20 × 10-14 SDU; b) Aug. 4.11, 2010. Levels are 0.20 × 10-13, 0.40 × 10-13, and 1.10 × 10-13 SDU; c) Sep. 6.04, 2010. Levels are 0.15 × 10-13, 0.40 × 10-13, and 1.10 × 10-13 SDU; d) Nov. 3.16, 2010. Levels are 0.55 × 10-13, 1.25 × 10-13, 4.00 × 10-13 SDU. See log of the observations in Table 1. |
As a result of the particle velocities obtained in Paper I, the characterization of 22P/Kopff in Moreno et al. (2012), the result presented by Fulle et al. (2010) to comet 67P/Churyumov-Gerasimenko, and this study, we found a definite relationship between the ejection velocities and the heliocentric distance. For example, for r = 1 cm particles, we found a power law given by 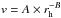 , where A and B parameters were given by A = 7.067 mB+1/s and B = 1.998. Thus, the ejection velocity law is roughly inversely proportional to ~
, where A and B parameters were given by A = 7.067 mB+1/s and B = 1.998. Thus, the ejection velocity law is roughly inversely proportional to ~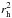 . This agrees with the results from hydrodynamical inner coma models by Crifo & Rodionov (1997) and disagrees with the
. This agrees with the results from hydrodynamical inner coma models by Crifo & Rodionov (1997) and disagrees with the 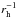 dependence by Whipple (1951). The result of the fit is displayed in Fig. 11, where in addition to the 11 comets studied between Paper I and this study, we add the ejection velocity of 1 cm particles of the comet 67P/Churyumov-Gerasimenko, obtained by Fulle et al. (2010). In that figure, one can see that 81P at ~2.0 AU and 22P at rh> 2.5 AU have deviated from this trend. In the case of 81P, this behavior it is due to the outburst I characterized in Sect. 4.1, and for 22P it comes from the strong dust ejection anisotropies at the large heliocentric distances identified by Moreno et al. (2012).
dependence by Whipple (1951). The result of the fit is displayed in Fig. 11, where in addition to the 11 comets studied between Paper I and this study, we add the ejection velocity of 1 cm particles of the comet 67P/Churyumov-Gerasimenko, obtained by Fulle et al. (2010). In that figure, one can see that 81P at ~2.0 AU and 22P at rh> 2.5 AU have deviated from this trend. In the case of 81P, this behavior it is due to the outburst I characterized in Sect. 4.1, and for 22P it comes from the strong dust ejection anisotropies at the large heliocentric distances identified by Moreno et al. (2012).
5. Dynamical history analysis
To obtain the dynamical evolution of the two comets studied in this paper, we followed the same procedure as described in Paper I, which is based on previous studies by Levison & Duncan (1994). We used version 6.2 of Mercury’s numerical integrator developed by Chambers (1999). We generated 99 clones having 2σ dispersion in three of the orbital elements: semimajor axis, a, inclination, i, and eccentricity, e, where σ is the uncertainty in the corresponding parameter as given in the JPL Horizons online solar system data2. The orbital parameters and the σ values are given in Table A.1. The 99 clones plus the real object give a total of 100 massless particles to perform the statistical study. The Sun and the eight planets are considered to be massive bodies. To control the close encounters of the massless particles with the massive bodies, we used the hybrid algorithm that combines a symplectic algorithm with a Burlisch-Stoer integrator (see Chambers 1999). The initial time step was eight days, and the clones were removed when their heliocentric distance was >1000 AU.
 |
Fig. 11 Ejection velocities of 1 cm particles versus the heliocentric distance for all comets in the sample plus the result obtained by Fulle et al. (2010) in the study of comet 67P/Churyumov-Gerasimenko. The complete set of comets are: 22P/Kopff, 30P/Reinmuth 1, 67P/Churyumov-Gerasimenko, 78P/Gehrels 2, 81P/Wild 2, 103P/Hartley 2 (Model I and Model II), 115P/Maury, 118P/Shoemaker-Levy 4, 123P/West-Hartley, 157P/Tritton, 185P/Petriew, and P/2011 W2 (Rinner). The color code is given in the legend. The solid black line is the best fit found for that distribution: |
We performed backward integrations of 15 Myr. The non-gravitational forces were neglected according to the same arguments posed by Lacerda (2013), where the change rate of the semimajor axis, da/ dt, is produced by a non-gravitational acceleration, T, created by single sublimation jet tangential to the comet’s orbit and affecting its motion during the life time of sublimation, tsub: ![\begin{eqnarray} &&\frac{{\rm d}a}{{\rm d}t}=\frac{2Va^{2}T}{GM_{\odot}} \\[-1mm] &&T=\frac{{\rm d}M_{\rm d}}{{\rm d}t}\times \frac{v_{\rm d}}{m_{\rm nuc}} \\[-1mm] &&t_{\rm sub}=m_{\rm nuc}\times \left(\frac{{\rm d}M_{\rm d}}{{\rm d}t}\right)^{-1}\cdot \end{eqnarray}](/articles/aa/full_html/2014/11/aa24331-14/aa24331-14-eq165.png) Therefore, the total deviation of the semimajor axis D would be
Therefore, the total deviation of the semimajor axis D would be 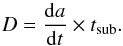 (5)In these equations, dMd/ dt is the dust mass loss rate, V the orbital velocity, a the semimajor axis, G the gravitational constant, M⊙ the Sun mass, vd is the dust velocity, and mnuc the mass of the nucleus. In Paper I, we estimated the highest deviation of the semimajor axis for the complete sample of comets as D = 0.32 AU. We found D81P = 0.24 AU, D103PModelI = 0.24 AU, and D103PModelII = 0.21 AU. These values are in the same range as those found in Paper I and in Lacerda (2013). For further details we refer the readers to Sect. 5 of Paper I.
(5)In these equations, dMd/ dt is the dust mass loss rate, V the orbital velocity, a the semimajor axis, G the gravitational constant, M⊙ the Sun mass, vd is the dust velocity, and mnuc the mass of the nucleus. In Paper I, we estimated the highest deviation of the semimajor axis for the complete sample of comets as D = 0.32 AU. We found D81P = 0.24 AU, D103PModelI = 0.24 AU, and D103PModelII = 0.21 AU. These values are in the same range as those found in Paper I and in Lacerda (2013). For further details we refer the readers to Sect. 5 of Paper I.
 |
Fig. 12 81P/Wild 2 backward in time orbital evolution during 1 Myr. Left panel: fraction of surviving clones (%) versus time from now (Myr). The colors represent the regions visited by the test particles (red: Jupiter family region; cyan: Centaur; blue: Transneptunian; yellow: Halley type). The resolution is 2 × 104 yr. Right bottom panel: the % of surviving clones versus time from now (Myr), where N = 100 is the number of the initial test massless particles. |
 |
Fig. 13 81P/wild 2 last 100 yr. fraction of surviving clones (%) versus time from now (yr). The colors represent the regions visited by the test particles (red: Jupiter family region; cyan: Centaur). The dashed line marks the bars with a confidence level equal or larger than 90% of the clones in the Jupiter family region. The resolution is 3 yr, and the number of the initial test particles is N = 100. |
5.1. Discussion
In Paper I, we concluded that after the 15 Myr backward integration, just 12 of the initial 900 massless particles survived, which means ~98.7% were ejected form the solar system and ~1.3% remained in it. This result agrees with Levison & Duncan (1994), where the authors concluded that ~1.5% endured in the solar system after integration. Thus, in Paper I, eleven of the twelve remaining particles were in Transneptunian region, while one was in Centaur region (see Fig. 10 in Paper I). In this study, just 3 three clones of the initial 200 particles remained in the solar system after the 15 Myr integration, which is ~1.5%. These clones were 81P/clon34 and 81P/clon94, which are in Transneptunian region, and 103P/clon57 in Centaur region. Therefore, this result agrees with the one obtained in Paper I, and with Levison & Duncan (1994).
After the analysis of the 15 Myr integration in Paper I, to obtain a general view of the regions visited by comets, we focused on the first 1 Myr of backward integration in the orbital evolution, where ~20% of the massless particles still remained in the solar system. We inferred that all of them have a Centaur and Transneptunian past, while the Halley Type region was the most unlikely source for those comets, as expected. This is consistent for the other comets, 81P and 103P, under study in this paper (see Figs. 12 and B.1).
After that, to obtain the time spent by each comet in the JFCs region, we displayed the last 5000 yr using a 100 yr temporal resolution. We found that all targets were relatively young in the JFCs region, with ages between 100 <t< 4000 years. The youngest comets of the sample were 22P/Kopff (~100 yr), 78P/Gehrels 2 (~500 yr), and 118P/Shoemaker-Levy 4 (~600 yr). On the other hand, the oldest comet was 123P with ~3 × 103 yr. In this study, following the same steps, we have inferred that 81P is ~40 yr, while 103P is ~1000 yr (see Figs. 13 and B.2). The result for 81P agrees with the current knowledge about it: Sekanina & Yeomans (1985) described a very close encounter with Jupiter in 1974, and, as result of that approach, the comet was inserted in the inner regions of the solar system.
Finally, in Paper I we related the annual dust production rate for each comet (Td) within the time spent in the JFCs region. We concluded that the most active comets in our sample were also the youngest ones, i.e., 22P, 78P, and 118P. Here we added the results obtained for 81P and 103P. We found that 81P is both the youngest and the most active comet in the whole sample. This result is displayed in Fig. 14, where the 11 comets under study are shown.
 |
Fig. 14 Annual dust production rate of our targets obtained in the dust analysis (see Sect. 4) versus the time in the JFCs region with a 90% C.L. derived from dynamical studies (see Sect. 5). Red circles are the results derived from Pozuelos et al. (2014); yellow circle is the comet 22P/Koppf, where dust analysis was carried out in Moreno et al. (2012); violet circles are the results of the comets 81P/Wild 2 and 103P/Hartley 2, studied in this work. The comets with arrows mean the Td given for them are lower limits (see text in Paper I). |
6. Summary and conclusions
To increase the number of comets analyzed in Paper I, in this work we extended the study to comets 81P/Wild 2 and 103P/Hartley 2, which are of special interest as targets of the spacecraft missions Stardust and EPOXI. We presented optical images of those comets and Afρ values as a function of the heliocentric distance provided by the amateur astronomical association Cometas-Obs. To fit the observational data, we used our Monte Carlo dust tail code (see e.g., Moreno 2009), from which we derived the dust parameters as a function of the heliocentric distance: dust loss rate, ejection velocities of particles, the size distribution, and the overall emission pattern.
The main results are as follows.
-
Comet 81P/Wild 2 was found to be the most active in the wholesample of eleven comets, with an annual dust production rate ofTd = 2.8 × 109 kg yr-1. Its emission pattern was established as anisotropic with active areas located from 45° to −30° on the surface. The rotational parameters, I and φ, were found to be I = (55 ± 5)° and φ = (300 ± 20)°. In addition, we found two small outbursts suffered by the comet, one inbound and one outbound, where the total dust emitted was mob.I ~ 9.2 × 108 kg and mob.II ~ 3.0 × 108 kg, respectively.
-
In the case of the comet 103P/Hartley 2, we proposed two models: Model I or the hyperactive model, where according to previous knowledge of this comet (see e.g., A’Hearn et al. 2011; Meech et al. 2011; Harmon et al. 2011), we forced the maximum size of particles to be in the range of rmax = 20 cm. The dust production rate of this model was obtained as Td = 1.7 × 109 kg yr-1. Model II or the standard model was carried out without the restriction in the maximum size of the particles. In that case, the result in the annual dust production rate was Td = 4.5 × 108 kg yr-1. The ejection of comet 103P, in both models, was found to be isotropic.
-
For both comets, the power index of the size distribution, δ, was found to be in the range −4 <δ − 3 <. In this range, the brightness and mass are decoupled, so the mass depends on the largest ejected grains, while the brightness depends on the micrometer-size grains. For this reason, the dust production rate in our models should be regarded as lower limits. In the case of 103P, the presence of large chunks from the EPOXI mission and radar observations were found in the tail. While the true nature of these chunks is still under study, the size of them is estimated as ~20 cm. Thus, in our study, Model I seems to be more realistic than Model II, which should be considered as a lower limit for this comet.
-
We concluded that the best match to the dust ejection velocity law is
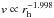 which agrees with
which agrees with 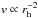 obtained by Crifo & Rodionov (1997) from hydrodynamical models of the inner cometary comae, for intermediate-sized particles.
obtained by Crifo & Rodionov (1997) from hydrodynamical models of the inner cometary comae, for intermediate-sized particles.
The second block of our study concerned determination of the dynamical evolution of the targets over the past 15 Myr. We used the numerical integrator developed by Chambers (1999). As in Paper I, the statistical study for each comet was implemented using 100 test massless particles: 1 real particle plus 99 clones with 2σ dispersion in the orbital parameters a, e, and i. In these integrations, the Sun and the eight planets were considered to be massive bodies, and close encounters between them and test particles were permitted. Therefore, from the initial 200 massless particles, we removed those that were beyond 1000 AU at any time during the integration. The main results were:
-
The analysis showed that ~1.5% of the massless particles remained in the solar system after the 15 Myr integration, and the most likely sources of them were the Centaur and Transneptunian regions. This result agrees with Paper I and with the studies of Levison & Duncan (1994).
-
We were able to deduce, with 90% confidence level, how long these targets spent as members of the JFCs: 81P ~40 yr and 103P ~1000 yr. Thus, 81P was found to be the youngest target in the whole sample of short-period comets studied between Paper I and this study.
In Fig. 14 we added the results from Paper I and the ones obtained from this work for the comets 81P and 103P. In that figure, we plotted the annual dust production rate [kg yr-1] (see Table 3 in this work, and Table 4 in Paper I) versus the time spent by the comets in the JFCs region with a 90% confidence level obtained in the dynamical analysis. From this figure, we concluded that 81P is both the youngest and the most active comet. Therefore, the relationship between activity and the time spent in JFCs, still seems to be evident. Despite the general trend in our sample of comets, this result should be taken with caution, because two exceptions to this trend were found in Paper I, 157P/Tritton and 123P/West-Hartley. To establish firmer conclusions about the cometary activity and the dynamical evolution, it would be desirable to perform more studies on other short-period comets.
Dust properties summary of the targets under study I.
Dust properties summary of the targets under study II.
Acknowledgments
We would like to thank Dr. Z.-Y. Lin and Dr. L.M. Lara for sharing the observations of comet 81P/Wild 2 carried out in Lulin Observatory (Taiwan) with us. We would also like to thank the entire Amateur Astronomical Association Cometas-Obs for always looking for comets. We would also like to thank Dr. Chambers for his help using his numerical integrator. We are grateful to the anonymous referee for comments and suggestions to improve this paper. This work was supported by contracts AYA2012-3961-CO2-01 and FQM-4555 (Proyecto de Excelencia, Junta de Andalucía).
References
- A’Hearn, M. F., Schleicher, D. G., Millis, R. L., Feldman, P. D., & Thompson, D. T. 1984, AJ, 89, 579 [NASA ADS] [CrossRef] [Google Scholar]
- A’Hearn, M. F., Belton, M. J. S., Delamere, W. A., et al. 2005, Science, 310, 258 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- A’Hearn, M. F., Belton, M. J. S., Delamere, W. A., et al. 2011, Science, 332, 1396 [NASA ADS] [CrossRef] [Google Scholar]
- Basilevsky, A. T., & Keller, H. U. 2006, Planet. Space Sci., 54, 808 [NASA ADS] [CrossRef] [Google Scholar]
- Basilevsky, A. T., & Keller, H. U. 2007, Sol. Syst. Res., 41, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Bauer, J. M., Walker, R. G., Mainzer, A. K., et al. 2011, ApJ, 738, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Belton, M. J. S. 2013, Icarus, 222, 653 [NASA ADS] [CrossRef] [Google Scholar]
- Belton, M. J. S., Thomas, P., Carcich, B., et al. 2013a, Icarus, 222, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Belton, M. J. S., Thomas, P., Li, J.-Y., et al. 2013b, Icarus, 222, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Bertini, I., Barbieri, C., Ho, T.-M., et al. 2012, A&A, 541, A159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boissier, J., Bockelée-Morvan, D., Biver, N., et al. 2014, Icarus, 228, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Brownlee, D. E., Horz, F., Newburn, R. L., et al. 2004, Science, 304, 1764 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Burns, J. A., Lamy, P. L., & Soter, S. 1979, Icarus, 40, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Chambers, J. E. 1999, MNRAS, 304, 793 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Crifo, J. F., & Rodionov, A. V. 1997, Icarus, 127, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Davidsson, B. J. R., & Gutierrez, P. J. 2004, in BAAS, 36, 1118 [Google Scholar]
- Duxbury, T. C., Newburn, R. L., & Brownlee, D. E. 2004, J. Geophys. Res. (Planets), 109, 12 [Google Scholar]
- Edoh, O. 1983, Univ. Arizona, USA [Google Scholar]
- Epifani, E., Colangeli, L., Fulle, M., et al. 2001, Icarus, 149, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Farnham, T. L., & Schleicher, D. G. 2005, Icarus, 173, 533 [NASA ADS] [CrossRef] [Google Scholar]
- Finson, M. J., & Probstein, R. F. 1968, ApJ, 154, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Fulle, M. 2004, in Motion of cometary dust, eds. M. C. Festou, H. U. Keller, & H. A. Weaver (University of Arizona Press), 565 [Google Scholar]
- Fulle, M., Colangeli, L., Agarwal, J., et al. 2010, A&A, 522, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Green, S. F., McDonnell, J. A. M., McBride, N., et al. 2004, J. Geophys. Res. (Planets), 109, 12 [Google Scholar]
- Groussin, O., Lamy, P., Jorda, L., & Toth, I. 2004, A&A, 419, 375 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grun, E., Zook, H. A., Fechtig, H., & Giese, R. H. 1985, Icarus, 62, 244 [NASA ADS] [CrossRef] [Google Scholar]
- Hadamcik, E., & Levasseur-Regourd, A. C. 2009, Planet. Space Sci., 57, 1118 [NASA ADS] [CrossRef] [Google Scholar]
- Hanner, M. S., & Hayward, T. L. 2003, Icarus, 161, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Harmon, J. K., Nolan, M. C., Howell, E. S., Giorgini, J. D., & Taylor, P. A. 2011, ApJ, 734, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Hsieh, H. H., Yang, B., & Haghighipour, N. 2012a, ApJ, 744, 9 [Google Scholar]
- Hsieh, H. H., Yang, B., Haghighipour, N., et al. 2012b, AJ, 143, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Jockers, K. 1997, Earth Moon and Planets, 79, 221 [Google Scholar]
- Kelley, M. S., Lindler, D. J., Bodewits, D., et al. 2013, Icarus, 222, 634 [NASA ADS] [CrossRef] [Google Scholar]
- Kirk, R. L., Duxbury, T. C., Hörz, F., et al. 2005, in 36th Annual Lunar and Planet. Sci. Conf., eds. S. Mackwell, & E. Stansbery, 2244 [Google Scholar]
- Knight, M. M., & Schleicher, D. G. 2013, Icarus, 222, 691 [NASA ADS] [CrossRef] [Google Scholar]
- Kolokolova, L., Hanner, M. S., Levasseur-Regourd, A.-C., & Gustafson, B. Å. S. 2004, in Physical properties of cometary dust from light scattering and thermal emission, ed. G. W. Kronk, 577 [Google Scholar]
- Lacerda, P. 2013, MNRAS, 428, 1818 [NASA ADS] [CrossRef] [Google Scholar]
- Lara, L. M., Lin, Z.-Y., & Meech, K. 2011, A&A, 532, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Levison, H. F., & Duncan, M. J. 1994, Icarus, 108, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Licandro, J., Moreno, F., de León, J., et al. 2013, A&A, 550, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lin, Z.-Y., Lara, L. M., Vincent, J. B., & Ip, W.-H. 2012, A&A, 537, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lisse, C. M., Fernandez, Y. R., Reach, W. T., et al. 2009, PASP, 121, 968 [NASA ADS] [CrossRef] [Google Scholar]
- Meech, K. J., & Jewitt, D. C. 1987, A&A, 187, 585 [NASA ADS] [Google Scholar]
- Meech, K. J., A’Hearn, M. F., Adams, J. A., et al. 2011, ApJ, 734, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Monet, D. G., Levine, S. E., Canzian, B., et al. 2003, AJ, 125, 984 [NASA ADS] [CrossRef] [Google Scholar]
- Moreno, F. 2009, ApJS, 183, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Moreno, F., Lara, L. M., Licandro, J., et al. 2011, ApJ, 738, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Moreno, F., Pozuelos, F., Aceituno, F., et al. 2012, ApJ, 752, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Moreno, F., Cabrera-Lavers, A., Vaduvescu, O., Licandro, J., & Pozuelos, F. 2013, ApJ, 770, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Moreno, F., Licandro, J., Álvarez-Iglesias, C., Cabrera-Lavers, A., & Pozuelos, F. 2014, ApJ, 781, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Mueller, B. E. A., Samarasinha, N. H., Farnham, T. L., & A’Hearn, M. F. 2013, Icarus, 222, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Pozuelos, F. J., Moreno, F., Aceituno, F., et al. 2014, A&A, 568, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Richardson, J. E., & Bowling, T. J. 2014, Icarus, 234, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Sekanina, Z. 1981, Ann. Rev. Earth Planetary Sci., 9, 113 [Google Scholar]
- Sekanina, Z. 2003, J. Geophys. Res. (Planets), 108, 8112 [NASA ADS] [CrossRef] [Google Scholar]
- Sekanina, Z., & Yeomans, D. K. 1985, AJ, 90, 2335 [NASA ADS] [CrossRef] [Google Scholar]
- Sekanina, Z., Brownlee, D. E., Economou, T. E., Tuzzolino, A. J., & Green, S. F. 2004, Science, 304, 1769 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Thomas, P., A’Hearn, M., Belton, M. J. S., et al. 2013a, Icarus, 222, 453 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, P. C., A’Hearn, M. F., Veverka, J., et al. 2013b, Icarus, 222, 550 [NASA ADS] [CrossRef] [Google Scholar]
- Tozzi, G. P., Epifani, E. M., Hainaut, O. R., et al. 2013, Icarus, 222, 766 [NASA ADS] [CrossRef] [Google Scholar]
- Veverka, J., Klaasen, K., A’Hearn, M., et al. 2013, Icarus, 222, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Whipple, F. L. 1951, ApJ, 113, 464 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Orbital parameters of comets 81P/Wild 2 and 103P/Hartley 2
In Table A.1 we show the orbital elements of the comets used during the dynamical studies in Sect. 5. They are extracted from JPL Horizons online solar system data3.
Orbital parameters of the short-period comets under study.
Appendix B: Dynamical analysis of comet 103P/Hartley 2
In Figs. B.1 and B.2, we show the dynamical analysis of the comet 103P/Hartley 2 described in Sect. 5. We present the fraction of the surviving clones versus time from now on different time scales. In both cases, the colored bars correspond to different regions visited by test particles: red to Jupiter family; cyan to Centaur; yellow to Haley type; blue to Transneptunian. The number of the initial test particles is N = 100.
 |
Fig. B.2 As in Fig. 13, but for the comet 103P/Hartley 2. The total plotted time is 5 × 103yr, with a resolution of 100 yr. |
All Tables
All Figures
 |
Fig. 1 Representative images of the observations obtained using a CCD camera at 1.52 m telescope at the Observatorio de Sierra Nevada in Granada, Spain. Right panel corresponds to 81P/Wild 2 on April 9, 2010. Isophote levels in solar disk units (SDU) are: 0.25 × 10-13, 0.77 × 10-13, 2.20 × 10-13. Left panel corresponds with comet 103P/Hartley 2 on August 4, 2010. Isophote levels are: 0.20 × 10-13, 0.40 × 10-13, 1.10 × 10-13. In both cases the directions of celestial north and east are given. The vertical bars correspond to 2 × 104 km in the sky. |
| In the text | |
 |
Fig. 2 81P/Wild 2 Afρ measurements by Cometas-Obs. Upper panel: original data and phase angle as a function of heliocentric distance. Lower panel: original Afρ data and corrected Afρ data by Eq. (1) (see text). |
| In the text | |
 |
Fig. 3 Best-fit modeled parameters to the dust environment of 81P/Wild 2 Afρ data and images (Figs. 4 and 5). All parameters are given as a function of the heliocentric distance. From top to bottom and left to right the panels are a) dust production rate [kg s-1]; b) ejection velocities of 1-cm particles [m s-1]; c) maximum size of particles [cm]; d) power index of the size distribution, δ. The solid red line corresponds to pre-perihelion and the dashed blue line to post-perihelion. |
| In the text | |
 |
Fig. 4 Comparison of observed and modeled Afρ data as a function of heliocentric distance. Parameter Afρ versus heliocentric distance. The Afρ measurements have been corrected using Eq. (1). Black dots: Afρ data from Cometas-Obs. Green triangles: Afρ data derived from OSN images. Blue diamonds: Afρ data from Lulin observatory images. The observations labeled (a) to (g) correspond to the Afρ derived from images (a) to (g) in Fig. 5. The outbursts I (inbound) and II (outbound) described in the text are marked with arrows. All the Afρ values refer to ρ = 104 km. |
| In the text | |
 |
Fig. 5 Isophote field comparison between observations and model. The black contours correspond to the observations and the red ones to the model. The dates and the SDU levels are a) Jan. 16.81, 2010. Levels are 0.80 × 10-13, 2.00 × 10-13, and 5.00 × 10-13 SDU; b) Apr. 9.06, 2010. Levels are 0.25 × 10-13, 0.77 × 10-13, and 2.20 × 10-13 SDU; c) Apr. 21.06, 2010. Levels are 0.25 × 10-13, 0.77 × 10-13, and 2.20 × 10-13 SDU; d) May 15.96, 2010. Levels are 0.10 × 10-13, 0.25 × 10-13, 0.77 × 10-13, and 2.20 × 10-13 SDU; e) Jun. 3.93, 2010. Levels are 0.10 × 10-13, 0.25 × 10-13, 0.77 × 10-13, and 2.20 × 10-13 SDU; f) Jul. 6.89, 2010. Levels are 0.08 × 10-13, 0.25 × 10-13, and 0.77 × 10-13 SDU; g) Aug. 21.85, 2010. Levels are 0.25 × 10-13, 0.77 × 10-13, and 2.20 × 10-13 SDU. See log of the observations in Table 1. |
| In the text | |
 |
Fig. 6 As Fig. 3 but for comet 103P/Hartley 2. Corresponding to Model I. This model fits the observations displayed in Figs. 9 and 8, where it is represented by the red line. |
| In the text | |
 |
Fig. 7 As in Fig. 3 but for comet 103P/Hartley 2. Corresponding to Model II. This model fits the observations displayed in Figs. 10 and 8 where it is represented by the blue line. |
| In the text | |
 |
Fig. 8 Comparison between observational data and the models proposed for the comet 103P/Hartley 2. Afρ measurements have been corrected using Eq. (1). Black dots are the data from Cometas-Obs, and green triangles marked from (a) to (d) are the observations at OSN telescope. The red line corresponds to Model I or Hyperactive model, which fits the observations in Fig. 9. The blue line is the Model II or Standard model, and its fits with observations can be checked in Fig. 10. All the Afρ values are referred to ρ = 104 km. |
| In the text | |
 |
Fig. 9 Isophote field comparison between observations and Model I or Hyperactive model. The black contours correspond to the observations and the red ones to the model. The dates and the SDU levels are a) Jul. 12.14, 2010. Levels are 0.30 × 10-14, 0.55 × 10-14, and 1.20 × 10-14 SDU; b) Aug. 4.11, 2010. Levels are 0.20 × 10-13, 0.40 × 10-13, and 1.10 × 10-13 SDU; c) Sep. 6.04, 2010. Levels are 0.15 × 10-13, 0.40 × 10-13, and 1.10 × 10-13 SDU; d) Nov. 3.16, 2010. Levels are 0.55 × 10-13, 1.25 × 10-13, 4.00 × 10-13 SDU. See log of the observations in Table 1. |
| In the text | |
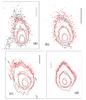 |
Fig. 10 As in Fig. 9 but for Model II or standard model. |
| In the text | |
 |
Fig. 11 Ejection velocities of 1 cm particles versus the heliocentric distance for all comets in the sample plus the result obtained by Fulle et al. (2010) in the study of comet 67P/Churyumov-Gerasimenko. The complete set of comets are: 22P/Kopff, 30P/Reinmuth 1, 67P/Churyumov-Gerasimenko, 78P/Gehrels 2, 81P/Wild 2, 103P/Hartley 2 (Model I and Model II), 115P/Maury, 118P/Shoemaker-Levy 4, 123P/West-Hartley, 157P/Tritton, 185P/Petriew, and P/2011 W2 (Rinner). The color code is given in the legend. The solid black line is the best fit found for that distribution: |
| In the text | |
 |
Fig. 12 81P/Wild 2 backward in time orbital evolution during 1 Myr. Left panel: fraction of surviving clones (%) versus time from now (Myr). The colors represent the regions visited by the test particles (red: Jupiter family region; cyan: Centaur; blue: Transneptunian; yellow: Halley type). The resolution is 2 × 104 yr. Right bottom panel: the % of surviving clones versus time from now (Myr), where N = 100 is the number of the initial test massless particles. |
| In the text | |
 |
Fig. 13 81P/wild 2 last 100 yr. fraction of surviving clones (%) versus time from now (yr). The colors represent the regions visited by the test particles (red: Jupiter family region; cyan: Centaur). The dashed line marks the bars with a confidence level equal or larger than 90% of the clones in the Jupiter family region. The resolution is 3 yr, and the number of the initial test particles is N = 100. |
| In the text | |
 |
Fig. 14 Annual dust production rate of our targets obtained in the dust analysis (see Sect. 4) versus the time in the JFCs region with a 90% C.L. derived from dynamical studies (see Sect. 5). Red circles are the results derived from Pozuelos et al. (2014); yellow circle is the comet 22P/Koppf, where dust analysis was carried out in Moreno et al. (2012); violet circles are the results of the comets 81P/Wild 2 and 103P/Hartley 2, studied in this work. The comets with arrows mean the Td given for them are lower limits (see text in Paper I). |
| In the text | |
 |
Fig. B.1 As in Fig. 12, but for comet 103P/Hartley 2. |
| In the text | |
 |
Fig. B.2 As in Fig. 13, but for the comet 103P/Hartley 2. The total plotted time is 5 × 103yr, with a resolution of 100 yr. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


