| Issue |
A&A
Volume 569, September 2014
|
|
|---|---|---|
| Article Number | A57 | |
| Number of page(s) | 8 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201424264 | |
| Published online | 24 September 2014 | |
Electron-capture supernovae exploding within their progenitor wind
1
Argelander Institute for Astronomy, University of Bonn,
Auf dem Hügel 71,
53121
Bonn,
Germany
e-mail:
moriyatk@astro.uni-bonn.de
2
Department of Physics, Faculty of Science and Engineering, Konan
University, 8-9-1 Okamoto, Kobe,
658-8501
Hyogo,
Japan
3
Kavli Institute for the Physics and Mathematics of the Universe
(WPI), Todai Institutes for Advanced Study, The University of Tokyo,
5-1-5 Kashiwanoha, Kashiwa,
277-8583
Chiba,
Japan
4
Institute for Theoretical and Experimental Physics,
Bolshaya Cheremushkinskaya
25, 117218
Moscow,
Russia
5
Sternberg Astronomical Institute, M.V. Lomonosov Moscow State
University, Universitetski pr. 13, 119992
Moscow,
Russia
Received:
23
May
2014
Accepted:
17
July
2014
The most massive stars on the asymptotic giant branch (AGB), or the so-called super-AGB stars, are thought to produce supernovae triggered by electron captures in their degenerate O+Ne+Mg cores. Super-AGB stars are expected to have slow winds with high mass-loss rates, so their circumstellar density is high. The explosions of super-AGB stars are therefore presumed to occur in this dense circumstellar environment. We provide the first synthetic light curves for such events by exploding realistic electron-capture supernova progenitors within their super-AGB winds. We find that the early light curve – that is, before the recombination wave reaches the bottom of the hydrogen-rich envelope of supernova ejecta (the plateau phase) – is not affected by the dense wind. However, after the luminosity drop following the plateau phase, the luminosity remains much higher when the super-AGB wind is taken into account. We compare our results to the historical light curve of SN 1054, the progenitor of the Crab Nebula, and show that the explosion of an electron-capture supernova within an ordinary super-AGB wind can explain the observed light curve features. We conclude that SN 1054 could have been a Type IIn supernova without any extra extreme mass loss, which was previously suggested to be necessary to account for its early high luminosity. We also show that our light curves match Type IIn supernovae with an early plateau phase or the so-called Type IIn-P supernovae, and suggest that they are electron-capture supernovae within super-AGB winds. Although some electron-capture supernovae can be bright in the optical spectral range due to the large progenitor radius, their X-ray luminosity from the interaction does not necessarily get as bright as other Type IIn supernovae whose optical luminosities are also powered by the interaction. Thus, we suggest that optically bright X-ray-faint Type IIn supernovae can emerge from electron-capture supernovae. Optically faint Type IIn supernovae, such as SN 2008S, can also originate from electron-capture supernovae if their hydrogen-rich envelope masses are small. We argue that some of them can be observed as Type IIn-b supernovae due to the small hydrogen-rich envelope mass.
Key words: stars: massive / supernovae: general / supernovae: individual: SN 1054 / supernovae: individual: SN 2009kn / stars: mass-loss
© ESO, 2014
1. Introduction
Massive stars are known to explode as supernovae (SNe) due to central core collapse. Stars with the zero-age main-sequence mass above around 10 M⊙ trigger the core collapse after the formation of an Fe core. However, it has been suggested that massive stars whose masses are slightly smaller than the masses required to form Fe cores can still make electron degenerate O+Ne+Mg cores, which can trigger core collapse through the electron-capture reactions (e.g., Miyaji et al. 1980; Nomoto et al. 1982; Nomoto 1984, 1985, 1987; Miyaji & Nomoto 1987). Core-collapse SNe triggered by the electron-capture reactions are called electron-capture SNe (ecSNe).
The ecSN progenitors are super-asymptotic giant branch (super-AGB) stars at the onset of the core collapse if they were single stars. Since there are many uncertainties in thermal pulses, mass loss, etc., in the evolution of super-AGB stars, the exact mass range of ecSN progenitors, or even the existence of them, is theoretically not well constrained (e.g., Langer 2012; Poelarends et al. 2008; Siess 2007, 2010; Jones et al. 2013; Takahashi et al. 2013). It has also been suggested that the binary evolution can help a star that explodes as an ecSN (Podsiadlowski et al. 2004; Nomoto 1985). While the exact mass range or the existence of ecSN progenitors remains uncertain, several first-principle numerical simulations of the O+Ne+Mg core collapse have succeeded in predicting the observational properties of ecSNe. The ecSNe are predicted to have small explosion energy (~1050 erg) and small 56Ni production (~10-3 M⊙) by the neutrino-driven explosion (Kitaura et al. 2006; Burrows et al. 2007; Janka et al. 2008; Hoffman et al. 2008; Wanajo et al. 2009).
Several SNe have been related to ecSNe based on the predicted ecSN properties (e.g.. Botticella et al. 2009; Thompson et al. 2009; Pumo et al. 2009; Kawabata et al. 2010). The most famous SN related to an ecSN is SN 1054 or the Crab Nebula (see Sect. 4.1). However, while several numerical simulations of the explosions of ecSNe have been performed by using the realistic progenitor model, there is little theoretical study on the LC properties of ecSNe. Recently, Tominaga et al. (2013, TBN13 hereafter) performed numerical LC calculations by using realistic ecSN progenitor models and provided the LC properties of ecSNe. They have shown that ecSNe can be bright (~−17 mag in optical bands) in spite of the small predicted explosion energy because of the large progenitor radius and the small H-rich envelope mass. Super-AGB stars are known to have high mass-loss rates (~10-4 M⊙ yr-1, e.g., Poelarends et al. 2008) and the ecSN progenitors can lose a large fraction of their H-rich envelope as a result of the large mass-loss during the super-AGB phase, which is quite distinct from a-little-more massive stars causing the Fe core collapse.
An important characteristic of ecSNe, which TBN13 did not consider, is the existence of the super-AGB wind around the ecSN progenitors. The ecSN progenitors should be within the circumstellar medium (CSM) created by the super-AGB wind when they explode if they are single stars. In addition to the high mass-loss rates, the wind velocities of super-AGB stars are ~10 km s-1, making the CSM density as high as those expected for Type IIn SNe (SNe IIn) in which we see the effect of the CSM interaction in their observational properties (e.g., Kiewe et al. 2012; Taddia et al. 2013; Fransson et al. 2013; Moriya et al. 2014; see Sect. 2.1.2). It is even suggested that most SNe IIn may come from the low-mass stars, which are consistent with ecSNe (Habergham et al. 2014; Anderson et al. 2012).
The fact that ecSNe can be bright despite the small explosion energy was already suggested by van Veelen (2010) by modeling the interaction between ecSN ejecta and expected dense CSM. Smith (2013) also discussed the effect of dense CSM on ecSN LCs. He suggested that the early large luminosity of SN 1054 from an ecSN indicates the existence of confined dense CSM from eruptive mass loss (see Sect. 4.1 for the discussion of SN 1054). However, as is shown by TBN13 and van Veelen (2010), ecSNe can be as bright as SN 1054 in spite of the low explosion energy because of the expected large progenitor radius and small mass of the H-rich envelope.
The previous numerical simulations of ecSN LCs do not take either the realistic ecSN progenitor model (van Veelen 2010) or the existence of the dense CSM around the ecSN progenitors (TBN13) into account. In this paper, we combine the two previous LC studies of ecSNe and perform the numerical LC simulation of ecSNe exploding in the super-AGB wind. We provide realistic ecSN LCs to compare with observations.
The rest of this paper is organized as follows. At first, in Sect. 2.1, we describe the progenitors and their CSM that we use for our LC modeling of ecSNe and the properties of the SN explosions. Then, we show the synthesized LCs in Sect. 3. The LCs are compared to observed SN LCs with special focus on SN 1054 and so-called “Type IIn-P” SNe in Sect. 4. We conclude this paper in Sect. 5.
2. Initial conditions
2.1. Progenitors and circumstellar media
2.1.1. Electron-capture SN progenitors
The super-AGB ecSN progenitors we use in this work are the same as those presented in TBN13. The progenitor models are constructed by attaching a H-rich envelope (Nomoto & Sugimoto 1972) to the thin He layer on the 1.377 M⊙ O+Ne+Mg ecSN progenitor that has been obtained by Nomoto et al. (1982); Nomoto (1984, 1987). Several ecSN progenitors with different envelope masses (Menv) and hydrogen fractions (Xenv) are constructed by TBN13. In this work, we take the model with Menv = 3.0 M⊙ and Xenv = 0.2 as a fiducial model. The LC from the model was compared to that of SN 1054 in TBN13. The hydrogen fraction is rather low in the model. The ² fraction affects the early plateau length in LCs, but the differences between the plateau lengths of the Xenv = 0.2 models and the Xenv = 0.7 models are less than 20 days (TBN13). The plateau luminosity is not strongly affected by the composition. The radius and luminosity of the model are 7 × 1013 cm (103 R⊙) and 3 × 1038erg s-1 (8 × 104 L⊙), respectively. See TBN13 for the detailed properties of the progenitors.
2.1.2. Circumstellar media
We put the CSM expected from super-AGB winds outside the aforementioned ecSN progenitors. However, the mass loss from super-AGB stars is uncertain. Poelarends et al. (2008) adopted several mass-loss prescriptions to follow the super-AGB evolution and found that the differences in the mass-loss prescriptions do not significantly affect the final results. The mass-loss rates are around 10-4 M⊙ yr-1 (Poelarends et al. 2008). We adopt three mass-loss rates in our LC calculations: 10-4, 5 × 10-5, and 10-5 M⊙ yr-1. Although we construct the CSM by assuming that the mass-loss rates are constant, super-AGB stars experience thermal pulses, and the mass-loss rates can alter significantly in a short timescale (e.g., Jones et al. 2013; Lau et al. 2012).
Another important quantity we need to know to estimate the CSM density is the wind velocity vwind. The escape velocity of our fiducial progenitor is 41 km s-1. The actual terminal wind velocity is, again, uncertain. van Veelen (2010) argued that the wind velocity can be as low as 30% of the escape velocity based on the formulation of Eldridge et al. (2006). Here, we take vwind = 20km s-1 as a representative wind velocity as was assumed in van Veelen (2010).
Given the mass-loss rate (Ṁ) and wind velocity (vwind), the
CSM density ρcsm(r) is set as
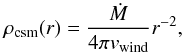 (1)where r is radius. The
super-AGB phase is assumed to continue for ~
104 years (e.g., Poelarends et al. 2008), and the dense CSM should reach ~6 × 1017 cm in the super-AGB
phase. However, the CSM radius boundary is arbitrarily set at 2 × 1016 cm in the initial
condition of the numerical simulations we performed. Thus, the effect of the dense CSM
on the LCs is expected to last longer than that we obtain, as discussed in the following
sections.
(1)where r is radius. The
super-AGB phase is assumed to continue for ~
104 years (e.g., Poelarends et al. 2008), and the dense CSM should reach ~6 × 1017 cm in the super-AGB
phase. However, the CSM radius boundary is arbitrarily set at 2 × 1016 cm in the initial
condition of the numerical simulations we performed. Thus, the effect of the dense CSM
on the LCs is expected to last longer than that we obtain, as discussed in the following
sections.
It is an important feature that the CSM density of the super-AGB wind is similar to those estimated in the CSM of typical SNe IIn. The CSM density is proportional to Ṁ/vwind (Eq. (1)). The typical CSM properties of SNe IIn are estimated to be Ṁ ~ 10-3 M⊙ yr-1 with vwind ~ 100 km s-1 (e.g., Kiewe et al. 2012; Taddia et al. 2013; Fransson et al. 2013; Moriya et al. 2014). While the mass-loss rates of the super-AGB stars (~ 10-4 M⊙ yr-1) are about one order of magnitude smaller than those estimated for SNe IIn, the wind velocity ~10 km s-1 is also one order of magnitude smaller. Thus, the CSM density from the super-AGB wind is presumed to be high enough to affect the LCs and spectra of ecSNe as much as we observe in SNe IIn.
2.2. Explosion properties and light curve calculations
The explosions of super-AGB stars are followed in the same way as in TBN13. The explosions of the ecSN progenitors are numerically followed with a one-dimensional multigroup radiation hydrodynamics code STELLA (e.g., Blinnikov et al. 2006, 1998). The explosions are initiated by putting thermal energy at the center. The explosion energy is set as 1.5 × 1050 erg, which is based on the numerical simulations performed with the first principles (Kitaura et al. 2006), unless otherwise mentioned. STELLA does not follow the explosive nucleosynthesis, and we need to provide the chemical yields from the explosive nucleosynthesis to obtain the opacity and the energy input from the nuclear decay of 56Ni. We use the chemical yields from the nucleosynthesis calculation of the self-consistent ecSN explosion performed with the same O+Ne+Mg core (Model ST in Wanajo et al. 2009). The amount of 56Ni produced in the model is 2.5 × 10-3 M⊙. We assume the envelope is not affected by the explosive nucleosynthesis. Finally, TBN13 has investigated the effect of the central pulsar to the LC but we do not take it into account in this paper.
 |
Fig. 1 Bolometric LCs of ecSNe exploding within the super-AGB wind. The LC model without CSM (TBN13) is also shown for comparison. The mass-loss rate of the model is indicated in the figure. The wind velocity is vwind = 20km s-1 for all models. |
3. Light curve properties
Synthetic bolometric LCs are presented in Fig. 1. The LC without CSM was already presented in TBN13. It stays bright until the photosphere located at the hydrogen recombination front resides in the H-rich envelope. This early phase is essentially the same as the plateau phase of Type IIP SNe. As is already shown by TBN13, the plateau phase is bright in spite of the low explosion energy. This is because of the large progenitor radius and the small H-rich envelope mass expected for super-AGB SN progenitors (cf. Kasen & Woosley 2009; Young 2004). The length of the plateau phase depends on the mass and composition of the H-rich envelope, and it can be longer than 100 days (TBN13). The luminosity drops by about two orders of magnitudes at the end of the plateau, and the LC starts to follow the decay of 56Co if there is no CSM.
Even if we take the effect of the CSM interaction into account, the early LCs during the plateau phase are still dominated by the light from the SN ejecta. The effect of the super-AGB wind on the LCs starts to appear after the plateau.
The effect of the interaction on the LCs is examined in detail in Fig. 2. In addition to the models with no CSM and 10-4 M⊙ yr-1
presented in Fig. 1, the analytic bolometric LC models
based on Moriya et al. (2013b) are shown (AN1 and
AN2). The analytic LC is expressed as 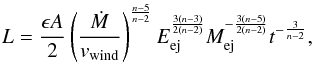 (2)where
(2)where
![\begin{equation} A=\left(\frac{n-3}{n-2}\right)^3 \left[ \frac{2}{(n-4)(n-3)(n-\delta)} \frac{[2(5-\delta)(n-5)]^{(n-3)/2}}{[(3-\delta)(n-3)]^{(n-5)/2}} \right]^{\frac{3}{n-2}}, \end{equation}](/articles/aa/full_html/2014/09/aa24264-14/aa24264-14-eq43.png) (3)t is the time since the
explosion, Eej is the SN kinetic energy,
Mej is the SN ejecta mass, n is the outer density slope
of the SN ejecta (ρej
∝ r−n), δ is the inner density slope
of the SN ejecta (ρej
∝ r−δ), and ϵ is the conversion
efficiency from kinetic energy to radiation. We refer to Moriya et al. (2013b) for further details. In this paper, we set n = 9 and δ = 0 to compare the model
with that of van Veelen (2010) but the LC does not
strongly depend on the choice of n and δ within the reasonable range (n ≃ 7–12 and δ ≃ 0–1). All the analytic
models shown in Fig. 2 assume Ṁ =
10-4 M⊙ yr-1 and vwind =
20km
s-1. The AN1 model in Fig. 2 assumes Eej = 1.5 × 1050 erg and
Mej =
3 M⊙. As discussed below, the conversion
efficiency ϵ is
uncertain in both the numerical and analytic models. The conversion efficiency
ϵ in AN1 is
chosen to match the later luminosity of the numerical 10-4 M⊙ yr-1
model (ϵ =
0.1).
(3)t is the time since the
explosion, Eej is the SN kinetic energy,
Mej is the SN ejecta mass, n is the outer density slope
of the SN ejecta (ρej
∝ r−n), δ is the inner density slope
of the SN ejecta (ρej
∝ r−δ), and ϵ is the conversion
efficiency from kinetic energy to radiation. We refer to Moriya et al. (2013b) for further details. In this paper, we set n = 9 and δ = 0 to compare the model
with that of van Veelen (2010) but the LC does not
strongly depend on the choice of n and δ within the reasonable range (n ≃ 7–12 and δ ≃ 0–1). All the analytic
models shown in Fig. 2 assume Ṁ =
10-4 M⊙ yr-1 and vwind =
20km
s-1. The AN1 model in Fig. 2 assumes Eej = 1.5 × 1050 erg and
Mej =
3 M⊙. As discussed below, the conversion
efficiency ϵ is
uncertain in both the numerical and analytic models. The conversion efficiency
ϵ in AN1 is
chosen to match the later luminosity of the numerical 10-4 M⊙ yr-1
model (ϵ =
0.1).
 |
Fig. 2 Comparison of several bolometric LC models. The “no CSM” model and the 10-4 M⊙ yr-1 model are the same as in Fig. 1. The AN1 model is the expected contribution of the luminosity from the interaction in the 10-4 M⊙ yr-1 model which is estimated with the analytic LC model of Moriya et al. (2013b). Adding the “no CSM” and AN1 models, we obtain the “no CSM + AN1” model, which roughly matches the overall LC evolution of the 10-4 M⊙ yr-1 model. The LC model of van Veelen (2010) is obtained from a numerical two-dimensional LC calculation with the similar initial conditions in the 10-4 M⊙ yr-1 model. The AN2 model is the analytic LC estimate for the van Veelen (2010) model. See Sect. 3 for details. |
The analytic model represents the contribution of the luminosity from the interaction. In Fig. 2, we also present a model in which the luminosities of the numerical “no CSM” model and the analytic AN1 model are added. This model can roughly explain the bolometric luminosity evolution of the numerical model with the super-AGB wind. Large differences between the numerical model and the added model appear in two phases: (i) just after the plateau phase at around 100 days and (ii) around 900 days when the numerical LC drops significantly. The earlier luminosity discrepancy (i) is caused by the higher photospheric temperature in the numerical interacting model. A similar kind of smooth transition is also found in the explosion models of red supergiants within dense CSM (Moriya et al. 2011). The sudden decline (ii) appears because the shock goes out of the dense CSM whose radius is arbitrarily set at 2 × 1016 cm. If the super-AGB phase continues for ~ 104 years with the wind speed of 20 km s-1, the dense CSM should actually be extended up to ~6 × 1017 cm. This means that the interaction should actually continue further, and the LC continues to be bright as we see in the analytic model.
In Fig. 2, we also show the numerical bolometric LC for the interaction between ecSN ejecta and dense CSM as obtained by van Veelen (2010). The bolometric LC is obtained with the hydrodynamics code ZEUS-MP that is combined with a cooling function, which is applicable to the optically thin system. The method is similar to that adopted by van Marle et al. (2010). The homologous SN ejecta is assumed to have two density components with n = 9 and δ = 0. The hydrodynamical calculation is performed in two dimensions. The SN ejecta mass is 3.15 M⊙, and the kinetic energy is 1050 erg. These parameters are almost the same as in our model. The SN ejecta is connected to the dense CSM by Ṁ = 10-4 M⊙ yr-1 and vwind = 20 km s-1 at 1014 cm.
Since the numerical interaction model of van Veelen (2010) does not take account of the recombination process in the SN ejecta, the early LC evolution is different from what we obtained. However, even at the epochs when our LC model is dominated by the luminosity from the interaction, the difference in the luminosity remains by a factor of about 3. The difference is likely to stem from the uncertainty in the conversion efficiency ϵ. We plot another analytic LC of Moriya et al. (2013b) (Eq. (2)) with Mej = 3.15 M⊙ and Eej = 1050 erg in Fig. 2 (AN2). The analytic model AN2 matches the numerical model of van Veelen (2010) well. The Mej and Eej in AN2 are almost the same as in AN1. The main difference between AN1 and AN2 is that the conversion efficiency ϵ is increased to 0.5 in AN2 from 0.1 in AN1. Thus, the main reason for the discrepancy in the two numerical models is the difference in the conversion efficiency achieved in these simulations.
The conversion efficiency is a parameter that is still not well-constrained. It is usually assumed to be ≃0.1–0.5 in the literature. The maximum conversion efficiency is ≃0.5 because of the conservation of momentum. In the one-dimensional code STELLA, the conversion efficiency is artificially reduced. The motivation for the reduction in the code is that the multidimensional instabilities may initiate additional motion in the dense shell, and more energy may remain as kinetic energy if the dimension is larger (Blinnikov et al. 1998; Moriya et al. 2013a). A recent multidimensional radiation hydrodynamics calculation of a pulsational pair-instability SN model of Woosley et al. (2007) by Chen et al. (2014) showed that the resulting luminosity is similar to that obtained by STELLA with the artificial reduction of the conversion efficiency. In the multidimensional simulations by van Veelen (2010), however, it is found that the Rayleigh-Taylor fingers formed by multidimensional instabilities make the density ahead of the shock higher, and thus, the luminosity is higher by a factor of 1.8 in the two-dimensional simulations. In summary, the artificial reduction in the conversion efficiency in STELLA and the larger effective conversion efficiency in multidimensional simulations by van Veelen (2010) due to the Rayleigh-Taylor fingers cause the difference in the conversion efficiency. We still do not know clearly how the multi-dimensionality affects the conversion efficiency. One possibility is that the conversion efficiency depends on the CSM density. The numerical simulations by Chen et al. (2014) are performed with the denser CSM than those in van Veelen (2010), which are closer to ours. In this case, the conversion efficiency may also be time dependent since the CSM density reduces as the shock propagates outward. Another possible reason for the difference is that the radiation is not coupled to hydrodynamics in the simulations by van Veelen (2010), while it is coupled in the simulations by Chen et al. (2014). The effect of the multidimensionality in SN IIn luminosity needs to be investigated more.
 |
Fig. 3 Multicolor LC of the model with 10-4 M⊙ yr-1. |
Figure 3 shows the multicolor LC of our numerical model with 10-4 M⊙ yr-1. The evolution during the early plateau phase is consistent with those of SNe IIP. After the early plateau, the evolution of multicolor LCs is similar to each other, but the magnitudes depend on the bands. The evolution of the optical LCs is similar to that of the bolometric LC in Fig. 1. When the shock is radiation-dominated (when the ratio of the radiation pressure to the gas pressure is above ≃5), the shock temperature does not become very high because of the large heat capacity of photons, so optical photons are mainly emitted from the shock (Weaver 1976; Blinnikov & Tolstov 2011; Tolstov et al. 2013). Even when the shock is not radiation-dominated, the high-energy photons produced at the shock are efficiently thermalized due to the large CSM density, so photons can be emitted in the optical wavelengths (cf. Chevalier & Irwin 2012).
Finally, we show the velocity structures of the models with and without CSM in Fig. 4 at around the middle of the plateau phase (t ≃ 50 days). The entire velocity in the model without CSM is homologous, while only the unshocked SN ejecta is homologous in the model with CSM. The photosphere is located at r = 1.1 × 1015 cm in the “no CSM” model, and it is located at r = 1.2 × 1015 cm in the model with the CSM. The photospheric velocity is almost the same (2300 km s-1) in the two models. The model with CSM has the velocity drop at r = 1.4 × 1015 cm where the SN ejecta collides to the CSM. The material in SN ejecta, which exists beyond this radius in the “no CSM” model, is accumulated in the cold dense shell at 1.4 × 1015 cm in the model with CSM.
 |
Fig. 4 Velocity structures of the models with and without CSM at t ≃ 50 days. |
4. Comparison with observations
In this section, we compare our ecSN LC models presented in the previous section to the observations, which may be related to ecSNe.
4.1. SN 1054 (Crab Nebula)
SN 1054 was a “guest star”, which is recorded mainly in Chinese and Japanese literature (see Stephenson & Green 2002, for a summary of the historical records). The proximity of the guest star to the Crab Nebula (M 1 or NGC 1952) was first pointed out by Lundmark (1921). The expansion of the Crab Nebula, which was discovered by Lampland (1921) and Duncan (1921), is consistent with the explosion occurring in 1054 (Hubble 1928; Rudie et al. 2008, but see also Trimble 1968; Wyckoff & Murray 1977; Nugent 1998). Thus, the Crab Nebula is quite likely the remnant of SN 1054.
The Crab Nebula is one of the best observed SN remnants (see Hester 2008; Davidson & Fesen 1985, for summaries). The observed chemical abundances (e.g., MacAlpine & Satterfield 2008; Satterfield et al. 2012) suggest that the Crab Nebula is a remnant of an ecSN (e.g., Nomoto et al. 1982). In addition, the estimated small ejecta mass (4.6 ± 1.8 M⊙, Fesen et al. 1997) and small kinetic energy (~1049 erg, e.g., Frail et al. 1995; Smith 2013) match the theoretical predictions of ecSN properties (e.g., Nomoto et al. 1982; Kitaura et al. 2006; Burrows et al. 2007). The above properties of the Crab Nebula suggest that SN 1054 was likely an ecSN.
Generally, SN LCs are an important clue to investigate their progenitors. The LC of SN 1054 deduced from the ancient records (see below) has been extensively discussed by many authors (e.g., Minkowski 1971; Chevalier 1977; Wheeler 1978). It has been argued that the LC of SN 1054 may be inconsistent with those expected from ecSNe. Sollerman et al. (2001) pointed out that the last observational record of SN 1054 is incompatible with the small amount of 56Ni production expected in ecSNe. Recently, Smith (2013) suggested that the relatively high early luminosity of SN 1054 is hard to be explained by the small explosion energy expected for ecSNe. However, TBN13 showed that the small explosion energy is consistent with the early high-luminosity of SN 1054 because of the progenitor’s large radius and the small H-rich envelope mass in ecSNe. Sollerman et al. (2001) proposed that the later high-luminosity of SN 1054 was powered by energy input from the central pulsar or the CSM interaction. The energy input from the pulsar was taken into account by TBN13. They found that the energy input from the pulsar can potentially explain the late luminosity, although their model with one-group radiation transport predicted a lower luminosity. We compare here our ecSN LC models with super-AGB winds to that of SN 1054 to show that ecSN exploded within super-AGB winds can actually explain the LC properties of SN 1054.
In Fig. 5, we compare our LC models with the LC of SN 1054 deduced from the historical records. The recorded brightness of SN 1054 at three epochs, which were observed with human eyes are adopted (Stephenson & Green 2002):
-
1.
The “guest star” appeared on AD 1054 July 4(JD 2 106 219)1, and it was as bright as Venus(~−4.5 mag).
-
2.
It was able to observe during the daytime for 23 days. Thus, the star was as bright as the sky in the daytime at 23 days since its discovery (JD 2 106 232), which is at ~−3 mag.
-
3.
It disappeared from the sky on AD 1056 April 6 (JD 2 106 858). We assume that SN 1054 became ~6 mag at this time.
The errors, especially in magnitude, are expected to be large. For example, the Japanese record reports that the star was as bright as Jupiter (mopt ~ −2 mag) instead of Venus (Stephenson & Green 2002). We assign a magnitude of error to the deduced magnitudes. The recorded date also has uncertainty. In addition, the star may not have been seen for a while because of the bad weather. Thus, we assign the error of 10 days in the recorded dates. The estimated observed magnitudes are corrected to the absolute ones with the distance of 2 kpc (Trimble 1973; Davidson & Fesen 1985) and the extinction of AV = 1.6 mag (Miller 1973).
 |
Fig. 5 LCs of SN 1054 and our ecSNe exploded within super-AGB winds. The V-band LCs of the models are shown. The observations of SN 1054 are based on human eyes, which are sensitive at around the V band (Vos 1978). Note that the V-band and R-band magnitudes are similar in our models (Fig. 3). |
Our LC models show that the explosion of an ecSN within super-AGB wind can explain the major characteristics of SN 1054. As has already been shown by TBN13, the early high luminosity of SN 1054 can be explained by the ecSN model. Smith (2013) suggested that a confined dense shell is required to explain the early high luminosity of SN 1054 with a low energy explosion of ecSNe but this is not necessarily the case (TBN13). The early luminosity can be solely explained by ecSNe without any confined dense shell. No extreme mass loss of the super-AGB star shortly before the explosion is required.
An essential difference between our models and those of TBN13 is the existence of the super-AGB wind in our models. As was discussed by Sollerman et al. (2001), the late luminosity of SN 1054 requires about 0.06 M⊙ of 56Ni, which is incompatible with the expected small 56Ni production of ecSNe (~10-3 M⊙). It was invoked by TBN13 that the luminosity input from the central pulsar to explain the late high luminosity. Our models, which include the luminosity from the interaction with dense CSM whose existence is naturally expected in the explosion of super-AGB stars, can describe the later luminosity of SN 1054 without invoking the energy input from the pulsar. This possibility was already proposed by Sollerman et al. (2001), and we confirmed it. Both the pulsar and interaction may contribute to the late time luminosity.
The difference in observational properties of the pulsar and interaction models appears in the spectra. The interaction is presumed to make SN 1054 Type IIn. The luminosity from the interaction dominates after the early plateau phase, but the strong narrow emission lines may have made SN 1054 Type IIn from early on. Observations of light echoes may be able to distinguish them as was suggested by Smith (2013). However, detection of SN IIn spectra does not necessarily indicate that SN 1054 was powered by the interaction from the earliest time as is shown here.
A remaining concern about our LC models for SN 1054 is the final observational record. The final LC point is based on the Chinese record that the guest star vanished at that epoch. However, the SN luminosity of our models stays constant. One can, of course, doubt the accuracy of the record, and the luminosity may have stayed more or less similar for longer time. Another possible interpretation is that the shock had gone through the dense part of the CSM at this time, and the LC declined suddenly as seen at around JD 2 107 000 in Fig. 5 in our models whose dense CSM radius is 2 × 1016 cm. The disappearance at JD 2 106 858 can be explained if the dense CSM only extends to ≃1.5 × 1016 cm. In this case, the super-AGB progenitor should have undergone the high mass-loss rate starting from ≃240 years before the explosion, assuming vwind = 20 km s-1. This may be possible if the mass loss from super-AGB stars is related to many thermal pulses of He shell burning, thus being strongly time-dependent.
4.2. Type IIn supernovae with LC plateau (Type IIn-P)
Some SNe IIn are known to be characterized by an early LC plateau followed by the sudden LC decline as seen in SNe IIP. They have been suggested to be related to ecSNe because of low estimated 56Ni masses (e.g., SN 1994W, Sollerman et al. 1998; SN 2009kn, Kankare et al. 2012; SN 2011ht, Mauerhan et al. 2013). This kind of SNe IIn is also called “Type IIn-P” SNe by some authors because of the LC plateau (e.g., Mauerhan et al. 2013).
In Fig. 6, we compare the ecSN LC model by interacting with a super-AGB wind with the LC of SN 2009kn (Kankare et al. 2012). The progenitor model is constructed by attaching the Ṁ = 10-4 M⊙ yr-1 and vwind = 20 km s-1 wind on top of the Menv = 4.7 M⊙ and Xenv = 0.5 progenitor presented in TBN13. The explosion energy is increased to 3.5 × 1050 erg to match the plateau luminosity of SN 2009kn. The 56Ni mass is the same as in the previous models (2.5 × 10-3 M⊙) for simplicity.
 |
Fig. 6 Comparison of the observed LC of SN 2009kn (Kankare et al. 2012) and the multicolor LC model of the ecSN exploded in the super-AGB wind. |
The overall LC properties of SN 2009kn are reproduced by the numerical model. The R-band brightness of the first three observed epochs is higher than the numerical LC. However, the multicolor LCs of the later plateau phase are consistent with the observations. The luminosities after the plateau are lower than observed ones. This may indicate that the mass-loss rate of the progenitor was larger than 10-4 M⊙ yr-1, and/or the wind velocity was smaller than 20km s-1.
For the LC drop after the plateau, two reasons have been suggested. (i) Chugai et al. (2004) suggested that the drop appears when the blast wave leaves the dense part of CSM. The major power input from the interaction terminates when the blast wave leaves the dense part of the CSM and the LC drop is observed. (ii) Dessart et al. (2009) related the drop to the recombination. Our model is close to the latter idea. In our model, however, the LC plateau is not related to the interaction as considered in Dessart et al. (2009) but is caused by exactly the same reason as in SNe IIP, which is the recombination in the H-rich layers of the SN ejecta.
As the emission from the early phase is dominated by the emission from the SN ejecta, one may expect to see SN IIP spectral features in these epochs. However, the photospheric velocity during the plateau phase is as low as ~2000 km s-1 (Sect. 3 and Fig. 4). Thus, the spectral features from the SN ejecta can be strongly diluted by the intermediate narrow-line components usually observed in SNe IIn, which typically have the width of ~1000 km s-1. The dense shell may also smear out the spectral features from the SN ejecta.
One observational property of these SNe IIn, which may not prefer our ecSN model, is the observed velocities of the narrow P-Cygni profiles. The small velocities of the narrow P-Cygni profiles in SNe IIn are generally related to the wind velocity of the progenitors. The velocities of the narrow components in the SNe IIn with the LC plateau are typically 100–1000 km s-1 (e.g., Chugai et al. 2004; Kankare et al. 2012; Mauerhan et al. 2013). This is inconsistent with the small wind velocities of the super-AGB wind. One possibility is that these features may come from the slowly-moving SN ejecta and other unobserved, much slower P-Cygni components in the spectra may exist. In addition, the detailed line formation mechanisms of SNe IIn are not well understood, and the detailed spectral modeling is required to see if the super-AGB model is able to explain the spectral properties.
Finally, one of the SNe IIn with the LC plateau, SN 2011ht, is found to have brightened a year before the major luminosity increase in 2011 (Fraser et al. 2013). If SN 2011ht is associated with a super-AGB star, the pre-outburst could be related to the thermal pulses of He-shell burning in the super-AGB progenitor. Several possible pre-burst events have been reported (Ofek et al. 2014), and some of them may be related to the AGB activities.
4.3. Other supernovae
Other SNe IIn, which have been suggested to be ecSNe, are faint from early times. For example, the peak bolometric magnitude of SN 2008S was about −14 mag (1041 erg, e.g., Botticella et al. 2009), and the progenitor was found to be around 10 M⊙ (Prieto et al. 2008). Our LC models, however, predict that ecSNe are not faint at early times. One possible way to make the early ecSN LCs faint is to reduce the mass of H-rich envelope. Then, the early bright phase gets as short as those in SNe IIb, and the subsequent luminosity is dominated by the interaction from early times because of the small 56Ni mass. The luminosities only from the interaction in our models are comparable to those of faint SNe IIn, which have been suggested to be ecSNe like SN 2008S (Fig. 2). The H-rich envelope may become small enough depending on the amount of mass loss from the progenitors if they are single stars. A large amount of mass can also be lost by ecSN progenitors from binary stars due to the binary evolution (cf. Podsiadlowski et al. 2004). Without the super-AGB wind, faint SNe IIn, such as SN 2008S, may have been observed as SNe IIb from ecSNe with very small mass H-rich envelopes. In some cases, the SN IIb features may be observed at early times and ecSNe with little H-rich envelope may be observed as “Type IIn-b”.
X-ray observations of SNe IIn can play an important role in identifying the SNe IIn of the ecSN origin. Although our ecSN LCs with the plateau phase are optically bright at early times, the high luminosity is not due to the interaction. This means that X-ray luminosities, which are mainly from the interaction, can be very low compared to other SNe IIn with similar optical luminosities, which are powered mainly by the interaction in the optical range as well. For example, the X-ray luminosities of ~1037erg s-1 in 0.1–10 keV at one year after the explosion is expected in our 10-4 M⊙ yr-1 model with the formalism of Fransson et al. (1996). SN IIn 2005ip, which had a similar optical luminosity to our ecSN model at the early plateau (Stritzinger et al. 2012), had an X-ray luminosity of ≃1041erg s-1 in 0.1–10 keV at one year after the explosion (Katsuda et al. 2014). Thus, optically bright but X-ray-faint SNe IIn can be promising candidates for ecSNe. However, if ecSN ejecta mass is small due to the mass loss or binary evolution, the luminosity from the interaction can also be high (van Veelen 2010, see Eq. (2)). In other words, the luminosities of ecSNe with little H-rich envelope would be dominated by the interaction from early times, and their X-ray luminosities can be as bright as those expected from the optical luminosities. Then, the corresponding SNe IIn can also be X-ray bright for a long time, as is observed in, for example, SN 1988Z (van Veelen 2010). Radio observations may also be used to trace the shock properties, but the radio luminosity can be low because of the strong free-free absorption by the dense CSM (cf. Chevalier 1998).
5. Conclusions
We performed numerical LC calculations of ecSNe that exploded within super-AGB winds and obtained the following results. The early bolometric LCs at the plateau phase are not affected by the dense CSM, and they are the same as those from the models without the dense CSM (TBN13). As is shown by TBN13, the early LCs of ecSNe can be as luminous as −17 mag in the optical bands in spite of the small explosion energy (1.5 × 1050 erg) because of the large radius and the small H-rich envelope mass of super-AGB stars. The effect of the super-AGB CSM on the LCs starts to appear after the plateau phase. If there is no CSM, the LCs start to follow the 56Co decay (L ∝ e− t/ (111 days)) after the plateau. However, if a dense CSM from the super-AGB stars exists, the interaction between the SN ejecta and the dense super-AGB CSM provides additional energy to illuminate ecSNe. The bolometric LCs decline much slower than the 56Co decay (L ∝ t−3 / (n −2), where n is the outer density slope of SN ejecta, ρej ∝ r−n, with n ≃ 7–12).
SN 1054 (Crab Nebula) has been suggested to be an ecSN. However, several observational properties have been argued to be difficult to be explained by ecSNe. Sollerman et al. (2001) argued that the final observational record at t ≃ 650 days after discovery indicates that SN 1054 was too bright to be an ecSN, which does not produce enough 56Ni. We confirmed that the interaction with the dense CSM expected from the super-AGB stars can explain the last observational record. Smith (2013) argued that early luminosity is also too bright to be ecSNe. However, it was shown by TBN13 and this work that the luminosity is consistent with ecSNe.
We also compare our LC model to the LCs in a subclass of SNe IIn, which show the LC plateau in the early phase (Type IIn-P). We show that our LC model is consistent and suggest that they are ecSNe exploding within the dense super-AGB CSM. Faint SNe IIn can be ecSNe with the dense CSM but with little H-rich envelope. They may be observed as “Type IIn-b”.
We show that SNe IIn with the LC plateau from ecSNe can be bright in optical at early times, even if the CSM is not dense enough to power the early optical luminosity by the interaction. Thus, their X-ray luminosities from the interaction can be faint in spite of the large optical luminosities in the SNe IIn. As a result, some ecSNe can be observed as optically bright but X-ray-faint SNe IIn. Since the luminosities of ecSNe with little H-rich envelope are dominated by the interaction from early on, their X-ray luminosities can be as bright as those expected from the optical luminosities.
The star was recorded to appear in late May in 1054 in Japanese literature (Meigetsuki), but it is likely that there is an error in the recorded month. The actual date is likely to be one month later, which is consistent with the Chinese records (Stephenson & Green 2002).
Acknowledgments
T.J.M. is supported by Japan Society for the Promotion of Science Postdoctoral Fellowships for Research Abroad (26·51). K.N. is supported by the Grant-in-Aid for Scientific Research (23224004, 23540262, 26400222) from the Japan Society for the Promotion of Science. Numerical computations were carried out on computers at Center for Computational Astrophysics, National Astronomical Observatory of Japan. This research is also supported by World Premier International Research Center Initiative (WPI Initiative), MEXT, Japan. The work in Russia was supported by RF Government grant 11.G34.31.0047, grants for supporting Scientific Schools 5440.2012.2 and 3205.2012.2, and joint RFBR-JSPS grant 13–02–92119.
References
- Anderson, J. P., Habergham, S. M., James, P. A., & Hamuy, M. 2012, MNRAS, 424, 1372 [NASA ADS] [CrossRef] [Google Scholar]
- Blinnikov, S. I., & Tolstov, A. G. 2011, Astron. Lett., 37, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Blinnikov, S. I., Eastman, R., Bartunov, O. S., Popolitov, V. A., & Woosley, S. E. 1998, ApJ, 496, 454 [NASA ADS] [CrossRef] [Google Scholar]
- Blinnikov, S. I., Röpke, F. K., Sorokina, E. I., et al. 2006, A&A, 453, 229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Botticella, M. T., Pastorello, A., Smartt, S. J., et al. 2009, MNRAS, 398, 1041 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, A., Dessart, L., & Livne, E. 2007, Supernova 1987A: 20 Years After: Supernovae and Gamma-Ray Bursters, AIP Conf. Proc., 937, 370 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, K.-J., Woosley, S., Heger, A., Almgren, A., & Whalen, D. 2014, ApJ, submitted [arXiv:1402.4134] [Google Scholar]
- Chevalier, R. A. 1977, in Supernovae, ASSL, 66, 53 [Google Scholar]
- Chevalier, R. A. 1998, ApJ, 499, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Chevalier, R. A., & Irwin, C. M. 2012, ApJ, 747, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Chugai, N. N., Blinnikov, S. I., Cumming, R. J., et al. 2004, MNRAS, 352, 1213 [NASA ADS] [CrossRef] [Google Scholar]
- Davidson, K., & Fesen, R. A. 1985, ARA&A, 23, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Dessart, L., Hillier, D. J., Gezari, S., Basa, S., & Matheson, T. 2009, MNRAS, 394, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Duncan, J. C. 1921, PNAS, 7, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Eldridge, J. J., Genet, F., Daigne, F., & Mochkovitch, R. 2006, MNRAS, 367, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Fesen, R. A., Shull, J. M., & Hurford, A. P. 1997, AJ, 113, 354 [NASA ADS] [CrossRef] [Google Scholar]
- Frail, D. A., Kassim, N. E., Cornwell, T. J., & Goss, W. M. 1995, ApJ, 454, L129 [NASA ADS] [CrossRef] [Google Scholar]
- Fransson, C., Lundqvist, P., & Chevalier, R. A. 1996, ApJ, 461, 993 [NASA ADS] [CrossRef] [Google Scholar]
- Fransson, C., Ergon, M., Challis, P. J., et al. 2013, ApJ, submitted [arXiv:1312.6617] [Google Scholar]
- Fraser, M., Magee, M., Kotak, R., et al. 2013, ApJ, 779, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Habergham, S. M., Anderson, J. P., James, P. A., & Lyman, J. D. 2014, MNRAS, 441, 2230 [NASA ADS] [CrossRef] [Google Scholar]
- Hester, J. J. 2008, ARA&A, 46, 127 [Google Scholar]
- Hoffman, R. D., Müller, B., & Janka, H.-T. 2008, ApJ, 676, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Hubble, E. P. 1928, Leaflet of the Astronomical Society of the Pacific, 1, 55 [NASA ADS] [Google Scholar]
- Janka, H.-T., Müller, B., Kitaura, F. S., & Buras, R. 2008, A&A, 485, 199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, S., Hirschi, R., Nomoto, K., et al. 2013, ApJ, 772, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Kankare, E., Ergon, M., Bufano, F., et al. 2012, MNRAS, 424, 855 [NASA ADS] [CrossRef] [Google Scholar]
- Kasen, D., & Woosley, S. E. 2009, ApJ, 703, 2205 [NASA ADS] [CrossRef] [Google Scholar]
- Katsuda, S., Maeda, K., Nozawa, T., Pooley, D., & Immler, S. 2014, ApJ, 780, 184 [NASA ADS] [CrossRef] [Google Scholar]
- Kawabata, K. S., Maeda, K., Nomoto, K., et al. 2010, Nature, 465, 326 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kiewe, M., Gal-Yam, A., Arcavi, I., et al. 2012, ApJ, 744, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Kitaura, F. S., Janka, H.-T., & Hillebrandt, W. 2006, A&A, 450, 345 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lampland, C. O. 1921, PASP, 33, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, N. 2012, ARA&A, 50, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Lau, H. H. B., Gil-Pons, P., Doherty, C., & Lattanzio, J. 2012, A&A, 542, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lundmark, K. 1921, PASP, 33, 225 [Google Scholar]
- MacAlpine, G. M., & Satterfield, T. J. 2008, AJ, 136, 2152 [NASA ADS] [CrossRef] [Google Scholar]
- Mauerhan, J. C., Smith, N., Silverman, J. M., et al. 2013, MNRAS, 431, 2599 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, J. S. 1973, ApJ, 180, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Minkowski, R. 1971, in The Crab Nebula, Proc. IAU Symp., 46, 241 [NASA ADS] [Google Scholar]
- Miyaji, S., & Nomoto, K. 1987, ApJ, 318, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Miyaji, S., Nomoto, K., Yokoi, K., & Sugimoto, D. 1980, PASJ, 32, 303 [Google Scholar]
- Moriya, T., Tominaga, N., Blinnikov, S. I., Baklanov, P. V., & Sorokina, E. I. 2011, MNRAS, 415, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Moriya, T. J., Blinnikov, S. I., Tominaga, N., et al. 2013a, MNRAS, 428, 1020 [NASA ADS] [CrossRef] [Google Scholar]
- Moriya, T. J., Maeda, K., Taddia, F., et al. 2013b, MNRAS, 435, 1520 [NASA ADS] [CrossRef] [Google Scholar]
- Moriya, T. J., Maeda, K., Taddia, F., et al. 2014, MNRAS, 439, 2917 [NASA ADS] [CrossRef] [Google Scholar]
- Nomoto, K. 1984, ApJ, 277, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Nomoto, K. 1985, in The Crab Nebula and Related Supernova Remnants, eds. M. C. Kafatos, & R. B. C. Henry (London: Cambridge University Press), 97 [Google Scholar]
- Nomoto, K. 1987, ApJ, 322, 206 [NASA ADS] [CrossRef] [Google Scholar]
- Nomoto, K., & Sugimoto, D. 1972, Prog. Theor. Phys., 48, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Nomoto, K., Sugimoto, D., Sparks, W. M., et al. 1982, Nature, 299, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Nugent, R. L. 1998, PASP, 110, 831 [NASA ADS] [CrossRef] [Google Scholar]
- Ofek, E. O., Sullivan, M., Shaviv, N. J., et al. 2014, ApJ, 789, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Poelarends, A. J. T., Herwig, F., Langer, N., & Heger, A. 2008, ApJ, 675, 614 [NASA ADS] [CrossRef] [Google Scholar]
- Podsiadlowski, P., Langer, N., Poelarends, A. J. T., et al. 2004, ApJ, 612, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- Prieto, J. L., Kistler, M. D., Thompson, T. A., et al. 2008, ApJ, 681, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Pumo, M. L., Turatto, M., Botticella, M. T., et al. 2009, ApJ, 705, L138 [NASA ADS] [CrossRef] [Google Scholar]
- Rudie, G. C., Fesen, R. A., & Yamada, T. 2008, MNRAS, 384, 1200 [NASA ADS] [CrossRef] [Google Scholar]
- Satterfield, T. J., Katz, A. M., Sibley, A. R., MacAlpine, G. M., & Uomoto, A. 2012, AJ, 144, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Siess, L. 2007, A&A, 476, 893 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Siess, L. 2010, A&A, 512, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, N. 2013, MNRAS, 434, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Sollerman, J., Cumming, R. J., & Lundqvist, P. 1998, ApJ, 493, 933 [NASA ADS] [CrossRef] [Google Scholar]
- Sollerman, J., Kozma, C., & Lundqvist, P. 2001, A&A, 366, 197 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stephenson, F. R., & Green, D. A. 2002, Historical supernovae and their remnants, International series in astronomy and astrophysics, 5 (Oxford: Clarendon Press) [Google Scholar]
- Stritzinger, M., Taddia, F., Fransson, C., et al. 2012, ApJ, 756, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Taddia, F., Stritzinger, M. D., Sollerman, J., et al. 2013, A&A, 555, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Takahashi, K., Yoshida, T., & Umeda, H. 2013, ApJ, 771, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, T. A., Prieto, J. L., Stanek, K. Z., et al. 2009, ApJ, 705, 1364 [NASA ADS] [CrossRef] [Google Scholar]
- Tolstov, A. G., Blinnikov, S. I., & Nadyozhin, D. K. 2013, MNRAS, 429, 3181 [NASA ADS] [CrossRef] [Google Scholar]
- Tominaga, N., Blinnikov, S. I., & Nomoto, K. 2013, ApJ, 771, L12 (TBN13) [NASA ADS] [CrossRef] [Google Scholar]
- Trimble, V. 1968, AJ, 73, 535 [Google Scholar]
- Trimble, V. 1973, PASP, 85, 579 [NASA ADS] [CrossRef] [Google Scholar]
- van Marle, A. J., Smith, N., Owocki, S. P., & van Veelen, B. 2010, MNRAS, 407, 2305 [NASA ADS] [CrossRef] [Google Scholar]
- van Veelen, B. 2010, Ph.D. Thesis, Utrecht University, The Netherlands [Google Scholar]
- Vos, J. J. 1978, Color Res. Appl., 3, 125 [CrossRef] [Google Scholar]
- Wanajo, S., Nomoto, K., Janka, H.-T., Kitaura, F. S., & Müller, B. 2009, ApJ, 695, 208 [NASA ADS] [CrossRef] [Google Scholar]
- Weaver, T. A. 1976, ApJS, 32, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Wheeler, J. C. 1978, ApJ, 225, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., Blinnikov, S., & Heger, A. 2007, Nature, 450, 390 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Wyckoff, S., & Murray, C. A. 1977, MNRAS, 180, 717 [NASA ADS] [CrossRef] [Google Scholar]
- Young, T. R. 2004, ApJ, 617, 1233 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Bolometric LCs of ecSNe exploding within the super-AGB wind. The LC model without CSM (TBN13) is also shown for comparison. The mass-loss rate of the model is indicated in the figure. The wind velocity is vwind = 20km s-1 for all models. |
| In the text | |
 |
Fig. 2 Comparison of several bolometric LC models. The “no CSM” model and the 10-4 M⊙ yr-1 model are the same as in Fig. 1. The AN1 model is the expected contribution of the luminosity from the interaction in the 10-4 M⊙ yr-1 model which is estimated with the analytic LC model of Moriya et al. (2013b). Adding the “no CSM” and AN1 models, we obtain the “no CSM + AN1” model, which roughly matches the overall LC evolution of the 10-4 M⊙ yr-1 model. The LC model of van Veelen (2010) is obtained from a numerical two-dimensional LC calculation with the similar initial conditions in the 10-4 M⊙ yr-1 model. The AN2 model is the analytic LC estimate for the van Veelen (2010) model. See Sect. 3 for details. |
| In the text | |
 |
Fig. 3 Multicolor LC of the model with 10-4 M⊙ yr-1. |
| In the text | |
 |
Fig. 4 Velocity structures of the models with and without CSM at t ≃ 50 days. |
| In the text | |
 |
Fig. 5 LCs of SN 1054 and our ecSNe exploded within super-AGB winds. The V-band LCs of the models are shown. The observations of SN 1054 are based on human eyes, which are sensitive at around the V band (Vos 1978). Note that the V-band and R-band magnitudes are similar in our models (Fig. 3). |
| In the text | |
 |
Fig. 6 Comparison of the observed LC of SN 2009kn (Kankare et al. 2012) and the multicolor LC model of the ecSN exploded in the super-AGB wind. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


