| Issue |
A&A
Volume 569, September 2014
|
|
|---|---|---|
| Article Number | A86 | |
| Number of page(s) | 11 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201424104 | |
| Published online | 29 September 2014 | |
Radio emissions from pulsar companions: a refutable explanation for galactic transients and fast radio bursts
1 LUTH, Observatoire de Paris, CNRS, Université Paris Diderot, 5 place Jules Janssen, 92190 Meudon, France
e-mail: fabrice.mottez@obspm.fr
2 LESIA, Observatoire de Paris, CNRS, UPMC, Université Paris Diderot, 5 place Jules Janssen, 92190 Meudon, France
e-mail: philippe.zarka@obspm.fr
Received: 30 April 2014
Accepted: 28 July 2014
Context. The six known highly dispersed fast radio bursts are attributed to extragalactic radio sources that are of unknown origin but extremely energetic. We propose here a new explanation that does not require an extreme release of energy and involves a body (planet, asteroid, white dwarf) orbiting an extragalactic pulsar.
Aims. We investigate a theory of radio waves associated with such pulsar-orbiting bodies. We focus our analysis on the waves emitted from the magnetic wake of the body in the pulsar wind. After deriving their properties, we compare them with the observations of various transient radio signals to determine whether they could originate from pulsar-orbiting bodies.
Methods. The analysis is based on the theory of Alfvén wings: for a body immersed in a pulsar wind, a system of two stationary Alfvén waves is attached to the body, provided that the wind is highly magnetised. When they are destabilised through plasma instabilities, Alfvén wings can be the locus of strong radio sources that are convected with the pulsar wind. By assuming a cyclotron maser instability operating in the Alfvén wings, we make predictions about the shape, frequencies, and brightness of the resulting radio emissions.
Results. Because of the beaming by relativistic aberration, the signal is seen only when the companion is perfectly aligned between its parent pulsar and the observer, as is the case for occultations. For pulsar winds with a high Lorentz factor (≥104), the whole duration of the radio event does not exceed a few seconds, and it is composed of one to four peaks that last a few milliseconds each and are detectable up to distances of several Mpc. The Lorimer burst, the three isolated pulses of PSR J1928+15, and the recently detected fast radio bursts are all compatible with our model. According to it, these transient signals should repeat periodically with the companion’s orbital period.
Conclusions. The search of pulsar-orbiting bodies could be an exploration theme for new- or next-generation radio telescopes.
Key words: pulsars: general / radiation mechanisms: non-thermal / relativistic processes / minor planets, asteroids: general / planet-star interactions
© ESO, 2014
1. Introduction
Lorimer et al. (2007) discovered the first highly dispersed, bright radio burst in a Parkes pulsar survey. The time–frequency dispersion of this burst perfectly followed a 1 /f-2 law with a dispersion measure (DM) ~375 pc.cm-3, out of which no more than 15% could be attributed to the wave path in our Galaxy. Therefore its origin was assumed to be extragalactic, with a source distance of about 500 Mpc (z = 0.12), well outside the local group of galaxies. As a consequence of this large distance and the strong burst intensity (30 Jansky – 1 Jy = 10-26 Wm-2 Hz-1), the inferred emitted power was extremely large, ~1033 J (Thornton et al. 2013). The fixed–frequency duration of this burst is ≤5 ms, with no detectable scatter–broadening, so that the natural origin of this exceptional burst was debated. But recently, five similar burtst (albeit less intense, 0.4–1.3 Jy) have been found in Parkes pulsar surveys (Keane et al. 2011; Thornton et al. 2013), and were called fast radio bursts (FRB). They emanate from different regions of the sky. Their fixed–frequency durations extend from shorter than 1.1 ms to 5.6 ms. Interestingly, one of these bursts also exhibits an exponential scattering tail, supporting its natural origin. With DMs between ~550 and 1100 pc cm-3, all these bursts are attributed to extragalactic radio sources at cosmological distances in the range 1.7–3.2 Gpc. Their physical origin is unknown but again assumed to be extremely energetic. No event such as a supernova or a gamma-ray burst was observed simultaneously with an FRB. Proposed explanations include the annihilation of a mini black hole (Keane et al. 2012), binary white dwarf mergers (Kashiyama et al. 2013), neutron star mergers (Totani 2013), or implosions of supra-massive neutron stars shortly after their birth (Zhang 2014). All these explanations imply that FRBs are isolated events that occur only once from a given source. Other scenarii might lead to irregularly repeatable pulses, such as a giant pulse from a young pulsar with a low burst rate (Keane et al. 2012), or rare eruptions of flaring main-sequence stars within one kpc (Loeb et al. 2014).
We propose here a new explanation that does not require an extreme release of energy, but is still consistent with the observations. This explanation involves a body orbiting a pulsar: planet, asteroid, white dwarf, or even another neutron star. Many such objects are known in our Galaxy. Most millisecond pulsars are in binary systems, the companion being in many cases a white dwarf (Savonije 1987) – possibly of low mass (Bailes et al. 2011) – or a neutron star (Deller et al. 2013). Triple systems containing at least a pulsar and a white dwarf have been found (Ransom et al. 2014). Five planets, distributed within three planetary systems, are known to orbit pulsars (Wolszczan & Frail 1992; Thorsett et al. 1993; Bailes et al. 2011). All of them were detected by analysing the shift of the pulsar period Pobs in terms of the position of the barycentre of the star, which led to the deduction that it was induced by the motion of orbiting planets. It is likely that other pulsar planets remain to be discovered. Finally, asteroid belts are likely to exist around pulsars, and they have been invoked by several authors to explain timing irregularities (Shannon et al. 2013), anti-glitches (Huang & Geng 2014), or burst intermittency (Cordes & Shannon 2008; Deneva et al. 2009; Mottez et al. 2013). In this paper we investigate the ability of these bodies immersed in a pulsar wind to produce radio waves.
Mottez & Heyvaerts (2011b) showed that a pulsar-orbiting body necessarily moves in the wind of the pulsar and not in the light-cylinder, and that its interaction with the wind causes a system of strong electric currents flowing along the body and in the plasma carried by the wind. The power associated with these currents can be higher than 1022 W. We explore what happens if a fraction of this power is converted into radio-frequency electromagnetic waves. Without needing to go into the detailed physics of the electromagnetic waves production, we can make predictions about the properties of the subsequent radio waves, and we study if and how this radio signal could be detected by ground-based radio-telescopes.
Our analysis is based on the electrodynamic interaction of the orbiting body and the pulsar wind derived in Mottez & Heyvaerts (2011a,b) and Heyvaerts et al. (2012). This interaction is the relativistic analogue of the Io-Jupiter interaction, which has been described in terms of a unipolar inductor circuit or a pair of Alfvén wings (see the review by Saur et al. 2004) and transposed to exoplanet-star interaction by Zarka et al. (2001), Willes & Wu (2005), and Zarka (2007). In our case, the magnetised plasma flow around the body is not corotating like in the previous papers, but is a wind as in Preusse et al. (2006), but here strongly relativistic.
In Sect. 2 we analyse the system of Alfvén wings generated by the interaction of the body with the pulsar wind. Then, after eliminating the possibility that the radio emission could come from the vicinity of the body (Sect. 3), we study the generation and characteristics of the radio emission produced by a wind-convected source along the Alfvén wings (Sect. 4). In Sect. 5 we compare our predictions with past observations of a few remarkable radio transients. Finally in Sect. 6 we address specific questions raised by our explanation, and provide perspectives for observations that can confirm or refute our theory.
2. Interaction with the pulsar wind
A body orbiting a pulsar with a period exceeding a few minutes is immersed in the pulsar wind, and the interaction between the pulsar and its companion is ruled by electrodynamic processes. The distance of the known pulsar companions is typically several hundreds of light cylinder radii (rLC).
Among the many pulsar wind models, those of Goldreich & Julian (1969) and Michel (1969), or more recent ones (Bucciantini et al. 2006), show that for a pulsar with an aligned magnetic field, beyond a distance of hundreds of rLC from the star, the plasma wind flow is radial (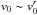 ), the magnetic field energy dominates the plasma kinetic energy (B2 ≫ μ0ργc2 – the wind is said to be “Poynting-flux dominated”), and the plasma velocity is highly relativistic. The Lorentz factor is unknown but expected to be in the range γ ~ 101 − 107. The magnetic field is quasi-azimuthal (B ~ Bφ ≫ Bpoloidal). The flow and Alfvén velocities (v0 and VA) are very close to the speed of light and, if the above-quoted models are correct, the wind is sub-Alfvénic: v0<VA (Mottez & Heyvaerts 2011b).
), the magnetic field energy dominates the plasma kinetic energy (B2 ≫ μ0ργc2 – the wind is said to be “Poynting-flux dominated”), and the plasma velocity is highly relativistic. The Lorentz factor is unknown but expected to be in the range γ ~ 101 − 107. The magnetic field is quasi-azimuthal (B ~ Bφ ≫ Bpoloidal). The flow and Alfvén velocities (v0 and VA) are very close to the speed of light and, if the above-quoted models are correct, the wind is sub-Alfvénic: v0<VA (Mottez & Heyvaerts 2011b).
2.1. Alfvén wings
Because the fast magnetosonic waves are even faster than VA, the wind is also slower than the fast magnetosonic waves, and there is thus no MHD shock ahead of an obstacle in the wind. The pulsar-orbiting body is thus in direct contact with the wind. Following the idea developed in Neubauer (1980) and applied by Mottez & Heyvaerts (2011b) in the context of pulsar winds, a pair of electric current circuits are induced by the body–wind interaction, carried by two stationary Alfvénic structures called Alfvén wings. These wings are attached to the body on one side, and extend far into space into the flowing plasma on the other side.
The azimuthal magnetic field of the pulsar wind is 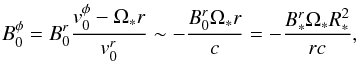 (1)where
(1)where 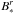 , Ω∗, and R∗ are respectively the star surface radial magnetic field, its rotation circular frequency, and radius. The convection electric field
, Ω∗, and R∗ are respectively the star surface radial magnetic field, its rotation circular frequency, and radius. The convection electric field 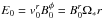 , directed perpendicularly to the wind flow and to the magnetic field, is the engine of the Alfvén wings. It induces a potential drop U = 2RbE0 along the body of radius Rb, that is the cause of a current flowing along the planet and in the surrounding plasma.
, directed perpendicularly to the wind flow and to the magnetic field, is the engine of the Alfvén wings. It induces a potential drop U = 2RbE0 along the body of radius Rb, that is the cause of a current flowing along the planet and in the surrounding plasma.
When the Alfvén velocity is close to c, as in a pulsar wind, the total electric current is 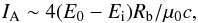 (2)where Ei is an electric field along the body caused by its ionospheric or surface finite conductivity. The power dissipated by Joule effect along the body is maximised when internal and external loads match, that is, when Ei = E0/ 2. For a pulsar with a rotation period of 1 s and an Earth-like orbiting body at 0.2 UA, IA ~ 1011 A. This current has the same order of magnitude as the current that powers the whole pulsar magnetosphere (Goldreich & Julian 1969). For bodies orbiting recycled (millisecond) pulsars, the Alfvén wing current is smaller than the Goldreich & Julian current by one or two orders of magnitude (~109 A) because of a weaker wind magnetic field, but it is still not negligible.
(2)where Ei is an electric field along the body caused by its ionospheric or surface finite conductivity. The power dissipated by Joule effect along the body is maximised when internal and external loads match, that is, when Ei = E0/ 2. For a pulsar with a rotation period of 1 s and an Earth-like orbiting body at 0.2 UA, IA ~ 1011 A. This current has the same order of magnitude as the current that powers the whole pulsar magnetosphere (Goldreich & Julian 1969). For bodies orbiting recycled (millisecond) pulsars, the Alfvén wing current is smaller than the Goldreich & Julian current by one or two orders of magnitude (~109 A) because of a weaker wind magnetic field, but it is still not negligible.
x ratio, Afvén wing angles δ+ and δ− with the radial wind direction, and proper time τ+ and τ− spent by the CMI sources in the wings as functions of the companion distance r and the wind Lorentz factor γ0.
For a pulsar whose magnetic dipole axis is aligned with the rotation axis and that has a radial wind flow and a mostly azimuthal magnetic field in the companion’s environment, the angle δ between the invariant vector Vs, i.e. the direction of the Alfvén wing, and the radial direction, can be estimated within simple models.
In most wind models for aligned pulsars (see Kirk et al. (2009) for a review), the wind is characterised by two invariants along its flow: the neutron star magnetic flux Ψ, and the mass flux f, defined as 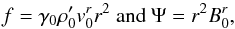 (3)with γ0 the Lorentz factor associated with the unperturbed wind velocity
(3)with γ0 the Lorentz factor associated with the unperturbed wind velocity 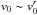 , and
, and 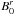 the radial magnetic field. Estimates of the Lorentz factor based on various observations and models vary over a fairly wide range from 101 to 107 (Kirk et al. 2009). The angle δs of the Alfvén wings relative to the local magnetic field is
the radial magnetic field. Estimates of the Lorentz factor based on various observations and models vary over a fairly wide range from 101 to 107 (Kirk et al. 2009). The angle δs of the Alfvén wings relative to the local magnetic field is ![\begin{equation} \label{eq_delta} \delta_s=s\arctan{ \left[\frac{x}{\gamma_0 \left(\sqrt{1+x^2}-s \right)}\right]}, \end{equation}](/articles/aa/full_html/2014/09/aa24104-14/aa24104-14-eq80.png) (4)where s = ± 1, and x is a dimensionless parameter defined by
(4)where s = ± 1, and x is a dimensionless parameter defined by 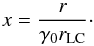 (5)Details of this computation are given in Appendix A.
(5)Details of this computation are given in Appendix A.
When x ≫ 1, with Eq. (A.7) and γ0 ≫ 1, Eq. (4) reduces to 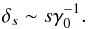 (6)This means that the two Alfvén wings make two symmetric and small angles relative to the radial direction. But we have no a priori evidence of the value of x. We might as well have x ≪ 1. In that case, the two Alfvén wings have an asymmetric configuration with an angle
(6)This means that the two Alfvén wings make two symmetric and small angles relative to the radial direction. But we have no a priori evidence of the value of x. We might as well have x ≪ 1. In that case, the two Alfvén wings have an asymmetric configuration with an angle 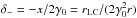 even smaller than in the previous case, and an angle δ+ = arctan2 /γ0x = 2rLC/r.
even smaller than in the previous case, and an angle δ+ = arctan2 /γ0x = 2rLC/r.
A few examples of δ± angles are displayed in Table 1 for various values of r and γ0.
We can consider two types of sources of radio-emissions: the source can be (1) attached to the companion body, or more precisely, to a plasma with a low velocity in the body’s frame of reference; or it can be (2) carried along with the pulsar wind plasma.
3. Radio emission from a source linked to the companion
The plasma close to the pulsar companion can be destabilised by the Alfvén wing’s current flowing along the body, and excite a high level of coherent electromagnetic waves. Then, in the reference frame of the companion, the radio emission may be sent at various angles, as is observed near solar system planets connected to Alfvén wings. For instance, Jupiter’s Galilean satellite Io is embedded in the co-rotating magnetosphere of Jupiter and is the source of two Alfvén wings (Neubauer 1980; Saur et al. 2004).
The wings in the vicinity of Jupiter are strong radio emitters of decametric waves that are observed with ground-based radio-telescopes. Their frequencies cover the range of local electron cyclotron frequencies in the source regions. It is not clear if the sources are fixed relative to the Alfvén wings or if they are convected by the co-rotating plasma, but in both cases, their velocity would be too low to be measured by Doppler shift.
For a pulsar companion, sources of radio waves attached to the companion or to the co-rotating plasma in its vicinity would also have a non-relativistic velocity relative to the observer. The relativistic aberration would be negligible as well and would not cause any focussing of the emitted energy. Therefore, even if the source is powerful, these radio waves would be very faint at interstellar distances and the chances to detect them from Earth would be very low. As a comparison, the intense Io-Jupiter radio emission is not detectable against the Galactic background beyond 1 pc distance even with the largest existing radio-telescopes (Farrell et al. 2004; Zarka 2004a). Detection at distances of the order of a kpc would thus require an emission >106 times more intense.
Because their emission would not be detectable from Earth, we did not investigate the assumption of radio sources attached to the companion further.
4. Sources of radio emission carried by the wind along the wings
Radio emissions might also be emitted from the plasma wind when it crosses the Alfvén wings, far from the pulsar companion. The sources would be convected with the wind along the Alfvén wings. Because the wind is relativistic, the sources would have a relativistic motion relative to an observer on Earth. More precisely, we assume that the source propagates along the Alfvén wing, and that the source velocity projected along the (radial) wind direction is the same as that of the wind. Then, the source velocity modulus is 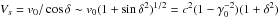 . The requirement that Vs<c implies
. The requirement that Vs<c implies 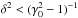 . It is satisfied with the two wings if x ≫ 1, and with the δ− wing only when x ≪ 1. Thus, at least one source can always exist.
. It is satisfied with the two wings if x ≫ 1, and with the δ− wing only when x ≪ 1. Thus, at least one source can always exist.
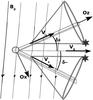 |
Fig. 1 Alfvénic wake of the pulsar’s companion body seen from above the equatorial plane. The velocity of the source regions Vs is assumed to be along the Alfvén wings. The thick grey lines represent the cones in which emitted radio waves are focussed. We call them the angular emission patterns. The observer’s frame related to the upper wing on the figure (making an angle δ+ with the wind) is indicated by the Ox and Oz axes. It is fixed relative to the pulsar companion. The two stars mark the region of the angular emission patterns of highest wave intensity (see Sect. 4). |
4.1. Plasma flow, instability, and radio waves
We define the observer’s frame in the Cartesian coordinate system where Oz is aligned with the Alfvén wing velocity Vs and where the magnetic field is contained in the plane xOz (cf. Fig. 1). The source frame has the same axes, but moves at velocity Vs = Vsez along Oz. The pulsar wind velocity in the observer’s frame is (v0sinδ,0,v0cosδ). The wind velocity in the source frame, noted v′, is given by ![\begin{eqnarray} v'_z = \frac{v_0 \cos \delta -V_s}{1-\frac{V_s^2 \cos \delta}{c^2}} &\mbox{ and }& v'_x= \gamma v_0 \sin \delta \left[1+\frac{V_s}{c^2}v'_z\right], \end{eqnarray}](/articles/aa/full_html/2014/09/aa24104-14/aa24104-14-eq101.png) (7)where
(7)where 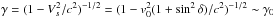 . If the source propagates with the wind, as assumed here, then Vs = v0cosδ,
. If the source propagates with the wind, as assumed here, then Vs = v0cosδ, 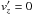 ,
, 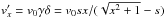 is a significant fraction of v0. While in the observer’s frame the magnetic field is mostly azimuthal (
is a significant fraction of v0. While in the observer’s frame the magnetic field is mostly azimuthal (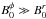 ), this is not true in the source frame. In that frame the magnetic field is
), this is not true in the source frame. In that frame the magnetic field is 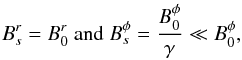 (8)thus a large component parallel to the wing exists, as illustrated in Fig. 2.
(8)thus a large component parallel to the wing exists, as illustrated in Fig. 2.
In terms of particle distribution (a Lorentz invariant), f(r,γmv) = f(r′,γmv′), so that a distribution that is shifted in the vz direction in the observer’s frame is shifted in the 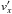 direction in the source frame. The particle distribution is then highly non-gyrotropic, since Ox is a direction that creates a large angle with the magnetic field in the source frame. This shifted distribution is expected to be a powerful energy source for the cyclotron maser instability (CMI; Freund et al. 1983; Wu 1985). We note that the CMI theory is based on special relativity effects, even when applied in the midly relativistic plasma of main-sequence stars and in the Io Alfvén wings. The CMI does not exist in a non-relativistic plasma; it requires a particle population with non-negligible v/c.
direction in the source frame. The particle distribution is then highly non-gyrotropic, since Ox is a direction that creates a large angle with the magnetic field in the source frame. This shifted distribution is expected to be a powerful energy source for the cyclotron maser instability (CMI; Freund et al. 1983; Wu 1985). We note that the CMI theory is based on special relativity effects, even when applied in the midly relativistic plasma of main-sequence stars and in the Io Alfvén wings. The CMI does not exist in a non-relativistic plasma; it requires a particle population with non-negligible v/c.
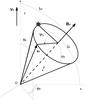 |
Fig. 2 Directions of the magnetic field and of the radio waves emitted in the source frame: the wave vectors are along a cone of summit angle αs, and of an axis parallel to the magnetic field Bs. The wave vector position on that cone is parametrised by the angle Ψs. The inclination of the magnetic field with the wing axis Oz is λs. The cylindrical angular coordinates θs and ϕs of the wave vector are defined relatively to the z axis. As in Fig. 1, the star (at Ψs = 0) marks the angle of emission of the most intense CMI waves. |
We did not compute the CMI growth rate here. It would require to know the precise shape of the particle distribution function, for which we have no measurement or theoretical arguments that would justify any choice at this stage. Nevertheless, the crucial part of the CMI theory concerns the cyclotron resonance condition. It is developed in the relativistic context without any approximation of the Lorentz factor (Wu 1985). In that general context, the most unstable waves have the following properties in the reference frame of the source:
-
The wave vectors are aligned along a cone of summitangle αs whose axis is the magnetic field in the source reference frame.
-
Because the average velocity of the distribution is low in the direction of the magnetic field, the wave vectors are expected to make a large angle with the magnetic field. We can consider that the unstable wave vectors lie along a cone of aperture half-angle αs in the range 85° − 90°.
-
The growth rate does not depend on the azimuth Ψs of the wave vector along the cone if the distribution function is gyrotropic (i.e. of the form f = f(r,p∥,p⊥)). In contrast, the growth rate can depend strongly on Ψs if f explicitly depends on the three components of p. In the present case, as shown above, the distribution is non-gyrotropic, and the intensities of the waves should depend on Ψs, the most intense waves on this cone corresponding to wave vectors k in the x direction, mostly in the direction of the wind (+ x for the δ + wing), and possibly also in the opposite direction.
-
The frequency of the emitted waves is close to the local electron gyrofrequency ω ≃ ωce in the linear approximation −x for the δ + wing.
-
When the growth rate is high, non-linear effects tend to produce harmonics and broaden the emitted frequency spectrum.
How much time does an element of plasma of the wind spend in the Alfvén wing? We assume that the diameter of the Alfvén wing is ηRb where η is of the order of one. The inclination angle of the wind relative to the Alfvén wing being δ = 1 /γ, an element of plasma of the wind spends a time τo ~ ηRb/δv0 in the wing, in the observer’s reference frame. In the reference frame of the source, this time is 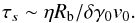 (9)A few values of τs are displayed in Table 1, where it is assumed that ηRb = 1000 km, and v0 ~ c. We can see that these times currently exceed a few milliseconds, especially in the δ− wing. This is much longer than the typical growth time of the CMI, which can reach saturation in tens to hundreds of microseconds in much less anisotropic and energetic plasmas (Pritchett 1986; Le Queau & Roux 1987; Le Queau 1988).
(9)A few values of τs are displayed in Table 1, where it is assumed that ηRb = 1000 km, and v0 ~ c. We can see that these times currently exceed a few milliseconds, especially in the δ− wing. This is much longer than the typical growth time of the CMI, which can reach saturation in tens to hundreds of microseconds in much less anisotropic and energetic plasmas (Pritchett 1986; Le Queau & Roux 1987; Le Queau 1988).
4.2. Direction of radio waves emitted by the cyclotron maser instability
Let θs and ϕs define the direction of the electromagnetic wave vector in the source frame (Fig. 2). Because of the relativistic aberration, these angles become in the observer’s frame: 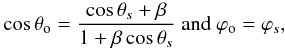 (10)where β = Vs/c. A well known consequence of Eq. (10) is that for high values of γ and for any radiation angle θs> 0, the corresponding angles θo in the observer’s frame are smaller than γ-1. We will show that this is correct provided that γ ≫ 103. The luminosity of the emission is also affected by the aberration. Let dWo/dΩo be the energy radiated in the solid angle Ωo in the observer’s reference frame, and dWs/dΩs the same ratio in the source frame, then
(10)where β = Vs/c. A well known consequence of Eq. (10) is that for high values of γ and for any radiation angle θs> 0, the corresponding angles θo in the observer’s frame are smaller than γ-1. We will show that this is correct provided that γ ≫ 103. The luminosity of the emission is also affected by the aberration. Let dWo/dΩo be the energy radiated in the solid angle Ωo in the observer’s reference frame, and dWs/dΩs the same ratio in the source frame, then 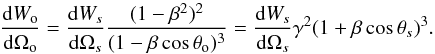 (11)For an isotropic radiation in the source frame,
(11)For an isotropic radiation in the source frame, 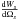 is constant and the main effect on
is constant and the main effect on 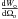 is the amplification by ~γ2 resulting from the transformation of the solid angle of emission from the source frame to the observer’s frame. For instance, all the radiation for θs> 0 is radiated in the observer’s frame in the solid angle dΩo ~ πγ-2 sr delimited by the cone of summit angle γ-1, which is very small if γ ≫ 1. Conversely, all the radiation for θs< 0 is emitted in the other directions corresponding to a solid angle Ω = π(4 − γ-2) sr. Therefore, the power angular density dWo/dΩo is much higher inside the cone of summit angle γ-1 than in the other directions. That is why we can say that most of the observable radiation is contained within the cone of angle γ-1. If γ ≫ 1, the amplitude of the signal is lower by orders of magnitude in the other directions.
is the amplification by ~γ2 resulting from the transformation of the solid angle of emission from the source frame to the observer’s frame. For instance, all the radiation for θs> 0 is radiated in the observer’s frame in the solid angle dΩo ~ πγ-2 sr delimited by the cone of summit angle γ-1, which is very small if γ ≫ 1. Conversely, all the radiation for θs< 0 is emitted in the other directions corresponding to a solid angle Ω = π(4 − γ-2) sr. Therefore, the power angular density dWo/dΩo is much higher inside the cone of summit angle γ-1 than in the other directions. That is why we can say that most of the observable radiation is contained within the cone of angle γ-1. If γ ≫ 1, the amplitude of the signal is lower by orders of magnitude in the other directions.
Theories of the CMI tell us, however, that the radio waves are not emitted isotropically, but rather along conical sheets of aperture angle αs varying with the frequency in a range close to 90°. If the particle distribution is non-gyrotropic, the intensity of the waves can be highly variable along the cone walls.
We first consider the direction of the wave vectors associated with a single Alfvén wing aligned with Oz. We consider waves whose vectors k form a cone of angle αs with the magnetic field in the source reference frame. What are the wave directions in the observer’s reference frame? Let λs be the angle between the emission cone axis and the z direction in the source frame (Fig. 2). Because the emission cone axis is parallel to the magnetic field, tanλs = r/γrLC. A single wave vector is characterised by the cone of axis B/B, of summit angle αs, and by its position along the cone, parametrised by the angle Ψs. This wave vector direction is characterised by the two angles θs and ϕs in the spherical coordinates frame associated with the Oz axis in the source frame. The coordinates of the unit vector parallel to the wave vector are 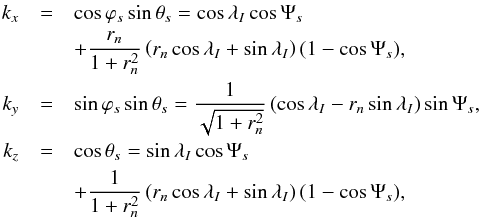 (12)where λI = π/ 2 − λs + αs and rn = r/γrLC = tanλs. The direction angles θs and ϕs can be easily derived and expressed in the observer’s frame following Eq. (10). When β is close to one, it is better to use the following relation which resolves a problem of numerical degeneracy,
(12)where λI = π/ 2 − λs + αs and rn = r/γrLC = tanλs. The direction angles θs and ϕs can be easily derived and expressed in the observer’s frame following Eq. (10). When β is close to one, it is better to use the following relation which resolves a problem of numerical degeneracy, 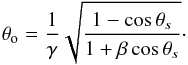 (13)The above angles are relative to a single Alfvén wing, and the z axis corresponds to the wing direction.
(13)The above angles are relative to a single Alfvén wing, and the z axis corresponds to the wing direction.
As mentioned, the luminosity is expected to be much higher in the direction corresponding to Ψs = 0.
When the two wings are considered, it is better to define a Z axis along the wind direction, and to shift the above values of θo (related to a wing z axis) by an angle δ− for one wing and δ+ for the other. The directions of the waves are plotted in Fig. 3 in the observer’s frame for a planet at 0.1 AU from the star, an emission angle αs = 85°, and γ = 10 (the low range of γ for a pulsar wind). The small grey disks represent the field illuminated by waves emitted at an angle ≤90° from each Alfvén wing axis in the source frame (cf. Fig. 2) in the approximation of very large γ. There is one such disk for each Alfvén wing, whose border corresponds to emission at 90° from the Alfvén wing axis in the source frame. These circles are the same as those that limit the cones represented on Fig. 1. Because these grey disks do not encompass the other circles, the approximation of a very large γ is not valid when γ = 10.
The angular emission patterns can be related to time intervals. We first neglect the oscillation of the (tilted) magnetic field with the pulsar spin frequency. The simplest trajectory of the line of sight to the observer on these figures is a straight line uniformly parametrised in time, deduced from the orbital motion of the pulsar companion. In Fig. 3, there would be four intersections of the emission beam (large circles) with this straight line, two of which are associated with a high-amplitude signal. An angle interval Δ corresponds to a time interval τ given by 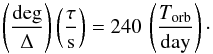 (14)When the oscillation of the magnetic field is taken into account, the whole figure rotates back and forth around the origin at the pulsar period with an angular amplitude depending mainly on the pulsar tilt angle. Then, provided that the time τ is longer than the pulsar spin period, we can have several pulses for each crossing of the beam pattern instead of one longer pulse when the oscillation is negligible.
(14)When the oscillation of the magnetic field is taken into account, the whole figure rotates back and forth around the origin at the pulsar period with an angular amplitude depending mainly on the pulsar tilt angle. Then, provided that the time τ is longer than the pulsar spin period, we can have several pulses for each crossing of the beam pattern instead of one longer pulse when the oscillation is negligible.
 |
Fig. 3 Directions of the radio waves in the observer’s frame. The two smaller tangent grey disks in the middle of the plot correspond to the waves that are beamed at ≤90° from the Alfvén wing axis in the source frame in the approximation of very high γ values (see text for the precise meaning of “very high”). The two large circles (black lines) are the radio-beaming patterns associated with the CMI. They are defined by x = δ± + θocosϕo and y = θosinϕo, with θo and ϕo the cylindrical angular coordinates of the wave vector in the observer’s reference frame of each Alfvén wing. θo and ϕo are related via Eq. (10) (or Eq. (13)) to the wave vector coordinates in the source frame θs and ϕs given by Eq. (12). The most intense emissions correspond to the innermost intersection of each large circle with the horizontal axis. Here γ = 10, r = 0.1 AU and αs = 85°. With these parameters, x = 78. The stars mark the directions of the most intense radio emissions. |
For γ = 10, the angle λs between the cone axis and Oz in the source frame is large, so that a large part of the emission cone of summit angle 85° is beamed at >90° from Oz. In the observer’s frame, we see in Fig. 3 that these radio emissions make a large angle – of tens of degrees – with the wind direction. Because of the orbital motion of the pulsar companion, a distant observer will cut the emission diagram along a horizontal line shifted from the horizontal axis of Fig. 3 by the inclination of the companion’s orbital plane as seen from Earth. If the pulsar magnetic field is tilted on its rotation axis, then the beaming pattern will oscillate at the pulsar spin period (and thus the observer will cut the emission diagram along a sinusoidal curve). In all cases, the observer probably intersects the radio emission diagram four times during a full companion’s orbit. Because of the relativistic transformation of solid angles and because Ψs = 0 corresponds to much more powerful emissions than in the other directions, however, the most intense emissions will be seen at the crossings of the radio-beaming diagram close to the origin, inside the grey disks.
The situation is quite different for γ = 1000, as shown in Fig. 4. The range of angles of emission is now much smaller than 1°. Therefore, the chances of being in the correct line of sight are much lower. If it is so, the observer can see the radio emission up to four times (out of which two correspond to intense emission) that are much closer in time to each other. At a distance of 0.1 AU from a pulsar with a mass of 1.4 M⊙, the orbital period is ~10 days, and the typical separation of 0.16° between the two innermost intersections of the radio-beaming pattern correspond to time intervals of ~6 minutes. Because of the already mentioned anisotropy of the distribution function, the two inner regions (near the two inner intersections with the horizontal line) correspond to much higher amplitudes than the two others.
Only the emission pattern associated with δ− is shown in Fig. 5 for γ = 106. As we can see in Table 1, the time spent by the CMI sources in the wing δ− is 85 s, while it is about 0.1 μs in the other wing. Furthermore, CMI source cannot propagate at the wind velocity along the δ+ wing when x ≪ 1. The directions of emission associated with the δ− wing almost coincide with the tangent circle that limits the grey disk (they coincide exactly for αs = 90°) and the corresponding angles are now of the order of 0.2′′. We chose a distance r = 0.01 AU, corresponding to Torb ~ 9 h (with a neutron star of 1.4 solar mass). According to Eq. (14), the time interval between two circle crossings is shorter than 5 ms. The vicinity of the intersection of the circle with the horizontal line, on the right-hand side, corresponds to the highest wave amplitude.
For γ = 105 and r = 0.1 UA, the figure (not shown) has the same aspect as in Fig. 5, with an anglular diameter ~2′′ instead of 0.2′′. This corresponds to a time interval of 1.3 s.
Because most pulsar wind models are based on highly relativistic flows, and because, as we show below, it may explain some already existing observations, we focus the following analysis on the cases where γ> 103.
 |
Fig. 4 Directions of the radio waves in the observer’s frame. Same as in Fig. 3, but for γ = 1000. As in Fig. 3, r = 0.1 AU and αs = 85°. These parameters correspond to x = 0.78. |
 |
Fig. 5 Directions of the radio waves in the observer’s frame. Same as in Fig. 3, but for γ = 106 and r = 0.01 AU. As in Fig. 3, αs = 85°. These parameters correspond to x = 0.78 × 10-5. Here only the emission pattern associated with δ− is represented. The star marks the direction of the most intense radio emissions. |
4.3. Range of frequencies
As mentioned in Sect. 4.1, we first considered that the waves are emitted at frequencies close to the local gyrofrequency fc,s in the reference frame of the sources. Then we converted the frequency to fc,o into the frame of the observer. Using Eqs. (1) and (8) and considering that 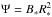 , the gyrofrequency in the source frame is
, the gyrofrequency in the source frame is 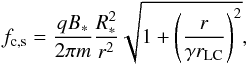 (15)with q and m the electron’s charge and mass. The Doppler-Fizeau shift along the line of sight towards the observer provides the observed frequency
(15)with q and m the electron’s charge and mass. The Doppler-Fizeau shift along the line of sight towards the observer provides the observed frequency ![\begin{eqnarray} \nonumber f_{\rm c,o}&=&25 \gamma \left(\frac{B_{*}}{10^5 \mbox{T}} \right) \left(\frac{1 \mbox{AU}}{r}\right)^{2} \left( \frac{R_*}{10^4 \mbox{m}} \right)^{2} \\ & & \times \left\{1+ \left[\frac{\pi \; 10^5}{\gamma} \left(\frac{10 \mbox{ms}}{T_{*}}\right)\left(\frac{r}{1 \mbox{AU}}\right) \right]^2\right\}^{1/2}\cdot \label{eq_omega_observer} \end{eqnarray}](/articles/aa/full_html/2014/09/aa24104-14/aa24104-14-eq205.png) (16)Figure 6 displays the observed frequency fc,o as a function of the Lorentz factor γ of the pulsar wind for various companion distances from a millisecond pulsar. For γ< 105 the frequencies are in the range of meter to decameter radio waves, typically reachable with LOFAR (van Haarlem et al. 2013) and (in the future) SKA1. The GHz range of frequencies is reached for companions within 0.2 AU when the Lorentz factor is higher than 106. The sub-millimeter range is reached only for very close planets and very fast pulsar winds (γ> 107).
(16)Figure 6 displays the observed frequency fc,o as a function of the Lorentz factor γ of the pulsar wind for various companion distances from a millisecond pulsar. For γ< 105 the frequencies are in the range of meter to decameter radio waves, typically reachable with LOFAR (van Haarlem et al. 2013) and (in the future) SKA1. The GHz range of frequencies is reached for companions within 0.2 AU when the Lorentz factor is higher than 106. The sub-millimeter range is reached only for very close planets and very fast pulsar winds (γ> 107).
Figure 7 displays the observed frequency/Lorentz factor relation for a standard pulsar of period T∗ = 1 s and magnetic field B∗ = 108 T. Up to now, no planet is known to orbit a standard pulsar, but other companions are likely to exist. For such systems, observed frequencies will be significantly higher than those associated with millisecond pulsar companions. They will remain in the radio range for distant companions, but could reach the infrared domain for close-by companions and high-speed winds.
 |
Fig. 6 Cyclotron frequency in the observer’s frame as a function of the pulsar wind Lorentz factor γ, from Eq. (16) for various distances of the companion. Values that are not varied are the same as in the text: the magnetic field is B∗ = 105 T and the spin period T∗ = 10 ms. |
 |
Fig. 7 Same as Fig. 6 for companions orbiting a standard pulsar with a magnetic field B∗ = 108 T and a spin period T∗ = 1 s. |
4.4. Brightness
The maximum power involved in an Alfvén wing is (Mottez & Heyvaerts 2011b) 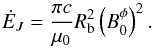 (17)This expression is the relativistic analogue of that derived in Zarka et al. (2001) for magnetised flow-obstacle interactions. From Eq. (1), this can be expressed as a function of the distance r and the radius Rb of the orbiting body
(17)This expression is the relativistic analogue of that derived in Zarka et al. (2001) for magnetised flow-obstacle interactions. From Eq. (1), this can be expressed as a function of the distance r and the radius Rb of the orbiting body 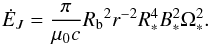 (18)From studies of planetary magnetospheric radio emissions in our solar system, it was found that the emitted radio power is proportional to the Poynting flux of the solar wind on the magnetospheric cross-section. The same relation of proportionality also relates satellite-induced (Io, Ganymede) radio emissions in the magnetosphere of Jupiter with the incident Poynting flux convected by the rotation of the planetary magnetic field on the obstacle (ionosphere of Io, magnetosphere of Ganymede). The general scaling law describing this relation has a constant of proportionality ϵ ~ 2 − 10 × 10-3 (Zarka et al. 2001; Zarka 2007).
(18)From studies of planetary magnetospheric radio emissions in our solar system, it was found that the emitted radio power is proportional to the Poynting flux of the solar wind on the magnetospheric cross-section. The same relation of proportionality also relates satellite-induced (Io, Ganymede) radio emissions in the magnetosphere of Jupiter with the incident Poynting flux convected by the rotation of the planetary magnetic field on the obstacle (ionosphere of Io, magnetosphere of Ganymede). The general scaling law describing this relation has a constant of proportionality ϵ ~ 2 − 10 × 10-3 (Zarka et al. 2001; Zarka 2007).
To test the possible saturation of this scaling law toward high Poynting fluxes and high radio powers, Zarka (2010) analysed the literature on radio emission from magnetised binary stars. Budding et al. (1998) and Richards et al. (2003) showed that the RS CVn system V711τ frequently emits radio bursts that reach 0.1 Jy at 2.3 GHz and 1 Jy at 8.4 GHz. With a distance of 29 pc and a bandwidth Δf ≥ 8 GHz, one deduces an isotropic radio power ~7 × 1019 − 20 W. Based on estimates from Saar (1996) and Budding et al. (1998), the RS CVn magnetic fields reach 1 − 3 × 103 G, which leads, based on the separation of the system V711τ (11.5 R⊙, Richards et al. 2003), to a magnetic field magnitude B ~ 10 − 30 G at the interaction region. The radius of this region is at most that of the secondary companion in V711τ (~1.3 R⊙). Assuming a stellar wind velocity V ~ 300 km s-1 and an interaction region size R ~ 1 − 9 × 108 m, the Poyinting flux convected on the obstacle is 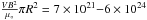 W. The constant of proportionality ϵ is thus in the range 10-1 to 10-5, but more reasonably (matching high and low estimates) in the range 10-2 to 10-4. In spite of the above uncertainties, the range of ϵ falls remarkably close to that deduced from the above scaling law, suggesting that it may remain valid with a constant of about a few 10-3 up to 10 orders of magnitude above the range of solar system planets.
W. The constant of proportionality ϵ is thus in the range 10-1 to 10-5, but more reasonably (matching high and low estimates) in the range 10-2 to 10-4. In spite of the above uncertainties, the range of ϵ falls remarkably close to that deduced from the above scaling law, suggesting that it may remain valid with a constant of about a few 10-3 up to 10 orders of magnitude above the range of solar system planets.
Therefore, we estimate that the power radiated in the form of non-thermal radio waves is in our case 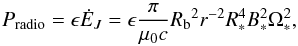 (19)with a conservative value of about 10-3 for ϵ.
(19)with a conservative value of about 10-3 for ϵ.
For a spectrum of emitted waves spreading along an interval Δf of frequencies, at a distance D from the source, the average flux density in Jy of radio waves inside the cone of emission is 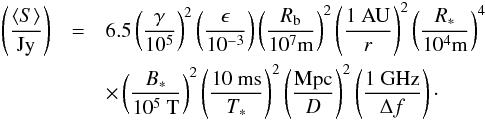 (20)The detected flux density will be S = ⟨ S ⟩ only if the radiation is isotropic in the source frame. If this is not the case, an additional amplification factor intrinsic to the emission mechanism is to be applied for specific directions of emissions inside the cone, whereas S can be null outside of these specific directions.
(20)The detected flux density will be S = ⟨ S ⟩ only if the radiation is isotropic in the source frame. If this is not the case, an additional amplification factor intrinsic to the emission mechanism is to be applied for specific directions of emissions inside the cone, whereas S can be null outside of these specific directions.
 |
Fig. 8 Distance, expressed in Mpc, at which the radio emission produced in the companion’s Alfvén wing can reach a flux density of 1 Jy, for various distances from the pulsar to its companion. The values that are not varied are the same as in the text. They correspond to a recycled millisecond pulsar and a coefficient ϵ = 10-3. The radio spectrum is assumed to be spread over a spectral range of 1 GHz. |
For the reference values of Eq. (20), Fig. 8 shows the distance D at which the radiation can be observed as a function of the Lorentz factor γ of the wind for various distances between the neutron star and its companion. For Lorentz factors larger than ~106, the radio emission can be observed as far 1 Gpc or more. For a radio emission produced for example by the CMI, an additional amplification factor ≥10 (already in the source frame) is to be taken into account relative to the isotropic power derived above (see Zarka et al. 2004 and references therein). Then, a Lorentz factor of ~105 allows detecting 1 Jy emission at 1 Gpc range. Within reasonable ranges for the parameters in Eq. (20), it is possible to produce 1 Jy radio emission at >1 Gpc range even for ϵ = 10-4 and not excessively high γ factors.
The power Pradio radiated in the form of radio waves in the companion’s wake of about 1018 W for the nominal values of the computation (1020 − 22 W for a companion at 0.1−0.01 AU), is weaker than or comparable to the radio power typically emitted by isolated pulsars (~1020 to 1022 W, as deduced from the ATNF pulsar catalogue, Manchester et al. 2005b,a). But the flux density is considerably higher for the companion-induced emission because of the very high degree of collimation of the radio beams that is caused by the highly relativistic motion of the sources and leads to an amplification of the flux density by a factor ~γ2. This high collimation and not the intrinsically high power of the source permits the beams detection at very large distances.
This phenomenon presents analogies with the high intensity of BL Lac galaxies: they are very bright because we (observers) are aligned with a collimated beam, and because of the relativistic motion of the sources. In the case of BL Lac, the local emission is caused by incoherent synchrotron and inverse Compton radiation at frequencies high above the cyclotron frequency. In the present case, we expect a coherent plasma process (like the CMI) to generate a radiation that, in the frame of the source, is at the local cyclotron frequency. We have not considered the possibility of a high-energy counterpart associated with synchrotron radiation from a hot-plasma component, but this counterpart, emitted by an incoherent process, would be much weaker. (Jupiter’s synchrotron emission is five orders of magnitude weaker than its auroral CMI radio emission, Zarka 2004b.)
5. Possible explanation of remarkable radio transients
5.1. Lorimer burst and fast radio bursts
We propose that the Lorimer burst and FRBs described in the introduction may be the signature of the above-described radio emission from pulsar companions. The inferred and surprisingly large distances deduced in Lorimer (2007) (0.5 Gpc), and even more in Thornton et al. (2013) (1.7–3.2 Gpc), are consistent with the energetics of the pulsar companion signal discussed in the previous section. The corresponding sources would indeed lie in other galaxies, at Gpc distances from us, but as explained above, the exceptionally high collimation of the radio emission allows us to detect these bursts with flux densities of several Jy. This high collimation is also consistent with the rare detection of FRBs, although we do not address this point quantitatively here (see rate calculations in Hassall et al. 2013). We discuss here the duration and frequency range of these bursts.
We first consider the duration of FRB signals to be ~5 ms (part of which may be due to scatter-broadening, Thornton et al. 2013). From Fig. 8, it appears that the Lorentz factor γ0 = 106 would allow for a detection at Gpc distance. The example displayed in Fig. 5 shows that a companion with an orbital period of a few hours, in a γ0 = 106 wind could provide a signal of adequate duration.
A value of Torb similar to or higher than a few hours is a reasonable value for the orbital period of a pulsar companion: more than 70 pulsar companions are known with Torb< 1 day, 10% of which have Torb< 0.1 day (Manchester et al. 2005b,a), not including possible low-mass planets and asteroids. Moreover, the value of Torb deduced above is consistent with the fact that no other pulse was observed during the 1.5 h following the observation of the Lorimer burst and other FRBs.
Considering the asymmetry of the intensity diagram along the circular emision pattern of Fig. 5, the crossing of a pattern corresponding to γ ~ 105 is also compatible with the observations, provided that the peak signal from one wing strongly dominates while the other is below the detection threshold.
If the emission is produced by a coherent plasma process such as the CMI, we expect that the radiation is produced along the Alfvén wings at the local cyclotron frequency. Figures 6 and 7 show that we can easily explain an emission at ~1 GHz. But the wide spectral range over which FRBs are observed (≥25%) implies that the emission probably is produced along the Alfvén wings across a wide radial range over which the wind magnetic field and/or γ factor vary in this proportion. Another, perhaps more appealing, explanation is that the shift of the velocity distribution of the whole wind along the 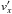 direction in the source frame (i.e. the perpendicular direction, at a particular azimuth) provides an enormous amount of free energy to the CMI, far beyond what is usually available in planetary magnetospheres where a small fraction of the particles are gyrotropically distributed at v⊥ ≠ 0. As a consequence, the emission excited by a pulsar companion could be extremely saturated, generating series of harmonics that possibly result in a quasi-continuous broad spectrum. One of the FRBs reported in Thornton et al. (2013) indeed shows 100 MHz-wide bright bands.
direction in the source frame (i.e. the perpendicular direction, at a particular azimuth) provides an enormous amount of free energy to the CMI, far beyond what is usually available in planetary magnetospheres where a small fraction of the particles are gyrotropically distributed at v⊥ ≠ 0. As a consequence, the emission excited by a pulsar companion could be extremely saturated, generating series of harmonics that possibly result in a quasi-continuous broad spectrum. One of the FRBs reported in Thornton et al. (2013) indeed shows 100 MHz-wide bright bands.
5.2. An event in the Galaxy
Deneva et al. (2009) reported the discovery of an event composed of three pulsar-like bursts from a source named PSR J1928+15. The bursts occured at intervals of 0.403 s from each other, with the middle pulse being brighter by an order of magnitude than the other two. The duration of each of the three dedispersed pulses was about 30 ms. The DM is 242 ps cm-3 which, for the galactic coordinates of PSR J1928+15 (longitude = 50.64°, latitude = −1.03°), is compatible with a signal from our Galaxy. In spite of several follow-up observations, the source was not detected again. Deneva et al. (2009) suggested – after Cordes & Shannon (2008) – that it might have been caused by the excitation of a dormant pulsar by accretion of material from an asteroid belt. But they did not provide any physical insight on the underlying mechanism, while Cordes & Shannon (2008) were mostly concerned with pulsar nullings, instead of isolated pulses from dormant pulsars.
We consider a companion orbiting a pulsar with a P∗ = 0.403 s period, in a γ0 = 103 wind at a distance r = 0.01 AU. From Table 1, we can see that (for a ~ 1000 km companion), the CMI sources spend τ− = 80 ms in the δ− wing, and only τ+ = 0.1 ms in the other. Therefore, the CMI develops only in the δ− wing. Because τ−/τ+ does not depend on the size Rb of the body, this is true for a smaller object as well. The high-amplitude part of the angular pattern caused by the particle distribution anisotropy of the δ− Alfvén wing can be crossed in about 1.5 s, and this would correspond to 3 pulses of 0.403 s. Each of these pulses would correspond to a slightly different value of αs, the second pulse (centre of the emission pattern) being the most intense. Other weaker pulses might have been seen with a lower noise level. The low-amplitude part of the emission angular pattern of the δ− wing would not have been seen either. Of course, the parameters γ0 = 103 and r = 0.01 AU are simply one possibility among many others. With a single observation, it is not possible to constrain the model more strictly. Nevertheless, the PSR J1928+15 signal is compatible with our pulsar companion model.
PSR J1928+15 is thought to be at a distance ~10 kpc, much closer than the sources of the Lorimer burst and FRBs. However, the signal amplitude (Speak ~ 180 mJy) is slightly weaker than that of the very distant FRBs. Therefore, the radio luminosity of this system is much lower. A possible explanation is that its orbiting companion is much smaller than those associated with the extragalactic FRBs. For instance, an asteroid (of radius ~km) would be a possible companion of such a standard pulsar. Because of the smaller size of the companion and according to Eq. (9) the wind plasma would spend less time in the Alfvén wings, allowing less time for the full development of the instability that causes the radio emissions. Because the initial phase of the instability growth is exponential, a variation of this duration by a factor of a few units can imply a difference of several orders of magnitude on the luminosity. The radio signature of such a small companion would not be detectable at extragalactic distances.
6. Discussion and conclusion
6.1. Why we do not necessarily see the radio emission from the central pulsar
According to our model, the radio emissions from pulsar companions are beamed along the pulsar-companion line. Because the orbital plane of the companion is likely to be very close to the pulsar’s equatorial plane, the radio emission from the companion is beamed nearly at a right angle from the rotation axis of the neutron star. Because the radio signals from a pulsar are emitted from its polar cap, a very steep tilt of the magnetic field is needed to be able to see the radio emissions from the pulsar and from the companion. In most cases, we will see only the pulsar signal, even if it possesses a companion, because the emission induced by the companion will never be directed toward Earth. This is why one has detected orbiting planets via a pulsar’s radio emission timing without necessarily detecting the planet-induced signal. Conversely, we see only the emission induced by the companion in the case of FRBs because the pulsar’s emission is never directed toward Earth (or simply because it is too weak to be detected at extragalactic distances).
Where the magnetic axis (or the companion’s orbital plane) is tilted enough relative to the pulsar’s rotational axis, however, we may be able to detect both signals, superimposed to each other. Because the companion’s signal is very rare (in time) compared with the pulsed signal from the neutron star, it may remain unnoticed except if explicitly searched for, and it will generally be invisible in the folded pulsar signal (at the pulsar period) except when it is very strong. Note also that because pulsar timing is based on the variations of distance from the neutron star to the observer, it is mostly efficient for distant companions, thus a low-mass companion orbiting close to the neutron star may well remain undetected by a time-of-arrival analysis.
6.2. Observational tests
The theories that have previously been proposed to explain the Lorimer burst and FRBs predict a unique event from a given source, or irregularly repeatable pulses. The latter are not consistent with the large observed DMs, however. In contrast, our explanation based on highly collimated emission from a pulsar companion’s wind wake implies that these pulses should be periodically observable at the orbital period of the companion. A decisive test of our theory would thus consist in detecting again a signal with similar characteristics coming from the direction of the source of the Lorimer burst, or of any known FRB, or from PSR J1928+15. We recommend to observe the same regions of the sky again. The difficulty is to observe continuously so as not to miss a pulse with a duration of a few msec that may occur at any time within hours, days, or more.
Another interesting target is the binary pulsar PSR J2222-0137, which contains a millisecond pulsar orbited by a companion of unknown nature (Deller et al. 2013). As the system is seen nearly edge-on (sini = 0.9985 ± 0.0005) and its orbital parameters are known, it is possible to observe it in search for the companion-induced signal around the transit time of the companion between the pulsar and Earth, or even to search for this signal in existing data.
Note that at frequencies about 1 GHz, an angular wandering of the source of the order of 10-3 arcsec and an angular broadening one order of magnitude larger is expected (Cordes 1990). Both effects are much weaker than 1 /γ and probably do not significantly influence the above discussion. However, intensity fluctuations due to strong scintillation may amplify or attenuate pulses, with an amplitude of fluctuation from one pulse to the other of up to 100%. Thus the detection of the Lorimer burst or of FRBs could have benefited from both a perfect alignment and a constructive scintillation.
Other possible tests of our theory related to the frequency range of the signal discussed in Sect. 4.3 include (i) the existence of periodic (in frequency) intensity fluctuations along the pulse that would be due to emission at harmonics of a given frequency (the fundamental being the frequency interval between bright spots); (ii) the existence of a low-frequency cutoff of the emission below the fundamental frequency predicted in Sect. 4.3; and (iii) the polarization of the radio signal: it is probably strongly circular or elliptical when produced by the CMI (Zarka 2004b).
6.3. Radio waves from pulsar companions as a probe of pulsar winds
Up to now, research on very low-mass pulsar companions has led to the discovery of five planets (Wolszczan & Frail 1992; Thorsett et al. 1993; Bailes et al. 2011) and speculations about orbiting asteroids (Cordes & Shannon 2008; Deneva et al. 2009; Shannon et al. 2013; Mottez et al. 2013). These objects raise a moderate interest in the field of planetology: they orbit stars that left the main sequence a long time ago (in a state that the Sun will never reach), they are exposed to the neutron star X-rays that probably prevent life from developing, they are embedded in a relativistic wind, and they are very far away from us.
By contrast, the study of these objects is of high interest for the understanding and probing of pulsar winds. If companion-induced radio signals are confirmed, then the underlying theory of Alfvén wings of bodies in a pulsar wind (Mottez & Heyvaerts 2011a,b; Heyvaerts et al. 2012) would be supported as well. This theory assumes a wind velocity lower than the Alfvén wave velocity (both are very close to c). This hypothesis, compatible with many theoretical models, is valid only if the pulsar wind at the companion distance is still Poynting-flux dominated. In spite of many discussions (see Bucciantini 2014 for review) there is no convincing proof of this hypothesis. Observational testing of our theory may provide this missing proof and unique measurements of the Lorentz factor of the wind at AU distances, a key ingredient for the theories of dissipation in pulsar winds. The distance range that could be probed is from 10–100 light cylinder radii (otherwise, the companion is destroyed by tidal effects) to a few AU (much closer than the wind termination shock, otherwise at thousands of AU the companion is practically gravitationally unbound from the neutron star).
If we find that the radio transients that we discussed in Sect. 5 are indeed periodic, the shortest measured period will be the orbital period of the companion Torb. As neutron stars have a narrow range of masses (1–3 M⊙), we can estimate the companion distance to the star. Then, measured pulse characteristics will allow us to deduce the value of the pulsar wind Lorentz factor γ and to know whether the wind is Poynting-flux dominated at the orbital distance of the companion, that is, far away from the light cylinder, and far away from the termination shock.
Acknowledgments
We thank Michal Bejger (Copernicus Astronomical Center, Polish Academy of Sciences) for suggesting the relevance of pulsar-planet physics to orbiting white dwarfs. This work was partly supported by the CNRS/INSU/PNHE Programme National Hautes Energies.
References
- Arons, J. 2004, Adv. Space Res., 33, 466 [Google Scholar]
- Bailes, M., Bates, S. D., Bhalerao, V., et al. 2011, Science, 333, 1717 [NASA ADS] [CrossRef] [Google Scholar]
- Bucciantini, N. 2014, Astron. Nachr., 335, 234 [Google Scholar]
- Bucciantini, N., Thompson, T. A., Arons, J., Quataert, E., & Del Zanna, L. 2006, MNRAS, 368, 1717 [NASA ADS] [CrossRef] [Google Scholar]
- Budding, E., Slee, O. B., & Jones, K. 1998, PASA, 15, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Cordes, J. M. 1990, in Low Frequency Astrophysics from Space, eds. N. E. Kassim, & K. W. Weiler (Berlin: Springer Verlag), Lect. Not. Phys., 362, 165 [Google Scholar]
- Cordes, J. M., & Shannon, R. M. 2008, ApJ, 682, 1152 [NASA ADS] [CrossRef] [Google Scholar]
- Deller, A. T., Boyles, J., Lorimer, D. R., et al. 2013, ApJ, 770, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Deneva, J. S., Cordes, J. M., McLaughlin, M. A., et al. 2009, ApJ, 703, 2259 [NASA ADS] [CrossRef] [Google Scholar]
- Farrell, W. M., Lazio, T. J. W., Zarka, P., et al. 2004, Planet. Space Sci., 52, 1469 [NASA ADS] [CrossRef] [Google Scholar]
- Freund, H. P., Wong, H. K., Wu, C. S., & Xu, M. J. 1983, Phys. Fluids, 26, 2263 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Julian, W. H. 1969, ApJ, 157, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Hassall, T. E., Keane, E. F., & Fender, R. P. 2013, MNRAS, 436, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Heyvaerts, J., Lehner, T., & Mottez, F. 2012, A&A, in press [Google Scholar]
- Huang, Y. F., & Geng, J. J. 2014, ApJ, 782, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Kashiyama, K., Ioka, K., & Mészáros, P. 2013, ApJ, 776, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Keane, E. F., Kramer, M., Lyne, A. G., Stappers, B. W., & McLaughlin, M. A. 2011, MNRAS, 415, 3065 [NASA ADS] [CrossRef] [Google Scholar]
- Keane, E. F., Stappers, B. W., Kramer, M., & Lyne, A. G. 2012, MNRAS, 425, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Kirk, J. G., Lyubarsky, Y., & Petri, J. 2009, in Astrophys. Space Sci. Lib. 357, ed. W. Becker, 421 [Google Scholar]
- Le Queau, D. 1988, in Planetary radio emissions II, Proc. of the Second International Workshop, Graz, Austria, Sept. 7–9, 1987 (A89-39951 17-91), eds. H. O. Rucker, S. J. Bauer, & B. M. Pedersen (Wien: Verlag der Oesterreichischen Akademie der Wissenschaften), 381 [Google Scholar]
- Le Queau, D., & Roux, A. 1987, Sol. Phys., 111, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Loeb, A., Shvartzvald, Y., & Maoz, D. 2014, MNRAS, in press [arXiv:1310.2419] [Google Scholar]
- Lorimer, D. 2007, in Chandra Proposal, 2411 [Google Scholar]
- Lorimer, D. R., Bailes, M., McLaughlin, M. A., Narkevic, D. J., & Crawford, F. 2007, Science, 318, 777 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Manchester, R. N., Hobbs, G. B., Teoh, A., & Hobbs, M. 2005a, VizieR Online Data Catalog: VII/245 [Google Scholar]
- Manchester, R. N., Hobbs, G. B., Teoh, A., & Hobbs, M. 2005b, ApJ, 129, 1993 [Google Scholar]
- Michel, F. C. 1969, ApJ, 158, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Mottez, F., & Heyvaerts, J. 2011a, A&A, 532, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mottez, F., & Heyvaerts, J. 2011b, A&A, 532, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mottez, F., Bonazzola, S., & Heyvaerts, J. 2013, A&A, 555, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neubauer, F. M. 1980, J. Geophys. Res., 85, 1171 [Google Scholar]
- Preusse, S., Kopp, A., Büchner, J., & Motschmann, U. 2006, A&A, 460, 317 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pritchett, P. L. 1986, Phys. Fluids, 29, 2919 [NASA ADS] [CrossRef] [Google Scholar]
- Ransom, S. M., Stairs, I. H., Archibald, A. M., et al. 2014, Nature, 505, 520 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Richards, M. T., Waltman, E. B., Ghigo, F. D., & Richards, D. S. P. 2003, ApJS Ser., 147, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Saar, S. H. 1996, in Stellar Surface Structure, eds. K. G. Strassmeier, & J. L. Linsky, IAU Symp., 176, 237 [Google Scholar]
- Saur, J., Neubauer, F. M., Connerney, J. E. P., Zarka, P., & Kivelson, M. G. 2004, in Plasma interaction of Io with its plasma torus (Cambridge University Press), 537 [Google Scholar]
- Savonije, G. J. 1987, Nature, 325, 416 [NASA ADS] [CrossRef] [Google Scholar]
- Shannon, R. M., Cordes, J. M., Metcalfe, T. S., et al. 2013, ApJ, 766, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Thornton, D., Stappers, B., Bailes, M., et al. 2013, Science, 341, 53 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Thorsett, S. E., Arzoumanian, Z., & Taylor, J. H. 1993, ApJ, 412, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Totani, T. 2013, PASJ, 65, L12 [NASA ADS] [CrossRef] [Google Scholar]
- van Haarlem, M. P., Wise, M. W., Gunst, A. W., et al. 2013, A&A, 556, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Willes, A. J., & Wu, K. 2005, A&A, 432, 1091 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wolszczan, A., & Frail, D. A. 1992, Nature, 355, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, C. S. 1985, Space Sci. Rev., 41, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Zarka, P. 2004a, in Extrasolar Planets: Today and Tomorrow, eds. J. Beaulieu, A. Lecavelier Des Etangs, & C. Terquem, ASP Conf. Ser., 321, 160 [Google Scholar]
- Zarka, P. 2004b, Adv. Space Res., 33, 2045 [NASA ADS] [CrossRef] [Google Scholar]
- Zarka, P. 2007, Planet. Space Sci., 55, 598 [NASA ADS] [CrossRef] [Google Scholar]
- Zarka, P. 2010, in Pathways Towards Habitable Planets, eds. V. Coudé du Foresto, D. M. Gelino, & I. Ribas, ASP Conf. Ser., 430, 175 [Google Scholar]
- Zarka, P., Treumann, R. A., Ryabov, B. P., & Ryabov, V. B. 2001, Ap&SS, 277, 293 [Google Scholar]
- Zarka, P., Cecconi, B., & Kurth, W. S. 2004, J. Geophys. Res., 109, 9 [Google Scholar]
- Zhang, B. 2014, ApJ, 780, L21 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Orientation of the Alfvén wings relative to the local magnetic field
The computation of the electric current of Alfvén waves involves a first invariant Vs, the vector defining the Alfvén characteristics, whose modulus is the speed of an Alfvénic perturbation along these characteristics. With s = ± 1 characterising the two wings, and v and B the perturbed flow velocity and magnetic field 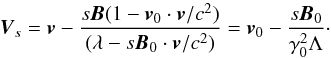 (A.1)The last term is an estimate of the invariant involving only unperturbed wind parameters. The parameter λ can be expressed as a function of the unperturbed wind parameters:
(A.1)The last term is an estimate of the invariant involving only unperturbed wind parameters. The parameter λ can be expressed as a function of the unperturbed wind parameters: ![\appendix \setcounter{section}{1} \begin{equation} \label{eq_definition_lambda} \lambda = \left[\mu_0 \rho_0'+c^{-2} {B}_{0}^{r2}+ c^{-2} \gamma_0^{-2} B_0^{ \phi 2} \right] ^{1/2}, \end{equation}](/articles/aa/full_html/2014/09/aa24104-14/aa24104-14-eq264.png) (A.2)where
(A.2)where 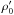 is the density in the moving frame of the wind (primed quantities refer hereafter to that frame), and
is the density in the moving frame of the wind (primed quantities refer hereafter to that frame), and 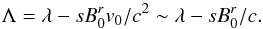 (A.3)The invariant Vs, related to the theory of uncompressible Alfvén waves, was derived in Mottez & Heyvaerts (2011b) following a linear approximation for the derivation of the general properties of relativistic Alfvén wings. This invariant was found again in Heyvaerts et al. (2012) in the context of the non-linear theory of relativistic simple Alfvén waves.
(A.3)The invariant Vs, related to the theory of uncompressible Alfvén waves, was derived in Mottez & Heyvaerts (2011b) following a linear approximation for the derivation of the general properties of relativistic Alfvén wings. This invariant was found again in Heyvaerts et al. (2012) in the context of the non-linear theory of relativistic simple Alfvén waves.
Because the direction of the Alfvén wings is those of Vs and because 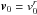 , the angle δ between the Alfvén wing and the radial direction is
, the angle δ between the Alfvén wing and the radial direction is 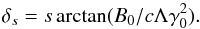 (A.4)When Λ is expressed as a function of the wind invariants, we find
(A.4)When Λ is expressed as a function of the wind invariants, we find ![\appendix \setcounter{section}{1} \begin{equation} \label{eq_delta_complet} \delta_s=s\arctan{ \left[\frac{x}{\gamma_0 \left(\sqrt{1+x^2(1+\frac{\gamma_0}{\sigma_0})}-s \right)}\right]}, \end{equation}](/articles/aa/full_html/2014/09/aa24104-14/aa24104-14-eq270.png) (A.5)where σ0 is the magnetization factor defined by
(A.5)where σ0 is the magnetization factor defined by 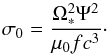 (A.6)The MHD models considering a relativistic radial wind (Arons 2004; Kirk et al. 2009) imply an asymptotic Lorentz factor scaling as
(A.6)The MHD models considering a relativistic radial wind (Arons 2004; Kirk et al. 2009) imply an asymptotic Lorentz factor scaling as 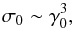 (A.7)and the term γ0/σ0 can be neglected. It is negligible as long as the wind is Poynting-flux dominated, which is the basic assumption that governs this paper. When γ0/σ0 is neglected, we obtain Eq. (4).
(A.7)and the term γ0/σ0 can be neglected. It is negligible as long as the wind is Poynting-flux dominated, which is the basic assumption that governs this paper. When γ0/σ0 is neglected, we obtain Eq. (4).
All Tables
x ratio, Afvén wing angles δ+ and δ− with the radial wind direction, and proper time τ+ and τ− spent by the CMI sources in the wings as functions of the companion distance r and the wind Lorentz factor γ0.
All Figures
 |
Fig. 1 Alfvénic wake of the pulsar’s companion body seen from above the equatorial plane. The velocity of the source regions Vs is assumed to be along the Alfvén wings. The thick grey lines represent the cones in which emitted radio waves are focussed. We call them the angular emission patterns. The observer’s frame related to the upper wing on the figure (making an angle δ+ with the wind) is indicated by the Ox and Oz axes. It is fixed relative to the pulsar companion. The two stars mark the region of the angular emission patterns of highest wave intensity (see Sect. 4). |
| In the text | |
 |
Fig. 2 Directions of the magnetic field and of the radio waves emitted in the source frame: the wave vectors are along a cone of summit angle αs, and of an axis parallel to the magnetic field Bs. The wave vector position on that cone is parametrised by the angle Ψs. The inclination of the magnetic field with the wing axis Oz is λs. The cylindrical angular coordinates θs and ϕs of the wave vector are defined relatively to the z axis. As in Fig. 1, the star (at Ψs = 0) marks the angle of emission of the most intense CMI waves. |
| In the text | |
 |
Fig. 3 Directions of the radio waves in the observer’s frame. The two smaller tangent grey disks in the middle of the plot correspond to the waves that are beamed at ≤90° from the Alfvén wing axis in the source frame in the approximation of very high γ values (see text for the precise meaning of “very high”). The two large circles (black lines) are the radio-beaming patterns associated with the CMI. They are defined by x = δ± + θocosϕo and y = θosinϕo, with θo and ϕo the cylindrical angular coordinates of the wave vector in the observer’s reference frame of each Alfvén wing. θo and ϕo are related via Eq. (10) (or Eq. (13)) to the wave vector coordinates in the source frame θs and ϕs given by Eq. (12). The most intense emissions correspond to the innermost intersection of each large circle with the horizontal axis. Here γ = 10, r = 0.1 AU and αs = 85°. With these parameters, x = 78. The stars mark the directions of the most intense radio emissions. |
| In the text | |
 |
Fig. 4 Directions of the radio waves in the observer’s frame. Same as in Fig. 3, but for γ = 1000. As in Fig. 3, r = 0.1 AU and αs = 85°. These parameters correspond to x = 0.78. |
| In the text | |
 |
Fig. 5 Directions of the radio waves in the observer’s frame. Same as in Fig. 3, but for γ = 106 and r = 0.01 AU. As in Fig. 3, αs = 85°. These parameters correspond to x = 0.78 × 10-5. Here only the emission pattern associated with δ− is represented. The star marks the direction of the most intense radio emissions. |
| In the text | |
 |
Fig. 6 Cyclotron frequency in the observer’s frame as a function of the pulsar wind Lorentz factor γ, from Eq. (16) for various distances of the companion. Values that are not varied are the same as in the text: the magnetic field is B∗ = 105 T and the spin period T∗ = 10 ms. |
| In the text | |
 |
Fig. 7 Same as Fig. 6 for companions orbiting a standard pulsar with a magnetic field B∗ = 108 T and a spin period T∗ = 1 s. |
| In the text | |
 |
Fig. 8 Distance, expressed in Mpc, at which the radio emission produced in the companion’s Alfvén wing can reach a flux density of 1 Jy, for various distances from the pulsar to its companion. The values that are not varied are the same as in the text. They correspond to a recycled millisecond pulsar and a coefficient ϵ = 10-3. The radio spectrum is assumed to be spread over a spectral range of 1 GHz. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


