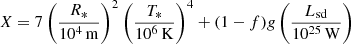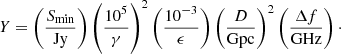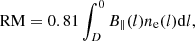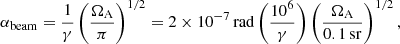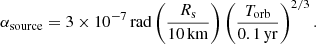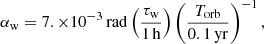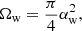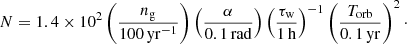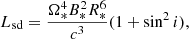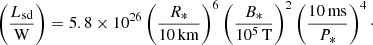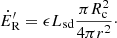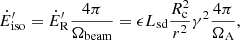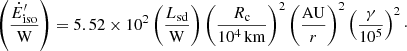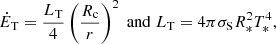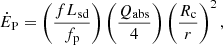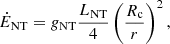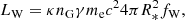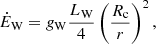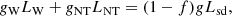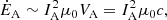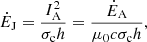| Issue |
A&A
Volume 644, December 2020
|
|
|---|---|---|
| Article Number | A145 | |
| Number of page(s) | 14 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202037751 | |
| Published online | 14 December 2020 | |
Repeating fast radio bursts caused by small bodies orbiting a pulsar or a magnetar
1
LUTH, Observatoire de Paris, PSL Research University, CNRS, Université de Paris, 5 Place Jules Janssen, 92190 Meudon, France
e-mail: fabrice.mottez@obspm.fr
2
LESIA, Observatoire de Paris, PSL Research University, CNRS, Université de Paris, Sorbonne Université, 5 Place Jules Janssen, 92190 Meudon, France
3
Jodrell Bank Centre for Astrophysics, Department of Physics and Astronomy, The University of Manchester, Manchester M19 9PL, UK
Received:
16
February
2020
Accepted:
1
October
2020
Context. Asteroids orbiting into the highly magnetized and highly relativistic wind of a pulsar offer a favorable configuration for repeating fast radio bursts (FRB). The body in direct contact with the wind develops a trail formed of a stationary Alfvén wave, called an Alfvén wing. When an element of wind crosses the Alfvén wing, it sees a rotation of the ambient magnetic field that can cause radio-wave instabilities. In the observer’s reference frame, the waves are collimated in a very narrow range of directions, and they have an extremely high intensity. A previous work, published in 2014, showed that planets orbiting a pulsar can cause FRBs when they pass in our line of sight. We predicted periodic FRBs. Since then, random FRB repeaters have been discovered.
Aims. We present an upgrade of this theory with which repeaters can be explained by the interaction of smaller bodies with a pulsar wind.
Methods. Considering the properties of relativistic Alfvén wings attached to a body in the pulsar wind, and taking thermal consideration into account, we conducted a parametric study.
Results. We find that FRBs, including the Lorimer burst (30 Jy), can be explained by small-size pulsar companions (1 to 10 km) between 0.03 and 1 AU from a highly magnetized millisecond pulsar. Some parameter sets are also compatible with a magnetar. Our model is compatible with the high rotation measure of FRB 121102. The bunched timing of the FRBs is the consequence of a moderate wind turbulence. An asteroid belt composed of fewer than 200 bodies would suffice for the FRB occurrence rate measured with FRB 121102.
Conclusions. After this upgrade, this model is compatible with the properties discovered since its first publication in 2014, when repeating FRBs were still unknown. It is based on standard physics and on common astrophysical objects that can be found in any type of galaxy. It requires 1010 times less power than (common) isotropic-emission FRB models.
Key words: radio continuum: general / pulsars: general / stars: magnetars / minor planets, asteroids: general / plasmas / magnetic fields
© F. Mottez et al. 2020
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
Mottez & Zarka (2014, hereafter MZ14) proposed a model of FRBs that involves common celestial bodies, neutron stars (NS), and planets orbiting them, well-proven laws of physics (electromagnetism), and a moderate energy demand that allows for a narrowly beamed continuous radio-emission from the source that sporadically illuminates the observer. When these ingredients are put together, the model is compatible with the localization of FRB sources at cosmological distances (Chatterjee et al. 2017), it can explain the millisecond burst duration, the flux densities above 1 Jy, and the range of observed frequencies.
MZ14 is based on the relativistic Alfvén wings theory of Mottez & Heyvaerts (2011), and the authors concluded that planetary companions of standard or millisecond pulsars could be the source of FRBs. In an erratum that reevaluated the magnetic flux and thus the magnetic field in the pulsar wind, Mottez & Heyvaerts (2020, hereafter MH20) revised the emitted radio frequency and flux density and concluded that observed FRB characteristics are rather compatible with companions of millisecond highly magnetized pulsars. These pulsar characteristics correspond to young neutron stars. This paper is an upgrade of this revised model, in the light of the discovery of repeating radio bursts made since the date of publication of MZ14 (Spitler et al. 2016; CHIME/FRB Collaboration 2019). The main purpose of this upgrade is modeling the random repeating bursts, and explaining the strong linear polarization that might be associated with huge magnetic rotation measures (Michilli et al. 2018; Gajjar et al. 2018).
The MZ14 model consists of a planet that orbits a pulsar and is embedded in its ultra-relativistic and highly magnetized wind. The model requires that wind and planet are in direct contact. Then, the disturbed plasma flow reacts by creating a strong potential difference at the companion. This is the source of an electromagnetic wake, called Alfvén wing, because it is formed of one or two stationary Alfvén waves. Alfvén wings support an electric current and an associated change in magnetic field direction. According to MZ14, when the wind crosses an Alfvén wing, it sees a temporary rotation of the magnetic field. This perturbation can be the cause of a plasma instability that generates coherent radio waves. Because the pulsar companion and the pulsar wind are permanent structures, this radio-emission process is most probably permanent as well. Because the source of these radio waves is the pulsar wind when it crosses the Alfvén wings, and because the wind is highly relativistic with Lorentz factors up to an expected value γ ∼ 106, the radio source has a highly relativistic motion relative to the radio-astronomers who observe it. Because of the relativistic aberration that results, all the energy in the radio waves is concentrated into a narrow beam of aperture angle ∼1/γ rad (the green cone attached to source S in Fig. 1). We only observe the waves when we cross the beam. The motion of the beam (its change of direction) results primarily from the orbital motion of the pulsar companion. The radio-wave energy was evaluated in MZ14 and MH20, as well as its focusing, and it was shown that it is compatible with a brief emission that can be observed at cosmological distances (∼1 Gpc) with flux densities higher than 1 Jy.
 |
Fig. 1. Schematic view of the wake of a pulsar companion. The pulsar is far to the left outside of the figure. The directions of the wind velocity vw, the wind magnetic field Bw, and the convection electric field Ew are plotted on the left-hand side. The shadow is shown in gray. The Alfvén wing is shown in blue. The region from which we expect radio emissions (in yellow) is inside the wing and outside the shadow. Its largest transverse radius is RS and its distance to the companion is l. Seen from the NS at a distance r, it subtends a solid angle Ωσ. Any point source S in the source region can generate radio waves. Because of the relativistic aberration, their directions are contained in a narrow beam (in green) of solid angle πγ−2. If the emission is not isotropic in the source reference frame, it is emitted in a subset of this cone (dark green tortuous line). Photons that emerge from this cone are marked with red arrows. Seen from the source point S, this dark green area subtends a solid angle Ωbeam. |
In the nonrelativistic regime, the Alfvén wings of planet-satellite systems and their radio emissions have been well studied because this electromagnetic structure characterizes the interaction of Jupiter and its rotating magnetosphere with its inner satellites Io, Europa, and Ganymede (Saur et al. 2004; Hess et al. 2007; Pryor et al. 2011; Louis et al. 2017; Zarka et al. 2018). It is also observed in the Saturn-Enceladus system (Gurnett et al. 2011).
The central question is how the pulsar wind can be in direct contact with the obstacle. The solution proposed in MZ14 was to assume that the pulsar wind is sub-Alfvénic.
Although the wind velocity is almost the speed of light c, the MZ14 model assumed that the wind is slower than Alfvén and fast magnetosonic waves. The planet was then supposed to orbit inside this sub-Alfvénic region of the wind. The Alfvénic mach number is
where vr is the radial wind velocity, and σ is the magnetization parameter, defined as the ratio of magnetic to kinetic energy densities (Mottez & Heyvaerts 2011). Because the Alfvén velocity is very close to c and the fast magnetosonic velocity is even closer to c (see Keppens et al. 2019), the fast magnetosonic Mach number is smaller but close to MA. However, assuming MF < 1 or MA < 1 implies a low plasma density, which is difficult to reconcile with current pulsar wind models (e.g., Timokhin & Harding 2015).
In this work, however, the necessity of a wind that would be lower than fast magnetosonic waves or than Alfvén waves vanishes because small bodies have no atmosphere. A bow shock is created by the interaction of a flow with a gaseous atmosphere, and because asteroids have no atmosphere, there will be no bow shock in front of the asteroid regardless of the Mach number of the pulsar wind. Then, the pulsar wind is directly in contact with the surface of the object, which is the only requirement of the Alfvén wing theory. With super-Alfvénic flows, we can allow the wind to have the larger Lorentz factors required to compensate for the smaller size of the companion. We indeed show in Sects. 3.2 and 3.3 that a Lorentz factor γ > 5.105 is needed for FRBs to be caused by asteroids instead of planets.
The upgraded model presented here is a generalization of MZ14. MZ14 assumed that the radiation mechanism was the cyclotron maser instability (CMI), a relativistic wave instability that is efficient in the above mentioned solar system Alfvén wings, with emissions at the local electron gyrofrequency and harmonics (Freund et al. 1983). Here, without entering into the details of the radio emission processes, we consider that other instabilities can also generate coherent radio emission at frequencies much lower than the gyrofrequency, as is the case in the highly magnetized inner regions of pulsar environments. Removing the constraint that the observed frequencies are above the gyrofrequency allows for FRB radiation sources, that is, pulsar companions, much closer to the neutron star. Then, it is possible to explore the possibility of FRB sources such as asteroid belts or streams at a close distance to the neutron star. The ability of these small companions to resist evaporation must be verified. We therefore include a detailed study of the thermal balance of the companion.
The model in MZ14 with a single planet leads to the conclusion that FRBs must be periodic, with a period equal to the companion orbital period, provided that propagation effects do not perturb the observation conditions too strongly. The possibility of asteroid clusters or belts might explain the existence of nonperiodic FRB repeaters such as those that have been discovered.
We also include a more elaborate reflection than in MZ14 of the duration of the observed bursts and of their nonperiodic repetition rates. The MZ14 model proposed a generation mechanism for FRB that led to predict isolated or periodic FRBs. We adapted this here to irregularly repeating FRBs. Nevertheless, we can already note that it contains a few elements that have been discussed separately in more recent papers. For instance, the energy involved in this model is lower by orders of magnitudes than the energy required by quasi-isotropic emission models because this model involves a very narrow beam of radio emission. This concept alone was discussed by Katz (2017), who concluded, as did MZ14, that a relativistic motion in the source, or of the source, can explain the narrowness of the radio beam. This point is key to the observability of a neutron star-companion system at cosmological distances.
The MZ14 proposed the basic mechanism. We broaden the range of companions. Using the main results of MZ14 and the thermal analysis summarized in Sect. 2, we perform a parametric study and select relevant solutions (Sect. 3). Compatibility with high rotation measures, for instance, as obtained for FRB 121102, is analyzed. In Sect. 4 we present an analysis of FRB timing. Before the conclusion, we present a short discussion and the number of asteroids required to explain the observed burst rates.
2. Pulsar companion in a pulsar wind: key results
We consider that the radio source is conveyed by the ultra-relativistic pulsar wind. The radio emission starts when the pulsar wind crosses the environment of a companion of radius Rc orbiting the pulsar.
2.1. Relativistic aberration and solid radiation angle
We considered a source of section σsource at a distance r from the neutron star. Each point of this source emits radio waves in a solid angle Ωbeam centered on the radial direction that connects it to the neutron star. The solid angle covered by this area as seen from the pulsar is Ωσ = σsource/r2. We characterized the source by an extent Rs (Fig. 1), then 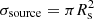 and Ωσ = π(Rs/r)2. Following MZ14, the source was attached to the pulsar wind when it crossed the companion’s environment. In the reference frame of the source, we assumed that the radio emission is contained in a solid angle ΩA that can be ≪4π. Because of the relativistic aberration, the radiation is emitted in a solid angle,
and Ωσ = π(Rs/r)2. Following MZ14, the source was attached to the pulsar wind when it crossed the companion’s environment. In the reference frame of the source, we assumed that the radio emission is contained in a solid angle ΩA that can be ≪4π. Because of the relativistic aberration, the radiation is emitted in a solid angle,
The total solid angle of the radio emissions in the observer frame is ΩT > Ωσ + Ωbeam = π(s/r)2 + πγ−2(ΩA/4π). The parametric study conducted in Sect. 3.2 shows that γ ∼ 106 and s < 500 m and r > 0.01 AU. Then, practically, ΩT ∼ Ωbeam = γ−2(ΩA/4). This value is used throughout the paper. The strong relativistic aberration favors the possibility of observing a moderately intense phenomenon over cosmological distances when the very narrow radiation beam is crossed.
2.2. Alfvén wings
We considered a pulsar companion in the ultra-relativistic wind of the pulsar. The wind velocity modulus is VW ∼ c. The magnetic field in the inner magnetosphere (distance to the neutron star r < rLC where rLC is the light cylinder radius) is approximately a dipole field. In the wind, its amplitude dominated by the toroidal component decreases as r−1, and the transition near rLC is continuous,
The orbiting companion is in direct contact with the pulsar wind. The wind velocity relative to the orbiting companion Vw crossed with the ambient magnetic field Bw is the cause of an induced electric structure associated with an average field E0 = Vw × Bw, called a unipolar inductor (Goldreich & Lynden-Bell 1969).
The interaction of the unipolar inductor with the conducting plasma generates a stationary Alfvén wave attached to the body, called Alfvén wing (Neubauer 1980). The theory of Alfvén wing has been revisited in the context of special relativity by Mottez & Heyvaerts (2011). In a relativistic plasma flow, the current system carried by each Alfvén wing (blue arrows in Fig. 1), “closed at infinity”, has an intensity IA related to the Alfvén wing power ĖA by
where μ0c = 1/377 mho is the vacuum conductivity. From Mottez & Zarka (2014) and MH20, the computation of the current IA in the relativistic Alfvén wing combined with the characteristics of the pulsar wind provides an estimate of the Alfvén wing power,
2.3. Alfvén wing radio emission
By extrapolation of known astrophysical systems, MZ14 showed that the Alfvén wing is a source of radio emissions of power
where 2 × 10−3 ≤ ϵ ≤ 10−2 (Zarka et al. 2001; Zarka 2007). The resulting flux density at distance D from the source is
where Δf is the spectral bandwidth of the emission, γ is the Lorentz factor of the pulsar wind, and γ2 in this expression is a consequence of the relativistic beaming: the radio emissions are focused into a cone of characteristic angle ∼γ−1 when γ ≫ 1.
The coefficient Acone is an anisotropy factor. Let ΩA be the solid angle in which the radio waves are emitted in the source frame. Then, Acone = 4π/ΩA. If the radiation is isotropic in the source frame, Acone = 1, otherwise, Acone > 1. For instance, with the CMI, Acone up to 100 (Louis et al. 2019).
Because the wing is powered by the pulsar wind, the observed flux density of Eq. (7) can be related to the properties of the pulsar by expressing ĖA as a function of P* and B*, which are the spin period and surface magnetic field of the neutron star, respectively, and the size of the object Rc. Thus, Eq. (7) becomes
Another way of presenting this result is in terms of equivalent isotropic luminosity Ėiso,S = 4πSD2 Δf, which in terms of reduced units reads
Observations of FRBs of known distances (up to ∼1 Gpc) reveal values of Ėiso,S in the range 1033−1037 W (Luo et al. 2020). This is compatible with the fiduciary values appearing in Eq. (9).
Another way of computing the radio flux is presented in Appendix A. It is found that
where the prime denotes the alternate way of computation. Without any explicit mention of Alfvén wings, Eqs. (9) and (10) should be compatible although they were introduced with different concepts. In the parametric study, we verify their expected similarity,
2.4. Frequencies
MZ14 proposed that the instability triggering the radio emissions is the cyclotron maser instability. Its low-frequency cutoff is the electron gyrofrequency. We show that for FRB 121102 and other repeaters, the CMI cannot always explain the observed frequencies in the context of our model.
In any case, we still use the electron gyrofrequency fce, o in the observer frame as a useful scale. According to MZ14 and MH20,
2.5. Pulsar spin-down age
The chances of observing an FRB triggered by asteroids orbiting a pulsar are proportional to the pulsar spin-down age τsd = P∗/2Ṗ∗. This definition combined with 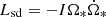 gives an expression depending on the parameters of our parametric study,
gives an expression depending on the parameters of our parametric study, 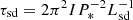 . In reduced units,
. In reduced units,
We verified for consistency with observational facts that a Crab-like pulsar (P* = 33 ms and Lsd = 1031 W) has a spin-down age τsd ∼ 6600 yr, which is compatible with its age since the supernova explosion in 1054.
2.6. Minimum asteroid size required against evaporation
The thermal equilibrium temperature Tc of the pulsar companion is
where σS is the Stefan-Boltzmann constant, and Rc and Tc are radius and temperature of the companion, respectively. Source ĖT is the blackbody radiation of the neutron star, ĖP is associated with inductive absorption of the Poynting flux, ĖNT is caused by the pulsar nonthermal photons, ĖW is associated with the impact of wind particles, and ĖJ is caused by the circulation of the Alfvén wing current IA into the companion.
These heat sources are investigated in Appendix B. In the appendix, we introduce two factors f and g that are used to abridge the sum ĖNT + ĖW = (1−f)gLsd into a single number that is kept in the parametric study.
The pulsar companion can survive only if it does not evaporate. As we show in the parametric studies, the current model works better with metallic companions. Therefore we anticipate this result and consider that its temperature must not exceed the iron fusion temperature Tmax ∼ 1400 K. Inserting Tmax in Eq. (14) provides an upper value of ĖA, whereas Eq. (7) with a minimum value S = 1 Jy provides a lower limit ĖA min of ĖA. The combination of these relations sets a constraint on the companion radius,
where EA min is given by Eq. (7) with S = 1 Jy, and
Because the coefficient of inductive energy absorption Qabs < Qmax = 10−6 and fp is a larger fraction of unity than f, we can neglect the contribution of the inductive heating ĖP. Combining this with Eq. (7), with Tmax = 1400 K for the iron fusion temperature and using normalized figures, we finally obtain the condition for the companion to remain solid,
where
and
We note that when for a given distance r, the factor of 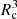 in Eq. (15) is negative, then no FRB-emitting object orbiting the pulsar can remain in solid state, regardless of its radius.
in Eq. (15) is negative, then no FRB-emitting object orbiting the pulsar can remain in solid state, regardless of its radius.
2.7. Clusters and belts of small bodies orbiting a pulsar
For FRB 121102, no periodicity was found in the time distribution of burst arrivals. Therefore we cannot consider that they are caused by a single body orbiting a pulsar. Scholz et al. (2016) have shown that the time distribution of the FRB 121102 bursts is clustered. Many radio surveys lasting more than 1000 s each and totaling 70 h showed no pulse occurrence, while six bursts were found within a 10 min period. The arrival time distribution is clearly highly non-Poissonian. This is somewhat at odds with FRB models based on pulsar giant pulses, which tend to be Poissonian (Karuppusamy et al. 2010).
We suggest that the clustered distribution of repeating FRBs might result from asteroid swarms. The hypothesis of clustered asteroids might be confirmed by the recent detection of a 16.35 ± 0.18 day periodicity of the pulses rate of the repeating FRB 180916.J0158+65 detected by the Canadian Hydrogen Intensity Mapping Experiment Fast Radio Burst Project (CHIME/FRB). Some cycles show no bursts, and some show multiple bursts (CHIME/FRB Collaboration 2020a).
Other irregular sources might be considered. We know that planetary systems exist around pulsars, if uncommon. One of them has four planets. It might also be a system formed of a massive planet and Trojan asteroids. In the Solar System, Jupiter is accompanied by about 1.6 × 105 Trojan asteroids with a radius larger than 1 km near the L4 point of the Sun-Jupiter system (Jewitt et al. 2000). Some of them reach larger scales: 588 Achilles measures about 135 kilometers in diameter, and 617 Patroclus is a binary system made up of two companions which are 140 km and 113 km in diameter.
Gillon et al. (2017) have shown that rich planetary systems with short-period planets are possible around main-sequence stars. Trappist-1 hosts seven Earth-sized planets, the farthest with an orbital period of only 20 days. We imagine a similar system with planets surrounded by satellites. The times at which the satellites would be aligned in a given direction would also seem quite irregular, non-Poissonian, and clustered.
The plausible detection of an asteroid belt around PSR B1937+21 (Shannon et al. 2013) whose effect is detected as timing red noise is also very interesting. It is reasonable to believe that other pulsars exist in which such belts might currently not be distinguishable from other sources of red noise (see, e.g., Shannon et al. 2014 and references therein). It is therefore reasonable to consider swarms of small bodies orbiting a pulsar, even if they are not yet considered as common according to current representations.
In conclusion of this section, the random character of the FRB timing might be due to a large number of asteroids or planets and satellites. These bodies might be clustered along their orbits, causing non-Poissonian FRB-clustered FRB timing. In Sect. 4.2 we discuss a different cause of clustered FRB occurrence: every single asteroid might be seen several times over a time interval ranging over some dozen minutes.
3. Parametric study
3.1. Minimum requirements
We tested whether medium and small solid bodies such as asteroids can produce FRBs. Thus we conducted a few parametric studies based on parameter sets that were compatible with neutron stars and their environment. They are based on the equations (Eqs. (8), (12), (17), (18), and (19)) presented above. We then selected the cases that met the following conditions: (1) the observed signal amplitude on Earth must exceed a minimum value Smin = 0.3 Jy, (2) the companion must be in solid state without current melting or evaporation, and (3) the radius of the source must exceed the maximum local Larmor radius. This last condition is a condition of validity of the magnetohydrodynamics (MHD) equations that support the theory of Alfvén wings (Mottez & Heyvaerts 2011). Practically, the larger Larmor radius might be associated with electron and positrons. In our analysis, this radius is compiled for hydrogen ions at the speed of light, so that condition (3) is checked conservatively.
Because the Roche limit for a companion density ρc ∼ 3000 kg m−3 is about 0.01 AU, we did not search for solutions for smaller separations of neutron star and asteroids r. This corresponds to orbital periods longer than 0.3 day for a neutron-star mass of 1.4 solar mass.
3.2. Pulsars and small-size companions
We first chose magnetic fields and rotation periods relevant to standard and recycled pulsars. Standard and recycled pulsars apparently do not produce FRBs that meet the minimum requirements defined in Sect. 3, however. Therefore we extended our exploration to the combinations of the parameters listed in Table 1. With ϵ = 2.×10−3, 400 031 (7.5%) of the 5 346 000 tested sets of parameters fulfill the minimum requirements. With the higher radio yield ϵ = 10−2, a larger number of 521 797 sets (9.8%) fulfill these conditions. According to the present model, they are appropriate for FRB production.
Parameter set of the first parametric study of FRBs produced by pulsar companions of medium and small size.
Because some of these solutions are more physically meaningful than others, we discuss a selection of realistic solutions.
A selection of representative examples of parameter sets that meet the above three requirements are displayed in Table 2. We considered a companion radius between 1 and 10 000 km. However, because the known repeating FRBs have high and irregular repetition rates, they are more probably associated with small and numerous asteroids. For instance, the volume of a single 100 km body is equivalent to the volumes of 103 asteroids of size Rc = 10 km. We therefore restricted the above parametric study to asteroids of size Rc ≤ 10 km. We also considered energy inputs (1 − f)gLsd > 1027 W because lower values would not be realistic for short-period pulsars with high magnetic fields (see Sect. 2.6 and Appendix B.5 for the definition of (1 − f)gLsd). We also required a pulsar spin-down age τsd ≥ 10 yr and a neutron star radius R* ≤ 12 km. We found 115 parameter sets that would allow for observable FRB at 1 Gpc. Cases 3−13 in Table 2 are taken from this subset of solutions.
We comment on Table 2. The examination of the spin-down age τsd shows that the pulsars allowing FRBs with small companions (cases 1−13, companion radius ≤10 km except for case 2, whose radius is 46 km) generally last shorter than a century (with a few exceptions, such as case 3). Most of the parameter sets involve a millisecond pulsar (P* = 3 or 10 ms, up to 32 ms for cases 1−2), with a Crab-like or higher magnetic field (B* ≥ 3 × 107 T). This means that only very young pulsars could allow for FRBs with asteroids (still with the exception displayed in case 3). The required Lorentz factor is γ ≥ 106. The constraints on the pulsar radius (R* down to 10 km) and temperature (tested up to 106 K) are weak. Orbital distances in the range 0.01 − 0.63 AU are found. A power input (1 − f)gLsd up to the maximum tested value of 1029 W is found, and with T* up to 106 K, this does not raise any significant problem for asteroid survival down to distances of 0.1 AU. The companion conductivity is found to lie between 102 and 107 mho, implying that the companion must be metal rich or must contain some metal. A metal-free silicate or carbon body could not explain the observed FRBs associated with small companion sizes. If the duration of the bursts were caused by the source size alone, this size would be between 0.21 and 0.53 km. This is compatible with even the smallest companion sizes (1−10 km). The electron cyclotron frequency varies in the range 40 GHz ≤ fce ≤ 28 THz, always above the observed FRB frequencies. Therefore the radio emission according to the present model cannot be the consequence of the CMI. The maximum ion Larmor radius, always smaller than a few meters, is much smaller than the source size, confirming that there is no problem with MHD from which the Alfvén wing theory derives.
We find that even a 2 km asteroid can cause FRBs (case 4). Most favorable cases for FRBs with small asteroids (Rc = 10 km or less) are associated with a radio-emission efficiency ϵ = 10−2, as expected. Nevertheless, the lower value ϵ = 2.×10−3 still allows for solutions for r = 0.1 AU (cases 12−13). Two parameter sets for small asteroids provide a flux density S > 20 Jy (such as case 8). Larger asteroids (Rc = 100 km) closer to the neutron star (r = 0.025 AU) could provide an S = 71 Jy burst, larger than the Lorimer burst (case 14). We also consider the case of a 316 km asteroid, at the same distance r = 0.025 AU, which could provide a 7 kJy burst (15*). Nevertheless, we added an asterisk to this case number because problematic effects enter: (1) the size of the asteroid is equal to the pulsar wavelength, so it must be heated by the pulsar wave Poynting flux, and it is probably undergoing evaporation; (2) it can also be tidally disrupted because it is not far from the Roche limit, and the self-gravitational forces for an asteroid of this size are important for its cohesion.
The 16.35-day periodicity of the repeating FRB 180916.J0158+65 (CHIME/FRB Collaboration 2020a) for a neutron star mass of 1.4 solar mass would correspond to a swarm of asteroids at a distance r = 0.14 AU. This fits the range of values from our parametric study. The case of FRB 180916.J0158+65 will be studied in more details in a forthcoming study where the emphasis will be placed on dynamical aspects of clustered asteroids.
Therefore we can conclude that FRBs can be triggered by 1−10 km sized asteroids orbiting a young millisecond pulsar, with a magnetic field B* comparable to that of the Crab pulsar or weaker, but with a shorter period. These pulsars might keep the ability to trigger FRBs that are visible at 1 Gpc at times τsd from shorter than a year up to a few centuries. Our results also provide evidence that the pulsar-companion model is valid as an explanation for repeating FRBs.
The question now is what observational constraints we can derive. Observations clearly cannot constrain the various pulsar parameters. Nevertheless, in the perspective of the discovery of a periodicity with repeating FRBs, such as with FR180916.J0158+65 (CHIME/FRB Collaboration 2019) and possibly FRB 121102 (Rajwade et al. 2020), it might be interesting to establish a flux-periodicity relation. Figure 2 shows the higher fluxes S as a function of the orbital periods Torb from the parameters displayed in Table 1. Moreover, the spin-down age τsd = P∗/2Ṗ∗ is the characteristic time of evolution of the pulsar period P*. For the nonevaporating asteroids considered in our study, the repeating FRBs can be observed over the time τsd with constant ranges of fluxes and frequencies. Over a longer duration t ≫ τsd, the flux S may fall below the sensitivity threshold of the observations. Therefore a prediction of this model is that repeaters fade away with time.
 |
Fig. 2. Maximum observable FRB flux density vs. orbital period from the parameter study described in Table 1. Each curve corresponds to a different constraint on pulsar spin-down age τsd, surface magnetic field B*, and companion radius Rc (see legend). |
3.3. Magnetars and small-size companions
We explored parameter sets describing small companions orbiting a magnetar. The list of parameters is displayed in Table 3.
Sets of input parameters for the parametric study for magnetars.
The current parameter list is intended for FRBs that should be observable from a 1 Gpc distance. The recently discovered FRB that is associated with a source (probably a magnetar) in our Galaxy (CHIME/FRB Collaboration 2020b; Bochenek et al. 2020) will be the object of a further dedicated study.
For each value of the radi -efficiency ϵ, this corresponds to 15 681 600 parameter sets. With ϵ = 10−2, we derived 20 044 solutions that met the minimum requirements defined in Sect. 3. All of them require a minimum size Rc = 46 km (from our parameter set), and a very short magnetar period P* ≤ 0.32 s. Therefore the spin-down age τsd does not exceed 10 or 20 years. An example is given in case 16 of Table 2. This means that it might be possible to trigger occasional FRBs with very young magnetars, but magnetars at 1 Gpc distance are not the best candidates for repeating FRBs associated with an asteroid belt.
3.4. Compatibility with the high Faraday rotation measure of FRB 121102
Michilli et al. (2018) have reported observations of 16 bursts associated with FRB 121102 at frequencies 4.1−4.9 GHz with the Arecibo radio-telescope. All of them are fully linearly polarized. The polarization angles PA have a dependence on f−2, where f is the wave frequency. This is interpreted as the Faraday effect. According to the theory that is generally used by radio astronomers, when a linearly polarized wave propagates through a magnetized plasma of ions and electrons, its polarization angles PA in the source reference frame varies as PA = PA∞ + θ = PA∞ + RMc2/f2, where PA∞ is a reference angle at infinite frequency. The RM factor is called the rotation measure and is given in rad m−2,
where B∥ is the magnetic field in μG projected along the line of sight, l is the distance in parsec, and ne is the electron number density in cm−3.
Michilli et al. (2018) reported very high values RMobs = ( + 1.027 ± 0.001)×105 rad m−2. With the cosmological expansion redshift RMsource = RMobs(1 + z)2 and z = 0.193, we have RMsource = 1.46 × 105 rad m−2. The RMobs are so large that they could not be detected at lower frequencies, 1.1−2.4 GHz, because of depolarization in the relatively coarse bandwidths of the detectors. Measurements performed later at the Green Bank Telescope at 4−8 GHz provided similar values: RMsource = 1.33 × 105 rad m−2 (Gajjar et al. 2018).
A pair-plasma does not produce any rotation measure. Therefore these RM are produced in an ion-electron plasma, which is assumed to be present well beyond the distances r of the pulsar companions of our model. Michilli et al. (2018) proposed that the rotation measure would come from a 1 pc HII region of density ne ∼ 102 cm−3. This would correspond to an average magnetic field B∥ ∼ 1 mG. For comparison, average magnetic fields in similar regions in our Galaxy correspond typically to 0.005 mG, however. Therefore it is suggested that the source is in the vicinity of a neutron star, and more plausibly, of a magnetar or a black hole.
Figure 3 plots the magnetic field as a function of the distance from the neutron star. It is approximated in the same way as in the remaining paper: a dipole field up to the light-cylinder, and then a magnetic field dominated by the toroidal component Bϕ that decreases as r−1 (see Eq. (3)). It is plotted for a highly magnetized magnetar (P* = 5 s, B* = 1012 T), for a Crab-like pulsar, for the very young pulsars that fit the parametric study of Sect. 3.2, and for a fast and short-lived magnetar (P* = 0.1 s, B* = 1011) that could provide FRBs with Rc = 50 km companions. At close distances from the neutron star, the highly magnetized magnetar and the fast magnetar have the strongest magnetic fields. Because their light cylinder is farther away than that of the fast young pulsars, however, the magnetar field beyond a distance r = 0.01 AU is lower than that caused by fast young pulsars.
 |
Fig. 3. Magnetic field as a function of the distance from the neutron star from Eq. (3). Beyond 10−2 AU, the magnetic field is stronger in the vicinity of a young pulsar (e.g., the Crab pulsar) than for a typical magnetar (blue curve). |
We therefore conclude that the high interstellar magnetic field in the 1 pc range of distances that can cause the large rotation measure associated with FRB 121102 is likely produced by the young pulsars that fit the quantitative model presented in Sect. 3.2.
4. Effects of the wind fluctuations on burst duration and multiplicity
The magnetic field varies in the pulsar wind, and its oscillations can explain why radio emission associated with a single asteroid cannot be seen at every orbital period Torb or can be seen several times. The direction of the wind magnetic field oscillates at the spin period P* of the pulsar, which induces a slight variation in the axis of the emission cone due to relativistic aberration (see MZ14). In the reference frame of the source, the strong slow oscillation (period P*) of the magnetic field can induce stronger effects on the plasma instability and therefore on the direction of the emitted waves. In the observer frame, this consequently changes the emission direction within the cone of relativistic aberration. These small changes in direction combined with the long distance between the source and us will affect our possibility of observing the signal. According to the phase of the pulsar rotation, we may or may not actually observe the source signal. It is also possible that for a fast rotating pulsar, we observe separate emission peaks, with a time interval P* ∼ 1 ms or more. Bursts with such multiple emission peaks (typically two or three) have been observed in FRB 181222, FRB 181226, and others (CHIME/FRB Collaboration 2019) and in FRB 121102 (Spitler et al. 2016).
The image of a purely stationary Alfvén wing described up to now in our model is a simplification of reality. In addition to the variations caused by the spinning of the pulsar, the wind is in any case unlikely to be purely stationary: the energy spectrum of its particles varies, as does the modulus and orientation of the embedded magnetic field. More importantly, because the flow in the equatorial plane of the neutron star is expected to induce magnetic reconnection at a distance of a few AU, we expect that turbulence has already started to develop at 0.1 AU (and probably even at 0.01 AU), so that fluctuations of the wind direction itself are possible. As a consequence, the wind direction does not coincide with the radial direction, but creates a small and fluctuating angle with it. These angular fluctuations must result in a displacement of the source region as well as of the direction of the emission beam. This wandering of the beam is bound to affect not only burst durations, but also their multiplicities.
4.1. Duration
Two characteristics must be discussed regarding the duration of the bursts: the narrowness, and the relatively small dispersion of their durations. The average duration of the first 17 events associated with FRB 121102 in the FRB Catalog (Petroff et al. 2016)1 is 5.1 ms and the standard deviation is 1.8 ms2.
Considering a circular Keplerian orbit of the NS companion, the time interval τ during which radio waves are seen is the sum of a time τbeam associated with the angular size of the beam αbeam (width of the dark green area inside the green cone in Fig. 1), and a time τsource associated with the size of the source αsource (size of the yellow region in Fig. 1). In MZ14, the term τsource was omitted, which caused an underestimate of τ. We take it into account here.
When we assume for simplicity that the emission beam is a cone of aperture angle αbeam, then the corresponding solid angle is 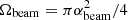 . Using Eq. (2), we obtain
. Using Eq. (2), we obtain
where ΩA is the intrinsic solid angle of emission defined in Sect. 2.1.
Similarly, the size of the source covers an angle αsource ∼ Rs/r, where RS is the size of the source and r is the distance of the companion to the pulsar. For a 1.4 M⊙ neutron star, this leads to
The angle αsource is an upper limit because the source can be farther down the wake.
When the line of sight lies in the orbital plane, then the transit time is equal to the time necessary for the line of sight to cross the angle of emission at a rate norb = 2π/Torb such that norbτ(beam/source) = α(beam/source), giving
which should be seen as maximum transit durations because in this simplified geometry, the line of sight crosses the widest section of the beam. Nonetheless, τ ∼ 0.2 s largely exceeds the average duration of 5 ms that has been recorded for FRB 121102.
This discrepancy can be resolved when the angular wandering of the source due to turbulence and intrinsic wind oscillations is considered. Let 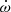 be the characteristic angular velocity of the beam as seen from the pulsar in the corotating frame. We now have
be the characteristic angular velocity of the beam as seen from the pulsar in the corotating frame. We now have 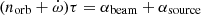 , where τ is the observed value τ ∼ 5 ms. This gives
, where τ is the observed value τ ∼ 5 ms. This gives 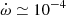 rad s−1 (or 0.7 days in terms of period) for Torb = 0.1 yr, Rs = 10 km, ΩA = 0.1 sr, and γ = 106. At a distance ∼r, this corresponds to a velocity of the source of vs ≃ 0.01c, which is much slower than the radial velocity of the wind, c, and therefore seems plausible. Because we do not generally expect that a burst corresponds to crossing the full width of the beam, this source velocity is to be seen as an upper limit.
rad s−1 (or 0.7 days in terms of period) for Torb = 0.1 yr, Rs = 10 km, ΩA = 0.1 sr, and γ = 106. At a distance ∼r, this corresponds to a velocity of the source of vs ≃ 0.01c, which is much slower than the radial velocity of the wind, c, and therefore seems plausible. Because we do not generally expect that a burst corresponds to crossing the full width of the beam, this source velocity is to be seen as an upper limit.
4.2. Burst multiplicity and rate
As underlined in Connor et al. (2016), a non-Poissonian repetition rate of bursts, as is observed, can have important consequences on the physical modeling of the sources. It is remarkable that many bursts come in groups gathered in a time interval of a few minutes. Zhang et al. (2018) used neural network techniques for the detection of 93 pulses from FRB 121102 in five hours, 45 of which were detected in the first 30 min. Some of them repeated within a few seconds. Many were short (typically 1 to 2 ms duration) and had low amplitudes (S frequently below 0.1 Jy).
We therefore consider in this section that the bunching of pulses over a wandering timescale τw ∼ 1 h is due to the turbulent motion of the beam of a single asteroid that crosses the line of sight of the observer several times. During this time, the asteroid moves on its orbit by an angle αw = norbτw ≫ α (see Sect. 4.1). In particular,
which implies that the beam only wanders across a small region. For the fiduciary values used in this formula, this corresponds to αw = 0.4°. That several bursts are visible also suggests that the beam covers the entire region during this time interval, possibly several times. This leads us to associate an effective solid angle with the emission of an asteroid, that is, the solid angle within which emission can be detected with a very high probability provided that we observe for a duration ∼τw. Further considering that this effective solid angle is dominated by the effect of wandering, we may define
where we assumed a conical shape, which is expected, for instance, in case of isotropic turbulence. We also note that in order to see two bursts separated by τw, the source must travel at a speed vs > rnorb = 2 × 10−4c(Torb/0.1 yr)−1/3, which is compatible with the findings of Sect. 4.1.
Thus, we propose that groups of bursts observed within a time interval of about τw result from one asteroid–pulsar interaction. When burst rates are estimated, it is therefore important to distinguish the number of bursts from the number of burst groups. According to our model, only the latter corresponds to the number of alignments of neutron star-asteroid-Earth. We emphasize that the meandering of the emission direction is an unpredictable function of time connected with the turbulent flow, which suggests that we will not observe precise periodic repetitions at each asteroid alignment (this effect comes in addition to the gravitational interactions mentioned in Sect. 2.7). We also note that the bunching mechanism we propose here does not predict a particular pattern for the properties of each bursts, which may vary randomly from one to another. This is distinct from an eruption-like phenomenon in which a strong energy release is followed by aftershocks of lower intensity, such as predicted by models of self-organized criticality (Aschwanden et al. 2016).
5. Discussion
5.1. What is new since the 2014 model with neutron stars and companions
MZ14, revised by MH20, showed that planets orbiting a pulsar, in interaction with its wind, might cause FRBs. Their model predicts that FRBs repeat periodically with the same period as the orbital period of the planet. An example of possible parameters given in MZ14 was a planet with a size ∼104 km at 0.1 AU from a highly magnetized millisecond neutron star. Chatterjee et al. (2017) more recently published the discovery of the repeating FRB 121102. The cosmological distance of the source (1.7 Gpc) was confirmed. The repeater FRB 121102, as well as the others discovered since then, is essentially not periodic, however.
We here considered that irregular repeating FRBs can be triggered by belts or swarms of small bodies orbiting a pulsar. After adding some thermal considerations that were not included in MZ14, we conducted several parametric studies that showed that repeating FRBs as well as nonrepeating ones can be generated by small bodies in the vicinity of a very young pulsar, and less likely, a magnetar. Some parameter sets even showed that 10 km bodies might cause FRBs seen at a distance of 1 Gpc with a flux of some dozen Janskys.
MZ14 assumed that the radio waves might be emitted by the cyclotron maser instability. The frequency of CMI waves is slightly higher than the electron gyrofrequency, which with the retained parameters is not compatible with observed radio frequencies. Another emission mechanism must therefore be at play. Determining its nature is left for a further study.
Regardless of the process that generates the radio emission, our parametric study is based on the hypothesis that the emission in the source reference frame is modestly beamed within a solid angle ΩA ∼ 0.1 to 1 sr. Our parametric study can be refined when we have better constrains on ΩA.
5.2. Comparisons with other models of bodies that interact with a neutron star
Many types of interactions have been studied between neutron stars and celestial bodies that orbiting them. Many of them involve interactions between the neutron star and its companion at a distance that is large enough for a significant part of the pulsar wind magnetic energy to dissipate. The pulsar wind energy is dominated by the kinetic energy of its particles. Moreover, the companion has an atmosphere, or a wind of its own if it is a star, and the companion-wind interface includes shock waves.
In our model, the distance to the companion is much smaller, and the wind energy is dominated by magnetic energy. The companion is asteroid-like, it has no atmosphere, and regardless of the Mach number of the pulsar wind, there is no shock-wave in front of it. The wind-companion interface takes the form of an Alfvén wing.
Our model is not alone in involving asteroids in the close vicinity of a neutron star. Dai et al. (2016) considered the free fall of an asteroid belt onto a highly magnetized pulsar, which is compatible with the repetition rate of FRB 121102. The asteroid belt was assumed to be captured by the neutron star from another star (see Bagchi 2017 for capture scenarios). The main energy source was the gravitational energy release related to tidal effects when the asteroid passes through the pulsar breakup radius. After Colgate & Petschek (1981), and with their fiduciary values, the authors estimated this power to be ĖG ∼ 1.2 × 1034 W. Even if this power is radiated isotropically from a source at a cosmological distance, it suffices to explain the observed FRB flux densities. Dai et al. (2016) developed a model to explain how a large fraction of this energy is radiated in the form of radio waves. As in MZ14, they invoked the unipolar inductor model. Their electric field had the form E2 = −vff × B, where vff is the free-fall asteroid velocity (we note it E2 as in Dai et al. 2016). Then, the authors argued that this electric field can accelerate electrons to a Lorentz factor γ ∼ 100, and the density was computed in a way similar to the Goldreich-Julian density in a pulsar magnetosphere. These accelerated electrons would cause coherent curvature radiation at frequencies of ∼1 GHz. Their estimate of the power associated with these radio waves was Ėradio ∼ 2.6 × 1033 W ∼ 0.2ĖG, under their assumption (simple unipolar inductor), which partially neglects the screening of the electric field by the plasma (in contrast to the Alfvén wing theory) and therefore overestimates the emitted power.
Conceptually, the Dai et al. (2016) model is more similar to ours than models related to shocks. In terms of distances to the neutron star, our model places the obstacle (asteroid or star) in between these two.
5.3. How many asteroids?
We considered a very simple asteroid belt where all the asteroids have a separation r with the neutron star, corresponding to an orbital period Torb, and their orbital inclination angles are smaller than α = Δz/r, where Δz is the extension in the direction perpendicular to the equatorial plane of the star.
Let Nv be the number of “visible” asteroids whose beams cross the observer line of sight at some point of their orbit. As explained in Sect. 4.2, we may consider that because of the angular wandering of the beam, an asteroid causes all the bursts that occur in a time window of τw ∼ 1 h. When the beam covers a conical area of aperture angle αw defined in Eq. (24), the visible asteroids are those that lie within ±αw/2 of the line of sight of the observer at inferior conjunction, the vertex of the angle being the pulsar. The total number N of asteroids in the belt is then related to the number of visible asteroids by N = Nvα/αw, assuming a uniform distribution. By definition, the number of groups of bursts per orbital period is Nv. It follows that the number of groups during a time Δt is given by Ng = NvΔt/Torb. Defining the rate ng = Ng/Δt, we obtain N = ngTorbα/αw.
About nine burst groups separated by more than one hour are listed in FRBcat for FRB 121102. Some FRB repeaters have been observed for dozens of hours without any burst, the record is 300 h of silence for FRB 180814.J0422+73 (Oostrum et al. 2020). When an interval of 100 h between bunches of bursts is considered, the event rate per year would be about 88. We adopt the figure of 100 events per year, giving
For the fiduciary values in Eq. (26), only 140 asteroids are therefore required to explain a FRB rate similar to that of the repeater FRB 121102. For comparison, in the Solar System, more than 106 asteroids larger than 1 km are known, about 104 of which are larger than 10 km.
6. Conclusion and perspectives
We summarize the characteristics of FRBs explained by our model. Their observed flux (including the 30 Jy Lorimer burst-like) can be explained by a moderately energetic system because of a strong relativistic aberration associated with a highly relativistic pulsar wind that interacts with metal-rich asteroids. A high pulsar wind Lorentz factor (∼106) is required in the vicinity of the asteroids. The FRB duration (about 5 ms) is associated with the asteroid orbital motion and the periodic variations of the wind caused by the pulsar rotation, and to a lesser extent, with pulsar wind turbulence. The model is compatible with the observations of FRB repeaters. The repetition rate might be very low, however, and FRBs considered up to now as nonrepeating might be repeaters with a low repetition rate. For repeaters, the bunched repetition rate is a consequence of a moderate pulsar wind turbulence. All the pulses associated with the same neutron star are expected to have the same DM (see Appendix C). The model is compatible with the high Faraday rotation measure observed in FRB 121102. Our model involves asteroids that orbit a young neutron star. We showed with the example of FRB 121102 that fewer than 200 asteroids with a size of a few dozen kilometer are required. This is far fewer than the number of asteroids of this type that orbit in the Solar System.
Nevertheless, we do not pretend to explain the entire phenomenology of FRBs, and it is possible that various FRBs are associated with different families of astrophysical sources.
We also describe the perspectives of technical improvements of the pulsar–asteroid model of FRB that deserve further work.
As described in Sect. 5.1, the radio emission process is left for a further study.
When thermal constraints were analyzed, we treated the Alfvén wing and the heating of the companion by the Poynting flux of the pulsar wave separately. For the latter, we used the Mie theory of diffusion, which takes the variability of the electromagnetic environment of the companion into account, but neglects the role of the surrounding plasma. On the other hand, the Alfvén wing theory in its current state takes the plasma into account, but neglects the variability in the electromagnetic environment. A unified theory of an Alfvén wing in a varying plasma would allow a better description of the interaction of the companion with its environment.
Another important (and often asked) question related to our model is the comparison of global FRB detection statistics with the population of young pulsars that host asteroids or planets in galaxies within a 1 or 2 Gpc range from Earth. This will be the subject of a forthcoming study.
Because our parametric study tends to favor 10- to 1000-year-old pulsars, the FRB source is expected to be surrounded by a young expanding supernova remnant (SNR) and a pulsar wind nebula driving a shock into the ejecta (Gaensler & Slane 2006). The effect of the SNR plasma on the dispersion measure of the radio waves will also be the topic of a further study. This question requires a model of the young SNR, and that is beyond the scope of this paper. We cannot exclude that this point brings new constraints on our model, and in particular, on the age of the pulsars causing the FRBs or on the mass of its progenitor.
We conclude this section with a vision. After upgrading the MZ14 FRB model (corrected by MH20) with the ideas of a cloud or belt of asteroids orbiting the pulsar and with turbulence in the pulsar wind, we have obtained a model that explains the observed properties of FRB repeaters and nonrepeaters in a unified frame. In this frame, the radio Universe contains myriads of pebbles that circle young pulsars in billions of galaxies, each with a highly collimated beam of radio radiation that meanders inside a larger cone (of perhaps a fraction of a degree) and sweeps through space like multitudes of small erratic cosmic lighthouses, detectable at gigaparsec distances. Each time one such beam crosses the Earth for a few milliseconds and illuminates radio telescopes, an FRB is detected, revealing a ubiquitous but otherwise invisible reality.
Acknowledgments
G. Voisin acknowledges support of the European Research Council, under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 715051, Spiders).
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010a, ApJ, 708, 1254 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010b, ApJ, 713, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ajello, M., Allafort, A., et al. 2013, ApJS, 208, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., Crosby, N. B., Dimitropoulou, M., et al. 2016, Space Sci. Rev., 198, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Bagchi, M. 2017, ApJ, 838, L16 [CrossRef] [Google Scholar]
- Becker, W. 2009, in Astrophysics and Space Science Library, ed. W. Becker, 357, 133 [Google Scholar]
- Bochenek, C. D., Ravi, V., Belov, K. V., et al. 2020, Nature, 587, 59 [CrossRef] [Google Scholar]
- Cerutti, B., & Philippov, A. A. 2017, A&A, 607, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chatterjee, S., Law, C. J., Wharton, R. S., et al. 2017, Nature, 541, 58 [NASA ADS] [CrossRef] [Google Scholar]
- CHIME/FRB Collaboration (Andersen, B. C., et al.) 2019, ApJ, 885, L24 [NASA ADS] [CrossRef] [Google Scholar]
- CHIME/FRB Collaboration (Amiri, M., et al.) 2020a, Nature, 582, 351 [CrossRef] [Google Scholar]
- CHIME/FRB Collaboration (Andersen, B. C., et al.) 2020b, Nature, 587, 54 [CrossRef] [Google Scholar]
- Colgate, S. A., & Petschek, A. G. 1981, ApJ, 248, 771 [CrossRef] [Google Scholar]
- Connor, L., Pen, U.-L., & Oppermann, N. 2016, MNRAS, 458, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Dai, Z. G., Wang, J. S., Wu, X. F., & Huang, Y. F. 2016, ApJ, 829, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Freund, H. P., Wong, H. K., Wu, C. S., & Xu, M. J. 1983, Phys. Fluids, 26, 2263 [NASA ADS] [CrossRef] [Google Scholar]
- Gaensler, B. M., & Slane, P. O. 2006, ARA&A, 44, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Gajjar, V., Siemion, A. P. V., Price, D. C., et al. 2018, ApJ, 863, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Gillon, M., Triaud, A. H. M. J., Demory, B.-O., et al. 2017, Nature, 542, 456 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Goldreich, P., & Lynden-Bell, D. 1969, ApJ, 156, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Gurnett, D. A., Averkamp, T. F., Schippers, P., et al. 2011, Geophys. Res. Lett., 38, L06102 [Google Scholar]
- Hess, S., Zarka, P., & Mottez, F. 2007, Planet. Space Sci., 55, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Hessels, J. W. T., Spitler, L. G., Seymour, A. D., et al. 2019, ApJ, 876, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Jewitt, D. C., Trujillo, C. A., & Luu, J. X. 2000, AJ, 120, 1140 [NASA ADS] [CrossRef] [Google Scholar]
- Karuppusamy, R., Stappers, B. W., & van Straten, W. 2010, A&A, 515, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Katz, J. I. 2017, MNRAS, 467, L96 [Google Scholar]
- Keppens, R., Goedbloed, H., & Durrive, J.-B. 2019, J. Plasma Phys., 85, 905850408 [CrossRef] [Google Scholar]
- Kirk, J. G., Skjæraasen, O., & Gallant, Y. A. 2002, A&A, 388, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kotera, K., Mottez, F., Voisin, G., & Heyvaerts, J. 2016, A&A, 592, A52 [CrossRef] [EDP Sciences] [Google Scholar]
- Lentz, W. J. 1976, Appl. Opt., 15, 668 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Louis, C. K., Lamy, L., Zarka, P., Cecconi, B., & Hess, S. L. G. 2017, J. Geophys. Res.: Space Phys., 122, 9228 [NASA ADS] [CrossRef] [Google Scholar]
- Louis, C. K., Hess, S. L. G., Cecconi, B., et al. 2019, A&A, 627, A30 [CrossRef] [EDP Sciences] [Google Scholar]
- Luo, R., Men, Y., Lee, K., et al. 2020, MNRAS, 494, 665 [CrossRef] [Google Scholar]
- Michilli, D., Seymour, A., Hessels, J. W. T., et al. 2018, Nature, 553, 182 [NASA ADS] [CrossRef] [Google Scholar]
- Mottez, F., & Heyvaerts, J. 2011, A&A, 532, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mottez, F., & Heyvaerts, J. 2020, A&A, 639, C2 [CrossRef] [EDP Sciences] [Google Scholar]
- Mottez, F., & Zarka, P. 2014, A&A, 569, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neubauer, F. M. 1980, J. Geophys. Res.: Space Phys., 85, 1171 [NASA ADS] [CrossRef] [Google Scholar]
- Ng, C. W., Takata, J., Strader, J., Li, K. L., & Cheng, K. S. 2018, ApJ, 867, 90 [CrossRef] [Google Scholar]
- Oostrum, L. C., Maan, Y., van Leeuwen, J., et al. 2020, A&A, 635, A61 [CrossRef] [EDP Sciences] [Google Scholar]
- Pétri, J. 2016, J. Plasma Phys., 82, 635820502 [CrossRef] [Google Scholar]
- Petroff, E., Barr, E. D., Jameson, A., et al. 2016, PASA, 33, e045 [NASA ADS] [CrossRef] [Google Scholar]
- Pryor, W. R., Rymer, A. M., Mitchell, D. G., et al. 2011, Nature, 472, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Rajwade, K. M., Mickaliger, M. B., Stappers, B. W., et al. 2020, MNRAS, 495, 3551 [CrossRef] [Google Scholar]
- Saur, J., Neubauer, F. M., Connerney, J. E. P., Zarka, P., & Kivelson, M. 2004, G., 1, 537 [Google Scholar]
- Scholz, P., Spitler, L. G., Hessels, J. W. T., et al. 2016, ApJ, 833, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Shannon, R. M., Cordes, J. M., Metcalfe, T. S., et al. 2013, ApJ, 766, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Shannon, R. M., Osłowski, S., Dai, S., et al. 2014, MNRAS, 443, 1463 [NASA ADS] [CrossRef] [Google Scholar]
- Spitkovsky, A. 2006, ApJ, 648, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Spitler, L. G., Scholz, P., Hessels, J. W. T., et al. 2016, Nature, 531, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Timokhin, A. N., & Arons, J. 2013, MNRAS, 429, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Timokhin, A. N., & Harding, A. K. 2015, ApJ, 810, 144 [CrossRef] [Google Scholar]
- Wilson, D. B., & Rees, M. J. 1978, MNRAS, 185, 297 [CrossRef] [Google Scholar]
- Zarka, P. 2007, Planet. Space Sci., 55, 598 [NASA ADS] [CrossRef] [Google Scholar]
- Zarka, P., Treumann, R. A., Ryabov, B. P., & Ryabov, V. B. 2001, Ap&SS, 277, 293 [Google Scholar]
- Zarka, P., Marques, M. S., Louis, C., et al. 2018, A&A, 618, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zavlin, V. E. 2009, in Astrophysics and Space Science Library, ed. W. Becker, 357, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Y. G., Gajjar, V., Foster, G., et al. 2018, ApJ, 866, 149 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Another way of computing the radio flux
As shown in Mottez & Heyvaerts (2011), the optimal power of the Alfvén wing ĖA is the fraction of the pulsar Poynting flux intercepted by the companion section. When we consider that at the companion separation r most of the pulsar spin-down power Lsd is in the form of the Poynting flux, 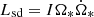 is a correct estimate of the Poynting flux. It can be derived from our parameter set. The fiduciary value of inertial momentum is I = 1038 kg m2. Our parameters do not explicitly include
is a correct estimate of the Poynting flux. It can be derived from our parameter set. The fiduciary value of inertial momentum is I = 1038 kg m2. Our parameters do not explicitly include 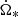 . Fortunately, we can use the approximate expression
. Fortunately, we can use the approximate expression
where i is the magnetic inclination angle (Spitkovsky 2006). We chose the conservative value i = 0°. With normalized values,
Following Eq. (6), the radio power is 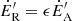 , where the prime denotes the present alternative computation,
, where the prime denotes the present alternative computation,
The equivalent isotropic luminosity is
where again the prime means “alternative to Eq. (9)”. In terms of reduced units,
Owing to the relativistic beaming factor γ2, this power can exceed the total pulsar spin-down power. This is possible because the radio beam covers a very small solid angle, which is at odds with the spin-down power that is a source of Poynting flux in almost any direction. Equation (10) is a simple combination of Eqs. (A.2) and (A.5).
Appendix B: Asteroid heating
B.1. Heating by thermal radiation from the neutron star
For heating by the stellar thermal radiation,
where LT is the thermal luminosity of the pulsar, R* and T* are the neutron star radius and temperature, σS is the Stefan-Boltzmann constant and in international system units, 4πσS = 7 × 10−7 Wm−2 K−4. For T* = 106 K, and T* = 3 × 105, the luminosities are 7 × 1025 W and 1024 W. This is consistent with the thermal radiation of Vela observed with Chandra, LT = 8 × 1025 W (Zavlin 2009).
B.2. Heating by the pulsar wave Poynting flux
Heating by the Poynting flux has been investigated in Kotera et al. (2016). Following their method,
where Lsd is the loss of pulsar rotational energy. The product fLsd is the part of the rotational energy loss that is taken by the pulsar wave. The dimensionless factor fp is the fraction of the sky into which the pulsar wind is emitted. The absorption rate Qabs of the Poynting flux by the companion was derived in Kotera et al. (2016) by applying the Mie theory with the Damie code based on Lentz (1976). For a metal-rich body smaller than 10−2RLC, Qabs < 10−6 (see their Fig. 1). We define the upper value of Qabs as Qmax.
The value Qmax = 10−6 may seem surprisingly low. For a large planet, we would have Qabs ∼ 1. To understand well what happens, we can compare this with the propagation of electromagnetic waves in a dusty interstellar cloud. The size of the dust grains is generally ∼1 μm. Visible light, with shorter wavelengths (∼500 nm), is scattered by these grains. Infrared light, however, with a wavelength longer than that of the dust grains, is not scattered in accordance with the Mie theory, and the dusty cloud is transparent to infrared light. With a rotating pulsar, the wavelength of the vacuum wave (Parker spiral) is λ ∼ 2c/Ω*, equal to twice the light cylinder radius rLC = c/Ω*. Dwarf planets are comparable in size with the light cylinder of a millisecond pulsar and much smaller than that of a 1 s pulsar, therefore smaller bodies always have a factor Q smaller or much smaller than 1. Asteroids up to 100 km are smaller than the light cylinder, therefore they do not scatter nor absorb the energy carried by the pulsar vacuum wave. This is expressed with Qmax = 10−6.
When the companion size is similar to the pulsar wavelength, that is, twice the light-cylinder distance 2rLC, then heating by the Poynting flux cannot be neglected. In this case, we can take Qabs = 1. For medium-size bodies for which gravitation was unable to retain an evaporated atmosphere, it is therefore important to verify if Rc < 2rLC.
B.3. Heating by the pulsar nonthermal radiation
For heating by the nonthermal stellar radiation,
where gNT is a geometrical factor induced by the anisotropy of nonthermal radiation. In regions above nonthermal radiation sources, gNT > 1, but in many other places, gNT < 1. The total luminosity associated with nonthermal radiation LNT depends largely on the physics of the magnetosphere, and it is simpler to use measured fluxes than those predicted by models and simulations.
With low-energy gamma-ray-silent pulsars, most of the energy is radiated in X-rays. Typical X-ray luminosities are in the range LX ∼ 1025 − 1029 W, corresponding to a proportion ηX = 10−2 − 10−3 of the spin-down luminosity Lsd (Becker 2009).
Gamma-ray pulsars are more energetic. It is reasonable to assume gamma-ray pulsar luminosity Lγ ∼ 1026 − 1029 W (Zavlin 2009; Abdo et al. 2013). The maximum of these values can be reached with young millisecond pulsars. For instance, the Crab pulsar (PSR B0531+21) with a period P* = 33 ms and 3.8 × 108 T has the second largest known spin-down power 4.6 × 1031 W and its X-ray luminosity is LX = 1029 W (Becker 2009). Its gamma-ray luminosity, estimated with Fermi, is Lγ = 6.25 × 1028 W above 100 MeV (Abdo et al. 2010a). Vela (P* = 89 ms, B* = 3.2 × 108 T) has a lower luminosity: LX = 6.3 × 1025 W in X-rays (including the already mentioned contribution of thermal radiation) and Lγ = 8.2 × 1027 W in gamma-rays (Abdo et al. 2010b).
We note for the geometrical factor gNT that most of the pulsar X-ray and gamma-ray radiations are pulsed. Because this pulsation is likely of geometrical origin, their emission is not isotropic. Without going into the diversity of models that have been proposed to explain the high-energy emission of pulsars, it is clear that (i) the high-energy flux impinging on the companion varies and is probably modulated by a duty cycle, and (ii) the companion may be located in a region of the magnetosphere where the high-energy flux is very different from what is observed, either weaker or stronger. It would be at least equal to or higher than the inter-pulse level.
If magnetic reconnection takes place in the stripped wind (see Pétri 2016 for a review), presumably in the equatorial region, then a fraction of the Poynting flux LP should be converted into high-energy particles, or X-ray and gamma-ray photons (or accelerated leptons, see Appendix B.4), which would also contribute to the irradiation. At which distance does this occur? Some models based on a low value of the wind Lorentz factor (γ = 250 in Kirk et al. 2002) evaluated the distance rdiss of the region of conversion at 10 to 100 rLC (we note “diss” for dissipation of magnetic energy). With pulsars with P ∼ 0.01 or 0.1 s, as we show below, the companions would be exposed to a high level of X-rays and gamma-rays. We also show below that the simple consideration of γ as low as 250 does not fit our model. More recently, Cerutti & Philippov (2017) showed with numerical simulations a scaling law for rdiss, which reads rdiss/RLC = πγκLC, where κLC is the plasma multiplicity at the light cylinder. (The plasma multiplicity is the number of pairs produced by a single primary particle.) With multiplicities of about 103 − 104 (Timokhin & Arons 2013) and γ > 104 (Wilson & Rees 1978; Ng et al. 2018), and the worst case P* = 1 ms, we have rdiss > 3 AU, which is beyond the expected distance r of the companions causing FRBs, as we show in the parametric study (Sect. 3).
Therefore we can consider that the flux of high-energy photons received by the pulsar companions is lower than the flux corresponding to an isotropic luminosity LNT, and we therefore consider that gNT ≤ 1.
B.4. Heating by the pulsar wind particles that hit the companion
Heating by absorption of the particle flux can be estimated on the basis of the density of electron-positron plasma that is sent away by the pulsar with an energy ∼γmcc2. Let n be the number density of electron-positron pairs, then we can write n = κρG/e, where ρG is the Goldreich-Julian charge density (also called corotation charge density), κ is the multiplicity of pair-creations, and e is the charge of the electron. We use the approximation ρG = 2ϵ0Ω*B*. Then,
where fW ≤ 1 is the fraction of the neutron star surface above which the particles are emitted. The flux ĖW is deduced from LW in the same way as in Eq. (B.1),
where gW is a geometrical factor depending on the wind anisotropy.
B.5. Added powers of the wind particles and of the pulsar nonthermal radiation
In Eq. (B.4) the estimate of LW depends on the ad hoc factors κ, γ, and f. Their estimates are highly dependent on the various models of pulsar magnetosphere. It is also difficult to estimate LNT. Then, it is convenient to note that there are essentially two categories of energy fluxes: those that are fully absorbed by the companion (high-energy particles, photons, and leptons), and those that may be only partially absorbed (the Poynting flux). In addition, all these fluxes should add up to the total rotational energy loss of the pulsar Lsd. Therefore the sum of the high-energy contributions may be rewritten as being simply
where f is the fraction of rotational energy loss into the pulsar wave, which is already accounted for in Eq. (B.2). This way of solving the problem allows an economy of ad hoc factors. The dependence of g is a function of the inclination i of the NS magnetic axis relative to the companion orbital plane as a consequence of the effects discussed in Appendix B.3. Following the discussion of the previous sections regarding gW and gNT, we assume generally that g is lower than one.
B.6. Heating by the companion Alfvén wing
One source of heat remains to be considered: the Joule dissipation associated with the Alfvén wing electric current. The total power associated with the Alfvén wing is
where VA ∼ c is the Alfvén velocity, and IA is the total electric current in the wing. A part ĖJ of this power is dissipated into the companion by Joule heating,
where σc is the conductivity of the material constituting the companion, and h is the thickness of the electric current layer. For a small body relative to the pulsar wavelength c/Ω*, we have h ∼ Rc. For a rocky companion, σc ∼ 10−3 mho m−1, whereas for iron, σc ∼ 107 mho m−1.
The Alfvén wing takes its energy from the pulsar wave Poynting flux, and we might consider that ĖA is also a fraction of the power fĖP. We might then conceal this term in the estimate of f. Nevertheless, we kept it explicitly for the estimate of the minimum companion size that might trigger an FRB because we need to know ĖA to estimate the FRB power.
Appendix C: Fluctuations of the dispersion measure
The groups of bursts from FRB 121102 analyzed in Zhang et al. (2018) show large variations in dispersion measure (DM). With an average value close to DM = 560 pc cm−3, the range of fluctuations ΔDM is larger than 100 pc cm−3, sometimes with large variations for bursts separated by less than one minute. Because the variations are strong and fast, we cannot expect perturbations of the mean plasma density over long distances along the line of sight. If real, the origin of these fluctuations must be sought over short distances. If the plasma density perturbation extends over a distance of 104 km, the corresponding density variation reaches Δn ∼ 1011 cm−3, that is, the Goldreich-Julian density near the neutron star surface. Such strong fluctuations are very unlikely in the much less dense pulsar wind, where radio wave generation takes place in our paper. Are these strong DM variations fatal for our model?
The DM fluctuations or the (less numerous) bursts from FRB 121102 listed in the FRBcat database are more than one order of magnitude weaker than those reported by Zhang et al. (2018). How reliable are the DM estimates in the latter paper? This question was investigated in Hessels et al. (2019). The authors note that the time-frequency sub-structure of the bursts, which is highly variable from burst to burst, biases the automatic determination of the DM. They argued that it is more appropriate to use a DM metrics that maximizes frequency-averaged burst structure than the usual frequency-integrated peak of the signal-to-noise ratio. The DM estimates based on frequency-averaged burst structure reveal a very small dispersion ΔDM ≤ 1 pc cm−3. They also note an increase by 1−3 pc cm−3 in four years, which is compatible with propagation effects into the interstellar and intergalactic medium.
This discussion is likely relevant to other FRB repeaters, such as FRB 180916.J0158+65, because all of them show analogous burst substructures. Thus we conclude that the large DM variations observed in Zhang et al. (2018), for instance, are apparent and actually related to burst substructures. They depend more on the method used to estimate the DM than on real variations of plasma densities. Therefore they do not constitute a problem for our pulsar–asteroid FRB model.
All Tables
Parameter set of the first parametric study of FRBs produced by pulsar companions of medium and small size.
All Figures
 |
Fig. 1. Schematic view of the wake of a pulsar companion. The pulsar is far to the left outside of the figure. The directions of the wind velocity vw, the wind magnetic field Bw, and the convection electric field Ew are plotted on the left-hand side. The shadow is shown in gray. The Alfvén wing is shown in blue. The region from which we expect radio emissions (in yellow) is inside the wing and outside the shadow. Its largest transverse radius is RS and its distance to the companion is l. Seen from the NS at a distance r, it subtends a solid angle Ωσ. Any point source S in the source region can generate radio waves. Because of the relativistic aberration, their directions are contained in a narrow beam (in green) of solid angle πγ−2. If the emission is not isotropic in the source reference frame, it is emitted in a subset of this cone (dark green tortuous line). Photons that emerge from this cone are marked with red arrows. Seen from the source point S, this dark green area subtends a solid angle Ωbeam. |
| In the text | |
 |
Fig. 2. Maximum observable FRB flux density vs. orbital period from the parameter study described in Table 1. Each curve corresponds to a different constraint on pulsar spin-down age τsd, surface magnetic field B*, and companion radius Rc (see legend). |
| In the text | |
 |
Fig. 3. Magnetic field as a function of the distance from the neutron star from Eq. (3). Beyond 10−2 AU, the magnetic field is stronger in the vicinity of a young pulsar (e.g., the Crab pulsar) than for a typical magnetar (blue curve). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} {M_{\rm A}}^2 = \left(\frac{v_{\rm r}}{c}\right)^2 \left[1 + \frac{\gamma }{\sigma } \left(\frac{v_{\rm r}}{c}\right)\right], \end{aligned} $$](/articles/aa/full_html/2020/12/aa37751-20/aa37751-20-eq1.gif)
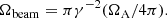
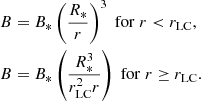
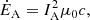
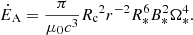
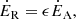

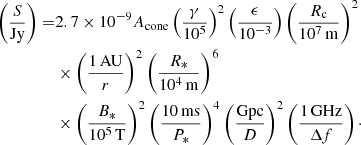
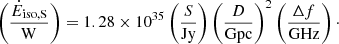
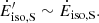
![$$ \begin{aligned} \left(\frac{f_{\rm ce,o}}{\mathrm{Hz}}\right)=&5.2 \times 10^4 \left(\frac{\gamma }{10^5}\right) \left(\frac{B_{*}}{10^5\,\mathrm{T}} \right)\nonumber \\& \times \left(\frac{1\,\mathrm{AU}}{r}\right)^{2} \left( \frac{R_*}{10^4\,\mathrm{m}} \right)^{3} \left(\frac{10\,\mathrm{ms}}{P_{*}}\right)\nonumber \\&\times \left\{ 1+ \left[\frac{\pi \, 10^5}{\gamma } \left(\frac{10\,\mathrm{ms}}{P_{*}}\right)\left(\frac{r}{1\,\mathrm{AU}}\right) \right]^2\right\} ^{1/2}. \end{aligned} $$](/articles/aa/full_html/2020/12/aa37751-20/aa37751-20-eq13.gif)
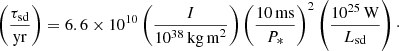
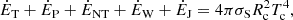
![$$ \begin{aligned} R_{\rm c}^3 \mu _0 c \sigma _{\rm c} \left[ 4 \pi \sigma _{\rm S} T_{\mathrm{max} }^4 -\frac{X}{4 r^2} \right] > \dot{E}_{\rm A\,min}, \end{aligned} $$](/articles/aa/full_html/2020/12/aa37751-20/aa37751-20-eq18.gif)
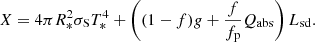
![$$ \begin{aligned}&R_{\rm c}^3 \left(\frac{\sigma _{\rm c}}{10^7\,\mathrm{mho}}\right) \left[2.7 \times 10^4 \left(\frac{T_{\rm c}}{1400\,\mathrm{K}}\right)^4 -\left(\frac{\mathrm{AU}}{r}\right)^2 X \right]\\&\qquad \qquad \qquad \qquad \qquad \qquad >2.7 \times {10^{15}} \frac{Y}{A_{\mathrm{cone} }}, \nonumber \end{aligned} $$](/articles/aa/full_html/2020/12/aa37751-20/aa37751-20-eq20.gif)