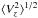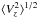| Issue |
A&A
Volume 567, July 2014
|
|
|---|---|---|
| Article Number | A17 | |
| Number of page(s) | 11 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201423656 | |
| Published online | 04 July 2014 | |
Long-time evolution of gas-free disk galaxies in binary systems
1
Coordenação de Astronomia e Astrofísica, Observatório
Nacional, Rua General José Cristino
77, São Cristóvão, CEP
20921–400
Rio de Janeiro
RJ
Brazil
e-mail: chan@on.br
2
Divisão Serviço da Hora, Observatório Nacional,
Rua General José Cristino 77, São
Cristóvão, CEP
20921–400
Rio de Janeiro, RJ, Brazil
e-mail: selma@on.br
Received:
17
February
2014
Accepted:
13
May
2014
We present the results of several detailed numerical N-body simulations of the dynamical interactions of two equal-mass disk galaxies. Both galaxies are embedded in spherical halos of dark matter and contain central bulges. Our analysis of the dynamical evolution of the binary system focuses on the morphological evolution of the stellar distribution of the disks. The satellite galaxy has coplanar or polar disk orientation in relation to the disk of the primary galaxy and their initial orbits are prograde eccentric (e = 0.1, e = 0.4 or e = 0.7). Both galaxies have mass and size similar to the Milky Way. We show that the merger of the two disk galaxies, depending on the relative orientation of the disks, can yield either a disk or lenticular remnant, instead of an elliptical one. These are the first reported simulations that show the formation of S0-like galaxies from protracted binary galaxy interactions. Additionally, we demonstrate that the time to merger increases linearly with the initial apocentric distance between the galaxies, and decreases with the initial orbital eccentricity. We also show that the tidal forces of the disks excite transient m = 1 and m = 2 wave modes, that is, lopsidedness, spiral arms, and bars. However, after the merging of the disks, these larger instabilities fade completely, and the remnant is thicker and more extended than the original disks. The maximum relative amplitude of these waves is at most about 15 times higher than the control case. The m = 2 wave mode is generated mainly by tidal interaction in the outer region of the disks. The m = 1 wave mode depends mostly on the interaction of the inner part of the disks, producing an off-centering effect of the wave mode center relative to the center of mass of the disk. These characteristics produce a time lag among the maximum formation of these two wave modes. Finally, the disk settles down quickly after the merger, in less than one outer disk rotation period.
Key words: galaxies: spiral / galaxies: evolution / galaxies: interactions / galaxies: kinematics and dynamics / galaxies: structure
© ESO, 2014
1. Introduction
Seventy percent of the galaxies in the nearby universe are characterized by a disk with prominent spiral arms, but our understanding of the origin of these patterns is incomplete, even after decades of theoretical study (Sellwood 2011, 2013). Several ideas have been proposed to explain the formation of spiral arms.
The latest simulations show that gravitational instabilities in the stars lead to flocculent and multi-armed spirals that persist for many Gyr (Oh et al. 2008; Fujii et al. 2011). However, the mechanism that produces and maintains two-armed grand design galaxies is still ambiguous.
Grand design galaxies, which exhibit symmetric two-armed spiral structures, represent a significant fraction of spiral galaxies. The production of such a spiral galaxy faces two main obstacles: first, inducing the m = 2 spiral structure, and secondly, maintaining it.
It is known that the spiral arms of disk galaxies can be excited by tidal interactions with nearby companion galaxies (Oh et al. 2008; Dobbs et al. 2010; Struck et al. 2011).
Oh et al. (2008) have investigated the physical properties of tidal structures in a disk galaxy created by gravitational interactions with a companion using numerical N-body simulations. They have considered a galaxy model consisting of a rigid halo/bulge and an infinitesimally thin stellar disk with Toomre parameter Q ≈ 2. The perturbing companion was treated as a pointmass moving on a prograde parabolic orbit, with varying mass and pericenter distance. They have shown that tidal interactions produce well-defined spiral arms and extended tidal features, such as bridge and tail, which are all transients.
Dobbs et al. (2010) modeled the disk galaxy M51 and its interaction with a companion point-mass NGC 5195, focusing primarily on the dynamics of the gas, and secondly on the stellar disk. The halo was represented by a rigid potential. The tidal interaction has produced spiral arms in the stars and in the gas. The resulting spiral structure has shown excellent agreement with that of M51.
Lotz et al. (2010) analyzed the effect of a gas fraction on the morphologies of a series of simulated disk galaxy mergers. Each galaxy was initially modeled as a disk of stars and gas, a stellar bulge, and a dark matter halo, with different number of particles and masses for each component. All the simulated mergers had the same orbital parameters. Each pair of galaxies started on a subparabolic orbit with eccentricity 0.95 and an initial pericentric radius of 13.6 kpc. The galaxies had a roughly prograde-prograde orientation relative to the orbital plane, with the primary galaxy tilted 30° from a pure prograde orientation. Their simulations have predicted that galaxy mergers would exhibit high asymmetries for longer periods of time if they had high gas fractions.
Struck and collaborators (Struck et al. 2011) have discovered long-lived waves in numerical simulations of fast (marginally bound or unbound) flyby galaxy collisions. The main galaxy had a rigid halo potential, and gas and the companion was modeled as a point mass. They have found that none of the simulations resulted in bar formation. They have also shown that while these waves propagate through the disk, they are maintained by the coherent oscillations initiated by the impulsive disturbance.
Snaith et al. (2012) have studied the properties and evolution of a simulated polar-disk galaxy. This galaxy was composed of two orthogonal disks, one of which contained old stars (old stellar disk) and the other both younger stars and cold gas (polar disk). They have confirmed that the polar disk galaxy is the result of the last major merger, where the angular moment of the interaction is orthogonal to the angle of the infalling gas.
In one of our previous works in kinematic and morphology of spiral galaxies we have shown a deep interaction between the dynamical and morphological properties of this type of galaxy (Chan & Junqueira 2003). With continuos satellite forcing, the final state was in the form of a slowly evolving wave pattern, as shown by the pattern speeds for stable m = 1 and m = 2 wave modes. The pattern speeds obtained from the density and the three positive-velocity component distributions are the same. This was also true for the negative velocity components.
Kinematics studies of spiral galaxies have revealed a remarkable variety of interesting behavior: some galaxies have large-scale asymmetries in their rotation curves as a signature of kinematic lopsidedness (Junqueira & Combes 1996), while in others the inner regions counter-rotate with the respect to the rest of the galaxy (Garcia-Burillo et al. 2000). Most of the spiral galaxies have asymmetric HI profiles and asymmetric rotation curves (Haynes et al. 2000; Andersen & Bershady 2013). Such intriguing kinematics might arise if these galaxies are the end-products of minor mergers (Haynes et al. 2000). Minor mergers and weak tidal interactions between galaxies occur with much higher frequency than major ones. By weak interactions between galaxies we mean those that do not destroy the disk of the primary galaxy. However, weak interactions may cause disk heating, and satellite remnants may build up the stellar halo.
Galaxy interactions probably play a key role in determining the morphology and the dynamical properties of disk galaxies. Careful examination shows that most disk galaxies are not truly symmetric but exhibit a variety of morphological peculiarities of which spiral arms and bars are the most pronounced. Disk galaxies currently show significant spiral-generating tidal perturbations by one or more small-mass companions, and nearly all have had tidal interactions at some time in the past.
After decades of efforts, we now know that these features may be driven by environmental disturbances acting directly on the disk, in addition to self-excitation of a local disturbance (e.g., by swing amplification, Toomre 1981). However, the disk is embedded within a halo and, therefore, the luminous disk is not dynamically independent (Combes 2008). The dark matter halo is disturbed by dwarf companions, neighboring galaxies in groups and clusters, and the tidal force from the overall cluster. If the halo can respond globally to these disturbances, it can affect the disk structure. Thus, because most spirals have dwarf companions, there are interactions with these companions and the inward propagation of external perturbations by the halo could be a dominant source of disk structure for all galaxies (Vesperini & Weinberg 2000).
To study the dynamical evolution of two disk galaxies and their morphological evolution, this paper explores the picture as follows: first, we assume a disk galaxy with the characteristics of the Milk Way (disk, bulge, and halo). Second, we let a secondary galaxy orbit on prograde coplanar or polar disk (orientation in relation to the primary disk galaxy). Although the gas is important in modeling a realistic disk galaxy, in this work we focus only on the morphological stellar properties.
As an example of a work on the evolution of stellar disk galaxies without gas, we mention the recently published work by Baba et al. (2013). Using N-body simulations, they analyzed the physical mechanisms of non-steady stellar spiral arms in disk galaxies, which are those without the gaseous component. They have studied the growing and damping phases of the spiral arms and confirmed that the spiral arms are formed by a swing amplification mechanism that reinforces density enhancement. The main motivation was that all the previous time-dependent simulation works have not been able to prove the existence of stationary density waves in a disk galaxy without external perturbations and a bar structure.
Thus, the main goal of the present work is, by utilising detailed numerical N-body simulations, to study the dynamical interactions of the two disks of the galaxies. In particular, we have investigated whether interactions can induce persistent and stable m = 1 or m = 2 patterns in disk galaxies.
The paper is organized as follows: in Sect. 2 we describe the numerical method used in the simulations. In Sect. 3 we present the initial conditions. In Sect. 4 we describe the results of the simulations. In Sect. 5 we show power spectra of the instabilities. Finally, in Sect. 6 we discuss and summarize the results.
Disk galaxy model properties.
2. Numerical method
The full N-body code used in the simulations was GADGET (Springel et al. 2001). The code was parallelized and the communication was made by means of the message passing interface (MPI). GADGET evolves self-gravitating collisionless fluids with the traditional N-body approach and a collisional gas by smoothed particle hydrodynamics. But in our case we used only the particle integration, which uses a tree algorithm to compute gravitational forces. The parallel version has been designed to run on massively parallel supercomputers with distributed memory.
Fortin, Athanassoula & Lambert (2011) published a comparison with different codes for galactic N-body simulations, in particular, the GADGET code and the Dehnen algorithm. They have shown that the serial implementation of the Dehnen algorithm is slower in terms of execution time than the parallelized implementation of the GADGET code, with 8 to 128 processors.
The GADGET code does not exactly conserve energy or momentum, but the energy is conserved to better than 0.3% over an entire evolution, and the center of mass moves a distance of at most 82ϵ (the softening parameter) from the initial system center mass, with a time step size Δt = 1.000 × 10-3 and ϵ = 8.000 × 10-4. Too large ϵ reduces the noise but increases the error in the calculation of the force because it fails to resolve the interactions of particles with scale lengths shorter than it. Conversely, too small value for ϵ produces a noisy estimate of the force because of the finite number of particles. The value of the optimal softening scale depends both on the mass distribution and on the number of particles used to represent it. For more particles the optimal softening scale is smaller. More highly concentrated mass distributions necessitate smaller softening scale. Several works have analyzed this problem carefully (Merritt 1996; Athanassoula et al. 2000; Rodionov & Sotnikova 2005). For example, Athanassoula et al. (2000) have shown that for a Dehnen sphere, ϵ = 4.000 × 10-3. Thus, the softening scale is motivated by a trade-off between accuracy and computational speed. We have run several simulations of the isolated disk galaxy to find the optimal ϵ and the longest integration time step. The criteria were to find the maximum softening parameter and integration time step such that it could minimize the heating of the disk, without changing the physical disk parameters too much, mainly Zd. When the scale ϵ was too big the disk heated up, which increased its width. Thus, the chosen softening parameter is smaller than the disk scale height Zd, so that the disk of the galaxies can be followed accurately.
For non-zero tolerance parameter θ, the treecode CPU time scales as O(Nlog N), but in the limit θ → 0 this method scales as O(N2), approaching to the direct code. At the very beginning of this work we used the GADGET-1 (Springel et al. 2001). Thus, we assumed for the tolerance parameter θ the value 0.577, to avoid pathological situations when using the treecode as described by (Salmon & Warren 1994). However, this value of θ needs a lot of CPU time but the error in the force calculation is minimized, although many authors studying disk galaxies have used θ > 0.7 (Oh et al. 2008; Minchev et al. 2012).
3. Initial conditions of the simulations
We used the nearly self-consistent disk-bulge-halo galaxy model proposed by (Kuijken & Dubinski 1995) in the simulations. We assumed a model that has mass distributions and rotation curves closely resembling those of the Milk Way, that is, the model MW-A of (Kuijken & Dubinski 1995). This galaxy disk model has a disk-bulge mass ratio of 2:1 and halo-disk mass ratio of 5:1 (see Table 1). The disk is warm with a Toomre parameter Q = 1.7 at the disk half-mass radius.
Our simulations are based on fewer particles than other works on disk galaxies. However, since we are the first to attempt to solve the problem proposed here, we have decided to run modest simulations using the computer clusters that were available, to have, at least, an initial dynamical study of these types of binary galaxies.
The disk follows approximately an exponential-sech law described by 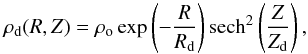 (1)where ρo is the central density that is related to the total mass of the disk. This approximation was used because the full potential equation obtained by Kuijken & Dubinski (1995) is analytically more complicated.
(1)where ρo is the central density that is related to the total mass of the disk. This approximation was used because the full potential equation obtained by Kuijken & Dubinski (1995) is analytically more complicated.
4. Results of the simulations
In Fig. 1 we show the contour plot of the primary galaxy at the beginning of the simulation (t = 0) and at the Hubble time of the simulation (t = tH). We note that the central density in the plane XY has increased slightly after one Hubble time of simulation, since the contour levels are the same for the two instants of time. In the XZ plane the scale height apparently has increased because of the two-body relaxation heating, but this quantity has changed very little (see Fig. 5).
 |
Fig. 1 Contour plot of the primary galaxy at the beginning of the simulation (t = 0) and at the Hubble time of the simulation (t = tH). The smoothing was made by averaging the 25 first and second neighbors of each pixel. Hereafter, the density levels in the planes XY and XZ at t = 0 will be used in all the contour plots, in the planes XY and XZ, respectively. |
 |
Fig. 2 Rotation curve at the time t = 0 of the disk Vc, the main component of the angular momentum per unit of mass Jz and the velocity dispersion in the Z direction |
 |
Fig. 3 Rotation curve at the time t = tH of the disk Vc, the main component of the angular momentum per unit of mass Jz and the velocity dispersion in the Z direction |
 |
Fig. 4 Time evolution of the scale radius (Rd). The projected particle number density on the XY plane was fitted using the approximation given by the Eq. (1). The coordinate R is the radius in cylindrical coordinates. The fitting parameters are Rd = (−0.7042 × 10-1 ± 0.2840 × 10-1) [ t/tH ] + (0.8819 ± 0.1620 × 10-1). |
 |
Fig. 5 Time evolution of the scale height (Zd). The projected particle number density on the XZ plane was fitted using the approximation given by the Eq. (1). The fitting parameters are Zd = (0.1791 × 10-2 ± 0.6320 × 10-3) [ t/tH ] + (0.9006 × 10-1 ± 0.3563 × 10-3). |
From comparing Figs. 2 and 3, we note from the quantity 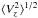 that the self-heating of the initial disk and the particle halo adds another significant source of heating in the disk. The gravitational softening can also cause the disk to puff up; this is the reason why we chose a such small softening parameter, 125 times smaller than the scalar disk height. Moreover, the total rotation curves Vc and the angular momentum in the Z direction have not changed after one Hubble time of simulation.
that the self-heating of the initial disk and the particle halo adds another significant source of heating in the disk. The gravitational softening can also cause the disk to puff up; this is the reason why we chose a such small softening parameter, 125 times smaller than the scalar disk height. Moreover, the total rotation curves Vc and the angular momentum in the Z direction have not changed after one Hubble time of simulation.
In Figs. 4 and 5 we present the time evolution of the scale radius (Rd) and the scale height (Zd). As expected, because of the heating of the disk the first quantity diminishes with the time while the second increases with the time. The linear fitting parameters of these two quantities are presented in the captions of these figures. Since the scale height has increased by less than 0.2%, we assumed throughout that this scale has not changed when we analyzed the data of the simulations.
The units used in the simulations are G = 1, [length] = 4.500 kpc, [mass] = 5.100 × 1010 M⊙, [time] = 1.993 × 107 years (H0 = 100 km s-1 Mpc) and [velocity] = 220.730 km s-1. All the physical quantities will be referred to these units. The particle softening radius was assumed to be 0.0008 or 1/125 of the disk scale height. The critical opening angle was set to θ = 0.577 and the forces between the cells and particles used the quadrupole correction. The longest integration step time was assumed to be 0.001 in units of simulation time. The Hubble time tH corresponds to 490 time units.
We ran several simulations, without satellite to check the initial instabilities of the galaxy model. The initial galaxy simulations were run in a SUN FIRE 6800 cluster with 16 CPU processors. Each simulation took about 50 days of CPU time. For the simulations with the primary and satellite galaxies we used several clusters with a variety of CPU processors: SUN BLADE X6250, SUN FIRE X2200, SGI ALTIX ICE 8200, SGI ALTIX 450/1350, SGI ALTIX-XE 340, IBM P750, INTEL PENTIUM QUAD CORE and INTEL PENTIUM DUAL CORE. The number of CPU processors varied from at least 8 to at most of 128. Each simulation took 90 days of CPU time in average.
Very often (Oh et al. 2008; Dobbs et al. 2010; Lotz et al. 2010; Struck et al. 2011; Bois et al. 2011), simulations of interactions between two disk galaxies have used initial conditions such as parabolic or hyperbolic orbits. However, the bounded eccentrically orbits in an interval of a Hubble time have not been studied because is very expensive in terms of CPU time. This is mainly because in this kind of simulation we must adequately integrate the internal dynamic of the disk galaxy during a very long cosmological time interval. We decided not to use cosmologically consistent initial conditions from publicly available simulations as done, e.g., by (Ruszkowski & Springel 2009) for two reasons. First, we would like to know what happened with the binary galaxies in bound orbits and, secondly, it would cost much more (in number of experiments and in CPU time) if we had begun our simulations from cosmologicaly unbound galaxies to arrive at eccentrically bound galaxies.
All the initial conditions of the numerical experiments are presented in Table 2. The orbits of the initial galaxies are eccentric (e = 0.1, 0.4 or 0.7) and the orientations of the disks are coplanar (Θ = 0) or polar (Θ = 90) to each other. The simulations began with the two galaxies at the apocentric positions.
Primary and secondary galaxy initial conditions.
Characteristics of the final stage of the orbits and merged disks.
In Fig. 6 we show the dependence of the time of merging (TM) (see Table 3) with the eccentricity (e) and the initial apocentric distance (Ra). The time of merging is defined as the time when the centers of mass of the two disks (primary and secondary galaxies) overlap (Chan & Junqueira 2001). The merging time increases linearly with the initial apocentric distance. The TM for different eccentricities is obtained by extrapolating the linear approximation for each eccentricity and determining TM for a fixed value of Ra. We obtained that the time of merging decreases with eccentricity.
 |
Fig. 6 Time of merging with the fitted straight lines, for each eccentricity, where Ra is the apocentric distance. The open circles represent the simulations with e = 0.1. The open triangles represent the simulations with e = 0.4. The open squares denote the experiments with e = 0.7. The best-fit parameters are: [ tM/tH ] = (0.039 ± 0.002)Ra + (−0.508 ± 0.056) (for e = 0.1), [ tM/tH ] = (0.049 ± 0.005)Ra + (−1.285 ± 0.020) (for e = 0.4) and [ tM/tH ] = (0.038 ± 0.006)Ra + (−1.635 ± 0.038) (for e = 0.7) (the far two points were obtained by extrapolating the time evolution of the distance between the two disks, using the simulation EXP17). |
There are two different kinds of merged remnants in our simulations. The first (coplanar disks) is a disk galaxy with scale radius and height very similar to the initial disk galaxy (see Table 3), but with a tidal radius that is at least five times larger than that of the initial galaxy (see Fig. 7). The second (polar disks) resembles a lenticular galaxy, but again with a tidal radius that is larger than the initial galaxy radius (see Fig. 7).
In Figs. 7 and 8 we present the contour snapshots of the result of the merger of the primary and secondary galaxies in the planes XY and XZ at the Hubble time of the simulation (t = tH). We show the simulations EXP13, 14, 16, 17, 19, 20, 22, 23, 25, 27, 28, 30, 31, 33, 34, and 36. In the simulations with coplanar disk orbits (EXP13, 14, 16, 17, 25, 27, 28, and 30) the resulting fused galaxies are still disk galaxies. Their fitted scale radii (Rd(12)) and heights (Zd(12)) using Eq. (1) are presented in Table 3. The merged disk galaxies are thicker and larger than the initial ones.
 |
Fig. 7 Contour snapshot of the merger of the primary and secondary galaxies (flat disk merged remnants) together in the planes XY and XZ at the Hubble time of the simulation (t = tH). Simulations EXP13, 14, 16, 17, 25, 27, 28 and 30. |
 |
Fig. 8 Contour snapshot of the merger of the primary and secondary galaxies (oblate disk merged remnants) together in the planes XY and XZ at the Hubble time of the simulation (t = tH). Simulations EXP19, 20, 22, 23, 31, 33, 34, and 36. |
However, for the simulations with polar disk orbits (EXP19, 20, 22, 23, 31, 33, 34, and 36) the resulting fused galaxies are no longer disk galaxies. In both planes, XY and XZ, the galaxies resemble lenticular galaxies. The outer contour level of the merged galaxy in EXP23 is clearly deformed, differently from other merged polar disks, maybe because of the number of orbits (see Table 3). This is the only simulation among all our experiments with the most orbits (2.5), with the longest time interval with tidal interaction between the two disk galaxies.
In Figs. 9 and 10 we show what happened to these galaxies using the simulation EXP31 at t = 0.5tH and at t = tH. These figures show the disks of the primary galaxy G1 and secondary G2. The polar characteristic of the G2 is still there at t = 0.5tH but this is lost at t = tH. At this time the polar disk is completely disrupted and its debris forms a stellar halo. From overlapping the contours of G1 and G2, we obtain Fig. 8 for the simulation EXP31.
 |
Fig. 9 Contour of the snapshot of the merger of the primary and secondary galaxies plotted separately in the plane XY and XZ at 50% of the Hubble time (t = 0.5tH). Simulation EXP31. |
 |
Fig. 10 Contour of the snapshot of the merger of the primary and secondary galaxies plotted separately in the plane XY and XZ at 60% of the Hubble time (t = 0.6tH). From overlapping the contours of G1 and G2, at t = tH, we obtain the contours of Fig. 8 for the simulation EXP31. |
5. Power spectrum analysis
The power spectrum analysis provides a useful and objective tool for studing the induced waves. This analysis uses the amplitude and phase of the Fourier components of the surface density of the stars, and allows us to show the spiral modes in our simulations. This analysis give us the pattern speed of all spiral perturbations and their relative positions.
The power spectrum method, known historically as periodogram, was used to search for periodicities in sparse, noisy, unevenly spaced data (Junqueira & Combes 1996).
If we take an N-point sample of the function c(t) at equal intervals of time t and compute its discrete Fourier transform (Press et al. 1992), we obtain the power spectrum P(Ω) of c(t).
We used the grid-expansion method to analyze the density distribution (128 × 128 × 128 pixels) to obtain the power spectrum.
Firstly, using a radial binning of 0.0125, we obtained the amplitude and the phase of the Fourier components. Secondly, using the snapshots of the slab of the disk density in a time interval 0.01tH, we calculated the superposition of the entire Fourier amplitude and phase for each radial bin and for each time interval. Finally, we obtained the power spectrum as a plot of the number density for each radial bin. The power spectrum analysis was made by studying the primary galaxy just before the merging time. The orientation of the disk was not followed dynamically because it has not deviated from the initial orientation angle, as we can see in Fig. 10.
Since we have a 3D particle disk, we limited the number of the particles within the planes Z = −Zmax and Z = Zmax to simplify the application of the grid expansion method (Chan & Junqueira 2003). We considered this thin slab between these two planes as the plane Z = 0 for the grid expansion. We denote this thin slab as Z = 0 in the equations. The chosen quantity Zmax = 0.1 is the value of the scale height of the disk (Zd). There are approximately 40% of the total disk particles (Nd) within these two planes. We assumed a largest radius of 5 length units throughout since we have 95% of the mass of the disk within this radius.
The basic assumption of the density wave theory is that spiral arms are not always composed of the same stars, but instead are the manifestation of the excess matter associated with the crest of a rotating-wave pattern. Two other assumptions were introduced from the onset, the linearity and quasi-stationarity of the wave. These assumptions allow us to write any perturbation of the axisymmetric background as superposition waves given by ![\begin{equation} \rho_{\rm d}(R,\phi,Z=0,t)=\sum_m \rho_m(R) {\rm e}^{{\rm i}[\Omega(m) t - m\phi]}, \label{rho} \end{equation}](/articles/aa/full_html/2014/07/aa23656-14/aa23656-14-eq108.png) (2)where ρd is the density. The summation index indicates the symmetry of the component: m = 0 corresponds to the axisymmetric background; m = 1 corresponds to the lopsided perturbation, and m = 2 corresponds to the symmetric two-arm perturbation (spiral, bar). Ω(m) is the pattern speed of the component m.
(2)where ρd is the density. The summation index indicates the symmetry of the component: m = 0 corresponds to the axisymmetric background; m = 1 corresponds to the lopsided perturbation, and m = 2 corresponds to the symmetric two-arm perturbation (spiral, bar). Ω(m) is the pattern speed of the component m.
We can rewrite Eq. (2) in the usual wave notation ![\begin{equation} \rho_{\rm d}(R,\phi,Z=0,t)=\sum_m p_m(R) {\rm e}^{{\rm i}[\Psi_m(R) + \Omega(m) t - m\phi]}, \label{rho1} \end{equation}](/articles/aa/full_html/2014/07/aa23656-14/aa23656-14-eq112.png) (3)where pm(R) is the amplitude of the wave and Ψm(R) is the phase angle of the mode m.
(3)where pm(R) is the amplitude of the wave and Ψm(R) is the phase angle of the mode m.
Now the density mode m can be obtained from ![\begin{equation} \rho_{\rm d}^m(R,\phi,Z=0,t)= p_m(R) \cos[ \Psi_m(R) + \Omega(m) t - m\phi ]. \label{rhodmr} \end{equation}](/articles/aa/full_html/2014/07/aa23656-14/aa23656-14-eq115.png) (4)We interpret the m = 1 and m = 2 plots in Figs. 11 and 12. They do not look like a clear one-armed spirals, or a clear asymmetry in the two arms, like in Fig. 13 of (Junqueira & Combes 1996), because in this present work they represent the Fourier analysis of a transient wave. Junqueira & Combes analyzed only the gaseous disk, but the analysis is similar to a stellar disk.
(4)We interpret the m = 1 and m = 2 plots in Figs. 11 and 12. They do not look like a clear one-armed spirals, or a clear asymmetry in the two arms, like in Fig. 13 of (Junqueira & Combes 1996), because in this present work they represent the Fourier analysis of a transient wave. Junqueira & Combes analyzed only the gaseous disk, but the analysis is similar to a stellar disk.
In Fig. 11 we show the transient wave modes m = 1 and m = 2 for the simulation EXP15 at two different instants of time 0.65tH and tH. Transient m = 1 wave modes are mostly present in the outer part of the disks. Furthermore, transient spiral arms (m = 2) are formed in the outer regions of the disks, and bars are present in the inner regions. Since they are transient m = 2 wave modes, the power spectrum for EXP15 (see Fig. 14) shows an undefined angular velocity for this mode.
 |
Fig. 11 Wave modes m = 1 and m = 2 for simulation EXP15 at two different instants of time 0.65tH and tH. The density levels for these plots are the same as used in m = 1 (t = 0.65tH). |
In Fig. 12 we show the transient wave modes m = 1 and m = 2 for the simulation EXP31 at two different instants of time 0.5tH and tH. The transient m = 1 wave mode at t = 0.5tH is mostly present in the outer part of the disks, except at t = tH. There is a large transient spiral arm (m = 2) at t = 0.5tH in the outer region of the disk and a prominent bar in the inner region of the disk at t = 0.6tH. As in EXP15, here we have transient m = 2 wave modes seen in the power spectrum for EXP31 (see Fig. 14). If we compare Figs. 12 and 13, the Fourier decompositions are very similar with the snaphots of the disks.
 |
Fig. 12 Wave modes m = 1 and m = 2 for simulation EXP31 at two different instants of time 0.5tH and 0.6tH. The density levels for these plots are the same as were used in EXP15 (m = 1, t = 0.65tH). |
 |
Fig. 13 Snapshots of the slabs Z = 0 for the simulation EXP15 at two different instants of time 0.65tH and tH. We also show the snapshots of the slabs Z = 0 for the simulation EXP31 at two different instants of time 0.5tH and 0.6tH. |
Figure 14 shows the power spectra for the m = 2 wave mode for simulations EXP00, 13, 14, 15, 16, 17, 19, 20, 21, 25, 28, and 31. We show only the m = 2 wave mode because we have not detected m = 1 wave mode in any simulation. Other experiments that presented an m = 2 wave mode and that are not shown in this figure are EXP22, 23, 27, and 33. These simulations were similar to that in Fig. 14. Other simulations did not show any sign of an m = 2 wave mode mostly because the primary and secondary halo did not touch each other during their evolution time (open disk interaction: see Table 3).
In Fig. 14, the first plot shows the power spectrum for the mode m = 2 for the simulation EXP00, without the secondary galaxy. This was made to analyze the existence of self-excited gravitational instabilities of the m = 2 wave mode in the disk. Evidently, there are not any wave modes.
Note the fuzzy small perturbations in the outer radii of the disks in Fig. 14 (note also that the density levels are three times higher than that used in the experiment EXP00). Most of the experiments in this figure have shown merged disks (see Table 3), except for the simulations EXP15 and 21 (grazing disks). There we can also see partial m = 2 wave modes in the outer radii of the disk with high clumpy density regions that do not extend to the inner part of the disks. Therefore, we cannot classify them as m = 2 stable wave modes because of these characteristics of the power spectra.
There are no discernable and significant substructures in Fig. 14. If there were a real stable wave we should have a plot like Fig. 16 of that (Junqueira & Combes 1996), a straight line parallel to the radial axis giving the pattern speed of the mode. Instead, since we have a transient wave, we obtain a fuzzy plot, more concentrated in the outer radial regions.
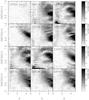 |
Fig. 14 Power spectrum for the mode m = 2 for the primary galaxy (G1) and for simulations EXP00, 13, 14, 15, 16, 17, 19, 20, 21, 25, 28, and 31 until the time of merging. The density levels are three times higher than that of the experiment EXP00. |
We integrated the wave amplitudes radially to derive the global Fourier amplitudes | pm | (Harsono et al. 2011), where m is the Fourier mode: ![\begin{equation} |p_m|(t) = \frac{1}{N_{\rm disk}}\sum_{R\,=\,0}^{R\,=\,5} |p_m(R) {\rm e}^{{\rm i}[\Psi_m(R) \, +\, \Omega(m) t \, -\, m\phi]}|, \end{equation}](/articles/aa/full_html/2014/07/aa23656-14/aa23656-14-eq121.png) (5)where pm(R) is giving by Eq. (3) and Ndisk is total number of particles in the disk within R = 5. The global amplitude analysis was made in two distinct ways: a) by studying the primary galaxy until the merging time, and b) by analyzing the compound galaxies after the merger, when they occur. The orientation of the disk was not followed dynamically because of the deformation of the disk in some simulations. In Fig. 15 we show the temporal evolution of the relative global integrated amplitudes for simulations EXP13, 14, 15, 16, 17, 19, 20, 21, 25, 28, and 31.
(5)where pm(R) is giving by Eq. (3) and Ndisk is total number of particles in the disk within R = 5. The global amplitude analysis was made in two distinct ways: a) by studying the primary galaxy until the merging time, and b) by analyzing the compound galaxies after the merger, when they occur. The orientation of the disk was not followed dynamically because of the deformation of the disk in some simulations. In Fig. 15 we show the temporal evolution of the relative global integrated amplitudes for simulations EXP13, 14, 15, 16, 17, 19, 20, 21, 25, 28, and 31.
 |
Fig. 15 Global integrated ratio amplitudes of the modes m = 1 (solid lines) and m = 2 (dotted lines) for the primary galaxy (G1) for the simulations 15 and 17 during a Hubble time. The | p00 | denotes the global amplitude of the control simulation EXP00. For simulations EXP13, 16, 25, and 28 we show the global ratio amplitudes for G1 until the merger time, denoted by the dashed lines. After the merge we show the global ratio amplitude of the compound galaxy (G1 + G2). For experiments EXP19, 20, and 31 (polar disk), we plot the evolution of G1 until the merger of G1 and G2, represented again by the dashed lines. |
Figure 15 shows that there is no possible kick due to uncosmological initial conditions. The reason is simply that all the simulations have begun at the apocentric distance, where the tidal interaction between the two binary galaxies is weaker.
Furthermore, all the waves are mostly driven shortly before merger, because the separations decreased, even in the cases with no merger.
We analyzed the special case EXP17 in Fig. 15. The simulation EXP17 presents three maxima for m = 2 wave mode. The first maximum is due to the formation of a bar, when the two disks are still far apart. The second and third ones are due to the formation of a two-arm spiral, when the disks already touch and deform each other.
Lopsided features are preferentially observed in the distribution of gas in late-type spiral galaxies. In several cases these features can be identified as one-armed spirals (m = 1 mode). More frequently, nuclei of galaxies are observed displaced with respect to the gravity center, as in M33 and M101. The nucleus of M31 reveals such an off-centering, which has been interpreted in terms of an m = 1 perturbation. Miller & Smith (1992) have studied through N-body simulations of disk galaxies a peculiar oscillatory motion of the nucleus with respect to the rest of the axisymmetric galaxy. They interpreted the phenomenon as an m = 1 instability, a density wave in orbital motion around the center of mass of the galaxy. Moreover, Junqueira & Combes (1996) have shown that stars and gas are off-centered with respect to the center of mass of the system. Figure 15 shows that the m = 1 and m = 2 modes are excited at different times. This is because the mode excitation comes from the outer region to the inner region of the disk. Thus, there is a time lag for this excitation to reache the inner disk region. Since the m = 1 mode needs an off-centered disk mode with respect to the center of mass and since the m = 2 mode is mostly excited from the outer disk region, this produces a time delay among the maxima of these two modes.
Figures 16 and 17 show the evolution of some halo contours containing, for example, about 40% and 90% the halo mass (EXP15). The early merger paper of Barnes & Hernquist (1996), which first discussed the halo mergers, has given attention only to the remnant halos at the end of the simulation. Our figures show that the strongest halo contour deformation (90%) coincides with the strongest disk deformation. After the passage of the secondary galaxy through the primary at the Hubble time, the halos settle down and their contours resemble the initial ones.
 |
Fig. 16 G1 halo contours of the EXP15 in the plane XY at three different times: t = 0, t = 0.68tH at the time of the maximum amplitude of the disk m = 2 component (see Fig. 15), and t = tH. The G1 disk contour of the EXP15 in the plane XY at the time t = 0.68tH. The two outer halo contour density levels correspond approximately to 40% of the total halo mass at the radius R ≈ 4 and 90% of the total halo mass at the radius R ≈ 11. The halo and the disk of the secondary galaxy G2 can be obtained by reflecting the respective contour image relative to the Y axis at X = 0, since the two galaxies have the same mass distribution. |
 |
Fig. 17 G1 halo contours of the EXP15 in the plane XZ at three different times: t = 0, t = 0.68tH at the time of the maximum amplitude of the disk m = 2 component (see Fig. 15), and t = tH. The G1 disk contour of the EXP15 in the plane XZ at the time t = 0.68tH. The two outer halo contour density levels correspond approximately to 40% of the total halo mass at the radius R ≈ 4 and 90% of the total halo mass at the radius R ≈ 11. The halo and the disk of the secondary galaxy G2 can be obtained by reflecting the respective contour image relative to the Y axis at X = 0, since the two galaxies have the same mass distribution. |
6. Discussion
We have dynamically evolved two disk galaxies with halo and bulge using N-body simulations. The initial disk model is stable against any self-excited m = 1 or m = 2 wave modes. The satellite galaxy has coplanar or polar disk orientation with respect to the disk of the primary galaxy and their initial orbits are prograde eccentric (e = 0.1, e = 0.4 or e = 0.7). Both galaxies have a similar mass and size as the Milk Way.
Most recent papers that studied the tidal interaction between two galaxies have used a fixed potential for the halo (Oh et al. 2008; Dobbs et al. 2010; Struck et al. 2011). This condition can be misleading because the halos are very important in transmiting angular momentum to the disk of the primary galaxy. The halo of the primary galaxy can respond globally to disturbance of the halo of the secondary galaxy, thus it can affect the disk structure in an inward effect. These effects can be clearly seen in the analysis of the power spectra (see Fig. 14).
This is the first published work, as far as we know, that has studied the secular evolution of bound disk binary galaxies. Nevertheless, we only compare our results with the global results of similar papers, since the numerical methods, initial conditions, time of integration, etc. are different from ours.
We showed that the merger of two coplanar (Θ = 0) pure stellar disk galaxies can result in a disk galaxy instead of an elliptical one, as was shown in other papers (Bournaud et al. 2005; Bois et al. 2011). If we have merger of two polar (Θ = 90) disk galaxies we can also have the formation of lenticular-like galaxies. These results are new to our knowledge.
In fact, none of our simulations resulted in elliptical galaxies. In a recent work, Bois et al. (2011) studied the formation of early-type galaxies through mergers with a sample of high-resolution numerical simulations of binary mergers of disk galaxies. The initial galaxy model had a real halo, bulge, disk, and gas. The orbits used in the merge simulations were all parabolic or hyperbolic, corresponding to initially unbound galaxy pairs, which is different from our simulations where the galaxy pairs were, from the very beginning, bound in eccentric orbits.
Furthermore, we demonstrated that the time of merging increases linearly with the initial apocentric distance of the galaxies and decreases with the eccentricity (see Fig. 6). Boylan-Kolchin & Quataert (2008) have studied the merging time of extended dark matter haloes using N-body simulations. Each of their simulations consisted of a host halo and a satellite halo; the ratio of the satellite to the host mass varied from 0.025 to 0.3 and the initial circularity of the satellite varied from 0.33 to 1, or in other words, the initial eccentricity varied from 0 to 0.67. They found that the merging time decreases exponentially with the eccentricity. This result partially agrees with our findings since the TM decreases with the eccentricity. However, we do not have enough simulations with different eccentricities to confirm the exponential behavior.
We also showed that the tidal forces of the disks can excite wave mode m = 1 and the wave mode m = 2, but they are not stable, meaning that they are transient wave modes (see Fig. 14). In a previous work (Chan & Junqueira 2003) we have shown that tidal interaction of a secondary point-mass galaxy could excite stable m = 1 and m = 2 wave modes in the density distribution as well as in the velocity distribution. In contrast to our previous paper, here we began the simulations with an apocentric distance where the halos did not touch. However, after the merging of the disks, when this occurred, these instabilities have faded away completely and the fused disk has become thicker and more extended.
Many authors (Oh et al. 2008; Lotz et al. 2010; Dobbs et al. 2010; Struck et al. 2011; Snaith et al. 2012) have shown that tidal interaction can trigger gravitational instabilities, such as spiral arms or lopsidedness. Our results confirmed these results: it was possible to create spiral arms, bars or lopsidedness through the tidal force, but they were transient phenomena.
The simulations with merger remnants the waves abruptly disappear after the merger are completed (in less than one outer disk rotation period). This point, illustrated in Fig. 15, shows that it is almost the opposite result reported by Struck et al. (2011), who have found that weak flybys induce waves that take a long time to nonlinearly break. The maximum relative amplitude of these waves is at most about 15 times larger than that of the control case. The m = 2 wave mode is generated mainly by tidal interaction in the outer region of the disks. The m = 1 wave mode depends mostly on an interaction of the inner part of the disks, producing an off-centering effect of the wave mode center with respect to the center of mass of the disk. These characteristics produce a time lag among the maximum formation of these two wave modes. The disk settles down quickly after the merger, in less than one outer disk rotation period. Furthermore, although the two disks may spend a long time in orbit, waves are only induced in the short time they are close together. The stellar disks can survive gentle merging, even with a massive companion, and the waves abruptly disappear after the merger is completed.
Finally, galaxy disks are born gas-rich, and the key to S0 formation is the evolutionary path from such progenitors. It is theoretically interesting that some form of disk can be preserved through some types of major merger. Practically, however, it is not likely that too many S0s are result of S0+S0 or early Sa+Sa mergers. A related, and more important point is that if
stellar disks can survive some gas-free major mergers, then they are also likely to survive multiple minor mergers, which may play a more important role in finishing the formation of S0s. The idea that minor mergers play such a role in ellipticals is very well known today, which makes it much more enlightening for S0s.
Acknowledgments
One of the authors (RC) acknowledges the financial support from FAPERJ (No. E-26/171.754/2000, E-26/171.533/2002 and E-26/170.951/2006 for construction of a cluster of 16 INTEL PENTIUM DUAL CORE PCs) and the other author (SJ) also acknowledges the financial support from FAPERJ (No. E-26/170.176/2003). The author (RC) also acknowledges the financial support from Conselho Nacional de Desenvolvimento Científico e Tecnológico – Brazil. We would also like to thank the generous amount of CPU time given by LNCC (Laboratório Nacional de Computação Científica), CESUP/UFRGS (Centro Nacional de Supercomputação da UFRGS), CENAPAD/UNICAMP (Centro Nacional de Processamento de Alto Desempenho da UNICAMP), NACAD/COPPE-UFRJ (Núcleo de Atendimento de Computação de Alto Desempenho da COPPE/UFRJ) in Brazil. In addition, this research has been supported by SINAPAD/Brazil. The authors would like to thank Vladimir Garrido Ortega for the useful discussions at the very beginning of this work. We acknowledge Curt Struck for the careful reading of the manuscript and giving many suggestions that improved this work.
References
- Andersen, D. R., & Bershady, M. A. 2013, ApJ, 768, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Athanassoula, E., Fady, E., Lambert, J. C., & Bosma, A. 2000, MNRAS, 314, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Baba, J., Saitoh, T. R., & Wada, K. 2013, ApJ, 763, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, J. E., & Hernquist, L. 1996, ApJ, 471, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Bois, M., Emsellem, E., Bournaud, F., et al. 2011, MNRAS, 416, 1654 [NASA ADS] [CrossRef] [Google Scholar]
- Bournaud, F., Jog, C. J., & Combes, F. 2005, A&A, 437, 69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boylan-Kolchin, M., Ma, C., & Quataert, E. 2008, MNRAS, 383, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Chan, R., & Junqueira, S. 2001, A&A, 366, 418 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chan, R., & Junqueira, S. 2003, ApJ, 586, 780 [NASA ADS] [CrossRef] [Google Scholar]
- Combes, F. 2008, Mem. S.A. It., 75, 281 [Google Scholar]
- Dobbs, C. L., Theis, C., Pringle, J. E., & Bate, M. R. 2010, MNRAS, 403, 625 [NASA ADS] [CrossRef] [Google Scholar]
- D’Onghia, E., Vogelsberger, M., & Hernquist, L. 2013, ApJ, 766, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Fujii, M. S., Baba, J., Saitoh, T. R., et al. 2011, ApJ, 730, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Garcia-Burillo, S., Sempere, M. J. L., Combes, F., Hunt, L. K., & Neri, R. 2000, A&A, 363, 869 [NASA ADS] [Google Scholar]
- Harsono, D., Alexander, R. D., & Levin, Y. 2011, MNRAS, 413, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Haynes, M. P., Jore, K. P., Barret, E. A., Broeils, A. H., & Murray, B. 2000, AJ, 120, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Junqueira, S., & Combes, F. 1996, A&A, 312, 703 [NASA ADS] [Google Scholar]
- Kuijken, K., & Dubinski, J. 1995, MNRAS, 277, 1341 [CrossRef] [Google Scholar]
- Lotz, J. M., Jonsson, P., Cox, T. J., & Primack, J. R. 2010, MNRAS, 404, 575 [NASA ADS] [CrossRef] [Google Scholar]
- Merritt, D. 1996, AJ, 111, 2462 [NASA ADS] [CrossRef] [Google Scholar]
- Minchev, I., Famaey, B., Quillen, A. C., et al. 2012, A&A, 548, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miller, R. H., & Smith, B. F. 1992, ApJ, 393, 508 [NASA ADS] [CrossRef] [Google Scholar]
- Oh, S. H., Kim, W., Lee, H. M., & Kim, J. 2008, ApJ, 683, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Roškar, R., Debattista, V. P., Quinn, T. R., & Wadsley, J. 2012, MNRAS, 426, 2089 [NASA ADS] [CrossRef] [Google Scholar]
- Rodionov, S. A., & Sotnikova, N. Ya. 2005, Astron. Rep., 49, 470 [NASA ADS] [CrossRef] [Google Scholar]
- Ruszkowski, M., & Springel, V. 2009, ApJ, 696, 1094 [NASA ADS] [CrossRef] [Google Scholar]
- Salmon, J. K., & Warren, M. S. 1994, J. Comput. Phys., 111, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Snaith, O. N., Gibson, B. K., Brook, C. B., et al. 2012, MNRAS, 425, 1967 [NASA ADS] [CrossRef] [Google Scholar]
- Sellwood, J. A. 2011, MNRAS, 410, 1637 [NASA ADS] [Google Scholar]
- Sellwood, J. A. 2013, ApJ, 769, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., Yoshida, N., & White, S. D. M. 2001, New Astron., 6, 79 [Google Scholar]
- Struck, C., Dobbs, C. L., & Hwang, J. 2011, MNRAS, 414, 2498 [NASA ADS] [CrossRef] [Google Scholar]
- Toomre, A. 1981, Proc. of the Advanced Study Institute (Cambridge University Press), 111 [Google Scholar]
- Vesperini, E., & Weinberg, M. D. 2000, ApJ, 534, 598 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Contour plot of the primary galaxy at the beginning of the simulation (t = 0) and at the Hubble time of the simulation (t = tH). The smoothing was made by averaging the 25 first and second neighbors of each pixel. Hereafter, the density levels in the planes XY and XZ at t = 0 will be used in all the contour plots, in the planes XY and XZ, respectively. |
| In the text | |
 |
Fig. 2 Rotation curve at the time t = 0 of the disk Vc, the main component of the angular momentum per unit of mass Jz and the velocity dispersion in the Z direction |
| In the text | |
 |
Fig. 3 Rotation curve at the time t = tH of the disk Vc, the main component of the angular momentum per unit of mass Jz and the velocity dispersion in the Z direction |
| In the text | |
 |
Fig. 4 Time evolution of the scale radius (Rd). The projected particle number density on the XY plane was fitted using the approximation given by the Eq. (1). The coordinate R is the radius in cylindrical coordinates. The fitting parameters are Rd = (−0.7042 × 10-1 ± 0.2840 × 10-1) [ t/tH ] + (0.8819 ± 0.1620 × 10-1). |
| In the text | |
 |
Fig. 5 Time evolution of the scale height (Zd). The projected particle number density on the XZ plane was fitted using the approximation given by the Eq. (1). The fitting parameters are Zd = (0.1791 × 10-2 ± 0.6320 × 10-3) [ t/tH ] + (0.9006 × 10-1 ± 0.3563 × 10-3). |
| In the text | |
 |
Fig. 6 Time of merging with the fitted straight lines, for each eccentricity, where Ra is the apocentric distance. The open circles represent the simulations with e = 0.1. The open triangles represent the simulations with e = 0.4. The open squares denote the experiments with e = 0.7. The best-fit parameters are: [ tM/tH ] = (0.039 ± 0.002)Ra + (−0.508 ± 0.056) (for e = 0.1), [ tM/tH ] = (0.049 ± 0.005)Ra + (−1.285 ± 0.020) (for e = 0.4) and [ tM/tH ] = (0.038 ± 0.006)Ra + (−1.635 ± 0.038) (for e = 0.7) (the far two points were obtained by extrapolating the time evolution of the distance between the two disks, using the simulation EXP17). |
| In the text | |
 |
Fig. 7 Contour snapshot of the merger of the primary and secondary galaxies (flat disk merged remnants) together in the planes XY and XZ at the Hubble time of the simulation (t = tH). Simulations EXP13, 14, 16, 17, 25, 27, 28 and 30. |
| In the text | |
 |
Fig. 8 Contour snapshot of the merger of the primary and secondary galaxies (oblate disk merged remnants) together in the planes XY and XZ at the Hubble time of the simulation (t = tH). Simulations EXP19, 20, 22, 23, 31, 33, 34, and 36. |
| In the text | |
 |
Fig. 9 Contour of the snapshot of the merger of the primary and secondary galaxies plotted separately in the plane XY and XZ at 50% of the Hubble time (t = 0.5tH). Simulation EXP31. |
| In the text | |
 |
Fig. 10 Contour of the snapshot of the merger of the primary and secondary galaxies plotted separately in the plane XY and XZ at 60% of the Hubble time (t = 0.6tH). From overlapping the contours of G1 and G2, at t = tH, we obtain the contours of Fig. 8 for the simulation EXP31. |
| In the text | |
 |
Fig. 11 Wave modes m = 1 and m = 2 for simulation EXP15 at two different instants of time 0.65tH and tH. The density levels for these plots are the same as used in m = 1 (t = 0.65tH). |
| In the text | |
 |
Fig. 12 Wave modes m = 1 and m = 2 for simulation EXP31 at two different instants of time 0.5tH and 0.6tH. The density levels for these plots are the same as were used in EXP15 (m = 1, t = 0.65tH). |
| In the text | |
 |
Fig. 13 Snapshots of the slabs Z = 0 for the simulation EXP15 at two different instants of time 0.65tH and tH. We also show the snapshots of the slabs Z = 0 for the simulation EXP31 at two different instants of time 0.5tH and 0.6tH. |
| In the text | |
 |
Fig. 14 Power spectrum for the mode m = 2 for the primary galaxy (G1) and for simulations EXP00, 13, 14, 15, 16, 17, 19, 20, 21, 25, 28, and 31 until the time of merging. The density levels are three times higher than that of the experiment EXP00. |
| In the text | |
 |
Fig. 15 Global integrated ratio amplitudes of the modes m = 1 (solid lines) and m = 2 (dotted lines) for the primary galaxy (G1) for the simulations 15 and 17 during a Hubble time. The | p00 | denotes the global amplitude of the control simulation EXP00. For simulations EXP13, 16, 25, and 28 we show the global ratio amplitudes for G1 until the merger time, denoted by the dashed lines. After the merge we show the global ratio amplitude of the compound galaxy (G1 + G2). For experiments EXP19, 20, and 31 (polar disk), we plot the evolution of G1 until the merger of G1 and G2, represented again by the dashed lines. |
| In the text | |
 |
Fig. 16 G1 halo contours of the EXP15 in the plane XY at three different times: t = 0, t = 0.68tH at the time of the maximum amplitude of the disk m = 2 component (see Fig. 15), and t = tH. The G1 disk contour of the EXP15 in the plane XY at the time t = 0.68tH. The two outer halo contour density levels correspond approximately to 40% of the total halo mass at the radius R ≈ 4 and 90% of the total halo mass at the radius R ≈ 11. The halo and the disk of the secondary galaxy G2 can be obtained by reflecting the respective contour image relative to the Y axis at X = 0, since the two galaxies have the same mass distribution. |
| In the text | |
 |
Fig. 17 G1 halo contours of the EXP15 in the plane XZ at three different times: t = 0, t = 0.68tH at the time of the maximum amplitude of the disk m = 2 component (see Fig. 15), and t = tH. The G1 disk contour of the EXP15 in the plane XZ at the time t = 0.68tH. The two outer halo contour density levels correspond approximately to 40% of the total halo mass at the radius R ≈ 4 and 90% of the total halo mass at the radius R ≈ 11. The halo and the disk of the secondary galaxy G2 can be obtained by reflecting the respective contour image relative to the Y axis at X = 0, since the two galaxies have the same mass distribution. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.