| Issue |
A&A
Volume 567, July 2014
|
|
|---|---|---|
| Article Number | A138 | |
| Number of page(s) | 8 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201423577 | |
| Published online | 30 July 2014 | |
Structure and evolution of solar supergranulation using SDO/HMI data
1 Institut de Recherche en Astrophysique et Planétologie, Université de Toulouse, CNRS, 14 avenue Édouard Belin, 31400 Toulouse, France
2 Astronomical Institute, Faculty of Mathematics and Physics, Charles University in Prague, V Holešovičkách 2, 18000, Prague 8, Czech Republic
3 Astronomical Institute, Academy of Sciences of the Czech Republic (v. v. i.), Fričova 298, 25165 Ondřejov, Czech Republic
4 LESIA, Observatoire de Paris, Section de Meudon, 92195 Meudon, France
5 Max-Planck-Institut für Sonnensystemforschung, Justus-von-Liebig-Weg 3, 37077 Göttingen, Germany
6 Institut für Astrophysik, Georg-August-Universität Göttingen, Friedrich-Hund-Platz 1, 37077 Göttingen, Germany
Received: 5 February 2014
Accepted: 20 June 2014
Context. Studying the motions on the solar surface is fundamental for understanding how turbulent convection transports energy and how magnetic fields are distributed across the solar surface.
Aims. From horizontal velocity measurements all over the visible disc of the Sun and using data from the Solar Dynamics Observatory/Helioseismic and Magnetic Imager (SDO/HMI), we investigate the structure and evolution of solar supergranulation.
Methods. Horizontal velocity fields were measured by following the proper motions of solar granules using a newly developed version of the coherent structure tracking code. With this tool, maps of horizontal divergence were computed. We then segmented and identified supergranular cells and followed their histories by using spatio-temporal labelling. With this data set we derived the fundamental properties of supergranulation, including their motion.
Results. We find values of the fundamental parameters of supergranulation similar to previous studies: a mean lifetime of 1.5 days and a mean diameter of 25 Mm. The tracking of individual supergranular cells reveals the solar differential rotation and a poleward circulation trend of the meridional flow. The shape of the derived differential rotation and meridional flow does not depend on the cell size. If there is a background magnetic field, the diverging flows in supergranules are weaker.
Conclusions. This study confirms that supergranules are suitable tracers that may be used to investigate the large-scale flows of the solar convection as long as they are detectable enough on the surface.
Key words: Sun: photosphere / Sun: granulation / Sun: general
© ESO, 2014
1. Introduction
The dynamics of the solar surface is still a main subject of research in solar physics. It is essential to understand the mechanisms at the origin of the solar magnetic fields and their redistribution to constrain the dynamo process or the solar wind generation. Indeed, the surface field patterns ultimately determine the coronal field topology and the photospheric footpoints of open field lines of the heliosphere (DeRosa & Toomre 2004). A recently published scenario of the origin of the solar wind in coronal holes (Yang et al. 2013) suggests that motions driven by supergranulation advect meso-scale closed loops toward supergranular borders. The horizontally moving loops impinge on an open funnel that is located at the supergranular cell boundary. This collision may trigger magnetic reconnection, which finally forms the nascent solar wind.
Thanks to spatial observatories (SOHO, SDO, Hinode, etc.), the Sun is the only star where large-scale (differential rotation, meridional circulation, etc.) and small-scales (supergranulation, granulation) flows can be observed continuously, with temporal scales of a few seconds to several months. Solar granulation is generally considered to be well understood (Nordlund et al. 2009), but the origin of supergranulation is currently unknown despite of many observations and analyses (Rieutord & Rincon 2010).
Different approaches have previously been used to study the supergranulation: correlation or tracking techniques applied to quiet-Sun images of CaII-K that record the emission of the magnetic elements in the magnetic network that surrounds the supergranular cells (Del Moro et al. 2007), Doppler features (DeRosa & Toomre 2004; Švanda et al. 2008, and others), or pattern of horizontal divergences of the smaller-scale flows (Gizon et al. 2003). Additional information about supergranulation was also obtained from the power spectral analyses (e.g. Williams et al. 2013).
Helioseismology represents a powerful tool for studying supergranules and the connected flows (e.g. Švanda 2013). The propagation of acoustic waves through the solar interior is affected by plasma motions, which in turn affects helioseismic observables such as frequencies or travel times of the waves. Inverse modelling can image the flows, but substantial time averaging is required to obtain results with a signal-to-noise ratio higher than unity.
The main goal of our study is to determine the properties of the supergranulation by using horizontal flow fields directly measured on the solar surface via solar granulation tracking computed by the coherent structure tracking (CST) code (Roudier et al. 2013; Rieutord et al. 2007; Tkaczuk et al. 2007).
The CST method allows determining plasma flows from scales as small as 2.5 Mm (Rieutord et al. 2001) up to almost the full disc (to be precise, up to 0.8 radius) of the Sun. Here we take advantage of the high spatial and temporal resolution of SDO/HMI continuum observations and use the granulation as tracers for direct measurements of the plasma flow.
The velocity field obtained by the CST code is represented on a wavelet basis that allows computating the field derivatives such as divergence or vertical vorticity.
The paper is organised in the following way: in Sect. 2 we explain the data reduction to isolate individual supergranules and their histories in the datacube. In Sect. 3 we describe the results obtained after applying the method. Conclusions and future perspectives follow.
2. SDO-HMI observations and horizontal flow field measurement
The Helioseismic and Magnetic Imager onboard the Solar Dynamics Observatory (HMI/SDO; Schou et al. 2012) supplies uninterrupted high-resolution observations of the full solar disc. This provides a unique opportunity for mapping surface flows on a wide range of scales (both spatial and temporal).
We used HMI/SDO white-light data from May 10 2011 to May 16 2011 (seven days without interruption) to derive horizontal velocity fields using a recent version of the CST algorithm (Roudier et al. 2013). The code tracked the motion of individual granules that were recorded in the frames with a time step of 45 s and a pixel size of 0.5 arcsec.
 |
Fig. 1 Horizontal divergence map white stands for positive divergence (left) and segmented divergence centres, black for positive divergence (right). |
 |
Fig. 2 Evolution of divergence: positive divergence in white (top), and the segmented counterpart, positive divergence in black (bottom). The time step is 30 min and the field of view of 179 × 179 arcsec2. |
 |
Fig. 3 Time-latitude slice of the horizontal divergence tracked at constant rotation rate (left) and the segmented slice (right). Linear vertical structures represent persistent outflow cells, with their lengths proportional to their lifetimes. |
The resulting horizontal velocity fields returned by CST map the motions of the solar surface plasma on scales larger than 2.5 Mm over almost the entire visible surface of the Sun with a time step of 30 min (Roudier et al. 2013). The reconstrution of the continuous velocity field is based on a wavelet multi-resolution analysis, by which one can obtain velocity fields at different scales. It also gives its derivatives such as the horizontal divergence or the vertical component of the vorticity. The algorithm also limits the propagation of noise and other errors (Rieutord et al. 2007). The measurements of horizontal flows by CST is strictly sensitive to the motions within the thin shell at the very top of the solar convection zone (Roudier et al. 1999). It is thus suitable for studies of solar supergranulation, especially in the region around the disc centre, whereas local helioseismology methods are sensitive to deeper layers and sample a thicker shell (at least 1 Mm) at the top of the convection zone. It was shown that the results from both methods are comparable, but not identical (Švanda et al. 2013).
It was described in earlier works (e.g. Beck & Duvall 2001; Gizon & Duvall 2003; Hirzberger et al. 2008) that a convenient way of identifying the individual supergranular cells is through the use of the horizontal divergence ∇h·v of the flow, 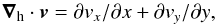 (1)where vx and vy are the horizontal components of the flow field in a local Cartesian coordinate system. The regions of positive divergence are typically regions of upflows, while regions with a negative horizontal divergence depict downflows. A supergranule in a flow map near the solar surface is defined as a compact region of positive divergence surrounded by lanes of negative divergence.
(1)where vx and vy are the horizontal components of the flow field in a local Cartesian coordinate system. The regions of positive divergence are typically regions of upflows, while regions with a negative horizontal divergence depict downflows. A supergranule in a flow map near the solar surface is defined as a compact region of positive divergence surrounded by lanes of negative divergence.
For this purpose we used the divergence derived directly from the CST. To characterize the supergranulation scale, similarly to Hirzberger et al. (2008) and DeRosa & Toomre (2004), we selected the low spatial resolution mode of the CST, with a scale cut-off of 14 arcsec (around 10 Mm). Meunier et al. (2007) showed that a scale cut-off of 10.2 Mm is well adapted to the typical size of supergranules.
The divergence patterns were tracked rigidly at the Carrington rate of 13.2°/day. Then, the divergence fields were remapped onto a latitude–longitude coordinate system using the Postel projection with a pixel size of 0.21°, which is equivalent to a grid size of 2.55 Mm. The time series spans seven days with a field of view centred on the equator with the limits in latitude (−28°, +32°) and in longitude (290°,330°) in Carrington coordinates. The tracked region remains visible on the disc and is located within about 30° of the limb.
3. Properties of supergranules
3.1. Evolution of the divergence field
We used the supergranular outflow core defined by DeRosa & Toomre (2004). This is the group of pixels of positive divergence where the local curvature of the function is negative, a segmentation criterion originally proposed by Strous (see Rieutord et al. 2007).
In Fig. 1 each positive divergence is easily identifiable in the segmented map. The segmentation processing was applied to all the 336 divergence maps of our seven day sequence. Figure 2 shows an example of the temporal evolution of the divergences and their segmented counterparts during five hours. In the selected field, three sunspots are present as a divergence centre, like supergranules. However their contribution is negligible compared with the total number of detected divergences. Figure 3 displays a time-latitude slice of the divergence (also from the segmented map) of the data cube, which exhibits the temporal evolution of supergranule cores. The lengths of the persistent flows are an indication of their lifetimes.
The proper determination of the lifetime of each cell requires cross-identifying of the supergranular centres between the consecutive frames of the 3D (x,y,t) datacube. For that purpose we used the time labelling described Roudier et al. (2003). This method was previously developed to track the evolution of solar granules, but has been fully adapted to tracking supergranular cores.
In the seven day-long datacube with a time sampling of 30 min we identified and tracked 4759 supergranular centres, which allowed us to follow their properties during their evolution. This number is close to the 4977 supergranular lifetime histories followed by Hirzberger et al. (2008) over a spatial window three times larger and a temporal window of five days which yielded a 3D datacube 2.15 times larger. The similarity of these numbers arises because our HMI/SDO data set has a higher resolution than the MDI/SOHO data used by Hirzberger et al. (2008). We thus detect twice as much supergranules which compensates for the smaller field of view needed to use a seven-day series.
 |
Fig. 4 Distribution of supergranular lifetimes for 3000 supergranules identified in the temporal sequence, with a bin of 12 h. The solid line represents an exponential fit to the feature-tracking data. |
The distribution of derived supergranular lifetimes is shown in Fig. 4. For a temporal bin of 12 h it may be fitted with an exponential distribution in the form ![\begin{equation} N(t)=N(0)\exp[-t/\tau], \end{equation}](/articles/aa/full_html/2014/07/aa23577-14/aa23577-14-eq12.png) (2)where τ is the mean lifetime. The best-fit exponential function (straight line in Fig. 4) gives τ = 1.5 days, in agreement with Hirzberger et al. (2008) for a temporal bin of 12 h.
(2)where τ is the mean lifetime. The best-fit exponential function (straight line in Fig. 4) gives τ = 1.5 days, in agreement with Hirzberger et al. (2008) for a temporal bin of 12 h.
3.2. Properties of supergranular cells
 |
Fig. 5 Supergranule outflow cores (divergences left) and the associated watershed basin cells (white middle), and cell area representation of the supergranules (right). |
A more detailed investigation of the supergranulation is required to properly identify each cell in the divergence map, following our definition of one supergranule as a compact region of positive divergence surrounded by lanes of the negative divergence. We detected the cells with a watershed basin segmentation applied to the divergence maps, similarly to Hirzberger et al. (2008). The divergence is treated as a topographic map, with the divergence magnitude corresponding to the height of various catchment basins (that are divergence cells). An example of such a detection is displayed in Fig. 5. In that plot we can clearly identify the cores of the cells (positive divergences) and the associated cells.
 |
Fig. 6 Number of supergranules versus their equivalent diameter. |
The segmented cells allowed us to state additional statistical properties. Figure 6 shows a histogram of a cell diameter that is peaked around 25 Mm (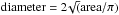 ). Our resulting mean cell diameter is slightly smaller than found by Hirzberger et al. (2008) – 27.1 Mm – and Del Moro et al. (2004) – 33 Mm –, because we detected smaller size divergence centres by our processing. By combining the high spatial resolution of HMI/SDO data with the velocity computed by CST we were able to take into account all sizes of the divergence centres in the field of view by using watershed basin segmentation.
). Our resulting mean cell diameter is slightly smaller than found by Hirzberger et al. (2008) – 27.1 Mm – and Del Moro et al. (2004) – 33 Mm –, because we detected smaller size divergence centres by our processing. By combining the high spatial resolution of HMI/SDO data with the velocity computed by CST we were able to take into account all sizes of the divergence centres in the field of view by using watershed basin segmentation.
This result clearly demonstrates that the definition of a typical supergranule (size, diameter, lifetime, etc.) strongly depends on the data set and the applied method. Therefore, it is very difficult to properly describe a typical supergranular cell when the method does not take into account some of the representatives (typically those with small sizes or weak divergence signals). To obtain proper physical characteristics of supergranulation the set of representatives must be complete. We are confident that this has been achieved in our analysis.
The relation between the area and maximum divergence reported previously by Hirzberger et al. (2008) and Meunier et al. (2007) is confirmed by our analysis. Figure 7 shows this relation with an extension toward low values. A linear relation appears to extend over the full range of values with a very large scatter toward larger cells.
 |
Fig. 7 Two-dimensional histogram of the maximum divergence versus supergranular cell area. |
 |
Fig. 8 Lifetime dependence of the area of the supergranule outflow core (cross) and lifetime dependence of the area of the 37 longest-living supergranules (solid line). |
 |
Fig. 9 Lifetime dependence of the maximun divergence of the supergranule outflow core (cross and Y coordinate axis left) and the temporal mean divergence of the 37 longest-living supergranules (solid line and Y coordinate axis right). |
The cross plots in Figs. 8 and 9, similar to Fig. 12 in Hirzberger et al. (2008), show the outflow core areas and the maximum divergences averaged over each lifetime history and, additionally, averaged over each bin of the histograms. We confirm the trend for larger supergranules to live longer. However, we do not observe that supergranules with larger divergences have longer lives – the divergences appears to be quite constant regardless of the lifetime of the supergranule.
The solid lines in Figs. 8 and 9 show the mean temporal evolution of the area and the divergence of the 37 longest-living supergranules. For the long-lived supergranules, we observe an increasing area during the first 1.5 days with an area more or less constant thereafter. The duration of such supergranules does not allow us to see the final phase of their evolution. The divergence intensity evolution shows an increasing phase during the first two or three days followed by a slow decrease toward the end of our sequence.
3.3. Advection of supergranules
It was also suggested by other authors (e.g. Snodgrass & Ulrich 1990; Švanda et al. 2006, 2008, 2009; Hathaway 2012) that supergranules may be treated as objects that are carried by an underlying large-scale velocity field, and hence may used as tracers for studies of such a velocity field. Organised motions could serve as evidence for example of giant cells (Hathaway et al. 2013). So far, most of these studies (if not all of them) were driven by some versions of correlation techniques, which did not follow individual supergranules, but rather a pattern of supergranulation. An additional filtering was used (e.g. by Hathaway 2012) to select scales that are to be tracked and hence discuss the possible flow dependence on the size of these cells. One should proceed with caution: without properly identifying the supergranular cells, the scales selected by the filtering do not have to really isolate only the supergranules with the appropriate size. Interpreting of such measurements may be rather complicated. Hathaway (2012) assumed that the vertical extent of supergranular cells correspond to their horizontal diameter and hence used the tracking of the supergranular pattern with various scales to investigate the weak meridional flow in depth. They concluded that the large supergranular cells (more precisely a pattern with large scales) already “feel” the return meridional flow some 50 Mm below the surface and hence move towards the equator. The hypothesis of the shallow meridional flow is supported by a multicellular model of the meridional flow, which came recently from local helioseismology (Zhao et al. 2013).
In contrast to the traditional methodology, we may follow the individual supergranular cells in time, and thus directly study the possible dependence of the motions of supergranular cells on their sizes. A drawback of this method is the significantly higher level of random noise, which may be only decreased by using more supergranular histories and averaging them, thus losing temporal resolution.
 |
Fig. 10 Zonal velocity component measured by tracking the supergranules cells (top). The differential rotation is clealy identified. The meridional component of the supergranule motion (bottom) shows a poleward motion, which does not depend on the size of supergranules. |
To collect a large statistical sample, the datacube covering seven days was split into four chunks, each 42 h long (84 frames). The splitting allowed us to use larger fields of view undisturbed by edge effects than if the datacube were used uninterrupted. Given the characteristic lifetime of 1.5 days we assume that we have captured the evolution of most of the supergranules in these chunks. We did not consider supergranules whose lifetime started or ended in the boundary frames; the history of such supergranules would not have been complete.
Altogether we identified 14 321 complete histories of individual supergranular cells. For each of these cell, its motion averaged over its lifetime was computed by means of the difference of positions of the gravity centre in the first frame, where the cell was detected, and the frame, where the cell was detected the last time. Because of the very discrete coverage of the field of view, we averaged the motions of supergranules over the bands of 5° in latitude.
The ensemble of supergranule results was split into three bins according to their effective size. The boundary values were chosen so that the bins were more or less equally populated. In this case, there were 3005 supergranules in the bin of 5–22 Mm, 5744 supergranules in the bin of 22–27 Mm and 5556 cells in the bin of 27–45 Mm.
Figure 10 shows the resulting velocity components additionally averaged in longitude. The noise level of each plotted point is estimated to be 10 m/s. Since the reference frame for tracking the frames in the datacube is the Carrington rotation rate, the differential rotation is clearly visible in the zonal component (upper panel). In the meridional component (lower panel) the trend of weak single-cell poleward meridional flow is visible.
Our results contradict those derived by Hathaway (2012). He reported (1) the decreasing amplitude of the poleward meridional flow with the size (more precisely wavelength) of supergranules, the flow eventually turned equatorward for supergranules with wavelengths longer than 50 Mm; and (2) the increasing amplitude of the zonal flow component with increasing size of supergranules. Our analysis shows that both zonal and meridional flows are independentof the supergranules size.
Hathaway (2012) claimed that the onset of the meridional flow reversal occurs for supergranule wavelengths longer than 50 Mm. Interestingly, in our sample of more than 14 000 supergranules with complete histories, there is only one supergranule longer than 50 Mm. A similar histogram by Hirzberger et al. (2008) points to a similar conclusion. The question therefore is what structures are represented by Fourier wavelengths of 50 Mm: obviously, it cannot be individual supergranules.
A possible improvement of this approach would be to use more supergranular cells as tracers, which would reduce the noise level and also allow for a better resolution in both latitude and size of supergranules.
3.4. Effect of the magnetic field
 |
Fig. 11 Map of the longitudinal magnetic field on 12 May 2011 showing the latitude of the concentrated magnetic activity. |
 |
Fig. 12 Divergence (larger than 0.0002876 s-1 in each frame) integrated over 7 days of observations (left). Identical plot with values higher than 0.000342 s-1 over the 7 days (right). We note in the right upper corner a lower density of the stronger divergence due to the magnetic activity at that location during the 7 days of the sequence. We also note the same density below a latitude − 20° in the bottom right corner, but the magnetic field was only active for 2 days. |
 |
Fig. 13 Comparison of the divergence distribution in the entire field of view (solid line) and in the upper right corner (dashed dotted), where a strong magnetic field is present. A Gaussian distribution with the same standard deviation is overplotted for comparison (dashed line). |
It is well established today that magnetic fields affect the dynamic of the solar convection. Figure 11 shows the magnetic context in field studied (dark rectangle) on May 12, 2011. The magnetic field is located in the top right part of our field of view. To test the possible influence of that magnetic activity on the amplitude of the divergence, we took thresholded divergences integrated over time defined as 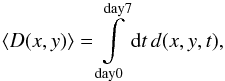 (3)where d(x,y,t) = ∇h·v(x,y,t) for (∇h·v)(x,y,t) >dthresh and d(x,y,t) = 0 otherwise.
(3)where d(x,y,t) = ∇h·v(x,y,t) for (∇h·v)(x,y,t) >dthresh and d(x,y,t) = 0 otherwise.
Figure 12 shows ⟨ D(x,y) ⟩ with a threshold dthresh = 0.0002876 s-1 and an identical plot with a threshold dthresh = 0.000342 s-1, corresponding to 2.5 and 3.0σ of the divergence fluctuations. Note that the lower density of the stronger divergence is centered on the upper right corner because of the magnetic activity at that location. This is confirmed by the histogram in Fig. 13, where the divergence distribution in the magnetic region is more concentrated at small amplitudes than is the full field-of-view divergence distribution. These distibutions clearly show a larger positive wing than that for the respective Gaussian distribution with the same standard-deviation.
3.5. Relation of the magnetic network with divergence amplitude
The magnetic network is known to be located at the edge of the supergranules. We studied the contribution of the large amplitude divergences (supergranules) to building the network. First, we used the hypothesis that the motions of supergranules accross the solar surface are purely horizontal. From the velocities measured by CST vx and vy, we computed the longitudinal vφ and latitudinal vθ components. These velocities were projected with a grid with a regular angle spacing of 0.2047 degrees in both φ and θ. From the projected vφ and vθ we computed the divergence field. Figure 14 displays the divergence. This distibution shows wings larger than that for the corresponding Gaussian, which reflects the intermittency of the supergranulation (Rieutord et al. 2008).
 |
Fig. 14 Divergences during the first 48h of the time sequence. A Gaussian distribution with the same standard deviation is overplotted for comparison (dashed line). |
4. Conclusions
By following the proper motions of the solar granules, we can revisit the dynamics of the solar surface at high spatial and temporal resolutions from hours to months and years with the SDO data. Applying the CST to HMI/SDO white-light images gives direct access to the solar plasma motion on the solar surface. The long continuous seven day series offers the opportunity of studying the properties of supergranulation and its evolution. The CST code and the multi-resolution technique directly produce the divergence field,which minimizes the error propagation during the scaling. The spatial window of 10.2 Mm is well adapted to the typical size of supergranules; thus we can use the divergence patterns as proxies of supergranules. We confirm most of the results described by Hirzberger et al. (2008), except for the divergence increase relative to the increasing lifetime. This is probably due to the different ways of calibrating the divergence amplitude.
We found the mean diameter of supergranular cells to be about 25 Mm, which is smaller than found previously. The reason might be a better detection of the small-scale divergences. We also observe a smaller amplitude of the divergence in the region of strong magnetic activity, which probably has some influence on the diffusion of the magnetic elements in this region.
Applying the tracking on divergence remapped onto a latitude-longitude coordinate system using the Postel projection, highlights the solar differential rotation and a poleward circulation trend of the meridian flow regardless of the size of supergranules. This result does not confirm the different behaviour of the largest cells found by Hathaway (2012), where the poleward meridional flow disappears. This trend must be confirmed with a longer sequence (one month at least) to reduce the noise, but this suggests that such a data analysis can be used to study the meridional flow with a smaller temporal window than for other methods. Improvements are expected with a longer data-set analysis on the meridional flow and its evolution during the solar cycle.
Acknowledgments
We thank the HMI team members for their hard work. We thank the German Data Center for SDO for providing SDO/HMI data. This work was granted access to the HPC resources of CALMIP under the allocation 2011-[P1115]. M.Š. is supported by the Czech Science Foundation (grant P209/12/P568). This work was supported by the project RVO:67985815 of the Czech academy of Sciences and the research plan MSM0021620860 of the Ministry of Education, Youth, and Sports of the Czech Republic. We would like to give special thanks to the anonymous referee for his or her helpful comments and recommendations.
References
- Beck, J. G., & Duvall, Jr., T. L. 2001, in SOHO 10/GONG 2000 Workshop: Helio- and Asteroseismology at the Dawn of the Millennium, eds. A. Wilson, & P. L. Pallé, ESA SP, 464, 577 [Google Scholar]
- Del Moro, D., Berilli, F., Duvall, T., & Kosovichev, A. G. 2004, Sol. Phys., 221, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Del Moro, D., Giordano, S., & Berrilli, F. 2007, A&A, 472, 599 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- DeRosa, M. L., & Toomre, J. 2004, ApJ, 616, 1242 [NASA ADS] [CrossRef] [Google Scholar]
- Gizon, L., & Duvall, Jr., T. L. 2003, in GONG+ 2002. Local and Global Helioseismology: the Present and Future, ed. H. Sawaya-Lacoste, ESA SP, 517, 43 [Google Scholar]
- Gizon, L., Duvall, T. L., & Schou, J. 2003, Nature, 421, 43 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hathaway, D. H. 2012, ApJ, 760, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Hathaway, D. H., Upton, L., & Colegrove, O. 2013, Science, 342, 1217 [NASA ADS] [CrossRef] [Google Scholar]
- Hirzberger, J., Gizon, L., Solanki, S. K., & Duvall, T. L. 2008, Sol. Phys., 251, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Meunier, N., Tkaczuk, R., Roudier, T., & Rieutord, M. 2007, A&A, 461, 1141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nordlund, Å., Stein, R. F., & Asplund, M. 2009, Liv. Rev. Sol. Phys., 6, 2 [Google Scholar]
- Rieutord, M., & Rincon, F. 2010, Liv. Rev. Sol. Phys., 7, 2 [Google Scholar]
- Rieutord, M., Roudier, T., Ludwig, H.-G., Nordlund, Å., & Stein, R. 2001, A&A, 377, L14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rieutord, M., Roudier, T., Roques, S., & Ducottet, C. 2007, A&A, 471, 687 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rieutord, M., Meunier, N., Roudier, T., et al. 2008, A&A, 479, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roudier, T., Rieutord, M., Malherbe, J., & Vigneau, J. 1999, A&A, 349, 301 [NASA ADS] [Google Scholar]
- Roudier, T., Lignières, F., Rieutord, M., Brandt, P. N., & Malherbe, J. M. 2003, A&A, 409, 299 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roudier, T., Rieutord, M., Prat, V., et al. 2013, A&A, 552, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schou, J., Scherrer, P. H., Bush, R. I., et al. 2012, Sol. Phys., 275, 229 [Google Scholar]
- Snodgrass, H. B., & Ulrich, R. K. 1990, ApJ, 351, 309 [Google Scholar]
- Tkaczuk, R., Rieutord, M., Meunier, N., & Roudier, T. 2007, A&A, 471, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Švanda, M. 2013, ApJ, 775, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Švanda, M., Klvaňa, M., & Sobotka, M. 2006, A&A, 458, 301 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Švanda, M., Klvaňa, M., Sobotka, M., & Bumba, V. 2008, A&A, 477, 285 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Švanda, M., Klvaňa, M., Sobotka, M., Kosovichev, A. G., & Duvall, T. L. 2009, New A, 14, 429 [Google Scholar]
- Švanda, M., Roudier, T., Rieutord, M., Burston, R., & Gizon, L. 2013, ApJ, 771, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, P. E., Pesnell, W. D., Beck, J. G., & Lee, S. 2013, Sol. Phys. [Google Scholar]
- Yang, L., He, J., Peter, H., et al. 2013, ApJ, 770, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, J., Bogart, R. S., Kosovichev, A. G., Duvall, Jr., T. L., & Hartlep, T. 2013, ApJ, 774, L29 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Horizontal divergence map white stands for positive divergence (left) and segmented divergence centres, black for positive divergence (right). |
| In the text | |
 |
Fig. 2 Evolution of divergence: positive divergence in white (top), and the segmented counterpart, positive divergence in black (bottom). The time step is 30 min and the field of view of 179 × 179 arcsec2. |
| In the text | |
 |
Fig. 3 Time-latitude slice of the horizontal divergence tracked at constant rotation rate (left) and the segmented slice (right). Linear vertical structures represent persistent outflow cells, with their lengths proportional to their lifetimes. |
| In the text | |
 |
Fig. 4 Distribution of supergranular lifetimes for 3000 supergranules identified in the temporal sequence, with a bin of 12 h. The solid line represents an exponential fit to the feature-tracking data. |
| In the text | |
 |
Fig. 5 Supergranule outflow cores (divergences left) and the associated watershed basin cells (white middle), and cell area representation of the supergranules (right). |
| In the text | |
 |
Fig. 6 Number of supergranules versus their equivalent diameter. |
| In the text | |
 |
Fig. 7 Two-dimensional histogram of the maximum divergence versus supergranular cell area. |
| In the text | |
 |
Fig. 8 Lifetime dependence of the area of the supergranule outflow core (cross) and lifetime dependence of the area of the 37 longest-living supergranules (solid line). |
| In the text | |
 |
Fig. 9 Lifetime dependence of the maximun divergence of the supergranule outflow core (cross and Y coordinate axis left) and the temporal mean divergence of the 37 longest-living supergranules (solid line and Y coordinate axis right). |
| In the text | |
 |
Fig. 10 Zonal velocity component measured by tracking the supergranules cells (top). The differential rotation is clealy identified. The meridional component of the supergranule motion (bottom) shows a poleward motion, which does not depend on the size of supergranules. |
| In the text | |
 |
Fig. 11 Map of the longitudinal magnetic field on 12 May 2011 showing the latitude of the concentrated magnetic activity. |
| In the text | |
 |
Fig. 12 Divergence (larger than 0.0002876 s-1 in each frame) integrated over 7 days of observations (left). Identical plot with values higher than 0.000342 s-1 over the 7 days (right). We note in the right upper corner a lower density of the stronger divergence due to the magnetic activity at that location during the 7 days of the sequence. We also note the same density below a latitude − 20° in the bottom right corner, but the magnetic field was only active for 2 days. |
| In the text | |
 |
Fig. 13 Comparison of the divergence distribution in the entire field of view (solid line) and in the upper right corner (dashed dotted), where a strong magnetic field is present. A Gaussian distribution with the same standard deviation is overplotted for comparison (dashed line). |
| In the text | |
 |
Fig. 14 Divergences during the first 48h of the time sequence. A Gaussian distribution with the same standard deviation is overplotted for comparison (dashed line). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


