| Issue |
A&A
Volume 567, July 2014
|
|
|---|---|---|
| Article Number | A24 | |
| Number of page(s) | 6 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201423524 | |
| Published online | 04 July 2014 | |
Sausage oscillations of coronal plasma slabs
1 Centre for Fusion, Space and Astrophysics, Department of Physics, University of Warwick, Coventry, CV4 7AL, UK
e-mail: christopher.hornsey@warwick.ac.uk
2 STFC Rutherford Appleton Laboratory, Chilton, Didcot, Oxon., OX11 0QX, UK
3 School of Space Research, Kyung Hee University, Yongin, 446-701, Gyeonggi, Korea
4 Central Astronomical Observatory of the Russian Academy of Sciences at Pulkovo, 196140 St Petersburg, Russia
Received: 28 January 2014
Accepted: 6 May 2014
Context. Sausage oscillations are observed in plasma non-uniformities of the solar corona as axisymmetric perturbations of the non-uniformity. Often, these non-uniformities can be modelled as field-aligned slabs of the density enhancement.
Aims. We perform parametric studies of sausage oscillations of plasma slabs, aiming to determine the dependence of the oscillation period on its parameters, and the onset of leaky and trapped regimes of the oscillations.
Methods. Slabs with smooth transverse profiles of the density of a zero-beta plasma are perturbed by an impulsive localised perturbation of the sausage symmetry. In particular, the slab can contain an infinitely thin current sheet in its centre. The initial value problem is then solved numerically. The numerical results are subject to spectral analysis. The results are compared with analytical solutions for a slab with a step-function profile and also with sausage oscillations of a plasma cylinder.
Results. We established that sausage oscillations in slabs generally have the same properties as in plasma cylinders. In the trapped regime, the sausage oscillation period increases with the increase in the longitudinal wavelength. In the leaky regime, the dependence of the period on the wavelength experiences saturation, and the period becomes independent of the wavelength in the long-wavelength limit. In the leaky regime the period is always longer than in the trapped regime. The sausage oscillation period in a slab is always longer than in a cylinder with the same transverse profile. In slabs with steeper transverse profiles, sausage oscillations have longer periods. The leaky regime occurs at shorter wavelengths in slabs with smoother profiles.
Key words: magnetohydrodynamics (MHD) / Sun: atmosphere / Sun: corona / Sun: magnetic fields / Sun: oscillations / waves
© ESO, 2014
1. Introduction
The sausage mode, also known as the m = 0, fast magnetoacoustic or peristaltic mode, is one of the main magnetohydrodynamic (MHD) modes of field-aligned plasma non-uniformities of the solar corona (see e.g. Zaitsev & Stepanov 2008; De Moortel & Nakariakov 2012; Stepanov et al. 2012, for recent reviews). This mode is a periodic expansion and contraction of the non-uniformity. In the low-β plasma, typical for coronal active regions, the plasma flows in the sausage mode are mainly transverse to the direction of the magnetic field, hence are essentially compressive (e.g. Gruszecki et al. 2012; Antolin & Van Doorsselaere 2013). If the wave-guiding non-uniformity is symmetric in the transverse direction, the transverse flows in the mode are described by an odd function: the flow is zero at the axis of the waveguide, so is not moved by this mode. The perturbations of the plasma density and of the magnetic field strength are described by even functions. Locally, this mode is a superposition of oblique fast magnetoacoustic waves. The presence of a wave-guiding non-uniformity of the plasma is a crucial element of this mode: the outer boundaries of the non-uniformity lead to the reflection or refraction of the fast waves back to the non-uniformity. Thus, globally, the fast waves propagate along the magnetic field (Edwin & Roberts 1982, 1983) in the waveguide. In the transverse direction, the waves are either confined to the wave-guide axis or radiate away.
In the context of MHD coronal seismology, the main interest in the sausage mode is connected with the interpretation of the quasi-periodic modulation of the microwave, white light, X-ray and gamma-ray emission generated in solar flares (see Nakariakov & Melnikov 2009, for a detailed review). The modulation is produced either directly by the variation in the macroscopic parameters of the plasma, such as the density and the magnetic field (e.g. Roberts et al. 1984; Nakariakov et al. 2003; Mossessian & Fleishman 2012), by the modulation of the non-thermal electron dynamics (Zaitsev & Stepanov 1982), or indirectly by periodic triggering of magnetic reconnection (Nakariakov et al. 2012). Also, sausage oscillations have been detected in cool loops (e.g. Srivastava et al. 2008) and EUV loops (e.g. Su et al. 2012). Details of these mechanisms remain debated, but in any case they transfer the periodicity of the MHD oscillation to the periodic variation of the observed plasma parameters.
Usually, wave-guiding plasma non-uniformities are modelled as a plasma cylinder (e.g. Rosenberg 1970; Edwin & Roberts 1983; Kopylova et al. 2007; Vasheghani Farahani et al. 2014) or a slab (Edwin & Roberts 1982; Pascoe et al. 2007b). Analytical calculations performed in the case of a step-function transverse profile of the plasma density show that there are two regimes of the linear sausage mode dynamics: shorter wavelength oscillations are trapped, while longer wavelengths are leaky (Cally 1986). The cut-off wavelength separating these two regimes corresponds to the threshold of the total internal reflection. The cut-off value is determined by the Alfvén speeds inside and outside the waveguide. Analytical solutions also exist in the case of a slab with the symmetric Epstein profile of the plasma density and show the same behaviour (Nakariakov & Roberts 1995; Cooper et al. 2003). This behaviour was studied in a series of numerical experiments. It was shown to be robust, and it exists, for instance, in multi-shell non-uniformities (Pascoe et al. 2007a), in high-β loops (Inglis et al. 2009), and in non-uniformities with the cross-sectional area varying in the longitudinal direction (Pascoe et al. 2009). Systematic numerical modelling of trapped fast magnetoacoustic waves in a plasma slab was performed in Murawski & Roberts (1993, 1994) and Ogrodowczyk & Murawski (2006, 2007), who include oscillations in a system of two parallel slabs. The results reproduced the “crazy tadpole” wavelet spectra and showed that they are a robust feature of the dynamics.
In the case of standing sausage waves, the non-linear dependence of the phase speed on the wavenumber leads to an interesting effect. If in the trapped regime the period grows with the wavelength (Nakariakov et al. 2003; Pascoe et al. 2007b), in the leaky regime the period becomes independent of the wavelength (Cally 1986; Kopylova et al. 2007). Very recently, numerical simulations demonstrated the transition from the regime where the period grows with the wavelength to the regime of its practical independence (Nakariakov et al. 2012). This result has strong potential for plasma diagnostics in situations when the wavelength of sausage oscillations cannot be resolved, e.g. in quasi-periodic pulsations in stellar flares. However, the results of Nakariakov et al. (2012) were obtained for a plasma cylinder, and need to be generalised for the plasma slab. Indeed, in a number of cases the waveguiding coronal plasma non-uniformity is rather a plane or curved slab than a cylinder. In particular, sausage perturbations can readily occur in coronal streamers and other current sheets (e.g. Smith et al. 1997), in dark lanes in post-flare supra-arcades (e.g. Verwichte et al. 2005; Costa 2011), and global oscillations of prominence slabs. Understanding the sausage mode dynamics is important for the mechanism for the peristaltic pumping in flaring current sheets (e.g. Scott et al. 2013). Also, propagating sausage wave trains guided by a current sheet are employed to the interpretation of radio fiber bursts (Jelínek & Karlický 2012; Karlický et al. 2013).
The aim of this paper is to generalise the results obtained in Nakariakov et al. (2012) on the slab geometry. We also aim to develop the work of Pascoe et al. (2007b) on the case of long wavelengths, studying the transition between trapped and leaky regimes, and comparison of the results obtained in both the geometries. The paper is organised as follows. Section 2 describes the model that was used to describe these oscillations in the slab geometry. Section 3 details the results of measurements made using this model, firstly studying how the period of the oscillations varies with the wavenumber for different shapes and depths of well, as well as how these values compare to the cylindrical case. Then the effect of varying the steepness of the well was considered in depth. Finally in this section the values of the cutoff wavelength, the value of the wavelength for which the oscillation transitions for being trapped to being leaky, were studied, and compared with analytical results in the case of an infinitely steep well. Section 4 summarises the conclusions.
2. Model
Consider a slab of a zero-β plasma of infinite extent in the x-direction. The plasma is penetrated by a straight and uniform magnetic field, B0 directed along the x axis. Here, the index “0” denotes the equilibrium quantities. The equilibrium density, ρ0, is ![\begin{eqnarray} \label{rho0} \rho_0 = \frac{4\pi B_0^2}{C_{\mathrm{A}\infty}^2}\left[1-\delta\exp \left(-\left(\frac{\mid z\mid}{d}\right)^\alpha\right)\right]^{-2}, \end{eqnarray}](/articles/aa/full_html/2014/07/aa23524-14/aa23524-14-eq6.png) (1)and the Alfvén speed, CA(z), obeys
(1)and the Alfvén speed, CA(z), obeys ![\begin{eqnarray} C_\mathrm{A}(z)=C_{\mathrm{A}\infty}\left[1-\delta \exp \left(-\left(\frac{\mid z\mid}{d}\right)^\alpha\right)\right], \label{CAprofile} \end{eqnarray}](/articles/aa/full_html/2014/07/aa23524-14/aa23524-14-eq8.png) (2)where CA∞ is the Alfvén speed at a large distance from the slab, where d is the slab half-width, the parameter 0 <δ< 1 controls the value of the Alfvén speed at the centre of the slab, and the parameter α controls the steepness of the profile of the Alfvén speed. The specific shape of the transverse profile of the equilibrium density was chosen to make it consistent with the profile used in Nakariakov et al. (2012). It allowed a direct comparison of the results obtained in the cylindrical and slab geometries. There are no steady flows in the considered equilibrium. The use of the zero-β limit is justified by the previous numerical experiments that showed that properties of sausage oscillations are practically independent of β, provided it is lower than unity (Inglis et al. 2009). As β is taken to zero, profile (2) of the Alfvén speed coincides with the profile of the fast magnetoacoustic speed,
(2)where CA∞ is the Alfvén speed at a large distance from the slab, where d is the slab half-width, the parameter 0 <δ< 1 controls the value of the Alfvén speed at the centre of the slab, and the parameter α controls the steepness of the profile of the Alfvén speed. The specific shape of the transverse profile of the equilibrium density was chosen to make it consistent with the profile used in Nakariakov et al. (2012). It allowed a direct comparison of the results obtained in the cylindrical and slab geometries. There are no steady flows in the considered equilibrium. The use of the zero-β limit is justified by the previous numerical experiments that showed that properties of sausage oscillations are practically independent of β, provided it is lower than unity (Inglis et al. 2009). As β is taken to zero, profile (2) of the Alfvén speed coincides with the profile of the fast magnetoacoustic speed, 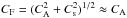 , where the sound speed, Cs is neglected in comparison with the Alfvén speed. Thus, the slab has a decrease in the fast magnetoacoustic speed and hence can act as a fast magnetoacoustic waveguide (Nakariakov & Roberts 1995). As the propagation of fast magnetoacoustic waves is not sensitive to whether the magnetic field is directed in the positive or negative direction along the x-axis in the considered geometry, our model is also applicable to infinitely thin current sheets situated at z = 0 and embedded in a plasma slab.
, where the sound speed, Cs is neglected in comparison with the Alfvén speed. Thus, the slab has a decrease in the fast magnetoacoustic speed and hence can act as a fast magnetoacoustic waveguide (Nakariakov & Roberts 1995). As the propagation of fast magnetoacoustic waves is not sensitive to whether the magnetic field is directed in the positive or negative direction along the x-axis in the considered geometry, our model is also applicable to infinitely thin current sheets situated at z = 0 and embedded in a plasma slab.
In the following we restrict ourselves to the consideration of ideal processes only, described by the ideal zero-β MHD equations:  where the notations are standard. The mass continuity and energy equations that are not needed for this study, are not shown.
where the notations are standard. The mass continuity and energy equations that are not needed for this study, are not shown.
Consider linear perturbations of the slab, that are confined to the xz-plane. For linear perturbations, labelled with the indices “1”, we obtain
 For the components of the vector quantities we obtain the equations
For the components of the vector quantities we obtain the equations 
Differentiating Eq. (7) by t, Eq. (8) by x and Eq. (9) by z, eliminating the variables Bz and Bx, and assuming that the perturbations are periodic in the x-direction with the wavelength 2π/kx, we obtain  (10)Equation (10) is a 1D wave equation describing the evolution of fast magnetoacoustic oscillations of a given longitudinal wavelength 2π/kx in the transverse direction, in a field-aligned zero-β plasma slab with a smooth transverse profile of the plasma density. This equation is a Cartesian analogue of Eq. (9) of Nakariakov et al. (2012).
(10)Equation (10) is a 1D wave equation describing the evolution of fast magnetoacoustic oscillations of a given longitudinal wavelength 2π/kx in the transverse direction, in a field-aligned zero-β plasma slab with a smooth transverse profile of the plasma density. This equation is a Cartesian analogue of Eq. (9) of Nakariakov et al. (2012).
The Fourier transform in the x-direction, made in the derivation of Eq. (10) is possible if the slab is uniform in the x-direction. This condition corresponds to the assumption that the wavelength of the perturbations is shorter than the non-uniformity along the magnetic field. Also, the slab is assumed to be uniform in the third, y-direction, that is perpendicular to both the magnetic field and the plasma density non-uniformity gradient. This allows us to assume the perturbations to be independent of the y-direction. These assumptions are standard in modelling plasma non-uniformities in the solar corona, e.g. current sheets in helmet streamers and above post-flaring arcades.
A parametric study of an initial value problem for Eq. (10) was performed numerically using the pdsolve command of Maple 16 that implements a second order (in space and time) centred finite difference scheme (see Nakariakov et al. 2012, for details). The initial conditions were chosen to be an impulsive anti-symmetric pulse centred at the axis of the slab, ![\begin{eqnarray} \label{initcon} v_z(z,t=0)=A_0z\exp\left[-\left(\frac{z}{d}\right)^2\right], \end{eqnarray}](/articles/aa/full_html/2014/07/aa23524-14/aa23524-14-eq29.png) (11)where A0 is the initial amplitude. The symmetry of the initial perturbation excludes the excitation of kink oscillations. All the energy of the initial pulse goes to sausage oscillations. As the initial pulse does not coincide with eigen functions of the slab, it can excite a number of transverse harmonics. However, as function (11) decreases monotonically with the increase in the distance from the slab central plane, the fundamental mode that has a similar structure is excited much more effectively than higher transverse harmonics. In the simulations the higher harmonics are practically absent. The boundary conditions were set as
(11)where A0 is the initial amplitude. The symmetry of the initial perturbation excludes the excitation of kink oscillations. All the energy of the initial pulse goes to sausage oscillations. As the initial pulse does not coincide with eigen functions of the slab, it can excite a number of transverse harmonics. However, as function (11) decreases monotonically with the increase in the distance from the slab central plane, the fundamental mode that has a similar structure is excited much more effectively than higher transverse harmonics. In the simulations the higher harmonics are practically absent. The boundary conditions were set as  (12)where z = 50d is the transverse extent of the simulation domain. This value for the boundary condition was chosen so as there would not be a discontinuity in the initial perturbation, as it is a requirement of the pdsolve command. (See Nakariakov et al. 2012, for details.) Thus, we use the symmetry of the problem to consider the perturbations in a half of the slab, in the domain z = [0,50d] only. The spatial structure of the velocity oscillations in the domain z = [ − 50d,0] is the same as in the considered domain, but in the anti-phase in time. The external boundary of the simulation domain was taken far enough from the slab axis, to avoid the interaction of the excited oscillations with the outer boundary in the duration of the simulation.
(12)where z = 50d is the transverse extent of the simulation domain. This value for the boundary condition was chosen so as there would not be a discontinuity in the initial perturbation, as it is a requirement of the pdsolve command. (See Nakariakov et al. 2012, for details.) Thus, we use the symmetry of the problem to consider the perturbations in a half of the slab, in the domain z = [0,50d] only. The spatial structure of the velocity oscillations in the domain z = [ − 50d,0] is the same as in the considered domain, but in the anti-phase in time. The external boundary of the simulation domain was taken far enough from the slab axis, to avoid the interaction of the excited oscillations with the outer boundary in the duration of the simulation.
Once excited, the perturbation oscillate almost harmonically (Fig. 1). As in the cylindrical case, the simulations show two regimes of oscillation: trapped and leaky.
 |
Fig. 1 Time-distance plots of transverse flows in sausage oscillations. Left panel: example of a trapped sausage oscillation in a plasma slab with the parameters: δ = 0.8 and α = 6 for the wave number kx = 1.5. Right panel: example of a leaky sausage oscillation in a plasma slab with the parameters: δ = 0.7 and α = 6, for kx = 0.4. The spatial coordinate is normalised such that the half-width of the slab, d = 1, and the time is measured in the units d/CA∞, where d is the slab half-width and CA∞ is the Alfvén speed outside the slab. |
 |
Fig. 2 Variation of the sausage oscillation period with the wavelength in a plasma slab with α = 6, for different values of δ: the solid line corresponds to δ = 0.5, the triple dot-dashed line corresponds to δ = 0.7, the dashed line to δ = 0.8, and the dot-dashed line to δ = 0.9. The thick straight line shows P = λ/CAe, that is the cutoff separating the trapped and leaky regimes. The thinner straight lines show P = λ/CA0 that correspond to the short wavelength asymptote in each case. |
In the trapped regime the oscillation is completely contained by the plasma inhomogeneity. It is determined from the simulation, as the amplitude of the oscillation inside the well remains constant (Fig. 1, left panel). These are the sausage oscillations described by Edwin & Roberts (1983), who found that these oscillations could only exist when CA0<ω/k<CA∞, which gives the extent of the trapped regime. These limits are shown by the straight lines in Figs. 2, 3.
The leaky regime is characterised by oscillations which do not remain contained by the plasma inhomogeneity, these oscillations continuously excite fast waves that propagate away from the centre of the simulation towards the boundary. These oscillations are identified by their decreasing amplitude inside the inhomogeneity (Fig. 1, right panel). However these oscillations generally remain of sufficient quality for the period to be measured and studied. This finding is consistent with the analytical estimation obtained in Terradas et al. (2005) for the long-wavelength (kxd ≪ 1) oscillations in a slab with a step-function profile of the Alfvén speed. Using Eqs. ((12)–(14)) from Terradas et al. (2005), and converting to the notation used in this study:  (13)where τD is the decay time of the oscillations, P is the period, and ωI and ωR are the imaginary and real parts of the oscillation frequency, respectively. Thus, the oscillation quality can be estimated as:
(13)where τD is the decay time of the oscillations, P is the period, and ωI and ωR are the imaginary and real parts of the oscillation frequency, respectively. Thus, the oscillation quality can be estimated as:  (14)Thus, Eq. (14) with δ = 0.5 gives Q = π. Our numerical results give, e.g. Q ≈ 4.02 for δ = 0.5, α = 8 and kx = 1. These two numbers are sufficiently close to each other. The small discrepancy should be attributed to the finite wavelength and finite smoothness of the profile, used in the numerical simulations.
(14)Thus, Eq. (14) with δ = 0.5 gives Q = π. Our numerical results give, e.g. Q ≈ 4.02 for δ = 0.5, α = 8 and kx = 1. These two numbers are sufficiently close to each other. The small discrepancy should be attributed to the finite wavelength and finite smoothness of the profile, used in the numerical simulations.
 |
Fig. 3 Comparison of the variation of period of these oscillations against longitudinal wavelength in the slab and cylindrical cases, both curves have values of α = 6 and δ = 0.5, the dotted line represents the cylindrical case (Nakariakov et al. 2012), the solid line represents the slab. The thick straight line shows P = λ/CA∞, that is the cutoff separating the trapped and leaky regimes. The thinner straight line shows P = λ/CA0 which corresponds to the short wavelength asymptote. |
Moreover, thus far sausage oscillations have been identified in the microwave and hard X-ray emission generated in the impulsive phase of solar flares (see Nakariakov & Melnikov 2009 for details). The observations do not show any evidence of the exponential damping, and their duration is determined by the duration of the impulsive phase of the flare. Our simulations show that the decay time in a number of cases is significantly longer than several periods of oscillation. This makes the damping time non-detectable in the observations limited by the duration of the impulsive phase of the flare. In this study we concentrate only on the dependence of the sausage oscillation period on the parameters of the problem, and do not discuss further the oscillation quality and the damping time. This limitation is similar to that implemented in Nakariakov et al. (2012).
For ease of visualisation the following normalisations were used: the spatial units are normalised such that the half-width of the inhomogeneity, d = 1, the temporal units were d/CA∞ where CA∞ = 1 is the external Alfvén speed. By order of magnitude, the half-width could be about 1 Mm, and the external Alfvén speed is about 2–3 Mm/s.
3. Results
Figure 2 shows the dependence of the sausage oscillation period on the wavelength for different density ratios. This figure extends the results obtained in Pascoe et al. (2007b) on the case of long wavelengths. It shows that, similarly to the cylindrical case, the sausage oscillation period becomes gradually independent of the wavelength. This figure is the slab equivalent to Fig. 3 in Nakariakov et al. (2012). Edwin & Roberts (1983) showed that the sausage oscillation exists as a trapped oscillation when CA0<ω/kx<CA∞. These are indicated by the straight lines on the plot, as such any oscillation to the right of the thick straight line is therefore leaky, and any to the left are trapped. It is consistent with the conclusion drawn for step-function profiles, that the same qualitative behaviour is observed in the slab geometry as in the cylindrical geometry (Edwin & Roberts 1982, 1983). Moreover, this similarity remains valid in the leaky regime too. For a given density ratio δ, the period P increases monotonically with the wavelength λ. For a given wavelength, a slab with a higher density ratio, in other words with a deeper well in the fast speed, oscillates with a longer period. The plot also demonstrates that the dependence saturates in the long wavelength limit for all depths of the well. This similarity with the cylindrical case is expected, as the nature of the oscillation has not changed.
An estimate for the typical period of sausage oscillations for typical coronal parameters can be obtained as follows. In a plasma slab of half-width d = 2000 km and an external Alfvén speed of CA∞ = 1000 km s-1 the normalised period Psaus ≈ 0.5d/CA∞ is about one second. For wider slabs, the period can be several times longer. This is consistent with typical observations e.g. in the radio band (e.g., Nakariakov & Melnikov 2009). Also, these typical periods are much shorter than the typical life-times of oscillating plasma non-uniformities, such as helmet streamers, flaring current sheets and supra-arcade flows.
Figure 3 shows a comparison of the dependences of the sausage oscillation period on the wavelength for the slab and cylindrical geometries, for the same profile of the transverse non-uniformity and its width. In the slab case the sausage period is longer. This result is consistent with the estimations obtained analytically in the case of the step-function profiles (Edwin & Roberts 1982, 1983) in the trapped regime. It can be illustrated, e.g., by the cut-off values of the wave numbers that are  (15)where CAe and CA0 are the Alfvén speed values outside and inside the waveguide, and d is the half-width of the waveguide (cf. the parameter d in Eq. (1)). The plasma inside and outside is taken to be of zero-β. It is clear that on the plane representing the dependence of the phase speed of the sausage mode on the longitudinal wave number the dispersion curve for a slab is situated lower than for a cylinder, when all parameters of the slab and the cylinder are the same. Thus, for the same wave number, the phase speed in the slab case is lower than in the cylinder. Hence, the sausage oscillation period in a slab is longer than in the cylinder. In the trapped regime, the quantitative difference between the slab and cylindrical cases can be readily understood. In both the cases the oscillation is confined to the non-uniformity, while in the cylindrical case this confinement is more efficient: if in the slab case the energy outside the slab decreases exponentially, in the cylindrical case such an exponential decrease has the additional 1/r-factor, where r is the transverse coordinate. Our results show that this behaviour is also seen in the leaky regime, and in non-uniformities with smooth transverse profiles.
(15)where CAe and CA0 are the Alfvén speed values outside and inside the waveguide, and d is the half-width of the waveguide (cf. the parameter d in Eq. (1)). The plasma inside and outside is taken to be of zero-β. It is clear that on the plane representing the dependence of the phase speed of the sausage mode on the longitudinal wave number the dispersion curve for a slab is situated lower than for a cylinder, when all parameters of the slab and the cylinder are the same. Thus, for the same wave number, the phase speed in the slab case is lower than in the cylinder. Hence, the sausage oscillation period in a slab is longer than in the cylinder. In the trapped regime, the quantitative difference between the slab and cylindrical cases can be readily understood. In both the cases the oscillation is confined to the non-uniformity, while in the cylindrical case this confinement is more efficient: if in the slab case the energy outside the slab decreases exponentially, in the cylindrical case such an exponential decrease has the additional 1/r-factor, where r is the transverse coordinate. Our results show that this behaviour is also seen in the leaky regime, and in non-uniformities with smooth transverse profiles.
Figure 4 shows the dependence of the sausage oscillation period on the steepness of the transverse profile, α, for a fixed value of the parameter δ. Each of the lines represents a fixed value of kx, for the line kx = 0.4 the oscillations are leaky for all values of α, for kx = 1.4 the oscillations are trapped for all values of α, and for kx = 0.7 the oscillations are leaky for values of α lower than 2.5, yet trapped for larger α. As expected for any given value of α a smaller value of kx, and hence longer longitudinal wavelength, results in a larger period of oscillation. This can be understood by considering the oscillations as a wave packet trapped inside the potential well of the fast magnetoacoustic speed, being reflected or refracted off the walls at either side, whilst also travelling along the well. As the longitudinal wavelength increases the effective distance between two reflections increases, resulting in the increase in the wave period.
 |
Fig. 4 Dependence of the period of trapped sausage oscillations on the steepness index, α, for different wave numbers: kx = 0.4 shown by the solid line, kx = 0.7 shown by the dotted line, and kx = 1.4 by the dashed line. The solid line stops where the oscillation becomes too leaky to accurately measure the period. For all the curves, the value of the parameter δ was fixed as 0.8. The period is measured in normalised units, equal to d/CA∞, where d is the slab half-width and CA∞ is the Alfvén speed outside the slab. |
For a fixed longitudinal wave number kx a larger value of α, and hence a steeper potential well, also results in a longer period of oscillations. Again this can be understood by considering the oscillation as a wave packet trapped in the potential well. In this case the distance between points of reflection is not changing, however the mean wave speed along the path is changing, and is higher for smaller values of α. To understand this consider two cases, firstly where α → ∞, and secondly α< ∞. For α → ∞, CA(r) = CA0 everywhere in −d<r<d (Eq. (2)). Thus, everywhere inside the potential well the speed has its minimal value. But, for a smooth profile with α< ∞, the value CA(r) is higher than CA0 = CA(r = 0) for all values of r except at the very axis of the slab, r = 0. Hence, the transverse travel time between two reflections decreases, decreasing the wave period.
Figure 5 shows the dependence of the cutoff wave number on the depth of the potential well in the slab geometry. The cutoff is defined as the value of the longitudinal wave number kc at which the oscillations transition from being trapped to leaky. For the cutoff wave number, the phase speed of the sausage mode equals to the Alfvén speed outside the slab, CAe. Thus, at the cut-off, the sausage oscillation period is  (16)It is evident that for all values of the steepness parameter α, the cutoff value of the longitudinal wave number increases with the increase in the Alfvén speed at the axis of the slab (i.e. at the bottom of the potential well). This result can be readily understood, as it is easier for the waves to escape the shallower potential well. Also, the cutoff wave number increases with the decrease in the steepness parameter α, as a smoother transverse profile is more suitable for fast wave leakage.
(16)It is evident that for all values of the steepness parameter α, the cutoff value of the longitudinal wave number increases with the increase in the Alfvén speed at the axis of the slab (i.e. at the bottom of the potential well). This result can be readily understood, as it is easier for the waves to escape the shallower potential well. Also, the cutoff wave number increases with the decrease in the steepness parameter α, as a smoother transverse profile is more suitable for fast wave leakage.
In Fig. 5, we also show the cutoff values determined analytically in the case of a step-function profile (Edwin & Roberts 1982). The analytical results are slightly different from the results obtained numerically in the case α → ∞. This small discrepancy can be attributed to the intrinsic difficulties in the determination of the cut-off value numerically: the transition from the trapped to leaky regimes is rather smooth and is not easy to determine precisely. However, the numerical results show the main tendency very well, and hence are reliable. In general, our results show that in a slab, as well as in a cylinder (Nakariakov et al. 2012), the steeper and deeper wells of the fast magnetoacoustic speed confine sausage oscillations to a greater degree.
Figure 6 shows a comparison of the cutoff longitudinal wave numbers calculated analytically and obtained numerically for both cylindrical and slab geometries, cf. Fig. 5. There is a good agreement between the analytical values and those obtained numerically for both the cylindrical and the slab geometries.
It is evident that the cutoff longitudinal wavenumber is larger in the cylindrical geometry than in the slab geometry, hence these oscillations are better confined in a cylindrical waveguide than a slab.
 |
Fig. 5 Dependence of the cutoff longitudinal wave number of a sausage oscillation on the internal Alfvén speed (and hence the potential well depth) for a fixed value of the external Alfvén speed and for different values of α. The long dashed line corresponds to α = 2, the triple-dot dashed line to α = 4, the dot dashed line to α = 6, the dashed line to α = 8, the dotted line to α = 10 and the solid line shows the step-function profile, i.e. α → ∞. The diamonds are the values for the cutoff in the case of a step-function profile, obtained analytically. The internal Alfvén speed is normalised such that the external Alfvén speed, CAe = 1, and the wavenumber is normalised such that the characteristic width of the slab, d = 1. |
 |
Fig. 6 Comparison of the variation in the cutoff longitudinal wave number with the internal Alfvén speed, in the slab and cylindrical cases with the step-function profiles, α → ∞. The solid line represents the numerically calculated values in the slab case, and the diamonds the analytical values; the dotted line represents the numerically calculated values in the cylindrical case (Nakariakov et al. 2012), and the crosses the analytical values. |
4. Conclusions
We considered sausage modes of a plasma slab stretched along the magnetic field, considering the effect of the smooth transverse profile of the fast magnetoacoustic speed. The slab could contain a thin (much thinner than the transverse size of the slab) current sheet with an anti-parallel magnetic field at its centre. Our attention is restricted to the case of waves propagating along the magnetic field in the zero-β plasma. In this case, a localised increase in the density of the plasma results in a localised decrease in the Alfvén speed, and hence in the fast magnetoacoustic speed. A localised decrease in the fast magnetoacoustic speed makes the slab a fast magnetoacoustic waveguide. Both trapped and leaky regimes of the oscillations were studied. It was found that sausage mode of the slabs have, in general, the same properties as sausage modes of plasma cylinders, studied in Nakariakov et al. (2012). Our results can be summarised as follows:
-
1.
Both leaky and trapped regimes of sausage oscillations can bereadily excited by an initial impulsive driver. The leaky regimeoccurs for longitudinal wavelengths longer than the trappedregime.
-
2.
In the trapped regime, the sausage oscillation period grows with the increase in the longitudinal wavelength. In the leaky regime, the dependence of the period on the wavelength experiences saturation, and the period becomes independent of the wavelength. In the leaky regime the period is always longer than in the trapped regime.
-
3.
In a plasma cylinder and a slab of the same half-width and the same parameters of the transverse profiles of the fast magnetoacoustic speed, the sausage oscillation period in the slab is always longer than in the cylinder. The difference can reach 50%.
-
4.
In slabs with steeper transverse profiles of the fast magnetoacoustic speed, the sausage oscillation periods are longer.
-
5.
For a given depth of the potential well, smoother profiles of the fast magnetoacoustic speed (with a smaller value of the parameter α), have bigger values of the cutoff longitudinal wave numbers. The cutoff values separate the leaky and trapped regimes.
-
6.
For the same potential wells, the cutoff wave numbers in a cylinder are always larger than in a slab.
In the presence of the current sheet at the centre of the slab the results remain the same, as our formalism in this case remains exactly the same. Indeed, the presence of the current sheet causes a singularity at the centre of the slab, that does not affect the sausage oscillations that have zero transverse flows at the slab centre and hence do not “feel” the singularity.
We would like to stress that both leaky and trapped regimes of sausage oscillations of plasma slabs in the solar corona are observed well, as the quality of leaky oscillations can be high. Also, results obtained for a slab can be applied to coronal current sheets, provided the magnetic field at either sides of the sheet is anti-parallel.
Acknowledgments
This work is supported by the European Research Council under the SeismoSun Research Project No. 321141, the Russian Foundation of Basic Research under grant 13-02-00044, and the BK21 plus program through the National Research Foundation (NRF) funded by the Ministry of Education of Korea (VMN). C.H. is supported by a studentship from the UK Science and Technology Facilities Council.
References
- Antolin, P., & Van Doorsselaere, T. 2013, A&A, 555, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cally, P. S. 1986, Sol. Phys., 103, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Cooper, F. C., Nakariakov, V. M., & Tsiklauri, D. 2003, A&A, 397, 765 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Costa, A. 2011, Plasma Physics and Controlled Fusion, 53, 074006 [NASA ADS] [CrossRef] [Google Scholar]
- De Moortel, I., & Nakariakov, V. M. 2012, Roy. Soc. London Phil. Trans. Ser. A, 370, 3193 [Google Scholar]
- Edwin, P. M., & Roberts, B. 1982, Sol. Phys., 76, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Edwin, P. M., & Roberts, B. 1983, Sol. Phys., 88, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Gruszecki, M., Nakariakov, V. M., & Van Doorsselaere, T. 2012, A&A, 543, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Inglis, A. R., van Doorsselaere, T., Brady, C. S., & Nakariakov, V. M. 2009, A&A, 503, 569 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jelínek, P., & Karlický, M. 2012, A&A, 537, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karlický, M., Mészárosová, H., & Jelínek, P. 2013, A&A, 550, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kopylova, Y. G., Melnikov, A. V., Stepanov, A. V., Tsap, Y. T., & Goldvarg, T. B. 2007, Astron. Lett., 33, 706 [NASA ADS] [CrossRef] [Google Scholar]
- Mossessian, G., & Fleishman, G. D. 2012, ApJ, 748, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Murawski, K., & Roberts, B. 1993, Sol. Phys., 144, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Murawski, K., & Roberts, B. 1994, Sol. Phys., 151, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Nakariakov, V. M., & Melnikov, V. F. 2009, Space Sci. Rev., 149, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Nakariakov, V. M., & Roberts, B. 1995, Sol. Phys., 159, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Nakariakov, V. M., Melnikov, V. F., & Reznikova, V. E. 2003, A&A, 412, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakariakov, V. M., Hornsey, C., & Melnikov, V. F. 2012, ApJ, 761, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Ogrodowczyk, R., & Murawski, K. 2006, Sol. Phys., 236, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Ogrodowczyk, R., & Murawski, K. 2007, A&A, 461, 1133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pascoe, D. J., Nakariakov, V. M., & Arber, T. D. 2007a, Sol. Phys., 246, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Pascoe, D. J., Nakariakov, V. M., & Arber, T. D. 2007b, A&A, 461, 1149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pascoe, D. J., Nakariakov, V. M., Arber, T. D., & Murawski, K. 2009, A&A, 494, 1119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roberts, B., Edwin, P. M., & Benz, A. O. 1984, ApJ, 279, 857 [NASA ADS] [CrossRef] [Google Scholar]
- Rosenberg, H. 1970, A&A, 9, 159 [NASA ADS] [Google Scholar]
- Scott, R. B., Longcope, D. W., & McKenzie, D. E. 2013, ApJ, 776, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, J. M., Roberts, B., & Oliver, R. 1997, A&A, 327, 377 [NASA ADS] [Google Scholar]
- Srivastava, A. K., Zaqarashvili, T. V., Uddin, W., Dwivedi, B. N., & Kumar, P. 2008, MNRAS, 388, 1899 [NASA ADS] [CrossRef] [Google Scholar]
- Stepanov, A. V., Zaitsev, V. V., & Nakariakov, V. M. 2012, Physics Uspekhi, 55, A260000 [Google Scholar]
- Su, J. T., Shen, Y. D., Liu, Y., Liu, Y., & Mao, X. J. 2012, ApJ, 755, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Terradas, J., Oliver, R., & Ballester, J. L. 2005, A&A, 441, 371 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vasheghani Farahani, S., Hornsey, C., Van Doorsselaere, T., & Goossens, M. 2014, ApJ, 781, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Verwichte, E., Nakariakov, V. M., & Cooper, F. C. 2005, A&A, 430, L65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zaitsev, V. V., & Stepanov, A. V. 1982, Sov. Astron. Lett., 8, 132 [NASA ADS] [Google Scholar]
- Zaitsev, V. V., & Stepanov, A. V. 2008, Physics Uspekhi, 51, 1123 [Google Scholar]
All Figures
 |
Fig. 1 Time-distance plots of transverse flows in sausage oscillations. Left panel: example of a trapped sausage oscillation in a plasma slab with the parameters: δ = 0.8 and α = 6 for the wave number kx = 1.5. Right panel: example of a leaky sausage oscillation in a plasma slab with the parameters: δ = 0.7 and α = 6, for kx = 0.4. The spatial coordinate is normalised such that the half-width of the slab, d = 1, and the time is measured in the units d/CA∞, where d is the slab half-width and CA∞ is the Alfvén speed outside the slab. |
| In the text | |
 |
Fig. 2 Variation of the sausage oscillation period with the wavelength in a plasma slab with α = 6, for different values of δ: the solid line corresponds to δ = 0.5, the triple dot-dashed line corresponds to δ = 0.7, the dashed line to δ = 0.8, and the dot-dashed line to δ = 0.9. The thick straight line shows P = λ/CAe, that is the cutoff separating the trapped and leaky regimes. The thinner straight lines show P = λ/CA0 that correspond to the short wavelength asymptote in each case. |
| In the text | |
 |
Fig. 3 Comparison of the variation of period of these oscillations against longitudinal wavelength in the slab and cylindrical cases, both curves have values of α = 6 and δ = 0.5, the dotted line represents the cylindrical case (Nakariakov et al. 2012), the solid line represents the slab. The thick straight line shows P = λ/CA∞, that is the cutoff separating the trapped and leaky regimes. The thinner straight line shows P = λ/CA0 which corresponds to the short wavelength asymptote. |
| In the text | |
 |
Fig. 4 Dependence of the period of trapped sausage oscillations on the steepness index, α, for different wave numbers: kx = 0.4 shown by the solid line, kx = 0.7 shown by the dotted line, and kx = 1.4 by the dashed line. The solid line stops where the oscillation becomes too leaky to accurately measure the period. For all the curves, the value of the parameter δ was fixed as 0.8. The period is measured in normalised units, equal to d/CA∞, where d is the slab half-width and CA∞ is the Alfvén speed outside the slab. |
| In the text | |
 |
Fig. 5 Dependence of the cutoff longitudinal wave number of a sausage oscillation on the internal Alfvén speed (and hence the potential well depth) for a fixed value of the external Alfvén speed and for different values of α. The long dashed line corresponds to α = 2, the triple-dot dashed line to α = 4, the dot dashed line to α = 6, the dashed line to α = 8, the dotted line to α = 10 and the solid line shows the step-function profile, i.e. α → ∞. The diamonds are the values for the cutoff in the case of a step-function profile, obtained analytically. The internal Alfvén speed is normalised such that the external Alfvén speed, CAe = 1, and the wavenumber is normalised such that the characteristic width of the slab, d = 1. |
| In the text | |
 |
Fig. 6 Comparison of the variation in the cutoff longitudinal wave number with the internal Alfvén speed, in the slab and cylindrical cases with the step-function profiles, α → ∞. The solid line represents the numerically calculated values in the slab case, and the diamonds the analytical values; the dotted line represents the numerically calculated values in the cylindrical case (Nakariakov et al. 2012), and the crosses the analytical values. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


