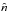| Issue |
A&A
Volume 566, June 2014
|
|
|---|---|---|
| Article Number | A21 | |
| Number of page(s) | 15 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201423881 | |
| Published online | 02 June 2014 | |
Populations of rotating stars
III. SYCLIST, the new Geneva population synthesis code
1
Astrophysics group, EPSAM, Keele University,
Lennard-Jones Labs,
Keele,
ST5 5BG,
UK
e-mail:
c.georgy@keele.ac.uk
2
Centre de Recherche Astrophysique de Lyon, École Normale
Supérieure de Lyon, 46 allée d’Italie, 69384
Lyon Cedex 07,
France
3
Geneva Observatory, University of Geneva,
Maillettes 51,
1290
Sauverny,
Switzerland
Received:
25
March
2014
Accepted:
22
April
2014
Context. Constraints on stellar models can be obtained from observations of stellar populations, provided the population results from a well defined star formation history.
Aims. We present a new tool for building synthetic colour–magnitude diagrams of coeval stellar populations. We study, from a theoretical point of view, the impact of axial rotation of stars on various observed properties of single-aged stellar populations: magnitude at the turnoff, photometric properties of evolved stars, surface velocities, surface abundances, and the impact of rotation on the age determination of clusters by an isochrone fitting. One application to the cluster NGC 663 is performed.
Methods. Stellar models for different initial masses, metallicities, and zero-age main sequence (ZAMS) rotational velocities are used for building interpolated stellar tracks, isochrones, and synthetic clusters for various ages and metallicities. The synthetic populations account for the effects of the initial distribution of the rotational velocities on the ZAMS, the impact of the inclination angle and the effects of gravity and limb darkening, unresolved binaries, and photometric errors. Interpolated tracks, isochrones, and synthetic clusters can be computed through a public web interface.
Results. For clusters with a metallicity in the range [0.002, 0.014] and an age between 30 Myr and 1 Gyr, the fraction of fast rotators on the main sequence (MS) band is the largest just below the turnoff. This remains true for two different published distributions of the rotational velocities on the ZAMS. This is a natural consequence of the increase in the MS lifetime due to rotation. The fraction of fast rotators one magnitude below the turnoff also increases with the age of the cluster between 30 Myr and 1 Gyr. The most nitrogen-rich stars are found just below the turnoff. There is an increase in the fraction of enriched stars when the metallicity decreases. We show that the use of isochrones computed from rotating stellar models with an initial rotation that is representative of the average initial rotation of the stars in clusters provides a reasonable estimate of the age, even though stars in a real cluster did not start their evolution with an identical initial rotation.
Key words: stars: general / stars: evolution / stars: rotation / stars: fundamental parameters / galaxies: star clusters: general / Hertzsprung-Russell and C-M diagrams
© ESO, 2014
1. Introduction
Populations of coeval stars such as those found in many open clusters in the Galaxy and the Magellanic Clouds represent an excellent benchmark to sample of stars with identical initial composition and age. The morphology of the distribution of stars in the colour–magnitude diagrams (CMDs) provides both very interesting constraints on stellar models and a way to obtain the age of the population, although of course ages are still model dependent.
Our aim in the present work is twofold. On the one hand, we present the new tool SYCLIST (for SYnthetic CLusters, Isochrones, and Stellar Tracks), which was developed to produce single-aged stellar populations built on recently published grids of stellar models (Ekström et al. 2012; Georgy et al. 2013a,b). This tool will be improved in the future, allowing non-coeval populations to be described. It is presently partially available through a web interface1. On the other hand, we present applications for investigating various effects. Among them we study the impact of the dispersion in the initial rotational velocities on the age determinations through the isochrone method. We also quantify the effects of gravity and limb darkening on the photometric appearance of a cluster. To our knowledge, these two darkening effects (or brightening, depending on the inclination) are for the first time accounted for in the building of CMDs. We discuss where the fast rotators and nitrogen-rich stars are located in clusters of various ages and metallicities. A complete discussion that includes the whole parameter space (age, metallicity, velocity, and inclination distributions, presence or not of the gravity- or limb-darkening, of unresolved binaries, calibrations between effective temperature-colours and bolometric corrections, accounting for photometric noise) is beyond the scope of this paper that aims only at approaching the impact these effects and their interplay might have on synthetic stellar populations. We eventually compare the output of the present tool with the cluster NGC 663 and show that a reasonable description of observed data can be achieved.
The SYCLIST code operates on the following stellar models libraries:
-
the large grids of models covering most of the stellar mass domain (between 0.8 and 120 M⊙), with two different initial equatorial velocities (Veq,ini/Vcrit = 0 and 0.4), and two metallicities: Z = 0.014 (solar metallicity, Ekström et al. 2012) and Z = 0.002 (SMC metallicity, Georgy et al. 2013a);
-
the grids centred on the B-type star mass domain (between 1.7 and 15 M⊙) with nine different initial rotation rates between Ωini/ Ωcrit = 0 and 0.95 (where
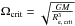 and Re,crit the equatorial radius when the
star rotates at the angular velocity Ωcrit) at three metallicities: Z = 0.014,
Z =
0.006 (LMC metallicity) and Z = 0.002 (Georgy et al. 2013b);
and Re,crit the equatorial radius when the
star rotates at the angular velocity Ωcrit) at three metallicities: Z = 0.014,
Z =
0.006 (LMC metallicity) and Z = 0.002 (Georgy et al. 2013b); -
in addition to the two previous sets of models, the online version also includes the grid of non-rotating stellar models from Mowlavi et al. (2012), with a very fine mesh covering the mass domain between 0.5 and 3.5 M⊙ and 6 metallicities between Z = 0.006 and Z = 0.04.
- 1.
Interpolated single stellar models: interpolated tracks are provided for any choice of the initial mass, metallicity, and equatorial rotational velocity. The range of allowed values are determined by the choice of the library;
- 2.
Isochrones: isochrones are computed with a given initial metallicity and rotational velocity;
- 3.
Synthetic coeval stellar populations: synthetic clusters of single-aged stellar populations are built, offering various optional settings for the initial distributions of the velocities (Huang & Gies 2006; Huang et al. 2010, Dirac) and of the inclination angles (random or Dirac), for the account for the gravity and limb darkening (von Zeipel 1924; Espinosa Lara & Rieutord 2011; Claret 2000). The effect of unresolved binaries and photometric noise can also be added. Various calibrations for the transformation of the theoretical quantities (luminosities and effective temperatures) to the observed magnitudes and colours can be used (see Sect. 2.3.4);
- 4.
Time evolution of star count: in this mode, the code computes the evolution of the relative numbers of various types of stars (spectral types, blue-, yellow-, and red-supergiants, Wolf-Rayet subtypes, stars in a given rotation rate range, etc.) as a function of time.
2. Description of the population synthesis code
Whatever the chosen output, the SYCLIST code relies on its ability to interpolate between existing stellar tracks. For this purpose, the electronic tables provided by the Geneva group (and used as input libraries in SYCLIST) are formatted as follows (see Ekström et al. 2012, for more details): 400 points (hereafter time-models) are extracted from a complete computed sequence of a few tens of thousands time-models. These 400 time-models are chosen carefully in order to fully describe the morphology of the tracks in the theoretical Hertzsprung-Russell diagram (HRD) ensuring that reasonable interpolations may be made between time-models having the same number in these tables.
2.1. Interpolated stellar tracks
In order to obtain an evolutionary track for a star with a given initial metallicity, mass and rotational rate ω, we perform linear interpolations3, first in ω, then in mass and finally in metallicity, using the 8 closest surrounding models in the chosen database. The models by Ekström et al. (2012), and Mowlavi et al. (2012) can be interpolated among various masses and metallicities. In addition, interpolation in ω is available for the grids by Georgy et al. (2013b), since these feature a dense coverage of initial rotation rates.
In case an extrapolation4 has to be performed, and for quantities that have a limited range of possible values or a threshold, such as the chemical abundances, the rotation rate, the mass-loss rates, etc., the interpolated values are constrained to not overstep the limit (for example, if the interpolated value of the central hydrogen abundance is −0.003, this value is reset to 0.0).
If the SYCLIST code is launched in the mode “interpolated stellar model”, an output is generated at this step and is formatted to be identical to the electronic tables described in Ekström et al. (2012). This tool is useful to attribute a mass and an age to a single star whose position in the HRD or in the MV versus B-V plane is known.
Obviously, an interpolated model represents only an approximation of a rigorously computed stellar model. In Sect. 3.1, we present examples of interpolated tracks and discuss their reliability when confronted to the computed tracks.
2.2. Isochrone building
An isochrone at a given age t is computed by interpolating a set of stellar models with initial mass in the range [Mmin,Mmax] with Mmin the minimal mass in the models library and Mmax the maximal mass of the stars that are still in a nuclear burning phase at time t. In a second step, all the pertinent quantities are obtained by performing for each interpolated model a new linear interpolation along the log (t) axis.
In “Isochrone” mode, the outputs of SYCLIST provide all the surface quantities of the stellar models (log (L/L⊙), log (Teff), magnitude, colours, abundances, rotation characteristics,...).
2.3. Synthetic clusters
To build synthetic clusters, we assume that each star is characterised by the following physical properties: its initial mass, metallicity, and rotational velocity, the inclination axis between the axis of rotation and the direction of the observer (i = 0 in case of a star seen pole-on, see Fig. 1), its age, the presence or absence of an unresolved companion5. For each star of the cluster, the initial mass, rotational velocity, and inclination angle is determined through a random draw performed in such a way that it follows the desired distribution6. In addition, calibration functions are needed to translate theoretical quantities (luminosity and effective temperature) into observed ones (magnitude and colour), and some uncertainties in the magnitudes and colours might be accounted for. In the following, we explain all the options that are implemented in the SYCLIST code for these settings.
 |
Fig. 1 Schematic representation of a meridional cut of a rotating star. The plane shown
contains the line connecting the centre of the star to the observer and the
rotational axis. In the text, the angle i is called the inclination angle
(i =
0 when the star is seen pole-on). A given point on the surface is
defined by the angle θ that we call the colatitude in the text. Note
that in a deformed rotating star, the unit vector perpendicular to the surface
|
2.3.1. The initial mass function, the initial distribution of rotational velocities and of inclinations
In the current version of SYCLIST, only the initial mass function (IMF) from Salpeter (1955), described by a power-law function with an index α = −2.35, has been implemented. Even though Salpeter’s work is almost 60 years old, newer and more complex IMFs found by other authors still show that this index is valid in the range of stellar masses considered in this work (see Kroupa 2002). This justifies the use in the present work of the simplest expression by Salpeter (1955). In the future, the code will offer a choice of various IMFs.
Four distributions of rotational velocities are currently implemented:
- 1.
the simplest distribution, is a Dirac distribution δ(ω), with ω between 0 and 1. The quantity ω is equal to Ωini/ Ωcrit where Ω is the surface angular velocity. With this distribution, it is possible to build a synthetic cluster (or isochrones) in which all the stars have the same ω on the ZAMS. This simple distribution is very practical to study the effect of rotation in stellar clusters, in particular when rapid rotators are considered;
- 2.
a uniform distribution with ω between 0 and 1 is also implemented. Although this distribution is certainly not a physical one, it allows to study the effect of the other parameters change, like the change of the angle of view of the star and also the effect of the age on the angular velocity distribution;
- 3.
from the literature, we get the Huang & Gies (2006) distribution, established from the observation of 496 galactic OB stars of the field and clusters of different ages;
- 4.
Huang et al. (2010) propose a distribution of rotational velocities for B stars. By measuring the projected velocity Vsin(i) of 220 young galactic B stars, they made a simple polynomial fit of the histogram data of Vsin(i) /Vcrit and then used a deconvolution algorithm to derive the distribution of Veq/Vcrit. They obtained a rotational velocity distribution for young stars for three ranges of masses: low mass (2 M⊙ ≤ M < 4 M⊙), middle mass (4 M⊙ ≤ M < 8 M⊙) and high mass range (M ≥ 8 M⊙).
For rotating stars, in particular if they are fast rotators, the inclination angle under which the star is seen will affect the observed temperature and luminosity due to gravity darkening. The angle of view is drawn from the following distributions:
-
1.
a Dirac one, with an open choice for the angle;
-
2.
a sin(i) probability;
2.3.2. Gravity-darkening effect and impact of inclination
The luminosity that we obtain from our evolutionary tracks, LMOD, is the bolometric power emitted by the star in all directions. We define the effective temperature given by our models by Teff, MOD = (LMOD/(σΣ))1/4, where σ is the Stefan-Boltzmann constant and Σ the actual total surface of the star.
LMOD is a theoretical quantity. Observations give access to the power emitted by the star in only one direction, that of the observer. In case the star emits radiation isotropically, a measurement along any direction is equivalent, and, from the measurement in one direction, the total luminosity of the star can be correctly estimated. However, when the emission is not isotropic, not all directions are equivalent. In this case, from a measurement in a given direction, the estimation of the luminosity, assuming isotropy, LMES, is different from LMOD.
Teff,MOD as defined above is the
theoretical surface averaged effective temperature. In case the star presents variations
of its temperature over its surface, the integration of the local radiative flux
(proportional to 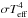 where
where
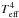 is the
local effective temperature) would still be equal to LMOD.
Observationally, the effective temperature of a star is obtained by spectroscopy or
through colours that are measured on the hemisphere facing the observer. Again, in case
of isotropy, any hemisphere is equivalent and such a measurement provides the effective
temperature of the star. In case of anisotropy, one has only access to Teff,MES =
(LMES/ (σΣp))1 /4, where Σp is the projected surface of the star on a plane
perpendicular to the line of sight. In order to generate observational quantities, we
first need to link LMES to LMOD and
Teff,MES to Teff,MOD.
is the
local effective temperature) would still be equal to LMOD.
Observationally, the effective temperature of a star is obtained by spectroscopy or
through colours that are measured on the hemisphere facing the observer. Again, in case
of isotropy, any hemisphere is equivalent and such a measurement provides the effective
temperature of the star. In case of anisotropy, one has only access to Teff,MES =
(LMES/ (σΣp))1 /4, where Σp is the projected surface of the star on a plane
perpendicular to the line of sight. In order to generate observational quantities, we
first need to link LMES to LMOD and
Teff,MES to Teff,MOD.
There is evidence indicating that the surface of a rotating star is, at least as a first approximation, well described by the Roche Model (e.g. Domiciano de Souza et al. 2003). In this model, the ratio of the equatorial radius to the polar radius of the star depends on ω, and is greater for more rapidly rotating stars. For the most rapidly rotating stars (ω> 0.7), the equatorial radius becomes significantly larger than the polar radius. As a consequence, the effective gravity of rotating stars with a radiative surface is latitude dependent. Because there is a relation between geff and Teff (von Zeipel 1924; Espinosa Lara & Rieutord 2011), the effective temperature is also latitude dependent (see e.g. Maeder 1999). The poles of a rotating star are hotter than the equatorial regions, which turn out to be cooler and less bright. This temperature and brightness contrast between the poles and the equator of a rotating star is known as gravity darkening.
Due to gravity darkening, a star seen pole-on will be observed as hotter and more luminous (bluer and brighter) than it would be if seen equator-on. Therefore, the angle of view under which we observe a star will influence its location in the HRD, by modifying the inferred luminosity and effective temperature.
The luminosity inferred by an observer in a direction d inclined
by an angle i with respect to the rotation axis is:
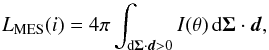 (1)with
I(θ) the specific intensity at the
colatitude θ. The integral is computed on the hemisphere that
is visible for the observer, i.e. the points of the stellar surface with
dΣ·d>
0. Assuming a black body radiation, this leads to:
(1)with
I(θ) the specific intensity at the
colatitude θ. The integral is computed on the hemisphere that
is visible for the observer, i.e. the points of the stellar surface with
dΣ·d>
0. Assuming a black body radiation, this leads to: 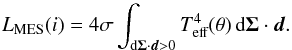 (2)LMES is thus
sensitive to the way the effective temperature is distributed over the surface. In the
SYCLIST code, two relations between Teff(θ) and the
colatitude are implemented:
(2)LMES is thus
sensitive to the way the effective temperature is distributed over the surface. In the
SYCLIST code, two relations between Teff(θ) and the
colatitude are implemented:
-
a formulation based on the von Zeipel theorem (von Zeipel 1924): in the framework of the Roche model, we have that
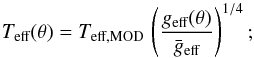 (3)
(3) -
the formulation proposed by Espinosa Lara & Rieutord (2011): their Eq. (31) can be re-written as
![\begin{eqnarray} T_\text{eff}(\theta)&=&\,T_\text{eff,MOD}\,\left( \frac{\Sigma}{4\,\pi\,R_\text{p,crit}^2} \right)^{1/4}\,\left[ \left( -\frac{1}{x^2}+\frac{8}{27}\omega^2x\,\sin^2(\theta) \right)^2\right. \notag\\ &&\left. + \left( \frac{8}{27}\omega^2x\,\sin(\theta)\cos(\theta) \right)^2 \right]^{1/8}\,\sqrt{\frac{\tan(\vartheta)}{\tan{\theta}}} \end{eqnarray}](/articles/aa/full_html/2014/06/aa23881-14/aa23881-14-eq74.png) (4)where
x =
R(θ)
/Rp,crit (with
Rp,crit the polar radius at the
critical velocity), and ϑ the solution of their Eq. (24).
(4)where
x =
R(θ)
/Rp,crit (with
Rp,crit the polar radius at the
critical velocity), and ϑ the solution of their Eq. (24).
In both cases, Teff(θ) can be
expressed as: 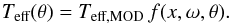 (5)In the Roche model
approximation, the shape of the stellar surface (given by the function x) only depends on
ω (e.g.
Maeder 2009). Thus, the function
f(x,ω,θ) is independent from the
stellar parameters and only depends on geometrical considerations.
(5)In the Roche model
approximation, the shape of the stellar surface (given by the function x) only depends on
ω (e.g.
Maeder 2009). Thus, the function
f(x,ω,θ) is independent from the
stellar parameters and only depends on geometrical considerations.
Inserting Eq. (5) in Eq. (2) yields:
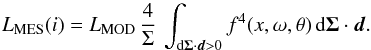 (6)Thus, the
observed luminosity of the star depends on the real luminosity corrected by a purely
geometrical factor CL(i,ω):
(6)Thus, the
observed luminosity of the star depends on the real luminosity corrected by a purely
geometrical factor CL(i,ω):
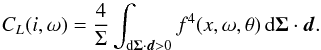 (7)This factor is
independent of the stellar parameters7.
(7)This factor is
independent of the stellar parameters7.
The observed Teff,MES is deduced by averaging the
flux on the projected stellar surface Σp:
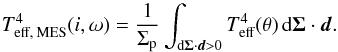 (8)Again with the
help of Eq. (5), we have:
(8)Again with the
help of Eq. (5), we have:
![\begin{equation} T_\text{eff, MES}(i,\omega) = T_\text{eff, MOD}\left[\frac{1}{\Sigma_\text{p}}\int_{\text{d}\vec{\Sigma}\cdot\vec{d} > 0} f^4(x,\omega,\theta)\,\text{d}\vec{\Sigma}\cdot\vec{d}\right]^\frac{1}{4}. \end{equation}](/articles/aa/full_html/2014/06/aa23881-14/aa23881-14-eq86.png) (9)Hence, also the
observed effective temperature is a function of average effective temperature, corrected
by the factor CTeff:
(9)Hence, also the
observed effective temperature is a function of average effective temperature, corrected
by the factor CTeff:
![\begin{equation} C_{T_\text{eff}}(i,\omega) = \left[\frac{1}{\Sigma_\text{p}}\int_{\text{d}\vec{\Sigma}\cdot\vec{d} > 0} f^4(x,\omega,\theta)\,\text{d}\vec{\Sigma}\cdot\vec{d}\right]^\frac{1}{4}.\label{Equ_CT} \end{equation}](/articles/aa/full_html/2014/06/aa23881-14/aa23881-14-eq88.png) (10)Both
CL and CTeff are
purely geometrical, and only depend on ω and i. One can therefore compute them once for
various inclinations and rotations, and use these values for performing interpolations.
(10)Both
CL and CTeff are
purely geometrical, and only depend on ω and i. One can therefore compute them once for
various inclinations and rotations, and use these values for performing interpolations.
2.3.3. Limb-darkening effect and impact of inclination
The gravity-darkening effect discussed above arises because each of the surface element has its own effective temperature. Considered alone, it is supposed that the specific intensity emitted by a surface element in a given direction does not depend on that direction. However, the atmosphere of a real star does not radiate as a true black body: the specific intensity will not be the same when the elementary surface is seen face-on or from a grazing viewing angle. Due to the structure of the atmosphere, the optical thickness is not the same along these two directions and thus the radiation received will come from more or less deep (and thus more or less warm) layers of the star. This is called the limb-darkening effect. For a uniformly bright star, it results in a dimming of the star’s disk from the centre towards the edge. To reproduce the emission from the hemisphere oriented towards us, we have to integrate the specific intensity arising from directions perpendicular to the surface in the centre of the hemisphere and directions tangent to the surface at the edge, with all the intermediate values in-between.
Let us first describe the equations used for a non-rotating star whose surface is
characterised by a single value of the effective temperature. The limb-darkening law is
expressed by ℓ(μ) = I(μ)/I(1), where I is the specific
intensity and 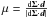 ,
the cosine of the angle between the normal to the surface and the direction towards the
observer. A value of μ =
1 corresponds to the centre of the stellar disk, whereas
μ = 0 to
the stellar edge or limb.
,
the cosine of the angle between the normal to the surface and the direction towards the
observer. A value of μ =
1 corresponds to the centre of the stellar disk, whereas
μ = 0 to
the stellar edge or limb.
To obtain the impact of this effect on the perceived luminosity we can use Eq. (1). Since the case considered here is the one
of a non-rotating star, we have that the perceived luminosity without any limb-darkening
effect would be 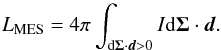 (11)The limb-darkening
effect implies that the specific intensity depends on μ. Since I(μ) =
ℓ(μ)I(1), one
can write
(11)The limb-darkening
effect implies that the specific intensity depends on μ. Since I(μ) =
ℓ(μ)I(1), one
can write 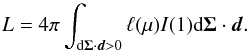 (12)To proceed, one
needs to find a relation between I(1) and the local effective temperature of the
surface element considered. For this purpose we can use the fact that the mean specific
intensity ⟨I⟩ is related to the effective temperature via the
relation
(12)To proceed, one
needs to find a relation between I(1) and the local effective temperature of the
surface element considered. For this purpose we can use the fact that the mean specific
intensity ⟨I⟩ is related to the effective temperature via the
relation 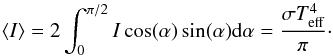 (13)It can be shown using
the definition of ℓ(μ) that
(13)It can be shown using
the definition of ℓ(μ) that
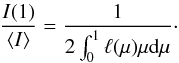 (14)Thus, replacing
I(1) by
(14)Thus, replacing
I(1) by
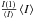 in Eq. (12), one has finally
in Eq. (12), one has finally  (15)In case there is no
limb-darkening, then ℓ(μ) = 1 and one obtains
(15)In case there is no
limb-darkening, then ℓ(μ) = 1 and one obtains
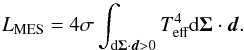 (16)Since
I is
equal to
(16)Since
I is
equal to 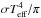 , then
one finds again Eq. (1).
, then
one finds again Eq. (1).
Following Claret (2000), we represent the
quantity ℓ(μ) by
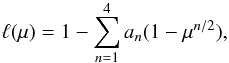 (17)where the
coefficients an depend on the
effective temperature and surface gravity of the star. In the present work, we use the
bolometric limb-darkening coefficients from the new grids of ATLAS9 models (Howarth 2011), which are given for a wide range of
surface gravities and effective temperatures.
(17)where the
coefficients an depend on the
effective temperature and surface gravity of the star. In the present work, we use the
bolometric limb-darkening coefficients from the new grids of ATLAS9 models (Howarth 2011), which are given for a wide range of
surface gravities and effective temperatures.
In the case of a rotating star, the surface gravity and Teff change with the colatitude θ. Therefore, in Eq. (12) the latitude-dependent temperature should be accounted for in the computation of the local I(1) and ⟨I⟩. However, in the range of Teff and log (g) values typical for intermediate and massive stars, ℓ(μ) does not vary much (according to the tables provided by Howarth 2011). Equation (15) thus remains valid. In this case, we take the latitude-dependent temperature of the star into account. However, we take representative values for the limb-darkening coefficients for the whole star, given by the mean Teff and log (g). In other words, we assume that I(1)/⟨I⟩ is constant over the surface.
This approach introduces only small errors: for temperatures higher than ~12 000 K, ℓ(μ) remains almost constant with Teff and varies very little with log (g). For temperatures lower than ~12 000 K, ℓ(μ) is almost independent of log (g) for all μ, albeit with a somehow stronger dependency on Teff: in this temperature domain, using Teff and a representative log (g) for the most rapidly rotating stars introduces an error in ℓ(μ) less than 10% for μ = 0.5 and less than 15% for μ = 0.1. We have to bear in mind that the current limb-darkening coefficients have been obtained for non rotating models. However, as far as we know, there does not exist a study with complete data for a broad range of Teff and log (g) for rotating models.
Then, for our rotating models with LMOD and Teff,MOD, we
obtain the limb-darkening coefficients for such a temperature and for a value of
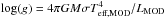 . By the mean of
Eq. (15), one obtains LMES.
Teff,MES is obtained by
. By the mean of
Eq. (15), one obtains LMES.
Teff,MES is obtained by
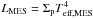 .
.
Figure 2 shows the value of the correcting factors in dex in case only gravity darkening is accounted for and in case both gravity darkening and limb darkening are taken into account. With the temperature profile given by Espinosa Lara & Rieutord (2011), a star seen pole-on becomes brighter by at most 0.2 dex, which represents an increase in about 50% in luminosity. The effective temperature appears to be higher by about 0.01 dex (2%). When the star is seen equator-on, the luminosity and the effective temperature are decreased: −0.13 dex (~−25%) and −0.01 dex (−3%) respectively. Also the limb-darkening effect reinforces the effect of gravity darkening particularly for fast rotation, and for stars seen pole- or equator-on. For instance, in the example presented in Fig. 2 for an object with Teff = 25 000 K and log (g) = 3.5 seen pole-on, the correction factors for luminosity and effective temperature become 0.21 dex (60%) and 0.01 dex (3%), respectively. For the same object seen equator-on, these values become −0.15 dex (− 30%) and −0.02 dex (−5%). Accounting for gravity-darkening alone (with either von Zeipel 1924 or Espinosa Lara & Rieutord 2011 prescription), or gravity- and limb-darkenening together is optional in SYCLIST.
 |
Fig. 2 Logarithm of the correcting factors for the effective temperature (left panels) and luminosity (right panels) as a function of ω and of the inclination angle i, with the gravity-darkening law by Espinosa Lara & Rieutord (2011). Top panels: gravity-darkening alone. Centre panels: gravity- and limb-darkening for Teff = 25 000 K and log (g) = 3.5. Bottom panels: same as middle panels for Teff = 5000 K and log (g) = 0.0. |
2.3.4. Calibration functions
A colour-Teff calibration and bolometric correction is required in order to transform our theoretical HRD to a CMD. SYCLIST offers two different choices:
- 1.
the calibrations used in the old grids (Schaller et al. 1992): for the MS stars (luminosity class V), the calibration relation between the effective temperature Teff and the colour index B − V is taken from Boehm-Vitense (1981), the bolometric correction from Malagnini et al. (1986) and the UBV relation from Schmidt-Kaler (1982); for giant type III and supergiant type Ia star, the Teff versus B − V relation and the bolometric correction are taken from Flower (1977), and the UBV relation from Schmidt-Kaler (1982);
- 2.
the newer colour-temperature calibration for stars proposed by Worthey & Lee (2011).
2.3.5. Binary population and photometric noise
The available libraries rely on single star tracks at the moment and thus do not account for the evolution of interacting binary systems8. However, it is possible to mimic the presence of unresolved binaries. The position of an unresolved binary depends on the mass of the primary and on the mass ratio. Once the mass of the primary star is set, the mass of the companion star is determined by a uniform random draw between 0.1 and 1 time the mass of the primary. The luminosity and the flux in the various filters of each component of the binary are summed. Because it is not easy to attribute a Teff to the pair, we assume that the Teff of the binary system is equivalent to that of the primary9.
Note that in case the mass of the secondary is lower than the minimal mass of the grid of stellar models used for the generation of the synthetic cluster, the star is tagged as a binary, but the secondary is not interpolated, and the fluxes are not corrected (only the flux of the primary is accounted for). In the HRD (or CMD), this produces a double tail near the lower limit of the IMF (one composed by the single stars and by the binaries for which only one component is accounted for, and the second composed by the binary with a mass-ratio close to one). As one moves towards higher mass, the gap between the two tails is progressively filled with binaries with various mass ratio. The fraction of unresolved binaries is an optional parameter of the code.
The photometric data of an observed cluster contains noise, which broadens the main sequence. In order to simulate the noise in the observed CMD, it is possible to add a Gaussian noise (parametrised by a typical standard deviation σ in the magnitude MV and the colour index B − V) to all the stars of the synthetic cluster.
 |
Fig. 3 To illustrate the accuracy of the interpolation, we compare a 7 M⊙ model with ωini = 0.5 (red solid curve) obtained by interpolation between 5 M⊙ (black) and 9 M⊙ (blue) models of identical ωini with the “real” 7 M⊙ model (red dashed curve) from Georgy et al. (2013b). |
 |
Fig. 4 Evolutionary tracks for 7 M⊙ stellar models at Z = 0.014 for various initial rotation rates, when the effects of gravity-darkening are accounted for. The blue dotted lines show the track for a star seen pole-on (i = 0°). The solid black and dashed red lines show the tracks with i = 45°, respectively 90° (equator-on). |
2.4. Evolution of star count ratios
The aim of the “star count” mode is to predict the fraction of different types of stars as a function of the age given a fiducial (e.g. a mass interval) for normalisation. The initial and final times between which the evolution is computed are an input for this option of the code. Then, a time step array is generated that ranges from the initial to the final time with a time step Δt.
Another input is the number of mass (m) and rotation rate (n) cells to be considered. Then, we have m + 1 values of initial mass, equally spaced in mass and n + 1 values of initial rotation rates equally spaced as well.
The four vertex given by (Mk,ωj), (Mk,ωj + 1), (Mk + 1,ωj), (Mk + 1,ωj + 1), with k between 1 and m and j between 1 and n define a box. For each box, we assign the average value for the mass Mk + 1/2 = (Mk + Mk + 1) /2. The fraction FM of stars over the total population with a mass between Mk and Mk + 1 is given by the IMF, as described in a previous section. For this box of mass Mk + 1 /2 we have a fraction Fω of stars with initial rotational rates between ωj and ωj + 1, given by the assumed initial velocity distribution. In this way, the fraction of stars over the total population in each box at the ZAMS is given by FM × Fω.
Then, the evolution of each box is characterised by the evolution of a model of mass Mk + 1/2, and its initial rotational rate ωj + 1/2. At each time step, we count in the different boxes the number of stars of a given type, taking into account that stars of a certain mass disappear at that age (e.g. explode as a supernova).
The quantities of interest for following throughout the evolution of a synthetic population include: the fraction of stars of a certain spectral type, such as B type stars (defined here as objects with effective temperatures between 10 000 K and 30 000 K), the fraction of stars rotating above a certain rotation rate (e.g. ω > 0.8), supergiant stars (with luminosities higher than 104.9 L⊙), red supergiant stars (RSG, with effective temperatures lower than 103.66 K) or the fraction of Be stars (which we consider to be dependent of the effective temperature, following Cranmer 2005, as explained in Granada et al. 2013).
3. Results
3.1. On single stellar models
We first check that interpolations of the tracks provide reasonable results by comparing tracks computed by the Geneva stellar evolution code with tracks obtained by interpolations of neighbouring tracks. An example of such an interpolation is shown on Fig. 3, where we compare a 7 M⊙ model at Z = 0.014 with an initial rotation rate ωini = 0.5 obtained by interpolation between a 5 M⊙ and a 9 M⊙ model with the same initial rotation rate, with a model that was rigorously computed with the Geneva stellar evolution code. We see that the MS and the HRD crossing, as well as the red supergiant (RSG) branch are well reproduced. For features depending on complex physical processes such as the blue loop, the interpolation provides less accurate results.
 |
Fig. 5 Analogous to Fig. 4 for blue loops. The shaded area represents the Cepheid instability strip according to Tammann et al. (2003). |
As explained in Sect. 2.3.2, tracks may be shifted in luminosity and effective temperature due to the gravity darkening effect. An illustration of this effect (with the temperature law by Espinosa Lara & Rieutord 2011) is shown in Fig. 4. As expected, tracks seen pole-on are more luminous and hotter than tracks seen equator-on (the effect of limb darkening is not accounted for here). The effect remains quite modest up to ωini = 0.5. Indeed the shift between the extreme points at the red turnoff at the end of the MS phase are at most of 0.005 dex in effective temperature and 0.04 dex in luminosity. At ωini = 0.95, the corresponding shifts are much larger: 0.027 dex in log (Teff) and 0.28 dex in log (L/L⊙).
In the plane MV versus B − V, these shifts are different. In this range of effective temperatures, B − V shows a very weak dependence on log (Teff) and thus the differences in effective temperature in the most extreme case (ωini = 0.95) will correspond to a change of only 0.002 dex in B − V (for values of B − V around − 0.18). The shift in MV is 0.105 dex for ωini = 0.50 and 0.668 dex for ωini = 0.95.
During the blue loops, the gravity darkening effect might also be noticeable, because the stars contract and their surface is thus accelerated, as illustrated in Fig. 5. However ω does not reach extreme values and the shift remains lower than what is seen during the MS. Up to ωini = 0.70, the shift increases for increasing ωini. For higher initial values, the maximal ω reached during the loop is similar, which explains the saturation of the gravity darkening effect that appears in Fig. 5 for the highest ωini.
In Fig. 6, the effect of limb-darkening has been added. It is barely visible on the MS for the relatively slowly rotating model shown in the left panel. It is more pronounced for the more rapid rotator shown in the right panel. The limb-darkening effect strengthens the effect of gravity darkening (see also Fig. 2). Indeed, when the star is seen pole-on, the brightest regions of the star are seen perpendicularly, which tends to increase the observed flux. The opposite is true when the star is seen equator-on.
3.2. On isochrones
Isochrone fitting is the most common technique of inferring the age of an observed cluster. It is thus interesting to study how the initial distribution of velocities among the cluster stars and the random orientation of the inclination angle impact the age determination via this method. We also study the way isochrones computed from a rotating stellar population differ with isochrones computed from non-rotating models.
In Fig. 7, we show isochrones in the MV versus B-V plane and in the log (L/L⊙) versus log (Teff) plane. These isochrones are computed assuming stars with an identical ωini. This is of course not realistic, although the isochrones corresponding to ωini = 0.3 and 0.5 should encompass most of the observed stars. Note that in “Isochrone” mode, the effects of gravity darkening are not taken into account.
The isochrones corresponding to initially fast rotating stars have turnoff at a higher luminosity and in general at a bluer colours than isochrones computed from slowly or non-rotating models. Comparing MV at the turnoff for the isochrones with ωini = 0.1 and 0.7, the difference amounts to 0.4 dex at log (t) = 7.2 and to 0.55 dex at log (t) = 9.0. At very high rotation (ωini = 0.95), the tracks may be shifted to the right (in cooler regions) because hydrostatic effects become dominant with respect to the mixing effect in the mass range considered.
 |
Fig. 7 Isochrones for various ages computed from stellar models with a Dirac initial velocity distribution. The initial velocities are indicated on the upper right panel. The mass at the turnoff for the logarithm of the ages of 7.2, 8.0 and 9.0 are around 12, 5 and 2 M⊙, respectively. |
3.3. On synthetic stellar clusters
In contrast to isochrones, synthetic CMDs account for the fact that a stellar population is not only composed of stars of various masses but also of stars with different initial rotation velocities and angles of view.
In this section, we use our population synthesis code as an instrument to analyse single-aged stellar populations from a purely theoretical point of view. The main questions we intend to address are the following: how does the velocity distribution evolve as a function of time? How does the inclusion of rotation impact the determination of the ages and of the mass at the turnoff? What is the impact of different distributions of initial rotation? How do gravity and limb-darkening distort the CMDs? Are the initially rapid rotators located in a peculiar place in the cluster CMD? Where are the most rapid rotators? Where are the nitrogen-enriched stars? What are the effects of stochasticity on the appearance of a given CMD cluster? How do the above properties change when the age increases?
3.3.1. Evolution of the velocity distribution
In this section, we study how the distribution of rotational velocities varies in clusters of different ages. To reduce the effects of stochasticity, we consider a population initially composed of 10 000 stars, distributed within the mass range 1.7 to 15 M⊙ according to a Salpeter’s IMF.
The first row of Fig. 8 (panels a, b, c) shows the time evolution of the distribution of rotational velocities between 10 Myr and 1 Gyr when the initial rotation velocity distribution by Huang et al. (2010) is used at solar metallicity (Z = 0.014). In panel a, the initial masses of stars span the whole mass interval between 1.7 and 15 M⊙. In panels b and c, the mass interval is reduced to respectively [1.7,5.7] and [1.7,2.4], due to the fact that more massive stars progressively disappear. Between 10 and 100 Myr, the maximum velocity of the distribution decreases and the peak of the distribution shifts toward a lower velocity. This is a quite general trend that comes from the decrease of the rotation rate occuring at the very beginning of the evolution (see for instance Fig. 6 in Georgy et al. 2013b or Granada et al. 2013). This effect depopulates the high velocity end of the distribution (Veq ≳ 300 km s-1). At 100 Myr, this braking has affected almost the whole mass range of the cluster. In addition, the strong braking that occurs after the end of the MS when the star evolves to become a red (super)giant progressively populates the very low velocity end of the distribution.
The second row of Fig. 8 (panels d, e, f) shows the same velocity distribution evolution at a lower metallicity Z = 0.002. The global trend is similar, except that there are generally more rapid rotators. Indeed the Huang et al. (2010) initial velocity distribution is given in terms of Vini/Vcrit which corresponds to slightly higher velocities when the metallicity decreases (the stars are more compact at low Z). In the 1 Gyr panel (f), the distribution becomes double-peaked. Two causes are identified: first, at this age, only the lowest mass stars are still on the MS, and in this mass range Veq increases during the MS (in contrast with the Z⊙ case). Second, rapid rotation significantly increases the MS duration in this mass domain, and for a given mass only the most rapid rotators are still on the MS.
The third row of Fig. 8 (panels g, h, i) shows the results obtained when the velocity distribution of Huang & Gies (2006) is used as the initial one. This distribution favours the moderate rotators. In particular, the peak of the velocity distribution at an age of 10 Myr is shifted from a value of approximately 280 km s-1 to a value of 150 km s-1 and the overall distribution is flatter than the one obtained with the Huang et al. (2010) initial velocity distribution.
The bottom row (panels j, k, l) shows the same distribution as shown in panels a, b, and c, albeit for a cluster with an initial number of stars of 400. This illustrates the impact of stochastic effects on the distribution, which is to produce fluctuations. However the general trends are preserved, and show that a few hundred stars provide a sufficient sampling for obtaining a good description of the velocity distribution.
 |
Fig. 8 Distribution of surface equatorial velocities in a cluster at three different ages (first column: 10 Myr, second column: 100 Myr, and third column: 1 Gyr). Top row (panels a), b), c)): Z⊙ cluster with the initial velocity distribution from Huang et al. (2010, see their Fig. 6). Second row (panels d), e), f)): same as above, but at Z = 0.002. Third row (panels g), h), i)): same as top row, but with the initial velocity distribution from Huang & Gies (2006). Bottom row (panels j), k), l)): same as top row but for a total number of stars of 400 instead of 10 000. |
3.3.2. Synthetic colour–magnitude diagram for a 100 Myr cluster
We first compute a synthetic cluster with 400 stars in the mass range between 1.7 and 15 M⊙ and an age of 100 Myr at Z⊙. The initial velocity distribution is the one from Huang et al. (2010), and the inclination angles follow a random distribution. The cluster contains 30% of unresolved binaries, following the result by Oudmaijer & Parr (2010)10. A Gaussian noise in the visible magnitudes and colours with standard deviation of 0.15 mag and 0.10 mag, respectively, has been added. We used the calibrations between colour, bolometric corrections and effective temperatures given by Worthey & Lee (2011).
 |
Fig. 9 Synthetic CMD for a 100 Myr old cluster at Z⊙, computed with the initial velocity distribution of Huang et al. (2010). A Gaussian noise with a standard deviation of 0.15 mag in MV and 0.1 mag in B − V has been added. Different characteristics are indicated by different symbols. Multiplicity: single stars (circles) or unresolved binaries (triangles); velocity: current ω< 0.85 (red), or ω ≥ 0.85 (blue), with filled symbols for ωini ≥ 0.85; inclination angle: i ≥ 70° (horizontal stroke), i < 10° (vertical stroke), intermediate inclinations (diagonal stroke); surface chemical enrichment: (N/C)/(N/C)ini ≥ 3 (surrounding square). The labelled stars are listed in Table 1. |
Figure 9 shows the CMD of this cluster. Fast rotators are more frequent towards the turnoff of the cluster sequence than below, along the MS band. Typically, in the magnitude range between −1 and −2, the total number of stars is 18. Among these, 5 stars have an ω > 0.85 (28% of the sample). Between the magnitudes 0 and − 1, there are 13 fast rotators among a total of 69 stars (18%). Indeed, rotation enhances the MS lifetime of a given initial mass star and increases its luminosity. This favours fast rotators in the upper part of the MS band.
Among the 18 fast rotators present in the whole CMD, all began their evolution with an initial fast rotation (ωini > 0.85).
The random angle distribution implies that very few stars will be seen pole-on. Actually, between the magnitudes 0 and − 2, only 1 star is seen nearly pole-on (i < 10°) and 33 stars are seen equator-on (i ≥ 70°) among a total of 87 stars.
All significantly nitrogen-enriched stars are either at the turnoff or evolved post-MS stars. The MS stars with a N/C greater than 3 times the initial ratio span the range of values between 3.1 (star M)11 and 6.4 (star P). Among the post-MS stars, the N/C enhancement factor lies between 1.8 (star 3) and 22.7 (star 6). Stars 2 and 5 lie nearly in the same position of the HRD, although their N/C ratios differ greatly. The enrichment in star 2 (8.5) is mainly due to the dredge-up process with only a small contribution from the rotational mixing, since it has ωini = 0.30. The star 5, on the other hand, has ωini = 0.68, which explains the much higher enhancement factor (16.9). There is no clear correlation between the actual surface velocity and the nitrogen enrichment. Other effects like the initial mass, and hence the evolutionary phase, produce some dispersion. The behaviour of the N/O and 12C/13C is generally the same as N/C. This is due to the fact that both of these ratio are affected by H burning via the CNO cycle, and thus follow the same trend as the N/C ratio.
Due to rotation, there is some overlap between the mass range of stars in the upper part of the MS band and the mass range of post-MS stars. The minimum initial mass of the post-MS stars is 5.16 M⊙ (star 1) and its maximum value is 5.51 M⊙ (star 9). On the MS band, the maximum mass is 5.24 M⊙ (star P). Thus the mass range between 5.16 and 5.24 M⊙ can be found both on the MS band and in the post-MS phases, depending on initial rotation. For instance, star P, which is still on the MS band, was initially a rapid rotator (ωini = 0.94), while star 2, which is an evolved star with roughly the same initial mass, was initially a slowly rotating star (ωini = 0.30).
Were this synthetic cluster an observed one, how would the age determination by the isochrone fitting method be impacted by not considering some of the effects mentioned in Sect. 2.3?
 |
Fig. 10 Same cluster as Fig. 9 with isochrones superimposed. Left panel: isochrones computed from non-rotating models. Right panel: isochrones computed from rotating models with Vini/Vcrit = 0.4. |
In Fig. 10 (left panel), isochrones obtained from non-rotating models are superimposed to the same cluster as in Fig. 9. The isochrone corresponding to the actual age of the cluster does not fit the magnitude of the turnoff. An isochrone at younger age (log (t) ≲ 7.8) would provide a better fit. However, the inferred age of the cluster would be younger by 40% than the true one. Moreover the mass at the turnoff for the Vini = 0 isochrone at log (t) = 7.8 is 5.8 M⊙, while the actual masses of stars at the turnoff (I, M, O, P) are between 4.8 and 5.2 M⊙.
When isochrones obtained from rotating models are used (Fig. 10, right panel), the situation is improved. However, the turnoff magnitude of the correct isochrone (log (t) = 8.0) is still fainter than the more luminous MS star of the cluster, and the best fit is provided by the log (t) = 7.9 isochrone, which underestimates the true age of the cluster by 20%. Figure 11, which presents the same cluster without photometric noise, shows that the age discrepancy remains and is thus mostly due to the rotational mixing acting inside star P.
Note that the isochrones were built from models with only one Vini/Vcrit (the average rotation rate Vini/Vcrit = 0.4). The extreme stars are not expected to be reproduced. However, as our grids of rotating stellar models were calibrated in order to match the observed features at solar metallicity (see Ekström et al. 2012), we expect the isochrones built from these models to give the best account for the clusters.
Figure 12 shows two clusters with the same characteristics as the one presented in Fig. 9, but where all stars are initially rapid rotators (ωini = 0.95) and are seen either pole-on (left panel) or equator-on (right panel), so that the impact of gravity- and limb-darkening is maximised. As expected, the turnoff is brighter by about 0.9 dex in MV in the pole-on cluster than in the equator-on one. Since these synthetic CMDs result from two different draws, stochastic effects produce some scatter, but the general trend is clear. Of course, this is an upper limit value due to the very extreme cases considered here. In B − V, there is also a shift, but it is so small that it is drowned in the photometric noise.
 |
Fig. 11 Same synthetic cluster as the one shown in Fig. 9 but where the photometric errors have been removed. |
 |
Fig. 12 Synthetic cluster with similar characteristics as the one shown in Fig. 9, but where all the stars began their evolution with ωini = 0.95. Isochrones for various initial rotation velocities and for an age of log (t) = 8 are also shown. Left panel: all stars are seen pole-on. Right panel: all stars are seen equator-on. |
 |
Fig. 13 Same synthetic cluster as the one shown in Fig. 9 but with a different initial distribution of the velocities (see text). |
The velocity distribution of Huang et al. (2010) has been obtained from young stars, and thus is convenient to be used as an initial velocity distribution in SYCLIST. Huang & Gies (2006) have also proposed a Veq distribution12, and it is interesting to weight the impact of the use of a different distribution (Fig. 13).
Table 2 presents the counts of MS stars in a given magnitude interval for the clusters computed with each velocity distribution. N⋆(0.85) counts the number of stars rotating with ω > 0.85. In the MV interval [−2.25, −1], the counts are rather similar for the two distributions, and thus the fraction of rapid rotators is about the same (~30%). In the interval [−1,0], the fraction of rapid rotators drops for both distribution. However, the drop is less steep for the Huang et al. (2010) distribution (18.8% against 7.5% for Huang & Gies 2006). Indeed, stars with a mass below 4 M⊙ appear in this magnitude interval, and in the Huang et al. (2010) work, the velocity distribution for the mass range 2−4 M⊙ peaks at higher velocity than the distribution for higher masses.
3.3.3. Synthetic colour-magnitude diagrams for different ages and metallicities
Figure 14 presents the CMD of various clusters for different ages and metallicities. The symbols are the same than in Fig. 9.
The turnoff of the isochrone is brighter at Z = 0.014 than at Z = 0.002. Since stars at lower metallicity are more luminous, we would expect the turnoff to be brighter. However, they have also shorter lifetimes, so the mass at the turnoff at a given age is lower at Z = 0.002 (MTO,100 Myr = 4.8 M⊙) than at Z⊙ (MTO,100 Myr = 5.2 M⊙). For clusters, it is less clear, because velocity and angle dispersions as well as noise blur the picture.
Generally, the fraction of rapid rotators among stars located one magnitude below the turnoff increases with increasing age. At log (t) = 7.2, there are no rapid rotators brighter than MV = −2. At log (t) = 8.0, the fraction is around 30−35%. At log (t) = 9.0 and Z⊙, this trend continues (45%). For the same age at Z = 0.002, the minimal mass of stars one magnitude below the turnoff drops below 1.7 M⊙, which is the minimal mass for the cluster, so the value obtained (28%) is not reliable. There is no clear trend with metallicity for the two ages where the populations are complete.
At Z⊙, the fraction of stars with (N/C)/(N/C)ini ≥ 3 decreases with age. The opposite trend applies at Z = 0.002. This is expected since at low Z, even low-mass stars get a surface enrichment strong enough to reach values higher than 3, while at solar metallicty, the lowest mass never reach such a level (see Fig. 8 in Georgy et al. 2013b). As time proceeds, the low-mass stars become the dominant population in clusters, explaining why the fraction of stars with (N/C)/(N/C)ini ≥ 3 increases with age at Z = 0.002.
As expected (see Georgy et al. 2013a), the evolved stars are shifted to bluer colours in low metallicity clusters.
For young clusters, it is very difficult to determine an age from isochrones in MV vs. B − V based only on the turnoff, because the stars remain at constant B − V for a while after the MS, extending from the turnoff13. For older clusters, the crossing of the CMD occurs immediately after the turnoff, making the age determination more obvious. In all cases (but particularly for young clusters), the presence of evolved stars is a great help to constrain the best fitting isochrone.
3.4. On the evolution of stellar count
Figure 15 shows the time evolution of the fraction of B stars with a rotational rate ω higher than 0.8, the fraction of early B stars with rate ω ≥ 0.80, as well as the RSG and yellow supergiants (YSG)14, normalised to the total number of B stars. This figure, corresponding to Z = 0.014, shows that the observation of different stellar groups could be helpful to constrain the age of a cluster15. It is unlikely to find RSG stars in clusters with an age below 14 or above 30 Myr. They are expected to be found only in massive clusters, with hundreds of B-type stars. Such clusters are also expected to host tens of rapidly rotating B-type stars, as observed by Marco & Negueruela (2013) in the case of the massive star cluster NGC 7419. In less massive clusters, RSG stars are expected to be very rare. In general, RSGs will be always more numerous than YSGs.
This mode of “star count evolution” for SYCLIST was also used in Granada et al. (2013) to study the time-evolution of Be populations in single-aged clusters.
 |
Fig. 15 Time evolution of different kinds of stellar populations, normalised to the total amount of B type stars at each time: B-type stars rotating with ω ≥ 0.80 (blue line), early B-type stars (cyan line) and early B-type stars rotating with ω ≥ 0.80 (green line), RSGs (red line), and YSGs (yellow line). |
 |
Fig. 16 Left panel: CMD of NGC 663. Black dots are the field stars from Pigulski et al. (2001). Red circles are cluster members with Hα photometry, blue circles are Be stars and magenta squares red giant stars that are confirmed cluster members (Mermilliod et al. 2008). Right panel: synthetic cluster of an age of log (t) = 7.3. Red points indicate stars with Teff higher than 10 000 K. Blue circles represent stars with ω > 0.8 and magenta squares stars with log (Teff) < 3.66. Isochrones at an age of log (t) = 7.3 are drawn (Vini/Vcrit = 0.40: solid lines, non-rotating: dashed lines). |
4. Application of SYCLIST to NGC 663 – a Be star-rich open cluster hosting red giant stars
Even though it is beyond the scope of the present article to make an extensive analysis of observed stellar populations, we present in this section an example demonstrating the potential of SYCLIST in the study of different stellar populations and dating of open clusters.
Pigulski et al. (2001) presented BV(RI)cHα of the central region of the open cluster NGC 663, covering 14 × 20 arcmin2. Their Hα photometry, complete down to magnitude Rc = 15.4 (corresponding to A5 spectral type for cluster members), allowed them to detect all the stars presenting Hα emission in B-type range, and to distinguish non-cluster stars which contaminate the field of NGC 663. They identified 392 cluster members with Rc ≤ 15.4, from which 26 are Hα emitters of spectral type B, identified thus as Be stars.
Figure 16 (left panel) shows the CMD of the stars in the above-mentioned field. We produced several synthetic clusters at various ages, assuming a Salpeter (1955) IMF and Huang et al. (2010) initial velocity distribution. They contain the same amount of stars in the B-type range as observed in NGC 663 by Pigulski et al. (2001). We considered in this case that the errors in colour and magnitude increase with increasing V, as obtained from the observations by these authors. The cluster at log (t) = 7.3 (20 Myr) appears to better describe the characteristics of NGC 663. This cluster is plotted in Fig. 16 (right panel), assuming a normal extinction law, E(B − V) = 0.83, and a true distance modulus of 11.6 mag (Pigulski et al. 2001). Isochrones at log (t) = 7.3, with and without rotation, are also shown.
Different authors obtain different ages between 10 and 30 Myr for NGC 663 (e.g. Pigulski et al. 2001; Pandey et al. 2005). As mentioned in the previous section, the expected fraction of RSG reaches a maximum value around 18 Myr. At this age, the fraction NRSG/NB-type = 1% (see Fig. 15). This implies an expected number of 2−6 RSGs in such a cluster. The observed value (2) is well in that range. NGC 663 exhibits also a relatively large fraction of Be stars below the turnoff. However, the Be stars at higher magnitudes are not expected in the framework of our models. At detailed study is deferred to a forthcoming paper.
NGC 663 exhibits also a relatively large fraction of rapid rotators, which is well in line with the findings of the previous section.
Even though our synthetic cluster has a remarkable resemblance to the observed one in Fig. 16, and the study of the evolution of stellar populations allows us to understand the presence of different stellar populations in the CMD at different ages, such as RSG stars or populations of rapidly rotating stars, there are some observed features that remain uncertain. The presence of blue supergiant stars is not an unusual feature in a cluster of this age, and 5 such BSGs are observed in NGC 663. However, their presence cannot be explained with our single stellar population synthesis. They could originate from the merger of stars in binary systems, or be rapidly rotating more massive stars that are not accounted for in this study (see Schneider et al. 2014).
5. Conclusions
We present the SYCLIST code, a new tool for interpolating between stellar tracks, building isochrones, creating synthetic clusters, and following the evolution of stellar populations. It includes an IMF, various initial velocity and viewing angle distributions, and is able to account for the gravity- and limb-darkening. The binary fraction and a photometric noise are additional options for the outputs of the “Synthetic cluster” mode.
In this paper we explain how these effects are implemented in the code, and study to which extent they impact the aspects of stellar tracks, isochrones, and synthetic clusters. We also study typical synthetic clusters at various ages and metallicities, and discuss their main features.
We briefly present the potential use of the SYCLIST code in comparison with observed clusters. More extensive studies and comparisons will be the subject of a forthcoming paper.
SYCLIST performs extrapolations, if models with initial rotation rates higher than 0.95 (maximal ω in Georgy et al. (2013b) are requested.
This list is obviously not exhaustive, and we consider here only the physical properties that we implemented in our grids of stellar models or in the SYCLIST code. Other physical processes, such as internal magnetic fields, or surface magnetic braking, could be added by using specific stellar tracks libraries.
The conversion from the original Veq distribution to a ω distribution is done in Ekström et al. (2008).
Acknowledgments
The authors thank the anonymous referee for her/his positive comments and constructive suggestions. C.G. acknowledges support from the European Research Council under the European Union’s Seventh Framework Programme (FP/2007-2013)/ERC Grant Agreement n. 306901.
References
- Boehm-Vitense, E. 1981, ARA&A, 19, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Claret, A. 2000, A&A, 363, 1081 [NASA ADS] [Google Scholar]
- Cranmer, S. R. 2005, ApJ, 634, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Domiciano de Souza, A., Kervella, P., Jankov, S., et al. 2003, A&A, 407, L47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ekström, S., Meynet, G., Maeder, A., & Barblan, F. 2008, A&A, 478, 467 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ekström, S., Georgy, C., Eggenberger, P., et al. 2012, A&A, 537, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Espinosa Lara, F., & Rieutord, M. 2011, A&A, 533, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Flower, P. J. 1977, A&A, 54, 31 [NASA ADS] [Google Scholar]
- Georgy, C., Ekström, S., Eggenberger, P., et al. 2013a, A&A, 558, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Georgy, C., Ekström, S., Granada, A., et al. 2013b, A&A, 553, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Granada, A., Ekström, S., Georgy, C., et al. 2013, A&A, 553, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Howarth, I. D. 2011, MNRAS, 413, 1515 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, W., & Gies, D. R. 2006, ApJ, 648, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, W., Gies, D. R., & McSwain, M. V. 2010, ApJ, 722, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2002, Science, 295, 82 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Maeder, A. 1999, A&A, 347, 185 [NASA ADS] [Google Scholar]
- Maeder, A. 2009, Physics, Formation and Evolution of Rotating Stars (Springer) [Google Scholar]
- Malagnini, M. L., Morossi, C., Rossi, L., & Kurucz, R. L. 1986, A&A, 162, 140 [NASA ADS] [Google Scholar]
- Marco, A., & Negueruela, I. 2013, A&A, 552, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mermilliod, J. C., Mayor, M., & Udry, S. 2008, A&A, 485, 303 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mowlavi, N., Eggenberger, P., Meynet, G., et al. 2012, A&A, 541, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oudmaijer, R. D., & Parr, A. M. 2010, MNRAS, 405, 2439 [NASA ADS] [Google Scholar]
- Pandey, A. K., Upadhyay, K., Ogura, K., et al. 2005, MNRAS, 358, 1290 [NASA ADS] [CrossRef] [Google Scholar]
- Pigulski, A., Kopacki, G., & Kołaczkowski, Z. 2001, A&A, 376, 144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Schaller, G., Schaerer, D., Meynet, G., & Maeder, A. 1992, A&AS, 96, 269 [Google Scholar]
- Schmidt-Kaler, T. 1982, in The Landolt-Börnstein Database – Numerical Data and Functional Relationships in Science and Technology, Stars and Star Clusters, eds. K. Schaifers, & H. H. Voigt (Berlin/Heidelberg: Springer-Verlag), 2b, 451 [Google Scholar]
- Schneider, F. R. N., Izzard, R. G., de Mink, S. E., et al. 2014, ApJ, 780, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Tammann, G. A., Sandage, A., & Reindl, B. 2003, A&A, 404, 423 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- von Zeipel, H. 1924, MNRAS, 84, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Worthey, G., & Lee, H.-C. 2011, ApJS, 193, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Schematic representation of a meridional cut of a rotating star. The plane shown
contains the line connecting the centre of the star to the observer and the
rotational axis. In the text, the angle i is called the inclination angle
(i =
0 when the star is seen pole-on). A given point on the surface is
defined by the angle θ that we call the colatitude in the text. Note
that in a deformed rotating star, the unit vector perpendicular to the surface
|
| In the text | |
 |
Fig. 2 Logarithm of the correcting factors for the effective temperature (left panels) and luminosity (right panels) as a function of ω and of the inclination angle i, with the gravity-darkening law by Espinosa Lara & Rieutord (2011). Top panels: gravity-darkening alone. Centre panels: gravity- and limb-darkening for Teff = 25 000 K and log (g) = 3.5. Bottom panels: same as middle panels for Teff = 5000 K and log (g) = 0.0. |
| In the text | |
 |
Fig. 3 To illustrate the accuracy of the interpolation, we compare a 7 M⊙ model with ωini = 0.5 (red solid curve) obtained by interpolation between 5 M⊙ (black) and 9 M⊙ (blue) models of identical ωini with the “real” 7 M⊙ model (red dashed curve) from Georgy et al. (2013b). |
| In the text | |
 |
Fig. 4 Evolutionary tracks for 7 M⊙ stellar models at Z = 0.014 for various initial rotation rates, when the effects of gravity-darkening are accounted for. The blue dotted lines show the track for a star seen pole-on (i = 0°). The solid black and dashed red lines show the tracks with i = 45°, respectively 90° (equator-on). |
| In the text | |
 |
Fig. 5 Analogous to Fig. 4 for blue loops. The shaded area represents the Cepheid instability strip according to Tammann et al. (2003). |
| In the text | |
 |
Fig. 6 Same as in Fig. 4, with the addition of the effect of limb-darkening (dashed lines). |
| In the text | |
 |
Fig. 7 Isochrones for various ages computed from stellar models with a Dirac initial velocity distribution. The initial velocities are indicated on the upper right panel. The mass at the turnoff for the logarithm of the ages of 7.2, 8.0 and 9.0 are around 12, 5 and 2 M⊙, respectively. |
| In the text | |
 |
Fig. 8 Distribution of surface equatorial velocities in a cluster at three different ages (first column: 10 Myr, second column: 100 Myr, and third column: 1 Gyr). Top row (panels a), b), c)): Z⊙ cluster with the initial velocity distribution from Huang et al. (2010, see their Fig. 6). Second row (panels d), e), f)): same as above, but at Z = 0.002. Third row (panels g), h), i)): same as top row, but with the initial velocity distribution from Huang & Gies (2006). Bottom row (panels j), k), l)): same as top row but for a total number of stars of 400 instead of 10 000. |
| In the text | |
 |
Fig. 9 Synthetic CMD for a 100 Myr old cluster at Z⊙, computed with the initial velocity distribution of Huang et al. (2010). A Gaussian noise with a standard deviation of 0.15 mag in MV and 0.1 mag in B − V has been added. Different characteristics are indicated by different symbols. Multiplicity: single stars (circles) or unresolved binaries (triangles); velocity: current ω< 0.85 (red), or ω ≥ 0.85 (blue), with filled symbols for ωini ≥ 0.85; inclination angle: i ≥ 70° (horizontal stroke), i < 10° (vertical stroke), intermediate inclinations (diagonal stroke); surface chemical enrichment: (N/C)/(N/C)ini ≥ 3 (surrounding square). The labelled stars are listed in Table 1. |
| In the text | |
 |
Fig. 10 Same cluster as Fig. 9 with isochrones superimposed. Left panel: isochrones computed from non-rotating models. Right panel: isochrones computed from rotating models with Vini/Vcrit = 0.4. |
| In the text | |
 |
Fig. 11 Same synthetic cluster as the one shown in Fig. 9 but where the photometric errors have been removed. |
| In the text | |
 |
Fig. 12 Synthetic cluster with similar characteristics as the one shown in Fig. 9, but where all the stars began their evolution with ωini = 0.95. Isochrones for various initial rotation velocities and for an age of log (t) = 8 are also shown. Left panel: all stars are seen pole-on. Right panel: all stars are seen equator-on. |
| In the text | |
 |
Fig. 13 Same synthetic cluster as the one shown in Fig. 9 but with a different initial distribution of the velocities (see text). |
| In the text | |
 |
Fig. 14 Synthetic CMD for various ages and metallicities. The symbols are the same as in Fig. 9. |
| In the text | |
 |
Fig. 15 Time evolution of different kinds of stellar populations, normalised to the total amount of B type stars at each time: B-type stars rotating with ω ≥ 0.80 (blue line), early B-type stars (cyan line) and early B-type stars rotating with ω ≥ 0.80 (green line), RSGs (red line), and YSGs (yellow line). |
| In the text | |
 |
Fig. 16 Left panel: CMD of NGC 663. Black dots are the field stars from Pigulski et al. (2001). Red circles are cluster members with Hα photometry, blue circles are Be stars and magenta squares red giant stars that are confirmed cluster members (Mermilliod et al. 2008). Right panel: synthetic cluster of an age of log (t) = 7.3. Red points indicate stars with Teff higher than 10 000 K. Blue circles represent stars with ω > 0.8 and magenta squares stars with log (Teff) < 3.66. Isochrones at an age of log (t) = 7.3 are drawn (Vini/Vcrit = 0.40: solid lines, non-rotating: dashed lines). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.