HTTP_Request2_Exception Unable to connect to tcp://think-ws.ca.edps.org:85. Error: php_network_getaddresses: getaddrinfo failed: Name or service not known A PCA-based automated finder for galaxy-scale strong lenses | Astronomy & Astrophysics (A&A)
EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 566 (June 2014) A&A, 566 (2014) A63 Full HTML
Free Access
Issue
A&A
Volume 566, June 2014
Article Number A63
Number of page(s) 10
Section Numerical methods and codes
DOI https://doi.org/10.1051/0004-6361/201423365
Published online 17 June 2014

© ESO, 2014

1. Introduction

With the many ongoing or planned sky surveys taking place in the optical and near-infrared, gravitational lensing has become a major scientific tool for studying the properties of massive structures on all spatial scales. On the largest scales, in the weak regime, gravitational lensing constitutes a crucial cosmological probe (e.g. Heymans et al. 2013; Frieman et al. 2008). On smaller scales, weak galaxy-galaxy lensing allows us to study the extended halo of individual galaxies or of groups of galaxies (e.g. Simon et al. 2012) and to constrain cosmology (e.g. Mandelbaum et al. 2013; Parker et al. 2007).

In the strong regime, when multiple images of a lensed source are seen, gravitational lensing offers an accurate way to weigh galaxy clusters (Bartelmann et al. 2013; Hoekstra et al. 2013; Meneghetti et al. 2013; Kneib & Natarajan 2011, for reviews), galaxy groups (e.g. Foëx et al. 2013; Limousin et al. 2009), and individual galaxies (e.g. Brownstein et al. 2012; Treu et al. 2011; Bolton et al. 2006). However, all the strongly lensed systems known today, combined together, represent only hundreds of objects. Wide field surveys have the potential to produce samples that are three orders of magnitude larger, allowing us to study statistically dark matter and its evolution in galaxies as a function, say, of morphological type, mass, stellar, and gas contents (see Gavazzi et al. 2012; Ruff et al. 2011; Sonnenfeld et al. 2013b,a). For example, Pawase et al. (2012) predicts that a survey like Euclid1 will find at least 60 000 galaxy-scale strong lenses. To find and to use them efficiently, it is vital to devise automated finders that can produce samples of lenses with high completeness and purity and with a well defined selection function. The lenses of Pawase et al. (2012) are source-selected. There is no volume-limited sample of lens-selected systems, so the number of 60 000 systems is only given here as an estimate of how many objects future wide-field surveys will have to deal with.

Several automated robots exist to find strong lenses. Among the best ones are Arcfinder (Seidel & Bartelmann 2007), which was developed primarily to find large arcs behind clusters and groups, and the algorithm by Alard (2006) used by Cabanac et al. (2007) and More et al. (2012) to look for arcs produced by individual galaxies and groups in the CFHT Strong Lensing Legacy Survey. Other automated robots consider any galaxy as a potential lens and predict where lensed images of a background source should be before trying to identify them on the real data (Marshall et al. 2009). To detect lenses with small Einstein radii or with faint rings, most of these algorithms rely on foreground lens subtraction (e.g. Gavazzi et al. 2012). So far, this subtraction has been performed through model fitting. An example of a ring detector is given in Sygnet et al. (2010). It selects objects with possible lensing configurations according to their lensing convergence, estimated from the Tully-Fisher relation. This algorithm relies on photometric information but requires a visual check of a large number of candidates.

In the present paper, we propose a “lens finder” that uses single-band images to find full and partial Einstein rings based on purely morphological criteria. The algorithm uses a pre-selection of potential lens galaxies as input, producing so-called “lens-selected” samples. The thereby work sets the basis of an algorithm using machine-learning techniques. Although focussed on finding Einstein rings, it can be adapted to other types of lenses, such as those consisting of multiple, relatively pointlike components.

This paper is organised as follows. In Sects. 2 and 3 we outline our algorithm and introduce the principles behind each step of the process. In Sect. 4 we show the performance of our algorithm using a set of simulations designed to reproduce Euclid images in the optical. We discuss the completeness and purity of our algorithm as a function of signal-to-noise ratio (S/N) and caustic radius of the lensing systems. Section 5 shows results of our galaxy subtraction algorithm compared to those of galfit software (Peng et al. 2011) on images from the CFHT optical imaging of SDSS stripe 82, and Sect. 6 summarises our main results.

2. A new automated lens finder

2.1. Principle of the algorithm

By construction, lens-selected samples display bright foreground lenses and faint background sources, otherwise the pre-selection of the lenses based on morphological type, luminosity, and colour would not be possible. As a consequence, faint Einstein rings are hidden in the glare of the foreground lenses, which must be properly removed before any search for lensed rings can be undertaken. An efficient “lens finder” therefore involves two main steps: 1- removal of the lens galaxy, 2- identification of rings in the lens-subtracted image.

A traditional way of subtracting galaxies is to fit a two-dimensional elliptical profile to the data, e.g. as done with the galfit software (Peng et al. 2011). While this is sufficient for characterising the main morphological properties of galaxies, it turns out to be insufficient for detecting faint arcs seen superposed on bright galaxies with a significant level of resolved structures.

One way to circumvent the problem is to build an empirical light model from the sample of galaxies itself, i.e. to use machine learning techniques such as principal component analysis (PCA; Jolliffe 1986). The sparsity and the diversity in terms of shape of the lensed objects (rings, arcs, multiple images) prevents them from being represented in the basis well enough, thus allowing for an accurate separation of lenses and sources. This has already been used to find lensed sources from PCA decomposition of quasar spectra (e.g. Courbin et al. 2012; Boroson & Lauer 2010). We now adopt a similar strategy to analyse images.

Once the foreground lenses have been properly removed, we analyse the residual rings using methods described in Sect. 3. The main steps of the algorithm can be summarised as follows:

  • 1.

    Pre-selection of the galaxies with a predefined range of shape parameters (size, ellipticities, magnitudes, colours, etc.);

  • 2.

    Construction of the PCA basis either from the selected sample of galaxies or from an adapted training set;

  • 3.

    Reconstruction of the central galaxies and subtraction from the original images;

  • 4.

    Detection of lensed objects using either island finding or polar transform on the residual image.

thumbnail Fig. 1

Examples of PCA components obtained using 1000 simulated galaxies from the Bologna Lens Factory (see Sect. 4).

2.2. Selection of galaxies

The first step in this method is to build stamp images of galaxies in which to look for lensed objects. This step strongly depends on the specific sample considered and may take advantage of algorithms such as SExtractor (Bertin & Arnouts 1996).

For the PCA decomposition to work well, a compromise has to be found between the number of objects used to build the PCA basis, the size of the objects in pixels, and the range in shape parameters. The more complex the galaxies are, the more galaxies should be included in the training set; i.e., the sparsity of the problem has to be evaluated carefully.

For relatively simple galaxy shapes, like elliptical galaxies, the pre-selection may focus on galaxies with similar sizes and ellipticities, which ensures better morphological similarities. This usually results in a satisfactory subtraction of the lens galaxy with only a few PCA components. However, the window in which the sizes and ellipticities are chosen has to be wide enough to allow a full representation of any shapes of galaxies in this range. The choice of this selection window is discussed later when applying the method to specific data.

Computational time is an important parameter to consider as well. Building the PCA basis involves finding the eigenvectors and the eigenvalues of a n2 × Ngal matrix, where n is the number of pixels per stamp and where Ngal is the number of stamps in the training set.

2.3. Building the PCA basis

Before computing the PCA basis, we rotate all the galaxies in the training set so that their major axes are all aligned, and we centre the galaxies in each stamp image. The rotation is performed using a polynomial transformation and a bilinear interpolation. This restricts the parameter space to be explored further and is fully justified given that position angle of galaxies on the sky are distributed in a random way: the position angle cannot be a principal component. We do not apply any other re-scaling, e.g. of parameters such as ellipticity, which do not distribute in a random way.

Any companions to the galaxies used to build the PCA basis are a possible source of artefacts. Companion galaxies are frequent enough to have a strong weight in the final basis. This can result in removing part of the lensed object at the end of the process or, conversely, to create fake lensed objects.

To avoid this effect, we selected only galaxies with no bright companions or with companions far away from the centre of light. This method of course results in reducing the size of the PCA basis. To include more “companion-free” galaxies, one often has to widen the original selection function, at least in surveys of limited volume, and this may result in a PCA basis that is less representative of the considered sample. To use galaxies with companions in the PCA basis, one has to devise a masking strategy. This can be an improvement to the algorithm presented in this paper and may depend on the specific properties of the sample of galaxies to be analysed.

thumbnail Fig. 2

Illustration of the ring finding process for two simulated Einstein rings from the Bologna Lens Factory (Sect. 4). For each row from left to right are shown 1- an example of simulated Einstein ring (64 × 64 pixels), along with its lens galaxy, 2- the lensed ring after PCA subtraction of the foreground galaxy, 3- the result of curvelet denoising, 4- the polar transform of the ring revealing a visible horizontal line whose position along the y-axis gives a measurement of the radius of the Einstein ring.

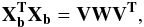The PCA analysis is computed by building a matrix Xb in which each of the n columns is an image from the basis set, reshaped as a vector of size n2. A singular value decomposition is performed on the covariance matrix of the elements of the basis, Xb, which boils down to finding V, and W verifying XbTXb=VWVT,\begin{eqnarray} \rm \bf X_b^{T} X_b = VWV^{T}, \end{eqnarray}(1)where W is a diagonal matrix. 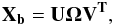The singular value decomposition of Xb is written Xb=UΩVT,\begin{eqnarray} \rm \bf X_b = U\Omega V^{T}, \end{eqnarray}(2)with Ω2 = W, and U the matrix of the eigenvectors for the decomposition of Xb. 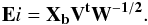Therefore, the eigenvectors Ei can be recovered from the singular value decomposition of the covariance matrix Ei=XbVtW−1/2.\begin{eqnarray} \rm {\bf E}{\it i} = {\bf X_{b}V^{t}W^{-1/2}}. 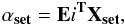\end{eqnarray}(3)The decomposition of an n × n image of galaxy reshaped as a column vector, Xset (not necessarily in the basis) can now be expressed as αset=EiTXset,\begin{eqnarray} \rm \bf \alpha_{set} ={\bf E}{\it i}^{T} {\bf X}_{set}, \end{eqnarray}(4)where αset is a Ngal-sized vector of PCA coefficients that represents the image Xset. A partial reconstruction of the image is done by using only the k-first coefficients of the PCA, i.e. the k most significant coefficients. The estimated reshaped image is ˜Xset=Ei[0..n2,0..k]αset[0..k].\begin{eqnarray} {\bf \tilde{X}}_{\rm set} = {\bf E}i_{[0..n^2, 0..k]}\alpha_{{\rm set}[0..k]}. \end{eqnarray}(5)Since the basis does not represent anything but the variations in shapes of the central parts of the galaxies, they will be the only reconstructed objects. The remaining companions are much less represented in the PCA basis. Rare structures such as Einstein rings or multiply imaged objects are represented very little in the PCA basis. Using a limited number of PCA coefficients during the reconstruction will therefore create images of lens galaxies without any significant lensed structure potentially present in the original data. The reconstructed PCA images can therefore be subtracted from the original data in order to unveil the lensing structures, when present. Figure 1 displays examples of the first PCA coefficients for the simulated Einstein rings described in Sect. 4.

To evaluate the quality of reconstruction in an objective way, we compute the reduced χ2 (per pixel) of the reconstruction in some circular area S containing NS pixels: q=1NS∑i=1N[di−miσi2]2\begin{eqnarray} q = \frac{1}{N_S}\sum_{i=1}^{N}\left[ \frac{d_i-m_{i}}{\sigma_i^2}\right] ^2 \label{quality} \end{eqnarray}(6)where di are the pixels in the original image along with their photometric error σi, and where mi are pixel values as predicted by the PCA model/reconstruction. The radius of the circular area S can be chosen to match the mean size of the galaxies in the sample.

A critical step in the PCA reconstruction is the choice of the number of PCA coefficients. If all of the coefficients are used, the reconstruction will include elements of the basis that represent the noise, hence resulting in an overfitting of the data and to an apparent smoothing of the residual image obtained after subtraction of the galaxy. This can be damaging when trying to detect faints rings and arcs. Conversely, if the number of coefficients is insufficient, the central galaxy will only be partially removed, leaving significant and undesired structures in the residual image.

In Sect. 4, we describe a way to choose the number of PCA coefficients in an objective way, using the reduced χ2, and we illustrate the effect of this choice using a set of simulated Einstein rings, as they would be seen with the ESA Euclid satellite (Laureijs et al. 2011).

3. Finding the lensed images, arcs and rings

Once a galaxy is removed from the image, the second step is to search for any residual lensed signal. In this paper, we focus on partial or full Einstein rings. We have investigated two different approaches. The first one uses a curvelet filter (Starck et al. 2002), optimised to enhance any arc-like structure, on images reshaped on a polar grid. The second method uses SExtractor (Bertin & Arnouts 1996) to identify the remaining sources in the residuals and to assess whether they are lensed images according to their orientation and elongation.

3.1. Polar transform

A simple way to detect full or partial rings can be devised by turning the Cartesian coordinate system of the data into the polar one. The polar coordinates (ρ,θ) are chosen so that the origin is the centre of the galaxy that has been removed using the PCA decomposition. The polar-transformed image is built by creating a new grid of pixels and by asking, for each pair of (ρ,θ) coordinates, the value of the pixels in the original (x,y) Cartesian grid. This involves an interpolation process giving the pixel intensities Ipol(ρ,θ) as a function of the pixel intensities in the original image I(x,y), with the standard relations x = ρcos(θ) and y = ρsin(θ).

By construction, the polar transform centred on the lens galaxy barycentre, turns a circle into a line, as illustrated in Fig. 2. The problem of ring detection is then reduced to a problem of line detection. The polar image’s columns are collapsed into a vector containing the median value of each column. If the original image contains a ring, this vector will present a spike, whose position gives the radius of the ring directly, as illustrated in Fig. 3. In practice, we define a threshold that determines whether the maximum of the vector stands for a ring or not. Figures 2 and 3 show the different steps in the ring detection.

thumbnail Fig. 3

Median pixel values along the pixel rows of the curvelet-filtered images shown in the third column of Fig. 2. The black line corresponds to the top row of Fig. 2, and the red line corresponds to the bottom row. A simple thresholding scheme allows us to detect the spike and to measure directly the size of the Einstein ring (see text).

Since the rings are not always perfectly circular but elliptical, their shape in polar coordinates can deviate significantly from a straight line. In most cases, looking for straight lines in polar coordinates is sufficient to detect rings, at least for moderate ellipticities. However, it is possible to refine the detection criterion by fitting an ellipse in polar coordinates, 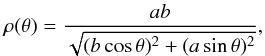ρ(θ)=ab(bcosθ)2+(asinθ)2,\begin{eqnarray} \rho(\theta) = \frac{a b}{\sqrt{(b \cos \theta)^2 + (a \sin \theta)^2}}, \end{eqnarray}(7)where a and b are the semi-major and semi-minor axes of the ellipse, and where the origin of the system is centred on the lensing galaxy. To find point-source components superposed on the rings (or simply lensed point sources), one can add simple Gaussian profiles to the fit or the actual instrumental/atmospheric PSF. Alternatively, one can implement the detection scheme of Meneghetti et al. (2008) to find brightness fluctuations along the arcs. Different typical lensing configurations are shown to illustrate this in Fig. 4.

thumbnail Fig. 4

Left panels: schematic view of rings (dashed line) and multiple images (blue dots along the ring tracks). Right panels: their corresponding transform in polar coordinates.

3.2. Island finding: the use of SExtractor parameters

An alternative method for assessing the presence of lensed structure in fields is to characterise all sources in the field, and use the measured parameters of these sources in order to identify patterns among them. This process begins with the use of SExtractor to identify sources in the field above a S/N threshold. The flux, ellipticity, tangentiality (closeness of the position angle to 90° to a vector from the field centre to the object), and distance from the field centre are measured. In addition, flux islands (which may contain one or more SExtractor components) are identified and the third moments of the flux distribution are measured. Third moments are sensitive to bent or arc-like structures, which are hard to detect from single components alone. 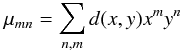For the current purpose, we define a combination of third moments ζ as ζ=12log10[(μ30+μ12)2+(μ21+μ03)2],\begin{eqnarray} \zeta = \frac{1}{2} \log_{10} \left[(\mu_{30}+\mu_{12})^2+(\mu_{21}+\mu_{03})^2\right] , \end{eqnarray}(8)where μmn=∑n,md(x,y)xmyn\begin{eqnarray} \mu_{mn}=\sum_{n, m} d(x,y) x^m y^n \end{eqnarray}(9)where d(x,y) is the data value in terms of offsets x and y from the brightest pixel in the island. This statistics, as a combination of third moments is sensitive to bending and is also invariant under scaling and rotation.

A point-score is then assigned to each component according to the elongation of the component and its tangential orientation with respect to the field centre. In addition, components with similar radii are weighted upwards in the point-score allocation, and components that are part of an island with significant third moment are also weighted up. Specifically, the point score is given by the following procedure, using free parameters pi where necessary:

thumbnail Fig. 5

Result of the galaxy removal on four of our simulated Einstein rings. The left panel displays the four original images. From left to right, the other panels display galaxy removals when 10, 50, and 200 PCA coefficients are used. The reduced χ2 are q = 1.74, q = 1.00 (i.e. optimal number of coefficients), and q = 0.9 respectively.

thumbnail Fig. 6

Results of the island-finding algorithm. Each panel shows the residual image after the PCA galaxy subtraction, with the point score of each component given separately and the total point score at the top (see text). The top row shows systems which have lenses and is ordered so that the highest point-score is on the left and the lowest on the right. Objects with high ellipticity and high curvature, tangential to the radius vector from the centre of the image, are preferred; lens systems without such objects are hard to recognise by eye and also tend to attract a lower point score. The bottom row shows a sample of non-lenses, again ordered by point score. High point-score objects are generally those in which chance coincidences produce configurations that mimic the presence of lensing.

  • Each component, unless it has a flux less than a threshold p0, is assigned a point score of 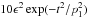10ϵ2exp(−t2/p12)\hbox{$10{\epsilon}^{2} \exp(-t^2/p_1^2)$}, where ϵ ≡ a/b is its elongation and t the difference between its tangentiality and the angle tangential to the radius vector to the point. In general, we use Gaussian penalty functions where we wish to select for a value close to one that would be expected for lensing, and power laws for quantities that we wish to maximise. The ϵ2 dependence results from a limited amount of experimentation by hand, although such dependencies can ideally be optimised on a larger sample.

  • The point score of any component within a factor of p2 in radius from its neighbour is multiplied by (1.0+N/p3)∗exp[−(r−1)2/p42]\hbox{$(1.0+N/p_3)* \exp[-(r-1)^2/p_4^2]$}, where N is the number of points assigned to the neighbour, and r is the ratio of their distances from the centre of the field. This selection favours multiple lensed images at the same radius, although the selection will have more effect if the individual images are themselves elongated and tangential.

  • If a component is part of an island with third moment ζ>p5, its point score is multiplied by [1 + (ζ − p5)] 2.

The six parameters pi are then optimised on a small training set of lenses before being applied to the dataset. A variable point-score threshold can be used for lens detection, completeness generally being achieved at the expense of purity of the resulting sample.

4. Application to Euclid-like simulated images

The “lens finder” described in Sect. 2 is designed to process large imaging data sets. Although the pre-selection of the galaxies to be searched for lensing may require colour information, the new algorithm proposed in this paper can be applied to single-band data to perform a purely morphological search. In the following, we evaluate the performances of the method using simulated images of Einstein rings as they would be seen with the ESA Euclid satellite (Laureijs et al. 2011).

The image simulations are provided through the Bologna Lens Factory (BLF) project2. This is a project dedicated to performing lensing simulations and providing realistic mock data for a wide variety of lensing studies from large scale weak lensing to galaxy cluster lensing and strongly lensed quasars. For the purposes of this work, images were created to specifically mimic the expected Euclid images in the visible instrument, as described in Laureijs et al. (2011). The pixel size is 0.1′′ and the PSF is Gaussian with a full-width half-maximum (FWHM) of 0.18′′. The surface brightness is translated into photon counts taking the expected instrumental throughput in the VIS band into account. Background counts from zodiacal light are added, assuming a brightness equal to 22.8 mag/arcsec2. Noise is then calculated by paying attention to Poisson statistics, flat-field error, and read-out (Meneghetti et al. 2008). The lensing and image construction is done with the GLAMER lensing code (Metcalf & Petkova 2013; Petkova et al. 2013). The pre-lensed galaxy surface brightness models and mass distribution are provided by the Millennium Run Observatory (MRObs; Overzier et al. 2013). Each galaxy is represented by a bulge and a disk component whose properties are predicted by a semi-analytic galaxy evolution model. The mass distribution consists of haloes identified in the Millennium Nbody simulation.

The lensing simulations were done as follows. The haloes in the catalogue are represented by NFW haloes (Navarro et al. 1997) with singular isothermal ellipsoids (SIEs) in their centres to represent the baryonic galaxy. This model has been shown to fit observed Einstein rings well (Gavazzi et al. 2007). The NFW profile is fit to the mass and peak circular velocity of the halo found in the Millennium simulation. The mass and velocity dispersion of the SIE component is set by the stellar mass to halo mass relation of Moster et al. (2010) and the Faber-Jackson relation (Faber & Jackson 1976). The lensed image of every source within a 0.1 deg2 light cone down to 28th magnitude in I band is constructed and put into a master image. This image contains only a few strongly lensed objects because the source density is low enough that it is rare to have a visible object within a caustic. To boost the number of strong galaxy-galaxy lenses, all the critical curves and their associated caustics in the field are found for a source redshift of zs = 2.5, and a source galaxy is moved to be near the caustic. The sources are taken randomly from galaxies within the light cone at a similar redshift. Then the lensed image of this source is constructed and added to a 200 × 200 pixel cutout stamp from the master image. Images with and without the added source are provided and an image with only the added lensed source is provided. All images are provided with and without the noise and PSF effects. A catalogue of all the critical curves and caustics is also provided, with their locations and properties such as average radius and area.

Since we are not concerned with predicting the statistical properties of the lenses in this paper, many of the precise details of these simulations are not important (for example the distribution of source and lens redshifts, morphologies, luminosities). The performance of the PCA lens finder will be stated in terms of the S/N of the Einstein ring so the simulations are only required to represent the variety of expected lenses and not their precise distribution.

The set of Euclid simulation images consists of 3000 galaxies with a full or partial background Einstein ring and of a training set of 1250 galaxies with no lensing. Among the 1250 non-lensing galaxies of the training set, 1000 are used to build the PCA basis in order to search for lensing in the 4250 images, 3000 of which containing Einstein rings. With real data, the training set can be the whole data set itself, as galaxies with lensing features are rare.

Building the PCA basis for the 1000 Euclid galaxies, which are 128 pixels on a side, takes about 40 min on a single processor. Using this PCA basis, doing the galaxy reconstruction and subtraction takes less than a minute more for the whole data set, i.e. 4250 images. In terms of cpu , the PCA method is therefore very well tractable and applicable to large data sets.

4.1. Quality of the central galaxy reconstruction

The quality of the PCA reconstruction depends on three main factors: 1- the range in galaxy sizes, 2- the presence of companions near the galaxies used to build the PCA basis, 3- the number of PCA coefficients to be used. To minimise the parameter space to explore, all galaxies are first centred on the central pixel of the FITS stamp and rotated so that their long-axis aligns with the image rows. If necessary, the resulting images are zero-padded and trimmed to a common size. In the present case we use 128 × 128 pixels.

In order to minimise the contamination of the PCA basis by companions to the galaxies in our sample, we only select the stamps that have no companion brighter than 50% of the maximum brightness of the main galaxy in a range of less than ten pixels to the patch’s centre, i.e. 1′′ given the Euclid pixel size of 0.1′′.

To estimate the number of PCA components, we carry out different reconstructions with an increasing number of PCA coefficients. We stop adding coefficients when reaching an acceptable quality, i.e. when there is no residual above the noise level. A good reduced χ2 is when q, (Eq. (6)) remains between 1 and 1.5, i.e. when the mean χ2 per pixel is on average close to 1σ. Indeed, if the pixels in the residuals are highly correlated owing to a reconstruction that includes coefficients representative of the noise, the reduced χ2 becomes smaller than 1. Conversely, when the residuals contain important patterns due to an insufficient reconstruction, q is much larger than 1. This is illustrated in Figs. 7 and 8 for the specific case of our Euclid simulation, where a good reconstruction is achieved for a number of PCA coefficients of about 50, i.e. the minimum number of coefficients required to reach q ~ 1.

4.2. The effect of galaxy sizes

Even for relatively smooth light distributions, like early type galaxies, a careful balance must be found between the number of galaxies in the training set and the range in galaxy sizes. We investigate in the following the influence of the size distribution of the galaxies for the specific case of our Euclid simulations.

To do so, we binned the sample in galaxy sizes, keeping 100 galaxies per bin and we built the PCA basis for each bin of size, as in Fig. 7. Rescaling the galaxies in Reff is also an alternative, but we try as much as we can to avoid alter the data before building the PCA basis. Rescaling in Reff may be considered for small samples of galaxies that cannot be binned in galaxy size. The images are then reconstructed using different number of coefficients. The quality of reconstruction, estimated using the median q factor over all images of the subsample, is then evaluated. Figure 7 suggests that 50–70 coefficients is an optimal number to reach a reduced χ2 close to 1.

Figure 8 shows how q rises when galaxies are getting bigger than a semi-major axis itself larger than three pixels. Because big galaxies are less represented in the PCA basis due to their scarcity, their reconstruction is less accurate, leading to larger χ2. It is therefore very important to carefully select the range of size that we want to investigate when building the PCA basis and to ensure that a sufficient number of galaxies are available to represent the full variety of structures in the sample. Indeed, for bigger galaxies, where Einstein rings are more likely to be found, the number of objects contributing to the basis is reduced, simply because big galaxies are rare.

thumbnail Fig. 7

Reduced χ2, as a function of the number of coefficients used in the reconstruction. Only 50–70 coefficients are needed to reach a reduced χ2 of q ~ 1 in the case of our Euclid simulations.

thumbnail Fig. 8

Quality of the reconstruction of the simulated Euclid lenses as a function of the average size of the galaxies in pixels, as measured with SExtractor . The pixel size of the images matches that of Euclid, i.e. 0.1′′. Since big galaxies are rare, they are less well represented in the PCA basis, hence less well modeled.

thumbnail Fig. 9

Completeness as a function of purity for different thresholds of Einstein radii (expressed in terms of critical curve here) and signal-to-noise ratio with the two methods described in Sect. 3: polar transform (in red) and island finding (in blue). The minimal radius in the sample is r = 0.02′′, which means that the top left panel shows the results over the whole sample.

4.3. Completeness and purity

To evaluate the efficiency of the algorithm, we performed tests of detection on simulated images for which the S/N and the caustic radius of the lensing galaxies are known. For this study we used a set of 3000 simulated full rings from the BLF. With these realistic Euclid-like ring images and the associated noise images we can compute the S/N, for each Einstein ring: 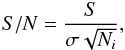S/N=SσNi,\begin{eqnarray} S/N = \frac{S}{\sigma\sqrt{N_i} },\label{SNR} \end{eqnarray}(10)where Ni is the number of non-zero pixels in the noise free ring image, σ the rms noise per pixel, and S the total flux in the ring. The simulated images analysed by building a PCA basis using 1000 galaxies from a set of non lensing galaxies. The detection algorithms, described in Sect. 3 were then applied to the 3000 images with lensing and to the 1250 images without lensing. The island-finding algorithm was trained on a set of 167 images of lensed rings provided by the BLF, together with another set of 200 images that did not contain lenses. The parameters were optimised here and then re-optimised on the dataset itself. The output of the process was compared to the known answer from the simulations to evaluate the completeness and the purity of the derived lens catalogues.

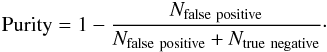Since the fraction of non-lens images in the sample is smaller than in reality, we instead defined the purity as the fraction of non-lens images that have not been detected instead of the fraction of true positive among all the detected lensed images: Purity=1−NfalsepositiveNfalsepositive+Ntruenegative·\begin{eqnarray} {\rm Purity} = 1-\frac{N_{\rm false\ positive}}{N_{\rm false\ positive} + N_{\rm true\ negative}}\cdot \label{equation:purity} \end{eqnarray}(11)The completeness is expressed as the fraction of actual lens images that have been detected over the whole sample of lenses: Compl.=NtruepositiveNtruepositive+Nfalsepositive·\begin{eqnarray} {\rm Compl.} = \frac{N_{\rm true\ positive}}{N_{\rm true\ positive} + N_{\rm false\ positive}}\cdot\label{equation:completeness} \end{eqnarray}(12)Figure 9 shows the purity as a function of completeness for both methods. Different thresholds in S/N and critical curve for the lensing have been considered. Although both methods are comparable at low completeness, at high completeness levels the SExtractor algorithm generally leads to lower purity, corresponding to more false positives. This problem appears worse at high S/N levels, because the number of false positive detections in the non-lens sample remains constant, while the number of true positives declines. This is likely to be due to the attempt to preserve at least some sensitivity to only marginally extended components, corresponding, for example, to quadruply imaged sources of modest extent. The algorithm is therefore more vulnerable to chance alignments between external components. Work is under way to alleviate this problem and, particularly, to use colour information to distinguish between genuine and chance alignments. In the context of the present work, we stick to single-band detections. The results tend to show that we can detect rings almost independently on the radius. For instance, with the polar transform method and a S/N higher than 30, one can reach a completeness of 90% for a purity of 86%.

thumbnail Fig. 10

Comparison of different galaxy-removal schemes applied to deep CFHT images. The first column shows the original image. The second shows the residual image after subtraction of a PCA reconstruction of the galaxy. The third and fourth columns show the subtraction of a single and double elliptical Sérsic profile respectively, using GALFIT3 . The PCA-subtracted images are rotated by construction of the PCA basis, but the GALFIT -subtracted images are not, in order to avoid interpolation when not mandatory.

5. Application to real data

In the above, we have tested our lens finder on simulated images that mimic Euclid images in the VIS band. An obvious question is whether the algorithm performs in a satisfactory way on real data. While carrying out a ring search on a large data set is beyond the scope of this paper, we can nevertheless test how our PCA decomposition of galaxies compares with other more traditional ways of removing lensing galaxies.

To do that, we used the deep and sharp optical images taken with MEGACAM at the CFHT to map SDSS stripe 82. Following the same procedure as with the Euclid simulations, we set the optimal number of PCA coefficients by checking that we can actually reach reduced χ21 < q < 1.2 depending on the seeing and on the physical size of the galaxies we wanted to subtract.

In Fig. 10, we compare our galaxy subtraction with what was done in other lens searches using single or double Sérsic profiles (e.g. Vegetti et al. 2012; Lagattuta et al. 2010). Not surprisingly, the subtraction with Sérsic profiles performs rather well with low S/N galaxies or with small galaxies, but leaves significant residuals for large galaxy sizes. Because these residuals often take the shape of a ring, they may lead to large numbers of false positives in a ring search.

The experiment we carry out here with real data uses only one single field of the CFHT data of stripe 82, i.e. one square degree out of the 180 available. This means that the PCA decomposition uses only a limited number of large galaxies. As a consequence, using the whole 180 fields has the potential to improve further the galaxy subtraction, while profile fitting will always be limited to the information in one single galaxy and does not benefit from the information on the shape of all galaxies present in the whole data set. In other words, increasing the survey size not only increases the number of potential lenses, but also increases the density of galaxies per bin of size, hence improving the quality of the PCA basis.

6. Conclusion

The two lens-finder algorithms developed here both rely on a good subtraction of lensing galaxies with machine-learning methods. Different ideas for ring detection then allow objects with different properties to be detected on the residual images:

  • The polar transform method enhances the signal in the residual image by applying curvelet denoising and uses a polar transform of the images to turn the problem of circle detection to a line detection. It is designed to detect full or partial rings with or without ellipticity.

  • The “Island-finding algorithm” uses SExtractor to detect structures in the PCA-subtracted images and to determine whether they correspond to lensed sources according to their elongation, orientation, and bending. This algorithm is expected to be more efficient at finding partial arcs and multiple images.

The method was successfully applied to Euclid-like simulations. With the polar transform method, a completeness of 90% was reached for data where the S/N in the Einstein ring is at least 30. The same simulations show that the purity of the derived ring sample reaches 86% of the non lensed galaxies detected as false positives.

The galaxy subtraction algorithm turns out to be efficient when applied to real data as well: our tests with CFHT images of SDSS Stripe 82 surpasses the subtraction obtained with direct model fitting in quality.

In future work, ways to increase the purity of the algorithms will be investigated by using adapted dictionary learning (e.g. Beckouche et al. 2013) for galaxy subtraction. The strength of those machine-learning methods should allow us to build bases adapted to more complicated problems, such as subtracting galaxies in clusters to detect rings produced by multiple galaxies. Better morphological selection based on PCA “clustering” or beamlet analysis (e.g. Donoho & Huo 2002) can be used to distinguish ring-like shapes, to classify rings and arcs, and to carry out galaxy classification in general, as done in the past with quasar spectra (Boroson & Lauer 2010) and, more recently, with galaxy multi-band photometry (Wild et al. 2014).

Acknowledgments

The authors would like to thank R. Cabanac, A. Fritz, R. Gavazzi, F. Lanusse, P. Marshall, J.-L. Starck, and A. Tramacere for helpful discussions on various aspects of this paper. This work is supported by the Swiss National Science Foundation (SNSF). G. Lemson is supported by Advanced Grant no. 246797 “GALFORMOD” from the European Research Council. B. Metcalf, F. Bellagamba, C. Giocoli and M. Petkova’s research is part of the project GLENCO, funded under the European Seventh Framework Programme, Ideas, Grant Agreement No. 259349. P. Hartley is supported by a Science & Technology Facilities Council (STFC) studentship. J.-P. Kneib is supported by the European Research Council (ERC) advanced grant Light on the Dark (LIDA).

References

  1. Alard, C. 2006, unpublished [arXiv:astro-ph/0606757] [Google Scholar]
  2. Bartelmann, M., Limousin, M., Meneghetti, M., & Schmidt, R. 2013, Space Sci. Rev., 177, 3 [NASA ADS] [CrossRef] [Google Scholar]
  3. Beckouche, S., Starck, J. L., & Fadili, J. 2013, A&A, 556, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Bolton, A. S., Burles, S., Koopmans, L. V. E., Treu, T., & Moustakas, L. A. 2006, ApJ, 638, 703 [NASA ADS] [CrossRef] [Google Scholar]
  6. Boroson, T. A., & Lauer, T. R. 2010, AJ, 140, 390 [NASA ADS] [CrossRef] [Google Scholar]
  7. Brownstein, J. R., Bolton, A. S., Schlegel, D. J., et al. 2012, ApJ, 744, 41 [NASA ADS] [CrossRef] [Google Scholar]
  8. Cabanac, R. A., Alard, C., Dantel-Fort, M., et al. 2007, A&A, 461, 813 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Courbin, F., Faure, C., Djorgovski, S. G., et al. 2012, A&A, 540, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Donoho, D. L., &Huo, X. 2002, in Multiscale and Multiresolution Methods Theory and Applications, eds. T. J. Barth, et al. (Springer), Lect. Notes Comput. Sci. Eng., 20, 149 [Google Scholar]
  11. Faber, S. M., & Jackson, R. E. 1976, ApJ, 204, 668 [NASA ADS] [CrossRef] [Google Scholar]
  12. Foëx, G., Motta, V., Limousin, M., et al. 2013, A&A, 559, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Frieman, J. A., Turner, M. S., & Huterer, D. 2008, ARA&A, 46, 385 [NASA ADS] [CrossRef] [Google Scholar]
  14. Gavazzi, R., Treu, T., Rhodes, J. D., et al. 2007, ApJ, 667, 176 [NASA ADS] [CrossRef] [Google Scholar]
  15. Gavazzi, R., Treu, T., Marshall, P. J., Brault, F., & Ruff, A. 2012, ApJ, 761, 170 [NASA ADS] [CrossRef] [Google Scholar]
  16. Heymans, C., Grocutt, E., Heavens, A., et al. 2013, MNRAS, 432, 2433 [NASA ADS] [CrossRef] [Google Scholar]
  17. Hoekstra, H., Bartelmann, M., Dahle, H., et al. 2013, Space Sci. Rev., 177, 75 [NASA ADS] [CrossRef] [Google Scholar]
  18. Jolliffe, I. T. 1986, Principal Component Analysis (Berlin; New York: Springer-Verlag) [Google Scholar]
  19. Kneib, J.-P., & Natarajan, P. 2011, A&AR, 19, 47 [Google Scholar]
  20. Lagattuta, D. J., Auger, M. W., & Fassnacht, C. D. 2010, ApJ, 716, L185 [NASA ADS] [CrossRef] [Google Scholar]
  21. Laureijs, R., Amiaux, J., Arduini, S., et al. 2011, unpublished [arXiv:1110.3193] [Google Scholar]
  22. Limousin, M., Cabanac, R., Gavazzi, R., et al. 2009, A&A, 502, 445 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Mandelbaum, R., Slosar, A., Baldauf, T., et al. 2013, MNRAS, 432, 1544 [NASA ADS] [CrossRef] [Google Scholar]
  24. Marshall, P. J., Hogg, D. W., Moustakas, L. A., et al. 2009, ApJ, 694, 924 [NASA ADS] [CrossRef] [Google Scholar]
  25. Meneghetti, M., Melchior, P., Grazian, A., et al. 2008, A&A, 482, 403 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Meneghetti, M., Bartelmann, M., Dahle, H., & Limousin, M. 2013, Space Sci. Rev., 177, 31 [NASA ADS] [CrossRef] [Google Scholar]
  27. Metcalf, R. & Petkova, M. 2013, MNRAS, submitted [arXiv:arXiv:1312.1128] [Google Scholar]
  28. More, A., Cabanac, R., More, S., et al. 2012, ApJ, 749, 38 [Google Scholar]
  29. Moster, B. P., Somerville, R. S., Maulbetsch, C., et al. 2010, ApJ, 710, 903 [NASA ADS] [CrossRef] [Google Scholar]
  30. Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
  31. Overzier, R., Lemson, G., Angulo, R. E., et al. 2013, MNRAS, 428, 778 [NASA ADS] [CrossRef] [Google Scholar]
  32. Parker, L. C., Hoekstra, H., Hudson, M. J., van Waerbeke, L., & Mellier, Y. 2007, ApJ, 669, 21 [NASA ADS] [CrossRef] [Google Scholar]
  33. Pawase, R. S., Faure, C., Courbin, F., Kokotanekova, R., & Meylan, G. 2012, MNRAS, accepted [arXiv:1206.3412] [Google Scholar]
  34. Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H.-W. 2011, Astrophys. Source Code Lib., ascl:1104.010 [Google Scholar]
  35. Petkova, M., Metcalf, R., & Giocoli, C. 2013, MNRAS, submitted [arXiv:1312.1536] [Google Scholar]
  36. Ruff, A. J., Gavazzi, R., Marshall, P. J., et al. 2011, ApJ, 727, 96 [NASA ADS] [CrossRef] [Google Scholar]
  37. Seidel, G., & Bartelmann, M. 2007, A&A, 472, 341 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Simon, P., Schneider, P., & Kübler, D. 2012, A&A, 548, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Sonnenfeld, A., Gavazzi, R., Suyu, S. H., Treu, T., & Marshall, P. J. 2013a, ApJ, 777, 97 [NASA ADS] [CrossRef] [Google Scholar]
  40. Sonnenfeld, A., Treu, T., Gavazzi, R., et al. 2013b, ApJ, 777, 98 [NASA ADS] [CrossRef] [Google Scholar]
  41. Starck, J.-L., Candès, E., & Donoho, D. 2002, ITIP 11, 131 [Google Scholar]
  42. Sygnet, J. F., Tu, H., Fort, B., & Gavazzi, R. 2010, A&A, 517, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Treu, T., Dutton, A. A., Auger, M. W., et al. 2011, MNRAS, 417, 1601 [NASA ADS] [CrossRef] [Google Scholar]
  44. Vegetti, S., Lagattuta, D. J., McKean, J. P., et al. 2012, Nature, 481, 341 [NASA ADS] [CrossRef] [Google Scholar]
  45. Wild, V., Almaini, O., Cirasuolo, M., et al. 2014, MNRAS, 440, 1880 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

thumbnail Fig. 1

Examples of PCA components obtained using 1000 simulated galaxies from the Bologna Lens Factory (see Sect. 4).
In the text
thumbnail Fig. 2

Illustration of the ring finding process for two simulated Einstein rings from the Bologna Lens Factory (Sect. 4). For each row from left to right are shown 1- an example of simulated Einstein ring (64 × 64 pixels), along with its lens galaxy, 2- the lensed ring after PCA subtraction of the foreground galaxy, 3- the result of curvelet denoising, 4- the polar transform of the ring revealing a visible horizontal line whose position along the y-axis gives a measurement of the radius of the Einstein ring.
In the text
thumbnail Fig. 3

Median pixel values along the pixel rows of the curvelet-filtered images shown in the third column of Fig. 2. The black line corresponds to the top row of Fig. 2, and the red line corresponds to the bottom row. A simple thresholding scheme allows us to detect the spike and to measure directly the size of the Einstein ring (see text).
In the text
thumbnail Fig. 4

Left panels: schematic view of rings (dashed line) and multiple images (blue dots along the ring tracks). Right panels: their corresponding transform in polar coordinates.
In the text
thumbnail Fig. 5

Result of the galaxy removal on four of our simulated Einstein rings. The left panel displays the four original images. From left to right, the other panels display galaxy removals when 10, 50, and 200 PCA coefficients are used. The reduced χ2 are q = 1.74, q = 1.00 (i.e. optimal number of coefficients), and q = 0.9 respectively.
In the text
thumbnail Fig. 6

Results of the island-finding algorithm. Each panel shows the residual image after the PCA galaxy subtraction, with the point score of each component given separately and the total point score at the top (see text). The top row shows systems which have lenses and is ordered so that the highest point-score is on the left and the lowest on the right. Objects with high ellipticity and high curvature, tangential to the radius vector from the centre of the image, are preferred; lens systems without such objects are hard to recognise by eye and also tend to attract a lower point score. The bottom row shows a sample of non-lenses, again ordered by point score. High point-score objects are generally those in which chance coincidences produce configurations that mimic the presence of lensing.
In the text
thumbnail Fig. 7

Reduced χ2, as a function of the number of coefficients used in the reconstruction. Only 50–70 coefficients are needed to reach a reduced χ2 of q ~ 1 in the case of our Euclid simulations.

In the text
thumbnail Fig. 8

Quality of the reconstruction of the simulated Euclid lenses as a function of the average size of the galaxies in pixels, as measured with SExtractor . The pixel size of the images matches that of Euclid, i.e. 0.1′′. Since big galaxies are rare, they are less well represented in the PCA basis, hence less well modeled.

In the text
thumbnail Fig. 9

Completeness as a function of purity for different thresholds of Einstein radii (expressed in terms of critical curve here) and signal-to-noise ratio with the two methods described in Sect. 3: polar transform (in red) and island finding (in blue). The minimal radius in the sample is r = 0.02′′, which means that the top left panel shows the results over the whole sample.
In the text
thumbnail Fig. 10

Comparison of different galaxy-removal schemes applied to deep CFHT images. The first column shows the original image. The second shows the residual image after subtraction of a PCA reconstruction of the galaxy. The third and fourth columns show the subtraction of a single and double elliptical Sérsic profile respectively, using GALFIT3 . The PCA-subtracted images are rotated by construction of the PCA basis, but the GALFIT -subtracted images are not, in order to avoid interpolation when not mandatory.

In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.