EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 566 (June 2014) A&A, 566 (2014) A52 Full HTML
Free Access
Issue
A&A
Volume 566, June 2014
Article Number A52
Number of page(s) 7
Section Atomic, molecular, and nuclear data
DOI https://doi.org/10.1051/0004-6361/201323298
Published online 11 June 2014

© ESO, 2014

1. Introduction

Identification of a wide variety of chemical compounds in space, as well as in planetary atmospheres (see, e.g., the Cologne database1 and the “astrochymist” website2) has been made possible through the spectral signatures of astronomical bodies (Tielens 2013). For their interpretation, laboratory measurements are essential, and rotational spectroscopy clearly plays here a leading role (e.g., Winnewisser et al. 1992). The detailed spectroscopic characterization of gaseous hydrogen sulfide (H2S) is very relevant in the fields of astrophysical investigations, because H2S is one of the most abundant sulfur-bearing gas-phase species in different astronomical objects, such as solar system giant planets, extrasolar planets, brown dwarfs, interstellar clouds, etc. (e.g., Thaddeus et al. 1972; Visscher et al. 2006; Zahnle et al. 2009). In particular, this molecule has been recognized as one of the key species for the detailed chemical and physical characterization of extrasolar planets. For that reason it has been included in the ExoMol project (Tennyson & Yurchenko 2012), which aims at systematically providing line lists for molecules of astronomical importance. From a spectroscopic point of view, hydrogen sulfide is a light asymmetric-top molecule (similar to water) and is characterized by strong centrifugal-distortion effects. As a consequence, the convergence of the model Hamiltonians used to describe the rotational spectrum is very slow, so a large number of high-order parameters are needed to reproduce the experimental data. In these cases, the reliability of the determined centrifugal-distortion constants and their physical meaning need to be carefully checked (Belov et al. 1995).

Molecular isotope studies provide a key to understanding the evolution of elemental enrichment in the interstellar medium, including both stellar nucleosynthesis and the large-scale mixing of interstellar gas (e.g., Ikeda et al. 2002; Tielens 2013). Isotopes are in fact formed by distinct nucleosynthetic processes whose efficiency can be quite distinct under different conditions. Various isotopic substitutions of hydrogen sulfide, namely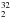 HS, H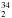S, HD32S, and D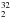S, have already been detected in space (Thaddeus et al. 1972; Ukita et al. 1983; Minh et al. 1989, 1990; Macdonald et al. 1996; Vastel et al. 2003). The first step toward detecting isotopic species is to know either the transition frequencies or the corresponding spectroscopic parameters with suitable accuracy. The aim of the present study is to provide such information for the 36S-containing isotopologue, whereas other rare isotopologues of hydrogen sulfide are only considered at the computational level.

thumbnail Fig. 1

The J = 54,1 ← 53,2 transition at 399.6 GHz (left side: P = 28 mTorr/3.7 Pa, mod. depth = 600 kHz) and the J = 42,3 ← 41,4 transition at 1023.4 GHz (right side: P = 57 mTorr/7.6 Pa, mod. depth = 1800 kHz) recorded in natural abundance.

The second issue to be addressed is the actual detectability in space of H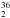S. It has to be noted that on Earth its natural abundance is about 200 times smaller than for the already detected H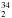S (288±1 in the solar system according to Ding et al. 2001), but it should be mentioned that two 36S-containing molecules have already been detected in space (Mauersberger et al. 1996, 2004). In Mauersberger et al. (1996) the detection of C36S in eight Galactic molecular hot cores was reported. A comparison with the spectra of other isotopic species of carbon monosulfide led to a 34S/36S abundance ratio of 115±17, which thus is smaller than in the solar system (Mauersberger et al. 1996). This ratio is consistent with what has been determined by Mauersberger et al. (2004), 107±15, from the observation of the J = 2 ← 1 and 3 ← 2 rotational lines of C36S and the J = 5 ← 4 and 6 ← 5 transitions of Si36S in the carbon star IRC+10216. In Mauersberger et al. (2004), the peculiar enhanced 36S abundance is discussed, but a number of open questions were left open, thus suggesting the need for further investigations. The observation of other 36S-containing isotopologues would therefore be very useful in elucidating the nucleosynthesis processes that led to the formation of different sulfur isotopes.

In view of the interest in H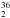S pointed out above, we decided to extend the study of Azzam et al. (2013) in the millimeter- and submillimeter-wave ranges in order to improve the accuracy of the spectroscopic parameters determined there. In fact, in Azzam et al. (2013), the rotational spectrum of H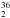S was measured at the SOLEIL synchrotron in the range of 1.8 to 6.7 THz with an accuracy of 15 MHz. However, such an investigation does not allow the rotational transitions to be predicted with the accuracy required for analyzing astronomical observations. Even worse is that, as demonstrated later in the text, the spectroscopic constants of Azzam et al. (2013) turn out to provide erroneous predictions for the rotational spectrum, at least in the millimeter- and submillimeter-wave frequency range.

To clarify this point, we decided to compare the rotational parameters for different isotopic species of hydrogen sulfide and to perform state-of-the art quantum-chemical calculations of the spectroscopic parameters involved. Making use of accurate experimental data for the main isotopologue (Cazzoli & Puzzarini 2014) and of an empirical scaling procedure, these computations endorsed the search and assignment of the rotational spectrum of H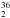S as well as provided reliable spectroscopic constants for other rare, i.e., mono- and bi-deuterated, isotopologues of hydrogen sulfide.

2. Experimental and computational details

2.1. Measurements

Measurements were performed with a frequency-modulated, computer-controlled spectrometer working from 65 GHz to 1.6 THz (Cazzoli & Puzzarini 2006; Puzzarini et al. 2012b), with the 167 GHz−1.6 THz frequency range considered in the present work. The millimeter- and submillimeter-wave sources employed, phase-locked to a rubidium frequency standard, were frequency multipliers driven by Gunn diode oscillators. The frequency modulation was obtained by sine-wave modulating the 72 MHz local oscillator of the synchronization loop with the modulation depth varied from 200 kHz to 2.4 MHz according to the transition frequency under consideration. Liquid-He-cooled InSb and Schottky diode detectors were used and their output processed by means of a Lock-in amplifier tuned to twice the modulation frequency (i.e., second harmonic detection is performed). A commercial sample of hydrogen sulfide was used with the 36S-containing isotopologue detected in natural abundance (0.02%). Pressure values in the range of 20 to 80 mTorr (2.7 to 10.7 Pa) were employed.

Figure 1 shows the J = 54,1 ← 53,2 and J = 42,3 ← 41,4 transitions of H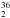S at 399.6 GHz and 1023.4 GHz, respectively. Despite the detection in natural abundance, it is apparent that the sensitivity of our spectrometer is such that we were able to record these transitions with a very good signal-to-noise ratio, thus retrieving the corresponding transition frequencies with an accuracy ranging from 30 to 100 kHz.

2.2. Computations

To support the experimental investigation, high-level quantum-chemical calculations of the relevant spectroscopic parameters involved, i.e., the rotational and centrifugal-distortion constants, were carried out (Puzzarini et al. 2010; Puzzarini 2013). The equilibrium rotational constants were derived in a straightforward manner from the equilibrium structure recently evaluated in Helgaker et al. (2013) by means of a state-of-the-art composite scheme (Heckert et al. 2005, 2006), which accounts for extrapolation to the complete basis-set limit as well as the inclusion of core correlation and higher excitations. Interested readers are referred to Helgaker et al. (2013) for a detailed account.

The ground-state rotational constants, 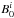, were then obtained by correcting the equilibrium rotational constants, 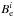, for vibrational effects via (e.g., Puzzarini et al. 2008; Mills 1972), 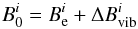(1)with 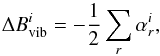(2)where the 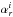’s are the vibration-rotation interaction constants with the sum running over all normal modes and the index i referring to the inertial axes (a, b, c). These constants were obtained by means of second-order vibrational perturbation theory (VPT2; Mills 1972), as described in Stanton et al. (1998). The required force fields were evaluated using coupled-cluster (CC) theory (Shavitt & Bartlett 2009) within the singles and doubles (CCSD) approximation augmented by a perturbative treatment of triple excitations (CCSD(T); Raghavachari et al. 1989), thereby using the correlation-consistent cc-pCVQZ basis set (Dunning 1989; Woon & Dunning 1993; Peterson & Dunning 2002). The harmonic force field was obtained using analytic second derivatives (Stanton & Gauss 1997), whereas the cubic force field was determined in a normal-coordinate representation via numerical differentiation of the analytically evaluated harmonic force constants (e.g., Stanton et al. 1998; Schneider & Thiel 1989; Stanton & Gauss 2000). In addition to the vibration-rotation interaction constants, the computed force fields also enabled determination of the quartic and sextic centrifugal-distortion constants (Mills 1972; Aliev & Watson 1985; Puzzarini et al. 2012a).

To show how the spectroscopic parameters change when moving from one isotopic species to another, the calculations described above were carried out for the main isotopic species, H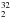S, as well as for the 33S-, 34S-, and 36S-containing isotopologues. To improve the theoretical predictions further, an empirical scaling procedure was employed, based on the available experimental spectroscopic constants for H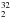S (Cazzoli & Puzzarini 2014). For a generic spectroscopic parameter X, the scaling is performed using the expression 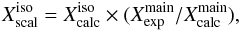(3)where the superscript iso refers to either 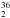HS, H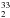S, or H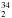S, while main indicates H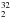S. In Eq. (3), scal, exp, and calc denote the scaled, experimental, and quantum-chemically calculated values for X, respectively. In a second step, the scaling procedure was applied to HD33S, HD34S, D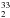S, and D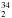S to provide reliable spectroscopic parameters for future experimental investigations of these species.

All quantum-chemical computations described above were carried out using the CFour program package (Stanton et al. 2013, http://www.cfour.de).

thumbnail Fig. 2

Portion of the recorded spectrum at 731 GHz (P = 60 mTorr/8.0 Pa, frequency modulation = 1.2 MHz): the J = 55,1 ← 54,2 transition of HS and the J = 107,3 ← 106,4 transition of HS are evident. The predicted position of the J = 55,1 ← 54,2 transition of HS according to the spectroscopic constants of Azzam et al. (2013) is also depicted.

3. Results and discussion

As already mentioned in the Introduction, the spectroscopic parameters recently determined by Azzam et al. (2013) turned out to be unable to correctly predict the rotational spectrum of H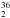S in the millimeter- and submillimeter-wave frequency ranges. This finding is illustrated in Fig. 2, which shows a portion of the rotational spectrum of hydrogen sulfide at 731 GHz. The recorded J = 55,1 ← 54,2 transition of H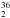S is displayed together with its predicted position according to the spectroscopic constants of Azzam et al. (2013): a mismatch of about 98 MHz is observed. Other attempts to observe rotational transitions for H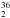S also indicated that the parameters reported in Azzam et al. (2013) are unreliable and thus not really useful for spectroscopic predictions. In fact, several centrifugal-distortion constants reported by Azzam et al. (2013) have opposite signs in comparison to those of the other isotopologues. Furthermore, three sextic terms were not determined despite the fact that higher-order constants were included in the fit.

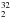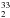A closer inspection of the rotational constants furthermore reveals that they do not comply with the trend seen when moving from one isotopologue to another. For this reason, we resorted to the computational investigations described above and proceeded as follows. First, we considered the computational results for HS, HS, and H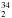S, for which reliable experimental data are available. The main purpose is here to validate the scaling procedure described in the previous section. Then, once its reliability has been demonstrated, the scaling was applied to the parameters of H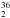S to check the constants given in Azzam et al. (2013) and to obtain reliable predictions for guiding the search and assignment of its rotational spectrum.

Table 1

Computed, scaled, and experimental spectroscopic constants (MHz) of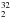 HS, H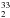S, and H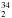S.

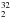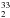The results obtained for HS, HS, and H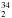S are collected in Table 1, where both the calculated rotational and quartic and sextic centrifugal-distortion constants are compared to the scaled ones, along with their experimental counterparts (Cazzoli & Puzzarini 2014; Azzam et al. 2013). Good agreement between the scaled and experimental results for H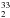S and H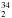S is noted, thus confirming the reliability of the scaling procedure. In detail, we note that the discrepancies with respect to experiment are negligible for the rotational constants, i.e., on the order of 0.0001%, while they range from ~0.001% to ~0.01% for the quartic centrifugal-distortion constants and amount to less than 1% for the sextic centrifugal terms. Subsequently, the scaling procedure applied to H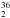S led to the results reported in Table 2, where they are compared to those of Azzam et al. (2013). We note that the rotational constants of this work deviate from our scaled estimates by 8 to 20 MHz. Large discrepancies are also observed for the centrifugal-distortion constants, with even a sign change in the case of the sextic h1 term. Figure 3 shows the comparison of the predicted rotational spectrum in the 700−800 GHz frequency range based on our scaled parameters with the one based on the spectroscopic constants of Azzam et al. (2013). We note that the deviations range from 30 to 184 MHz. In the lefthand inset, the actually recorded lines are depicted as well, thus demonstrating the good agreement of the observed spectrum with the present prediction.

Based on the scaled spectroscopic parameters, we searched for and assigned the rotational transitions of H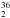S in the 167 GHz−1.6 THz range mentioned above (the complete list of measured transitions is available in electronic form at the CDS). These were then included in a global fit that also involves the frequency values for the vibrational ground state up to about 6.7 THz from Azzam et al. (2013). As for the other isotopic species of hydrogen sulfide (Cazzoli & Puzzarini 2014; Azzam et al. 2013), the fitting procedure was carried out with Pickett’s SPFIT program (2009; Pickett 1991) employing Watson’s S-reduced Hamiltonian in the Ir representation (Watson 1977) with each transition weighted proportionally to the inverse square of its experimental uncertainty. In total, 112 distinct frequency lines were used for obtaining 24 distinct constants up to the eighth-order centrifugal-distortion terms (plus one decic constant). The results are collected in Table 2, and they show the same good agreement with the scaled parameters as the one we already noted for the other isotopologues. This further confirms that the parameters of Azzam et al. (2013) are not reliable, despite being rather well determined. The problem in the spectroscopic analysis reported in Azzam et al. (2013) is probably due to the lack of transitions recorded in the low-frequency regime.

Table 2

Computed, scaled, and experimental spectroscopic constants (MHz) of H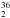S.

The present case is thus an illustrative example of the importance of having good theoretical estimates to rely on when a spectroscopic characterization is carried out for the first time: that is, with the availability of such estimates, the determination of unreliable parameters in Azzam et al. (2013) could have been avoided. The use of theoretical data is particularly important when a limited set of data is available, since this can easily lead to different sets of parameters from fits that all show acceptable standard deviations. In fact, none of the transitions from Azzam et al. (2013) was discarded from our fit. By comparing the present results with those by Azzam et al. (2013), it is also evident that, as a consequence of the deviations affecting the rotational and quartic centrifugal-distortion constants, some sextic and octic centrifugal-distortion constants could not be determined. On the other hand, in Azzam et al. (2013) inclusion of higher-order terms was required to reproduce the measured transition frequencies, while in the present study we demonstrated that they are not needed.

A final comment concerns the very first attempt to observe the rotational spectrum of H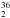S. In Saleck et al. (1995), the authors investigated the millimeter- and submillimeter-wave spectra of various rare isotopologues of hydrogen sulfide. While they provided a rather good spectroscopic characterization of the 33S- and 34S-containing species, they only tentatively assigned three rotational transitions to H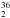S. As pointed out in Azzam et al. (2013), only one of the latter (the J = 20,2 ← 11,1 transition at 686.8 GHz) actually belongs to the molecule under consideration, while the other two show deviations of several hundred MHz from the actual lines of H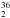S.

Finally, to provide reliable spectroscopic parameters for future experimental investigations, the scaling procedure described above was also applied to several rare mono- and bi-deuterated isotopologues of hydrogen sulfide. Owing to the considerable change in the spectroscopic parameters upon deuteration, HD32S and D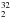S were used here as parent species for the mono- and bi-deuterated species, respectively. The scaled spectroscopic parameters of HD33S, HD34S, D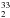S, and D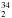S are collected in Table 3 (the calculated spectroscopic constants of HD32S, HD33S, HD34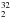S, DS, D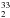S, and D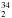S are found in the Appendix: Supplementary Table A.1), where they are compared with the limited experimental data available for HD34S and D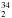S (Camy-Peyret et al. 1985). For HD32S, the experimental rotational and centrifugal-distortion constants are those recently obtained by the present authors (Cazzoli et al., in prep.), while for D2S the experimental parameters were obtained from a fit of the transitions available in the Cologne database (Müller et al. 2001; Müller et al. 2005), thereby using Watson’s S reduction. (The reader is also referred to the original works: Hillger & Strandberg 1951; Camy-Peyret et al. 1985.) For D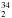S, good agreement is observed, thus suggesting that the rotational and quartic centrifugal-distortion constants of Camy-Peyret et al. (1985) should be considered reliable. With the present study, we therefore can only improve the spectroscopic characterization by providing reliable sextic terms. In Camy-Peyret et al. (1985), the sextic and higher order terms were kept fixed at the corresponding values for D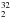S. For HD34S, the differences between the scaled and experimental rotational constants range from 5 MHz for A to ~37 MHz for C and ~39 MHz for B. In view of the proved reliability of our scaled parameters, an experimental re-investigation is deserved for this isotopic species. For HD33S and D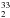S, our scaled parameters provide the first isotopic characterization.

thumbnail Fig. 3

Rotational spectrum of HS in the 700−800 GHz frequency range: the predictions obtained using our scaled parameters (in blue) and those based on the spectroscopic constants of Azzam et al. (2013) are compared. In the insets, this comparison is shown in more detail; on the left side, a comparison with the recorded spectra is provided.

Table 3

Spectroscopic constants (MHz) of the mono- and bi-deuterated isotopologues of hydrogen sulfide.

4. Conclusions

In the present work we have presented the first complete, accurate spectroscopic characterization of the rotational spectrum of H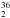S. A key point was the interplay of theory and experiment, which revealed the incorrectness of the previously reported spectroscopic constants and provided reliable parameters to guide the experimental investigation. The latter was made possible thanks to the high sensitivity of our millimeter-/submillimeter-wave spectrometer, which permitted the rotational spectrum of this rare isotopologue to be recorded in natural abundance (0.02%) with an extremely good signal-to-noise ratio. The present study was complemented by providing accurate predictions for other rare isotopic species, namely HD33S, HD34S, D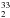S, and D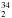S.

According to Mauersberger et al. (2004), 36S is one of the stable nuclei in nature with possible different nucleosynthesis scenarios being discussed, and a number of questions are still open. It would therefore be of great interest to extend the detection in space to other 36S-containing compounds than CS and SiS, as well as to other astronomical sources. By reporting accurate spectroscopic parameters for H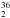S, the 36S-containing isotopologue of one of the most abundant sulfur-bearing gas-phase species in different astronomical objects, we thus offer a reliable opportunity for accomplishing this task.

Appendix A

Table A.1

Calculated spectroscopic constants (MHz) of the mono- and bi-deuterated isotopologues of hydrogen sulfide.

Acknowledgments

This work has been supported by Italian MIUR (PRIN 2012 funds) and the University of Bologna (RFO funds), as well as in Mainz by the Deutsche Forschungsgemeinschaft (DFG GA 370/5-1) and the Fonds der Chemischen Industrie.

References

  1. Aliev, M. R. & Watson, J. K. G. 1985, in Molecular Spectroscopy: Modern Research, Vol. III, ed. K. N. Rao (New York: Academic Press), 1 [Google Scholar]
  2. Azzam, A. A. A., Yurchenko, S. N., Tennyson, J., Martin-Drumel, M.-A., & Pirali, O. 2013, J. Quant. Spectrosc. Radiat. Transf., 130, 341 [NASA ADS] [CrossRef] [Google Scholar]
  3. Belov, S. P., Yamada, K. M. T., Winnewisser, G., et al. 1995, J. Mol. Spectrosc., 173, 380 [NASA ADS] [CrossRef] [Google Scholar]
  4. Camy-Peyret, C., Flaud, J.-M., & Lechuga-Fossat, L. 1985, J. Mol. Spectrosc., 109, 300 [NASA ADS] [CrossRef] [Google Scholar]
  5. Cazzoli, G., & Puzzarini, C. 2006, J. Mol. Spectrosc., 240, 153 [NASA ADS] [CrossRef] [Google Scholar]
  6. Cazzoli, G., & Puzzarini, C. 2014, J. Mol. Spectrosc., 298, 31 [NASA ADS] [CrossRef] [Google Scholar]
  7. Ding, T., Valkiers, S., Kipphardt, H., et al. 2001, Geochim. Cosmochim. Acta, 65, 2433 [Google Scholar]
  8. Dunning, Jr., T. H. 1989, J. Chem. Phys., 90, 1007 [NASA ADS] [CrossRef] [Google Scholar]
  9. Heckert, M., Kállay, M., & Gauss, J. 2005, Mol. Phys., 103, 2109 [NASA ADS] [CrossRef] [Google Scholar]
  10. Heckert, M., Kállay, M., Tew, D. P., Klopper, W., & Gauss, J. 2006, J. Chem. Phys., 125, 044108 [NASA ADS] [CrossRef] [Google Scholar]
  11. Helgaker, T., Gauss, J., Cazzoli, G., & Puzzarini, C. 2013, J. Chem. Phys., 139, 244308 [NASA ADS] [CrossRef] [Google Scholar]
  12. Hillger, R. E., & Strandberg, M. W. P. 1951, Phys. Rev., 83, 575 [NASA ADS] [CrossRef] [Google Scholar]
  13. Ikeda, M., Hirota, T., Yamamoto, S. 2002, ApJ, 575, 250 [NASA ADS] [CrossRef] [Google Scholar]
  14. Macdonald, G. H., Gibb, A. G., Habing, R. J., & Millar, T. J. 1996, A&AS, 119, 333 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Mauersberger, R., Henkel, C., Langer, N., & Chin, Y.-N. 1996, A&A, 313, L1 [NASA ADS] [Google Scholar]
  16. Mauersberger, R., Ott, U., Henkel, C., Cernicharo, J., & Gallino, R. 2004, A&A, 426, 219 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Mills, I. M. 1972, in Molecular Spectroscopy: Modern Research, eds. K. N. Rao, & C. W. Mathews (New York: Academic), 115 [Google Scholar]
  18. Minh, Y. C., Irvine, W. M., & Ziurys, L. M. 1989, ApJ, 345, L63 [NASA ADS] [CrossRef] [Google Scholar]
  19. Minh, Y. C., Irvine, W. M., McGonagle, D., & Ziurys, L. M. 1990, ApJ, 360, 136 [NASA ADS] [CrossRef] [Google Scholar]
  20. Müller, H. S. P., Thorwirth, S., Roth, D. A., & Winnewisser, G. 2001, A&A, 370, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [NASA ADS] [CrossRef] [Google Scholar]
  22. Peterson, K. A., & Dunning, Jr., T. H. 2002, J. Chem. Phys., 117, 10548 [NASA ADS] [CrossRef] [Google Scholar]
  23. Pickett, H. M. 1991, J. Mol. Spectrosc., 148, 371 [Google Scholar]
  24. Pickett, H. M. 2009, SPFIT/SPCAT package, available at http://spec.jpl.nasa.gov [Google Scholar]
  25. Puzzarini, C. 2013, Phys. Chem. Chem. Phys., 15, 6595 [CrossRef] [PubMed] [Google Scholar]
  26. Puzzarini, C., Heckert, M., & Gauss, J. 2008, J. Chem. Phys., 128, 194108 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  27. Puzzarini, C., Stanton, J. F., & Gauss, J. 2010, Int. Rev. Phys. Chem., 29, 273 [CrossRef] [Google Scholar]
  28. Puzzarini, C., Cazzoli, G., López, J. C., et al. 2012a, J. Chem. Phys., 137, 024310 [NASA ADS] [CrossRef] [Google Scholar]
  29. Puzzarini, C., Cazzoli, G., & Gauss, J. 2012b, J. Chem. Phys., 137, 154311 [NASA ADS] [CrossRef] [Google Scholar]
  30. Raghavachari, K., Trucks, G. W., Pople, J. A., & Head-Gordon, M. 1989, Chem. Phys. Lett., 157, 479 [NASA ADS] [CrossRef] [Google Scholar]
  31. Saleck, A. H., Tanimoto, M., Belov, S. P., Klaus, T., & Winnewisser, G. 1995, J. Mol. Spectrosc., 171, 481 [NASA ADS] [CrossRef] [Google Scholar]
  32. Schneider, W., & Thiel, W. 1989, Chem. Phys. Lett., 157, 367 [NASA ADS] [CrossRef] [Google Scholar]
  33. Shavitt, I., & Bartlett, R. J. 2009, Many-Body Methods in Chemistry and Physics: MBPT and Coupled-Cluster Theory (Cambridge: Cambridge University Press) [Google Scholar]
  34. Stanton, J. F., & Gauss, J. 1997, Chem. Phys. Lett., 276, 70 [NASA ADS] [CrossRef] [Google Scholar]
  35. Stanton, J. F., & Gauss, J. 2000, Int. Rev. Phys. Chem., 19, 61 [CrossRef] [Google Scholar]
  36. Stanton, J. F., Lopreore, C. L., & Gauss, J. 1998, J. Chem. Phys., 108, 7190 [NASA ADS] [CrossRef] [Google Scholar]
  37. Stanton, J. F., Gauss, J., Harding, M. E., Szalay, P. G., et al. 2013, For the current version, see http://www.cfour.de [Google Scholar]
  38. Tennyson, J., & Yurchenko, S. N. 2012, MNRAS, 425, 21 [Google Scholar]
  39. Thaddeus, P., Kutner, M. L., Penzias, A. A., Wilson, R. W., & Jefferts, K. B. 1972, ApJ, 176, L73 [NASA ADS] [CrossRef] [Google Scholar]
  40. Tielens, A. G. G. M. 2013, Rev. Mod. Phys., 85, 1021 [NASA ADS] [CrossRef] [Google Scholar]
  41. Ukita, N., & Morris, M. 1983, A&A, 121, 15 [NASA ADS] [Google Scholar]
  42. Vastel, C., Phillips, T. G., Ceccarelli, C., & Pearson, J. C. 2003, ApJ, 593, L97 [NASA ADS] [CrossRef] [Google Scholar]
  43. Visscher, C., Lodders, K., & Fegley, Jr., B. 2006, A&A, 648, 1181 [Google Scholar]
  44. Watson, J. K. G. 1977, in Vibrational Spectra and Structure, Vol. 6, ed. J. R. Durig (Amsterdam, The Netherlands: Elsevier), 1 [Google Scholar]
  45. Winnewisser, G., Herbst, E., & Ungerechts, H. 1992, in Spectroscopy of the Earth’s Atmosphere and Interstellar Medium, eds. K. N. Rao, & A. Weber (San Diego, USA: Academic Press), 423 [Google Scholar]
  46. Woon, D. E., & Dunning, Jr., T. H. 1993, J. Chem. Phys., 98, 1358 [CrossRef] [Google Scholar]
  47. Zahnle, K., Marley, M. S., Freedman, R. S., Lodders, K., & Fortney, J. J. 2009, ApJ, 701, L20 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Computed, scaled, and experimental spectroscopic constants (MHz) of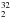 HS, H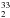S, and H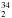S.

In the text
Table 2

Computed, scaled, and experimental spectroscopic constants (MHz) of HS.

In the text
Table 3

Spectroscopic constants (MHz) of the mono- and bi-deuterated isotopologues of hydrogen sulfide.

In the text
Table A.1

Calculated spectroscopic constants (MHz) of the mono- and bi-deuterated isotopologues of hydrogen sulfide.

In the text

All Figures

thumbnail Fig. 1

The J = 54,1 ← 53,2 transition at 399.6 GHz (left side: P = 28 mTorr/3.7 Pa, mod. depth = 600 kHz) and the J = 42,3 ← 41,4 transition at 1023.4 GHz (right side: P = 57 mTorr/7.6 Pa, mod. depth = 1800 kHz) recorded in natural abundance.

In the text
thumbnail Fig. 2

Portion of the recorded spectrum at 731 GHz (P = 60 mTorr/8.0 Pa, frequency modulation = 1.2 MHz): the J = 55,1 ← 54,2 transition of HS and the J = 107,3 ← 106,4 transition of HS are evident. The predicted position of the J = 55,1 ← 54,2 transition of HS according to the spectroscopic constants of Azzam et al. (2013) is also depicted.
In the text
thumbnail Fig. 3

Rotational spectrum of HS in the 700−800 GHz frequency range: the predictions obtained using our scaled parameters (in blue) and those based on the spectroscopic constants of Azzam et al. (2013) are compared. In the insets, this comparison is shown in more detail; on the left side, a comparison with the recorded spectra is provided.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.