| Issue |
A&A
Volume 566, June 2014
|
|
|---|---|---|
| Article Number | A117 | |
| Number of page(s) | 7 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201322008 | |
| Published online | 23 June 2014 | |
Research Note
Constraints on the height of the inner disk rim in pre-main-sequence stars⋆
1 Physics Department, University of Split, Nikole Tesle 12, 21000 Split, Croatia
e-mail: vinkovic@pmfst.hr
2 Science and Society Synergy Institute, Bana J. Jelačića 22B, 40000 Čakovec, Croatia
e-mail: dejan@iszd.hr
Received: 3 June 2013
Accepted: 24 April 2014
The structure of inner region of protoplanetary disks around young pre-main-sequence stars is still poorly understood. This part of the disk is shaped by various forces that influence dust and gas dynamics, and by dust sublimation, which creates abrupt drops in the dust density. This region also emits strong near-infrared excess that cannot be explained by classical accretion disk models, which suggests the existence of some unusual dust distribution or disk shape. The most prevalent explanation to date is the puffed-up inner disk rim model, where the disk exhibits an optically thin cavity around the star up to the distance of dust sublimation. The critical parameter in this model is the inner disk rim height zmax relative to the rim distance from the star Rin. Observations often require zmax/Rin ≳ 0.2 to reproduce the near-infrared excess in the spectra. We compile a comprehensive list of processes that can shape the inner disk rim and combine them into a self-consistent model. Two of them, radiation pressure force and the gas velocity profile, have never been applied in this context before. The aim was to find the most plausible theoretical values of zmax/Rin. The results show that this value is ≲0.13 for Herbig Ae stars, ≲0.11 for T Tau stars, and ≲0.10 for young brown dwarfs. This is lower than the observational requirements for Herbig Ae stars. We argue that the same problem exists in T Tau stars as well. We conclude that the puffed-up inner rim model cannot be the sole explanation for the near-infrared excess in young pre-main-sequence stars.
Key words: accretion, accretion disks / stars: pre-main sequence / protoplanetary disks / infrared: stars
Appendix is available in electronic form at http://www.aanda.org
© ESO, 2014
1. Introduction
Protoplanetary disks surrounding young pre-main-sequence stars have been a subject of intense theoretical and observational scrutiny in recent decades (Williams & Cieza 2011). Since these disks are expected to host planet formation, particular focus has been on dust properties and dust distribution within the disks. While this led to an advanced understanding of the dust evolution beyond ~1 AU from the star, the inner disk region within ≲1 AU remained a controversial topic (Millan-Gabet et al. 2007; Dullemond & Monnier 2010). The main obstacle is the inability of current telescopes to spatially resolve this region, except by the near-infrared interferometry, which in itself depends on modeling assumptions and currently provides valuable but still limiting information on the disk structure (Wolf et al. 2012).
The inner disk rim is observable at near-infrared wavelengths because dust emission in this part of the disk comes from dust temperatures above 1000 K. Even the most resilient dust grains sublimate in these conditions, but the exact sublimation distance from the star depends on the grain size and chemistry and on the local gas pressure. Removal of dust grains creates large steps in the opacity gradient, which complicates modeling the dusty disk structure (Kama et al. 2009; Vinković 2012). Modeling efforts have therefore been devoted to approximate methods, motivated by the peculiar near-infrared bump in the spectral energy distribution of many pre-main-sequence stars.
This bump was first noticed in Herbig Ae/Be stars by Hillenbrand et al. (1992), while Chiang et al. (2001) showed that ordinary accretion disk models do not produce enough flux to explain the bump. Dullemond et al. (2001) introduced the most popular explanation for this phenomenon to date, based on the assumption that the disk gas is optically thin close to the star in the zone where dust grains cannot survive. This allows stellar radiation to heat the whole vertical profile of the inner dusty disk rim, including the disk interior, which is typically much colder than the disk surface. This causes the disk to expand vertically, or “puff-up”, which also increases the emitting area of the hot dusty disk rim. The near-infrared bump is then merely a measure of how much the disk expands vertically.
That assumption of an optically thin hole was confirmed by near-infrared interferometry (Millan-Gabet et al. 2001, 2007), which boosted the popularity of the puffed-up disk model. The model was additionally improved (e.g. Dullemond & Dominik 2004a,b; Isella & Natta 2005; Tannirkulam et al. 2007; Thi et al. 2011) and is still the most prevalent description of the inner disk structure (Dullemond & Monnier 2010). However, over the years, two main concerns about the plausibility of the model have been raised. One concern is that the near-infrared excess predicted by the puffed-up disk model is too low to explain the strongest near-infrared bumps, unless physically unrealistic vertical puffing is invoked, with heights several times above hydrostatic equilibrium (D’Alessio et al. 2006; Vinković et al. 2006; Meijer et al. 2008; Schegerer et al. 2008; Acke et al. 2009; Verhoeff et al. 2010, 2011; Mulders & Dominik 2012; McClure et al. 2013a). In addition, as Mulders & Dominik (2012) explain in their Appendix C, such strong puffing up casts a shadow over large parts of the outer disk, which would decrease the disk temperature and reduce its mid-infrared emission below the observed levels. Moreover, the claim that an optically thin hole does not contribute to the near-infrared excess and images has been challenged recently by some interferometry observations (Akeson et al. 2005; Tannirkulam et al. 2008; Benisty et al. 2010, 2011) and also theoretically (Vinković 2006; Kama et al. 2009).
The other concern is that the theoretical approaches to the modeling of the inner disk have been lacking some critical physical elements and therefore cannot correctly describe its structure. Small grains have often been included into the dust opacity of the inner rim, but now we know that the shape of inner disk rim is dictated solely by big grains (≳1 μm) because they are more resilient to sublimation than smaller grains. Hence, big grains populate the inner disk surface and shield smaller grains in the disk interior from direct stellar radiation (Kama et al. 2009; Vinković 2012). An unexpected consequence of radiative transfer in big grains is that the location of the inner disk rim becomes a nontrivial problem, with the temperature inversion effect producing a local temperature maximum within the dust cloud (see Appendix A). Here we focus only on the height and shape of optically thick disk, where we use the simple prescription for the rim radius presented by Vinković (2006).
Moreover, processes such as vertical gas velocity profile (Takeuchi & Lin 2002) or radiation pressure on dust grains (Takeuchi & Lin 2003; Vinković 2009) have been lacking from the debate on the puffed-up rim model. In this paper we construct a model that takes into consideration a comprehensive list of physical processes that influence the rim shape. Our goal is to find zmax/Rin for a wide range of disk parameters and determine constraints on the applicability of the puffed-up inner rim model.
2. Physics of the inner disk structure
 |
Fig. 1 Sketch of the disk and processes used in our calculations. Three shades of gray show the regions clear of dust, with optically thin dust, and with optically thick dust. The beginning of the optically thick disk at Rin is defined as the disk rim. White dots mark the zone dominated by big grains, L∗ is the stellar luminosity, Lacc is the accretion luminosity, VH the viscous heating, TD the turbulent diffusion, G the gravity, C the centrifugal force, DS the dust settling due to the gas drag force, PG the gas pressure gradient, RP the radiation pressure, and VP is the gas velocity profile. |
We implemented various physical processes discussed previously in the context of protoplanetary disks, although not necessarily applied to the problem of inner disk rim. A detailed list of equations used in our calculation is given in Appendix A, while here we present only a short version. A list of the physical processes together with a sketch of the disk geometry is given in Fig. 1. We considered an axially symmetric disk, described with a cylindrical coordinate system where r is in the disk midplane and z is in the direction of the disk symmetry axis. We used 1 AU as the unit of distance and one year as the unit of time.
The concept of puffed-up inner rim model is related to the optically thick disk surface. Hence, we define the location of the inner rim Rin as the midplane distance of optically thick dust from the star (Vinković 2006) ![\begin{equation} \label{Rin_thin_thick} R_{\rm in}=0.0344\Psi\left( \frac{1500~{\rm K}}{T_{\rm sub}} \right)^2 \sqrt{\frac{L_*+L_{\rm acc}}{L_\odot}} \,\,\,\,\,\mathrm{[AU]}, \end{equation}](/articles/aa/full_html/2014/06/aa22008-13/aa22008-13-eq16.png) (1)where L∗ is the stellar luminosity, Lacc is the accretion luminosity, and Ψ = 2 is the coefficient accounting for the effect of optically thick dust back-heating. This is also the place of local temperature maximum equal to local values of Tsub (see Fig. 3 in Kama et al. 2009). High-resolution radiative transfer calculation shows that the entire inner rim experiences temperatures close to Tsub, with dominantly radial temperature variation close to the rim (Vinković 2012). Hence, a vertically isothermal disk is a good approximation as long as we consider only the rim properties. The disk temperature in this narrow zone is then described with
(1)where L∗ is the stellar luminosity, Lacc is the accretion luminosity, and Ψ = 2 is the coefficient accounting for the effect of optically thick dust back-heating. This is also the place of local temperature maximum equal to local values of Tsub (see Fig. 3 in Kama et al. 2009). High-resolution radiative transfer calculation shows that the entire inner rim experiences temperatures close to Tsub, with dominantly radial temperature variation close to the rim (Vinković 2012). Hence, a vertically isothermal disk is a good approximation as long as we consider only the rim properties. The disk temperature in this narrow zone is then described with 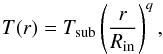 (2)where we treat q as a free parameter, while dust sublimation Tsub depends on the local gas density ρgas (Pollack et al. 1994).
(2)where we treat q as a free parameter, while dust sublimation Tsub depends on the local gas density ρgas (Pollack et al. 1994).
The gas is in vertical hydrostatic equilibrium 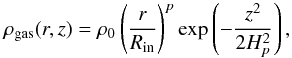 (3)where ρ0 = ρgas(Rin,0) is the midplane gas density at the inner disk rim, Hp(r) = cs(r) / ΩK(r) is the disk scale height that varies with r, cs is the isothermal sound speed, and ΩK is the Keplerian angular velocity at the midplane.
(3)where ρ0 = ρgas(Rin,0) is the midplane gas density at the inner disk rim, Hp(r) = cs(r) / ΩK(r) is the disk scale height that varies with r, cs is the isothermal sound speed, and ΩK is the Keplerian angular velocity at the midplane.
Accretion of the gas onto the star contributes with accretion luminosity to the total energy that heats the inner rim (Muzerolle et al. 2004). To accommodate for this effect we calculated the accretion luminosity using the accretion rate Ṁacc derived from the vertical profile of the gas density and the horizontal velocity of gas flow (see Appendix A). We used the horizontal component of the gas velocity derived by Takeuchi & Lin (2002)![\begin{equation} {v}_{\rm r,gas}(r,z)=-\frac{\alpha c_{\rm s} H_p}{r}\left( 3p+2q+6+\frac{5q+9}{2}\frac{z^2}{H_p^2} \right) \left[\mathrm{ \frac{AU}{year} }\right], \end{equation}](/articles/aa/full_html/2014/06/aa22008-13/aa22008-13-eq28.png) (4)who used the α-prescription for the viscous effect of turbulence (Shakura & Sunyaev 1973; Pringle 1981). The inward accretion exists only if p + 3(q + 1) / 2 > − 2 (Takeuchi & Lin 2002). The accretion rate depends on the distance from the star, except for q = −0.5 when the radial velocity is independent of r and the disk is in steady-state. We focused our attention on a very small part of the disk around Rin, where Ṁacc varies slowly with r. Hence, we define the accretion rate as Ṁacc(Rin). In Appendix A, we show Ṁacc ∝ ρ0 and how we derive ρ0 from Ṁacc, which is in turn derived from Lacc ∝ Ṁacc.
(4)who used the α-prescription for the viscous effect of turbulence (Shakura & Sunyaev 1973; Pringle 1981). The inward accretion exists only if p + 3(q + 1) / 2 > − 2 (Takeuchi & Lin 2002). The accretion rate depends on the distance from the star, except for q = −0.5 when the radial velocity is independent of r and the disk is in steady-state. We focused our attention on a very small part of the disk around Rin, where Ṁacc varies slowly with r. Hence, we define the accretion rate as Ṁacc(Rin). In Appendix A, we show Ṁacc ∝ ρ0 and how we derive ρ0 from Ṁacc, which is in turn derived from Lacc ∝ Ṁacc.
The local viscous dissipation of energy in accretion disks contributes to the local disk temperature, and we determined this effect. Hence, the net temperature at Rin is the combination 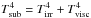 (Ciesla & Cuzzi 2006) of the temperature from stellar irradiation and from viscous heating (see Appendix A for details). This condition has to be checked iteratively during the determination of Rin.
(Ciesla & Cuzzi 2006) of the temperature from stellar irradiation and from viscous heating (see Appendix A for details). This condition has to be checked iteratively during the determination of Rin.
Another process we considered is the radial migration of dust particles in the gas disk. We followed the prescription by Takeuchi & Lin (2002), where dust particles are driven by gas drag and their radial velocity depends on the distance from the midplane. The source of this vertical velocity variation is the gas pressure gradient, which causes two effects: gas rotation is different from Keplerian rotation above the midplane, and the gas drag force depends on gas density.
Without gas drag, dust particles would follow Keplerian orbits. We considered particles smaller than the mean free path of gas molecules. Their motion is described with Epstein’s gas drag law. We also considered turbulent disks where the gas turbulent motion stirs up dust particles to higher altitudes and prevents dust sedimentation. The equilibrium distribution of dust particles is reached when the sedimentation due to gas drag and the diffusion due to turbulence are balanced. Using the α-prescription for the viscous effect of turbulence, the dust density distribution is (Takeuchi & Lin 2002) 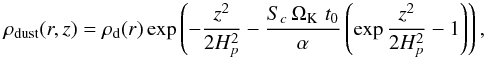 (5)where ρd(r) is the midplane dust density profile and t0(r) is given in Appendix A. The Schmidt number Sc is a measure of the coupling between the particles and the gas. Even though Sc ~ 1 for the particle sizes used in our paper, we adopted the expression for Sc suggested by (Youdin & Lithwick 2007; see Appendix A for details).
(5)where ρd(r) is the midplane dust density profile and t0(r) is given in Appendix A. The Schmidt number Sc is a measure of the coupling between the particles and the gas. Even though Sc ~ 1 for the particle sizes used in our paper, we adopted the expression for Sc suggested by (Youdin & Lithwick 2007; see Appendix A for details).
Takeuchi & Lin (2003) showed that stellar radiation pressure force slowly erodes the dusty disk surface, but they did not investigate the impact of this force on the surface of inner disk rim. We used their methodology to include the radiation pressure force into the dust velocity profiles. We ignored the complicated infrared radiation pressure force of photons from the disk interior because this force can only enhance the disk erosion (Vinković 2009). Hence, the radial component of dust velocity is (Takeuchi & Lin 2003) ![\begin{equation} \mathrm{v}_{\rm r,dust}(r,z)=\frac{\mathrm{v}_{\rm r,gas}+(\beta-\eta)\,r\,t_{\rm drag}\,\Omega_{\rm K}^2} {1+t_{\rm drag}^2\Omega_{\rm K}^2} \left[\mathrm{ \frac{AU}{year} }\right] , \end{equation}](/articles/aa/full_html/2014/06/aa22008-13/aa22008-13-eq42.png) (6)where β is the ratio between the stellar radiation pressure force and gravity and η is a parameter given in Appendix A.
(6)where β is the ratio between the stellar radiation pressure force and gravity and η is a parameter given in Appendix A.
Our goal is to find the relative height zmax/Rin above which the outward flow vr,dust> 0removes dust from the disk rim. The disk volume below the height zmax can be populated entirely by dust on long timescales, but above this limit dust grains are quickly eroded. From the radiative transfer point of view, the ratio zmax/Rin measures the maximum fraction of the stellar radiation intercepted by the disk rim, which in turn is the maximum energy reemitted into the near-infrared.
Parameters of our disk model and their range of values.
3. Results
 |
Fig. 2 Example of model results showing the variation of horizonal velocities with height above the midplane (measured in scale heights). Lines show velocities of gas (dotted line), dust without the force of radiation pressure (long-dashed line), dust with the force (solid line), and zero velocity separating inflow from outflow (horizonal short-dashed line). Model parameters used in this result are T∗ = 10 000 K, L∗ = 40 L⊙, Lacc = 5 L⊙, M∗ = 2.5 M⊙, q = −0.5, p = −2.25, a = 1 μm, ρgrain = 3 g/cm3, and α = 0.01. The model output is ρ0 = 2.6 × 10-9 g/cm3, Ṁacc = 1.7 × 10-7M⊙/year, and Rin = 0.54 AU. The dusty disk is truncated at a height of zmax = 3.24Hp = 0.11Rin (the point where dust turns from inflow to outflow). |
We explored a wide range of parameters (see Table 1) for Herbig Ae and T Tau stars and brown dwarfs. The ranges of accretion luminosities are based on observational data (Natta et al. 2006; Herczeg et al. 2009; Donehew & Brittain 2011; Mendigutía et al. 2012). In total, more than 6000 models were calculated. Some models result in unrealistically large disk masses (that would lead to gravitational instabilities), but nevertheless, we did not exclude them from the analysis. The accretion rates are lower than 10-6M⊙ yr-1, which is consistent with the assumption of optically thin gas within Rin (Muzerolle et al. 2004). The dust optical constants are taken from Dorschner et al. (1995). We used two extreme types of grains: solids with 3 g/cm3 in density and highly porus, fluffy aggregates with 0.1 g/cm3.
Figure 2 shows a typical model outcome. The horizontal component of the dust velocity at Rin depends on height and directs the flow of gas. The flow varies with height between outflow and inflow regimes. Dust motion is dictated by gas within a couple of gas scale heights from the midplane. Depending on the radial gas density profile, this flow can start as a slow outflow in the midplane before it turns into inflow above the midplane. The gas flow would dictate the dust dynamics even at larger heights, but the radiation pressure force starts to dominate and dust drifts into outflow. The transition from inflow to outflow is at zmax. Without the radiation pressure dust grains would follow the gas until gas and dust decouple and the results would be identical to the work by Takeuchi & Lin (2002).
 |
Fig. 3 Shape of inner disk surface defined as the radial optical depth of τ = 1 (solid line). The model parameters are the same as in Fig. 2. The inner disk radius Rin is marked with the dotted line (the velocity profiles in Fig. 2 follow this line). The dust density scale is set by using the spatial length of 10-5 AU in the midplane between Rin and τ = 1. The radiation pressure force dominates the region above the dot-dot-dashed line and moves dust particles outward. The disk surface without radiation pressure would extend as far as the dashed line. |
The inability of the dust to move inward in the zone above zmax has consequences for the shape of the inner disk surface. An estimate of the inner disk edge shape is shown in Fig. 3, based on the model from Fig. 2. The shape is defined as the surface where the radial optical depth is τ = 1. The dust density scale ρ0 is defined by setting the spatial depth of τ = 1 at Rin in the midplane (this depth is so low that Rin can be treated as the distance of optically thick surface from the star). The figure shows how the surface curves because of dust density drop with height (as was also shown by Tannirkulam et al. 2007), but only at heights below the dust outflow zone created by the radiation pressure force. The dust density can be increased to boost the disk surface height, but only within the dust inflow zone.
 |
Fig. 4 Distribution of zmax/Rin values relative to the mass accretion rate Ṁacc (in units of M⊙ yr-1), the power law p of the disk density change from Eq. (3), the temperature power law q from Eq. (2), and the inner disk radius Rin from Eq. (1). Results are shown for three types of objects, as indicated in the figure: Herbig Ae, T Tau, and brown dwarfs. The box-and-whisker plots at the far right show the range of results for each object: boxes show the median line and the first and third quartile, while the whiskers show the 10th and 90th percentile. |
Dust sublimation does not enter as a sharp boundary condition into the shaping of the disk surface, as is typically assumed (e.g. Isella & Natta 2005; Tannirkulam et al. 2007), because big dust grains can survive in the optically thin zone closer to the star than Rin (see examples by Kama et al. 2009 and Vinković 2012). Hence, in this estimate we ignored optically thin dust within Rin because we have no information on its density structure (Vinković 2012).
The main result is shown in Fig. 4. The values of zmax/Rin in all models are ≲0.13 for Herbig Ae stars, ≲0.11 for T Tau stars, and ≲0.10 for young brown dwarfs. The figure shows that the values vary with Ṁacc, p, q and Rin, where variations of values used for Lacc create a spread in Ṁacc and Rin.
4. Discussion
If the near-infrared excess is purely caused by the dusty disk emission, the amount of near-infrared excess at ~ 2 μm is a direct measure of the inner disk rim height (Vinković et al. 2006; Mulders & Dominik 2012). Measurements of spectral energy distribution of Herbig Ae stars imply that for many objects the rim height must be zmax/Rin ≳ 0.2 (Akeson et al. 2005; Vinković et al. 2006; Eisner et al. 2007; Meijer et al. 2008; Schegerer et al. 2008; Acke et al. 2009; Mulders & Dominik 2012). This implies that the inner rim heights shown in Fig. 4 are not sufficient to explain strong near-infrared bumps. Some additional sources of the near-infrared excess must be present.
Moreover, the heights in our model do not produce a self-shadowing of the disk (Fig. 3), which was one of the important consequences of the puffed-up rim model (Dullemond & Monnier 2010). High values of rim heights were derived by Dullemond & Dominik (2004a) using hydrostatic equilibrium disk models with very steep radial density profiles. They demonstrated self-shadowing for p = −4, but this implies a disk with almost all of its mass within the inner 1 AU from the star, which is unrealistic (as was pointed out by D’Alessio et al. 2006). Their models did not take into account the role of big dust grains in shaping the rim either. Their improved models that combine hydrostatic equilibrium, vertical dust settling, and turbulent mixing (Dullemond & Dominik 2004b) did not show the near-infrared bump. A comparison of these models with the data was performed recently by Mulders & Dominik (2012), who concluded that the models cannot explain the near-infrared bump.
Another important problem is the shape of the inner disk rim. The initial simple puffed-up rim model had a vertical wall (Dullemond et al. 2001), which does not agree with the near-infrared interferometry data (Dullemond & Monnier 2010). Therefore, the rim curvature has been modeled by several authors, but so far without the radiation pressure force and with a limited set of physical phenomena. Radiative transfer methods used by Isella & Natta (2005) and Tannirkulam et al. (2007; for Herbig Ae stars) and Mayne & Harries (2010; for brown dwarfs) were not appropriate for calculating temperature inversion effect at the inner rim. Furthermore, since they did not use grain size separation, where big grains shield small grains from the direct stellar radiation, the rim shape is not correct either. The drawbacks of these models were discussed by Kama et al. (2009), who also emphasized the importance of the temperature inversion effect in shaping the inner disk.
Our results imply that at least a fraction of the near-infrared excess must originate from some extension to the inner disk rim geometry. In the absence of detailed constraints, simple halo structures above the inner disk have been gaining popularity in recent years as a method to model the near-infrared observations (e.g. Vinković et al. 2006; Schegerer et al. 2008; Mulders et al. 2010; Verhoeff et al. 2011; Mulders & Dominik 2012; Kreplin et al. 2013; Mosoni et al. 2013). The assumption is that some dynamical process (or a combination of them) lifts dust out of the disk and creates an optically thin halo-like structure, such as magnetocentrifugally driven disk wind (Bans & Königl 2012), buoyancy due to magnetorotational instability (Turner et al. 2013), charged dust in the magnetic field (Ke et al. 2012), non-radial radiation pressure (Vinković 2009), and temperature decoupling in the disk surface between dust and gas (Thi et al. 2011).
Recent near-infrared observations of T Tau stars by McClure et al. (2013a) suggest that the inner rim of disks around their sample of T Tau stars has zmax/Rin ~ 0.2 − 0.4– too high to be explained solely by the puffed-up disk. They used a black-body fit to the near-infrared flux, which is equivalent to assuming that the emission from inner disk wall is dominated by big grains. Vinković et al. (2006) showed with exact 2D radiative transfer calculations that changing the grain size in the inner disk wall cannot reduce zmax/Rin and keeps the flux at the same level. However, McClure et al. (2013b) achieved this by using multiple rim walls of different grain size composition. Including viscous heating can explain their success for stars with Ṁacc ≳ 10-8M⊙/yr, but it is unclear how that worked for lower accretion rates or extreme wall heights. The discrepancy is probably due to their approximation of the inner rim surface as a mixture of grain sizes, while in reality grains separate by size and do not form multigrain surfaces (Vinković 2012). This approximation overestimates the inner disk radius and boosts the flux. Thus, our work, combined with previous 2D radiative transfer calculations, suggests that the extreme near-infrared excess detected in T Tau stars by McClure et al. (2013a) is difficult to explain by a puffed-up inner rim or its curvature.
5. Conclusions
We investigated the inner disk rim height using a self-consistent dust dynamics model based on a long list of physical processes: big dust grains populating the disk surface as the dust grains most resilient to the direct stellar heating, the temperature inversion effect that affects the position of the inner disk radius, accretion luminosity, viscous heating, turbulent diffusion, dust settling due to the gas drag force, vertical hydrostatic equilibrium, radiation pressure force, and the gas velocity profile. The last two processes have never been included in such an analysis before. The objects under consideration were Herbig Ae stars, T Tau stars, and brown dwarfs.
A wide range of parameters was explored, resulting in more than 6000 models of the rim height. The results were compared with the rim height implied by the observations of near-infrared excess from protoplanetary disks. Comparison showed that although we built a comprehensive self-consistent model, the modeled rim heights are insufficient to explain the observed flux of Herbig Ae stars. This confirms some previous studies that reached the same conclusion using models that incorporate a smaller list of physical processes. It also implies that some additional physical processes are influencing dust dynamics in such a way that they increase the overall volume of observed hot optically thin dust. This problem is closely related to the question of the shape (i.e. curvature) of the inner disk rim. We showed that radiation pressure creates a cut-off height above which the
dust flows outward. This means that the dusty disk cannot exist above this height unless some other forces counterbalance the radiation pressure force. We argued that recent observations of extreme near-infrared excess in T Tau stars are also indicative of extensions of the puffed-up inner rim model.
Online material
Appendix A: Theoretical model
First we devised a method for calculating the inner disk radius. The traditional approach was to use the dust sublimation temperature Tsub as a unique well-defined boundary condition, based on the assumption that the temperature drops with the distance from the star. However, it has been shown numerically (Kama et al. 2009; Vinković 2012) and theoretically (Vinković 2006) that the temperature of the big grains that populate the surface of the inner disk actually increases with distance within the optically thin dusty zone (see sketch in Fig. 1) before it starts to monotonically decrease within the optically thick dust. This temperature inversion effect results in a local temperature maximum within the dust cloud (see Fig. 3 in Kama et al. 2009), where dust can overheat. A precise calculation of the dust distribution that includes this effect requires information on the spatial dust distribution within the optically thin zone. Since the density structure of the optically thin dust zone cannot be geometrically constrained, we are left with a highly ambiguous concept of the inner disk rim.
Vinković (2006) proposed using two inner disk radii that distinguish between two coexisting – optically thin and thick – disk zones around a star of luminosity L∗: ![\appendix \setcounter{section}{1} \begin{equation} \label{A:Rin_thin_thick} R_{\rm in}=0.0344\Psi\left( \frac{1500~{\rm K}}{T_{\rm sub}} \right)^2 \sqrt{\frac{L_*+L_{\rm acc}}{L_\odot}} \,\,\,\,\,\mathrm{[AU]}, \end{equation}](/articles/aa/full_html/2014/06/aa22008-13/aa22008-13-eq77.png) (A.1)where Rin is the disk radius in the midplane, Lacc is the accretion luminosity described below and Ψ = 2 and Ψ ~ 1.2 are used for the optically thick and thin inner radii, respectively. Here we considered only optically thick disks with Tsub as the dust sublimation temperature of the inner disk rim surface. The sublimation temperature depends on the gas density ρgas. Based on the fit to the data from Pollack et al. (1994), we used:
(A.1)where Rin is the disk radius in the midplane, Lacc is the accretion luminosity described below and Ψ = 2 and Ψ ~ 1.2 are used for the optically thick and thin inner radii, respectively. Here we considered only optically thick disks with Tsub as the dust sublimation temperature of the inner disk rim surface. The sublimation temperature depends on the gas density ρgas. Based on the fit to the data from Pollack et al. (1994), we used: ![\appendix \setcounter{section}{1} \begin{equation} \label{A:Tsub} T_{\rm sub}=2127\left(\frac{\rho_{\rm gas}}{\mathrm{g/cm^3}}\right)^{0.0216} \mathrm{[K]} . \end{equation}](/articles/aa/full_html/2014/06/aa22008-13/aa22008-13-eq79.png) (A.2)This is sufficient for the range of gas densities used in our model. A more detailed description of Tsub is given by Kama et al. (2009).
(A.2)This is sufficient for the range of gas densities used in our model. A more detailed description of Tsub is given by Kama et al. (2009).
The surface of the inner disk is directly exposed to stellar heating, which creates a vertical temperature structure very close to isothermal in the narrow spatial region of our interest. The high-resolution radiative transfer calculation by Vinković (2012) showed that this is a good approximation for the inner rim of the disk. This approximation can only overestimate the dusty disk height because in reality the temperature slightly drops with the height above midplane. The radial temperature change is approximated with 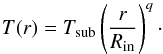 (A.3)The gas is in vertical hydrostatic equilibrium when the gas density structure is described as
(A.3)The gas is in vertical hydrostatic equilibrium when the gas density structure is described as
where ρ0 = ρgas(Rin,0) is the midplane gas density at the inner disk rim, Hp is the disk scale height, cs is the isothermal sound speed, ΩK is the Keplerian angular velocity at the midplane, M∗ is the stellar mass, μgas = 2.33 is the mean molecular weight in units of the proton mass mp, and k is Boltzmann’s constant.
Takeuchi & Lin (2002) showed that the vertical component of the gas velocity is much smaller than the horizontal component vr,gas, given by ![\appendix \setcounter{section}{1} \begin{equation} \label{A:V_r} {v}_{\rm r,gas}(r,z)=- \frac{\alpha c_{\rm s} H_p}{r}\left( 3p+2q+6+\frac{5q+9}{2}\frac{z^2}{H_p^2} \right) \left[\mathrm{ \frac{AU}{year} }\right]\cdot \end{equation}](/articles/aa/full_html/2014/06/aa22008-13/aa22008-13-eq88.png) (A.8)Accretion of the gas onto the star contributes with its luminosity to the total energy that heats the inner rim. To accommodate for this effect we used the accretion luminosity (Calvet & Gullbring 1998; Muzerolle et al. 2004) in Eq. (A.1)
(A.8)Accretion of the gas onto the star contributes with its luminosity to the total energy that heats the inner rim. To accommodate for this effect we used the accretion luminosity (Calvet & Gullbring 1998; Muzerolle et al. 2004) in Eq. (A.1) ![\appendix \setcounter{section}{1} \begin{equation} \label{A:Lacc} L_{\rm acc}=\xi\frac{GM_*\dot{M}_{\rm acc}}{R_*}=3.18 \xi \,\left(\frac{M_*}{M_\odot }\right)\left(\frac{R_\odot}{R_*}\right) \left(\frac{\dot{M}_{\rm acc}}{10^{-7}M_\odot/{\rm year}}\right) [L_\odot] , \end{equation}](/articles/aa/full_html/2014/06/aa22008-13/aa22008-13-eq89.png) (A.9)where M∗ is the stellar mass, ξ ~ 0.8 is the correction factor for the magnetospheric truncation of the disk, G is the gravitational constant, and R∗ is the stellar radius.
(A.9)where M∗ is the stellar mass, ξ ~ 0.8 is the correction factor for the magnetospheric truncation of the disk, G is the gravitational constant, and R∗ is the stellar radius.
The accretion rate Ṁacc can be calculated from the vertical profile of the gas density (Eq. (A.4)) and the horizontal velocity (Eq. (A.8)) 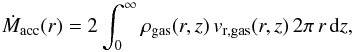 (A.10)which exists as inflow only if
(A.10)which exists as inflow only if 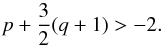 (A.11)The accretion rate depends on the distance from the star, which drives the disk evolution, except for q = −0.5 when the radial velocity is independent of r and the disk is in steady-state. We focused our attention on a very small part of the disk around Rin, where Ṁacc varies slowly. Hence, we define the accretion rate as Ṁacc(Rin). Equation (A.10) also shows that Ṁacc ∝ ρ0. We used this to derive ρ0 from Ṁacc, which is in turn derived from Lacc ∝ Ṁacc in Eq. (A.9).
(A.11)The accretion rate depends on the distance from the star, which drives the disk evolution, except for q = −0.5 when the radial velocity is independent of r and the disk is in steady-state. We focused our attention on a very small part of the disk around Rin, where Ṁacc varies slowly. Hence, we define the accretion rate as Ṁacc(Rin). Equation (A.10) also shows that Ṁacc ∝ ρ0. We used this to derive ρ0 from Ṁacc, which is in turn derived from Lacc ∝ Ṁacc in Eq. (A.9).
The local viscous dissipation of energy in the accretion disks contributes to the local disk temperature, and we checked for this effect. The net temperature at Rin is the combination 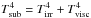 (Ciesla & Cuzzi 2006) of the stellar irradiation (Eq. (A.1), with Tsub replaced by Tirr) and viscous heating
(Ciesla & Cuzzi 2006) of the stellar irradiation (Eq. (A.1), with Tsub replaced by Tirr) and viscous heating 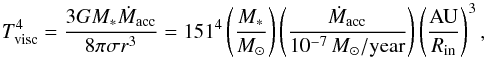 (A.12)where σ is the Stefan-Boltzmann constant. If
(A.12)where σ is the Stefan-Boltzmann constant. If 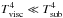 , we used Eq. (A.1) to derive Rin and if
, we used Eq. (A.1) to derive Rin and if 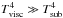 , we used Eq. (A.12). These conditions have to be checked iteratively when calculating Rin.
, we used Eq. (A.12). These conditions have to be checked iteratively when calculating Rin.
The long-term stability of the inner disk rim depends on the radial migration of the dust particles. We followed the prescription by Takeuchi & Lin (2002) where dust particles are driven by gas drag and their radial velocity depends on the distance from the midplane. The source of this vertical velocity variation is the gas pressure gradient, which causes two effects: the gas rotation is different from Keplerian rotation above the midplane, and the gas drag force depends on gas density. Without the gas drag the dust particles would follow Keplerian orbits. We considered particles smaller than the mean free path of gas molecules. This condition is described with Epstein’s gas drag law that gives the gas drag stopping time:
![\appendix \setcounter{section}{1} \begin{eqnarray} &&\label{A:tdrag} t_{\rm drag}(r,z) = \frac{\rho_{\rm grain} \,\,a}{\rho_{\rm gas} v_{\rm th}} = t_0(r) \exp\left(\frac{z^2}{2H_p^2}\right) , \\ &&\label{A:tdrag0} t_0 (r) = \frac{10^{-15}}{3}\left(\frac{\rho_{\rm grain}}{\rho_0}\right) \left(\frac{a/\mu {\rm m}}{\sqrt{T_{\rm sub}}}\right) \left(\frac{R_{\rm in}}{r}\right)^{p+q/2} [\mathrm{year}] , \end{eqnarray}](/articles/aa/full_html/2014/06/aa22008-13/aa22008-13-eq99.png) where ρgrain is the dust grain solid density, a is the dust grain radius, and
where ρgrain is the dust grain solid density, a is the dust grain radius, and 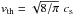 is the mean thermal velocity of gas.
is the mean thermal velocity of gas.
We considered turbulent disks where the gas turbulent motion stirs up dust particles to higher altitudes to prevent dust sedimentation. The equilibrium distribution of dust particles is reached when the sedimentation due to gas drag and the diffusion due to turbulence are balanced. Using the α-prescription for the viscous effect of turbulence (Shakura & Sunyaev 1973; Pringle 1981), the dust density distribution is (Takeuchi & Lin 2002) 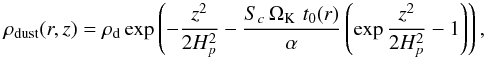 (A.15)where ρd(r) is the midplane dust density profile. The Schmidt number Sc is a measure of the coupling between the particles and the gas. Sc ~ 1 for the small particles used in our paper and increases to infinity for very big particles. This means that very big particles are not influenced by the gas turbulence and they accumulate in the midplane. The expression of Sc is a matter of debate, and we adopted the expression suggested by Youdin & Lithwick (2007) for diffusion driven by anisotropic turbulence
(A.15)where ρd(r) is the midplane dust density profile. The Schmidt number Sc is a measure of the coupling between the particles and the gas. Sc ~ 1 for the small particles used in our paper and increases to infinity for very big particles. This means that very big particles are not influenced by the gas turbulence and they accumulate in the midplane. The expression of Sc is a matter of debate, and we adopted the expression suggested by Youdin & Lithwick (2007) for diffusion driven by anisotropic turbulence 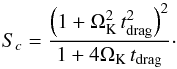 (A.16)Takeuchi & Lin (2003) showed that the stellar radiation pressure force slowly erodes the dusty disk surface, but they did not investigate the impact of this force on the surface of inner disk rim. We used their methodology to include the radiation pressure force in the dust velocity profiles. We ignored the complicated radiation pressure force from the near-infrared photons from the disk interior (Vinković 2009), but this force can only enhance the disk erosion and reduce the height of the optically thick disk. The stellar radiation pressure force compares to the stellar gravity by a factor of (Vinković 2009)
(A.16)Takeuchi & Lin (2003) showed that the stellar radiation pressure force slowly erodes the dusty disk surface, but they did not investigate the impact of this force on the surface of inner disk rim. We used their methodology to include the radiation pressure force in the dust velocity profiles. We ignored the complicated radiation pressure force from the near-infrared photons from the disk interior (Vinković 2009), but this force can only enhance the disk erosion and reduce the height of the optically thick disk. The stellar radiation pressure force compares to the stellar gravity by a factor of (Vinković 2009) 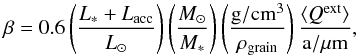 (A.17)where ⟨ Qext ⟩ is the dust extinction coefficient averaged over the stellar spectrum. We used a stellar black-body spectrum to calculate ⟨ Qext ⟩ from olivine dust grains. However, the result is close
(A.17)where ⟨ Qext ⟩ is the dust extinction coefficient averaged over the stellar spectrum. We used a stellar black-body spectrum to calculate ⟨ Qext ⟩ from olivine dust grains. However, the result is close
to ⟨ Qext ⟩ ~ 2 because the stellar radiation peaks at wavelengths shorter than the size of big grains that populate the inner disk surface. The radial component of the dust velocity with included radiation pressure was derived by Takeuchi & Lin (2003) as
![\appendix \setcounter{section}{1} \begin{eqnarray} \label{A:v_r_dust} &&{v}_{\rm r,dust}(r,z)=\frac{{v}_{\rm r,gas}+(\beta-\eta)\,r\,t_{\rm drag}\,\Omega_{\rm K}^2} {1+t_{\rm drag}^2\Omega_{\rm K}^2} \left[\mathrm{ \frac{AU}{year} }\right] , \\[2.5mm] && \eta = -\left(p+q+\frac{q+3}{2}\frac{z^2}{H_p^2}\right) \left(\frac{H_p}{r}\right)^2 \cdot \end{eqnarray}](/articles/aa/full_html/2014/06/aa22008-13/aa22008-13-eq108.png) Our goal is to find the relative height zmax/Rin that separates the inflow below this height from the outflow vr,dust(Rin,zmax) > 0above zmax. We varied the parameters listed in Table 1 and iteratively searched for ρ0 consistent with Ṁacc, which in turn has to be consistent with Lacc. The pseudocode describing the computational procedure is the following:
Our goal is to find the relative height zmax/Rin that separates the inflow below this height from the outflow vr,dust(Rin,zmax) > 0above zmax. We varied the parameters listed in Table 1 and iteratively searched for ρ0 consistent with Ṁacc, which in turn has to be consistent with Lacc. The pseudocode describing the computational procedure is the following:

Acknowledgments
The author acknowledges the Technology Innovation Centre Međimurje for computational resources. The author thanks the anonymous referee for the critical reviewing of the manuscript and constructive comments.
References
- Acke, B., Min, M., van den Ancker, M. E., et al. 2009, A&A, 502, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Akeson, R. L., Walker, C. H., Wood, K., et al. 2005, ApJ, 622, 440 [NASA ADS] [CrossRef] [Google Scholar]
- Bans, A., & Königl, A. 2012, ApJ, 758, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Benisty, M., Natta, A., Isella, A., et al. 2010, A&A, 511, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benisty, M., Renard, S., Natta, A., et al. 2011, A&A, 531, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calvet, N., & Gullbring, E. 1998, ApJ, 509, 802 [NASA ADS] [CrossRef] [Google Scholar]
- Chiang, E. I., Joung, M. K., Creech-Eakman, M. J., et al. 2001, ApJ, 547, 1077 [NASA ADS] [CrossRef] [Google Scholar]
- Ciesla, F. J., & Cuzzi, J. N. 2006, Icarus, 181, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Cuzzi, J. N., Hogan, R. C., Paque, J. M., & Dobrovolskis, A. R. 2001, ApJ, 546, 496 [NASA ADS] [CrossRef] [Google Scholar]
- D’Alessio, P., Calvet, N., Hartmann, L., Franco-Hernández, R., & Servín, H. 2006, ApJ, 638, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Donehew, B., & Brittain, S. 2011, AJ, 141, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Dorschner, J., Begemann, B., Henning, T., Jaeger, C., & Mutschke, H. 1995, A&A, 300, 503 [NASA ADS] [Google Scholar]
- Dullemond, C. P., & Dominik, C. 2004a, A&A, 417, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dullemond, C. P., & Dominik, C. 2004b, A&A, 421, 1075 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dullemond, C. P., & Monnier, J. D. 2010, ARA&A, 48, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Dullemond, C. P., Dominik, C., & Natta, A. 2001, ApJ, 560, 957 [NASA ADS] [CrossRef] [Google Scholar]
- Eisner, J. A., Hillenbrand, L. A., White, R. J., et al. 2007, ApJ, 669, 1072 [NASA ADS] [CrossRef] [Google Scholar]
- Herczeg, G. J., Cruz, K. L., & Hillenbrand, L. A. 2009, ApJ, 696, 1589 [Google Scholar]
- Hillenbrand, L. A., Strom, S. E., Vrba, F. J., & Keene, J. 1992, ApJ, 397, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Isella, A., & Natta, A. 2005, A&A, 438, 899 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kama, M., Min, M., & Dominik, C. 2009, A&A, 506, 1199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ke, T. T., Huang, H., & Lin, D. N. C. 2012, ApJ, 745, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Kreplin, A., Weigelt, G., Kraus, S., et al. 2013, A&A, 551, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mayne, N. J., & Harries, T. J. 2010, MNRAS, 409, 1307 [NASA ADS] [CrossRef] [Google Scholar]
- McClure, M. K., D’Alessio, P., Calvet, N., et al. 2013a, ApJ, 775, 114 [NASA ADS] [CrossRef] [Google Scholar]
- McClure, M. K., Calvet, N., Espaillat, C., et al. 2013b, ApJ, 769, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Meijer, J., Dominik, C., de Koter, A., et al. 2008, A&A, 492, 451 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mendigutía, I., Mora, A., Montesinos, B., et al. 2012, A&A, 543, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Millan-Gabet, R., Schloerb, F. P., & Traub, W. A. 2001, ApJ, 546, 358 [NASA ADS] [CrossRef] [Google Scholar]
- Millan-Gabet, R., Malbet, F., Akeson, R., et al. 2007, Protostars and Planets V (Tucson: University of Arizona Press), 539 [Google Scholar]
- Mosoni, L., Sipos, N., Ábrahám, P., et al. 2013, A&A, 552, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mulders, G. D., & Dominik, C. 2012, A&A, 539, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mulders, G. D., Dominik, C., & Min, M. 2010, A&A, 512, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muzerolle, J., D’Alessio, P., Calvet, N., & Hartmann, L. 2004, ApJ, 617, 406 [NASA ADS] [CrossRef] [Google Scholar]
- Natta, A., Testi, L., & Randich, S. 2006, A&A, 452, 245 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pollack, J. B., Hollenbach, D., Beckwith, S., et al. 1994, ApJ, 421, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Pringle, J. E. 1981, ARA&A, 19, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Schegerer, A. A., Wolf, S., Ratzka, T., & Leinert, C. 2008, A&A, 478, 779 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Starkey, N. A., & Franchi, I. A. 2013, GeCoA, 105, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Takeuchi, T., & Lin, D. N. C. 2002, ApJ, 581, 1344 [NASA ADS] [CrossRef] [Google Scholar]
- Takeuchi, T., & Lin, D. N. C. 2003, ApJ, 593, 524 [NASA ADS] [CrossRef] [Google Scholar]
- Tannirkulam, A., Harries, T. J., & Monnier, J. D. 2007, ApJ, 661, 374 [NASA ADS] [CrossRef] [Google Scholar]
- Tannirkulam, A., Monnier, J. D., Harries, T. J., et al. 2008, ApJ, 689, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Thi, W.-F., Woitke, P., & Kamp, I., 2011, MNRAS, 412, 711 [NASA ADS] [Google Scholar]
- Turner, N. J., Benisty, M., Dullemond, C. P., & Hirose, S. 2014, ApJ, 780, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Verhoeff, A. P., Min, M., Acke, B., et al. 2010, A&A, 516, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verhoeff, A. P., Min, M., Pantin, E., et al. 2011, A&A, 528, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vinković, D. 2006, ApJ, 651, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Vinković, D. 2009, Nature, 459, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Vinković, D. 2012, MNRAS, 420, 1541 [NASA ADS] [CrossRef] [Google Scholar]
- Vinković, D., Ivezić, Ž., Miroshnichenko, A. S., & Elitzur, M. 2003, MNRAS, 346, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Vinković, D., Ivezić, Ž., Jurkić, T., & Elitzur, M. 2006, ApJ, 636, 348 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, J. P., & Cieza, L. A. 2011, ARA&A, 49, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, S., Malbet, F., Alexander, R., et al. 2012, A&AR, 20, 52 [Google Scholar]
- Youdin, A. N., & Lithwick, Y. 2007, Icarus, 192, 588 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Sketch of the disk and processes used in our calculations. Three shades of gray show the regions clear of dust, with optically thin dust, and with optically thick dust. The beginning of the optically thick disk at Rin is defined as the disk rim. White dots mark the zone dominated by big grains, L∗ is the stellar luminosity, Lacc is the accretion luminosity, VH the viscous heating, TD the turbulent diffusion, G the gravity, C the centrifugal force, DS the dust settling due to the gas drag force, PG the gas pressure gradient, RP the radiation pressure, and VP is the gas velocity profile. |
| In the text | |
 |
Fig. 2 Example of model results showing the variation of horizonal velocities with height above the midplane (measured in scale heights). Lines show velocities of gas (dotted line), dust without the force of radiation pressure (long-dashed line), dust with the force (solid line), and zero velocity separating inflow from outflow (horizonal short-dashed line). Model parameters used in this result are T∗ = 10 000 K, L∗ = 40 L⊙, Lacc = 5 L⊙, M∗ = 2.5 M⊙, q = −0.5, p = −2.25, a = 1 μm, ρgrain = 3 g/cm3, and α = 0.01. The model output is ρ0 = 2.6 × 10-9 g/cm3, Ṁacc = 1.7 × 10-7M⊙/year, and Rin = 0.54 AU. The dusty disk is truncated at a height of zmax = 3.24Hp = 0.11Rin (the point where dust turns from inflow to outflow). |
| In the text | |
 |
Fig. 3 Shape of inner disk surface defined as the radial optical depth of τ = 1 (solid line). The model parameters are the same as in Fig. 2. The inner disk radius Rin is marked with the dotted line (the velocity profiles in Fig. 2 follow this line). The dust density scale is set by using the spatial length of 10-5 AU in the midplane between Rin and τ = 1. The radiation pressure force dominates the region above the dot-dot-dashed line and moves dust particles outward. The disk surface without radiation pressure would extend as far as the dashed line. |
| In the text | |
 |
Fig. 4 Distribution of zmax/Rin values relative to the mass accretion rate Ṁacc (in units of M⊙ yr-1), the power law p of the disk density change from Eq. (3), the temperature power law q from Eq. (2), and the inner disk radius Rin from Eq. (1). Results are shown for three types of objects, as indicated in the figure: Herbig Ae, T Tau, and brown dwarfs. The box-and-whisker plots at the far right show the range of results for each object: boxes show the median line and the first and third quartile, while the whiskers show the 10th and 90th percentile. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\appendix \setcounter{section}{1} \begin{eqnarray} \label{A:gas_density} && \rho_{\rm gas}(r,z) = \rho_0 \left(\frac{r}{R_{\rm in}}\right)^p \exp\left(-\frac{z^2}{2H_p^2}\right) ,\\ && \label{A:Hp} H_p(r) \! =\! \frac{c_s}{\Omega_{\rm K}}\! =\! 2\times 10^{-3}\!\sqrt{T_{\rm sub}\frac{M_\odot}{M_*}}* \left( \frac{r}{R_{\rm in}} \right)^{q/2} \!\left( \frac{r}{\mathrm{AU}} \right)^{3/2} [\mathrm{AU}] ,~~~~~~~~~~~ \\ &&\label{A:cs} c_{\rm s} (r) = \sqrt{\frac{k \,\, T(r)}{\mu_{\rm gas}\,m_{\rm p}}} = 0.0126 \sqrt{T_{\rm sub}} \left( \frac{r}{R_{\rm in}} \right)^{q/2} \left[\mathrm{ \frac{AU}{year} }\right] , \\ &&\label{A:OmegaK} \Omega_{\rm K}\,(r) = 2\pi \sqrt{\frac{M_*}{M_\odot}} \left( \frac{\mathrm{AU}}{r}\right)^{3/2} \left[\mathrm{\frac{1}{year} }\right], \end{eqnarray}](/articles/aa/full_html/2014/06/aa22008-13/aa22008-13-eq81.png)