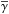| Issue |
A&A
Volume 565, May 2014
|
|
|---|---|---|
| Article Number | A94 | |
| Number of page(s) | 9 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201323091 | |
| Published online | 16 May 2014 | |
Large-scale magnetic fields in Bok globules⋆
1
University of Kiel, Institute of Theoretical Physics and
Astrophysics,
Leibnizstr. 15,
24118
Kiel,
Germany
e-mail:
gbertrang@astrophysik.uni-kiel.de
2
Assam University, Department of Physics,
788 011
Silchar,
India
Received: 20 November 2013
Accepted: 27 March 2014
Context. The role of magnetic fields in the star formation process is a contentious matter of debate. In particular, no clear observational proof exists of a general influence by magnetic fields during the initial collapse of molecular clouds.
Aims. Our aim is to examine magnetic fields and their influence on a wide range of spatial scales in low-mass star-forming regions.
Methods. We trace the large-scale magnetic field structure on scales of 103−105 AU in the local environment of Bok globules through optical and near-infrared polarimetry and combine these measurements with existing submillimeter measurements, thereby characterizing the small-scale magnetic field structure on scales of 102−103 AU.
Results. For the first time, we present polarimetric observations in the optical and near-infrared of the three Bok globules B335, CB68, and CB54, combined with archival observations in the submillimeter and the optical. We find a significant polarization signal (P ≳ 2%,P/σP > 3) in the optical and near-infrared for all three globules. Additionally, we detect a connection between the structure on scales of 102−103 AU to 103−104 AU for both B335 and CB68. Furthermore, for CB54, we trace ordered polarization vectors on scales of ~105 AU. We determine a magnetic field orientation that is aligned with the CO outflow in the case of CB54, but nearly perpendicular to the CO outflow for CB68. For B335 we find a change in the magnetic field oriented toward the outflow direction, from the inner core to the outer regions.
Conclusions. We find strongly aligned polarization vectors that indicate dominant magnetic fields on a wide range of spatial scales.
Key words: magnetic fields / polarization / stars: formation / stars: low-mass / ISM: clouds / instrumentation: polarimeters
© ESO, 2014
1. Introduction
Magnetic fields are observed in a wide range of astronomical scales: from the entire galaxy and giant molecular clouds (Beck et al. 1996; Beck 2001), to smaller molecular clouds with low-mass star formation and protostellar disks (see, e.g., Girart et al. 2008; Henning et al. 2001; Wolf et al. 2004), to circumstellar disks where they drive outflows, jets, and the accretion onto the central star (see, e.g., Pudritz et al. 2007; Suzuki & Inutsuka 2009; Gullbring et al. 1998). Magnetic fields have been discussed as playing an important role in star formation (see, e.g., Galli 2009). In general, they can influence the contraction timescale, the gas-dust coupling, and the shape of cloud fragments, and they host jets and outflows (see, e.g., McKee & Ostriker 2007).
In the dusty envelopes around young stellar objects, polarization of background starlight due to dichroic extinction and thermal emission by non-spherical dust grains is the most important signature of magnetic fields (see, e.g., Weintraub et al. 2000; Girart et al. 2008; Clemens & Kraemer 1999). The dust grains become partially aligned to the magnetic field, with their long axes perpendicular to the magnetic field lines (see, e.g., Lazarian 2007). The thermal emission of the dust grains thus becomes polarized, with a polarization direction perpendicular to the magnetic field, projected onto the plane of sky. Additionally, the light of background stars that shines through the star-forming region becomes polarized by dichroic absorption by the dust grains. Here, the resulting polarization maps directly trace the magnetic field lines, projected onto the plane of sky (see, e.g., Weintraub et al. 2000). Such polarization observations allow an assessment of the relative importance of uniform and tangled magnetic fields: a high level of polarization, uniform in direction, indicates a well-ordered field that is not significantly tangled on scales smaller than the beam size, i.e., a magnetic field that plays an important role in the evolution of the local density structure during the star formation.
A very good environment for studying the role of magnetic fields is given in low-mass star-forming regions, so-called Bok globules. These objects are less affected by large-scale turbulences and other nearby star-forming events. Bok globules are small in diameter (0.1–2 pc), simply structured, and are relatively isolated molecular clouds with masses of 2–100 M⊙ (Clemens et al. 1991; Bok 1977; Leung 1985).
Given the sensitivity of millimeter/submillimeter (sub-mm) telescopes that allow for polarimetric observations, the thermal emission of the dust grains, observable in the sub-mm, traces the densest, central part of a Bok globule. The less dense, outer parts are traced with polarized observations of background starlight that is dichroicly absorbed and observable in the near-infrared (near-IR)/optical. Thus, multiwavelength observations that combine sub-mm, near-IR, and optical polarization observations reveal the magnetic field geometry from the smallest to the largest scales of the Bok globule. So far, there have only been about two dozen sub-mm polarization observations of Bok globules, while only about half a dozen of these show ordered magnetic field structures (Matthews et al. 2009; Dotson et al. 2010). The majority of the sub-mm polarization observations show tangled field patterns, an indicator for negligible magnetic fields. Contrary to that, the near-IR and optical observations of Alves et al. (2011), Stephens et al. (2013), and Sen et al. (2000) revealed ordered field structures in the less dense, outer parts, indicating dominant magnetic fields in these parts of low-mass star-forming regions. Motivated by this, we performed a polarization study of Bok globules with two morphologically different globule types: B335 and CB68 are simply structured, small globules, whereas CB54 is a more complexly structured, larger Bok globule. In this work, we present polarization observations in the optical and near-IR of the three Bok globules B335, CB68, and CB54, combined with archival sub-mm and optical observations, for the first time.
We start with a description of the sources and the selection criteria in Sect. 2. In Sect. 3 we describe the observations, and in Sect. 4 the data reduction. In Sect. 5 we analyze the polarization maps, and in Sects. 6 and 7 we discuss the magnetic field and the correlation between the magnetic field structure and the CO outflows. In Sect. 8 we discuss the observability of the gap regions between the sub-mm and near-IR observations that we find and summarize our results.
2. Description of the sources
Our aim is to observe the polarization structure and, by this, the magnetic field structure on a wide range of scales with as few external influences as possible, e.g., nearby star-forming activity or reflection nebulae. This restricts us to isolated and compact Bok globules with available archival sub-mm polarization maps that show regular magnetic field structures. Additionally, the globules ought to have a high number of potential background stars in the particular wavelength range and to be observable from sites with access to optical or near-IR polarimeters. We applied these selection criteria to the legacy catalogs of the 350 μm polarimeter, Hertz, at the Caltech Submillimeter Observatory (CSO, Dotson et al. 2010) and the 850 μm polarimeter for SCUBA, SCUPOL, at the James Clerk Maxwell Telescope (JCMT, Matthews et al. 2009) and find that these criteria are satisfied only by the three Bok globules B335, CB68, and CB54.
B335 is a Bok globule at a distance of only ~100 pc (Olofsson & Olofsson 2009), and it accommodates one of the best-studied low-mass protostellar cores (see, e.g., Harvey et al. 2003; Evans et al. 2005). Its protostar drives a collimated bipolar outflow with a dynamical age of ~3 × 104 yr (see, e.g., Chandler & Sargent 1993). The dense core in B335 is generally recognized as the best protostellar collapse candidate, and the emission from different molecular lines has been successfully modeled in terms of an inside-out collapse (Shu 1977) with an infall age of ~105 yr and a current protostar mass of ~0.4 M⊙ (see, e.g., Choi et al. 1995). A total envelope mass of ~4 M⊙ within a radius of 1.5 × 104 AU was derived from sub-mm observations by Wolf et al. (2003).
CB68 is a globule in a distance of only ~160 pc (Launhardt & Henning 1997). It is remarkable for the very high percentage of polarization near 850 μm (Vallée et al. 2000). The small core of CB68 with a mass of ~0.9 M⊙ and a diameter of 0.03 pc is just below the critical size scale of 0.05 pc, identified as the diameter where there is a break in star formation processes and below which there is a coherent core (Vallée et al. 2000). Roughly perpendicular to its bipolar CO outflow, there is an elongated structure seen in both dense gas and dense dust, indicating a pseudodisk (Vallée et al. 2003). Sub-mm polarization data obtained with SCUBA/JCMT implies an hourglass-type magnetic field structure (Vallée & Fiege 2007).
CB54 is a large Bok globule, associated with the molecular cloud BWW 4 in a distance of ~1.1 kpc (Brand & Blitz 1993). The globule contains a massive dense core of MH ~ 100 M⊙ that drives a bipolar molecular outflow (Launhardt & Henning 1997; Yun & Clemens 1994). At near-IR wavelengths, a small, deeply embedded young stellar cluster becomes visible (Wolf et al. 2004). CB54 shows a randomly oriented polarization pattern in the sub-mm (Henning et al. 2001, see Fig. 3b). However, in the optical the polarization pattern appears more homogenous (Sen et al. 2000, see Fig. 3c).
3. Observations
The observations were performed in the near-IR with ISAAC/ VLT and SOFI/NTT and in the optical with IFOSC/IGO (see Table 1).
Summary of the observations.
Polarization standard stars.
3.1. Near-IR observations
The near-IR observations were carried out in March–May 2012 and January 2013 at ESOs Very Large Telescope (VLT) and the New Technology Telescope (NTT). We observed with the instruments Infrared Spectrometer And Array Camera (ISAAC) and Son OF ISAAC (SOFI), which are mounted at the Nasmyth A foci of the 8 m VLT (UT3), respectively of the 3.58 m NTT, both equipped with a 1024 × 1024 Hawaii Rockwell array optimized for wavelengths of 1–2.5 μm.
In both ISAAC/VLT and SOFI/NTT a single Wollaston prism is used for polarization observations. In this observing mode, the polarized flux is measured simultaneously at two different angles that differ by 90°. To derive the linear polarization degree and orientation of an object, two observations must be performed at each pointing of the telescope with different orientations of the Wollaston prism, typically 0° and 45°. For ISAAC/VLT and SOFI/NTT, this is realized by a rotation of the complete instrument. To avoid overlapping between different polarization images an aperture mask of three alternating opaque and transmitting strips of about 20′′ × 150′′ for ISAAC/VLT and 40′′ × 300′′ for SOFI/NTT is used.
We carried out Js-band polarization observations of five fields of B335 and CB68 with ISAAC/VLT and of four fields of CB54 with SOFI/NTT.
3.2. Optical observations
The optical observations in R band were carried out in March 2012 at the 2 m IUCAA Girawali Observatory (IGO, India). The IUCAA Faint Object Spectrograph & Camera (IFOSC), attached at IGOs Cassegrain focus, is equipped with an EEV 2K × 2K CCD camera optimized for a wavelength range of 350–850 nm (for details, see Gupta et al. 2002).
IFOSC/IGOs polarimetry mode makes use of a single Wollaston prism combined with a half-wave plate. The linear polarization degree and orientation is derived through two observations with two different half-wave plate orientations. The field of view for the polarimetry mode is about 4′ × 4′. IFOSC/IGO does not use an aperture mask like ISAAC/VLT or SOFI/NTT. The unambiguous assignment of the observed point sources to the corresponding direction of polarization is done as part of the data reduction procedure.
We performed polarization observations of four fields of CB68 with IFOSC/IGO.
4. Data reduction
The data reduction was performed with pipelines specialized for each instrument (for details of polarimetric data reduction and calibration see, e.g., Wolf et al. 2002). These pipelines are used for bias correction, flat-fielding, and instrumental polarization removal. The Stokes parameters I,Q, and U are computed through aperture photometry. During the observations with ISAAC/VLT, we observed at orientations of the Wollaston prism of 0°,45°. During the SOFI/NTT and IFOSC/IGO observations, we observed respectively with the Wollaston prism and the half-plate at four different orientations of 0°,22.5°,45°,67.5°. Unpolarized and polarized standard stars have been observed to determine the instrumental polarization. Table 2 summarizes the general information for these stars.
Observational results for the polarized standard star of CB54.
For ISAAC/VLT, we find a dependency between the instrumental polarization and the airmass of the object. This effect varies the observed Stokes parameters, Q and U, significantly on scales of 10% and is taken into account in the data analysis (see Appendix A for details). For the SOFI/NTT data set, we applied a correction technique based on the correction of the ISAAC/VLT data. As a successful test, the observational results of the polarized standard star of the SOFI/NTT observations after bias correction correspond well to the literature values (see Tables 2, 3).
 |
Fig. 1 B335 – Left: DSS-map with overlaid near-IR polarization vectors observed with ISAAC/VLT. The length of the vectors shows the degree of polarization, and the direction gives the position angle. Only vectors with P/σP > 3 are plotted. The contour lines represent the 12CO(2–1) OTF channel maps obtained with the HHT on Mount Graham. The black (gray) contour lines give the blueshifted (redshifted) eastern (western) outflow lobe. The contour levels are |
 |
Fig. 2 CB68 – a) DSS-map with overlaid near-IR polarization vectors observed with ISAAC/VLT. The length of the vectors shows the degree of polarization, and the direction gives the position angle. Only vectors with P/σP > 3 are plotted. The contour lines represent the 12CO(3–2) spectral channel maps obtained with the JCMT. The black contour lines give the blueshifted (south-eastern), the grey, dotted contour lines give the redshifted (north-western) outflow lobe. Contour levels at 0.25,0.50,0.75,... K (from Vallée et al. 2000, HPBW of 14′′; reproduced by permission of the AAS). b.1–3) Same as a) but with polarization vectors obtained with IFOSC/IGO in the optical. c) Intensity map overlaid with polarization vectors obtained with SCUBA/JCMT in the sub-mm (Vallée et al. 2003, reproduced by permission of the AAS). |
 |
Fig. 3 CB54 – a) DSS-map with overlaid near-IR polarization vectors observed with ISAAC/VLT. The length of the vectors shows the degree of polarization, and the direction gives the position angle. Only vectors with P/σP > 3 are plotted. Blue vectors have a better error statistic than the red vectors, since they are based on more than one set of observations. The contour lines represent the 12CO(1–0) spectral channel maps obtained with the Five College Radio Astronomy Observatory. The solid contour lines give the blueshifted (south-western), and the dotted contour lines give the redshifted (north-eastern) outflow lobe. Contour levels are spaced at 0.3 K km s-1 intervals of 1.7 K km s-1 (blue), and 0.15 K km s-1 intervals of 0.45 K km s-1 (red), respectively (from Yun & Clemens 1994, beam size of 48′′; reproduced by permission of the AAS). b) Intensity map overlaid with polarization vectors obtained with SCUBA/JCMT in the sub-mm (Henning et al. 2001, reproduced by permission of the AAS). c) Intensity map overlaid with polarization vectors obtained with IMPOL/GIRT in the optical (Sen et al. 2000). |
 |
Fig. 4 Distribution of the degree of polarization, P for P/σP > 3, counts given by N(P), of B335, CB68, and CB54, observed in the near-IR. |
 |
Fig. 5 Distribution of the polarization angle, γ, counts given by N(γ), of B335, CB68, and CB54, observed in the near-IR. The dashed lines represent the mean polarization angles, |
5. Polarization maps
In this section, we present the polarization maps in the sub-mm, in the near-IR, and in the optical of the three Bok globules B335, CB68, and CB54. For comparing the sub-mm maps with the near-IR and optical maps, it has to be taken into account that the polarization arises from two different physical processes: while thermal emission is observed in the sub-mm, dichroic absorption is observed in the near-IR and the optical. Thus, the polarization of a dust grain observed in the sub-mm is oriented perpendicular to the polarization of the very same dust grain observed in the near-IR or optical.
The sub-mm maps of our three objects are each available in two versions, the originally published maps by Wolf et al. (2003), Vallée et al. (2003), and Henning et al. (2001), as well as rereduced maps by Matthews et al. (2009). Matthews et al. (2009) reduced all polarization observations again that have been executed with SCUBA/JCMT and cover a huge variety of objects, from planets up to galaxies, in a single procedure. In doing so, Matthews et al. (2009) applied very strict criteria for the decision of including or omitting science data of an object and remark that data that was omitted by these generalized regulations may still be usable, and even part of publications, but would require too much individual assessment to meet the requirements of their systematic rereduction. For this reason, we decided to use the originally reduced and published sub-mm polarization maps in our discussion (see, Figs. 1–3).
In the following, we discuss the polarization maps seperately for each observed wavelength, as well as in comparison to the maps of the additional wavelength ranges.
5.1. Bok globules with simple morphology: B335 and CB68
The polarization maps of the Bok globules B335 and CB68 are shown in Figs. 1 and 2. Both globules disclose a significant polarization signal (P ≳ 1%,P/σP > 3) in their outer, less dense parts in the near-IR as well as in the optical for CB68 (see Fig. 4). The near-IR polarization vectors appear ordered very well in the case of CB68 (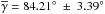 , see Fig. 5) and largely well-ordered in the case of B335 (
, see Fig. 5) and largely well-ordered in the case of B335 (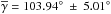 , see Figs. 1, 5). According to ESO regulations, there are no observations of polarized standard stars for the near-IR data observed with ISAAC/VLT. Thus, no independent quantitative measure of the reliability of the observed polarization angles exists.
, see Figs. 1, 5). According to ESO regulations, there are no observations of polarized standard stars for the near-IR data observed with ISAAC/VLT. Thus, no independent quantitative measure of the reliability of the observed polarization angles exists.
In both globules, a clear spatial gap remains between the polarization vectors in the sub-mm and in the near-IR. The gap width in B335 amounts to about 70′′ (≈7 × 103 AU) and to about 100′′ (≈1.6 × 104 AU) in CB68. Launhardt et al. (2013) observed the hydrogen column densities, NH, of CB68 and B335. In the region traced by SCUBA/JCMT, they determine NH ≳ 1022 cm-2 and in the region traced by ISAAC/VLT and SOFI/NTT they find NH ≲ 1021 cm-2. This gives us a benchmark for the feasibility to observe the morphology of the globules with the applied observing techniques and instrumentation and explains the gap.
In the case of B335, the orientation of the near-IR polarization vectors in the eastern and southern part of the globule fits to the orientation of the sub-mm polarization vectors very well. In the north-western part the polarization orientation shows local varieties in the sub-mm but not in the near-IR, even though the near-IR polarization pattern appears slightly unordered (see, Fig. 1).
In the case of CB68, there are near-IR polarization vectors with P/σP > 3 only in the western and in the south-eastern part. Vallée et al. (2003) observed a spiral polarization pattern in the sub-mm. One polarization “spiral-arm” points toward the southeastern globule part and thus, fits well to the near-IR polarization vectors. For the polarization vectors in the western part, this is not the case. However, one has to keep in mind that there can also be an influence by that arm of the globule that stretches in the northwestern direction. The optical polarization vectors of CB68 in the most outer parts of the globule are rather unordered. However, the polarization vectors in the northern part (see Fig. 2b.2) follow the smaller gas-dust branch that is perpendicular to the north-western arm of CB68. Additionally, in the southern part (see Fig. 2b.3, upper half of the left field) the optical polarization vectors follow the small extension of the globule, too. There is a slight deviation of the orientation of the polarization vectors observed in the optical from those observed in the near-IR. The most straight forward explanation is that the different vectors trace the magnetic field in different regions of the globule.
Gas densities, gas velocities, polarization, and magnetic field strengths of the outer parts of B335 traced in the near-IR.
5.2. Bok globule with more complex morphology: CB54
The polarization map of the Bok globule CB54 is shown in Fig. 3. We observe a significant polarization signal (P ≳ 2%,P/σP > 3) in the near-IR across the entire globule (see Fig. 4). As in the case of the globules CB68 and B335, we also find a clear spatial gap with a width of about 1′ (corresponding to about 7 × 104 AU) between the polarization vectors observed in the sub-mm and in the near-IR in CB54.
Figure 3 displays polarization vectors that cover the globule on scales from 103−104 AU up to 105 AU. Given the complex structure of this Bok globule, it is not necessarily expected to find uniformly ordered polarization vectors across such large scales. However, on smaller scales (~104 AU), by a factor of ≳2 larger than the region traced by the sub-mm map, our near-IR observations and the optical obvervations by Sen et al. (2000) reveal ordered polarization vectors.
The southern field of the optical data (Fig. 3c, lower field) overlaps with a part of our near-IR data. The optical polarization degree is about one order of magnitude stronger than that in the near-IR. This factor is significantly higher than the difference of about a factor of two which we expect from dust properties obtained from Mie theory (Mie 1908). However, in terms of the orientation, the optical and near-IR vectors fit well to each other (Δγ ≲ 10°).
The region around the sub-mm map is of particular interest. In the sub-mm, Wolf et al. (2003) observed randomly oriented polarization vectors. However, our near-IR observations reveal ordered polarization vectors on larger scales around the sub-mm map (see Fig. 3a).
6. Magnetic fields
In our analysis we assume that the magnetic field is oriented perpendicular to the measured polarization vectors in the sub-mm and parallel oriented to the measured polarization vectors in the near-IR and in the optical. This widely applied concept is based on the finding that, independently of the alignment mechanism, charged interstellar dust grains would have a substantial magnetic moment leading to a rapid precession of the grain angular momentum around the magnetic field direction, implying a net alignment of the grains with the magnetic field (see, e.g., Draine & Weingartner 1997; Lazarian 2007). However, one has to keep in mind that polarization observations strongly suffer from projectional effects along the line-of-sight (LOS). Thus, for a comprehensive understanding of the magnetic field structure additional 3D radiative transfer modeling is essential but beyond the scope of this study.
In general, a high degree of polarization is connected to a magnetic field that is strong enough to align enough dust grains along the LOS to prevent the annihilation of the polarized signal that is expected from randomly oriented grains along the LOS. In our observations of all three Bok globules, B335, CB68, and CB54, we find strongly ordered magnetic fields. Additionally, our observations show well-ordered polarization vectors on scales of ≲104 AU for all three Bok globules. Thus our observations imply magnetic fields that are strongly ordered over large parts of the globules. And finally, in the case of B335 and CB68, our near-IR and optical observations trace polarization patterns that fit to the polarization patterns observed in the sub-mm by Wolf et al. (2003) and Vallée et al. (2003), which implies strong and ordered magnetic fields on scales from 102−103 AU to 104 AU.
Besides this analysis of the magnetic field, Chandrasekhar & Fermi (1953) give an estimate for the magnetic field strength in the plane-of-sky (POS; CF method): 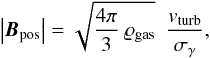 (1)where ϱgas is the gas density in units of g cm-3, vturb the rms turbulence velocity in units of cm s-1, and σγ the standard deviation of the polarization position angles in radians. Here, it is assumed that the magnetic field is frozen in the cloud material. For a detailed discussion of this equation, we refer to Crutcher (2012), and for an extension of the mean magnetic field strength, we refer to Houde (2004).
(1)where ϱgas is the gas density in units of g cm-3, vturb the rms turbulence velocity in units of cm s-1, and σγ the standard deviation of the polarization position angles in radians. Here, it is assumed that the magnetic field is frozen in the cloud material. For a detailed discussion of this equation, we refer to Crutcher (2012), and for an extension of the mean magnetic field strength, we refer to Houde (2004).
For B335, we use the hydrogen number densities and the turbulence velocity from Frerking et al. (1987), for details see Table 4. To account for helium and heavier elements, we derive the total gas density ρgas from 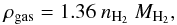 (2)where MH2 = 2.0158 amu is the mass of a H2 molecule. The corresponding values are listed in Table 4.
(2)where MH2 = 2.0158 amu is the mass of a H2 molecule. The corresponding values are listed in Table 4.
We can estimate the mean magnetic field strength in the region north of the center, northwest of the center, and east of the center of B335 (see Table 4). We find similar magnetic field strengths in the different regions, BB335, near−IR ≈ (12−40) μG, which are less, by a factor of 3–10, than the estimated field strength in the sub-mm, BB335, smm ≈ 130 μG (Wolf et al. 2003). Considering the inaccuracies in the estimations of the densities, the temperatures, and the gas velocities, we do not find any significant difference in the magnetic field strengths in the inner and outer parts of B335.
For CB68 and CB54, information about the gas densities, temperatures, and turbulence velocities in the parts of the globules that we traced in the near-IR and in the optical is not available. However, in the sub-mm, Vallée et al. (2003) and Henning et al. (2001) estimate the magnetic field strengths of CB68 and CB54 to BCB68, smm ≈ 150 μG and BCB54, smm ≈ 60 μG.
7. Correlation between magnetic field structure and the CO outflow of the Bok globules
Magnetic fields are believed not only to influence the collapse of Bok globules but also the formation of circumstellar disks and outflows. Many observations show a preferential alignment of the outflow axis along the cloud-scale magnetic field (e.g., Cohen et al. 1984; Vrba et al. 1986; Jones & Amini 2003), but misaligned orientations of the outflow axes and magnetic field direction have been reported as well (e.g., Hull et al. 2013; Wolf et al. 2003). Based on MHD simulations, Matsumoto et al. (2006) find that the degree of alignment between outflow and magnetic field depends on the magnetic field strength: the stronger the magnetic field, the better the alignment. However, one has to keep in mind that these simulations consider only the most inner regions of globules with outflows on scales of 150–200 AU. Thus, it is uncertain whether the findings of Matsumoto et al. (2006) can be extended to the scales of our observations.
In the following, we examine the relative positions of the outflow axes and the magnetic field directions for our observations of the three Bok globules, B335, CB68, and CB54, which all contain protostellar cores and drive collimated CO outflows (Chandler & Sargent 1993; Vallée et al. 2000; Yun & Clemens 1994).
In discussing the relative orientation between the CO outflow and the magnetic field structure, one has to consider that only one component of the spatial orientation of the outflow (vsini) is known from velocity measurements and that polarization vectors only trace the magnetic field structure projected on the plane of sky. In the sub-mm, Wolf et al. (2003) and Vallée et al. (2003) find the polarization vectors aligned with the CO outflows and discuss the relation to the magnetic field structure traced by the polarization maps. We extend this analysis to the outer, less dense regions traced by our near-IR and optical observations. Consistent with the sub-mm studies, we assume that the magnetic field is oriented parallel to the observed polarization vectors in the near-IR and the optical (for details see Sect. 6).
B335 (Fig. 1) – Our near-IR observations trace the outflow region in the eastern part of this globule. Here, the near-IR polarization vectors are oriented by an angle 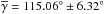 with respect to the outflow axis
with respect to the outflow axis 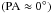 . The sub-mm polarization vectors are aligned nearly parallel to the outflow axis (Wolf et al. 2003). The globule itself is clearly elongated in the north-south direction (see Fig. 1). Therefore, the magnetic field orientation changes from the inner 7 × 103 AU, where it is perpendicular to the outflow and parallel to the globule, to the outer 2 × 104 AU, where it is inclined toward the outflow.
. The sub-mm polarization vectors are aligned nearly parallel to the outflow axis (Wolf et al. 2003). The globule itself is clearly elongated in the north-south direction (see Fig. 1). Therefore, the magnetic field orientation changes from the inner 7 × 103 AU, where it is perpendicular to the outflow and parallel to the globule, to the outer 2 × 104 AU, where it is inclined toward the outflow.
CB68 (Fig. 2) – The observed extent of the CO outflow is limited to the inner 1.6 × 104 AU, and thereby traced only by the near-IR polarization vectors in the southeastern part of this globule. These polarization vectors are oriented roughly perpendicular 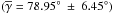 to the outflow axis
to the outflow axis 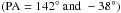 (Vallée et al. 2000). Relative to the pseudodisk (PA ≈ 51° ± 1°), which is located in the center of this globule (<103 AU), Vallée et al. (2003) also find twisted sub-mm polarization vectors that they interpret as influenced by the outflow. However, on scales of about 2 × 103 AU, the magnetic field orientation is nearly perpendicular to the outflow axis, and thereby almost parallel to the pseudodisk.
(Vallée et al. 2000). Relative to the pseudodisk (PA ≈ 51° ± 1°), which is located in the center of this globule (<103 AU), Vallée et al. (2003) also find twisted sub-mm polarization vectors that they interpret as influenced by the outflow. However, on scales of about 2 × 103 AU, the magnetic field orientation is nearly perpendicular to the outflow axis, and thereby almost parallel to the pseudodisk.
CB54 (Fig. 3) – Our near-IR observations trace the redshifted CO outflow very well. We find polarization vectors that are almost perfectly aligned with the outflow axis. This corresponds well to the findings of Wolf et al. (2003) in the sub-mm, where a mean polarization orientation perpendicular to the outflow direction was found. The blueshifted outflow lobe is barely traced by our near-IR polarization vectors that are almost perpendicular to the outflow lobe. However, one has to consider that the distance between the polarization vectors and the CO contour lines is large, and the CO outflow shows a dip toward the vectors. The magnetic field direction is clearly parallel to the redshifted CO outflow lobe on scales of about 5 × 104 AU.
Following the discussion by Matsumoto et al. (2006), our observations indicate that the magnetic field of B335 is stronger relative to the outflow in the very outer parts of the globule than in the inner core and the other way around in the case of CB68, while the magnetic field of CB54 dominates the outflow along its complete extent. These findings cannot be verified by our analysis of the magnetic field strength in B335 by using the CF method (for details, see Sect. 6). However, one has to keep in mind that these interpretation may be highly influenced by projectional effects.
8. Summary
For the first time, we have obtained multiwavelength polarization maps that cover the extent of Bok globules over a range of 102−105 AU, covering optically thin and optically thick regions. We observed the three globules B335, CB68, and CB54 in the near-IR and in the optical, and combined our observations with archival sub-mm and optical data. The major results follow.
-
1.
The polarization degrees in the near-IRand in the optical amount to several percent
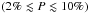 .
. -
2.
In the case of B335 and CB68, two simple structured Bok globules, the orientation of the sub-mm polarization vectors in the dense inner part (102−103 AU) of the globules continue to the outer, less dense globule parts (104−105 AU).
-
3.
In the case of CB54, a globule with large-scale turbulences, the orientation of the polarization vectors in the near-IR is well-ordered on scales of ~104AU.
-
4.
In the case of B335, we found comparable magnetic field strengths in the globule parts traced by our near-IR observations and in the parts traced by sub-mm observations, by using the CF method.
-
5.
We do not find a general correlation between the magnetic field structure and the CO outflow of the Bok globule. In CB54 we find a magnetic field orientation parallel to the CO outflow, while B335 shows a change in the orientation of the magnetic field toward the outflow axis from the inner core to the outer regions. In CB68, we find a magnetic field orientation nearly perpendicular to the CO outflow.
-
6.
The instrumental polarization of ISAAC/VLT depends significantly on the airmass of the observed object. For our unpolarized standard star, EGGR118, we determined the deviation of the polarization degree, ΔP ≈ 1.4%.
The well-ordered polarization vectors indicate dominant magnetic fields from scales of 102−103 AU to scales of 104−105 AU. In the particular case of CB54, the randomly oriented polarization pattern in the sub-mm can be explained by, e.g., a change in the orientation from the region south of the sub-mm map to the region north of the sub-mm map (see Fig. 3).
A gap remains with a width of about 1′−2′ between the sub-mm observations done with SCUBA/JCMT and the near-IR observations performed with ISAAC/VLT and SOFI/NTT of B335, CB68, and CB54. Launhardt et al. (2013) derive typical hydrogen column densities for the region traced by the SCUBA/JCMT observations in Bok globules of NH ≳ 1022 cm-2, as well as NH ≲ 1021 cm-2, for the regions observed with ISAAC/VLT and SOFI/NTT. To close the gap and, finally, spatially connect the magnetic field observations from the smallest to the largest scale, obvervations that trace the region of 1021 cm-2 ≲ NH ≲ 1022 cm-2 need to be done. Based on the flux level determined at the edges of the sub-mm map of B335 and CB54 observed with SCUBA/JCMT (Wolf et al. 2003; Henning et al. 2001), we estimate that these observations can be performed in less than one hour with ALMA since cycle 2.
The key to understanding the influence of magnetic fields on the low-mass star formation process is knowledge about the three-dimensional structures of the magnetic field and the object itself. Our observations, as well as all observations, suffer from projectional effects along the line of sight. Thus, it is necessary to do three-dimensional modeling of Bok globules, which includes a proper description of dust, dust grain alignment, gaseous outflows, and polarimetric radiative transfer, in addition to polarimetric observations. However, this type of analysis is beyond the scope of this study.
Acknowledgments
Gesa Bertrang gratefully acknowledges financial support by the DFG under contract WO857/11-1 within the frame of the DFG Priority Program 1573: The Physics of the Interstellar Medium.
References
- Alves, F. O., Acosta-Pulido, J. A., Girart, J. M., Franco, G. A. P., & López, R. 2011, AJ, 142, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, R. 2001, Space Sci. Rev., 99, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, R., Brandenburg, A., Moss, D., Shukurov, A., & Sokoloff, D. 1996, ARA&A, 34, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Bok, B. J. 1977, PASP, 89, 597 [NASA ADS] [CrossRef] [Google Scholar]
- Brand, J., & Blitz, L. 1993, A&A, 275, 67 [NASA ADS] [Google Scholar]
- Chandler, C. J., & Sargent, A. I. 1993, ApJ, 414, L29 [CrossRef] [Google Scholar]
- Chandrasekhar, S., & Fermi, E. 1953, ApJ, 118, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Choi, M., Evans, II, N. J., Gregersen, E. M., & Wang, Y. 1995, ApJ, 448, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Clayton, G. C., & Martin, P. G. 1981, AJ, 86, 1518 [NASA ADS] [CrossRef] [Google Scholar]
- Clemens, D. P., & Kraemer, K. E. 1999, in AAS Meeting Abstracts #194, BAAS, 31, 890 [NASA ADS] [Google Scholar]
- Clemens, D. P., Yun, J. L., & Heyer, M. H. 1991, ApJS, 75, 877 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, R. J., Rowland, P. R., & Blair, M. M. 1984, MNRAS, 210, 425 [NASA ADS] [Google Scholar]
- Crutcher, R. M. 2012, ARA&A, 50, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Dotson, J. L., Vaillancourt, J. E., Kirby, L., et al. 2010, ApJS, 186, 406 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Weingartner, J. C. 1997, ApJ, 480, 633 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, II, N. J., Lee, J.-E., Rawlings, J. M. C., & Choi, M. 2005, ApJ, 626, 919 [NASA ADS] [CrossRef] [Google Scholar]
- Fossati, L., Bagnulo, S., Mason, E., & Landi Degl’Innocenti, E. 2007, in The Future of Photometric, Spectrophotometric and Polarimetric Standardization, ed. C. Sterken, ASP Conf. Ser., 364, 503 [Google Scholar]
- Frerking, M. A., Langer, W. D., & Wilson, R. W. 1987, ApJ, 313, 320 [NASA ADS] [CrossRef] [Google Scholar]
- Galli, D. 2009, Mem. Soc. Astron. Italiana, 80, 54 [Google Scholar]
- Girart, J. M., Rao, R., & Marrone, D. P. 2008, Ap&SS, 313, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Gullbring, E., Hartmann, L., Briceno, C., & Calvet, N. 1998, ApJ, 492, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Gupta, R., Burse, M., Das, H. K., Kohok, A., & Ramaprakash, A. N. 2002, Bull. Astron. Soc. India, 30, 785 [Google Scholar]
- Harvey, D. W. A., Wilner, D. J., Myers, P. C., & Tafalla, M. 2003, ApJ, 596, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Henning, T., Wolf, S., Launhardt, R., & Waters, R. 2001, ApJ, 561, 871 [NASA ADS] [CrossRef] [Google Scholar]
- Houde, M. 2004, ApJ, 616, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Hull, C. L. H., Plambeck, R. L., Bolatto, A. D., et al. 2013, ApJ, 768, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, T. J., & Amini, H. 2003, AJ, 125, 1418 [NASA ADS] [CrossRef] [Google Scholar]
- Launhardt, R., & Henning, T. 1997, A&A, 326, 329 [NASA ADS] [Google Scholar]
- Launhardt, R., Stutz, A. M., Schmiedeke, A., et al. 2013, A&A, 551, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lazarian, A. 2007, J. Quant. Spectrosc. Radiat. Transf., 106, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Leung, C. M. 1985, in Protostars and Planets II, eds. D. C. Black, & M. S. Matthews (Tucson: University of Arizona press), 104 [Google Scholar]
- Matsumoto, T., Nakazato, T., & Tomisaka, K. 2006, ApJ, 637, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Matthews, B. C., McPhee, C. A., Fissel, L. M., & Curran, R. L. 2009, ApJS, 182, 143 [NASA ADS] [CrossRef] [Google Scholar]
- McKee, C. F., & Ostriker, E. C. 2007, ARA&A, 45, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Mie, G. 1908, Ann. Phys., 330, 377 [Google Scholar]
- Olofsson, S., & Olofsson, G. 2009, A&A, 498, 455 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pudritz, R. E., Ouyed, R., Fendt, C., & Brandenburg, A. 2007, Protostars and Planets V (Tucson: University of Arizona press), 277 [Google Scholar]
- Russell, D. M., & Fender, R. P. 2008, MNRAS, 387, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Sen, A. K., Gupta, R., Ramaprakash, A. N., & Tandon, S. N. 2000, A&AS, 141, 175 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shu, F. H. 1977, ApJ, 214, 488 [NASA ADS] [CrossRef] [Google Scholar]
- Stephens, I. W., Looney, L. W., Kwon, W., et al. 2013, ApJ, 769, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Stutz, A. M., Rubin, M., Werner, M. W., et al. 2008, ApJ, 687, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Suzuki, T. K., & Inutsuka, S.-I. 2009, ApJ, 691, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Turnshek, D. A., Bohlin, R. C., Williamson, II, R. L., et al. 1990, AJ, 99, 1243 [NASA ADS] [CrossRef] [Google Scholar]
- Vallée, J. P., & Fiege, J. D. 2007, AJ, 134, 628 [NASA ADS] [CrossRef] [Google Scholar]
- Vallée, J. P., Bastien, P., & Greaves, J. S. 2000, ApJ, 542, 352 [NASA ADS] [CrossRef] [Google Scholar]
- Vallée, J. P., Greaves, J. S., & Fiege, J. D. 2003, ApJ, 588, 910 [NASA ADS] [CrossRef] [Google Scholar]
- Vrba, F. J., Luginbuhl, C. B., Strom, S. E., Strom, K. M., & Heyer, M. H. 1986, AJ, 92, 633 [NASA ADS] [CrossRef] [Google Scholar]
- Weintraub, D. A., Goodman, A. A., & Akeson, R. L. 2000, Protostars and Planets IV (Tucson: University of Arizona press), 247 [Google Scholar]
- Whittet, D. C. B., Martin, P. G., Hough, J. H., et al. 1992, ApJ, 386, 562 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, S., Vanzi, L., & Ageorges, N. 2002, How To Reduce SOFI/NTT Polarimetric Data [Google Scholar]
- Wolf, S., Launhardt, R., & Henning, T. 2003, ApJ, 592, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, S., Launhardt, R., & Henning, T. 2004, Ap&SS, 292, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Yun, J. L., & Clemens, D. P. 1994, ApJS, 92, 145 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Airmass-dependent instrumental polarization
Our ISAAC/VLT observations were performed in service mode between March 27 and May 27, 2012. Each night, we made two observations of unpolarized standard stars, GJ1178 and EGGR118. When its right ascension meant that GJ1178 was no longer observable, two observations of EGGR118 were made in the same night. Thus, we have observations of EGGR118 for the complete observing interval of two months, always performed with the very same procedure.
 |
Fig. A.1 Determined correction factors, CJs, of EGGR118 over the corresponding airmasses and the fit to the data points, a polynomial of the 2nd degree. The coefficients of the polynomial are given by the ai, beginning with the leading coefficient. |
 |
Fig. A.2 Determination of the corresponding correction factors, CJs, of the globules airmass intervals by using the polynomial fit (see Fig. A.1). The errorbars in airmass direction give the airmass interval of the observation of each field. The errorbars in CJs-direction give the error of the estimated correction factor of each data point, including photometric and fitting errors. |
Every instrument or telescope may influence the polarization state of the incoming light, through its instrumental polarization. Therefore, the instrumental polarization needs to be considered during the data reduction process. The assumption here is that the instrumental polarization is mainly created by a non-ideal transmission ratio of the Wollaston prism. The ideal transmission ratio would be a 50:50 ratio of the intensities of the upper, iu, and lower, il, beams that are created by the Wollaston prism. To correct the signal for deviations in the ideal transmission ratio, a wavelength-dependent correction factor, Cλ, is applied (Wolf et al. 2002):  To determine the instrumental polarization, Cλ has to be adjusted in such a way that the measured polarization of the unpolarized standard star is minimal.
To determine the instrumental polarization, Cλ has to be adjusted in such a way that the measured polarization of the unpolarized standard star is minimal.
We determine an instrumental polarization that shows a strong dependence on the airmass of the object. In Fig. A.1 we plot the correction factor, CJs, over the airmass of EGGR118, observed in the Js band throughout two months. The correction factor varies about 10% between the beginning of the observations (airmass ≈1) to the end of the observations (airmass ≈2.4). Since the Stokes parameters, Q and U, are linearly dependent on Cλ, the instrumental polarization itself changes significantly with the airmass of the observed object. For EGGR118, we find ΔP ≈ 1.4%.
To correct this effect, we fit a second-degree polynomial to the values of CJs that we determine for the different airmasses at which we observed EGGR118 (see Fig. A.1). Then, we take the airmass intervals of the Bok globule observations of each field and use the polynomial fit to determine their corresponding correction factors (see Fig. A.2).
The airmass dependency of the instrumental polarization clearly shows the invalidity of the assumption that the non-ideal Wollaston prism is the only source of the instrumental polarization that has to be considered. Since ISAAC/VLT does not contain any components that move after the basic setup of the instrument is completed, this dependency indicates significant influence by either the telescope itself or the atmosphere. Additional sources of the instrumental polarization can be the deformation of the mirrors when the telescopes points to different airmasses or rather zenith angles, causing artifical polarization in the moment when the beam is reflected.
All Tables
Gas densities, gas velocities, polarization, and magnetic field strengths of the outer parts of B335 traced in the near-IR.
All Figures
 |
Fig. 1 B335 – Left: DSS-map with overlaid near-IR polarization vectors observed with ISAAC/VLT. The length of the vectors shows the degree of polarization, and the direction gives the position angle. Only vectors with P/σP > 3 are plotted. The contour lines represent the 12CO(2–1) OTF channel maps obtained with the HHT on Mount Graham. The black (gray) contour lines give the blueshifted (redshifted) eastern (western) outflow lobe. The contour levels are |
| In the text | |
 |
Fig. 2 CB68 – a) DSS-map with overlaid near-IR polarization vectors observed with ISAAC/VLT. The length of the vectors shows the degree of polarization, and the direction gives the position angle. Only vectors with P/σP > 3 are plotted. The contour lines represent the 12CO(3–2) spectral channel maps obtained with the JCMT. The black contour lines give the blueshifted (south-eastern), the grey, dotted contour lines give the redshifted (north-western) outflow lobe. Contour levels at 0.25,0.50,0.75,... K (from Vallée et al. 2000, HPBW of 14′′; reproduced by permission of the AAS). b.1–3) Same as a) but with polarization vectors obtained with IFOSC/IGO in the optical. c) Intensity map overlaid with polarization vectors obtained with SCUBA/JCMT in the sub-mm (Vallée et al. 2003, reproduced by permission of the AAS). |
| In the text | |
 |
Fig. 3 CB54 – a) DSS-map with overlaid near-IR polarization vectors observed with ISAAC/VLT. The length of the vectors shows the degree of polarization, and the direction gives the position angle. Only vectors with P/σP > 3 are plotted. Blue vectors have a better error statistic than the red vectors, since they are based on more than one set of observations. The contour lines represent the 12CO(1–0) spectral channel maps obtained with the Five College Radio Astronomy Observatory. The solid contour lines give the blueshifted (south-western), and the dotted contour lines give the redshifted (north-eastern) outflow lobe. Contour levels are spaced at 0.3 K km s-1 intervals of 1.7 K km s-1 (blue), and 0.15 K km s-1 intervals of 0.45 K km s-1 (red), respectively (from Yun & Clemens 1994, beam size of 48′′; reproduced by permission of the AAS). b) Intensity map overlaid with polarization vectors obtained with SCUBA/JCMT in the sub-mm (Henning et al. 2001, reproduced by permission of the AAS). c) Intensity map overlaid with polarization vectors obtained with IMPOL/GIRT in the optical (Sen et al. 2000). |
| In the text | |
 |
Fig. 4 Distribution of the degree of polarization, P for P/σP > 3, counts given by N(P), of B335, CB68, and CB54, observed in the near-IR. |
| In the text | |
 |
Fig. 5 Distribution of the polarization angle, γ, counts given by N(γ), of B335, CB68, and CB54, observed in the near-IR. The dashed lines represent the mean polarization angles, |
| In the text | |
 |
Fig. A.1 Determined correction factors, CJs, of EGGR118 over the corresponding airmasses and the fit to the data points, a polynomial of the 2nd degree. The coefficients of the polynomial are given by the ai, beginning with the leading coefficient. |
| In the text | |
 |
Fig. A.2 Determination of the corresponding correction factors, CJs, of the globules airmass intervals by using the polynomial fit (see Fig. A.1). The errorbars in airmass direction give the airmass interval of the observation of each field. The errorbars in CJs-direction give the error of the estimated correction factor of each data point, including photometric and fitting errors. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.