| Issue |
A&A
Volume 565, May 2014
|
|
|---|---|---|
| Article Number | A52 | |
| Number of page(s) | 10 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201321119 | |
| Published online | 06 May 2014 | |
Properties of sunspot umbrae observed in cycle 24
Kiepenheuer-Institut für Sonnenphysik,
Schöneckstr. 6,
7104
Freiburg,
Germany
e-mail: kiess@kis.uni-freiburg.de; rrezaei@kis.uni-freiburg.de; wolfgang@kis.uni-freiburg.de
Received:
16
January
2013
Accepted:
6
February
2014
Aims. There is an ongoing debate whether the solar activity cycle is overlaid with a long-term decline that may lead to another grand minimum in the near future. We used the size, intensity, and magnetic field strength of sunspot umbrae to compare the present cycle 24 with the previous one.
Methods. We used data of the Helioseismic and Magnetic Imager on board the Solar Dynamics Observatory and selected all sunspots between May 2010 and October 2012, using one image per day. We created two subsets of this dataset with a manual tracking algorithm, both without duplication. One contains each sunspot (910 umbrae within 488 spots) and was used to analyze the distribution of umbral areas, selected with an automated thresholding method. The other subset contains 205 fully evolved sunspots. We estimated their magnetic field and the total magnetic flux and discuss the relations between umbral size, minimum continuum intensity, maximum field strength, and total magnetic flux.
Results. We find non-linear relations between umbral minimum intensity and size and between maximum magnetic field strength and size. The field strength scales linearly with the intensity and the umbral size scales roughly linearly with the total magnetic flux, while the size and field strength level off with stronger flux. When separated into hemispheres and averaged temporally, the southern umbrae show a temporal increase in size and the northern umbrae remain constant. We detected no temporal variation in the umbral mean intensity. The probability density function of the umbral area in the ascending phase of the current solar cycle is similar to that of the last solar cycle.
Conclusions. From our investigation of umbral area, magnetic field, magnetic flux, and umbral intensity of the sunspots of the rising phase of cycle 24, we do not find a significant difference to the previous cycle, and hence no indication for a long-term decline of solar activity.
Key words: sunspots / Sun: photosphere
© ESO, 2014
1. Introduction
Sunspots are the most conspicuous manifestations of the solar magnetic activity in white-light images (Bray & Loughhead 1964; Wittmann & Xu 1987). They are at the top of the hierarchy of the photospheric magnetic structures, being about three orders of magnitude larger than magnetic flux tubes (Keller 1992; Wiehr et al. 2004; Rouppe van der Voort et al. 2005; Solanki et al. 2006; Lagg et al. 2010). Diameters of sunspot umbrae span a range of 1 to 20 Mm and their areas cover two orders of magnitude (Solanki 2003; Rempel & Schlichenmaier 2011; Borrero & Ichimoto 2011). The umbrae of the largest sunspots are the coolest structures observed in the solar photosphere, their temperature is some 2000 K lower than that of the quiet-Sun photosphere (Maltby et al. 1986; Kopp & Rabin 1992; Balthasar & Schmidt 1993; Martinez Pillet & Vazquez 1993; Collados et al. 1994). The orientation of the magnetic field is close to the local vertical in umbrae (Beckers & Schröter 1969; Keppens & Martinez Pillet 1996; Mathew et al. 2003; Beck 2008).
The periodic variation of sunspot number, that is, the solar cycle, was observed for more than 400 years (Athay & Warwick 1961; Harvey 1992; Spruit 2012; Usoskin 2013). It is traced with several quantities, including the number and area of sunspots (Hoyt & Schatten 1996; Hathaway et al. 2002; Usoskin 2008; Hathaway 2010). The cyclic variation of umbral properties such as intensity and magnetic field strength was subject of several investigations (Livingston 2002; Penn & Livingston 2006; Penn & MacDonald 2007; Penn & Livingston 2011; Livingston et al. 2012; Pevtsov et al. 2013). Among others, Albregtsen & Maltby (1978) and Albregtsen et al. (1984) found that the umbral intensity fluctuates in phase with the solar cycle such that the umbrae are brighter at the end of a cycle. Norton & Gilman (2004) found a decrease in the umbral intensity from early- to mid-phase of cycle 23 and an increase after the maximum of the cycle. In contrast, Mathew et al. (2007) reported a constant umbral intensity throughout cycle 23. This is accompanied with a periodic variation of the maximum field strength of umbrae with solar cycle phase (Watson et al. 2011; Pevtsov et al. 2011; Rezaei et al. 2012a).
The fraction of umbral area to sunspot area is apparently independent of the solar cycle. Using Greenwich photoheliographic results, Jensen et al. (1955), Tandberg-Hanssen (1956), and Ringnes (1964) reported a weak tendency for the average penumbra-to-umbra radius to change in phase with the solar cycle. Steinegger et al. (1990) and Brandt et al. (1990) found umbra-penumbra area ratios of 0.24 and 0.32 for small and large spots, respectively. Beck & Chapman (1993) found the umbra-penumbra area ratio to be independent of the sunspot complexity and magnetic field strength and only weakly correlated with the umbral area. Mathew et al. (2007) found no variation of umbral radius with solar cycle. They noted a weak tendency of a secular trend in the northern hemisphere, however. Penn & MacDonald (2007) and Rezaei et al. (2012a) found no significant variation of the umbral area as a function of solar cycle. Schad & Penn (2010, hereafter SP) observed a small variation in umbral size correlated with the variation of umbral intensity and solar cycle.
The general view in early observations was that smaller sunspots have a higher continuum intensity and a lower magnetic field strength (Bray & Loughhead 1964). The underestimation of stray light in earlier works was noticed by Zwaan (1965), who argued that much of the dependency of the continuum intensity on the sunspot size can be explained by stray light (see also Rossbach & Schröter 1970). More recent investigations challenged the idea that the continuum-area dependency is an artefact of stray light (McIntosh 1981; Stellmacher & Wiehr 1988; Martinez Pillet & Vazquez 1993). Most recent observations indicate that the continuum-area dependency is real and exists even after removal of stray light (Mathew et al. 2007; Wesolowski et al. 2008; Schad & Penn 2010; Rezaei et al. 2012a).
Measurements of umbral physical properties are prone to systematic and random errors. Intensity measurements of umbrae are affected by scattered light (Mattig 1971; Martinez Pillet 1992; Chae et al. 1998; Beck et al. 2011). The field strength measurements in sunspot umbrae using the Zeeman splitting of spectral lines are contaminated on the one hand by molecular blends (Wittmann 1972) and on the other hand by inaccurate atomic data (Borrero et al. 2003). The uncertainty in the measurements of the umbral area is due to the umbral fine structures (Sobotka et al. 1993; Schmidt & Balthasar 1994; Lites et al. 2004; Rimmele 2008; Shimizu et al. 2009). Umbrae are more stable than penumbrae (Robinson & Boice 1982; Leka & Skumanich 1998; Schlichenmaier et al. 2010b; Rezaei et al. 2012b; Louis et al. 2012). Larger spots tend to have darker umbrae, a higher magnetic field strength, and a longer lifetime than smaller spots (e.g., Schrijver 1987). However, there is a significant intrinsic scatter (Lites & Skumanich 1990; Martinez Pillet & Vazquez 1993; Schlichenmaier & Collados 2002).
Bogdan et al. (1988, hereafter BOG) and SP studied the umbral size distribution from 1917 to 1982 and during the solar cycle 23, respectively. They found that there is no significant temporal variation in the size distribution from one cycle to the next. This invariance in the umbral area distribution is noteworthy considering the drastic difference in the number of sunspots in different solar cycles. The distribution can be fitted with a lognormal function, motivated by the fragmentation and random processes relevant to sunspot formation (Bogdan et al. 1988, and references therein). The size distribution of sunspot groups in the Greenwich photoheliographic sunspot records was studied by Baumann & Solanki (2005), who found a lognormal distribution both for the instantaneous area (corresponding to BOG selection) and for the maximum area of sunspots.
The end product of a multiplicative and fragmentary process is a lognormal distribution (Kolmogorov 1941). There are many applications of lognormal distributions in different branches of science (e.g., Pauluhn et al. 2000; Yurchyshyn et al. 2005; Kobayashi et al. 2011). In the photosphere, a lognormal distribution of the umbral area observed in about three orders of magnitude hints at a fragmentation origin for umbrae. BOG speculated that a lognormal distribution of emerging flux tubes indicates that they are probably the result of fragmentation of a large flux tube. As pointed out by Baumann & Solanki (2005), it is unlikely that sunspots are entirely the result of such fragmentation. It is perhaps more reasonable to imagine that they are the joint product of fragmentation and coalescence of flux patches, as discussed by Zwaan (1992) and Schlichenmaier et al. (2010b).
This size distribution provides insights into the nature of the solar dynamo mechanism (Parker 1979a; Ossendrijver 2003). However, most of the umbrae observed by BOG and SP were in their decay phase, therefore one needs to be careful about using their distribution as an argument for the origin of sunspot flux trunks in the convection zone. The fragmentation of the rising flux tube also occurs near the solar surface (Zwaan 1978; Brandenburg 2005). In a 16 Mm deep domain, Rempel (2011) found fragmentation of the flux trunk down to the bottom boundary. This subsurface fragmentation causes fragmentation in the photosphere, as observed for instance by Louis et al. (2012).
To distinguish between two sunspot formation scenarios (fragmentation or coalescence), one needs to evaluate the distribution in an early stage of spot development, when the decay has not redistributed the surfaced flux. It would be interesting to evaluate the umbral area beneath the photosphere and before their photospheric appearance. If lognormal, this would hint at a fragmentation process in the convection zone. To be as close as possible to such a pre-emergence situation, we have evaluated the umbral area distribution in an early stage, when the decay has not significantly redistributed the surfaced flux yet (Sect. 2.3).
Magnetohydrodynamic simulations of emerging flux tubes (Fan 2008), active regions (Cheung et al. 2010), pores (Cameron et al. 2007), and sunspots (Rempel et al. 2009) became available recently. The flux emergence simulations model the rise of a twisted flux tube in the convection zone, its expansion, and fragments near the solar surface. In contrast, in sunspot and pore simulations, the field lines are imposed on a relaxed hydrodynamic domain. Then, the dispersed flux elements partially evacuate and merge (Kitiashvili et al. 2010) to form pores and sunspots. The coalescence of the emerged flux elements in the simulations agrees with observations of Bernasconi et al. (2002) and Schlichenmaier et al. (2010a), for example. The tethered-balloon model of Spruit (1981) predicts that the coalescence of small flux patches (Pariat et al. 2004; Rezaei et al. 2012a) is a surface phenomenon since these flux elements are deeply anchored. In other words, the emergence of large flux tubes does not fundamentally affect their integrity.
Because of the broad range of parameters, simulations usually focus on some aspects of sunspot properties instead of addressing all problems. Umbrae in these simulations perform convective energy transport by umbral dots and transient light-bridges. Rempel (2011, his Fig. 11) presented a sunspot with a minimum (bolometric) umbral intensity of about 0.3 Ic. In another simulation he found a minimum umbral intensity of about 0.22 Ic (Rempel 2012, his Fig. 5). In both cases, the unsigned flux of the simulated spot is about 1022 Mx. Using the SIR code (Ruiz Cobo & del Toro Iniesta 1992; Bellot Rubio 2003), we performed spectral synthesis of the Rempel (2012) umbra and found a minimum continuum intensity of 0.08 Ic at a wavelength of 630 nm. This minimum intensity is close to what one expects for such a big sunspot (compare with the sunspot of Nov. 19, 2013).
Rempel (2011) presented a simulated sunspot in a domain 16 Mm deep. In this simulation, a considerable amount of a subsurface magnetic field is fragmented due to convection. The photospheric manifestation of this fragmentation is the appearance of light-bridges or flux separation. He found a deep-reaching outflow beneath the photosphere down to the bottom boundary of the simulation domain. Such an axisymmetric outflow presumably supports the monolithic subsurface structure of sunspots (Parker 1979b). It is unclear which role the supergranulation flow plays in this process.
Sunspots decay as a result of fragmentation (Petrovay
& van Driel-Gesztelyi 1997; Martínez Pillet
2002). The decay rate, which in turn determines the sunspot lifetime, is a function
of anchoring depth and the corresponding convection timescales in such depths (Moradi et al. 2010). The lifetime of sunspots,
T, falls in
between two extremes: ![\begin{eqnarray*} \frac{H_p}{\it{v}_{\mathrm{rms}}} \ll T \ll \left(\frac{r_0}{10\,\mathrm{Mm}}\right)^2 \times10\,[\mathrm{days}], \end{eqnarray*}](/articles/aa/full_html/2014/05/aa21119-13/aa21119-13-eq4.png) where
Hp is the pressure scale
height, vrms is a typical convection velocity, and
r0
the maximal radius of the spot (Petrovay &
Moreno-Insertis 1997; Schlichenmaier et al.
1999).
where
Hp is the pressure scale
height, vrms is a typical convection velocity, and
r0
the maximal radius of the spot (Petrovay &
Moreno-Insertis 1997; Schlichenmaier et al.
1999).
McIntosh (1981) reported on a long-lived sunspot in Aug. 1966, which survived five solar rotations (137 days). While the convection timescale (the lower limit) is about 6 h at a depth of 15 Mm, Rempel (2011) speculated that the lifetime of a sunspot is roughly an order of magnitude longer than the convection timescale (at the corresponding anchoring depth). The trend found in his simulation cannot be extrapolated to broader ranges since the aforementioned long-lived sunspot will need an anchoring depth of about four times the depth of the convection zone.
The prolonged duration of the minimum of the last solar cycle (23) raised speculations about a lower activity level in solar cycle 24 and the possible approach of a new grand minimum (Tripathy et al. 2010; Jain et al. 2011). There are also indications that the population of small sunspots compared with the large ones in solar cycle 23 might be different than in previous cycles (Clette & Lefèvre 2012). This motivated us to study properties of umbrae in the current solar cycle (24) and compare them with those of previous cycles.
In this contribution, we measure the umbral area, evaluate the maximum field strength and minimum intensity of sunspot umbrae in solar cycle 24 based on the data obtained with the Helioseismic and Magnetic Imager (HMI, Scherrer et al. 2012; Schou et al. 2012), a filter instrument on board the Solar Dynamics Observatory (SDO, Pesnell et al. 2012). From May 2010 until October 2012, 4229 sunspots were observed with some 6892 (910 unique) umbrae. The criteria for the data selection are discussed in Sect. 2. We analyze the data and interpret the results in Sects. 3 and 4, respectively. A summary and conclusions are presented in Sect. 5.
2. Observations and data analysis
HMI records six equidistant wavelength positions around the center wavelength of the neutral iron line at 617.33 nm (Norton et al. 2006; Fleck et al. 2011). HMI filters have a full width at half maximum (FWHM) of about 7.6 pm. With a spatial sampling of about 0.5″, the spatial resolution of each full-disk image is about 1″. The image size is 4096 × 4096 pixels and the cadence of full Stokes maps is 12 min1.
2.1. Range of observation
The current solar cycle (24) started on January 04, 2008, when a new active region with reversed polarity in the northern hemisphere at a high latitude was observed by the Solar and Heliospheric Observatory (SOHO, Scherrer et al. 1995) Michelson Doppler Imager (MDI, Scherrer et al. 1995). Figure 1 shows the monthly and smoothed sunspot number in cycle 24 (SIDC-team 2008). The activity level was very low throughout the rest of 2008. A significant rise of the sunspot number only occurred in early 2009 (Fig. 1).
Our observations (01/05/2010 to 31/10/2012) cover the rising phase of cycle 24. After a small dip in early 2013, the spot number increased again in the second quarter of 2013. We analyzed one image of the continuum intensity per day and selected all sunspots in the data.
 |
Fig. 1 SIDC monthly sunspot number (black line). The gray line shows the smoothed sunspot number. The dashed vertical lines mark the range of our data. |
2.2. Correction for limb-darkening
As a first step, each image was normalized to its mean value, derived from a 100″ square at disk center, avoiding sunspots. To derive the limb-darkening curve, images from twelve days with no activity were chosen, and μ, the cosine of the heliocentric angle, was computed for each pixel. We used a smoothed version of the intensity as a function of μ to correct for limb-darkening. This curve represents our empirical limb-darkening function. For each data pixel, the heliocentric angle was calculated and the intensity was divided by the corresponding value of our limb-darkening function.
2.3. Selection of umbrae
We analyzed one image per day and manually marked a total of 4229 sunspots (6892 umbrae) on the visible solar hemisphere. Because most sunspots live for several days, we applied an algorithm to reduce the data such that no sunspot was counted multiple times.
Starting with the first spot in our data, we calculated its expected positions during its passage across the solar disk (maximum 14 days), taking the differential rotation depending on the latitude θ into account. We used the empirical formula Ω [ deg/day ] = 14.522−2.84 sin2(θ) given by Howard et al. (1984). For these 14 days we then simultaneously plotted all sunspots closer than 15 degrees to the expected positions of the first spot. From this series of images we then manually selected the sunspots of interest and skipped the rest. This algorithm was successively used on the remaining sunspots in our original dataset (4229 spots).
We applied the described algorithm using two different selection criteria. For the first subset of data we focused on young spots with well-developed umbrae. None of the selected spots had a heliocentric angle greater than 60 degrees (μ ≥ 0.5). This subset containing 488 spots was used for statistical analysis of umbral sizes described in Sect. 3.1. For the second subset we focused on fully evolved sunspots with penumbrae. To reduce scatter, no complex spots were selected. This led to a subset of 205 sunspots that was used to analyze the correlation of umbral properties.
 |
Fig. 2 AR11520 on 14/07/2012 is an example of a sunspot with a large umbra. The red contour shows the threshold level (0.6 of mean quiet-Sun intensity) used to select the umbra. The spot has a heliocentric angle of μ = 0.86. The total area of the largest four umbrae is 206 MHS. |
2.3.1. Large sample
The first subset (488 sunspots) was used for an analysis of the distribution of umbral sizes. We applied a threshold method to select the umbrae, see for instance, Brandt et al. (1990), Mathew et al. (2007), Wesolowski et al. (2008), and SP. This threshold was chosen as 0.6 of the mean quiet-Sun intensity. The minimum size for an umbra to be selected was chosen to be 0.5 microhemispheres (MHS). OneMHS is 10-6 of the visible solar surface and corresponds to 3.05 Mm2 or 5.79 arcsec2. We counted distinct umbrae within one sunspots separately, which led to a total of 910 umbrae within 488 sunspots. A threshold value of 0.6 ensured that all umbrae were sampled, while it does not capture umbral light bridges as seen in Fig. 2 (Muller 1979). To evaluate the umbral size distribution we created a histogram with fifty bins. A logarithmic bin size was used to ensure that there was still a fair number of umbrae in the bins covering higher values of the size spectrum. We considered an uncertainty of ±1 pixel for the umbral radius in each measurement. The relative uncertainty of the umbral size decreases with increasing umbral area. Since logarithmic binning was chosen, the bins for small spots are narrower than the bins for large ones. For the first bin (0.5 MHS) the width is about the same as the uncertainty of the umbral area.
2.3.2. Small sample
For each of the 205 spots we used a threshold of 0.52 of the mean quiet-Sun intensity to select its umbra (see Sect. 4.7.2 for the influence of the intensity threshold). From a circle with the same area as the umbra we calculated an equivalent radius. We also derived the minimum relative intensity (the darkest pixel) and the maximum magnetic field strength. We furthermore marked the penumbra manually and calculated the total magnetic flux of the sunspot. Using this sample, we studied relations between size, intensity, field strength, and flux of sunspots. We also analyzed the variation of minimum intensity and size measurements in each hemisphere as a function of time. We grouped these data using ten measurements in each but the last bin. The radii in the large and small sample are not directly comparable, since we applied different thresholds, and in the small sample we did not distinguish between multiple umbrae within one sunspot.
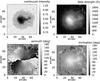 |
Fig. 3 Inversion results for one of our sunspots. From top left clockwise: continuum intensity, magnetic field strength, inclination, and azimuth. |
2.4. Inversion of HMI data
We inverted the HMI data using an updated version of the Very Fast Inversion of the Stokes Vector (VFISV, Borrero et al. 2007, 2011) code to retrieve the magnetic field. Assuming a source function that varies linearly with optical depth, the code uses a Milne-Eddington approximation to solve the radiative transfer equation. The best-fit solution of the code then returns the height-independent values of the magnetic field strength, inclination and azimuth along with the velocity and other parameters. The inversion was performed for all sunspots of the small sample. An example of the results is shown in Fig. 3. The standard deviation of the estimated error of the magnetic field strength is about 87 Gauss (G). Because HMI samples only six wavelength positions, systematic errors in the magnetic field strength are possible. Although the magnetic field strength in magnetograms suffers from saturation effects (Liu et al. 2007, 2012), we do not see saturation in the inverted field strength. There are, however, limitations on the maximum retrieved field strength using HMI data. This is mainly due to the low light level in the center of dark umbrae, the spacecraft velocity, presence of molecular blends, as well as strong Zeeman splitting compared with the spectral range of HMI. We did not use the spurious field strength, which appeared only on a few large sunspots in our sample, but used the maximum field strength where the inversion succeeded.
 |
Fig. 4 Variation of umbral maximum field strength as a function of radius. Parameters of a linear fit (solid red line) and power law fit (solid blue line) and correlation coefficients are given in Table 1. The dashed lines mark the one-sigma confidence level for each fit. The yellow and purple lines mark the adopted linear fits from Kopp & Rabin (1992) and SP, respectively. The upper x-axis shows the area corresponding to the given radius. |
 |
Fig. 5 Variation of umbral minimum intensity vs. radius. For a more detailed description, see caption of Fig. 4. |
 |
Fig. 6 Maximum field strength of umbra vs. minimum intensity. For a more detailed description, see caption of Fig. 4. |
3. Results
3.1. Size, intensity, and field strength
We studied the umbral maximum field strength, minimum continuum intensity, and area (or its equivalent radius) in our data. To this end, we selected 205 mature sunspots close to disk center, with a relatively simple structure, and approximately after the end of their initial growth phase. Figure 3 shows a typical spot of this sample.
Figures 4 and 5 show scatter plots of maximum field strength and minimum intensity as a function of umbral radius, respectively. Figure 6 shows the relation between field strength and intensity. We plot power law and linear fits in all three cases. Fit parameters can be found in Table 1.
A power law fit reproduces the observed data better than a linear fit in Figs. 4 and 5. This non-linearity motivated us to fit a power law in the intensity-magnetic field strength relation (Fig. 6) as well. The three power exponents are consistent, that is, 0.23 ≈ (–0.96) * (–0.26), cf. Table 1. We also provide linear fits for comparison with other authors (see Sect. 4).
 |
Fig. 7 Variation of umbral parameters with magnetic flux (Φ). Left: maximum field strength vs. Φ, center: radius vs. Φ, right: minimum intensity vs. Φ. Parameters of a linear fit (solid red line) and power law fit (solid blue line) and correlation coefficients are given in Table 1. |
3.2. Magnetic flux
We used the inclination maps from the inversions (Sect. 2.4) to measure the total (unsigned) magnetic flux Φ of each sunspot in the small sample. Figure 7 shows scatter plots of the umbral size, intensity, and field-strength versus flux. Maximum field strength and minimum intensity show non-linear relations with the flux. The total magnetic flux of a sunspot is an integral quantity like the size. The umbral equivalent radius shows a quite linear dependence on flux and has a tight correlation (middle panel). The field strength and intensity show larger scatter compared with size and non-linear behavior. We used power law relations to fit these data.
3.3. Northern and southern hemispheres
There are about 50% more sunspots in the northern hemisphere than in the southern one in our full data (6892 umbrae). In a six-month interval statistics, the northern hemisphere had more sunspots than the southern except for the very last six month in our data. This might indicate a time lag between the two hemispheres. Therefore, we tried to analyze the temporal variation of the radius and intensity of umbrae in each hemisphere (Fig. 8). The northern hemisphere does not show a significant variation of the umbral radius vs. the solar cycle phase, that is, between 2 years and 4.5 years after the beginning of the cycle, while there is a marginally significant change in the southern hemisphere (2σ). The temporal variation of the intensity (lower panel) does not show any significant variation in either hemisphere. This is an important finding, and we return to this point in Sect. 4.6.
 |
Fig. 8 Variation of intensity and size of sunspots in each hemisphere vs. time. Each point represents the average of ten sunspots. |
3.4. Distribution of the umbral area
We used the sample of 910 unique umbrae (each counted once) and the whole dataset of 6892 umbrae to study the area distribution. To approach the underlying probability density function (PDF), ρ, the histogram was normalized such that its area was unity. A Levenberg-Marquard least-squares procedure (Press et al. 1992) was used to fit a lognormal function (Eq. (1)) to this distribution. To weight the bins, the errors were taken proportional to the inverse of the square root of the number of entries in each bin.
The lognormal distribution is 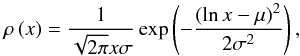 (1)where x is the umbral size in
MHS, and μ
and σ are the
two fit parameters. Table 2 lists the fit
parameters and their uncertainties. The mean value of the umbral area and the mean of the
PDF in the observed range are the same (13 MHS). The standard deviation of the data
(20 MHS) is similar to the value of the PDF (26 MHS). The top panel of Fig. 9 shows our data and the fit with uncertainties. The
bottom panel of Fig. 9 shows the lognormal fits of
the large sample and all data. The shapes of the two curves are very similar. Neither
counting each umbra only once, nor reducing the data to fully evolved sunspots drastically
modifies the distribution compared with the full dataset. This means that we do not see an
influence of the evolution of sunspots on the distribution of umbral sizes in our data.
(1)where x is the umbral size in
MHS, and μ
and σ are the
two fit parameters. Table 2 lists the fit
parameters and their uncertainties. The mean value of the umbral area and the mean of the
PDF in the observed range are the same (13 MHS). The standard deviation of the data
(20 MHS) is similar to the value of the PDF (26 MHS). The top panel of Fig. 9 shows our data and the fit with uncertainties. The
bottom panel of Fig. 9 shows the lognormal fits of
the large sample and all data. The shapes of the two curves are very similar. Neither
counting each umbra only once, nor reducing the data to fully evolved sunspots drastically
modifies the distribution compared with the full dataset. This means that we do not see an
influence of the evolution of sunspots on the distribution of umbral sizes in our data.
 |
Fig. 9 Umbral size distribution. Error bars in x-direction mark the width of the bins. The error bars in y-direction are proportional to the inverse of the square root of entries in each bin. Top: the black data points and curve show our data and the lognormal fit, respectively. The colored curves are adopted from SP and show their fit (after normalizing its area) to the rising phase (red) and maximum (blue) of solar cycle 23. The red arrow marks the data range used by SP. Bottom: comparison of the complete sample of 6892 umbrae and the unique sample of 910 umbrae (no repetition). The dashed lines give the one-sigma errors of the fit. |
4. Discussion
We carefully selected sunspots, taking mostly leading spots after the initial growth phase when most of the flux had emerged. About half of the selected sunspots have a μ value higher than 0.9 (heliocentric angle θ< 26°). In the following, we discuss our results and compare them with earlier works.
4.1. Relation between umbral size and field strength
Nicholson (1933) already found that the magnetic field strength scales non-linearly with the umbral size, although his results for field strengths lower than 2000 G are biased by systematic errors. Since then, this relationship was confirmed by several authors (von Klüber 1948; Kopp & Rabin 1992; Livingston 2002; Rezaei et al. 2012a). In Fig. 4 we compare linear fits of SP (Fe i 868.8 nm) and Kopp & Rabin (1992, Fe i 1.56 μ with our results. Because these spectral lines sample slightly different layers of the solar atmosphere than the Fe i 617.3 nm line (HMI), we evaluated the systematic offset in the received field strength. We used the COOL umbra model of Collados et al. (1994) and the SIR code (Ruiz Cobo & del Toro Iniesta 1992; Bellot Rubio 2003) to synthesize this model atmosphere for the given lines and invert them as in case of VFISV. As expected, the Fe i 1.56 μm line samples deeper layers of the atmosphere and returns stronger field strengths (than the HMI line), while the Fe i 868.8 nm line samples slightly higher layers, resulting in lower values. Therefore, we applied a fixed correction (changing the ordinate) before overplotting the curves of SP (purple) and Kopp & Rabin (yellow) in Fig. 4. The line of SP is quite parallel to our line, with an offset of about 300 G.
4.2. Size–intensity relation
Figure 5 shows a non-linear relationship between the minimum continuum intensity and the umbral radius. The umbral intensity contrast decreases with increasing wavelength. This complicates a direct comparison of the size–intensity and the intensity-field strength relation with the results of other authors, which is why we do not show adopted curves. This not only requires a correction factor to account for different wavelengths, but also requires individual correction for stray-light removal applied in each study. A power law fit matches the observed values better than a linear fit. SP presented a quadratic fit, while Mathew et al. (2007) found that a power law fit better reproduced the observations. The exponent of our power law fit compares well with the exponent given by Mathew et al. (2007). These authors used a wavelength range close to the HMI line.
4.3. Relation of field strength to intensity
It is generally believed that the sunspot umbra is darker because of a partial inhibition of convective energy transport in presence of a strong magnetic field (Biermann 1941). There is a well-known relation between the field strength and the intensity of umbrae (e.g. Martinez Pillet & Vazquez 1993). Both maximum field strength and minimum intensity show a non-linear dependence on the size of umbrae with noticeable intrinsic scatter. The darkest umbrae in our data have minimum continuum intensities as low as six percent of the quiet-Sun intensity, which indicates a low amount of stray light (Fig. 6). SP fit a power law function to the relation of field strength to intensity, while Rezaei et al. (2012a) used a linear relation alone. The power law exponent in our fit (–0.26) is lower than the one presented by SP because of the weaker umbral contrast in the near infrared. The correlation between minimum intensity and maximum field strength is significantly higher than the one between size and intensity. Therefore, if no polarimetric measurements are available, the umbral intensity is a better proxy for a rough estimation of the magnetic field strength than the size, as suggested by Norton & Gilman (2004).
4.4. Magnetic flux
The generally adopted scenario of a forming active region is the rise of a buoyant flux tube in the convection zone (Parker 1955; Spruit 1981; Caligari et al. 1995). The buoyancy requires definite values of the magnetic field strength, and the rise of a buoyant flux tube is accompanied by a horizontal expansion. Cheung et al. (2007) found in simulations that a scaling relation forms between the field strength and the plasma density before the emergence on the solar surface. The final field strength is the result of the interaction between the rising flux tube and the turbulent convection in an stratified atmosphere. The total magnetic flux is one of the parameters that determines the size, intensity, and field strength of a sunspot. During the formation process, pores and small flux patches migrate and accumulate enough flux to form sunspots (Zwaan 1992; Leka & Skumanich 1998; Schlichenmaier et al. 2010a). The total flux of a sunspot is lower than the total flux of the corresponding flux tube because a fraction of flux disperses in plages and cancellations (e.g., Cheung et al. 2010).
For a better understanding of the interplay between the flux and maximum field strength
as well as size and intensity, we plot these parameters vs. flux in Fig. 7. The scatter in the plot of the relation of field
strength to flux (left panel) is reminiscent of the scatter in the plot of field strength
to size (Fig. 4). The umbral field strength perhaps
also depends on the fraction of penumbral flux. Steinegger et al. (1990) found that the ratio of the umbra to penumbra area is
positively correlated with the spot size. The linearity of the relation of sunspot radius
vs. flux (Fig. 7, middle panel) suggests that one
might use the sunspot size as a proxy for its flux. From this point of view, the left and
right panel of Fig. 7 are similar to Figs. 4 and 5,
respectively. Umbral sizes oscillate during the lifetime of spots, in particular for
long-lived spots with a timescale of 3–5 days (Robinson
& Boice 1982). This is much longer than the dynamical timescale: the
Alfv n
and sound timescale (at τ =
1 level) in a moderate-sized spot is on the order of an hour (Rempel & Schlichenmaier 2011). It needs to be
investigated whether these size oscillations leave traces in the maximum field strength of
spots.
n
and sound timescale (at τ =
1 level) in a moderate-sized spot is on the order of an hour (Rempel & Schlichenmaier 2011). It needs to be
investigated whether these size oscillations leave traces in the maximum field strength of
spots.
4.5. Maximum field strength and strength of a cycle
At first glance, Fig. 4 suggests that the maximum field strength of sunspots level off at a certain value. In principle, the maximum field strength is a result of the horizontal pressure balance of umbrae and the surrounding atmosphere (e.g., Ossendrijver 2003). This simple picture, however, cannot explain the scatter in the left panel of Fig. 7. As seen in this figure, the maximum field strength does not increase much from sunspots with a flux of 5 to 15 × 1021 Mx (≈3.2 kG and ≈3.4 kG, respectively). Livingston (2002, their Fig. 2) and Rezaei et al. (2012a, their Fig. 3) also did not find field strengths higher than about 4 kG in cycles 22 and 23, respectively.
The strongest umbra in cycle 24 in our data has a field strength of 3.4 kG, comparable with cycle 23 (3.6 kG using infrared lines, Rezaei et al. 2012a). Our results agree with Norton et al. (2013), who found no variation in the maximum field strength of umbrae between cycle 23 and 24. Livingston et al. (2006) compiled old observations and reported maximum field strengths of up to 6 kG. The number of sunspots with a very strong field strength, however, dropped sharply in the last few cycles. Does the Sun fail to generate large and strong sunspots? Livingston et al. (2006) found a fraction of 0.2% for umbrae with a field strength stronger than 4 kG. In our sample of 205 spots we would expect 0.4 spots and do not observe such a strong field strength.
The strength of solar cycles is determined by the number of sunspots, their darkness, and by the field strength. Cameron & Schüssler (2012) proposed that the strength of a cycle changes as a function of cross-equator flux transport and near-surface flows (see also Durrant et al. 2004; Cameron et al. 2013). They used the open flux parameter (Wang & Sheeley 2009) as a precursor of the next solar cycle. These authors found that the non-linear growth of disturbances caused by an occasional emergence of a large active region near the solar equator can significantly amplify or weaken the next solar cycle. Hence it is perhaps too early to conclude that no sunspot appears in cycle 25, as proposed by Livingston et al. (2012).
4.6. Hemispheric asymmetry and temporal variation
We present the temporal variation of intensity and size of umbrae in Fig. 8 and find no significant trend for the umbral intensity in either hemisphere during the rising phase of cycle 24. Our finding is in contrast to results reported by Norton & Gilman (2004), who found a decrease in umbral intensity in the rising phase of cycle 23. These authors used the MDI instrument with a spatial resolution of about 2″. In comparison, HMI data have a spatial resolution of 1″. No stray-light correction was applied in either study. Mathew et al. (2007) found a decrease in the umbral intensity in the northern hemisphere, but attributed it to variations of umbral size in that time interval and considered it insignificant. The time interval of our data is about half of that of Mathew et al. (2007). Our finding also agrees with Norton et al. (2013), who found no variation in umbral intensity during the rising phase of cycle 24, as well as de Toma et al. (2013) who find no variation in the umbral intensity from 1986 to 2012.
In our data the number of sunspots in the northern hemisphere is about 50% larger than in the southern one. This either indicates that there is a time lag between the two hemispheres, or that there is a significant difference regardless of the phase of the solar cycle (Knaack et al. 2004). There are several reports of the hemispheric asymmetry in meridoinal flow (Howard & Gilman 1986), polar field reversal (Durrant & Wilson 2003), and the magnetic activity (Temmer et al. 2002; Brajša et al. 2005). McIntosh et al. (2013) found that overall in cycles, the northern hemisphere experienced a larger number of spots since 1965, while the southern hemisphere had an excess in sunspot number in the declining stage of the last four cycles. Hence, our finding of a leading northern hemisphere agrees with the latter authors. An increase of the umbral radius is seen only in spots in the southern hemisphere (Fig. 8).
4.7. Umbral size distribution
4.7.1. Comparison with BOG and SP
To compare our result for cycle 24 with those of previous cycles, one has to convert
the fit parameters reported in SP and BOG into our definition. These authors used a
different definition of the lognormal function, 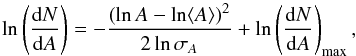 (2)where
A is the
umbral size, (dN/
dA) is the density function, ⟨ A ⟩ the mean and
σA the width of the
distribution. With this definition, the function is normalized to its maximum and not
its integral (
(2)where
A is the
umbral size, (dN/
dA) is the density function, ⟨ A ⟩ the mean and
σA the width of the
distribution. With this definition, the function is normalized to its maximum and not
its integral (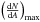 scales the
distribution). To normalize Eq. (2) to
its area, that is, make it a PDF, one has to select
scales the
distribution). To normalize Eq. (2) to
its area, that is, make it a PDF, one has to select
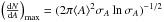 .
It is straightforward to show that these two definitions are mathematically identical.
The conversion factors are the following:
.
It is straightforward to show that these two definitions are mathematically identical.
The conversion factors are the following:  (3)These relations
allow one to convert the fit parameters given by SP and BOG into our definition
(Table 2).
(3)These relations
allow one to convert the fit parameters given by SP and BOG into our definition
(Table 2).
The top panel of figure 9 shows the lognormal fit of the umbral size distribution in the current solar cycle and the previous one. The red curve was calculated using the results of SP for the ascending phase of solar cycle 23. We converted their parameters into our definition using Eq. (3). The curves of the rising part of solar cycle 23 and 24 are similar (the fit parameters of these two fits are listed in Table 2). Although our fit parameters differ from those published by SP, the distributions are close in the relevant part of the size spectrum (i.e., between 0.5 and 200 MHS where we actually fitted the data) and the strongest deviation belongs to the smallest umbral radii. This also agrees with the invariant umbral area distribution reported by BOG and SP. Therefore, we conclude that the umbral size distribution of the current solar cycle (24) is similar to the distribution of the previous one. Note that BOG did not use a threshold method to determine the umbral size, which makes the results not exactly comparable. Also note that they considered only spots within ±7.5 deg from the meridian, while SP and we included all sunspots except those at the very limb.
For umbrae larger than 100 MHS there is a deviation between the fit and the data (Fig. 9), which is also the case for cycle 23 in SP (their Fig. 1). Although in both cases this difference is within the given errors, one might argue that the assumption of a lognormal distribution fails in this part of the size spectrum in the early stage of the cycle.
4.7.2. Influence of the intensity threshold
The continuum intensity at the umbra-penumbra border was assumed to be 0.6. For a discussion of the influence of this on the umbra-penumbra area ratio, see Steinegger et al. (1996) and Gyori (1998). We repeated our analysis for several intensity thresholds between 0.5 and 0.6 of quiet-Sun mean intensity. Table 2 contains the fit parameters for the umbral size distributions for thresholds of 0.5 and 0.6 Ic. The size distribution is very robust with respect to this parameter, the distributions do not show a significant difference. We chose a lower threshold (0.52) for the analysis of umbral properties in the 205 sunspots for which we inverted the magnetic field. This decision was made to reduce the risk of contamination of the umbra with penumbral light.
4.7.3. Temporal invariance of the size distribution
Our umbral area distribution (Fig. 9) is similar to that of SP. These authors compared different parts of cycle 23 and found only a weak variation in the umbral size distribution. BOG noted that the distribution function does not change from one cycle to the next. This is in contrast to other umbral properties such as umbral brightness (Albregtsen & Maltby 1978; Albregtsen et al. 1984) or magnetic field strength (Livingston et al. 2012; Rezaei et al. 2012a), which vary within the solar cycle or show a long-term trend (Nagovitsyn et al. 2012).
4.8. Error discussion
Intensity measurements always have to be taken with caution because they are to some degree biased by stray light. We did not correct for this because when we analyzed the data no point spread function (PSF) was available for HMI. Fortunately, the low minimum umbral intensities we found in this work indicate a low degree of stray-light contamination, or at least a very narrow PSF compared with the size of large umbrae. See Yeo et al. (2014) for recent results regarding the PSF of HMI.
The errors to the curve fits in the scatter plots between intensity, magnetic field strength, radius, and magnetic flux (Figs. 4 – 7) were calculated using the errors of the individual measurements, which are the spatial resolution of the telescope for the radius and an uncertainty of 150 G for the magnetic field strength. Our findings might still be biased by random errors, especially since the statistics covers only 2.5 years of data. Therefore the relations for large spots have to be taken with caution, since the intrinsic scattering in all parameters is high.
The same argument holds for the umbral size distribution. Our histogram falls below the lognormal curve for umbrae larger than 100 MHS, but since there are very few measurements in this part of the histogram, this may just be coincidence because our statistics covers only 2.5 years. Owing to the limited statistics, the errors for the temporal variation of umbrae are large and an observed trend is barely significant. On the other hand, short as they are, our statistics are complete and cover all sunspots during the rising phase of the current cycle (24).
5. Summary and conclusion
We used HMI data to investigate properties of sunspots in the ascending phase of solar cycle 24. We used one solar image per day and applied an automated thresholding method to measure the umbral area. The data were corrected for limb-darkening and foreshortening effects. We performed an inversion to retrieve the magnetic field vector for a hand-selected subset of 205 sunspots. We used the large sample (910 unique umbrae) to analyze the distribution of umbral sizes, while the small sample enabled us to study empirical relations and temporal variations of size, magnetic field strength, and continuum intensity. The relations between magnetic field strength, continuum intensity, and size of the umbrae are similar to previous studies, an invariant size-field strength relationship very likely exists.
The relation between umbral intensity and size shows a power law behavior with an exponent similar that of the previous cycle. Compared with a linear fit, a power law function fits the dependency of intensity on magnetic field strength and size better. The continuum intensity is a good proxy of the field strength, while the sunspot flux closely follows the umbral area. The umbral radius shows an increase in the southern hemisphere, while no significant temporal variation in the northern hemisphere was observed. The umbral intensity does not show a temporal variation in the ascending phase of cycle 24 similar to cycle 23. The umbral size distribution is also similar to that in the rising phase of cycle 23. Using sunspot properties in the ascending phase of cycle 24, we found no evidence for a significant decrease in solar activity, as was suggested for instance by Livingston et al. (2012). We will continue to monitor sunspot properties and their changes through the rest of this cycle to examine the likelihood of a long-term decrease of the solar activity.
Data are available at http://jsoc.stanford.edu/, see also http://hmi.stanford.edu/ for information about the instrument.
Acknowledgments
The data used here are courtesy of NASA/SDO and the AIA, EVE, and HMI science teams. R.R. acknowledges financial support by the DFG grant RE 3282/1-1. We acknowledge fruitful discussions at the workshops on “Filamentary Structure and Dynamics of Solar Magnetic Fields” as well as “Extracting Information from spectropolarimetric observations: comparison of inversion codes” at the ISSI in Bern. We thank Rolf Schlichenmaier for insightful discussions. We also thank the anonymous referee for helpful suggestions. We are grateful to Juan Manuel Borrero for instructions on using his latest version of VFISV code. We used data provided by M. Rempel at the National Center for Atmospheric Research (NCAR). The National Center for Atmospheric Research is sponsored by the National Science Foundation.
References
- Albregtsen, F., & Maltby, P. 1978, Nature, 274, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Albregtsen, F., Joras, P. B., & Maltby, P. 1984, Sol. Phys., 90, 17 [Google Scholar]
- Athay, R. G., & Warwick, C. S. 1961, Adv. Geophys., 8, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Balthasar, H., & Schmidt, W. 1993, A&A, 279, 243 [NASA ADS] [Google Scholar]
- Baumann, I., & Solanki, S. K. 2005, A&A, 443, 1061 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, C. 2008, A&A, 480, 825 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, C., Rezaei, R., & Fabbian, D. 2011, A&A, 535, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, J. G., & Chapman, G. A. 1993, Sol. Phys., 146, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Beckers, J. M., & Schröter, E. H. 1969, Sol. Phys., 10, 384 [NASA ADS] [CrossRef] [Google Scholar]
- Bellot Rubio, L. R. 2003, Inversion of Stokes profiles with SIR (Freiburg: Kiepenheuer Institut für Sonnenphysik) [Google Scholar]
- Bernasconi, P. N., Rust, D. M., Georgoulis, M. K., & Labonte, B. J. 2002, Sol. Phys., 209, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Biermann, L. 1941, Vierteljahrsschr. Astr. Gesellsch., 76, 194 [Google Scholar]
- Bogdan, T. J., Gilman, P. A., Lerche, I., & Howard, R. 1988, ApJ, 327, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Borrero, J. M., & Ichimoto, K. 2011, Liv. Rev. Sol. Phys., 8, 4 [Google Scholar]
- Borrero, J. M., Bellot Rubio, L. R., Barklem, P. S., & del Toro Iniesta, J. C. 2003, A&A, 404, 749 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borrero, J. M., Tomczyk, S., Norton, A., et al. 2007, Sol. Phys., 240, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Borrero, J. M., Tomczyk, S., Kubo, M., et al. 2011, Sol. Phys., 273, 267 [Google Scholar]
- Brajša, R., Wöhl, H., Vršnak, B., et al. 2005, Sol. Phys., 231, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A. 2005, ApJ, 625, 539 [Google Scholar]
- Brandt, P. N., Schmidt, W., & Steinegger, M. 1990, Sol. Phys., 129, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Bray, R. J., & Loughhead, R. E. 1964, Sunspots (Chapman Hall) [Google Scholar]
- Caligari, P., Moreno-Insertis, F., & Schüssler, M. 1995, ApJ, 441, 886 [NASA ADS] [CrossRef] [Google Scholar]
- Cameron, R. H., & Schüssler, M. 2012, A&A, 548, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cameron, R., Schüssler, M., Vögler, A., & Zakharov, V. 2007, A&A, 474, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cameron, R. H., Dasi-Espuig, M., Jiang, J., et al. 2013, A&A, 557, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chae, J., Yun, H. S., Sakurai, T., & Ichimoto, K. 1998, Sol. Phys., 183, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Cheung, M. C. M., Schüssler, M., & Moreno-Insertis, F. 2007, A&A, 467, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cheung, M. C. M., Rempel, M., Title, A. M., & Schüssler, M. 2010, ApJ, 720, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Clette, F., & Lefèvre, L. 2012, J. Space Weather Space Clim., 2, A06 [Google Scholar]
- Collados, M., Martinez Pillet, V., Ruiz Cobo, B., del Toro Iniesta, J. C., & Vazquez, M. 1994, A&A, 291, 622 [NASA ADS] [Google Scholar]
- de Toma, G., Chapman, G. A., Cookson, A. M., & Preminger, D. 2013, ApJ, 771, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Durrant, C. J., & Wilson, P. R. 2003, Sol. Phys., 214, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Durrant, C. J., Turner, J. P. R., & Wilson, P. R. 2004, Sol. Phys., 222, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, Y. 2008, ApJ, 676, 680 [NASA ADS] [CrossRef] [Google Scholar]
- Fleck, B., Couvidat, S., & Straus, T. 2011, Sol. Phys., 271, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Gyori, L. 1998, Sol. Phys., 180, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Harvey, K. L. 1992, in The Solar Cycle, ASP Conf. Ser., 27, 335 [NASA ADS] [Google Scholar]
- Hathaway, D. H. 2010, Liv. Rev. Sol. Phys., 7, 1 [Google Scholar]
- Hathaway, D. H., Wilson, R. M., & Reichmann, E. J. 2002, Sol. Phys., 211, 357 [Google Scholar]
- Howard, R., & Gilman, P. A. 1986, ApJ, 307, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Howard, R., Gilman, P. I., & Gilman, P. A. 1984, ApJ, 283, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Hoyt, D. V., & Schatten, K. H. 1996, Sol. Phys., 165, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Jain, K., Tripathy, S. C., & Hill, F. 2011, ApJ, 739, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Jensen, E., Nordø, J., & Ringnes, T. S. 1955, Astrophys. Norvegica, 5, 167 [NASA ADS] [Google Scholar]
- Keller, C. U. 1992, Nature, 359, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Keppens, R., & Martinez Pillet, V. 1996, A&A, 316, 229 [NASA ADS] [Google Scholar]
- Kitiashvili, I. N., Kosovichev, A. G., Wray, A. A., & Mansour, N. N. 2010, ApJ, 719, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Knaack, R., Stenflo, J. O., & Berdyugina, S. V. 2004, A&A, 418, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kobayashi, N., Kuninaka, H., Wakita, J.-i., & Matsushita, M. 2011, J. Phys. Soc. Jpn, 80, 072001 [NASA ADS] [CrossRef] [Google Scholar]
- Kolmogorov, A. 1941, Akademiia Nauk SSSR Doklady, 31, 99 [Google Scholar]
- Kopp, G., & Rabin, D. 1992, Sol. Phys., 141, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Lagg, A., Solanki, S. K., Riethmüller, T. L., et al. 2010, ApJ, 723, L164 [NASA ADS] [CrossRef] [Google Scholar]
- Leka, K. D., & Skumanich, A. 1998, ApJ, 507, 454 [NASA ADS] [CrossRef] [Google Scholar]
- Lites, B. W., & Skumanich, A. 1990, ApJ, 348, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Lites, B. W., Scharmer, G. B., Berger, T. E., & Title, A. M. 2004, Sol. Phys., 221, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, Y., Norton, A. A., & Scherrer, P. H. 2007, Sol. Phys., 241, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, Y., Hoeksema, J. T., Scherrer, P. H., et al. 2012, Sol. Phys., 279, 295 [Google Scholar]
- Livingston, W. 2002, Sol. Phys., 207, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Livingston, W., Harvey, J. W., Malanushenko, O. V., & Webster, L. 2006, Sol. Phys., 239, 41 [Google Scholar]
- Livingston, W., Penn, M. J., & Svalgaard, L. 2012, ApJ, 757, L8 [Google Scholar]
- Louis, R. E., Ravindra, B., Mathew, S. K., et al. 2012, ApJ, 755, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Maltby, P., Avrett, E. H., Carlsson, M., et al. 1986, ApJ, 306, 284 [Google Scholar]
- Martinez Pillet, V. 1992, Sol. Phys., 140, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez Pillet, V. 2002, Astron. Nachr., 323, 342 [NASA ADS] [CrossRef] [Google Scholar]
- Martinez Pillet, V., & Vazquez, M. 1993, A&A, 270, 494 [NASA ADS] [CrossRef] [Google Scholar]
- Mathew, S. K., Lagg, A., Solanki, S. K., et al. 2003, A&A, 410, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathew, S. K., Martínez Pillet, V., Solanki, S. K., & Krivova, N. A. 2007, A&A, 465, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mattig, W. 1971, Sol. Phys., 18, 434 [NASA ADS] [CrossRef] [Google Scholar]
- McIntosh, P. S. 1981, in The Physics of Sunspots, eds. L. E. Cram & J. H. Thomas, 7 [Google Scholar]
- McIntosh, S. W., Leamon, R. J., Gurman, J. B., et al. 2013, ApJ, 765, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Moradi, H., Baldner, C., Birch, A. C., et al. 2010, Sol. Phys., 267, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Muller, R. 1979, Sol. Phys., 61, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Nagovitsyn, Y. A., Pevtsov, A. A., & Livingston, W. C. 2012, ApJ, 758, L20 [Google Scholar]
- Nicholson, S. B. 1933, PASP, 45, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Norton, A. A., & Gilman, P. A. 2004, ApJ, 603, 348 [NASA ADS] [CrossRef] [Google Scholar]
- Norton, A. A., Graham, J. P., Ulrich, R. K., et al. 2006, Sol. Phys., 239, 69 [Google Scholar]
- Norton, A. A., Jones, E. H., & Liu, Y. 2013, J. Phys. Conf. Ser., 440, 012038 [NASA ADS] [CrossRef] [Google Scholar]
- Ossendrijver, M. 2003, A&ARv, 11, 287 [Google Scholar]
- Pariat, E., Aulanier, G., Schmieder, B., et al. 2004, ApJ, 614, 1099 [Google Scholar]
- Parker, E. N. 1955, ApJ, 121, 491 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1979a, Cosmical Magnetic Fields: Their Origin and Their Activity (NewYork: Oxford University Press) [Google Scholar]
- Parker, E. N. 1979b, ApJ, 230, 905 [NASA ADS] [CrossRef] [Google Scholar]
- Pauluhn, A., Solanki, S. K., Rüedi, I., Landi, E., & Schühle, U. 2000, A&A, 362, 737 [NASA ADS] [Google Scholar]
- Penn, M. J., & Livingston, W. 2006, ApJ, 649, L45 [Google Scholar]
- Penn, M. J., & Livingston, W. 2011, in IAU Symp., 273, 126 [Google Scholar]
- Penn, M. J., & MacDonald, R. K. D. 2007, ApJ, 662, L123 [NASA ADS] [CrossRef] [Google Scholar]
- Pesnell, W. D., Thompson, B. J., & Chamberlin, P. C. 2012, Sol. Phys., 275, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Petrovay, K., & Moreno-Insertis, F. 1997, ApJ, 485, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Petrovay, K., & van Driel-Gesztelyi, L. 1997, Sol. Phys., 176, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Pevtsov, A. A., Nagovitsyn, Y. A., Tlatov, A. G., & Rybak, A. L. 2011, ApJ, 742, L36 [Google Scholar]
- Pevtsov, A. A., Bertello, L., Tlatov, A. G., et al. 2013, Sol. Phys., 289, 593 [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical recipes in FORTRAN. The art of scientific computing, 2nd edn. (Cambridge University Press) [Google Scholar]
- Rempel, M. 2011, ApJ, 740, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Rempel, M. 2012, ApJ, 750, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Rempel, M., & Schlichenmaier, R. 2011, Liv. Rev. Sol. Phys., 8, 3 [Google Scholar]
- Rempel, M., Schüssler, M., & Knölker, M. 2009, ApJ, 691, 640 [NASA ADS] [CrossRef] [Google Scholar]
- Rezaei, R., Beck, C., & Schmidt, W. 2012a, A&A, 541, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rezaei, R., Bello González, N., & Schlichenmaier, R. 2012b, A&A, 537, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rimmele, T. 2008, ApJ, 672, 684 [NASA ADS] [CrossRef] [Google Scholar]
- Ringnes, T. S. 1964, Astrophys. Norvegica, 8, 303 [NASA ADS] [Google Scholar]
- Robinson, R. D., & Boice, D. C. 1982, Sol. Phys., 81, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Rossbach, M., & Schröter, E. H. 1970, Sol. Phys., 12, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Rouppe van der Voort, L. H. M., Hansteen, V. H., Carlsson, M., et al. 2005, A&A, 435, 327 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ruiz Cobo, B., & del Toro Iniesta, J. C. 1992, ApJ, 398, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Schad, T. A., & Penn, M. J. 2010, Sol. Phys., 262, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Scherrer, P. H., Bogart, R. S., Bush, R. I., et al. 1995, Sol. Phys., 162, 129 [Google Scholar]
- Scherrer, P. H., Schou, J., Bush, R. I., et al. 2012, Sol. Phys., 275, 207 [Google Scholar]
- Schlichenmaier, R., & Collados, M. 2002, A&A, 381, 668 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlichenmaier, R., Bruls, J. H. M. J., & Schüssler, M. 1999, A&A, 349, 961 [NASA ADS] [Google Scholar]
- Schlichenmaier, R., Bello Gonzalez, N., Rezaei, R., & Waldmann, T. A. 2010a, Astron. Nachr., 331, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Schlichenmaier, R., Rezaei, R., Bello González, N., & Waldmann, T. A. 2010b, A&A, 512, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schmidt, W., & Balthasar, H. 1994, A&A, 283, 241 [NASA ADS] [Google Scholar]
- Schou, J., Scherrer, P. H., Bush, R. I., et al. 2012, Sol. Phys., 275, 229 [Google Scholar]
- Schrijver, C. J. 1987, A&A, 180, 241 [NASA ADS] [Google Scholar]
- Shimizu, T., Katsukawa, Y., Kubo, M., et al. 2009, ApJ, 696, L66 [NASA ADS] [CrossRef] [Google Scholar]
- SIDC-team 2008, Monthly Report on the International Sunspot Number, online catalogue [Google Scholar]
- Sobotka, M., Bonet, J. A., & Vazquez, M. 1993, ApJ, 415, 832 [NASA ADS] [CrossRef] [Google Scholar]
- Solanki, S. K. 2003, A&ARv, 11, 153 [Google Scholar]
- Solanki, S. K., Inhester, B., & Schüssler, M. 2006, Rep. Prog. Phys., 69, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Spruit, H. C. 1981, in The Physics of Sunspots, eds. L. E. Cram, & J. H. Thomas, 98 [Google Scholar]
- Spruit, H. 2012, Prog. Theor. Phys. Suppl., 195, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Steinegger, M., Brandt, P. N., Schmidt, W., & Pap, J. 1990, Ap&SS, 170, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Steinegger, M., Vazquez, M., Bonet, J. A., & Brandt, P. N. 1996, ApJ, 461, 478 [NASA ADS] [CrossRef] [Google Scholar]
- Stellmacher, G., & Wiehr, E. 1988, A&A, 191, 149 [NASA ADS] [Google Scholar]
- Tandberg-Hanssen, E. 1956, Astrophys. Norvegica, 5, 207 [NASA ADS] [Google Scholar]
- Tapping, K. F., & Valdés, J. J. 2011, Sol. Phys., 334 [Google Scholar]
- Temmer, M., Veronig, A., & Hanslmeier, A. 2002, A&A, 390, 707 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tripathy, S. C., Jain, K., Hill, F., & Leibacher, J. W. 2010, ApJ, 711, L84 [NASA ADS] [CrossRef] [Google Scholar]
- Usoskin, I. G. 2008, Liv. Rev. Sol. Phys., 5, 3 [Google Scholar]
- Usoskin, I. G. 2013, Liv. Rev. Sol. Phys., 10, 1 [Google Scholar]
- von Klüber, H. 1948, ZAp, 24, 121 [NASA ADS] [Google Scholar]
- Wang, Y.-M., & Sheeley, N. R. 2009, ApJ, 694, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Watson, F. T., Fletcher, L., & Marshall, S. 2011, A&A, 533, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wesolowski, M. J., Walton, S. R., & Chapman, G. A. 2008, Sol. Phys., 248, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Wiehr, E., Bovelet, B., & Hirzberger, J. 2004, A&A, 422, L63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wittmann, A. 1972, Sol. Phys., 23, 294 [NASA ADS] [CrossRef] [Google Scholar]
- Wittmann, A. D., & Xu, Z. T. 1987, A&AS, 70, 83 [NASA ADS] [Google Scholar]
- Yeo, K. L., Feller, A., Solanki, S. K., et al. 2014, A&A, 561, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yurchyshyn, V., Yashiro, S., Abramenko, V., Wang, H., & Gopalswamy, N. 2005, ApJ, 619, 599 [Google Scholar]
- Zwaan, C. 1965, Recherches Astronomiques de l’Observatoire d’Utrecht, 17 [Google Scholar]
- Zwaan, C. 1978, Sol. Phys., 60, 213 [Google Scholar]
- Zwaan, C. 1992, in Sunspots. Theory and Observations, eds. J. H. Thomas, & N. O. Weiss, NATO ASIC Proc., 375, 75 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 SIDC monthly sunspot number (black line). The gray line shows the smoothed sunspot number. The dashed vertical lines mark the range of our data. |
| In the text | |
 |
Fig. 2 AR11520 on 14/07/2012 is an example of a sunspot with a large umbra. The red contour shows the threshold level (0.6 of mean quiet-Sun intensity) used to select the umbra. The spot has a heliocentric angle of μ = 0.86. The total area of the largest four umbrae is 206 MHS. |
| In the text | |
 |
Fig. 3 Inversion results for one of our sunspots. From top left clockwise: continuum intensity, magnetic field strength, inclination, and azimuth. |
| In the text | |
 |
Fig. 4 Variation of umbral maximum field strength as a function of radius. Parameters of a linear fit (solid red line) and power law fit (solid blue line) and correlation coefficients are given in Table 1. The dashed lines mark the one-sigma confidence level for each fit. The yellow and purple lines mark the adopted linear fits from Kopp & Rabin (1992) and SP, respectively. The upper x-axis shows the area corresponding to the given radius. |
| In the text | |
 |
Fig. 5 Variation of umbral minimum intensity vs. radius. For a more detailed description, see caption of Fig. 4. |
| In the text | |
 |
Fig. 6 Maximum field strength of umbra vs. minimum intensity. For a more detailed description, see caption of Fig. 4. |
| In the text | |
 |
Fig. 7 Variation of umbral parameters with magnetic flux (Φ). Left: maximum field strength vs. Φ, center: radius vs. Φ, right: minimum intensity vs. Φ. Parameters of a linear fit (solid red line) and power law fit (solid blue line) and correlation coefficients are given in Table 1. |
| In the text | |
 |
Fig. 8 Variation of intensity and size of sunspots in each hemisphere vs. time. Each point represents the average of ten sunspots. |
| In the text | |
 |
Fig. 9 Umbral size distribution. Error bars in x-direction mark the width of the bins. The error bars in y-direction are proportional to the inverse of the square root of entries in each bin. Top: the black data points and curve show our data and the lognormal fit, respectively. The colored curves are adopted from SP and show their fit (after normalizing its area) to the rising phase (red) and maximum (blue) of solar cycle 23. The red arrow marks the data range used by SP. Bottom: comparison of the complete sample of 6892 umbrae and the unique sample of 910 umbrae (no repetition). The dashed lines give the one-sigma errors of the fit. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


