| Issue |
A&A
Volume 564, April 2014
|
|
|---|---|---|
| Article Number | A122 | |
| Number of page(s) | 11 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201423597 | |
| Published online | 17 April 2014 | |
Chemical evolution of fluorine in the bulge⋆,⋆⋆
High-resolution K-band spectra of giants in three fields
1 Lund Observatory, Department of Astronomy and Theoretical Physics, Lund University, Box 43, 221 00 Lund, Sweden
e-mail: henrikj@astro.lu.se
2 School of Physics, Trinity College, 2 Dublin, Ireland
3 Observatório Nacional, Rua General José Cristino, 77, 20921-400 São Cristóvão, Rio de Janeiro, RJ, Brazil
4 Observatoire de la Côte d’Azur, Boulevard de l’Observatoire, BP 4229, 06304 Nice Cedex 4, France
5 Department of Physics and Astronomy, Uppsala University, Box 516, 751 20 Uppsala, Sweden
6 Centre for Astrophysics Research, University of Hertfordshire, Hatfield AL10 9AB, UK
7 National Optical Astronomy Observatory, 950 North Cherry Avenue, Tucson, AZ 85719, USA
8 Instituto de Astrofisica, Pontifica Universidad Catolica de Chile, Casilla 306 Santiago 22, Chile
Received: 7 February 2014
Accepted: 11 March 2014
Context. Possible main formation sites of fluorine in the Universe include asymptotic giant branch (AGB) stars, the ν-process in Type II supernova, and/or Wolf-Rayet stars. The importance of the Wolf-Rayet stars has theoretically been questioned and they are probably not needed in modeling the chemical evolution of fluorine in the solar neighborhood. It has, however, been suggested that Wolf-Rayet stars are indeed needed to explain the chemical evolution of fluorine in the bulge. The molecular spectral data, needed to determine the fluorine abundance, of the often used HF-molecule has not been presented in a complete and consistent way and has recently been debated in the literature.
Aims. We intend to determine the trend of the fluorine-oxygen abundance ratio as a function of a metallicity indicator in the bulge to investigate the possible contribution from Wolf-Rayet stars. Additionally, we present here a consistent HF line list for the K- and L-bands including the often used 23 358.33 Å line.
Methods. High-resolution near-infrared spectra of eight K giants were recorded using the spectrograph CRIRES mounted at the VLT. A standard setting was used that covered the HF molecular line at 23 358.33 Å. The fluorine abundances were determined using spectral fitting. We also re-analyzed five previously published bulge giants observed with the Phoenix spectrograph on Gemini using our new HF molecular data.
Results. We find that the fluorine-oxygen abundance in the bulge probably cannot be explained with chemical evolution models that only include AGB stars and the ν-process in supernovae Type II, that is a significant amount of fluorine production in Wolf-Rayet stars is most likely needed to explain the fluorine abundance in the bulge. For the HF line data, we find that a possible reason for the inconsistencies in the literature, where two different excitation energies were used, is two different definitions of the zero-point energy for the HF molecule and therefore also two accompanying different dissociation energies. Both line lists are correct as long as the corresponding consistent partition function is used in the spectral synthesis. However, we suspect this has not been the case in several earlier works, which led to fluorine abundances ~0.3 dex too high. We present a line list for the K- and L-bands and an accompanying partition function.
Key words: Galaxy: bulge / Galaxy: evolution / stars: abundances / infrared: stars
Based on observations collected at the European Southern Observatory, Chile (ESO programs 71.B-0617(A), 073.B0074(A), and 079.B-0338(A)) and observations obtained at the Gemini Observatory, which is operated by the Association of Universities for Research in Astronomy, Inc., under a cooperative agreement with the NSF on behalf of the Gemini partnership: the National Science Foundation (United States), the National Research Council (Canada), CONICYT (Chile), the Australian Research Council (Australia), CNPq (Brazil), and CONICRT (Argentina), as program GS-2004A-Q-20.
Figure 4 and Tables 5 and 6 are available in electronic form at http://www.aanda.org
© ESO, 2014
1. Introduction
From a nucleosynthetic perspective fluorine is a very interesting element, and its cosmic origin is truly intriguing. Its creation and destruction in stellar interiors is very sensitive to the physical conditions (see for example Lucatello et al. 2011), meaning that observations of fluorine abundances can provide strong constraints to stellar models. It will also be possible to observationally constrain the main stellar nuclear production sites of fluorine in the Universe at different epochs and in different stellar populations. To do this, observations of the chemical evolution of fluorine as a function of metallicity for different stellar populations have to be compared with model predictions.
Theoretical considerations have offered three main production mechanisms that all should work under prevailing conditions during different phases of stellar evolution. Their relative importance at different stages of evolution and in different stellar populations is only starting to be investigated. The different production sites of 19F, the only stable isotope of fluorine, that have been proposed are the following:
-
νnucleosynthesis in supernovae Type II. The corecollapse of a massive star, following a supernovaType II (SN II) explosion, leads to a prodigiousneutrino flux. In spite of the small cross sections, the large amountof neutrinos gives rise to a significant spallation of 20Ne to 19F (Woosley & Haxton 1988) in the overlying(neon-rich) shells of the core. Hartmannet al. (1991) estimated the total(mu- and tau-) neutrino energy to beEν = 3 × 1053 erg. Kobayashi et al. (2011a) investigated the importance of this total neutrino energy for the ν-process reactions for the evolution of fluorine in the solar neighborhood. They concluded that the ν nucleosynthesis probably is a major fluorine production mechanism and that its relative contribution is largest for low metallicities.
-
Thermal-pulsing asymptotic giant branch stars. Low-mass (2 ≲ M/M⊙ ≲ 4) thermal-pulsing asymptotic giant branch (TP-AGB) stars have been suggested to produce fluorine in different burning phases during the thermal pulse stage by nuclear reaction chains starting from 14N (Forestini et al. 1992; Jorissen et al. 1992; Abia et al. 2011; Kobayashi et al. 2011a; Gallino et al. 2010). Fluorine is then transported up to the surface by the third dredge-up. Fluorine production in AGB stars is expected to be accompanied by the slow neutron-capture nucleosynthesis (the s-process), producing elements such as Sr, Y, Zr, Nb, Ba, and La (e.g. Mowlavi et al. 1998; Goriely & Mowlavi 2000; Abia et al. 2009). It has been demonstrated observationally that AGB stars produce fluorine, see for example Jorissen et al. (1992) and Abia et al. (2011).
-
Wolf-Rayet stars. Meynet & Arnould (1993, 1996, 2000) suggested that Wolf-Rayet (W-R) stars might contribute significantly to the Galactic fluorine budget. 19F is produced in the convective cores of W-R stars during the core He-burning phase. Due to a large mass loss caused by a metallicity-dependent, radiatively driven wind, the destruction of 19F by the (α, p) reaction is prevented because the convective core shrinks. The fluorine left behind is eventually exposed at the surface when the heavy mass loss strips the star of the outer layers. This mechanism depends on key parameters such as initial mass, metallicity, and rotational velocity. Fluorine is produced from 14N, which means that the more 14N is available, the more fluorine is expected. A second metallicity-dependent effect is the metallicity-dependent winds. Both circumstances favor the fluorine production at higher metallicities. Palacios et al. (2005) showed that when incorporating newer yields and including models of rotating W-R stars, the yields from this mechanism are significantly reduced, implying that W-R stars might not be a major contributor of fluorine. However, these authors concluded that due to large uncertainties in key nuclear-reaction rates and mass-loss rates, the question of the contribution to Galactic 19F from W-R stars is still an open question.
Using a semi-analytic multizone chemical-evolution model, Renda et al. (2004) showed for the first time the impact of the AGB and W-R star contributions to the Galactic chemical evolution of fluorine. They showed that ν nucleosynthesis was dominant in the early Universe and that the AGB stars’ significance successively grows. Based on the old yields and nonrotating models, they also showed that the contribution of W-R stars is significant for solar and supersolar metallicities, increasing the [F/O] ratio by a factor of two at solar metallicities. Their conclusion was that all three production sites are needed to explain the Galactic chemical evolution of fluorine for a range of metallicities.
Kobayashi et al. (2011a) modeled the evolution of fluorine in the solar neighborhood by including AGB stars and ν nucleosynthesis with two different neutrino energies (Eν = 3 × 1053 erg and Eν = 9 × 1053 erg). Note that the contributions from W-R stars are underestimated in these models, because elements such as C, N, and possibly F, which are newly produced and have been lost via stellar winds before supernova explosions, are not included. The models agree well with field stars of higher metallicities. At lower metallicities the models cannot reproduce the observations of Li et al. (2013), but the model that fits best still includes the ν-process with Eν = 3 × 1053 erg.
The abundance of fluorine in stars is difficult to measure because of a paucity of suitable spectral lines. Highly ionized F v and F vi lines in the UV have been used by Werner et al. (2005) in extremely hot post-AGB stars, and a handful of F i lines between 6800−7800 Å have been used in extreme helium stars and R Coronae Borealis stars (Pandey 2006; Pandey et al. 2008). All other studies we are aware of have been conducted using HF molecular lines in the K-band and mostly the HF(1 − 0) R9 line at 23 358.329 Å.
Relevant for the observations we present here, is the study by Cunha et al. (2008), who presented the first study of the chemical evolution of fluorine in the Galactic bulge by investigating six red giants in Baade’s Window (five of these spectra are re-analyzed in this paper). They found that the fluorine-to-oxygen abundance ratio in the bulge follows and extends the solar neighborhood trend. The trend at higher metallicities needs other sources of fluorine in addition to the ν-process contribution, which is sufficient at lower metallicities. These are the AGB star and W-R star contributions. By investigating the correlation with abundances of s-process elements, the authors concluded that, for the bulge the W-R wind contribution to the fluorine budget probably is important and larger than for the Disk. They therefore suggested that W-R stars might have played a vital role in the chemical evolution of the Galactic bulge.
In this paper, we observationally investigate the chemical evolution of fluorine in the bulge by analyzing red giants from three fields. We discuss the relative contributions of the different main nucleosynthetic sites suggested by comparing our derived abundances with the latest and most updated models for the evolution of fluorine in the bulge. Our main conclusion is that a significant fluorine production in W-R stars is most likely needed to explain the fluorine abundance in the bulge, meaning that the production in AGB stars and SNe II is probably not enough.
2. Observations
We have observed eight K giants in the Galactic bulge using the spectrometer CRIRES (Käufl et al. 2004, 2006; Moorwood 2005) mounted on the VLT. The K-band observations we explore are, with one exception, of the same stars as the H-band observations analyzed in Ryde et al. (2010), which in turn is a subsample of the full visual sample used in Zoccali et al. (2006), Lecureur et al. (2007), and Barbuy et al. (2013). The basic data of our stars are listed in Table 1, and the Fig. 1 shows the location of our three fields (B3, BW, and B6) in comparison with the COBE/DIRBE outline of the Galactic bulge (Weiland et al. 1994) and the microlensed bulge dwarfs of Bensby et al. (2013).
Basic data for the observed red giants.
 |
Fig. 1 Location of the four fields (B3, BW, B6, and BL) of Lecureur et al. (2007) in comparison with the COBE/DIRBE outline of the Galactic bulge (Weiland et al. 1994) and the study of Bensby et al. (2013). Our stellar sample is a subset of the B3, BW, and B6 stars. The five re-analyzed stars from Cunha et al. (2008) are in the BW field. |
The stars were observed with the CRIRES-setting 24/-1/i, which provides a spectral coverage from approximately 23 070 Å to 23 510 Å and therefore includes the HF-line at 23 358.33 Å. The spectral resolution is about R = 40 000, as determined from narrow telluric lines. The observations were reduced using the CRIRES pipeline and the continua were normalized with the the IRAF task continuum. Subsequently, the telluric lines plaguing this part of the IR spectra, were carefully removed by dividing the normalized spectra with that of a telluric standard of high signal-to-noise ratio, which we observed in the same setting and reduced in the same way, using the IRAF task telluric.
The stellar parameters were re-determined from the visual observations with the UVES spectrometer described in Lecureur et al. (2007), and the oxygen abundances were re-determined from the H-band data described in Ryde et al. (2010). The UVES observations were carried out May-Aug. 2003−2004 and the CRIRES observations in May-Aug. 2007−2008. A summary of the observations and the S/N reached is presented in Table 2. The high optical extinction in the bulge direction is the cause of the large differences in exposure times between the visual and the infrared observations. The extinction in the K band is a factor of 10 lower that in the V band (Cardelli et al. 1989).
In addition to these eight giants, K-band spectra from three K giants and two M giants in Cunha et al. (2008) (in turn from Cunha & Smith 2006) were re-analyzed. These stars are all in Baade’s Window and were observed using the Phoenix spectrograph at Gemini-South (Hinkle et al. 1998). For a complete description of these observations, see Cunha et al. (2008) and Cunha & Smith (2006).
Summary of the observations with VLT/UVES and VLT/CRIRES.
3. Analysis
The visual and the infrared spectra were analyzed using the software Spectroscopy Made Easy (SME, Valenti & Piskunov 1996). SME simultaneously fits a chosen number of parameters by fitting calculated synthetic spectra to parts of an observed spectrum using χ2-minimization. The parts, called line masks and continuum masks, mark regions with spectral lines of interest and points that SME should treat as continuum points. The latter are used if a linear rectification in predefined narrow windows of the already continuum-normalized observed spectrum is needed (see Sect. 2).
SME uses spherical symmetric, [α/Fe]-enhanced, LTE MARCS-models. Within the Gaia-ESO collaboration (Gilmore et al. 2012) it has also been developed to handle NLTE for many iron lines (Lind et al. 2012; Bergemann et al. 2012). We have no knowledge of estimated 3D-effects on the fluorine line used in the analysis for our stellar parameters, but Li et al. (2013) have calculated 3D-corrections for more metal-poor stars and showed that the corrections are small.
3.1. Stellar parameters
For consistency, we used SME in our analysis for both our optical and infrared spectra. We therefore also redetermined the stellar parameters for our stars based on the method described in Jönsson et al. (in prep.). In short, we determined all the stellar parameters (Teff, log g, [Fe/H], and ξmicro) simultaneously, with SME using a well-chosen line-list of weak, unblended Fe i, Fe ii, and Ca i lines and gravity-sensitive Ca i-wings. All lines except some Fe ii-lines have lab-measured oscillator strengths with excellent accuracy (according to the Gaia-ESO line-list categorization of Heiter et al., in prep.), and for all iron lines NLTE-corrections were used (Lind et al. 2012; Bergemann et al. 2012). The resulting parameters are listed in Table 3 and those agree within uncertainties with those in Ryde et al. (2010).
In Table 3 we also list the stellar parameters used for the bulge stars of Cunha et al. (2008) for which we re-determined the fluorine abundance (stellar parameters from Cunha & Smith 2006). These stellar parameters were determined from a combination of photometry and IR spectroscopy, which might lead to systematic differences to the stellar parameters of the B3-BW-B6 data set. Note also that the two M giants are cooler and have a lower surface gravity than the rest of the stars, which perhaps leads to systematic differences as well.
Determined stellar parameters for the reference star Arcturus and our program stars.
The uncertainties in our method of determining the stellar parameters from optical spectra and their dependence on the S/N will be described in Jönsson et al. (in prep.). In short, we degraded the Arcturus spectrum of Hinkle et al. (2000) to different S/N and determined the stellar parameters for these spectra. The estimated uncertainties for the stars in this paper following this method are δTeff ≲ 70 K, δlog g ≲ 0.2, δ [Fe/H] ≲ 0.1, and δξmicro ≲ 0.1.
3.2. Line data
All optical line data we used were collected and/or determined within the Gaia-ESO collaboration (Heiter et al., in prep). The infrared line data except for HF were extracted from the VALD database (Valenti & Piskunov 1996; Ryabchikova et al. 1997; Kupka et al. 1999, 2000). The line data of the [O i]-line, the three Zr i-lines, and the OH-lines used are listed in Table 4. We calculate the excitation energies and transition probabilities for HF in Sect. 3.2.1.
Atomic and molecular data for the spectral lines used for O and Zr abundance determination.
3.2.1. HF molecule
The excitation energies and transition probabilities for HF have not been presented previously in a complete and comprehensive manner. The values of Jorissen et al. (1992), who cited private communications with Tipping, are often used. Lucatello et al. (2011), D’Orazi et al. (2013), and Nault & Pilachowski (2013), however, used the excitation energy for the 23 358.329 Å-line from Decin (2000), in turn from private communications with Sauval, which differs from the Tipping value by 0.25 eV. As long as the excitation energy and partition function are consistent, both energies can be used for abundance determinations. Otherwise, there will be an ~0.3 dex difference in abundance, just as Lucatello et al. (2011), D’Orazi et al. (2013), and Nault & Pilachowski (2013) showed. Since it is unclear which partition function is used in most works, it is difficult to compare the resulting abundance values. We here intend to explicitly present which excitation energies, transition probabilities, and partition function we used so that our data can be easily compared with future studies.
The partition function is defined as  (1)where gi and χi are the statistical weight and the excitation energy of level i. The consistent excitation energies have to be used when calculating the number density of a certain lower level for a transition,
(1)where gi and χi are the statistical weight and the excitation energy of level i. The consistent excitation energies have to be used when calculating the number density of a certain lower level for a transition,  (2)The zero-point energy of the levels used (which is a problem for molecules, but not for atoms), must correspond to the one used to calculate the partition function. Thus, as long as there is no mis-match, it does not matter which is used since the zero-point energies can be factored out in Eq. (2).
(2)The zero-point energy of the levels used (which is a problem for molecules, but not for atoms), must correspond to the one used to calculate the partition function. Thus, as long as there is no mis-match, it does not matter which is used since the zero-point energies can be factored out in Eq. (2).
We used the partition function from MARCS/BSYN and SME (Gustafsson et al. 2008, and references therein), which is an updated version of the one from Sauval & Tatum (1984). This partition function is shown in Eq. (3) and in Fig. 2.  (3)The dissociation energy used is the same as in Sauval & Tatum (1984): D0(HF) = 5.869 eV. We suspect that the 0.25 eV difference between different excitation energies used comes from that the Tipping-list uses the dissociation energy of the energy potential, De(HF), and not, like Sauval, the true energy required for dissociation, D0(HF). The former is higher than the latter due to the zero point of the energy of the lowest vibrational level. The difference is 0.25 eV for HF (Zemke et al. 1991a). We stress once again that it does not matter which energies are used as long as the consistent partition function is used.
(3)The dissociation energy used is the same as in Sauval & Tatum (1984): D0(HF) = 5.869 eV. We suspect that the 0.25 eV difference between different excitation energies used comes from that the Tipping-list uses the dissociation energy of the energy potential, De(HF), and not, like Sauval, the true energy required for dissociation, D0(HF). The former is higher than the latter due to the zero point of the energy of the lowest vibrational level. The difference is 0.25 eV for HF (Zemke et al. 1991a). We stress once again that it does not matter which energies are used as long as the consistent partition function is used.
 |
Fig. 2 Partition function of the HF molecule used in the MARCS code and SME for a relevant temperature range. |
We computed the HF line data from available molecular data consistent with the partition function and dissociation energy above. The excitation energies were calculated from the energy-level expression and coefficients of Leblanc et al. (1994). They fitted measured HF-line frequencies to the energy-level expression given by ![\begin{eqnarray} E(v,J)&=& T_v+B_vJ(J+1)-D_v[J(J+1)]^2+ H_v[J(J+1)]^3 \notag \\&&+L_v[J(J+1)]^4, \end{eqnarray}](/articles/aa/full_html/2014/04/aa23597-14/aa23597-14-eq60.png) (4)obtaining the rotational constants Tv, Bv, Dv, Hv, and Lv, especially for the vibrational states of interest for us, namely v = 0 and v = 1. These are provided in Table III of Leblanc et al. (1994). The calculated energy levels are good to 10-4 cm-1 or better. The excitation energies of the lower energy levels of the ro-vibrational lines of HF are presented in Col. 6 in Tables 5 and 6.
(4)obtaining the rotational constants Tv, Bv, Dv, Hv, and Lv, especially for the vibrational states of interest for us, namely v = 0 and v = 1. These are provided in Table III of Leblanc et al. (1994). The calculated energy levels are good to 10-4 cm-1 or better. The excitation energies of the lower energy levels of the ro-vibrational lines of HF are presented in Col. 6 in Tables 5 and 6.
From this we calculated the transition frequencies (and wavelengths) from the differences of the energy levels of the upper and lower level of the lines. The wavenumbers and wavelengths of the HF lines in the 22 700−25 000 Å region (R branch, including the band head at 22 700 Å) and 25 500−39 200 Å region (P branch) are given in Cols. 4 and 5 in Tables 5 and 6, respectively. The R-branch lines lie in the K band, whereas the P-branch lines, which originates from higher rotational levels, lie in the L band.
We also computed the HF ro-vibrational Einstein coefficients for spontaneous emission using the transition matix-element expansion coefficients given by Arunan et al. (1992). These authors used accurate dipole-moment functions based on experimental data to find these coefficients:  (5)where m = J′′ + 1 for the R branch, i.e. J′ ← (J′′ − 1) and m = −J′′ for the P branch, that is, J′ ← (J′′ + 1). The upper state is designed with a prime, ′, and the lower state with a double prime, ′′. The transition matrix elements, Rv′ → v′′(m), are given by Rv′ → v′′(m) = a0 + a1m + a2m2 + a3m3, where the expansion coefficients, ai, are given in a Table VI in Arunan et al. (1992). Finally, the log gf values were calculated from
(5)where m = J′′ + 1 for the R branch, i.e. J′ ← (J′′ − 1) and m = −J′′ for the P branch, that is, J′ ← (J′′ + 1). The upper state is designed with a prime, ′, and the lower state with a double prime, ′′. The transition matrix elements, Rv′ → v′′(m), are given by Rv′ → v′′(m) = a0 + a1m + a2m2 + a3m3, where the expansion coefficients, ai, are given in a Table VI in Arunan et al. (1992). Finally, the log gf values were calculated from  (6)see, for example, Larsson (1983). The calculated log (gf)-values are given in Col. 9 in Tables 5 and 6. Arunan et al. (1992) claimed that these transition probabilities are reliable and well-established, and that they agree with ab initio calculations of Zemke et al. (1991b), which provides confidence in the values.
(6)see, for example, Larsson (1983). The calculated log (gf)-values are given in Col. 9 in Tables 5 and 6. Arunan et al. (1992) claimed that these transition probabilities are reliable and well-established, and that they agree with ab initio calculations of Zemke et al. (1991b), which provides confidence in the values.
For an overview of which lines might be important for abundance determinations, we plot in Fig. 3 the relative line strengths in the form of gf e− χexc/kT at T = 4000 K, a typical temperature of the line-forming regions of a red giant. The R9-line used in this and many other works is highlighted together with some other lines. The equivalent widths of the lines for a typical model atmosphere in principle show the same relative strengths.
 |
Fig. 3 Relative line strengths of the ro-vibrational HF lines (the R and P branches of the v′′ = 0 to v′ = 1 band) given by gf e− χexc/kT at T = 4000 K. The K and L infrared transmission bands are indicated. |
3.3. Stellar abundances
All abundances for the B3-BW-B6 stars were determined using SME and the stellar parameters described in Table 3. The abundances from the visual spectra were determined using the macro-turbulence determined simultaneously with the stellar parameters, but when we determined the abundances from the IR-spectra the macro-turbulence was a global free parameter.
The uncertainties in the determined abundances from the uncertainties in the stellar parameters, see Sect. 3.1, are given in Table 7.
Uncertainties in the determined abundances caused by uncertainties in the stellar parameters.
We note that all abundances are most sensitive to the temperature and that they all increase with higher temperature. This will mean that uncertainties, caused by uncertainties in the stellar parameters in the ratios [F/O] and [Zr/F] used in Figs. 6 and 7 will be smaller than the quadratic addition of the two uncertainties. For the total uncertainties in the abundances we also have to include the uncertainties in the continuum fitting around the O-, HF-, and Zr-lines used, but they are much smaller in most cases. Altogether, we estimate the total uncertainties in the abundances to approximately be 0.15 dex and in the abundance ratios lower than 0.1 dex.
The re-determination of the fluorine abundances for the sample of stars previously analyzed in Cunha et al. (2008) was made using the same LTE MARCS model atmospheres as for the B3-BW-B6 stars, but using MOOG (Sneden 1973) instead of SME. Our tests show that using the same model atmosphere, SME and MOOG give the same result to a very good precision. For a discussion on the uncertainties of the stellar parameters and the abundances of the BMB-I-IV stars, see Cunha & Smith (2006) and Cunha et al. (2008). In particular, the most metal-poor star, IV-329, is challenging to analyze because of telluric lines.
4. Results
The part of the spectra that contains the lines used in our investigation together with our best-fit synthetic spectra is presented in Fig. 4, and the resulting abundances are presented in Table 8. In Fig. 5 we plotted [F/Fe] and [O/Fe] as functions of [Fe/H], in Fig. 6 we plotted our abundances together with our chemical evolution models. The fluorine abundances derived here for the stars from Cunha et al. (2008, light-green circles) are systematically lower than those derived previously from the different excitation energies and partition functions used (as described in Sect. 3.2.1), but also because in this study we used newer, alpha-enhanced stellar model atmospheres.
Determined abundances.
 |
Fig. 5 [F/Fe] and [O/Fe] as functions of [Fe/H] for the B3-BW-B6 stars. The stars are color-coded as the corresponding fields in Fig. 1. The black dots are the microlensed bulge dwarfs of Bensby et al. (2013) that are also marked in Fig. 1. Conservative estimates of the uncertainties are marked in the upper corners. |
 |
Fig. 6 Our fluorine abundances compared with the predictions of our bulge models including AGB stars, excluding and including the ν-process with two different energies, and excluding W-R stars. The abundances have been transformed to the scale of the models with log ϵ(F)⊙ = 4.56 and log ϵ(O)⊙ = 8.93 (Anders & Grevesse 1989). The stars are color-coded as the corresponding fields in Fig. 1 with the BW-stars of Cunha et al. (2008) added in the right panel in light green. Conservative estimates of the uncertainties are marked in the upper left-hand corners. We note that the star BMB-78, still after the re-analysis, falls below the rest of the trend; see Sect. 5 for possible explanations. |
5. Discussion
From the color-coding in Figs. 5−7, which designates the three different bulge fields observed (see Fig. 1), we are unable to trace any spatial variation of the fluorine abundance for the different fields. More stars in every field are needed to start discussing abundance trends. Therefore, we discuss all our abundances as following a general bulge-trend below.
In the right panel of Fig. 5 we see the expected decline of oxygen with respect to [Fe/H] because of the large production of iron in SNe type Ia. Our trend closely follows that of the microlensed bulge stars of Bensby et al. (2013). In the left panel we do not see a decline in [F/Fe] for the same range of [Fe/H], and if the upper limit of fluorine abundance in the star B3-b1 is ignored, the trend in [F/Fe] increases for the same metallicity range. This would indicate that there must be a production site of fluorine that (over-) compensates for the increase in iron around the same time scale as SN type I.
 |
Fig. 7 Abundance ratios of fluorine and zirconium in our sample as a function of the solar normalized fluorine abundance. The negative slope indicated by this plot suggests that W-R stars might be important for producing fluorine in the bulge. The stars are color-coded as the corresponding fields in Fig. 1, and conservative estimates of the uncertainties are marked in the lower right-hand corner. |
Kobayashi et al. (2011b) modeled the evolution of fluorine including “normal” nucleosynthesis in supernovae and synthesis in AGB stars, excluding the ν-process and yields from W-R-winds for different populations of the Galaxy, including the bulge. Kobayashi et al. (2011a) showed models that included the ν-process in SNe II, with two different neutrino energies, but only for the solar neighborhood. The two energies chosen were Eν = 3 × 1053 erg (the energy estimated by Hartmann et al. 1991 and best reproducing the values of Li et al. 2013 in the solar neighborhood) and Eν = 9 × 1053 erg (the theoretically highest possible value). In Fig. 6 we present for the first time the combination of the bulge model as described in Kobayashi et al. (2011b) with the ν-process as modeled in Kobayashi et al. (2011a). If we ignore for the moment the light-green values for the re-analyzed Cunha et al. (2008) stars, we find, just like Li et al. (2013) did for the solar neighborhood, that the fluorine-oxygen abundance trend in the bulge is best described with the model that includes AGB stars and Eν = 3 × 1053 erg, but that the models do not to reproduce the trend of the lower-metallicity stars: there seems to be a steeper slope in the observed data than in the models, see left panel of Fig. 6. This might be because the ν-process-contribution in the bulge is more metallicity-dependent than in the models, or because its contribution in the bulge is lower and another, more metallicity-dependent source (possibly W-R-stars) is needed.
When including the light-green stars from Cunha et al. (2008), the trend becomes somewhat more scattered, and we treat their fluorine abundance for the star IV-329 as an upper limit. At this star’s temperature and metallicity, the HF line is only 4% deep and may be significantly affected by imperfect telluric division. The recent discussion by de Laverny & Recio-Blanco (2013) noted that in low-metallicity stars where the HF R9 line becomes very weak, uncertain telluric-line removal at the 1−2% level (which they maintain is typical) results in large fluorine abundance uncertainties. The authors suggest caution in interpreting fluorine abundances derived from such a weak HF R9 line. Furthermore, since the figure shows [F/O] as a function of [O/H], the accuracy of the oxygen abundance plays a vital role in defining the trend. As an example of how severe the impact of the oxygen abundance is on the trend of Fig. 6 we note that decreasing the oxygen abundance of the peculiar star BMB-78 by 0.3 dex to better follow the B3-BW-B6-stars in Fig. 5 will shift it into the B3-BW-B6-trend in Fig. 6. The oxygen-abundances of the Cunha et al. (2008) stars will be re-determined using newer, alpha-enhanced model atmospheres to see whether this will influence the [F/O]-trend amongst these stars in Fig. 6 (Cunha & Smith, in prep.). At present we cannot rule out that the peculiar fluorine abundance of BMB-78 is a result of inhomogeneous chemical evolution in the bulge (see Cunha et al. (2008) for a more detailed discussion). The other Cunha et al. (2008)-stars agree well with the B3-BW-B6 data set in spite of the systematic differences expected from different methods of determining the stellar parameters and the fact that BMB-289 is an M-giant, while the entire B3-BW-B6 data set consists of K-giants.
To investigate in more detail whether W-R stars might be needed to explain the fluorine abundance in the bulge, we determined the abundance of the s-element zirconium, which is mainly produced in low-mass AGB stars (Travaglio et al. 2004), and compared it with the abundance of fluorine, see Fig. 7. The negative slope in this plot, which shows [Zr/F] as a function of [F/H], suggests that the most fluorine-rich stars have been enhanced in fluorine by a source that does not produce zirconium, in other words that the contribution from AGB stars seems small. Thus, the additional sources needed might either be the ν-process, W-R stars, or both. The ν-process does not seem to be metal dependent in our [O/H]-range, while the W-R stars are, meaning that the slope is best explained with W-R stars. However, Zr is not exclusively produced in AGB stars, but there is some minor r-process and weak s-process production in massive stars as well (Travaglio et al. 2004; Bisterzo et al. 2011). The contribution of these stars to the bulge Zr-abundance is not known as far as we know. To evaluate this more detailed modeling is needed.
Concerning the role of W-R stars for the chemical evolution in the bulge, the discussion on the oxygen and magnesium trends in the bulge (for a review, see Rich 2013) is also of interest. Since the metallicity-dependent, radiation-driven winds of W-R stars can be massive and cause the outer layers of the stars to be pealed off (Maeder 1992), the contribution from these stars might explain the decline of oxygen in the bulge (Fulbright et al. 2007; McWilliam et al. 2008). At the same time, these massive stars might be an important formation site for carbon in the Galaxy (see for example Gustafsson et al. 1999; Mattsson 2010). Fulbright et al. (2007) and McWilliam et al. (2008) discussed the decline in [O/Mg] and [O/Fe] at solar metallicities, Cescutti et al. (2009) the [C/O] versus [O/H] trends in the bulge showed that these are best fitted with models that include massive star yields altered by metallicity-dependent winds, just as for W-R stars. Note, however, that Alves-Brito et al. (2010) and Ryde et al. (2010) did not find the strong increase in the carbon abundance in the bulge, which would have been expected if the W-R stars had played an important role. Therefore, the question of the role of W-R stars in the bulge remains open. It will, however, be able to be tested with more observations of the sort that already exist. Detailed modeling is needed, and improved data may solve this problem (Rich 2013).
Since fluorine is produced from nitrogen in both AGB stars and W-R stars, but it is produced from neon in the ν-process, it would be of interest to investigate the trend of F vs. N in the bulge, but since our stellar sample consists of giants, it is hard to establish the “cosmic” nitrogen abundance to the needed accuracy because newly produced nitrogen is dredged-up into the atmosphere of the star.
6. Conclusion
At low metallicity, our observed fluorine-oxygen abundance trend in the bulge is lower than predicted in our bulge model that includes the ν-process, showing a steeper slope than the model. This might suggest a metal-dependent production source of fluorine. This source cannot be the ν-process in SNe II because it is not metal-dependent over our metallicity range, and it cannot be AGB stars because they produce s-elements at the same time as fluorine and would probably not give rise to the observed decline in [Zr/F] for increasing [F/H] (as shown in Fig. 7). Therefore our data corroborate the findings of Cunha et al. (2008) that W-R stars might be an important source of fluorine in the bulge. To fully evaluate this we need galactic chemical evolution models that include full sets of yields of AGB stars, W-R stars, and supernova explosions.
Some of the earlier reports of high fluorine abundances might have been caused by the use of mismatching molecular data for the HF-molecule, but this has to be investigated. To help with this we have presented an HF line-list with a consistent partition function for lines in the K- and L-bands.
Online material
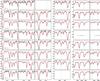 |
Fig. 4 Observed spectra in black and synthetic spectra in red for the B3-BW-B6 stars. The three Zr-lines, the [O i]-line, the OH-lines, and the HF-line used are marked. The exact wavelengths are listed in Table 4. The OH-lines with obvious cosmic hits were excluded from the fit. Note the different flux scales. An example of the HF-line in the re-analyzed BMB-I-IV can be found in Cunha et al. (2008). |
Acknowledgments
This research has been partly supported by the Royal Physiographic Society in Lund, Stiftelsen Walter Gyllenbergs fond and Märta och Erik Holmbergs donation. Support from the Swedish Research Council, VR, project number 621-2008-4245, is also acknowledged. N.R. is a Royal Swedish Academy of Sciences Research Fellow supported by a grant from the Knut and Alice Wallenberg Foundation. N.R. would like to thank the Aspen Center for Physics (and the NSF Grant #1066293) for hospitality during the bulge/Bar workshop in September 2011, at which part of this work was initiated. M.Z. acknowledges support by Proyecto Fondecyt Regular 1110393, the BASAL Center for Astrophysics and Associated Technologies PFB-06, and by the Chilean Ministry for the Economy, Development, and Tourism’s Programa Iniciativa Científica Milenio through grant P07-021-F, awarded to The Milky Way Millennium Nucleus. This publication made use of the SIMBAD database, operated at CDS, Strasbourg, France, NASA’s Astrophysics Data System, and the VALD database, operated at Uppsala University, the Institute of Astronomy RAS in Moscow, and the University of Vienna.
References
- Abia, C., Recio-Blanco, A., de Laverny, P., et al. 2009, ApJ, 694, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Abia, C., Cunha, K., Cristallo, S., et al. 2011, ApJ, 737, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Alves-Brito, A., Meléndez, J., Asplund, M., Ramírez, I., & Yong, D. 2010, A&A, 513, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Arunan, E., Setser, D. W., & Ogilvie, J. F. 1992, J. Chem. Phys., 97, 1734 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, Ann. Rev. Astron. Astrophys., 47, 481 [CrossRef] [Google Scholar]
- Barbuy, B., Hill, V., Zoccali, M., et al. 2013, A&A, 559, 5 [Google Scholar]
- Bensby, T., Yee, J. C., Feltzing, S., et al. 2013, A&A, 549, 147 [Google Scholar]
- Bergemann, M., Lind, K., Collet, R., Magic, Z., & Asplund, M. 2012, MNRAS, 427, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Biemont, E., Grevesse, N., Hannaford, P., & Lowe, R. M. 1981, ApJ, 248, 867 [NASA ADS] [CrossRef] [Google Scholar]
- Bisterzo, S., Gallino, R., Straniero, O., Cristallo, S., & Käppeler, F. 2011, MNARS, 418, 284 [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Cescutti, G., Matteucci, F., McWilliam, A., & Chiappini, C. 2009, A&A, 505, 605 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cunha, K., & Smith, V. V. 2006, ApJ, 651, 491 [NASA ADS] [CrossRef] [Google Scholar]
- Cunha, K., Smith, V. V., & Gibson, B. K. 2008, ApJ, 679, L17 [NASA ADS] [CrossRef] [Google Scholar]
- de Laverny, P., & Recio-Blanco, A. 2013, A&A, 560, 74 [Google Scholar]
- Decin, L. 2000, Ph.D. Thesis, Catholique University of Leuven, 16 [Google Scholar]
- D’Orazi, V., Lucatello, S., Lugaro, M., et al. 2013, ApJ, 763, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Forestini, M., Goriely, S., Jorissen, A., & Arnould, M. 1992, A&A, 261, 157 [NASA ADS] [Google Scholar]
- Fulbright, J. P., McWilliam, A., & Rich, R. M. 2007, ApJ, 661, 1152 [NASA ADS] [CrossRef] [Google Scholar]
- Gallino, R., Bisterzo, S., Cristallo, S., & Straniero, O. 2010, Mem. Soc. Astron. It., 81, 998 [NASA ADS] [Google Scholar]
- Gilmore, G., Randich, S., Asplund, M., et al. 2012, The Messenger, 147, 25 [NASA ADS] [Google Scholar]
- Goldman, A., Schoenfeld, W. G., Goorvitch, D., et al. 1998, J. Quant. Spectrosc. Radiat. Transf., 59, 453 [Google Scholar]
- Goriely, S., & Mowlavi, N. 2000, A&A, 362, 599 [NASA ADS] [Google Scholar]
- Gustafsson, B., Karlsson, T., Olsson, E., Edvardsson, B., & Ryde, N. 1999, A&A, 342, 426 [NASA ADS] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartmann, D. H., Haxton, W. C., Hoffman, R. D., & Woosley, S. E. 1991, Nucl. Phys. A, 527, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Hinkle, K., Wallace, L., & Livingston, W. C. 1995, Infrared Atlas of the Arcturus Spectrum, 0.9-5.3 microns (San Francisco: ASP) [Google Scholar]
- Hinkle, K., Wallace, L., Valenti, J., & Harmer, D. 2000, Visible and Near Infrared Atlas of the Arcturus Spectrum 3727-9300 A (San Francisco: ASP) [Google Scholar]
- Hinkle, K. H., Cuberly, R. W., Gaughan, N. A., et al. 1998, Proc. SPIE, 3354, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Jorissen, A., Smith, V. V., & Lambert, D. L. 1992, A&A, 261, 164 [NASA ADS] [Google Scholar]
- Käufl, H.-U., Ballester, P., Biereichel, P., et al. 2004, in Ground-based Instrumentation for Astronomy, eds. A. F. M. Moorwood, & I. Masanori. Proc. SPIE, ESO, Germany, 5492, 1218 [Google Scholar]
- Käufl, H. U., Amico, P., Ballester, P., et al. 2006, The Messenger, 126, 32 [NASA ADS] [Google Scholar]
- Kobayashi, C., Izutani, N., Karakas, A. I., et al. 2011a, ApJ, 739, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Kobayashi, C., Karakas, A. I., & Umeda, H. 2011b, MNRAS, 414, 3231 [NASA ADS] [CrossRef] [Google Scholar]
- Kupka, F., Piskunov, N., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Kupka, F. G., Ryabchikova, T. A., Piskunov, N. E., Stempels, H. C., & Weiss, W. W. 2000, Baltic Astron., 9, 590 [Google Scholar]
- Larsson, M. 1983, A&A, 128, 291 [NASA ADS] [Google Scholar]
- Leblanc, R. B., White, J. B., & Bernath, P. F. 1994, J. Mol. Spectrosc., 164, 574 [Google Scholar]
- Lecureur, A., Hill, V., Zoccali, M., et al. 2007, A&A, 465, 799 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, H. N., Ludwig, H. G., Caffau, E., Christlieb, N., & Zhao, G. 2013, ApJ, 765, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Lind, K., Bergemann, M., & Asplund, M. 2012, MNRAS, 427, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Lucatello, S., Masseron, T., Johnson, J. A., Pignatari, M., & Herwig, F. 2011, ApJ, 729, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A. 1992, A&A, 264, 105 [NASA ADS] [Google Scholar]
- Mattsson, L. 2010, A&A, 515, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McWilliam, A., Matteucci, F., Ballero, S., et al. 2008, ApJ, 136, 367 [Google Scholar]
- Meynet, G., & Arnould, M. 1993, Nuclei in the Cosmos; 2: 1992, Proc. of the 2nd International Symposium on Nuclear Astrophysis (BIOP Publishing), 503 [Google Scholar]
- Meynet, G., & Arnould, M. 1996, Wolf-Rayet stars in the framework of stellar evolution, Liège: Université de Liège, 33, 89 [NASA ADS] [Google Scholar]
- Meynet, G., & Arnould, M. 2000, A&A, 355, 176 [NASA ADS] [Google Scholar]
- Moorwood, A. 2005, High Resolution Infrared Spectroscopy in Astronomy, Proc. of and Workshop, Germany, eds. H. U. Käuflr, R. Siebenmargen, & A. Moorwood, 15 [Google Scholar]
- Mowlavi, N., Jorissen, A., & Arnould, M. 1998, A&A, 334, 153 [NASA ADS] [Google Scholar]
- Nault, K. A., & Pilachowski, C. A. 2013, ApJ, 146, 153 [Google Scholar]
- Palacios, A., Arnould, M., & Meynet, G. 2005, A&A, 443, 243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pandey, G. 2006, ApJ, 648, L143 [NASA ADS] [CrossRef] [Google Scholar]
- Pandey, G., Lambert, D. L., & Rao, N. K. 2008, ApJ, 674, 1068 [NASA ADS] [CrossRef] [Google Scholar]
- Renda, A., Fenner, Y., Gibson, B. K., et al. 2004, MNRAS, 354, 575 [NASA ADS] [CrossRef] [Google Scholar]
- Rich, R. M. 2013, Planets, 271 [Google Scholar]
- Ryabchikova, T. A., Piskunov, N. E., Kupka, F., & Weiss, W. W. 1997, Baltic Astron., 6, 244 [Google Scholar]
- Ryde, N., Gustafsson, B., Edvardsson, B., et al. 2010, A&A, 509, 20 [Google Scholar]
- Sauval, A. J., & Tatum, J. B. 1984, ApJS, 56, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Sneden, C. 1973, ApJ, 184, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Storey, P. J., & Zeippen, C. J. 2000, MNRAS, 312, 813 [Google Scholar]
- Travaglio, C., Gallino, R., Arnone, E., et al. 2004, ApJ, 601, 864 [NASA ADS] [CrossRef] [Google Scholar]
- Valenti, J. A., & Piskunov, N. 1996, A&AS, 118, 595 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weiland, J. L., Arendt, R. G., Berriman, G. B., et al. 1994, ApJ, 425, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, K., Rauch, T., & Kruk, J. W. 2005, A&A, 433, 641 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wiese, W. L., Smith, M. W., & Glennon, B. M. 1966, NSRDS-NBS 4, Washington, D.C.: US Department of Commerce, National Bureau of Standards, J. Phys. Chem. Ref. Data [Google Scholar]
- Woosley, S. E., & Haxton, W. C. 1988, Nature, 334, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Zemke, W. T., Stwalley, W. C., Coxon, J. A., & Hajigeorgiou, P. G. 1991a, Chem. Phys. Lett., 177, 412 [NASA ADS] [CrossRef] [Google Scholar]
- Zemke, W. T., Stwalley, W. C., Langhoff, S. R., Valderrama, G. L., & Berry, M. J. 1991b, J. Chem. Phys., 95, 7846 [NASA ADS] [CrossRef] [Google Scholar]
- Zoccali, M., Lecureur, A., Barbuy, B., et al. 2006, A&A, 457, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Determined stellar parameters for the reference star Arcturus and our program stars.
Atomic and molecular data for the spectral lines used for O and Zr abundance determination.
Uncertainties in the determined abundances caused by uncertainties in the stellar parameters.
All Figures
 |
Fig. 1 Location of the four fields (B3, BW, B6, and BL) of Lecureur et al. (2007) in comparison with the COBE/DIRBE outline of the Galactic bulge (Weiland et al. 1994) and the study of Bensby et al. (2013). Our stellar sample is a subset of the B3, BW, and B6 stars. The five re-analyzed stars from Cunha et al. (2008) are in the BW field. |
| In the text | |
 |
Fig. 2 Partition function of the HF molecule used in the MARCS code and SME for a relevant temperature range. |
| In the text | |
 |
Fig. 3 Relative line strengths of the ro-vibrational HF lines (the R and P branches of the v′′ = 0 to v′ = 1 band) given by gf e− χexc/kT at T = 4000 K. The K and L infrared transmission bands are indicated. |
| In the text | |
 |
Fig. 5 [F/Fe] and [O/Fe] as functions of [Fe/H] for the B3-BW-B6 stars. The stars are color-coded as the corresponding fields in Fig. 1. The black dots are the microlensed bulge dwarfs of Bensby et al. (2013) that are also marked in Fig. 1. Conservative estimates of the uncertainties are marked in the upper corners. |
| In the text | |
 |
Fig. 6 Our fluorine abundances compared with the predictions of our bulge models including AGB stars, excluding and including the ν-process with two different energies, and excluding W-R stars. The abundances have been transformed to the scale of the models with log ϵ(F)⊙ = 4.56 and log ϵ(O)⊙ = 8.93 (Anders & Grevesse 1989). The stars are color-coded as the corresponding fields in Fig. 1 with the BW-stars of Cunha et al. (2008) added in the right panel in light green. Conservative estimates of the uncertainties are marked in the upper left-hand corners. We note that the star BMB-78, still after the re-analysis, falls below the rest of the trend; see Sect. 5 for possible explanations. |
| In the text | |
 |
Fig. 7 Abundance ratios of fluorine and zirconium in our sample as a function of the solar normalized fluorine abundance. The negative slope indicated by this plot suggests that W-R stars might be important for producing fluorine in the bulge. The stars are color-coded as the corresponding fields in Fig. 1, and conservative estimates of the uncertainties are marked in the lower right-hand corner. |
| In the text | |
 |
Fig. 4 Observed spectra in black and synthetic spectra in red for the B3-BW-B6 stars. The three Zr-lines, the [O i]-line, the OH-lines, and the HF-line used are marked. The exact wavelengths are listed in Table 4. The OH-lines with obvious cosmic hits were excluded from the fit. Note the different flux scales. An example of the HF-line in the re-analyzed BMB-I-IV can be found in Cunha et al. (2008). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


