| Issue |
A&A
Volume 564, April 2014
|
|
|---|---|---|
| Article Number | A21 | |
| Number of page(s) | 14 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201323170 | |
| Published online | 28 March 2014 | |
Ammonia observations in the LBV nebula G79.29+0.46
Discovery of a cold ring and some warm spots ⋆,⋆⋆
1
Centro de Astrobiología (INTA-CSIC), Ctra. M-108, km. 4, 28850 Torrejón de Ardoz,
Madrid,
Spain
e-mail:
ricardo@cab.inta-csic.es
2
Institut de Ciències de l’Espai (CSIC-IEEC), Campus UAB Facultat
de Ciències, Torre C5-parell
2, 08193
Bellaterra,
Spain
3
Suffolk University, Madrid Campus, C/ Valle de la Viña 3,
28003
Madrid,
Spain
4
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69, 53121
Bonn,
Germany
5
Astronomy Department, King Abdulaziz University,
PO Box 80203, Jeddah
21589, Saudi
Arabia
Received:
2
December
2013
Accepted:
29
January
2014
Context. The surroundings of luminous blue variable (LBV) stars are excellent laboratories to study the effects of their high UV radiation, powerful winds, and strong ejection events onto the surrounding gas and dust.
Aims. We aim at determining the physical parameters of the dense gas near G79.29+0.46, an LBV-candidate located at the centre of two concentric infrared rings, which may interact with the infrared dark cloud (IRDC) G79.3+0.3.
Methods. The Effelsberg 100 m telescope was used to observe the NH3 (1, 1) and (2, 2) emission in a field of view of 7′ × 7′ including the infrared rings and a part of the IRDC. In addition, we observed particular positions in the NH3 (3,3) transition toward the strongest region of the IRDC, which is also closest to the ring nebula.
Results. We report here the first coherent ring-like structure of dense NH3 gas associated with an evolved massive star. It is well traced in both ammonia lines, surrounding an already known infrared ring nebula; its column density is two orders of magnitude lower than the IRDC. The NH3 emission in the IRDC is characterized by a low and uniform rotational temperature (Trot~10 K) and moderately high opacities in the (1, 1) line. The rest of the observed field is spotted by warm or hot zones (Trot>30 K) and characterized by optically thin emission of the (1, 1) line. The NH3 abundances are about 10-8 in the IRDC, and 10-10–10-9 elsewhere. The warm temperatures and low abundances of NH3 in the ring suggest that the gas is being heated and photo-dissociated by the intense UV field of the LBV star. An outstanding region is found to the south-west (SW) of the LBV star within the IRDC. The NH3 (3, 3) emission at the centre of the SW region reveals two velocity components tracing gas at temperatures >30 K. Of particular interest is the northern edge of the SW region, which coincides with the border of the ring nebula and a region of strong 6 cm continuum emission; here, the opacity of the (1, 1) line and the NH3 abundance do not decrease as expected in a typical clump of an isolated cold dark cloud. This strongly suggests some kind of interaction between the ring nebula (powered by the LBV star) and the IRDC. We finally discuss the possibility of NH3 evaporation from the dust grain mantles due to the already known presence of low-velocity shocks in the area.
Conclusions. The detection of the NH3 associated with this LBV ring nebula, as well as the special characteristics of the northern border of the SW region, confirm that the surroundings of G79.29+0.46 constitute an exemplary scenario, which merits to be studied in detail by other molecular tracers and higher angular resolutions.
Key words: stars: massive / stars: mass-loss / ISM: individual objects: G79.29+0.46 / ISM: molecules / ISM: structure
NH3 (1, 1) and (2, 2) spectra are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/564/A21
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2014
1. Introduction
Massive stars are probably the most important sources providing thermal and mechanical energy to the interstellar medium (ISM). They are few in number and remain on the main sequence only for some million years. One of the shortest (up to a few 104 yr) and most spectacular stages of their evolution is reached when they become luminous blue variable (LBV) stars. With bolometric luminosities >3 × 105L⊙, LBV stars are characterized by their heavy mass loss and both photometric and spectroscopic variability, and are assumed to be the progenitors of Wolf-Rayet (WR) stars (Langer et al. 1994; Maeder & Meynet 1994) or, as suggested by other authors, even the direct progenitors of type II supernovae with dense circumstellar material (e.g. Gal-Yam et al. 2007; Smith 2007). A key subject of current study about the LBV stars is the mechanism that drives the variability and episodic mass ejections. Since the winds and mass ejections leave their fingerprints on the surrounding material, the study of the distribution, composition, and physical properties of the circumstellar gas and dust would put constraints on the stellar wind models (e.g. Garcia-Segura & Mac Low 1995).
This circumstellar material, at up to 1 pc distance from the star, has been traditionally studied in the optical/IR, tracing emission nebulae consisting of ionized and neutral atomic gas and the (often) warm dust. However, the LBV environment is presumably also rich in molecules, (1) because the stars are active dust producers; and (2) because there should be shocks, caused by the stellar wind, triggering a shock-induced chemistry. In addition, since the atmospheric abundances of LBVs are expected to be He-enriched and near nuclear-CNO equilibrium, it is theoretically expected that the ejecta from LBVs will be rich in nitrogenated species (e.g. Smith et al. 1998, and references therein).
A clear-cut case of an environment rich in molecules is NGC 2359. In this WR nebula, Rizzo et al. (2001a) have detected the NH3 (1, 1) and (2, 2) metastable lines, which was the first detection of a polyatomic molecule in the surroundings of an evolved massive star. NH3 was detected towards a peak of the CO emission (Rizzo et al. 2001b, 2003a), in coincidence with other complex molecules (such as HCO+, CS, CN, and HCN; see Rizzo et al. 2003b). These findings revealed the presence of dense and warm molecular gas, which can be traced by N-bearing molecules. The high ammonia abundance and kinetic temperature derived (10-8 and 30 K, respectively) are interpreted in terms of a shock-induced chemistry. The same molecules detected in NGC 2359 (and some isotopomers) were later reported in the Homunculus, the circumstellar nebula around the well-known LBV η Carina (Smith et al. 2006; Loinard et al. 2012).
Among the N-bearing molecules usually studied, NH3 is particularly interesting because of its relatively high abundance and ubiquity. Moreover, its properties allow an accurate determination of the kinetic temperature, avoiding common observational problems like calibration and pointing (Ho & Townes 1983). The detection of NH3 in the environment of NGC 2359 and η Carina encourages studies of additional LBV star environments.
The nebula G79.29+0.46 constitutes an excellent testbed to pursue this type of studies. The combined effect of the strong UV field, the steady powerful winds and the violent mass ejections have produced conspicuous structures in the nebula and beyond. G79.29+0.46, firstly discovered by its free-free emission (Higgs et al. 1994), is a ring-like nebula formed and excited by an LBV candidate, surrounded by an outstanding pair of concentric rings seen in the infrared up to 24 μm (see Fig. 1 of Jiménez-Esteban et al. 2010), which is most likely formed by material ejected by the central object in at least two different mass-loss episodes. The detection of a CO structure around the nebula, as observed in the J = 2 → 1 and J = 3 → 2 lines (Rizzo et al. 2008), demonstrated the existence of warm and/or high-density molecular gas. Immersed within the CO structure, there is a higher density clump that is claimed to be associated with the south-western side of the infrared nebula. This work also provided evidences for a low-velocity shock with velocities about 14–15 km s-1 toward this CO clump. Subsequent CO J = 4 → 3 emission (Jiménez-Esteban et al. 2010) revealed two concentric slabs in the same region of the clump, filling the space between the two shells detected at 24 μm, and in coincidence with a region of strong 6 cm continuum emission of the nebula (Umana et al. 2011).
G79.29+0.46 is part of the very complex Cygnus X region. It is projected in between two star-forming regions: the Hii region DR 15 to the south-east (see Fig. 11 of Kraemer et al. 2010), and the infrared dark cloud IRDC G79.3+0.3 (hereafter the IRDC) towards the southern and western borders (Redman et al. 2003). The local arm is seen tangentially in this direction (Dame & Thaddeus 1985; Rygl et al. 2012), which makes it difficult to determine distances and to identify mutual associations among targets associated with the Cyg X region. An update of the information currently available and a brief discussion of the distance is presented below, in Sect. 5.1.
In this paper, we present NH3(1, 1) and (2, 2) maps observed with the Effelsberg 100-m radio telescope towards the LBV nebula G79.29+0.46 and the nearby IRDC. In Sect. 2 we describe the observations. In Sect. 3 we present the structure of ammonia emission in different velocity ranges, revealing a ring-like structure associated with the previously known infrared shell, as well as spectra of NH3 (3, 3) towards two positions in the south-western region. In Sect. 4 we analyse the ammonia data in the field, and study the properties of the dense gas associated with the LBV nebula and with the IRDC. Finally, in Sect. 5, we discuss the most relevant properties of the dense gas in the region, and the possible interaction of the LBV nebula with the IRDC. The main conclusions are summarized in Sect. 6.
2. Observations
We have used the Effelsberg 100-m radio telescope of the Max-Planck-Institut für Radioastronomie to map the distribution of the (1, 1) and (2, 2) inversion lines of NH3, in a ~7′ × 7′ field around G79.29+0.46. The observations have been carried out in March 2008.
The 1.3 cm HEMT receiver was tuned to 23.7086 GHz, a frequency lying midway between the rest frequencies of the two observed lines. We used the FFTS spectrometer, which provides a bandwidth of 100 MHz and a frequency resolution of ~6 kHz (0.08 km s-1). This spectrometer allowed the simultaneous observation of the two lines, with excellent velocity resolution. The whole data were processed using the CLASS software1. After baseline subtraction and calibration, the spectra were smoothed to a resolution of 0.24 km s-1 for further analysis.
The telescope beam size (half power beam width, HPBW) at the observed frequency is ~40′′, and the main beam efficiency is 0.52. We used NGC 7027 for continuum calibration, assuming an absolute flux of 5.58 Jy at 23.7 GHz (Ott et al. 1994). We also used DR21 (close to the observed field) as a line calibrator. Pointing was regularly checked, typically once every hour, and is accurate to within 7′′.
We observed throughout in position-switching mode, with the relative reference position at 200′′ in azimuth. Integration times per point varied between 5 and 10 min on-source, depending on weather conditions and elevations. Due to variable weather the system temperature varied between 30 K and 94 K, resulting in an rms noise (1-sigma) between 50 mK and 350 mK for a velocity spacing of 0.24 km s-1. All temperatures throughout this paper are on a main-beam scale (TMB).
The whole field was initially sampled every 40′′. A particular region of interest, corresponding to a multiple layered morphology in CO (Rizzo et al. 2008) was fully sampled (i.e. every 20′′); this region is indicated in Figs. 1 to 4 by a square and is referred to as “the SW region” hereafter.
Furthermore, two deep-integration pointed observations of the (3, 3) line were made towards specific positions. These positions correspond to NH3 and CO peaks, as explained in Sect. 3.3. Identical technical conditions were applied in this case.
All the positions throughout this paper are offsets from the equatorial coordinates
(J2000.0) of the exciting star, at (RA, Dec) = 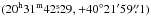 .
.
 |
Fig. 1 NH3 (1, 1) line intensity map in the direction toward G79.29+0.46. Only the main component has been integrated, in the velocity range indicated at the top right corner. On greyscale, the 1.2 mm continuum image of the MAMBO cameras at the IRAM 30 m telescope is also plotted (Motte et al. 2007). The logarithmic intensity scale used is indicated in the top bar. NH3 starting contours and spacing are 0.2 K km s-1. Equatorial coordinates refer to the star position (Sect. 2). The region was fully sampled within the square indicated at the south-west, and every 40′′elsewhere. The white contour, taken from the MAMBO data, is plotted to indicate the boundaries of the IRDC. Most of the NH3 (1, 1) emission seems associated with the cold dust traced by the 1.2 mm continuum, although some low-level features are also noted (see text). |
 |
Fig. 2 Same as Fig. 1 for the NH3 (2, 2) line. Contours start at 0.22 K km s-1, and are spaced by 0.11 K km s-1. Although the most extended emission is well correlated to the dark cloud in the south and west, the peak of the (2, 2) line arises from the (0″, −40″) position and is not correlated to the 1.2 mm emission. |
3. Results
3.1. Overall emission
The whole velocity range of NH3 emission, from −3 km s-1 to +3 km s-1, falls within the regions corresponding to Cyg X and the Great Rift (Schneider et al. 2006; Gottschalk et al. 2012). Channel maps of the emission of the (1, 1) and (2, 2) lines are presented in the Appendix, and the spectra are also accessible for download at the CDS. The velocity-integrated maps of both lines, in the interval (−3, +3) km s-1, are shown in Figs. 1 and 2. In Fig. 1, the (1, 1) contours are superimposed on the 1.2 mm continuum image from the MAMBO and MAMBO-2 cameras at the IRAM 30 m telescope (Motte et al. 2007), smoothed to an angular resolution of ~26′′. The figure shows that the most intense NH3 and 1.2 mm emission arises from the IRDC, extending from the south-east to the west of our field of view, and consisting of four main clumps. The peaks of ammonia do not agree with those of the 1.2 mm continuum. The SW region (the area inside the square) is the closest in projection to the ring of ionized nebula (Higgs et al. 1994; Umana et al. 2011). It is worth noting that while the southern clump and the SW region are physically connected, the connection between the SW region and the western clump suffers a discontinuity both in dust and gas, even taking into account that their overall structure suggests they are part of the same large-scale cloud. There is also some weak emission, traced by the low-level contours; this low-level emission is particularly visible at the northern and western part of the field, and also close to its centre, near the LBV star.
The NH3 (2, 2) line emission shares some of the (1, 1) features. Figure 2 plots the NH3 (2, 2) emission in the same velocity range as in Fig. 1. Again, the most extended emission appears correlated to the 1.2 mm continuum, and consequently to the IRDC; furthermore, some emission at the centre and the west is also present. It is remarkable that the peak of the whole map arises from a position close to the LBV star, at (0″, −40″). The central part of the field is devoid of NH3 (2, 2) emission, except at the (0″, −40″) position.
 |
Fig. 3 NH3 (1, 1) and (2, 2) integrated line emission in the velocity range (−1.2, +0.5) km s-1, overlaid on the 70 μm continuum of Herschel/PACS. The white contour is the same as depicted in Figs. 1 and 2. The fully sampled area is indicated by the white square. The white triangle (circle) points to the position of the NH3 (CO) peak. NH3(1, 1) starting and spacing contours (yellow) are 0.12 and 0.06 K km s-1, respectively. NH3(2, 2) starting and spacing contours (blue) are 0.04 K km s-1. In this velocity range, the ammonia emission is dominated by a ring-like structure towards the outer part of the ring nebula (see text). |
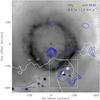 |
Fig. 4 Same as Fig. 3, but for the the velocity range (+0.5, +1.2) km s-1. Starting contours and spacing of the NH3 (1, 1) line (yellow) are 0.6 K km s-1 and 0.2 K km s-1, respectively. For the NH3 (2, 2) line, the starting contours and spacing (blue) are 0.09 and 0.03 K km s-1, respectively. At this velocity range, the ammonia emission is particularly intense towards the SW region (e.g., within the white square), in coincidence with the most prominent CO emission. Another outstanding feature is the (2, 2) spot around (0″, −40″), which has no (1, 1) counterpart. |
3.2. NH3 associated with the LBV nebula
To identify and further characterize the ammonia associated with G79.29+0.46, we thoroughly studied the NH3 emission in different velocity bins. After this analysis, two velocity ranges are particularly interesting. In Figs. 3 and 4, the emission of the (1, 1) and (2, 2) lines are sketched in these velocity intervals.
Figure 3 shows the ammonia emission in the velocity range (−1.2, +0.5) km s-1, overlaid on a Herschel/PACS image at 70 μm 2. An outstanding morphological correlation with the ring nebula (especially in the (1, 1) line) is noted in this figure, where a large portion of the 70 μm ring is surrounded by an ammonia feature. This NH3 ring-like structure bounds the 70 μm ring to the north and west, but is projected above it towards the south. The (2, 2) line also shows a similar morphology, although not as clear as the (1, 1) line. The lowest-level contours of the (1, 1) and (2, 2) lines corresponds to a signal-to-noise (S/N) ratio higher than 4 and 1.5, respectively, which explains the lack of a better correlation in the (2, 2) line.
Moreover, the inner part of the nebula is also partially filled by (1, 1) emission, without a (2, 2) counterpart. Because of the undersampling and the limited S/N ratio, it is not possible to determine whether a physical connection between the ammonia ring and the emission at the field centre exists. If so, most of the NH3 associated with the LBV nebula might be the surviving part of a formerly complete NH3 shell.
Figure 4 is similar to Fig. 3, but covers the second velocity range of interest: (+0.5, +1.2) km s-1. Here, the NH3 emission of both lines is concentrated towards the SW region, approximately at the centre of the fully sampled area. The (2, 2) line emission also depicts a strong spot around (0″, −40″) without a counterpart in the (1, 1) line.
The velocity of the NH3 ring does not match the values reported for the CO shell (see Figs. 6 and 7 of Jiménez-Esteban et al. 2010), which are around −3 km s-1 and +3 km s-1. This contradictory result is only apparent because it accounts for intrinsic differences in the molecules under comparison. CO is very abundant and ubiquitous, optically thick and with a low critical density; therefore, the CO emission is expected to trace ambients with a wider range of physical conditions than NH3. The velocity of the NH3 ring fits well within the whole range of emission associated with the CO shell (−5 to +5 km s-1; see Rizzo et al. 2008), but is close to the velocity of the local arm in this direction, and also to the velocity of Cygnus X and the Great Cygnus Rift. The velocity ranges of the CO slabs reported by Jiménez-Esteban et al. (2010) are merely those where the confusion effects are minor and a clear correlation with the infrared shell is noted.
In projection, the NH3 ring bounds the ring nebula and the CO slabs, although the presence of any positional differences between CO and NH3 should take into consideration the arguments presented above, and the fact that the comparison is made at different velocities. As we discuss below, the lack of ammonia in the ring nebula is consistent with the destruction of this molecule by the strong UV field.
3.3. NH3 (3, 3) in the SW region
We devoted special attention to the SW region, because it hosts a multiply layered CO structure (Rizzo et al. 2008; Jiménez-Esteban et al. 2010), and is also claimed to be a site of interaction between the LBV nebula and its environs (Umana et al. 2011).
The CO (Rizzo et al. 2008; Jiménez-Esteban et al. 2010) and dust-continuum emission (Figs. 1 and 2) are very well correlated in this region. Ammonia also depicts a strong and compact emission in the SW region, although it does not peak at the same position as CO and dust. Hereafter, we refer to the peaks of emission of ammonia and CO as the NH3 peak and the CO peak. The NH3 peak is near the centre of the SW region, at ~(−54″, −131″), while the CO peak is shifted with respect to the NH3 peak approximately by (−20″, +20″). To better analyse these two points, we performed deep integrations of the (3, 3) line.
 |
Fig. 5 NH3 (3, 3) observations in the south-western part of the field. Two positions (the NH3 and the CO peaks) have been observed, indicated above the boxes. The (1, 1) and (2, 2) spectra towards the same positions are also plotted for comparison. Note that the (1, 1) intensity scale is reduced by a factor of two, and the (3, 3) spectra are multiplied by 20. The (3, 3) spectrum towards the CO peak has been smoothed to 0.7 km s-1. Dashed vertical lines are plotted at +0.3 and +1.9 km s-1 to facilitate further comparisons among the lines, and to separate the three components present in the (3, 3) line towards the NH3 peak. |
 |
Fig. 6 Distribution of the rotational temperatures, overlaid on the 8 μm image of Spitzer. The values derived from hyperfine fitting of the (1, 1) line are labelled in blue; those derived from Gaussian fitting of both lines are shown in yellow; red labels correspond to the positions with the highest values of Trot (see text). In all cases, fitting of the (2, 2) has been obtained with a single Gaussian component. The low temperatures associated with the IRDC, and higher values elsewhere are clearly revealed. |
The two (3, 3) spectra are presented in Fig. 5, together with the corresponding (1, 1) and (2, 2) lines. Dashed velocity marks have been added at +0.3 and +1.9 km s-1 to facilitate the comparisons.
The first feature in the figure is the lack of (3, 3) emission in the CO peak. The ratio of the areas between the NH3 peak and the CO peak –computed in the velocity range (+0.3, +1.9) km s-1of the (3, 3) line– is higher than 16. On the other hand, the same ratios computed for the (1, 1) and (2, 2) lines are 1.8 and 2.8, respectively. Therefore, the absence of emission in the (3, 3) towards the CO peak is statistically significant.
A second feature in Fig. 5 is the presence of three velocity components in the (3, 3) line towards the NH3 peak. The velocity of the central component, roughly between the velocity marks, agrees with those of the (1, 1) and (2, 2) lines. However, the lower (blue) and higher (red) velocity components of the (3, 3) line do not have any counterpart in the (1, 1) or (2, 2) line emission. As we analyse below, the blue and red components are characterized by higher temperatures than the central component.
4. Analysis of the NH3 emission
4.1. Derivation of physical parameters
Ammonia is a rather ubiquitous molecule. Heavily destroyed in UV fields (e.g. Fuente et al. 1990, and references therein), it is present in cold dark clouds (Jijina et al. 1999; Sepúlveda et al. 2011) and also in regions affected by shocks (Tafalla & Bachiller 1995; Zhang et al. 2002; Palau et al. 2007). Since the very beginnings of molecular spectroscopy, it has been widely recognized as an excellent thermometer of the ISM (Ho & Townes 1983; Guesten et al. 1985; Maret et al. 2009).
From the joint analysis of the (1, 1) and (2, 2) metastable lines, we derived several physical properties of the NH3 gas. The details of the formulation are explained in the Appendix. We analysed every position with significant emission (>3σ) in any of the two lines.
The (1, 1) line emission arising from the IRDC is mostly optically thick, and the opacities were estimated through a hyperfine (hf) fitting. No satellite lines were detected elsewhere, and only a Gaussian fitting was performed. All the positions with significant emission in the (2, 2) line were also fitted by Gaussian profiles.
To estimate the ammonia abundance, X(NH3), we used the 1.2 mm map of Motte et al. (2007) and computed the H2 column density following Motte et al. (1998). Assumptions and formulation are also detailed in the Appendix.
In the NH3 peak of the SW region, where the (3, 3) line was observed and detected, we proceeded with a Boltzmann diagram approach to determine the rotational temperature and column densities of the three velocity components. The procedure is also described in the Appendix.
4.2. Rotational and kinetic temperatures
The distribution of the rotational temperatures (Trot) is sketched in Fig. 6. The values are written at their corresponding positions, superimposed to a Spitzer image at 8 μm.
The blue labels correspond to the points where hf fitting was possible. All these positions belong to the IRDC (as said above), and are characterized by a very low and uniform Trot, in the range 7–11 K. The points with two values of Trot correspond to the cases where two velocity components were fitted.
The yellow labels correspond to the points with both lines fitted by Gaussian profiles, and with derived values of Trot lower than 40 K. In case of a non-detection of the (2, 2) line, the values are expressed as upper limits. None of these points are correlated to the IRDC, and it is hard to establish a tendency across the observed field.
The red labels correspond to the positions where the (1, 1) line remains undetected, and therefore the values of Trot are lower limits. These “hot spots” are spread across the whole observed field, but again avoiding the IRDC positions. As the hot spots are located in the under-sampled area, we have to interpret them as small regions (smaller than 40″) with specific local conditions. The peak of the (2, 2) line in Fig. 4 – offset (0′′, −40′′) – has a lower limit of Trot of 63 K.
 |
Fig. 7 Distribution of the opacities in all the positions where a hyperfine fitting of the (1, 1) line was possible, i.e. mostly in the IRDC. |
 |
Fig. 8 Distribution of the ammonia column density in units of 1012 cm-3. Colours are the same as in Fig. 6. Details about the computation of N(NH3) are provided in the text. The large difference between the IRDC and the other positions is remarkable (see text). |
The general picture of the region consists, therefore, of a very cold and massive IRDC, spotted by tenuous areas, some of them depicting moderately high temperatures. This strong difference in the temperatures among the IRDC and the other positions is even more pronounced if we consider the kinetic temperatures (Tk), because the ratio between Tk and Trot increases with Trot (Danby et al. 1988; Tafalla et al. 2004). At the IRDC, Tk is in the range 8–12 K, while the positions with yellow labels may have Tk between 25 and 47 K. It is hard to constrain Tk in the hot spots, although high values, 100 K or even more, are possible.
4.3. Opacities in the IRDC
Figure 7 depicts the opacities of the main group (τm in the Appendix), derived when hf fitting was possible. The positions correspond to the IRDC and are labelled in blue, as in Fig. 6. Positions with two opacities correspond to the cases with two velocity components. As expected in the case of dark clouds, the higher opacities are found toward the inner part of the IRDC. A notable exception is found in the SW region, where the opacity remains high in the northern edge of the region, close to the border of the ring nebula.
4.4. Column densities and abundances
Figure 8 depicts the distribution of the column density, N(NH3), in the observed field. The colour code is the same as in Fig. 6. The estimates of N(NH3) in the hot spots (red labels) where only lower limits to Trot are determined, were made by assuming Trot = 50 K; all lower limits to Trot are higher than 50 K and, therefore, the values of N(NH3) are lower limits in all these cases. At the positions where we determined upper limits (yellow labels), we assumed Trot = 10 K. When there were two velocity components, the sum of both N(NH3) are depicted.
The differences between the IRDC and the rest of the field are striking in Fig. 8. N(NH3) varies from several 1014 to some 1016 cm-3 at the IRDC positions, and is in the range from 1012 to 1013 cm-3 elsewhere.
This wide range of the N(NH3) values also affects the estimates of abundances with respect to H2, X(NH3). Figure 9 shows the X(NH3) distribution in the field, with the same colour codes as previous figures. To compute the NH3 abundance, we had to estimate the H2 column density (N(H2) at all positions. This is inferred from the 1.2 mm continuum, which is considered a dust tracer. Assumed dust temperatures were 10 K at the IRDC positions and 50 K elsewhere (see the Appendix for details about the criteria used).
The lowest values of the abundances, in the range from several 10-11 to some 10-9, are spread all across the observed field except in the IRDC, where the abundance grows to some 10-8. Interestingly, the abundance in the SW region remains high at its northern and south-western borders. This is not the tendency expected in a quiescent clump of a dark cloud like, for instance, the other clumps of the IRDC.
 |
Fig. 9 Distribution of the ammonia abundances in units of 10-11 overlaid on an image of Spitzer/MIPS at 24 μm to highlight the second infrared ring. See details of the computation of H2 column densities in the text. Considerable differences between the IRDC and the rest of the field are again noted; furthermore, high values appear in the northern and south edges of the SW region, coinciding with the position of the first and second infrared rings, respectively (see text). |
4.5. NH3 peak
In Fig. 10, we show the Boltzmann diagram of the NH3 peak after fitting the (3, 3) spectrum to three Gaussian velocity components. The velocity ranges and the velocity-integrated line intensities of the fitting are shown in Table 1. We named the components central, blue, and red according to their velocity ranges.
Boltzmann diagram results in the NH3 peak.
As said above, the (1, 1) and (2, 2) lines were not detected in the red or blue velocity components; in these cases, upper detection limits (3-sigma) were computed in the corresponding velocity ranges.
The results of the Boltzmann diagram are shown in the last two columns of Table 1. Trot and N(NH3) can be determined only for the central component. For the others, we only derived lower limits of Trot. Because we also considered the column densities up to the first four metastable levels (see Appendix), the resulting values of N(NH3) are therefore upper limits.
Most of the gas (of the order of 1015 cm-2) arises in the central component and has a low value of Trot (11 K); these values of Trot and N(NH3) are those typically measured in the IRDC.
But strikingly, there is much low amount of gas (three orders of magnitude lower) at higher temperatures, above 28 K and 40 K. This finding confirms the scenario depicted by the (1, 1) and (2, 2) lines in the whole field: most of the dense gas is in cold form and associated with the IRDC, which in turn is embedded in a field dotted by low amounts of warm/hot gas.
 |
Fig. 10 Rotational diagram corresponding to the NH3 peak. The column densities have been computed for the three velocity components depicted in Fig. 5, also indicated in Table 1. The best-fit lines are sketched. The rotational temperature is only determined for the central component, while for the others (blue and red) only lower limits can be derived. |
4.6. Anomalous NH3(1, 1) spectra in the SW region
We found anomalous satellite ratios in the NH3(1, 1) spectra at four positions of the SW region. Figure 11 shows the spectra together with their locations. The positions affected by this anomalous emission lie at the outer edges of the SW region, two of them close to the CO peak.
The blue outer satellite hyperfine components are stronger than those of the red side. This has been proposed to be a signpost of contracting motions, both theoretically (Park 2001) and observationally (e.g. Fontani et al. 2012).
Alternatively, the anomaly could be caused by non-LTE emission due to hyperfine selective photon trapping, because this only affects the outer satellites. However, this effect would produce the opposite result; the red satellite would become stronger than the blue one (Stutzki & Winnewisser 1985).
 |
Fig. 11 Anomalous spectra in the SW region. The greyscale displays the Spitzer/IRAC 8 μm emission, and the yellow contours the NH3 (1, 1) integrated emission. Blue dots mark the positions of the anomalous spectra. These spectra are shown in the smaller boxes outside the map. Offsets are indicated in the top right corner of each spectrum. The observed spectra are in black and the fitting in red. The TMB scale has been chosen to improve the visibility of satellite lines. |
5. Discussion
5.1. Critical revision of the distances
The most recent distance estimate to some star-forming regions of Cygnus X is 1.4 kpc, based on spectroscopic parallaxes of their maser-emitting regions (Rygl et al. 2012). This distance is only slightly smaller than previous estimates using the same technique (Torres-Dodgen et al. 1991), and consistent with other works based on stellar classification (e.g. Hanson 2003). On the other hand, several studies locate DR15 at a lower distance, about 700–800 pc (Wendker et al. 1991; Uyanıker et al. 2001; Redman et al. 2003).
However, the distance to the IRDC is still a matter of debate, with distances ranging from 800 to 1700 pc (Redman et al. 2003; Kraemer et al. 2010). A close inspection of the infrared images and submillimeter continuum emission of a large field of view (20′ × 20′) including G79.29+0.46 reveals that the IRDC is interrupted in two positions: the SW region (e.g. Kraemer et al. 2010; Jiménez-Esteban et al. 2010; Umana et al. 2011), and the position of DR15 (see Fig. 2 of Redman et al. 2003). At first sight, the IRDC is farther away than both DR15 and the LBV nebula. However, the presence of a dark filamentary structure extending to the north of the IRDC and crossing the LBV nebula up to the position of the LBV star suggests that part of the IRDC is also in front of the LBV nebula (Figs. 6–8, and 11). Therefore, provided that part of the IRDC seems to be in front of the LBV nebula, and part of it seems to be behind, it seems reasonable to consider that the IRDC and the LBV nebula lie at similar distances of 1.4 kpc.
In addition, the overall NH3 (1, 1) and 1.2 mm emissions shown in Fig. 1 reveal a discontinuity separating the SW region and the westernmost clump of the IRDC, which is coincident with a bright 8 μm structure extending from the infrared ring farther to the south-west (Figs. 6–8, and 11). This has been proposed as an interaction zone of the LBV star with the surrounding medium (Umana et al. 2011) and favours the association of the LBV star with the IRDC.
The finding of hot spots with low column density in the field of view toward G79.29+0.46 leads us to associate the most tenuous ammonia to the Cygnus X star-forming region, or even to G79.29+0.46 itself. In this scenario, the warm/hot spots may represent the relics of the clumps of the ancient molecular cloud, which are being photo-evaporated by the UV field from G79.29+0.46, perhaps supported by other neighbouring massive stars. This idea is reinforced by the low abundance of NH3 measured near G79.29+0.46, compatible with the idea of NH3 being photo-dissociated by the strong UV radiation present in the region. The high temperatures found in the nebula are consistent with the high dust temperature previously found in the same region (Waters et al. 1996; Jiménez-Esteban et al. 2010).
In summary, we provide sufficient arguments that favour the possibility of some co-existence of the IRDC and G79.29+0.46 in close volumes. Therefore, the interplay between these two objects should be explored in more detail.
5.2. Hints of a possible interaction in the SW region
As said above, the fraction of the IRDC that we mapped is roughly divided into four regions, more or less aligned from the south-east corner of the map to its western border. In some aspects, the SW region (one of these four regions) presents a number of peculiarities compared with the other three regions.
The opacities measured in the SW region do not clearly decrease at the borders, which is not the expected behaviour in a typical cold dark cloud. In particular, the opacity in the northern edge – roughly a strip from (0′′, −120′′) to (−80′′, −100′′) – remains as high as in the centre. The abundance is also high in some points of the same strip, up to one order of magnitude higher than the NH3 peak (located at the centre of the SW region). The southern border – a strip from (−30′′, −200′′) to (−120′′, −150′′) – also depicts some points of high relative abundance. The anomalous (1, 1) satellite emission (Sect. 4.6) in the external parts of the SW region is another peculiarity.
The large differences in some parameters of the SW region, compared with the rest of the IRDC, are probably caused by different physical conditions. An increase of the abundances towards the borders is not the expected tendency in the parts of a cold cloud most exposed to external UV radiation. The abundance of NH3 in a harsh environment may be enhanced by sputtering in the presence of a C-type shock (Flower & Pineau des Forêts 1994; Draine 1995), which releases volatile molecules from the surface of the dust grains. This is a reasonable hypothesis taking into account the presence of a low-velocity shock (about 14 km s-1) at the north-western side of the SW region, close to the CO peak (Rizzo et al. 2008). It is also worth noting that the northern edge of the SW region coincides with a morphological disturbance of the 6 cm continuum emission, which is claimed as an evidence of some interaction with the surrounding ISM (Umana et al. 2011). Therefore, these ammonia observations may have unveiled the molecular counterpart of such disturbance, and also a new molecular component associated with the shocks discovered in CO (Rizzo et al. 2008).
The positions of abundance enhancement towards the southern border of the SW region agree with those of the external infrared shell, better seen in 24 μm (Jiménez-Esteban et al. 2010, and Fig. 9 of this work).
The scenario of the LBV star interacting with the IRDC is also consistent with the (3, 3) spectrum towards NH3 peak, which reveals two velocity components tracing gas at temperatures ≳30 K, clearly higher than the typical temperatures measured in the IRDC, of ~10 K.
Therefore, a number of observational findings points to a possible interaction of the nebula and the nested molecular shells with the SW region. Definitive evidence will come from observations with high angular resolution.
5.3. Triggered star formation in the SW region
If the LBV star is interacting with the SW region, this might affect the star formation that is currently ongoing in the area (Vink et al. 2008). The dynamical time scale of the ejection events that produced the CO and infrared nested shells is 4–5 yr (Rizzo et al. 2008; Umana et al. 2011). This is similar to the age of the brightest young stellar object embedded in the SW region, assuming it is in the Class 0 phase (Greene et al. 1994; Kenyon & Hartmann 1995; Enoch et al. 2009; Evans et al. 2009). Thus, while it seems unlikely that the ejection events of the LBV could have triggered the collapse of the young stellar objects embedded in the SW region, an interesting possibility would be to explore whether they are affecting the formation and evolution of the young stellar objects already formed.
After some 104−105 yr of evolution, G79.29+0.46 will become a Wolf-Rayet star and the NH3 ring will eventually disappear. The stellar wind regime will change at this stage, turning it out to higher velocity and lower wind density (Langer et al. 1994; Maeder & Meynet 1994; Garcia-Segura & Mac Low 1995). This will produce new shocks in the surrounding gas and dust, which may release volatile molecules from the icy grain mantles (Flower & Pineau des Forêts 1994) and consequently increase the ammonia abundance again. This line of reasoning is supported by the significantly high NH3 abundance seen to the north and south-western borders of the SW region, a trend also found in the molecular cloud around the WR nebula NGC 2359 (Rizzo et al. 2001a), and the Galactic Center (Flower et al. 1995; Martín-Pintado et al. 1999). The young stellar objects formed in the SW region will probably suffer photo-evaporation and heating of their envelopes.
6. Conclusions
To study the molecular gas in the infrared ring nebula of the LBV star G79.29+0.46 and its nearby IRDC, we used the Effelsberg telescope to map the NH3 (1, 1) and NH3(2, 2) emission in the G79.29+0.46 field. We additionally observed NH3(3, 3) in particular positions of the strongest NH3(1, 1) emission. Our main findings are summarized as follows:
-
1.
While the strongest emission of NH3 (1, 1) and (2, 2) matches the infrared-dark structure of the IRDC, mainly detected at velocities > 1 km s-1, the emission in the velocity range from −1.2 km s-1 to +0.5 km s-1 reveals a coherent structure closely following the infrared ring surrounding the LBV star, also partially seen in the (2, 2) transition. This is the first NH3 structure associated with an evolved massive star known so far.
-
2.
We derived the rotational temperature and NH3 column density of the dense gas in the entire field of view, and found that the rotational temperature is uniform and in the range 7–11 K in the IRDC, while it is >30 K in particular positions or hot spots of the infrared ring nebula and a couple of points within 30′′ of the LBV star. The NH3 column density in the IRDC is in the range 1014–1015 cm-2, while it is about two orders of magnitude lower near the LBV and the infrared ring. Using the 1.2 mm continuum emission in the field, we inferred NH3 abundances of about 10-8 in the IRDC, and 10-10–10-9 near the LBV star. The warm temperatures and low abundances of NH3 near the LBV star and its infrared-ring suggest that the gas is being heated and photo-dissociated by the intense UV-field of the LBV star.
-
3.
An outstanding region is recognized beyond the ring nebula towards its south-western part, which is also part of the IRDC (the SW region). The NH3 (3, 3) emission towards the centre of the SW region reveals three velocity components. One of them is associated with the IRDC and has a rotational temperature of 11 K, while the other two are associated with small dense cores with temperatures >30 K. In the northern edge of the SW region, the opacity of the (1, 1) line keeps a value as high as in the clump centre. The NH3 abundance tends to be higher at the clump edges than in the clump centre. All these features, together with the results of previous works reporting a shock within this region and hints of interaction with the LBV star, strongly suggests that a mass-loss ejection event of the LBV star is interacting with the SW region and releasing NH3 molecules back to the gas phase, thus increasing its abundance at the outer edges of the clump.
G79.29+0.46 is providing increasing evidence of being an excellent laboratory to study the history of a high-mass star evolution. Because LBVs are the precursors of core-collapse supernovae (through a Wolf-Rayet stage), the knowledge of the different actors present in this field may also help to learn about this topic. The ammonia ring-like structure associated with G79.29+0.46 and the SW region deserve follow-up observations with high angular resolution. Furthermore, the observation of other molecular tracers are of particular interest.
Online material
Appendix A: Channel maps
The proper channel maps of the two ammonia lines observed are presented in Figs. A.1 and A.2. The collection of spectra are also available at the CDS.
 |
Fig. A.1 Channel maps of the NH3 (1, 1) emission. Only the main hyperfine component is depicted. LSR velocities are indicated at the top centre of each map. Contours are 0.15, 0.30, 0.45, 0.60, 0.90, 1.20, 1.50, 1.80, 2.25, 2.70, 3.15, 3.60, 4.20, and 4.8 K. |
 |
Fig. A.2 Channel maps of the NH3 (2, 2) emission. Only the main hyperfine component is depicted. LSR velocities are indicated at the top centre of each map. Contours are 0.18, 0.36, 0.54, 0.72, and 1.08 K. |
Appendix B: Formulation
In this Appendix we summarize the formulae used to determine some physical properties (opacities, rotational temperatures, column densities, and abundances) from the observed NH3 lines. This corresponds to the standard interpretation previously discussed and presented by several authors, such as Ungerechts et al. (1986) and Busquet et al. (2009).
Appendix B.1: Hyperfine and Gaussian fitting
The NH3 lines are split by the quadrupole hyperfine interaction (Ho & Townes 1983). From the relative intensities of the main hf group and the four satellite ones, it is possible to directly derive the optical depth of the main hf group (Pauls et al. 1983). When the satellite (1, 1) lines were detected, a CLASS method was used for this fitting. The output is: (1) A τm = f [Jν(Texc) − Jν(Tbg)] τm; (2) LSR velocity (VLSR); (3) line width at half maximum (Δv); and (4) τm, the opacity of the main hf group. f is the beam-filling factor, and Jν(T) is Rayleigh-Jeans temperature, defined as Jν(T) = (h ν/k) (eh ν/k T − 1)-1, Tbg = 2.73 K is the background temperature, and h and k are the Planck and Boltzmann constants, respectively.
This formulation assumes that all the hf levels are populated according to local
thermodynamic equilibrium (LTE) conditions, and a Gaussian velocity distribution. The
level population is characterized by the excitation temperature Texc, which
can be cleared from the fitting by
![\appendix \setcounter{section}{2} \begin{eqnarray} T_\mathrm{exc}=\frac{{\mathrm h} \nu / {k}}{\ln[1+{\mathrm h} \nu / {k}\ \ W^{-1}]}, \end{eqnarray}](/articles/aa/full_html/2014/04/aa23170-13/aa23170-13-eq89.png) (B.1)where
W = Jν(Texc) = A/f + Jν(Tbg).
(B.1)where
W = Jν(Texc) = A/f + Jν(Tbg).
The column density of a NH3(J,K) level, N(J,K), is obtained by
 (B.2)where
ν is
the line frequency in GHz, τtot is the “total” opacity of all
the hf components, and Δv and Texc are in km s-1 and K, respectively. The
above equation results from solving the transport equation for the NH3 molecule (Wilson et al. 2009), using a dipole moment
μ = 1.469 D, and assuming Texc≫Tbg.
(B.2)where
ν is
the line frequency in GHz, τtot is the “total” opacity of all
the hf components, and Δv and Texc are in km s-1 and K, respectively. The
above equation results from solving the transport equation for the NH3 molecule (Wilson et al. 2009), using a dipole moment
μ = 1.469 D, and assuming Texc≫Tbg.
When hyperfine fitting was possible, we estimated the column density of the (1, 1)
level, N(1, 1), using the above equation. Numerically, it
is computed by  (B.3)where
a rough assumption of τtot = 2 τm
was used.
(B.3)where
a rough assumption of τtot = 2 τm
was used.
When hyperfine fitting was not possible, we assumed optically thin emission. In this
case, Eq. (B.2) for the (1, 1) line results in
 (B.4)In
the above equation, all the hf components are included in the integral. If the
integration only extends to the main group, the coefficient needs to be multiplied by
a factor of 2.
(B.4)In
the above equation, all the hf components are included in the integral. If the
integration only extends to the main group, the coefficient needs to be multiplied by
a factor of 2.
In the case of the (2, 2) line, the equivalent expression is
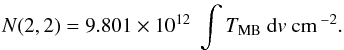 (B.5)Provided
N(1, 1) and N(2,2), the rotational temperature
Trot can be computed (Townes & Schawlow 1975; Ho & Townes 1983) by
(B.5)Provided
N(1, 1) and N(2,2), the rotational temperature
Trot can be computed (Townes & Schawlow 1975; Ho & Townes 1983) by
 (B.6)which
results from a two-level system approximation (Ho
& Townes 1983).
(B.6)which
results from a two-level system approximation (Ho
& Townes 1983).
The partition function is given by
 (B.7)where
gJK = (2J + 1) gop
and EJK are the
statistical weight and the energy of the level (J,K), and
gop is the statistical weight for the
ortho and para species. In the above equation we summed to the first four levels3 and assumed that (1) only the metastable levels are
populated; (2) the levels are characterized by the LTE temperature T; and (3)
gop equals to 2 and 1 for the ortho
and para species, respectively.
(B.7)where
gJK = (2J + 1) gop
and EJK are the
statistical weight and the energy of the level (J,K), and
gop is the statistical weight for the
ortho and para species. In the above equation we summed to the first four levels3 and assumed that (1) only the metastable levels are
populated; (2) the levels are characterized by the LTE temperature T; and (3)
gop equals to 2 and 1 for the ortho
and para species, respectively.
The total column density of all the metastable lines may be computed from a single
line and by assuming a partition function characterized by T = Trot (e.g.
Ungerechts et al. 1986; Busquet et al. 2009):
 (B.8)In
particular, for the (1, 1) line the above equation becomes
(B.8)In
particular, for the (1, 1) line the above equation becomes
![\appendix \setcounter{section}{2} \begin{eqnarray} N(\mathrm{NH}_3)&=&N(1,~1)\Bigg[\frac{1}{3}{\rm e}^{23.4/T_\mathrm{rot}}+1+ \frac{5}{3}{\rm e}^{-41.5/T_\mathrm{rot}}\nonumber\\[2mm] &&+\frac{14}{3}{\rm e}^{-101.2/T_\mathrm{rot}}\Bigg]. \end{eqnarray}](/articles/aa/full_html/2014/04/aa23170-13/aa23170-13-eq112.png) (B.9)When
the (2, 2) line is the only one detected, an equivalent formula to (B.9) is
(B.9)When
the (2, 2) line is the only one detected, an equivalent formula to (B.9) is
![\appendix \setcounter{section}{2} \begin{eqnarray} N(\mathrm{NH}_3)&=&N(2, 2)\Bigg[\frac{1}{5}{\rm e}^{64.9/T_\mathrm{rot}}+ \frac{3}{5}{\rm e}^{41.5/T_\mathrm{rot}}+1\nonumber\\[2mm] &&+\frac{14}{5}{\rm e}^{-59.6/T_\mathrm{rot}}\Bigg]. \end{eqnarray}](/articles/aa/full_html/2014/04/aa23170-13/aa23170-13-eq113.png) (B.10)
(B.10)
Appendix B.2: Abundances
The NH3
abundance is computed by  (B.11)where
N(H2) is the H2 column density. To estimate it, we used the survey
of the Cygnus region conducted by Motte et al.
(2007) in the 1.2 mm continuum emission.
(B.11)where
N(H2) is the H2 column density. To estimate it, we used the survey
of the Cygnus region conducted by Motte et al.
(2007) in the 1.2 mm continuum emission.
At this wavelength, most of the flux arises from thermal dust emission, which is optically thin. By assuming a constant gas-to-dust ratio, the 1.2 mm flux is directly related to the total amount of molecular gas. We therefore used the formulation of Motte et al. (1998), adapted to our case.
More precisely, we used their Eq. (1), which computes N(H2) as a function of the 1.2 mm flux, the dust temperature (Tdust) and κ1.2 mm, the dust opacity per unit mass column density.
The map of Motte et al. (2007) was convolved to 40′′ to match the angular resolution of the 100 m telescope. For κ1.2 mm we adopted a value of 0.01 g-1 (cm-2)-1, which corresponds to dust particles covered by thin ice mantles (Ossenkopf & Henning 1994), and is also a geometrical average between the values commonly adopted for pre-stellar dense clumps and circumstellar envelopes in young stellar objects of class II (Motte et al. 2007).
Under these assumptions, the resulting formula is
 (B.12)where
S is
the flux at 1.2 mm in the convolved map. Tdust is assumed as 10 K in the IRDC
positions, and 50 K elsewhere, consistent with the two dust populations previously
reported in the region (Umana et al. 2011).
(B.12)where
S is
the flux at 1.2 mm in the convolved map. Tdust is assumed as 10 K in the IRDC
positions, and 50 K elsewhere, consistent with the two dust populations previously
reported in the region (Umana et al. 2011).
For the IRDC, the assumed value of 10 K is compatible with the Trot derived from the hf fitting, because Tk≈Trot at low temperatures, and the gas is thermalised at the dust temperature. At the other positions – particularly in the ring nebula and its interior – the continuum emission is bright at shorter wavelengths, such as 24 μm, indicating a probably higher dust temperature. By assuming a conservative value of 50 K, the derived values of N(H2) have to be considered as upper limits and thus X(NH3) as lower limits.
Appendix B.3: Rotational diagrams
The rotational diagram, also known as the Boltzmann diagram approach, is a rather common methodology used to derive the rotational temperature and column density of a given species. The method is described in many works (see, for example, Goldsmith & Langer 1999) and assumes a population of the levels characterized by Trot, under LTE conditions.
By taking logarithms to Eq. (B.8), and after some algebra, we obtain
![\appendix \setcounter{section}{2} \begin{eqnarray} \log\left[N(J,K)/g_{JK}\right]&=&-\frac{\log e}{T_\mathrm{rot}}\nonumber\\[4mm] &&\times \left(E_{JK}/{k}\right) \!+ \! \log\left[N(\mathrm{NH}_3)/Q(T_\mathrm{rot})\right]. \end{eqnarray}](/articles/aa/full_html/2014/04/aa23170-13/aa23170-13-eq121.png) (B.13)We
see in the above equation that the energy of the upper levels is linearly related to
the logarithms of the column densities.
(B.13)We
see in the above equation that the energy of the upper levels is linearly related to
the logarithms of the column densities.
If three or more lines of a given species are measured, we can define the abscissa
x as
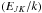 ,
and the ordinate y as log [N(J,K)/gJK].
x and
y are
related by the usual linear equation y = a x + b,
and we can therefore find the least-squares regression line. Trot and
N(NH3) can be obtained from the slope a and the constant term
b by
,
and the ordinate y as log [N(J,K)/gJK].
x and
y are
related by the usual linear equation y = a x + b,
and we can therefore find the least-squares regression line. Trot and
N(NH3) can be obtained from the slope a and the constant term
b by
 (B.14)and
(B.14)and
 (B.15)
(B.15)
CLASS is part of the GILDAS software, developed by IRAM. See http://www.iram.fr/IRAMFR/GILDAS/
The Level-2 PACS image (Poglitsch et al. 2010) was obtained from the Herschel public archive (ObsID: 1342196767).
Acknowledgments
We are deeply grateful to Gemma Busquet and Álvaro Sánchez-Monge for observing the final part of the map. We also acknowledge the kind and professional support of the Effelsberg staff during the observations. The constructive comments from the anonymous referee have significantly improved the paper. J.R.R. acknowledges support from MICINN (Spain) grants CSD2009-00038, AYA2009-07304, and AYA2012-32032. A.P. is supported by a JAE-Doc CSIC fellowship co-funded with the European Social Fund under the program “Junta para la Ampliación de Estudios”, by the MICINN grant AYA2011-30228-C03-02 (co-funded with FEDER funds), and by the AGAUR grant 2009SGR1172 (Catalonia). F.J.-E. acknowledges support from MICINN grant AYA2011-24052 and the CoSADIE Coordination Action (FP7, Call INFRA-2012-3.3 Research Infrastructures, project 312559). This work has benefited from research funding from the European Community’s sixth Framework Programme under RadioNet R113CT 2003 5058187.
References
- Busquet, G., Palau, A., Estalella, R., et al. 2009, A&A, 506, 1183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dame, T. M., & Thaddeus, P. 1985, ApJ, 297, 751 [NASA ADS] [CrossRef] [Google Scholar]
- Danby, G., Flower, D. R., Valiron, P., Schilke, P., & Walmsley, C. M. 1988, MNRAS, 235, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 1995, Ap&SS, 233, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Enoch, M. L., Evans, N. J., II, Sargent, A. I., & Glenn, J. 2009, ApJ, 692, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, N. J., II, Dunham, M. M., Jørgensen, J. K., et al. 2009, ApJS, 181, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, D. R., & Pineau des Forêts, G. 1994, MNRAS, 268, 724 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, D. R., Pineau des Forêts, G., & Walmsley, C. M. 1995, A&A, 294, 815 [NASA ADS] [Google Scholar]
- Fontani, F., Palau, A., Busquet, G., et al. 2012, MNRAS, 423, 1691 [NASA ADS] [CrossRef] [Google Scholar]
- Fuente, A., Martin-Pintado, J., Bachiller, R., & Cernicharo, J. 1990, A&A, 237, 471 [NASA ADS] [Google Scholar]
- Gal-Yam, A., Leonard, D. C., Fox, D. B., et al. 2007, ApJ, 656, 372 [NASA ADS] [CrossRef] [Google Scholar]
- Garcia-Segura, G., & Mac Low, M.-M. 1995, ApJ, 455, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Goldsmith, P. F., & Langer, W. D. 1999, ApJ, 517, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Gottschalk, M., Kothes, R., Matthews, H. E., Landecker, T. L., & Dent, W. R. F. 2012, A&A, 541, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Greene, T. P., Wilking, B. A., Andre, P., Young, E. T., & Lada, C. J. 1994, ApJ, 434, 614 [NASA ADS] [CrossRef] [Google Scholar]
- Güsten, R., Walmsley, C. M., Ungerechts, H., & Churchwell, E. 1985, A&A, 142, 381 [NASA ADS] [Google Scholar]
- Hanson, M. M. 2003, ApJ, 597, 957 [NASA ADS] [CrossRef] [Google Scholar]
- Higgs, L. A., Wendker, H. J., & Landecker, T. L. 1994, A&A, 291, 295 [NASA ADS] [Google Scholar]
- Ho, P. T. P., & Townes, C. H. 1983, ARA&A, 21, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Jijina, J., Myers, P. C., & Adams, F. C. 1999, ApJS, 125, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Jiménez-Esteban, F. M., Rizzo, J. R., & Palau, A. 2010, ApJ, 713, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Kenyon, S. J., & Hartmann, L. 1995, ApJS, 101, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Kraemer, K. E., Hora, J. L., Egan, M. P., et al. 2010, AJ, 139, 2319 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, N., Hamann, W.-R., Lennon, M., et al. 1994, A&A, 290, 819 [NASA ADS] [Google Scholar]
- Loinard, L., Menten, K. M., Güsten, R., Zapata, L. A., & Rodríguez, L. F. 2012, ApJ, 749, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Longmore, S. N., Burton, M. G., Barnes, P. J., et al. 2007, MNRAS, 379, 535 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A., & Meynet, G. 1994, A&A, 287, 803 [Google Scholar]
- Maret, S., Faure, A., Scifoni, E., & Wiesenfeld, L. 2009, MNRAS, 399, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Martín-Pintado, J., Gaume, R. A., Rodríguez-Fernández, N., de Vicente, P., & Wilson, T. L. 1999, ApJ, 519, 667 [NASA ADS] [CrossRef] [Google Scholar]
- Motte, F., Andre, P., & Neri, R. 1998, A&A, 336, 150 [NASA ADS] [Google Scholar]
- Motte, F., Bontemps, S., Schilke, P., et al. 2007, A&A, 476, 1243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ossenkopf, V., & Henning, T. 1994, A&A, 291, 943 [NASA ADS] [Google Scholar]
- Ott, M., Witzel, A., Quirrenbach, A., et al. 1994, A&A, 284, 331 [NASA ADS] [Google Scholar]
- Palau, A., Estalella, R., Girart, J. M., et al. 2007, A&A, 465, 219 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Park, Y.-S. 2001, A&A, 376, 348 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pauls, A., Wilson, T. L., Bieging, J. H., & Martin, R. N. 1983, A&A, 124, 23 [NASA ADS] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Redman, R. O., Feldman, P. A., Wyrowski, F., et al. 2003, ApJ, 586, 1127 [NASA ADS] [CrossRef] [Google Scholar]
- Rizzo, J. R., Martín-Pintado, J., & Henkel, C. 2001a, ApJ, 553, L181 [NASA ADS] [CrossRef] [Google Scholar]
- Rizzo, J. R., Martín-Pintado, J., & Mangum, J. G. 2001b, A&A, 366, 146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rizzo, J. R., Martín-Pintado, J., & Desmurs, J.-F. 2003a, A&A, 411, 465 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rizzo, J. R., Martín-Pintado, J., & Desmurs, J.-F. 2003b, IAU Symp., 212, 742 [NASA ADS] [Google Scholar]
- Rizzo, J. R., Jiménez-Esteban, F. M., & Ortiz, E. 2008, ApJ, 681, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Rygl, K. L. J., Brunthaler, A., Sanna, A., et al. 2012, A&A, 539, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, N., Bontemps, S., Simon, R., et al. 2006, A&A, 458, 855 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sepúlveda, I., Anglada, G., Estalella, R., et al. 2011, A&A, 527, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, N. 2007, AJ, 133, 1034 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, N., Brooks, K. J., Koribalski, B. S., & Bally, J. 2006, ApJ, 645, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, L. J., Nota, A., Pasquali, A., et al. 1998, ApJ, 503, 278 [NASA ADS] [CrossRef] [Google Scholar]
- Stutzki, J., & Winnewisser, G. 1985, A&A, 144, 13 [NASA ADS] [Google Scholar]
- Tafalla, M., & Bachiller, R. 1995, ApJ, 443, L37 [Google Scholar]
- Tafalla, M., Myers, P. C., Caselli, P., & Walmsley, C. M. 2004, A&A, 416, 191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Torres-Dodgen, A. V., Carroll, M., & Tapia, M. 1991, MNRAS, 249, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Townes, C. H., & Schawlow, A. L. 1975, Microwave spectroscopy (New York: Dover Publications) [Google Scholar]
- Umana, G., Buemi, C. S., Trigilio, C., et al. 2011, ApJ, 739, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Ungerechts, H., Winnewisser, G., & Walmsley, C. M. 1986, A&A, 157, 207 [NASA ADS] [Google Scholar]
- Uyanıker, B., Fürst, E., Reich, W., Aschenbach, B., & Wielebinski, R. 2001, A&A, 371, 675 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vink, J. S., Drew, J. E., Steeghs, D., et al. 2008, MNRAS, 387, 308 [NASA ADS] [CrossRef] [Google Scholar]
- Waters, L. B. F. M., Izumiura, H., Zaal, P. A., et al. 1996, A&A, 313, 866 [NASA ADS] [Google Scholar]
- Wendker, H. J., Higgs, L. A., & Landecker, T. L. 1991, A&A, 241, 551 [NASA ADS] [Google Scholar]
- Wilson, T. L., Rohlfs, K., Hüttemeister, S. 2009, Tools of Radio Astronomy (Berlin: Springer-Verlag) [Google Scholar]
- Zhang, Q., Hunter, T. R., Sridharan, T. K., & Ho, P. T. P. 2002, ApJ, 566, 982 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 NH3 (1, 1) line intensity map in the direction toward G79.29+0.46. Only the main component has been integrated, in the velocity range indicated at the top right corner. On greyscale, the 1.2 mm continuum image of the MAMBO cameras at the IRAM 30 m telescope is also plotted (Motte et al. 2007). The logarithmic intensity scale used is indicated in the top bar. NH3 starting contours and spacing are 0.2 K km s-1. Equatorial coordinates refer to the star position (Sect. 2). The region was fully sampled within the square indicated at the south-west, and every 40′′elsewhere. The white contour, taken from the MAMBO data, is plotted to indicate the boundaries of the IRDC. Most of the NH3 (1, 1) emission seems associated with the cold dust traced by the 1.2 mm continuum, although some low-level features are also noted (see text). |
| In the text | |
 |
Fig. 2 Same as Fig. 1 for the NH3 (2, 2) line. Contours start at 0.22 K km s-1, and are spaced by 0.11 K km s-1. Although the most extended emission is well correlated to the dark cloud in the south and west, the peak of the (2, 2) line arises from the (0″, −40″) position and is not correlated to the 1.2 mm emission. |
| In the text | |
 |
Fig. 3 NH3 (1, 1) and (2, 2) integrated line emission in the velocity range (−1.2, +0.5) km s-1, overlaid on the 70 μm continuum of Herschel/PACS. The white contour is the same as depicted in Figs. 1 and 2. The fully sampled area is indicated by the white square. The white triangle (circle) points to the position of the NH3 (CO) peak. NH3(1, 1) starting and spacing contours (yellow) are 0.12 and 0.06 K km s-1, respectively. NH3(2, 2) starting and spacing contours (blue) are 0.04 K km s-1. In this velocity range, the ammonia emission is dominated by a ring-like structure towards the outer part of the ring nebula (see text). |
| In the text | |
 |
Fig. 4 Same as Fig. 3, but for the the velocity range (+0.5, +1.2) km s-1. Starting contours and spacing of the NH3 (1, 1) line (yellow) are 0.6 K km s-1 and 0.2 K km s-1, respectively. For the NH3 (2, 2) line, the starting contours and spacing (blue) are 0.09 and 0.03 K km s-1, respectively. At this velocity range, the ammonia emission is particularly intense towards the SW region (e.g., within the white square), in coincidence with the most prominent CO emission. Another outstanding feature is the (2, 2) spot around (0″, −40″), which has no (1, 1) counterpart. |
| In the text | |
 |
Fig. 5 NH3 (3, 3) observations in the south-western part of the field. Two positions (the NH3 and the CO peaks) have been observed, indicated above the boxes. The (1, 1) and (2, 2) spectra towards the same positions are also plotted for comparison. Note that the (1, 1) intensity scale is reduced by a factor of two, and the (3, 3) spectra are multiplied by 20. The (3, 3) spectrum towards the CO peak has been smoothed to 0.7 km s-1. Dashed vertical lines are plotted at +0.3 and +1.9 km s-1 to facilitate further comparisons among the lines, and to separate the three components present in the (3, 3) line towards the NH3 peak. |
| In the text | |
 |
Fig. 6 Distribution of the rotational temperatures, overlaid on the 8 μm image of Spitzer. The values derived from hyperfine fitting of the (1, 1) line are labelled in blue; those derived from Gaussian fitting of both lines are shown in yellow; red labels correspond to the positions with the highest values of Trot (see text). In all cases, fitting of the (2, 2) has been obtained with a single Gaussian component. The low temperatures associated with the IRDC, and higher values elsewhere are clearly revealed. |
| In the text | |
 |
Fig. 7 Distribution of the opacities in all the positions where a hyperfine fitting of the (1, 1) line was possible, i.e. mostly in the IRDC. |
| In the text | |
 |
Fig. 8 Distribution of the ammonia column density in units of 1012 cm-3. Colours are the same as in Fig. 6. Details about the computation of N(NH3) are provided in the text. The large difference between the IRDC and the other positions is remarkable (see text). |
| In the text | |
 |
Fig. 9 Distribution of the ammonia abundances in units of 10-11 overlaid on an image of Spitzer/MIPS at 24 μm to highlight the second infrared ring. See details of the computation of H2 column densities in the text. Considerable differences between the IRDC and the rest of the field are again noted; furthermore, high values appear in the northern and south edges of the SW region, coinciding with the position of the first and second infrared rings, respectively (see text). |
| In the text | |
 |
Fig. 10 Rotational diagram corresponding to the NH3 peak. The column densities have been computed for the three velocity components depicted in Fig. 5, also indicated in Table 1. The best-fit lines are sketched. The rotational temperature is only determined for the central component, while for the others (blue and red) only lower limits can be derived. |
| In the text | |
 |
Fig. 11 Anomalous spectra in the SW region. The greyscale displays the Spitzer/IRAC 8 μm emission, and the yellow contours the NH3 (1, 1) integrated emission. Blue dots mark the positions of the anomalous spectra. These spectra are shown in the smaller boxes outside the map. Offsets are indicated in the top right corner of each spectrum. The observed spectra are in black and the fitting in red. The TMB scale has been chosen to improve the visibility of satellite lines. |
| In the text | |
 |
Fig. A.1 Channel maps of the NH3 (1, 1) emission. Only the main hyperfine component is depicted. LSR velocities are indicated at the top centre of each map. Contours are 0.15, 0.30, 0.45, 0.60, 0.90, 1.20, 1.50, 1.80, 2.25, 2.70, 3.15, 3.60, 4.20, and 4.8 K. |
| In the text | |
 |
Fig. A.2 Channel maps of the NH3 (2, 2) emission. Only the main hyperfine component is depicted. LSR velocities are indicated at the top centre of each map. Contours are 0.18, 0.36, 0.54, 0.72, and 1.08 K. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


