| Issue |
A&A
Volume 564, April 2014
|
|
|---|---|---|
| Article Number | A102 | |
| Number of page(s) | 20 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201322139 | |
| Published online | 14 April 2014 | |
The Besançon Galaxy model renewed⋆
I. Constraints on the local star formation history from Tycho data
1 Departament d’Astronomia i Meteorologia and IEEC-ICC-UBUniversitat de Barcelona, Martí i Franquès 1, 08028 Barcelona, Spain
e-mail: mczekaj@am.ub.es
2 Institut Utinam, CNRS UMR6213, Université de Franche-Comté, OSU THETA de Franche-Comté-Bourgogne, 25010 Besançon, France
3 GEPI, Observatoire de Paris, CNRS, Université Paris Diderot, 92190 Meudon, France
Received: 25 June 2013
Accepted: 14 January 2014
Context. The understanding of Galaxy evolution can be facilitated by the use of population synthesis models, which allows us to test hypotheses on the star formation history, star evolution, and chemical and dynamical evolution of the Galaxy.
Aims. The new version of the Besançon Galaxy model (BGM) aims to provide a more flexible and powerful tool to investigate the initial mass function (IMF) and star formation rate (SFR) of the Galactic disc.
Methods. We present a new strategy for the generation of thin disc stars, which assumes the IMF, SFR and evolutionary tracks as free parameters. We have updated most of the ingredients for the star count production and, for the first time, binary stars are generated in a consistent way. The local dynamical self-consistency is maintained in this new scheme. We then compare simulations from the new model with Tycho-2 data and the local luminosity function, as a first test to verify and constrain the new ingredients. The effects of changing thirteen different ingredients of the model are systematically studied.
Results. For the first time, a full sky comparison is performed between BGM and data. This strategy allows us to constrain the IMF slope at high masses, which is found to be close to 3.0 and excludes a shallower slope such as Salpeter’s one. The SFR is found decreasing whatever IMF is assumed. The model is compatible with a local dark matter density of 0.011 M⊙ pc-3 implying that there is no compelling evidence for the significant amount of dark matter in the disc. While the model is fitted to Tycho-2 data, which is a magnitude limited sample with V< 11, we check that it is still consistent with fainter stars.
Conclusions. The new model constitutes a new basis for further comparisons with large scale surveys and is being prepared to become a powerful tool for the analysis of the Gaia mission data.
Key words: Galaxy: disk / Galaxy: evolution / galaxies: structure / Galaxy: general / solar neighborhood / Galaxy: stellar content
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2014
1. Introduction
The understanding of the origin and evolution of the Milky Way is one of the primary goals of the Gaia mission (ESA, launched December 2013). The use of its data to test different hypotheses and scenarios of galaxy formation and evolution requires the availability of an adaptable Galaxy model to provide simulated data for comparison. Kinematic and photometric data with the ages and metallicities of the stars and their statistics allows us to characterise galaxy’s populations and, from that, the overall Galactic gravitational potential. One of the most promising procedures to reach such a goal is to optimize the present population synthesis models by fitting robust statistical techniques, the large and small scale structure, and kinematics parameters that best reproduce Gaia data. The work presented in this paper is focused on the optimization of the structure parameters of the Milky Way Galactic disc in the Besançon Galaxy model (BGM) by comparing the simulations to real data to study the process of Galaxy evolution.
The development of Galaxy models started in the early 80s when several needs for star count predictions for the sake of preparing observations, in particular HST mission. For example, Bahcall & Soneira (1980) built a model based on simple assumptions on density laws and luminosity functions, while Wainscoat et al. (1992) developed a model in the infrared using a more complex set of luminosity functions but leading to a very large number of free parameters. From the beginning, the aim of the BGM was not only to be able to simulate reasonable star counts but further to test scenarios of Galactic evolution from assumptions on the rate of star formation, initial mass function (IMF), and stellar evolution. This was the spirit of the Tinsley (1972) formalism of decomposition of the star-creation process in these two functions of mass and time, which are assumed independent. Crézé (1979) and Crézé & Robin (1983) conceived the starting point of a model to be able to generate samples of stars directly comparable with observations. The idea was that simulations can be efficiently compared with data because all observational bias can easily be taken into account. Then statistical tests and fitting processes can be applied to constrain model parameters and hypothesis, such as the IMF, the density laws, etc. The initial BGM from Robin & Crézé (1986) was improved for taking into account dynamical constraints (see Bienaymé et al. 1987). Further developments concerned the stellar and Galactic evolution constraints from the Hipparcos input catalogue, the high latitude star counts (Haywood et al. 1997b), constraints on the thick disc population (Robin et al. 1996; Reylé & Robin 2001), the halo (Robin et al. 2000), and the bulge (Picaud & Robin 2004). This leads to a version, which was released to the community on the web1 and described in Robin et al. (2003). Since this work, we continued to develop it, partly for giving improved fit to available data and partly to constrain Galactic structure and scenarios of galaxy formation, especially in the Galactic plane, thanks to the 3D extinction model developed (Marshall et al. 2006), the study of the Galactic warp and flare (Derrière & Robin 2001; Reylé et al. 2009), and, lastly, the bar and bulge regions (Robin et al. 2012b).
In recent years, other population synthesis models have been developed, such as those by Ng et al. (1997), Vallenari et al. (1999), Girardi et al. (2005), and that known as tri-dimensional model of the galaxy (TRILEGAL). These models are also based on stellar evolutionary tracks and assumptions on SFH and IMF. However, none of them have yet used dynamical constraints, as BGM has. The model TRILEGAL benefits for a wide coverage of all the photometric systems used in observations. It uses slightly different model parameters; the atmosphere model used are the one from Padova, while we use semi-empirical grids from BaSeL2.2 (Lejeune et al. 1997, 1998) or 3.1 (Westera et al. 2002) complemented at low temperatures by NextGen models in BGM. The colour predictions are then significantly different in the low mass region. The TRILEGAL model uses essentially the same kind of parametrization for the thin disc with a scale height changing with age but with an exponential or secant squared while BGM uses Einasto ellipsoids. A simple diffuse extinction model from an exponential or sech2 function is used for modelling the interstellar absorption, and the warp and flare in the outer disc are not yet taken into account in TRILEGAL. Bulge parameters, as proposed by Vanhollebeke et al. (2009) are sensitively different than in BGM (Robin et al. 2012b). Ng et al. (1997) and Vallenari et al. (1999) models have only been compared to data in a limited number of directions of observations, and their parameters are less well established and constrained.
Just & Jahreiß (2010) proposed a new scheme, using local dynamical constraints to create a local model of the Galaxy. This model only accounts for main sequence stars and have not been compared with large scale surveys, but it produced interesting constraints on the local star formation history and on the IMF. Gao et al. (2013) attempted to combine the Just & Jahreiß (2010) approach with TRILEGAL code to fit some parameters and improved the fit to SDSS data towards high latitudes. However, they conclude that TRILEGAL has not enough flexibility to obtain a satisfactory fit to these data and show that BGM (2003 version) does not compare well with SDSS data. However, this was a version of the BGM that was not calibrated for the ugriz photometric system yet.
Galaxia (Sharma et al. 2011) is another type of approach, which makes use of the BGM (the 2003 version) in order to create large simulations to be compared with large scale surveys. It can take any Galaxy model as an input but is not a new Galaxy model by itself. It is also a very useful tool to translate N-body simulations into an observable catalogue.
For a long time, we have identified a systematic disagreement between BGM and real data concerning bright stars. A comparison to the Hipparcos catalogue showed that the A-F dwarfs are over-represented by 20−30% while the quality of star count predictions are at the level of a few percent at fainter magnitudes (Robin et al. 2003; Ibata et al. 2007). It appears that faint star counts (typically V ≥ 15) are dominated by thick disc and halo populations at or slightly below the turnoff, while the contribution of the thin disc is dominated by K and M dwarfs, a region of the HR diagram where the history of star formation is not important. With these stars being unevolved, this occurs because their density depends on the integral of the star formation rate (SFR) over the age of the disc and not on the detailed history of the SFR. Since the study of Haywood et al. (1997a) on the Hipparcos input catalogue, which showed that the SFR should be nearly constant or not varying by more than a factor of 3 over the age of the thin disc, we assumed a constant star formation for the thin disc in BGM. The A-F dwarfs, which constitute a large contribution to bright data sets, as Hipparcos and Tycho-2, are indeed very sensitive to the history of the SFR, and we concluded that it was necessary to specifically study this aspect using these dwarfs in the solar neighbourhood to get rid of the discrepancy of the BGM. In doing so, the Tycho-2 catalogue is the best homogeneous data set available for the whole sky and complete to about magnitude V ~ 11. This is the specific subject of the present study.
In the era of Gaia, a model able to analyse stellar population distributions to constrain Galaxy evolution would be very welcome. The BGM is in this respect a very useful tool and should be able to “measure” the star formation history in different regions of the Milky Way. However, the old scheme of BGM, based on the evolution scheme from Haywood et al. (1997a) does not have enough flexibility to change the IMF and SFR in the thin disc. Moreover, it does not allow us to generate binary stars easily. This is why we have undertaken the present work to modify the BGM code to be able to change these parameters easily to use different ones in different regions of the Milky Way if necessary and to account for stellar binarity at the same time. To test this scheme and to constrain the star formation history, the new code presented here has been compared and tested using the Tycho-2 catalogue and the local luminosity function (LF). We consider this as a first step for furnishing a reliable model for interpretation of future large scale surveys, such as Gaia, but also for RAVE, APOGEE, Gaia-ESO, and other future data.
In Sect. 2, the new approach and the overall structure of the code are presented. In Sect. 3, we present the observables and tools used in our analysis. In Sect. 4, we detail the model ingredients, which have been investigated. In Sect. 5, we show the results obtained from the multiple comparisons of our model with the Tycho-2 data and the LF; additionally it is our first check of how the new model reproduces deep star counts.
2. The new version of Besançon Galaxy model
In this work, we have focused on the Galactic thin disc; thus, the developments presented here concern the treatment of that population only. The thin disc population represents ~92−98% of the sample used in the present analysis. Work is in progress to apply the same scheme to other populations. For the sake of comparison to Tycho data, the other components, the thick disc, and the halo are simulated by single bursts of star formation, as in Robin et al. (2003), and the corresponding Hess diagrams are used, where the bulge is negligible locally.
2.1. A new approach to the BGM
2.1.1. The overall structure
The version of the BGM presented here is based on a new approach to the star simulation procedure. Rather than using a fixed Hess diagram, we have turned the IMF, SFR, and evolutionary tracks into free parameters. The model performs the star-creation process assuming an IMF, a SFR along the age of the Galactic disc, and an age–metallicity relation. Created stars follow a set of evolutionary tracks and may finish as remnants. To generate a simulated Galaxy from these fundamental buildingblocks, we have implemented important changes in the BGM code.
Figure 1 presents the scheme of the new model’s ingredients and the information they provide. First, we draw the mass, the age, and the metallicity of an object, according to the chosen functions. With the obtained values we search the location of the star in the HR diagram by interpolating the evolutionary tracks. If such a solution is found, then a star with the given L/L⊙, log g, and Teff is created. Using the atmosphere models, we then compute its observed parameters and include the extinction effects and optionally the estimations of the observational errors. From the a priori knowledge on the space density distributions, we know how much mass is to be converted into stars at various distances within the Galactic disc. Combining all this information, we get the picture of the thin disc at the present time. The stars for which a solution on the tracks was not found, meaning that the combination of their age and mass does not correspond to an alive star, are moved to the “remnants cemetery”.
A still missing feature in this new thin disc treatment is a correct treatment of white dwarfs, which we are not yet producing in a consistent way using their evolutionary tracks. This is left for future work. At the moment, they are produced following the scheme of the old model.
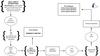 |
Fig. 1 General scheme describing the ingredients needed to build the evolutionary model and the information they provide. In italics we have marked the ingredients, which are under study, in this paper. |
2.1.2. Determination of the mass model
As explained in Robin & Crézé (1986), the definition of the mass density ρ(r,l,b,i) at heliocentric distance r in the direction of the galactocentric coordinates (l,b) for each age subcomponent i requires the following:
-
1.
an estimation of the mass density of each subcomponent at theSun position,
-
2.
a mathematical law capable of reproducing the trend of the density from the solar neighborhood to remote distances, and
-
3.
evaluations of both the scale heights and the scale lengths of each subcomponent to constrain free parameters of the mathematical expression.
As explained in Robin et al. (2003), the BGM thin disc is divided into seven age subcomponents. This division is maintained in the new model and could be easily changed to a larger number of subcomponents if required. Each supcomponent is modelled by the Einasto density law, as seen in Table 3 of Robin et al. (2003). It was chosen to represent the thin disc because it assures the continuity and derivability in the plane. The Einasto law ellipsoids are defined by a scale length and an eccentricity ϵ. The eccentricities for all disc subcomponents are obtained from dynamic considerations, as explained later in this section. Applying the Einasto law, we calculate the relative density at the (x,y,z) position. Depending on the age subcomponent and the user specifications, it may include the warp, flare, and spiral arms.
 |
Fig. 2 Normalization iterative process to derive the mass model. The local volume density |
The process of determining the mass model parameters is presented in Fig. 2. Block A is a local mass normalization, which provides the values of local volume mass density 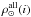 for each age subcomponent i. Block B is where we perform the simulations of the local neighborhood and derive the percentage of alive stars and remnants for each thin disc subcomponent. Thus, the procedure presented in blocks A and B simply splits the stellar local volume mass density
for each age subcomponent i. Block B is where we perform the simulations of the local neighborhood and derive the percentage of alive stars and remnants for each thin disc subcomponent. Thus, the procedure presented in blocks A and B simply splits the stellar local volume mass density 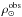 (at all ages) into seven disc subpopulations according to the SFR and includes the secular heating process to get
(at all ages) into seven disc subpopulations according to the SFR and includes the secular heating process to get 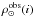 . In Block C, we impose the dynamical constraints to get the excentricities of the ellipsoidal density distribution ϵ(i) from the Boltzmann equation. The whole procedure is a normalization iterative process, which uses the observational and dynamical constraints, provides the values of
. In Block C, we impose the dynamical constraints to get the excentricities of the ellipsoidal density distribution ϵ(i) from the Boltzmann equation. The whole procedure is a normalization iterative process, which uses the observational and dynamical constraints, provides the values of 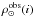 and ϵ(i), and that constructs the mass model to be applied in simulations in this way. Initially, some estimates are assigned to eccentricities ϵ(i) and to the local surface density
and ϵ(i), and that constructs the mass model to be applied in simulations in this way. Initially, some estimates are assigned to eccentricities ϵ(i) and to the local surface density 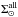 . Due to the subdivision of the thin disc into seven age subcomponents, the SFR is introduced into the model by the means of the intensity of star formation history at each epoch SFR(i). Block A requires two conditions to be fulfilled. The first one is that the surface density of each age subcomponent
. Due to the subdivision of the thin disc into seven age subcomponents, the SFR is introduced into the model by the means of the intensity of star formation history at each epoch SFR(i). Block A requires two conditions to be fulfilled. The first one is that the surface density of each age subcomponent 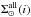 has to be proportional to the intensity of SFR in its corresponding age bin SFR(i), and the second one requires that the sum of calculated volume densities of all disc subcomponents
has to be proportional to the intensity of SFR in its corresponding age bin SFR(i), and the second one requires that the sum of calculated volume densities of all disc subcomponents 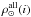 must fit the value of the imposed total volume density
must fit the value of the imposed total volume density 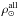 . When the iteration finishes we get the local volume density split into seven components
. When the iteration finishes we get the local volume density split into seven components 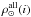 . Subsequently, we perform the simulations of a sphere around the Sun to get the values of the local volume density of alive stars split into seven components
. Subsequently, we perform the simulations of a sphere around the Sun to get the values of the local volume density of alive stars split into seven components 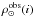 . In Block C, we treat the dynamics: this is where the disc eccentricities ϵ(i) are calculated and the dynamical self-consistency is ensured. The full description of this process is given in Bienaymé et al. (1987). The values of the velocity dispersion σW for each subcomponent i are adopted from observations (see Sect. 4.6). First, all mass components-thin disc
. In Block C, we treat the dynamics: this is where the disc eccentricities ϵ(i) are calculated and the dynamical self-consistency is ensured. The full description of this process is given in Bienaymé et al. (1987). The values of the velocity dispersion σW for each subcomponent i are adopted from observations (see Sect. 4.6). First, all mass components-thin disc 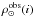 , thin disc white dwarfs
, thin disc white dwarfs 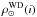 , thick disc ρthick, halo ρhalo, bulge ρbulge and interstellar medium ρISM-enter the Poisson equation and impose a potential Φ. Then the dark halo (ρDH) and bulge parameters are adjusted until the potential produces an acceptable rotation curve. The new potential combined with the velocity dispersions in the Boltzmann equation produce new values of ϵ(i) modifying the density distribution of each stellar component. The process is iterated until the mass model stabilizes by producing a self-consistent solution. It is important to emphasize that each time an evolutionary ingredient of the model changes (see Fig. 1) the mass model has to be rederived.
, thick disc ρthick, halo ρhalo, bulge ρbulge and interstellar medium ρISM-enter the Poisson equation and impose a potential Φ. Then the dark halo (ρDH) and bulge parameters are adjusted until the potential produces an acceptable rotation curve. The new potential combined with the velocity dispersions in the Boltzmann equation produce new values of ϵ(i) modifying the density distribution of each stellar component. The process is iterated until the mass model stabilizes by producing a self-consistent solution. It is important to emphasize that each time an evolutionary ingredient of the model changes (see Fig. 1) the mass model has to be rederived.
2.2. The code and its implementation
2.2.1. The thin disc treatment
The BGM provides star-counts prediction towards a selected direction in the sky. Either a line of sight or a zone can be simulated. The outermost loops of the new code have not changed, and as in Robin et al. (2003), they are the coordinates and distance loops. Together, they form the volume element loop; thus, stars are produced with distance steps while moving from the Sun until the chosen distance limit. In each volume element, the objects belonging to the basic Galactic components are generated. Here, we present and discuss the new thin disc treatment. We start with the general outline of the new code, which is sketched in Fig. 3.
The outermost loop of the thin disc treatment is the age loop. Each disc’s subcomponent – seven for the time being – simulates an age interval to cover the total disc age in fine resolution. In each age bin, the mass available to be spent on star production in a given volume element is the mass reservoir. It is the amount of mass that is expected to be found in stars at the specified position (volume element) according to the predefined evolutionary (IMF and SFR) and density (density laws) parameters. It is calculated from the expression 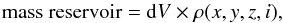 (1)where i denotes the thin disc age subcomponent. This equation is the backbone of the thin disc simulation.
(1)where i denotes the thin disc age subcomponent. This equation is the backbone of the thin disc simulation.
 |
Fig. 3 Organigram of the new model’s thin disc treatment. |
The densities ρ(x,y,z,i) are obtained taking into account the density law, SFR, and secular heating that corresponds to a given i-th subcomponent after performing the local mass normalizations. Then, the mass reservoir, which is calculated for a given volume element and disc subcomponent, is divided into three bins corresponding to three IMF ranges. By construction the model works with three mass ranges, and it allows the introduction of at most three-slope power law IMFs. This division is directly related to the power law description of the IMF,which is most commonly used in literature, and has proved to fit the observational data (Kroupa et al. 1993). In the future, other analytical functions, such as the ones proposed by Chabrier (2005), can be easily implemented as well. The drawing of the stars is done separately for each of the three mass intervals always by starting from the high mass bin (see the mass range loop in Fig. 3). To divide the mass reservoir into three parts that correspond to three IMF slopes, mass normalization factors are computed. They are presented later in this section.
At short distances from the Sun, the volume elements for a given line of sight are small. Consequently, the mass available to spend on stars is also small and could introduce a bias towards creating too many low-mass objects. Basically, whenever the mass is not sufficient to produce a more massive star, too many low mass ones are drawn instead, thus significantly biasing the shape of the IMF. To avoid that bias, we have implemented a correction for the small volume elements, as explained in Appendix A.1.
In each mass range, the star production proceeds until there is no more mass to convert into stars (null mass reservoir). We verify that there is no bias in the masses drawn in each mass range. Once the mass of an object is drawn from the given IMF, we check if the reservoir of mass is enough to create this object. The high mass bin corresponds to the long and steep tail of the IMF, so it can happen that a mass drawn for a star candidate exceeds the total mass available in that case, although resources are relatively big. A similar situation applies to the remaining two mass regions, but with a smaller rate of occurrence. Losing that mass would produce a bias in the mass distribution. To correct for that, we introduce a random drawing, according to Poisson statistics, to either generate or not this drawn star in the remaining mass reservoir, and we correct the reservoir value accordingly. We verify a posteriori that the drawn masses and the IMF are correct globally.
Once an object is created we assign to it an age and metallicity. The ages are drawn randomly from the uniform distribution in the interval of the given age subcomponent. The metallicity is drawn for each star from its own age, according to the age–metallicity relation adopted, while the mean age of the bin was assigned instead in the previous version of BGM. This results in a smoother age–metallicity relation in the resulting simulated stars.
When the age, mass, and metallicity are established, we interpolate the evolutionary tracks and find the position of the star in the HR diagram. If the solution is found, we consider that a star is alive, while the star is added to the remnant pool if a solution is not found. If the star is alive, its intrinsic parameters are calculated and then, according to a given probability, it is decided if that star is single or if it is the primary component of a binary system. Subsequently, the observables are assigned to that object and the extinction effect is included. Optionally, the observational errors are added, and the star is written to the catalogue. If the produced star was flagged as a primary, we create its secondary, place it on the evolutionary tracks, calculate its intrinsic parameters, and write it to the catalogue of secondaries. The mass of the second component is subtracted from the massreservoir. The merging of binary systems is performed later (see Sect. 2.2.2). We then keep producing stars subsequently from the three mass ranges as long as there is mass left in the given pool. The procedure continues for all age subcomponents and for all volume elements.
The IMF takes the form of three segments of power law, where for each one, 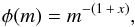 (2)where m is the mass, x is the slope and (1 + x) is also commonly denoted as the α parameter. Our code is designed to deal with three slope IMF. To get the mass locked within each mass interval one must solve ∫mφ(m)dm for all three ranges. The sum of those three numbers must be normalized to one. The relative mass locked within each mass interval, MInti is computed as follows:
(2)where m is the mass, x is the slope and (1 + x) is also commonly denoted as the α parameter. Our code is designed to deal with three slope IMF. To get the mass locked within each mass interval one must solve ∫mφ(m)dm for all three ranges. The sum of those three numbers must be normalized to one. The relative mass locked within each mass interval, MInti is computed as follows: 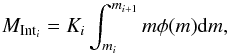 (3)where Ki are the continuity coefficients. The sum of those values is normalized to one, so when we multiply the mass reservoir (total mass within a given volume element) by each of them, we distribute the available mass over three ranges in a given volume element for a given subpopulation.
(3)where Ki are the continuity coefficients. The sum of those values is normalized to one, so when we multiply the mass reservoir (total mass within a given volume element) by each of them, we distribute the available mass over three ranges in a given volume element for a given subpopulation.
2.2.2. Binarity
The new BGM is able to generate binary systems. Binaries are implemented by following the scheme proposed by Arenou (2011), which is applied in the Gaia simulator (Robin et al. 2012a). The thorough explanation of the algorithm and the observational data, which were used to set the empirical relations adopted in this scheme, can be found in those articles. Here, we provide the general description of how that procedure was implemented in the model. It is presented in the core of the thin disc treatment in Fig. 3. Every new created star is decided to be a single or a primary component of a double system according to a probability, which depends on the object’s mass and luminosity class (see Sect. 4.3). If a star, which has just been created is determined to be a primary, we subsequently create its secondary using the following steps. The separation of the system is estimated from the probability distribution function of the semi-major axis derived empirically from observations (see Arenou 2011). The mass ratio statistics are also estimated from observations, which takes into account the spectral type of the primary and the binary period. We want to emphasize that we have preferred to apply the empirical law for the derivation of the mass distribution of the secondary stars instead of a theoretical imposed IMF. The small differences between these two approaches are evaluated in Appendix A.2. We assign the same age and metallicity to the secondary component as the primary object, and then it is placed on the evolutionary tracks and its intrinsic parameters are determined. We are not considering interacting binaries, which may follow different evolutionary tracks due to the presence of the companion. The secondary star is always found alive, since it has been already checked at this point that its primary, which is more massive, is alive.
After its creation, the system is randomly inclined with respect to the line of sight and then is projected on the sky. Subsequently, the angular separation is computed and the decision of whether the system is going to be a resolved or unresolved binary system depends on the imposed resolution of the catalogue.
It must be emphasized that the constraint on the local stellar mass density is conserved when generating the binaries. It is a strong advantage of the new BGM scheme that the total mass is constrained previously to simulations through the dynamical self-consistency calculations. This means that the mass is established before and after the stars, whether single or double, which are created from the available mass reservoir.
2.3. New processing modes
The BGM has several different modes in which simulations can be performed. There was a strong need for performing volume limited simulations in the solar neighbourhood, especially when reproducing the local observed LF and calculating the SFR normalization in a cylinder. For that, we have incorporated two new processing modes in the model: we can simulate a sphere (with a constant spatial density) or a cylinder centred at the Sun position and perpendicular to the Galactic plane. The spherical volume element is used to calculate the synthetic LF and compare it to the observed one. Using a cylinder mode, we have tested the algorithms of star production and checked if we are able to reproduce the imposed theoretical SFR integrated in the perpendicular direction z.
3. Observed data sets
We decided to compare simulations by two observational sets: the Tycho-2 data up to the magnitude VT = 11.0 and the single star luminosity function LF. In the first case, we were interested to compare the simulated star counts and the (B − V)T distributions with Tycho-2 data over the whole sky. In the second case, we have performed the simulations of the local sphere (see Sect. 2.3) for each model and obtained the synthetic LF, which were compared with the observed LF.
3.1. The Tycho-2 Catalogue
The Tycho-2 catalogue (Høg et al. 2000) provides positions, proper motions, and BT and VT magnitudes of the 2.5 million brightest stars across the entire sky. Stars until magnitude VT ~ 11.0 were chosen ensuring a completeness of 99 percent up to this magnitude (864 816 stars). We decided to work in the space of observables, so we transformed our simulations done in the Johnson photometric system into the Tycho system. Different photometry transformations were evaluated (see Appendix B).
As it is shown in Sect. 5, Tycho data shows a bi-modal colour distribution. In the blue peak, we mainly have B, A, and F type main-sequence stars, which are on average young, while the red peak is dominated by giant stars covering a wide age range. Most of the stars fall within the absolute magnitude range − 1 <MV< 5 mag.
To reduce the computational time, the systematic comparison between simulated and Tycho-2 data was done by considering three established reference regions: the whole Galactic north pole at b> 70°; the region at intermediate latitude at 160°<l< 180° and 20°< b < 40° and the region within the plane at 70°< l < 90° and –10°<b< 10°. These regions have been selected to be representative of the full longitude range at the corresponding latitude, meaning that their colour distribution shows the same characteristics as one of the full longitude stripes at the specified latitude. In addition to these regions, whenever a more general comparison was required, a whole-sky analysis was performed and eventually, sky maps of mean colours and relative number of objects was produced.
3.2. The local luminosity function
Three observed LFs have been considered: Jahreiß & Wielen (1997), Kroupa (2001), and Reid et al. (2002). All of them are the LF of single stars. Whereas Kroupa (2001) and Reid et al. (2002) provide only the LF for the stars on or near the main sequence, Jahreiß & Wielen (1997) also provides the total LF, which included the evolved stars. Differences among them are observed at both, the bright end and faint end of the LF.
As we work with Tycho data, we are interested in the bright side of the LF, that is, at MV< 5. In this region, although the Hipparcos survey provided completeness at a 25 pc distance limit, one can notice some differences in LFs from different authors. These differences reflect Poisson uncertainties and are mainly attributed to the slightly different volume considered by each author.
4. Model ingredients
In this section, we describe the analytical expressions and the empirical relations tested for all the model ingredients detailed in Table 5. As indicated in Fig. 2, a new mass model was derived and the Galactic gravitational potential was recalculated when any of the model’s ingredients listed in the top boxes of Fig. 2 were changed.
4.1. The initial mass function and star formation history
Table 1 lists the eleven IMFs, which were tested in our study. All the considered IMFs are power-laws (see Eq. (2)), which differ only in the number and values of slopes and the corresponding mass ranges.
List of eleven IMFs applied in our simulations.
From literature, we considered the following six IMFs: Scalo (1986), Haywood et al. (1997a), Haywood et al. (1997b) with a corrected slope at the low masses as proposed by Robin et al. (2003) (hereafter called Haywood-Robin IMF), Vallenari et al. (2006), Kroupa (2008), and Just & Jahreiß (2010). We extended the low mass range of Vallenari et al. (2006) IMF from 0.2 to 0.09 M⊙. After several tests, we proposed five new IMFs, which are different combinations of Kroupa (2008) at low masses and Haywood et al. (1997b) at high masses. To merge the two functions, we looked for their intersection above 1 M⊙. It was found to be at 1.53 M⊙. The IMF called KH-v1 (from Kroupa-Haywood version 1) keeps the IMF of Kroupa (2008) below that value and the Haywood et al. (1997b) above. Subsequently, other IMFs were defined by slightly changing the slopes and/or the limiting masses. Table 1 presents the five that provide a better fit to Tycho data.
Constant and decreasing SFRs are considered. To test a declining scenario, we used two approaches. We considered the Aumer & Binney (2009) simple exponential function SFR(τ) ∝ exp(−γt), where γ is a parameter and t is time with γ to be 0.12 (one of the Aumer & Binney (2009) good fits). As a second approach, we took the more complex expression proposed by Just & Jahreiß (2010). Those two decreasing SFRs are depicted in Fig. 4.
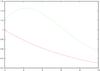 |
Fig. 4 Two decreasing SFRs as a function of time t. SFR of model A by Just & Jahreiß (2010) (dashed green line) and (Aumer & Binney 2009) single exponential with γ = 0.12 (solid red line). Normalizations are arbitrary. |
4.2. Evolutionary tracks sets
Table 2 lists the different sets implemented in the BGM since 1986. As mentioned in Fig. 2, we tested two evolutionary tracks sets named package E1 and E2 (see Table 2). Package E2 uses Bertelli et al. (2008) tracks for masses ≥0.7 M⊙, and Chabrier & Baraffe (1997) tracks at lower masses.
Evolutionary tracks used in subsequent versions of BGM.
4.3. Binarity
To compare our simulations with Tycho-2, data a spatial resolution of 0.8 arcsec was assumed, meaning that all the binary systems generated below this angular separation were considered as unresolved. We have checked that values of 0.5 or 1.0 arcsec do not change much colour histograms as most of the simulated binaries turn out to have much smaller separations.
4.4. The local stellar and ISM mass densities
In our model, the local stellar mass density of the thin disc component is a critical parameter (see Fig. 2). In Table 3, we present the most used values derived from observations: Wielen (1974), hereafter referred as LMD1, and Jahreiß & Wielen (1997), which are obtained using Hipparcos data and are referred here as LMD2. As can be seen in Table 3, this last value is in good agreement with the value derived by Reid et al. (2002), which is also from Hipparcos data. We varied only the density corresponding to main sequence and giant stars (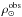 ), which maintains a value 0.007 M⊙ pc-3 for white dwarfs in both cases. Thus, the tested values for
), which maintains a value 0.007 M⊙ pc-3 for white dwarfs in both cases. Thus, the tested values for 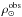 are 0.039 M⊙ pc-3 (LMD1) and 0.033 M⊙ pc-3 (LMD2). The way in which the local stellar mass density is distributed over the seven subcomponents of the thin disc is illustrated in Fig. 2.
are 0.039 M⊙ pc-3 (LMD1) and 0.033 M⊙ pc-3 (LMD2). The way in which the local stellar mass density is distributed over the seven subcomponents of the thin disc is illustrated in Fig. 2.
In Robin et al. (2003), the mass density assumed for the interstellar medium was 0.02 M⊙ pc-3. In the present work, we change that value to 0.05 M⊙ pc-3 as proposed by Binney & Tremaine (2008). As it is known, this parameter is very uncertain and its influence in the process of the derivation of the total dynamical mass is discussed in Sect. 5.4.
Values of the thin disc local stellar volume mass density derived from observations (units: M⊙ pc-3).
4.5. Atmosphere models
Three different sets of atmosphere models were tested: the BaSeL 2.2 (Lejeune et al. 1997, 1998), BaSeL 3.1 (Westera et al. 2002), and the giant MARCS grid (Houdashelt et al. 2000). In the last case, MARCS models for giants were combined with BaSeL3.1 for other stars.
4.6. Age–metallicity and age–velocity relations
Two age–metallicity relations have been considered, the one from Twarog (1980, used in the old model) and the one proposed by Haywood (2006). Twarog’s relation assigns significantly lower metallicities than Haywood’s one. Straight lines were fitted to both relations and dispersion curves. We checked that the new mechanism (see Sect. 2.2.1) of assigning the metallicity diminishes the step-like form and smooths out the resulting relation. The intrinsic scatter of the metallicity is taken into account. The scatter has a specific value for each age and follows the relation given by Haywood (2006) in his Fig. 13c. This scatter is increasing with age, a trend that has been interpreted as due to the pollution by stars that come from both the inner and outer disc (Haywood 2008; Haywood et al. 2013).
Table 4 shows the values of the two age–velocity relation (AVR) tested here, the Gómez et al. (1997) relation, used in the old model, and the new Holmberg et al. (2009) relation, which have significantly higher velocity dispersion perpendicular to the plane, for the old disc.
Comparison of the age–velocity dispersion relation by Gómez et al. (1997) and Holmberg et al. (2009).
4.7. The age of the thin disc
In the old BGM, the age of the formation of the thin disc was set to 10 Gyr. Two more values, the values of 12 Gyr (one of the favoured values by Aumer & Binney (2009)) and 9 Gyr, proposed by del Peloso et al. (2005), who derived an age of 8.8 ± 1.7 Gyr from Th/Eu nucleocosmochronology were tested here.
4.8. The thick disc
As described in Reylé & Robin (2001), the thick disc density law is assumed to be a truncated exponential characterised by three parameters: hz the scale height, ρthick the local density and xl the distance above the plane, where the density law becomes exponential. Reylé & Robin (2001) have shown that there is a degeneracy in the parameter determination because the local density and the scale height are anti-correlated when using star counts at high latitudes as constraints. Hence, they consider a family of solutions having a fixed parameter df ∝local density 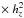 . We have tested two solutions here: model TkD1 with hz = 1200 pc, xl = 72 pc, and 7.23 × 10-4M⊙ pc-3 and model TkD2 with hz = 800 pc, xl = 400 pc, and ρ0 = 2.9 × 10-3M⊙ pc-3. The xl parameter is fitted using the Boltzmann equation. The metallicity assumed for the thick disc is –0.48 dex and the dispersion is 0.30. The comparison of the two presented models is shown in Sect. 5.6 and discussed in Sect. 6.
. We have tested two solutions here: model TkD1 with hz = 1200 pc, xl = 72 pc, and 7.23 × 10-4M⊙ pc-3 and model TkD2 with hz = 800 pc, xl = 400 pc, and ρ0 = 2.9 × 10-3M⊙ pc-3. The xl parameter is fitted using the Boltzmann equation. The metallicity assumed for the thick disc is –0.48 dex and the dispersion is 0.30. The comparison of the two presented models is shown in Sect. 5.6 and discussed in Sect. 6.
4.9. Extinction model
Both the Drimmel & Spergel (2001) and the Marshall et al. (2006) extinction models are implemented in the BGM. Marshall et al. (2006) covers only the region –100°< l < 100° and − 10°< b < 10°, whereas the Drimmel & Spergel (2001) extinction model covers the full sky and has saturation problems in the complex regions near the Galactic centre.
4.10. Radial scale length
In the old model, the values of radial scale length were fitted to hR = 5000 pc for the young disc subpopulation (τ< 150 Myr) and hR = 2400 pc for older stars. We shall refer to these values as model SL1. To check the influence of this parameter, alternative values were tested. A large scale length for the young population was implemented: hR = 5500 pc for the stars with τ< 150 Myr; hR = 5000 pc for stars with 150 Myr <τ< 1 Gyr; hR = 3500 pc for 1 Gyr <τ< 2 Gyr and hR = 2400 pc for τ> 2 Gyr (model SL2). The aim was not to adjust the scale length of the thin disc, which would be difficult with Tycho data only, but to test its influence in the present analysis on the star counts and colour distribution within the Galactic plane.
5. Results
5.1. The old model vs. Tycho-2
Figure 5 presents the comparison between the colour distributions from the old BGM from Robin et al. (2003) and from Tycho-2 data. The ingredients of the old model are presented synthetically in the second column of Table 5. When comparing the old model to Tycho-2 data, one notices several important discrepancies:
-
1.
The red peak of the modelled (B − V)T distribution is shifted by about 0.2 mag to the red.
-
2.
The excess of the total number of stars: the model produces two times more stars than the Tycho-2 sample.
-
3.
The excess of the blue stars around (B − V)T ~ 0.15 mag.
 |
Fig. 5 Whole sky (B − V)T distributions of the old model (solid grey line) and Tycho-2 data (dashed green line). |
Most important ingredients of the old and new model, which have been analysed.
5.2. Defining a default model
Our strategy was to analyse the impact on the results when each of the ingredients presented in Sect. 4 was changed independently from the others. We must emphasize that several ingredients are highly correlated. Thus, we also study the combinations of parameters which are correlated, for example, the IMF, SFR and the local mass density. A detailed analysis, simulations of different regions, and comparisons with Tycho-2 data allowed us to establish and justify the composition of a default model, defined as a combination of a new set of ingredients that significantly improve the fit to Tycho data. In the third and fourth columns of Table 5, we present the list of these ingredients. We present two default models, A and B because there are two IMFs that we favour, as shown later on in Sect. 5.5. As we found that the IMF is correlated with the local stellar mass density, our default models assume different values for these two ingredients. The differences are indicated by model A and B in lines corresponding to the IMF and local stellar mass density. The remaining model components presented in the third column are the same for the default model A or B. In subsequent sections, we show how each model ingredient influences the results and by presenting the best fit to data for each of them we justify the values chosen to compose our default models.
As the investigation of different combinations of IMF and SFR in solar neighbourhood was the central point of our study, it is extensively discussed in Sect. 5.4. For other ingredients, we checked two or three different scenarios, while the updated ingredients (evolutionary tracks, binarity, atmosphere models, and ISM local density) are systematically considered. The implementation of binarity is undoubtly an important update. The fraction of multiple stars in our Galaxy is still unknown, however, most studies suggest that binaries can account for about 50% of the total stellar content of the Milky Way (Arenou 2011). Nevertheless, the simulations without binaries are also presented to study the effect of simulating systems. All analysis were made by comparing star counts and (B − V)T colour distributions between data and simulations. For each test, new simulations were performed in one of the reference regions presented in Sect. 3.1. The simulations within the Galactic plane, at intermediate latitudes, or at the Galactic pole were done depending on where the expected effect is stronger. Colour histograms were plotted always in the same range and with the same number of bins. To evaluate quantitatively the effect of assigning different values to each ingredient with respect to Tycho-2 data, we have applied a χ2-type statistics test. Two different tests were used to check: to evaluate the adequacy of the stellar densities globally and to test the shape of the colour distribution, which is sensitive to the relative star densities as a function of mass and age. Considering that Ri stands for the counts in the model histogram and Si for the counts in the Tycho-2 histogram, and Nbin is the number of bins. We apply the following:
-
Definition of χ2 as used to test the null hypothesis that a given dataset has been drawn from a given distribution,
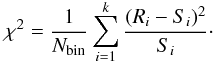 With this definition, we are taking the approximation that the Tycho-2 histograms can be used to exactly represent actual distribution, and, thus, use them as an absolute reference (we assume that the Tycho-2 data set is complete). In this case we are checking the absolute number of objects per bin with respect to the Tycho-2 data.
With this definition, we are taking the approximation that the Tycho-2 histograms can be used to exactly represent actual distribution, and, thus, use them as an absolute reference (we assume that the Tycho-2 data set is complete). In this case we are checking the absolute number of objects per bin with respect to the Tycho-2 data. -
Definition of χ2 as used to test the null hypothesis that two datasets have been drawn from the same underlying distribution,
 This definition allows to check the similarity of the shape of the two histograms but does not take into account the differences in the total number of stars. Thus, this test is of secondary importance but helps to analyse the normalized shapes of the resulting (B − V)T distributions.
This definition allows to check the similarity of the shape of the two histograms but does not take into account the differences in the total number of stars. Thus, this test is of secondary importance but helps to analyse the normalized shapes of the resulting (B − V)T distributions.
Table 6 presents the results of both tests for different model ingredients as discussed in the following sections. They are divided into three groups: the first group concerns the disc evolution ingredients, the second the updated ingredients, and the third one the additional tests. In the second column, we specify the region of the sky where the simulations were performed. Options (1) and (2) in the third and fourth column stand for two different values of a given model ingredient that are compared. In some cases, more than two values were tested; however, this table provides a general information about the representative examples and a more detailed comparison is explained later on in this section. To construct Table 6 and for the sake of the more detailed analysis presented in the following sections, all simulations were performed with the default model B. Only when testing the extinction models, both default models A and B were checked. For the IMF, just an example of comparison is presented in the table, as it is extensively discussed in Sect. 5.7. Three different values of the thin disc age were tested, which are presented in two rows. The two values for each ingredient; (1) and (2), are tested against Tycho-2 data (T).
5.3. Updating a first set of model ingredients
Here, we discuss how the updates of the atmosphere model, the evolutionary tracks, the binarity treatment, and the age–metallicity relation have significantly improved the position of the red peak. In Fig. 6, we compare simulations using BaSeL 2.2 and BaSeL 3.1 atmosphere model libraries. The use of the new BaSeL 3.1 library moves the red peak by more than 0.1 mag towards bluer colours, improving the fit to Tycho-2 distribution, as seen in the figure and in the statistics test in the Table 6. We have checked that the improvement is observed at all Galactic latitudes. The MARCS models for giants, when applied, produce a red peak in between the peaks given by the two BaSeL libraries, which is not red enough for a good fit to Tycho data. From Fig. 6 and the χ2 statistics, it is clear that BaSeL 3.1 makes the BGM fit Tycho-2 data much better.
The χ2 tests for eleven model ingredients with respect to the Tycho-2 data.
 |
Fig. 6 Testing atmosphere models. (B − V)T distributions in the reference region at intermediate latitudes. Tycho-2 data (dashed green line) is compared with the simulations obtained with the default model B and BaSeL 3.1 library (solid blue line) and the default model B and BaSeL 2.2 (dotted red line). |
The update of the stellar evolutionary tracks from those used in Robin et al. (2003) to the package E1 and E2 (Table 2) was a necessary improvement to take into account better physics in stellar models. When trying both packages, the resulting colour histograms differ slightly in the red peak of the colour distribution such that the package E2 leads to 13% less stars in the red peak than when package E1 is used. The results of the χ2 tests show a slight improvement when using E2 package, which justifies to use the new tracks from Bertelli et al. (2008) and Bertelli et al. (2009) in the default model (package E2).
The age–metallicity relation plays also an important role on the position of the giants peak. Table 6 shows that the new Haywood (2006) relation clearly reproduces the Tycho-2 data better. It performs better in both the blue and the red peak. It is possible that an intermediate age–metallicity relation could fit data even better, although the differences in the counts are small in regard to the effect of other parameters.
Contribution of all mass components (in M⊙ pc-3) to the total dynamical mass in the default models A and B.
5.4. The dynamical mass and the age–velocity relation
As shown in Fig. 2, the dynamical mass density and the age–velocity relation (AVR) are the most significant input parameters derived from observations that enter into the process of dynamical self-consistency (see Block C in Fig. 2). However, the total local dynamical mass is not directly imposed in the model but it is obtained summing up all mass components. If the assumption about the input value of any mass component changes the total dynamical mass also changes. The estimation of the local dynamical mass density by Crézé et al. (1998) was 0.076 ± 0.015 M⊙ pc-3. Holmberg & Flynn (2000) derives it to be 0.102 ± 0.010 M⊙ pc-3 and similarly Korchagin et al. (2003) gives 0.100 M⊙ pc-3, while van Leeuwen (2007) proposes a bit higher value 0.122 ± 0.019 M⊙ pc-3. Table 7 presents the contribution of all mass components to the total dynamical mass density obtained here in case of both default models. In italics, we give the components whose density is an input value taken from external studies not adjusted in this study. The thin disc local mass density took two values derived from observations 0.039 M⊙ pc-3 (LMD1) and 0.033 M⊙ pc-3 (LMD2). The best fitted thick disc density was set to 2.9 × 10-3M⊙ pc-3 (see Sect. 5.6), and for the stellar halo, we fixed 0.92 × 10-5M⊙ pc-3. As can be seen in Fig. 2, the local mass density of the dark halo is recomputed each time in the iterative process. The values of the local dark matter density derived in case of model A and B are 0.01051 and 0.01085M⊙ pc-3, respectively. They are only slightly higher than 0.008 ± 0.003 M⊙ pc-3 proposed by Bovy & Tremaine (2012) and 0.0075 ± 0.0021 M⊙ pc-3, which is recently obtained by Zhang et al. (2013) using SDSS/SEGUE data. Our values are at less than 2σ from the values derived by these authors. They also agree with the values 0.012 M⊙ pc-3 derived by Bienaymé et al. (2006) from the kinematics and 0.008 M⊙ pc-3 obtained by de Boer (2005) from diffuse Galactic gamma rays for a spherical dark halo. This parameter is still much uncertain as discussed in Burch & Cowsik (2013). These authors perform a self-consistent calculation of the spatial distribution of dark matter and try to contrain it by comparing it with kinematic observables. They find the local dark matter density to be greater than the recent estimates: 0.015 and 0.019 M⊙ pc-3. Depending on which local stellar volume mass density was assumed for the thin disc, the total dynamical mass density slightly changes. However, by taking into account the error bars, both values are in a good agreement with the results of Holmberg & Flynn (2000) and Korchagin et al. (2003). Undoubtedly, the derived values are highly dependent on the density assumed for the ISM (see Sect. 4.4).
The age–velocity dispersion relation (AVR) investigation is presented in Fig. 7 and Table 6. It shows that the Gómez et al. (1997) AVR leads to better results at the Galactic pole than the Holmberg et al. (2009) AVR. The latter produces too many giants and bright stars within the Galactic plane.
 |
Fig. 7 (B − V)T distributions towards the Galactic north pole showing the effect of changing the age–velocity dispersion relation (AVR) against the default model B. Tycho-2 data (dashed green line) and the simulations based on the default model B (solid blue line) are shown. The dotted red line is based on simulations using an AVR of Holmberg et al. (2009) rather than of Gómez et al. (1997) but leaving all other parameters unchanged. |
5.5. Ingredients for star generation in mass and time
As expected, the IMF, SFR, and the local stellar volume mass density are very correlated; this is why we studied these three ingredients collectively. In this section, we also discuss the effect of binarity on the simulations. Different combinations were tested using two approaches. The first one was to compare the synthetic LF produced by the given combination with the observed LF. The second step was to check the fitting of the obtained simulations to Tycho-2 data.
5.5.1. Comparison with the LF
When fitting the local LF, we have considered the total LF from Jahreiß & Wielen (1997) data. The procedure of comparing the synthetic and observed LFs was repeated for all tested combinations of eleven IMFs, four SFRs (Sect. 4.1) and two values of the local stellar volume mass density (Sect. 4.4). For some of the combinations, we also have performed a secondary test that excludes the giants from the simulations and compares them to the Kroupa (2001) and Reid et al. (2002) luminosity function of main sequence stars.
Using both values of the local stellar mass density, the LMD1 and LMD2, the constant SFR was tested along with all eleven IMFs proposed in Table 1. Most IMFs combined with a constant SFR produce many more bright objects than the observed LF, except for two of them, the Haywood-Robin and Kroupa (2008) IMF, for which the solution agrees with the observational LF from Jahreiß & Wielen (1997). As shown in Sect. 5.5.2, Tycho-2 data turns out to be an even stronger constraint when evaluating constant SFR.
Secondly, all IMFs were combined with a decreasing SFR and both values of the local stellar volume mass density. In most cases when using the LMD2, the simulated LFs have a better fit to data than when we assume the LMD1. Some of the combinations led to a good fit in one range of magnitudes and a bit worse in the other. This is the case of Kroupa (2008) IMF. This function fits well the observed LF in the range of bright magnitudes. However, in the region of 4 <MV< 8 mag, the default models A and B give a much better fit than the combination with Kroupa (2008) IMF. The Vallenari et al. (2006) IMF combined with a decreasing SFR and two values of the local stellar volume mass density always produces a LF above the observational values.
In Fig. 8, we present the comparison of the observed LF with the synthetic LF, as obtained with the default model B (Table 5) and two values of the local stellar mass density, LMD1 and LMD2 (in both cases simulations with and without binaries). As expected, changing the value of the local mass density from LMD1 to LMD2 shifts the whole LF downward. Binarity produces a second order effect, which is discussed in the comparison with Tycho data (Sect. 5.5.2).
In Fig. 8, it is shown that the default model B with the Kroupa-Haywood v6 IMF and a decreasing SFR (Aumer & Binney (2009)) reproduces better the local LF in the range of absolute magnitude [4;12] when using the LMD2 than when the LMD1 is applied. At the bright tail of the LF, both solutions are within the big error bars. Performing the same comparisons with the default model A, LMD1 provides a LF, which is closer to the observations. TIn the following, we consider two default models, the model A (Haywood-Robin IMF) with LMD1 and model B (Kroupa-Haywood v6 IMF) with LMD2. Figure 9 shows the comparison of the total and main-sequence LFs produced by the default model A with the observations.
 |
Fig. 8 Comparing the observed LF with the synthetic LF that is obtained with the default model B and two values of local stellar mass density, LMD1 and LMD2 (in both cases simulations with and without binaries). Total LF from Jahreiß & Wielen (1997) (red dots), main sequence LF from Kroupa (2001) (black triangles), and Reid et al. (2002) (black dots) are shown. |
 |
Fig. 9 Comparison of the observed LF with simulated one from model A: total LF (solid blue line) and main sequence LF (dashed magenta line). Symbols for observed data are same as in Fig. 8. |
 |
Fig. 10 Testing a constant and decreasing SFR with different IMFs. All three panels show the (B − V)T distributions of the reference region within the Galactic plane. Tycho data in all panels is plotted using dashed green line. The top panel corresponds to Kroupa (2008) IMF, the middle to Haywood-Robin IMF and the bottom to Kroupa-Haywood v6 IMF (see Table 1). In red dotted line the simulations, which are obtained with constant SFR, and in solid yellow, orange, and blue lines, the simulations obtained with the decreasing SFR of Aumer & Binney (2009) and each IMF respectively. |
Taking into account big error bars at the bright and faint ends of the observed LF, we can conclude that most of the model LFs do not differ much from the observations. However, in the following section we show that this conclusion arises from the uncertainties on the local luminosity function mainly due to Poisson statistics for bright stars. In next section we show that Tycho-2 data gives stronger constraints and are able to distinguish between several hypothesis on the IMF. As an example, the default model with IMF changed to the one of Scalo (1986) and the LMD2 local density fits well the Jahreiß & Wielen (1997) LF for MV< 8 mag, but it does not fit well the Tycho-2 (B − V)T distribution. Most of the Tycho-2 sample covers the range of absolute magnitude MV = [−1,5]. It includes the region where the LF has large error bars (MV< 3).
5.5.2. Comparison with Tycho-2 data
The (B − V)T colour distributions of Tycho-2 data allow us to distinguish the blue main sequence stars from the giants, while they are both at about the same absolute magnitude in the LF. Figure 10 presents the colour distributions when three IMFs were combined with a constant and a decreasing SFR. When Kroupa (2008) and Kroupa-Haywood v6 IMFs are combined with a constant SFR, many more blue (on average young) objects are produced than when a decreasing SFR is applied. In the case of the Kroupa-Haywood v6 IMF and both SFRs, we have performed a χ2 statistics presented in Table 6. There is a clear improvement of the fit when assuming a decreasing SFR. Only when the Haywood-Robin IMF is combined with the constant SFR, the excess of the blue stars is small. For all other IMFs that we have tested, the excess of blue stars is very significant and, in some cases, even bigger than presented in Fig. 10 (for example Scalo (1986) and Vallenari et al. (2006) IMF). We conclude that we are getting unrealistic star counts on the blue part of the (B − V)T distribution within the Galactic plane when imposing a constant SFR along with eleven IMFs that we tested. Only in the case of Haywood-Robin IMF, this excess of stars is less significant. Tycho data strongly favour a decreasing SFR. This is most likely one of the main reasons of the disagreement between the old model and Tycho data.
Then, we have combined all tested IMFs with the decreasing SFR from Aumer & Binney (2009). The IMF from Just & Jahreiß (2010) was additionally combined with their best fit SFR (see model A from their paper). We refer this combination of SFR and IMF as the Just & Jahreiß (2010) best fit. The details of the analysis made for all IMFs are presented in Czekaj (2012). Many of the combinations led to a significant excess of the blue and bright stars within the Galactic plane (in particular Scalo (1986), Kroupa (2008), Vallenari et al. (2006) and KrH v8 IMFs). Other IMF produced far too few objects (KrH v1, KrH v4 and Haywood et al. 1997a).
 |
Fig. 11 Testing different IMFs. The (B − V)T distributions correspond to the (top) entire Galactic plane | b | < 10, (middle) entire stripe of the sky at 10 < | b | ≤ 30, and (bottom) the stripe of the sky at 30 < | b | ≤ 90. In dotted orange line the simulations, which are obtained with the default model A (Haywood-Robin IMF); in solid blue line we have the default model B (Kroupa-Haywood v6 IMF), and the default model combined with the best fit SFR and IMF from Just & Jahreiß (2010) is in dash-dotted magenta line. The Tycho-2 data is in dashed green line. |
The best fit was obtained when Haywood-Robin and Kroupa-Haywood v6 IMF were combined with a decreasing SFR of Aumer & Binney (2009). These two combinations were used in default models A and B respectively (see Table 5). The best fit SFR and IMF from Just & Jahreiß (2010), as combined with the default model (for the rest of the ingredients) (hereafter the JJ model) also provides a good solution. In Fig. 11, we show the whole sky (B − V)T distributions obtained with the two default models and the JJ model. These distributions were divided into three latitude ranges corresponding to Galactic plane, intermediate latitudes and the Galactic poles. At the intermediate latitudes, the best fit is provided by the model B, and at the Galactic poles, both the model B and the JJ model are the best. It can be seen that Haywood-Robin IMF (model A) fits the star counts of Tycho-2 within the Galactic plane the best. However, the fit provided by model B is one of the best when compared to all other tested IMFs. The JJ model produces more stars than the model B. When looking at the Galactic plane, we can notice that there are still some discrepancies present. The Galactic plane is where many different factors interplay and finding a good fit is a very complex task (see Sect. 5.6).
 |
Fig. 12 Testing binarity. (B − V)T distribution in our reference region within the Galactic plane. Tycho-2 data (dashed green line), the simulations obtained with the default model B and binarity (solid blue line) and simulations with the default model B without binarity (dotted red line) are shown. |
In Fig. 12, we present the simulations with and without binaries. As expected, when adding binarity, we increase the number of objects at the low-mass tail of the LF and decrement the high masses, as also seen on the LF in Fig. 8. One notices the decrease of star counts in the simulations with binaries in Fig. 12. This is because the stars up to magnitude VT ≤ 11 correspond to the bright end of the LF. As can be seen in this figure, the simulations with binaries give a better fit to Tycho-2 distribution, although we have to take into account that we are testing this parameter here independently from the others. We have also checked the number of produced binaries in the whole sky simulations. As expected, the percentage of created binaries is the same for both default models. In the whole sky sample, 45% of stars are unresolved binaries, 12% are resolved systems, and 35% are single stars (the rest are thick disc stars).
5.6. Additional tests
In this section, we discuss more ingredients that are critical within the Galactic plane. Work is in progress to constrain them using additional data sets.
Two extinction models (Sect. 4.9) were compared in the stripe at | l | <100 and | b | <10. As can be seen in Fig. 13, the difference in star counts is significant. It is possible that the Marshall et al. (2006) extinction model underestimates the absorption at the very short distances, what could be caused by the lack of data in the local sphere (they used K giants from 2MASS and these stars are very few at short distances). This could explain the excess of blue stars. On the contrary, the Drimmel & Spergel (2001) extinction model produces a deficiency of giant stars and a shift of their peak to redder colours. This could be explained by an overestimate of the extinction at large distances. From the χ2 test (Table 6), it seems that the general fit obtained with Marshall et al. (2006) extinction model is worse, although it performs better in the red peak. Changing the extinction model in only the Galactic plane stripe | l | < 100 and | b | < 10 leads to a change in the all sky star counts, which reaches ~10% for the bluest and bright objects ((B − V)T< 0.4). As expected, the extinction model is a crucial input of BGM. However, several parameters influence the star counts within the plane. Complementary analysis would be needed to derive any sensible conclusions.
 |
Fig. 13 Testing two different extinction models. The presented (B − V)T distributions correspond to a part of the Galactic plane | l | < 100 and | b | < 10. Top: default model A. Bottom: default model B. Two different extinction models are also used: dotted red line is Drimmel & Spergel (2001) (in both cases), solid orange line is model A with Marshall et al. (2006), solid blue line is model B with Marshall et al. (2006) and dashed green is Tycho data. |
We now explore the effect of the age adopted for the thin disc. It appears that the effect is sensitive to different values when we look at different latitudes. At the Galactic pole, the samples simulated with 9, 10, and 12 Gyr behave similarly in the blue peak, while the solution obtained with 12 Gyr produces more old stars and fits better Tycho-2 data in the red peak. This is due to the fact that older stars have a larger scale height following the increase of the velocity dispersion. At intermediate latitudes, the same effect is visible but then the number of giants is larger than in Tycho sample. At these latitudes the best solution is provided by simulations with a 9 Gyr or 10 Gyr old thin disc. In the Galactic plane, the difference between the three ages are very small, as seen in the χ2 tests (Table 6). The differences are mostly observed in the blue peak, while the giant peak is nearly insensitive to this parameter. If one extends the age of the thin disc to 12 Gyr, stars that are a bit less blue and young are produced within the plane, which makes the fit to Tycho-2 data slightly better. However, the Galactic plane is a problematic region, where extinction, spiral arms and many other effects can play and compensate the effect of the age. Hence, we keep the conservative value of 10 Gyr, which provides the best fit to intermediate and high latitudes.
The Tycho-2 data do not reach large distances (from the solar neighbourhood) giving relatively poor constraints on the radial scale length, as compared to more remote star counts. The χ2 tests in Table 6 show that the change, as expected, is negligible towards the rotation but is significant towards the Galactic centre (main sequence) and anticentre (giants). As the new scale length improves in one case and degrades in the other, it might be due to another effect, which plays at low latitudes. We thus keep the default value.
Finally, two different sets of thick disc density parameters (Sect. 4.8) have been tested in simulations and compared to Tycho data. As we are limited to VT = 11, the thick disc provides a small contribution to the whole sky statistics: the relative number of thick disc stars in our sample is 7.3% for the Reylé & Robin (2001) best fit model and only 2% in the other case. The model that assumes a larger local density for the thick disc provides a better fit to Tycho-2 data, as shown by the χ2 tests, in Table 6. It fits better the red giants peak and significantly contributes at intermediate colours in between the peaks. Deriving a firm conclusion about the thick disc parameters requires a specific analysis of large scale surveys.
5.7. Looking for the best fit with Tycho-2 data
In Fig. 14, we present the whole-sky (B − V)T distributions of the two new default models, the old model and Tycho-2 data. Notice the enormous changes in the (B − V)T histogram of the new model with respect to the old one: we have significantly decreased the number of objects in both peaks making it in much better agreement with the Tycho-2 sample. The red peak of giant stars has been shifted by more than 0.1 mag towards the blue colours, which fits significantly better the giant peak of Tycho-2 data. The excess of the blue stars around (B − V)T ~ 0.1 and 0.5 mag has been significantly reduced. Table 8 summarizes the observed star counts and the behavior of the models in different latitude ranges.
 |
Fig. 14 Whole sky (B − V)T distributions of the old model (dash-dotted grey line), Tycho-2 data (dashed green line), and two new default models: model A in dotted orange line (Haywood-Robin IMF) and model B in solid blue line (Kroupa-Haywood v6 IMF). |
From Fig. 11, we also derive the conclusions that the default model A (Haywood-Robin IMF) reproduces the (B − V)T distribution within the Galactic plane very well, while it produces, respectively, 15 and 12% less stars than Tycho-2 data at intermediate and higher latitudes. The default model B (Kroupa-Haywood v6 IMF) differs from the data more significantly at the Galactic plane but it performs very well at intermediate and high latitudes.
As a complementary test, a clustering technique was performed on the (B − V)T distributions to separate the sample into two groups, the blue and the red. Figure 15 shows sky maps of the relative differences (NModel − NTycho) /NTycho in the number of objects (whole sky, default model B) for the blue group (top) and the red group (bottom). As expected, the Galactic plane is the most problematic region due to high interstellar extinction and its somewhat clumpy distribution. The largest discrepancies in the relative number of objects are correlated with the discrepancies in the mean colours. The regions within the plane where there are fewer Tycho-2 star counts than in the model are also clearly seen in Fig.1 from Høg et al. (2000). The two most problematic regions can be associated with dust clouds, the Taurus dark cloud at l = 174° and 175 pc and the large complex Aquila rift between l = 10° and l = 55° that runs from 50 pc to 375 pc (Lucke 1978). The extinction models used here are not realistic in those close dark clouds. Some other structures not considered in the comparisons can interfere as well, such as a spiral structure, star-forming regions, Gould belt, etc. In spite of these localized discrepancies, we have significantly improved (by at least a factor of two) the accuracy of star count predictions obtained with the new model when compared with old model (Czekaj 2012).
Star count comparisons between model A, model B, and the old model with respect to Tycho-2 data for VT ≤ 11 in three latitude ranges.
χ2 statistics of colour histograms for the old model, two default models (A and B), and the Just & Jahreiß (2010) best fit for IMF and SFR with respect to the Tycho-2 histogram in different latitude ranges.
In Table 9, χ2 tests are applied to the whole sky distributions. The most striking result from this table is that the new default models A and B and the JJ model provide a huge improvement with respect to the old model. The most significant improvement is observed for | b | > 10, while the Galactic plane is the most problematic region, where the modelling of the extinction causes a large part of the discrepancies. According to the second χ2 test with scaling factors, the model A is best at all latitudes, meaning that the shape of the distributions produced by this model is the closest to data. In absolute terms (the minimum χ2 test), model B fits better the observed data for all the sky outside the plane (| b | < 10). The results obtained with JJ model at high latitudes are also very good in terms of absolute star counts and the distribution’s shape. As for model B, it becomes less realistic within the Galactic plane.
Despite of the huge improvement with respect to the old model it is clear that, the simulations differ from the data by much more than expected from purely Poissonian statistics, which accounts for all remaining uncertainties in the model inputs, including stellar physics, interstellar extinction, inhomogeneties and non-axisymetries in the Galaxy components. We look forward to continue to improve the model by further investigations.
 |
Fig. 15 Sky maps of the relative number of objects (model B – Tycho)/Tycho between model B and Tycho data for two colour groups as defined by a clustering technique. Top blue group, bottom: red group. |
5.8. Deep star counts at the Galactic pole
As the new models improve the fit at magnitudes up to 11 it does not guarantee that they perform well at larger magnitudes. Figure 16 shows a preliminary test made to check the performance of these models A and B at a magnitude up to 21 towards the Galactic pole. Simulated star counts are compared with various data sets from the CDS (5 <V< 8 mag), Gilmore et al. (1995) (12 <V< 18 mag), Bok & Basinski (1964) (8 <V< 16 mag), Yoshii et al. (1987) (10 <V< 17 mag), and M. Crézé (priv. comm.) (17 <V< 21 mag). Both models perform well at deep magnitudes. Most of the stars with the apparent magnitude between 10 and 17 have the absolute magnitude within the range 4−10. As expected from their LF presented in Figs. 8 and 9, these models do not differ much in this range.
 |
Fig. 16 Star count predictions in the V band at the Galactic north pole (| b | > 80). We show the original Tycho-2 stars, which are used in our analysis (VT ≤ 11 mag) (green dahsed line) and the simulations obtained with model A (dotted magenta line) and model B (blue solid line). Black crosses indicate various observed counts taken from CDS (5 <V< 8 mag), Gilmore et al. (1995) (12 <V< 18 mag), Bok & Basinski (1964) (8 <V< 16 mag), Yoshii et al. (1987) (10 <V<17 mag), and Crézé (priv. comm.) (17 <V< 21 mag). |
6. Conclusions and future work
We have designed, implemented, and tested a new version of the Besançon Galaxy model. The new code implements an important change in the star production philosophy of the thin disc population, where the IMF, SFR, and stellar evolutionary tracks are treated as free parameters. The new code can be tested by comparing simulations by assuming different IMF and SFR, which could also be different in different parts of the Galaxy. The code also produces binary systems that take into account the observational spatial resolution.
We have updated and analysed several of the model’s inputs (see Table 5) using two observational sets, the Tycho-2 data, and the local luminosity function. The extinction model is one of the most crucial inputs at low latitudes. Significant differences in the Galactic plane are observed when using Drimmel & Spergel (2001) or Marshall et al. (2006) extinction models. Our results indicate that Drimmel & Spergel (2001) overestimates the extinction at large distances and Marshall et al. (2006) underestimates the extinction at very short distances. In absence of a better alternative, we have selected the Marshall et al. (2006) whenever it is available and the Drimmel & Spergel (2001) for the rest of the sky.
One of the most crucial parts of our investigation was to look for the best IMF and SFR, which are able to reproduce the whole sky Tycho-2 data. When a constant SFR is assumed, no matter which IMF is used, we are not able to reproduce the Tycho-2 star counts. The model always shows a significant excess of blue stars. This result strongly favours a decreasing SFR. The new decreasing SFR adopted here does not alter the overall good agreement obtained with the previous model (constant SFR) at fainter magnitudes. This is due to the fact that fainter stars (V> 14) of the thin disc are on the lower main sequence where the stellar density is sensitive to the integral of the SFR over the disc age and not to the detailed evolution in time.
When looking for the best fit IMF, we notice the following:
-
A slope α = 2.3 at high masses, which has been used by Vallenari et al. (2006) and Kroupa (2008) produces a strong excess of blue stars. As already mentioned by Haywood et al. (1997a), a Salpeter IMF is certainly inappropriate for our Galaxy. A steeper slope in this mass range is recommended.
-
The Just & Jahreiß (2010) IMF used with their best fit decreasing SFR, and our default model reproduces the Tycho-2 (B − V)T distribution at intermediate and high latitudes well, but it performs a bit worse within the plane.
We conclude that Kroupa-Haywood v6 and Haywood-Robin IMF combined with the decreasing SFR of Aumer & Binney (2009) provide the best fit to Tycho data.
All the thin disc ingredients cannot be constrained using nearby photometric data alone. A better solution would require a higher amount of observational constraints (in particular deeper star counts) and a robust statistical model fitting algorithm (as for instance Markov chain Monte carlo method). Nevertheless, we have learned that Tycho data is able to impose strong observational constraints to the SFR and the IMF in the bright star/intermediate mass domain in the solar vicinity.
A complementary investigation of the thick disc is underway using SDSS and 2MASS surveys to characterise the thick disc properties and constrain the scenario of its formation. We believe that using this new scheme and a better knowledge of the thin disc itself will help to perform this analysis, getting rid of the uncertainties on the structural parameters due to the degeneracies of parameters and to the thin disc contamination. Scenarios, such as the decomposition of populations of mono-abundances from Bovy et al. (2012), the question of the role of migration, in situ formation, or formation by mergers will then be possibly tested.
The next step will be to test the stellar kinematics and metallicity link to constrain the chemo-dynamical evolution of the Galaxy using RAVE data. The availability of even deeper spectroscopic probes, like the Gaia-ESO survey or APOGEE, will also allow us to constrain the SFR on a larger scale and to specifically study the link between the local thin and thick discs and more problematic populations of the bar and the bulge in the inner Galaxy. We expect that the new tool presented here will be very efficient for the analysis and understanding of future large scale surveys, such as Gaia. Work is in progress to make the new default models available online.
Online material
Appendix A: Statistical treatments
Appendix A.1: Small volume elements treatment
A simple test was performed to demonstrate the problem due to the use of small volume elements at short heliocentric distances. We have performed the simulations of a standard region (40 square degrees) until 100 pc. When no additional treatment is applied in the volume elements, the resulting mass distribution presents significant discontinuities (see Fig. A.1). They are caused by too low mass enclosed inside the volume being processed. We checked that this effect is less significant when no cut in distance is applied, because the further volume elements with more mass smooth out the dip. To correct this effect, the code is able to enlarge the volume element by a given factor and draw the masses from that enlarged pool. Through fitting, we estimated that a factor of 50 is enough to avoid the bias. This strategy assures that the mass calculated for that enlarged volume element is big enough for different masses to be drawn with no bias. Later on, we (randomly) keep only a fraction of the drawn objects, which corresponds to the original small volume element. As shown in Fig. A.1, this treatment avoids the underestimation of the number of stars from the high-mass IMF tail and leads to no discontinuities in the mass distribution of the simulated sample.
 |
Fig. A.1 Simulated mass distributions. Three slope IMF was assumed in these simulations: α1=1.3 for 0.09 <m< 0.5 M⊙, α2 = 2.3 for 0.5 <m< 1.53 M⊙ and α3 = 3.0 for 1.53 <m< 120 M⊙. In red the sample biased due to the problem of small volume elements and in blue the simulations obtained after the implementation of small volume elements treatment (the correcting factor was set to 50). |
Appendix A.2: What is the IMF of secondary stars?
As discussed is Sect. 2.2.2, we have preferred to produce the masses of the secondary stars from the empirical relations (Arenou 2011) and not from the IMF that is assumed for single
and primary stars. To verify the differences between both IMFs, we performed the simulations of the sphere around the Sun (100 and 180 pc) with and without binaries. In both cases, we saved the masses of all ever produced stars (alive and remnants). In Fig. A.2, we compare the mass distribution of primaries and secondary stars.
 |
Fig. A.2 Difference in the IMF of single (blue) and secondary (green) stars for the full sky sample (r< 100 pc). |
In Fig. A.3, we show the relative difference of the number of objects when using the binarity treatment N1 that contains single, primary, and secondary stars and the sample without binaries N2 (that is the IMF of single stars). We only plot the mass range m = [0:4]M⊙ because of the low statistics at higher masses. There is a difference at the level of 6% due to secondary stars. Thus, in conclusion, the IMF is not preserved. The IMF of secondary stars is not known enough, and it has no strong reason to be the same as the single star IMF. We decide to keep the constraint from the statistics of observed binaries, rather than the unverified theroretical hypothesis that the IMF of secondaries is the same as the primaries and singles.
 |
Fig. A.3 Relative difference of the number of objects when using the binarity treatment N1 containing single, primary and secondary stars, and the sample without binaries N2 that is the IMF of single stars. |
Appendix B: Photometry transformations
To find the best transformation between the Johnson and Tycho systems, we have analysed four different approaches. First, we considered the standard transformation published in the Vol. 1 of ESA (1997) (see Sects. 1.3 and 2.2)  (B.1)The second approach was the linear interpolation of the values, as specified in Table 1.3.4. of the same publication. In this case, the slope of the (B − V)J versus (BT − VT) relation, or the so called G-factor, is different in each of the six presented colour intervals.
(B.1)The second approach was the linear interpolation of the values, as specified in Table 1.3.4. of the same publication. In this case, the slope of the (B − V)J versus (BT − VT) relation, or the so called G-factor, is different in each of the six presented colour intervals.
In a third approach, we used equations of giant-like stars (luminosity class III with low reddening) for the whole sample (also from Vol. 1 of ESA (1997)).
The fourth method of transformation comes from Mark Kidger. On his website2, he derives the following relations: 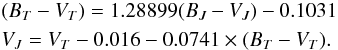 (B.2)In Fig. B.1, we present the (B − V)J distributions of the Tycho sample (cut at VT< = 11 mag) transformed into a Johnson system by the four discussed methods. Both the standard transformation, and the relation derived by Mark Kidger propose a unique slope for all the colour ranges. These standard equations are a rough approximation because they impose the same transformation for all types of stars. Perryman & ESA (1997) suggest a more sophisticated method of transformation such as the linear interpolation approach. As expected, the giants and linear interpolation methods show very similar results for the giants peak, while significant differences appear in the blue peak. In this paper, we use the linear interpolation transformation method, so we have inverted it and transformed the photometry of our simulations from Johnson to Tycho-2 system.
(B.2)In Fig. B.1, we present the (B − V)J distributions of the Tycho sample (cut at VT< = 11 mag) transformed into a Johnson system by the four discussed methods. Both the standard transformation, and the relation derived by Mark Kidger propose a unique slope for all the colour ranges. These standard equations are a rough approximation because they impose the same transformation for all types of stars. Perryman & ESA (1997) suggest a more sophisticated method of transformation such as the linear interpolation approach. As expected, the giants and linear interpolation methods show very similar results for the giants peak, while significant differences appear in the blue peak. In this paper, we use the linear interpolation transformation method, so we have inverted it and transformed the photometry of our simulations from Johnson to Tycho-2 system.
 |
Fig. B.1 (B − V)J distribution of Tycho-2 catalogue (after cutting at VT = 11 mag) transformed using four different photometry transformations. Top: standard (red), linear interpolation (green), and giants (blue) methods. Bottom: linear interpolation (green) and Mark Kidger’s (magenta) methods. |
Acknowledgments
We thank O. Bienaymé and M. Crézé for useful discussions and suggestions. We also wish to thank to F. Arenou for providing us the detailed strategy for binarity implementation. The anonymous referee is thanked for proposing improvements to clarify the paper. M. A. Czekaj was supported as an Early Stage Researcher of the Marie Curie Research Training Network “European Leadership in Space Astrometry” (ELSA) MRTN-CT-2006-033481 of the VIth Framework Programm – European Community and the MICINN (Spanish Ministry of Science and Innovation) – FEDER through grant AYA2009-14648-C02-01. We acknowledge the support of the French Agence Nationale de la Recherche under contract ANR-2010-BLAN-0508-01OTP. This thesis has been carried out at the Department d’Astronomia i Meteorologia (Universitat de Barcelona) and the Observatoire de Besançon (France). This study was partially supported by the Gaia Research for European Astronomy Training (GREAT) 08-RNP-118 European Science Foundation (European RNP FP7) and the MICINN – AYA2009-08488-E/AYA.
References
- Arenou, F. 2011, in International Workshop Double and Multiple Stars: Dynamics, Physics, and Instrumentation, eds. J. A. Docobo, V. S. Tamazian, & Y. Y. Balega, AIP Conf. Ser., 1346, 107 [Google Scholar]
- Aumer, M., & Binney, J. J. 2009, MNRAS, 397, 1286 [NASA ADS] [CrossRef] [Google Scholar]
- Bahcall, J. N., & Soneira, R. M. 1980, ApJS, 44, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Becker, S. A., Iben, J. I., & Tuggle, R. S. 1977, ApJ, 218, 633 [NASA ADS] [CrossRef] [Google Scholar]
- Bertelli, G., Bressan, A., Chiosi, C., Fagotto, F., & Nasi, E. 1994, A&A, 106, 275 [Google Scholar]
- Bertelli, G., Girardi, L., Marigo, P., & Nasi, E. 2008, A&A, 484, 815 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertelli, G., Nasi, E., Girardi, L., & Marigo, P. 2009, A&A, 508, 355 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bienaymé, O., Robin, A. C., & Crézé, M. 1987, A&A, 180, 94 [Google Scholar]
- Bienaymé, O., Soubiran, C., Mishenina, T. V., Kovtyukh, V. V., & Siebert, A. 2006, A&A, 446, 933 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Binney, J., & Tremaine, S. 2008, Galactic Dynamics: Second Edition (Princeton University Press) [Google Scholar]
- Bok, B. J., & Basinski, J. 1964, Memoires of the Mount Stromlo Observervatory, 16, [Google Scholar]
- Bovy, J., & Tremaine, S. 2012, ApJ, 756, 89 [Google Scholar]
- Bovy, J., Rix, H.-W., Liu, C., et al. 2012, ApJ, 753, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Burch, B., & Cowsik, R. 2013, ApJ, 779, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Castellani, V., Chieffi, A., & Straniero, O. 1992, ApJS, 78, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2005, in The Initial Mass Function 50 Years Later, eds. E. Corbelli, F. Palla, & H. Zinnecker, Astrophys. Space Sci. Lib., 327, 41 [Google Scholar]
- Chabrier, G., & Baraffe, I. 1997, A&A, 327, 1039 [NASA ADS] [Google Scholar]
- Chiosi, C., Nasi, E., & Sreenivasan, S. R. 1978, A&A, 63, 103 [NASA ADS] [Google Scholar]
- Crézé, M. 1979, in Compte-rendu de Ecole de Goutelas (Département Etoiles et galaxies, Observatoire de Meudon) [Google Scholar]
- Crézé, M., & Robin, A. 1983, in Nearby Stars and the Stellar Luminosity Function, eds. A. G. D. Philip, & A. R. Upgren, IAU Colloq., 76, 391 [Google Scholar]
- Crézé, M., Chereul, E., Bienaymé, O., & Pichon, C. 1998, A&A, 329, 920 [NASA ADS] [Google Scholar]
- Czekaj, M. A. 2012, Ph.D. thesis, University of Barcelona, Spain [Google Scholar]
- de Boer, W. 2005, New A Rev., 49, 213 [Google Scholar]
- del Peloso, E. F., da Silva, L., Porto de Mello, G. F., & Arany-Prado, L. I. 2005, A&A, 440, 1153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Derrière, S., & Robin, A. C. 2001, in The New Era of Wide Field Astronomy, eds. R. Clowes, A. Adamson, & G. Bromage, ASP Conf. Ser., 232, 229 [Google Scholar]
- Drimmel, R., & Spergel, D. N. 2001, ApJ, 556, 181 [NASA ADS] [CrossRef] [Google Scholar]
- ESA. 1997, ESA SP-1200, 1 [Google Scholar]
- Gao, S., Just, A., & Grebel, E. K. 2013, A&A, 549, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gilmore, G., Wyse, R. F. G., & Jones, J. B. 1995, AJ, 109, 1095 [NASA ADS] [CrossRef] [Google Scholar]
- Girardi, L., Groenewegen, M. A. T., Hatziminaoglou, E., & da Costa, L. 2005, A&A, 436, 895 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gómez, A. E., Grenier, S., Udry, S., et al. 1997, in Hipparcos – Venice 97, eds. R. M. Bonnet, E. Høg, P. L. Bernacca, et al., ESA SP, 402, 621 [Google Scholar]
- Haywood, M. 2006, MNRAS, 371, 1760 [NASA ADS] [CrossRef] [Google Scholar]
- Haywood, M. 2008, MNRAS, 388, 1175 [NASA ADS] [CrossRef] [Google Scholar]
- Haywood, M., Robin, A. C., & Crézé, M. 1997a, A&A, 320, 428 [NASA ADS] [Google Scholar]
- Haywood, M., Robin, A. C., & Crézé, M. 1997b, A&A, 320, 440 [NASA ADS] [Google Scholar]
- Haywood, M., Di Matteo, P., Lehnert, M., Katz, D., & Gomez, A. 2013, A&A, 560, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Høg, E., Fabricius, C., Makarov, V. V., et al. 2000, A&A, 355, L27 [NASA ADS] [Google Scholar]
- Holmberg, J., & Flynn, C. 2000, MNRAS, 313, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Holmberg, J., Nordström, B., & Andersen, J. 2009, A&A, 501, 941 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Houdashelt, M. L., Bell, R. A., & Sweigart, A. V. 2000, AJ, 119, 1448 [Google Scholar]
- Ibata, R., Martin, N. F., Irwin, M., et al. 2007, ApJ, 671, 1591 [NASA ADS] [CrossRef] [Google Scholar]
- Jahreiß, H., & Wielen, R. 1997, in Hipparcos – Venice 97, eds. R. M. Bonnet, E. Høg, P. L. Bernacca, et al., ESA SP, 402, 675 [Google Scholar]
- Just, A., & Jahreiß, H. 2010, MNRAS, 402, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Korchagin, V. I., Girard, T. M., Borkova, T. V., Dinescu, D. I., & van Altena, W. F. 2003, AJ, 126, 2896 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2001, in Dynamics of Star Clusters and the Milky Way, eds. S. Deiters, B. Fuchs, A. Just, R. Spurzem, & R. Wielen, ASP Conf. Ser., 228, 187 [Google Scholar]
- Kroupa, P. 2008, in Pathways Through an Eclectic Universe, eds. J. H. Knapen, T. J. Mahoney, & A. Vazdekis, ASP Conf. Ser., 390, 3 [Google Scholar]
- Kroupa, P., Tout, C. A., & Gilmore, G. 1993, MNRAS, 262, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Lejeune, T., Cuisinier, F., & Buser, R. 1997, A&AS, 125, 229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lejeune, T., Cuisinier, F., & Buser, R. 1998, A&A, 130, 65 [Google Scholar]
- Lucke, P. B. 1978, A&A, 64, 367 [NASA ADS] [Google Scholar]
- Marshall, D. J., Robin, A. C., Reylé, C., Schultheis, M., & Picaud, S. 2006, A&A, 453, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mengel, J. G., Demarque, P., Sweigart, A. V., & Gross, P. G. 1979, ApJS, 40, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Ng, Y. K., Bertelli, G., Chiosi, C., & Bressan, A. 1997, A&A, 324, 65 [NASA ADS] [Google Scholar]
- Perryman, A., & ESA 1997, The Hipparcos and Tycho catalogues: astrometric and photometric star catalogues derived from the ESA Hipparcos Space Astrometry Mission, ESA SP, 1200 [Google Scholar]
- Picaud, S., & Robin, A. C. 2004, A&A, 428, 891 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reid, I. N., Gizis, J. E., & Hawley, S. L. 2002, AJ, 124, 2721 [NASA ADS] [CrossRef] [Google Scholar]
- Reylé, C., & Robin, A. C. 2001, A&A, 373, 886 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reylé, C., Marshall, D. J., Robin, A. C., & Schultheis, M. 2009, A&A, 495, 819 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robin, A., & Crézé, M. 1986, A&A, 157, 71 [Google Scholar]
- Robin, A. C., Haywood, M., Crézé, M., Ojha, D. K., & Bienaymé, O. 1996, A&A, 305, 125 [NASA ADS] [Google Scholar]
- Robin, A. C., Reylé, C., & Crézé, M. 2000, A&A, 359, 103 [NASA ADS] [Google Scholar]
- Robin, A. C., Reylé, C., Derrière, S., & Picaud, S. 2003, A&A, 409, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robin, A. C., Luri, X., Reylé, C., et al. 2012a, A&A, 543, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robin, A. C., Marshall, D. J., Schultheis, M., & Reylé, C. 2012b, A&A, 538, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scalo, J. M. 1986, Fundamentals of Cosmic Physics (Springer Verlag), 11, 1 [Google Scholar]
- Schaller, G., Schaerer, D., Meynet, G., & Maeder, A. 1992, A&A, 96, 269 [Google Scholar]
- Sharma, S., Bland-Hawthorn, J., Johnston, K. V., & Binney, J. 2011, ApJ, 730, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Sweigart, A. V., & Gross, P. G. 1978, ApJS, 36, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Tinsley, B. M. 1972, A&A, 20, 383 [NASA ADS] [Google Scholar]
- Twarog, B. A. 1980, ApJS, 44, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Vallenari, A., Bertelli, G., Bressan, A., & Chiosi, C. 1999, Balt. Astron., 8, 147 [NASA ADS] [Google Scholar]
- Vallenari, A., Pasetto, S., Bertelli, G., et al. 2006, A&A, 451, 125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Leeuwen, F., ed. 2007, Hipparcos, the New Reduction of the Raw Data, Astrophys. Space Sci. Lib. (Springer), 350 [Google Scholar]
- Vanhollebeke, E., Groenewegen, M. A. T., & Girardi, L. 2009, A&A, 498, 95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wainscoat, R. J., Cohen, M., Volk, K., Walker, H. J., & Schwartz, D. E. 1992, ApJS, 83, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Westera, P., Lejeune, T., Buser, R., Cuisinier, F., & Bruzual, G. 2002, A&A, 381, 524 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wielen, R. 1974, Highlights of Astronomy, 3, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Yoshii, Y., Ishida, K., & Stobie, R. S. 1987, AJ, 93, 323 [Google Scholar]
- Zhang, L., Rix, H.-W., van de Ven, G., et al. 2013, ApJ, 772, 108 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Values of the thin disc local stellar volume mass density derived from observations (units: M⊙ pc-3).
Comparison of the age–velocity dispersion relation by Gómez et al. (1997) and Holmberg et al. (2009).
Contribution of all mass components (in M⊙ pc-3) to the total dynamical mass in the default models A and B.
Star count comparisons between model A, model B, and the old model with respect to Tycho-2 data for VT ≤ 11 in three latitude ranges.
χ2 statistics of colour histograms for the old model, two default models (A and B), and the Just & Jahreiß (2010) best fit for IMF and SFR with respect to the Tycho-2 histogram in different latitude ranges.
All Figures
 |
Fig. 1 General scheme describing the ingredients needed to build the evolutionary model and the information they provide. In italics we have marked the ingredients, which are under study, in this paper. |
| In the text | |
 |
Fig. 2 Normalization iterative process to derive the mass model. The local volume density |
| In the text | |
 |
Fig. 3 Organigram of the new model’s thin disc treatment. |
| In the text | |
 |
Fig. 4 Two decreasing SFRs as a function of time t. SFR of model A by Just & Jahreiß (2010) (dashed green line) and (Aumer & Binney 2009) single exponential with γ = 0.12 (solid red line). Normalizations are arbitrary. |
| In the text | |
 |
Fig. 5 Whole sky (B − V)T distributions of the old model (solid grey line) and Tycho-2 data (dashed green line). |
| In the text | |
 |
Fig. 6 Testing atmosphere models. (B − V)T distributions in the reference region at intermediate latitudes. Tycho-2 data (dashed green line) is compared with the simulations obtained with the default model B and BaSeL 3.1 library (solid blue line) and the default model B and BaSeL 2.2 (dotted red line). |
| In the text | |
 |
Fig. 7 (B − V)T distributions towards the Galactic north pole showing the effect of changing the age–velocity dispersion relation (AVR) against the default model B. Tycho-2 data (dashed green line) and the simulations based on the default model B (solid blue line) are shown. The dotted red line is based on simulations using an AVR of Holmberg et al. (2009) rather than of Gómez et al. (1997) but leaving all other parameters unchanged. |
| In the text | |
 |
Fig. 8 Comparing the observed LF with the synthetic LF that is obtained with the default model B and two values of local stellar mass density, LMD1 and LMD2 (in both cases simulations with and without binaries). Total LF from Jahreiß & Wielen (1997) (red dots), main sequence LF from Kroupa (2001) (black triangles), and Reid et al. (2002) (black dots) are shown. |
| In the text | |
 |
Fig. 9 Comparison of the observed LF with simulated one from model A: total LF (solid blue line) and main sequence LF (dashed magenta line). Symbols for observed data are same as in Fig. 8. |
| In the text | |
 |
Fig. 10 Testing a constant and decreasing SFR with different IMFs. All three panels show the (B − V)T distributions of the reference region within the Galactic plane. Tycho data in all panels is plotted using dashed green line. The top panel corresponds to Kroupa (2008) IMF, the middle to Haywood-Robin IMF and the bottom to Kroupa-Haywood v6 IMF (see Table 1). In red dotted line the simulations, which are obtained with constant SFR, and in solid yellow, orange, and blue lines, the simulations obtained with the decreasing SFR of Aumer & Binney (2009) and each IMF respectively. |
| In the text | |
 |
Fig. 11 Testing different IMFs. The (B − V)T distributions correspond to the (top) entire Galactic plane | b | < 10, (middle) entire stripe of the sky at 10 < | b | ≤ 30, and (bottom) the stripe of the sky at 30 < | b | ≤ 90. In dotted orange line the simulations, which are obtained with the default model A (Haywood-Robin IMF); in solid blue line we have the default model B (Kroupa-Haywood v6 IMF), and the default model combined with the best fit SFR and IMF from Just & Jahreiß (2010) is in dash-dotted magenta line. The Tycho-2 data is in dashed green line. |
| In the text | |
 |
Fig. 12 Testing binarity. (B − V)T distribution in our reference region within the Galactic plane. Tycho-2 data (dashed green line), the simulations obtained with the default model B and binarity (solid blue line) and simulations with the default model B without binarity (dotted red line) are shown. |
| In the text | |
 |
Fig. 13 Testing two different extinction models. The presented (B − V)T distributions correspond to a part of the Galactic plane | l | < 100 and | b | < 10. Top: default model A. Bottom: default model B. Two different extinction models are also used: dotted red line is Drimmel & Spergel (2001) (in both cases), solid orange line is model A with Marshall et al. (2006), solid blue line is model B with Marshall et al. (2006) and dashed green is Tycho data. |
| In the text | |
 |
Fig. 14 Whole sky (B − V)T distributions of the old model (dash-dotted grey line), Tycho-2 data (dashed green line), and two new default models: model A in dotted orange line (Haywood-Robin IMF) and model B in solid blue line (Kroupa-Haywood v6 IMF). |
| In the text | |
 |
Fig. 15 Sky maps of the relative number of objects (model B – Tycho)/Tycho between model B and Tycho data for two colour groups as defined by a clustering technique. Top blue group, bottom: red group. |
| In the text | |
 |
Fig. 16 Star count predictions in the V band at the Galactic north pole (| b | > 80). We show the original Tycho-2 stars, which are used in our analysis (VT ≤ 11 mag) (green dahsed line) and the simulations obtained with model A (dotted magenta line) and model B (blue solid line). Black crosses indicate various observed counts taken from CDS (5 <V< 8 mag), Gilmore et al. (1995) (12 <V< 18 mag), Bok & Basinski (1964) (8 <V< 16 mag), Yoshii et al. (1987) (10 <V<17 mag), and Crézé (priv. comm.) (17 <V< 21 mag). |
| In the text | |
 |
Fig. A.1 Simulated mass distributions. Three slope IMF was assumed in these simulations: α1=1.3 for 0.09 <m< 0.5 M⊙, α2 = 2.3 for 0.5 <m< 1.53 M⊙ and α3 = 3.0 for 1.53 <m< 120 M⊙. In red the sample biased due to the problem of small volume elements and in blue the simulations obtained after the implementation of small volume elements treatment (the correcting factor was set to 50). |
| In the text | |
 |
Fig. A.2 Difference in the IMF of single (blue) and secondary (green) stars for the full sky sample (r< 100 pc). |
| In the text | |
 |
Fig. A.3 Relative difference of the number of objects when using the binarity treatment N1 containing single, primary and secondary stars, and the sample without binaries N2 that is the IMF of single stars. |
| In the text | |
 |
Fig. B.1 (B − V)J distribution of Tycho-2 catalogue (after cutting at VT = 11 mag) transformed using four different photometry transformations. Top: standard (red), linear interpolation (green), and giants (blue) methods. Bottom: linear interpolation (green) and Mark Kidger’s (magenta) methods. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.