| Issue |
A&A
Volume 564, April 2014
|
|
|---|---|---|
| Article Number | A102 | |
| Number of page(s) | 20 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201322139 | |
| Published online | 14 April 2014 | |
Online material
Appendix A: Statistical treatments
Appendix A.1: Small volume elements treatment
A simple test was performed to demonstrate the problem due to the use of small volume elements at short heliocentric distances. We have performed the simulations of a standard region (40 square degrees) until 100 pc. When no additional treatment is applied in the volume elements, the resulting mass distribution presents significant discontinuities (see Fig. A.1). They are caused by too low mass enclosed inside the volume being processed. We checked that this effect is less significant when no cut in distance is applied, because the further volume elements with more mass smooth out the dip. To correct this effect, the code is able to enlarge the volume element by a given factor and draw the masses from that enlarged pool. Through fitting, we estimated that a factor of 50 is enough to avoid the bias. This strategy assures that the mass calculated for that enlarged volume element is big enough for different masses to be drawn with no bias. Later on, we (randomly) keep only a fraction of the drawn objects, which corresponds to the original small volume element. As shown in Fig. A.1, this treatment avoids the underestimation of the number of stars from the high-mass IMF tail and leads to no discontinuities in the mass distribution of the simulated sample.
 |
Fig. A.1
Simulated mass distributions. Three slope IMF was assumed in these simulations: α1=1.3 for 0.09 <m< 0.5 M⊙, α2 = 2.3 for 0.5 <m< 1.53 M⊙ and α3 = 3.0 for 1.53 <m< 120 M⊙. In red the sample biased due to the problem of small volume elements and in blue the simulations obtained after the implementation of small volume elements treatment (the correcting factor was set to 50). |
| Open with DEXTER | |
Appendix A.2: What is the IMF of secondary stars?
As discussed is Sect. 2.2.2, we have preferred to produce the masses of the secondary stars from the empirical relations (Arenou 2011) and not from the IMF that is assumed for single
and primary stars. To verify the differences between both IMFs, we performed the simulations of the sphere around the Sun (100 and 180 pc) with and without binaries. In both cases, we saved the masses of all ever produced stars (alive and remnants). In Fig. A.2, we compare the mass distribution of primaries and secondary stars.
 |
Fig. A.2
Difference in the IMF of single (blue) and secondary (green) stars for the full sky sample (r< 100 pc). |
| Open with DEXTER | |
In Fig. A.3, we show the relative difference of the number of objects when using the binarity treatment N1 that contains single, primary, and secondary stars and the sample without binaries N2 (that is the IMF of single stars). We only plot the mass range m = [0:4]M⊙ because of the low statistics at higher masses. There is a difference at the level of 6% due to secondary stars. Thus, in conclusion, the IMF is not preserved. The IMF of secondary stars is not known enough, and it has no strong reason to be the same as the single star IMF. We decide to keep the constraint from the statistics of observed binaries, rather than the unverified theroretical hypothesis that the IMF of secondaries is the same as the primaries and singles.
 |
Fig. A.3
Relative difference of the number of objects when using the binarity treatment N1 containing single, primary and secondary stars, and the sample without binaries N2 that is the IMF of single stars. |
| Open with DEXTER | |
Appendix B: Photometry transformations
To find the best transformation between the Johnson and Tycho systems, we have analysed four different approaches. First, we considered the standard transformation published in the Vol. 1 of ESA (1997) (see Sects. 1.3 and 2.2) 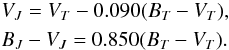 (B.1)The second approach was the linear interpolation of the values, as specified in Table 1.3.4. of the same publication. In this case, the slope of the (B − V)J versus (BT − VT) relation, or the so called G-factor, is different in each of the six presented colour intervals.
(B.1)The second approach was the linear interpolation of the values, as specified in Table 1.3.4. of the same publication. In this case, the slope of the (B − V)J versus (BT − VT) relation, or the so called G-factor, is different in each of the six presented colour intervals.
In a third approach, we used equations of giant-like stars (luminosity class III with low reddening) for the whole sample (also from Vol. 1 of ESA (1997)).
The fourth method of transformation comes from Mark Kidger. On his website2, he derives the following relations: 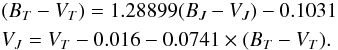 (B.2)In Fig. B.1, we present the (B − V)J distributions of the Tycho sample (cut at VT< = 11 mag) transformed into a Johnson system by the four discussed methods. Both the standard transformation, and the relation derived by Mark Kidger propose a unique slope for all the colour ranges. These standard equations are a rough approximation because they impose the same transformation for all types of stars. Perryman & ESA (1997) suggest a more sophisticated method of transformation such as the linear interpolation approach. As expected, the giants and linear interpolation methods show very similar results for the giants peak, while significant differences appear in the blue peak. In this paper, we use the linear interpolation transformation method, so we have inverted it and transformed the photometry of our simulations from Johnson to Tycho-2 system.
(B.2)In Fig. B.1, we present the (B − V)J distributions of the Tycho sample (cut at VT< = 11 mag) transformed into a Johnson system by the four discussed methods. Both the standard transformation, and the relation derived by Mark Kidger propose a unique slope for all the colour ranges. These standard equations are a rough approximation because they impose the same transformation for all types of stars. Perryman & ESA (1997) suggest a more sophisticated method of transformation such as the linear interpolation approach. As expected, the giants and linear interpolation methods show very similar results for the giants peak, while significant differences appear in the blue peak. In this paper, we use the linear interpolation transformation method, so we have inverted it and transformed the photometry of our simulations from Johnson to Tycho-2 system.
 |
Fig. B.1
(B − V)J distribution of Tycho-2 catalogue (after cutting at VT = 11 mag) transformed using four different photometry transformations. Top: standard (red), linear interpolation (green), and giants (blue) methods. Bottom: linear interpolation (green) and Mark Kidger’s (magenta) methods. |
| Open with DEXTER | |
© ESO, 2014
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


