| Issue |
A&A
Volume 563, March 2014
|
|
|---|---|---|
| Article Number | A47 | |
| Number of page(s) | 6 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201323256 | |
| Published online | 05 March 2014 | |
A population synthesis study of the luminosity function of hot white dwarfs
1
Departament de Física AplicadaUniversitat Politècnica de
Catalunya,
c/Esteve Terrades 5,
08860
Castelldefels,
Spain
e-mail:
enrique.garcia-berro@upc.edu
2
Institute for Space Studies of Catalonia,
c/Gran Capità 2–4, Edif. Nexus
104, 08034
Barcelona,
Spain
3
Mt. Suhora Observatory, Cracow Pedagogical University,
ul. Podchorazych 2,
30-084
Cracow,
Poland
4
Gemini Observatory, 670 N. A’Ohoku Place, Hilo
HI
96720,
USA
Received:
14
December
2013
Accepted:
7
February
2014
Context. We present a coherent and detailed Monte Carlo simulation of the population of hot white dwarfs. We assess the statistical significance of the hot end of the white dwarf luminosity function and the role played by the bolometric corrections of hydrogen-rich white dwarfs at high effective temperatures.
Aims. We use the most up-to-date stellar evolutionary models and implement a full description of the observational selection biases to obtain realistic simulations of the observed white dwarf population.
Methods. Our theoretical results are compared with the luminosity function of hot white dwarfs obtained from the Sloan Digital Sky Survey (SDSS), for both DA and non-DA white dwarfs.
Results. We find that the theoretical results are in excellent agreement with the observational data for the population of white dwarfs with hydrogen deficient atmospheres (non-DA white dwarfs). For the population of white dwarfs with hydrogen-rich atmospheres (white dwarfs of the DA class), our simulations show some discrepancies with the observations for the brightest luminosity bins, namely those corresponding to luminosities larger than ~10 L⊙. These discrepancies can be attributed to the way in which the masses of the white dwarfs contributing to this luminosity bin have been computed, as most of them have masses smaller than the theoretical lower limit for carbon-oxygen white dwarfs.
Conclusions. We conclude that the way in which the observational luminosity function of hot white dwarfs is obtained is very sensitive to the particular implementation of the method used to derive the masses of the sample. We also provide a revised luminosity function for hot white dwarfs with hydrogen-rich atmospheres.
Key words: stars: luminosity function, mass function / white dwarfs
© ESO, 2014
1. Introduction
White dwarfs are the most common end-point of stellar evolution. In fact, more than ~95% of the stars in our Galaxy, namely those with masses smaller than ~10 M⊙, will end their lives as white dwarfs. Hence, the white dwarf population carries very valuable information about the evolution of the vast majority of stars in our Galaxy. Moreover, their structural and evolutionary properties are relatively well understood – see, for instance, the recent review of Althaus et al. (2010). Consequently, the characteristics of white dwarf populations can be used to constrain the evolutionary models of their progenitor stars. For instance, the white dwarf population can be used to assess the amount of mass lost by their progenitors, a process that plays a key role in stellar evolution. Additionally, since the mass ejected in the late stages of stellar evolution is enriched in heavy elements, the study of the Galactic white dwarf population is important to model the chemical evolution of our Galaxy. These, however, are not the only useful applications of studying the population of white dwarfs. It is worth mentioning that the study of the local white dwarf population provides interesting constraints on the local star formation rate (Diaz-Pinto et al. 1994; Rowell 2013) and on the age of the Galactic disk in the solar neighborhood (Winget et al. 1987; García-Berro et al. 1988a,b) and other Galactic populations, including open (García-Berro et al. 2010) and globular clusters – see, for example, Hansen et al. (2007). Furthermore, the ensemble characteristics of the population of white dwarfs can be used to constrain the mass of weakly interacting particles, like axions (Isern et al. 2008), neutrino emission rates (Lamb & van Horn 1975) and the nature of the baryonic dark matter content of our Galaxy – see, for instance, Isern et al. (1998), Torres et al. (2002), and García-Berro et al. (2004), and references therein. Finally, the population of white dwarfs can also be used to study alternative theories of gravity (García-Berro et al. 2011; García-Berro et al. 1995).
All these investigations require not only accurate evolutionary white dwarf cooling sequences, but also reliable determinations of the observed ensemble properties of the white dwarf population, namely its luminosity function and its mass distribution. Thus, to address all these questions, we need large white dwarf samples of known completeness. The Sloan Digital Sky Survey (SDSS) – see, e.g., York et al. (2000) – has provided us with a very large sample of white dwarfs and from it, a reliable white dwarf luminosity function for hot white dwarfs – namely those with effective temperatures in excess of 23 500 K – has been recently obtained (Krzesinski et al. 2009). This white dwarf luminosity function has the interesting benefit that it has been obtained using solely spectroscopically-confirmed white dwarfs from the SDSS DR4 and it is thus an excellent testbed to check not only the white dwarf cooling sequences at high luminosities, but also our ability to model reliably some Galactic inputs necessary to compute the luminosity function. Here we describe the results of a comprehensive set of Monte Carlo simulations aimed to model the hot part of the white dwarf luminosity function for both hydrogen-rich (DA) white dwarfs and non-DA (hydrogen deficient) stars.
2. The population synthesis code
Our population synthesis code has been extensively described in previous papers (García-Berro et al. 1999, 2004; Torres et al. 2002), and has proven to be a very valuable tool to simulate successfully the Galactic disk and halo populations, as well as the populations of Galactic clusters. Hence, we will only describe here its most relevant aspects, and we refer the interested reader to previous publications for detailed descriptions of the relevant physical and astronomical inputs. Specifically, we simulated a synthetic population of disk white dwarfs in the solar neighborhood in a sphere of radius 3 kpc. This radius is sufficiently large to avoid possible biases due to the sampling procedure, which for the case under study could be important given that we are dealing with the brightest population of white dwarfs. We also adopted a disk age of 10.5 Gyr, a constant star formation rate, and a standard initial mass function (Kroupa 2001). However, let us note that the results presented in this paper do not sensitively depend on the precise choice of the initial mass function. In particular, when the initial mass function of Scalo (1998) is adopted we find negligible changes in our results. Velocities were obtained taking into account the differential rotation of the Galaxy, the peculiar velocity of the Sun, and a dispersion law which depends on the Galactic scale height. We used a double exponential profile with a scale height h = 250 pc and a scale length l = 1.3 kpc, and adopted the initial-final relationship of Catalán et al. (2008a) and Catalán et al. (2008b). The cooling sequences employed varied per the mass of the white dwarf, MWD. If MWD ≤ 1.1 M⊙, a CO core was adopted, while if MWD > 1.1 M⊙, an ONe core was used. In the case of CO white dwarfs with H-rich envelopes we used the evolutionary calculations of Renedo et al. (2010), while for white dwarfs with ONe cores we used those of Althaus et al. (2007). For H-deficient white dwarfs, we used the cooling sequences of Benvenuto & Althaus (1997), which correspond to pure He atmospheres, and the bolometric corrections of Bergeron et al. (1995). Finally, we used the same selection criteria in our model population as Krzesinski et al. (2009) employed to cull their observational sample. Specifically, we selected only white dwarf models with g > 14 and a fully de-reddened magnitude go < 19 that satisfied the color cuts −1.5 < (u − g)o < 0 and −1.5 < (g − r)o < 0.
 |
Fig. 1 White dwarf luminosity functions for hot DA and non-DA white dwarfs for two different models – see text Sect. 3 for details. The solid line with filled squares is the luminosity function of Krzesinski et al. (2009), while the dashed lines with empty squares show the results of our simulations. |
3. The luminosity function of hot white dwarfs
In Fig. 1 we show the model luminosity functions for hot hydrogen-rich (DA) and hydrogen-deficient (non-DA) white dwarfs for two different assumptions about the ratio of DA to non-DA white dwarfs. Each model luminosity function shown in this figure is the ensemble average of 50 independent Monte Carlo realizations for which we also computed the corresponding standard deviations as an estimate of the associated sampling errors. In the canonical set of simulations we adopt the standard DA/non-DA ratio fDA/non−DA = 0.80, independent of effective temperature. In the fiducial set of simulations, we use a ratio dependent on the effective temperature, Teff, adopting the ratio obtained from the SDSS (Krzesinski et al. 2009). The solid lines in Fig. 1 represent the white dwarf luminosity function of Krzesinski et al. (2009), while the dashed lines show our synthetic luminosity functions, obtained from the model population of hot white dwarfs computed with the procedure outlined in the previous section. The upper panels of Fig. 1 clearly show that the luminosity function of hot DA white dwarfs barely depends on the choice of the DA/non-DA ratio, whilst that of non-DA white dwarfs depends sensitively on it. Also, it is quite apparent that the agreement with the observational data is excellent for the fiducial model in which the ratio of non-DA to DA white dwarfs depends on effective temperature.
There is one puzzling characteristic of the observational luminosity function of hot DA white dwarfs clearly seen in Fig. 1 – namely, the existence of a plateau at luminosities around log (L/L⊙) ≈ 1, or equivalently Mbol ≈ 2.0 that is not reproduced in our synthetic luminosity functions. Interestingly, the luminosity function of hot non-DA white dwarfs does not have a similar plateau and there is excellent agreement between the synthetic and observational data. Thus, the origin of this feature in the DA luminosity function cannot be attributed to a global Galactic input – like the initial mass function or to a recent burst of star formation – because if this were the case, the feature would be present in the luminosity functions of both the DA and non-DA white dwarfs. Also, the existence of this plateau cannot be a consequence of the gross evolutionary properties of the progenitor stars – like the choice of the initial-final mass relationship – since again in this case we would find a similar feature in the luminosity function of non-DA white dwarfs. Instead, the presence of this plateau must be related to the intrinsic way in which the luminosity function of hot DA white dwarfs is derived. Hence, we are left with three possible alternatives to explain its origin, although other explanations cannot be obviously discarded “a priori”. Either the model atmospheres of hot DA white dwarfs are not complete for this range of effective temperatures and there is a piece of physics that has not been properly taken into account in the model atmospheres, or the theoretical cooling sequences are not entirely reliable at these luminosities – possibly influenced by the initial conditions of the cooling models, or by the model atmospheres employed to derive the colors and the bolometric magnitude – or alternatively, the observational error bars inherent to the 1/Vmax method have been underestimated – a reasonable possibility given that at this range of luminosities the number of objects is relatively small, see Geijo et al. (2006) – and the plateau corresponds to a statistical fluctuation. We study all three possibilities in detail.
In a first attempt to explore the origin of the plateau in the DA white dwarf luminosity function, we studied the effect of the adopted atmospheres in the analysis of the population of hot DA white dwarfs. Specifically, we analyzed the effects of the NLTE corrections and of the presence of metals in the atmospheres of these stars. For this purpose we adopted the NLTE corrections of Napiwotzki et al. (1999). These corrections are provided in a tabular form for temperatures 30 000 K < Teff < 100 000 K and gravities 6.50 < log g < 9.75. Additionally, we assumed that 50% of hot DA white dwarfs have metals in their atmospheres, although the results are essentially the same when different percentages of white dwarfs contaminated by metals are adopted. According to the results of Napiwotzki et al. (1999), the effective temperatures (and consequently, the luminosities) of DA white dwarfs with metal-contaminated atmospheres are overestimated by 20% at 80 000 K, while at 40 000 K, no corrections are needed. These effective temperatures correspond to approximately the correct range of luminosities for which the plateau in the luminosity function of hot DA white dwarfs is found. With all these inputs, we ran our Monte Carlo code to obtain a population of hot DA white dwarf models with metal-contaminated atmospheres. The results of this set of calculations are shown in the top panel of Fig. 2 by a dashed line connecting the open squares. This synthetic luminosity function includes both the effects of NLTE corrections and those of the metallic contamination of hot DA atmospheres. The solid line connecting the filled squares corresponds to the observed hot DA white dwarf luminosity function from the SDSS. As can be seen, these two additional effects have a very limited impact on the simulated white dwarf luminosity functions, and consequently they cannot be at the origin of the plateau. Another possibility is that for these luminosities the so-called “Balmer-line problem” – see Gianninas et al. (2010) and references therein – affects the determination of the bolometric magnitudes of very hot white dwarfs in such a way that the shape of the luminosity function could be substantially modified. To study this possibility we adopted the following procedure. First, we assumed that a considerable (20%) fraction of very hot DA white dwarfs (namely, those with effective temperatures larger than 40 000 K) present the Balmer-line problem. This fraction is twice the observed one, but in this way we maximize the possible effects of the Balmer-line problem. Then, to these white dwarfs we applied the corrections of Fig. 12 of Gianninas et al. (2010), and we recomputed the luminosity function of DA white dwarfs, keeping the rest of the inputs the same. The result of this procedure is shown in the second panel of Fig. 2. As can be seen, our simulations are again unable to correctly reproduce the existence of the plateau in the luminosity function. Therefore, we now explore our next possible solution.
 |
Fig. 2 Synthetic luminosity function of hot white dwarfs obtained using different assumptions about the atmospheric composition of hot DA white dwarfs and two sets of model atmospheres, compared to the observational luminosity function of the SDSS (Krzesinski et al. 2009) – solid line and filled squares. The top two panels show the synthetic luminosity functions of hot DA white dwarfs when NLTE corrections and metal contamination, and when the corrections of Gianninas et al. (2010) to the so-called Balmer-line problem are considered. The two bottom panels display the results of our simulations when the cooling tracks of Renedo et al. (2010) are employed – that is, our fiducial model – whereas in the second bottom panel we display the results obtained when the model atmospheres of Tremblay et al. (2011) are used. In all four panels the results of the population synthesis calculations are plotted using dashed lines and open squares. |
A second possibility worth exploring is that the cooling sequences used to compute the theoretical luminosity function of the population of DA white dwarfs are not reliable for this range of effective temperatures. To explore the effects of a different choice of the DA white dwarf cooling tracks, we adopted a completely different set of cooling sequences which incorporate different prescriptions for the model atmospheres from Tremblay et al. (2011), and have been computed with very different stellar evolutionary codes that incorporate different physical inputs. Additionally, we recall that both sets of cooling sequences – that is, those of Fontaine et al. (2001) and those of Renedo et al. (2010) – have been evolved from different initial models. The results of this new set of calculations are displayed in the bottom two panels of Fig. 2. As can be seen in this figure, the impact on the shape of the white dwarf luminosity function of DA white dwarfs of the adopted evolutionary sequences is minimal. In particular, although using the evolutionary cooling tracks of Fontaine et al. (2001) the bins of higher luminosities – say, those with Mbol ≲ 1.0 – are more populated, the overall shape of the luminosity function remains almost unchanged, and moreover the apparent plateau of the white dwarf luminosity function is not reproduced, while both sets of evolutionary sequences are in close agreement for luminosities smaller than this value. Hence, we can safely discard the hypothesis that the plateau is an artifact produced by our choice of model atmospheres or a poor description of the initial phases of white dwarf cooling.
Now we turn our attention to the third possibility previously envisaged – that there is an
observational bias in the way in which the DA white dwarf luminosity function is computed.
In particular, it may be possible that the observed plateau is a consequence of an
unexpected larger number of objects in the corresponding luminosity bins. However, it should
be kept in mind that the 1/Vmax method is
specifically designed to compensate for the bias due to an observational magnitude limit cut
and consequently, that the contribution of each individual star to the luminosity function
depends on its magnitude. Specifically, the contribution of each star to the luminosity
function is obtained from the maximum volume at which it could be found:
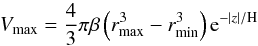 (1)where
rmax and rmin are the
maximum and minimum distances for which an object with apparent magnitude m can be detected within the
magnitude limits of the survey, β is the sky solid angle of the sample of stars,
z is the
vertical Galactic coordinate, and H is the Galactic scale height, for which we adopt
250 pc, as in Krzesinski et al. (2009). Therefore,
for a given absolute magnitude M the maximum and minimum distances are a function of
the apparent magnitude cut, so the maximum volume is given by:
(1)where
rmax and rmin are the
maximum and minimum distances for which an object with apparent magnitude m can be detected within the
magnitude limits of the survey, β is the sky solid angle of the sample of stars,
z is the
vertical Galactic coordinate, and H is the Galactic scale height, for which we adopt
250 pc, as in Krzesinski et al. (2009). Therefore,
for a given absolute magnitude M the maximum and minimum distances are a function of
the apparent magnitude cut, so the maximum volume is given by:
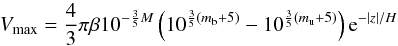 (2)where
mu
and mb are represent the range of selected
magnitudes. Note that for a given magnitude cut, the term inside the parenthesis is
constant. Hence, the contribution of a given object to the luminosity function, which is the
inverse of the maximum volume, is then:
(2)where
mu
and mb are represent the range of selected
magnitudes. Note that for a given magnitude cut, the term inside the parenthesis is
constant. Hence, the contribution of a given object to the luminosity function, which is the
inverse of the maximum volume, is then:
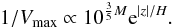 (3)This last equation
implies that the contribution of an object to the luminosity function only depends on its
absolute magnitude and its Galactic height, z. Since there is no physical reason to suspect that
the Galactic scale height depends on the luminosity, or conversely that white dwarfs (and
their corresponding progenitor stars) born at different times come from Galactic populations
with different scale heights, it ends up that the contribution of each individual object to
the luminosity function only depends on its absolute magnitude. Moreover, if it were the
case that the Galactic scale height depends on the luminosity, a similar feature would also
be present in the luminosity function of non-DA white dwarfs, which is not the case.
(3)This last equation
implies that the contribution of an object to the luminosity function only depends on its
absolute magnitude and its Galactic height, z. Since there is no physical reason to suspect that
the Galactic scale height depends on the luminosity, or conversely that white dwarfs (and
their corresponding progenitor stars) born at different times come from Galactic populations
with different scale heights, it ends up that the contribution of each individual object to
the luminosity function only depends on its absolute magnitude. Moreover, if it were the
case that the Galactic scale height depends on the luminosity, a similar feature would also
be present in the luminosity function of non-DA white dwarfs, which is not the case.
 |
Fig. 3 Top panel: luminosity function of DA white dwarfs of Krzesinski et al. (2009) – solid line and filled squares – and our fiducial white dwarf luminosity function – dashed line and empty squares. Middle panel: total number of objects of Krzesinski et al. (2009) – solid line and filled symbols – and that obtained in our fiducial model – dashed line and open squares. In this panel we also plot the antilogarithm of the observed white dwarf luminosity function – dotted line and empty circles. Bottom panel: average contribution per object, as obtained from the data of Krzesinski et al. (2009) and from our population synthesis simulations – dashed line and empty squares. The solid line connecting the filled squares shows the average contribution of DA white dwarfs, while the dotted line connecting the empty circles shows that of non-DA white dwarfs. |
To clarify this issue, Fig. 3 displays the luminosity function of DA white dwarfs in the SDSS and several other interesting quantities. In the top panel of this figure, we show both the observed luminosity function (solid line with solid symbols) from Krzesinski et al. (2009) and our fiducial model (dashed line and open symbols). The middle panel of Fig. 3 depicts the total number of white dwarfs for each luminosity bin of the Krzesinski et al. (2009) luminosity function (solid line and filled symbols). Note that the total number of objects is monotonically decreasing with luminosity. Also shown in this panel are the total number of DA white dwarfs obtained in our fiducial simulation (dashed line connecting open squares), and the antilogarithm of the white dwarf luminosity function (dotted line connecting hollow circles) derived from the SDSS – that is, the antilogarithm of the luminosity function shown in the top panel, which allows to gain more insight on the statistical behavior of the luminosity function. All three curves have been normalized to the luminosity bin with log (L/L⊙) = −0.5 (that is, Mbol = 3.45). This panel clearly demonstrates that because our theoretical simulations yield more white dwarfs in the luminosity range of the plateau than does the observed white dwarf luminosity function, their contribution to the number density of stars in the region of the plateau must therefore be smaller. Moreover, it is interesting to note that although the number of objects in the SDSS is monotonically increasing with fainter luminosities, the antilogarithm of the white dwarf luminosity function is not, thus pointing towards an artifact existing in the observational white dwarf luminosity function. Finally, in the bottom panel of Fig. 3, we show the average 1/Vmax contribution for each luminosity bin in the SDSS sample of DA white dwarfs (solid line and filled squares), in our fiducial simulation (dashed line and open squares), and in the SDSS sample of non-DA white dwarfs (dotted line and hollow circles). These curves show that for the population of DA white dwarfs, the average value of 1/Vmax presents a peak at the range of appropriate luminosities which is ~20 times larger than expected, pointing towards an artifact produced by one or several of the objects of the observational sample. Moreover, given that our simulations predict a larger number of objects in the relevant range of effective temperatures, we conclude that the origin of the plateau does not reside in an excess of objects in these luminosity bins, but rather in that their contribution to the luminosity function is somehow larger than it should be.
 |
Fig. 4 Distribution of distances above the Galactic plane of DA white dwarfs in the sample of Krzesinski et al. (2009) and in our simulated sample as a function of the magnitude. The small symbols correspond to the results of our Monte Carlo simulations, while the large ones represent the observational data. Empty symbols correspond to white dwarfs with derived masses smaller than 0.49 M⊙, whereas filled symbols represent white dwarfs with measured masses larger than this value. The top panel presents the original data of Krzesinski et al. (2009), while the bottom panel shows revised distances obtained assuming that the mass of each of these white dwarfs is 0.49 M⊙. |
 |
Fig. 5 Luminosity functions of DA white dwarfs for several mass cuts. See text for details. The solid line with filled squares represents the original Krzesinski et al. (2009) DA white dwarf luminosity function, the dashed line with empty squares is our simulated luminosity function, and the dotted line with filled triangles is the Krzesinski et al. (2009) DA luminosity function with our mass adjustments as described in the text. |
To investigate this point in detail, the top half of Fig. 4 shows the distribution of distances above the Galactic plane of DA white dwarfs in the sample of Krzesinski et al. (2009) – large symbols – as well as that obtained in a typical Monte Carlo realization – small symbols. Our simulation matches remarkably well the distribution of vertical distances of the white dwarfs in the SDSS sample except in the region of the plateau. which in this plot is delimited by the vertical dashed lines. In particular, there is a group of white dwarfs in this region of the SDSS luminosity function with noticeable large distances above the Galactic plane that our population synthesis model does not reproduce. Upon inspecting the original sample of Krzesinski et al. (2009), we found that most of these white dwarfs have masses well below 0.49 M⊙ – the theoretical lower limit of a carbon-oxygen white dwarf – and thus cannot be single white dwarfs. To highlight the effects of the mass determination in the luminosity function, we highlight these low-mass white dwarfs using open squares whereas those white dwarfs with masses compatible with the theoretical lower limit for carbon-oxygen white dwarfs are displayed using solid squares. Clearly, the vast majority of white dwarfs in the region where the DA white dwarf luminosity function has a plateau have determined masses smaller than 0.49 M⊙. To explore the effect of these low mass determinations, the lower panel of Fig. 4 shows revised distances above the Galactic plane calculated assuming that the masses of all the less than 0.49 M⊙ white dwarfs are instead the minimum mass of a carbon-oxygen core white dwarf, 0.49 M⊙. Now, the discrepancy between the observed and simulated samples largely disappears, and although there are white dwarfs with large distances above the Galactic plane the relative number of these white dwarfs agrees with our simulations.
Figure 5 explores the effects of the DA mass determinations in the SDSS DA white dwarf luminosity function. Since white dwarfs with masses smaller than 0.49 M⊙ cannot be single carbon-oxygen white dwarfs, either these white dwarfs are members of unresolved binaries and thus, they should be excluded from the observational sample, or the mass determination of these white dwarfs is an artifact of the reduction procedure, and therefore its mass should be at least the minimum mass for a white dwarf with a carbon-oxygen core. To explore the first possibility, we apply different mass cuts to the as published SDSS sample and we compute the DA white dwarf luminosity function excluding all stars with masses smaller than the mass cut. Fig. 5 shows the results. With a mass cut Mcut = 0.48 M⊙, the resulting luminosity function – shown as a dotted line connecting triangles – is barely affected and is very similar to the original luminosity function of Krzesinski et al. (2009) – solid line connecting solid squares – and very different from our simulated result – dashed line connecting open squares. However, with a Mcut = 0.49 M⊙ mass cut, the situation changes completely and the updated observational luminosity function perfectly agrees with the simulated one. If the mass cut is increased to Mcut = 0.50 M⊙, the agreement between luminosity functions is poor, as expected, and a significant paucity of hot DA white dwarfs becomes rather evident. Finally, in the bottom panel of Fig. 5, we simply assume that DA white dwarfs with masses smaller than MWD < 0.49 M⊙ have erroneously determined masses and that their real masses should be precisely 0.49 M⊙. Here again, we see remarkable agreement between the simulated and the observational luminosity functions, very similar to that obtained applying a mass cut Mcut = 0.49 M⊙ to the SDSS sample. All in all, we conclude that the luminosity function of DA white dwarfs of Krzesinski et al. (2009) must be revised, since it is very sensitive to the mass determinations of DA white dwarfs. We provide the values of the corrected luminosity function in Table 1, where we list the bolometric magnitude, the space density and the number of stars in each bin, assuming that the minimum mass of the white dwarfs in the sample of Krzesinski et al. (2009) is 0.49 M⊙.
4. Conclusions
Observed DA white dwarf luminosity function dwarfs after applying the correction for those objects with masses below 0.49 M⊙.
We presented a set of simulations of the luminosity function of hot white dwarfs. Our results are in excellent agreement with the observations for non-DA stars, while for DA white dwarfs we found that a plateau present in the luminosity function at Mbol ≈ 2.0 – or, equivalently, log (L/L⊙) ≈ 1 – cannot be reproduced by our simulations. We first discarded that this plateau could be due to a global Galactic input, like a recent burst of star formation, because if this were the case, the luminosity function of hot non-DA white dwarfs should show a similar plateau. We then investigated other possible origins of this plateau. In particular, we studied the possible role of NLTE effects and metal contamination in the atmospheres of hydrogen-rich white dwarfs, the role of the so-called Balmer-line problem for very hot white dwarfs, and the possibility that the available cooling sequences were severely affected by the initial conditions adopted to compute them, and the statistical uncertainties in the white dwarf sample. We found that at the relevant luminosities of the plateau, the effects of NLTE corrections are limited and that metal contamination plays a minor role in shaping the luminosity function. This is also the case when the Balmer-line problem is taken into account. We also discarded the explanation that the available cooling tracks are severely affected by the choice of initial conditions. Thus, we were left with a possible statistical fluctuation, which we investigated in detail. We found that even though our theoretical simulations yield more white dwarfs in the luminosity range of the plateau than exist in the Krzesinski et al. (2009) sample, their contribution to the number density of stars in this region is smaller than that of the SDSS sample, thus pointing towards an artifact in the derivation of the SDSS luminosity function.
We therefore analyzed the distribution of masses and distances of the SDSS sample and we found that within the range of luminosities of the plateau, the SDSS white dwarf luminosity function is almost completely dominated by the contributions of a handful of white dwarfs with masses smaller than 0.49 M⊙, the lower theoretical mass for a carbon-oxygen white dwarf. Thus, either these objects are members of unresolved binaries, or they
have erroneously determined masses. We found that once these objects are excluded from the calculation of the DA white dwarf luminosity function, the agreement with our simulated luminosity function is excellent. Additionally, we computed the distances setting the mass of each of these <0.49 M⊙ white dwarfs at 0.49 M⊙, again finding excellent agreement with our simulated luminosity functions and that obtained with a 0.49 M⊙ mass cut applied to the SDSS sample. We therefore conclude that the luminosity function of hot DA white dwarfs of Krzesinski et al. (2009) is contaminated by white dwarfs with incorrectly determined low masses (below 0.49 M⊙) and we provide a revised white dwarf luminosity function in Table 1. The analysis presented in this paper also confirms the validity of the white dwarf theoretical cooling sequences at high effective temperatures via the good match of our model luminosity functions to that of the SDSS observations. We also emphasize that the way in which the observational luminosity function of hot white dwarfs is obtained is very sensitive to the particular implementation of the method used to derive the masses of the sample.
Acknowledgments
This research was supported by AGAUR, by MCINN grant AYA2011–23102, by the European Union FEDER funds, and by the ESF EUROGENESIS project (grant EUI2009-04167).
References
- Althaus, L. G., García-Berro, E., Isern, J., Córsico, A. H., & Rohrmann, R. D. 2007, A&A, 465, 249 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., Córsico, A. H., Isern, J., & García-Berro, E. 2010, A&ARv, 18, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Benvenuto, O. G., & Althaus, L. G. 1997, MNRAS, 288, 1004 [NASA ADS] [CrossRef] [Google Scholar]
- Bergeron, P., Wesemael, F., & Beauchamp, A. 1995, PASP, 107, 1047 [NASA ADS] [CrossRef] [Google Scholar]
- Catalán, S., Isern, J., García-Berro, E., & Ribas, I. 2008a, MNRAS, 387, 1693 [NASA ADS] [CrossRef] [Google Scholar]
- Catalán, S., Isern, J., García-Berro, E., et al. 2008b, A&A, 477, 213 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Diaz-Pinto, A., García-Berro, E., Hernanz, M., Isern, J., & Mochkovitch, R. 1994, A&A, 282, 86 [NASA ADS] [Google Scholar]
- Fontaine, G., Brassard, P., & Bergeron, P. 2001, PASP, 113, 409 [NASA ADS] [CrossRef] [Google Scholar]
- García-Berro, E., Hernanz, M., Isern, J., & Mochkovitch, R. 1988a, Nature, 333, 642 [NASA ADS] [CrossRef] [Google Scholar]
- García-Berro, E., Hernanz, M., Mochkovitch, R., & Isern, J. 1988b, A&A, 193, 141 [NASA ADS] [Google Scholar]
- García-Berro, E., Hernanz, M., Isern, J., & Mochkovitch, R. 1995, MNRAS, 277, 801 [NASA ADS] [CrossRef] [Google Scholar]
- García-Berro, E., Torres, S., Isern, J., & Burkert, A. 1999, MNRAS, 302, 173 [NASA ADS] [CrossRef] [Google Scholar]
- García-Berro, E., Torres, S., Isern, J., & Burkert, A. 2004, A&A, 418, 53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García-Berro, E., Torres, S., Althaus, L. G., et al. 2010, Nature, 465, 194 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- García-Berro, E., Lorén-Aguilar, P., Torres, S., Althaus, L. G., & Isern, J. 2011, JCAP, 5, 21 [Google Scholar]
- Geijo, E. M., Torres, S., Isern, J., & García-Berro, E. 2006, MNRAS, 369, 1654 [NASA ADS] [CrossRef] [Google Scholar]
- Gianninas, A., Bergeron, P., Dupuis, J., & Ruiz, M. T. 2010, ApJ, 720, 581 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, B. M. S., Anderson, J., Brewer, J., et al. 2007, ApJ, 671, 380 [NASA ADS] [CrossRef] [Google Scholar]
- Isern, J., García-Berro, E., Hernanz, M., Mochkovitch, R., & Torres, S. 1998, ApJ, 503, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Isern, J., García-Berro, E., Torres, S., & Catalán, S. 2008, ApJ, 682, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Krzesinski, J., Kleinman, S. J., Nitta, A., et al. 2009, A&A, 508, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lamb, D. Q., & van Horn, H. M. 1975, ApJ, 200, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Napiwotzki, R., Green, P. J., & Saffer, R. A. 1999, ApJ, 517, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Renedo, I., Althaus, L. G., Miller Bertolami, M. M., et al. 2010, ApJ, 717, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Rowell, N. 2013, MNRAS, 434, 1549 [NASA ADS] [CrossRef] [Google Scholar]
- Scalo, J. 1998, in The Stellar Initial Mass Function (38th Herstmonceux Conference), eds. G. Gilmore, & D. Howell, ASP Conf. Ser., 142, 201 [Google Scholar]
- Torres, S., García-Berro, E., Burkert, A., & Isern, J. 2002, MNRAS, 336, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Tremblay, P.-E., Bergeron, P., & Gianninas, A. 2011, ApJ, 730, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Winget, D. E., Hansen, C. J., Liebert, J., et al. 1987, ApJ, 315, L77 [NASA ADS] [CrossRef] [Google Scholar]
- York, D. G., Adelman, J., Anderson, Jr., J. E., et al. 2000, AJ, 120, 1579 [Google Scholar]
All Tables
Observed DA white dwarf luminosity function dwarfs after applying the correction for those objects with masses below 0.49 M⊙.
All Figures
 |
Fig. 1 White dwarf luminosity functions for hot DA and non-DA white dwarfs for two different models – see text Sect. 3 for details. The solid line with filled squares is the luminosity function of Krzesinski et al. (2009), while the dashed lines with empty squares show the results of our simulations. |
| In the text | |
 |
Fig. 2 Synthetic luminosity function of hot white dwarfs obtained using different assumptions about the atmospheric composition of hot DA white dwarfs and two sets of model atmospheres, compared to the observational luminosity function of the SDSS (Krzesinski et al. 2009) – solid line and filled squares. The top two panels show the synthetic luminosity functions of hot DA white dwarfs when NLTE corrections and metal contamination, and when the corrections of Gianninas et al. (2010) to the so-called Balmer-line problem are considered. The two bottom panels display the results of our simulations when the cooling tracks of Renedo et al. (2010) are employed – that is, our fiducial model – whereas in the second bottom panel we display the results obtained when the model atmospheres of Tremblay et al. (2011) are used. In all four panels the results of the population synthesis calculations are plotted using dashed lines and open squares. |
| In the text | |
 |
Fig. 3 Top panel: luminosity function of DA white dwarfs of Krzesinski et al. (2009) – solid line and filled squares – and our fiducial white dwarf luminosity function – dashed line and empty squares. Middle panel: total number of objects of Krzesinski et al. (2009) – solid line and filled symbols – and that obtained in our fiducial model – dashed line and open squares. In this panel we also plot the antilogarithm of the observed white dwarf luminosity function – dotted line and empty circles. Bottom panel: average contribution per object, as obtained from the data of Krzesinski et al. (2009) and from our population synthesis simulations – dashed line and empty squares. The solid line connecting the filled squares shows the average contribution of DA white dwarfs, while the dotted line connecting the empty circles shows that of non-DA white dwarfs. |
| In the text | |
 |
Fig. 4 Distribution of distances above the Galactic plane of DA white dwarfs in the sample of Krzesinski et al. (2009) and in our simulated sample as a function of the magnitude. The small symbols correspond to the results of our Monte Carlo simulations, while the large ones represent the observational data. Empty symbols correspond to white dwarfs with derived masses smaller than 0.49 M⊙, whereas filled symbols represent white dwarfs with measured masses larger than this value. The top panel presents the original data of Krzesinski et al. (2009), while the bottom panel shows revised distances obtained assuming that the mass of each of these white dwarfs is 0.49 M⊙. |
| In the text | |
 |
Fig. 5 Luminosity functions of DA white dwarfs for several mass cuts. See text for details. The solid line with filled squares represents the original Krzesinski et al. (2009) DA white dwarf luminosity function, the dashed line with empty squares is our simulated luminosity function, and the dotted line with filled triangles is the Krzesinski et al. (2009) DA luminosity function with our mass adjustments as described in the text. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


