EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 563 (March 2014) A&A, 563 (2014) A57 Full HTML
Free Access
Issue
A&A
Volume 563, March 2014
Article Number A57
Number of page(s) 16
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/201322653
Published online 06 March 2014

© ESO, 2014

1. Introduction

Besides mapping the innermost regions of active galactic nuclei (AGN), the hardest X-rays ≳ 15 keV present the further advantage of not being affected by absorption, provided that the hydrogen column density NH along the line of sight is lower than a few 1023 cm-2. As a result, hard X-rays can be effectively used to study the intrinsic properties of AGN emission, testing the validity of unification models that in first approximation explain the differences between the different AGN classes as a function of the viewing angle (e.g., Beckmann & Shrader 2012). In radio quiet AGN, the hard X-ray emission is postulated to originate in a two-phase medium, where the soft disk photons are Comptonized by electrons in a hot plasma above the disk (Haardt & Maraschi 1993). In radio loud objects, an additional contribution from inverse Compton scattering from relativistic electrons in the jet, as well as synchrotron radiation, can dominate the X-ray output.

Moreover, AGN are known to exhibit variability at all observed frequencies, whose study can provide important information about the physics, the structure, and the dynamics of the emitting source. In the softer X-ray domain (≲ 10 keV), extensive variability studies have been carried out, especially in the recent years thanks to the numerous monitoring campaigns with RXTE and XMM-Newton, covering time scales from hours to years. Many important results have been obtained with these observations, such as the complex correlation of the X-rays with the emission at other wavelengths (e.g., McHardy et al. 2007; Soldi et al. 2008; Bell et al. 2011; Mehdipour et al. 2011; Chatterjee et al. 2011), in particular, in the optical-UV band (e.g., Shemmer et al. 2003; Uttley 2005; Arévalo et al. 2008b; Breedt et al. 2010); the study of X-ray lag spectra (e.g., Arévalo et al. 2008a; Zoghbi et al. 2010; De Marco et al. 2013); the correlations between variability properties and black hole mass (e.g., Czerny et al. 2001; Lu & Yu 2001; Uttley et al. 2002; Papadakis 2004) and accretion rate (McHardy et al. 2006; Körding et al. 2007). See McHardy (2010) for a review of X-ray variability and its scaling from stellar to super-massive black holes. On the other hand, the large majority of the hard X-ray variability studies performed in the last years focused on the spectral variability of AGN at different flux levels for single bright sources or for small samples of selected objects, thanks to pointed observations of the BeppoSAX (e.g., Petrucci et al. 2000; Nicastro et al. 2000; de Rosa et al. 2007), INTEGRAL (e.g., Pian et al. 2006, 2011; Beckmann et al. 2008; Lubiński et al. 2010; Soldi et al. 2011a; Petrucci et al. 2013) and Suzaku (e.g., Reeves et al. 2007; Itoh et al. 2008; Terashima et al. 2009; Fukazawa et al. 2011; Reis et al. 2012) satellites. These X-ray studies suggest different origins for the observed variability, such as changes in the amount of absorption or of its ionization, fluctuations in the seed photon flux, intrinsic modifications of the corona properties or geometry (or of the jet parameters, in case of radio loud AGN), or a variable contribution of different spectral components, with at least some of these scenarios driven by accretion rate variations.

However, with the only exception being the CGRO/BATSE instrument, detecting only a handful of AGN (Harmon et al. 2004), long-term hard X-ray monitoring has not been possible until recent years, because of the observing strategy of the hard X-ray satellites and the limited size of the field of view of their instruments. Furthermore, latest generation and future hard-X-ray telescopes such as NuSTAR will have small fields of view and relatively inflexible scheduling capabilities, so future studies may tend to be limited to either short time scales or in the number of observed objects. Since November 2004, the Burst Alert Telescope (BAT, Barthelmy et al. 2005) instrument on board the Swift satellite (Gehrels et al. 2004) has been observing the sky in the 14–195 keV energy range. Thanks to its large field of view of ~1.4 sr and to Swift’s observing strategy, the BAT has been monitoring a large number of hard X-ray sources (Cusumano et al. 2010; Baumgartner et al. 2013), providing a long-term and sufficiently sampled data set for the first time. Swift/BAT light curves on different time scales and energy bands and extracted with different methods are provided through the hard X-ray transient monitoring pages1 (Krimm et al. 2013) and for the BAT 58-month hard X-ray survey2 that includes more than 1000 objects, about 60% of which are AGN. The latter has been recently updated to cover 70 months of observations (Baumgartner et al. 2013).

A first study of the variability of hard X-ray-selected AGN using BAT data has been presented by Beckmann et al. (2007a). It includes 44 AGN detected with high significance over the first nine months of BAT observations. The variability study in the 14–195 keV band was performed using a maximum likelihood estimator and the structure function analysis. Among the main results of this work, Seyfert 2/obscured objects were found to be more variable than Seyfert 1/unobscured ones, and an anti-correlation was detected between variability and luminosity.

Preliminary studies of the five years BAT observations but with limited numbers of AGN have been presented by Soldi et al. (2010), Ricci et al. (2011a), and Caballero-Garcia et al. (2012). In particular this last study focused on five bright AGN, detecting spectral  variability  in three of them, which is consistent with

the electron plasma temperature decreasing with increasing flux, within the Comptonization scenario.

Shimizu & Mushotzky (2013, hereafter SM13) have calculated the power density spectra (PDS) of 30 AGN for the first time in hard X-rays (all these objects are also included in our study), using BAT 14–150 keV data covering time scales from one week to a few years (νPDS ~ 10-8−10-6 Hz). All but one PDS were found to be well fitted by a simple power law with slope α ~ −0.8, similar to the PDS measured in the 2–10 keV domain at time frequencies lower than a break frequency 1/TB. In fact, the PDS of AGN in the 2–10 keV domain has a characteristic power law shape with index αPDS = −1 for long time scales, steepening to αPDS = −2 for times scales shorter than a source-specific break time TB (Uttley 2005; González-Martín & Vaughan 2012), which is found to scale with black hole mass and accretion rate following the relation described by McHardy et al. (2006). The lack of correlations between variability and luminosity, and between variability and black hole mass, in the sample presented by Shimizu & Mushotzky (2013) has, therefore, been ascribed to the long time scales probed by this study. No decisive evidence was found to determine whether AGN long-term variability is energy dependent.

We present here our variability analysis of the largest AGN sample with a sufficient hard X-ray monitoring to perform this kind of study. Our analysis provides an orthogonal approach to the one presented by SM13, since we consider the frequency-independent variations of the full long-term light curves, and therefore we are able to extend our study to a much larger AGN sample, while for the PDS analysis, a high signal-to-noise ratio (S/N) is required, thus limiting the use of this technique to the 30 objects already presented by SM13. Furthermore, we are also able to investigate the dependence of variability on energy in the hard X-ray band.

A description of the AGN light curves in the BAT 58-month survey is presented in Sect. 2, along with the estimate of the systematic uncertainties. In Sect. 3 the maximum likelihood estimator for variability is introduced and the selected sample of 110 AGN described. The correlation analysis between variability and the AGN fundamental parameters is detailed in Sect. 4, while Sect. 5 presents the study of spectral variability within the BAT energy range. We discuss our results (Sect. 6) with particular emphasis on the comparison between hard X-ray and soft X-ray variability, since this can provide important insight into the mechanisms responsible for the observed emission across the high-energy spectrum. A summary of our conclusions is given in Sect. 7.

Considering the importance of the analyzed time scales in the results presented here, we generally refer to long time scales (and low time frequencies) for variability studies considered to sample the PDS above the break TB, and to short time scales (and high time frequencies) below the break. In the following we use a ΛCDM cosmology with ΩM = 0.3, ΩΛ = 0.7, and H0 = 73 km s-1 Mpc-1.

2. Swift/BAT light curve analysis

Among the 1092 sources detected in the BAT 58-month survey, 625 are AGN. We exclude from this list the six pairs of AGN whose sky positions are too close to safely avoid contamination of the light curves, i.e., objects with BAT coordinates within 2 arcmin of each other. For these 613 AGN, we retrieved the publicly available light curves covering the time from the beginning of the mission up to May 2010, therefore including up to 66 months of data3. The light curves have been extracted from the snapshot (i.e. a single Swift pointing lasting about 20 min) images corrected for off-axis effects. The images were created in eight energy bands, i.e., 14–20, 20–24, 24–35, 35–50, 50–75, 75–100, 100–150, and 150–195 keV. To convert count rates in the total 14–195 keV band to fluxes, we assume a Crab-like spectrum (Γ = 2.15; Tueller et al. 2010) with a flux of FCrab,14−195 keV = 2.44 × 10-8 erg cm-2 s-1 corresponding to a count rate of xCrab,14−195 keV = 0.0418 counts s-1 detector-1 (average from the Crab snapshot light curve). The complete description of the BAT data analysis and light curve extraction is provided in Tueller et al. (2010) and Baumgartner et al. (2013).

The reference light curves used for our analysis are obtained from the combined 14–195 keV light curves first rebinned to 30 days and then filtered to exclude points with exposure time shorter than one day and data points with error bars larger than ΔFcut,30 days = 1.7 mCrab. To derive this value, the histogram of the flux uncertainties for all light curves was built in logarithmic space, and the histogram peak and minimum identified. The value ΔFcut,30 days = 2 × ΔFpeak − ΔFmin (i.e., as far above the peak of the distribution as the minimum is below) is considered to mark the beginning of the high-value tail of the distribution of flux uncertainties and is, therefore, used as the cut-off value, ΔFcut,30 days.

2.1. Light curve systematic errors

Residual systematic uncertainties can affect the light curves and need to be taken into account before a variability analysis can be performed. Among them, the most important contributions come from a component σsys,A = sysA × F, which is proportional to the source flux, a component σsys,B = sysB × σstat that can be derived from empty sky positions and a term σsys,C = sysC × σstat due to summing up energy and time bins that are somehow correlated. The term σsys,A is estimated using the Crab light curve under the assumption that it is constant. Fitting the Crab orbital light curve with a constant, a σsys,A = 0.06 × F systematic error needs to be added to obtain a reduced χ2 equal to 1. A further source of uncertainty is expected following the finding of long-term variability in the Crab light curve (up to ~7% on a year time scale; Wilson-Hodge et al. 2011); therefore, the value of the sysA term is likely to be overestimated here. Owing to the difficulty of disentangling the systematic component from the intrinsic Crab variability, we prefer to choose a conservative approach and to adopt the sysA = 0.06 value. In any case, even when reducing this term to 0.01, the amplitude of the variations increases on average by only 2% to 3%, largely within the estimated uncertainties on the variability estimator (see Sect. 3.1).

The component σsys,B is estimated by constructing orbital light curves from blank sky positions and building the histogram of all the resulting significances. By selecting sky positions with no sources, a Gaussian distribution centered on zero for the significances is expected. Any significant deviation from a zero mean value or from a width equal to one would point towards systematic uncertainties. Indeed, the statistical errors need to be increased by σsys,B = 0.08 × σstat in order to obtain a Gaussian fit to the histogram of significances with width equal to one.

Finally, from the comparison between the 14–195 keV monthly light curves extracted from the one-month integrated mosaic images and the monthly light curves obtained by rebinning the orbital light curves and summing up eight energy bands over the full 14–195 keV range, we estimate that an additional statistical error contribution, σsys,C = 0.08  ×  σstat, is needed to take the effects of correlated energy and time bins into account. The final statistical plus systematic error is given by σtot=(sysA×F)2+[σstat(1+sysB+sysC)]2\hbox{$\sigma_{\rm tot} = \sqrt{({\rm sys}_{\rm A} \times F)^2 + [\sigma_{\rm stat} (1 + {\rm sys}_{\rm B} + {\rm sys}_{\rm C})]^2}$}. Figure 1 presents five example light curves with different S/Ns and variability.

thumbnail Fig. 1

Examples of 30-d binned, 14–195 keV BAT light curves for objects presenting different variability levels (increasing from top to bottom) and with different signal-to-noise ratios. The estimator SV represents the intrinsic variability of a light curve, renormalized to the average flux and in percentage (see Sect. 3.1).

thumbnail Fig. 2

Histograms of the time-averaged 14–195 keV flux (top), of the variability index V from the χ2 test (middle; the vertical dashed line indicates V = 1.3), and of the variability amplitude estimator SV (bottom) for the total sample of 613 AGN (black) and for the selected sample of 110 AGN (red hatched). We assigned V = 10 to those objects with Pχ2 < 10-6. SV could be computed for 464 of the BAT-detected AGN.

3. Hard X-ray variability properties

As an initial estimate of the variability of our AGN sample, we fit the 30-day binned light curves of the 613 AGN with a constant function, and apply a χ2 test. The variability index V is defined as V = −log (1 − Pχ2), where Pχ2 is the null hypothesis probability to obtain such a χ2 if the source were constant. For 36% of the light curves in the sample the fit to a constant intensity source results in V > 1.3 (i.e., Pχ2 ≤ 5%; Paolillo et al. 2004; Lanzuisi et al. 2013), indicating that these objects exhibit significant variability (Fig. 2). In particular, 34% of the Seyfert galaxies are found to be variable against the 44% of the radio loud population. Among Seyfert galaxies, about 41% of type-2 objects show variability, contrary to only 29% of the type-1 objects.

3.1. Amplitude of the variations

Several methods can be used to quantify the amplitude of the variations in a light curve, e.g. excess variance or fractional variability amplitude (Vaughan et al. 2003; Ponti et al. 2004; Soldi et al. 2008). Almaini et al. (2000) proposed a numerical approach, arguing that this is a more appropriate method in the presence of non-uniform measurement uncertainties, while recently Allevato et al. (2013) have shown that it provides results equivalent to the normalized excess variance. The Almaini method is based on a maximum-likelihood estimate of the σQ parameter, representing the variability of the light curve. In the case of constant measurement uncertainties (σi = const.), it reduces to the excess variance (σQ = σXS). The σQ parameter is defined so as to satisfy the following equation (see Almaini et al. 2000; and Beckmann et al. 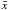2007a, for more details): ∑i=1N[(xi−x̅)2−(σi2+σQ2)](σi2+σQ2)2=0\begin{equation} \sum^{N}_{i=1} \frac{[(x_{\rm i}-\bar{x})^2 - (\sigma_{\rm i}^2+\sigma_{\rm Q}^2)]}{(\sigma_{\rm i}^2+\sigma_{\rm Q}^2)^2} = 0 \end{equation}(1)where \hbox{$\bar{x}$} is the mean value of the light curve xi with measurement uncertainties σi. The maximum-likelihood estimator has also been successfully used in, say, Mateos et al. (2007) and in Chitnis et al. (2009). For continuity and comparison with Beckmann et al. (2007a), we choose to apply the Almaini method here. Unlike the original prescription, we use the weighted rather than the arithmetic mean to compute σQ, because it provides more stable results in general, being less sensitive to the presence of outlier points. Nevertheless, we verified that equivalent results are obtained in both cases when analyzing the final AGN sample presented here.

To compare the variability of different objects, we renormalize σQ to the average flux ⟨F⟩ of the source, obtaining the SV = σQ/ ⟨F⟩ × 100% variability estimator (Fig. 2). Therefore, SV measures, in percentage units, the amplitude of the intrinsic variability of a light curve, corrected by measurement uncertainties and renormalized to the average flux. Unlike in Beckmann et al. (2007a), the systematic uncertainties deduced from the Crab and blank sky positions have already been included in the orbital light curves and no further correction to SV is therefore required.

Table 1

Average properties of the BAT AGN in our variability sample, as a function of the AGN class and the amount of intrinsic absorption.

In computing SV, the uncertainty σmeas is determined with a bootstrap technique (Simpson & Mayer-Hasselwander 1986). For each object, 100 000 light curves are randomly drawn from the original one, with the same total number of points and allowing the same data point to be drawn more than once. The variability estimator SV is then computed for each simulated light curve and its frequency distribution built. The 15.9th and 84.1th percentiles of this distribution are taken as an estimate of the 1σ confidence intervals (see also Vaughan et al. 2003). Owing to the stochastic nature of variability, a further source of uncertainty σsampl is introduced by the uneven sampling of the light curves. This contribution can be understood as the dispersion of SV values measured on the same light curve on which different samplings are applied. We estimate this contribution with the bootstrap method, but this time using the initial, unfiltered light curves (i.e., all having regular 30-day sampling). For each object, 10 000 light curves with N points are randomly drawn from the original one, where N is the number of points of the filtered light curve and where every data point cannot be drawn more than once. The 15.9th and 84.1th percentiles of the SV frequency distribution are taken as an estimate of the 1σ confidence intervals. The final uncertainty on SV is obtained by combining in quadrature σmeas and σsampl.

3.2. Sample selection

The final sample of 110 AGN was selected based on the following two criteria: 1) the average value of the S/N of the points in the light curve is larger than 2; 2) SV can be measured for the given 30-day binned, filtered light curve, i.e., the uncertainties are smaller than the measurable intrinsic variability. The first criterion is essentially (but not exactly) equivalent to using a flux threshold of F(14−195 keV) > 3.8 × 10-11 erg cm-2 s-1 or a S/N over the full light curve larger than 15, and it selects 115 sources (Fig. 2). The second criterion excludes only five additional sources. The filtering applied to the light curves (see Sect. 2) excludes no more than 22% (~10% on average) of the data for the objects in the selected sample4. The resulting sample is composed of 88 Seyfert galaxies (36 Seyfert 1, 17 of intermediate type, 32 Seyfert 2, and 3 Narrow Line Seyfert 1), 9 radio galaxies and 13 blazars. These sources cover a range of 14–195 keV fluxes between F = 10-11 and 10-9 erg cm-2 s-1 (Fig. 2) and redshifts up to z = 2.5 (see Fig. 1 in Soldi et al. 2012 for the redshift distribution of the sample). The non-blazar objects belong to the local AGN population with redshifts up to z = 0.1 and an average value of ⟨z⟩ = 0.024 (Table 1).

In Table 2 the values of SV are reported for the 110 AGN selected for the variability amplitude analysis. The blazar population shows a larger average variability (⟨SV⟩ bla = 33 ± 2%) compared to the radio quiet objects (⟨SV⟩ Sey = 19.3 ± 0.5%). A Kolmogorov-Smirnov test provides a probability PKS ≥ 98% that the blazar and Seyfert samples are not drawn from the same parent population. Nevertheless, extreme cases of high variability are present in both the blazar and Seyfert classes. An average variability SV > 90% is in fact detected in the two gamma-ray bright blazars QSO B0033 +595 and Mrk 421 and in the Seyfert 2 galaxy 2MASX J04440903+2813003.

The radio galaxies present an intermediate behavior between blazars and Seyferts, with ⟨SV⟩ RG = 24.0 ± 1.4%. Within the Seyfert class, intermediate and type 2 objects (⟨SV⟩ Sey1.5 + 2 = 20.8  ±  0.6%) are found to be only slightly more variable than type 1 (⟨SV⟩ Sey1 = 16.5  ±  0.9%), and a KS-test probability PKS ≥ 94% indicates that the Seyfert 1 and Seyfert 1.5–2 samples could be drawn from the same parent distribution. Furthermore, no difference is found in the average variability of absorbed and unabsorbed Seyfert galaxies (with NH = 1022 cm-2 the dividing line), with ⟨SV⟩ abs = 19.7 ± 0.6% and ⟨SV⟩ unabs = 19 ± 1%. The average properties of the different AGN classes are summarized in Table 1.

3.3. Black hole mass, hydrogen column density, and Eddington ratio

To test the dependence of variability on different AGN parameters, we collected the values of black hole masses MBH and hydrogen column density NH for our sample from the literature. The masses have been calculated with different methods, and when not available in the literature, the uncertainties on the values were estimated from the typical accuracy provided by the method following Beckmann et al. (2009). Out of the 110 objects, 92 have mass estimates (only an upper limit for MR 2251−178; Table 2), 86 have NH values, and for 23 only NH upper limits could be found.

For 63 objects (56 Seyferts, 4 radio galaxies, and 3 blazars), we collected the bolometric luminosities from the literature, selecting those estimated from the fitting of the spectral energy distributions (Woo & Urry 2002; Vasudevan & Fabian 2007, 2009; Vasudevan et al. 2009, 2010; Table 2). To estimate the bolometric luminosity from the X-ray one, constant corrections (Winter et al. 2009; Beckmann et al. 2009) and corrections that depend on the luminosity (Marconi et al. 2004), on the Eddington ratio (Vasudevan & Fabian 2007), on the spectral shape (Fabian et al. 2009), or on the intrinsic absorption (Vasudevan et al. 2010) have been proposed, but all fail to reproduce the large scatter of bolometric versus X-ray luminosity. However, to extend the sample for which we are able to compute the Eddington ratio, we also considered two of those bolometric corrections. The first one follows Beckmann et al. (2009), i.e., assumes that the bolometric luminosity Lbol is two times higher than the 1–200 keV luminosity, where L1−200 keV = 1.8 × L14−195 keV for a simple power law spectrum with photon index Γ = 1.9. The second one is based on the relation provided by Marconi et al. (2004) to compute Lbol using a luminosity-dependent bolometric correction. Since these corrections allow having estimates of Lbol for an additional 29 objects (19 Seyfert) and since they trace the bolometric luminosities computed from the SED fitting for our sample sufficiently well, we consider Lbol, SED throughout the paper but compare the results to those obtained with X-ray based Lbol estimates on a larger sample. The Eddington ratio is then computed as λEdd = Lbol/LEdd, where LEdd = 1.26 × 1038MBH/M⊙ erg s-1.

thumbnail Fig. 3

Variability estimator SV versus luminosity in the 14–195 keV band for the Seyfert galaxies in our sample. Yellow triangles represent the average of the variability estimator in different luminosity bins following Allevato et al. (2013).

thumbnail Fig. 4

Variability estimator SV versus intrinsic absorption for the Seyfert galaxy sample. Upper limits on NH are indicated with arrows. Yellow triangles represent the average of the variability estimator in different absorption bins.

4. Correlation analysis

To test for the dependence of the hard X-ray variability on the properties of the selected objects, we correlate the variability estimator SV with the X-ray luminosity L14−195 keV, black hole mass MBH, Eddington ratio λEdd, intrinsic hydrogen column density NH, and spectral shape Γ. We exclude the radio loud sources from the correlation analysis in order to have a uniform, local Seyfert sample for which it is not necessary to correct variability and luminosity for redshift and beaming effects, and for which the hard X-ray emission is dominated by accretion processes, with no jet contribution. In addition, the results for the Seyfert sample are easily comparable to previous studies that also focus on radio quiet objects.

We do not find any significant correlation of SV with luminosity (Fig. 3) or with absorption (Fig. 4). Variability appears to be marginally anti-correlated with Eddington ratio when using Lbol, SED to compute λEdd, with a Spearman ranking correlation coefficient of Rcorr = −0.3 corresponding to a probability for chance occurrence of Pcorr = 0.03 (Fig. 5, left panel). However, the correlation disappears when using a larger sample and the X-ray based bolometric corrections to estimate λEdd. 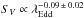When fitting the SV versus Eddington ratio relation with a power law model, we find SV∝λEdd−0.044±0.014\hbox{$S_{V} \propto \lambda_{\rm Edd}^{-0.044 \pm 0.014}$}, which steepens to SV∝λEdd−0.09 ± 0.02\hbox{$S_{V} \propto \lambda_{\rm Edd}^{-0.09 \,\pm \,0.02}$} when excluding the three sources at super-Eddington rates.

Unlike what is observed in the 2–10 keV band, we do not detect any anti-correlation between the 14–195 keV variability and the black hole mass (Rcorr = 0.06, Pcorr = 0.64; Fig. 6). This agrees with what was found by Shimizu & Mushotzky (2013) on a smaller sample (Fig. 6). On the other hand, Caballero-Garcia et al. (2012) report a trend toward decreasing variability with increasing black hole mass for the five brightest Seyfert galaxies at hard X-rays, with 20–50 keV BAT light curves rebinned to two days. However, when computing Fvar for the two-days binned, 14–195 keV light curves as presented in our work for the same five sources, and applying a Spearman rank correlation test (more robust than the linear/Pearson correlation one; e.g., Press et al. 2007), we do not find any anti-correlation between variability and black hole mass (Rcorr = −0.1, Pcorr = 0.87).

thumbnail Fig. 5

Left: variability estimator SV versus Eddington ratio for the Seyfert sample. Yellow triangles represent the average of the variability estimator in different Eddington ratio bins. Middle: photon index versus Eddington ratio for the Seyfert sample. Right: variability estimator SV versus photon index for all the Seyfert galaxies in our sample, separated into the different types. Empty black circles indicate those sources with 1023 < NH < 4 × 1023 cm-2.

The lack of an SV − MBH anti-correlation is most likely because the BAT survey samples time scales that are longer than the power density spectrum (PDS) break, TB. In fact, the X-ray PDS of AGN has a characteristic power law shape with index αPDS = −1 for long time scales and αPDS = −2 for times scales shorter than a source-dependent break time TB (typically of hours to weeks; Uttley 2005; Arévalo et al. 2008a; Markowitz 2009, 2010; González-Martín & Vaughan 2012), which is found to scale with black hole mass and bolometric luminosity following the relation described by McHardy et al. (2006). This implies a scaling of the variability amplitude with the same AGN properties when time scales close to or shorter than TB are considered. Above 15 keV the PDS obtained with BAT data on time scales of weeks to years show for 29 out of 30 objects a single power law with index αPDS ~ −0.8 (SM13), consistent with the 2–10 keV results and providing an upper limit of 26 days for the hard X-ray TB of these objects. However, if one assumed that TB is independent of energy and can be estimated using the McHardy et al. (2006) relation, one would find that for 12 Seyferts in our sample TB, pred is predicted to be longer than three years. This suggests the possibility that for those AGN, BAT has measured the variability at frequencies above the PDS break and that therefore a scaling of variability with black hole mass should be expected5. Nonetheless, no correlation is detected (Fig. 6). Recently, based on the 0.2–10 keV PDS analysis of 104 AGN and on the detection of a break in 15 of them, González-Martín & Vaughan (2012) have recomputed the TB − MBH − Lbol relation finding a weaker dependence on Lbol than in the McHardy et al. (2006) formulation. Therefore, considering the large uncertainties on the mass determination and bolometric luminosity estimate, and on the TB − MBH − Lbol relation, it is not possible to derive from the above arguments whether or not this relation is also valid at hard X-rays.

5. Spectral variability

5.1. Variability, photon index, and Eddington ratio

A significant anti-correlation is found between variability and photon index for Seyfert galaxies, in the sense that AGN with harder spectra are more variable (Rcorr = −0.5, Pcorr = 2 × 10-6, Fig. 5 right panel). The photon index used here is the result of a simple power law fit to the BAT spectrum. Even when excluding the objects with NH > 3 × 10-23 cm-2 for which absorption might start to have a noticeable influence on the hard X-ray spectrum, the anti-correlation is still significant (Pcorr = 6  ×  10-4).

A correlation is also identified between photon index and Eddington ratio (Rcorr = 0.56, Pcorr = 10-5; Fig. 5 middle panel), similar to what is observed in the 2–10 keV band on year time scales (Sobolewska & Papadakis 2009). The best fit to the data with a power law model results in 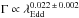Γ∝λEdd0.022 ± 0.002\hbox{$\Gamma \propto \lambda_{\rm Edd}^{0.022 \,\pm\, 0.002}$} (Γ∝λEdd0.039 ± 0.003\hbox{$\Gamma \propto \lambda_{\rm Edd}^{0.039\, \pm\, 0.003}$} when considering only sources with λEdd < 1). The correlation is also significant when using the X-ray bolometric corrections to compute λEdd. This relation has been suggested to be based on the geometry of the accretion flow, with stronger accreting objects having accretion disks whose inner radius is closer to the innermost circular stable orbit, so it can cool the hot corona more efficiently, resulting in softer X-ray spectra (Sobolewska & Papadakis 2009).

The marginal anti-correlation between variability and Eddington ratio (Fig. 5, left panel) could therefore be induced by the combination of the Γ − λEdd and SV − Γ ones (SV ∝ Γ−2.5  ±  0.3 for the total Seyfert sample).

thumbnail Fig. 6

Variability estimator SV versus black hole mass for the Seyfert galaxies in the sample. Empty circles highlight AGN with predicted break time longer than 3 years, while blue empty squares point out the Seyferts from the SM13 sample. The arrow indicates the MBH upper limit for MR 2251−178. Yellow triangles represent the average of the variability estimator in different black hole mass bins.

thumbnail Fig. 7

35–100 keV versus 14–24 keV variability estimator for the AGN in our sample. The dashed line indicates where objects with the same variability in the two bands would lie. Even though the variations in the two bands are well correlated, the variations in the lower-energy band are larger than those at higher energies for the majority of the radio quiet objects. Some of the most extreme outliers are labeled.

5.2. Variability in the 14–24 and 35–100 keV bands

To compare the variability at different energies, we use the 30-day binned light curves in the 14–24 and 35–100 keV bands (see Table 2). These energy bands were selected to provide comparable significance for a typical hard X-ray AGN spectrum with power law shape and photon index Γ = 1.8.

For a sample of 68 AGN (50 Seyferts, 9 radio galaxies, 9 blazars), we were able to estimate SV for the two selected bands (Fig. 7). In general, the variations are correlated well between the two bands (Rcorr = 0.6, Pcorr = 5 × 10-7). However, there is an average 10% shift of the Seyfert population towards higher amplitude of the variations at lower energies, aside from a very few exceptions. A Kolmogorov-Smirnov test indicates a probability PKS ≥ 98% that the variations in the two energy bands are different for the 50 Seyferts in this subsample. This is also true when separating the sample into the 13 unabsorbed (NH < 1022 cm-2) and 26 absorbed objects: absorbed and unabsorbed sources show the same average variability amplitude, with the lower energy band presenting greater variability (⟨SV⟩ unabs,14−24 keV = 26  ±  2%, ⟨SV⟩ abs,14−24 keV = 28  ±  1%, ⟨SV⟩ unabs,35−100 keV = 17 ± 2%, ⟨SV⟩ abs,35−100 keV = 16  ±  1%). On the other hand, on average the 18 radio loud AGN do not display a significant dependence of variability on energy.

thumbnail Fig. 8

Hardness ratio versus 14–195 keV flux for the 18 AGN showing spectral variability (13 Seyfert galaxies on the three top rows and 5 radio loud AGN on the bottom row). The black dots are from the 1-month binned light curves, and red squares indicate the average hardness ratio in different flux bins.

It is important to stress that the 14–24 and 35–100 keV bands have been selected specifically to have similar S/N for a typical AGN spectrum, therefore excluding the possibility that the behavior observed could be due to a bias introduced by the different uncertainties in the two bands. In fact, on average the difference between the S/N in the low- and high-energy band is 3% for the total sample (−1.4% for the Seyferts and 11% for the radio loud sources), with about half of the sample having higher S/N in the high-energy band.

When testing the possibility that the additional variability in the lower energy band could be ascribed to variations in the intrinsic absorption, we find that large and frequent variations would be needed. In fact, if we consider a simple power law spectrum (Γ = 1.9) with full-coverage absorption, variations on the order of ΔNH ~ 5−10 × 1023 cm-2 would be needed to produce flux variations of ΔF14−24 keV ~ 8−16% and ΔF35−100 keV < 0.7%. This would imply a 10% difference between the low- and high-energy flux variations within two observations and correspond to a ΔF14−195 keV ~ 3−6% contribution to the variability in the full band. However, to measure an increase in SV by 10% given our sampling baseline and rate, unrealistically large (⟨ΔNH⟩ at least up to ~1025 cm-2) and frequent (on average over 50% of the light curve points) variations in the absorbing column would be required, and would imply even larger variations in the energy band <10 keV. Even though variable absorbers are indeed common (Risaliti et al. 2002), such extreme variations are very rarely observed (see, e.g., NGC 1365, Risaliti et al. 2007).

5.3. Hardness ratio versus flux

To compare the spectral variability within the single sources, for each object we compute the hardness ratio on month time scale, defined as HR=F35−100 keV−F14−24 keVF35−100 keV+F14−24 keV·\begin{equation} HR = \frac{F_{35-100 \rm \, keV}-F_{14-24 \rm \, keV}}{F_{35-100 \rm \, keV}+F_{14-24 \rm \, keV}} \cdot \end{equation}(2)The dependence of HR on time is then fitted with a constant function, a χ2 test is applied, and the corresponding variability index V is computed (as defined in Sect. 3). Based on this, we select a subsample of 18 objects for which V > 1.3, as those presenting spectral variability. These are mostly the brightest objects in the sample, with a few exceptions (e.g., MCG−05−23−016, Circinus galaxy). The relatively low fraction of sources showing significant spectral variability agrees with the results presented by Mateos et al. (2007), who find spectral variability to be less common than flux variability on long time scales in the 0.2−12 keV band. In Fig. 8 the hardness ratios as a function of flux (normalized to the mean flux of each object) are presented. For eight Seyferts there is a clear trend toward spectral softening when the source brightens (Mrk 3, NGC 3516, NGC 4151, NGC 4507, NGC 4945, IC 4329A, NGC 5506, AX J1737.4−2907), while no significant correlation is detected for the other radio quiet objects. Our results agree with those reported by Caballero-Garcia et al. (2012) for NGC 4945, NGC 2110, and IC 4329, while different trends are observed for NGC 4388 and NGC 4151. This is possibly due to the different energy bands used to compute HR (20–50 and 50–100 keV in Caballero-Garcia et al. 2012).

There is no correlation between flux and spectral variations for radio loud objects, with the exception of Mrk 421 and Cen A, which exhibit marginal spectral hardening with increasing flux. Cen A has been observed to present a harder-when-brighter spectrum also during Suzaku observations (Fukazawa et al. 2011). This behavior has been interpreted as due to the increased contribution in the brighter state of a hard tail produced in the jet.

6. Discussion

6.1. Variability of the different AGN classes

Radio loud objects show larger amplitudes of the variations compared to Seyfert galaxies, as expected if their hard X-ray emission is dominated by the extreme processes taking place in a relativistic jet (e.g., Lichti et al. 2008), while hard X-ray emission from Seyfert galaxies is instead dominated by thermal Comptonization. This is even more evident considering that the variability of higher redshift blazars (4 out of 13 objects have z > 0.4) will actually increase when taking the effect of cosmological time dilation into account. Among radio loud objects, the radio galaxies seem to show rather intermediate variability amplitudes between the blazars and the radio quiet class, in agreement with the idea that the jet and the coronal emissions are probably both contributing. This makes it difficult to disentangle the relative importance of these components in the hard X-ray spectra of radio galaxies, as shown, for example, in Centaurus A (Beckmann et al. 2011), 3C 111 (de Jong et al. 2012), and in other radio galaxies (Grandi et al. 2006).

Among Seyfert galaxies, there are indications that type 1.5–2 objects are slightly more variable than type 1, as already found at hard X-rays in Beckmann et al. (2007a). A similar behavior has been reported by Saxton et al. (2011) when studying long-term X-ray variability properties of a sample of more than 1000 AGN detected by ROSAT and within the XMM-Newton slew survey. Following their study, the Seyfert 2 class has the highest fraction of sources with large variability in the 0.2–2 keV range, but it is not clear if the observed variability is due to changes in the line-of-sight column density, or it is instead intrinsic to the central engine. On the other hand, while in Beckmann et al. (2007a) there was a tentative trend toward more absorbed sources being more variable, here we do not observe any correlation between variability and absorption column density. Therefore, the global properties of variability as a function of AGN class point to general agreement with the basic formulation of AGN unification models, in which the differences are driven in first approximation only by AGN orientation and by the presence or absence of a relativistic jet.

Within our sample, there are three NLS1 galaxies, a class that is known to show peculiar characteristics in the soft X-ray domain, like a steep spectral continuum, and strong and fast variability. Most of these distinctive properties of NLS1s have been interpreted in the context of relatively small black hole masses undergoing rapid evolution, powered by higher accretion rates than their broad line equivalent (Peterson et al. 2000). The average hard X-ray photon index of the NLS1 in our sample is indeed slightly larger than for the rest of the Seyfert class (⟨Γ⟩ NLS1 = 2.2 ± 0.1, ⟨Γ⟩ Sey1 = 2.01 ± 0.02), as also derived from INTEGRAL observations on 14 NLS1s (Ricci et al. 2011b; Panessa et al. 2011). On the other hand, the average variability amplitude is consistent with what is observed for broad line Seyfert 1 (⟨SV⟩ NLS1 = 15 ± 3%). Even though our NLS1 sample is too small to draw any firm conclusion, the discrepancy between the soft and hard X-rays results could be due to the different time scales probed in these studies: while NLS1s do show strong variability on short time scales, on long time scales above the PDS time break, their timing characteristics do not differ significantly from those of the general type-1 Seyfert population. This agrees with Saxton et al. (2011), who find substantially the same long-term variability in narrow and broad line Seyfert 1 within their 0.2–2 keV survey study.

6.2. Long-term variability, luminosity and black hole mass

Due to the rather long time scales probed by BAT, the anti-correlations of variability with luminosity (Barr & Mushotzky 1986; Green et al. 1993; Papadakis 2004) and with black hole mass (Papadakis & McHardy 1995; Zhou et al. 2010; Kelly et al. 2011, 2013; Ponti et al. 2012) often observed below 10 keV on short time scales are not detected in our hard X-ray study (Figs. 3 and 6). This agrees with results obtained in the soft X-ray band when year time scales are investigated. For example, Saxton et al. (2011) do not find any relation between long-term variability and luminosity when studying a 0.2–2 keV AGN sample and argue that this is expected since the sampled time scales are substantially longer than the typical PDS break times of AGN. Moreover, Markowitz & Edelson (2004) analyzed a sample of 27 AGN with ASCA and RXTE data in the 2–12 keV energy range. Even though they do detect anti-correlations between variability and luminosity and variability and black hole mass on day time scales, the significance of these relations decreases when studying longer time scales (a month to years), and the slope of the linear fit to the data approaches zero, indicating that there is no anti-correlation observed on long time scales. Zhang (2011) used RXTE/ASM data, monitoring 27 AGN for about 14 years in the 1.5–12 keV band. The excess variance computed on the 300-day binned light curves does not correlate with the black hole mass. The author argues that this points to AGN being in a high/soft state rather than in a low/hard state, based on an analogy with Galactic black holes (GBH) when solely their timing behavior is considered. In fact, PDS of GBHs in low/hard state are observed to present a second break at even lower time frequencies, and therefore if a similar behavior has to be expected from AGN, a mass dependence of the excess variance should also be observed on long time scales, which is instead not detected.

Finally, considering that the BAT PDS on long time scales appear to have a slope consistent with αPDS ~ 1 (SM13), SV computed in this time frequency range is proportional to the PDS normalization. Therefore, the lack of correlation between SV and MBH and LX indicates that the PDS normalization does not seem to scale with black hole mass or luminosity. Moreover, the average variability for Seyfert galaxies is ⟨SV⟩ Sey = 19% with 68% of the objects having SV values in the range ~10−35%. The total variability range is smaller by a factor of ~6 with respect to the range measured on shorter time scales by Ponti et al. (2012) in the 2–10 keV energy band. This suggests that the BAT SV, hence the normalization of the PDS on long time scales, could be very similar in all local Seyfert galaxies.

6.3. Spectral variability

A significant correlation is detected between variability in the 14–24 and 35–100 keV energy ranges, with Seyfert galaxies being on average more variable in the lower energy band (Fig. 7). The detected correlation suggests that the same process is likely to be at the origin of the variability in the two bands. Moreover, the presence of such large average variations, even in the 35−100 keV range, is incompatible with hard X-ray variability being entirely due to variations in the hydrogen column density along the line of sight. In fact, as an indication, a variation of ΔNH ~ 5 × 1024 cm-2 would imply only a 3% variation in the 35–100 keV flux, yet a limited fraction of the additional variability observed at lower (14–24 keV) energies could be due to absorption variations.

Several studies have detected decreasing variability with increasing X-ray energies in the 0.2–12 keV band, either through excess variance or PDS amplitude (e.g., Nandra 2001; McHardy et al. 2004; Markowitz & Edelson 2004; Ponti 2007; Ponti et al. 2012), and both on short (≲1 day) and long time scales (≳30 days). The same finding extends to hard X-ray energies, with the 14–24 keV band showing on average larger variations than the 35–100 keV one in Seyfert galaxies. A similar result has been obtained by Chitnis et al. (2009) when comparing the 1.5–12 keV RXTE/ASM variability to that measured in the 14−195 keV band by BAT. Shimizu & Mushotzky (2013) did not detect an energy dependence of the PDS parameters for the three Seyferts for which this investigation was possible, but the corresponding excess variance (computed using the PDS parameters) decreases through the 14–24, 24–50, and 50–150 keV bands they studied. If for observations below 10 keV changes of the amount of the absorbing material or of its ionization could play a role (Risaliti et al. 2002; Ponti et al. 2012), in the BAT band such mechanisms are unlikely to be able to fully explain the observed properties.

The variations could instead originate directly at the X-ray source. For example, if a power law spectrum pivots at energies ≳50 keV, the 14–24 keV flux would be expected to vary more strongly than the 35–100 keV one (Gierliński & Zdziarski 2005). If we assume a standard Comptonization model based on a two-phase accretion disk (Haardt & Maraschi 1993), the hard X-ray variability could be driven by changes in the seed photon flux (Nandra et al. 2000; Arévalo et al. 2005) or by physical variations in the corona (temperature and optical depth; Nicastro et al. 2000; Lubiński et al. 2010). Petrucci et al. (2000) point out that in order to have a pivoting point at high energies an increase in the cooling is required rather than a decrease in the heating, which would instead determine a low-energy pivoting point.

In addition, the superposition of two components, one constant (e.g., the reflected continuum) and the other one variable (for example, the Comptonized continuum) could contribute further to the observed spectral variations (Shih et al. 2002; Markowitz & Edelson 2004; Ponti et al. 2006; Papadakis et al. 2009; Sobolewska & Papadakis 2009). In the 14–24 keV and 35–100 keV bands, the contribution of reflection to the observed flux is about 30–40% for a reflection fraction R = 1 and typical AGN spectra with Γ = 1.6−2.1, NH = 1−100 × 1022 cm-2, and a high-energy cut-off at EC = 100−300 keV. For such spectra, a larger contribution from reflection is measured in the total 35–100 keV flux compared to the 14–24 keV one, but only by a few percentage points. Therefore, reflection alone cannot fully explain the difference observed in the two hard X-ray bands, even though a contribution from it is expected.

The scenario of a pivoting spectrum superposed on a constant reflection is in general also consistent with a steepening of the hard X-ray spectrum when the source brightens. This is indeed observed for the majority of the Seyferts in our sample that show some spectral variability (Fig. 8) and follows an established trend observed in the X-ray emission of numerous local radio quiet AGN (Markowitz & Edelson 2004; Sobolewska & Papadakis 2009; Caballero-Garcia et al. 2012) and also in higher redshift objects (Paolillo et al. 2004). Within the Comptonization frame, the softer-when-brighter behavior can be understood if an increase in the seed photon power illuminating the corona determines a more efficient cooling of the hot electrons, with a resulting drop in the coronal temperature, which causes the X-ray spectrum to steepen.

The correlation between Eddington ratio and photon index is another known property of AGN samples below 10 keV (Sobolewska & Papadakis 2009), and it is confirmed by our study at hard X-rays (Fig. 5, middle panel), in agreement with Middleton et al. (2008), who suggest this relation to explain possible differences in hard X-ray spectral slopes for different AGN classes.

thumbnail Fig. 9

14–195 keV versus 2–10 keV normalized excess variance σrms2\hbox{$\sigma^2_{\rm rms}$} for 10 Seyfert galaxies and 3 radio loud AGN (3C 273, 3C 390.3, Cen A) in our sample for which 2–10 keV PDS with a measured frequency break have been reported in the literature. The dashed line indicates where objects with the same variability at soft and hard X-rays would lie.

A different behavior arises when comparing the hard X-ray to the soft X-ray variability. We collected from the literature the PDS parameters for 13 AGN in our sample, i.e., those objects with measured soft X-ray PDS and with detected frequency break (González-Martín & Vaughan 2012, SM13, and references therein). We compare the normalized excess variance σrms2\hbox{$\sigma^2_{\rm rms}$} in the 14–195 keV band to the 2–10 keV one, computed by extrapolating the soft X-ray PDS to low frequencies in order to cover the same time scales as the BAT data set, i.e., between νmin = 6 × 10-9 Hz and νmax = 4 × 10-7 Hz. The variability amplitude at hard X-rays is found to be equal to or larger than the one in the soft X-rays (Fig. 9). This is consistent with what has been found by Caballero-Garcia et al. (2012) and Shimizu & Mushotzky (2013), yet it is surprising, since it seems to be an opposite trend to those observed within the soft and hard X-rays bands alone. One reason could be that, when extrapolating the 2–10 keV PDS to year time scales, the uncertainties on the measurement of the PDS slope introduce a large scatter in the estimated excess variance. Indeed, for 6 out of 13 objects, the low-frequency PDS slope has been fixed to α = −1 (from González-Martín & Vaughan 2012). Slightly steeper slopes by Δα = 0.1−0.2 would imply a comparable or larger variability at soft rather than at hard X-rays.

If instead the hard X-rays are indeed more variable than the soft X-rays on long time scales, this might indicate an even more complex dependence of variability on energy. The difference between soft and hard X-ray variability could be, for example, related to the size of the emitting region. If the high-energy plasma is located inside the accretion disk or above its inner part (Zdziarski et al. 1999; Lubiński et al. 2010), while the low-energy emitting region is associated to some outflow from the disk or a second plasma with lower temperature (Petrucci et al. 2013), then the high-energy emission could be more variable than the lower-energy emission. However, the change in relative dominance of the two components would have to happen exactly at energies of 10–15 keV. In addition, it would be necessary to explain why this trend is inverted within the soft and hard X-ray bands, with the higher energy emission in general less variable than the lower energy emission.

6.3.1. Variability and photon index anti-correlation

Another interesting difference compared to the lower energies and lower time frequencies is the trend of harder sources to be more variable at hard X-rays (Fig. 5, right panel). In fact, several papers report the opposite trend for softer sources to be more variable on time scales close to or below a day, even though with different degrees of confidence. O’Neill et al. (2005) find a marginal correlation between photon index and excess variance, while Green et al. (1993) and Grupe et al. (2001) find a more significant correlation in the 1–8 keV (EXOSAT) and 0.2–2 keV band (ROSAT), respectively. One has to keep in mind, though, that a contribution from absorption variations could be important in the ROSAT data. The largest soft X-ray sample for this kind of study has been presented by Ponti et al. (2012). They confirm the correlation between excess variance and photon index, which they ascribe to the fact that accretion rate correlates with both variability and photon index in their sample. In contrast, at hard X-rays and low time frequency, it seems more likely that the correlation between accretion rate and photon index and the anti-correlation between photon index and variability are the origin of the marginal anti-correlation between accretion rate and variability (Fig. 5).

The photon index versus variability anti-correlation is instead commonly observed in Galactic black holes (GBH), which show larger variability during the hard state, i.e., when the corona rather than the accretion disk emission is believed to dominate the X-ray spectrum (e.g., Muñoz-Darias et al. 2011). Moreover, a decreasing variability with the softening of the spectrum is detected in the so-called hard-intermediate state, when the less variable accretion disk component starts contributing to the X-ray spectrum of GBHs (Belloni et al. 2011). This might indicate that the larger variability in the harder BAT sources could be associated to their stronger Comptonization.

thumbnail Fig. 10

Measured photon index versus intrinsic absorption for the Seyfert galaxy sample. The lines correspond to the measured photon index obtained from a simple power law fit of simulated power law spectra with intrinsic photon index Γ = 1.6, 1.9, and 2.2 (from bottom to top) modified by the corresponding NH. Upper limits on NH are indicated with arrows.

The anti-correlation between variability and photon index in our sample could, at least partly, be induced by the effect of different reflection fractions. On one hand, if one assumes that the bulk of reflection is mostly constant, objects with larger reflection would be expected to be less variable. Constant or slowly variable reflection components observed in a number of objects have been explained as either due to a distant reflector, with light travel time damping out variability (e.g., Miller et al. 2008; Bianchi et al. 2009), or as a consequence of strong gravitational light bending in the close vicinity of the black hole (e.g., Miniutti & Fabian 2004; Ponti et al. 2006; Miniutti et al. 2007). On the other hand, there are indications that objects with larger reflection have softer X-ray spectra. In fact, Zdziarski et al. (1999) reported a strong correlation indicating that intrinsically softer sources have larger reflection fractions, possibly due to the reflector also being the source of seed photons for the Comptonization emission. In addition to this effect, when fitting with a simple power law model spectra with different reflection strengths and the same intrinsic continuum, the measured photon index in the 14–195 keV band results steeper for larger reflection, with ΔΓ ≲ 7% (depending on the intrinsic continuum shape and on the position of the high-energy spectral turnover) for a reflection fraction R changing from 0 to 2. Reflection fractions R > 1 might be the result of peculiar geometries (causing, e.g., high covering factors; Malzac 2001), of light bending effects in the vicinity of the black hole (Miniutti & Fabian 2004), or of a variable continuum combined with a delayed answer of the reflected component, due to the distance of the reflector (Malzac & Petrucci 2002).

When the accretion disk is considered as the main reflector, a larger reflection component is expected from face-on compared to edge-on AGN. Indeed, when dividing our sample into the different AGN classes, Seyfert 1 appear at the higher end of the photon index distribution, consistent with larger reflection being associated to softer spectra. Furthermore, Ricci et al. (2011b) and Vasudevan et al. (2013) have recently shown that objects with absorption in the range 1023 < NH < 1024 cm-2 present a stronger reflection component than those at lower NH. When looking at the distribution of photon indexes as a function of NH, sources in the range 1023 < NH < 4 × 1023 cm-2 have a softer spectrum than the rest of the Seyfert 2 population and comparable to the average Seyfert 1 one (Fig. 10), possibly pointing out a stronger reflection component. We note that the photon index drop at NH > 4 × 1023 cm-2 cannot be simply explained by our fitting not taking absorption into account. In fact, when simulating absorbed spectra and fitting them with a simple power law, the measured photon index decreases much less dramatically as a function of NH than is observed in the data (see lines in Fig. 10).

However, caution should be used since for highly absorbed sources simple absorption models fail to correctly reproduce the spectra in the presence of strong reprocessed emission (Lubinski et al., in prep.; Yaqoob 2012; Braito et al. 2013), and since stacked spectra might be influenced by the effects of combining objects with different spectral shapes contributing with varying weight to the different energy bands. In addition, the validity of the Γ−R correlation reported by Zdziarski et al. (1999) is still being debated. Some later studies have confirmed this relation (Mattson et al. 2007; Dadina 2008; Winter et al. 2012), whereas others did not (Molina et al. 2009; de Rosa et al. 2012), pointing out the difficulty in disentangling a real physical relation from the degeneracies among photon index, reflection, and high-energy cut-off in the commonly used X-ray fitting models (Mattson et al. 2007; Winter et al. 2012).

An alternative explanation could come from a similar trend observed in NGC 7469 (Nandra & Papadakis 2001), which presented a higher excess variance when the spectrum of the source was harder. Nandra & Papadakis (2001) suggest that this and other timing properties of this AGN could be explained if the inner regions of the corona were hotter than the outer ones. The hard X-ray emission would then be produced in the innermost parts of the corona and therefore be more variable and have shorter time scales than the soft X-ray one, produced in the larger and cooler outer zone. However, these results are based on a 30-day observation at <15 keV, so the time scales and energies are different than those of our work. Similarly, in the model first proposed by Lyubarskii (1997) and then reconsidered by others (Churazov et al. 2001; Arévalo & Uttley 2006), different variability patterns at different energies and on different time scales are explained with accretion disk fluctuations propagating inward and illuminating a corona with emissivity gradient, which would therefore modulate the X-ray source.

7. Conclusions

We have characterized the 14–195 keV variability of the largest sample of hard X-ray-selected AGN provided by Swift/BAT to date. The amplitude of the variations was quantified and their dependence on energy and on basic AGN properties, such as black hole mass, luminosity, Eddington ratio, and intrinsic absorption, were investigated. The average characteristics of hard X-ray variability generally agree with the unified models, indicating larger variability in jetted sources and no clear dependence of the variations on AGN orientation. The amplitude of the hard X-ray variations and its spectral properties indicate that variability cannot be driven by absorption variations. On the other hand for radio quiet AGN, it is rather consistent with changes of a power law continuum over a constant component, with the power law pivoting around ≳50 keV. Such variations in the continuum emission would be achieved for example with a change in the corona temperature, determining a shift of the high-energy cut-off at hard X-rays, either due to intrinsic coronal variations or to a change in the seed photon flux.

In general, variability at hard X-rays has very similar properties to that in the softer X-ray band, when similar time scales are compared, compatible with variability being driven by the same mechanism across the full X-ray band. However, some discrepancies, like AGN with harder spectra being more variable and the apparent lower variability in the 2–10 keV band, could be ascribed to additional components in either band (e.g., reflection, absorption), and in any case they could provide interesting insight into the intrinsic differences of the emission in the soft and hard X-ray bands, such as for the emitting regions and their sizes.

The lack of dependence of the long-term variability on black hole mass and luminosity, and the relatively narrow range of variability measured in Seyfert galaxies, suggest that the normalization of the X-ray power spectrum is independent of black hole mass and luminosity and might have a similar value for all local Seyfert galaxies.

Thanks to the Swift/BAT ongoing observations, it will be possible to further extend the studied time scales and increase the available AGN sample, obtaining the best hard X-ray AGN variability sample for some time to come. At the same time, pointed observations with Suzaku, INTEGRAL, and NuSTAR will continue to investigate the spectral variability in bright and well studied AGN, as already successfully done in a number of sources (Reeves et al. 2007; Itoh et al. 2008; Terashima et al. 2009; Fukazawa et al. 2011; Beckmann et al. 2007b; Soldi et al. 2010, 2011b; Lubiński et al. 2010).

Online material

Table 2

Variability estimator SV, black hole mass, and bolometric luminosity for the selected Swift/BAT AGN sample.

3

We note that even though 58 months of BAT data were used for source detection, the light curves used in this work extend beyond this data set, i.e. up to 66 months.

4

The values of SV computed on the filtered and unfiltered light curves are compatible, with an average scatter of ≤2% for the selected sample, well within the estimated uncertainties on SV. On the other hand, for the BAT AGN excluded from the analysis the scatter is on average 4 times larger, further justifying our choice to limit the analysis to a sample of light curves for which the variability measurement is not so strongly influenced by single data points.

5

For the majority of the objects in the SM13 sample (20 out of 23) TB, pred is close to or shorter than 30 days, consistent with no TB detected by SM13 in the BAT time frequency range.

Acknowledgments

The authors thank Jerome Rodriguez for useful discussions of Galactic black holes, and the anonymous referee for the valuable suggestions that helped to improve this paper. S.S. acknowledges the Centre National d’Études Spatiales (CNES) for financial support. G.P. acknowledges support via an EU Marie Curie Intra-European fellowship under contract No. FP-PEOPLE-2012-IEF-331095. This work has been partly supported by the LabEx UnivEarthS6 project “Impact of black holes on their environment”, and by the Polish NCN grants N N203 581240 and 2012/04/M/ST9/00780. This article commemorates our colleague Jack Tueller who passed away during the study.

References

  1. Allevato, V., Paolillo, M., Papadakis, I., & Pinto, C. 2013, ApJ, 771, 9 [NASA ADS] [CrossRef] [Google Scholar]
  2. Almaini, O., Lawrence, A., Shanks, T., et al. 2000, MNRAS, 315, 325 [NASA ADS] [CrossRef] [Google Scholar]
  3. Arévalo, P., & Uttley, P. 2006, MNRAS, 367, 801 [NASA ADS] [CrossRef] [Google Scholar]
  4. Arévalo, P., Papadakis, I., Kuhlbrodt, B., & Brinkmann, W. 2005, A&A, 430, 435 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Arévalo, P., McHardy, I. M., & Summons, D. P. 2008a, MNRAS, 388, 211 [NASA ADS] [CrossRef] [Google Scholar]
  6. Arévalo, P., Uttley, P., Kaspi, S., et al. 2008b, MNRAS, 389, 1479 [NASA ADS] [CrossRef] [Google Scholar]
  7. Barr, P., & Mushotzky, R. F. 1986, Nature, 320, 421 [NASA ADS] [CrossRef] [Google Scholar]
  8. Barthelmy, S. D., Barbier, L. M., Cummings, J. R., et al. 2005, Space Sci. Rev., 120, 143 [NASA ADS] [CrossRef] [Google Scholar]
  9. Baumgartner, W. H., Tueller, J., Markwardt, C. B., et al. 2013, ApJS, 207, 19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Beckmann, V., & Shrader, C. R. 2012, Active Galactic Nuclei (Wiley–VCH) [Google Scholar]
  11. Beckmann, V., Barthelmy, S. D., Courvoisier, T. J.-L., et al. 2007a, A&A, 475 [Google Scholar]
  12. Beckmann, V., Gehrels, N., & Tueller, J. 2007b, ApJ, 666, 122 [NASA ADS] [CrossRef] [Google Scholar]
  13. Beckmann, V., Courvoisier, T. J.-L., Gehrels, N., et al. 2008, A&A, 492, 93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Beckmann, V., Soldi, S., Ricci, C., et al. 2009, A&A, 505, 417 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Beckmann, V., Jean, P., Lubiński, P., Soldi, S., & Terrier, R. 2011, A&A, 531, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Bell, M. E., Tzioumis, T., Uttley, P., et al. 2011, MNRAS, 411, 402 [NASA ADS] [CrossRef] [Google Scholar]
  17. Belloni, T. M., Motta, S. E., & Muñoz-Darias, T. 2011, Bull. Astron. Soc. Ind., 39, 409 [Google Scholar]
  18. Bian, W., & Gu, Q. 2007, ApJ, 657, 159 [NASA ADS] [CrossRef] [Google Scholar]
  19. Bianchi, S., Piconcelli, E., Chiaberge, M., et al. 2009, ApJ, 695, 781 [NASA ADS] [CrossRef] [Google Scholar]
  20. Braito, V., Ballo, L., Reeves, J. N., et al. 2013, MNRAS, 428, 2516 [NASA ADS] [CrossRef] [Google Scholar]
  21. Breedt, E., McHardy, I. M., Arévalo, P., et al. 2010, MNRAS, 403, 605 [NASA ADS] [CrossRef] [Google Scholar]
  22. Caballero-Garcia, M. D., Papadakis, I. E., Nicastro, F., & Ajello, M. 2012, A&A, 537, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Chatterjee, R., Marscher, A. P., Jorstad, S. G., et al. 2011, ApJ, 734, 43 [Google Scholar]
  24. Chitnis, V. R., Pendharkar, J. K., Bose, D., et al. 2009, ApJ, 698, 1207 [NASA ADS] [CrossRef] [Google Scholar]
  25. Churazov, E., Gilfanov, M., & Revnivtsev, M. 2001, MNRAS, 321, 759 [NASA ADS] [CrossRef] [Google Scholar]
  26. Cusumano, G., La Parola, V., Segreto, A., et al. 2010, A&A, 524, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Czerny, B., Nikołajuk, M., Piasecki, M., & Kuraszkiewicz, J. 2001, MNRAS, 325, 865 [NASA ADS] [CrossRef] [Google Scholar]
  28. Dadina, M. 2008, A&A, 485, 417 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. de Jong, S., Beckmann, V., & Mattana, F. 2012, A&A, 545, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. De Marco, B., Ponti, G., Cappi, M., et al. 2013, MNRAS, 431, 2441 [NASA ADS] [CrossRef] [Google Scholar]
  31. de Rosa, A., Piro, L., Perola, G. C., et al. 2007, A&A, 463, 903 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. de Rosa, A., Panessa, F., Bassani, L., et al. 2012, MNRAS, 420, 2087 [NASA ADS] [CrossRef] [Google Scholar]
  33. Denney, K. D., Peterson, B. M., Pogge, R. W., et al. 2010, ApJ, 721, 715 [NASA ADS] [CrossRef] [Google Scholar]
  34. Fabian, A. C., Vasudevan, R. V., Mushotzky, R. F., Winter, L. M., & Reynolds, C. S. 2009, MNRAS, 394, L89 [NASA ADS] [CrossRef] [Google Scholar]
  35. Fukazawa, Y., Hiragi, K., Yamazaki, S., et al. 2011, ApJ, 743, 124 [NASA ADS] [CrossRef] [Google Scholar]
  36. Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [NASA ADS] [CrossRef] [Google Scholar]
  37. Gierliński, M., & Zdziarski, A. A. 2005, MNRAS, 363, 1349 [NASA ADS] [CrossRef] [Google Scholar]
  38. González-Martín, O., & Vaughan, S. 2012, A&A, 544, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Grandi, P., Malaguti, G., & Fiocchi, M. 2006, ApJ, 642, 113 [NASA ADS] [CrossRef] [Google Scholar]
  40. Green, A. R., McHardy, I. M., & Lehto, H. J. 1993, MNRAS, 265, 664 [NASA ADS] [Google Scholar]
  41. Greenhill, L. J., Booth, R. S., Ellingsen, S. P., et al. 2003, ApJ, 590, 162 [NASA ADS] [CrossRef] [Google Scholar]
  42. Grier, C. J., Peterson, B. M., Pogge, R. W., et al. 2012, ApJ, 755, 60 [NASA ADS] [CrossRef] [Google Scholar]
  43. Grupe, D., Thomas, H.-C., & Beuermann, K. 2001, A&A, 367, 470 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Haardt, F., & Maraschi, L. 1993, ApJ, 413, 507 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  45. Harmon, B. A., Wilson, C. A., Fishman, G. J., et al. 2004, ApJS, 154, 585 [NASA ADS] [CrossRef] [Google Scholar]
  46. Itoh, T., Done, C., Makishima, K., et al. 2008, PASJ, 60, 251 [NASA ADS] [Google Scholar]
  47. Kaspi, S., Brandt, W. N., Maoz, D., et al. 2007, ApJ, 659, 997 [NASA ADS] [CrossRef] [Google Scholar]
  48. Kelly, B. C., Sobolewska, M., & Siemiginowska, A. 2011, ApJ, 730, 52 [NASA ADS] [CrossRef] [Google Scholar]
  49. Kelly, B. C., Treu, T., Malkan, M., Pancoast, A., & Woo, J.-H. 2013, ApJ, 779, 187 [NASA ADS] [CrossRef] [Google Scholar]
  50. Körding, E. G., Migliari, S., Fender, R., et al. 2007, MNRAS, 380, 301 [NASA ADS] [CrossRef] [Google Scholar]
  51. Krimm, H. A., Holland, S. T., Corbet, R. H. D., et al. 2013, ApJS, 209, 14 [NASA ADS] [CrossRef] [Google Scholar]
  52. Lanzuisi, G., Ponti, G., Salvato, M., et al. 2013, ApJ, submitted [Google Scholar]
  53. Lichti, G. G., Bottacini, E., Ajello, M., et al. 2008, A&A, 486, 721 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Lu, Y., & Yu, Q. 2001, MNRAS, 324, 653 [NASA ADS] [CrossRef] [Google Scholar]
  55. Lubiński, P., Zdziarski, A. A., Walter, R., et al. 2010, MNRAS, 408, 1851 [NASA ADS] [CrossRef] [Google Scholar]
  56. Lyubarskii, Y. E. 1997, MNRAS, 292, 679 [NASA ADS] [CrossRef] [Google Scholar]
  57. Malizia, A., Bassani, L., Bird, A. J., et al. 2008, MNRAS, 389, 1360 [NASA ADS] [CrossRef] [Google Scholar]
  58. Malzac, J. 2001, MNRAS, 325, 1625 [NASA ADS] [CrossRef] [Google Scholar]
  59. Malzac, J., & Petrucci, P.-O. 2002, MNRAS, 336, 1209 [NASA ADS] [CrossRef] [Google Scholar]
  60. Marconi, A., Risaliti, G., Gilli, R., et al. 2004, MNRAS, 351, 169 [NASA ADS] [CrossRef] [Google Scholar]
  61. Markowitz, A. 2009, ApJ, 698, 1740 [NASA ADS] [CrossRef] [Google Scholar]
  62. Markowitz, A. 2010, ApJ, 724, 26 [NASA ADS] [CrossRef] [Google Scholar]
  63. Markowitz, A., & Edelson, R. 2004, ApJ, 617, 939 [NASA ADS] [CrossRef] [Google Scholar]
  64. Mateos, S., Barcons, X., Carrera, F. J., et al. 2007, A&A, 473, 105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Mattson, B. J., Weaver, K. A., & Reynolds, C. S. 2007, ApJ, 664, 101 [NASA ADS] [CrossRef] [Google Scholar]
  66. McHardy, I. 2010, in Lect. Notes Phys. 794, ed. T. Belloni (Berlin Springer Verlag), 203 [Google Scholar]
  67. McHardy, I. M., Papadakis, I. E., Uttley, P., Page, M. J., & Mason, K. O. 2004, MNRAS, 348, 783 [NASA ADS] [CrossRef] [Google Scholar]
  68. McHardy, I. M., Koerding, E., Knigge, C., Uttley, P., & Fender, R. P. 2006, Nature, 444, 730 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  69. McHardy, I., Lawson, A., Newsam, A., et al. 2007, MNRAS, 375, 1521 [NASA ADS] [CrossRef] [Google Scholar]
  70. Mehdipour, M., Branduardi-Raymont, G., Kaastra, J. S., et al. 2011, A&A, 534, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  71. Middleton, M., Done, C., & Schurch, N. 2008, MNRAS, 383, 1501 [NASA ADS] [CrossRef] [Google Scholar]
  72. Miller, L., Turner, T. J., & Reeves, J. N. 2008, A&A, 483, 437 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. Miniutti, G., & Fabian, A. C. 2004, MNRAS, 349, 1435 [NASA ADS] [CrossRef] [Google Scholar]
  74. Miniutti, G., Fabian, A. C., Anabuki, N., et al. 2007, PASJ, 59, 315 [NASA ADS] [Google Scholar]
  75. Molina, M., Bassani, L., Malizia, A., et al. 2009, MNRAS, 399, 1293 [NASA ADS] [CrossRef] [Google Scholar]
  76. Muñoz-Darias, T., Motta, S., & Belloni, T. M. 2011, MNRAS, 410, 679 [NASA ADS] [CrossRef] [Google Scholar]
  77. Nandra, K. 2001, in Probing the Physics of Active Galactic Nuclei, eds. B. M. Peterson, R. W. Pogge, & R. S. Polidan, ASP Conf. Ser., 224, 167 [Google Scholar]
  78. Nandra, K., & Papadakis, I. E. 2001, ApJ, 554, 710 [NASA ADS] [CrossRef] [Google Scholar]
  79. Nandra, K., Le, T., George, I. M., et al. 2000, ApJ, 544, 734 [NASA ADS] [CrossRef] [Google Scholar]
  80. Nicastro, F., Piro, L., De Rosa, A., et al. 2000, ApJ, 536, 718 [NASA ADS] [CrossRef] [Google Scholar]
  81. Nikolajuk, M., Papadakis, I. E., & Czerny, B. 2004, MNRAS, 350, L26 [NASA ADS] [CrossRef] [Google Scholar]
  82. O’Neill, P. M., Nandra, K., Papadakis, I. E., & Turner, T. J. 2005, MNRAS, 358, 1405 [NASA ADS] [CrossRef] [Google Scholar]
  83. Padovani, P., & Rafanelli, P. 1988, A&A, 205, 53 [NASA ADS] [Google Scholar]
  84. Panessa, F., de Rosa, A., Bassani, L., et al. 2011, MNRAS, 417, 2426 [NASA ADS] [CrossRef] [Google Scholar]
  85. Paolillo, M., Schreier, E. J., Giacconi, R., Koekemoer, A. M., & Grogin, N. A. 2004, ApJ, 611, 93 [NASA ADS] [CrossRef] [Google Scholar]
  86. Papadakis, I. E. 2004, MNRAS, 348, 207 [NASA ADS] [CrossRef] [Google Scholar]
  87. Papadakis, I. E., & McHardy, I. M. 1995, MNRAS, 273, 923 [NASA ADS] [Google Scholar]
  88. Papadakis, I. E., Sobolewska, M., Arevalo, P., et al. 2009, A&A, 494, 905 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  89. Peterson, B. M., McHardy, I. M., Wilkes, B. J., et al. 2000, ApJ, 542, 161 [NASA ADS] [CrossRef] [Google Scholar]
  90. Petrucci, P. O., Haardt, F., Maraschi, L., et al. 2000, ApJ, 540, 131 [NASA ADS] [CrossRef] [Google Scholar]
  91. Petrucci, P.-O., Paltani, S., Malzac, J., et al. 2013, A&A, 549, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  92. Pian, E., Foschini, L., Beckmann, V., et al. 2006, A&A, 449, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  93. Pian, E., Ubertini, P., Bazzano, A., et al. 2011, A&A, 526, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  94. Ponti, G. 2007, Ph.D. Thesis, Università di Bologna [Google Scholar]
  95. Ponti, G., Cappi, M., Dadina, M., & Malaguti, G. 2004, A&A, 417, 451 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  96. Ponti, G., Miniutti, G., Cappi, M., et al. 2006, MNRAS, 368, 903 [NASA ADS] [CrossRef] [Google Scholar]
  97. Ponti, G., Papadakis, I., Bianchi, S., et al. 2012, A&A, 542, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  98. Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 2007, Numerical recipes: The art of scientific computing [Google Scholar]
  99. Reeves, J. N., Awaki, H., Dewangan, G. C., et al. 2007, PASJ, 59, 301 [NASA ADS] [Google Scholar]
  100. Reis, R. C., Fabian, A. C., Reynolds, C. S., et al. 2012, ApJ, 745, 93 [NASA ADS] [CrossRef] [Google Scholar]
  101. Ricci, C., Paltani, S., Soldi, S., & Courvoisier, T. J. L. 2011a, in Fast X-ray Timing and Spectroscopy at Extreme Count Rates (HTRS 2011) [arXiv:1106.3997] [Google Scholar]
  102. Ricci, C., Walter, R., Courvoisier, T. J.-L., & Paltani, S. 2011b, A&A, 532, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  103. Risaliti, G., Elvis, M., & Nicastro, F. 2002, ApJ, 571, 234 [NASA ADS] [CrossRef] [Google Scholar]
  104. Risaliti, G., Elvis, M., Fabbiano, G., et al. 2007, ApJ, 659, L111 [NASA ADS] [CrossRef] [Google Scholar]
  105. Saxton, R., Read, A., Esquej, P., Miniutti, G., & Alvarez, E. 2011, in Narrow-Line Seyfert 1 Galaxies and their Place in the Universe PoS(NLS1)008 [Google Scholar]
  106. Shemmer, O., Uttley, P., Netzer, H., & McHardy, I. M. 2003, MNRAS, 343, 1341 [NASA ADS] [CrossRef] [Google Scholar]
  107. Shih, D. C., Iwasawa, K., & Fabian, A. C. 2002, MNRAS, 333, 687 [NASA ADS] [CrossRef] [Google Scholar]
  108. Shimizu, T. T., & Mushotzky, R. F. 2013, ApJ, 770, 60, SM13 [NASA ADS] [CrossRef] [Google Scholar]
  109. Simpson, G., & Mayer-Hasselwander, H. 1986, A&A, 162, 340 [NASA ADS] [Google Scholar]
  110. Sobolewska, M. A., & Papadakis, I. E. 2009, MNRAS, 399, 1597 [NASA ADS] [CrossRef] [Google Scholar]
  111. Soldi, S., Türler, M., Paltani, S., et al. 2008, A&A, 486, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  112. Soldi, S., Ponti, G., Beckmann, V., & Lubinski, P. 2010, in Proc. of The Extreme sky: Sampling the Universe above 10 keV Conf. [arXiv:1001.4348] [Google Scholar]
  113. Soldi, S., Beckmann, V., Gehrels, N., de Jong, S., & Lubiński, P. 2011a, in Narrow-Line Seyfert 1 Galaxies and their Place in the Universe [arXiv:1105.5993] [Google Scholar]
  114. Soldi, S., Beckmann, V., Gehrels, N., et al. 2011b, in Proc. of the 8th INTEGRAL Workshop The Restless Gamma-ray Universe [arXiv:1102.4959] [Google Scholar]
  115. Soldi, S., Baumgartner, W., Beckmann, V., et al. 2012, in Proc. of An INTEGRAL view of the high-energy sky (the first 10 years) (INTEGRAL 2012) [Google Scholar]
  116. Stalin, C. S., Jeyakumar, S., Coziol, R., Pawase, R. S., & Thakur, S. S. 2011, MNRAS, 416, 225 [NASA ADS] [Google Scholar]
  117. Terashima, Y., Gallo, L. C., Inoue, H., et al. 2009, PASJ, 61, 299 [Google Scholar]
  118. Tueller, J., Baumgartner, W. H., Markwardt, C. B., et al. 2010, ApJS, 186, 378 [NASA ADS] [CrossRef] [Google Scholar]
  119. Uttley, P. 2005, in Proc. of the AGN Variability from X-rays to Radio Waves Conf. [arXiv:0501157] [Google Scholar]
  120. Uttley, P., McHardy, I. M., & Papadakis, I. E. 2002, MNRAS, 332, 231 [NASA ADS] [CrossRef] [Google Scholar]
  121. Vasudevan, R. V., & Fabian, A. C. 2007, MNRAS, 381, 1235 [NASA ADS] [CrossRef] [Google Scholar]
  122. Vasudevan, R. V., & Fabian, A. C. 2009, MNRAS, 392, 1124 [NASA ADS] [CrossRef] [Google Scholar]
  123. Vasudevan, R. V., Mushotzky, R. F., Winter, L. M., & Fabian, A. C. 2009, MNRAS, 399, 1553 [NASA ADS] [CrossRef] [Google Scholar]
  124. Vasudevan, R. V., Fabian, A. C., Gandhi, P., Winter, L. M., & Mushotzky, R. F. 2010, MNRAS, 402, 1081 [NASA ADS] [CrossRef] [Google Scholar]
  125. Vasudevan, R. V., Mushotzky, R. F., & Gandhi, P. 2013, ApJ, 770, L37 [NASA ADS] [CrossRef] [Google Scholar]
  126. Vaughan, S., Edelson, R., Warwick, R. S., & Uttley, P. 2003, MNRAS, 345, 1271 [NASA ADS] [CrossRef] [Google Scholar]
  127. Wilson-Hodge, C. A., Cherry, M. L., Case, G. L., et al. 2011, ApJ, 727, L40 [NASA ADS] [CrossRef] [Google Scholar]
  128. Winter, L. M., Mushotzky, R. F., Reynolds, C. S., & Tueller, J. 2009, ApJ, 690, 1322 [NASA ADS] [CrossRef] [Google Scholar]
  129. Winter, L. M., Veilleux, S., McKernan, B., & Kallman, T. R. 2012, ApJ, 745, 107 [NASA ADS] [CrossRef] [Google Scholar]
  130. Woo, J.-H., & Urry, C. M. 2002, ApJ, 579, 530 [NASA ADS] [CrossRef] [Google Scholar]
  131. Yaqoob, T. 2012, MNRAS, 423, 3360 [NASA ADS] [CrossRef] [Google Scholar]
  132. Zdziarski, A. A., Lubiński, P., & Smith, D. A. 1999, MNRAS, 303, L11 [NASA ADS] [CrossRef] [Google Scholar]
  133. Zhang, Y.-H. 2011, ApJ, 726, 21 [NASA ADS] [CrossRef] [Google Scholar]
  134. Zhou, X.-L., Zhang, S.-N., Wang, D.-X., & Zhu, L. 2010, ApJ, 710, 16 [NASA ADS] [CrossRef] [Google Scholar]
  135. Zoghbi, A., Fabian, A. C., Uttley, P., et al. 2010, MNRAS, 401, 2419 [Google Scholar]

All Tables

Table 1

Average properties of the BAT AGN in our variability sample, as a function of the AGN class and the amount of intrinsic absorption.

In the text
Table 2

Variability estimator SV, black hole mass, and bolometric luminosity for the selected Swift/BAT AGN sample.

In the text

All Figures

thumbnail Fig. 1

Examples of 30-d binned, 14–195 keV BAT light curves for objects presenting different variability levels (increasing from top to bottom) and with different signal-to-noise ratios. The estimator SV represents the intrinsic variability of a light curve, renormalized to the average flux and in percentage (see Sect. 3.1).
In the text
thumbnail Fig. 2

Histograms of the time-averaged 14–195 keV flux (top), of the variability index V from the χ2 test (middle; the vertical dashed line indicates V = 1.3), and of the variability amplitude estimator SV (bottom) for the total sample of 613 AGN (black) and for the selected sample of 110 AGN (red hatched). We assigned V = 10 to those objects with Pχ2 < 10-6. SV could be computed for 464 of the BAT-detected AGN.

In the text
thumbnail Fig. 3

Variability estimator SV versus luminosity in the 14–195 keV band for the Seyfert galaxies in our sample. Yellow triangles represent the average of the variability estimator in different luminosity bins following Allevato et al. (2013).
In the text
thumbnail Fig. 4

Variability estimator SV versus intrinsic absorption for the Seyfert galaxy sample. Upper limits on NH are indicated with arrows. Yellow triangles represent the average of the variability estimator in different absorption bins.
In the text
thumbnail Fig. 5

Left: variability estimator SV versus Eddington ratio for the Seyfert sample. Yellow triangles represent the average of the variability estimator in different Eddington ratio bins. Middle: photon index versus Eddington ratio for the Seyfert sample. Right: variability estimator SV versus photon index for all the Seyfert galaxies in our sample, separated into the different types. Empty black circles indicate those sources with 1023 < NH < 4 × 1023 cm-2.

In the text
thumbnail Fig. 6

Variability estimator SV versus black hole mass for the Seyfert galaxies in the sample. Empty circles highlight AGN with predicted break time longer than 3 years, while blue empty squares point out the Seyferts from the SM13 sample. The arrow indicates the MBH upper limit for MR 2251−178. Yellow triangles represent the average of the variability estimator in different black hole mass bins.
In the text
thumbnail Fig. 7

35–100 keV versus 14–24 keV variability estimator for the AGN in our sample. The dashed line indicates where objects with the same variability in the two bands would lie. Even though the variations in the two bands are well correlated, the variations in the lower-energy band are larger than those at higher energies for the majority of the radio quiet objects. Some of the most extreme outliers are labeled.

In the text
thumbnail Fig. 8

Hardness ratio versus 14–195 keV flux for the 18 AGN showing spectral variability (13 Seyfert galaxies on the three top rows and 5 radio loud AGN on the bottom row). The black dots are from the 1-month binned light curves, and red squares indicate the average hardness ratio in different flux bins.
In the text
thumbnail Fig. 9

14–195 keV versus 2–10 keV normalized excess variance σrms2\hbox{$\sigma^2_{\rm rms}$} for 10 Seyfert galaxies and 3 radio loud AGN (3C 273, 3C 390.3, Cen A) in our sample for which 2–10 keV PDS with a measured frequency break have been reported in the literature. The dashed line indicates where objects with the same variability at soft and hard X-rays would lie.

In the text
thumbnail Fig. 10

Measured photon index versus intrinsic absorption for the Seyfert galaxy sample. The lines correspond to the measured photon index obtained from a simple power law fit of simulated power law spectra with intrinsic photon index Γ = 1.6, 1.9, and 2.2 (from bottom to top) modified by the corresponding NH. Upper limits on NH are indicated with arrows.

In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.