| Issue |
A&A
Volume 562, February 2014
|
|
|---|---|---|
| Article Number | A124 | |
| Number of page(s) | 24 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201322707 | |
| Published online | 19 February 2014 | |
Magnetic activity of F stars observed by Kepler⋆
1
Laboratoire AIM, CEA/DSM-CNRS-Université Paris Diderot;
IRFU/SAp,
Centre de Saclay,
91191
Gif-sur-Yvette Cedex,
France
e-mail:
savita.mathur@gmail.com; rgarcia@cea.fr
2
Space Science Institute, 4750 Walnut street Suite#205, Boulder
CO
80301,
USA
e-mail:
smathur@spacescience.org
3
CNRS, Institut de Recherche en Astrophysique et Planétologie,
14 avenue Edouard
Belin, 31400
Toulouse,
France
e-mail:
jerome.ballot@irap.omp.eu
4
Université de Toulouse, UPS-OMP, IRAP, 31400
Toulouse,
France
5
Laboratoire Lagrange, UMR7293, Université de Nice
Sophia-Antipolis, CNRS, Observatoire de la Côte d’Azur, BP 4229, 06304
Nice Cedex 4,
France
e-mail:
salabert@oca.eu
6
Stellar Astrophysics Centre, Aarhus University,
8000
Aarhus C,
Denmark
7
Instituto de Astrofísica de Canarias, 38200, La Laguna, Tenerife, Spain
e-mail:
crr@iac.es
8
Departamento de Astrofísica, Universidad de La
Laguna, 38206, La
Laguna, Tenerife,
Spain
9
Instituut voor Sterrenkunde, University of Leuven,
Celestijnenlaan 200
D, 3001
Leuven,
Belgium
10
Department of Astrophysics, IMAPP, Radboud University
Nijmegen, PO Box
9010, 6500 GL
Nijmegen, The
Netherlands
Received: 18 September 2013
Accepted: 17 December 2013
Context. The study of stellar activity is important because it can provide new constraints for dynamo models when combined with surface rotation rates and the depth of the convection zone. We know that the dynamo mechanism, which is believed to be the main process that rules the magnetic cycle of solar-like stars, results from the interaction between (differential) rotation, convection, and magnetic field. The Kepler mission has already been collecting data for a large number of stars during four years allowing us to investigate magnetic stellar cycles.
Aims. We investigated the Kepler light curves to look for magnetic activity or even hints of magnetic activity cycles. Based on the photometric data we also looked for new magnetic indexes to characterise the magnetic activity of the stars.
Methods. We selected a sample of 22 solar-like F stars that have a rotation period shorter than 12 days. We performed a time-frequency analysis using the Morlet wavelet yielding a magnetic proxy for our sample of stars. We computed the magnetic index Sph as the standard deviation of the whole time series and the index ⟨ Sph ⟩, which is the mean of standard deviations measured in subseries of length five times the rotation period of the star. We defined new indicators, such as the contrast between high and low activity, to take into account the fact that complete magnetic cycles are not observed for all the stars. We also inferred the Rossby number of the stars and studied their stellar background.
Results. This analysis shows different types of behaviour in the 22 F stars. Two stars show behaviour very similar to magnetic activity cycles. Five stars show long-lived spots or active regions suggesting the existence of active longitudes. Two stars in our sample seem to have a decreasing or increasing trend in the temporal variation of the magnetic proxies. Finally, the last group of stars shows magnetic activity (with the presence of spots) but no sign of cycle.
Key words: asteroseismology / stars: solar-type / stars: activity / stars: general / methods: data analysis
Appendix A is available in electronic fom at http://www.aanda.org
© ESO, 2014
1. Introduction
The magnetic activity of the Sun observed as a star shows clear signatures of rotational modulation superimposed on longer-term variations due to the 11-year sunspot cycle. Similar behaviour can also be seen in other stars by tracking their magnetic variations spectroscopically with observations of the Ca ii H (396.8 nm) and K (393.4 nm) lines, or through careful photometric monitoring to reveal the brightness changes associated with dark spots and bright faculae (e.g. see Lockwood et al. 2007). The most comprehensive spectroscopic survey for these variations was conducted at the Mount Wilson observatory over more than 30 years (Wilson 1978; Baliunas et al. 1995), leading to the first large sample of magnetic activity and rotation data to help validate models of stellar dynamos.
The Mount Wilson sample established that both the mean activity level and the stellar cycle period seemed to scale with the Rossby number, which tracks the stellar rotation period normalized by the convective timescale (as defined by Noyes et al. 1984). Essentially, the shortest activity cycles were observed in the most rapidly rotating stars, while more slowly rotating stars generally showed cycle periods comparable to the Sun or longer. Subsequent analysis revealed two distinct relationships between rotation period and cycle period, with an “active” sequence of stars rotating faster than the Sun showing a stellar cycle every few hundred rotations and an “inactive” sequence of more slowly rotating stars showing a stellar cycle every ~100 rotations (Saar & Brandenburg 1999). Some stars with intermediate rotation periods (10−25 days) exhibited stellar cycles on both sequences simultaneously. This led Böhm-Vitense (2007) to suggest that the two sequences might represent distinct dynamos in different regions of the star, driven either in a shear layer at the base of the convection zone (a so-called tachocline) or in a near-surface shear layer like that seen in helioseismic inversions (Thompson et al. 1996).
 |
Fig. 1 Wavelet analysis of KIC 3733735 (groups C and L). Top panel: temporal variation of the flux after the corrections applied as in García et al. (2011) and rebinned to 2 h. Middle panel: wavelet power spectrum as a function of time and period. The green grid represents the cone of influence that takes into account the edge effects and delimits the reliable rein in the WPS. Red and dark colours correspond to strong power while blue corresponds to weak power. Bottom upper panel: projection of the WPS on the time axis between periods of 1 and 4.1 days. Bottom lower panel: temporal variation of the standard deviation for KIC 3733735 for subseries of length 5 × Prot. The black dashed line represents the mean value of the standard deviation of the subseries, i.e. the magnetic index ⟨ Sph ⟩. The triple dot-dashed line represents the mean magnetic index for the low-activity subseries (⟨ Sph(nlow) ⟩) and the dash-dot line corresponds to the mean magnetic index for the high-activity subseries ⟨ Sph(nhigh) ⟩. |
Evidence of the existence of this second class of short-period stellar cycles has been growing over the past few years. Fletcher et al. (2010) used helioseismic data to identify a quasi-biennial (~2 year) variation in the Sun, with an amplitude that appeared to be modulated by the dominant 11-year signal. They speculated that buoyant magnetic flux, created near the tachocline during the maximum of the 11-year sunspot cycle, would rise toward the surface and pump up the amplitude of this short-period cycle. However, other explanations, like the beating between different configurations of the dynamo, were also given to justify this second modulation (Simoniello et al. 2013). García et al. (2010) found asteroseismic signatures of a short stellar cycle in the F2V star HD 49933 using observations from the CoRoT satellite. The solar-like pattern of anti-correlated changes in the oscillation frequencies and amplitudes suggested a cycle period longer than 120 days, and the size of the shifts showed a similar frequency dependence to that observed in the Sun (Libbrecht & Woodard 1990; Salabert et al. 2011). Metcalfe et al. (2010) discovered a record-breaking 1.6-year activity cycle in the F8V star ι Hor (HD 17051), which has subsequently been confirmed with X-ray observations of the stellar corona (Sanz-Forcada et al. 2013). Most recently, Metcalfe et al. (2013) documented dual magnetic cycles with periods of 3 years and 13 years in the K2V star ϵ Eri (HD 22049), falling squarely on the two activity sequences identified by Saar & Brandenburg.
The Kepler mission represents an unprecedented opportunity to study the short-period magnetic cycles that have been observed in some rapidly rotating F stars. The high precision time-series photometry collected every 30 min over the past four years can be used to measure rotation periods from spot modulation and to monitor the longer term brightness changes associated with the stellar cycle. Furthermore, for targets that have also been observed in short-cadence (Gilliland et al. 2010), the one-minute sampling allows a characterisation of the star through asteroseismology – including quantities such as the depth of the surface convection zone (e.g. Mathur et al. 2012; Mazumdar et al. 2012) and radial differential rotation – although for more evolved stars (Beck et al. 2012; Deheuvels et al. 2012), which provide useful constraints for dynamo models. The asteroseismic data can also be used to monitor the p-mode frequencies over time, allowing a search for the same pattern of changes that have been seen for the Sun and HD 49933 in response to their magnetic cycles. Rapidly rotating F stars are the ideal targets because they are expected to show the shortest cycle periods, and the size of the frequency variations is predicted to be larger than in the Sun (Metcalfe et al. 2007), as has also been suggested by observations (García et al. 2010; Salabert et al. 2011). In addition, the F star tau Boo belongs to the handful of stars where a magnetic activity cycle has been detected through Zeeman measurement of its magnetic field (Fares et al. 2009).
In this paper, we aim to characterise magnetic activity in a sample of rapidly rotating F stars using photometric measurements from the Kepler mission. Our goal is to better understand the development of regular magnetic cycles, and to place strong constraints on the physical processes that govern them. Our sample includes F stars with surface rotation periods shorter than 12 days that have also been observed with short-cadence for at least 3 months continuously, where the p-mode oscillations and rotation are both clearly detected. We provide an overview of the observations in Sect. 2 and define a new photometric index of magnetic activity in Sect. 3. We present our results in Sect. 4 and discuss them in Sect. 5. A summary of our conclusions is presented in Sect. 6.
2. Observations and data analysis
In this work we use high-quality and long photometric data provided by the NASA Kepler satellite (Borucki et al. 2010). As we are only interested in studying periodic modulations in the light curves that are longer than a few hours, we are able to use long-cadence data (29.43 min, Gilliland et al. 2010) that have been recorded since the beginning of the mission for most of the stars. Thus, 1440 days (Quarters 0 to 16) are used. In Fig. 1 (top) we show an example of a light curve for the Kepler target KIC 3733735. The light curves were corrected for instrumental effects and filtered with a 20-day triangular smooth (García et al. 2011; Mathur et al., in prep.). To minimise the impact of wrong corrections in our data processing, we have also used PDC-msMAP light curves (Smith et al. 2012; Stumpe et al. 2012), as described in the data release notes (DRN) 21 for Q0-Q14 and DRN20 and 21 for Q15 and Q16, respectively (Thompson 2013b,a). Although PDC-msMAP high-pass filters the light curves at periods below about 20 days, this does not affect our sample of stars because they have been selected to have rotation periods shorter than 12 days. Hence, we have verified that the retrieved rotation periods and the activity related modulations remained the same.
A sample of 196 solar-like stars were observed by Kepler since Q5 for at least three months in short cadence (58.85 s, Gilliland et al. 2010) as part of the Kepler Asteroseismic Science Consortium (KASC) programme. Short-cadenced data are necessary to extract the seismic global properties of the stars in order to infer reliable stellar masses and radii as well as the structure of the stellar interior, in particular, the extension of their convective envelope.
The surface rotation period of these stars at the active latitudes can be studied by looking at the photometric modulation induced by the star’s active regions crossing the stellar visible disk (Mosser et al. 2009; Ballot et al. 2011; Campante et al. 2011; Mathur et al. 2011a; García et al., in prep.). We expect that fast rotators have shorter cycle periods as shown from observations by Böhm-Vitense (2007). Following this idea, we selected 22 stars that have rotation periods shorter than 12 days to look for magnetic activity cycles within the observation time of the Kepler mission (~3.7 years so far). We focus on F stars with Teff > 6000 K, where the Teff values were taken from Pinsonneault et al. (2012). F stars are interesting because they have thinner convective zone and present a strong increase in differential rotation (e.g. Augustson et al. 2012). Except the Sun, we note that so far the only star for which a cycle-like magnetic modulation has been detected using seismology is the F star HD 49933 (García et al. 2010). It is therefore suitable to concentrate our analysis on this subset of stars.
In Table 1 we present the seismic global parameters of the subset of 22 stars studied in this work. They were obtained with the A2Z pipeline (Mathur et al. 2010b) and are in agreement with the results from Chaplin et al. (2014; listed as M∗ in Table 1), 19 of them at a 1σ level. For the other three stars, the agreement in νmax is at a 2σ level. A visual inspection of the power spectra and the global seismic parameters of these stars showed that the disagreements can be explained. The difference between the two analyses can be attributed to the longer datasets we are using here compared to the Chaplin et al. (2014) datasets, which are based on 1-month Kepler data from the survey phase. Moreover, KIC 9289275 and 1016239 have what is known as a double bump acoustic (p)-mode envelope that complicates the determination of νmax (Bedding et al. 2010).
List of the 22 stars analysed in this study.
Appourchaux et al. (2012b) have already extracted the p-mode frequencies for 11 stars in our sample (indicated in Table 1). The complete study of the individual p modes of these stars is out of the scope of this paper. For our purposes, we can compute their masses and radii relying on the scaling relations as defined by Kjeldsen & Bedding (1995, 2011) and validated later by different methods (e.g. Huber et al. 2011; Mathur et al. 2012; Silva Aguirre et al. 2012). The values that we obtain agree within 1σ (except KIC 3733375 which is within 2σ) with the grid-based modelling results presented in Chaplin et al. (2014). We note that we used the observed mean large separation in the scaling relations, but the use of the asymptotic mean large separation as described in Mosser et al. (2013) leads to smaller radii and masses, which also agree within the uncertainties with the values listed in Table 1.
The rotation periods obtained by García et al. (in prep.) are also given in Table 1 with the associated uncertainties. Briefly, to extract the rotation periods we apply two different techniques to the two above-mentioned datasets. On the one hand, we perform a time-frequency analysis of the light curves using a Morlet transform and we project the result on the frequency domain (e.g. Mathur et al. 2010a,b, 2013). In most of the cases, the rotation period would be the highest peak in this periodogram. Sometimes, when there are two active longitudes in each side of the star, the highest peak retrieved is not the rotation period but the second harmonic. To avoid this case we also extract the second highest peak in the periodogram and we check if they correspond to a harmonic. On the other hand, we compute the autocorrelation of the temporal signal to extract a second estimation of the rotation rate. The autocorrelation is a powerful method as has been demonstrated by McQuillan et al. (2013). The use of both algorithms, wavelets and autocorrelation, allows us to minimise any false detection or ambiguities among the harmonics of the signal.
We also checked the stability of the autocorrelation function to study the lifetime of the starspots or active regions (at active longitudes) crossing the visible disk of the star. McQuillan et al. (2013) used the stability of the autocorrelation function to point out possible classical pulsators for which low-frequency modes are very stable, but this stability can also be due to long-lived active regions or stable groups of starspots at a given active longitude on the star (e.g. Frasca et al. 2011; Strassmeier 2009). These long-lived structures, if they are rotating at close rates (due to differential rotation), can produce a beating in the light curve that mimics the effect of activity cycles.
In Fig. 2, we show a seismic Hertzsprung-Russell (H-R) diagram with the 22 stars in our sample, where we used the mean large frequency separation (⟨ Δν ⟩) instead of the luminosity on the vertical axis. There could be a small difference between the mass derived by Chaplin et al. (2014) and the position of the star on the HR diagram that could be due to differences in metallicity.
In order to verify that the modulations observed in the light curves were genuine and not due to pollution from nearby stars (active or classical pulsators), the pixel data of each star were examined. We first checked the full frame image of the corresponding channels provided by the Mikulski Archive for Space Telescopes (MAST) to ensure that the considered stars were not included in the halo of a nearby pulsating star, which could account for a false modulation of the obtained light curve. This was not the case for any of the stars in our study. We then performed a more thorough verification using the pixel data itself (see Mathur et al., in prep.). For each star, we divided the selected stellar mask into several areas, typically four quadrants, and looked for the modulation in the light curves extracted from these sub masks. The presence of a nearby pulsating star in the mask of the observed star could have led to the presence of a modulation of the signal in a limited area of the mask. As this was not the case for the stars studied in this paper, we can reasonably consider that the observed modulations of their light curves are intrinsic.
 |
Fig. 2 Modified HR diagram showing the sample of 22 F stars analysed. Red symbols represent the stars that are discussed in Sect. 4.2: with long-lived features, with cycle-like behaviour, or with a trend in the magnetic proxy. Blue symbols correspond to stars where no clear cycle is observed for the duration of the observations also referred as the “Other” category in Table 2. The size of the symbols is inversely proportional to the surface rotation period of the star. The position of the Sun is indicated by the ⊙ symbol, and evolution tracks from Aarhus Stellar Evolution Code (ASTEC) are shown for a range of masses at solar composition (Z⊙ = 0.0246). Median uncertainties on ⟨ Δν ⟩ and Teff are shown in the lower left corner of the figure. |
Different indexes obtained for the 22 stars.
3. Magnetic index
It would be interesting to compute a magnetic index to quantify the level of magnetic activity of different stars and be able to compare them. To do so, we need to define a magnetic index – similar to the average Mount Wilson S-index (Middelkoop 1982) – based on photometric observations instead of chromospheric ones. While studying the CoRoT star HD 49933, García et al. (2010) defined a magnetic index that is the standard deviation of 30-day-long subseries in the light curve, yielding a magnetic-cycle proxy computed as the temporal variation of this standard deviation. This calculation was later taken by Chaplin et al. (2011) to study the impact of stellar magnetic activity on the acoustic modes and their detectability. They slightly modified the computation of the index by measuring the standard deviation of the Kepler light curves that were low-pass filtered and smoothed by a 1 h boxcar.
In this paper, we propose to use the standard deviation of the whole time series as a magnetic index of each star. We call this index Sph as a counterpart of the spectroscopic S-index. It is sensitive to the stellar variability but also to the photon noise σph. There are several ways of estimating the contribution of σph in the Kepler light curves. Here we used the approach proposed by Jenkins et al. (2010). They used a sample of 1639 stars obtained with one month of Kepler data in long cadence to infer an empirical relation between the apparent magnitude of the stars and σph. This relation was then successfully used by Mathur et al. (2011b) to characterise the long-cadence background of more than a thousand Kepler red giants. We note that this relation depends on the magnitude of the stars and on the way the light curves are extracted (e.g. the size of the masks used in each star).
As said before, Sph is obtained for the whole time series. This allows us to minimise the effects of any instrumental glitch in the data. However, Sph is sensitive to the presence or to the absence of magnetic cycles during the observations, which can bias the magnetic index (as happens with the S-index). To assess the existence of variations in the activity levels in a given star we also compute Sph locally, during low and high activity periods, to determine the ratio or contrast between periods with different average activity. To do so, we first measure the standard deviation for independent subseries of length k × Prot, where k is fixed to 5. Indeed, we have verified that when k > 3, the standard deviation converges towards a constant value ensuring the universal character of this index. Then we select the subseries where the standard deviation is smaller (nlow) or greater (nhigh) than Sph. We also define another global index ⟨ Sph ⟩ as the mean value of all the subseries we have, after removing the null values. This parameter is very close to Sph. Figure 1 (bottom lower panel) shows an example of the sigma computed for the different subseries for one star in our sample: KIC 3733735. The dashed line represents the mean value of the standard deviation ⟨ Sph ⟩. We also note that these indexes are sensitive to the inclination angle of the star. The ratio 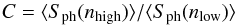 (1)gives a value of the contrast between periods of high activity and low activity during the observations. This is a useful way to disentangle stars potentially showing a magnetic activity cycle during the observations.
(1)gives a value of the contrast between periods of high activity and low activity during the observations. This is a useful way to disentangle stars potentially showing a magnetic activity cycle during the observations.
In Table 2 the global ⟨ Sph ⟩ index corrected for the photon noise as computed above, as well as the local indexes, also corrected for the photon noise: ⟨ Sph(nlow) ⟩ and ⟨ Sph(nhigh) ⟩, are given for the 22 F stars and the Sun using subseries of length 5 × Prot. To compute the solar magnetic index ⟨ Sph, ⊙ ⟩ we used the photometric data recorded by the Sun Photometers (SPM), belonging to the VIRGO (Variability of solar Irradiance and Gravity Oscillations; Fröhlich et al. 1995) instrument on board the Solar and Heliospheric Observatory (SoHO). We summed the two channels (green and red) to be close to the Kepler bandwidth and rebinned the data so that they have a sampling of 30 min like the Kepler long-cadence data. We obtained a value of ⟨ Sph, ⊙ ⟩ = 166.1 ppm for the mean activity level of the Sun integrated over the last 16 years (most of cycle 23 and the rising phase of cycle 24) (see García et al. 2013, for more details). Finally, we computed the associated statistical uncertainties ϵ by taking the dispersion between the different subseries used for the calculation of ⟨ Sph ⟩.
Figure 3 shows the mean activity index ⟨ Sph ⟩ for the 22 stars and the Sun. We notice that ⟨ Sph ⟩ varies between 70 to 900 ppm with an average activity level for our sample of stars at around 220 ppm showing that the magnetic activity of our set of stars is in general slightly larger than the mean activity level of the Sun. This is not in agreement with the results by Baliunas et al. (1995) who concluded that the F stars observed by the Mount Wilson survey had low S-indexes with a rather flat behaviour or a long-term variability, which they attributed to the lower chromospheric activity of these stars. Our analysis suggests that the photospheric activity is larger compared to the Sun. However, we have not taken into account any projection effects due to lower inclination stellar angles. Finally, KIC 7668623 has the largest value of the magnetic index. This case is further discussed in Sect. 4.2.
 |
Fig. 3 Mean magnetic index ⟨ Sph ⟩ identified by the star number given in Table 1. The stars are represented with different symbols according to their category in Table 2: L (red triangles), C (blue filled circle), T (pink squares), and O (open circles). KIC 3733735 is represented with the blue star since it belongs to both categories L and C. We superimposed the mean index of the Sun ⟨ Sph, ⊙ ⟩ = 166.1 ± 2.6 ppm (dashed line), the index at low activity ⟨ Sph(nlow) ⟩, (dot dash line), and the index at high activity ⟨ Sph(nhigh) ⟩ (triple dot dash line) obtained with the VIRGO data. |
We also show the contrast, C, between the maximum and minimum activity (Fig. 4). While most of the stars lie between 1 and 2, the Sun stands higher at 2.7. Only one star is close to the Sun, KIC 10644253, and we come back to it in the discussion.
Finally, we compute the range or variability index Rvar defined by Basri et al. (2011, 2013). They take subseries of 30 days and compute this index by ranking all the points of the light curve and removing the 5% of the points with the lowest and highest flux values. Then they measure the difference between the highest flux and the lowest flux remaining, which gives the range of flux spanned by the time series. The final index is the median value of all the subseries. Because this analysis is done for subseries of 30 days, it assumes that the rotation period of the star is shorter than 30 days, otherwise we cannot follow the change of the active regions. Fortunately for our stars, the rotation periods are below 12 days. The values of Rvar are given in Table 2 and they are also corrected for the photon noise. We notice that some stars with large values of ⟨ Sph ⟩ do not have large values of Rvar. This is an inherent consequence of the definition of Rvar. Assuming a proper correction of the light curve, the truncation of the highest 5% of the signal removes the highest activity points and results in a lower index relative to ⟨ Sph ⟩.
 |
Fig. 4 Contrast, C, between high and low magnetic activity for the 22 F stars for k = 5. The dashed line represents the contrast for the Sun obtained with the VIRGO data. Same legend as in Fig. 3. |
4. Time-frequency analysis: Magnetic cycle proxy
It is also interesting to study the temporal evolution of the magnetic activity of the stars and look for signatures of any cycle-like behaviour. To perform a time-frequency analysis, we used the wavelets tool developed by Torrence & Compo (1998), including the correction by Liu et al. (2007), and adapted for asteroseismology by Mathur et al. (2010b). It consists of looking for the correlation between the time series and a mother wavelet with a given period. We chose the Morlet wavelet, which is the convolution between a Gaussian function and a sinusoid. Then we slide the wavelet along time in the time series and we vary the period in a given range. This produces the wavelet power spectrum (WPS) represented in Fig. 1 (middle panel). Given the stellar rotation period, we project the WPS on the time axis in a small region around this period. This leads to the scale average variance (SAV, bottom panel in Fig. 1), which corresponds to a magnetic proxy of any magnetic activity cycle. This ensures that the magnetic proxy is only related to structures rotating with the rotation period of the star and is not affected by a localised problem due to a bad correction of the Kepler data.
4.1. The Sun
For this analysis, we used the VIRGO/SPM data again. García et al. (2013) applied the same methodology that we have used in this work to 16 years of solar data measured by SoHO. In Fig. 5 of this paper the scale average variance was compared to a typical solar magnetic activity proxy, the solar radio flux at 10.7 cm. We also note in their plot that during the rising phases of cycles 23 and 24 and during the maximum of cycle 23, some spikes appear in the magnetic proxy with a much higher amplitude compared to the minimum magnetic activity period. These features were also present in the solar radio flux, reinforcing the idea that the scale average variance is a good magnetic activity proxy at all temporal scales.
 |
Fig. 5 Wavelet analysis of VIRGO data for subseries of 2000 days. For each subseries, we show the wavelet power spectrum (red and dark areas are correspond to high power) and the average variance that is the magnetic proxy obtained by projecting the WPS between 6- and 60-day periods on the x-axis. Plots from top left to bottom right correspond to the increase in cycle 23 to the decrease in cycle 23. |
From the Kepler observations, we do not expect to observe many complete activity cycles. This might be possible only for a handful of stars among the fastest rotators. We investigate here if the SAV is able to disentangle the different phases of a cycle when the observations span only part of it. This analysis will also allow us to characterise features that could help us later to identify at which moment of the magnetic cycle the stars are observed when only a portion of their activity cycles is sampled.
To better interpret the results of the wavelet analysis for our sample of F stars, we divided the VIRGO/SPM data into chunks of 2000 days starting on 11 April 1996. This corresponds to an observation length that is 70 times the equatorial rotation period of the Sun, which is ~26 days. This is the case for our sample of Kepler stars, for which the rotation periods are shorter than 12 days ,and for which we have observed at least 70 rotation periods. The different subseries that we analysed are representative of different periods in the magnetic activity cycle of the Sun: the rising phase of cycle 23, the maximum activity of this cycle, its decrease, and the extended minimum between cycles 23 and 24. For the following study, the scale average variance was obtained projecting all the wavelets between 6 and 60 days to be very conservative and to include the second harmonic or the rotation period of ~13 days.
The top left panel in Fig. 5 corresponds to the increase in activity for cycle 23. We see that in the first 1000 days the magnetic proxy is very flat. After that flat period, the magnetic proxy increases, so the wavelet analysis is able to see the rise in the magnetic cycle.
The analysis of the period between 1000 and 3000 days, which includes the rising phase and the maximum of the magnetic activity cycle, is shown in the top right panel in Fig. 5. We notice that the magnetic proxy has quite a few high peaks whose amplitudes increase slightly. But having only these 2000 days of data at this given moment would not have allowed us to determine in which exact period of the cycle we are observing the Sun, except that it is quite active.
The bottom left panel in Fig. 5 represents the analysis of the maximum of cycle 23 and the beginning of the decrease of the cycle between 2000 and 4000 days. The magnetic proxy is flatter than the previous phase with amplitude peaks that are not as high. In particular, the last 800 days are flat and very similar to the first 1000 days of data.
Finally, the bottom right panel in Fig. 5 corresponds to the decrease of cycle 23 and the extended minimum between cycles 23 and 24. A few peaks are still present during the decrease of the cycle but after 4000 days the magnetic proxy is even flatter than the top left panel of the figure, so our magnetic proxy does see the extended minimum.
From this thorough analysis, we can say that the magnetic proxy SAV allows us to flag a rise or decrease in a magnetic activity cycle and therefore to uncover a cycle-like behaviour. However, if we observe most of the maximum activity cycle, it is very complicated to determine if the star is close to the rise or the dawn of the cycle. This is where the magnetic index Sph intervenes and can help to disentangle in which situation the star is observed.
We note that this analysis is done for the Sun, which has an inclination angle of 90°, but this will not be the case for all our stars. We come back to this problem in Sect. 5.2.
4.2. The Kepler F stars
We performed a time-frequency analysis by applying the wavelets to the 22 stars in our sample (see Fig. 1 and Appendix A) yielding their magnetic activity proxy as defined above. The projection on the time axis was computed in a range of periods that takes into account the power seen in the WPS. The range used for each star is given in the caption of the figures. We notice different patterns that could correspond to different magnetic behaviour that is intrinsic in the stars and we divide our sample into four groups: stars with long-lived features (probably spots or active regions), stars with a cycle-like behaviour, stars that show an increase or decrease in the magnetic proxy, and stars that do not show any clear modulation in the magnetic proxy.
The first group consists of six stars: KIC 3733735, KIC 7206837, KIC 7668623, KIC 9226926, KIC 10355856, and KIC 11070918. We call this group “L” for long-lived features. For these six stars, we note that their WPS have a high level of power throughout almost all of the observation period. This suggests that there are spots or active regions that are present around the same region (or longitude) at the surface of the stars for a long period of time. Two of these stars, KIC 3733735 and KIC 9226926, have their magnetic proxies that increase and decrease with time. This could be due to either an increase in the number of spots (similar to what we observe for the Sun) or a beating between two close frequencies that are very stable with time (active regions or modes). This is developed further in Sect. 5.1. In addition, KIC 7206837, KIC 7668623, KIC 10355856, and KIC 11070918 have strong power in the second and sometimes third harmonics of the main period of rotation. This is probably due to the existence of several long-lived active regions at given longitudes on the surface of the stars. In particular, the magnetic proxy of KIC 9226926 shows a modulation of about 540 days on average while KIC 10355856 has a modulation of approximately 30 days in the magnetic proxy. We also note that KIC 7668623 has some large peaks in the SAV, which could be related to a low inclination angle of the star.
The case of KIC 3733735 is very interesting because we observe two different modulations. The one of ~90 days seems very similar to the previous stars suggesting the presence of stable active regions. This modulation appears to be triggered by the other modulation, which corresponds to a flat magnetic proxy during the first 600 days of observations followed by a progressive increase and decrease. This large envelope is very similar to what we observe in the Sun during one cycle giving us a hint that one magnetic cycle is observed for this star.
The second group of stars (listed as “C” in Table 2) corresponds to those with cycle-like behaviour: KIC 3733735 (also in the previous category of long-lived spots) and KIC 10644253. The second star shows a few large peaks in the magnetic proxy suggesting that this star is observed with a low inclination angle and for which two magnetic cycles could have been observed.
The third group (listed as “T” in Table 2) contains two stars that show some trend in the magnetic activity proxy. KIC 1435467 seems to show a slight increase in the magnetic proxy. The SAV of KIC 12009504 has a slight decrease and then an increase in the magnetic proxy. This might correspond to the observation of the transition from one cycle to the following one. Unfortunately, since it is difficult to interpret these trends when we do not see any flat behaviour, more data are needed to confirm these conclusions.
The fourth and last group contains 13 stars (category “O” in Table 2) that do not show any modulation that looks like a cycle. The magnetic proxy of these stars is more chaotic. A few simple explanations can be given for these stars: 1) the cycle period is longer than the observation length preventing us from observing a cycle; 2) these stars do not have regular cycles; or 3) their inclination angles are low.
Since the magnetic proxy depends on the range of periods where we project the WPS, we cannot directly compare the absolute values of our stars with our study of the Sun. However, we can still compare the global behaviour of the proxy.
The stars KIC 1430163, 5371516, 5773345, 7103006, 9812850, and 10016239 show a large number of peaks in the magnetic proxy as well as an almost continuous power in the wavelet power spectrum. This suggests that these stars have active regions that evolve, appear, and disappear with time. This looks very similar to the analysis of the VIRGO data during the rise and maximum of the cycle (top right panel in Fig. 5). As said before, these stars could be in a non-cycling state or being observed during a maximum of a much longer activity cycle.
We note that KIC 4638884 has large peaks in the magnetic proxy. This could be related to the inclination angle of the stars and the position of the active latitudes. We discuss these cases further in the next section.
We find six stars (KIC 6508366, 7771282, 7940546, 8026226, 9289275, and 10162436) that have very erratic behaviour preventing us from confirming any cycle or magnetic-related cycles detection.
5. Discussion
5.1. Long-lived features
In Sect. 4.2, we mentioned two stars, KIC 3733735 and KIC 9226926, where we see an interesting modulation in the magnetic proxy that could be due to the magnetic activity cycle of the stars. One of these stars has a rather high magnetic index ⟨ Sph ⟩ of 249.9 ppm while the other star has a rather low value of 103.7 ppm. We looked in more detail into the low-frequency part of their power spectra around the rotation period found. We noticed that these stars have two or three high-amplitude peaks very close to each other. The existence of two close frequencies, f1 and f2, leads to a beating effect generating a sine wave of frequency f1 + f2 modulated by an envelope with a frequency f2 − f1.
For KIC 3733735, the two highest peaks are located at 4.4 and 4.5 μHz. The envelope of the beating should have a frequency of 0.1 μHz, i.e. 116 days. By computing the Fourier transform of the magnetic proxy, we obtain a peak at 0.13 μHz, i.e. 89 days. So the modulation observed is probably due to the beating of two frequencies. KIC 9226926 also has two main peaks in the power spectrum that have frequencies of 5.237 μHz and 5.259 μHz. The beating effect leads to a frequency of 0.022 μHz, i.e. 513 days. We also computed the Fourier transform of the magnetic proxy and found a frequency of 0.025 μHz, i.e. 463 days. This also confirms that we are not observing the magnetic cycles of the star but a result of the beating effect. The detection of two frequencies for the rotation measurement implies that for these two stars we are observing the signature of the latitudinal differential rotation.
We also looked at the phase of these features and noticed that their phases are very stable with time, i.e. the features are present around the same region on the surface for a long period of time (approximately 1000 days). These long-lived features can be produced by long-lived spots or active regions, by the presence of active longitudes yielding to the appearance of spots at a given longitude, or by classical pulsations. We favour the first two explanations for two reasons. According to their fundamental parameters, we do not expect these stars to be in the instability strip. In addition, the morphology of their light curves is typical of spotted stars. If we were in the presence of pulsations, the modulation of the light curve would be strictly sinusoidal possibly with a modulation due to starspots superimposed. However what we observe is a nearly sinusoidal signal during the minima of the modulation and a sine wave more or less truncated at the maxima. This truncated sinusoidal signal is characteristic of starspots, where the nearly flat part corresponds to the continuum of the luminosity because of a low number of spots. Figure 6 illustrates this with 20 days of data for KIC 3733735, where this effect is clearly visible. This figure can be directly compared to the one obtained through simulation by Walkowicz et al. (2013, their Fig. 1). They also point out that the visibility of this continuum increases with the inclination of the star, a correlation corroborated by the inclination angle of 30° for this star.
 |
Fig. 6 Light curve of KIC 3733735 at a maximum of the amplitude (black). The blue line is a sine wave whose frequency corresponds to the maximum of the light curve spectrum. The truncated upper parts of the real light curve are clearly visible while the lower parts are very similar to the pure sine wave. This shape is characteristic of starspots with surface rotation. |
After ruling out the pulsation scenario, two explanations remain: the active regions are very stable or they are generated at the same longitude, also called the active longitudes. These active longitudes or active nests have been observed in the Sun (de Toma et al. 2000) and seem to last for several rotation periods. This has also been seen in stars with a nearby companion (e.g. Lanza et al. 2011) whose interaction would generate a stable spot on the surface of the star. However, no signature of such a companion has been detected for these two stars. We notice that the long-term feature appears in KIC 3733735 once the second modulation (attributed to a magnetic cycle here) increases. This would mean that these active longitudes are related to internal changes, such as the dynamo mechanisms occurring inside the star. In particular this has been studied theoretically with dynamo models (Berdyugina et al. 2006; Weber et al. 2013).
5.2. Magnetic index and other parameters
Having defined a magnetic index and a magnetic cycle proxy for all the stars, we can study if the combination of both pieces of information can help to better understand the magnetic activity of the stars and the existence of regular cycles.
The two stars that show an increase or decrease in activity, i.e. a slope in the magnetic proxy, have a magnetic index ⟨ Sph ⟩ lower than the maximum activity of the Sun (⟨ Sph(nhigh) ⟩) so unfortunately we cannot say anything more about these stars. We also notice that stars with high amplitude peaks in the magnetic proxy usually have larger magnetic indexes, while the stars with a more erratic behaviour have lower indexes in general (although with a few outliers).
Finally, the two stars with broad peaks in the magnetic proxy (KIC 7668623 and KIC 10644253) have the highest values of ⟨ Sph ⟩. As said in Sect. 4.2, these stars might reflect a configuration where the inclination angle of their rotation axis is low but high enough so that we can see the signature of the rotation.
For 16 stars in our sample, Bruntt et al. (2012) could estimate a vsini. Using these values in combination with the estimation of the radius of the star from scaling relations and the rotation periods we have inferred, we can deduce the inclination angle i. It appears that in general i varies between 20 and 60°. For three stars (KIC 7940546, 10016239, and 12009504), the sini was a little larger than 1 but also slightly lower than 1 with the uncertainties. So we assumed that their inclination angle must be close to 90°. This could be due to some errors in the seismic parameters. The angle of inclination is an important parameter because it affects the observation of the magnetic cycle as studied by Vázquez Ramió et al. (2011). They showed that the maximum occurs later and has a lower amplitude than in the 90° case. This means that the minimum appears to be longer. In addition, they noted that the second harmonic of the rotation disappears. The star KIC 4638884 has an inclination angle around 25° and this could explain the shape of the magnetic proxy. The other star with a similar proxy (KIC 10644253) has an inclination angle of ~43°. The large uncertainty associated with this angle does not rule out the low inclination angle scenario.
One thing that is unknown for the stars is the latitude where the starspots or active regions appear. If the star is observed pole on and the active regions appear close to the pole, then we would be sensitive to the lifetime of the active region. If the active latitudes are located around 30° like the Sun and the star is observed almost pole on, we would still be able to determine the surface rotation period of the star but the effect of the active region will be weakened in the light curve because of projection effects that will diminish the observed size of the pattern.
A relation between the S-index and the rotation period has been established by Saar & Brandenburg (2002). In Fig. 7 we show ⟨ Sph ⟩ as a function of Prot. At first sight no clear correlation appears, but if we look at the stars that show evidence of long-lived features (red triangles), a slight correlation seems to be present. Saar & Brandenburg (2002) observed the opposite, that there was an anti-correlation, but we note that their result concerns stars where they observed magnetic cycles while our subsample only shows long-lived features.
 |
Fig. 7 Magnetic index ⟨ Sph ⟩ versus Prot using the same legend as in Fig. 3. The dashed line represents the magnetic index for the Sun. |
We looked for evidence of correlation between the magnetic index of our stars (⟨ Sph ⟩) and a few stellar parameters we have access to. It would be interesting to see if the hottest stars have generally larger magnetic indexes or not. According to Lovis et al. (2011), who measured the CaHK index  for 300 FGK, stars with an effective temperature above 5600 K showed a magnetic cycle semi-amplitude smaller than for cooler stars. The F stars in our sample show a slight anti-correlation where hotter stars have smaller magnetic indexes, going in the same direction as the Lovis et al. (2011) results.
for 300 FGK, stars with an effective temperature above 5600 K showed a magnetic cycle semi-amplitude smaller than for cooler stars. The F stars in our sample show a slight anti-correlation where hotter stars have smaller magnetic indexes, going in the same direction as the Lovis et al. (2011) results.
We expect that magnetic activity declines with age. The mean large separation Δν gives a hint about the evolutionary stage of a star. However, we did not find any clear correlation between ⟨ Sph ⟩ and Δν.
The contrast as a function of the evolutionary stage (Fig. 8) presents a slight correlation, which could suggest that more evolved stars seem to show a smaller contrast, which means that the change in luminosity due to magnetic activity becomes less prominent. However, the correlation rate is 40%, which is not negligible. We still have to be cautious because for most of the stars we do not see a complete cycle, if such a cycle exists in all F stars, which could bias our analysis.
 |
Fig. 8 Contrast between maximum and minimum activity regions as a function of the mean large separation (Δν). Using the same legend as in Fig. 3. The Sun is represented with the symbol ⊙. |
5.3. Rossby number
Noyes et al. (1984) studied the magnetic activity of low main-sequence stars that had Ca ii H and K line measurements at the Mount Wilson. They showed that chromospheric activity directly depends on the Rossby number Ro = Prot/τc, where τc is the convective turnover time. Saar & Brandenburg (2002) showed that the magnetic activity cycle period and the rotation rate were also linked through this quantity. We computed the Rossby numbers for our sample of stars. To ease comparisons with previous works, we computed a convective turnover time from the colour B − V, as done in Noyes et al. (1984). Colours are derived from the Tycho2 catalog (Høg et al. 2000). We have to keep in mind, however, that this approach, where τc is only parametrized with a colour, is very crude. Moreover, it is not necessarily well suited for F stars that may have very shallow convective envelopes. These numbers are quoted in Table 3.
However, seismology allows us to perform accurate modelling of the internal structure of observed stars. It is possible to compute Rossby numbers from these tailored models. Eight stars have been modelled by the Asteroseismic Modeling Portal (Metcalfe et al. 2009; Mathur et al. 2012, Metcalfe et al., in prep.). Using the mixing length theory, we defined a local Rossby number Rol and a global Rossby number Rog. For the first, the convective turnover time scale is computed as τcl = Λ/vMLT, where Λ is the mixing length and vMLT is the convective velocity evaluated half a pressure scale height above the base of the convective envelope. For Rog, the convective turnover time scale is computed through the whole envelope as 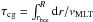 , where rbce is the position of the base of the convective envelope and R the stellar radius. These results are given in Table 3. We verify that Rol and Rog are closely linked and vary similarly. We note that the large values for the Rossby number of 12 and 125 correspond to the stars that have the shallowest convective zones (depths of 5 and 2%).
, where rbce is the position of the base of the convective envelope and R the stellar radius. These results are given in Table 3. We verify that Rol and Rog are closely linked and vary similarly. We note that the large values for the Rossby number of 12 and 125 correspond to the stars that have the shallowest convective zones (depths of 5 and 2%).
Among the two stars for which a cycle has been observed, only KIC 3733735 has seismic constraints that allow structure modelling. The Rossby number found for this star is high enough to suggest a long cycle period Pcyc compared to its rotation period Prot. Indeed, by renormalizing the cycle period to the rotation period for this star we find Pcyc > 540Prot (since only one cycle was observed), whereas for the Sun, Pcyc ≈ 150Prot. These observations should give constraints for dynamo theory that makes predictions for the link between Pcyc/Prot and Ro (see Thomas & Weiss 2008).
We finally searched for a correlation between the magnetic index and the local Rossby number. Noyes et al. (1984) showed that there was a clear anti-correlation between the Ca II HK flux  and Ro. Recently, Marsden et al. (2013) analysed a large number of solar-type stars with high-resolution spectropolarimetric observations and found a similar anti-correlation between the strength of the magnetic field and Ro. However, with our sample of stars we could not find any significant anti-correlation between ⟨ Sph ⟩, and the local Rossby number. However, we found a small anti-correlation between the contrast C and the Rossby number (see Fig. 9); this result does not agree with the results of Saar & Brandenburg (2002) who did not find any clear correlation between the cycle amplitude and Ro.
and Ro. Recently, Marsden et al. (2013) analysed a large number of solar-type stars with high-resolution spectropolarimetric observations and found a similar anti-correlation between the strength of the magnetic field and Ro. However, with our sample of stars we could not find any significant anti-correlation between ⟨ Sph ⟩, and the local Rossby number. However, we found a small anti-correlation between the contrast C and the Rossby number (see Fig. 9); this result does not agree with the results of Saar & Brandenburg (2002) who did not find any clear correlation between the cycle amplitude and Ro.
 |
Fig. 9 Magnetic contrast C as a function of the Rossby number of the stars modelled by AMP. The Rossby number was obtained from the stellar models (squares) and with the equation of Noyes et al. (1984) based on colour measurements of Tycho2 (triangles). |
Rotation periods, inclination angle, and Rossby numbers for the 22 stars computed with different approaches.
5.4. Hints in the background
It has been observed that the increase in the Sun’s magnetic activity is usually accompanied by the presence of bright points (or faculae) (e.g. Karoff 2012). To investigate the background of the power spectrum and extract its parameters for the 22 stars, we fitted it following the A2Z method described in Mathur et al. (2011b).
In order to have the most complete power spectrum, we used the short cadence data allowing us to measure the photon noise. Following Karoff et al. (2013a) we fitted the background with one and two Harvey-like functions (Harvey 1985) by fixing the slopes to 3.5 for the granulation component and 6.2 for the higher frequency component (i.e. the bright points) to ensure the stability of the fits. According to Karoff (2012), the second Harvey component could be due to faculae, then linked to the magnetic activity. However, within our sample of F stars, there is no evidence of a correlation between the magnetic index ⟨ Sph ⟩ and the characteristic parameters of the second Harvey component.
6. Conclusions
We have analysed 22 F stars that have a rotation period shorter than 12 days to determine their magnetic indexes and study their magnetic proxies. We defined some new indicators of the magnetic activity based on photometric observations. We studied the magnetic index ⟨ Sph ⟩, which is the mean value of the standard deviations of the subseries of length 5 × Prot. We showed that in general, most of the stars we studied have a mean activity index that is slightly larger than the one of the Sun.
We combined the measurement of the magnetic index with the magnetic proxy obtained with the wavelet analysis. This analysis showed a variety of behaviour in the magnetic activity of the F stars. Two stars show cycle-like behaviour. The magnetic proxy of KIC 3733735 is clearly flat over a period of 500 days and shows an increase and decrease during the rest of the observations suggesting a cycle period of at least 1400 days. The other star, KIC 10644253, has a magnetic proxy with two large peaks that can be explained by the observation of two cycles for a star that has a low inclination angle.
For two stars, KIC 3733735 and KIC 9226296, we detected the signature of latitudinal differential rotation as we observed the beating of two close frequencies. A group of five stars show a clear signature of long-lived features on their surface suggesting the existence of active longitudes on these stars.
We observed stars that present a slight increase or decrease in the magnetic proxy, suggesting a modulation of the magnetic activity. Finally, the last category gathers stars where no clear modulation is seen. These stars have either a large number of high amplitude peaks, or result from the observation with an inclination angle and more erratic stars.
This is very interesting because it means that stars with similar spectroscopic constraints and rotation periods can have very different magnetic activity behaviour: cycle-like behaviour, long-lived features, chaotic activity, or flat activity. To understand these differences, it is important to measure the magnetic field of these stars but also have a detailed description of their structure, such as the depth of their convection zones. For the former point, four in our sample of stars (KIC 1435467, 3733735, 7206837, and 12009504) have been monitored by the FIES spectrograph at the Nordic Optical Telescope (Karoff et al. 2013b). The analysis agrees that the star with the largest average S-index of 0.182 ± 0.001 is KIC 3733735. For the study of the structure a deeper analysis will be done for the stars with long short-cadence data.
Online material
Appendix A
 |
Fig. A.1 Wavelet analysis of KIC 1430163 (group O). Top panel: temporal variation of the flux after the corrections applied as in García et al. (2011). Middle panel: wavelet power spectrum as a function of time and period. The green grid represents the cone of influence that takes into account the edge effects and delimits the reliable rein in the WPS. Red and dark colours correspond to strong power while blue corresponds to weak power. Bottom panel: projection of the WPS on the time axis between periods of 1 and 7 days. |
 |
Fig. A.2 Wavelet analysis of KIC 1435467 (group T). Same representation as in Fig. A.1. The magnetic proxy (bottom panel) was computed between periods of 1.7 and 11 days. |
 |
Fig. A.3 Wavelet analysis of KIC 3733735 (group L+C). Same representation as in Fig. A.1. The magnetic proxy (bottom panel) was computed between periods of 1 and 4.1 days. |
 |
Fig. A.4 Wavelet analysis of KIC 4638884 (group O). Same representation as in Fig. A.1. The magnetic proxy (bottom panel) was computed between periods of 2.5 and 12 days. |
 |
Fig. A.5 Wavelet analysis of KIC 5371516 (group O). Same representation as in Fig. A.1. The magnetic proxy (bottom panel) was computed between periods of 1.5 and 10 days. |
 |
Fig. A.6 Wavelet analysis of KIC 5773345 (group O). Same representation as in Fig. A.1. The magnetic proxy (bottom panel) was computed between periods of 3.8 and 20 days. |
 |
Fig. A.7 Wavelet analysis of KIC 6508366 (group O). Same representation as in Fig. A.1. The magnetic proxy (bottom panel) was computed between periods of 2 and 6 days. |
 |
Fig. A.8 Wavelet analysis of KIC 7103006 (group O). Same representation as in Fig. A.1. The magnetic proxy (bottom panel) was computed between periods of 2 and 8 days. |
 |
Fig. A.9 Wavelet analysis of KIC 7206837 (group L). Same representation as in Fig. A.1. The magnetic proxy (bottom panel) was computed between periods of 1.2 and 7 days. |
 |
Fig. A.10 Wavelet analysis of KIC 7668623 (group L). Same representation as in Fig. A.1. The magnetic proxy (bottom panel) was computed between periods of 1.9 and 8 days. |
 |
Fig. A.11 Wavelet analysis of KIC 7771282 (group O). Same representation as in Fig. A.1. The magnetic proxy (bottom panel) was computed between periods of 3 and 20 days. |
 |
Fig. A.12 Wavelet analysis of KIC 7940546 (group O). Same representation as in Fig. A.1. The magnetic proxy (bottom panel) was computed between periods of 3 and 18 days. |
 |
Fig. A.13 Wavelet analysis of KIC 8026226 (group O). Same representation as in Fig. A.1. The magnetic proxy (bottom panel) was computed between periods of 2 and 16 days. |
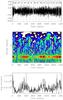 |
Fig. A.14 Wavelet analysis of KIC 9226926 (group L). Same representation as in Fig. A.1. The magnetic proxy (bottom panel) was computed between a period of 1 and 4 days. |
 |
Fig. A.15 Wavelet analysis of KIC 9289275 (group O). Same representation as in Fig. A.1. The magnetic proxy (bottom panel) was computed between periods of 2.3 and 17 days. |
 |
Fig. A.16 Wavelet analysis of KIC 9812850 (group O). Same representation as in Fig. A.1. The magnetic proxy (bottom panel) was computed between periods of 1.8 and 10 days. |
 |
Fig. A.17 Wavelet analysis of KIC 10016239 (group O). Same representation as in Fig. A.1. The magnetic proxy (bottom panel) was computed between periods of 1.8 and 10 days. |
 |
Fig. A.18 Wavelet analysis of KIC 10162436 (group O). Same representation as in Fig. A.1. The magnetic proxy (bottom panel) was computed between periods of 3.8 and 17 days. |
 |
Fig. A.19 Wavelet analysis of KIC 10355856 (group L). Same representation as in Fig. A.1. The magnetic proxy (bottom panel) was computed between periods of 1.7 and 8 days. |
 |
Fig. A.20 Wavelet analysis of KIC 10644253 (group C). Same representation as in Fig. A.1. The magnetic proxy (bottom panel) was computed between periods of 5 and 18 days. |
 |
Fig. A.21 Wavelet analysis of KIC 11070918 (group L). Same representation as in Fig. A.1. The magnetic proxy (bottom panel) was computed between periods of 0.8 an 5 days. |
 |
Fig. A.22 Wavelet analysis of KIC 12009504 (group T). Same representation as in Fig. A.1. The magnetic proxy (bottom panel) was computed between periods of 1.8 and 15 days. |
Acknowledgments
This work was partially supported by the NASA grant NNX12AE17G. S.M. and R.A.G. acknowledge the support of the European Community’s Seventh Framework Programme (FP7/2007-2013) under grant agreement No. 269194 (IRSES/ASK). R.A.G. acknowledges the support of the French ANR/IDEE grant. The authors thank K. Augustson, A. S. Brun, S. Mathis, and B. Mosser for very useful discussions. The research leading to these results has received funding from the European Research Council under the European Community’s Seventh Framework Programme (FP7/2007–2013)/ERC grant agreement n°227224 (PROSPERITY), as well as from the Research Council of the KU Leuven under grant agreement GOA/2013/012. S.B. is supported by the Foundation for Fundamental Research on Matter (FOM), which is part of the Netherlands Organisation for Scientific Research (NWO).
References
- Appourchaux, T., Benomar, O., Gruberbauer, M., et al. 2012a, A&A, 537, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Appourchaux, T., Chaplin, W. J., García, R. A., et al. 2012b, A&A, 543, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Augustson, K. C., Brown, B. P., Brun, A. S., Miesch, M. S., & Toomre, J. 2012, ApJ, 756, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Baliunas, S. L., Donahue, R. A., Soon, W. H., et al. 1995, ApJ, 438, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Ballot, J., Gizon, L., Samadi, R., et al. 2011, A&A, 530, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Basri, G., Walkowicz, L. M., Batalha, N., et al. 2011, AJ, 141, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Basri, G., Walkowicz, L. M., & Reiners, A. 2013, ApJ, 769, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, P. G., Montalban, J., Kallinger, T., et al. 2012, Nature, 481, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Bedding, T. R., Kjeldsen, H., Campante, T. L., et al. 2010, ApJ, 713, 935 [NASA ADS] [CrossRef] [Google Scholar]
- Berdyugina, S. V., Moss, D., Sokoloff, D., & Usoskin, I. G. 2006, A&A, 445, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Böhm-Vitense, E. 2007, ApJ, 657, 486 [NASA ADS] [CrossRef] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bruntt, H., Basu, S., Smalley, B., et al. 2012, MNRAS, 423, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Campante, T. L., Handberg, R., Mathur, S., et al. 2011, A&A, 534, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chaplin, W. J., Bedding, T. R., Bonanno, A., et al. 2011, ApJ, 732, L5 [Google Scholar]
- Chaplin, W. J., Basu, S., Huber, D., et al. 2014, ApJS, 210, 1 [NASA ADS] [CrossRef] [Google Scholar]
- de Toma, G., White, O. R., & Harvey, K. L. 2000, ApJ, 529, 1101 [Google Scholar]
- Deheuvels, S., García, R. A., Chaplin, W. J., et al. 2012, ApJ, 756, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Fares, R., Donati, J.-F., Moutou, C., et al. 2009, MNRAS, 398, 1383 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Fletcher, S. T., Broomhall, A., Salabert, D., et al. 2010, ApJ, 718, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Frasca, A., Fröhlich, H.-E., Bonanno, A., et al. 2011, A&A, 532, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fröhlich, C., Romero, J., Roth, H., et al. 1995, Sol. Phys., 162, 101 [NASA ADS] [CrossRef] [Google Scholar]
- García, R. A., Mathur, S., Salabert, D., et al. 2010, Science, 329, 1032 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- García, R. A., Hekker, S., Stello, D., et al. 2011, MNRAS, 414, L6 [NASA ADS] [CrossRef] [Google Scholar]
- García, R. A., Salabert, D., Mathur, S., et al. 2013, J. Phys. Conf. Ser., 440, 012020 [NASA ADS] [CrossRef] [Google Scholar]
- Gilliland, R. L., Jenkins, J. M., Borucki, W. J., et al. 2010, ApJ, 713, L160 [NASA ADS] [CrossRef] [Google Scholar]
- Harvey, J. 1985, in Future Missions in Solar, Heliospheric & Space Plasma Physics, eds. E. Rolfe, & B. Battrick, ESA SP, 235, 199 [Google Scholar]
- Høg, E., Fabricius, C., Makarov, V. V., et al. 2000, A&A, 355, L27 [NASA ADS] [Google Scholar]
- Huber, D., Bedding, T. R., Stello, D., et al. 2011, ApJ, 743, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, J. M., Caldwell, D. A., Chandrasekaran, H., et al. 2010, ApJ, 713, L120 [NASA ADS] [CrossRef] [Google Scholar]
- Karoff, C. 2012, MNRAS, 421, 3170 [NASA ADS] [CrossRef] [Google Scholar]
- Karoff, C., Campante, T. L., Ballot, J., et al. 2013a, ApJ, 767, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Karoff, C., Metcalfe, T. S., Chaplin, W. J., et al. 2013b, MNRAS, 433, 3227 [NASA ADS] [CrossRef] [Google Scholar]
- Kjeldsen, H., & Bedding, T. R. 1995, A&A, 293, 87 [NASA ADS] [Google Scholar]
- Kjeldsen, H., & Bedding, T. R. 2011, A&A, 529, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lanza, A. F., Boisse, I., Bouchy, F., Bonomo, A. S., & Moutou, C. 2011, A&A, 533, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Libbrecht, K. G., & Woodard, M. F. 1990, Nature, 345, 779 [Google Scholar]
- Liu, Y., Liang, X., & Weisberg, R. 2007, J. Atmos. Ocean Technol., 24, 2093 [Google Scholar]
- Lockwood, G. W., Skiff, B. A., Henry, G. W., et al. 2007, ApJS, 171, 260 [NASA ADS] [CrossRef] [Google Scholar]
- Lovis, C., Dumusque, X., Santos, N. C., et al. 2011, A&A, submitted [arXiv:1107.5325] [Google Scholar]
- Marsden, S. C., Petit, P., Jeffers, S. V., et al. 2013 [arXiv:1310.6507] [Google Scholar]
- Mathur, S., García, R. A., Catala, C., et al. 2010a, A&A, 518, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathur, S., García, R. A., Régulo, C., et al. 2010b, A&A, 511, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathur, S., Handberg, R., Campante, T. L., et al. 2011a, ApJ, 733, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Mathur, S., Hekker, S., Trampedach, R., et al. 2011b, ApJ, 741, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Mathur, S., Metcalfe, T. S., Woitaszek, M., et al. 2012, ApJ, 749, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Mathur, S., García, R. A., Morgenthaler, A., et al. 2013, A&A, 550, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mazumdar, A., Monteiro, M. J. P. F. G., Ballot, J., et al. 2012, Astron. Nachr., 333, 1040 [NASA ADS] [Google Scholar]
- McQuillan, A., Aigrain, S., & Mazeh, T. 2013, MNRAS, 432, 1203 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Metcalfe, T. S., Dziembowski, W. A., Judge, P. G., & Snow, M. 2007, MNRAS, 379, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Metcalfe, T. S., Creevey, O. L., & Christensen-Dalsgaard, J. 2009, ApJ, 699, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Metcalfe, T. S., Basu, S., Henry, T. J., et al. 2010, ApJ, 723, L213 [NASA ADS] [CrossRef] [Google Scholar]
- Metcalfe, T. S., Buccino, A. P., Brown, B. P., et al. 2013, ApJ, 763, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Middelkoop, F. 1982, A&A, 107, 31 [NASA ADS] [Google Scholar]
- Mosser, B., Baudin, F., Lanza, A. F., et al. 2009, A&A, 506, 245 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosser, B., Michel, E., Belkacem, K., et al. 2013, A&A, 550, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noyes, R. W., Hartmann, L. W., Baliunas, S. L., Duncan, D. K., & Vaughan, A. H. 1984, ApJ, 279, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Pinsonneault, M. H., An, D., Molenda-Żakowicz, J., et al. 2012, ApJS, 199, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Saar, S. H., & Brandenburg, A. 1999, ApJ, 524, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Saar, S. H., & Brandenburg, A. 2002, Astron. Nachr., 323, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Salabert, D., Régulo, C., Ballot, J., García, R. A., & Mathur, S. 2011, A&A, 530, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sanz-Forcada, J., Stelzer, B., & Metcalfe, T. S. 2013, A&A, 553, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- SilvaAguirre, V., Casagrande, L., Basu, S., et al. 2012, ApJ, 757, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Simoniello, R., Jain, K., Tripathy, S. C., et al. 2013, ApJ, 765, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, J. C., Stumpe, M. C., Van Cleve, J. E., et al. 2012, PASP, 124, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Strassmeier, K. G. 2009, in IAU Symp., 259, 363 [Google Scholar]
- Stumpe, M. C., Smith, J. C., Van Cleve, J. E., et al. 2012, PASP, 124, 985 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, J. H., & Weiss, N. O. 2008, Sunspots and Starspots (Cambridge University Press) [Google Scholar]
- Thompson, S. E. 2013a, Kepler Data Release Notes 20 (Moffet Filed CA: NASA Ames Research Center) [Google Scholar]
- Thompson, S. E. 2013b, Kepler Data Release Notes 21 (Moffet Filed CA: NASA Ames Research Center) [Google Scholar]
- Thompson, M. J., Toomre, J., Anderson, E., et al. 1996, Science, 272, 1300 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Torrence, C., & Compo, G. P. 1998, Bull. Am. Meteorol. Soc., 79, 61 [Google Scholar]
- Vázquez Ramió, H., Mathur, S., Régulo, C., & García, R. A. 2011, J. Phys. Conf. Ser., 271, 012056 [NASA ADS] [CrossRef] [Google Scholar]
- Walkowicz, L. M., Basri, G., & Valenti, J. A. 2013, ApJS, 205, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Weber, M. A., Fan, Y., & Miesch, M. S. 2013, ApJ, 770, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, O. C. 1978, ApJ, 226, 379 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Rotation periods, inclination angle, and Rossby numbers for the 22 stars computed with different approaches.
All Figures
 |
Fig. 1 Wavelet analysis of KIC 3733735 (groups C and L). Top panel: temporal variation of the flux after the corrections applied as in García et al. (2011) and rebinned to 2 h. Middle panel: wavelet power spectrum as a function of time and period. The green grid represents the cone of influence that takes into account the edge effects and delimits the reliable rein in the WPS. Red and dark colours correspond to strong power while blue corresponds to weak power. Bottom upper panel: projection of the WPS on the time axis between periods of 1 and 4.1 days. Bottom lower panel: temporal variation of the standard deviation for KIC 3733735 for subseries of length 5 × Prot. The black dashed line represents the mean value of the standard deviation of the subseries, i.e. the magnetic index ⟨ Sph ⟩. The triple dot-dashed line represents the mean magnetic index for the low-activity subseries (⟨ Sph(nlow) ⟩) and the dash-dot line corresponds to the mean magnetic index for the high-activity subseries ⟨ Sph(nhigh) ⟩. |
| In the text | |
 |
Fig. 2 Modified HR diagram showing the sample of 22 F stars analysed. Red symbols represent the stars that are discussed in Sect. 4.2: with long-lived features, with cycle-like behaviour, or with a trend in the magnetic proxy. Blue symbols correspond to stars where no clear cycle is observed for the duration of the observations also referred as the “Other” category in Table 2. The size of the symbols is inversely proportional to the surface rotation period of the star. The position of the Sun is indicated by the ⊙ symbol, and evolution tracks from Aarhus Stellar Evolution Code (ASTEC) are shown for a range of masses at solar composition (Z⊙ = 0.0246). Median uncertainties on ⟨ Δν ⟩ and Teff are shown in the lower left corner of the figure. |
| In the text | |
 |
Fig. 3 Mean magnetic index ⟨ Sph ⟩ identified by the star number given in Table 1. The stars are represented with different symbols according to their category in Table 2: L (red triangles), C (blue filled circle), T (pink squares), and O (open circles). KIC 3733735 is represented with the blue star since it belongs to both categories L and C. We superimposed the mean index of the Sun ⟨ Sph, ⊙ ⟩ = 166.1 ± 2.6 ppm (dashed line), the index at low activity ⟨ Sph(nlow) ⟩, (dot dash line), and the index at high activity ⟨ Sph(nhigh) ⟩ (triple dot dash line) obtained with the VIRGO data. |
| In the text | |
 |
Fig. 4 Contrast, C, between high and low magnetic activity for the 22 F stars for k = 5. The dashed line represents the contrast for the Sun obtained with the VIRGO data. Same legend as in Fig. 3. |
| In the text | |
 |
Fig. 5 Wavelet analysis of VIRGO data for subseries of 2000 days. For each subseries, we show the wavelet power spectrum (red and dark areas are correspond to high power) and the average variance that is the magnetic proxy obtained by projecting the WPS between 6- and 60-day periods on the x-axis. Plots from top left to bottom right correspond to the increase in cycle 23 to the decrease in cycle 23. |
| In the text | |
 |
Fig. 6 Light curve of KIC 3733735 at a maximum of the amplitude (black). The blue line is a sine wave whose frequency corresponds to the maximum of the light curve spectrum. The truncated upper parts of the real light curve are clearly visible while the lower parts are very similar to the pure sine wave. This shape is characteristic of starspots with surface rotation. |
| In the text | |
 |
Fig. 7 Magnetic index ⟨ Sph ⟩ versus Prot using the same legend as in Fig. 3. The dashed line represents the magnetic index for the Sun. |
| In the text | |
 |
Fig. 8 Contrast between maximum and minimum activity regions as a function of the mean large separation (Δν). Using the same legend as in Fig. 3. The Sun is represented with the symbol ⊙. |
| In the text | |
 |
Fig. 9 Magnetic contrast C as a function of the Rossby number of the stars modelled by AMP. The Rossby number was obtained from the stellar models (squares) and with the equation of Noyes et al. (1984) based on colour measurements of Tycho2 (triangles). |
| In the text | |
 |
Fig. A.1 Wavelet analysis of KIC 1430163 (group O). Top panel: temporal variation of the flux after the corrections applied as in García et al. (2011). Middle panel: wavelet power spectrum as a function of time and period. The green grid represents the cone of influence that takes into account the edge effects and delimits the reliable rein in the WPS. Red and dark colours correspond to strong power while blue corresponds to weak power. Bottom panel: projection of the WPS on the time axis between periods of 1 and 7 days. |
| In the text | |
 |
Fig. A.2 Wavelet analysis of KIC 1435467 (group T). Same representation as in Fig. A.1. The magnetic proxy (bottom panel) was computed between periods of 1.7 and 11 days. |
| In the text | |
 |
Fig. A.3 Wavelet analysis of KIC 3733735 (group L+C). Same representation as in Fig. A.1. The magnetic proxy (bottom panel) was computed between periods of 1 and 4.1 days. |
| In the text | |
 |
Fig. A.4 Wavelet analysis of KIC 4638884 (group O). Same representation as in Fig. A.1. The magnetic proxy (bottom panel) was computed between periods of 2.5 and 12 days. |
| In the text | |
 |
Fig. A.5 Wavelet analysis of KIC 5371516 (group O). Same representation as in Fig. A.1. The magnetic proxy (bottom panel) was computed between periods of 1.5 and 10 days. |
| In the text | |
 |
Fig. A.6 Wavelet analysis of KIC 5773345 (group O). Same representation as in Fig. A.1. The magnetic proxy (bottom panel) was computed between periods of 3.8 and 20 days. |
| In the text | |
 |
Fig. A.7 Wavelet analysis of KIC 6508366 (group O). Same representation as in Fig. A.1. The magnetic proxy (bottom panel) was computed between periods of 2 and 6 days. |
| In the text | |
 |
Fig. A.8 Wavelet analysis of KIC 7103006 (group O). Same representation as in Fig. A.1. The magnetic proxy (bottom panel) was computed between periods of 2 and 8 days. |
| In the text | |
 |
Fig. A.9 Wavelet analysis of KIC 7206837 (group L). Same representation as in Fig. A.1. The magnetic proxy (bottom panel) was computed between periods of 1.2 and 7 days. |
| In the text | |
 |
Fig. A.10 Wavelet analysis of KIC 7668623 (group L). Same representation as in Fig. A.1. The magnetic proxy (bottom panel) was computed between periods of 1.9 and 8 days. |
| In the text | |
 |
Fig. A.11 Wavelet analysis of KIC 7771282 (group O). Same representation as in Fig. A.1. The magnetic proxy (bottom panel) was computed between periods of 3 and 20 days. |
| In the text | |
 |
Fig. A.12 Wavelet analysis of KIC 7940546 (group O). Same representation as in Fig. A.1. The magnetic proxy (bottom panel) was computed between periods of 3 and 18 days. |
| In the text | |
 |
Fig. A.13 Wavelet analysis of KIC 8026226 (group O). Same representation as in Fig. A.1. The magnetic proxy (bottom panel) was computed between periods of 2 and 16 days. |
| In the text | |
 |
Fig. A.14 Wavelet analysis of KIC 9226926 (group L). Same representation as in Fig. A.1. The magnetic proxy (bottom panel) was computed between a period of 1 and 4 days. |
| In the text | |
 |
Fig. A.15 Wavelet analysis of KIC 9289275 (group O). Same representation as in Fig. A.1. The magnetic proxy (bottom panel) was computed between periods of 2.3 and 17 days. |
| In the text | |
 |
Fig. A.16 Wavelet analysis of KIC 9812850 (group O). Same representation as in Fig. A.1. The magnetic proxy (bottom panel) was computed between periods of 1.8 and 10 days. |
| In the text | |
 |
Fig. A.17 Wavelet analysis of KIC 10016239 (group O). Same representation as in Fig. A.1. The magnetic proxy (bottom panel) was computed between periods of 1.8 and 10 days. |
| In the text | |
 |
Fig. A.18 Wavelet analysis of KIC 10162436 (group O). Same representation as in Fig. A.1. The magnetic proxy (bottom panel) was computed between periods of 3.8 and 17 days. |
| In the text | |
 |
Fig. A.19 Wavelet analysis of KIC 10355856 (group L). Same representation as in Fig. A.1. The magnetic proxy (bottom panel) was computed between periods of 1.7 and 8 days. |
| In the text | |
 |
Fig. A.20 Wavelet analysis of KIC 10644253 (group C). Same representation as in Fig. A.1. The magnetic proxy (bottom panel) was computed between periods of 5 and 18 days. |
| In the text | |
 |
Fig. A.21 Wavelet analysis of KIC 11070918 (group L). Same representation as in Fig. A.1. The magnetic proxy (bottom panel) was computed between periods of 0.8 an 5 days. |
| In the text | |
 |
Fig. A.22 Wavelet analysis of KIC 12009504 (group T). Same representation as in Fig. A.1. The magnetic proxy (bottom panel) was computed between periods of 1.8 and 15 days. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


