| Issue |
A&A
Volume 562, February 2014
|
|
|---|---|---|
| Article Number | A83 | |
| Number of page(s) | 20 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201322386 | |
| Published online | 12 February 2014 | |
Interstellar chemistry of nitrogen hydrides in dark clouds⋆
1 Université Joseph Fourier/CNRS, Institut de Planétologie et d’Astrophysique de Grenoble (IPAG) UMR 5274, 38041 Grenoble, France
e-mail: romane.legal@obs.ujf-grenoble.fr; pierre.hily-blant@obs.ujf-grenoble.fr; alexandre.faure@obs.ujf-grenoble.fr
2 Institut Universitaire de France, France
3 Université de Paris-Sud/CNRS, IAS (UMR 8617), 91405 Orsay Cedex, France
4 LERMA/CNRS (UMR 8112)/Observatoire de Paris, 75014 Paris, France
Received: 29 July 2013
Accepted: 18 November 2013
Nitrogen, amongst the most abundant metals in the interstellar medium, has a peculiar chemistry that differs from those of carbon and oxygen. Recent observations of several nitrogen-bearing species in the interstellar medium suggest abundances in sharp disagreement with current chemical models. Although some of these observations show that some gas-grain processes are at work, gas-phase chemistry needs first to be revisited. Strong constraints are provided by recent Herschel observations of nitrogen hydrides in cold gas. The aim of the present work is to comprehensively analyse the interstellar chemistry of nitrogen, focussing on the gas-phase formation of the smallest polyatomic species and, in particular, on nitrogen hydrides. We present a new chemical network in which the kinetic rates of critical reactions have been updated based on recent experimental and theoretical studies, including nuclear spin branching ratios. Our network thus treats the different spin symmetries of the nitrogen hydrides self-consistently, together with the ortho and para forms of molecular hydrogen. This new network is used to model the time evolution of the chemical abundances in dark cloud conditions. The steady-state results are analysed, with special emphasis on the influence of the overall amounts of carbon, oxygen, and sulphur. Our calculations are also compared with Herschel/HIFI observations of NH, NH2, and NH3 detected towards the external envelope of the protostar IRAS 16293-2422. The observed abundances and abundance ratios are reproduced for a C/O gas-phase elemental abundance ratio of ~0.8, provided that the sulphur abundance be depleted by a factor greater than 2. The ortho-to-para ratio of H2 in these models is ~ 10-3. Our models also provide predictions for the ortho-to-para ratios of NH2 and NH3 of ~2.3 and ~0.7, respectively. We conclude that the abundances of nitrogen hydrides in dark cloud conditions are consistent with the gas-phase synthesis predicted with our new chemical network.
Key words: astrochemistry / ISM: abundances / ISM: molecules
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2014
1. Introduction
Nitrogen-bearing species have commonly been observed in the interstellar medium (ISM) ever since the discovery of ammonia, the first polyatomic interstellar species, by Cheung et al. (1968). Nitrogenated species are useful probes of the physics and chemistry of the ISM over a broad range of conditions. Inversion lines of ammonia serve as temperature probes in molecular clouds (Ho & Townes 1983; Maret et al. 2009) and rotational lines of diazenylium (N2H+) and its deuterated isotopologue, N2D+, may be used at much higher densities (n ~ 105 cm-3, Pagani et al. 2007; Crapsi et al. 2007). In the diffuse ISM, CN absorption lines allowed the first estimate of the CMB temperature (Thaddeus 1972). Owing to its sensitivity to Zeeman splitting and to its hyperfine structure, CN is also a powerful tool for measuring the line-of-sight magnetic field intensity in dense regions (Crutcher 2012).
The reservoir of nitrogen in molecular clouds is still controversial, but is expected to be gaseous, either in atomic or molecular forms. Atomic nitrogen in the diffuse ISM is observed through absorption lines in the UV (Nieva & Przybilla 2012). Searches for the N2 molecule in interstellar space have been unfruitful until its first detection in the far-ultraviolet by Knauth et al. (2004), in absorption against the background star HD 124314. The derived column density of N2, 4.6 × 1013 cm-2, is several orders of magnitude lower than that of atomic nitrogen (2.0 × 1017 cm-2), indicating that nitrogen is mainly atomic. The total visual extinction is 1.5 mag or Nh = 2.8 × 1021 cm-2(assuming standard grain properties), leading to abundances, with respect to hydrogen nuclei, of 7.2 × 10-5 and 1.6 × 10-8 for atomic and molecular nitrogen, respectively. The column density of N2 is also about one order of magnitude higher than the predictions of Li et al. (2013) for translucent clouds, which take the photo-dissociation of N2 into account. Strong discrepancy between observations and model predictions suggests that nitrogen chemistry in such diffuse-to-translucent environments remains poorly understood.
In dense molecular clouds, where hydrogen is molecular, the situation is even worse, because NI and N2 are not observable directly. Constraints on their abundances are thus only indirect. In dense clouds, N2H+, a direct chemical product of N2, has been observed by Womack et al. (1992) and Maret et al. (2006), who concluded that atomic N is most likely the dominant reservoir of nitrogen. In addition, in prestellar cores with gas densities ~105 cm-3, Hily-Blant et al. (2010b) derived an upper limit on the gas-phase abundance of atomic nitrogen which suggested that nitrogen may be predominantly hidden in ices coating dust grains. More recently, Daranlot et al. (2012) have found that gaseous nitrogen is mostly atomic in dense clouds, but that the dominant reservoir of nitrogen is indeed in the form of ammonia ices at the surface of dust grains. Neverthess, as stressed by these authors, the predicted amount of icy ammonia is larger than what is observed in dark clouds and much larger than what is observed in comets. From the above, one can safely consider that the question of the reservoir of gaseous (and solid) nitrogen in dark clouds still remains an open issue.
In recent years, additional observations have challenged our understanding of the first steps of the chemistry of nitrogen (e.g. Hily-Blant et al. 2010b; Persson et al. 2012). By first steps we here refer to the synthesis of the smallest N-bearing molecules. One such discrepancy between observations and models is shown by the CN:HCN abundance ratio towards several starless dark clouds, the value of which is underpredicted in the models of Hily-Blant et al. (2010b). Another concern is the HCN:HNC abundance ratio. These two isomers are the products of the dissociative recombination (hereafter denoted DR) of HCNH+, with equally measured branching ratio (Mendes et al. 2012). The predicted abundance ratio HCN:HNC is thus expected to be close to unity (Herbst et al. 2000). Observed ratios, however, show a large scatter around unity (Hirota et al. 1998) that may reflect different chemical routes to these molecules.
Another fundamental question is how ammonia is formed in dense clouds. Le Bourlot (1991) suggested that the gas-phase synthesis through the N+ + H2 reaction, followed by hydrogen abstractions and DR reactions, was efficient enough to reproduce the observed amounts. Very recently, however, Dislaire et al. (2012) have revisited the experimental data available for the N+ + H2 reaction. The new rate is significantly lower, and it falls below the critical value inferred by Herbst et al. (1987) to explain the observed abundances of ammonia. The efficiency of the gas-phase synthesis of ammonia versus the hydrogenation of atomic nitrogen on the surfaces of dust grains remains an open question (e.g. Tielens & Hagen 1982; D’Hendecourt et al. 1985; Charnley & Rodgers 2002; Hidaka et al. 2011). Observational constraints on the amount of ammonia locked into ices coating dust grains are rare, because the N-H vibrational feature at 2.95 μm is heavily obscured by the 3 μm deep water-ice bands. However, observations of NH3 ices in young star formation regions indicate that an abundance of 5% relative to water seems to be a reasonable value (Bottinelli et al. 2010). Up to now, N2 ices have not been detected in dense regions (Sandford et al. 2001). Perhaps related to the ammonia issue is a new constraint based on the abundance ratios of nitrogen hydrides NH:NH2:NH3 towards the Class 0 protostar IRAS 16293-2422, obtained with the HIFI (Heterodyne Instrument for the Far-Infrared) instrument onboard the Herschel satellite in the framework of the CHESS key programme (Ceccarelli et al. 2010). The absorption lines arising from the low-lying rotational levels of these hydrides lead to abundance ratios NH:NH2:NH3 = 5:1:300. These abundance ratios could not be reproduced by model calculations in dark gas at a temperature of 10 K and a gas density of 104 cm-3(Hily-Blant et al. 2010a). Last, in diffuse-to-translucent environments, Herschel/HIFI observations of the ortho and para forms of ammonia indicate an ortho-to-para ratio of ~0.7 that could not be explained with the standard nitrogen chemistry (Persson et al. 2012).
The present paper is devoted to the chemistry of nitrogen in dense regions of the ISM that are efficiently shielded from ultraviolet photons by the dust and molecular hydrogen. One major difficulty for progress on the issue of nitrogen chemistry in the dense ISM is that neither N nor N2 are observable. Determination of their abundances thus relies on observations of trace nitrogen-containing molecules. Chemical models are then essential. Such carriers usually include NH3, CN, HCN, HNC, and N2H+, together with 13C, D, and 15N isotopologues, and to a lesser extent NO. For the major isotopologues, the typical abundances with respect to the total H nuclei are ≈10-10 − 10-9, except for NO, whose abundance may be as high as 10-8 (Suzuki et al. 1992; Gerin et al. 1992; Akyilmaz et al. 2007; Hily-Blant et al. 2010b; Padovani et al. 2011).
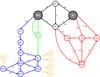 |
Fig. 1 Principal gas-phase reactions involved in the first stages of nitrogen interstellar chemistry in dark clouds. Nitrogen hydrides (blue, left) and nitriles (red, right) have been clearly separated. The main formation route of NH is highlighted (green). Chemical pathways from nitrogen hydrides to nitriles, which are efficient at specific C/O ratio ranges, are also represented (dashed yellow). Adapted from Hily-Blant et al. (2013a). |
Chemical models allow predictions to be made for the abundances of chemical species under specified physical conditions (for a review, see Wakelam et al. 2010). Time-dependent models follow the abundances with time, until the steady state is eventually reached. In the ISM, however, the steady state does not coincide with the thermodynamical equilibrium, and models should thus solve the time-dependent chemical and physical equations in a self-consistent fashion (e.g. Tassis et al. 2012). However, a full coupling, e.g. including the impact of the chemical abundances on the thermodynamical state of the gas through radiative transfer, remains beyond current numerical capabilities. Simplifications must be made, such as adopting analytical prescriptions for the time evolution of the gas physical conditions (Bergin & Langer 1997; Flower et al. 2005). Regarding the chemical processes, the cornerstone of any chemical model is really the network of chemical reactions that describe the formation and destruction of the chemical species. The determination, either theoretically or experimentally, of the kinetic rates of these reactions at the low temperatures prevailing in the diffuse, translucent, and dense ISM (5−80 K) is extremely time-demanding. This task is simply out of reach for the few thousand reactions involved in current chemical networks. It is thus crucial to identify the key reactions whose rates have a major effect on the chemistry (Wakelam et al. 2010, 2012).
In recent years, to meet the above challenges, rate constants for several key reactions involved in the chemistry of interstellar nitrogen have been computed (e.g. Jorfi et al. 2009; Jorfi & Honvault 2009) and measured (e.g. Bergeat et al. 2009; Daranlot et al. 2011, 2012) down to ~10 and ~50 K, respectively. These challenges also triggered theoretical investigations. Separate collisional rates were computed for HCN and HNC with H2by Sarrasin et al. (2010). They show, in particular, very different rates for the (1−0) rotational transition. Using those new rates, Padovani et al. (2011) derived an abundance ratio HCN:HNC ≈ 1 in three starless cores, in agreement with model predictions, suggesting that the current chemical route to HCN and HNC is consistent with observations. Further observations are, however, needed to put this result on a firmer basis.
A theoretical investigation of the ortho-para chemistry of ammonia in the cold ISM was done by Rist et al. (2013). They calculated separate branching ratios for the hydrogen abstractions and DR reactions leading to the ortho and para forms of nitrogen hydrides, taking nuclear spin selection rules into account. With these new rates and the new chemical network fully described in this paper, Faure et al. (2013) showed that the ortho-to-para ratio of ~0.7 for ammonia, observed by Persson et al. (2012), is in fact consistent with gas-phase chemistry in a para-enriched H2gas. In this model the anomalous values of the ortho-to-para ratios of nitrogen hydrides are a consequence of the low ortho-to-para ratio of H2 and result from the conservation of nuclear spin in chemical reactions. In a similar fashion, Dislaire et al. (2012) show that the NH:NH2 abundance ratio in the envelope of IRAS 16923-2422 can be reproduced only for an ortho-to-para ratio of H2≈ 10-3.
These recent experimental and theoretical results motivated the present work aimed at presenting a new network of the nitrogen chemistry in dense clouds, thus superseding the classical networks of Herbst & Klemperer (1973) and Pineau des Forêts et al. (1990). This work puts special emphasis on nitrogen hydrides for which the ortho and para forms are treated self-consistently along with the ortho and para forms of H2 The outline of the paper is as follows. In Sect. 2, we present our new nitrogen network. Section 3 describes our model calculations, with in particular, a discussion of initial abundances. Results and comparisons with Herschel observations of nitrogen hydrides are the subject of Sect. 4. Section 5 summarises our new findings and suggests further lines of investigation.
2. Chemical network
2.1. General considerations
The formation of nitrogen hydrides (NH, NH2, and NH3) is similar to that of carbon and oxygen hydrides, but has a different origin. First, unlike carbon, N+ is not available directly because the ionisation potential of N (14.53 eV) is greater than that of H. In addition, the reaction 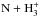 → NH+ + H2 – whose analogue is responsible for the production of CH+ and OH+ in dark gas – is endothermic because the proton affinity of N (3.55 eV) is lower than that of H2 (4.38 eV). The alternative exothermic pathway,
→ NH+ + H2 – whose analogue is responsible for the production of CH+ and OH+ in dark gas – is endothermic because the proton affinity of N (3.55 eV) is lower than that of H2 (4.38 eV). The alternative exothermic pathway, 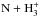 → NH
→ NH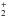 + H, shows a high activation energy (Herbst et al. 1987). As a result, in the current understanding of nitrogen chemistry, the production of N+ results from molecular nitrogen reacting with He+. This reaction is found to be more efficient than the direct cosmic-ray ionisation of atomic nitrogen. Once N+ is formed, rapid hydrogen-abstraction reactions initiated with
+ H, shows a high activation energy (Herbst et al. 1987). As a result, in the current understanding of nitrogen chemistry, the production of N+ results from molecular nitrogen reacting with He+. This reaction is found to be more efficient than the direct cosmic-ray ionisation of atomic nitrogen. Once N+ is formed, rapid hydrogen-abstraction reactions initiated with 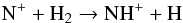 (1)lead to the NH+,
(1)lead to the NH+, 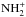 ,
, 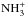 , and
, and 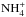 ions that, by dissociative recombinations, generate the formation of neutral nitrogen hydrides (see Fig. 1).
ions that, by dissociative recombinations, generate the formation of neutral nitrogen hydrides (see Fig. 1).
In addition, because the proton affinity of molecular nitrogen is 5.12 eV, the reaction of N2 with 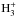 yielding N2H+ is exothermic and proceeds at a significant rate. The DR of N2H+ then leads to NH. The formation of nitrogen hydrides has accordingly its origin in N2. On the other hand, nitriles (such as HCN) derive from atomic nitrogen, through ion-neutral reactions with
yielding N2H+ is exothermic and proceeds at a significant rate. The DR of N2H+ then leads to NH. The formation of nitrogen hydrides has accordingly its origin in N2. On the other hand, nitriles (such as HCN) derive from atomic nitrogen, through ion-neutral reactions with 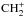 and
and 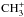 . The formation of nitrogen hydrides is therefore a relatively slow process compared to carbon and oxygen hydrides, precisely because the first step involves the synthesis of molecular nitrogen, which is thought to proceed through neutral-neutral reactions (Pineau des Forêts et al. 1990; Hily-Blant et al. 2010b):
. The formation of nitrogen hydrides is therefore a relatively slow process compared to carbon and oxygen hydrides, precisely because the first step involves the synthesis of molecular nitrogen, which is thought to proceed through neutral-neutral reactions (Pineau des Forêts et al. 1990; Hily-Blant et al. 2010b):  and
and  We anticipate that in those instances where the C/O gas-phase elemental abundance ratio is lower than unity, reaction (5) is expected to dominate the formation of CN over reaction (4).
We anticipate that in those instances where the C/O gas-phase elemental abundance ratio is lower than unity, reaction (5) is expected to dominate the formation of CN over reaction (4).
Reaction (1) consequently appears to be a key reaction for the synthesis of nitrogen hydrides. In fact, it was studied in detail by Le Bourlot (1991), who derived separate rates for the reaction with ortho- and para-H2 (denoted H2(o) and H2(p), respectively, in the remainder of the text). The reaction with H2(p) was assumed to occur with a 170 K activation energy, while being barrierless with H2(o), which makes the rate of reaction (1) strongly dependent on the ortho-to-para ratio of H2 (denoted o/p (H2) hereafter). More recently, Dislaire et al. (2012) have revised those rates (see Table B.1) using available experimental data (Marquette et al. 1988; Gerlich 1993) for H2(p), normal-H2(i.e. o/p (H2) = 3:1), and H2(p) containing admixtures of H2(o), leading to a rate at 10 K typically two orders of magnitude lower than in Le Bourlot (1991). In particular, for o/p (H2) ≲10-2, the new rate is below the critical value of 10-13 cm3 s-1 required to account for the observed amounts of gas-phase ammonia (Herbst et al. 1987). Nevertheless, Dislaire et al. (2012) could reproduce the abundance of ammonia observed towards IRAS 16293-2422, provided the total C/O gas-phase abundance ratio was lower than 0.4. Recent measurements by Zymak et al. (2013) have confirmed the rate used by Dislaire et al. (2012), although issues related to the fine-structure relaxation of N+ deserve further experimental and theoretical studies. Dislaire et al. (2012) also show that a branching ratio <10% for the channel of N2H+ + e− leading to NH is sufficient to reproduce the observed amount of NH. The abundance of NH is thus independent of the o/p (H2), unlike NH2 and NH3, which proceed from reaction (1). One consequence is that the NH:NH2 abundance ratio depends on the o/p (H2). Using the NH:NH2 abundance ratio, Dislaire et al. (2012) could finally determine an o/p (H2) of ≈10-3. However, these authors did not explicitly treat the formation of H2(o) and H2(p).
In the following, we discuss the new reaction rates that have been implemented to self-consistently model the formation of nitrogen hydrides of H2(o) and H2(p). This new network is an updated version of the gas-phase network of Flower et al. (2006a), as detailed below.
2.2. The ortho-to-para ratio of H2
The o/p (H2) plays a significant role in the chemistry of nitrogen hydrides, making it important to understand the processes that may affect its value, in order to self-consistently model the chemistry. As H2is not directly observable in the cold gas, its o/p (H2) ratio derives from indirect measurements (e.g. Troscompt et al. 2009, and references therein). An upper limit of 0.01 has been proposed by Pagani et al. (2009) to explain the large deuteration fraction of N2D+ in cold cores. Values consistent with this upper limit were predicted by the models of Flower et al. (2006b), with o/p (H2) ≈ 10-3. Molecular hydrogen is assumed to form on dust grain surfaces (Hollenbach & Salpeter 1971), in a strongly exothermic reaction (≈4.5 eV) such that the outcoming H2(o) and H2(p) should be in the ratio 3:1, imposed by their nuclear spin statistical weights. This corresponds to the maximum value permitted under thermal equilibrium. At temperatures lower than 100 K, only the first rotational levels of H2(p) and H2(o) (lying 170.5 K above H2(p)) are populated significantly, and the equilibrium value of o/p (H2) is given by the usual low-temperature approximation 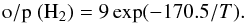 (7)In the ISM, the characteristic timescale for radiative spontaneous spin flip from J = 1 of H2(o) to J = 0 of H2(p) is ≈1013 yr (Raich & Good 1964; Pachucki & Komasa 2008), much longer than the lifetime of molecular clouds. As a consequence, the ortho and para forms may be viewed as two different chemical species, and gas-phase conversion from one form to the other is expected to take place only through ion-neutral reactions between H2 and protonated ions (Dalgarno et al. 1973; Crabtree et al. 2011). In a general fashion, these reactions can be written as
(7)In the ISM, the characteristic timescale for radiative spontaneous spin flip from J = 1 of H2(o) to J = 0 of H2(p) is ≈1013 yr (Raich & Good 1964; Pachucki & Komasa 2008), much longer than the lifetime of molecular clouds. As a consequence, the ortho and para forms may be viewed as two different chemical species, and gas-phase conversion from one form to the other is expected to take place only through ion-neutral reactions between H2 and protonated ions (Dalgarno et al. 1973; Crabtree et al. 2011). In a general fashion, these reactions can be written as 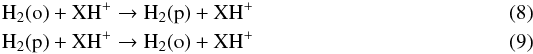 where XH+ stands primarily for H+,
where XH+ stands primarily for H+, 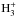 , and HCO+. If both exchange reactions proceed much more rapidly than the formation of H2 on grains, the o/p (H2) is expected to tend towards a value imposed by the detailed balance relation between the rates of reactions (8)−(9) that is the thermal value of Eq. (7). In contrast, if the formation rate on dust grains is much faster than any of the two exchange reactions, the o/p (H2) value will stay equal to 3:1. As said previously, there is some evidence that the o/p of H2significantly deviates from both 3:1 and the thermodynamical value of ≈3 × 10-7 at 10 K. This indicates that certain conversion processes do take place on timescales comparable to or even shorter than the formation process on dust grains.
, and HCO+. If both exchange reactions proceed much more rapidly than the formation of H2 on grains, the o/p (H2) is expected to tend towards a value imposed by the detailed balance relation between the rates of reactions (8)−(9) that is the thermal value of Eq. (7). In contrast, if the formation rate on dust grains is much faster than any of the two exchange reactions, the o/p (H2) value will stay equal to 3:1. As said previously, there is some evidence that the o/p of H2significantly deviates from both 3:1 and the thermodynamical value of ≈3 × 10-7 at 10 K. This indicates that certain conversion processes do take place on timescales comparable to or even shorter than the formation process on dust grains.
The gas-phase conversion between H2(o) and H2(p) has received particular attention in the past few years. We have therefore adopted the most recent theoretical results summarised in Table B.1. In particular, the conversion through reactions with protons has been computed by Honvault et al. (2011, 2012) using state-to-state quantum time-independent calculations. Exchange reactions with 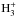 have been studied using a state-to-state micro-canonical statistical method by Hugo et al. (2009). The
have been studied using a state-to-state micro-canonical statistical method by Hugo et al. (2009). The 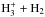 reaction was also studied experimentally below 100 K by Grussie et al. (2012), confirming the micro-canonical model. The rates of Hugo et al. (2009) are available for temperatures below 50 K, restricting the validity of our network to this low-temperature range.
reaction was also studied experimentally below 100 K by Grussie et al. (2012), confirming the micro-canonical model. The rates of Hugo et al. (2009) are available for temperatures below 50 K, restricting the validity of our network to this low-temperature range.
In addition to the formation of H2 on grains and to the ortho-to-para exchange reactions between H2and protonated ions, the formation and destruction of the 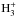 ion also play an important role in setting the o/p(H2) value. We have therefore updated the rate coefficients and branching ratios for the reaction
ion also play an important role in setting the o/p(H2) value. We have therefore updated the rate coefficients and branching ratios for the reaction 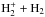 and the dissociative recombination
and the dissociative recombination 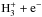 . To this aim, we have combined the most recent theoretical and experimental values of the overall rate coefficients with the Oka’s formalism (Oka 2004) to derive the nuclear spin branching ratios. Briefly, this formalism accounts for the selection rules that result from conserving the nuclear spin of identical nuclei. The approach of Oka (2004) is based on angular momentum algebra applied to the total nuclear spins of the reactants. For each allowed nuclear spin of the intermediate complex, the distribution of product states is deduced from the nuclear-spin conservation for the reverse reaction. Full details can be found in Oka (2004). It should be noted that these pure nuclear spin branching ratios are applicable to processes in which many rotational states of the products are populated, in particular exothermic reactions. In this work, these branching ratios were used for strongly exothermic ion-molecule and DR reactions where the products are expected to form rotationally hot, along with full proton scrambling. The corresponding new rate coefficients are listed in Tables B.1 and B.2. We note that most measurements have no temperature dependence since they were only performed at room temperature.
. To this aim, we have combined the most recent theoretical and experimental values of the overall rate coefficients with the Oka’s formalism (Oka 2004) to derive the nuclear spin branching ratios. Briefly, this formalism accounts for the selection rules that result from conserving the nuclear spin of identical nuclei. The approach of Oka (2004) is based on angular momentum algebra applied to the total nuclear spins of the reactants. For each allowed nuclear spin of the intermediate complex, the distribution of product states is deduced from the nuclear-spin conservation for the reverse reaction. Full details can be found in Oka (2004). It should be noted that these pure nuclear spin branching ratios are applicable to processes in which many rotational states of the products are populated, in particular exothermic reactions. In this work, these branching ratios were used for strongly exothermic ion-molecule and DR reactions where the products are expected to form rotationally hot, along with full proton scrambling. The corresponding new rate coefficients are listed in Tables B.1 and B.2. We note that most measurements have no temperature dependence since they were only performed at room temperature.
Very recently, Faure et al. (2013) have shown that these new rates do not significantly change the o/p (H2) at steady state with respect to the results of Flower et al. (2006b). A constant o/p (H2) of ~10-3 was thus found below 15 K. Above this temperature, the o/p (H2) was shown to converge towards the thermal value, as expected from the competition between the H2 formation on grains and the exchange reactions with protonated ions. This point will be further discussed elsewhere.
2.3. Atomic to molecular nitrogen conversion
As previously mentioned in Sect. 2.1, the atomic-to-molecular conversion is the first step towards synthesis of nitrogen hydrides in dark clouds. The rates of reactions (2)–(6) have been uncertain at low temperatures, and in particular the existence of low activation energy (≈20 K) has been suggested by the CN:NO abundance ratio (Akyilmaz et al. 2007). The rates for the NO + N and CN + N reactions have been revisited experimentally by Daranlot et al. (2011, 2012) using the CRESU technique down to temperatures of ≈50 K and further extrapolated down to 10 K. The new rates implemented in our network are summarised in Table B.3. We note that these rates present positive and negative temperature dependences (see Table B.3) and that they all lie between 4 × 10-12 cm3 s-1 and 2 × 10-10 cm3 s-1 at 10 K. These radical-neutral reactions are therefore moderately fast, but they provide the main routes in converting N to N2. The typical chemical timescales of nitrogen chemistry are discussed below.
2.4. Nitrogen hydrides synthesis
As previously emphasised, the o/p (H2) has a strong effect on the chemistry of nitrogen hydrides. To take the o/p (H2) into account self-consistently, some care must be taken in the dissociative recombinations of ionic nitrogen hydrides, 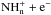 (n = 3, 4), since these reactions produce H2(o) and H2(p), in amounts that depend on the nuclear spin branching ratios. The associated hydrogen abstractions
(n = 3, 4), since these reactions produce H2(o) and H2(p), in amounts that depend on the nuclear spin branching ratios. The associated hydrogen abstractions 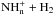 (n = 0−3) are also crucial in driving the nuclear spin distributions. The corresponding branching ratios were determined by Rist et al. (2013) using Oka’s formalism discussed above and assuming full scrambling. These branching ratios were found to be significantly different from those derived by Flower et al. (2006a). In this pioneering study, where the conservation of the total nuclear spin angular momentum was included, the branching ratios were indeed derived from simple statistical considerations without recourse to the angular momentum rules of Oka (2004; see also Sipilä et al. 2013, for a recent similar work). The new branching ratios derived by Rist et al. (2013) were employed very recently by Faure et al. (2013) in their work on the o/p of ammonia in the cold interstellar gas.
(n = 0−3) are also crucial in driving the nuclear spin distributions. The corresponding branching ratios were determined by Rist et al. (2013) using Oka’s formalism discussed above and assuming full scrambling. These branching ratios were found to be significantly different from those derived by Flower et al. (2006a). In this pioneering study, where the conservation of the total nuclear spin angular momentum was included, the branching ratios were indeed derived from simple statistical considerations without recourse to the angular momentum rules of Oka (2004; see also Sipilä et al. 2013, for a recent similar work). The new branching ratios derived by Rist et al. (2013) were employed very recently by Faure et al. (2013) in their work on the o/p of ammonia in the cold interstellar gas.
It should be noted that interconversion processes between the nuclear states of ionic hydrides, of the form 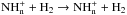 (n = 2−4), are ignored in this work. Indeed, these proton scrambling reactions were studied experimentally using deuterated analogues, and H-D exchanges were not observed, setting small upper limits for the rate coefficients (see the discussion in Faure et al. 2013). In addition, Faure et al. (2013) explicitly studied the
(n = 2−4), are ignored in this work. Indeed, these proton scrambling reactions were studied experimentally using deuterated analogues, and H-D exchanges were not observed, setting small upper limits for the rate coefficients (see the discussion in Faure et al. 2013). In addition, Faure et al. (2013) explicitly studied the 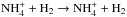 thermalisation reaction and showed that this reaction must be negligible in order to explain the observed non-thermal o/p of NH3 (~0.7).
thermalisation reaction and showed that this reaction must be negligible in order to explain the observed non-thermal o/p of NH3 (~0.7).
 |
Fig. 2 Time evolution of the abundances of the main nitrogenated species and species involved in the N-to-N2 conversion. For this particular model (our best model), the total gas-phase abundance ratio C/O is 0.8 and the total gas-phase abundance of sulphur is 8.0 × 10-8. |
Crucial, too, is the branching ratio of the DR of N2H+. As emphasised by Dislaire et al. (2012), the channel leading to NH was pivotal in explaining the observed NH:NH2 ratio that is greater than unity. These authors show that a branching ratio lower than 10% is sufficient, and recent storage ring measurements by Vigren et al. (2012) confirm this value, with a branching ratio of 7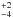 %. Branching ratios for the DR of the
%. Branching ratios for the DR of the 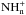 (n = 2−4) ions are taken from Mitchell (1990), Thomas et al. (2005), Jensen et al. (2000), and Öjekull et al. (2004) (see Table B.2), following Hily-Blant et al. (2010a).
(n = 2−4) ions are taken from Mitchell (1990), Thomas et al. (2005), Jensen et al. (2000), and Öjekull et al. (2004) (see Table B.2), following Hily-Blant et al. (2010a).
We summarise, in Tables B.1−B.3, all the updates and improvements from the Flower et al. network, including the ortho- and para-forms of hydrogen and nitrogen species1.
3. Modelling
3.1. General description
The 104 gas-phase chemical species considered in our network.
The complete network contains 104 species (see Table 1) and 917 reactions. The physical conditions, which are fixed, are typical of dark clouds: the gas has a constant number density of hydrogen nuclei nH = n(H) + 2n(H2) of 104 cm-3, shielded from the UV photons by ten magnitudes of visual extinction, and the kinetic temperature is kept constant at 10 K. Ionisation is driven by cosmic rays, with secondary photons included, and the ionisation rate of hydrogen is ζ = 1.3 × 10-17 s-1, a standard value usually attributed to dense regions (Prasad & Huntress 1980; Caselli et al. 1998; Wakelam et al. 2005). The processes involving dust grains are charge exchange, DR reactions, and the formation of H2 We adopt a single dust grain radius of 0.1 μm, following Walmsley et al. (2004), satisfying a dust-to-gas mass ratio of 1%. The abundances of all species are followed with time, until a steady state is reached. A typical illustrative result is shown in Fig. 2.
Even though we compute the time evolution of all the abundances, we focus our analysis on the steady state, which is reached typically after ~1 Myr for carbon- and oxygen-bearing species, ~3 − 5 Myr for NO, N2H+, and NH, and after ~10 Myr for nitrogen-bearing species (see Fig. 2). We note that these timescales are probably upper limits since they correspond to initial conditions where all elements (except hydrogen) are in atomic form. As mentioned earlier, nitrogen hydrides are late-time species, a consequence of the slow neutral-neutral reactions needed to build N2. The timescale of 10 Myr is longer than the gravitational free-fall timescale of ~0.5 Myr but comparable to the ambipolar diffusion timescale of ~10 Myr at a density of 104 cm-3 (Tassis & Mouschovias 2004; Bergin & Tafalla 2007). Indeed, in their chemical models of collapsing cores, Tassis et al. (2012) also considered delay times (before collapse starts) up to 10 Myr.
Another assumption of our model is that freeze-out, which occurs on a typical timescale of ~1010/nH yr (Bergin & Tafalla 2007), is not considered during the time evolution of the gas, although observations show depletion of several species in pre-stellar cores (e.g. Tafalla et al. 2004). However, observations also show that an important fraction of molecular species remains in the gas phase, such that desorption mechanisms are required (Hasegawa & Herbst 1993). Those are highly uncertain and depend critically on binding energies of the adsorbed species. Nevertheless, molecular mantles are observed in the core of dense dark clouds (Whittet et al. 1983; Boogert et al. 2011), indicating that molecular condensation on grains occurs efficiently. This effect is crudely accounted for in our model by adopting initially depleted elemental abundances in the gas phase. We also note that although steady state is rather unlikely, both steady-state and time-dependent modelling have their own limitations. Time-dependent calculations depend critically on the assumed initial abundances, which are poorly known, whilst steady-state models do not. In addition, focussing on the steady state does not prevent identifying key reactions and general trends, while avoiding the uncertainties described above.
3.2. Elemental abundances
The choice of the gas-phase elemental abundances is not a trivial task, nonetheless, and the abundances of the elements strongly influence the chemical state of the gas. One example is the relative amount of carbon and oxygen, which is known to strongly affect the chemistry (van Dishoeck & Blake 1998; Le Bourlot et al. 1995). For most of the elements, including nitrogen, we follow Flower et al. (2005), who have estimated gas-phase elemental abundances by combining observational constraints from the diffuse ISM and infrared signatures of ices (Gibb et al. 2000), and assuming the composition for the refractory core of dust grains. Nevertheless, the abundances of carbon, oxygen, and sulphur deserve special attention.
The elemental gas-phase abundance of sulphur, noted [S]tot, is very poorly constrained. It can vary by almost three orders of magnitude if we consider the range delimited by the so-called low metal abundance and high metal abundance cases defined originally by Graedel et al. (1982). The first category is suggested by the low electron abundance in dense clouds and may be more representative of the chemistry in such environments, whilst the second category reflects the standard ζ Oph sightline. Further studies of dense dark clouds have corroborated the low metal sulphur gas-phase abundance, even where elemental carbon, oxygen, and nitrogen are depleted by only factors of a few (Ruffle et al. 1999). In the well studied TMC-1 and L183 dark clouds, Tieftrunk et al. (1994) found that the sum of all detected S-bearing molecules represents only 0.1% of the elemental sulphur solar abundance [S]tot ≈ 1.5 × 10-5 (Przybilla et al. 2008; Asplund et al. 2009). In the following, we have applied depletion factors from the gas phase of 200, 20, and 2, or abundances with respect to H nuclei of 8.0 × 10-8, 8.0 × 10-7, and 8.0 × 10-6, respectively.
The reference cosmic abundance for oxygen is 575 ppm (Przybilla et al. 2008). Based on 56 diffuse sightlines, Cartledge et al. (2004) have shown that the gas-phase abundance of oxygen decreases with increasing sightline mean density, reflecting the uptake of oxygen in silicate and oxides into grain cores. They found an average gas-phase atomic oxygen abundance of 280 ppm for densities greater than 1.5 cm-3, suggesting that up to 300 ppm of oxygen have been removed from the gas phase. This idea has been further developed by Whittet (2010), who performed a comprehensive oxygen budget up to densities ~1000 cm-3, and shows that ~100 ppm and ~120 ppm are locked into ices and silicates or oxydes, respectively. Taking into account that ~50 ppm is in gaseous CO, it must be recognised that up to ~300 ppm of oxygen are in unknown carriers. The depletion of oxygen not accounted for by known carriers is also demonstrated by Nieva & Przybilla (2012) who compared the abundances derived by Cartledge et al. with their Cosmic Abundance Standard based on B-stars.
Depletion of carbon is surprisingly not well constrained (see e.g. Fig. 5 of Jenkins 2009), essentially for observational limitations. In addition, the column densities derived so far in the literature may overestimate the amount of gas-phase carbon, because of an underestimated oscillator strength for the CII transition at 2325 Å (Sofia et al. 2011). The error could be up to a factor of two.
To reflect the large uncertainties in the gas-phase elemental abundances of carbon and oxygen, we decided to vary the carbon-to-oxygen gas-phase elemental abundance ratio, [C]tot/[O]tot, simply noted C/O hereafter. To do so, we have assumed a constant elemental abundance of carbon, [C]tot = 8.3 × 10-5, and varied that of oxygen from 50 ppm to 280 ppm. The lower limit is imposed by gaseous CO, and the upper limit is taken from Cartledge et al. (2004). The corresponding range in C/O is 0.3 to 1.5. The upper value of 280 ppm implicitely requires that ~230 ppm of oxygen have been taken from the various reservoirs (solid, ices, unknown carriers) and released in the gas phase by some unspecified processes. Our strategy is therefore analogous in some respects to the one adopted by Terzieva & Herbst (1998) and Tassis et al. (2012), who considered a similar range of elemental C/O ratios. However, the main difference with our model is that we do not consider gas-grain processes apart from charge exchange with grains and H2formation, such that the total amount of gas-phase carbon and oxygen remain constant during the time evolution. For each value of C/O, three models, corresponding to the three sulphur abundances discussed above, were performed. The initial gas-phase elemental abundances are summarised in Table 2.
4. Results
4.1. Influence of the C/O ratio
The steady-state abundances of several nitrogenated species, together with chemically related species, are shown in Fig. 3, as a function of the elemental C/O gas-phase abundance ratio, for three sulphur abundances. We first focus on the low metal sulphur abundance (left panel). For all values of C/O, atomic and molecular nitrogen are the most abundant species, except at high C/O, where CN becomes more abundant than N. Our model predicts that, at low and high C/O, molecular nitrogen is the dominant carrier of nitrogen. Oxygen-bearing species such as NO and OH see their abundance decreasing with increasing C/O, by 2 to 5 orders of magnitude. This is a consequence of the decreasing total amount of oxygen available in the gas-phase. In contrast, the abundances of CN and CH increase by the same amount. Nevertheless, for the latter species, this is not due to an increase in the total amount of carbon, but to an increase in the amount of carbon available in the gas phase, since less carbon is locked into the very stable CO molecule. The turning point between the low- and high-C/O regimes occurs around 0.9. In this intermediate regime (0.8 ≤ C/O ≤ 1.0), molecular nitrogen is no longer the main reservoir of nitrogen because OH and CH, which ensure the conversion from N to N2, are two orders of magnitude less abundant. The above reasoning remains true for a total gas-phase sulphur abundance of 8.0 × 10-7, although the mid-C/O regime now extends up to 1.1. At an even higher total gas-phase abundance of sulphur, the high-C/O regime in which N:N2 < 1 is not recovered.
The evolution of nitrogen hydrides with C/O is not uniform. For sulphur abundances up to 8.0 × 10-7, the NH abundance varies by less than an order of magnitude over the whole range of the C/O ratio, in sharp contrast with NH2 whose abundance decreases from 10-8 in the low-C/O regime to 10-10 in the high-C/O regime. The abundance of ammonia is a few 10-8 in both the low- and high-C/O regimes, but drops to 10-9 in the mid-C/O regime. When [S]tot = 8.0 × 10-6, the behaviour of [NH] is similar to that of [NH2], and drops by more than an order of magnitude from the low- to high-C/O regimes. For ammonia, the same trend holds, but unlike [NH] or [NH2], [NH3] manages to increase with C/O, although not recovering its value of the low-C/O regime.
 |
Fig. 3 Steady-state abundances of several nitrogen-bearing and nitrogen-chemistry related species, as a function of the gas-phase elemental abundance ratio of C/O, for three different values of gas-phase elemental abundance of sulphur (from left to right: [S]tot = 8.0 × 10-8, 8.0 × 10-7, 8.0 × 10-6). C/O values include 0.3, 0.4, 0.5, 0.6, 0.7, 0.75, 0.8, 0.9, 1.0, 1.1, 1.2, 1.3, 1.4, 1.5, and 0.67, which was the ratio employed in the previous studies of Flower et al. 2006. Top panels: molecules involved in the atomic-to-molecular conversion of nitrogen. Bottom panels: nitrogen hydrides. |
We here provide explanations for the observed abundance behaviours, focussing on the low metal sulphur abundance case. The evolution with C/O of the balance between N and N2 is explained by the fact that as C/O increases, more oxygen and less carbon – relative to the total – are locked into CO. Therefore, there is less oxygen available in the gas phase, and the abundances of NO and OH drop. The contrary holds true for carbon: there is more CH and CN. Since the N-to-N2 conversion proceeds through NO and/or CN, this explains the peak of N:N2 ratio for C/O ~ 1. As a consequence, the modelled abundances of all nitrogen hydrides, which strongly depend on the conversion of N into N2, decrease at C/O ~ 1. However, that ammonia recovers its low-C/O abundance at high C/O, when NH and NH2 do not, stems from the fact that these two radicals are primarily destroyed by reactions with atomic carbon, while ammonia is not. Reaction of NH with neutral carbon forms CN, and NH2 + C produces HCN and HNC. On the other hand, NH3 is not destroyed by neutral carbon but by 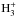 (whose abundance does not strongly depend on C/O), HCO+, and C+. As a consequence, in the high-C/O regime, the large amount of carbon not locked into CO enhances mostly the destruction of NH and NH2. At the same time, the N-to-N2 conversion restarts through CN, and the formation of ammonia increases.
(whose abundance does not strongly depend on C/O), HCO+, and C+. As a consequence, in the high-C/O regime, the large amount of carbon not locked into CO enhances mostly the destruction of NH and NH2. At the same time, the N-to-N2 conversion restarts through CN, and the formation of ammonia increases.
4.2. Influence of the sulphur abundance
We now further analyse the influence of the total sulphur abundance on the steady-state abundances of nitrogen hydrides. As shown in the top panels of Fig. 3, models with [S]tot = 8.0 × 10-8 and 8.0 × 10-7 are very similar, and the only change is the broadening of the mid-C/O regime mentioned above. For [S]tot = 8.0 × 10-6, CN and CH abundances drop by more than an order of magnitude at high C/O, whereas those of NO and OH increase.
The broadening of the mid-C/O regime as [S]tot increases results from a combination of several chemical effects. As already mentioned, in this regime, characterised by N:N2 > 1, the conversion from N to N2 is weak, because of the low abundances of CH and OH. Comparing models with [S]tot = 8.0 × 10-7 and 8.0 × 10-6, [CH] drops by about two orders of magnitude at high C/O, while [OH] is only marginally affected. Although [NO] increases by more than a factor 10, it remains 100 times less abundant than CN and does not compensate for the drop of [CN]. The net effect is a global decrease of the conversion partners. As a result, N remains more abundant than N2 up to C/O = 1.5. Thus, the effect of [S]tot must be traced back to CH, through the reaction 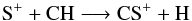 (10)which removes CH. A similar reaction holds for OH, but its abundance decreases only slightly. To understand this behaviour, we notice that OH is formed through the DR of H3O+, the abundance of which decreases with [S]tot. Indeed the ionisation potential of S (10.36 eV) is lower than that of H, and increasing [S]tot drives up the ionisation fraction. The resulting enhanced DR destruction of H3O+ thus compensates for the destruction of OH by S+. In the mid-C/O regime at low-to-intermediate sulphur abundances, there is such a combination of effects that both OH and CH remain too rare to ensure an efficient conversion of N into N2, leading to a well-defined C/O range in which N:N2 > 1. In this parameter space, the enhanced destruction of CH by S+ dominates the increase of atomic carbon in the gas phase, and the increase of H3O+ does not compensate for the destruction of OH by S+.
(10)which removes CH. A similar reaction holds for OH, but its abundance decreases only slightly. To understand this behaviour, we notice that OH is formed through the DR of H3O+, the abundance of which decreases with [S]tot. Indeed the ionisation potential of S (10.36 eV) is lower than that of H, and increasing [S]tot drives up the ionisation fraction. The resulting enhanced DR destruction of H3O+ thus compensates for the destruction of OH by S+. In the mid-C/O regime at low-to-intermediate sulphur abundances, there is such a combination of effects that both OH and CH remain too rare to ensure an efficient conversion of N into N2, leading to a well-defined C/O range in which N:N2 > 1. In this parameter space, the enhanced destruction of CH by S+ dominates the increase of atomic carbon in the gas phase, and the increase of H3O+ does not compensate for the destruction of OH by S+.
Regarding nitrogen hydrides, a variation from low-to-intermediate sulphur abundance does not change the abundances dramatically. This is not true when going from intermediate to high [S]tot. At high C/O, [NH] drops by a factor of 5, while NH2 is unaffected and remains at a very low abundance. The most dramatic change is that of [NH3], which drops by a factor of 20. This is due to the combination of the two reactions 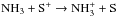 and
and 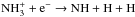 , which get greatly enhanced at high [S]tot. Their net effect is to transfer nitrogen from ammonia to NH. Nevertherless, the latter sees its amount divided by a factor 5 because the destruction path NH + N becomes important in the N:N2> 1 regime.
, which get greatly enhanced at high [S]tot. Their net effect is to transfer nitrogen from ammonia to NH. Nevertherless, the latter sees its amount divided by a factor 5 because the destruction path NH + N becomes important in the N:N2> 1 regime.
4.3. Comparison with observations
Before the launch of the Herschel space telescope, the only astronomical source where the three hydrides NH, NH2, and NH3 were detected was Sgr B2, with the ratios NH:NH2:NH3~ 1:10:100 (Goicoechea et al. 2004). However, this line of sight encompasses a variety of physical conditions (e.g. shocks), and the NH:NH2:NH3 ratios measured in Sgr B2 may therefore not be representative of cold dense clouds. Recent Herschel/HIFI observations towards the solar-type protostar IRAS 16293-2422, however, allowed putting strong constraints on the nitrogen hydride chemistry in dark gas (Hily-Blant et al. 2010a; Bacmann et al. 2010).
IRAS 16293-2422 is situated deep within a high column density core in a filament of the ρOph cloud complex. From the results of extensive interferometric and single dish-mapping at centimetre, millimetre, and far-infrared wavelengths, detailed models of the physical structure of the source have been constructed (e.g. Crimier et al. 2010, and references therein). The region can be divided into four components: the ambient molecular cloud, the circumbinary envelope, the three protostellar sources A1, A2, and B, and the outflow components (see Loinard et al. 2013, and references therein). The total column density of H2towards IRAS 16293-2422 is ~2 × 1023 cm-2 (van Dishoeck et al. 1995). In the most external part of the source where nitrogen hydrides are seen in absorption, the column density is necessarily much lower. Radiative transfer computations where we have coupled non-local thermodynamic equilibrium (non-LTE) calculations with a simple physical model of the source (see Appendix A) have shown that the absorbing region must have an H2 density ≲104 cm-3 (i.e. nH ≲ 2 × 104 cm-3), which corresponds not to the circumbinary envelope but to the ambient cloud (although the distinction is artificial since the density profile is continuous). For this component, the H2 column density is rather uncertain but we adopted the value derived from C18O observations by van Dishoeck et al. (1995), N(H2) = 1.5 × 1022 cm-2. We note that Hily-Blant et al. (2010a) employed a different value, N(H2) = (5.5 ± 2.5) × 1022 cm-2, based on an extrapolation of the Crimier et al. profile. The NH3 column density derived by Hily-Blant et al. (2010a) was highly uncertain because, in contrast to NH and NH2, the hyperfine structure was not resolved. Guessed excitation temperatures of 8−10 K were therefore employed within an LTE treatment. In the present work, non-LTE radiative transfer calculations for NH and NH3 were performed, as described in Appendix A. The best agreement with the observations (see Fig. A.1) is obtained for a total ammonia column density of 1.4 × 1015 cm-2. The associated gas temperature is 11 K, which is fully consistent with standard dark cloud conditions. The spectrum of NH is also reproduced well (see Fig. A.2). The column density of NH2 has also been revised, since it had been estimated by Hily-Blant et al. (2010a) based on the NH2(o) alone and assuming that the NH2(p) abundance was negligible. However, our models, as well as Faure et al. (2013), show that this should not be the case and that the o/p ratio of NH2 is more likely ~2.3. We have therefore increased the total column density of NH2 from 5.0 × 1013 to 7.5 × 1013 cm-2. Finally, the column densities of NH, NH2, and NH3 used in this work are (2.2 ± 0.8) × 1014, (7.5 ± 3.0) × 1013, and (1.4 ± 1.0) × 1015 cm-2, respectively, or abundance ratios NH:NH2:NH3 ~ 3:1:19. The corresponding abundances relative to the total H nuclei are then obtained using NH = 2 × N(H2) = (3.0 ± 1.5) × 1022 cm-2.
 |
Fig. 4 Steady-state abundances of NH, NH2, and NH3 as a function of the C/O gas-phase elemental abundance ratio for three different values of gas-phase elemental abundance of sulphur (from left to right: [S]tot = 8.0 × 10-8, 8.0 × 10-7, 8.0 × 10-6). C/O values include 0.3, 0.4, 0.5, 0.6, 0.67, 0.7, 0.75, 0.8, 0.9, 1.0, 1.1, 1.2, 1.3, 1.4, 1.5. In each panel, the solid line refers to the model predictions and the vertical dashed lines locate C/O = 0.67 (Flower et al. 2006 value) and 0.8 (our best model value). For NH2 and NH3, the ortho and para abundances are shown separately (dashed and dotted lines respectively). The observed abundances towards IRAS 16293-2422 are represented by the hatched boxes, considering an o/p ratio of NH2~ 2, as predicted by our model. |
 |
Fig. 5 Steady-state abundance ratios of the N-hydrides as a function of the gas-phase elemental abundance ratio of C/O for three different values of the gas-phase elemental abundance of sulphur (from left to right: [S]tot = 8.0 × 10-8, 8.0 × 10-7, 8.0 × 10-6). C/O values include 0.3, 0.4, 0.5, 0.6, 0.67, 0.7, 0.75, 0.8, 0.9, 1.0, 1.1, 1.2, 1.3, 1.4, 1.5. In all panels, the vertical dashed lines locate C/O = 0.67 (Flower et al. 2006 value) and 0.8 (our best model value). The abundances derived from Herschel/HIFI observations towards IRAS 16293-2422 are represented by the hatched boxes, considering an o/p ratio of NH2~ 2, as predicted by our model. |
Abundances and abundance ratios of nitrogen hydrides at steady state predicted using several chemical networks.
The abundances of NH, NH2, and NH3 towards IRAS 16293-2422 are compared in Fig. 4 to the set of models described previously. Overall, the predicted abundances match the observations only within a narrow range of C/O ratios, which is found to be 0.7−0.8. However, as discussed above, the uncertainties on the abundances are rather large due to the difficulty to estimate the H2 column density in the absorbing layers. In contrast, abundance (or column density) ratios circumvent this caveat, and are thus more robust. The ratios NH2:NH and NH3:NH are plotted in Fig. 5. At low and intermediate sulphur abundance, the NH2:NH ratio delineates a narrow range of C/O values of 0.75−0.80 consistent with the above constraints. At intermediate sulphur abundance, the NH3:NH ratio further constrains the C/O ratio to 0.75. For a high sulphur abundance, however, there is no C/O that allows both abundance ratios to be reproduced simultaneously. From Fig. 2, which shows the evolution with time of the abundances, we note that the observed abundance ratios NH:NH2:NH3 are also well reproduced at very early times ≈4 × 104 yr. However, at such early times, the fractional abundances of the N-hydrides are more than an order of magnitude smaller than observed. Although there was no minimisation attempt, the best agreement with the observations is found for the set of parameters [S]tot = 8.0 × 10-8 and C/O = 0.8, which will be referred to as our best model.
We conclude that the steady-state abundances predicted by our gas-phase chemical model are consistent with the observational constraints on the abundances and abundance ratios of NH, NH2, and NH3, provided that the C/O ratio is ~0.8. The elemental abundance of sulphur is less constrained, but must be depleted by more than a factor of 2.
4.4. Impact of the new rates
To show the influence of the new rates adopted in our network, we performed a calculation using the Flower network combined with our best model parameters. The abundances of NH2 and NH3 are similar to those found with our updated network, with differences less than 30%. However, this is not true for NH abundance, which is one order of magnitude lower with the old network. This large increase in our model is due to the dissociative recombination channel of N2H+ forming NH, as already noted in Dislaire et al. (2012). When looking into more detail, the relatively small change of the abundances of NH2 and NH3 in fact results from a combination of three effects. First, the updated rate of the reaction N+ + H2 lowers the abundances of NH2 and NH3 by more than a factor of 10. For ammonia, this effect is partially compensated for by the updated branching ratios of the 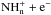 dissociative recombinations. The abundance of NH2 and that of ammonia are finally recovered when updating the rate and branching ratios of the reaction
dissociative recombinations. The abundance of NH2 and that of ammonia are finally recovered when updating the rate and branching ratios of the reaction 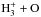 . This reaction produces more OH+ and H2O+, thus enhancing the amount of OH, hence the N to N2 conversion. This demonstrates that updating all those reaction rates is essential for reproducing the abundances of nitrogen hydrides. We note that the Dislaire et al. (2012) model, based on the osu.09.2008 chemical network2, predicts abundances that are too small for all three species, which may result from the large sulphur abundance assumed by these authors, although the comparison is not direct because the two chemical networks may contain different rate coefficients for non-negligible reactions.
. This reaction produces more OH+ and H2O+, thus enhancing the amount of OH, hence the N to N2 conversion. This demonstrates that updating all those reaction rates is essential for reproducing the abundances of nitrogen hydrides. We note that the Dislaire et al. (2012) model, based on the osu.09.2008 chemical network2, predicts abundances that are too small for all three species, which may result from the large sulphur abundance assumed by these authors, although the comparison is not direct because the two chemical networks may contain different rate coefficients for non-negligible reactions.
The impact of the new rates is further proven by the o/p of NH2 and NH3 predicted by our models, which are 2.3 and 0.7, respectively (see Table 3). These values are significantly higher than those obtained with the Flower et al. (2006a) network (1 and 0.3, respectively, see Table 3). It should be noted that both o/p ratios are below the statistical values of 3 and 1, respectively, which are lower limits under thermal equilibrium. In addition, these o/p ratios were found to depend only very weakly on the C/O value, as expected since the o/p of nitrogen hydrides are driven by the o/p ratio of H2(see Sect. 2.4 and Fig. 4).
5. Discussion and conclusions
We have presented a new gas-phase, ortho/para, chemical network devoted to the interstellar chemistry of nitrogen under typical dark cloud physical conditions. More specifically, this work focussed on nitrogen hydrides because these species, which are linked by a small number of chemical reactions, have been observed with high accuracy with the Herschel/HIFI instrument. The absorption lines of NH, NH2, and NH3 trace the cold, UV-shielded, and moderately dense envelope of the IRAS 16293-2422 protostar, and therefore provide direct observational tests of the chemistry of nitrogen in such environments. Although the comparison deals with a single object, the present work aims at understanding general processes of nitrogen chemistry in dark cloud conditions.
Our network is based on the gas-phase network of Flower et al. (2006a) where the following major improvements have been implemented: i) the nitrogen chemistry was revised using the most recent experimental results, in particular for the conversion of N to N2 through radical-radical reactions and for the dissociative recombinations of the 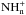 (n = 2 − 4) ions; ii) we adopted recent theoretical results for the ortho-to-para conversion of H2 by H+ and
(n = 2 − 4) ions; ii) we adopted recent theoretical results for the ortho-to-para conversion of H2 by H+ and 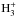 ; iii) we employed the formalism of Oka (2004), as detailed in Rist et al. (2013) and Faure et al. (2013), to derive the nuclear spin branching ratios for all primary reactions involved in the formation and destruction of H2(p), H2(o), NH, NH2(p), NH2(o), NH3(p), and NH3(o).
; iii) we employed the formalism of Oka (2004), as detailed in Rist et al. (2013) and Faure et al. (2013), to derive the nuclear spin branching ratios for all primary reactions involved in the formation and destruction of H2(p), H2(o), NH, NH2(p), NH2(o), NH3(p), and NH3(o).
Our findings may be summarised as follows. First, we found that the abundances of the nitrogen hydrides strongly depend on the gas-phase elemental C/O ratio adopted in the model. A similar result was noted in earlier works (e.g. Terzieva & Herbst 1998; Hily-Blant et al. 2010b; Tassis et al. 2012), although we here provided a detailed analysis of the influence of the C/O ratio, by focussing on a smaller set of species. The influence of the C/O ratio stems from the fact that nitrogen hydrides derive from N2 that is formed via either N + CH or N + OH. Two regimes corresponding to C/O < 0.8 and C/O > 1 are clearly identified where the N2/N ratio is greater than 1 and the abundance of ammonia is a few 10-8. In contrast, the abundances of NH and NH2 are much lower at high C/O because these radicals are efficiently destroyed by atomic carbon. Second, we have shown that increasing the elemental gas-phase abundance of sulphur [S]tot significantly reduces the efficiency of the N to N2 conversion. Thus a high abundance of sulphur (i.e. 8.0 × 10-6) was found to reduce the abundance of several N-bearing species by up to two orders of magnitude.
The steady-state abundances predicted by our model were compared to the Herschel/HIFI observations of NH, NH2, and NH3, towards the low-mass protostar IRAS 16293-2422. Our chemical model reproduces both the observed abundances and abundance ratios of the three hydrides well. A key point is that our network produces more NH than NH2, as observed. Our best model, which leads to NH:NH2:NH3 abundance ratios of 3:1:3 (see Table 3), is obtained for a C/O ratio of 0.8 and a low sulphur abundance [S]tot = 8.0 × 10-8. Although it is consistent with the 3:1:19 observed ratios, the predicted abundance of ammonia is at the lower end of the allowed range. Higher values for [S]tot are also possible, but a high abundance of 8.0 × 10-6 is clearly excluded by our models, as well as C/O ratios outside the range 0.7−0.8. We note that at earlier times (~2−5 Myr), the observations can be reproduced with a similar [S]tot (i.e. <8.0 × 10-6) and slightly higher C/O ratios, in the range 0.9 to 1.1.
Our model calculations thus show that chemical reactive processes on dust grains are not needed to explain the gas-phase abundances of nitrogen hydrides in typical dark cloud conditions. This of course does not preclude the possibility that a fraction of atomic nitrogen can also form ammonia ices by hydrogenation on the grain mantles. This process is in fact certainly necessary to account for the high abundance of ammonia (~10-6) detected in e.g. shock regions, where grain mantles are released in the gas phase (Umemoto et al. 1999). We note that our best model corresponds to a regime where N/N2 ≈ 1. The exact amount of gaseous N2, however, depends on the competition between its formation in the gas and the depletion of atomic nitrogen onto grains, which was neglected in the present work. Several nitrogenated species were shown observationally to resist depletion in cold prestellar cores, in contrast to CO and many other species. This is the case for NH3, N2H+, and CN (Tafalla et al. 2004; Crapsi et al. 2007; Hily-Blant et al. 2008), and also for HCN (and HNC), although for the last there seems to exist some variability amongst sources (Hily-Blant et al. 2010b; Padovani et al. 2011; Pagani et al. 2012). This observational result indicates that enough atomic N is always available in the gas phase, which is also slowly converted into N2. However, in similar objects, Akyilmaz et al. (2007) observes that NO disappears from the gas phase at high densities where CN does not, which was interpreted as freeze-out onto grains. The different behaviours among N-bearing species with respect to depletion could result from a combination of several factors, such as different molecular properties (e.g. the binding energy) and/or the timescales of the gas-phase chemical reactions. Further attempts to reproduce, in a comprehensive fashion, the behaviours of the observed species, may need to consider all these aspects taking the time-dependent competition between gas-phase and gas-grain processes into account.
Gas-phase synthesis of N-hydrides is further supported by the ortho-to-para ratios of NH3 and NH2 predicted by our model. Persson et al. (2012) measured the ortho- and para-ammonia column densities in diffuse molecular clouds along the sight lines towards the high-mass star-forming regions W49N and G10.6-0.4, and found o/p(NH3) ≈ 0.5−0.7. This ratio is in excellent agreement with our prediction. For NH2, preliminary Herschel measurements indicate ortho-to-para values in the range 1.5−3.5 in diffuse gas along the line of sight towards G10.6-0.4 (C.M. Persson et al., priv. comm.), again in very good agreement with our prediction. The NH, NH2, and NH3 abundances (relative to total hydrogen) derived by Persson et al. (2010) are 5.6 × 10-9, 3.0 × 10-9, and 3.2 × 10-9, respectively, or abundance ratios NH:NH2:NH3 = 2:1:1. The NH and NH2 abundances are thus similar to those in the envelope surrounding IRAS 16293-2422 (see Table 3), although that of ammonia is one order of magnitude lower. Their abundance ratios are in fact similar to the prediction of our best model (see Table 3). However, our calculations are not likely to apply to a warmer and more tenuous diffuse gas, which requires dedicated models (gas density of ~103 cm-3 and temperature of ~30 K). In particular, the C/O ratio and [S]tot abundance may take different values in the diffuse ISM. Photodissociation of ammonia may also play a role, as discussed by Persson et al. (2010), although we do not expect the UV to significantly alter the o/p of NH2 and NH3 which are driven by proton exchange reactions.
The present work gives rise to several questions. First, additional observations of NH, NH2, and NH3 in various objects are needed to confirm the gas-phase chemical processes mentioned above. The determination of the ortho-to-para ratio towards others Class 0 protostars would also be extremely useful. Another critical issue is related to the abundances of other N-bearing species such as N2H+, CN, and nitriles (e.g. HCN) in dark clouds. Observations in dark clouds are already available for these species, but were not discussed in this paper. The reason is that we believe that such a comprehensive comparison with all the observations first requires assessing the completeness of the current chemical network with respect to all those simple nitrogen-bearing species.
Here, we have focussed on nitrogen hydrides, and this allowed us to understand several effects and explain various observational facts. Of course, chemistry is highly non-linear (e.g. Le Bourlot et al. 1995), and we cannot exclude that in some peculiar range of parameters, new rates, e.g. in the formation of HCN, could affect the above results. However, by exploring such a broad range of initial abundances, we have been able to emphasise robust trends and processes. Our approach is complementary to other strategies that quantify the sensitivity of chemical networks to rate uncertainties (e.g. Wakelam et al. 2010). Time-dependent aspects must also be explored, taking gas-grain processes into account and/or including the effect of gas dynamics (e.g. Brown & Charnley 1990; Flower et al. 2006a; Tassis et al. 2012).
Concerning future improvements of our network, we are currently implementing new reaction rates and nuclear spin branching ratios for the deuterated isotopologues of several nitrogen-bearing species. Both deuterated and 15N isotopologues were not considered in the present work. However, both are detected in the cold ISM with significant abundances. The molecular D/H and 15N/14N ratios are sensitive probes of the chemistry, and future works will explore gas-phase fractionation processes and the possible link with the D and 15N-enrichments observed in solar system objects (see e.g. Wirström et al. 2012; Hily-Blant et al. 2013a, and references therein). We note in this context the recent detection of C15N and NH3D+ in cold prestellar cores by Hily-Blant et al. (2013b) and Cernicharo et al. (2013), respectively.
Online material
Appendix A: Radiative transfer modelling
Our one-dimensional spherical source model consists in two-layers with uniform density and kinetic temperature. The inner layer, close to the protostar, has a radius of 104 AU, a dust temperature of 30 K, and a total (front + back) column density N(H2) = 6.6 × 1022 cm-2 – hence, a density – and we assume this layer does not contain gas-phase nitrogen hydrides. Furthermore, the dust opacity is assumed to vary as a power-law of the wavelength, with a spectral index (β) of 2.8 and a dust opacity at 250 GHz of 1 g cm-2. The values of N(H2) and β were adjusted so that the continuum observed with HIFI towards that source is reproduced well by our model.
The external layer has the same H2column density, so that the total column density is 1.3 × 1023 cm-2 or 140 mag of visual extinction. We modelled the emergent telescope-convolved spectrum of all the observed transitions of ammonia, by solving the radiative transfer with the Monte-Carlo code RATRAN (Hogerheijde & van der Tak 2000). The collisional rates for NH3-H2(p) are taken from Maret et al. (2009). The o/p of NH3 was fixed at 0.7, as predicted by our chemistry model. The free parameters are the density, the gas temperature, and the NH3 column density in the external, absorbing, layer. The radii are set by the H2column density and the density of that layer. The emergent spectra were then fitted simultaneously to match the observed ones, and a χ2 used to select the best-fit model. We found that the self-absorbed profile of the 1−0 transition tightly constrains the H2density in the outer layer to less than 104 cm-3, since for higher densities the predicted profile no longer shows absorption. As a result, the absorbing ammonia molecules reside in the most external layer of the circumbinary envelope of IRAS 16293-2422.
 |
Fig. A.1 Comparison between the observed NH3 spectrum (black) from Hily-Blant et al. (2010a) and the best-fit model (red). The + and − signs in the transition labelling are the same as in Maret et al. (2009). |
 |
Fig. A.2 Same as in Fig. A.1 for the NH multiplets, using the same physical model as for NH3 and adopting a single NH column density of 2.2 ± 0.8 × 1014 cm-2. |
An ensemble of solutions is then found for the ammonia column density and the kinetic temperature, with the best agreement corresponding to N(NH3) = 1.4 × 1015 cm-2 and T =11 K, respectively (see Fig. A.1). This column density is a factor of 2.5 below the lower limit of Hily-Blant et al. (2010a). A cross-check of the best agreement was performed by computing the emergent hyperfine spectra of NH. To this aim, we used the LIME radiative transfer code (Brinch & Hogerheijde 2010), which takes line blending into account. The collisional rates for NH-H2(p) are scaled from the NH-He rates of Dumouchel et al. (2012) by applying the standard reduced mass ratio of 1.33. The model that best reproduces the three hyperfine multiplets of NH (see Fig. A.2) has a column density of NH in the foreground layer of 2.0 × 1014 cm-2, in excellent agreement with the determination of Bacmann et al. (2010) based on the “HFS” method of the CLASS software. Therefore this simple 2-layers model succesfully reproduces both the NH and NH3 spectra. The NH2(o) column density was not re-analysed owing to the lack of collisional rates. However, the column density of NH2(o) was derived by Hily-Blant et al. (2010a) using the same method and under the same assumptions as those for NH by Bacmann et al. (2010), and is thus expected to be reliable as well. In addition, here, we assumed an o/p(NH2) of 2 to estimate the total column density of NH2.
Appendix B: Chemical updates
New ion-neutral chemical reaction rates and ortho-para branching ratios.
New dissociative recombination (DR) reaction rates and branching ratios.
Neutral-neutral chemical reaction rates and branching ratios considered.
Acknowledgments
We thank our anonymous referee for a careful reading and useful comments that improved the manuscript. This work has been supported by “Région Rhône-Alpes” (CIBLE programme), the Agence Nationale de la Recherche (ANR-HYDRIDES), contract ANR-12-BS05-0011-01, and by the CNRS national programme “Physico-Chimie du Milieu Interstellaire”.
References
- Akyilmaz, M., Flower, D. R., Hily-Blant, P., Pineau des Forêts, G., & Walmsley, C. M. 2007, A&A, 462, 221 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anicich, V. G., & Huntress, Jr., W. T. 1986, ApJS, 62, 553 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Bacmann, A., Caux, E., Hily-Blant, P., et al. 2010, A&A, 521, L42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bergeat, A. 1999, Chem. Phys. Lett., 308, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Bergeat, A., Hickson, K. M., Daugey, N., Caubet, P., & Costes, M. 2009, Phys. Chem. Chem. Phys., 11, 8149 [CrossRef] [PubMed] [Google Scholar]
- Bergin, E. A., & Langer, W. D. 1997, ApJ, 486, 316 [NASA ADS] [CrossRef] [Google Scholar]
- Bergin, E. A., & Tafalla, M. 2007, ARA&A, 45, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Boogert, A. C. A., Huard, T. L., Cook, A. M., et al. 2011, ApJ, 729, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Bottinelli, S., Boogert, A. C. A., Bouwman, J., et al. 2010, ApJ, 718, 1100 [NASA ADS] [CrossRef] [Google Scholar]
- Brinch, C., & Hogerheijde, M. R. 2010, A&A, 523, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, P. D., & Charnley, S. B. 1990, MNRAS, 244, 432 [NASA ADS] [Google Scholar]
- Cartledge, S. I. B., Lauroesch, J. T., Meyer, D. M., & Sofia, U. J. 2004, ApJ, 613, 1037 [NASA ADS] [CrossRef] [Google Scholar]
- Caselli, P., Walmsley, C. M., Terzieva, R., & Herbst, E. 1998, ApJ, 499, 234 [Google Scholar]
- Ceccarelli, C., Bacmann, A., Boogert, A., et al. 2010, A&A, 521, L22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cernicharo, J., Tercero, B., Fuente, A., et al. 2013, ApJ, 771, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Charnley, S. B., & Rodgers, S. D. 2002, ApJ, 569, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Chastaing, D., Le Picard, S. D., & Sims, I. R. 2000, J. Chem. Phys., 112, 8466 [Google Scholar]
- Cheung, A. C., Rank, D. M., Townes, C. H., Thornton, D. D., & Welch, W. J. 1968, Phys. Rev. Lett., 21, 1701 [Google Scholar]
- Crabtree, K. N., Indriolo, N., Kreckel, H., Tom, B. A., & McCall, B. J. 2011, ApJ, 729, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Crapsi, A., Caselli, P., Walmsley, M. C., & Tafalla, M. 2007, A&A, 470, 221 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crimier, N., Ceccarelli, C., Maret, S., et al. 2010, A&A, 519, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crutcher, R. M. 2012, ARA&A, 50, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Dalgarno, A., Black, J. H., & Weisheit, J. C. 1973, Astrophys. Lett., 14, 77 [NASA ADS] [Google Scholar]
- Daranlot, J., Jorfi, M., Xie, C., et al. 2011, Science, 334, 1538 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Daranlot, J., Hincelin, U., Bergeat, A., et al. 2012, Proc. National Academy of Science, 109, 10233 [Google Scholar]
- D’Hendecourt, L. B., Allamandola, L. J., & Greenberg, J. M. 1985, A&A, 152, 130 [NASA ADS] [Google Scholar]
- Dislaire, V., Hily-Blant, P., Faure, A., et al. 2012, A&A, 537, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dos Santos, S. F., Kokoouline, V., & Greene, C. H. 2007, J. Chem. Phys., 127, 124309 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Dumouchel, F., Kłos, J., Toboła, R., et al. 2012, J. Chem. Phys., 137, 114306 [NASA ADS] [CrossRef] [Google Scholar]
- Faure, A., Hily-Blant, P., Le Gal, R., Rist, C., & Pineau des Forêts, G. 2013, ApJ, 770, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, D. R., Pineau des Forêts, G., & Walmsley, C. M. 2005, A&A, 436, 933 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Flower, D. R., Pineau des Forêts, G., & Walmsley, C. M. 2006a, A&A, 456, 215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Flower, D. R., Pineau des Forêts, G., & Walmsley, C. M. 2006b, A&A, 449, 621 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gerin, M., Viala, Y., Pauzat, F., & Ellinger, Y. 1992, A&A, 266, 463 [NASA ADS] [Google Scholar]
- Gerlich, D. 1993, J. Chem. Soc. Faraday Trans., 89, 2199 [CrossRef] [Google Scholar]
- Gibb, E. L., Whittet, D. C. B., Schutte, W. A., et al. 2000, ApJ, 536, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Goicoechea, J. R., Rodríguez-Fernández, N. J., & Cernicharo, J. 2004, ApJ, 600, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Graedel, T. E., Langer, W. D., & Frerking, M. A. 1982, ApJS, 48, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Grussie, F., Berg, M. H., Crabtree, K. N., et al. 2012, ApJ, 759, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Hasegawa, T. I., & Herbst, E. 1993, MNRAS, 261, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Herbst, E., & Klemperer, W. 1973, ApJ, 185, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Herbst, E., Defrees, D. J., & McLean, A. D. 1987, ApJ, 321, 898 [NASA ADS] [CrossRef] [Google Scholar]
- Herbst, E., Terzieva, R., & Talbi, D. 2000, MNRAS, 311, 869 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hidaka, H., Watanabe, M., Kouchi, A., & Watanabe, N. 2011, Phys. Chem. Chem. Phys., 13, 15798 [NASA ADS] [CrossRef] [Google Scholar]
- Hily-Blant, P., Walmsley, M., Pineau des Forêts, G., & Flower, D. 2008, A&A, 480, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hily-Blant, P., Maret, S., Bacmann, A., et al. 2010a, A&A, 521, L52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hily-Blant, P., Walmsley, M., Pineau des Forêts, G., & Flower, D. 2010b, A&A, 513, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hily-Blant, P., Bonal, L., Faure, A., & Quirico, E. 2013a, Icarus, 223, 582 [Google Scholar]
- Hily-Blant, P., Pineau des Forêts, G., Faure, A., Le Gal, R., & Padovani, M. 2013b, A&A, 557, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hirota, T., Yamamoto, S., Mikami, H., & Ohishi, M. 1998, ApJ, 503, 717 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, P. T. P., & Townes, C. H. 1983, ARA&A, 21, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Hogerheijde, M. R., & van der Tak, F. F. S. 2000, A&A, 362, 697 [NASA ADS] [Google Scholar]
- Hollenbach, D., & Salpeter, E. E. 1971, ApJ, 163, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Honvault, P., Jorfi, M., González-Lezana, T., Faure, A., & Pagani, L. 2011, Phys. Chem. Chem. Phys., 13, 19089 [CrossRef] [Google Scholar]
- Honvault, P., Jorfi, M., González-Lezana, T., Faure, A., & Pagani, L. 2012, Phys. Rev. Lett., 108, 109903 [NASA ADS] [CrossRef] [Google Scholar]
- Hugo, E., Asvany, O., & Schlemmer, S. 2009, J. Chem. Phys., 130, 164302 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Jenkins, E. B. 2009, ApJ, 700, 1299 [NASA ADS] [CrossRef] [Google Scholar]
- Jensen, M. J., Bilodeau, R. C., Safvan, C. P., et al. 2000, ApJ, 543, 764 [NASA ADS] [CrossRef] [Google Scholar]
- Jorfi, M., & Honvault, P. 2009, J. Phys. Chem. A, 113, 10648 [CrossRef] [Google Scholar]
- Jorfi, M., Honvault, P., & Halvick, P. 2009, Chem. Phys. Lett., 471, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Knauth, D. C., Andersson, B.-G., McCandliss, S. R., & Warren Moos, H. 2004, Nature, 429, 636 [NASA ADS] [CrossRef] [Google Scholar]
- Le Bourlot, J. 1991, A&A, 242, 235 [NASA ADS] [Google Scholar]
- Le Bourlot, J., Pineau des Forêts, G., Roueff, E., & Flower, D. R. 1995, A&A, 302, 870 [NASA ADS] [Google Scholar]
- Li, X., Heays, A. N., Visser, R., et al. 2013, A&A, 555, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Loinard, L., Zapata, L. A., Rodríguez, L. F., et al. 2013, MNRAS, 430, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Maret, S., Bergin, E. A., & Lada, C. J. 2006, Nature, 442, 425 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Maret, S., Faure, A., Scifoni, E., & Wiesenfeld, L. 2009, MNRAS, 399, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Marquette, J. B., Rebrion, C., & Rowe, B. R. 1988, J. Chem. Phys., 89, 2041 [NASA ADS] [CrossRef] [Google Scholar]
- Marquette, J. B., Rebrion, C., & Rowe, B. R. 1989, A&A, 213, L29 [NASA ADS] [Google Scholar]
- McCall, B. J., Huneycutt, A. J., Saykally, R. J., et al. 2004, Phys. Rev. A, 70, 052716 [NASA ADS] [CrossRef] [Google Scholar]
- Mendes, M. B., Buhr, H., Berg, M. H., et al. 2012, ApJ, 746, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Mitchell, B. 1990, Phys. Rep., 186, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Nieva, M.-F., & Przybilla, N. 2012, A&A, 539, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Öjekull, J., Andersson, P. U., Någård, M. B., et al. 2004, J. Chem. Phys., 120, 7391 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Oka, T. 2004, J. Mol. Spectr., 228, 635 [Google Scholar]
- Pachucki, K., & Komasa, J. 2008, Phys. Rev. A, 77, 030501 [NASA ADS] [CrossRef] [Google Scholar]
- Padovani, M., Walmsley, C. M., Tafalla, M., Hily-Blant, P., & Pineau des Forêts, G. 2011, A&A, 534, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pagani, L., Bacmann, A., Cabrit, S., & Vastel, C. 2007, A&A, 467, 179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pagani, L., Vastel, C., Hugo, E., et al. 2009, A&A, 494, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pagani, L., Bourgoin, A., & Lique, F. 2012, A&A, 548, L4 [CrossRef] [EDP Sciences] [Google Scholar]
- Persson, C. M., Black, J. H., Cernicharo, J., et al. 2010, A&A, 521, L45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Persson, C. M., De Luca, M., Mookerjea, B., et al. 2012, A&A, 543, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pineau des Forêts, G., Roueff, E., & Flower, D. R. 1990, MNRAS, 244, 668 [NASA ADS] [Google Scholar]
- Prasad, S. S., & Huntress, Jr., W. T. 1980, ApJS, 43, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Przybilla, N., Nieva, M.-F., & Butler, K. 2008, ApJ, 688, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Raich, J. C., & Good, Jr., R. H. 1964, ApJ, 139, 1004 [NASA ADS] [CrossRef] [Google Scholar]
- Rist, C., Faure, A., Hily-Blant, P., & Le Gal, R. 2013, J. Phys. Chem. A, 117, 9800 [Google Scholar]
- Ruffle, D. P., Hartquist, T. W., Caselli, P., & Williams, D. A. 1999, MNRAS, 306, 691 [NASA ADS] [CrossRef] [Google Scholar]
- Sandford, S. A., Bernstein, M. P., Allamandola, L. J., Goorvitch, D., & Teixeira, T. C. V. S. 2001, ApJ, 548, 836 [NASA ADS] [CrossRef] [Google Scholar]
- Sarrasin, E., Abdallah, D. B., Wernli, M., et al. 2010, MNRAS, 404, 518 [NASA ADS] [Google Scholar]
- Sipilä, O., Caselli, P., & Harju, J. 2013, A&A, 554, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sofia, U. J., Parvathi, V. S., Babu, B. R. S., & Murthy, J. 2011, AJ, 141, 22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Suzuki, H., Yamamoto, S., Ohishi, M., et al. 1992, ApJ, 392, 551 [NASA ADS] [CrossRef] [Google Scholar]
- Tafalla, M., Myers, P. C., Caselli, P., & Walmsley, C. M. 2004, A&A, 416, 191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tassis, K., & Mouschovias, T. C. 2004, ApJ, 616, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Tassis, K., Willacy, K., Yorke, H. W., & Turner, N. J. 2012, ApJ, 753, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Terzieva, R., & Herbst, E. 1998, ApJ, 501, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Thaddeus, P. 1972, ARA&A, 10, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, R. D., Hellberg, F., Neau, A., et al. 2005, Phys. Rev. A, 71, 032711 [NASA ADS] [CrossRef] [Google Scholar]
- Tieftrunk, A., Pineau des Forêts, G., Schilke, P., & Walmsley, C. M. 1994, A&A, 289, 579 [NASA ADS] [Google Scholar]
- Tielens, A. G. G. M., & Hagen, W. 1982, A&A, 114, 245 [NASA ADS] [Google Scholar]
- Troscompt, N., Faure, A., Maret, S., et al. 2009, A&A, 506, 1243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Umemoto, T., Mikami, H., Yamamoto, S., & Hirano, N. 1999, ApJ, 525, L105 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- van Dishoeck, E. F., & Blake, G. A. 1998, ARA&A, 36, 317 [NASA ADS] [CrossRef] [Google Scholar]
- van Dishoeck, E. F., Blake, G. A., Jansen, D. J., & Groesbeck, T. D. 1995, ApJ, 447, 760 [NASA ADS] [CrossRef] [Google Scholar]
- Vigren, E., Zhaunerchyk, V., Hamberg, M., et al. 2012, ApJ, 757, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Wakelam, V., Selsis, F., Herbst, E., & Caselli, P. 2005, A&A, 444, 883 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wakelam, V., Smith, I. W. M., Herbst, E., et al. 2010, Space Sci. Rev., 156, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Wakelam, V., Herbst, E., Loison, J.-C., et al. 2012, ApJS, 199, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Walmsley, C. M., Flower, D. R., & Pineau des Forêts, G. 2004, A&A, 418, 1035 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Whittet, D. C. B. 2010, ApJ, 710, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Whittet, D. C. B., Bode, M. F., Baines, D. W. T., Longmore, A. J., & Evans, A. 1983, Nature, 303, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Wirström, E. S., Charnley, S. B., Cordiner, M. A., & Milam, S. N. 2012, ApJ, 757, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Womack, M., Ziurys, L. M., & Wyckoff, S. 1992, ApJ, 393, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Zymak, I., Hejduk, M., Mulin, D., et al. 2013, ApJ, 768, 86 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Abundances and abundance ratios of nitrogen hydrides at steady state predicted using several chemical networks.
All Figures
 |
Fig. 1 Principal gas-phase reactions involved in the first stages of nitrogen interstellar chemistry in dark clouds. Nitrogen hydrides (blue, left) and nitriles (red, right) have been clearly separated. The main formation route of NH is highlighted (green). Chemical pathways from nitrogen hydrides to nitriles, which are efficient at specific C/O ratio ranges, are also represented (dashed yellow). Adapted from Hily-Blant et al. (2013a). |
| In the text | |
 |
Fig. 2 Time evolution of the abundances of the main nitrogenated species and species involved in the N-to-N2 conversion. For this particular model (our best model), the total gas-phase abundance ratio C/O is 0.8 and the total gas-phase abundance of sulphur is 8.0 × 10-8. |
| In the text | |
 |
Fig. 3 Steady-state abundances of several nitrogen-bearing and nitrogen-chemistry related species, as a function of the gas-phase elemental abundance ratio of C/O, for three different values of gas-phase elemental abundance of sulphur (from left to right: [S]tot = 8.0 × 10-8, 8.0 × 10-7, 8.0 × 10-6). C/O values include 0.3, 0.4, 0.5, 0.6, 0.7, 0.75, 0.8, 0.9, 1.0, 1.1, 1.2, 1.3, 1.4, 1.5, and 0.67, which was the ratio employed in the previous studies of Flower et al. 2006. Top panels: molecules involved in the atomic-to-molecular conversion of nitrogen. Bottom panels: nitrogen hydrides. |
| In the text | |
 |
Fig. 4 Steady-state abundances of NH, NH2, and NH3 as a function of the C/O gas-phase elemental abundance ratio for three different values of gas-phase elemental abundance of sulphur (from left to right: [S]tot = 8.0 × 10-8, 8.0 × 10-7, 8.0 × 10-6). C/O values include 0.3, 0.4, 0.5, 0.6, 0.67, 0.7, 0.75, 0.8, 0.9, 1.0, 1.1, 1.2, 1.3, 1.4, 1.5. In each panel, the solid line refers to the model predictions and the vertical dashed lines locate C/O = 0.67 (Flower et al. 2006 value) and 0.8 (our best model value). For NH2 and NH3, the ortho and para abundances are shown separately (dashed and dotted lines respectively). The observed abundances towards IRAS 16293-2422 are represented by the hatched boxes, considering an o/p ratio of NH2~ 2, as predicted by our model. |
| In the text | |
 |
Fig. 5 Steady-state abundance ratios of the N-hydrides as a function of the gas-phase elemental abundance ratio of C/O for three different values of the gas-phase elemental abundance of sulphur (from left to right: [S]tot = 8.0 × 10-8, 8.0 × 10-7, 8.0 × 10-6). C/O values include 0.3, 0.4, 0.5, 0.6, 0.67, 0.7, 0.75, 0.8, 0.9, 1.0, 1.1, 1.2, 1.3, 1.4, 1.5. In all panels, the vertical dashed lines locate C/O = 0.67 (Flower et al. 2006 value) and 0.8 (our best model value). The abundances derived from Herschel/HIFI observations towards IRAS 16293-2422 are represented by the hatched boxes, considering an o/p ratio of NH2~ 2, as predicted by our model. |
| In the text | |
 |
Fig. A.1 Comparison between the observed NH3 spectrum (black) from Hily-Blant et al. (2010a) and the best-fit model (red). The + and − signs in the transition labelling are the same as in Maret et al. (2009). |
| In the text | |
 |
Fig. A.2 Same as in Fig. A.1 for the NH multiplets, using the same physical model as for NH3 and adopting a single NH column density of 2.2 ± 0.8 × 1014 cm-2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


