| Issue |
A&A
Volume 561, January 2014
|
|
|---|---|---|
| Article Number | A143 | |
| Number of page(s) | 12 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201322632 | |
| Published online | 27 January 2014 | |
Measurement of the TCMB evolution from the Sunyaev-Zel’dovich effect
1
Institut d’Astrophysique Spatiale, CNRS (UMR8617) Université Paris-Sud
11, Bâtiment 121,
91405
Orsay Cedex,
France
e-mail:
ghurier@ias.u-psud.fr
2
CNRS, IRAP, 9
Av. colonel Roche, BP
44346, 31028
Toulouse Cedex 4,
France
3
Université de Toulouse, UPS-OMP, IRAP,
31400
Toulouse,
France
Received:
9
September
2013
Accepted:
27
November
2013
In the standard hot cosmological model, the black-body temperature of the cosmic microwave background (CMB), TCMB, increases linearly with redshift. Across the line of sight CMB photons interact with the hot (~ 107−8 K ) and diffuse gas of electrons from galaxy clusters. This interaction leads to the well-known thermal Sunyaev-Zel’dovich effect (tSZ), which produces a distortion of the black-body emission law, depending on TCMB. Using tSZ data from the Planck satellite, it is possible to constrain TCMB below z = 1. Focusing on the redshift dependance of TCMB, we obtain TCMB(z) = (2.726 ± 0.001) × (1 + z)1−β K with β = 0.009 ± 0.017, which improves on previous constraints. Combined with measurements of molecular species absorptions, we derive β = 0.006 ± 0.013. These constraints are consistent with the standard (i.e. adiabatic, β = 0) Big-Bang model.
Key words: cosmology: observations / cosmic background radiation / galaxies: clusters: general
© ESO, 2014
1. Introduction
The cosmic microwave background (CMB) radiation is a fundamental observational probe of the hot Big-Bang model. In standard ΛCDM cosmology, the CMB black-body temperature evolution as a function of redshift reads TCMB(z) = TCMB(z = 0) (1 + z)1−β, with β = 0 and TCMB(z = 0) is the temperature measured today in the local Universe.
A violation of this evolution would imply deeper theoretical consequences (e.g., Uzan et al. 2004). Alternative cosmological models predict a nonlinear scaling law between temperature and redshift (see e.g., Matyjasek 1995; Overduin & Cooperstock 1998; Puy 2004). A deviation from β = 0 can be induced by a violation of the equivalence principle or by a non-conservation of the photon number without any spectral distortion of the CMB. In the first case, it can be associated with fundamental constant variations (see e.g., Murphy et al. 2003; Srianand et al. 2004). In the second case, it can be associated with decaying dark-energy models (see e.g., Freese et al. 1987; Lima & Trodden 1996; Jetzer et al. 2011) or with axion-photon-like coupling process (see Jaeckel & Ringwald 2010, for a recent review).
The CMB temperature has been measured in our galaxy at high precision using CN excitation in molecular clouds by Roth et al. (1993). Next, it has been measured using the COBE-FIRAS experiment (Fixsen et al. 1996; Mather et al. 1999) and more recently, using the WMAP data (Bennett et al. 2003) to recalibrate the COBE-FIRAS (Fixsen 2009) measurements.
In addition to the measurement of TCMB at z = 0, there are currently two direct observational methods to measure TCMB at redshifts z > 0. The first one uses the excitation of interstellar atomic or molecular species by CMB photons (e.g. Losecco et al. 2001). This approach was used even before the CMB discovery (see Thaddeus 1972, for a review of early observations). When in radiative equilibrium with the CMB radiation, the excitation temperature of molecular species equals that of the CMB. Thus, these species allow one to measure the CMB temperature (Bahcall & Wolf 1968). The fact that the CMB is not the only heating source of the interstellar medium and the lack of a detailed knowledge of the physical conditions in the absorbing clouds are the main sources of systematics and uncertainties (Combes & Wiklind 1999). They lead to upper limits or large error bars (ΔT ≥ 0.6 K) on the value of TCMB (Meyer et al. 1986; Songaila et al. 1994a,b; Lu et al. 1996; Roth & Bauer 1999). Recently, Muller et al. (2013) have performed a comprehensive analysis that overcomes parts of the limitations. In particular, they have made use of various atomic and molecular species simultaneously in order to completely model the observed cloud properties and hence to provide tight constraints on TCMB.
The second observational approach consists in measuring a weak spectral distortion of the CMB black-body in the direction of galaxy clusters that is caused by the thermal Sunyaev-Zel’dovich (tSZ) effect (Zel’dovich & Sunyaev 1969; Sunyaev & Zel’dovich 1972). This technique was originally proposed by Fabbri et al. (1978) and Rephaeli (1980). Predictions for these measurement with Planck have been discussed by Horellou et al. (2005) and de Martino et al. (2012). They predicted, in an optimistic case, an uncertainty on the TCMB evolution of Δβ ~ 0.011. Actual measurements were already performed (Battistelli et al. 2002; Luzzi et al. 2009) and provided ΔT ≤ 0.3 K on a small number of clusters of galaxies. The Planck satellite now offers a new and large sample of galaxy clusters (Planck Collaboration 2014i) observed via the tSZ effect that allows us to derive much tighter constraints on the evolution of the CMB temperature.
Galaxy cluster catalogs that reach deeper (e.g. SPT, Reichardt et al. 2013 and ACT, Hasselfield et al. 2013) or larger (e.g. MCXC, Piffaretti et al. 2011) can also be used to complement the constraint from the Planck SZ clusters.
In this work, we focus on improving in the measurement of TCMB at redshifts z > 0 from the Planck data using the tSZ effect from galaxy clusters. In Sect. 2 we present the Planck intensity maps and galaxy cluster catalog that were used. Sect. 3 briefly presents the tSZ effect. Then in Sect. 4, we present the stacking method used to extract the tSZ flux in the different Planck frequency channels to constrain TCMB. In Sect. 5, we estimate the uncertainty levels on our measurement that are caused, on the one hand, by foreground/background contributions to Planck intensity maps and, on the other hand, by instrumental systematic effects. Next in Sect. 6, we carefully model our measurement to determine TCMB from the tSZ spectral law. In Sect. 7, we present our results and compare them with previous measurements. Finally in Sect. 8, we discuss our results and their cosmological implications.
2. Data
2.1. Planck intensity maps
We used the six channel maps, 100 to 857 GHz, from the Planck satellite (Planck Collaboration 2014a). We refer to the Planck Collaboration (2014c) and Planck Collaboration (2014e) for the generic scheme of time ordered information processing and map-making, as well as for the characteristics of the Planck frequency maps. We used the Planck channel maps in HEALPix (Górski et al. 2005) Nside = 2048 at full resolution. Here, we approximate the Planck beams by effective circular Gaussians (see Planck Collaboration 2014d, for more details).
2.2. Planck SZ catalog
We also used the Planck catalog of tSZ detections (Planck Collaboration 2014i, PSZ,). It contains 1227 sources, which is about six times larger than the Planck Early SZ (ESZ; Planck Collaboration 2011a) sample and is currently the largest tSZ-selected catalog. The PSZ contains 861 confirmed clusters to date.
In the following, we only consider the sample of 813 Planck cluster with redshifts up to ~1 (Planck Collaboration 2011d). This sample consists of high-significance SZ detections in the Planck channel maps and thus allows us to constrain TCMB up to z ~ 1, avoiding strong contamination by point sources or galactic emission.
2.3. Other catalogs of galaxy clusters
We complemented our analysis of the Planck SZ-cluster catalog using X-ray selected clusters from the Meta Catalog of X-ray Clusters (MCXC; Piffaretti et al. 2011); and tSZ selected clusters from the Atacama Cosmological Telescope (ACT; Hincks et al. 2010; Hasselfield et al. 2013) and the South Pole Telescope (SPT) tSZ catalogs (Chang et al. 2009; Song et al. 2012; Reichardt et al. 2013). Table 1 summarizes the main characteristics of these catalogs. In particular, for the present study, we considered subsamples from the MCXC, ACT, and SPT catalogs that consist of clusters not included in the PSZ catalog; for the MCXC clusters we also imposed that M500 ≥ 1014 M⊙.
2.4. Radio-source catalogs
Emission from radio point sources is a source of contamination in the estimation of the tSZ flux (Planck Collaboration 2014i) that can lead to biases in tSZ Compton-y signal (see e.g. Hurier et al. 2013, for an example on the Virgo and Perseus galaxy clusters).
The NRAO VLA Sky Survey (NVSS; Condon et al. 1998) is a 1.4 GHz continuum survey covering the entire sky north of Dec > −40°. The associated catalog of discrete sources contains over 1.8 million radio sources. South of Dec < −30° and at galactic latitudes | b| > 10°, the Sydney University Molonglo Sky Survey (SUMSS; Mauch et al. 2003, 2008) is a 843 MHz continuum survey also providing a radio source catalog. SUMSS and NVSS have a similar sensitivity and angular resolutions, and combined they cover the whole sky.
We used these two surveys as tracers of the radio emission that contaminated our estimation of the tSZ flux to estimate the level of bias in our measure.
3. The tSZ effect
The tSZ effect is a distortion of the CMB black-body radiation through inverse Compton
scattering. CMB photons receive an average energy boost by collision with hot (a few keV)
ionized electrons of the intra-cluster medium. The tSZ Compton parameter in a given
direction, n, on the sky is given by 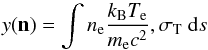 (1)where
ds is the distance along the line-of-sight, and
ne and Te are the electron
number-density and temperature. In units of CMB temperature, the tSZ effect at a frequency
ν is
(1)where
ds is the distance along the line-of-sight, and
ne and Te are the electron
number-density and temperature. In units of CMB temperature, the tSZ effect at a frequency
ν is 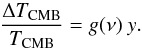 (2)Neglecting corrections due
to the weakly relativistic high-end of the velocity distribution for the thermal electrons,
we have
(2)Neglecting corrections due
to the weakly relativistic high-end of the velocity distribution for the thermal electrons,
we have ![\begin{equation} g(\nu) = \left[ x\coth \left(\frac{x}{2} \right) - 4 \right], \label{szspec} \end{equation}](/articles/aa/full_html/2014/01/aa22632-13/aa22632-13-eq32.png) (3)with the
dimensionless frequency
x = hν/(kBTCMB).
h and kB represent the Planck and the
Boltzmann constants. At z = 0, where
TCMB(z = 0) = 2.726 ± 0.001 K, the tSZ
effect signal is negative below 217 GHz and positive at higher frequencies. This
characteristic spectral signature is a unique tool for detecting of galaxy clusters. The
spectral signature is directly related to TCMB through the
x variable. They depend on the convolution of the tSZ intensity with the
Planck frequency responses.
(3)with the
dimensionless frequency
x = hν/(kBTCMB).
h and kB represent the Planck and the
Boltzmann constants. At z = 0, where
TCMB(z = 0) = 2.726 ± 0.001 K, the tSZ
effect signal is negative below 217 GHz and positive at higher frequencies. This
characteristic spectral signature is a unique tool for detecting of galaxy clusters. The
spectral signature is directly related to TCMB through the
x variable. They depend on the convolution of the tSZ intensity with the
Planck frequency responses.
Main characteristics of the galaxy cluster catalogs.
4. Methodology
In this section, we describe the procedure that was used to extract the tSZ signal from the full-sky Planck intensity maps. We start by considering clusters from the Planck catalog, because they have a high signal-to-noise ratio and a low level of contamination. Then, we discuss the case of additional clusters from the samples listed in Sect. 2.3.
In a first step, we set all Planck frequency channels to a common angular resolution of 10′, corresponding roughly to the angular resolution the lowest resolution channel at 100 GHz. Then, we extracted individual patches centered on the location of Planck galaxy clusters and stacked them. Next, we cleaned the obtained stacked patches from IR emission from galactic dust and extragalactic IR galaxies using the 857 GHz channel. Finally, we estimated the tSZ flux in each cleaned stacked patch.
4.1. Stacking
To increase the significance of the tSZ signal per frequency, we performed a stacking
analysis in multiple redshift bins. Our sample consists of 813 clusters with known
redshifts, distributed in 20 redshift bins from z = 0 to
z = 1, with a binsize Δz = 0.05. The redshift bins and
number of clusters per bin are listed in Table 3.
Note that the mean redshift  and the weighted mean over Y500,
zeff only differs at the third decimal. This shows that the
SZ flux distribution over the bin is homogeneous and that the choice of bins is a fair
sampling of the redshift distribution for the considered cluster sample. In the following,
we use zeff as the mean value for our redshift bin.
and the weighted mean over Y500,
zeff only differs at the third decimal. This shows that the
SZ flux distribution over the bin is homogeneous and that the choice of bins is a fair
sampling of the redshift distribution for the considered cluster sample. In the following,
we use zeff as the mean value for our redshift bin.
We constructed a stacked patch per redshift bin. We thus extracted individual patches of 2° × 2°1 from the full-sky intensity maps with pixels of 1.7′. The individual patches were centered on the positions of the clusters in the considered redshift bin. The individual patches were re-projected using a nearest neighbor interpolation on a grid of 0.2′ pixels in gnomonic projection. This conserves the cluster flux. Note that re-projection effects are the same for all frequencies and consequently do not bias the estimation of TCMB since the latter only depends on the shape of the tSZ spectral law.
For each redshift bin individual patches are cleaned from point-source contamination. To do this, we masked all sources from the Planck Catalog of Compact Sources (Planck Collaboration 2014j) detected above 10σ in one of the six highest frequency channels of Planck within an area of 30′ from the cluster center. Sources within a radius of 20′ from the considered cluster were not masked. This process avoids biases in the dust-cleaning process (see Sect. 4.2).
Finally in each redshift bin, the individual patches per frequency were co-added with a constant weight. This choice is a two-fold one. It accounts for the fact that the main contribution to the noise due to CMB is similar from one patch to the other. Furthermore, it avoids cases where a particular cluster will dominate the stacked signal. It is worth noting that this a choice is not optimized for the signal-to-noise ratio of the flux.
We verified that we derive similar results when applying random rotations to the extracted patches before stacking. This test demonstrated that our stacking is not sensitive to specific orientations, produced, for example, by the thermal dust emission from the Galactic plane.
4.2. Dust cleaning
To remove thermal dust contamination in stacked patches per frequency, we used the 857 GHz channel. The thermal dust emission is known to have a varying spectral energy distribution (SED) across the sky (Planck Collaboration 2013c). To compute the effective thermal dust SED for each stacked patch per frequency, we assumed that in a field of 2° × 2° the thermal dust spectral properties can be well described by a single SED.
This cleaning was performed for each redshift bin δ and for each
frequency i by computing the scale factor,
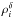 , between the
stacked patch at 857 GHz,
, between the
stacked patch at 857 GHz, 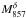 , and other
stacked patches from 100 to 545 GHz,
, and other
stacked patches from 100 to 545 GHz, 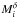 . To avoid
biases produced by correlations between IR emission and the tSZ effect, we computed
. To avoid
biases produced by correlations between IR emission and the tSZ effect, we computed
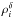 by removing
the central region of r < 30′, with
r the angular distance to the clusters position. We checked that
performing the cleaning per cluster instead of per redshift bin provides comparable
results.
by removing
the central region of r < 30′, with
r the angular distance to the clusters position. We checked that
performing the cleaning per cluster instead of per redshift bin provides comparable
results. 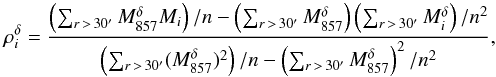 (4)where n
is the number of pixels satisfying the condition
r > 30′. Then, the stacked patches
cleaned from thermal dust were obtained by subtracting the 857 GHz from the other
channels:
(4)where n
is the number of pixels satisfying the condition
r > 30′. Then, the stacked patches
cleaned from thermal dust were obtained by subtracting the 857 GHz from the other
channels: 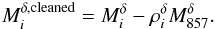 (5)This cleaning
process has an impact solely on 353 and 545 GHz channels with
(5)This cleaning
process has an impact solely on 353 and 545 GHz channels with
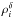 values
varying only by 10% and 5% at 353 and 545 GHz, from bin to bin. Dust-cleaned stacked
patches for each redshift bin are presented in Figs. 1 and 2. We clearly observe (as reported in
Planck Collaboration 2014i) the intensity
decrement at low frequency (<217 GHz), the null effect at 217 GHz
and the positive emission at high frequency (>217 GHz). Note that
we report a clear detection of the tSZ effect even in the 545 GHz Planck
channel for redshifts up to 0.6.
values
varying only by 10% and 5% at 353 and 545 GHz, from bin to bin. Dust-cleaned stacked
patches for each redshift bin are presented in Figs. 1 and 2. We clearly observe (as reported in
Planck Collaboration 2014i) the intensity
decrement at low frequency (<217 GHz), the null effect at 217 GHz
and the positive emission at high frequency (>217 GHz). Note that
we report a clear detection of the tSZ effect even in the 545 GHz Planck
channel for redshifts up to 0.6.
 |
Fig. 1 From left to right: stack of Planck intensity maps from 100 to 545 GHz cleaned by the 857 GHz channel, centered on the location of Planck tSZ detected clusters. From top to bottom: stacked signal from tSZ detected clusters in different redshifts bins (from z = 0.0 to z = 0.5), see Table 4 for the redshift bins. Each stacked map represents an area of 2° × 2°. |
4.3. Flux estimate
To measure the flux from the cleaned stacked patches at 100, 143, 217, 353, and 545 GHz, we first derived the shape of the tSZ signal in the stacked patches. To do this, we computed a Compton-y parameter map for each cluster individually using the MILCA method (Hurier et al. 2013). Computing the y-map on a stacked patch would lead to a poorer tSZ reconstruction. We then stacked the reconstructed y-maps for the clusters within a given redshift bin. We refer to them as tSZ filter or template.
The tSZ signal in the stacked patches presents a circular symmetry. We therefore computed
the radial profile of the tSZ filter and re-projected it to construct a denoised tSZ
filter, 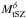 . We used
. We used
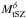 as a shape
filter to measure the tSZ flux,
as a shape
filter to measure the tSZ flux, 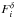 , in each
cleaned stacked patch
, in each
cleaned stacked patch 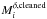 .
.
The tSZ flux was obtained by computing a linear fit of the denoised tSZ filter on the
cleaned stacked patches per frequency in a radius of 20’ around the cluster center,
assuming homogeneous noise and the following modeling 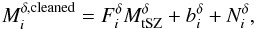 (6)with
(6)with
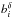 a constant
baseline accounting for large-scale (>20′) residual
contamination and
a constant
baseline accounting for large-scale (>20′) residual
contamination and 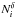 the noise
component including astrophysical emissions and instrumental noise.
the noise
component including astrophysical emissions and instrumental noise.
From Eq. (6), we derived a tSZ emission
law, 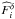 ,
for each redshift bin δ. The estimator
,
for each redshift bin δ. The estimator
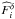 of
of 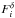 was obtained
by adjusting both
was obtained
by adjusting both 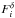 and
and
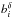 . Figure 3 presents the derived emission law for the tSZ effect
for each redshift bin. The standard model is displayed as a dashed red line. Measured
fluxes,
. Figure 3 presents the derived emission law for the tSZ effect
for each redshift bin. The standard model is displayed as a dashed red line. Measured
fluxes, 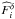 ,
were used to derive the value of
,
were used to derive the value of  for each
redshift bin in Sect. 6.
for each
redshift bin in Sect. 6.
Note that using of a tSZ template induces no prior on the tSZ spectral law (considering
that the spatial distribution of the tSZ signal is the same in all channels) and thus on
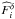 .
The small difference between tSZ filters from bin to bin is due to the difference in
cluster extensions since the profiles used here were not rescaled with respect to their
angular sizes contrary to Arnaud et al. (2010) and
the Planck Collaboration (2013a).
.
The small difference between tSZ filters from bin to bin is due to the difference in
cluster extensions since the profiles used here were not rescaled with respect to their
angular sizes contrary to Arnaud et al. (2010) and
the Planck Collaboration (2013a).
 |
Fig. 3 From left to right and top to bottom: measured tSZ emission law in units of KCMB for each redshift bin form 0 to 1, with Δz = 0.05. Note that bins with 0.80 ≤ z < 0.85 and 0.90 ≤ z < 0.95 do not contain any cluster. Black stars denote the data and dashed red lines the theoretical tSZ emission law. Error bars are strongly correlated between the different frequency channels, see Table 2. |
5. Statistical and systematic uncertainties
We now discuss the sources of uncertainties and systematic errors on the measured fluxes
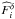 .
We first focus on the uncertainties produced by background and foreground signals, including
instrumental noise. Then we address the astrophysical components correlated to the tSZ
emission, and finally we discuss the systematic errors caused by the instrument spectral
responses.
.
We first focus on the uncertainties produced by background and foreground signals, including
instrumental noise. Then we address the astrophysical components correlated to the tSZ
emission, and finally we discuss the systematic errors caused by the instrument spectral
responses.
5.1. Background and foreground contamination
To estimate the uncertainty on 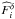 caused by contamination by other sources signal, we extracted the flux at 1000 random
positions across the sky for each denoised tSZ filter. We avoided the galactic plane area,
which is not represented in our cluster distribution.
caused by contamination by other sources signal, we extracted the flux at 1000 random
positions across the sky for each denoised tSZ filter. We avoided the galactic plane area,
which is not represented in our cluster distribution.
In the stacking process each cluster was considered to be uncorrelated with others. Consequently, we derived the full covariance matrix for the flux estimate in frequency channels from 100 to 545 GHz. An example of correlation matrix is presented in Table 2. This correlation matrix only accounts for uncertainties produced by uncorrelated components (with respect to the tSZ effect) in the flux estimation. This correlation matrix has a determinant of 10-4, which quantifies the volume occupied by the swarm of data samples in our five-dimension subspace (cleaned frequencies from 100 to 545 GHz).
At 100 to 217 GHz, the CMB anisotropies are the main source of uncertainties. This explains the high level of correlation in the estimated fluxes. At higher frequencies, instrumental noise and dust residuals become an important contribution to the total uncertainties, which explains the lower level of correlation.
Correlation matrix of statistical uncertainties for the measurement of tSZ flux
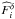 ,
estimated from 1000 random positions across the sky.
,
estimated from 1000 random positions across the sky.
5.2. Correlated foreground contamination
Uncertainties produced by uncorrelated foregrounds, for instance, CMB, can be fairly estimated from measurements at random positions over the sky. However, these measurements do not account for noise or bias produced by correlated emissions, such as, radio sources at low frequency, cosmic infrared background (CIB) at high frequency, and the kinetic SZ effect.
5.2.1. Cosmic infrared background
The CMB temperature measure is directly related to the frequency at which tSZ effect is
null, making it a key frequency in our analysis. At 217 GHz, a contribution from the CIB
(the integrated IR emission from dust in distant galaxies (see e.g., Hauser & Dwek 2001; Kashlinsky 2005; Lagache et al.
2005, for reviews)) is significant and is correlated to the tSZ signal (e.g.,
Addison et al. 2012). In the following, we
assumed a conservative situation of full correlation between tSZ and CIB,
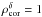 . Note that the cluster sample
used here does not contain all clusters at
z < 1. Consequently, the actual correlation
factor
. Note that the cluster sample
used here does not contain all clusters at
z < 1. Consequently, the actual correlation
factor 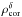 is lower than one
and depends on the completeness with respect to the redshift (see Planck Collaboration 2014i, for more details).
is lower than one
and depends on the completeness with respect to the redshift (see Planck Collaboration 2014i, for more details).
Considering the CIB intensity at 217 GHz, 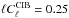 μK2.sr,
given by the Planck Collaboration (2011c), the
CMB power spectrum at ℓ = 1000,
μK2.sr,
given by the Planck Collaboration (2011c), the
CMB power spectrum at ℓ = 1000, 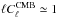 μK2 sr,
given in Planck Collaboration (2014f) and
considering the contribution to tSZ power spectrum from our sample
μK2 sr,
given in Planck Collaboration (2014f) and
considering the contribution to tSZ power spectrum from our sample
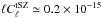 y2 sr
(Planck Collaboration 2014h), we can compute
the bias due to the CIB contribution. We furthermore assumed that 90% of the CIB is
cleaned by the dust-cleaning process discussed in Sect. 4.2 and we defined fclean = 0.9.
y2 sr
(Planck Collaboration 2014h), we can compute
the bias due to the CIB contribution. We furthermore assumed that 90% of the CIB is
cleaned by the dust-cleaning process discussed in Sect. 4.2 and we defined fclean = 0.9.
We used the following equation for the bias induced by tSZ × CIB correlation for a
given redshift bin δ:
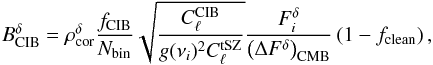 (7)fCIB ~ 0.05
is the fraction of CIB emission produced by objects at redshift
<1, Nbin is the number of redshift
bins, and
(7)fCIB ~ 0.05
is the fraction of CIB emission produced by objects at redshift
<1, Nbin is the number of redshift
bins, and 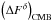 is the
contribution of the CMB to the uncertainties over
is the
contribution of the CMB to the uncertainties over
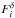 .
.
We derived a ratio between CMB and CIB fluctuations of about 0.2% on average per cluster. At most, we use about one hundred clusters in a single redshift bin. This reduced the CMB fluctuations by a factor 10. Consequently, in a conservative case, the CIB at 217 GHz contributes at the level of 2% of the intensity of CMB and can therefore be neglected.
5.2.2. Radio point sources
Radio sources within galaxy clusters can produce an overestimate of the flux at low frequencies, which in turn leads to an underestimate of TCMB(z).
Using the NVSS and the SUMSS catalogs of radio point sources, we estimated the radio
point-source contamination on the measured tSZ flux. To do this, we projected the NVSS
and the SUMSS catalogs on a full-sky map (considering only SUMSS sources at
Dec < −40°, and extrapolating their fluxes from
853 MHz to 1.4 GHz with a spectral index of −1). Then, we smoothed the obtained map at
10′. We thus obtained a full-sky map of the combined radio sources at 1.4
GHz on which we estimate the radio flux 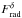 for each stacked
patch and redshift bin δ using the approach described in Sect. 4.3. Finally, we extrapolated the radio emission from
1.4 GHz to Planck frequencies, assuming a spectral index of −1. We
estimated the spectral index by computing the cross power spectrum between the NVSS
catalog projected map and the Planck 100 GHz channel. We derived an
averaged spectral index of −0.995 ± 0.010.
for each stacked
patch and redshift bin δ using the approach described in Sect. 4.3. Finally, we extrapolated the radio emission from
1.4 GHz to Planck frequencies, assuming a spectral index of −1. We
estimated the spectral index by computing the cross power spectrum between the NVSS
catalog projected map and the Planck 100 GHz channel. We derived an
averaged spectral index of −0.995 ± 0.010.
The radio fluxes within the tSZ filter, 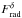 , expressed in
terms of percentage of the measured tSZ flux at 100 GHz are summarized in Table 3. Under the simple assumption of a single spectral
index −1, we show that the contamination by radio source emission on the measured tSZ
flux at 100 GHz is lower than 15%. In the analysis described in Sect. 6.2.2, we show how this contribution was modeled,
fitted, and accounted for in the estimate of the uncertainties.
, expressed in
terms of percentage of the measured tSZ flux at 100 GHz are summarized in Table 3. Under the simple assumption of a single spectral
index −1, we show that the contamination by radio source emission on the measured tSZ
flux at 100 GHz is lower than 15%. In the analysis described in Sect. 6.2.2, we show how this contribution was modeled,
fitted, and accounted for in the estimate of the uncertainties.
Reshift binning used for our analysis.
5.2.3. Kinetic Sunyaev-Zel’dovich effect
The kinetic SZ effect, kSZ, is the Doppler shift of CMB photons that scatter the intracluster electrons. This effect is faint, one order of magnitude lower than the tSZ. It has the same spectral dependance as the CMB and is spatially correlated to the tSZ signal. The kSZ effect can produce positive or negative CMB temperature anisotropies. Consequently, this effect will not bias the tSZ measurement, but will enlarge the CMB dispersion at the clusters position and therefore the error-bars. At Planck resolution, the increase in CMB variance due to the kSZ is small (Planck Collaboration 2013b) and can be neglected in our analysis.
In some nonstandard inhomogenous cosmological models (see e.g. Goodman 1995; Clarkson 2012), the kSZ monopole is different from zero. This could induce a bias in the tSZ measurement. However, these models are now strongly constrained by Planck data (Planck Collaboration 2013b).
5.3. Effects of bandpass and calibration uncertainties
To measure the tSZ emission law in the Planck channels we integrated the
tSZ emission law, 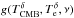 (see
Eq. (3)), over the Planck
spectral responses (i.e., bandpasses), see Planck
Collaboration (2014b), Hi, in the
following manner:
(see
Eq. (3)), over the Planck
spectral responses (i.e., bandpasses), see Planck
Collaboration (2014b), Hi, in the
following manner: 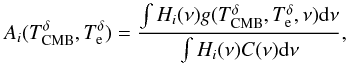 (8)with,
Ai the tSZ transmission in the
ith Planck channel,
C(ν) the emission law of the calibrators, CMB, and
planets (Planck Collaboration 2014e), and
(8)with,
Ai the tSZ transmission in the
ith Planck channel,
C(ν) the emission law of the calibrators, CMB, and
planets (Planck Collaboration 2014e), and
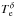 the effective
cluster temperature per redshift bin.
the effective
cluster temperature per redshift bin.
The bandpasses present uncertainties that depend on the tSZ spectral law. Given that
 and
and
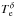 produce small
variations of the tSZ, we can assume that the bandpass uncertainties are constant. We
propagated the uncertainties on the bandpasses
Hi in our analysis by computing the
uncertainties on the tSZ emission law
produce small
variations of the tSZ, we can assume that the bandpass uncertainties are constant. We
propagated the uncertainties on the bandpasses
Hi in our analysis by computing the
uncertainties on the tSZ emission law 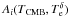 after integrating over the
bandpass. These turn into uncertainties on the recovered value of
after integrating over the
bandpass. These turn into uncertainties on the recovered value of
 . We derived
a systematic uncertainty of 0.010 K at z = 0 for
. We derived
a systematic uncertainty of 0.010 K at z = 0 for
 ; it becomes
0.010 × (1 + zeff) K for each redshift bin.
; it becomes
0.010 × (1 + zeff) K for each redshift bin.
At low frequencies, the Planck data were calibrated with respect to CMB
dipole (TCMB(z = 0)). Uncertainties on the
calibration can also lead to bias in 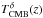 . However, this source of
uncertainties is small, about 0.2% at 100 to 217 GHz channels (Planck Collaboration 2014e). It was neglected in the following.
. However, this source of
uncertainties is small, about 0.2% at 100 to 217 GHz channels (Planck Collaboration 2014e). It was neglected in the following.
6. Analysis
6.1. Modeling the signal
Our measurement at the ith Planck frequency can be
modeled as 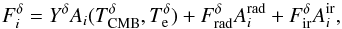 (9)with
Yδ = ∫δ∫ydΩdz
the integrated Compton parameter for a redshift bin δ,
(9)with
Yδ = ∫δ∫ydΩdz
the integrated Compton parameter for a redshift bin δ,
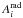 the radio
source spectrum with spectral index −1 normalized to 1 at 100 GHz, and
the radio
source spectrum with spectral index −1 normalized to 1 at 100 GHz, and
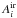 is the IR
spectrum with dust temperature Td = 17 K and spectral index
βd = 1.8 (Planck
Collaboration 2011b) normalized to 1 at 353 GHz. We verified that this
is the IR
spectrum with dust temperature Td = 17 K and spectral index
βd = 1.8 (Planck
Collaboration 2011b) normalized to 1 at 353 GHz. We verified that this
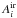 SED
theoretical model is consistent with the spectrum derived from our cleaning procedure.
SED
theoretical model is consistent with the spectrum derived from our cleaning procedure.
The adjustable parameters are Yδ,
 ,
,
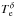 ,
,
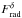 the radio
source flux and
the radio
source flux and 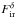 the IR
contamination level including CIB emission.
the IR
contamination level including CIB emission.
 |
Fig. 4 Likelihood function of the measured tSZ emission law as a function of
|
6.2. Sensitivity analysis
In the following, we perform a sensitivity analysis between
 and the
other parameters of the model.
and the
other parameters of the model.
6.2.1. Impact of relativistic corrections
The relativistic corrections to the tSZ emission law has been computed numerically (see
e.g. Rephaeli 1995; Pointecouteau et al. 1998; Itoh
et al. 1998). If we assume that the relativistic corrections can be described
as a first-order approximation,  (10)the averaged tSZ
emission law can be described with an averaged temperature fitted as an effective
temperature,
(10)the averaged tSZ
emission law can be described with an averaged temperature fitted as an effective
temperature, 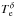 , for the
stacked tSZ signal (see Nozawa et al. 2000, for a
more detailed fitting formula).
, for the
stacked tSZ signal (see Nozawa et al. 2000, for a
more detailed fitting formula).
Figure 4 presents the likelihood function in the
plane ( ,
,
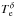 ) for
clusters in the redshift bin 0.05 to 0.10. The other redshift bins present similar
behaviors. The value we derived for
) for
clusters in the redshift bin 0.05 to 0.10. The other redshift bins present similar
behaviors. The value we derived for 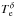 is below
10 keV at 1σ level and below 15 keV at 3σ level, with
a best-fitting value around 5 keV. This is consistent with the X-ray derived
temperatures for typical clusters in the Planck sample. Figure 4 shows no correlation between the recovered value of
is below
10 keV at 1σ level and below 15 keV at 3σ level, with
a best-fitting value around 5 keV. This is consistent with the X-ray derived
temperatures for typical clusters in the Planck sample. Figure 4 shows no correlation between the recovered value of
 and
and
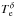 . This
Indicates that we can safely neglect relativistic corrections in our analysis.
. This
Indicates that we can safely neglect relativistic corrections in our analysis.
 |
Fig. 5 Top panel: Likelihood function of the measured tSZ emission law
as a function of |
6.2.2. Radio and IR contaminations
Figure 5 presents the likelihood function in the
plane of the radio contamination, 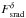 , and
, and
 (top panel), and
in the plane of the IR contamination,
(top panel), and
in the plane of the IR contamination, 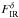 , and
, and
 (bottom panel)
for clusters within a redshift bin 0.10 to 0.15. The other redshift bins present similar
behaviors. We found that the IR contamination, including CIB residuals, is compatible
with 0 and does not bias our estimate of the tSZ flux. We also note that the derived
value of
(bottom panel)
for clusters within a redshift bin 0.10 to 0.15. The other redshift bins present similar
behaviors. We found that the IR contamination, including CIB residuals, is compatible
with 0 and does not bias our estimate of the tSZ flux. We also note that the derived
value of 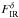 is consistent
with all fclean > 0.8 at
6σ level, consistent with the conservative case discussed in Sect.
5.2.1.
is consistent
with all fclean > 0.8 at
6σ level, consistent with the conservative case discussed in Sect.
5.2.1.
Furthermore, we observed that the radio source contamination produces some bias on the
 measurement. This
bias translates into
measurement. This
bias translates into 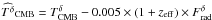 .
.
6.3. Profile likelihood analysis
Given the results of the sensitivity analysis discussed above, we can simplify the model
in Eq. (9) to 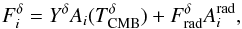 (11)considering only
the relevant parameters Yδ,
(11)considering only
the relevant parameters Yδ,
 and
and
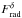 .
.
To fit  in each
redshift bin, we used a profile likelihood approach. First, we computed, through an
unbiased linear fit, the tSZ flux,
in each
redshift bin, we used a profile likelihood approach. First, we computed, through an
unbiased linear fit, the tSZ flux, 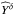 ,
of our measured spectral law for each value of
,
of our measured spectral law for each value of  and
and
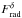 . Given the
similar amplitudes of the uncertainties on the measurement (mainly CMB contamination) and
the model (bandpasses), we used the following estimator for
Yδ:
. Given the
similar amplitudes of the uncertainties on the measurement (mainly CMB contamination) and
the model (bandpasses), we used the following estimator for
Yδ:
![\begin{equation} \widehat{Y}^\delta = \left[ {\vec A}^{\rm T}{\cal W}{\vec A} - {\mathrm{Tr}({\cal C}_{A}^{\rm T}{\cal W}}) \right]^{-1}\left[ {\vec A}^{\rm T}{\cal W}\widehat{\bold F}^\delta \right], \end{equation}](/articles/aa/full_html/2014/01/aa22632-13/aa22632-13-eq139.png) (12)with A the
tSZ transmission vector defined in Eq. (8),
(12)with A the
tSZ transmission vector defined in Eq. (8),
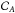 the A covariance matrix2,
the A covariance matrix2,
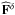 the measured tSZ emission law (see Eq. (6)), and
the measured tSZ emission law (see Eq. (6)), and 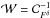 the inverse of the noise covariance matrix on
the inverse of the noise covariance matrix on 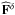 .
.
Measured value of  in Kelvin
derived from the tSZ emission law per redshift bin.
in Kelvin
derived from the tSZ emission law per redshift bin.
 |
Fig. 6 Measured |
Then, we computed the χ2, for each paire of parameters
( ,
,
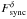 ) as
) as
![\begin{equation} \chi^2 = \left(\widehat{\bold F}^\delta - {\bold F}^\delta \right)^{\rm T} \left[{\cal C}_{F^\delta} + \left(\widehat{Y}^{\delta}\right)^2 {\cal C}_A \right]^{-1} \left(\widehat{\bold F}^\delta - {\bold F}^\delta \right). \end{equation}](/articles/aa/full_html/2014/01/aa22632-13/aa22632-13-eq147.png) (13)Finally, we
estimated the value of
(13)Finally, we
estimated the value of  by
marginalizing over
by
marginalizing over 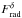 ,
considering a flat prior
,
considering a flat prior 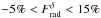 (as observed in Sect. 5.2.2); and by computing the first-order moment of the
likelihood function, ℒ = e−χ2/2
with respect to
(as observed in Sect. 5.2.2); and by computing the first-order moment of the
likelihood function, ℒ = e−χ2/2
with respect to  3.
3.
We computed the uncertainties on  using the
second-order moment of ℒ. Note that the uncertainties only differ at the fourth decimal at
68% confidence level. We also computed the covariance between each
using the
second-order moment of ℒ. Note that the uncertainties only differ at the fourth decimal at
68% confidence level. We also computed the covariance between each
 and
separated the statistical uncertainties that are fully uncorrelated between redshift bins,
and the systematic errors that are fully correlated from one bin to another.
and
separated the statistical uncertainties that are fully uncorrelated between redshift bins,
and the systematic errors that are fully correlated from one bin to another.
Table 4 summarizes our results for the derived TCMB(z) and the associated statistical and systematic uncertainties. We verified that removing clusters contaminated by very bright radio sources (S ≥ 250 mJy at 1.4 GHz) does not affect our results.
7. Results
The measurement of the tSZ emission law allows us to constrain the value of TCMB at z = 0 and its redshift dependance. We explore these two constraints separately. We present the results for the sample of Planck clusters, which constitutes our base dataset. We also discuss other cluster samples and finally we give the tightest constraints obtained by combining tSZ measures from Planck clusters and measures from molecular and atomic absorptions.
 |
Fig. 7 Derived β values for each redshift bin δ considering TCMB(z = 0) = 2.726. Red filled circles show our measurements, light- and dark-blue shaded regions show the 1 and 2σ levels. Errors bars are displayed centered on β = 0 to facilitate the comparison between uncertainties in the different redshift bins δ. The dashed black line represents β = 0 for standard evolution. |
 |
Fig. 8 Top panel: TCMB as a function of redshift. The red filled circles represent TCMB measured from the tSZ emission law in redshift bins of Planck clusters. The green star shows COBE-FIRAS measurement at z = 0 (Fixsen 2009). The orange crosses show TCMB measurements using individual clusters (Battistelli et al. 2002; Luzzi et al. 2009). Dark-blue triangles represent measurements from CI and CII absorption (Cui et al. 2005; Ge et al. 1997; Srianand et al. 2000; Molaro et al. 2002) at z = (1.8,2.0,2.3,3.0). Blue diamonds show the measurements from CO absorption lines (Srianand et al. 2008; Noterdaeme et al. 2011), and finally the light-blue asterisk is the constraint from various molecular species analyses by Muller et al. (2013). The solid black line presents the standard evolution for TCMB and the dashed black line represents our best-fitting model combining all the measurements. The 1 and 2σ envelopes are displayed as shaded dark and light-gray regions. Bottom panel: deviation from the standard evolution in units of standard deviation. The dashed and dotted black lines correspond to the 1 and 2σ levels. |
7.1. Constraints on CMB temperature
We computed the χ2 per degree of freedom (dof) between our
measurements of  (red filled
circles in Fig. 6) and the adiabatic evolution of the
CMB temperature (solid line in Fig. 6), with
TCMB(z = 0) = 2.726 ± 0.001 K. We obtained
(red filled
circles in Fig. 6) and the adiabatic evolution of the
CMB temperature (solid line in Fig. 6), with
TCMB(z = 0) = 2.726 ± 0.001 K. We obtained
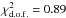 .
This implies that our measurements are consistent with the standard
TCMB evolution.
.
This implies that our measurements are consistent with the standard
TCMB evolution.
If we assume an adiabatic expansion, TCMB(z)
is written as 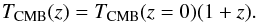 (14)We derived
TCMB(z = 0) from the estimated
(14)We derived
TCMB(z = 0) from the estimated
 for all the
redshift bins δ probed by our sample of Planck clusters.
The measurements are presented in Fig. 6 as red
filled circles. We observe that all measurements are within a 2σ from the
adiabatic expansion evolution. The best fit, using all redshift bins, gives
TCMB(z = 0) = 2.720 ± 0.009 ± 0.011 K with
statistical and systematics uncertainties, respectively. Note that the errors are
dominated by the systematic uncertainty from the spectral responses. It is fully
correlated between redshift bins, and thus cannot be reduced. Our measurement of
TCMB(z = 0) from the tSZ emission law
cannot compete, in terms of accuracy, with the COBE-FIRAS
TCMB(z = 0) = 2.726 ± 0.001 K (Fixsen 2009). However, it is fully consistent.
for all the
redshift bins δ probed by our sample of Planck clusters.
The measurements are presented in Fig. 6 as red
filled circles. We observe that all measurements are within a 2σ from the
adiabatic expansion evolution. The best fit, using all redshift bins, gives
TCMB(z = 0) = 2.720 ± 0.009 ± 0.011 K with
statistical and systematics uncertainties, respectively. Note that the errors are
dominated by the systematic uncertainty from the spectral responses. It is fully
correlated between redshift bins, and thus cannot be reduced. Our measurement of
TCMB(z = 0) from the tSZ emission law
cannot compete, in terms of accuracy, with the COBE-FIRAS
TCMB(z = 0) = 2.726 ± 0.001 K (Fixsen 2009). However, it is fully consistent.
7.2. Constraints on the redshift evolution
Our analysis was based on a sample of 813 Planck clusters covering a
redshift range from 0 to 1. If we express
TCMB(z) as in Lima et al. (2000),
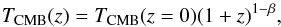 (15)it is possible to
test the TCMB evolution in adiabatic expansion. We fit
β using a maximum-likelihood analysis and a flat prior. Figure 7 presents the best-fitting value of β
for each individual redshift bin δ, considering
TCMB(z = 0) = 2.726. We observe that all
redshift bins are consistent with β = 0 at 2σ and that
redshift bins from z = 0.05 to z = 0.7 provide similar
constraints on β. Figure 7 also
illustrates that our constraint on β are not dominated by a given bin,
but that it uses the entire redshift range.
(15)it is possible to
test the TCMB evolution in adiabatic expansion. We fit
β using a maximum-likelihood analysis and a flat prior. Figure 7 presents the best-fitting value of β
for each individual redshift bin δ, considering
TCMB(z = 0) = 2.726. We observe that all
redshift bins are consistent with β = 0 at 2σ and that
redshift bins from z = 0.05 to z = 0.7 provide similar
constraints on β. Figure 7 also
illustrates that our constraint on β are not dominated by a given bin,
but that it uses the entire redshift range.
We derived β = 0.009 ± 0.017 from the tSZ emission law in the 18 redshift bins used in the analysis, consistent with no deviation from adiabatic evolution. Note that in contrast to the TCMB(z = 0) measurement, β is not affected by bandpass uncertainties because they are fully correlated for all redshift bins.
We compared our result on β with the different constraints obtained either from other tSZ measurements or molecular and atomic absorptions.
Previous analyses have measured TCMB(z) either at low redshift (Luzzi et al. 2009) using the tSZ effect on a small number of clusters, or at higher redshifts (Cui et al. 2005; Ge et al. 1997; Srianand et al. 2000; Molaro et al. 2002; Muller et al. 2013) using atomic and molecular absorption. These TCMB measurements are presented in Fig. 8 with the standard adiabatic evolution shown as a solid black line.
We derived for the above-mentioned measurements constraints on β using the same fitting procedure and a flat prior as in our analysis. Table 5 summarizes the results. We found that the tSZ emission law from Planck clusters provides the tightest constraint on β. Errors are smaller by about a factor of two compared with previous constraints, separately. Our result, β = 0.009 ± 0.017, from tSZ effect in Planck clusters is at the same level of precision and accuracy as the tightest constraint, β = 0.009 ± 0.019, reported by Muller et al. (2013), combining all the constraints from molecular and atomic lines and tSZ clusters before Planck.
By furthermore combining our new limit on β with the previous data sets, we improved the derived constraint on the TCMB evolution. We found β = 0.006 ± 0.013. It is worth noting that in this combination the fit is driven by our own analysis and the measurements from Muller et al. (2013) and Noterdaeme et al. (2011) which have uncertainties of 0.017, 0.031, and 0.033, respectively.
Measured values of TCMB and β re-derived, with our fitting procedure, from different subsamples of TCMB(z) measurements based on the tSZ effect and atomic/molecular absorptions.
8. Discussion
Our basic results presented in Sect. 7 were derived from the analysis of tSZ emission law of 813 clusters from Planck up to z ~ 1. We found β = 0.009 ± 0.017, which shows that even with a moderately deep sample tSZ is a competitive observational way of constraining the evolution of TCMB.
To explore the variation of this result with other cluster samples, we performed the same analysis, as in Sect. 6, on the MCXC (Piffaretti et al. 2011) catalog. This allowed us to select a large number of massive clusters (see Table 1). To avoid significant radio contamination of the tSZ measurement, we considered only clusters with an intensity lower than 500 μKCMB in the 100 GHz channel. This process only removes three clusters from our initial MCXC sample (see Sect. 2.3). We thus performed our analysis, and with the obtained TCMB measures ranging from z = 0 to 0.35, we found β = 0.07 ± 0.10. This poor constraint is mainly due to the reduced redshift range and to the relatively low tSZ flux associated with a large portion of the considered clusters. We also analyzed the SPT (Reichardt et al. 2013) and ACT (Hasselfield et al. 2013) catalogs. Again, we derived poor constraints on β, because the tSZ signal in the Planck intensity maps from the selected clusters is faint. Consequently, we did not include these measurements in the analysis. Combining the constraints from the tSZ emission law with other direct measurement using molecular and atomic absorption, we found the tightest limit on the TCMB evolution to be β = 0.006 ± 0.013, consistent with a standard TCMB evolution.
Departures from an adiabatic evolution of TCMB can be tested
through indirect measurements. In particular when CMB photon number is not conserved,
β can be constrained by the distance duality relation violation (Avgoustidis et al. 2012, and references therein) or by
combining the CMB and galaxy distribution (as in, e.g., Opher & Pelinson 2005). These indirect measurements yield
β = 0.010 ± 0.020 and β ≤ 0.0034, consistent with our
analysis. Our tSZ-based measurements can also test deviations from the
TCMB-redshift relation in decaying dark-energy (DE) models.
Jetzer et al. (2011) predicted the following
relation: 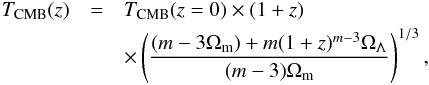 (16)with
Ωm and ΩΛ the matter and DE energy densities at
z = 0, and m = 3(weff + 1) is
related to the effective equation of state of the decaying DE,
weff. Considering a flat Universe and
Ωm = 0.314 ± 0.020 (Planck Collaboration
2014g), we derive weff = −0.995 ± 0.011, which
improves previous constraint from Noterdaeme et al. (e.g.,
2011).
(16)with
Ωm and ΩΛ the matter and DE energy densities at
z = 0, and m = 3(weff + 1) is
related to the effective equation of state of the decaying DE,
weff. Considering a flat Universe and
Ωm = 0.314 ± 0.020 (Planck Collaboration
2014g), we derive weff = −0.995 ± 0.011, which
improves previous constraint from Noterdaeme et al. (e.g.,
2011).
The evolution of TCMB with redshift can also be affected by
time-varying fundamental constants (see Uzan 2011,
for a recent review). Specifically for the tSZ-based constraints, variations of
h and kB in Eq. (3) lead to deviations of β from
zero 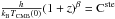 . However,
variations of the fundamental constants become small after the Universe enters its current
DE-dominated epoch (Barrow et al. 2002), and
consequently tSZ variations are less sensitive to these changes at
z < 1.
. However,
variations of the fundamental constants become small after the Universe enters its current
DE-dominated epoch (Barrow et al. 2002), and
consequently tSZ variations are less sensitive to these changes at
z < 1.
9. Conclusion
We have performed an analysis of the Planck intensity data in the range of 100 to 857 GHz, aimed at deriving the CMB temperature and its evolution via the tSZ emission law. Based on the Planck SZ catalog, we measured TCMB(z) in the redshift range 0 < z < 1. This is the first measurement of TCMB(z) on such a large tSZ sample of clusters. It demonstrates the ability of exploring the low-redshift range which cannot be covered by the traditionally used optical/UV quasar absorption systems.
We showed that clustered CIB and relativistic corrections to the tSZ spectral law do not produce any significant bias on our result. We note that the main uncertainties are caused by the Planck instrumental spectral responses, CMB contamination, and the radio source contamination. They were modeled and accounted for in the error bars in the determination of TCMB(z).
Our measurement of TCMB(z) below z = 1 reaches a precision of about 5% below z = 0.65, about 1% for all bins below z = 0.3, and better than 0.6% for the redshift between z = 0.05 and z = 0.10. This is the most precise measurement at z > 0 to date. Combining TCMB(z) at low redshifts with results from Muller et al. (2013) and references presented in Fig. 8, we obtained the tightest constraints so far on the TCMB(z) = TCMB(z = 0)(1 + z)1−β law, with β = 0.006 ± 0.013. Our result confirms that the CMB temperature evolution is consistent with an adiabatic expansion.
The discovery of new massive high-z (z > 0.5) clusters will bring a major improvement in TCMB(z) measurement from the tSZ emission law. In particular, SZ surveys such as Planck and SPT-3G and optical surveys such as the Dark Energy Survey (The Dark Energy Survey Collaboration 2005) and Pan-STARRS (Kaiser et al. 2002; Tonry et al. 2012) will provide us with much larger and deeper cluster samples. In the future, even larger and deeper samples of massive clusters will be constructed from from EUCLID (Amiaux et al. 2012; Amendola et al. 2013), the Large Synoptic Survey Telescope (LSST Science Collaboration et al. 2009), and SRG-eROSITA (Merloni et al. 2012; Pillepich et al. 2012). In combination with the fourth-generation CMB space mission, the tSZ emission law from clusters will strongly improve existing constraints on TCMB(z) up to z = 2.
The uncertainties on the response 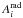 are lower
than 1% and neglected. In contrast, the uncertainties on the response for the tSZ in the
217 GHz channel is about 25% (Planck Collaboration
2014b).
are lower
than 1% and neglected. In contrast, the uncertainties on the response for the tSZ in the
217 GHz channel is about 25% (Planck Collaboration
2014b).
Acknowledgments
We thank the anonymous referee for his or her comments. We are grateful to J. F. Macías-Pérez, J. M. Diego, and R. Genova-Santos for their comments and suggestions. Some of the results in this paper have been derived using the HEALPix package (Górski et al. 2005). We acknowledge the support of the French Agence Nationale de la Recherche under grant ANR-11-BD56-015. The development of Planck has been supported by: ESA; CNES and CNRS/INSU-IN2P3-INP (France); ASI, CNR, and INAF (Italy); NASA and DoE (USA); STFC and UKSA (UK); CSIC, MICINN and JA (Spain); Tekes, AoF and CSC (Finland); DLR and MPG (Germany); CSA (Canada); DTU Space (Denmark); SER/SSO (Switzerland); RCN (Norway); SFI (Ireland); FCT/MCTES (Portugal); and The development of Planck has been supported by: ESA; CNES and CNRS/INSU-IN2P3-INP (France); ASI, CNR, and INAF (Italy); NASA and DoE (USA); STFC and UKSA (UK); CSIC, MICINN and JA (Spain); Tekes, AoF and CSC (Finland); DLR and MPG (Germany); CSA (Canada); DTU Space (Denmark); SER/SSO (Switzerland); RCN (Norway); SFI (Ireland); FCT/MCTES (Portugal); and PRACE (EU).
References
- Addison, G. E., Dunkley, J., & Spergel, D. N. 2012, MNRAS, 427, 1741 [NASA ADS] [CrossRef] [Google Scholar]
- Amendola, L., Appleby, S., Bacon, D., et al. 2013, Liv. Rev. Rel., 16, 6 [Google Scholar]
- Amiaux, J., Scaramella, R., Mellier, Y., et al. 2012, in SPIE Conf. Ser., 8442 [Google Scholar]
- Arnaud, M., Pratt, G. W., Piffaretti, R., et al. 2010, A&A, 517, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Avgoustidis, A., Luzzi, G., Martins, C. J. A. P., & Monteiro, A. M. R. V. L. 2012, JCAP, 2, 13 [Google Scholar]
- Bahcall, J. N., & Wolf, R. A. 1968, ApJ, 152, 701 [NASA ADS] [CrossRef] [Google Scholar]
- Barrow, J. D., Sandvik, H. B., & Magueijo, J. 2002, Phys. Rev. D, 65, 063504 [NASA ADS] [CrossRef] [Google Scholar]
- Battistelli, E. S., De Petris, M., Lamagna, L., et al. 2002, ApJ, 580, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Bennett, C. L., Halpern, M., Hinshaw, G., et al. 2003, ApJS, 148, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Chang, C. L., Ade, P. A. R., Aird, K. A., et al. 2009, in AIP Conf. Ser., 1185, eds. B. Young, B. Cabrera, & A. Miller, 475 [Google Scholar]
- Clarkson, C. 2012, C. R. Phys., 13, 682 [Google Scholar]
- Combes, F., & Wiklind, T. 1999, in Highly Redshifted Radio Lines, eds. C. L. Carilli, S. J. E. Radford, K. M. Menten, & G. I. Langston, ASP Conf. Ser., 156, 210 [Google Scholar]
- Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693 [NASA ADS] [CrossRef] [Google Scholar]
- Cui, J., Bechtold, J., Ge, J., & Meyer, D. M. 2005, ApJ, 633, 649 [Google Scholar]
- de Martino, I., Atrio-Barandela, F., da Silva, A., et al. 2012, ApJ, 757, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Fabbri, R., Melchiorri, F., & Natale, V. 1978, Ap&SS, 59, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Fixsen, D. J. 2009, ApJ, 707, 916 [Google Scholar]
- Fixsen, D. J., Cheng, E. S., Gales, J. M., et al. 1996, ApJ, 473, 576 [NASA ADS] [CrossRef] [Google Scholar]
- Freese, K., Adams, F. C., Frieman, J. A., & Mottola, E. 1987, Nucl. Phys. B, 287, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Ge, J., Bechtold, J., & Black, J. H. 1997, ApJ, 474, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, J. 1995, Phys. Rev. D, 52, 1821 [NASA ADS] [CrossRef] [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Hasselfield, M., Hilton, M., Marriage, T. A., et al. 2013, JCAP, 07, 008 [Google Scholar]
- Hauser, M. G., & Dwek, E. 2001, ARA&A, 39, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Hincks, A. D., Acquaviva, V., Ade, P. A. R., et al. 2010, ApJS, 191, 423 [Google Scholar]
- Horellou, C., Nord, M., Johansson, D., & Lévy, A. 2005, A&A, 441, 435 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hurier, G., Hildebrandt, S. R., & Macias-Perez, J. F. 2013 [arXiv:1007.1149] [Google Scholar]
- Itoh, N., Kohyama, Y., & Nozawa, S. 1998, ApJ, 502, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Jaeckel, J., & Ringwald, A. 2010, Ann. Rev. Nucl. Sci., 60, 405 [Google Scholar]
- Jetzer, P., Puy, D., Signore, M., & Tortora, C. 2011, Gen. Relativ. Gravit., 43, 1083 [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, N., Aussel, H., Burke, B. E., et al. 2002, in SPIE Conf. Ser. 4836, eds. J. A. Tyson, & S. Wolff, 154 [Google Scholar]
- Kashlinsky, A. 2005, Phys. Rep., 409, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Lagache, G., Puget, J.-L., & Dole, H. 2005, ARA&A, 43, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Lima, J. A. S., & Trodden, M. 1996, Phys. Rev. D, 53, 4280 [NASA ADS] [CrossRef] [Google Scholar]
- Lima, J. A. S., Silva, A. I., & Viegas, S. M. 2000, MNRAS, 312, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Losecco, J. M., Mathews, G. J., & Wang, Y. 2001, Phys. Rev. D, 64, 123002 [NASA ADS] [CrossRef] [Google Scholar]
- LSST Science Collaboration, Abell, P. A., Allison, J., et al. 2009 [arXiv:0912.0201] [Google Scholar]
- Lu, L., Sargent, W. L. W., Barlow, T. A., Churchill, C. W., & Vogt, S. S. 1996, ApJS, 107, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Luzzi, G., Shimon, M., Lamagna, L., et al. 2009, ApJ, 705, 1122 [NASA ADS] [CrossRef] [Google Scholar]
- Mather, J. C., Fixsen, D. J., Shafer, R. A., Mosier, C., & Wilkinson, D. T. 1999, ApJ, 512, 511 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matyjasek, J. 1995, Phys. Rev. D, 51, 4154 [NASA ADS] [CrossRef] [Google Scholar]
- Mauch, T., Murphy, T., Buttery, H. J., et al. 2003, MNRAS, 342, 1117 [NASA ADS] [CrossRef] [Google Scholar]
- Mauch, T., Murphy, T., Buttery, H. J., et al. 2008, VizieR Online Data Catalog: VIII/081 [Google Scholar]
- Merloni, A., Predehl, P., Becker, W., et al. 2012 [arXiv:1209.3114] [Google Scholar]
- Meyer, D. M., York, D. G., Black, J. H., Chaffee, Jr., F. H., & Foltz, C. B. 1986, ApJ, 308, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Molaro, P., Levshakov, S. A., Dessauges-Zavadsky, M., & D’Odorico, S. 2002, A&A, 381, L64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muller, S., Beelen, A., Black, J. H., et al. 2013, A&A, 551, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murphy, M. T., Webb, J. K., & Flambaum, V. V. 2003, MNRAS, 345, 609 [Google Scholar]
- Noterdaeme, P., Petitjean, P., Srianand, R., Ledoux, C., & López, S. 2011, A&A, 526, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nozawa, S., Itoh, N., Kawana, Y., & Kohyama, Y. 2000, ApJ, 536, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Opher, R., & Pelinson, A. 2005, Braz. J. Phys., 35, 1206 [NASA ADS] [CrossRef] [Google Scholar]
- Overduin, J. M., & Cooperstock, F. I. 1998, Phys. Rev. D, 58, 043506 [NASA ADS] [CrossRef] [Google Scholar]
- Piffaretti, R., Arnaud, M., Pratt, G. W., Pointecouteau, E., & Melin, J.-B. 2011, A&A, 534, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pillepich, A., Porciani, C., & Reiprich, T. H. 2012, MNRAS, 422, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration 2011a, A&A, 536, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011b, A&A, 536, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011c, A&A, 536, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011d, A&A, 536, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2013a, A&A, 550, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2013b, A&A, 561, A97 [Google Scholar]
- Planck Collaboration 2013c, A&A, submitted [arXiv:1307.6815] [Google Scholar]
- Planck Collaboration 2014a, A&A, submitted [arXiv:1303.5062] [Google Scholar]
- Planck Collaboration 2014b, A&A, submitted [arXiv:1303.5070] [Google Scholar]
- Planck Collaboration 2014c, A&A, submitted [arXiv:1303.5067] [Google Scholar]
- Planck Collaboration 2014d, A&A, submitted [arXiv:1303.5068] [Google Scholar]
- Planck Collaboration 2014e, A&A, submitted [arXiv:1303.5069] [Google Scholar]
- Planck Collaboration 2014f, A&A, submitted [arXiv:1303.5075] [Google Scholar]
- Planck Collaboration 2014g, A&A, submitted [arXiv:1303.5076] [Google Scholar]
- Planck Collaboration 2014h, A&A, submitted [arXiv:1303.5081] [Google Scholar]
- Planck Collaboration 2014i, A&A, submitted [arXiv:1303.5089] [Google Scholar]
- Planck Collaboration 2014j, A&A, submitted [arXiv:1303.5088] [Google Scholar]
- Pointecouteau, E., Giard, M., & Barret, D. 1998, A&A, 336, 44 [NASA ADS] [Google Scholar]
- Puy, D. 2004, A&A, 422, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reichardt, C. L., Stalder, B., Bleem, L. E., et al. 2013, ApJ, 763, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Rephaeli, Y. 1980, ApJ, 241, 858 [NASA ADS] [CrossRef] [Google Scholar]
- Rephaeli, Y. 1995, ARA&A, 33, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Roth, K. C., & Bauer, J. M. 1999, ApJ, 515, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Roth, K. C., Meyer, D. M., & Hawkins, I. 1993, ApJ, 413, L67 [NASA ADS] [CrossRef] [Google Scholar]
- Song, J., Zenteno, A., Stalder, B., et al. 2012, ApJ, 761, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Songaila, A., Cowie, L. L., Hogan, C. J., & Rugers, M. 1994a, Nature, 368, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Songaila, A., Cowie, L. L., Vogt, S., et al. 1994b, Nature, 371, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Srianand, R., Petitjean, P., & Ledoux, C. 2000, Nature, 408, 931 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Srianand, R., Chand, H., Petitjean, P., & Aracil, B. 2004, Phys. Rev. Lett., 92, 121302 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Srianand, R., Noterdaeme, P., Ledoux, C., & Petitjean, P. 2008, A&A, 482, L39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sunyaev, R. A., & Zel’dovich, Y. B. 1972, Comments Astrophys. Space Phys., 4, 173 [NASA ADS] [EDP Sciences] [Google Scholar]
- Thaddeus, P. 1972, ARA&A, 10, 305 [NASA ADS] [CrossRef] [Google Scholar]
- The Dark Energy Survey Collaboration 2005 [arXiv:astro-ph/0510346] [Google Scholar]
- Tonry, J. L., Stubbs, C. W., Lykke, K. R., et al. 2012, ApJ, 750, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Uzan, J.-P. 2011, Liv. Rev. Rel., 14, 2 [Google Scholar]
- Uzan, J.-P., Aghanim, N., & Mellier, Y. 2004, Phys. Rev. D, 70, 083533 [NASA ADS] [CrossRef] [Google Scholar]
- Zel’dovich, Y. B., & Sunyaev, R. A. 1969, Ap&SS, 4, 301 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Correlation matrix of statistical uncertainties for the measurement of tSZ flux
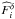 ,
estimated from 1000 random positions across the sky.
,
estimated from 1000 random positions across the sky.
Measured values of TCMB and β re-derived, with our fitting procedure, from different subsamples of TCMB(z) measurements based on the tSZ effect and atomic/molecular absorptions.
All Figures
 |
Fig. 1 From left to right: stack of Planck intensity maps from 100 to 545 GHz cleaned by the 857 GHz channel, centered on the location of Planck tSZ detected clusters. From top to bottom: stacked signal from tSZ detected clusters in different redshifts bins (from z = 0.0 to z = 0.5), see Table 4 for the redshift bins. Each stacked map represents an area of 2° × 2°. |
| In the text | |
 |
Fig. 2 Same as Fig. 1, but for redshift bins from z = 0.5 to z = 1.0. |
| In the text | |
 |
Fig. 3 From left to right and top to bottom: measured tSZ emission law in units of KCMB for each redshift bin form 0 to 1, with Δz = 0.05. Note that bins with 0.80 ≤ z < 0.85 and 0.90 ≤ z < 0.95 do not contain any cluster. Black stars denote the data and dashed red lines the theoretical tSZ emission law. Error bars are strongly correlated between the different frequency channels, see Table 2. |
| In the text | |
 |
Fig. 4 Likelihood function of the measured tSZ emission law as a function of
|
| In the text | |
 |
Fig. 5 Top panel: Likelihood function of the measured tSZ emission law
as a function of |
| In the text | |
 |
Fig. 6 Measured |
| In the text | |
 |
Fig. 7 Derived β values for each redshift bin δ considering TCMB(z = 0) = 2.726. Red filled circles show our measurements, light- and dark-blue shaded regions show the 1 and 2σ levels. Errors bars are displayed centered on β = 0 to facilitate the comparison between uncertainties in the different redshift bins δ. The dashed black line represents β = 0 for standard evolution. |
| In the text | |
 |
Fig. 8 Top panel: TCMB as a function of redshift. The red filled circles represent TCMB measured from the tSZ emission law in redshift bins of Planck clusters. The green star shows COBE-FIRAS measurement at z = 0 (Fixsen 2009). The orange crosses show TCMB measurements using individual clusters (Battistelli et al. 2002; Luzzi et al. 2009). Dark-blue triangles represent measurements from CI and CII absorption (Cui et al. 2005; Ge et al. 1997; Srianand et al. 2000; Molaro et al. 2002) at z = (1.8,2.0,2.3,3.0). Blue diamonds show the measurements from CO absorption lines (Srianand et al. 2008; Noterdaeme et al. 2011), and finally the light-blue asterisk is the constraint from various molecular species analyses by Muller et al. (2013). The solid black line presents the standard evolution for TCMB and the dashed black line represents our best-fitting model combining all the measurements. The 1 and 2σ envelopes are displayed as shaded dark and light-gray regions. Bottom panel: deviation from the standard evolution in units of standard deviation. The dashed and dotted black lines correspond to the 1 and 2σ levels. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


