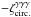| Issue |
A&A
Volume 561, January 2014
|
|
|---|---|---|
| Article Number | A53 | |
| Number of page(s) | 26 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201322146 | |
| Published online | 23 December 2013 | |
Source-lens clustering and intrinsic-alignment bias of weak-lensing estimators⋆
Institut de Physique Théorique, CEA Saclay, CNRS, URA 2306, 91191 Gif-sur-Yvette Cedex, France
e-mail: patrick.valageas@cea.fr
Received: 26 June 2013
Accepted: 11 October 2013
Aims. We estimate the amplitude of the source-lens clustering bias and of the intrinsic-alignment bias of weak-lensing estimators of the two-point and three-point convergence and cosmic-shear correlation functions.
Methods. We use a linear galaxy bias model for the galaxy-density correlations, as well as a linear intrinsic-alignment model. For the three-point and four-point density correlations, we use analytical or semi-analytical models, based on a hierarchical ansatz or a combination of one-loop perturbation theory with a halo model.
Results. For two-point statistics, we find that the source-lens clustering bias is typically several orders of magnitude below the weak-lensing signal, except when we correlate a very low-redshift galaxy (z2 ≲ 0.05) with a higher redshift galaxy (z1 ≳ 0.5), where it can reach 10% of the signal for the shear. For three-point statistics, the source-lens clustering bias is typically on the order of 10% of the signal, as soon as the three galaxy source redshifts are not identical. The intrinsic-alignment bias is typically about 10% of the signal for both two-point and three-point statistics. Thus, both source-lens clustering bias and intrinsic-alignment bias must be taken into account for three-point estimators aiming at a better than 10% accuracy.
Key words: gravitational lensing: weak / large-scale structure of Universe
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
Weak gravitational lensing of background galaxies by foreground large-scale structures is an important probe of both the geometry of the Universe and the growth of these large-scale structures. This makes it a powerful tool when studying the distribution of dark matter and the nature of dark energy (Albrecht et al. 2006). This effect arises from the deflection of light rays from distant galaxies by the fluctuations of the gravitational potential along the line of sight (Bartelmann & Schneider 2001; Munshi et al. 2008). This yields both a deformation of the shape of the images of distant galaxies (associated with the “cosmic shear” γ, at lowest order) and a magnification of their flux (associated with the “convergence” κ). Because we do not know a priori the shape or luminosity of individual background galaxies, cosmological studies use statistical averages over many galaxies to detect the coherent shear due to large-scale structures (typically on angular scales of a few arcmin), assuming that background galaxies are statistically isotropic. Thus, in practice we use the cosmic shear (through the coherent orientation of galaxies on arcmin scales that it induces) rather than the convergence as a probe of gravitational lensing (because it is difficult to predict the luminosity distribution of background galaxies with a good accuracy and we lack a standard candle). Moreover, we usually do not measure a shear or convergence map from a galaxy survey, that is, the fields γ(θ) or κ(θ) on some region of the sky, but the two-point correlation ⟨γiγj⟩ (θ), by averaging over all galaxy pairs (i,j) separated by an angular distance θ.
More precisely, weak gravitational lensing is measured from the ellipticities of galaxies, ϵobs, which are related to the cosmological shear distortions γ by ϵobs = ϵs + γ, where ϵs is the intrinsic galaxy ellipticity. Then, assuming that intrinsic galaxy ellipticities are independent and decorrelated from the shear, one measures the gravitational lensing signal by averaging over pairs of galaxies. This gives estimators (that we denote with a hat) of the form 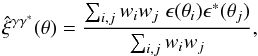 (1)where we sum over all galaxy pairs in the survey with an angular distance | θi − θj | that falls within some bin around θ. (In this example, we correlate ϵ with its complex conjugate ϵ∗ to obtain nonzero results, as the shear and the ellipticity are spin-2 quantities.) The weights wi may be chosen to diminish the importance of noisy objects, to improve the signal-to-noise ratio. This provides an estimator of the real-space two-point shear correlation function
(1)where we sum over all galaxy pairs in the survey with an angular distance | θi − θj | that falls within some bin around θ. (In this example, we correlate ϵ with its complex conjugate ϵ∗ to obtain nonzero results, as the shear and the ellipticity are spin-2 quantities.) The weights wi may be chosen to diminish the importance of noisy objects, to improve the signal-to-noise ratio. This provides an estimator of the real-space two-point shear correlation function 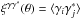 . By summing over all pairs that are separated by a distance shorter than some angular radius θ, one also obtains the integral of ξγγ∗ within this scale or the variance of the smoothed shear or of the aperture mass (e.g., Bartelmann & Schneider 2001; Munshi et al. 2008; Kilbinger et al. 2013).
. By summing over all pairs that are separated by a distance shorter than some angular radius θ, one also obtains the integral of ξγγ∗ within this scale or the variance of the smoothed shear or of the aperture mass (e.g., Bartelmann & Schneider 2001; Munshi et al. 2008; Kilbinger et al. 2013).
In this fashion, the two-point correlation (Bacon et al. 2000; Van Waerbeke et al. 2000; Wittman et al. 2000; Hamana et al. 2003; Jarvis et al. 2006; Semboloni et al. 2006; Fu et al. 2008; Schrabback et al. 2010) and three-point correlation (Bernardeau et al. 2002b; Semboloni et al. 2011) of the cosmic shear have been detected and measured on scales of a few arcmin.
In Eq. (1), ϵ may be taken as the tangential or cross-component or as the component along a given axis. One can also consider different redshift bins for zi and zj, as in tomographic studies that make use of the redshift dependence of the lensing signal (Hu 1999; Heymans et al. 2013). Next, one may take the Fourier transform of 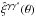 to obtain an estimator of the weak lensing power spectrum. This is more convenient than first taking the Fourier transform of the ellipticity field and second taking its variance, because the masks and intricate boundaries of galaxy surveys make it difficult to compute the Fourier transform of the field.
to obtain an estimator of the weak lensing power spectrum. This is more convenient than first taking the Fourier transform of the ellipticity field and second taking its variance, because the masks and intricate boundaries of galaxy surveys make it difficult to compute the Fourier transform of the field.
In practice, different sources of noise can bias the estimator (1). In addition to the instrumental noise itself (that may be included in the statistical properties of ϵs), intrinsic galaxy alignments must be taken care of. They come either through the correlation between nearby galaxies, 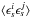 (Heavens et al. 2000; Croft & Metzler 2000; Catelan et al. 2001; Brown et al. 2002), or the correlation between the ellipticity of a foreground galaxy i and the local density field, which contributes to the shear of a background galaxy j and gives rise to a correlation
(Heavens et al. 2000; Croft & Metzler 2000; Catelan et al. 2001; Brown et al. 2002), or the correlation between the ellipticity of a foreground galaxy i and the local density field, which contributes to the shear of a background galaxy j and gives rise to a correlation 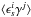 (Hirata & Seljak 2004; Hirata et al. 2007; Mandelbaum et al. 2011; Heymans et al. 2013).
(Hirata & Seljak 2004; Hirata et al. 2007; Mandelbaum et al. 2011; Heymans et al. 2013).
Another source of bias arises from the fact that galaxies are not located at random in space. Indeed, they are correlated with the density field, and this gives rise to a “source-lens clustering” bias (Bernardeau 1998; Hamana et al. 2002). For instance, in terms of the convergence κ, if galaxies were only located behind overdense regions their luminosity would appear systematically enhanced. This effect is expected to be rather small for measures of the two-point shear correlation, as compared with the full gravitational lensing signal, because it is restricted to density fluctuations close to the observed galaxies whereas the full signal arises from density fluctuations along the whole line of sight. It is further suppressed by the fact that the lensing efficiency (the kernel g in Eq. (9) below) vanishes at the source plane. Moreover, on large scales this bias scales as ξ2 whereas the weak lensing signal scales as ξ (where ξ is the matter density correlation), so that this bias should be subdominant. Nevertheless, in view of the increasing accuracy of future surveys, it is interesting to have an estimate of the magnitude of this systematic effect, to check that it can indeed be neglected (as in all current studies).
On the other hand, for measures of the shear three-point correlation, both the signal and the source-lens clustering bias scale as ξ2 and one can expect a significant contamination, especially for triplets of galaxies that are at different redshifts, so that the lensing kernel g is nonzero. Moreover, at leading order the bias writes as a sum of product of two terms. The first term again involves the correlation between a foreground galaxy and nearby density fluctuations along another line of sight, but the second term now involves the correlations between density fluctuations along two full lines of sight as in the cosmological signal and is not suppressed by the ratio of the density correlation length to the Hubble length.
The source-lens clustering effect has already been investigated in Bernardeau (1998) and Hamana et al. (2002), using perturbation theory and numerical simulations, for the skewness of the smoothed convergence as derived from a convergence map. In this paper, to keep close to current observational procedures, we investigate the source-lens clustering effect on estimators of the form of Eq. (1), without assuming a convergence map is first measured in the data analysis. As we explain in Sect. 6 below, the source-lens clustering bias associated with such two-point and three-point estimators is rather different from the one associated with the one-point estimator studied in Bernardeau (1998) and Hamana et al. (2002). In particular, it has the opposite sign. Moreover, we consider both the convergence κ (this allows us to introduce our approach in a simple fashion) and the cosmic shear γ. Then, we consider the bias due to galaxy intrinsic alignments, both for two-point and three-point shear correlation estimators. This allows us to extend previous works that focused on the two-point shear correlation to the case of the three-point shear correlation and to compare with the source-lens clustering bias.
We develop an analytical formalism to estimate these weak lensing biases and for numerical computations we use a linear bias model for the galaxy distribution and a linear intrinsic alignment model. We use semi-analytic models for the matter density two-, three- and four-point correlations.
This paper is organized as follows. We first study the source-lens clustering bias for estimators of the two-point correlation of the convergence in Sect. 2 and of the cosmic shear in Sect. 3. Then, we consider estimators of the three-point correlation of the convergence in Sect. 4 and of the cosmic shear in Sect. 5. We compare our approach with some previous works in Sect. 6. Next, we investigate the intrinsic-alignment bias in Sect. 7, for both estimators of the two- and three-point cosmic shear correlations. We conclude in Sect. 8.
2. Two-point convergence correlation function
2.1. Weak lensing convergence κ
For simplicity, we first consider the estimator of the two-point correlation function of the convergence κ, which is a scalar rather than a spin-2 quantity. Then, Eq. (1) becomes 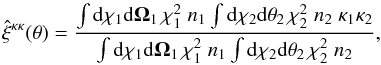 (2)where χ(z) is the comoving radial and angular distance (we assume a flat universe) and ni = n(xi) is the observed galaxy number density (a sum of Dirac peaks at the observed galaxy positions). We did not write weighting factors wi, which are not important for our purposes (and may be absorbed within the number densities ni). In Eq. (2), we count all pairs by first counting all galaxies i in the survey, of total angular area (ΔΩ), and next integrating over all their neighbors j at the angular distance θ2. We did not explicitly write the boundaries of the redshift and angular bins in the integration signs.
(2)where χ(z) is the comoving radial and angular distance (we assume a flat universe) and ni = n(xi) is the observed galaxy number density (a sum of Dirac peaks at the observed galaxy positions). We did not write weighting factors wi, which are not important for our purposes (and may be absorbed within the number densities ni). In Eq. (2), we count all pairs by first counting all galaxies i in the survey, of total angular area (ΔΩ), and next integrating over all their neighbors j at the angular distance θ2. We did not explicitly write the boundaries of the redshift and angular bins in the integration signs.
The estimator (2) is somewhat academic, because in practice we do not measure the convergences κi but only the ellipticities ϵi (which boil down to γi if we discard intrinsic alignments and instrumental noise). However, it provides a simpler presentation of our approach. Moreover, it will be interesting to compare the results obtained for the convergence and the shear, to see whether the latter could be estimated from the former ones.
For a sufficiently wide survey, we can neglect the fluctuations of the denominator in Eq. (2). Indeed, defining 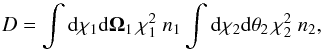 (3)we obtain (assuming for simplicity thin redshift and angular bins Δχ and Δθ)
(3)we obtain (assuming for simplicity thin redshift and angular bins Δχ and Δθ) 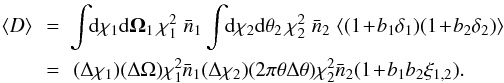 (4)Here, δi = δ(xi) is the matter density contrast,
(4)Here, δi = δ(xi) is the matter density contrast, 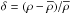 , ξ1,2 = ⟨δ1δ2⟩ its two-point correlation function, and bi is the mean bias of galaxies at redshift i, assuming a linear bias model,
, ξ1,2 = ⟨δ1δ2⟩ its two-point correlation function, and bi is the mean bias of galaxies at redshift i, assuming a linear bias model, 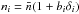 . The second order moment of D reads as
. The second order moment of D reads as 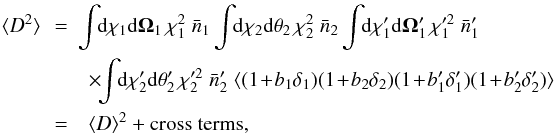 (5)where the cross terms correspond to contributions that involve correlations between δi and
(5)where the cross terms correspond to contributions that involve correlations between δi and 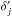 . They are negligible if | x′ − x | ≫ x0, where x0 is the correlation length, and this restricts the integral over
. They are negligible if | x′ − x | ≫ x0, where x0 is the correlation length, and this restricts the integral over 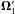 to
to 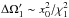 . Therefore, in terms of the scaling with respect to the survey width, we have
. Therefore, in terms of the scaling with respect to the survey width, we have 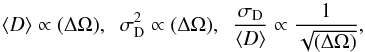 (6)where
(6)where 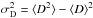 is the variance of the denominator of Eq. (2). Thus, the relative amplitude of the fluctuations of this denominator vanish as 1/
is the variance of the denominator of Eq. (2). Thus, the relative amplitude of the fluctuations of this denominator vanish as 1/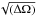 for large surveys.
for large surveys.
Then, neglecting the fluctuations of the denominator1 (there is no shot noise because of the nonzero angular separation), the expectation value of Eq. (2) reads as 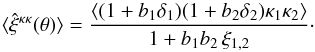 (7)Here, we have chosen infinitesimally thin redshift and angular bins, to avoid being too specific. Averaging over finite redshift bins for z1 and z2, and a finite angular bin for θ, gives the appropriate results for a given survey strategy.
(7)Here, we have chosen infinitesimally thin redshift and angular bins, to avoid being too specific. Averaging over finite redshift bins for z1 and z2, and a finite angular bin for θ, gives the appropriate results for a given survey strategy.
Next, the weak lensing convergence κi of a distant galaxy i due to density fluctuations along the line of sight is given by (in the Born approximation, Bartelmann & Schneider 2001; Munshi et al. 2008) 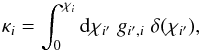 (8)where the lensing kernel gi′,i is given by
(8)where the lensing kernel gi′,i is given by 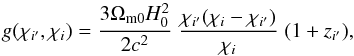 (9)and i′ denotes the point along the line of sight to the galaxy i. (Hereafter, primed indices or coordinates refer to points along the line of sight, which contribute to the weak lensing signal, whereas unprimed indices or coordinates refer to the background source galaxies.) Then, the average (7) can be split into four components,
(9)and i′ denotes the point along the line of sight to the galaxy i. (Hereafter, primed indices or coordinates refer to points along the line of sight, which contribute to the weak lensing signal, whereas unprimed indices or coordinates refer to the background source galaxies.) Then, the average (7) can be split into four components, 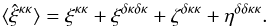 (10)The first component, which does not include cross-correlations between the galaxies and the density fluctuations along the lines of sight, is the weak lensing signal,
(10)The first component, which does not include cross-correlations between the galaxies and the density fluctuations along the lines of sight, is the weak lensing signal, 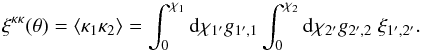 (11)The second component involves products of the two-point correlations between a galaxy and a line of sight,
(11)The second component involves products of the two-point correlations between a galaxy and a line of sight, ![\begin{eqnarray} \xi^{\delta\kappa\delta\kappa} & = & \frac{b_1 b_2}{1+b_1 b_ 2 \, \xi_{1,2}} \; [ \lag \delta_1 \kappa_1 \rag \lag \delta_2 \kappa_2 \rag + \lag \delta_1 \kappa_2 \rag \lag \delta_2 \kappa_1 \rag ] \label{xi-deltakappa-01} \\ & = & \frac{b_1 b_2}{1\!+\!b_1 b_ 2 \, \xi_{1,2}} \int \dd\chi_{1'} \dd\chi_{2'} \, g_{1',1} g_{2',2} \nonumber \\ && \times ~[ \xi_{1,1'} \xi_{2,2'} \! + \xi_{1,2'} \xi_{2,1'} ] , \label{xi-deltakappa-1} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22146-13/aa22146-13-eq69.png) while the third and fourth components involve the three- and four-point density correlations ζ and η,
while the third and fourth components involve the three- and four-point density correlations ζ and η, ![\begin{eqnarray} \zeta^{\delta\kappa\kappa} & = & \frac{b_1 \lag \delta_1 \kappa_1 \kappa_2 \rag + b_2 \lag \delta_2 \kappa_1 \kappa_2 \rag}{1+b_1 b_ 2 \, \xi_{1,2}} \\ & = & \frac{1}{1\!+\!b_1 b_ 2 \, \xi_{1,2}} \int \dd\chi_{1'} \dd\chi_{2'} \, g_{1',1} g_{2',2} \nonumber \\ && \times~[ b_1 \zeta_{1,1',2'} \! + b_2 \zeta_{2,2',1'} ] , \label{zeta-1}\\ \eta^{\delta\delta\kappa\kappa} & = & \frac{b_1 b_2}{1+b_1 b_ 2 \, \xi_{1,2}} \; \lag \delta_1 \delta_2 \kappa_1 \kappa_2 \rag_{\rm c}\\ & = & \frac{b_1 b_2}{1\!+\!b_1 b_ 2 \, \xi_{1,2}} \int \dd\chi_{1'} \dd\chi_{2'} \, g_{1',1} g_{2',2} \; \eta_{1,2,1',2'} . \label{eta-1} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22146-13/aa22146-13-eq72.png) Thus, the last three terms in Eq. (10) bias the estimator (2) of cosmological gravitational lensing. Of course, they vanish when the galaxy bias bi goes to zero, that is, when the galaxy positions are uncorrelated with the density fluctuations along the lines of sight. This source-lens clustering bias does not depend on the size of the survey (we assumed a survey window that is large as compared with the angular scale θ at which we probe the gravitational lensing correlation), because it is due to the intrinsic correlations of the galaxy and matter distributions and not to shot noise effects.
Thus, the last three terms in Eq. (10) bias the estimator (2) of cosmological gravitational lensing. Of course, they vanish when the galaxy bias bi goes to zero, that is, when the galaxy positions are uncorrelated with the density fluctuations along the lines of sight. This source-lens clustering bias does not depend on the size of the survey (we assumed a survey window that is large as compared with the angular scale θ at which we probe the gravitational lensing correlation), because it is due to the intrinsic correlations of the galaxy and matter distributions and not to shot noise effects.
2.2. Analytical approximations
To estimate the source-lens clustering bias for estimators of the two-point correlations, as in Eq. (10), we need the matter density three- and four-point correlation functions ζ and η. Because we are only interested in orders of magnitude estimates and do not require a 10% or better accuracy, we use a simple hierarchical ansatz for these high-order density correlations (Groth & Peebles 1977; Peebles 1980). Thus, we write the three-point density correlation as a sum of products of two-point correlations, ![\begin{equation} \zeta_{1,2,3} = \frac{S_3}{3} [ \xi_{1,2} \xi_{1,3} + \xi_{2,1} \xi_{2,3} + \xi_{3,1} \xi_{3,2} ] , \label{zeta-def} \end{equation}](/articles/aa/full_html/2014/01/aa22146-13/aa22146-13-eq73.png) (18)and in a similar fashion for the four-point density correlation,
(18)and in a similar fashion for the four-point density correlation, ![\begin{equation} \eta_{1,2,3,4} = \frac{S_4}{16} [ \xi_{1,2} \xi_{1,3} \xi_{1,4} + 3 {\rm cyc.} + \xi_{1,2} \xi_{2,3} \xi_{3,4} + 11 {\rm cyc.} ] , \label{eta-def} \end{equation}](/articles/aa/full_html/2014/01/aa22146-13/aa22146-13-eq74.png) (19)where “3 cyc.” and “11 cyc.” stand for three and eleven terms that are obtained from the previous one by permutations over the labels “1, 2, 3, 4” of the four points. For the normalization factors Sn in Eqs. (18), (19), we interpolate from the large-scale quasilinear limit (Bernardeau et al. 2002a) (where we take an angular average to neglect the angular dependence of S3 that would arise in the exact leading-order perturbative result)
(19)where “3 cyc.” and “11 cyc.” stand for three and eleven terms that are obtained from the previous one by permutations over the labels “1, 2, 3, 4” of the four points. For the normalization factors Sn in Eqs. (18), (19), we interpolate from the large-scale quasilinear limit (Bernardeau et al. 2002a) (where we take an angular average to neglect the angular dependence of S3 that would arise in the exact leading-order perturbative result) 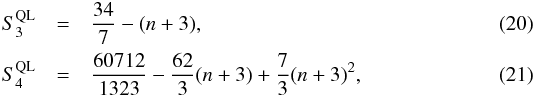 to the highly nonlinear HEPT approximation (Scoccimarro & Frieman 1999)
to the highly nonlinear HEPT approximation (Scoccimarro & Frieman 1999) 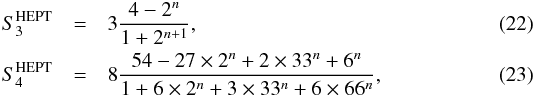 as
as 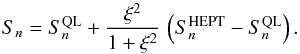 (24)Here, ξ is the two-point correlation at the scale of interest and n the local slope of the linear matter power spectrum. Thus, in the quasilinear regime, where ξ ≪ 1, we have
(24)Here, ξ is the two-point correlation at the scale of interest and n the local slope of the linear matter power spectrum. Thus, in the quasilinear regime, where ξ ≪ 1, we have 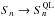 , while in the highly nonlinear regime, where ξ ≫ 1, we have
, while in the highly nonlinear regime, where ξ ≫ 1, we have 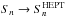 . Since the density correlations only contribute on much smaller scales (~8 h-1 Mpc) than the cosmological scales (c/H0 ~ 3000 h-1 Mpc), in the integrals such as (11) or (17) it is sufficient to use for the two-point correlations ξi,j and the coefficients Sn the mean redshift of the relevant points. (For Sn, we also use the geometrical mean of the relevant scales to compute n and ξ in Eqs. (20)−(24).)
. Since the density correlations only contribute on much smaller scales (~8 h-1 Mpc) than the cosmological scales (c/H0 ~ 3000 h-1 Mpc), in the integrals such as (11) or (17) it is sufficient to use for the two-point correlations ξi,j and the coefficients Sn the mean redshift of the relevant points. (For Sn, we also use the geometrical mean of the relevant scales to compute n and ξ in Eqs. (20)−(24).)
 |
Fig. 1 Skewness S3 and kurtosis S4 at redshift z = 0.35. The solid lines are the analytical approximation (24) and the symbols are results from numerical simulations (Nishimichi & Taruya 2011) for top-hat cumulants. |
This ansatz is the simplest model that is in qualitative agreement with large-scale theoretical predictions (because ζ ~ ξ2 and η ~ ξ3 at leading order in perturbation theory, see Goroff et al. 1986; Bernardeau et al. 2002a) and with numerical simulations on nonlinear scales (Colombi et al. 1996). It was already used to estimate the covariance matrices of galaxy surveys (Bernstein 1994; Szapudi & Colombi 1996) or X-ray cluster surveys (Valageas et al. 2011; Valageas & Clerc 2012). Its generalization to all-order density correlations was also used to compute the high-order cumulants and the probability distributions of the smoothed convergence and cosmic shear, providing a good agreement with results from ray-tracing in N-body simulations (Valageas et al. 2004; Barber et al. 2004; Munshi et al. 2004; Munshi & Valageas 2005).
For completeness, we check the approximation (24) in Fig. 1, where we plot the coefficients Sn as defined by Eq. (24) and the skewness and kurtosis of the density contrast within spherical cells of radius x measured in numerical simulations (Nishimichi & Taruya 2011). The latter are defined from the cumulants of the density contrast as 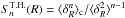 , where the superscript “T.H.” refers to the top-hat filter. These two definitions only coincide if we neglect the scale dependence of the two-point correlations and of the coefficients Sn when we compute the cumulants
, where the superscript “T.H.” refers to the top-hat filter. These two definitions only coincide if we neglect the scale dependence of the two-point correlations and of the coefficients Sn when we compute the cumulants 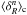 from the three- and four-point correlations (18) and (19). However, this is sufficient for our purpose because in our numerical computations of the cosmic shear bias below, we also factor out the coefficients Sn, using their value at the typical angular scale of interest, so that geometrical integrations over angles, including the typical spin-2 factor e2iα, can be done analytically. Thus, Fig. 1 shows that our approximation provides the correct order of magnitude for three- and four-point correlations. On these scales, the match is better than 20% for the skewness and 35% for the kurtosis. It might be possible to improve the agreement with the simulations by using another interpolation form, such as αξβ / (1 + αξβ) where α and β are best-fit parameters, but in this paper we keep the simple interpolation (24), which is sufficient for our purposes.
from the three- and four-point correlations (18) and (19). However, this is sufficient for our purpose because in our numerical computations of the cosmic shear bias below, we also factor out the coefficients Sn, using their value at the typical angular scale of interest, so that geometrical integrations over angles, including the typical spin-2 factor e2iα, can be done analytically. Thus, Fig. 1 shows that our approximation provides the correct order of magnitude for three- and four-point correlations. On these scales, the match is better than 20% for the skewness and 35% for the kurtosis. It might be possible to improve the agreement with the simulations by using another interpolation form, such as αξβ / (1 + αξβ) where α and β are best-fit parameters, but in this paper we keep the simple interpolation (24), which is sufficient for our purposes.
Since galaxies have a bias of order unity, and we are only interested in general-purpose estimates, we take bi = 1 in our numerical computations (and our results may be multiplied by the appropriate factors bi if needed, as in Eqs. (13)−(17)). For the nonlinear density correlation function ξ(x), we use the semi-analytic model developed in Valageas et al. (2013), which combines one-loop perturbation theory with a halo model to predict the matter density power spectrum and correlation function with a percent accuracy on quasilinear scales and a ten-percent accuracy on highly nonlinear scales. For cosmological parameters, we use the best fit ΛCDM cosmology from Planck observations (Planck Collaboration 2013).
In numerical computations, we keep the real-space expressions (11)−(17), rather than going to Fourier space. This avoids integrations over oscillatory kernels, such as Bessel functions, and the use of Limber’s approximation. Indeed, in configuration-space expressions such as Eq. (11), which involves the correlation ξ1′,2′ between density fluctuations δ1′ and δ2′ along two lines of sight, Limber’s approximation corresponds to setting χ1′ = χ2′ in cosmological kernels such as the lensing efficiency g(χ′,χ) (Limber 1953; Munshi et al. 2008). This is because the density correlation is negligible beyond x0 ~ 8 h-1 Mpc whereas cosmological kernels vary on much larger scales ~c / H0 ~ 3000 h-1 Mpc. However, if we use this approximation in Eqs. (13)−(17), we obtain ξδκδκ = ζδκκ = ηδδκκ = 0, because g(χ′,χ) = 0 at χ′ = χ. This also means that the source-lens clustering contributions in Eq. (10) will be suppressed by a factor ~x0 / (c / H0) (which vanishes in Limber’s limit) and that the computation of this source-lens clustering bias requires going beyond Limber’s approximation. (This is no longer the case for the three-point estimators studied in Sects. 4 and 5, where we use Limber’s approximation because the source-lens clustering contributions do not vanish in this limit).
2.3. Numerical results
 |
Fig. 2 Relative source-lens clustering bias of the weak lensing convergence two-point correlation ξκκ, as a function of the angular scale θ, for the three pairs of coincident source redshifts z1 = z2 = 0.5, 1, and 2, from top to bottom. In each panel, we show the ratios ξδκδκ / | ξκκ | (lower black line), ζδκκ / | ξκκ | (middle red line), and ηδδκκ / | ξκκ | (upper blue line). The spike for ζδκκ is due to a change of sign and this contribution to the bias is negative at large angles (in all figures in this paper, a positive/negative bias is shown by a solid/dotted line). |
 |
Fig. 3 Same as in Fig. 2, but for pairs of different source redshifts, (z1,z2) = (0.5,1), (0.5,2), and (1,2). The contribution ηδδκκ is negative as shown by the dotted line. |
 |
Fig. 4 Relative source-lens clustering bias of the weak lensing convergence two-point correlation, (ξδκδκ + ζδκκ + ηδδκκ) / | ξκκ |, as a function of the second galaxy redshift z2, for a fixed first galaxy redshift z1 = 0.5,1, or 2. We consider the angular scales θ = 1, 10, and 100 arcmin, from the upper to the lower panels. All total biases are positive. |
We show our results for cases where the two galaxy redshifts are the same in Fig. 2. Throughout this paper, a positive (resp. negative) bias is shown by a solid (resp. dotted) line in the figures.
On small angular scales, the total bias is dominated by the four-point correlation contribution (17), because it scales as ξ3 and grows faster than the other terms in the nonlinear regime. This arises from correlations between the two nearby source galaxies and close density fluctuations on the two lines of sight. On very large scales, the bias is dominated by the first term in Eq. (13), which does not depend on the angular scale θ because it arises from the correlation between each galaxy and density fluctuations along its line of sight, whereas the other terms and the weak lensing signal ξκκ itself decrease for larger angles θ as they involve correlations between the two lines of sight.
In all cases, the last three terms in Eq. (10) only give rise to a relative bias of the weak lensing estimator that is smaller than about 10-4. This can be safely neglected for all practical purposes. This is due to the fact that:
-
(a)
this bias only arises from density fluctuations close to thesource galaxies, whereas the weak lensing signal is generated bydensity fluctuations along the whole line of sight,
-
(b)
the lensing efficiency g(χi′,χi) of Eq. (9) vanishes at the source plane, χi′ = χi, which further suppresses the bias by a factor of order x0/(c / H0), where x0 ~ 8 h-1 Mpc is the typical correlation length, and
-
(c)
the bias scales as ξ2 whereas the signal scales as ξ.
We show our results for cases where the two galaxy redshifts are different in Fig. 3. Let us choose for instance z1 < z2. Then, the contribution ξδκδκ is now always dominated by the first term in Eq. (13), because the correlation ξ2,1′ in the second term in Eq. (13) is very small since z1′ ≤ z1 < z2. Nevertheless, this gives an overall contribution ξδκδκ to the relative bias that is again smaller than about 10-5, as for the similar coincident redshifts of Fig. 2. In contrast, the four-point correlation η1,2,1′,2′ and its bias contribution (17) are now very small, several orders of magnitude below the corresponding contribution obtained for similar coincident redshifts, as expected because it involves correlations between density fields at different redshifts. The only significant contribution that is left is the first term in Eq. (15), which involves the three-point correlation ζ1,1′,2′, because it is still possible for the three points { 1,1′,2′ } to be located at about the same redshift. Moreover, this contribution is now much greater than for coincident redshifts and can reach 1%. This is because this contribution is dominated by configurations where the points 1′ and 2′ are at about the redshift z1, and while the lensing kernel g1′,1 is still suppressed by a factor of order x0 / (c/H0), the kernel g2′,2 is now of the same order as its typical value along the line of sight to galaxy 2, because z2′ is now significantly different from z2 since z2′ ≃ z1 < z2.
To see more clearly the redshift dependence of the source-lens clustering bias, we show our results as a function of the second galaxy redshift z2, for a fixed first galaxy redshift z1, in Fig. 4. In agreement with the discussion above, the relative bias (ξδκδκ + ζδκκ + ηδδκκ) / ξκκ is minimum for z2 = z1 because of the vanishing of both lensing kernels g1′,1 and g2′,2 for z1′ = z2′ = z1 = z2. For z2 ≫ z1, the lensing signal ξκκ saturates because it is dominated by density fluctuations in the common redshift range, z1′ ≃ z2′ ≤ min(z1,z2) = z1, whereas the bias is dominated by the three-point correlation ζ1,1′,2′ (with a similar kernel g2′,2), so that the relative bias also saturates and remains small. For z2 ≪ z1, the lensing signal decreases with the length of the common redshift range, z1′ ≃ z2′ ≤ min(z1,z2) = z2, while the bias is dominated by the three-point correlation ζ2,2′,1′. This leads to a steep growth of the relative bias for very small z2 (because the short line of sight diminishes the signal, which only arises from scales where the three-point correlation is significant and contributes to the bias). The comparison between the panels shows that the relative amplitude of the bias decreases on larger angular scales, because the three-point correlation is smaller.
Thus, most of the source-lens clustering bias arises from the three-point correlation between a low-redshift source galaxy, nearby density fluctuations on its line of sight, and density fluctuations at about the same redshift on the line of sight to a second higher redshift source galaxy. Figure 4 shows that this source-lens clustering bias is almost always negligible, except when we cross-correlate the gravitational lensing distortions of a low-redshift galaxy, z2 ≲ 0.2, with a higher redshift galaxy, z1 ≳ 0.5 (the effect being larger for higher z1 and smaller θ). There, the bias can actually dominate the weak lensing signal.
3. Two-point cosmic shear correlation function
3.1. Weak lensing shear γ
The measure of the convergence κ from galaxy surveys is not easy, because galaxies do not have a unique luminosity that could serve as a standard candle. In practice, one rather measures the two-point correlation function of the cosmic shear from the galaxy ellipticities, as in Eq. (1). Using in the following the flat sky approximation (which is sufficient for small angular scales), the shear γ is given by 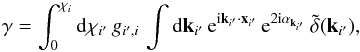 (25)where
(25)where 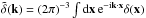 is the Fourier transform of the density contrast, xi′ = (χi′,χi′θi′) is the position of point i′ along the line of sight, and αk is the polar angle of the wave vector k in the plane that is orthogonal to the line of sight. The shear γ is a complex quantity, γ = γx + iγy, where γx and γy are the real components along the two axis ex and ey in the transverse plane. Because of the factor e2iαk, it is also a spin-2 quantity (Bartelmann & Schneider 2001; Munshi et al. 2008). This additional factor makes the computations somewhat heavier than for the convergence κ. From the shear γ one may compute several correlation functions, such as ⟨γγ∗⟩, ⟨γxγx⟩, ⟨γyγy⟩, ⟨γtγt⟩, ⟨γ×γ×⟩, where γt and γ× are the tangential and cross-components, with respect to the direction of the pair in the transverse plane. They can all be expressed in terms of the convergence two-point correlation (11) and have similar magnitudes (Kaiser 1992; Bartelmann & Schneider 2001; Munshi et al. 2008). For our purposes we focus on the full shear correlation, ⟨γγ∗⟩, as in Eq. (1). Then, in a fashion similar to Eq. (7), the average of this estimator writes as
is the Fourier transform of the density contrast, xi′ = (χi′,χi′θi′) is the position of point i′ along the line of sight, and αk is the polar angle of the wave vector k in the plane that is orthogonal to the line of sight. The shear γ is a complex quantity, γ = γx + iγy, where γx and γy are the real components along the two axis ex and ey in the transverse plane. Because of the factor e2iαk, it is also a spin-2 quantity (Bartelmann & Schneider 2001; Munshi et al. 2008). This additional factor makes the computations somewhat heavier than for the convergence κ. From the shear γ one may compute several correlation functions, such as ⟨γγ∗⟩, ⟨γxγx⟩, ⟨γyγy⟩, ⟨γtγt⟩, ⟨γ×γ×⟩, where γt and γ× are the tangential and cross-components, with respect to the direction of the pair in the transverse plane. They can all be expressed in terms of the convergence two-point correlation (11) and have similar magnitudes (Kaiser 1992; Bartelmann & Schneider 2001; Munshi et al. 2008). For our purposes we focus on the full shear correlation, ⟨γγ∗⟩, as in Eq. (1). Then, in a fashion similar to Eq. (7), the average of this estimator writes as 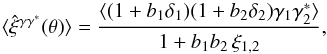 (26)where again the indices 1 and 2 refer to the two lines of sight separated by the angular distance θ. This average can be split into four components,
(26)where again the indices 1 and 2 refer to the two lines of sight separated by the angular distance θ. This average can be split into four components, 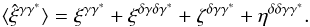 (27)The first component is again the weak lensing signal and it is equal to the convergence correlation (11),
(27)The first component is again the weak lensing signal and it is equal to the convergence correlation (11), 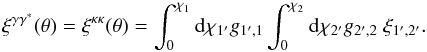 (28)The second component involves products of the two-point correlations between the galaxies and the density fluctuations along the line of sight,
(28)The second component involves products of the two-point correlations between the galaxies and the density fluctuations along the line of sight,  (29)As compared with Eq. (12), there is no term
(29)As compared with Eq. (12), there is no term 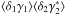 because it vanishes thanks to the spin-2 factor ei2α. This is not the case for the cross term
because it vanishes thanks to the spin-2 factor ei2α. This is not the case for the cross term 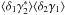 , where each product breaks the rotational invariance as it connects two different lines of sight (which defines a prefered direction) and the final contribution is nonzero (this direction is the same for the two terms so that averaging over the direction θ does not yield a null result).
, where each product breaks the rotational invariance as it connects two different lines of sight (which defines a prefered direction) and the final contribution is nonzero (this direction is the same for the two terms so that averaging over the direction θ does not yield a null result).
Whereas scalar quantities like the convergence only involve the matter density two-point correlation function, ξ(x), which is the the Fourier transform of the power spectrum, 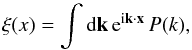 (30)for quantities that involve the spin-2 cosmic shear, we also need the integral with a spin-2 factor e2iαk,
(30)for quantities that involve the spin-2 cosmic shear, we also need the integral with a spin-2 factor e2iαk, 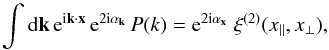 (31)where x∥ and x⊥ are the longitudinal and transverse components of the separation vector x with respect to the line of sight. As shown in Appendix A.1, this correlation function reads as
(31)where x∥ and x⊥ are the longitudinal and transverse components of the separation vector x with respect to the line of sight. As shown in Appendix A.1, this correlation function reads as 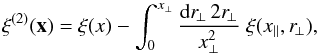 (32)and ξ(2)(x) = 0 if x⊥ = 0. Then, Eq. (29) also reads as (see Appendix A.1)
(32)and ξ(2)(x) = 0 if x⊥ = 0. Then, Eq. (29) also reads as (see Appendix A.1) 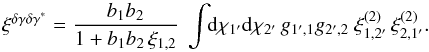 (33)As compared with Eq. (13), the first product ξ1,1′ξ2,2′ vanishes because of the spin-2 factor ei2α, as explained above, whereas in the second product ξ1,2′ξ2,1′ the scalar correlation ξ is replaced by the “spin-2 correlation” ξ(2). Because of the subtraction in Eq. (32), associated with the constraint ξ(2)(x) = 0 if x⊥ = 0, | ξ(2) | is usually smaller than | ξ |. Therefore, the spin-2 factor ei2α decreases the amplitude of the source-lens clustering bias of the cosmic shear, as compared with the convergence.
(33)As compared with Eq. (13), the first product ξ1,1′ξ2,2′ vanishes because of the spin-2 factor ei2α, as explained above, whereas in the second product ξ1,2′ξ2,1′ the scalar correlation ξ is replaced by the “spin-2 correlation” ξ(2). Because of the subtraction in Eq. (32), associated with the constraint ξ(2)(x) = 0 if x⊥ = 0, | ξ(2) | is usually smaller than | ξ |. Therefore, the spin-2 factor ei2α decreases the amplitude of the source-lens clustering bias of the cosmic shear, as compared with the convergence.
The third and fourth components involve the three- and four-point density correlations and read as 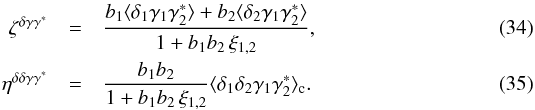 For instance, using Eq. (25), the first average that enters the numerator in Eq. (34) reads as
For instance, using Eq. (25), the first average that enters the numerator in Eq. (34) reads as 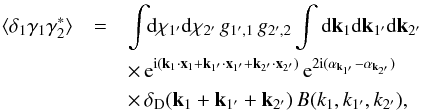 (36)where B(k1,k2,k3;z) is the matter density bispectrum. Because this contribution is dominated by configurations where the points { 1,1′,2′ } are nearby and at almost the same redshift (otherwise the three-point correlation is negligible), the bispectrum can be taken at the mean redshift of these three points.
(36)where B(k1,k2,k3;z) is the matter density bispectrum. Because this contribution is dominated by configurations where the points { 1,1′,2′ } are nearby and at almost the same redshift (otherwise the three-point correlation is negligible), the bispectrum can be taken at the mean redshift of these three points.
 |
Fig. 5 Relative source-lens clustering bias of the weak lensing shear two-point correlation ξγγ∗, as a function of the angular scale θ, for the three pairs of coincident source redshifts z1 = z2 = 0.5, 1, and 2. The lower curves show the two-point contribution (33) and the upper curves the three-point contribution (34). The spike for ζδγγ∗ is due to a change of sign and at large angles this contribution to the bias is negative (dotted lines). |
 |
Fig. 6 Same as in Fig. 5, but for pairs of different source redshifts, (z1,z2) = (0.5,1), (0.5,2), and (1,2). Solid lines correspond to positive bias and dotted lines to negative bias. |
 |
Fig. 7 Relative source-lens clustering bias of the weak lensing shear two-point correlation, (ξδγδγ∗ + ζδγγ∗) / | ξγγ∗ | (we neglect the four-point contribution), as a function of the second galaxy redshift z2, for a fixed first galaxy redshift z1 = 0.5,1, or 2. We consider the angular scales θ = 1, 10, and 100 arcmin, from the upper to the lower panels. |
3.2. Analytical approximations
For the shear, computations are not as straightforward because of the spin-2 factor e2iα. As we have seen in Sect. 2.3, the source-lens clustering bias is only important when we correlate a high-redshift galaxy, z2 ≳ 0.5, with a low-redshift galaxy, z1 ≲ 0.2. Then, the bias is dominated by the first term in Eq. (34), which involves the three-point correlation between the low-redshift galaxy with density fluctuations at almost the same redshift on the two lines of sight. Therefore, we neglect the four-point contribution (35) and we only consider the contributions (33) and (34). In Fourier space, neglecting the scale dependence of the coefficient S3, the ansatz (18) yields the factorized bispectrum ![\begin{eqnarray} B(k_1,k_2,k_3) & = & \frac{S_3}{3} [ P(k_2) P(k_3) + P(k_1) P(k_3) + P(k_1) P(k_2) ] . \label{bispectrum-def} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22146-13/aa22146-13-eq216.png) (37)As described in Appendix A.2, substituting the ansatz (37) into Eq. (36) gives
(37)As described in Appendix A.2, substituting the ansatz (37) into Eq. (36) gives ![\begin{equation} \lag \delta_1 \gamma_1 \gamma_2^* \rag = \int \!\! \dd\chi_{1'} \dd\chi_{2'} \, g_{1',1} \, g_{2',2} \frac{S_3}{3} \left[ \zeta_{1,1',2'}^{(1,1')} + \zeta_{1,1',2'}^{(1,2')} \right] , \label{zeta-gamma-3} \end{equation}](/articles/aa/full_html/2014/01/aa22146-13/aa22146-13-eq217.png) (38)where
(38)where 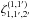 and
and 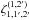 are given by Eqs. (A.11) and (A.16) (and the contribution
are given by Eqs. (A.11) and (A.16) (and the contribution 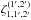 vanishes because of the spin-2 factor e2iα). A symmetric expression gives
vanishes because of the spin-2 factor e2iα). A symmetric expression gives 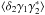 and this yields the three-point contribution (34).
and this yields the three-point contribution (34).
3.3. Numerical results
We show our results for galaxy pairs at the same redshift in Fig. 5. As compared with the case of the convergence shown in Fig. 2, the three-point contribution is somewhat smaller while the two-point contribution is several orders of magnitude smaller. This is because of the spin-2 factor that replaces the density correlation ξ by the smaller correlation ξ(2) in Eq. (33) and removes the contribution 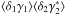 . This implies that the contribution ξδγδγ∗ now decreases at large angles θ so that the relative bias does not show the faster growth found in Fig. 2. In any case, Fig. 5 shows that as for the convergence the source-lens clustering bias is negligible for same-redshift sources.
. This implies that the contribution ξδγδγ∗ now decreases at large angles θ so that the relative bias does not show the faster growth found in Fig. 2. In any case, Fig. 5 shows that as for the convergence the source-lens clustering bias is negligible for same-redshift sources.
We show our results for cases where the two galaxy redshifts are different in Fig. 6. We find again that the three-point contribution is somewhat smaller than for the case of the convergence shown in Fig. 3, especially on small scales, where it only reaches 0.1% instead of 1%. The two-point contribution is several orders of magnitude smaller than for the convergence. This is because it only involves the cross correlation 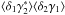 , which correlates the high-redshift galaxy 2 with low-redshift density fluctuations 1′ with z1′ ≤ z1 < z2, as the term
, which correlates the high-redshift galaxy 2 with low-redshift density fluctuations 1′ with z1′ ≤ z1 < z2, as the term 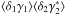 is zero by symmetry.
is zero by symmetry.
We show the dependence of the source-lens clustering bias on the second galaxy redshift z2, for a fixed first galaxy redshift z1, in Fig. 7. We obtain behaviors that are similar to those found in Fig. 4 for the convergence, with a minimum at the coincident redshift z2 = z1, a saturation at high redshift z2 ≫ z1, and a steep increase for z2 → 0 (but the bias is no longer always positive). The amplitude of the bias is somewhat smaller than in Fig. 4, especially for small angular scales. This leads to an even smaller range of redshifts at z2 ≲ 0.05 where the bias reaches 10% of the signal or more.
Therefore, as for the convergence, we find that the source-lens clustering bias of estimators of the cosmic shear two-point correlation function is almost always negligible. It is only relevant when we cross-correlate the shear of a low-redshift galaxy, z2 ≲ 0.05, with the shear of a higher redshift galaxy, z1 ≳ 0.5 (the effect being larger for higher z1 and smaller θ). For z1 ≲ 0.01, the bias can actually dominate the weak lensing signal. In practice, it would be sufficient to remove such pairs from the data analysis, because they are a very small fraction of the pairs measured in a survey and their cosmological information is highly redundant with other pairs (where both galaxies are at the same low redshift or at possibly different redshifts above 0.05).
4. Three-point convergence correlation function
4.1. Source-lens clustering bias
We now consider the impact of the source-lens clustering bias on estimators of the three-point weak lensing correlation functions. As for the two-point correlation, we first investigate the simpler case of the weak lensing convergence κ. Then, the generalization of Eqs. (2)−(7) to three-point statistics, obtained by measuring triplets of galaxies, gives 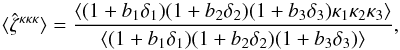 (39)for the estimator of the three-point convergence correlation. As seen in Sect. 2, because the lensing kernel g(χ′,χ) vanishes for χ′ = χ, the source-lens clustering bias is only significant when a foreground galaxy i correlates with the density fluctuations j′ along the line of sight to a background galaxy j, with zj′ ≃ zi < zj. Therefore, to simplify the analysis, we neglect correlations that correspond to a vanishing lensing efficiency kernel g (that at next order give a damping factor x0 / (c/H0) instead of zero) or that involve different redshifts. This allows us to use Limber’s approximation (which gives zero for the discarded terms). Then, assuming without loss of generality z1 ≤ z2 ≤ z3, δ1 can only be correlated with { δ2,δ3,κ2,κ3 }, δ2 with { δ1,δ3,κ3 }, and δ3 with { δ1,δ2 }. Then, the average (39) reads as
(39)for the estimator of the three-point convergence correlation. As seen in Sect. 2, because the lensing kernel g(χ′,χ) vanishes for χ′ = χ, the source-lens clustering bias is only significant when a foreground galaxy i correlates with the density fluctuations j′ along the line of sight to a background galaxy j, with zj′ ≃ zi < zj. Therefore, to simplify the analysis, we neglect correlations that correspond to a vanishing lensing efficiency kernel g (that at next order give a damping factor x0 / (c/H0) instead of zero) or that involve different redshifts. This allows us to use Limber’s approximation (which gives zero for the discarded terms). Then, assuming without loss of generality z1 ≤ z2 ≤ z3, δ1 can only be correlated with { δ2,δ3,κ2,κ3 }, δ2 with { δ1,δ3,κ3 }, and δ3 with { δ1,δ2 }. Then, the average (39) reads as 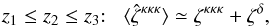 (40)where the source-lens clustering contribution (that we denote with the superscript δ) writes as
(40)where the source-lens clustering contribution (that we denote with the superscript δ) writes as ![\begin{eqnarray} \zeta^{\delta} & = & \left[ b_1 b_2 \lag\delta_1\delta_2\kappa_3\rag \lag\kappa_1\kappa_2\rag + (1 \!+\! b_1 b_3 \xi_{1,3} ) b_2 \lag\delta_2\kappa_3\rag \lag\kappa_1\kappa_2\rag \right. \nonumber \\ && \left. + ( 1 \!+\! b_2 b_3 \xi_{2,3} ) b_1 ( \lag\delta_1\kappa_2\rag \lag\kappa_1\kappa_3\rag \!+\! \lag\delta_1\kappa_3\rag \lag\kappa_1\kappa_2\rag ) \right] \nonumber \\ && \times \left[ 1 \!+\! b_1 b_2 \xi_{1,2} \!+\! b_2 b_3 \xi_{2,3} \!+\! b_1 b_3 \xi_{1,3} \!+\! b_1 b_2 b_3 \zeta_{1,2,3} \right]^{-1} \!. \label{hzeta-kappa-2} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22146-13/aa22146-13-eq240.png) (41)Here we note again ξi,j = ⟨δiδj⟩ the density-density correlation (which arises from the galaxy-galaxy correlations).
(41)Here we note again ξi,j = ⟨δiδj⟩ the density-density correlation (which arises from the galaxy-galaxy correlations).
In contrast with the case of the two-point estimator (10), the source-lens clustering bias is no longer dominated by contributions that involve the density three-point correlation, but by contributions that involve products of the density two-point correlation. In particular, for the generic case of three different source redshifts, the galaxy-galaxy correlations are negligible and Eq. (41) simplifies as 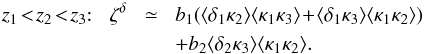 (42)Therefore, the source-lens clustering bias is much easier to evaluate for the three-point convergence correlation functions than for the two-point statistics studied in Sects. 2 and 3. Nevertheless, in the following we use Eq. (41) to include the case where galaxy redshifts coincide.
(42)Therefore, the source-lens clustering bias is much easier to evaluate for the three-point convergence correlation functions than for the two-point statistics studied in Sects. 2 and 3. Nevertheless, in the following we use Eq. (41) to include the case where galaxy redshifts coincide.
On large scales, whereas in Eq. (10) the two-point weak lensing signal ξκκ scales as the linear density correlation ξL and the bias ζδκκ obeys the higher-order scaling 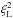 , in Eq. (42) the three-point weak lensing signal ζκκκ and its bias ⟨δκ⟩ ⟨κκ⟩ show the same scaling
, in Eq. (42) the three-point weak lensing signal ζκκκ and its bias ⟨δκ⟩ ⟨κκ⟩ show the same scaling 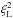 . Therefore, the impact of the source-lens clustering bias is expected to be greater for measures of three-point lensing correlations than for two-point lensing correlations (see also Bernardeau 1998).
. Therefore, the impact of the source-lens clustering bias is expected to be greater for measures of three-point lensing correlations than for two-point lensing correlations (see also Bernardeau 1998).
The first contribution in Eq. (40) is the weak lensing signal,  (43)Using Limber’s approximation (Limber 1953; Kaiser 1992; Munshi et al. 2008), that is, neglecting the variation of the lensing kernels g on scales where the density correlations are not negligible, this writes as
(43)Using Limber’s approximation (Limber 1953; Kaiser 1992; Munshi et al. 2008), that is, neglecting the variation of the lensing kernels g on scales where the density correlations are not negligible, this writes as 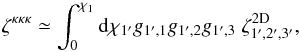 (44)where we introduced the 2D three-point density correlation obtained by integrating along two lines of sight,
(44)where we introduced the 2D three-point density correlation obtained by integrating along two lines of sight, 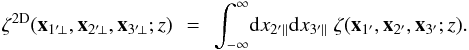 (45)Using again Limber’s approximation, the two-point functions that enter Eq. (41) read as (for z1 ≤ z2),
(45)Using again Limber’s approximation, the two-point functions that enter Eq. (41) read as (for z1 ≤ z2), 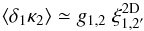 (46)and
(46)and 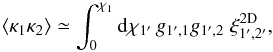 (47)where we introduced the 2D two-point density correlation obtained by integrating along one line of sight,
(47)where we introduced the 2D two-point density correlation obtained by integrating along one line of sight, 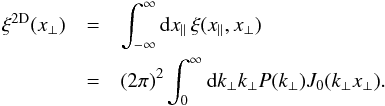 (48)The term ⟨δ1δ2κ3⟩ in Eq. (41) is only significant for the rare cases where | z2 − z1 | ≲ x0 / (c/H0). Therefore, it is sufficient to use the ansatz (18) (which we compare with a more precise model in App. D). This gives
(48)The term ⟨δ1δ2κ3⟩ in Eq. (41) is only significant for the rare cases where | z2 − z1 | ≲ x0 / (c/H0). Therefore, it is sufficient to use the ansatz (18) (which we compare with a more precise model in App. D). This gives ![\begin{eqnarray} \lag\delta_1\delta_2\kappa_3\rag \!\! & \simeq & \!\! \frac{S_3}{3} \left[ \xi_{1,2} \left( \lag\delta_1\kappa_3\rag \!+\! \lag\delta_2\kappa_3\rag \right) \! + \!\! \int \!\! \dd\chi_{3'} \, g_{3',3} \, \xi_{3',1} \xi_{3',2} \right] \! . \label{zeta-d1d2k3} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22146-13/aa22146-13-eq256.png) (49)
(49)
4.2. Numerical computations
 |
Fig. 8 Relative source-lens clustering bias of the equilateral weak lensing convergence three-point correlation |
 |
Fig. 9 Relative source-lens clustering bias of the equilateral weak lensing convergence three-point correlation |
As shown in Eqs. (41), (42), the source-lens clustering bias of three-point lensing statistics is dominated by terms that only involve the two-point matter and galaxy correlation functions. Therefore, the density three-point correlation is mainly needed to compute the lensing signal to estimate the relative amplitude of the source-lens clustering bias. Nevertheless, because this bias is no longer negligible, in contrast with the case of two-point statistics studied in Sects. 2 and 3, it is useful to go beyond orders of magnitude estimates for the three-point lensing correlation. Therefore, instead of the ansatz (18) we now use the more accurate modeling described in Valageas & Nishimichi (2011b). It combines one-loop standard perturbation theory and a halo model to predict the density 3D bispectrum and three-point correlation. This provides in turn the weak lensing bispectrum and three-point correlation and gives a good agreement with ray-tracing numerical simulations (Valageas et al. 2012a,b). (In this model, the bispectrum is split as usual as a sum of three-halo, two-halo, and one-halo contributions. The three-halo term is identified with the perturbative contribution and is given by the standard one-loop perturbation theory. The two-halo term involves the correlation between halos (taken proportional to the linear correlation), as well as the halo profiles (we use the NFW profile from Navarro et al. 1997) and mass function (as in Valageas & Nishimichi 2011a), which also fully determine the one-halo term.)
We also compared these results with the ansatz (18), where ![\begin{equation} \zeta^{\rm 2D}_{1',2',3'} \simeq \frac{S_3}{3} \left[ \xi^{\rm 2D}_{1',2'} \xi^{\rm 2D}_{1',3'} + \xi^{\rm 2D}_{2',1'} \xi^{\rm 2D}_{2',3'} + \xi^{\rm 2D}_{3',1'} \xi^{\rm 2D}_{3',2'} \right] , \label{zeta-kappa-3} \end{equation}](/articles/aa/full_html/2014/01/aa22146-13/aa22146-13-eq260.png) (50)and found that both approximations agree to better than a factor 1.5 for θ < 10′ and a factor 3 for θ < 40′, as illustrated in Fig. D.1. The agreement degrades on large scales because they do not change sign at exactly the same scale, which gives rise to large relative deviations around the scale where either one prediction goes through zero. However, this is not a serious problem for such purposes, because the three-point convergence correlation becomes very small on large scales and most of the information from weak lensing surveys comes from smaller scales, θ ≲ 10′, where the signal can be discriminated from the different sources of noise (Semboloni et al. 2011). Thus, the simple approximation (50), which enables fast and simple numerical computations, would actually be sufficient to estimate the magnitude of the convergence three-point correlation, whence of the relative bias.
(50)and found that both approximations agree to better than a factor 1.5 for θ < 10′ and a factor 3 for θ < 40′, as illustrated in Fig. D.1. The agreement degrades on large scales because they do not change sign at exactly the same scale, which gives rise to large relative deviations around the scale where either one prediction goes through zero. However, this is not a serious problem for such purposes, because the three-point convergence correlation becomes very small on large scales and most of the information from weak lensing surveys comes from smaller scales, θ ≲ 10′, where the signal can be discriminated from the different sources of noise (Semboloni et al. 2011). Thus, the simple approximation (50), which enables fast and simple numerical computations, would actually be sufficient to estimate the magnitude of the convergence three-point correlation, whence of the relative bias.
4.3. Numerical results
We show our results for equilateral configurations in Fig. 8, as a function of the angular width θ of the triangle sides. On these scales, the source-lens clustering bias is typically of order 10% for the convergence three-point correlation. Within the Limber approximation, the source-lens clustering bias is nonzero as soon as the three galaxy redshifts are not identical (as explained in Sect. 4.1, to obtain a better estimate at identical redshifts one needs to go beyond the Limber approximation, which will however give a small bias because of the suppression factor x0 / (c/H0)).
On small scales, the relative bias is somewhat higher for the cases where z1 = z2. This is due to the term ⟨δ1δ2κ3⟩ ⟨κ1κ2⟩ in Eq. (41), which is only significant when z1 ≃ z2. Moreover, this contribution typically scales as ξ3 because it involves the product of a three-point and a two-point correlations, see also Eq. (49). This leads to a significant growth on small scales provided the condition z1 ≃ z2 is satisfied.
We show the redshift dependence of the source-lens clustering bias in Fig. 9 (here we no longer have the ordering z1 ≤ z2 ≤ z3 since we let z3 vary from 0 to 2 at fixed { z1,z2 }). The upward spikes correspond to redshifts z3 such that the two lowest redshifts of the triplet { z1,z2,z3 } are equal. As explained above for Fig. 8, this is due to the clustering of the two foreground galaxies with nearby density fluctuations on the third line of sight, through the factor ⟨δ1δ2κ3⟩ ⟨κ1κ2⟩ in Eq. (41). This effect occurs in a narrow redshift band of width x0 / (c/H0) set by the galaxy correlation length. Therefore, for generic galaxy redshifts drawn from actual surveys, this amplification should be rare and the typical bias is of order 10%. The right panels in Fig. 9 correspond to closer pairs { z1,z2 }. We obtain similar results as in the left panels but with a broad valley as z3 becomes close to the pair { z1,z2 }. This is due to the effect of the lensing kernels gi′,i that vanish on the source plane and lead to a zero bias when z1 = z2 = z3 within our approximations. This yields suppression factors x0 / (c / H0) and a decrease of the bias for z1 ≃ z2 ≃ z3, as found in Sects. 2 and 3 in the case z1 ≃ z2 for two-point estimators. When z3 = min(z1,z2) we recover the localized upward spike. When z3 is far from the pair { z1,z2 } we recover a bias of about 10% of the signal as in the left panels.
As for the case of the convergence two-point correlation shown in Fig. 4, the bias becomes more important as one of the galaxies lies at a small redshift. Indeed, the shorter line of sight decreases the signal, as in Eq. (44), and lessens the impact of the suppression factor x0 / (c / H0) associated with the source-lens clustering. Then, for θ ≲ 1′ the bias becomes of the same order as the signal for z1 ≲ 0.1.
5. Three-point cosmic shear correlation function
5.1. Source-lens clustering bias
We now consider the three-point correlation function of the cosmic shear γ. Because of the spin-2 factor e2iα computations are somewhat heavier. To simplify the analysis we focus on the geometrical average 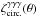 ,
, 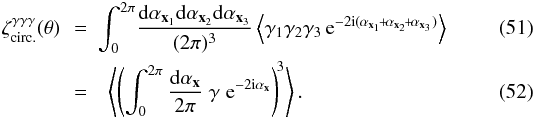 Here αxi is again the polar angle of the line of sight to the galaxy i. The exponential factors in the term ⟨..⟩ ensure that the full product is a spin-0 quantity and does not vanish by symmetry. In Eq. (51), the three lines of sight are at the same angular separation θ from a fixed center O and we integrate over their angles αxi with respect to this central point. Therefore,
Here αxi is again the polar angle of the line of sight to the galaxy i. The exponential factors in the term ⟨..⟩ ensure that the full product is a spin-0 quantity and does not vanish by symmetry. In Eq. (51), the three lines of sight are at the same angular separation θ from a fixed center O and we integrate over their angles αxi with respect to this central point. Therefore, 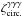 is the geometrical mean of the shear three-point correlation ζγγγ over all triangles with a circumcircle of radius θ. (It is identical to the correlations
is the geometrical mean of the shear three-point correlation ζγγγ over all triangles with a circumcircle of radius θ. (It is identical to the correlations 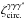 (where the factor e− 2iαx3 is changed to e2iαx3),
(where the factor e− 2iαx3 is changed to e2iαx3), 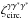 , and
, and 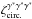 .) The fully symmetric three-point correlation (51) provides simpler expressions than the correlation ζγγγ(θ12,θ23,θ31), associated with a single triangular shape, thanks to the independent integrations over the polar angles αxi. As shown by the second equality (52), this is also the third-order cumulant of the complex aperture mass M (with a Dirac weight), the usual E-mode aperture mass Map being defined as Map = Re(M), which can be expressed in terms of the tangential shear γt (Schneider et al. 1998; Jarvis et al. 2004; Schneider et al. 2005). Here we have
.) The fully symmetric three-point correlation (51) provides simpler expressions than the correlation ζγγγ(θ12,θ23,θ31), associated with a single triangular shape, thanks to the independent integrations over the polar angles αxi. As shown by the second equality (52), this is also the third-order cumulant of the complex aperture mass M (with a Dirac weight), the usual E-mode aperture mass Map being defined as Map = Re(M), which can be expressed in terms of the tangential shear γt (Schneider et al. 1998; Jarvis et al. 2004; Schneider et al. 2005). Here we have 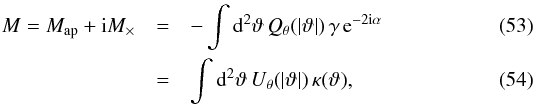 with
with 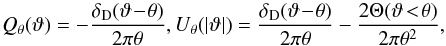 (55)where Θ(ϑ < θ) is the unit top-hat. As is well known, gravitational lensing only gives rise to E modes, so that M× = 0 as seen from Eq. (54), within the Born approximation. Then
(55)where Θ(ϑ < θ) is the unit top-hat. As is well known, gravitational lensing only gives rise to E modes, so that M× = 0 as seen from Eq. (54), within the Born approximation. Then 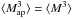 . However, this is no longer the case when we include additional observational effects, such as source clustering (Schneider et al. 2002) or galaxy intrinsic alignments (this depends on the properties of the latter, e.g., whether they follow a linear or quadratic dependence on the density field, Crittenden et al. 2001). Here we do not investigate the E/B modes separation and focus on the overall amplitude of the source-lens clustering bias as compared with the gravitational lensing signal and the intrinsic-alignment bias.
. However, this is no longer the case when we include additional observational effects, such as source clustering (Schneider et al. 2002) or galaxy intrinsic alignments (this depends on the properties of the latter, e.g., whether they follow a linear or quadratic dependence on the density field, Crittenden et al. 2001). Here we do not investigate the E/B modes separation and focus on the overall amplitude of the source-lens clustering bias as compared with the gravitational lensing signal and the intrinsic-alignment bias.
Using the vanishing of the lensing kernel g on the source plane as in Sect. 4.1, Eqs. (40) and (41) become 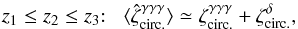 (56)and
(56)and ![\begin{eqnarray} \zeta^{\delta}_{\rm circ.} \!\!\!\! & = & \!\! \left[ b_1 b_2 \lag\delta_1\delta_2\gamma_3\rag_{\alpha} \lag\gamma_1\gamma_2\rag_{\alpha} \!+\! (1 \!+\! b_1 b_3 \xi_{1,3} ) b_2 \lag\delta_2\gamma_3\rag_{\alpha} \lag\gamma_1\gamma_2\rag_{\alpha} \right. \nonumber \\ && \left. + ( 1 \!+\! b_2 b_3 \xi_{2,3} ) b_1 ( \lag\delta_1\gamma_2\rag_{\alpha} \lag\gamma_1\gamma_3\rag_{\alpha} \!+\! \lag\delta_1\gamma_3\rag_{\alpha} \lag\gamma_1\gamma_2\rag_{\alpha} ) \right] \nonumber \\ && \times \left[ 1 \!+\! b_1 b_2 \xi_{1,2} \!+\! b_2 b_3 \xi_{2,3} \!+\! b_1 b_3 \xi_{1,3} \!+\! b_1 b_2 b_3 \zeta_{1,2,3} \right]^{-1} \! . \label{hzeta-gamma-2} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22146-13/aa22146-13-eq298.png) (57)The subscripts “α” denote the factors e− 2iαxi and the integrations over the angles αxi, as in Eq. (51). To simplify the computations, we only perform the geometrical average (51) for the terms that involve the shear γ and we factor out the galaxy-galaxy correlations ξi,j by simply using their values at the angular scale θ. This should be sufficient for our purposes because, as seen in the previous sections, these terms are only important when zi = zj. Again, for the generic case where the three galaxy redshifts are different, Eq. (57) simplifies as
(57)The subscripts “α” denote the factors e− 2iαxi and the integrations over the angles αxi, as in Eq. (51). To simplify the computations, we only perform the geometrical average (51) for the terms that involve the shear γ and we factor out the galaxy-galaxy correlations ξi,j by simply using their values at the angular scale θ. This should be sufficient for our purposes because, as seen in the previous sections, these terms are only important when zi = zj. Again, for the generic case where the three galaxy redshifts are different, Eq. (57) simplifies as 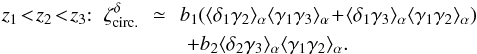 (58)Thus, the source-lens clustering bias of the shear three-point correlation is dominated by contributions that only involve the density two-point correlation.
(58)Thus, the source-lens clustering bias of the shear three-point correlation is dominated by contributions that only involve the density two-point correlation.
The first contribution in Eq. (56) is the weak lensing signal. Using Limber’s approximation, it reads as (for z1 ≤ z2 ≤ z3) 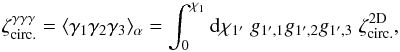 (59)with
(59)with ![\begin{eqnarray} \zeta_{\rm circ.}^{\rm 2D} & = & \int_{-\infty}^{\infty} \dd x_{2'\parallel} \dd x_{3'\parallel} \int_0^{2\pi} \! \frac{\dd\alpha_{\vx_1}\dd\alpha_{\vx_2}\dd\alpha_{\vx_3}}{(2\pi)^3} \nonumber \\ && \hspace{-0.cm} \times \int \dd\vk_{1'}\dd\vk_{2'}\dd\vk_{3'} \; {\rm e}^{\ii [ \vk_{1'}\cdot\vx_{1'}+\vk_{2'}\cdot\vx_{2'}+\vk_{3'}\cdot\vx_{3'}]} \nonumber \\ && \hspace{-0.cm} \times \; \delta_{\rm D}(\vk_{1'}+\vk_{2'}+\vk_{3'}) \; B(k_{1'},k_{2'},k_{3'}) \; \nonumber \\ && \hspace{-0.cm} \times \; {\rm e}^{2\ii (\alpha_{\vec{k}_{1'}}+\alpha_{\vk_{2'}}+\alpha_{\vk_{3'}} - \alpha_{\vx_1} - \alpha_{\vx_2} - \alpha_{\vx_3})} . \label{zetap-circ-B} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22146-13/aa22146-13-eq303.png) (60)Expressing the bispectrum in terms of the density three-point correlation and using Eq. (A.4) this also writes as
(60)Expressing the bispectrum in terms of the density three-point correlation and using Eq. (A.4) this also writes as ![\begin{eqnarray} \zeta_{\rm circ.}^{\rm 2D} & = & \int \frac{\dd \vr_{1\perp} \dd \vr_{2\perp} \dd \vr_{3\perp}}{(2\pi)^3} \; \zeta^{\rm 2D}(\vr_{1\perp},\vr_{2\perp},\vr_{3\perp}) \nonumber \\ && \times \prod_{i\,=\,1}^3 \left[ \frac{\delta_{\rm D}(r_{i\perp}-d)}{d} - \frac{2 \, \Theta(r_{i\perp}<d)}{d^2} \right] , \label{zetap-circ-zeta2D} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22146-13/aa22146-13-eq304.png) (61)where d = χ1′θ is the radius of the circumcircle at radial distance χ1′, Θ(ri ⊥ < d) is the unit top-hat, and ζ2D is the 2D three-point density correlation introduced in Eq. (45). This could be obtained at once from Eqs. (54) and (55).
(61)where d = χ1′θ is the radius of the circumcircle at radial distance χ1′, Θ(ri ⊥ < d) is the unit top-hat, and ζ2D is the 2D three-point density correlation introduced in Eq. (45). This could be obtained at once from Eqs. (54) and (55).
Thus, as compared with the circular average 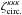 of the three-point convergence correlation, the shear introduces a non-local dependence. As for the two-point “spin-2” correlation (32), this comes through a counterterm that involves the integral of the two- or three-point correlation over smaller angular scales. This decreases the amplitude of the weak lensing signal, as compared with the convergence case. For instance, if we generalize the geometrical average (51) to
of the three-point convergence correlation, the shear introduces a non-local dependence. As for the two-point “spin-2” correlation (32), this comes through a counterterm that involves the integral of the two- or three-point correlation over smaller angular scales. This decreases the amplitude of the weak lensing signal, as compared with the convergence case. For instance, if we generalize the geometrical average (51) to 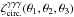 , so that the three lines of sight { x1,x2,x3 } are at different radii { θ1,θ2,θ3 } from a given center, we can see from the generalization of Eq. (61) that
, so that the three lines of sight { x1,x2,x3 } are at different radii { θ1,θ2,θ3 } from a given center, we can see from the generalization of Eq. (61) that 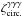 goes to zero when one radius θi vanishes while the other two radii remain finite (because ζ2D(r1 ⊥,r2 ⊥,r3 ⊥) remains finite in this limit). This is related to the well-known property that the aperture mass (53) can be written in terms of the convergence with a compensated window function Uθ, as in Eq. (54).
goes to zero when one radius θi vanishes while the other two radii remain finite (because ζ2D(r1 ⊥,r2 ⊥,r3 ⊥) remains finite in this limit). This is related to the well-known property that the aperture mass (53) can be written in terms of the convergence with a compensated window function Uθ, as in Eq. (54).
Therefore, in contrast with measures of the two-point correlation, where ξγγ∗ = ξκκ in Eq. (28), for the three-point statistics the spin-2 factor e2iα of the shear does not fully cancel (because the three-point Dirac factor δD(k1 + k2 + k3) no longer ensures e2i(αk1 + αk2 + αk3) = 1). This yields a smaller signal and a non-local dependence in terms of real-space correlations. Nevertheless, for the circular statistics 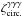 this non-locality does not extend to the whole transverse plane. It only involves the three point function ζ2D within radius θ, with simple weights, and
this non-locality does not extend to the whole transverse plane. It only involves the three point function ζ2D within radius θ, with simple weights, and 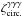 could still provide a good probe of ζ2D.
could still provide a good probe of ζ2D.
The term ⟨δ1γ2⟩ α of Eq. (57) writes as (for z1 ≤ z2) ![\begin{eqnarray} \lag\delta_1\gamma_2\rag_{\alpha} \!\! & = & \! g_{1,2} \int_{-\infty}^{\infty} \!\! \dd x_{2'\parallel} \int_0^{2\pi} \frac{\dd\alpha_{\vx_2}}{2\pi} \int \! \frac{\dd\vr}{(2\pi)^3} \int \!\! \dd\vk_1 \dd\vk_{2'} \nonumber \\ && \times \; {\rm e}^{\ii[\vk_1\cdot(\vx_1+\vr)+\vk_{2'}\cdot(\vx_{2'}+\vr)]} P(k_1) {\rm e}^{2\ii(\alpha_{\vk_{2'}}-\alpha_{\vx_2})} , \end{eqnarray}](/articles/aa/full_html/2014/01/aa22146-13/aa22146-13-eq321.png) (62)where we again assumed that variations of g2′,2 can be neglected on scales where the correlation ξ1,2′ is significant. Integrating over the longitudinal components { x2′ ∥,k2′ ∥,r∥,k1 ∥ }, and the angles { αx2,αk2′,αr,αk1 }, we obtain
(62)where we again assumed that variations of g2′,2 can be neglected on scales where the correlation ξ1,2′ is significant. Integrating over the longitudinal components { x2′ ∥,k2′ ∥,r∥,k1 ∥ }, and the angles { αx2,αk2′,αr,αk1 }, we obtain 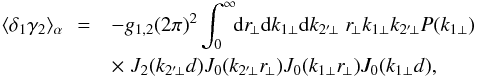 (63)where d = χ1θ. Then, writing the transverse power spectrum as in Eq. (B.4) and using the properties (A.15) and (A.4), we can perform the integrations over wavenumbers. This yields
(63)where d = χ1θ. Then, writing the transverse power spectrum as in Eq. (B.4) and using the properties (A.15) and (A.4), we can perform the integrations over wavenumbers. This yields 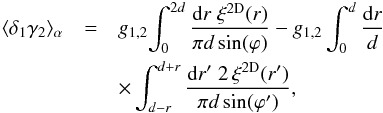 (64)where the angles ϕ and ϕ′ are given by
(64)where the angles ϕ and ϕ′ are given by 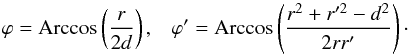 (65)In a similar fashion, the term ⟨γ1γ2⟩ α reads as (z1 ≤ z2)
(65)In a similar fashion, the term ⟨γ1γ2⟩ α reads as (z1 ≤ z2) ![\begin{eqnarray} \lag\gamma_1\gamma_2\rag_{\alpha} & \! = & - \int_0^{\chi_1} \dd\chi_{1'} \, g_{1',1} g_{1',2} \; \Bigg\{ \int_0^{2d} \frac{\dd r \, r \, \xi^{\rm 2D}(r)}{\pi d^2} \nonumber \\ && \times \left[ 2 \varphi - \frac{d}{r \sin(\varphi)} \right] - \int_0^d \frac{\dd r \, 2r}{d^2} \left( \xi^{\rm 2D}(r) \left[ \frac{d-r}{d}\right]^2 \right. \nonumber \\ && \left. + \int_{d-r}^{d+r} \frac{\dd r' \, r' \, \xi^{\rm 2D}(r')}{\pi d^2} \left[ 2 \varphi' - \frac{d^2}{r \, r' \sin(\varphi')} \right] \right) \Bigg\} , \label{xi-g1-g2} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22146-13/aa22146-13-eq332.png) (66)where we used Eq. (B.6) and the angles ϕ and ϕ′ are given by Eq. (65).
(66)where we used Eq. (B.6) and the angles ϕ and ϕ′ are given by Eq. (65).
The term ⟨δ1δ2γ3⟩ α in Eq. (57) is only significant for the rare cases where | z2 − z1 | ≲ x0 / (c/H0). Therefore, we simply use the ansatz (37), which gives ![\begin{eqnarray} \lag\delta_1\delta_2\gamma_3\rag_{\alpha} & \! \simeq & \frac{S_3}{3} \Bigg\{ \xi_{1,2} \left( \lag\delta_1\gamma_3\rag_{\alpha} \!+\! \lag\delta_2\gamma_3\rag_{\alpha} \right) + \int \dd\chi_{3'} \, g_{3',3} \nonumber \\ && \hspace{0cm} \times \int_0^{2\pi} \frac{\dd\alpha_1\dd\alpha_2}{(2\pi)^2} \int_0^{\infty} \dd x_{3' \!\perp} \, x_{3'\!\perp} \; \xi_{3',1} \xi_{3',2} \nonumber \\ && \hspace{0cm} \times \left[ \frac{\delta_{\rm D}(x_{3' \!\perp} \!-\! d)}{d} - \frac{2\Theta(x_{3' \!\perp} \!<\!d)}{d^2} \right] \Bigg\} \cdot \label{zeta-d1d2g3} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22146-13/aa22146-13-eq334.png) (67)Here d = (χ1 + χ2)θ / 2 and we made the simplifying approximation of factorizing the angular integrations over αxi of the factors ⟨δ1δ2γ3⟩ α and ⟨γ1γ2⟩ α.
(67)Here d = (χ1 + χ2)θ / 2 and we made the simplifying approximation of factorizing the angular integrations over αxi of the factors ⟨δ1δ2γ3⟩ α and ⟨γ1γ2⟩ α.
 |
Fig. 10 Relative source-lens clustering bias of the circular weak lensing shear three-point correlation |
 |
Fig. 11 Relative source-lens clustering bias of the circular weak lensing shear three-point correlation |
5.2. Numerical computations
As for the case of the weak lensing convergence, the source-lens clustering bias in Eqs. (57) and (58) mainly depends on the density two-point correlation function (within our approximations). The density three-point correlation is only needed to compute the weak lensing signal (59) (whence the relative amplitude of the bias) and the term ⟨δ1δ2γ3⟩ α in Eq. (57), which is only significant for z1 ≃ z2. To improve the accuracy of our computations, as in Sect. 4, we use the more accurate modeling described in Valageas & Nishimichi (2011b) and Valageas et al. (2012a,b), instead of the hierarchical ansatz (18), to compute the weak lensing signal (59).
Nevertheless, we also compared these results with the ansatz (37). Then, Eq. (60) also writes as Eq. (B.7), see Appendix B. This provides an expression in terms of the real-space density correlation, without oscillatory kernels and with lower-dimensional integrals.
Then, we found that both approximations agree to better than a factor 1.5 for θ < 30′, as illustrated in Fig. D.1. The three-point cosmic shear correlation function becomes very small on large scales and most of the information from weak lensing surveys comes from smaller scales, θ ≲ 10′, where the signal can be discriminated from the noise (Semboloni et al. 2011). Therefore, the simple approximation (37), whence Eq. (B.7), would be sufficient to estimate the relative importance of various sources of noise such as the source-lens clustering bias.
5.3. Numerical results
We show our results as a function of the angular radius θ in Fig. 10. As for the convergence three-point correlation shown in Fig. 8, the relative amplitude of the source-lens clustering bias is of order 10%. However, it does not significantly decrease on larger scales (in this range 1′ < θ < 50′) and is about ten times larger than would be estimated from a study of the convergence alone on scales θ ~ 50′. This is due to the fact that the shear correlations are not simply proportional to the convergence statistics because of the spin-2 factor e2iα. This leads to counterterms as in Eq. (61), associated with the non-local dependence of the shear, which make the shear also depend on the slope of the lensing correlation functions. For instance, as seen in Fig. D.1, the ratio 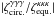 grows with the angular scale θ together with the slope of
grows with the angular scale θ together with the slope of 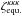 . The angular dependence of the density bispectrum also changes with scale, as we go from the small scale one-halo regime to the large-scale perturbative regime, and this also makes the ratio
. The angular dependence of the density bispectrum also changes with scale, as we go from the small scale one-halo regime to the large-scale perturbative regime, and this also makes the ratio 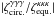 grows with θ (as shown by the comparison between the solid and dashed lines in Fig. D.1). Therefore, it is useful to go beyond the convergence case and to compute the shear case itself (or the statistics of interest in each specific data analysis), even though the computations are somewhat heavier.
grows with θ (as shown by the comparison between the solid and dashed lines in Fig. D.1). Therefore, it is useful to go beyond the convergence case and to compute the shear case itself (or the statistics of interest in each specific data analysis), even though the computations are somewhat heavier.
As for the convergence, the relative bias on small scales is somewhat higher if z1 = z2, because of the term ⟨δ1δ2γ3⟩ α ⟨γ1γ2⟩ α in Eq. (57).
We show the redshift dependence of the source-lens clustering bias in Fig. 11. Again, the upward spikes correspond to redshifts z3 such that the two lowest galaxy redshifts of the triplet { z1,z2,z3 } are equal. (The features at z3 ~ 0.1 for θ = 1′ are due to changes of sign of  , which make the ratio
, which make the ratio 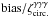 diverge.) In agreement with Fig. 10, for both angular scales θ = 1′ and 10′ the relative amplitude of the source-lens clustering bias is of order 10%. Therefore, although it is subdominant and can be neglected in current weak lensing surveys, where the signal-to-noise ratio is about unity for three-point statistics (Semboloni et al. 2011), it could be necessary to take this bias into account in future surveys such as Euclid (Refregier et al. 2010).
diverge.) In agreement with Fig. 10, for both angular scales θ = 1′ and 10′ the relative amplitude of the source-lens clustering bias is of order 10%. Therefore, although it is subdominant and can be neglected in current weak lensing surveys, where the signal-to-noise ratio is about unity for three-point statistics (Semboloni et al. 2011), it could be necessary to take this bias into account in future surveys such as Euclid (Refregier et al. 2010).
As for the convergence, the right panels, which correspond to closer pairs { z1,z2 }, show a decrease of the bias for z3 close to { z1,z2 }, because of the vanishing of the lensing kernels on the source plane, which yields a zero bias (in our approximations) for z1 = z2 = z3. When z3 is farther from the pair { z1,z2 } we recover a 10% bias as in the left panels.
6. Comparison with some previous works on the source-lens clustering bias
The source-lens clustering bias has already been studied in Bernardeau (1998) and Hamana et al. (2002) but from a different point of view. They consider the measure of a κ-map from an estimator of the form 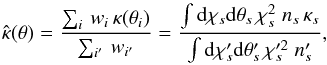 (68)where in the second equality we used notations similar to Eq. (2), and ns is the observed galaxy density at position (χs,θs). (For the clarity of the discussion below, we denote the dummy variables i′ and
(68)where in the second equality we used notations similar to Eq. (2), and ns is the observed galaxy density at position (χs,θs). (For the clarity of the discussion below, we denote the dummy variables i′ and 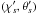 with a prime in the denominator, but both numerator and denominator are integrated over the same source distribution.) Thus, one measures the convergence κ(θ) in each direction on the sky from the galaxies in a small area around this direction. This is mostly suited for studies on large angular scales, so that there are enough galaxies in each direction bin to obtain a meaningful average. As shown by Eq. (68), Bernardeau (1998) and Hamana et al. (2002) actually consider a one-point statistics,
with a prime in the denominator, but both numerator and denominator are integrated over the same source distribution.) Thus, one measures the convergence κ(θ) in each direction on the sky from the galaxies in a small area around this direction. This is mostly suited for studies on large angular scales, so that there are enough galaxies in each direction bin to obtain a meaningful average. As shown by Eq. (68), Bernardeau (1998) and Hamana et al. (2002) actually consider a one-point statistics, 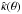 , which is smoothed on the scale θs of the angular bin, and next estimate the variance, skewness, and kurtosis of this one-point quantity.
, which is smoothed on the scale θs of the angular bin, and next estimate the variance, skewness, and kurtosis of this one-point quantity.
In contrast, in this paper we directly consider two-point or three-point estimators such as Eq. (1), which read for the convergence as
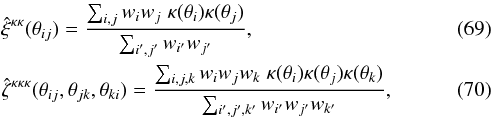 without building an intermediate κ-map, which is closer to current observational practice (for the same reason, we also consider estimators of the shear correlations in addition to the convergence). (Again, we denote with a prime the dummy indices in the denominator, but { i,j,k } and { i′,j′,k′ } run over the same set.) This also allows one to probe smaller angular scales, because the statistical sum in Eq. (69), or Eq. (70), is taken over all pairs of separation θij, or triplets of separation { θij,θjk,θki }, over the full survey and one is not limited by the binning width of the κ-map.
without building an intermediate κ-map, which is closer to current observational practice (for the same reason, we also consider estimators of the shear correlations in addition to the convergence). (Again, we denote with a prime the dummy indices in the denominator, but { i,j,k } and { i′,j′,k′ } run over the same set.) This also allows one to probe smaller angular scales, because the statistical sum in Eq. (69), or Eq. (70), is taken over all pairs of separation θij, or triplets of separation { θij,θjk,θki }, over the full survey and one is not limited by the binning width of the κ-map.
This also implies that contributions due to source-lens clustering appear both in the numerator and denominator in Eq. (68), through the fluctuations of the galaxy densities in each direction bin (independently of the total survey area), whereas in Eqs. (69) and (70) we can neglect the fluctuations of the denominator as they scale as 1/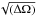 over the survey area (ΔΩ) (and we assume a sufficiently large survey) (the clustering of the sources contributes to the denominator, as shown by the terms ξi,j or ζi,j,k in the denominator of Eqs. (7) or (41), but for a survey area that is much larger than the galaxy correlation length, the sample variance of the denominator becomes negligible in relative terms, as 1/
over the survey area (ΔΩ) (and we assume a sufficiently large survey) (the clustering of the sources contributes to the denominator, as shown by the terms ξi,j or ζi,j,k in the denominator of Eqs. (7) or (41), but for a survey area that is much larger than the galaxy correlation length, the sample variance of the denominator becomes negligible in relative terms, as 1/ , see Eq. (6)).
, see Eq. (6)).
From a physical point of view, this also means that the source-lens clustering effects studied in Bernardeau (1998) and Hamana et al. (2002) are rather different from those studied in this article. Two effects come into play for the one-point estimator (68). A first positive bias comes from the coupling in the numerator between  and κs, on the same line of sight, as large-scale overdensities around the source plane χs yield both a positive convergence (due to matter overdensities in front of the source) and a positive galaxy number density fluctuation δs. A second negative bias, due to the finite redshift width of the source distribution, comes from the coupling between the convergence κs in the numerator and the galaxy number density fluctuations
and κs, on the same line of sight, as large-scale overdensities around the source plane χs yield both a positive convergence (due to matter overdensities in front of the source) and a positive galaxy number density fluctuation δs. A second negative bias, due to the finite redshift width of the source distribution, comes from the coupling between the convergence κs in the numerator and the galaxy number density fluctuations 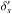 in the denominator, with
in the denominator, with 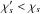 . Indeed, a large-scale overdensity at
. Indeed, a large-scale overdensity at 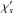 yields both a positive galaxy number density fluctuation
yields both a positive galaxy number density fluctuation 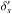 and a positive convergence κs. This damps the contributions with a positive convergence to the estimator (68), because the same effect associated with a large positive background κi also produces a great number of foreground galaxies i′ so that the contribution of κi to Eq. (68) is diluted. (Mathematically, the negative sign of this bias comes from the fact that expanding a fluctuation in the denominator gives a term
and a positive convergence κs. This damps the contributions with a positive convergence to the estimator (68), because the same effect associated with a large positive background κi also produces a great number of foreground galaxies i′ so that the contribution of κi to Eq. (68) is diluted. (Mathematically, the negative sign of this bias comes from the fact that expanding a fluctuation in the denominator gives a term 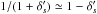 .) This is also briefly described in Sect. 2 in Hamana et al. (2002). The first effect, which involves correlations at the source plane, is suppressed by a factor of order x0/(c / H0) because of the vanishing of the lensing efficiency kernel g(χ′,χ) at χ′ = χ (as also discussed in Sect. 2 for our two-point estimators). Therefore, the second effect dominates provided the redshift source distribution is broad enough. Thus, Bernardeau (1998) and Hamana et al. (2002) find a negative bias that becomes more important as the width of the redshift source distribution increases (the convergence is defined with an opposite sign in Bernardeau 1998).
.) This is also briefly described in Sect. 2 in Hamana et al. (2002). The first effect, which involves correlations at the source plane, is suppressed by a factor of order x0/(c / H0) because of the vanishing of the lensing efficiency kernel g(χ′,χ) at χ′ = χ (as also discussed in Sect. 2 for our two-point estimators). Therefore, the second effect dominates provided the redshift source distribution is broad enough. Thus, Bernardeau (1998) and Hamana et al. (2002) find a negative bias that becomes more important as the width of the redshift source distribution increases (the convergence is defined with an opposite sign in Bernardeau 1998).
In this paper, the source-lens clustering bias arises in a different manner. Indeed, since we can neglect the fluctuations of the denominators in Eqs. (69) and (70), source-lens clustering effects come from the coupling in the numerators between different lines of sight. This difference from the case studied in Bernardeau (1998) and Hamana et al. (2002) is clearly due to the fact that (68) is a one-point estimator while (69) and (70) are two-point and three-point estimators. Then, we typically obtain a positive bias on small angular scales, see Figs. 4 and 9, as a large-scale overdensity around (χi,θi) yields a positive galaxy fluctuation δi and a positive convergence κi along the same line of sight (this is also the first effect described for the one-point estimator (68), which is suppressed by a factor of order x0 / (c / H0)) but also positive convergences κj and κk along the other lines of sight of background galaxies along the directions θj and θk. The latter effect is the dominant one for the three-point estimator (70).
Thus, it is not possible to make a direct comparison between our results and those obtained in Bernardeau (1998) and Hamana et al. (2002), because we consider different estimators that lead to different source-lens clustering effects (as clearly shown by the fact that they have different signs). Indeed, as explained above, the one-point estimator (68) is associated with a dominant negative bias, so that its skewness 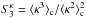 is decreased by the source-lens clustering effects (see also the discussion in Sect. 2 in Hamana et al. 2002), whereas we find a positive bias for the estimator (70) of the three-point correlation function. Nevertheless, we may note that for the skewness of the convergence, Bernardeau (1998) finds a relative bias that goes from − 3%, for a source distribution with a redshift width of Δzs = 0.15, to − 27% for Δzs = 0.87 (and typical redshifts zs ~ 1). In our case, we can see from the right panels in Fig. 9 that for three source redshifts at zs ≃ 1 with Δzs ≃ 0.1, we obtain a relative bias of + 1% for θ = 1′ and somewhat below + 1% for θ = 10′. From the left and right panels, we can see that we obtain a relative bias that can reach more than + 50% for θ = 1′, or + 10% for θ = 10′, when one source redshift is significantly lower than the other two with z1 ≲ 0.1, and Δzs ≳ 0.5. Thus, we find similar behaviors, in terms of absolute amplitudes, as in Bernardeau (1998), but with a somewhat lower bias (if we consider our results at 10′). Apart from the different set of cosmological parameters, these differences and the opposite signs come from the fact that we consider different estimators, as explained above. Nevertheless, the similar orders of magnitude could be expected from dimensional analysis, since we probe the same physical process. Next, from the two-point estimator (69) we explicitly estimate the source-lens clustering bias of two-point statistics, see Sect. 2, which was not considered in Bernardeau (1998) and Hamana et al. (2002) because it is a higher-order effect (~ξ2 while the signal scales as ξ). This allows us to check at a quantitative level that this bias is indeed negligible for most practical purposes.
is decreased by the source-lens clustering effects (see also the discussion in Sect. 2 in Hamana et al. 2002), whereas we find a positive bias for the estimator (70) of the three-point correlation function. Nevertheless, we may note that for the skewness of the convergence, Bernardeau (1998) finds a relative bias that goes from − 3%, for a source distribution with a redshift width of Δzs = 0.15, to − 27% for Δzs = 0.87 (and typical redshifts zs ~ 1). In our case, we can see from the right panels in Fig. 9 that for three source redshifts at zs ≃ 1 with Δzs ≃ 0.1, we obtain a relative bias of + 1% for θ = 1′ and somewhat below + 1% for θ = 10′. From the left and right panels, we can see that we obtain a relative bias that can reach more than + 50% for θ = 1′, or + 10% for θ = 10′, when one source redshift is significantly lower than the other two with z1 ≲ 0.1, and Δzs ≳ 0.5. Thus, we find similar behaviors, in terms of absolute amplitudes, as in Bernardeau (1998), but with a somewhat lower bias (if we consider our results at 10′). Apart from the different set of cosmological parameters, these differences and the opposite signs come from the fact that we consider different estimators, as explained above. Nevertheless, the similar orders of magnitude could be expected from dimensional analysis, since we probe the same physical process. Next, from the two-point estimator (69) we explicitly estimate the source-lens clustering bias of two-point statistics, see Sect. 2, which was not considered in Bernardeau (1998) and Hamana et al. (2002) because it is a higher-order effect (~ξ2 while the signal scales as ξ). This allows us to check at a quantitative level that this bias is indeed negligible for most practical purposes.
7. Intrinsic alignments
As noticed in the introduction, another well-known source of noise for weak-lensing measurements is the intrinsic alignment of galaxies. Indeed, each galaxy ellipticity may be correlated with the ellipticities of other galaxies and with the local density field that gives rise to the lensing distortion of background galaxies. When we average over the product of observed ellipticities of pairs of galaxies, the first effect leads to an “intrinsic–intrinsic” contribution (“II”) and the second effect to a “lensing–intrinsic” effect (“GI”). Following Heymans et al. (2013); Bridle & King (2007), we may use a version of the linear tidal field alignment model described in Catelan et al. (2001); Hirata & Seljak (2004), and write the observed galaxy ellipticity as 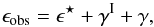 (71)where γ is the gravitational lensing contribution as in previous sections, ϵ⋆ is a random uncorrelated component that does not give rise to any bias, and γI is the component of the intrinsic galaxy ellipticity that is correlated with the large-scale density field, as
(71)where γ is the gravitational lensing contribution as in previous sections, ϵ⋆ is a random uncorrelated component that does not give rise to any bias, and γI is the component of the intrinsic galaxy ellipticity that is correlated with the large-scale density field, as 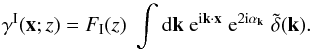 (72)In particular, galaxy ellipticities are only cross-correlated through their correlation to the same density field. Equation (72) may be seen as the simplest alignment model, where we linearize the dependence of the intrinsic ellipticity γI on the matter density field (as for the galaxy number density fluctuations δg, where we often use a linear bias model with δg = b(M,z)δ). As compared with the spin-0 quantity δg, the spin-2 factor e2iαk can be understood from the spin-2 character of the ellipticity and it is identical to the factor that appears in the expression (25) of the cosmic shear. Thus, the form of Eq. (72) is rather generic, once we decide to keep only the linear term, and follows from symmetry constraints (we assume there is no intrinsic B mode). If we introduce a new scale, such as the galaxy radius R, we can consider other contributions, where we replace
(72)In particular, galaxy ellipticities are only cross-correlated through their correlation to the same density field. Equation (72) may be seen as the simplest alignment model, where we linearize the dependence of the intrinsic ellipticity γI on the matter density field (as for the galaxy number density fluctuations δg, where we often use a linear bias model with δg = b(M,z)δ). As compared with the spin-0 quantity δg, the spin-2 factor e2iαk can be understood from the spin-2 character of the ellipticity and it is identical to the factor that appears in the expression (25) of the cosmic shear. Thus, the form of Eq. (72) is rather generic, once we decide to keep only the linear term, and follows from symmetry constraints (we assume there is no intrinsic B mode). If we introduce a new scale, such as the galaxy radius R, we can consider other contributions, where we replace 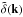 in Eq. (72) by higher-derivative terms, such as
in Eq. (72) by higher-derivative terms, such as 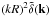 , or add some explicit smoothing, such as
, or add some explicit smoothing, such as 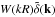 with W(kR) ~ e− (kR)2 (they are also scalar quantities and the length R is required for dimensional reasons). However, as compared with the contribution (72), these new contributions or modifications are suppressed by a factor (R/d)2, where d = χθ is the typical angular scale between the lines of sight.
with W(kR) ~ e− (kR)2 (they are also scalar quantities and the length R is required for dimensional reasons). However, as compared with the contribution (72), these new contributions or modifications are suppressed by a factor (R/d)2, where d = χθ is the typical angular scale between the lines of sight.
However, in practice we never measure the intrinsic ellipticity γI(x) itself, seen as a continuous field in the limit R → 0, but the galaxy-density weighted intrinsic ellipticity 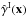 (Hirata & Seljak 2004),
(Hirata & Seljak 2004), 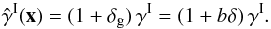 (73)Indeed, in a fashion similar to Eq. (1), estimators of the intrinsic-ellipticity–galaxy correlation function write for instance as
(73)Indeed, in a fashion similar to Eq. (1), estimators of the intrinsic-ellipticity–galaxy correlation function write for instance as 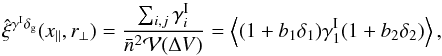 (74)where
(74)where 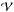 is the total survey volume or simulation box (in the redshift slice of interest) and (ΔV) the small volume of the separation bin Δx∥2πr⊥Δr⊥. In a similar fashion, the estimator of the intrinsic-ellipticity auto-correlation is of the form
is the total survey volume or simulation box (in the redshift slice of interest) and (ΔV) the small volume of the separation bin Δx∥2πr⊥Δr⊥. In a similar fashion, the estimator of the intrinsic-ellipticity auto-correlation is of the form 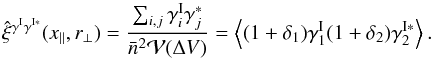 (75)In practice, one considers the tangential and cross components of the ellipticity and may use Landy-Szalay estimators (Landy & Szalay 1993) to reduce the noise (Mandelbaum et al. 2006, 2011). In any case, because we only measure the intrinsic ellipticities at galaxy locations, observations and simulations constrain the galaxy-density weighted intrinsic ellipticity
(75)In practice, one considers the tangential and cross components of the ellipticity and may use Landy-Szalay estimators (Landy & Szalay 1993) to reduce the noise (Mandelbaum et al. 2006, 2011). In any case, because we only measure the intrinsic ellipticities at galaxy locations, observations and simulations constrain the galaxy-density weighted intrinsic ellipticity 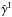 rather than γI. Then, following the usual practice (which is sometimes implicit in published works), we assume that the galaxy-density weight (1 + δg) only renormalizes the linear model (72) and we write
rather than γI. Then, following the usual practice (which is sometimes implicit in published works), we assume that the galaxy-density weight (1 + δg) only renormalizes the linear model (72) and we write 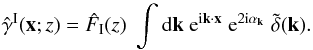 (76)Then, the “II” and “GI” power spectra are related to the matter power spectrum as
(76)Then, the “II” and “GI” power spectra are related to the matter power spectrum as 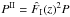 and
and 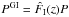 , as in Heymans et al. (2013). In most previous works, one directly works with these power spectra, which are typically fitted to simulations or observations, without relying on the explicit model (76). This is more general, because one could use different cross- and auto-correlation normalizations,
, as in Heymans et al. (2013). In most previous works, one directly works with these power spectra, which are typically fitted to simulations or observations, without relying on the explicit model (76). This is more general, because one could use different cross- and auto-correlation normalizations, 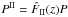 and
and 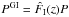 , or even different power spectrum shapes, whereas the model (76) implies
, or even different power spectrum shapes, whereas the model (76) implies  . Nevertheless, this is not a serious drawback as compared with previous works that often assume
. Nevertheless, this is not a serious drawback as compared with previous works that often assume  (to avoid introducing too many parameters). In our case, we need the explicit model (76) to compute three-point correlations (otherwise we would need an additional model for the intrinsic-alignment bispectra).
(to avoid introducing too many parameters). In our case, we need the explicit model (76) to compute three-point correlations (otherwise we would need an additional model for the intrinsic-alignment bispectra).
This distinction between γI and 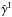 is important in this paper because we explicitly consider the source-lens clustering effects, that is, the factors δi in statistical averages such as Eq. (7), and we cannot “forget” them when we include intrinsic-alignment contributions. The linear tidal field model itself only gives Eq. (72), because it is based on the continuous dark matter tidal field (Catelan et al. 2001). Then, the density weighted shear would read as
is important in this paper because we explicitly consider the source-lens clustering effects, that is, the factors δi in statistical averages such as Eq. (7), and we cannot “forget” them when we include intrinsic-alignment contributions. The linear tidal field model itself only gives Eq. (72), because it is based on the continuous dark matter tidal field (Catelan et al. 2001). Then, the density weighted shear would read as 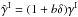 (Hirata & Seljak 2004). However, if we use such a model we face small-scale problems when we consider two- or three-point estimators such as Eq. (26). Indeed, this gives rise to factors such as
(Hirata & Seljak 2004). However, if we use such a model we face small-scale problems when we consider two- or three-point estimators such as Eq. (26). Indeed, this gives rise to factors such as 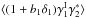 , which involve the three-point correlation
, which involve the three-point correlation 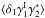 . However, this quantity is divergent for a power spectrum that decreases more slowly than k-3 at high k, that is, where ξ(0) = ∞. Indeed, using for instance the ansatz (37), we obtain a term that behaves as
. However, this quantity is divergent for a power spectrum that decreases more slowly than k-3 at high k, that is, where ξ(0) = ∞. Indeed, using for instance the ansatz (37), we obtain a term that behaves as 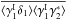 , which corresponds to the coincident limit x1′ → x1 in Eq. (A.16). (The overbar denotes that the two averages cannot be separated and the angular average requires some care and gives a nonzero result. In contrast, coincident two-point correlations such as
, which corresponds to the coincident limit x1′ → x1 in Eq. (A.16). (The overbar denotes that the two averages cannot be separated and the angular average requires some care and gives a nonzero result. In contrast, coincident two-point correlations such as 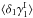 vanish by symmetry, but this is no longer the case for
vanish by symmetry, but this is no longer the case for 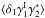 because of the explicit coupling to the extra factor
because of the explicit coupling to the extra factor 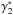 , associated with the second line of sight, which breaks the previous symmetry.)
, associated with the second line of sight, which breaks the previous symmetry.)
In the current ΛCDM cosmology, this quantity does not really diverge, and ξ(0) is finite, but this still means that the contribution 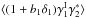 can be very large and depends on the shape of the power spectrum at very small scales, which does not make much physical sense. (We checked numerically that within this approach, terms such as
can be very large and depends on the shape of the power spectrum at very small scales, which does not make much physical sense. (We checked numerically that within this approach, terms such as 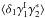 would dominate over
would dominate over 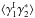 , even when we introduce a small-scale cutoff at R = 1 h-1 Mpc, and would give rise to a too large intrinsic-alignment bias.) In fact, this problem only warns us that the simple intrinsic-alignment model (72) is not sufficient to compute the three-point correlation
, even when we introduce a small-scale cutoff at R = 1 h-1 Mpc, and would give rise to a too large intrinsic-alignment bias.) In fact, this problem only warns us that the simple intrinsic-alignment model (72) is not sufficient to compute the three-point correlation 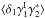 . Indeed, by discarding the galaxy length-scale R in Eq. (72), we have assumed that we consider much larger scales, so that the limit R → 0 is meaningful. In the three-point correlation
. Indeed, by discarding the galaxy length-scale R in Eq. (72), we have assumed that we consider much larger scales, so that the limit R → 0 is meaningful. In the three-point correlation 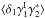 this is no longer the case, as one distance goes to zero (between δ1 and
this is no longer the case, as one distance goes to zero (between δ1 and 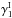 , which correspond to the same galaxy). Then, we should include the galaxy scale R, for instance through a smoothing kernel W(kR), in the intrinsic alignment model (72) (and also in the galaxy bias model δg = bδ).
, which correspond to the same galaxy). Then, we should include the galaxy scale R, for instance through a smoothing kernel W(kR), in the intrinsic alignment model (72) (and also in the galaxy bias model δg = bδ).
In practice, we consider the same-point combination (1 + bδ)γI as a new quantity 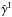 with a “renormalized” amplitude
with a “renormalized” amplitude 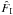 , as in Eq. (76), rather than considering the “bare” intrinsic ellipticity γI. This makes sense from both theoretical and observational/practical points of view. Indeed, three-point correlations such as ⟨(1 + bδ1)γ1γ2⟩ are dominated by contributions of the form ξ1,1ξ1,2, which decay linearly over ξ1,2 with the distance between the two lines of sight while ξ1,1 behaves as a scale-independent prefactor, whereas contributions of the form ξ1,2ξ1,2 are negligible at large distance. Thus, for two-point and higher-order correlations between different lines of sight, the product (1 + bδ1)γ1 can be considered as a single quantity and correlations with distant objects can be expected to scale as ξ1,2, which is satisfied by the renormalized model (76). On the other hand, because measures only deal with the density-weighted intrinsic ellipticity, as in Eqs. (74), (75), they directly constrain the “renormalized” factor
, as in Eq. (76), rather than considering the “bare” intrinsic ellipticity γI. This makes sense from both theoretical and observational/practical points of view. Indeed, three-point correlations such as ⟨(1 + bδ1)γ1γ2⟩ are dominated by contributions of the form ξ1,1ξ1,2, which decay linearly over ξ1,2 with the distance between the two lines of sight while ξ1,1 behaves as a scale-independent prefactor, whereas contributions of the form ξ1,2ξ1,2 are negligible at large distance. Thus, for two-point and higher-order correlations between different lines of sight, the product (1 + bδ1)γ1 can be considered as a single quantity and correlations with distant objects can be expected to scale as ξ1,2, which is satisfied by the renormalized model (76). On the other hand, because measures only deal with the density-weighted intrinsic ellipticity, as in Eqs. (74), (75), they directly constrain the “renormalized” factor 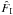 of Eq. (76), rather than the “bare” factor FI of Eq. (72). Therefore, we can directly work with the model (76) and forget (or rather bypass) the “bare” model (72). Then, the structure of Eq. (76) can be motivated by the same symmetry and long-distance arguments discussed below Eq. (72).
of Eq. (76), rather than the “bare” factor FI of Eq. (72). Therefore, we can directly work with the model (76) and forget (or rather bypass) the “bare” model (72). Then, the structure of Eq. (76) can be motivated by the same symmetry and long-distance arguments discussed below Eq. (72).
We choose for 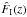 the relation used in previous works (Hirata & Seljak 2004; Bridle & King 2007; Joachimi et al. 2011; Heymans et al. 2013)
the relation used in previous works (Hirata & Seljak 2004; Bridle & King 2007; Joachimi et al. 2011; Heymans et al. 2013) 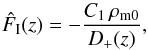 (77)where D+(z) is the linear growth factor normalized to unity today and the normalization constant is
(77)where D+(z) is the linear growth factor normalized to unity today and the normalization constant is 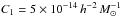 Mpc3. This redshift dependence follows from the linear theory model described in Hirata & Seljak (2004), but as in Bridle & King (2007) and Heymans et al. (2013), we use the nonlinear density contrast in Eq. (76), because its form is more general than a linear theory over δL.
Mpc3. This redshift dependence follows from the linear theory model described in Hirata & Seljak (2004), but as in Bridle & King (2007) and Heymans et al. (2013), we use the nonlinear density contrast in Eq. (76), because its form is more general than a linear theory over δL.
A first improvement to the model (76) would be to include a dependence on mass for the prefactor 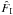 (as for the ordinary number-density bias b(M,z)). Alternatively, one can include a dependence on galaxy type (e.g., elliptical vs spiral galaxies), as done in Semboloni et al. (2008) in N-body simulations (with a phenomenological model to align elliptical galaxies with the host halo and spiral galaxies transverse to the halo spin) or as observed from the comparison between simulations and galaxy surveys (Joachimi et al. 2013a). In particular, spiral galaxies are expected to be governed by the angular momentum of the halo, which gives a quadratic dependence on the density field (Catelan et al. 2001; Crittenden et al. 2001). This would give a small residual value for
(as for the ordinary number-density bias b(M,z)). Alternatively, one can include a dependence on galaxy type (e.g., elliptical vs spiral galaxies), as done in Semboloni et al. (2008) in N-body simulations (with a phenomenological model to align elliptical galaxies with the host halo and spiral galaxies transverse to the halo spin) or as observed from the comparison between simulations and galaxy surveys (Joachimi et al. 2013a). In particular, spiral galaxies are expected to be governed by the angular momentum of the halo, which gives a quadratic dependence on the density field (Catelan et al. 2001; Crittenden et al. 2001). This would give a small residual value for 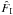 (if there remains a small linear dependence on the halo ellipticity) and a higher-order quadratic term that is not included in our study (and that we assume to be negligible, for instance if the galaxy sample is mostly made of elliptical galaxies). A second generalization would be to include a stochastic component to
(if there remains a small linear dependence on the halo ellipticity) and a higher-order quadratic term that is not included in our study (and that we assume to be negligible, for instance if the galaxy sample is mostly made of elliptical galaxies). A second generalization would be to include a stochastic component to 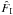 . These improvements may be obtained from numerical simulations, but for our general purpose we keep the simple parameterization (77). For specific galaxy samples with different normalizations C1, our results should be rescaled by the appropriate factors.
. These improvements may be obtained from numerical simulations, but for our general purpose we keep the simple parameterization (77). For specific galaxy samples with different normalizations C1, our results should be rescaled by the appropriate factors.
 |
Fig. 12 Relative intrinsic-alignment bias of the weak lensing shear two-point correlation, ξI / | ξγγ∗ |, as a function of the angular scale θ, for three pairs of different source redshifts, (z1,z2) = (0.5,1),(0.5,2), and (1,2). All total biases are negative. |
 |
Fig. 13 Relative intrinsic-alignment bias of the weak lensing shear two-point correlation, ξI / | ξγγ∗ |, as a function of the second galaxy redshift z2, for a fixed first galaxy redshift z1 = 0.5,1, or 2. We consider the angular scales θ = 1, 10, and 100 arcmin, from the upper to the lower panels. |
7.1. Two-point shear correlation function
Taking into account the intrinsic ellipticities, the average of the estimator 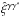 in Eq. (26) now writes as
in Eq. (26) now writes as 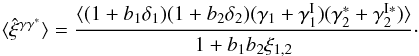 (78)As compared with Eq. (27), this gives the additional contributions
(78)As compared with Eq. (27), this gives the additional contributions 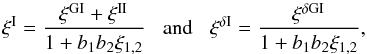 (79)where the usual “lensing–intrinsic” and “intrinsic–intrinsic” contributions are
(79)where the usual “lensing–intrinsic” and “intrinsic–intrinsic” contributions are 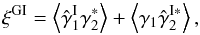 (80)and
(80)and 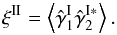 (81)The new “source-lens clustering–intrinsic” contribution, which involves the coupling of the source-lens clustering and intrinsic-alignment effects, is
(81)The new “source-lens clustering–intrinsic” contribution, which involves the coupling of the source-lens clustering and intrinsic-alignment effects, is 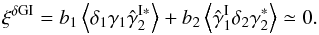 (82)It is negligible because of the vanishing of the lensing efficiency kernel g(χ′,χ) of Eq. (9) at the source plane χ′ = χ.
(82)It is negligible because of the vanishing of the lensing efficiency kernel g(χ′,χ) of Eq. (9) at the source plane χ′ = χ.
We do not treat the products (1 + bδ)γ and (1 + bδ)γI in the same manner, because as explained below Eq. (76), we consider (1 + bδ)γI as a single quantity 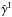 , while as in Sect. 3 we consider (1 + bδ) and γ as two separate quantities. This is because (1 + bδ)γI is a one-point quantity, whereas (1 + bδ)γ is a two-point quantity that involves the source and foreground fluctuations on its line of sight.
, while as in Sect. 3 we consider (1 + bδ) and γ as two separate quantities. This is because (1 + bδ)γI is a one-point quantity, whereas (1 + bδ)γ is a two-point quantity that involves the source and foreground fluctuations on its line of sight.
Then, from the intrinsic alignment model (76) we obtain 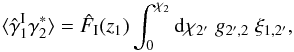 (83)and
(83)and  (84)We show our results in Figs. 12 and 13. In agreement with previous works, we find a bias of order 10% for the shear two-point correlation (Heymans et al. 2013; Joachimi et al. 2013b). The relative effect increases for small source redshifts, zs ≲ 0.5, and can become greater than unity, because the shorter line of sight implies a smaller gravitational lensing signal. Indeed, the comparison between Eq. (28) and Eq. (83) gives ξγγ∗ ~ χg2x0ξ and
(84)We show our results in Figs. 12 and 13. In agreement with previous works, we find a bias of order 10% for the shear two-point correlation (Heymans et al. 2013; Joachimi et al. 2013b). The relative effect increases for small source redshifts, zs ≲ 0.5, and can become greater than unity, because the shorter line of sight implies a smaller gravitational lensing signal. Indeed, the comparison between Eq. (28) and Eq. (83) gives ξγγ∗ ~ χg2x0ξ and 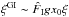 , where x0 is the typical correlation length, whence ξGI / ξγγ∗ ~ 1 / (χg) ~ [c / (H0χ)] 2 increases for a small source redshifts.
, where x0 is the typical correlation length, whence ξGI / ξγγ∗ ~ 1 / (χg) ~ [c / (H0χ)] 2 increases for a small source redshifts.
When the two galaxy redshifts z1 and z2 are well separated, | z2 − z1 | ≫ x0H0 / c (typically | z2 − z1 | > 0.01), the intrinsic–alignment bias ξI is dominated by the lensing–intrinsic contribution (80) and the intrinsic–intrinsic contribution (81) is negligible (because the correlation between the two source galaxies is negligible). Because the function 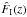 in Eq. (77) is negative this yields a negative bias. When the two galaxy redshifts are very close, their intrinsic ellipticities are significantly correlated and the intrinsic–intrinsic contribution (81) becomes dominant. As seen from Eq. (84), this now gives a positive bias because for these close pairs ξ1,2 > 0. This gives rise to the positive spikes in Fig. 13 for z1 ≃ z2.
in Eq. (77) is negative this yields a negative bias. When the two galaxy redshifts are very close, their intrinsic ellipticities are significantly correlated and the intrinsic–intrinsic contribution (81) becomes dominant. As seen from Eq. (84), this now gives a positive bias because for these close pairs ξ1,2 > 0. This gives rise to the positive spikes in Fig. 13 for z1 ≃ z2.
The comparison of Fig. 12 with Fig. 6, and of Fig. 13 with Fig. 7, shows that the intrinsic-alignment bias is much greater than the source-lens clustering bias. Thus, for practical purposes one does not need to worry about the source-lens clustering bias of two-point statistics. This remains true when one implements nulling techniques to eliminate the intrinsic-alignment bias because this also removes the source-lens clustering bias by the same effect. Indeed, considering for instance z1 < z2, this method corresponds to integrating over a distribution of background source redshifts n(z2) so that ∫dz2 g2′,2n(z2) = 0 at the plane z2′ = z1 (Joachimi & Schneider 2008). This damps all contributions that arise at z2′ ≃ z1, both the source-lens clustering contribution 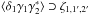 and the intrinsic-alignment contribution
and the intrinsic-alignment contribution 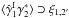 .
.
7.2. Three-point shear correlation function
As for the case of the two-point estimator, the galaxy intrinsic alignments add new contributions 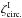 and
and 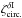 to the average of the three-point estimator
to the average of the three-point estimator 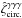 in Eq. (56), which can be split as
in Eq. (56), which can be split as 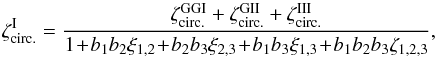 (85)and
(85)and 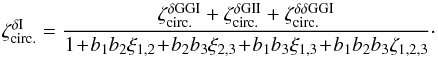 (86)For z1 ≤ z2 ≤ z3, the non-negligible “usual” intrinsic contributions are (because of the vanishing of the lensing kernel g(χ′,χ) at the source plane)
(86)For z1 ≤ z2 ≤ z3, the non-negligible “usual” intrinsic contributions are (because of the vanishing of the lensing kernel g(χ′,χ) at the source plane) 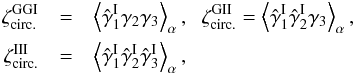 (87)where the subscript “α” denotes the integration over the angles αxi and the factor e− 2i(αx1 + αx2 + αx3), as in Eq. (51). When all redshifts are different, only the contribution
(87)where the subscript “α” denotes the integration over the angles αxi and the factor e− 2i(αx1 + αx2 + αx3), as in Eq. (51). When all redshifts are different, only the contribution  is left:
is left: 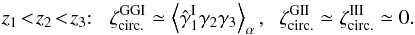 (88)The new “source-lens clustering–intrinsic” contributions read as (with z1 ≤ z2 ≤ z3)
(88)The new “source-lens clustering–intrinsic” contributions read as (with z1 ≤ z2 ≤ z3) 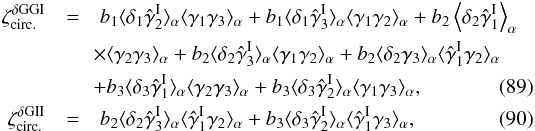 and
and 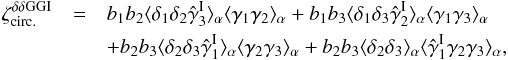 (91)where the superscripts “δ”, “G”, and “I”, count the number of terms δ, γ, and
(91)where the superscripts “δ”, “G”, and “I”, count the number of terms δ, γ, and  . When the three source redshifts are different, only the contribution
. When the three source redshifts are different, only the contribution  is left:
is left: 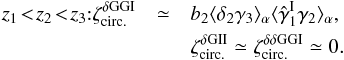 (92)
(92)
 |
Fig. 14 Relative intrinsic-alignment bias of the circular weak lensing shear three-point correlation |
 |
Fig. 15 Relative intrinsic-alignment bias of the circular weak lensing shear three-point correlation |
7.2.1. Usual intrinsic-alignment bias
Using the intrinsic alignment model (76), the first lensing–intrinsic contribution reads as (compare with Eq. (59)) 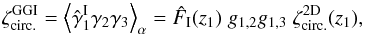 (93)where
(93)where 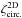 was defined in Eqs. (60) or (61). Here, as in Sect. 5, we used Limber’s approximation. The “GII” contribution, which is only relevant when z1 ≃ z2 (we consider the ordering z1 ≤ z2 ≤ z3), writes as
was defined in Eqs. (60) or (61). Here, as in Sect. 5, we used Limber’s approximation. The “GII” contribution, which is only relevant when z1 ≃ z2 (we consider the ordering z1 ≤ z2 ≤ z3), writes as 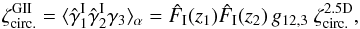 (94)where g12,3 = g((χ1 + χ2) / 2,χ3) and we introduced
(94)where g12,3 = g((χ1 + χ2) / 2,χ3) and we introduced ![\begin{eqnarray} \zeta^{\rm 2.5D}_{\rm circ.} & = & \int_{-\infty}^{\infty} \dd x_{3'\parallel} \int_0^{2\pi} \! \frac{\dd\alpha_{\vx_1}\dd\alpha_{\vx_2}\dd\alpha_{\vx_3}}{(2\pi)^3} \nonumber \\ && \times \int \dd\vk_1\dd\vk_2\dd\vk_{3'} \; {\rm e}^{\ii [ \vk_1\cdot\vx_1+\vk_2\cdot\vx_2+\vk_{3'}\cdot\vx_{3'}]} \nonumber \\ && \times \; \delta_{\rm D}(\vk_1+\vk_2+\vk_{3'}) \; B(k_1,k_2,k_{3'}) \; \nonumber \\ && \times \; {\rm e}^{2\ii (\alpha_{\vk_1}+\alpha_{\vk_2}+\alpha_{\vk_{3'}} - \alpha_{\vx_1} - \alpha_{\vx_2} - \alpha_{\vx_3})} . \label{zeta-2.5D--1} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22146-13/aa22146-13-eq496.png) (95)The superscript “2.5D” refers to the fact that this quantity is intermediate between the 2D correlation (60), which involves two integrations along the lines of sight, and the 3D correlation, which has no integration along the lines of sight. To simplify the computations, we again use the hierarchical ansatz (37) for the bispectrum. As described in Appendix C, this gives
(95)The superscript “2.5D” refers to the fact that this quantity is intermediate between the 2D correlation (60), which involves two integrations along the lines of sight, and the 3D correlation, which has no integration along the lines of sight. To simplify the computations, we again use the hierarchical ansatz (37) for the bispectrum. As described in Appendix C, this gives 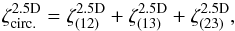 (96)where the three components are given by Eqs. (C.5) and (C.9) (and
(96)where the three components are given by Eqs. (C.5) and (C.9) (and 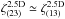 when z1 ≃ z2). The “III” contribution, which is only relevant when z1 ≃ z2 ≃ z3, writes as
when z1 ≃ z2). The “III” contribution, which is only relevant when z1 ≃ z2 ≃ z3, writes as 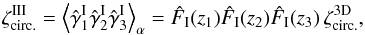 (97)with
(97)with ![\begin{eqnarray} \zeta^{\rm 3D}_{\rm circ.} & = & \int_0^{2\pi} \! \frac{\dd\alpha_{\vx_1}\dd\alpha_{\vx_2}\dd\alpha_{\vx_3}}{(2\pi)^3} \int \dd\vk_1\dd\vk_2\dd\vk_3 \; B(k_1,k_2,k_3) \nonumber \\ && \hspace{-0.cm} \times \; {\rm e}^{\ii [ \vk_1\cdot\vx_1+\vk_2\cdot\vx_2+\vk_3\cdot\vx_3]} \; \delta_{\rm D}(\vk_1+\vk_2+\vk_3) \nonumber \\ && \hspace{-0.cm} \times \; {\rm e}^{2\ii (\alpha_{\vk_1}+\alpha_{\vk_2}+\alpha_{\vk_3} - \alpha_{\vx_1} - \alpha_{\vx_2} - \alpha_{\vx_3})} . \label{zeta-3D--1} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22146-13/aa22146-13-eq500.png) (98)Using again the hierarchical ansatz (37) for the bispectrum, we obtain
(98)Using again the hierarchical ansatz (37) for the bispectrum, we obtain 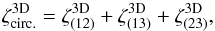 (99)where the three components are given by permutations over Eq. (C.12), as described in Appendix C.
(99)where the three components are given by permutations over Eq. (C.12), as described in Appendix C.
We show our results in Figs. 14 and 15. The overall behavior is similar to the one found in Figs. 12 and 13 for the two-point correlation function, with a relative bias that varies between 1% and more than unity, depending on the angular scale and the redshifts of the sources. These orders of magnitude are consistent with previous works (Semboloni et al. 2008) (but the different redshift distributions and galaxy models make a precise comparison difficult). Again, the relative bias increases for low source redshifts because of the shorter lines of sight, which give rise to factors χg in the weak lensing signal that decrease as χ → 0. Then, as noticed in Semboloni et al. (2008), by removing or focusing on low-redshift galaxies, one can separate (or amplify the relative weight of) the cosmic-shear or intrinsic-alignement signals. This allows one to obtain on one hand a better constraint on cosmology from weak lensing and on the other hand a better understanding of intrinsic alignments. However, this requires reliable photometric or spectroscopic redshifts.
Because our three source redshifts never coincide, the “III” contribution is always negligible as compared with the other two terms in Eq. (85). For most redshifts in Fig. 15, where the three source redshifts are significatly separated, the intrinsic alignment bias is dominated by the contribution  , associated with the correlation of the intrinsic alignment of the foreground galaxy z1 with the local density field that gives rise to lensing distortions of the two more distant galaxies z2 and z3. In our case, this yields a positive bias, whereas the cosmic shear signal
, associated with the correlation of the intrinsic alignment of the foreground galaxy z1 with the local density field that gives rise to lensing distortions of the two more distant galaxies z2 and z3. In our case, this yields a positive bias, whereas the cosmic shear signal  is negative. As for the two-point correlation case shown in Fig. 13, this opposite sign is due to the negative sign in the model (77). When the lowest two source redshifts become close (i.e., z3 ≃ z1 in Fig. 15), the contribution
is negative. As for the two-point correlation case shown in Fig. 13, this opposite sign is due to the negative sign in the model (77). When the lowest two source redshifts become close (i.e., z3 ≃ z1 in Fig. 15), the contribution  becomes dominant and gives a negative bias. This gives rise to the (negative) spikes in Fig. 15.
becomes dominant and gives a negative bias. This gives rise to the (negative) spikes in Fig. 15.
The comparison of Fig. 15 with Fig. 11 shows that the intrinsic-alignment bias can be either greater or smaller than the source-lens clustering bias, depending on the source redshifts and angular scale. For low redshifts, zi ≲ 0.5, the intrinsic-alignment bias is typically greatest, while for high redshifts, zi ≳ 1, the source-lens clustering bias is greatest. This is different from the case of the two-point shear correlation, where the intrinsic-alignment bias was typically much greater than the source-lens clustering bias, which can be neglected for practical purposes. We can note that the scaling with the amplitude of the matter power spectrum (or correlation function) is different:  Thus, whereas for the two-point estimator, the signal and the intrinsic-alignment bias are of the same order ~ξ while the source-lens clustering bias is of higher order ~ζ ~ ξ2; for the three-point estimator, the signal, the intrinsic-alignment bias, and the source-lens clustering bias, are all of the same order ~ζ ~ ξ2. Then, for three-point statistics both the intrinsic-alignment bias and the source-lens clustering bias should be taken into account, if we aim at an accuracy better than 10%.
Thus, whereas for the two-point estimator, the signal and the intrinsic-alignment bias are of the same order ~ξ while the source-lens clustering bias is of higher order ~ζ ~ ξ2; for the three-point estimator, the signal, the intrinsic-alignment bias, and the source-lens clustering bias, are all of the same order ~ζ ~ ξ2. Then, for three-point statistics both the intrinsic-alignment bias and the source-lens clustering bias should be taken into account, if we aim at an accuracy better than 10%.
 |
Fig. 16 Relative source-lens clustering–intrinsic-alignment bias of the circular weak lensing shear three-point correlation |
 |
Fig. 17 Relative source-lens clustering–intrinsic-alignment bias of the circular weak lensing shear three-point correlation |
Another difference with the case of two-point statistics is that nulling techniques devised for the removal of intrinsic-alignment bias no longer automatically remove the source-lens clustering bias. Indeed, considering source redshifts in non-overlapping bins with z1 < z2 < z3, the intrinsic-alignment bias is dominated by the contribution 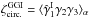 of Eq. (87), and as for the two-point case it is sufficient to use a weight T(χ3) such that ∫dχ3T(χ3)g(χ3′,χ3) vanishes at χ3′ = χ1 to remove this bias (Shi et al. 2010). This also removes the contributions ⟨δ1γ2⟩α⟨γ1γ3⟩ α + ⟨δ1γ3⟩ α ⟨γ1γ2⟩ α of the source-lens clustering bias in Eq. (58), but this does not erase the third contribution ⟨δ2γ3⟩α⟨γ1γ2⟩α that involves galaxy-density fluctuations at the second redshift z2. Thus, to remove both the intrinsic-alignment bias and the source-lens clustering bias we need the weight T(χ3) to satisfy a second constraint, ∫dχ3T(χ3)g(χ3′,χ3) = 0 at χ3′ = χ2, to erase the correlations in both planes z1 and z2. We leave a study of this problem to future work.
of Eq. (87), and as for the two-point case it is sufficient to use a weight T(χ3) such that ∫dχ3T(χ3)g(χ3′,χ3) vanishes at χ3′ = χ1 to remove this bias (Shi et al. 2010). This also removes the contributions ⟨δ1γ2⟩α⟨γ1γ3⟩ α + ⟨δ1γ3⟩ α ⟨γ1γ2⟩ α of the source-lens clustering bias in Eq. (58), but this does not erase the third contribution ⟨δ2γ3⟩α⟨γ1γ2⟩α that involves galaxy-density fluctuations at the second redshift z2. Thus, to remove both the intrinsic-alignment bias and the source-lens clustering bias we need the weight T(χ3) to satisfy a second constraint, ∫dχ3T(χ3)g(χ3′,χ3) = 0 at χ3′ = χ2, to erase the correlations in both planes z1 and z2. We leave a study of this problem to future work.
7.3. Coupled source-lens clustering–intrinsic-alignment bias
The coupled source-lens clustering–intrinsic alignment contributions (89)−(91) involve new terms of the form 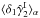 ,
, 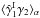 , and
, and 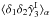 . The first two terms can be read from Eqs. (64) and (66), where an integration factor along the line of sight, ∫dχ g, is replaced by a factor
. The first two terms can be read from Eqs. (64) and (66), where an integration factor along the line of sight, ∫dχ g, is replaced by a factor 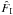 . Thus, Eq. (64) becomes
. Thus, Eq. (64) becomes 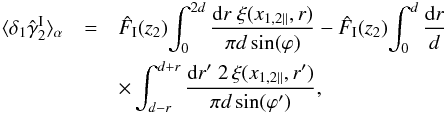 (102)while Eq. (66) becomes
(102)while Eq. (66) becomes ![\begin{eqnarray} \lag\hat{\gamma}_1^{\rm I}\gamma_2\rag_{\alpha} & = & - \hat{F}_{\rm I}(z_1) g_{1,2} \; \Bigg\{\int_0^{2d} \frac{\dd r \, r \, \xi^{\rm 2D}(r)}{\pi d^2} \left[ 2 \varphi - \frac{d}{r \sin\varphi} \right] \nonumber \\ && - \int_0^d \frac{\dd r \, 2r}{d^2} \left( \! \xi^{\rm 2D}(r) \left[ \frac{d\!-\!r}{d}\right]^2 \!+\! \int_{d-r}^{d+r} \frac{\dd r' \, r' \, \xi^{\rm 2D}(r')}{\pi d^2} \right. \nonumber \\ && \left. \times \left[ 2 \varphi' - \frac{d^2}{r \, r' \sin\varphi'} \right] \right) \Bigg\}. \label{xi-gI1-g2} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22146-13/aa22146-13-eq525.png) (103)From the property (54), the third term writes as
(103)From the property (54), the third term writes as 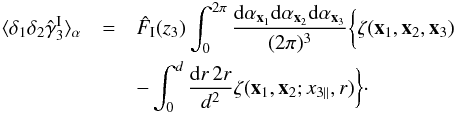 (104)We show the amplitude of this coupled contribution
(104)We show the amplitude of this coupled contribution  in Figs. 16 and 17. The comparison of Fig. 16 with Fig. 14 shows that when two source redshifts are identical source-lens clustering effects amplify the intrinsic-alignment bias. This yields a bias of order unity for a large range of source redshifts and angular scales. However, when the three source redshifts are different (the single case {z1,z2,z3} = {0.5,1,2} in these two figures), the coupled source-lens clustering–intrinsic alignment effects reduce to the contribution (92) and only give rise to a bias of about 1%. This is not surprising, because for this redshift triplet we can see in Figs. 10 and 14 that the pure source-lens clustering and intrinsic alignment effects are of order 10%, and we could expect their combination to be approximately 1%.
in Figs. 16 and 17. The comparison of Fig. 16 with Fig. 14 shows that when two source redshifts are identical source-lens clustering effects amplify the intrinsic-alignment bias. This yields a bias of order unity for a large range of source redshifts and angular scales. However, when the three source redshifts are different (the single case {z1,z2,z3} = {0.5,1,2} in these two figures), the coupled source-lens clustering–intrinsic alignment effects reduce to the contribution (92) and only give rise to a bias of about 1%. This is not surprising, because for this redshift triplet we can see in Figs. 10 and 14 that the pure source-lens clustering and intrinsic alignment effects are of order 10%, and we could expect their combination to be approximately 1%.
Figure 17 confirms that, except for the coincident source redshifts that give rise to high peaks for this bias, the coupled source-lens clustering–intrinsic alignment bias is usually very small. As the other sources of bias, its relative amplitude with respect to the signal increases for low source redshifts, and it becomes of order unity at zi ≲ 0.1, but the usual intrinsic alignment bias has already grown further in such cases. Thus, for most practical purposes, the coupled contribution  is negligible or subdominant.
is negligible or subdominant.
Equations (88) and (92) show that when the three source redshifts are different, both the pure intrinsic-alignment and the coupled source-lens clustering–intrinsic alignment contributions involve the lowest-redshift intrinsic alignment 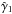 . However, the first bias involves the three-point correlation
. However, the first bias involves the three-point correlation 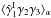 whereas the second one involves the two-point correlation
whereas the second one involves the two-point correlation 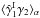 . This means that to remove the intrinsic-alignment bias through a nulling technique (Shi et al. 2010) one can integrate with a suitable weight T2(χ2) or T3(χ3) over the redshift distribution of either the intermediate or the farthest source plane, whereas the coupled bias can only be removed by the integration with the weight T2(χ2) over the intermediate source plane (or with a new weight
. This means that to remove the intrinsic-alignment bias through a nulling technique (Shi et al. 2010) one can integrate with a suitable weight T2(χ2) or T3(χ3) over the redshift distribution of either the intermediate or the farthest source plane, whereas the coupled bias can only be removed by the integration with the weight T2(χ2) over the intermediate source plane (or with a new weight 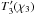 that removes the contributions from the plane z2). Therefore, to remove both contributions with a single weight, one must integrate over the intermediate source plane.
that removes the contributions from the plane z2). Therefore, to remove both contributions with a single weight, one must integrate over the intermediate source plane.
8. Conclusion
In this paper, we have estimated the source-lens clustering bias of two-point and three-point weak lensing estimators. This arises from the fact that galaxies are not located at random in space: their distribution is correlated with the density fluctuations that give rise to the weak lensing signal we wish to measure. Our approach does not rely on perturbation theory, which only applies to very large angular scales, or on the measure of a “convergence map” from galaxy surveys. Following the strategy used in practice in weak lensing surveys, we consider estimators of the real-space two-point and three-point weak lensing correlation functions, obtained by summing over pairs or triplets of source galaxies over the survey area. This leads to a (typically positive) source-lens clustering bias that is different from the (typically negative) source-lens clustering bias associated with one-point estimators of the κ-map. We study both the case of convergence correlations (which are not observed in current surveys but enable simpler computations) and shear correlations (which correspond to the current observational probes but lead to somewhat heavier computations).
For two-point weak lensing correlation functions, the source-lens clustering bias is typically several orders of magnitude below the weak lensing signal, because
-
(a)
it only arises from density fluctuations close to at least one ofthe source galaxies, whereas the lensing signal is generated bydensity fluctuations along the lines of sight up to the lowest galaxyredshift.
-
(b)
the lensing efficiency kernel g(χ′,χ) vanishes at the source plane, which yields additional suppression factors x0 / (c/H0), where x0 is the typical correlation length. Moreover, the bias is smaller for the shear than for the convergence because of some cancellations due to the spin-2 factor e2iα.
-
(c)
it is quadratic over the density correlation (~ξ2 + ξ3) whereas the signal is linear (~ξ).
The only case where the bias is significant, and can even be larger than the signal, is when we cross-correlate the gravitational lensing distortions of a very low-redshift galaxy, z2 ≲ 0.05, with a higher redshift galaxy (z1 ≳ 0.5), as in tomographic studies where we bin the galaxy population in several redshift bins. Then, the bias is set by the three-point correlation between the low-redshift galaxy, at z2, and density fluctuations on the two lines of sight at nearby redshifts, z2′ ≃ z1′ ≃ z2. This increase in the bias, with respect to other galaxy configurations, is due to the facts that one lensing kernel, g1′,1, is no longer small (because we are far from the distant galaxy redshift), three-point correlations are larger at low redshift, and the lensing signal itself is smaller, as the common depth of the two lines of sight, up to min(z1,z2), is smaller.
In principles, one may subtract the main contamination ζδγγ∗ from the estimator 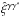 to measure the weak lensing signal from Eq. (27). However, in cases where this bias is relevant, it involves the three-point galaxy–matter–matter correlation function, which is not predicted to much better than 10% (we must take the inaccuracies of the matter three-point correlation and of the galaxy bias into account). Therefore, in practical analysis of cosmic shear surveys, it is probably more convenient not to include the cross-correlation between low redshifts (z2 ≲ 0.05) and higher redshift galaxies (z1 ≳ 0.5). This should not remove much of the weak lensing signal, which usually comes from galaxies at z ~ 1, where the galaxy number density of the survey is greatest. A simple implementation would be to discard any pair {i,j} in the estimator (1) whenever ζδγγ∗ is larger than ten percent of ξγγ∗.
to measure the weak lensing signal from Eq. (27). However, in cases where this bias is relevant, it involves the three-point galaxy–matter–matter correlation function, which is not predicted to much better than 10% (we must take the inaccuracies of the matter three-point correlation and of the galaxy bias into account). Therefore, in practical analysis of cosmic shear surveys, it is probably more convenient not to include the cross-correlation between low redshifts (z2 ≲ 0.05) and higher redshift galaxies (z1 ≳ 0.5). This should not remove much of the weak lensing signal, which usually comes from galaxies at z ~ 1, where the galaxy number density of the survey is greatest. A simple implementation would be to discard any pair {i,j} in the estimator (1) whenever ζδγγ∗ is larger than ten percent of ξγγ∗.
For three-point weak lensing correlation functions, the source-lens clustering bias is typically of order 10% of the signal, both for the convergence and the shear. In contrast to the case of two-point estimators, as soon as the three source galaxy redshifts are not identical the bias is not suppressed by a factor x0 / (c/H0) associated with the vanishing of the lensing kernel g(χ′,χ) at the source plane. Moreover, the bias is not dominated by three-point galaxy-matter correlation functions but by two-point correlations and on large scales the signal and the bias show the same scaling ∝ξ2 over the density correlation. These features explain the greater significance of the source-lens clustering bias for three-point estimators than for two-point estimators.
Next, we have considered the intrinsic-alignment bias of these weak lensing estimators. Using a simple intrinsic-alignment model, which assumes a linear relationship between the galaxy and halo ellipticities, that has been used in previous works for two-point statistics, we have extended this approach to three-point statistics. We find that the intrinsic-alignment bias is about 10% of the signal for estimators of either the two-point or three-point shear correlations, but there is a significant dependence on scale and redshift. In particular, the intrinsic-alignment bias becomes greater than unity for low source redshifts zs ≲ 0.3. As noticed in Semboloni et al. (2008), low-redshift galaxies could be used to understand intrinsic alignments while high-redshift galaxies would be used for measures of the cosmic shear, but this requires reliable redshifts.
We have also investigated the coupling of source-lens clustering and intrinsic-alignment effects. They are negligible for two-point estimators. For three-point estimators, they are negligible or smaller than the usual intrinsic-alignment bias, provided the three source redshifts are different (otherwise they can be larger than the usual intrinsic-alignment bias).
Thus, for two-point statistics one can neglect the source-lens clustering bias and focus on the intrinsic-alignment bias. Moreover, in this case nulling techniques simultaneously remove the source-lens clustering and intrinsic-alignment biases. For three-point statistics, such biases of 10% are sufficiently small to be neglected in current surveys. However, it may be necessary to take them into account in future surveys such as Euclid (Refregier et al. 2010).
One approach is to explicitly include these effects in the analysis by building a model for these two biases (which may contain a few free nuisance parameters that are estimated from the same observations). For the source-lens clustering bias, a convenient feature is that it should be possible to obtain reasonably good estimates of its amplitude because it is dominated by two-point density–density and galaxy–density correlations (rather than three- or higher-order correlations). However, it shows a linear dependence on the galaxy bias (in the generic case where the three galaxy redshifts are different, as in Eq. (58)), within a linear galaxy bias model. This may limit the accuracy of predictions for this source-lens clustering bias to about 10% (because of the measure of the galaxy bias and the limited validity of the linear bias approximation), but in practice this bias parameter may be treated as a free parameter to be constrained by the same observations. The intrinsic-alignment bias involves the three-point density correlation (for a linear model), which is more difficult to model with a high accuracy in the nonlinear regime. Moreover, the intrinsic alignment is much less well understood than the galaxy number density bias. In particular, its dependence on galaxy type and mass it not constrained to a very high accuracy. There remains work to be done in this direction.
A second approach is to use a nulling technique, where one integrates over the background source redshift distribution with a suitable weight T(z3) to remove the dependence on density fluctuations at the redshift z1 of the lowest-redshift galaxy. However, in contrast with the case of two-point statistics, this no longer simultaneously removes all contributions to the source-lens clustering bias, because there remains a contribution associated with fluctuations at the redshift of the intermediate galaxy z2. Therefore, one may need to impose a second constraint on T(z3) to remove the dependence on both planes z1 and z2. It remains to be seen whether this is really needed to lower the bias to a sufficiently low level, and whether the loss of information entailed by such a procedure is not to high. We leave this to future works.
Online material
Appendix A: Two-point cosmic shear correlation
Appendix A.1: Density-shear two-point correlation
The product of two-point correlations in Eq. (29) reads as 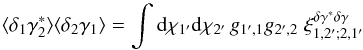 (A.1)where we introduced
(A.1)where we introduced 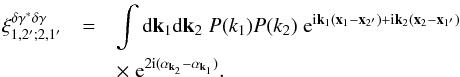 (A.2)This involves the spin-2 correlation defined in Eq. (31). Writing the power spectrum in terms of the two-point correlation function, integrating over the longitudinal direction and the polar angles of r⊥ and k⊥, Eq. (31) also reads as
(A.2)This involves the spin-2 correlation defined in Eq. (31). Writing the power spectrum in terms of the two-point correlation function, integrating over the longitudinal direction and the polar angles of r⊥ and k⊥, Eq. (31) also reads as 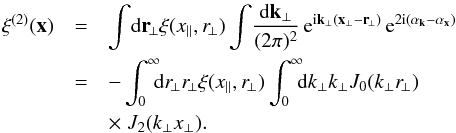 (A.3)(Here we note
(A.3)(Here we note 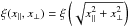 .) The integral over two Bessel functions satisfies
.) The integral over two Bessel functions satisfies
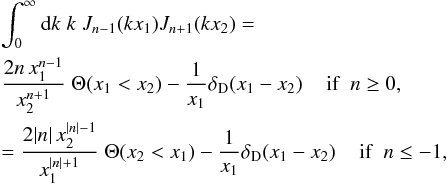 (A.4)where Θ is the Heaviside function. This yields Eq. (32) and Eq. (A.2) writes as
(A.4)where Θ is the Heaviside function. This yields Eq. (32) and Eq. (A.2) writes as 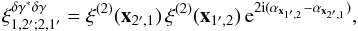 (A.5)where we note x1,2 = x2 − x1. Since we have αx1′,2 = αx1,2 and αx2′,1 = αx2,1 = αx1,2 + π, Eq. (A.5) gives Eq. (33).
(A.5)where we note x1,2 = x2 − x1. Since we have αx1′,2 = αx1,2 and αx2′,1 = αx2,1 = αx1,2 + π, Eq. (A.5) gives Eq. (33).
Appendix A.2: Density–shear–shear three-point correlation
Substituting the expression (37) of the bispectrum into Eq. (36), we are led to compute the quantity ![\appendix \setcounter{section}{1} \begin{align} \zeta_{1,1',2'}^{(1',2')} \!+\! \zeta_{1,1',2'}^{(1,1')} \!+\! \zeta_{1,1',2'}^{(1,2')} & = \int \!\! \dd\vk_1 \dd\vk_{1'}\dd\vk_{2'} \, \delta_{\rm D}(\vk_1 \!+\! \vk_{1'} \!+\! \vk_{2'} \!) \nonumber \\ & \times {\rm e}^{\ii (\vk_1\cdot\vx_1+\vk_{1'}\cdot\vx_{1'}+\vk_{2'}\cdot\vx_{2'})} \, {\rm e}^{2\ii (\alpha_{\vk_{1'}}-\alpha_{\vk_{2'}})} \nonumber \\ & \times [ P(k_{1'}) P(k_{2'})\! +\! P(k_1) P(k_{1'}) \!+ \!P(k_1) P(k_{2'}) ] , \label{zeta-P-gamma-1} \end{align}](/articles/aa/full_html/2014/01/aa22146-13/aa22146-13-eq577.png) (A.5)where the superscripts in the three terms in the left-hand side refer to the arguments of the power spectra in the three terms in the bracket in the right hand side. Here and in the following, we use the flat sky approximation and the fact that the three points, 1, 1′, and 2′, are at the same redshift (i.e., within radial distances of order ~8 h-1Mpc). By symmetry, the first term vanishes,
(A.5)where the superscripts in the three terms in the left-hand side refer to the arguments of the power spectra in the three terms in the bracket in the right hand side. Here and in the following, we use the flat sky approximation and the fact that the three points, 1, 1′, and 2′, are at the same redshift (i.e., within radial distances of order ~8 h-1Mpc). By symmetry, the first term vanishes, 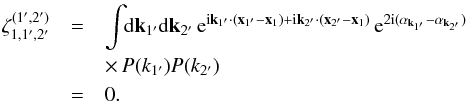 (A.7)Indeed, x1 and x1′ are along the same line of sight, hence their projected separation in the transverse plane is zero, x1′ ⊥ − x1 ⊥ = 0, and the angular integration over the polar angle αk1′ vanishes.
(A.7)Indeed, x1 and x1′ are along the same line of sight, hence their projected separation in the transverse plane is zero, x1′ ⊥ − x1 ⊥ = 0, and the angular integration over the polar angle αk1′ vanishes.
Using the exponential representation of the Dirac factor, the second term reads as 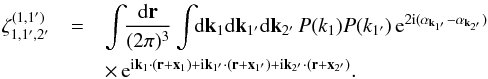 (A.8)Using Eqs. (30) and (31) in Eq. (A.8) gives
(A.8)Using Eqs. (30) and (31) in Eq. (A.8) gives 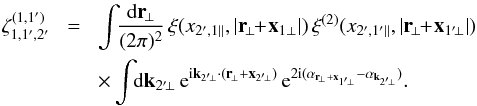 (A.9)Using the fact that x1′ ⊥ = x1 ⊥, we make the change of variables
(A.9)Using the fact that x1′ ⊥ = x1 ⊥, we make the change of variables  . Then, using the Jacobi-Anger expansion,
. Then, using the Jacobi-Anger expansion,  (A.10)and Eq. (A.4), we can perform the integration over k2′ ⊥, which gives
(A.10)and Eq. (A.4), we can perform the integration over k2′ ⊥, which gives 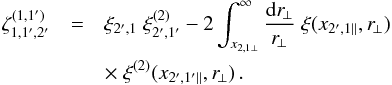 (A.11)As compared with the factor ξ2′,1ξ2′,1′ that arises for the convergence, as in Eq. (15), the source-lens clustering bias of the cosmic shear is suppressed by the spin-2 factor e2iα. It replaces one correlation ξ by a correlation ξ(2), which is smaller because of the subtraction in Eq. (32), and it yields a second subtraction in Eq. (A.11).
(A.11)As compared with the factor ξ2′,1ξ2′,1′ that arises for the convergence, as in Eq. (15), the source-lens clustering bias of the cosmic shear is suppressed by the spin-2 factor e2iα. It replaces one correlation ξ by a correlation ξ(2), which is smaller because of the subtraction in Eq. (32), and it yields a second subtraction in Eq. (A.11).
In a similar fashion, the third term of Eq. (A.5) also reads as 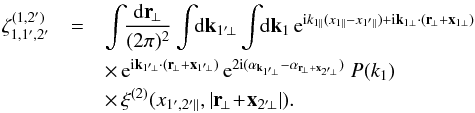 (A.12)Then, making the change of variable
(A.12)Then, making the change of variable 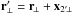 and using the expansion (A.10) we can integrate over angles. Next, using the property (A.4) and the summation rule
and using the expansion (A.10) we can integrate over angles. Next, using the property (A.4) and the summation rule  , we obtain
, we obtain 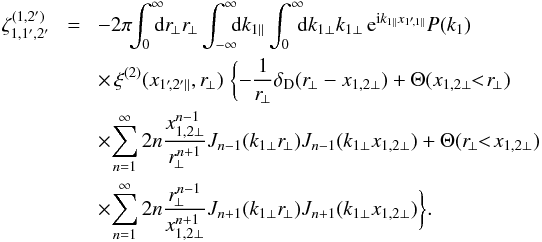 (A.13)Then, expressing P(k1) in terms of the two-point correlation function, as in
(A.13)Then, expressing P(k1) in terms of the two-point correlation function, as in 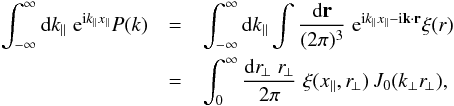 (A.14)and using the property
(A.14)and using the property ![\appendix \setcounter{section}{1} \begin{eqnarray} \lefteqn{\int_0^{\infty} \dd k \, k J_0(a k) J_n(b k) J_n(c k) = \Theta(|b-c|<a<b+c) \; \frac{\cos(n\varphi)}{\pi b c \sin(\varphi)}} \nonumber \\ && \mbox{with} \;\;\; \varphi = \mbox{Arccos}\left[ \frac{b^2+c^2-a^2}{2bc} \right] , \label{J0JnJn} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22146-13/aa22146-13-eq597.png) (A.15)where a > 0,b > 0,c > 0, n is integer, and Θ is a unit top-hat with obvious notations (i.e., unity when the conditions are satisfied and zero otherwise), we can integrate over k1 and we obtain
(A.15)where a > 0,b > 0,c > 0, n is integer, and Θ is a unit top-hat with obvious notations (i.e., unity when the conditions are satisfied and zero otherwise), we can integrate over k1 and we obtain 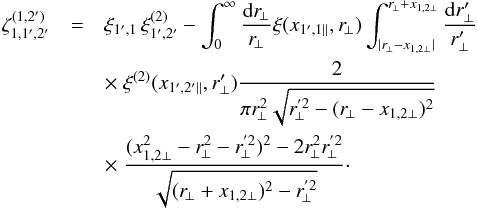 (A.16)Again, as compared with the factor ξ1′,1 ξ1′,2′ that arises for the convergence, the spin-2 factor e2iα suppresses the source-lens clustering bias by replacing a factor ξ by ξ(2) and introducing another subtraction.
(A.16)Again, as compared with the factor ξ1′,1 ξ1′,2′ that arises for the convergence, the spin-2 factor e2iα suppresses the source-lens clustering bias by replacing a factor ξ by ξ(2) and introducing another subtraction.
Appendix B: Three-point cosmic shear correlation
Using the exponential representation of the Dirac distribution, Eq. (60) also writes as ![\appendix \setcounter{section}{2} \begin{eqnarray} \zeta_{\rm circ.}^{\rm 2D} & = & \int_{-\infty}^{\infty} \dd x_{2'\parallel} \dd x_{3'\parallel} \int_0^{2\pi} \! \frac{\dd\alpha_{\vx_1}\dd\alpha_{\vx_2}\dd\alpha_{\vx_3}}{(2\pi)^3} \int \frac{\dd\vr}{(2\pi)^3} \nonumber \\ && \times \int \! \dd\vk_{1'}\dd\vk_{2'}\dd\vk_{3'} \, {\rm e}^{\ii [ \vk_{1'}\cdot(\vx_{1'}+\vr)+\vk_{2'}\cdot(\vx_{2'}+\vr)+\vk_{3'}\cdot(\vx_{3'}+\vr)]} \nonumber \\ && \times \; B(k_{1'},k_{2'},k_{3'}) \; {\rm e}^{2\ii (\alpha_{\vk_{1'}}+\alpha_{\vk_{2'}}+\alpha_{\vk_{3'}} - \alpha_{\vx_1} - \alpha_{\vx_2} - \alpha_{\vx_3})} . \label{zetap-circ-1} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22146-13/aa22146-13-eq602.png) (B.1)Integrating one after the other over the longitudinal components, { x2′ ∥,x3′ ∥ }, { k2′ ∥,k3′ ∥ }, { r∥,k1′ ∥ }, the angles { αx1,αx2,αx3 }, { αk1′,αk2′,αk3′ }, and αr, we obtain
(B.1)Integrating one after the other over the longitudinal components, { x2′ ∥,x3′ ∥ }, { k2′ ∥,k3′ ∥ }, { r∥,k1′ ∥ }, the angles { αx1,αx2,αx3 }, { αk1′,αk2′,αk3′ }, and αr, we obtain 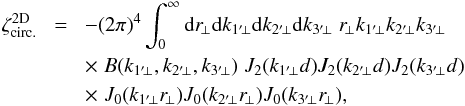 (B.2)where d = χ1′θ is the radius of the circumcircle at radial distance χ1′. Using the ansatz (37), this reads as
(B.2)where d = χ1′θ is the radius of the circumcircle at radial distance χ1′. Using the ansatz (37), this reads as 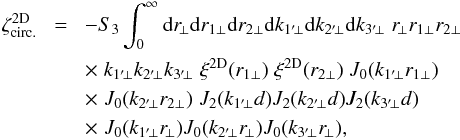 (B.3)where we used Eq. (A.14) to write
(B.3)where we used Eq. (A.14) to write 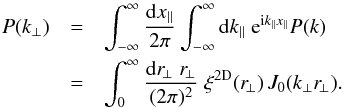 (B.4)Using the property (A.15) and
(B.4)Using the property (A.15) and ![\appendix \setcounter{section}{2} \begin{eqnarray} \lefteqn{\int_0^{\infty} \dd k J_1(a k) J_0(b k) J_0(c k)\! =\! \Theta( |b \!-\! c| \!<\! a \!<\! b+c) \frac{\varphi}{\pi a} + \frac{\Theta(a \!>\! b \!\!+\!\! c)}{a} } \nonumber \\ &&\hspace*{-3mm} \mbox{with} \;\;\; \varphi = \mbox{Arccos}\left[ \frac{b^2+c^2-a^2}{2bc} \right] , \label{J0J0J1} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22146-13/aa22146-13-eq612.png) (B.5)with the relation J0(z) + J2(z) = 2J1(z) / z, we obtain
(B.5)with the relation J0(z) + J2(z) = 2J1(z) / z, we obtain ![\appendix \setcounter{section}{2} \begin{eqnarray} \int_0^{\infty} \dd k \, k J_2(a k) J_0(b k) J_0(c k) & = & \frac{2\Theta(a \!>\! b \!+\! c)}{a^2} \nonumber \\ && \hspace{-1cm} + \frac{\Theta( |b \!-\! c| \!<\! a \!<\! b+c)}{\pi a^2} \left( 2\varphi - \frac{a^2}{bc\sin\varphi}\right) \nonumber \\ && \hspace{-4.2cm} \mbox{with} \;\;\; \varphi = \mbox{Arccos}\left[ \frac{b^2+c^2-a^2}{2bc} \right] \cdot \label{J2J0J0} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22146-13/aa22146-13-eq614.png) (B.6)Then, using Eqs. (A.4) and (B.6), we can integrate Eq. (B.3) over wavenumbers, which yields
(B.6)Then, using Eqs. (A.4) and (B.6), we can integrate Eq. (B.3) over wavenumbers, which yields ![\appendix \setcounter{section}{2} \begin{eqnarray} \zeta_{\rm circ.}^{\rm 2D} & = & S_3 \left( \int_0^{2d} \frac{\dd r \, r \, \xi^{\rm 2D}(r)} {\pi d^2} \left[ 2 \varphi - \frac{d}{r \sin(\varphi)} \right] \right)^{\!\!2} \!\! - S_3 \! \int_0^d \! \frac{\dd r \, 2r}{d^2} \nonumber \\ && \times \left( \int_{d-r}^{d+r} \frac{\dd r' \, r' \, \xi^{\rm 2D}(r')}{\pi d^2} \left[ 2 \varphi' - \frac{d^2}{r \, r' \sin(\varphi')} \right] \right. \nonumber \\ && \left. + \int_0^{d-r} \frac{\dd r' \; 2 r'}{d^2} \; \xi^{\rm 2D}(r') \right)^{\!\!2} , \label{zetap-circ-4} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22146-13/aa22146-13-eq615.png) (B.7)where the angles ϕ and ϕ′ are given by Eq. (65).
(B.7)where the angles ϕ and ϕ′ are given by Eq. (65).
Appendix C: Three-point lensing–intrinsic shear correlations
To compute the lensing–intrinsic three-point correlations (95) and (98) we proceed as in Appendix B. Using the exponential representation of the Dirac distribution, Eq. (95) also writes as ![\appendix \setcounter{section}{3} \begin{eqnarray} \zeta_{\rm circ.}^{\rm 2.5D} & \! = \! & \int_{-\infty}^{\infty} \dd x_{3'\parallel} \int_0^{2\pi} \! \frac{\dd\alpha_{\vx_1}\dd\alpha_{\vx_2}\dd\alpha_{\vx_3}}{(2\pi)^3} \int \frac{\dd\vr}{(2\pi)^3} \nonumber \\ && \times \int \! \dd\vk_1\dd\vk_2\dd\vk_{3'} \, {\rm e}^{\ii [ \vk_1\cdot(\vx_1+\vr)+\vk_2\cdot(\vx_2+\vr)+\vk_{3'}\cdot(\vx_{3'}+\vr)]} \nonumber \\ && \times \; B(k_1,k_2,k_{3'}) \; {\rm e}^{2\ii (\alpha_{\vk_1}+\alpha_{\vk_2}+\alpha_{\vk_{3'}} - \alpha_{\vx_1} - \alpha_{\vx_2} - \alpha_{\vx_3})} . \label{zeta-circ-2.5D-1} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22146-13/aa22146-13-eq616.png) (C.1)Integrating one after the other over the longitudinal components, { x3′ ∥,k3′ ∥ }, the angles { αx1,αx2,αx3 }, { αk1,αk2,αk3′ }, and αr, we obtain
(C.1)Integrating one after the other over the longitudinal components, { x3′ ∥,k3′ ∥ }, the angles { αx1,αx2,αx3 }, { αk1,αk2,αk3′ }, and αr, we obtain ![\appendix \setcounter{section}{3} \begin{eqnarray} \zeta_{\rm circ.}^{\rm 2.5D} & \! = \! & - (2\pi)^2 \!\! \int_{-\infty}^{\infty} \!\! \dd r_{\parallel} \dd k_{1\parallel} \dd k_{2\parallel} \int_0^{\infty} \!\! \dd r_{\!\perp} \dd k_{1\perp} \dd k_{2\perp} \dd k_{3'\!\perp} \; r_{\!\perp} k_{1\perp} k_{2\perp} \nonumber \\ && \times \; k_{3'\!\perp} \; {\rm e}^{\ii[ k_{1\parallel}(x_{1\parallel}+r_{\parallel}) +k_{2\parallel}(x_{2\parallel}+r_{\parallel}) ]} \, B(k_1,k_2,k_{3'\!\perp}) J_2(k_{1\perp} d) \nonumber \\ && \times \; J_2(k_{2\perp} d) J_2(k_{3'\!\perp} d) \; J_0(k_{1\perp} r_{\!\perp}) J_0(k_{2\perp} r_{\!\perp}) J_0(k_{3'\!\perp} r_{\!\perp}) , \label{zetap-circ-2.5D-2} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22146-13/aa22146-13-eq619.png) (C.2)where d = (χ1 + χ2)θ / 2 is the radius of the circumcircle at radial distance (χ1 + χ2) / 2 (this three-point correlation is only relevant when the two redshifts z1 and z2 are very close). Next, using the hierarchical ansatz (37), we can split
(C.2)where d = (χ1 + χ2)θ / 2 is the radius of the circumcircle at radial distance (χ1 + χ2) / 2 (this three-point correlation is only relevant when the two redshifts z1 and z2 are very close). Next, using the hierarchical ansatz (37), we can split 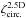 into three contributions. The first term, associated with the product P(k1)P(k2) in the bispectrum ansatz, writes as
into three contributions. The first term, associated with the product P(k1)P(k2) in the bispectrum ansatz, writes as ![\appendix \setcounter{section}{3} \begin{eqnarray} \zeta_{(12)}^{\rm 2.5D} & \! = \! & (2\pi)^2 \frac{S_3}{3} \!\! \int_{-\infty}^{\infty} \!\! \dd r_{\parallel} \dd k_{1\parallel} \dd k_{2\parallel} \int_0^{\infty} \!\! \dd r_{\!\perp} \dd k_{1\perp} \dd k_{2\perp} \; r_{\!\perp} k_{1\perp} k_{2\perp} \nonumber \\ && \times \; \left[ \frac{\delta_{\rm D}(r_{\perp}\!-\!d)}{d} - \frac{2\Theta(r_{\perp}\!<\!d)}{d^2} \right] {\rm e}^{\ii[ k_{1\parallel}(x_{1\parallel}+r_{\parallel}) +k_{2\parallel}(x_{2\parallel}+r_{\parallel}) ]} \nonumber \\ && \times \; J_2(k_{1\perp} d) J_2(k_{2\perp} d) \; J_0(k_{1\perp} r_{\!\perp}) J_0(k_{2\perp} r_{\!\perp}) P(k_1) P(k_2) , \label{zetap-circ-2.5D-12-1} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22146-13/aa22146-13-eq623.png) (C.3)where we used Eq. (A.4) to integrate over k3′ ⊥. Next, writing the power spectra in terms of the two-point correlation functions, we can integrate over { k1 ∥,k2 ∥ }. This yields
(C.3)where we used Eq. (A.4) to integrate over k3′ ⊥. Next, writing the power spectra in terms of the two-point correlation functions, we can integrate over { k1 ∥,k2 ∥ }. This yields ![\appendix \setcounter{section}{3} \begin{eqnarray} \zeta_{(12)}^{\rm 2.5D} & \! = \! & \frac{S_3}{3} \!\! \int_{-\infty}^{\infty} \!\! \dd r_{\parallel} \int_0^{\infty} \!\! \dd r_{\!\perp} \dd k_{1\perp} \dd k_{2\perp} \dd r_{1\perp} \dd r_{2\perp} \; r_{\!\perp} k_{1\perp} k_{2\perp} r_{1\perp} r_{2\perp} \nonumber \\ && \times \; \left[ \frac{\delta_{\rm D}(r_{\perp}\!-\!d)}{d} - \frac{2\Theta(r_{\perp}\!<\!d)}{d^2} \right] \, \xi(x_{1\parallel} \!+\! r_{\parallel},r_{1\perp}) \, \xi(x_{2\parallel} \!+\! r_{\parallel},r_{2\perp}) \nonumber \\ && \times \; J_2(k_{1\perp} d) J_2(k_{2\perp} d) \; J_0(k_{1\perp} r_{\!\perp}) J_0(k_{2\perp} r_{\!\perp}) \; J_0(k_{1\perp} r_{1\perp}) \nonumber \\ && \times \; J_0(k_{2\perp} r_{2\perp}) . \label{zetap-circ-2.5D-12-2} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22146-13/aa22146-13-eq626.png) (C.4)Using Eq. (B.6) we can integrate over { k1 ⊥,k2 ⊥ }, which yields
(C.4)Using Eq. (B.6) we can integrate over { k1 ⊥,k2 ⊥ }, which yields ![\appendix \setcounter{section}{3} \begin{eqnarray} \zeta_{(12)}^{\rm 2.5D} & \! = \! & \frac{S_3}{3} \int_{-\infty}^{\infty} \dd r_{\parallel} \biggl\lbrace \int_0^{2d} \frac{\dd r_1 \, r_1}{\pi d^2} \xi(x_{1\parallel} \!+\! r_{\parallel},r_1) \left[ 2 \varphi_1 - \frac{d}{r_1 \sin\varphi_1} \right] \nonumber \\ && \times \int_0^{2d} \frac{\dd r_2 \, r_2}{\pi d^2} \xi(x_{2\parallel}\! +\! r_{\parallel},r_2) \left[ 2 \varphi_2 - \frac{d}{r_2 \sin\varphi_2} \right] - \int_0^d \! \frac{\dd r_{\perp} \, 2r_{\perp}}{d^2} \nonumber \\ && \times \left( \int_{d-r_{\perp}}^{d+r_{\perp}} \frac{\dd r_1' \, r_1'}{\pi d^2} \xi(x_{1\parallel} \!+ \!r_{\parallel},r_1') \left[ 2 \varphi_1' - \frac{d^2}{r_{\perp} \, r_1' \sin\varphi_1'} \right] \right. \nonumber \\ && \left. + \int_0^{d-r_{\perp}}\! \frac{\dd r_1' \; 2 r_1'}{d^2} \, \xi(x_{1\parallel} \!+\! r_{\parallel},r_1') \right) \left( \int_{d-r_{\perp}}^{d+r_{\perp}} \frac{\dd r_2' \, r_2'}{\pi d^2} \xi(x_{2\parallel} \!+ \! r_{\parallel},r_2') \right. \nonumber \\ && \left. \times \left[ 2 \varphi_2' \!-\! \frac{d^2}{r_{\perp} \, r_2' \sin\varphi_2'} \right] \!+\! \int_0^{d-r_{\perp}} \! \frac{\dd r_2' \; 2 r_2'}{d^2} \xi(x_{2\parallel}\! +\! r_{\parallel},r_2') \! \right) \! \biggl \rbrace , \label{zetap-circ-2.5D-12-3} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22146-13/aa22146-13-eq628.png) (C.5)where the angles ϕi and
(C.5)where the angles ϕi and  are given by
are given by 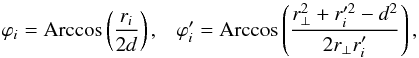 (C.6)as in Eq. (65). The second term in Eq. (C.2), associated with the product P(k1)P(k3), writes as
(C.6)as in Eq. (65). The second term in Eq. (C.2), associated with the product P(k1)P(k3), writes as ![\appendix \setcounter{section}{3} \begin{align} \zeta_{(13)}^{\rm 2.5D} =\ & (2\pi)^2 \frac{S_3}{3} \!\! \int_{-\infty}^{\infty} \!\! \dd r_{\parallel} \dd k_{1\parallel} \dd k_{2\parallel} \int_0^{\infty} \!\! \dd r_{\!\perp} \dd k_{1\perp} \dd k_{3'\!\perp} \; r_{\!\perp} k_{1\perp} k_{3'\!\perp} \nonumber \\ & \times \; \left[ \frac{\delta_{\rm D}(r_{\perp}\!-\!d)}{d} - \frac{2\Theta(r_{\perp}\!<\!d)}{d^2} \right] {\rm e}^{\ii[ k_{1\parallel}(x_{1\parallel}+r_{\parallel}) +k_{2\parallel}(x_{2\parallel}+r_{\parallel}) ]} \nonumber \\ & \times \; J_2(k_{1\perp} d) J_2(k_{3'\!\perp} d) \; J_0(k_{1\perp} r_{\!\perp}) J_0(k_{3'\!\perp} r_{\!\perp}) P(k_1) P(k_{3'\!\perp}) , \label{zetap-circ-2.5D-13-1} \end{align}](/articles/aa/full_html/2014/01/aa22146-13/aa22146-13-eq633.png) (C.6)where we used Eq. (A.4) to integrate over k2 ⊥. Next, writing the power spectra in terms of the two-point correlation functions, with Eq. (B.4) for P(k3′ ⊥), we can integrate over { k2 ∥,r∥,k1 ∥ }. This yields
(C.6)where we used Eq. (A.4) to integrate over k2 ⊥. Next, writing the power spectra in terms of the two-point correlation functions, with Eq. (B.4) for P(k3′ ⊥), we can integrate over { k2 ∥,r∥,k1 ∥ }. This yields ![\appendix \setcounter{section}{3} \begin{eqnarray} \zeta_{(13)}^{\rm 2.5D} & \! = \! & \frac{S_3}{3} \int_0^{\infty} \!\! \dd r_{\!\perp} \dd k_{1\perp} \dd k_{3'\!\perp} \dd r_{1\perp} \dd r_{3\perp} \; r_{\!\perp} k_{1\perp} k_{3'\!\perp} r_{1\perp} r_{3\perp} \nonumber \\ && \times \; \left[ \frac{\delta_{\rm D}(r_{\perp}\!-\!d)}{d} - \frac{2\Theta(r_{\perp}\!<\!d)}{d^2} \right] \, \xi(x_{1\parallel} \!-\! x_{2\parallel},r_{1\perp}) \, \xi^{\rm 2D}(r_{3\perp}) \nonumber \\ && \times \; J_2(k_{1\perp} d) J_2(k_{3'\!\perp} d) \; J_0(k_{1\perp} r_{\!\perp}) J_0(k_{3'\!\perp} r_{\!\perp}) \; J_0(k_{1\perp} r_{1\perp}) \nonumber \\ && \times \; J_0(k_{3'\!\perp} r_{3\perp}) . \label{zetap-circ-2.5D-13-2} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22146-13/aa22146-13-eq637.png) (C.8)Using Eq. (B.6) we can integrate over { k1 ⊥,k3′ ⊥ }, which yields
(C.8)Using Eq. (B.6) we can integrate over { k1 ⊥,k3′ ⊥ }, which yields ![\appendix \setcounter{section}{3} \begin{eqnarray} \zeta_{(13)}^{\rm 2.5D} & \! = \! & \frac{S_3}{3} \int_0^{2d} \frac{\dd r_1 \, r_1}{\pi d^2} \xi(x_{1\parallel} \!-\! x_{2\parallel},r_1) \left[ 2 \varphi_1 - \frac{d}{r_1 \sin\varphi_1} \right] \nonumber \\ && \times \; \int_0^{2d} \frac{\dd r_3 \, r_3}{\pi d^2} \xi^{\rm 2D}(r_3) \left[ 2 \varphi_3 - \frac{d}{r_3 \sin\varphi_3} \right] - \frac{S_3}{3} \int_0^d \! \frac{\dd r_{\perp} \, 2r_{\perp}}{d^2} \nonumber \\ && \times \; \left( \int_{d-r_{\perp}}^{d+r_{\perp}} \frac{\dd r_1' \, r_1'}{\pi d^2} \xi(x_{1\parallel} \!-\! x_{2\parallel},r_1') \left[ 2 \varphi_1' - \frac{d^2}{r_{\perp} \, r_1' \sin\varphi_1'} \right] \right. \nonumber \\ && \left. + \int_0^{d-r_{\perp}} \frac{\dd r_1' \; 2 r_1'}{d^2} \, \xi(x_{1\parallel} \!-\! x_{2\parallel},r_1') \right) \left( \int_{d-r_{\perp}}^{d+r_{\perp}} \frac{\dd r_3' \, r_3'}{\pi d^2} \xi^{\rm 2D}(r_3') \right. \nonumber \\ && \left. \times \left[ 2 \varphi_3' - \frac{d^2}{r_{\perp} \, r_3' \sin\varphi_3'} \right] \!+\! \int_0^{d-r_{\perp}} \! \frac{\dd r_3' \; 2 r_3'}{d^2} \, \xi^{\rm 2D}(r_3') \! \right) , \label{zetap-circ-2.5D-13-3} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22146-13/aa22146-13-eq639.png) (C.9)where the angles ϕi and
(C.9)where the angles ϕi and 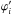 are given by Eq. (C.6). The third contribution
are given by Eq. (C.6). The third contribution 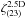 is obtained in the same manner, and within our approximation z1 ≃ z2 we have
is obtained in the same manner, and within our approximation z1 ≃ z2 we have 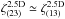 .
.
In a similar fashion, integrating over the angles { αx1,αx2,αx3 }, { αk1,αk2,αk3 }, and αr, Eq. (98) writes as ![\appendix \setcounter{section}{3} \begin{eqnarray} \zeta_{\rm circ.}^{\rm 3D} & \! = \! & - 2\pi \!\! \int_{-\infty}^{\infty} \!\! \dd r_{\parallel} \dd k_{1\parallel} \dd k_{2\parallel} \dd k_{3\parallel} \int_0^{\infty} \!\!\! \dd r_{\!\perp} \dd k_{1\perp} \dd k_{2\perp} \dd k_{3\perp} \; r_{\!\perp} k_{1\perp} k_{2\perp} \nonumber \\ && \times \; k_{3\perp} \; {\rm e}^{\ii[ k_{1\parallel}(x_{1\parallel}+r_{\parallel}) +k_{2\parallel}(x_{2\parallel}+r_{\parallel}) +k_{3\parallel}(x_{3\parallel}+r_{\parallel}) ]} \, B(k_1,k_2,k_3) \nonumber \\ && \times \; J_2(k_{1\perp} d) J_2(k_{2\perp} d) J_2(k_{3\perp} d) J_0(k_{1\perp} r_{\!\perp}) J_0(k_{2\perp} r_{\!\perp}) J_0(k_{3\perp} r_{\!\perp}) , \nonumber \\ && \label{zetap-circ-3D-2} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22146-13/aa22146-13-eq642.png) (C.10)where d = (χ1 + χ2 + χ3)θ / 3 is the radius of the circumcircle at radial distance (χ1 + χ2 + χ3) / 3 (this three-point correlation is only relevant when the three redshifts are very close). Next, using again the hierarchical ansatz (37), we can split
(C.10)where d = (χ1 + χ2 + χ3)θ / 3 is the radius of the circumcircle at radial distance (χ1 + χ2 + χ3) / 3 (this three-point correlation is only relevant when the three redshifts are very close). Next, using again the hierarchical ansatz (37), we can split 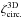 into three contributions. The first term, associated with the product P(k1)P(k2) in the bispectrum ansatz, writes as
into three contributions. The first term, associated with the product P(k1)P(k2) in the bispectrum ansatz, writes as ![\appendix \setcounter{section}{3} \begin{eqnarray} \zeta_{(12)}^{\rm 3D} & \! = \! & (2\pi)^2 \frac{S_3}{3} \!\! \int_{-\infty}^{\infty} \!\! \dd k_{1\parallel} \dd k_{2\parallel} \int_0^{\infty} \!\! \dd r_{\!\perp} \dd k_{1\perp} \dd k_{2\perp} \; r_{\!\perp} k_{1\perp} k_{2\perp} \nonumber \\ && \times \; \left[ \frac{\delta_{\rm D}(r_{\perp}\!-\!d)}{d} - \frac{2\Theta(r_{\perp}\!<\!d)}{d^2} \right] {\rm e}^{\ii[ k_{1\parallel}(x_{1\parallel}-x_{3\parallel}) +k_{2\parallel}(x_{2\parallel}-x_{3\parallel}) ]} \nonumber \\ && \times \; J_2(k_{1\perp} d) J_2(k_{2\perp} d) \; J_0(k_{1\perp} r_{\!\perp}) J_0(k_{2\perp} r_{\!\perp}) \; P(k_1) P(k_2) , \label{zetap-circ-3D-12-1} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22146-13/aa22146-13-eq646.png) (C.11)where we used Eq. (A.4) to integrate over k3 ⊥ and we also integrated over { k3 ∥,r∥ }. Next, writing the power spectra in terms of the two-point correlation functions, we can integrate over wavenumbers by using Eq. (B.6). This yields
(C.11)where we used Eq. (A.4) to integrate over k3 ⊥ and we also integrated over { k3 ∥,r∥ }. Next, writing the power spectra in terms of the two-point correlation functions, we can integrate over wavenumbers by using Eq. (B.6). This yields ![\appendix \setcounter{section}{3} \begin{eqnarray} \zeta_{(12)}^{\rm 3D} & \! = \! & \frac{S_3}{3} \int_0^{2d} \frac{\dd r_1 \, r_1}{\pi d^2} \; \xi(x_{1,3\parallel},r_1) \left[ 2 \varphi_1 - \frac{d}{r_1 \sin\varphi_1} \right] \nonumber \\ && \times \int_0^{2d} \! \frac{\dd r_2 \, r_2}{\pi d^2} \, \xi(x_{2,3\parallel},r_2) \left[ 2 \varphi_2 \!-\! \frac{d}{r_2 \sin\varphi_2} \right] \!-\! \frac{S_3}{3} \! \int_0^d \! \frac{\dd r_{\perp} \, 2r_{\perp}}{d^2} \nonumber \\ && \times \; \left( \int_{d\,-\,r_{\perp}}^{d+r_{\perp}} \frac{\dd r_1' \, r_1'}{\pi d^2} \, \xi(x_{1,3\parallel},r_1') \left[ 2 \varphi_1' - \frac{d^2}{r_{\perp} \, r_1' \sin\varphi_1'} \right] \right. \nonumber \\ && \left. + \int_0^{d\,-\,r_{\perp}} \frac{\dd r_1' \; 2 r_1'}{d^2} \, \xi(x_{1,3\parallel},r_1') \right) \left( \int_{d-r_{\perp}}^{d\,+\,r_{\perp}} \frac{\dd r_2' \, r_2'}{\pi d^2} \, \xi(x_{2,3\parallel},r_2') \right. \nonumber \\ && \left. \times \left[ 2 \varphi_2' - \frac{d^2}{r_{\perp} \, r_2' \sin\varphi_2'} \right] \!+\! \int_0^{d-r_{\perp}} \! \frac{\dd r_2' \; 2 r_2'}{d^2} \, \xi(x_{2,3\parallel},r_2') \! \right) , \label{zetap-circ-3D-12-2} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22146-13/aa22146-13-eq649.png) (C.12)where xi,j ∥ = xi ∥ − xj ∥ and the angles ϕi and
(C.12)where xi,j ∥ = xi ∥ − xj ∥ and the angles ϕi and 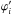 are given by Eq. (C.6). The second and third contributions
are given by Eq. (C.6). The second and third contributions 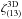 and
and 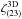 are also given by Eq. (C.12) through permutations over the indices { 1,2,3 }.
are also given by Eq. (C.12) through permutations over the indices { 1,2,3 }.
Appendix D: Comparison of models for the lensing three-point functions
 |
Fig. D.1 Convergence and shear three point correlations |
We compare in Fig. D.1 the predictions for three-point weak lensing correlations from the model of Valageas et al. (2012a,b),
which combines one-loop perturbation theory with a halo model (Valageas & Nishimichi 2011b) and has been checked against ray-tracing numerical simulations, with the predictions from the hierarchical ansatz (18). We consider the source redshift triplet { 0.5,1,2 } but other redshifts give similar results.
The shear three-point correlation is typically smaller than the convergence one because of the spin-2 factor e2iα, which leads to some cancellations as seen from the counterterms in Eq. (61) for the circular average (51). This effect is larger on smaller scales where the slope of 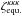 is lower.
is lower.
Figure D.1 shows that the hierarchical ansatz (18) provides the correct order of magnitude for weak lensing three-point functions on scales θ ≲ 50′. More precisely, both approximations agree to better than a factor 1.5 for θ < 10′ and a factor 3 for θ < 40′, for 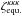 ; and to better than a factor 1.5 for θ < 30′ for
; and to better than a factor 1.5 for θ < 30′ for 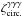 . Because most of the cosmological information from weak lensing three-point correlations measured in galaxy surveys comes from θ ≲ 10′, as the amplitude of the signal decreases on larger scales, the hierarchical ansatz (18) would be sufficient to estimate the relative importance of the source-lens clustering bias (which itself is dominated by contributions that only depend on the two-point density correlation) or of other sources of noise. This provides significantly faster numerical computations.
. Because most of the cosmological information from weak lensing three-point correlations measured in galaxy surveys comes from θ ≲ 10′, as the amplitude of the signal decreases on larger scales, the hierarchical ansatz (18) would be sufficient to estimate the relative importance of the source-lens clustering bias (which itself is dominated by contributions that only depend on the two-point density correlation) or of other sources of noise. This provides significantly faster numerical computations.
This is possible for a sufficiently wide survey because the denominator sums all pairs of separation θ over the survey. In contrast, if we consider the one-point estimator for a convergence map κ(θ), as in the analysis of Bernardeau (1998), for each direction θ on the sky the numerator and denominator only sum the small number of galaxies included within the smoothing radius θs. Then, the numerator and denominator show significant correlated fluctuations that must be taken into account. See the discussion in Sect. 6.
Acknowledgments
We thank T. Nishimichi for sending us the skewness and kurtosis measured in numerical simulations (Nishimichi & Taruya 2011) that we used in Fig. 1 to check the model (24). We thank M. Kilbinger for discussions. This work is supported in part by the French Agence Nationale de la Recherche under Grant ANR-12-BS05-0002.
References
- Albrecht, A., Bernstein, G., Cahn, R., et al. 2006 [arXiv:astro-ph/0609591] [Google Scholar]
- Bacon, D. J., Refregier, A. R., & Ellis, R. S. 2000, MNRAS, 318, 625 [NASA ADS] [CrossRef] [Google Scholar]
- Barber, A. J., Munshi, D., & Valageas, P. 2004, MNRAS, 347, 667 [NASA ADS] [CrossRef] [Google Scholar]
- Bartelmann, M., & Schneider, P. 2001, Phys. Rep., 340, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Bernardeau, F. 1998, A&A, 338, 375 [NASA ADS] [Google Scholar]
- Bernardeau, F., Colombi, S., Gaztañaga, E., & Scoccimarro, R. 2002a, Phys. Rep., 367, 1 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Bernardeau, F., Mellier, Y., & van Waerbeke, L. 2002b, A&A, 389, L28 [Google Scholar]
- Bernstein, G. M. 1994, ApJ, 424, 569 [NASA ADS] [CrossRef] [Google Scholar]
- Bridle, S., & King, L. 2007, New J. Phys., 9, 444 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, M. L., Taylor, A. N., Hambly, N. C., & Dye, S. 2002, MNRAS, 333, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Catelan, P., Kamionkowski, M., & Blandford, R. D. 2001, MNRAS, 320, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Colombi, S., Bouchet, F. R., & Hernquist, L. 1996, ApJ, 465, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Crittenden, R. G., Natarajan, P., Pen, U.-L., & Theuns, T. 2001, ApJ, 559, 552 [NASA ADS] [CrossRef] [Google Scholar]
- Croft, R. A. C., & Metzler, C. A. 2000, ApJ, 545, 561 [NASA ADS] [CrossRef] [Google Scholar]
- Fu, L., Semboloni, E., Hoekstra, H., et al. 2008, A&A, 479, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goroff, M. H., Grinstein, B., Rey, S.-J., & Wise, M. B. 1986, ApJ, 311, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Groth, E. J., & Peebles, P. J. E. 1977, ApJ, 217, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Hamana, T., Colombi, S. T., Thion, A., et al. 2002, MNRAS, 330, 365 [Google Scholar]
- Hamana, T., Miyazaki, S., Shimasaku, K., et al. 2003, ApJ, 597, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Heavens, A., Refregier, A., & Heymans, C. 2000, MNRAS, 319, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Heymans, C., Grocutt, E., Heavens, A., et al. 2013, MNRAS [Google Scholar]
- Hirata, C. M., & Seljak, U. 2004, Phys. Rev. D, 70, 063526 [NASA ADS] [CrossRef] [Google Scholar]
- Hirata, C. M., Mandelbaum, R., Ishak, M., et al. 2007, MNRAS, 381, 1197 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, W. 1999, ApJ, 522, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Jarvis, M., Bernstein, G., & Jain, B. 2004, MNRAS, 352, 338 [NASA ADS] [CrossRef] [Google Scholar]
- Jarvis, M., Jain, B., Bernstein, G., & Dolney, D. 2006, ApJ, 644, 71 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Joachimi, B., & Schneider, P. 2008, A&A, 488, 829 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Joachimi, B., Mandelbaum, R., Abdalla, F. B., & Bridle, S. L. 2011, A&A, 527, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Joachimi, B., Semboloni, E., Bett, P. E., et al. 2013a, MNRAS, 431, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Joachimi, B., Semboloni, E., Hilbert, S., et al. 2013b, MNRAS, 436, 819 [Google Scholar]
- Kaiser, N. 1992, ApJ, 388, 272 [NASA ADS] [CrossRef] [Google Scholar]
- Kilbinger, M., Fu, L., Heymans, C., et al. 2013, MNRAS, 430, 2200 [NASA ADS] [CrossRef] [Google Scholar]
- Landy, S. D., & Szalay, A. S. 1993, ApJ, 412, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Limber, D. N. 1953, ApJ, 117, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Mandelbaum, R., Hirata, C. M., Ishak, M., Seljak, U., & Brinkmann, J. 2006, MNRAS, 367, 611 [NASA ADS] [CrossRef] [Google Scholar]
- Mandelbaum, R., Blake, C., Bridle, S., et al. 2011, MNRAS, 410, 844 [NASA ADS] [CrossRef] [Google Scholar]
- Munshi, D., & Valageas, P. 2005, MNRAS, 360, 1401 [NASA ADS] [CrossRef] [Google Scholar]
- Munshi, D., Valageas, P., & Barber, A. J. 2004, MNRAS, 350, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Munshi, D., Valageas, P., van Waerbeke, L., & Heavens, A. 2008, Phys. Rep., 462, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Nishimichi, T., & Taruya, A. 2011, Phys. Rev. D, 84, 043526 [NASA ADS] [CrossRef] [Google Scholar]
- Peebles, P. J. E. 1980, The large-scale structure of the universe (Princeton, N.J.: Princeton University Press) [Google Scholar]
- Planck Collaboration 2013, A&A, submitted [arXiv:1303.5076] [Google Scholar]
- Refregier, A., Amara, A., Kitching, T. D., et al. 2010 [arXiv:1001.0061] [Google Scholar]
- Schneider, P., van Waerbeke, L., Jain, B., & Kruse, G. 1998, MNRAS, 296, 873 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, P., van Waerbeke, L., & Mellier, Y. 2002, A&A, 389, 729 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, P., Kilbinger, M., & Lombardi, M. 2005, A&A, 431, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schrabback, T., Hartlap, J., Joachimi, B., et al. 2010, A&A, 516, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scoccimarro, R., & Frieman, J. A. 1999, ApJ, 520, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Semboloni, E., Mellier, Y., van Waerbeke, L., et al. 2006, A&A, 452, 51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Semboloni, E., Heymans, C., van Waerbeke, L., & Schneider, P. 2008, MNRAS, 388, 991 [NASA ADS] [CrossRef] [Google Scholar]
- Semboloni, E., Schrabback, T., van Waerbeke, L., et al. 2011, MNRAS, 410, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Shi, X., Joachimi, B., & Schneider, P. 2010, A&A, 523, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Szapudi, I., & Colombi, S. 1996, ApJ, 470, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Valageas, P., & Clerc, N. 2012, A&A, 547, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valageas, P., & Nishimichi, T. 2011a, A&A, 527, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valageas, P., & Nishimichi, T. 2011b, A&A, 532, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valageas, P., Barber, A. J., & Munshi, D. 2004, MNRAS, 347, 654 [NASA ADS] [CrossRef] [Google Scholar]
- Valageas, P., Clerc, N., Pacaud, F., & Pierre, M. 2011, A&A, 536, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valageas, P., Sato, M., & Nishimichi, T. 2012a, A&A, 541, A161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valageas, P., Sato, M., & Nishimichi, T. 2012b, A&A, 541, A162 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valageas, P., Nishimichi, T., & Taruya, A. 2013, Phys. Rev. D, 87, 083522 [NASA ADS] [CrossRef] [Google Scholar]
- Van Waerbeke, L., Mellier, Y., Erben, T., et al. 2000, A&A, 358, 30 [NASA ADS] [Google Scholar]
- Wittman, D. M., Tyson, J. A., Kirkman, D., Dell’Antonio, I., & Bernstein, G. 2000, Nature, 405, 143 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
All Figures
 |
Fig. 1 Skewness S3 and kurtosis S4 at redshift z = 0.35. The solid lines are the analytical approximation (24) and the symbols are results from numerical simulations (Nishimichi & Taruya 2011) for top-hat cumulants. |
| In the text | |
 |
Fig. 2 Relative source-lens clustering bias of the weak lensing convergence two-point correlation ξκκ, as a function of the angular scale θ, for the three pairs of coincident source redshifts z1 = z2 = 0.5, 1, and 2, from top to bottom. In each panel, we show the ratios ξδκδκ / | ξκκ | (lower black line), ζδκκ / | ξκκ | (middle red line), and ηδδκκ / | ξκκ | (upper blue line). The spike for ζδκκ is due to a change of sign and this contribution to the bias is negative at large angles (in all figures in this paper, a positive/negative bias is shown by a solid/dotted line). |
| In the text | |
 |
Fig. 3 Same as in Fig. 2, but for pairs of different source redshifts, (z1,z2) = (0.5,1), (0.5,2), and (1,2). The contribution ηδδκκ is negative as shown by the dotted line. |
| In the text | |
 |
Fig. 4 Relative source-lens clustering bias of the weak lensing convergence two-point correlation, (ξδκδκ + ζδκκ + ηδδκκ) / | ξκκ |, as a function of the second galaxy redshift z2, for a fixed first galaxy redshift z1 = 0.5,1, or 2. We consider the angular scales θ = 1, 10, and 100 arcmin, from the upper to the lower panels. All total biases are positive. |
| In the text | |
 |
Fig. 5 Relative source-lens clustering bias of the weak lensing shear two-point correlation ξγγ∗, as a function of the angular scale θ, for the three pairs of coincident source redshifts z1 = z2 = 0.5, 1, and 2. The lower curves show the two-point contribution (33) and the upper curves the three-point contribution (34). The spike for ζδγγ∗ is due to a change of sign and at large angles this contribution to the bias is negative (dotted lines). |
| In the text | |
 |
Fig. 6 Same as in Fig. 5, but for pairs of different source redshifts, (z1,z2) = (0.5,1), (0.5,2), and (1,2). Solid lines correspond to positive bias and dotted lines to negative bias. |
| In the text | |
 |
Fig. 7 Relative source-lens clustering bias of the weak lensing shear two-point correlation, (ξδγδγ∗ + ζδγγ∗) / | ξγγ∗ | (we neglect the four-point contribution), as a function of the second galaxy redshift z2, for a fixed first galaxy redshift z1 = 0.5,1, or 2. We consider the angular scales θ = 1, 10, and 100 arcmin, from the upper to the lower panels. |
| In the text | |
 |
Fig. 8 Relative source-lens clustering bias of the equilateral weak lensing convergence three-point correlation |
| In the text | |
 |
Fig. 9 Relative source-lens clustering bias of the equilateral weak lensing convergence three-point correlation |
| In the text | |
 |
Fig. 10 Relative source-lens clustering bias of the circular weak lensing shear three-point correlation |
| In the text | |
 |
Fig. 11 Relative source-lens clustering bias of the circular weak lensing shear three-point correlation |
| In the text | |
 |
Fig. 12 Relative intrinsic-alignment bias of the weak lensing shear two-point correlation, ξI / | ξγγ∗ |, as a function of the angular scale θ, for three pairs of different source redshifts, (z1,z2) = (0.5,1),(0.5,2), and (1,2). All total biases are negative. |
| In the text | |
 |
Fig. 13 Relative intrinsic-alignment bias of the weak lensing shear two-point correlation, ξI / | ξγγ∗ |, as a function of the second galaxy redshift z2, for a fixed first galaxy redshift z1 = 0.5,1, or 2. We consider the angular scales θ = 1, 10, and 100 arcmin, from the upper to the lower panels. |
| In the text | |
 |
Fig. 14 Relative intrinsic-alignment bias of the circular weak lensing shear three-point correlation |
| In the text | |
 |
Fig. 15 Relative intrinsic-alignment bias of the circular weak lensing shear three-point correlation |
| In the text | |
 |
Fig. 16 Relative source-lens clustering–intrinsic-alignment bias of the circular weak lensing shear three-point correlation |
| In the text | |
 |
Fig. 17 Relative source-lens clustering–intrinsic-alignment bias of the circular weak lensing shear three-point correlation |
| In the text | |
 |
Fig. D.1 Convergence and shear three point correlations |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.