| Issue |
A&A
Volume 561, January 2014
|
|
|---|---|---|
| Article Number | A47 | |
| Number of page(s) | 13 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201321581 | |
| Published online | 23 December 2013 | |
High spectral resolution spectroscopy of the SiO fundamental lines in red giants and red supergiants with VLT/VISIR⋆,⋆⋆
Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
e-mail: kohnaka@mpifr.de
Received: 26 March 2013
Accepted: 29 October 2013
Context. The mass-loss mechanism in red giants and red supergiants is not yet understood well. The SiO fundamental lines near 8 μm are potentially useful for probing the outer atmosphere, which is essential for clarifying the mass-loss mechanism. However, these lines have been little explored until now.
Aims. We present high spectral resolution spectroscopic observations of the SiO fundamental lines near 8.1 μm in 16 bright red giants and red supergiants. Our sample consists of seven normal (i.e., non-Mira) K–M giants (from K1.5 to M6.5), three Mira stars, three optically bright red supergiants, two dusty red supergiants, and the enigmatic object GCIRS3 near the Galactic center.
Methods. Our program stars were observed between 8.088 μm and 8.112 μm with a spectral resolution of 30 000 using VLT/VISIR.
Results. We detected SiO fundamental lines in all of our program stars except for GCIRS3. The SiO lines in normal K and M giants as well as optically bright (i.e., not dusty) red supergiants do not show P-Cyg profiles or blueshifts, which means the absence of systematic outflows in the SiO line forming region. We detected P-Cyg profiles in the SiO lines in the dusty red supergiants VY CMa and VX Sgr, with the latter object being a new detection. These SiO lines originate in the outflowing gas with the thermal dust continuum emission seen as the background. The outflow velocities of the SiO line forming region in VY CMa and VX Sgr are estimated to be 27 km s-1 and 17 km s-1, respectively. We derived basic stellar parameters (effective temperature, surface gravity, luminosity, and mass) for the normal K–M giants and optically bright red supergiants in our sample and compared the observed VISIR spectra with synthetic spectra predicted from MARCS photospheric models. Most of the SiO lines observed in the program stars warmer than ~3400 K are reasonably reproduced by the MARCS models, which allowed us to estimate the silicon abundance as well as the 28Si/29Si and 28Si/30Si ratios. However, we detected possible absorption excess in some SiO lines. Moreover, the SiO lines in the cooler red giants and red supergiant cannot be explained by the MARCS models at all, even if the dust emission is taken into account. This disagreement may be a signature of the dense, extended molecular outer atmosphere.
Key words: infrared: stars / techniques: spectroscopic / stars: AGB and post-AGB / stars: late-type / stars: atmospheres / supergiants
Based on VISIR observations made with the Very Large Telescope of the European Southern Observatory. Program ID: 087.D-0522(A).
Reduced spectra are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/561/A47
© ESO, 2013
1. Introduction
Mass loss in red giants and red supergiants is a long-standing problem in stellar astrophysics. The combination of large-amplitude stellar pulsation and momentum transfer from radiation to dust is often believed to be responsible for mass loss (see, e.g., Höfner 2011, for recent review). However, as Höfner (2011) notes, there are stars with stellar parameters outside the range of this “pulsation-enhanced dust-driven wind scenario”, for example, stars with much smaller pulsation amplitudes and/or with little or no dust. This suggests that we may not yet understand the major physical processes responsible for driving mass outflows in red giants and red supergiants in general.
Summary of the VISIR observations.
To understand the mass-loss mechanism, it is essential to study the region between the photosphere and the innermost region of the circumstellar envelope, where the wind acceleration takes place. The molecule SiO is important in the atmosphere and circumstellar envelope of oxygen-rich cool evolved stars. Hinkle et al. (1976) revealed significant time variations in the SiO first overtone bands near 4 μm in Mira stars. The SiO first overtone bands have also been used to test the model atmospheres of red giants (e.g., Aringer et al. 1999; Lebzelter et al. 2001). Tsuji et al. (1994) determined the elemental abundance of silicon as well as its isotope ratios in M giants and M supergiants from high-resolution spectra of the SiO first overtone lines. Their analysis also reveals that while the weak and moderate SiO lines can be explained well by the hydrostatic photospheric models, the strong SiO lines in the latest M giants (M7–8III) show excess emission originating in an extended outer atmosphere. This extended outer atmosphere, the so-called MOLsphere (Tsuji 2000b), cannot be accounted for by hydrostatic photospheric models. The presence of the MOLsphere in normal (i.e., non-Mira) K–M giants, Mira stars, and red supergiants has been confirmed by IR spectroscopic and interferometric observations of molecules such as CO and H2O (e.g., Tsuji et al. 1997; Tsuji 2000a,b, 2001; Perrin et al. 2004a,b, 2005; Wittkowski et al. 2007, 2008, 2011; Woodruff et al. 2008, 2009; Le Bouquin et al. 2009; Martí-Vidal 2011; Ohnaka 2004a,b, 2012, 2013; Ohnaka et al. 2011, 2013).
The current MOLsphere models consist of ad hoc layers placed above the photosphere, and the density, temperature, and radius of the extended molecular outer atmosphere are determined to fit observed data. For Mira stars, dynamical model atmospheres have been developed (e.g., Ireland et al. 2011; Bladh et al. 2013) that predict the density and temperature distribution, as well as molecular abundances in the outer atmosphere in a self-consistent manner. These models can be compared to observed spectra. Unfortunately, dynamical model atmospheres for normal red giants and red supergiants, whose variability amplitudes are much smaller than in Mira stars, have not been studied as much. Probing the physical properties of the outer atmosphere using the ad hoc models is useful for gleaning information about the as-yet-unidentified physical process responsible for forming the extended molecular outer atmosphere.
The SiO fundamental lines near 8 μm are ideal for studying the physical properties of the outer atmosphere and the innermost circumstellar envelope. Geballe et al. (1979) observed the SiO fundamental lines in the dusty red supergiant VY CMa with a spectral resolution of 13 000. They discovered SiO lines with the P-Cyg profile originating in an expanding circumstellar envelope. The SiO lines with the P-Cyg profile in VY CMa were also detected much later by Richter et al. (2001) with a higher spectral resolution of 100 000. Keady & Ridgway (1993) detected weak, blueshifted SiO lines in the dusty carbon star IRC+10216 originating in the inner envelope. These studies suggest that the SiO fundamental lines are potentially useful for probing the outer atmosphere and the innermost circumstellar envelope. However, there are only a few high-resolution spectroscopic studies of the SiO fundamental lines in red giants and red supergiants in the literature. In this paper, we present the results of high-resolution spectroscopic observations of the poorly explored SiO fundamental lines in a sample of red giants and red supergiants with VLT/VISIR.
2. Observations
2.1. Sample
Our sample consists of seven normal (i.e., non-Mira-type) K–M giants, three Mira stars, five red supergiants, and the enigmatic object toward the Galactic center GCIRS3. We selected these stars to cover a range of spectral types, luminosity classes, and variabilities in order to systematically study the dependence of the SiO lines on the stellar parameters. As summarized in Table 1, seven K–M giants in our sample cover the spectral type from K1.5III to M6.5III. All of these stars, except for L2 Pup and θ Aps, show very little or no dust, as shown by the dust emission contrast (DEC), which is defined as the ratio of the dust emission to the emission from the star integrated over the spectral range between 7.67 and 14.03 μm (Sloan & Price 1998). The DEC values in Table 1 were taken from Sloan & Price (1998) except for α Boo, γ Cru, and VY CMa, which are not included in their list. We estimated the DEC values of α Boo and γ Cru to be zero based on the absence of an IR excess up to ~1000 μm (Dehaes et al. 2011). We estimated the DEC value of VY CMa from the model fitting of the spectral energy distribution presented by Harwit et al. (2001). The negative DEC values for ε Mus and α Her from Sloan & Price (1998) probably result from the uncertainty in defining the stellar continuum. We interpret them as showing no dust emission. Our sample includes three Mira stars, R Hya, R Aql, and W Hya. While this last star is classified as a semiregular variable on Simbad, it is often regarded as Mira-like because its variability amplitude is larger than usual semiregular variables, and it shows clear periodicity (e.g., Woodruff et al. 2009; Zhao-Geisler et al. 2011). The variability phase at the time of our VISIR observations was estimated from the light curves available at the American Association of Variable Star Observers (AAVSO). The red supergiants in our sample consist of three optically bright stars (α Ori, α Sco, and α Her) and two dusty stars (VY CMa and VX Sgr). The nature of the last object in our sample, GCIRS3, is not clear yet. Based on high spatial resolution mid-IR observations, Pott et al. (2008) suggest that it may be a dust-enshrouded carbon star, despite the strong silicate absorption at 10 μm. We included this object because some molecular lines may reveal the nature of the object.
2.2. VLT/VISIR observations and data reduction
We observed our program stars on 2011 April 19 between 8.088 μm and 8.112 μm with VLT/VISIR (Lagage et al. 2004). We used the high-resolution long-slit (HR) mode with a slit width of 0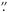 4, which resulted in a spectral resolution 30 000. We selected this spectral window, because it is not severely affected by telluric lines, except for the strong ones at 8.091 and 8.107 μm. A summary of the observations of the science targets and the calibrators is given in Table 1. The data were reduced with the VISIR pipeline ver. 3.0.0 provided by ESO (Lundin et al. 2008). The output of the pipeline reduction is the 1D spectra of the targets. The wavelength calibration was carried out using the telluric lines. The uncertainty in the wavelength calibration is ~7.0 × 10-5μm (2.6 km s-1). The telluric lines were removed by dividing the spectra of the science targets with those of the calibrators. In most cases, we used the calibrators that were observed before or after the science target within 0.5−1 h at similar airmasses (differences smaller than ~0.2). In the case of α Boo, it was necessary to use the calibrator observed with a time interval as long as 4.5 h. In either case, however, the strong telluric lines at 8.091 μm and 8.107 μm could not be completely removed, and so, we excluded these wavelengths from the analysis. The spectra are normalized by the local continuum level defined by the highest flux points in the observed spectral window. Because most of our program stars are very bright, we achieved signal-to-noise ratios of 100–200. The exception is GCIRS3, for which we achieved a signal-to-noise ratio of only 20.
4, which resulted in a spectral resolution 30 000. We selected this spectral window, because it is not severely affected by telluric lines, except for the strong ones at 8.091 and 8.107 μm. A summary of the observations of the science targets and the calibrators is given in Table 1. The data were reduced with the VISIR pipeline ver. 3.0.0 provided by ESO (Lundin et al. 2008). The output of the pipeline reduction is the 1D spectra of the targets. The wavelength calibration was carried out using the telluric lines. The uncertainty in the wavelength calibration is ~7.0 × 10-5μm (2.6 km s-1). The telluric lines were removed by dividing the spectra of the science targets with those of the calibrators. In most cases, we used the calibrators that were observed before or after the science target within 0.5−1 h at similar airmasses (differences smaller than ~0.2). In the case of α Boo, it was necessary to use the calibrator observed with a time interval as long as 4.5 h. In either case, however, the strong telluric lines at 8.091 μm and 8.107 μm could not be completely removed, and so, we excluded these wavelengths from the analysis. The spectra are normalized by the local continuum level defined by the highest flux points in the observed spectral window. Because most of our program stars are very bright, we achieved signal-to-noise ratios of 100–200. The exception is GCIRS3, for which we achieved a signal-to-noise ratio of only 20.
We converted the wavelength scale to the heliocentric frame and then to the laboratory frame. The heliocentric systemic velocities of our program stars are listed in Table 1 with the uncertainties. We took the systemic velocities measured by radio CO observations in the literature if available (references are also listed in the table). The systemic velocities derived from the CO lines originating in the expanding circumstellar envelope are not subject to atmospheric motions induced by pulsation and/or convection, which can affect the determination of the systemic velocity using spectral lines in the visible. In case velocities derived from different radio CO lines are available, we took the mean of the velocities and adopted a half of the maximum and minimum velocities as the uncertainty. For α Boo, γ Cru, σ Lib, V806 Cen, ε Mus, α Sco, and α Her, no radio CO observations are available. For these stars, we took the radial velocities from Gontcharov (2006), which were derived from spectral lines in the visible. These data represent well the systemic velocity for K and early/mid-M giants whose variability amplitude is small. For example, the time variation in the radial velocity in α Boo and γ Cru is ± 0.3 km s-1 and ± 0.6 km s-1, respectively (Hatzes & Cochran 1993; Murdoch et al. 1992). No radial velocity monitoring is available in the literature for σ Lib, V806 Cen, and ε Mus. Therefore, for these stars we adopted the same uncertainty of ± 0.6 km s-1 as in γ Cru.
Conversely, the visible spectral lines in the red supergiants α Sco and α Her show time variations in the radial velocity of up to ~10 km s-1 due to the atmospheric motions (Smith et al. 1989). We adopted these time variations as the uncertainty in the systemic velocity of α Sco and α Her. While α Sco and α Her both have binary companions, the effect of the orbital motion on the radial velocity is much smaller than the time variations due to the atmospheric motions for the following reason. The red supergiant α Sco A has a B2.5V companion. Using the binary parameters presented in Braun et al. (2012), we estimated the orbital velocity of α Sco A to be 2 km s-1, which is much smaller than 10 km s-1. The system α Her includes the red supergiant α1 Her and a secondary (α2 Her) with a separation of 4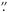 6, which corresponds to 504 AU at a distance of 110 pc (from the Hipparcos parallax; van Leeuwen 2007). The secondary α2 Her itself is a spectroscopic binary with a G8III star (α2 Her A) and an A9IV-V star (α2 Her B) with a separation of 0.17 AU and a period of 51.6 days (Deutsch 1956). Assuming an edge-on circular orbit around the red supergiant α1 Her for this spectroscopic binary and adopting the mass of 2.7, 2.6, and 2.0 M⊙ for α1 Her, α2 Her A, and α2 Her B, respectively (based on the results of Moravveji et al. 2013), the orbital velocity of α1 Her is estimated to be ~2 km s-1, which is again much smaller than the 10 km s-1 caused by the atmospheric motions.
6, which corresponds to 504 AU at a distance of 110 pc (from the Hipparcos parallax; van Leeuwen 2007). The secondary α2 Her itself is a spectroscopic binary with a G8III star (α2 Her A) and an A9IV-V star (α2 Her B) with a separation of 0.17 AU and a period of 51.6 days (Deutsch 1956). Assuming an edge-on circular orbit around the red supergiant α1 Her for this spectroscopic binary and adopting the mass of 2.7, 2.6, and 2.0 M⊙ for α1 Her, α2 Her A, and α2 Her B, respectively (based on the results of Moravveji et al. 2013), the orbital velocity of α1 Her is estimated to be ~2 km s-1, which is again much smaller than the 10 km s-1 caused by the atmospheric motions.
For GCIRS3, no radial velocity measurement is available. Therefore, the wavelength scale is converted only to the heliocentric frame.
 |
Fig. 1 Observed VISIR spectra of the SiO fundamental lines in seven K–M giants. The positions of the 28SiO, 29SiO, and 30SiO lines relatively free from blends with other species are marked by the black, red, and green arrows, respectively. The identification of these lines are also given (in case of multiple transitions within one feature, only the main contributor is given). The positions of the 28SiO, 29SiO, 30SiO, and H2O lines are shown by the black, red, green, and blue ticks, respectively (H2O lines are plotted only for L2 Pup and θ Aps). The dotted lines show the local continuum. |
 |
Fig. 2 Observed VISIR spectra of the SiO fundamental lines in three optically bright (i.e., not very dusty) red supergiants, shown in the same manner as in Fig. 1. |
3. Results
3.1. Optically bright red giants and red supergiants
Figure 1 shows the observed spectra of seven normal K–M giants in our sample with the positions of the 28Si16O, 29Si16O, and 30Si16O lines (hereafter simply denoted as 28SiO, 29SiO, and 30SiO), that are taken from the line list recently published by Barton et al. (2013). For the spectra of L2 Pup and θ Aps, the positions of the H2O lines taken from the line list of Barber et al. (2006) are also plotted. Most of the observed features are blends of different Si isotopes. Several lines that are relatively free from the blend of other species are marked and identified in the figure. In particular, the 29SiO lines at 8.0925 and 8.1077 μm, as well as the 30SiO lines at 8.0933 and 8.0944 μm are nearly free from the blend of different isotope species. Tsuji et al. (1994) derived 28Si/29Si = 13–20 and 28Si/30Si = 17–29 for M5–8 giants from the SiO first overtone lines near 4 μm. We estimate the silicon isotope ratios using the observed SiO fundamental lines in Sect. 4.
The SiO lines can already be seen in the K1.5 giant α Boo and they are stronger in M giants (γ Cru, σ Lib, V806 Cen, and ε Mus) than in α Boo but without clear dependence on the spectral type. The lack of clear correlation between the strengths of the SiO fundamental lines and the spectral type (or effective temperature) is already found in the spectra with lower spectral resolutions (Cohen & Davis 1995; Sloan & Price 1998; Heras et al. 2002). We will return to this point in Sect. 4.2.1, where we compare the observed data with synthetic spectra from hydrostatic photospheric models. The SiO lines become weaker in L2 Pup and θ Aps than in the earlier M giants. As the DEC values in Table 1 suggest, these two stars show noticeable dust emission, which makes the SiO lines appear weaker. However, as shown in Sect. 4.2.2, the observed spectra of L2 Pup and θ Aps cannot be explained just by the photospheric models with the dust emission, suggesting the possible effects of the MOLsphere on the SiO fundamental lines.
Figure 2 shows the observed spectra of the optically bright red supergiants α Ori, α Sco, and α Her. The SiO lines in α Ori and α Sco are significantly broader than those observed in the K–M giants, reflecting the larger turbulent velocities found in these red supergiants (e.g., Ohnaka et al. 2009, and references therein).
The observed SiO line positions of the K–M giants and optically bright red supergiants agree well with those from the line list within the uncertainty of the wavelength calibration. No P-Cyg profiles and/or blueshifts, which would be a signature of outflows, were detected. This suggests that the SiO fundamental lines form in the photosphere and also possibly in the MOLsphere, where the material is not yet systematically outflowing.
 |
Fig. 3 Observed VISIR spectra of the SiO fundamental lines in two dusty red supergiants. The positions of the 28SiO lines with the P-Cyg profile are shown by the arrows. |
3.2. Dusty red supergiants
Figure 3 shows the observed spectra of two dusty red supergiants, VY CMa and VX Sgr, which show much more prominent dust emission than do the red giants and red supergiants discussed above. The observed VISIR spectra reveal the 28SiO line at 8.0952 μm (1 − 0 R(3)) with the P-Cyg profile. The mid-IR spectra of these stars are dominated by the dust emission, which is responsible for the continuum. Given that the SiO lines originating in the photosphere and MOLsphere are masked by the prominent dust emission, the observed SiO line with the P-Cyg profile originates in the circumstellar envelope. The P-Cyg profile in the SiO line in VY CMa is consistent with what is reported in Richter et al. (2001). On the other hand, the SiO line with the P-Cyg profile has been detected for the first time toward VX Sgr. Richter et al. (2001) report the detection of the P-Cyg profile in the SiO line at 8.1044 μm (1 − 0 R(2)) as well. However, the line profile in our spectra of VY CMa and VX Sgr does not indicate the P-Cyg profile as clearly as the SiO line at 8.0952 μm. This might be due to the lower spectral resolution (λ/Δλ ≈ 30 000) compared to the 105 achieved by Richter et al. (2001).
 |
Fig. 4 Modeling of the P-Cyg profile of the SiO line 1 − 0 R(3) observed in VY CMa panel a) and VX Sgr panel b). In each panel, the red solid line represents the observed spectrum, while the black solid line represents the model spectrum. |
To estimate the outflow velocities in VY CMa and VX Sgr, we computed the profile of the SiO line at 8.0952 μm using a simple model of a spherically expanding shell with a constant velocity. This model consists of a dust shell, which emits as the blackbody of 1500 K and provides the continuum, and an expanding SiO layer with a temperature of 500 K placed at some distance from the continuum-forming dust layer. The free parameters are the expansion velocity, radius, SiO column density, and microturbulent velocity of the SiO layer. The SiO line profile was computed assuming local thermodynamical equilibrium (LTE). Figure 4 shows a comparison of the predicted and observed line profiles for VY CMa and VX Sgr. The observed P-Cyg profiles of VY CMa and VX Sgr are reasonably reproduced by an expansion velocity of 27 km s-1 and 17 km s-1, respectively. The radius of the SiO layer in VY CMa and VX Sgr is 2.5 and 2 times larger than the radius of the continuum-forming dust layer, respectively. A microturbulent velocity of 7 km s-1 was found to fit the observed profiles well. The SiO column density derived for VY CMa and VX Sgr is 5 × 1017 cm-2 and 4 × 1017 cm-2, respectively. The column density derived for VY CMa is in rough agreement with the 7 × 1017 cm-2 estimated by Geballe et al. (1979) from the P-Cyg profile of the SiO line at 8.309 μm. However, the strength of the absorption and emission components in the P-Cyg profile depends on the combination of the temperature, radius, and column density of the SiO layer, and these parameters cannot be unambiguously constrained by our observations of the single SiO line alone. Nevertheless, the wavelength shifts of the absorption and emission components are primarily determined by the outflow velocity. Therefore, the derived outflow velocities are not significantly dependent on the uncertainties in the other parameters. Given the terminal wind velocities of 44–48 km s-1 and 22–26 km s-1 for VY CMa and VX Sgr, respectively (Kemper et al. 2003), this SiO line at 8.0952 μm originates in the region, where the material has reached approximately 60–70% of the terminal velocity and is being further accelerated.
 |
Fig. 5 Observed VISIR spectra of the SiO fundamental lines in three Mira stars, shown in the same manner as in Fig. 1. |
3.3. Mira stars
Figure 5 shows the observed spectra of three Mira stars, R Aql, R Hya, and W Hya. The spectral features in R Hya and R Aql are systematically weaker than the dust-free M4–5 giants shown in Fig. 1, but are comparable to the M6.5 giant θ Aps. Given that the dust emission in θ Aps (DEC = 0.29) is similar to R Aql and R Hya (DEC = 0.36 and 0.24, respectively), the contribution of the dust emission is probably (at least partially) responsible for making the SiO lines appear weaker (but we note that the dust emission alone cannot account for the weak spectral features in θ Aps, as we discuss in Sect. 4.2.2). This can also explain why the SiO lines in W Hya, whose DEC value (0.10) is lower than in R Aql and R Hya, are more pronounced.
As the figure shows, there are a number of H2O lines in the observed spectral window, but many of them are blended with the SiO lines. The only H2O feature relatively free from the blend with the SiO lines is the broad absorption between 8.0995 μm and 8.1 μm. The only SiO line relatively free from the blend of H2O lines is the 29SiO line at 8.0925 μm, as marked in the figure. This 29SiO line in R Aql and R Hya is broader compared to the normal K–M giants shown in Fig. 1. In the case of R Hya, the line is redshifted by 7.8 km s-1, although the H2O lines at 8.093 μm may also be partially responsible for the apparent wavelength shift. The same line in W Hya is narrower than in R Aql and R Hya, but is redshifted by 5.4 km s-1. While it cannot be entirely excluded that an unidentified blend is responsible for the broadening of this 29SiO line, it may also be due to the line doubling caused by different radial velocities at different layers. For example, Hinkle & Barnes (1979) and Hinkle et al. (1982) revealed line doubling in the near-IR H2O and CO lines in Mira stars. They also report time variations in the radial velocity of these lines with an amplitude of 10–20 km s-1. Therefore, the SiO fundamental lines provide a useful tool for probing the atmospheric dynamics. Monitoring observations are necessary to better understand the effects of the pulsation on the formation layer of the SiO fundamental lines.
3.4. GCIRS3
The nature of GCIRS3 is not yet clear. While the deep silicate absorption feature at 10 μm indicates its oxygen-rich nature, Pott et al. (2008) propose that it is a dust-enshrouded carbon star based on their mid-IR interferometric observations. The observed spectrum of GCIRS3 plotted in Fig. 6 shows only weak features. We compared the spectrum of GCIRS3 with those of the Mira stars in our sample, but we could not identify the SiO or H2O lines in GCIRS3. It does not show SiO lines in the P-Cyg profile unlike VY CMa and VX Sgr, although the spectral energy distribution of GCIRS3 suggests that the star is dust-enshrouded. Therefore, the absence of the SiO and H2O lines lends support to the hypothesis of Pott et al. (2008) that GCIRS3 is a dust-enshrouded carbon star.
4. Comparison with model atmospheres
4.1. Determination of basic stellar parameters
4.1.1. K–M giants and optically bright red supergiants
We compared the observed SiO spectra with those predicted by photospheric models. For the normal K–M giants and optically bright red supergiants shown in Figs. 1 and 2, we used the MARCS photospheric models (Gustafsson et al. 2008)1, which represent plane-parallel or spherical non-gray hydrostatic photospheres with the molecular and atomic line opacities taken into account with the opacity sampling technique. We used spherical MARCS models for our study. Each MARCS model is specified by the effective temperature (Teff), surface gravity (log 1), stellar mass (M⋆), microturbulent velocity (νmicro), and chemical composition.
Basic stellar parameters, silicon abundance, and 28Si/29Si and 28Si/30Si ratios of the K–M giants and optically bright red supergiants in our sample.
For two K–M giants (α Boo and σ Lib) and three optically bright red supergiants (α Ori, α Sco, and α Her), most of the basic stellar parameters, in particular Teff and log 1, are available in the literature and are summarized in Table 2. For the other stars (γ Cru, V806 Cen, ε Mus, L2 Pup, and θ Aps), we derived Teff, M⋆, and log 1 in the following manner. We determined Teff using the observed bolometric flux and the angular diameter. While the angular diameter measurement is available for γ Cru (Glindemann et al. 2001), the angular diameter of the remaining stars was estimated from the relationship between the angular size and the (V − K) color derived by van Belle (1999). We used the relationship for normal giants and supergiants from van Belle (1999) for V806 Cen, ε Mus, and θ Aps. The relationship for variable stars was adopted for L2 Pup because this star shows a larger variability amplitude than the other stars. The bolometric flux of each star was computed from photometric data from the visible to the mid-IR (~20 μm) taken from the literature (Johnson et al. 1966; Morel & Magnenat 1978; Mermilliod 1991; Ducati 2002; NOMAD Catalog, Zacharias et al. 2005; 2MASS, Skrutskie et al. 2006; WISE All-Sky Data Release, Cutri et al. 2012). The photometric data were de-reddened using the interstellar extinction Aλ estimated as follows. We derived AV using the 3D model of the interstellar extinction of Arenou et al. (1992). Assuming AV = 3.1E(B − V) and Aλ/E(B − V) from Savage & Mathis (1979), we obtained the interstellar extinction Aλ in each photometric band. We confirmed that the Teff derived for σ Lib in this manner agrees with the value determined with the infrared flux method (Tsuji 2008), lending support to the reliability of our method for Teff determination.
The error in the derived Teff results from the uncertainty in the estimated angular diameter and the bolometric flux. Van Belle (1999) mentions that the accuracy in the angular diameter derived from the (V − K) color is approximately 10%. The uncertainty in the bolometric flux results from the fact that our stars are semiregular or irregular variables with a variability amplitude of ΔV ≲ 1.5 mag, and the photometric data in different bands were not taken contemporaneously. We assumed an uncertainty of 13% in the bolometric flux, adopting the value derived for the red supergiant Betelgeuse, which shows a similar variability amplitude (Ohnaka et al. 2013).
We note that L2 Pup started a dimming event around 1994, which is probably caused by episodic dust formation (Bedding et al. 2002). The dimming event was still in progress at the time of our VISIR observation. However, Bedding et al. (2002) conclude that the effective temperature or the luminosity is unlikely to have changed with respect to the pre-dimming state. Therefore, we used the (V − K) color of L2 Pup in the pre-dimming state to estimate Teff, because the photometric data during the dimming event are affected by the newly formed dust and, therefore, do not reflect the color of the star itself.
Because the distance to our program stars is known thanks to the Hipparcos parallax (van Leeuwen 2007), it is straightforward to estimate the luminosity (L⋆) from the de-reddened bolometric flux and the distance. Using the Teff and L⋆ determined in this manner, our program stars are plotted on the H-R diagram, as shown in Fig. 7. Also plotted are theoretical evolutionary tracks for 0.6, 1, and 1.5 M⊙ stars taken from Bertelli et al. (2008) and for a 2 M⊙ star from Herwig (2005)2. Comparison with these evolutionary tracks allows us to estimate the stellar mass. Combining the stellar mass with the stellar radius, which can be computed from Teff and L⋆, results in the surface gravity.
The chemical composition, in particular [Fe/H] and the CNO abundances, is also necessary to specify the MARCS models. However, the analysis of the chemical composition is available only for two K and M giants, α Boo and σ Lib, and two red supergiants, α Ori and α Her. The CNO abundances derived for α Boo, σ Lib, and α Her (Decin et al. 2003; Ramirez et al. 2011; Smith et al. 2013; Tsuji 2008) roughly agree with the moderately CN-cycled composition from the MARCS model grid. We assumed this chemical composition from the MARCS model grid for the M giants (with the exception of α Boo and σ Lib as the CNO abundances are determined for these two stars). On the other hand, the CNO abundances derived for the red supergiant α Ori (Tsuji 2006) are closer to the heavily CN-cycled composition from the MARCS grid. For the red supergiant α Sco, we adopted the same CNO abundances as α Ori, based on the similarity in Teff, log 1, and M⋆ (Ohnaka et al. 2013). The metallicity ([Fe/H]) is determined only for α Boo ([Fe/H] = −0.5, Decin et al. 2003; Ramirez et al. 2011) and α Ori ([Fe/H] = 0.1, Lambert et al. 1984). Therefore, we assumed the solar metallicity for the M giants and supergiants except α Boo, for which we adopted [Fe/H] = −0.5.
We used a microturbulent velocity of 2.5 km s-1 for the K–M giants in our sample and the red supergiant α Her and 5 km s-1 for the red supergiants α Ori and α Sco based on the analyses of Smith & Lambert (1990), Tsuji (2006; 2008), and Tsuji et al. (1994).
For each star, we selected the MARCS model with parameters closest to the ones derived as described above. The derived basic stellar parameters and the MARCS models adopted for our program stars are listed in Table 2.
 |
Fig. 7 H-R diagram. The observationally derived positions of seven K–M giants in our sample are plotted by the filled diamonds with error bars. The theoretical evolutionary track from the main sequence to the asymptotic giant branch for a 2 M⊙ star from Herwig (2005) is shown by the solid line. The evolutionary tracks from Bertelli et al. (2008) for 0.6, 1, and 1.5 M⊙ stars with the solar metallicity (Z = 0.017) and a 1 M⊙ star with a subsolar metallicity (Z = 0.004, appropriate for α Boo) are shown by the dots. |
4.1.2. Mira stars
Because the effective temperature and luminosity (and thus the radius) of Mira stars are expected to change with phase, it is necessary to determine the stellar parameters at the time of our VISIR observations to specify model atmospheres. Recently Ireland et al. (2011) have presented time series of dynamical model atmospheres for Mira stars. To check whether there are models appropriate for the Mira stars that we observed, we estimated the luminosity of our program stars at the phase of our VISIR observations. For R Aql, using the bolometric flux of (351.2 ± 52.7) × 10-8 erg cm-2 s-1 (Hofmann et al. 2000) and the distance of 240 pc (Whitelock et al. 2000), we obtain L⋆ = 6300 L⊙ (phase = 0.18). For R Hya and W Hya, we estimated the luminosity at the phase of our VISIR observations from the bolometric magnitude and its amplitude obtained by Whitelock et al. (2000). The resulting luminosity of R Hya and W Hya is 7200 L⊙ (phase = 0.44) and 9900 L⊙ (phase = 0.00), respectively. While some models in Ireland et al. (2011) have approximately the same luminosities as the observationally derived ones at the corresponding phases, the models have either periods that are too long or variability amplitudes that are too large compared to R Aql, R Hya, and W Hya. The models of Ireland et al. (2011) were computed for stellar parameters appropriate for o Cet, R Leo, and R Cas. Therefore, comparison of the VISIR spectra of our Mira stars with the models should be carried out, when dynamical models with parameters appropriate for our program stars become available.
4.2. Comparison between VISIR spectra and MARCS models
Using the temperature and pressure stratifications of the MARCS models, we computed synthetic spectra including the SiO fundamental lines and H2O lines. We used the SiO line list recently published by Barton et al. (2013)3, which is more complete than the line list of Langhoff & Bauschlicher (1993) that has been widely used. The H2O line list was taken from Barber et al. (2006)4. Details of the computation of the synthetic spectra are described in the Appendix of Ohnaka (2013).
 |
Fig. 8 Comparison of the synthetic spectra based on the MARCS models with the observed VISIR spectra of seven K–M giants. The observed and synthetic spectra are shown by the black and red solid lines, respectively. The relatively isolated 28SiO, 29SiO, and 30SiO lines are marked by the black, red, and green arrows, respectively. See Fig. 1 for their identification. The 28SiO lines with absorption excess are marked by the blue dots. |
4.2.1. K–M giants warmer than ~3400 K
Figures 8a–8e show a comparison of the VISIR spectra of five K–M giants warmer than ~3400 K with the MARCS synthetic spectra, which are already convolved with a Gaussian that represents the instrumental resolution and the macroturbulence. We adopted a macroturbulent velocity of 3 km s-1 for these K–M giants based on the analysis of the CO first overtone lines by Tsuji (1986).
The relatively isolated 28SiO lines marked by the black arrows in the figure allow us to estimate the silicon abundance. For α Boo, we first computed a synthetic spectrum with log ASi = 7.01 (the abundance is given on the scale of log AH = 12), which corresponds to the solar value of log ASi = 7.51 (Asplund et al. 2009)5 scaled to [Fe/H] = −0.5. However, the synthetic spectrum predicts the SiO lines to be too weak. We found that the observed spectrum can be reproduced well by the increased silicon abundance of log ASi = 7.5 ± 0.1. Given the error in the derived silicon abundance, this value roughly agrees with log ASi = 7.45 (errors smaller than 0.1 dex) derived by Peterson et al. (1993) and log ASi = 7.32 ± 0.04 derived more recently by Ramirez et al. (2011) from the atomic Si lines in the visible. The observed spectra of γ Cru, σ Lib, V806 Cen, and ε Mus are consistent with the solar silicon abundance of log ASi = 7.51. The uncertainty in the silicon abundance is ±0.2 dex for γ Cru and σ Lib and ±0.3 dex for V806 Cen and ε Mus. The reason for the larger uncertainty in cooler stars is that the strength of the 28SiO lines observed in our spectral window becomes insensitive to the silicon abundance in cooler stars.
Using the 29SiO lines at 8.0925, 8.1012, 8.1033, and 8.1077 μm, as well as the 30SiO lines at 8.0933, 8.0944, and 8.1030 μm, we estimated the 28Si/29Si and 28Si/30Si ratios. The observed 29SiO and 30SiO lines in α Boo, γ Cru, and V806 Cen are reasonably reproduced by 28Si/29Si = 15 and 28Si/30Si = 25, which are the average values in M giants analyzed by Tsuji et al. (1994). On the other hand, we found (28Si/29Si, 28Si/30Si) = (30, 50) and (15, 50) for σ Lib and ε Mus, respectively. The errors in the 28Si/29Si and 28Si/30Si ratios are ±30% and ±40%, respectively. The relatively large errors result from the small number of 29SiO and 30SiO lines used in the analysis. The derived silicon abundance and isotope ratios are summarized in Table 2.
There are slight wavelength shifts in the observed positions of some SiO lines compared to the synthetic spectra (e.g., 8.094 and 8.096 μm). However, given the uncertainty in the wavelength calibration of 2.6 km s-1, these wavelength shifts, which are 3 km s-1 at most, cannot be definitively regarded as evidence of the atmospheric motions.
In Sect. 3.1, we mentioned the apparent lack of clear correlation between the SiO line strength and the spectral type among the M giants discussed here. To better understand this observational result, we show in Fig. 9 the synthetic SiO spectra predicted from the MARCS models with Teff = 3400 and 3600 K and log 1 = 0.0 and 1.0 (other parameters are M⋆ = 1 M⊙, νmicro = 2 km s-1, [Fe/H] = 0.0, and moderately CN-cycled composition). The figure shows that the SiO lines become stronger with decreasing Teff and increasing log 1 in the Teff and log 1 range relevant to our M giants. In our sample, the cooler stars tend to have lower surface gravities. Therefore, the increase in the SiO line strength due to lower Teff can be canceled out by the decrease in the line strength due to lower log 1, which results in a weak dependence of the SiO line strength on the spectral type.
 |
Fig. 9 Synthetic spectra of the SiO lines for Teff = 3600 K and 3400 K and log 1= 0.0 and 1.0 (other parameters are M⋆ = 1 M⊙, νmicro = 2 km s-1, [Fe/H] = 0.0, and moderately CN-cycled composition). The dashed line represents the continuum. We included no lines at either edge of the spectral range to show the continuum level. |
 |
Fig. 10 Comparison of the synthetic spectra from the MARCS models with the observed VISIR spectra of three optically bright red supergiants, shown in the same manner as in Fig. 8. See Fig. 2 for the identification of the lines. |
While the observed spectra of α Boo and σ Lib are explained well by the MARCS models, there is noticeable disagreement between the observed and synthetic spectra for some SiO lines in γ Cru, V806 Cen, and ε Mus. The 28SiO lines at 8.0939 (2−1 R(12)), 8.0991 (3–2 R(21)), and 8.1025 μm (2−1 R(11)), marked by the blue dots in Fig. 8, are stronger than predicted by the MARCS models. Increasing the silicon abundance does not reconcile this problem, because the agreement for the other 28SiO lines marked by the black arrows would not be as good. The lines at 8.0939 and 8.0991 μm include blends of weaker 29SiO and 30SiO lines, respectively. However, increasing the abundance of these isotopic species would lead to poorer agreement for other 29SiO and 30SiO lines marked by the red and green arrows. Changing the stellar parameters within their uncertainties does not improve the agreement either.
The 28SiO lines with the absorption excess have low excitation potentials (0.16–0.30 eV), while the weaker 28SiO lines reproduced well by the models have higher excitation potentials of 0.77–1.40 eV. This is similar to what is found for the SiO first overtone lines in latest M giants by Tsuji et al. (1994), which is interpreted as the indication of the MOLsphere, as outlined in Sect. 1. Therefore, the absorption excess in the SiO fundamental lines with low excitation potentials may also be a signature of the MOLsphere. However, as described in Sect. 4.1, we assumed the CNO abundances and [Fe/H] for γ Cru, V806 Cen, and ε Mus, because no quantitative analysis of the chemical composition is available in the literature. Therefore, we cannot exclude the possibility that the absorption excess may be due to this assumed chemical composition. To confirm that the absorption excess is indeed a signature of the MOLsphere, the determination of the CNO abundances and [Fe/H] in these stars is necessary.
4.2.2. Cool M giants with Teff ≈ 2800 K: L2 Pup and θ Aps
As Figs. 8f and 8g show, the agreement between the observed and synthetic spectra is very poor for L2 Pup and θ Aps. In these stars, which are much cooler (Teff = 2800–2900 K) than the stars discussed above, the MARCS models predict the H2O lines to be strong. Most of the features in the synthetic spectra shown in Figs. 8f and 8g are due to H2O. However, the shape and depth of the spectral features predicted by the models show little correspondence to the observed spectra.
Because L2 Pup and θ Aps show dust emission (DEC = 0.60 and 0.29, respectively), we tentatively added a fractional contribution of the continuum dust emission of 50% in the synthetic spectra. Changing the fractional contribution of the dust continuum emission does not reconcile the disagreement, because it only makes all spectral features appear weaker or stronger and cannot alter the relative strengths of different spectral features. On the other hand, if there is emission from the extended MOLsphere, it can fill in the absorption and make the resultant spectrum (i.e., integrated over the entire stellar image in the sky) appear very different from the photospheric spectrum. Therefore, the disagreement between the observed and photospheric model spectra in L2 Pup and θ Aps may be, again, a signature of the MOLsphere.
In Figs. 8f and 8g, the normalized flux of the synthetic spectra is higher than 1 at some wavelengths that are masked by the strong telluric lines (e.g., 8.088 μm). This is not emission, but has occurred simply because we attempted to obtain the best match to the VISIR data at the wavelengths not severely affected by the telluric lines. In other words, the wavelengths of the strong telluric lines were excluded from the fitting.
4.2.3. Optically bright red supergiants
Figure 10 shows a comparison between the observed and synthetic spectra for the three optically bright red supergiants. For α Ori, α Sco, and α Her, we adopted (log ASi, 28Si/29Si, 28Si/30Si) = (7.45, 20, 25), (7.44, 13, 25), and (7.26, 20, 29), respectively, based on the results from the SiO first overtone lines by Tsuji et al. (1994). Because the 28Si/30Si ratio could not be determined for α Ori and α Sco in Tsuji et al. (1994), we assumed it to be the same as the average value among M giants. We note that these silicon abundances were already corrected for the difference in the 1f-values used in Tsuji et al. (1994) and this work. We adopted a macroturbulent velocity of 10 km s-1 for α Ori (Tsuji 2006) and assumed the same value for α Sco, while we used a macroturbulent velocity of 3 km s-1 for α Her (Tsuji 1986). The figure shows that the VISIR spectra of α Ori and α Sco are reproduced by the MARCS models, although the agreement is not as good as in the warm K–M giants discussed in Sect. 4.2.1. The agreement is much worse for α Her. The model predicts many features to be too strong. We computed synthetic spectra using models with slightly different parameters but could not improve the fit. Given that α Her shows little dust emission, the disagreement cannot be solved by adding the dust emission either. As in the cases of L2 Pup and θ Aps discussed above, this disagreement may be attributed to the emission from the extended MOLsphere.
The fair agreement between the observed and model spectra for α Ori is a little surprising, because Tsuji (2006) demonstrates that the SiO absorption bands observed longward of 7.5 μm with a spectral resolution of 1600 are much weaker than predicted by the photospheric model, suggesting the contribution of H2O and possibly also SiO emission from the extended MOLsphere. However, the signature of the MOLsphere can be masked in spatially unresolved spectra, because the additional absorption due to the MOLsphere can be filled in by the extended emission from the MOLsphere itself. This can make the resultant, spatially unresolved spectrum appear nearly unchanged. For example, Ohnaka et al. (2012) and Ohnaka (2013) demonstrate that although the spatially unresolved spectra of the 2.3 μm CO first overtone lines in K and M giants can be reproduced well by the MARCS photospheric models alone and show very little signature of the MOLsphere, spatially resolved spectro-interferometric observations clearly reveal the presence of the extended MOLsphere. This means that constraining the parameters of the MOLsphere from spatially unresolved spectra alone is not necessarily straightforward.
Therefore, to probe the properties of the MOLsphere from the SiO fundamental lines, it would be useful to combine the present VISIR spectra with interferometric observations. The mid-IR interferometric instrument MIDI at the ESO’s Very Large Telescope Interferometer (VLTI), as well as the next generation VLTI instrument MATISSE, can spatially resolve our program stars from 8 μm to 13 μm. Although the spectral resolution is much lower (~200 at most with MIDI), a combination of the spatially unresolved, high spectral resolution VISIR data and spatially resolved data with a lower spectral resolution taken with MIDI or MATISSE would enable us to constrain the parameters of the MOLsphere more reliably. We plan to present such an analysis for α Sco and α Her, for which we have obtained MIDI data, in a forthcoming paper.
5. Concluding remarks
We have obtained high-resolution spectra of the 8.1 μm SiO fundamental lines in 16 cool evolved stars, consisting of seven normal (i.e., non-Mira) K and M giants, five red supergiants, three Mira stars, and the enigmatic object GCIRS3 toward the Galactic center. The SiO lines detected in the K–M giants, as well as in the optically bright red supergiants, do not show a signature of systematic outflows. On the other hand, we detected SiO lines with the P-Cyg profile in the dusty red supergiants VY CMa and VX Sgr, with the latter object being a new detection. A simple modeling of the observed P-Cyg profiles suggests an outflow velocity of 27 km s-1 and 17 km s-1 in VY CMa and VX Sgr, respectively. We also detected a broadening and/or redshift in an 29SiO line in Mira stars. In GCIRS3, no SiO or H2O lines can be identified, which is consistent with the previous suggestion that this object is a dust-enshrouded carbon star, despite the presence of the 10 μm silicate feature.
The observed spectra of K–M giants warmer than ~3400 K are reasonably reproduced by the MARCS photospheric models. However, the MARCS models cannot explain the observed spectra of the cooler (Teff ≈ 2800 K) M giants at all, even if the dust emission is taken into account. Similarly, while the observed spectra of the red supergiants α Ori and α Sco (Teff ≈ 3700 K) can be fairly reproduced by the MARCS models, the observed spectrum of the cooler red supergiant α Her (Teff ≈ 3300 K) shows noticeable disagreement with the MARCS model. This disagreement in the cooler M giants and red supergiant may be a signature of the MOLsphere. Combination of VISIR high-resolution spectroscopy and mid-IR spectro-interferometry would be necessary to probe the contribution of the MOLsphere in the SiO fundamental lines. Given that silicon plays an important role in dust formation in oxygen-rich stars, studying the physical properties of the SiO gas in the MOLsphere is indispensable for understanding the dust formation in oxygen-rich stars.
Available at http://marcs.astro.uu.se
Available at http://www.exomol.com/data/molecules/SiO
Available at http://www.exomol.com/data/molecules/H2O
The silicon abundance log ASi = 7.51 was determined with a 3D solar model atmosphere, while we used 1D MARCS models. However, Asplund et al. (2009) show that the difference in the silicon abundance derived from the 3D and 1D solar model atmospheres is only 0.02 dex.
Acknowledgments
We thank the ESO VLT team for supporting our VISIR observations. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France. We acknowledge with thanks the variable star observations from the AAVSO International Database contributed by observers worldwide and used in this research. This publication makes use of data products from the Wide-field Infrared Survey Explorer, which is a joint project of the University of California, Los Angeles, and the Jet Propulsion Laboratory/California Institute of Technology, funded by the National Aeronautics and Space Administration. This publication also makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation.
References
- Arenou, F., Grenon, M., & Gómez, A. 1992, A&A, 258, 104 [NASA ADS] [Google Scholar]
- Aringer, B., Höfner, S., Wiedemann, G., et al. 1999, A&A, 342, 799 [NASA ADS] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Barber, R. J., Tennyson, J., Harris, G. J., & Tolchenov, R. N. 2006, MNRAS, 368, 1087 [NASA ADS] [CrossRef] [Google Scholar]
- Barton, E. J., Yurchenko, S. N., & Tennyson, J. 2013, MNRAS, 434, 1469 [NASA ADS] [CrossRef] [Google Scholar]
- Bedding, T., Zijlstra, A. A., Jones, A., et al. 2002, MNRAS, 337, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Bertelli, G., Girardi, L., Marigo, P., & Nasi, E. 2008, A&A, 484, 815 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bladh, S., Höfner, S., Nowotny, W., Aringer, B., & Eriksson, K. 2013, A&A, 553, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Braun, K., Baade, R., Reimers, D., & Hagen, H.-J. 2012, A&A, 546, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cohen, M., Davies, J. K. 1995, MNRAS, 276, 715 [NASA ADS] [CrossRef] [Google Scholar]
- Cutri, R. M. et al. 2012, Vizier On-line Data Catalog, II/311 [Google Scholar]
- Decin, L., Vandenbussche, B., Waelkens, C., et al. 2003, A&A, 400, 709 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dehaes, S., Bauwens, E., Decin, L., et al. 2011, A&A, 533, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deutsch, A. 1956, ApJ, 123, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Ducati, J. R. 2002, Catalogue of Stellar Photometry in Johnson’s 11-color system, CDS/ADC Collection of Electronic Catalogues, 2237 [Google Scholar]
- Geballe, T. R., Lacy, J. H., & Beck, S. C. 1979, ApJ, 230, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Glindemann, A., Bauvir, B., Delplancke, F., et al. 2001, ESO Messenger, 104, 2 [NASA ADS] [Google Scholar]
- Gontscharov, G. A. 2006, Astron. Lett., 32, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harper, G. M., Brown, A., & Guinan, E. 2008, AJ, 135, 1430 [NASA ADS] [CrossRef] [Google Scholar]
- Harwit, M., Malfait, K., Decin, L., et al. 2001, ApJ, 557, 844 [NASA ADS] [CrossRef] [Google Scholar]
- Hatzes, A., & Cochran, W. D. 1993, ApJ, 413, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Heras, A. M., Shipman, R. F., Price, S. D., et al. 2002, A&A, 394, 539 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Herwig, F. 2005, ARA&A, 43, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Hinkle, K. H., & Barnes, T. G. 1979, ApJ, 227, 923 [NASA ADS] [CrossRef] [Google Scholar]
- Hinkle, K. H., Barnes, T. G., Lambert, D. L., & Beer, R. 1976, ApJ, 210, L141 [NASA ADS] [CrossRef] [Google Scholar]
- Hinkle, K. H., Hall, D. N. B., & Ridgway, S. 1982, ApJ, 252, 697 [NASA ADS] [CrossRef] [Google Scholar]
- Hofmann, K.-H., Beckmann, U., Blöcker, T., et al. 2000, SPIE Proc., 4006, 688 [NASA ADS] [CrossRef] [Google Scholar]
- Höfner, S. 2011, in Why Galaxies Care About AGB stars II: Shining examples and common inhabitants, eds. F. Kerschbaum, T. Lebzelter, & R. Wing, ASP Conf. Ser. 445, 193 [Google Scholar]
- Ireland, M., Scholz, M., & Wood, P. R. 2011, MNRAS, 418, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, H. L., Iriarte, B., Mitchell, R. I., & Wisniewskj, W. Z. 1966, Comm. Lunar & Planetary Lab. 4, 99 [Google Scholar]
- Keady, J. J., & Ridgway, S. T. 1993, ApJ, 406, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Kemper, F., Stark, R., Justtanont, K., et al. 2003, A&A, 407, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kerschbaum, F., & Olofsson, H. 1999, A&AS, 138, 299 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lacour, S., Meimon, S., Thiébaut, E., et al. 2008, A&A, 485, 561 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lagage, P.O., Pel, J. W., Authier, M., et al. 2004, The Messenger, 117, 12 [NASA ADS] [Google Scholar]
- Lambert, D. L., Brown, J. A., Hinkle, K. H., & Johnson, H. R. 1984, ApJ, 284, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Langhoff, S. R., & Bauschlicher, C. W., Jr. 1993, Chem. Phys. Lett., 211, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Le Bouquin, J.-B., Lacour, S., Renard, S., et al. 2009, A&A, 496, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lebzelter, T., Hinkle, K. H., & Aringer, B. 2001, A&A, 377, 617 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lundin, K. L., Ballester, P., & Peron, M. 2008, VLT VISIR Pipeline User Manual (ESO) [Google Scholar]
- Martí-Vidal, I., Marcaide, J. M., Quirrenbach, A., et al. 2011, A&A, 529, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mermilliod, J.C. 1991, Catalogue of Homogeneous Means in the UBV System, Institut d’Astronomie, Université de Lausanne [Google Scholar]
- Moravveji, E., Guinan, E., Khosroshahi, H., & Wasatonic, R. 2013, AJ, 146, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Morel, M., & Magnenat, P. 1978, A&AS, 34 477 [Google Scholar]
- Murdoch, K., Clark, M., & Hearnshaw, J. B. 1992, MNRAS, 254, 27 [NASA ADS] [Google Scholar]
- O’Gorman, E., Harper, G. M., Brown, J. M., et al. 2012, AJ, 144, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Ohnaka, K. 2004a, A&A, 421, 1149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ohnaka, K. 2004b, A&A, 424, 1011 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ohnaka, K. 2013, A&A, 553, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ohnaka, K., Hofmann, K.-H., Benisty, M., et al. 2009, A&A, 503, 183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ohnaka, K., Weigelt, G., Millour, F., et al. 2011, A&A, 529, A163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ohnaka, K., Hofmann, K.-H., Schertl, D., et al. 2012, A&A, 537, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ohnaka, K., Hofmann, K.-H., Schertl, D., et al. 2013, A&A, 555, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perrin, G., Ridgway, S. T., Coudé du Foresto, V., et al. 2004a, A&A, 418, 675 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perrin, G., Ridgway, S. T., Mennesson, B., et al. 2004b, A&A, 426, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perrin, G., Ridgway, S. T., Verhoelst, T., et al. 2005, A&A, 436, 317 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peterson, R., Dalle Ore, C. M., & Kurucz, R. 1993, ApJ, 404, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Pott, J.-U., Eckart, A., Glindemann, A., et al. 2008, A&A, 480, 115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramírez, I., & Allen de Prieto, C. 2011, ApJ, 743, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Richter, M. J., Lacy, J. H., Greathouse, T. K., & Jaffe, D. T. 2001, Rev. Mex. Astron. Astrophys., 10, 53 [NASA ADS] [Google Scholar]
- Savage, B., & Mathis, J. S. 1979, ARA&A, 17, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Sloan, G.C., & Price, S. D. 1998, ApJS, 119, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, V. V., & Lambert, D. L. 1990, ApJS, 72, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, M. A., Patten, B. M., & Goldberg, L. 1989, AJ, 98, 2233 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, V. V., Cunha, K., Shetrone, M. D., et al. 2013, ApJ, 765, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Tsuji, T. 1986, A&A, 156, 8 [NASA ADS] [Google Scholar]
- Tsuji, T. 2000a, ApJ, 538, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Tsuji, T. 2000b, ApJ, 540, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Tsuji, T. 2001, A&A, 376, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tsuji, T. 2006, ApJ, 645, 1448 [NASA ADS] [CrossRef] [Google Scholar]
- Tsuji, T. 2008, A&A, 489, 1271 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tsuji, T., Ohnaka, K., Hinkle, K. H., & Ridgway, S. T. 1994, A&A, 289, 469 [NASA ADS] [Google Scholar]
- Tsuji, T., Ohnaka, K., Aoki, W., & Yamamura, I. 1997, A&A, 320, L1 [NASA ADS] [Google Scholar]
- van Belle, G. 1999, PASP, 111, 1515 [NASA ADS] [CrossRef] [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Whitelock, P., Marang, F., & Feast, M. 2000, MNRAS, 319, 728 [NASA ADS] [CrossRef] [Google Scholar]
- Wittkowski, M., Boboltz, D. A., Ohnaka, K., Driebe, T., & Scholz, M. 2007, A&A, 470, 191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wittkowski, M., Boboltz, D. A., Driebe, T., et al. 2008, A&A, 479, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wittkowski, M., Boboltz, D. A., Ireland, M., et al. 2011, A&A, 532, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woodruff, H. C., Tuthill, P. G., Monnier, J. D., et al. 2008, ApJ, 673, 418 [NASA ADS] [CrossRef] [Google Scholar]
- Woodruff, H. C., Ireland, M. J., Tuthill, P. G., et al. 2009, ApJ, 691, 1328 [NASA ADS] [CrossRef] [Google Scholar]
- Young, K. 1995, ApJ, 445, 872 [NASA ADS] [CrossRef] [Google Scholar]
- Zacharias, N., Monet, D. G., Levine, S. E., et al. 2005, NOMAD Catalog, VizieR On-line Data Catalog, I/297 [Google Scholar]
- Zhao-Geisler, R., Quirrenbach, A., Köhler, R., Lopez, B., & Leinert, C., 2011, A&A, 530, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Basic stellar parameters, silicon abundance, and 28Si/29Si and 28Si/30Si ratios of the K–M giants and optically bright red supergiants in our sample.
All Figures
 |
Fig. 1 Observed VISIR spectra of the SiO fundamental lines in seven K–M giants. The positions of the 28SiO, 29SiO, and 30SiO lines relatively free from blends with other species are marked by the black, red, and green arrows, respectively. The identification of these lines are also given (in case of multiple transitions within one feature, only the main contributor is given). The positions of the 28SiO, 29SiO, 30SiO, and H2O lines are shown by the black, red, green, and blue ticks, respectively (H2O lines are plotted only for L2 Pup and θ Aps). The dotted lines show the local continuum. |
| In the text | |
 |
Fig. 2 Observed VISIR spectra of the SiO fundamental lines in three optically bright (i.e., not very dusty) red supergiants, shown in the same manner as in Fig. 1. |
| In the text | |
 |
Fig. 3 Observed VISIR spectra of the SiO fundamental lines in two dusty red supergiants. The positions of the 28SiO lines with the P-Cyg profile are shown by the arrows. |
| In the text | |
 |
Fig. 4 Modeling of the P-Cyg profile of the SiO line 1 − 0 R(3) observed in VY CMa panel a) and VX Sgr panel b). In each panel, the red solid line represents the observed spectrum, while the black solid line represents the model spectrum. |
| In the text | |
 |
Fig. 5 Observed VISIR spectra of the SiO fundamental lines in three Mira stars, shown in the same manner as in Fig. 1. |
| In the text | |
 |
Fig. 6 Observed VISIR spectrum of GCIRS3. Unlike in Figs. 1–5, the wavelength scale is heliocentric. |
| In the text | |
 |
Fig. 7 H-R diagram. The observationally derived positions of seven K–M giants in our sample are plotted by the filled diamonds with error bars. The theoretical evolutionary track from the main sequence to the asymptotic giant branch for a 2 M⊙ star from Herwig (2005) is shown by the solid line. The evolutionary tracks from Bertelli et al. (2008) for 0.6, 1, and 1.5 M⊙ stars with the solar metallicity (Z = 0.017) and a 1 M⊙ star with a subsolar metallicity (Z = 0.004, appropriate for α Boo) are shown by the dots. |
| In the text | |
 |
Fig. 8 Comparison of the synthetic spectra based on the MARCS models with the observed VISIR spectra of seven K–M giants. The observed and synthetic spectra are shown by the black and red solid lines, respectively. The relatively isolated 28SiO, 29SiO, and 30SiO lines are marked by the black, red, and green arrows, respectively. See Fig. 1 for their identification. The 28SiO lines with absorption excess are marked by the blue dots. |
| In the text | |
 |
Fig. 9 Synthetic spectra of the SiO lines for Teff = 3600 K and 3400 K and log 1= 0.0 and 1.0 (other parameters are M⋆ = 1 M⊙, νmicro = 2 km s-1, [Fe/H] = 0.0, and moderately CN-cycled composition). The dashed line represents the continuum. We included no lines at either edge of the spectral range to show the continuum level. |
| In the text | |
 |
Fig. 10 Comparison of the synthetic spectra from the MARCS models with the observed VISIR spectra of three optically bright red supergiants, shown in the same manner as in Fig. 8. See Fig. 2 for the identification of the lines. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


