| Issue |
A&A
Volume 561, January 2014
|
|
|---|---|---|
| Article Number | A64 | |
| Number of page(s) | 19 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201219270 | |
| Published online | 03 January 2014 | |
A Gemini/GMOS study of the physical conditions and kinematics of the blue compact dwarf galaxy Mrk 996⋆,⋆⋆
1 Observatório Nacional, Rua José Cristino 77, 20921-400 Rio de Janeiro, Brazil
e-mail:
etelles@on.br
2 Astronomy Department, University of Virginia, PO Box 400325, Charlottesville VA 22904, USA
3 Institut d’Astrophysique, 98 bis Boulevard Arago, 75014 Paris, France
e-mail:
txt@virginia.edu
4 Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
5 Main Astronomical Observatory, Ukrainian National Academy of Sciences, Zabolotnoho 27, 03680 Kyiv, Ukraine
e-mail:
izotov@mao.kiev.ua
6 Gemini Observatory/AURA, Southern Operations Center, 603 Casilla, La Serena, Chile
e-mail:
rcarrasco@gemini.edu
Received: 22 March 2012
Accepted: 25 October 2013
Aims. We present an integral field spectroscopic study with the Gemini Multi-Object Spectrograph (GMOS) of the unusual blue compact dwarf (BCD) galaxy Mrk 996.
Methods. We show through velocity and dispersion maps, emission-line intensity and ratio maps, and by a new technique of electron density limit imaging that the ionization properties of different regions in Mrk 996 are correlated with their kinematic properties.
Results. From the maps, we can spatially distinguish a very dense high-ionization zone with broad lines in the nuclear region, and a less dense low-ionization zone with narrow lines in the circumnuclear region. Four kinematically distinct systems of lines are identified in the integrated spectrum of Mrk 996, suggesting stellar wind outflows from a population of Wolf-Rayet (WR) stars in the nuclear region, superposed on an underlying rotation pattern. From the intensities of the blue and red bumps, we derive a population of ~473 late nitrogen (WNL) stars and ~98 early carbon (WCE) stars in the nucleus of Mrk 996, resulting in a high N(WR)/N(O+WR) of 0.19. We derive, for the outer narrow-line region, an oxygen abundance 12 + log (O/H) = 7.94 ± 0.30 (~0.2 Z⊙) by using the direct Te method derived from the detected narrow [O iii]λ4363 line. The nucleus of Mrk 996 is, however, nitrogen-enhanced by a factor of ~20, in agreement with previous CLOUDY modeling. This nitrogen enhancement is probably due to nitrogen-enriched WR ejecta, but also to enhanced nitrogen line emission in a high-density environment. Although we have made use here of two new methods – principal component analysis (PCA) tomography and a method for mapping low- and high-density clouds – to analyze our data, new methodology is needed to further exploit the wealth of information provided by integral field spectroscopy.
Key words: galaxies: individual: Mrk 996 / galaxies: kinematics and dynamics / galaxies: star formation / galaxies: ISM / galaxies: abundances
Based on observations obtained at the Gemini Observatory, which is operated by the Association of Universities for Research in Astronomy, Inc., under a cooperative agreement with the NSF on behalf of the Gemini partnership: the National Science Foundation (United States), the Science and Technology Facilities Council (United Kingdom), the National Research Council (Canada), CONICYT (Chile), the Australian Research Council (Australia), Ministério da Ciência e Tecnologia (Brazil), and SECYT (Argentina).
Reduced and calibrated data cubes are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/561/A64
© ESO, 2014
1. Introduction
The blue compact dwarf (BCD) galaxy Mrk 996 (MB = −16.9) is a very unusual galaxy. It stands out from its counterparts because of its extremely large nuclear electron density, of the order of 106 cm-3 instead of the usual several 100 cm-3 for H ii regions. Much work has been done to study the unusual physical properties of Mrk 996. Hubble Space Telescope (HST) V and I images by Thuan et al. (1996) show that the bulk of the star formation occurs in a compact, roughly circular, high surface brightness nuclear region of radius 340 pc, with evident dust patches to the north of it. The nucleus (n) is located within an elliptical (E) low surface brightness (LSB) component, so that Mrk 996 belongs to the relatively rare class of nE BCDs (Loose & Thuan 1985). It may also be classified as a Type I H ii galaxy according to Telles et al. (1997). Thuan et al. (1996) found the extended envelope to show a distinct asymmetry. The envelope is more extended to the northeast side than to the southwest side, perhaps the sign of a past merger. This asymmetry is also seen in the spatial distribution of the globular clusters around Mrk 996, seen mainly to the south of the galaxy. The extended LSB component possesses an exponential disc structure with a small scale length of 0.42 kpc. While Mrk 996 does not show an obvious spiral structure in the disc, there is a spiral-like pattern in the nuclear star-forming region, which is no larger than 160 pc in radius. This galaxy has a heliocentric radial velocity of 1622 km s-1 (Thuan et al. 1999), which gives it a distance of 21.7 Mpc, adopting a Hubble constant of 75 km s-1 Mpc-1 and including a very small correction for the Virgocentric flow. Table 1 summarizes the basic information on Mrk 996. At the adopted distance, 1′′ corresponds to a linear size of 105 pc.
Basic data on Mrk 996.
The UV and optical spectra of the nuclear star-forming region of Mrk 996 (Thuan et al. 1996) show remarkable features, suggesting very unusual physical conditions. The He i line intensities are 2–4 times larger than those in normal BCDs. In the UV range, the N iii] λ 1750 and C iii] λ 1909 are particularly intense. Moreover, the line width depends on the degree of ionization of the ion. Thus, low-ionization forbidden emission lines such as [O ii] λ3726, 3729, [S ii] λ6717, 6731, and [N ii] λ6548, 6584 have narrow widths, similar to those in other H ii regions, while high-ionization emission lines such as the helium lines, the [O iii] λ4959, 5007, and [Ne iii] λ3868 nebular lines consist of narrow and broad components, and all auroral lines such as [O iii] λ4363, [N ii] λ5755, and [S iii] λ6312 are broad with line widths of ≥500 km s-1. These correlations of line widths with the degree of excitation suggest different ionization zones with very distinct kinematic properties. Thuan et al. (1996) found that the usual one-zone, low-density, ionization-bounded H ii region model cannot be applied to the nuclear star-forming region of Mrk 996 without leading to unrealistic helium and heavy-element abundances. Instead, they showed that a two-zone, density-bounded H ii region model that includes an inner compact region with a central density of 106 cm-3 (about 4 orders of magnitude greater than the densities of normal H ii regions) together with an outer region with a lower density of ~450 cm-3 (comparable to those of other H ii regions), is needed to account for the observed line intensities. The large density gradient is probably caused by a mass outflow driven by the large population of Wolf-Rayet (WR) stars present in the galaxy. The gas outflow motions may account for the line widths of the high-ionization lines originating in the dense inner region being much broader than the low-ionization lines originating in the less dense outer region. The high intensities of [N iii] λ1750, [C iii] λ1909, and He i can be understood by collisional excitation of these lines in the high-density region. In the context of this model, the oxygen abundance of Mrk 996 is 12 + log O/H = 8.0. If we adopt 12 + log O/H = 8.70 for the Sun (Asplund et al. 2009), then Mrk 996 has a heavy element mass fraction of 0.2 solar. The 2-zone CLOUDY models with element abundance ratios typical of low-metallicity BCDs reproduce well the observed line intensities, except for nitrogen. With an enhancement factor of ~5 or greater, the nitrogen line intensities can be reproduced. Thuan et al. (1996) attribute this nitrogen enhancement to local pollution from WR stars.
Thuan et al. (2008) have used the Spitzer satellite to study Mrk 996 in the mid-infrared (MIR). They also found that a CLOUDY model that accounts for both the optical and MIR lines requires that they originate in two distinct H ii regions: a very dense H ii region where most of the optical lines arise, with densities declining from 106 cm-3 at the center to a few hundred cm-3 at the outer radius of ~580 pc, and a H ii region with a density of ~300 cm-3 that is hidden in the optical, but seen in the MIR. The infrared lines arise mainly in the optically obscured H ii region, while they are strongly suppressed by collisional deexcitation in the optically visible one. The presence of the [O iv] 25.89 μm emission line implies the presence of ionizing radiation as hard as 54.9 eV. This hard ionizing radiation is most likely due to fast radiative shocks propagating in a dense interstellar medium (ISM).
Because of the presence in it of distinct ionization zones with different electron densities and kinematic properties, a very dense nuclear high-ionization zone with broad emission lines and a less dense low-ionization zone with narrow emission lines in the circumnuclear region, Mrk 996 is a prime target for observation with the Gemini Multi-object Spectrograph. This allows us to carry out a two-dimensional (2D) study of the kinematics and ionization structure of Mrk 996 with exquisite spatial and spectral resolution. In the same spirit, James et al. (2009) have also recently carried a 2D study of Mrk 996 with the VLT VIMOS integral field unit, although with less spatial and spectral resolution. Those authors found that most of the emission lines of Mrk 996 show two components: a narrow central Gaussian with a full width at half-maximum FWHM ~ 110 km s-1 superposed on a broad component with FWHM ~ 400 km s-1. The [O iii] λ4363 and [N ii] λ5755 lines show only a broad component and are detected only in the inner region. The broad line region shows N/H and N/O enhanced by a factor of ~20, while the abundances of the other elements are normal. An oxygen abundance of 12 + log (O/H) = 8.37, greater than 0.5 that of the Sun, and a very large WR (~3000) and O star (~150 000) population were derived. A follow-up Chandra study to explore the presence of an intermediate-mass black hole in the heart of Mrk 996 which may account for the presence of the [O iv] 25.89 μm line was undertaken by Georgakakis et al. (2011). No active galactic nuclei (AGN) were found.
We discuss the observations and the data reduction in Sect. 2. The integrated spectrum is considered in Sect. 3. We discuss here the systems of emission lines with different kinematics, the collisional excitation of hydrogen and helium lines, and the WR stellar population. The 2D kinematics data are presented in Sect. 4 in the form of velocity and velocity dispersion maps. In Sect. 5 we present a technique to delimit the spatial extent of the high electron density region. In Sect. 6 we apply a recently developed method for exploiting data cubes and extracting uncorrelated physical information, called principal component analysis (PCA) tomography. The 2D description of the physical conditions is presented in Sect. 7 through extinction, electron temperature and density, excitation, and WR feature maps. We summarize our conclusions in Sect. 8.
2. Observations and data reduction
The observations were obtained with the Gemini Multi-Object Spectrograph (GMOS; Hook et al. 2004) and the Integral Field Unit (IFU; Allington-Smith et al. 2002) hereafter GMOS/IFU, at the Gemini South Telescope in Chile. They were made during the nights of October 20, 2008, using the grating B1200+ _G5321 (B1200) covering the wavelength region from 3667 Å to 5142 Å with a spectral resolution of 0.24 Å, and of November 6, 2008, using the grating R831+ _G5322 (R831) with a spectral resolution of 0.34 Å, covering the wavelength region from 5095 Å to 7223 Å, with an overlap of ~50 Å between the red and blue spectral ranges, in the one-slit mode. The GMOS/IFU in this mode composes a pattern of 750 hexagonal elements, each with a projected diameter of 0 2, covering a total 3
2, covering a total 3 5 × 5′′ field of view, where 250 of these elements are dedicated to sky observation. The detector is made up of three 2048 × 4608 CCDs with 13.5 μm pixels, with a scale of 0
5 × 5′′ field of view, where 250 of these elements are dedicated to sky observation. The detector is made up of three 2048 × 4608 CCDs with 13.5 μm pixels, with a scale of 0 073 pixel-1. The CCDs create a mosaic of 6144 × 4608 pixels with a small gap of 37 columns between the chips. Figure 1 shows the inner 20′′ of the HST Wide Field Camera F569W filter image of Mrk 996 from Thuan et al. (1996) with the location of our GMOS field of view superimposed on it, with a linear contrast (left) and with a logarithmic stretch (right) to emphasize the compact nuclear region.
073 pixel-1. The CCDs create a mosaic of 6144 × 4608 pixels with a small gap of 37 columns between the chips. Figure 1 shows the inner 20′′ of the HST Wide Field Camera F569W filter image of Mrk 996 from Thuan et al. (1996) with the location of our GMOS field of view superimposed on it, with a linear contrast (left) and with a logarithmic stretch (right) to emphasize the compact nuclear region.
 |
Fig. 1 The GMOS 3 |
Observational setup.
Table 2 shows the observing log which gives the instrumental setup, the mean airmass and exposure times, the dispersion, the final instrumental resolution (σinst = FWHMinst/2.355), and the seeing (FWHM) of each observation. The data were reduced using the Gemini package version 1.8 inside IRAF1. All science exposures, comparison lamps, spectroscopic twilight, and GCAL flats were overscan/bias subtracted and trimmed. The spectroscopic GCAL flats were processed by removing the calibration unit with GMOS spectral response and the uneven illumination of the calibration unit. Twilight flats were used to correct for the illumination pattern in the GCAL lamp flat using the task gfresponse in the GMOS package. The twilight spectra were divided by the response map obtained from the lamp flats and the resulting spectra were averaged in the dispersion direction, giving the ratio of sky to lamp response for each fiber. The final response maps were then obtained by multiplying the GCAL lamp flat by the derived ratio. The resulting extracted spectra were then wavelength calibrated, corrected by the relative fiber throughputs, and extracted. The residual values in the wavelength solution for 40 and 60 points, using a Chebyshev polynomial of the fourth or fifth order, typically yielded rms values of ~0.08 Å and ~0.07 Å for the red and blue gratings, respectively. The final spectra cover wavelength intervals of ~3667–5142 Å and ~5095–7223 Å for data taken with the B1200 and R813 gratings, respectively.
The flux calibration was performed using the sensitivity function derived from observations of the stars Feige 110 and LTT1020 for both gratings. The 2D data images were transformed into a 3D data cube (x,y,λ), re-sampled as square pixels with 0 1 spatial resolution and corrected for differential atmospheric refraction (DAR) using the gfcube routine2. The three cubes with different exposures were combined to produce a single data cube for each grating. The flux maps on selected emission lines, radial velocity, and velocity dispersion maps, as well as 1D spectra of various apertures, were created by an extensive use of QFitsview, developed by Thomas Ott3. Both reduced and calibrated data cubes are available in electronic form at the CDS.
1 spatial resolution and corrected for differential atmospheric refraction (DAR) using the gfcube routine2. The three cubes with different exposures were combined to produce a single data cube for each grating. The flux maps on selected emission lines, radial velocity, and velocity dispersion maps, as well as 1D spectra of various apertures, were created by an extensive use of QFitsview, developed by Thomas Ott3. Both reduced and calibrated data cubes are available in electronic form at the CDS.
 |
Fig. 2 Integrated GMOS spectrum of the nucleus of Mrk 996 within a 1 |
3. Integrated spectrum
3.1. Selecting our extraction apertures
We have simulated apertures for the extraction of the integrated spectrum in order to compare our results with those of the similar IFU VIMOS work of James et al. (2009), as well as those of the HST work of Thuan et al. (1996) on the nuclear spectral properties of this peculiar galaxy. James et al. (2009) used a 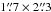 2 aperture for the core region and a
2 aperture for the core region and a 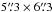 2 aperture for the outer part outside the core, and Thuan et al. (1996) obtained a nuclear spectrum with a 0
2 aperture for the outer part outside the core, and Thuan et al. (1996) obtained a nuclear spectrum with a 0 86 circular aperture with HST. The results of this simulated aperture analysis indicates that the VIMOS data of James et al. (2009) show similar line ratios for both the narrow and broad components for most lines, but the absolute fluxes are a factor of 4–5 higher than our data for the nuclear aperture. A direct comparison with the outer region was not possible because our field of view (
86 circular aperture with HST. The results of this simulated aperture analysis indicates that the VIMOS data of James et al. (2009) show similar line ratios for both the narrow and broad components for most lines, but the absolute fluxes are a factor of 4–5 higher than our data for the nuclear aperture. A direct comparison with the outer region was not possible because our field of view (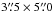 2) is slightly smaller than that of VIMOS. On the other hand, our HST simulated aperture fluxes and flux ratios give a good match to those of the HST spectrum of Thuan et al. (1996). Because of the flux discrepancy with the VIMOS data, we have re-reduced the whole data set using the more recent software that was developed by one of us (ERC, responsible for GMOS). We have thus double-checked our measurements by a new and independent data reduction, and confirmed our calibration.
2) is slightly smaller than that of VIMOS. On the other hand, our HST simulated aperture fluxes and flux ratios give a good match to those of the HST spectrum of Thuan et al. (1996). Because of the flux discrepancy with the VIMOS data, we have re-reduced the whole data set using the more recent software that was developed by one of us (ERC, responsible for GMOS). We have thus double-checked our measurements by a new and independent data reduction, and confirmed our calibration.
Having established the accuracy of our data reduction, by both internal and external checks, we decided to present the results for the integrated spectrum using a circular aperture of 1 6 in diameter, representative of the nuclear region of Mrk 996. This aperture size is consistent with the full width at zero intensity (FWZI) of the point spread function (PSF) of our calibration star, using the same instrument and setup on the same night. The second aperture used in this work contains the outer region, consisting of the spaxels within our field of view, but not considering the inner 1
6 in diameter, representative of the nuclear region of Mrk 996. This aperture size is consistent with the full width at zero intensity (FWZI) of the point spread function (PSF) of our calibration star, using the same instrument and setup on the same night. The second aperture used in this work contains the outer region, consisting of the spaxels within our field of view, but not considering the inner 1 3 radius (5 pixels from the nucleus aperture). Although both apertures used in the present work (the nuclear and the outer regions) are similar to those used by James et al. (2009), ours encompass smaller areas than theirs.
3 radius (5 pixels from the nucleus aperture). Although both apertures used in the present work (the nuclear and the outer regions) are similar to those used by James et al. (2009), ours encompass smaller areas than theirs.
3.2. Systems of emission lines with different kinematics
In Fig. 2, we show the integrated nuclear spectrum of Mrk 996 over the entire spectral range covered by the two gratings, within a 1 6 circular aperture centered on the nucleus. While this aperture is very similar to the core region aperture of James et al. (2009), as mentioned above, it is not identical.
6 circular aperture centered on the nucleus. While this aperture is very similar to the core region aperture of James et al. (2009), as mentioned above, it is not identical.
This spectrum has a higher spectral resolution (a factor of ~10 in the blue and of ~4 in the red) and a considerably higher signal-to-noise ratio (S/N) than the spectrum of James et al. (2009). It also covers a larger wavelength range. The spectrum has not been smoothed. The continuum levels of the blue and red parts of the integrated spectrum in the overlapping region at ~5100 Å match well although the two data cubes were taken on different nights. This, again, confirms that our data reduction and calibration are correct. We note that in the bluest part, for λ < 4000 Å, the continuum is not monotonically increasing to the blue, implying a poorer calibration due to the known low sensitivity of GMOS in that wavelength region. However, the remaining continuum is monotonically increasing from the red to the blue, in agreement with the spectrum of Thuan et al. (1996). By comparison, the continuum in the red part of the James et al. (2009) spectrum is nearly flat, probably indicating the contribution of the more spatially extended red old stellar population, due to the use of a considerably larger aperture (5 3 by 6
3 by 6 3).
3).
The high spectral resolution of the GMOS/IFU observations allows us to resolve the [O ii] λ3726, 3729 doublet lines. The hydrogen Balmer lines all show a narrow and a broad component. The total flux in the broad component of Hα is comparable to the total flux in its narrow component. The He i lines (λ4471, λ5876, λ6678, λ7065) are clearly broadened. The broad component is dominant in the [O iii] λ4363, [N ii] λ5755, and [S iii] λ6312 auroral lines, while the low-ionization species [S ii]λλ 6717, 6731, [O ii]λλ 3726, 3729, [N ii] λλ 6548, 6584, and [O i]λλ 6300, 6363 lines are all narrow, with no broad component. These general trends agree with those discussed by Thuan et al. (1996) and James et al. (2009).
 |
Fig. 3 Example of the deblend fitting procedure with the Hα line. Upper panel: the integrated profile of the Hα line as in Fig. 2 (black solid line). The red-dotted line shows the resulting fit to the broad component. The blue-dashed line shows the resulting fit to the narrow component. The integrated fluxes in the broad and narrow components in Table 3 are derived in this manner. Lower panel: residuals to the fit. |
Thanks to the high spectral resolution of our data, the narrow and broad components of emission lines are well separated. Therefore, using the IRAF splot routine we first fit the narrow component by a single Gaussian and subtract it from the line profile. Then we fit the broad component again by a single Gaussian. Additionally, very broad low-intensity Hα emission is present with a FWZI of ~100 Å, suggesting rapid outflow with a velocity of several thousand km s-1. This low-intensity Hα emission was not discussed by James et al. (2009), probably because of the lower S/N of their spectrum. In principle, a multi-Gaussian fitting to emission line profiles should have been used, including more than two components for each line. However, this approach is subjective. When more Gaussians are used for profile-fitting, the fit is better, without necessarily reflecting the real physical situation. Additionally, this procedure significantly complicates studies of the kinematic structure. Therefore, we have decided to fit line profiles in the simplest way, each of their narrow and broad components being fitted by a single Gaussian. Figure 3 shows an example of our deblend fits for deriving our fluxes in our line-fitting procedure. The lower panel shows the residuals of the fit. It can be seen that the broad component is flat on top, rather than being a perfect Gaussian. For the purpose here the measured fluxes are little affected by this deviation. We show in Table 3 the results of the line-fitting for the integrated nucleus spectrum within the 1 6 circular aperture . In this table, λ0 is the rest-frame wavelength and Ne(crit) is the critical density of the forbidden line. The flux is in units of 100 × Fnar/Fnar(Hβ) for the narrow component and of 100 × Fbr/Fbr(Hβ) for the broad component; v(rad) is the radial velocity in km s-1, and FWHM is the line full width at half maximum in km s-1. Errors in radial velocities are negligible and are not quoted. All measurements were performed by hand with the task splot within IRAF, and also by running non-interactively the profile fitting task fitprofs, providing initial guesses for positions and widths of the lines. The results of these non-interactive fits are, in most cases, identical to our measurements with splot. The advantage is that fitprofs computes error estimates for the fitted parameters by using a Monte Carlo technique that automatically takes into account the properties of our data. The details of this technique is given in the fitprofs help pages. We have chosen a large number of iterations for better error estimates. These are the errors quoted in Table 3. The errors introduced by flat-fielding the data is <1%. A larger error of 3–4% is introduced when the correction by the relative fiber throughputs is performed (response map). This will result in a 4–5% total error, to be added in quadrature to the listed errors in Table 3.
6 circular aperture . In this table, λ0 is the rest-frame wavelength and Ne(crit) is the critical density of the forbidden line. The flux is in units of 100 × Fnar/Fnar(Hβ) for the narrow component and of 100 × Fbr/Fbr(Hβ) for the broad component; v(rad) is the radial velocity in km s-1, and FWHM is the line full width at half maximum in km s-1. Errors in radial velocities are negligible and are not quoted. All measurements were performed by hand with the task splot within IRAF, and also by running non-interactively the profile fitting task fitprofs, providing initial guesses for positions and widths of the lines. The results of these non-interactive fits are, in most cases, identical to our measurements with splot. The advantage is that fitprofs computes error estimates for the fitted parameters by using a Monte Carlo technique that automatically takes into account the properties of our data. The details of this technique is given in the fitprofs help pages. We have chosen a large number of iterations for better error estimates. These are the errors quoted in Table 3. The errors introduced by flat-fielding the data is <1%. A larger error of 3–4% is introduced when the correction by the relative fiber throughputs is performed (response map). This will result in a 4–5% total error, to be added in quadrature to the listed errors in Table 3.
Emission line parameters derived from the integrated spectrum within a 1 6 aperture.
6 aperture.
Since the critical densities for collisional deexcitation differ according to the line (Table 3), different forbidden lines trace distinct zones of the H ii region in Mrk 996. Additionally, ionization structure plays a role. Emission lines of higher ionization species, [O iii] for example, originate in the inner part of the H ii region, while the emission of lower ionization species, [O i] for example, is produced in the outer part. As for permitted lines of hydrogen and helium, they trace both the inner and outer parts of the H ii region. Again, broad-line emission emerges in the inner part while narrow-line emission traces its outer part. Narrow-lines are also seen in the direction of the galaxy center because all lines of sight to the central part have to go through the outer part of the galaxy. The very high electron number density in the center of Mrk 996 is implied by the extremely high broad [O iii] λ4363/λ5007 flux ratio of ~25% (Table 3), while typical values in high-excitation H ii regions are only 1–3%. Such a high [O iii] λ4363/λ5007 flux ratio for the broad component in Mrk 996 occurs because the [O iii] λ5007 emission line is suppressed by collisional deexcitation, while the [O iii] λ4363 emission line is not.
Based on their radial velocities and FWHMs (Table 3), we can identify four kinematically distinct systems of lines, in order of increasing distance from the center and decreasing line widths. Since the density in the inner part of the central H ii region in Mrk 996 is very high, it probably cannot be resolved because of its small linear extent. Given a constant Hβ luminosity, the radius of the emitting region scales as ~Ne−2/3. Therefore, a region with an electron number density of ~106 cm-3 will have a radius ~500 times lower than a region with an electron number density of ~102 cm-3 and a similar Hβ luminosity. However, spectral information presents an advantage in that it allows the physical conditions to be traced even in unresolved regions. This is analogous to the studies of broad and narrow line regions in the spectra of distant AGN and QSOs.
The densest part of the H ii region appears to be located around the central ionizing stellar cluster. The first system of lines is related to the WR stars in this cluster. This system is composed of the broad permitted N iii 4640 and He ii 4686 lines (the blue bump) and of the C iv 5801 permitted line (the red bump). These WR lines have FWHM ~ 1300−2000 km s-1 and they are blue-shifted by ~100–200 km s-1 with respect to the narrow component of the Hβ emission line. These are produced in the dense stellar winds of WR stars.
The second system of lines probes the innermost zone of the dense H ii region. It consists of a single forbidden [O iii] λ4363 emission line with a critical density of 2.6 × 107 cm-3, the highest among all forbidden lines shown in Table 3. It has a FWHM of ~470 km s-1 and is blue-shifted by 60 km s-1 relative to the narrow Hβ emission line. The line profile of λ4363 is not smooth and seems to be complex. This possibly indicates multiplicity, although we cannot convincingly investigate this issue further without deciding arbitrarily on the number of line components present. In any case, a very weak peak is seen on the top of the line profile which coincides with the systemic velocity as given by the narrow component of Hβ, and may be real. This may be the narrow component seen in the regions outside the nucleus and is discussed below. Its existence will be confirmed independently by other techniques in Sect. 7.5.
The third system of lines consists of broad components of permitted hydrogen and helium emission lines, of forbidden emission lines of doubly ionized ions and of the auroral [N ii] λ5755 emission line (but excluding the [O iii] λ4363 and [Cl iii] λ5717, 5737 emission lines). These lines are blue-shifted by 20–30 km s-1 relative to the narrow Hβ emission line and have FWHMs of 450–500 km s-1, similar to the FWHM of the [O iii] λ4363 emission line. This lower blueshift indicates that the third line system originates in regions farther away from the center than does the second line system.
Finally, the fourth system consists only of lines with narrow components (FWHM ~ 100 km s-1). These are all narrow lines and narrow components of emission lines with composite profiles. Their radial velocities are, within the errors, the same as that of the narrow Hβ emission line.
A global picture consistent with the observed properties of the above four line systems would be the following. The first system of lines arises in the dense circumstellar envelopes of WR stars. All other line systems originate in the H ii region around the ionizing stellar cluster. The second and third systems of lines are formed as a result of the outflow of ionized ISM from the central part of the galaxy, and are due to stellar winds from the WR stars. Finally, the fourth system of lines arises in the outer less dense part of the H ii region that is not perturbed by the ionized gas outflow. We have been able to spatially identify this fourth system in the lines of sight away from the nucleus and extract the outer region spectrum from which a more precise determination of the H ii region abundances could be derived. These results are presented below.
3.3. Collisional excitation of hydrogen and helium lines
In general, the electron number density of H ii regions in star-forming galaxies is low, ~100 cm-2. At these densities, the deviations of hydrogen and He i line intensities from their recombination values are expected to be small. Then, deviations of the hydrogen emission line intensity ratios from their theoretical values are attributed to extinction. However, in the case of the dense H ii region in Mrk 996 the effect of collisional excitation of hydrogen and helium lines is expected to be large, especially in the densest part of the H ii region where the broad emission lines originate, as described above. Among the hydrogen lines, this effect is highest for the Hα emission line. If collisional excitation is high, then the Balmer decrement cannot be used for the determination of the extinction coefficient without correction for that effect.
Table 3 shows that the Hα/Hβ flux ratios for both narrow and broad components are significantly larger than the theoretical value of ~2.9. However, the Hγ/Hβ, Hδ/Hβ and H9/Hβ flux ratios for both narrow and broad components are close to the theoretical values. For the narrow component, such a small deviation can be attributed to line flux uncertainties caused by imperfect flux calibration and differential atmospheric refraction. For the broad component, the deviation of ~50% of the Hα/Hβ ratio from its theoretical value is too high to be explained in this way. We suggest that collisional excitation of hydrogen plays an important role in the central part of Mrk 996, enhancing the Hα/Hβ ratio (e.g., Stasińska & Izotov 2001; Peimbert et al. 2007). Using CLOUDY photo-ionized H ii region models for the range of the ionization parameter appropriate for Mrk 996 (logU = −3−2), we find that a broad Hα/Hβ flux ratio of ~4.6 corresponds to an electron number density Ne ~ (1−5) × 106 cm-3. This range of Ne is consistent with that derived by Thuan et al. (1996, 2008), but is somewhat lower than Ne ≳ 107 cm-3 obtained by James et al. (2009) from the analysis of the [O iii] λ4363/λ1663 and λ5007/λ4363 flux ratios, although it is consistent with their lower limit of 3 × 106 cm-3. Adopting an electron number density ≳107 cm-3 would lead to a broad Hα/Hβ flux ratio greater than ~5–6. We note that our value of the broad Hα/Hβ flux ratio is not corrected for extinction. If extinction is non-zero, then the true Hα/Hβ flux ratio would decrease, giving a smaller Ne. The low extinction-corrected broad Hα/Hβ flux ratio (~2.9) of James et al. (2009, their Table 2) is inconsistent with their best estimate of high density. Additionally, the [O iii] λ4363/λ1663 flux ratio is highly sensitive to the adopted extinction coefficient and the reddening curve. Thus, we conclude that the high central density of ≳107 cm-3 derived by James et al. (2009) from the broad [O iii] λ5007/λ4363 flux ratio is most likely overestimated. However, the electron density derived by James et al. (2009) from the [Fe iii] λ4881/λ4658 and λ5270/λ4658 ratios, in the range (0.5–3) × 106 cm-3, is in good agreement with ours.
In addition to the hydrogen lines, the He i emission lines are also subject to important collisional excitation from the meta-stable 23S level. Moreover, the He i λ3889 line is optically thick, as seen below. This results in a decrease in the intensity of this line and a fluorescent enhancement of other He i emission lines in the optical spectrum. If both effects are absent, then the expected intensities of the He i λ3889, λ4471, λ5876, λ6678, and λ7065 emission lines relative to the Hβ line are, respectively, ~0.10, 0.04, 0.11, 0.03, and 0.01 (e.g., Porter et al. 2005). Since the He i λ3889 emission line is blended with the H8 λ3889 emission line with a similar intensity of ~0.1 relative to the Hβ line, the total recombination intensity of the blend He i + H8 λ3889 is ~0.2 relative to the Hβ emission line.
It can be seen from Table 3 that the narrow He i emission lines are subject to both collisional and fluorescent enhancements. The importance of fluorescent enhancement is implied by the weakness of the He i + H8 λ3889 line. Subtracting the intensity of the H8 hydrogen line, we obtain an intensity of ~0.04 for the He i λ3889 emission line. This suggests that the He iλ3889 emission line is optically thick in the region emitting in narrow lines. On the other hand, the intensity of the He iλ7065 line is higher by a factor of ~4. This line is very sensitive to both collisional and fluorescent enhancements, contrary to the other He iλ4471, λ5876 and λ6678 emission lines.
The collisional and fluorescent enhancements of the He i emission lines are more pronounced in the region with broad lines. The intensity of the He i + H8 λ3889 blend is ~0.13, suggesting that He i λ3889 emission is nearly absent because of the high optical depth. On the other hand, the He i λ7065 emission line is enhanced by a factor of ~30, while other He i lines are enhanced by a factor of ~3. These enhancements are much higher than those in H ii regions of other blue compact dwarf galaxies (see, e.g., Izotov et al. 2007) and mean that Mrk 996 is not suitable for He abundance determination.
James et al. (2009) have derived the He abundance of Mrk 996, using only one emission line, He iλ5876, and He i emissivities from Porter et al. (2005). They find an He abundance of 0.08–0.10 in Mrk 996, typical of dwarf emission-line galaxies, with no radial variation. Several other He i emission lines were also present in the optical spectrum of James et al. (2009). However, no attempt was made to compare He abundances derived from different lines. In addition, Porter et al. (2005) emissivities do not take into account fluorescent excitation of He i emission lines (Robbins 1968), making the He abundance determination somewhat uncertain.
3.4. Wolf-Rayet population
Two types of WR stars are present in Mrk 996. The N iii λ4640 and He ii λ4686 emission lines, responsible for the blue bump, are due to late nitrogen (WNL) stars, while the C iv λ5801 emission line, responsible for the red bump, indicates the presence of early carbon (WCE) stars (Guseva et al. 2000). We derive the number of WR stars from the fluxes of broad lines in the spectrum with the 1 6 aperture. The maps in Fig. 14 (to be discussed later) also show that all of the WR emission comes from this circular region. We have also checked the fluxes of these lines in larger apertures and find that they do not change, also suggesting that all WR stars are located in the central compact region. No WR feature is detected in the integrated spectrum outside the nucleus, as presented below in Sect. 7.5.
6 aperture. The maps in Fig. 14 (to be discussed later) also show that all of the WR emission comes from this circular region. We have also checked the fluxes of these lines in larger apertures and find that they do not change, also suggesting that all WR stars are located in the central compact region. No WR feature is detected in the integrated spectrum outside the nucleus, as presented below in Sect. 7.5.
 |
Fig. 4 Radial velocity maps. Left: map of the narrow component of the Hα line. This map is representative of all other narrow-line maps (e.g., narrow [O iii] λ5007, [O i] λ6300, [S ii] λ6717). Right: map of the He i λ7065 line. This map is representative of other broad-line maps (e.g., [O iii] λ4363, broad Hα). Contours are the monochromatic intensity of the corresponding emission-line from decreasing intensity intervals of 2 × 10-17 erg cm2 s-1 in peak intensity for Hα and 10-18 erg cm2 s-1 for He i. Only pixels above 3σ of the noise are shown for He i. In both panels, north is up and east is to the left. |
The observed flux of WNL stars (N iii + He ii emission) is F(WNL) = 1.68 × 10-14 erg s-1 cm-2, and that of WCE stars (C iv emission) is F(WCE) = 5.90 × 10-15 erg s-1 cm-2 (Table 3). These fluxes have not been corrected for extinction because the collisional excitation of the hydrogen lines makes the determination of the extinction coefficient uncertain (see previous section). At a distance of 21.7 Mpc, these fluxes correspond to luminosities L(WNL) = 9.46 × 1038 erg s-1 and L(WCE) = 2.95 × 1038 erg s-1. Adopting the luminosity of a single WNL star to be 2.0 × 1036 erg s-1, and that of a single WCE star to be 3.0 × 1036 erg s-1 (Schaerer & Vacca 1998), the numbers of WR stars are N(WNL) = 473 and N(WCE) = 98, their ratio N(WCE)/N(WNL) being 0.20. These values are typical of WR galaxies (Guseva et al. 2000).
The total observed flux of the Hβ emission line (including both broad and narrow components, Table 3) is equal to F(Hβ) = 1.98 × 10-13 erg s-1 cm-2. This corresponds to a luminosity L(Hβ) = 1.12 × 1040 erg s-1 and a number of ionizing photons Q(H) = 2.34 × 1052 s-1. The number of O stars can then be derived from the equation 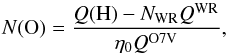 (1)where η0 is the ratio of the number of O7V stars to the number of all OV star. It is equal to 0.5 for a starburst age of 4 Myr (derived from the equivalent width of Hβ and using the dependence of η0 on EW(Hβ) in Schaerer & Vacca 1998). The number of ionizing photons emitted by a single WR or O7V star is QWR = QO7V = 1 × 1049 s-1 (Schaerer & Vacca 1998). Then, the number of O stars in Mrk 996 is N(O) = 2345, giving N(WR)/N(O + WR) = 0.19. This number of WR stars relative to that of O stars is among the highest found for WR galaxies (Guseva et al. 2000).
(1)where η0 is the ratio of the number of O7V stars to the number of all OV star. It is equal to 0.5 for a starburst age of 4 Myr (derived from the equivalent width of Hβ and using the dependence of η0 on EW(Hβ) in Schaerer & Vacca 1998). The number of ionizing photons emitted by a single WR or O7V star is QWR = QO7V = 1 × 1049 s-1 (Schaerer & Vacca 1998). Then, the number of O stars in Mrk 996 is N(O) = 2345, giving N(WR)/N(O + WR) = 0.19. This number of WR stars relative to that of O stars is among the highest found for WR galaxies (Guseva et al. 2000).
Our estimates of the number of WNL and WNC stars are very similar to those given by Thuan et al. (1996): N(WNL) = 601 and N(WCE) = 74. On the other hand, our estimates of WNL, WCE, and O stars do not agree with those derived by James et al. (2009). Their very high values (~3000 WR stars and ~150 000 O stars) are partly a consequence of estimates made using the flux integrated over the entire galaxy, rather than just the core region, and partly due to their erroneously high Hβ flux (their Table 2), a factor of ~5 higher than ours, when duly compared with our simulated VIMOS aperture. Such a high Hβ flux is inconsistent with our many observations of Mrk 996. Furthermore, their observed Hα flux (narrow+broad) of 3.65 × 10-12 erg cm-2 s-1 is ~7 times higher than the total Hα flux of (5.4 ± 0.7) × 10-13 erg cm-2 s-1 obtained by Gil de Paz et al. (2003) from Hα integrated photometry over the whole extent of the line emission. On the other hand, our value of 9.03 ± 0.13 × 10-13 erg cm-2 s-1 for the Hα flux in a 1 6 aperture is more consistent with the Gil de Paz et al. (2003) value.
6 aperture is more consistent with the Gil de Paz et al. (2003) value.
4. Mapping the kinematics of broad and narrow lines
4.1. Velocity maps
As discussed above, there are two main regions in Mrk 996 with distinct kinematic properties (see also Thuan et al. 1996; James et al. 2009): the central high-ionization broad-line emission zone and the outer low-ionization narrow-line emission zone. We now present maps of both regions in the strongest emission lines and use them to discuss the kinematics of the broad and narrow components. All maps presented here made extensive use of the QFitsView astronomical package4. In particular, the function velmap goes through a datacube and fit a Gaussian to a line. The arguments CENTER and FWHM, provided by the user, are used as initial estimates for the gauss-fit. The task then returns the results of the best fit, primarily the fit line center and fit line FWHM, producing the corresponding radial velocity and velocity dispersion maps.
 |
Fig. 5 Velocity dispersion maps. Left: map of the narrow component of the Hα line, representative of all other narrow-line maps (narrow [O iii] λ5007, [O i] λ6300, [S ii] λ6717). Right: map of the He i λ7065 line, representative of all other broad-line maps ([O iii] λ4363, broad Hα). The contours and orientation are the same as in Fig. 4. |
Figure 4 (left panel) shows the radial velocity maps for the narrow component of the Hα line. Velocity maps of other narrow lines such as [O i] λ6300, [S ii] λ6717, and narrow [O iii] λ5007 are similar to the Hα narrow-component map, and are not shown. All maps are consistent with a systemic velocity of ~1640 km s-1, in agreement with the velocities of the narrow lines in the integrated spectrum (Table 3). Examination of the Hα narrow component velocity map reveals a blueshift in the SW direction and a redshift in the NE direction, indicative of an overall rotation pattern. The kinematic pattern changes in the inner 2 ′′ where the symmetry axis becomes oriented in the EW direction. Such a twisted velocity map suggests an isotropic gas outflow from the center, superimposed on a rotation pattern of the underlying disk. We also note the presence of a high-velocity feature, perhaps produced by an outflow blob, in the SE direction, at the position x = 0 2 and y = 1
2 and y = 1 8. This high-velocity component is seen only in the direction diametrically opposite to the region of high extinction in the NW discussed below. We will discuss this high-velocity feature further below.
8. This high-velocity component is seen only in the direction diametrically opposite to the region of high extinction in the NW discussed below. We will discuss this high-velocity feature further below.
Figure 4 (right panel) shows the radial velocity map for the broad He i λ7065 line emission in the central region. In contrast to the narrow Hα line emission map, it shows no overall rotation pattern. The velocity of the nuclear broad-line emission is blueshifted with respect to that of the narrow component, in agreement with the broad-line velocities in the integrated spectrum (Table 3). There is some indication of slightly higher radial velocities in regions around the nuclear region. This ring-like velocity structure may indicate isotropic motions around the central region. There is, however, one striking exception: the radial velocity map of the [O iii] λ4363 line does not give a systemic velocity in agreement with the one in the nuclear region for other broad lines. The broad [O iii] λ4363 line emission is concentrated in the central 2′′, and it is clearly blueshifted by ΔV ~ 60 km s-1 with respect to the systemic velocity. This is seen not only in the velocity map, but also in the integrated spectrum, as discussed in Sect. 3.2. We will discuss the kinematics of [O iii] λ4363 in greater detail below.
4.2. Velocity dispersion maps
Figure 5 (left panel) shows the velocity dispersion maps, the left panel for the narrow component of Hα, and the right panel for the broad He i λ7065. Again, the narrow Hα map is representative of all dispersion maps for the narrow lines, such as narrow [O iii] λ,λ4959, 5007, [O i] λ6300 and [S ii] λ6717. These maps show a high central value of σ (FWHM/2.355) of ~45 km s-1, in agreement with the value given by the integrated spectrum (Table 3). The velocity dispersion then decreases outwards with radius. In the left panel, there is a clear increase in the velocity dispersion towards the outflow blob seen in the radial velocity map, in the SE direction. There are also two low-dispersion regions to the NE and NW, which appear to be related to the high-extinction region seen in the HST color map of Thuan et al. (1996). An additional low-dispersion region is seen in the SW direction. The NE and SW low-dispersion regions are aligned with the overall rotation pattern axis seen in Fig. 4, while the outflow blob shows kinematic features about an axis perpendicular to that axis. A patchy velocity dispersion map may indicate the presence of regions with different densities due to the presence of bubbles or shells as seen, for instance, in the study of the internal kinematics of the prototypical HII galaxy II Zw 40 (Bordalo et al. 2009).
Figure 5 (right panel) shows the velocity dispersion map for the He i λ7065 line. As before, this map is similar to those of other broad lines originating from the dense nuclear region. The He i velocity dispersion peaks at the center, with σ ~ 190 km s-1 (see also Table 3 for the integrated spectrum), and decreases outwards to values typical of the narrow-line region (σ of 50–100 km s-1). The width of the He i line is similar to that of the broad component of the Hα and Hβ lines, and of the [O iii] λ4363 and [N ii] λ5755 auroral lines which we discuss next.
4.3. The peculiar kinematics of the [O III] λ4363 and [N II] λ5755 lines
 |
Fig. 6 The peculiar kinematics of the [O iii] λ4363 line (upper panels) and of [N ii]λ5755 (lower panels). Contours are the monochromatic intensity of the corresponding emission-line from decreasing intensity intervals of 10-18 erg cm2 s-1in peak intensity. Pixels within the contours are 3σ above noise. North is up and east is left. |
Figure 6 shows the velocity fields of [O iii] λ4363 and [N ii] λ5755. Both lines are totally dominated by the broad emission: the narrow lines, if present, are undetected in the spatially resolved maps. The velocity dispersion of [O iii] λ4363 is very similar to that of He i λ7065 (Fig. 5), with some structures in the SE-NW direction and an integrated σ ~ 200 km s-1. A peak is also seen in the SW direction, but in a region of lower S/N per pixel, so we will not consider it real. The [N ii] λ5755 line is also broad, though with a somewhat smaller integrated value. The radial velocity maps of these lines have one intriguing peculiarity: both lines are blueshifted with respect to the systemic velocity of the galaxy, by some 60 km s-1 in the case of [O iii] λ4363, and by ~20 km s-1 in the case of [N ii] λ5755. In addition, [N ii] λ5755 also shows some structures in the SE-NW in the radial velocity map, suggestive of bipolar outflow motions from the nucleus. The kinematics of the narrow-line region outside the nucleus are, however, not correlated with those of the inner regions, suggesting that the strong motions associated with the broad lines observed are decoupled from motions in the narrow-line region. This interpretation is consistent with the assumption that the outflow motions originate from WR stars in the nuclear region, as is also implied from the flux and velocity maps of the WR blue and red bumps observed in the original data cube. This is also in agreement with the interpretation drawn in Sect. 3.2 for the different systems of emission lines seen in the integrated spectrum.
5. Matching the spatially resolved kinematics with the two-density model
The [S ii] λ6717/λ6731 ratio has been widely used in aperture spectroscopy to derive the electron density in H ii regions. The disadvantage is that it only gives an average value of the physical conditions in the region, masking any electron density variation or gradient or any nonuniformity and inhomogeneity in the ionization structure. That the density structure in Mrk 996 is not uniform has been discussed by Thuan et al. (1996, 2008), and James et al. (2009). Thuan et al. (1996, 2008) had to invoke a CLOUDY model with two zones of different electron densities to account for the integrated optical, near-, and mid-infrared spectra of Mrk 996.
 |
Fig. 7 Maps of low (left) and high (right) electron density emission. The orientation is the same as in Fig. 4. |
Here, we use a method for mapping low- and high-density clouds in astrophysical nebulae recently devised by Steiner et al. (2009a). This method aims to distinguish regions of low electron densities from those of high electron densities by using individual forbidden line emission images, as opposed to their ratio which may often have low S/N in the outer regions and give untrustworthy results. We will apply this method to the [S ii] λ6717 and [S ii] λ6731 emission line images of Mrk 996 to test the hypothesis of a two-density model for the galaxy. These two images are transformed into new images of low-(Iij(ld)) and high- (Iij(hd)) density emission by applying the Steiner et al. (2009a) formula 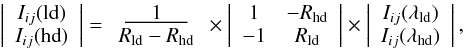 where Iij(λld) is the [S ii]λ6717 image, Iij(λhd) is the [S ii]λ6731 image, Rld is the low-density limit ratio of [S ii] λ6717/λ6731, and Rhd is its high-density limit ratio. From Table 1 in Steiner et al. (2009a), we find Rld = 1.44 and Rhd = 0.44, corresponding to number densities of 81 cm-3 and 5900 cm-3, respectively. The latter value should be considered an upper limit to the number density of the gas to which the [S ii] diagnostics can be applied since the critical densities for collisional deexcitation for [S ii] λ6717 and λ6731 are 1400 and 3600 cm-3, respectively (Table 3).
where Iij(λld) is the [S ii]λ6717 image, Iij(λhd) is the [S ii]λ6731 image, Rld is the low-density limit ratio of [S ii] λ6717/λ6731, and Rhd is its high-density limit ratio. From Table 1 in Steiner et al. (2009a), we find Rld = 1.44 and Rhd = 0.44, corresponding to number densities of 81 cm-3 and 5900 cm-3, respectively. The latter value should be considered an upper limit to the number density of the gas to which the [S ii] diagnostics can be applied since the critical densities for collisional deexcitation for [S ii] λ6717 and λ6731 are 1400 and 3600 cm-3, respectively (Table 3).
We can apply this method to our integral field observations to assess density variations along the line of sight to the central region of Mrk 996. Figure 7 (left panel) shows the low-density image (Iij(ld)) and the right panel shows the high-density image Iij(hd). If the [S ii] emission came only from low-density clouds, all emission would be seen in the left panel only, and none would be seen in the right one. We see clearly that, in Mrk 996, we do have emission along the line of sight from a low-density cloud (left panel) which covers the whole field and emits more in the EW direction. The high-density image (right panel) shows emission concentrated only in the nuclear region. This technique shows clearly that a single low-density regime is ruled out and that an additional regime of high density must be present. These clouds in the nuclear region are probably associated with the broad-line emission shown by some ionic species (e.g., Fig. 4b) and with the WR stars discussed below (see Fig. 14). By performing surface photometry on the high-density image Iij(hd), we derive the diameter of the high-density region to be ~1 6 or ~160 pc, about the size of the inner spiral structure discussed by Thuan et al. (1996) and James et al. (2009). This size coincides with our chosen aperture for the integrated nuclear spectrum shown in Fig. 2.
6 or ~160 pc, about the size of the inner spiral structure discussed by Thuan et al. (1996) and James et al. (2009). This size coincides with our chosen aperture for the integrated nuclear spectrum shown in Fig. 2.
6. PCA tomography
 |
Fig. 8 Tomogram (left) and eingeinvector (E1) in red cube (5700–7200 Å). Bottom right: the spectrum from the original data cube; upper right: the extracted spectrum from the reconstructed data cube, using the PCA tomography results (eigenvector 1 and tomogram 1) (see Steiner et al. 2009b). |
 |
Fig. 9 Tomogram (left) and eingeinvector (E2) in red cube 5700–7200 Å (right). The eigenvector shown in the lower-right panel is a zoom in a shorter wavelength range for a better visualization of the features of interest. |
 |
Fig. 10 Tomogram (left) and eingeinvector (E3) in blue cube 4300–5100 Å (right). The eigenvector shown in the lower-right panel is a zoom in a shorter wavelength range for a better visualization of the features of interest. |
To fully exploit the wealth and complexity of the information that integral field spectroscopic (IFS) data provide, we need analysis techniques that are more sophisticated than those commonly used in one-dimensional long-slit spectroscopy. However, this new methodology is still scarce, and most IFS studies simply reduce the data cube to one-dimensional spectra and two-dimensional maps, so that the usual well-known spectroscopy and imaging techniques can be applied to analyze the data. Here, we use a technique that has been introduced recently to extract spatial and spectral information from data cubes in a statistical manner, so that it can be used to derive physical information. This technique is called principal component analysis tomography. It combines the statistical PCA analysis, widely used in astronomy, with tomography which is also used in astronomy and other sciences to represent certain types of information derived from imaging techniques. A short presentation of the technique can be found in Steiner et al. (2010).
What PCA tomography basically does is to extract hidden information by transforming a large set of correlated data, in our case the wavelength pixels, into a new set of uncorrelated variables, ordered by their eigenvalues. Each new component, or eigenvector, carries the combined information of the original data, ordered by their significance as measured by their relative variance. The new coordinates can then be represented by their eigenvector and their respective projection called a tomogram. The combined analysis of the eigenvectors and tomograms allows for interpretations of physical phenomena that may not be directly seen in an usual spectrum or image.
Hair et al. (1998) devised a so-called scree test, which was used by Steiner et al. (2009b), and it allows the assessment of the most interesting eigenvectors and tomograms, those that contain most of the relevant information from the data. This test applied to our PCA results shows that the first five eigenvectors and tomograms are sufficient to reconstruct the data cube with the most significant information on the uncorrelated physical properties of the original data.
PCA Eigenvalues (blue and red cubes).
Table 4 presents the PCA results from the analysis of the GMOS/IFU data cubes for the red and blue gratings. Column 1 shows the eigenvalue numbers and Cols. 2 and 3 show the resulting variances for the first 10 principal components in the cases of the red and blue gratings, respectively. From these, one can see that the first four principal components carry 99.5% of all uncorrelated information contained in the data.
The first eigenvector in the red cube, which accounts for 98.15% of the data cube variance, is shown in Fig. 8. We note that the reconstructed data cube, using only the first principal component (eigenvector 1 and tomogram 1), is able to reproduce the original integrated spectrum. The upper-right panel in Fig. 8 shows the representative integrated spectrum obtained by using a reconstructed data cube with only the first eigenvector. This spectrum is identical to the one extracted from the original data cube. The added contribution of eigenvectors 2–5 accounts for only ≤2% of the variance in the data cube. With the simultaneous analysis of tomogram 1 and the corresponding eigenvector 1, we can reproduce most of the information that can be obtained from a direct broadband image and from an integrated spectrum of the corresponding field of view. This shows the great redundancy of this type of data, allowing for discriminating non-redundant information. The power of this technique lies in the fact that by removing the effects of the strongest correlations, one can look for the less significant ones.
Eigenvector 2 still contributes significantly (>1%) and its tomogram reveals distinct bipolar motions originating from the nucleus (Fig. 9). In this case, the y-axis does not represent flux, and the eigenvector is not a spectrum. The point to note is that the eigenvectors are not spectra but vectors of correlations. Here, the anti-correlations (up and down spikes) are seen in the narrow lines only. This means that this particular phenomenon is affecting only the narrow lines. In addition, the feature shows an anti-behavior of the blue side vs. the red side of the lines which leads us to interpret that we are seeing motions in the narrow lines only (e.g., [S ii] 6717, 6730). The respective tomogram in Fig. 9 (left) shows higher order kinematics of the narrow line. This feature cannot be seen in a classical way as if it were in a direct spectrum, but rather as a residual hidden phenomenon carrying only 1% of the variance. One may interpret this anti-correlation as representing the second-order rotation of a low-density cloud system in the circumnuclear region. Therefore, the broad lines observed in Mrk 996 are probably not due to a turbulent mixing layer, as postulated by James et al. (2009). The present interpretation is more consistent with the hypothesis that the broad lines originate from stellar wind outflows from WR stars in the nuclear region, as implied from the flux and velocity maps of the WR blue and red bumps observed in the original data cube, convoluted with some rotation of the low-density gas within this unresolved inner region. Our analysis is based on two independent data sets, the blue and the red cubes. The features observed in the eigenvectors and tomograms of both data sets are all very similar, which lends credibility to our interpretations.
 |
Fig. 11 Left: logarithmic extinction coefficient map derived from the Balmer decrement using integrated line profiles (broad + narrow components). Pixels with high noise at the border were masked out. Right: Hβ equivalent width map (per pixel in Å). The orientation is the same as in Fig. 4. |
Eigenvector 3 contributes about 0.5% of the variance of the blue cube. It also reveals a strong feature from its tomogram (Fig. 10, left) which seems to indicate a distinct intensity contribution from the narrow lines originating in the region surrounding the nucleus, which is different than that of the broad lines. It is noteworthy that the highest intensity features correspond to the positive correlation shown in the broad lines. These features are mapped as white and black pixels in the tomogram and coincide with the broad-line and high-density emission region as extensively discussed above. The lower intensity negative correlation corresponds to the narrow-line and low-density emission region as mapped with gray pixels in the tomogram, but the most important feature can be seen in the zoomed eigenvector (Fig. 10, bottom right) where a narrow contribution to the [O iii]λ 4363 line is unequivocally detected. This narrow component is not directly seen in the integrated spectrum, but it shows up in this third eigenvector as a dip feature. It is a fundamental finding for our purpose and validates our effort to extract a spatially resolved integrated spectrum which excludes the nuclear region. This will allow for the direct and precise determination of chemical abundances in Mrk 996 (see below) without having to resort to modeling as Thuan et al. (1996) did. We note that this direct and precise mapping of the narrow component of the [O iii]λ 4363 line could not be achieved with the data of James et al. (2009) because the narrow component was not detected in their observations with a lower signal-to-noise ratio.
Eigenvector 4 (not shown) contributes only ~0.1% of the variance, but it contains a visible feature in the NW direction. This feature is not related to the emission lines but to the continuum. It may represent, in a statistical way, the effect of dust obscuration. Extinction in that direction has been noted above from analysis of the original cube, through mapping of the Balmer decrement. It can also be seen from the HST broadband images (Thuan et al. 1996). Eigenvector 5 (not shown) contributes less than 0.1% of the variance, and it carries virtually no additional information on uncorrelated physical properties. The higher order eigenvectors and tomograms become more difficult to interpret and/or reach noise features or fingerprints that may not be real, but are instead associated with detector defects and other artificial features. We note that the PCA tomography technique can be used to eliminate higher order noise of the original data by the suppression of detector defects (fingerprints), noise, and by the reconstruction of the data cube accounting only for the first meaningful eigenvectors. A lengthier discussion of this topic is beyond the scope of the present paper. Admittedly, the interpretation of the PCA tomography is not straightforward, but it becomes robust when combined with all other information available. The use of PCA tomography for analyses similar to the one presented here can be found in more recent works, such as Steiner et al. (2013), Sanmartim et al. (2013), Riffel et al. (2011), Ricci et al. (2011), and Schnorr Müller et al. (2011).
7. Mapping the physical conditions
7.1. Extinction and Hβ equivalent width maps
The extinction map in Fig. 11 (left panel) was derived by the ratio of the broad+narrow components of the Hα and Hβ emission lines. It shows that the nuclear region of Mrk 996 has a higher extinction (C(Hβ) ~ 0.7). It is surrounded by a region of lower extinction, with C(Hβ) decreasing to zero. Some higher extinction extension towards the NW and E directions are seen in this map. The central part of the high C(Hβ) region coincides with the broad-line high-density region. As emphasized in Sect. 3.3, the Hα/Hβ ratio in this region cannot be used for extinction measurements, as collisional excitation of hydrogen in the nuclear region may make the Balmer decrement and the derived extinction value there artificially high (Fig. 11, left). The regions outside the nucleus show C(Hβ) ~ 0.4, in good agreement with the extinction derived from the integrated spectrum outside the nucleus (see below Table 5). Figure 11 (right panel) shows the map of Hβ equivalent widths [EW(Hβ)] per pixel. It appears that the highest values are not centered on the nucleus but rather in the NW direction, or in a circular ring just outside the nuclear region. Since the broad component in Hβ is primarily seen in the central part of the galaxy, the integrated EW(Hβ) per pixel drops steeply outwards.
Emission line parameters derived from the outer spectrum within a 2 7 × 4
7 × 4 4 excluding the inner circle with 1
4 excluding the inner circle with 1 3 radius.
3 radius.
 |
Fig. 13 Excitation maps: BPT diagram of narrow emission line ratios. Left: log ([O iii] λ5007/Hβ). Middle: log ([N ii] λ6584/Hα). Right: log ([S ii] λ6717,6731/Hα). The orientation is the same as in Fig. 4. |
7.2. Maps of line ratios sensitive to electron temperature and density
Figure 12 shows the spatial distribution of the [S ii] λ6717/ [S ii] λ6731 ratio. Low values (corresponding to the high-density regime, Ne ≥ 103 cm-3) of this ratio are seen in the central region, with a gradient towards higher values (corresponding to the low-density regime, Ne ≤ 102 cm-3) outside the nucleus, in good agreement with Fig. 7.
The ratio of the [O iii] emission from an upper level (the auroral line, λ4363) relative to that from lower levels (the nebular lines, λλ4959,5007) is known to be highly temperature sensitive. For the low-density region, the electron temperatures with the low-density approximation, typical of the warm ionized gas in H ii regions, range from 10 000 K to 20 000 K. However, as mentioned above, the very high flux ratios we find in the central regions is due to the very high density and thus the low-density approximation for temperature determination is no longer applicable. Mapping this ratio over the whole extent of our FOV is more difficult in our case, since in the nuclear region the narrow line is unresolved and in the outer region the broad line is not present. The integrated (broad+narrow) line ratio would yield an unphysical result since, as mentioned in Sect. 3.2, the different line systems originate from regions with completely different physical conditions. We have only used this ratio in the integrated spectrum of the region surrounding the nucleus (outer spectrum) in order to derive the chemical abundances directly, as described below.
7.3. Diagnostic diagrams
 |
Fig. 14 Maps of Wolf-Rayet spectral features. Left: blue bump (without the [Fe iii] emission). Right: red bump. The fluxes in the bumps are given in units of 10-16 erg s-1 cm-2. The orientation is the same as in Fig. 4. |
Figure 13 shows maps of some narrow emission-line ratios of interest such as log ([O iii] λ5007/Hβ) (left panel), log ([N ii] λ6584/Hα) (middle panel), and log ([S ii] λ6717, 6731/Hα) (right panel). These ratios are often used in a diagnostic diagram, known as the Baldwin et al. (1981, BPT) diagram, to identify the source of excitation in narrow emission-line galaxies. We have used the mapping of these ratios to assess the source of ionization in individual patches of the ISM in Mrk 996 (see also Lagos et al. 2009, 2012). Examination of the spatial distribution of these diagnostic ratios shows that regions of intense emission of high-ionization species ([O iii]) are coincident with those of weak emission of low-ionization species ([N ii], [S ii]), implying a single source of ionization, namely the UV radiation from massive stars. The conclusion is the same if we plot the BPT diagram pixel by pixel (not shown here) instead of using maps of individual ratios. Similar results and conclusions were obtained by James et al. (2009). All points fall in the locus predicted by models of photo-ionization by massive stars (e.g., Osterbrock & Ferland 2006). However, it has been shown by Stasińska et al. (2006) and Groves et al. (2006) that an AGN hosted by a low-metallicity galaxy would not be easily distinguished in such a diagram, even if the active nucleus contributed significantly to the emission lines. In fact, the presence of the [O iv] λ25.89 μm in the MIR spectrum of Mrk 996 (Thuan et al. 2008) implies the presence of harder ionizing radiation than the stellar one. Thuan et al. (2008) analyzed several possible sources of this radiation, including the presence of an AGN, and concluded that the most probable source is photo-ionization by fast shocks plowing through a dense ISM. In a Chandra X-ray study of Mrk 996, Georgakakis et al. (2011) did not find evidence for an AGN and also attributed the [O iv] λ25.89 μm emission to shocks associated with supernova explosions and stellar winds.
7.4. Wolf-Rayet star emission
 |
Fig. 15 Spatially narrow-line region spectrum (lower red spectrum) displayed with the integrated spectrum of the nuclear region (upper black spectrum). |
Thuan et al. (1996) and James et al. (2009) found a large population of WR stars in the central part of Mrk 996. Figure 14 shows maps of the spectral features associated with this WR stellar population. These maps were created by summing the fluxes within the wavelength range of interest, and subtracting the adjacent continuum. We have excluded from it the narrow [Fe iii] λ4658 line.
The left panel shows the map of the blue bump which includes the [N iii] λ4640 and He ii λ4686 emission features. The right panel shows the map of the red bump due to the weaker C iv λ5808 emission. The blue bump emission appears to be more extended spatially than the red bump emission, though this is just a consequence of the lower S/N in the red bump feature. The maps show that the blue and red bumps are coincident spatially and that their spatial distributions are identical to those of the broad He i and Hα emissions. This implies that the WR stars are located and concentrated solely in the nuclear region of Mrk 996.
The total observed (uncorrected for extinction) flux of the blue bump is 3.87 × 10-14 erg s-1 cm-2, while that of the red bump is 1.14 × 10-14 erg s-1 cm-2. These fluxes derived directly from the maps are a factor of ~2 larger than those derived from the integrated spectrum as described in Sect. 3.4. The origin of this discrepancy is probably due to our not performing here a proper deblending of the nebular lines (i.e., [Fe iii] λ4658, [Fe iii] λ4702, and He i 4713). Thus, a more detailed quantitative comparison with the integrated spectrum is not warranted. With the maps, we wish only to show the region where the WR emission originates.
7.5. Physical conditions and oxygen and nitrogen abundances of the outer narrow-line region
The integrated nucleus spectrum of Fig. 2 clearly shows the presence of blended broad and narrow lines. Table 3 presents the emission line fluxes of both broad and narrow components derived from this integrated nucleus spectrum (obtained through a ~1 6 aperture) after line deblending. As discussed in Sect. 5, we have been able to separate spatially the nuclear broad-line region from the surrounding narrow-line region by using the electron density diagnostic map (Fig. 7). The broad-line region, where the He i, [O iii] λ4363, and [N ii] λ5755 lines, and the WR blue and red bumps originate, coincides with the high-density region, with a diameter of ~1
6 aperture) after line deblending. As discussed in Sect. 5, we have been able to separate spatially the nuclear broad-line region from the surrounding narrow-line region by using the electron density diagnostic map (Fig. 7). The broad-line region, where the He i, [O iii] λ4363, and [N ii] λ5755 lines, and the WR blue and red bumps originate, coincides with the high-density region, with a diameter of ~1 6, in the electron density diagnostic maps. The diameter of ~160 pc of the nuclear broad-line and high electron density region is consistent with the size derived by Thuan et al. (1996) by CLOUDY photo-ionization modeling of the nuclear emission of Mrk 996.
6, in the electron density diagnostic maps. The diameter of ~160 pc of the nuclear broad-line and high electron density region is consistent with the size derived by Thuan et al. (1996) by CLOUDY photo-ionization modeling of the nuclear emission of Mrk 996.
 |
Fig. 16 Comparison of the measured line fluxes in the integrated spectrum of the outer region outside the nucleus (Table 5) with the fluxes measured in the narrow components of the integrated spectrum of the nucleus of Mrk 996 (Table 3). |
Having spatially resolved the broad-line and high-density region of Mrk 996 by the use of the various diagnostic maps, we can now go one step further: we can exclude the nuclear region and extract an integrated spectrum of the light that comes exclusively from the narrow-line region surrounding the nucleus. Figure 15 shows the outer narrow-line region spectrum in red lines (lower spectrum). For comparison, the integrated spectrum of the nuclear region is shown by a black line (upper spectrum). We emphasize that the narrow lines are not derived from a decomposition of the blended lines, but they are measured from the actual integrated spectrum in the region outside the nucleus. The three panels in Fig. 15 show several lines of interest, and are labeled [O iii] λ4363, Hα, and He i λ6678. It can be seen that the narrow component of [O iii]λ4363 in the outer region is very weak, but clearly detected at a 7σ level. This weak line is swamped by the broad component in the nuclear region and not detectable at lower S/N observations. One can also see that the narrow line of [O iii] λ4363 in the outer region, as opposed to the broad line of [O iii] λ4363 in the integrated nucleus region, is not blueshifted. It falls in the same systemic recession velocity derived from the narrow components of the lines in the integrated nucleus region. The existence of this narrow component originating from the low-density region has also been demonstrated by a completely independent technique, that of PCA tomography, as discussed in Sect. 6. The [N ii] and [S ii] lines show a narrow component everywhere, independent of the density. We note the high value of the [S ii] λ6717/λ6731 ratio in the narrow-line region, indicative of a low electron density.
We can now use the measured line fluxes, shown in Table 5 from the spatially separated narrow-line region spectrum (red-line lower spectra in Fig. 15) to derive the physical conditions and element abundances in the low-density outer region. As expected, the line fluxes measured outside the nucleus are in good agreement with the measured fluxes of the narrow components of the integrated spectrum in the nuclear region, as shown in Fig. 16, corroborating our statement that this zone of low density is on the line of sight of the inner broad-line dense nucleus. By scaling the intensity of the [O iii] λ4363 in the outer region with the narrow Hβ flux ratio of the outer region to the nuclear region, we estimate that the narrow component of the [O iii] λ4363 in the nuclear region must be ~4 fainter than the integrated line, which explains the difficulty in detecting this line directly in the integrated nuclear spectrum.
7.5.1. Oxygen abundances
We make use of the nebular package available in the stsdas external package under IRAF to derive abundances. The tasks in this package are based on a five-level atom model developed by De Robertis et al. (1987). The detection of [O iii] λ4363 allows a direct determination of the electron temperature Te(O++) = 1.29 × 104 K, while the ratio of the [S ii] lines permits us to determine a low electron density in this narrow-line region of Ne ~ 71 cm-3. We obtain 12 + log (O/H) = 7.94 ± 0.30 using C(Hβ) = 0.31, that is, Z⊙/6 by adopting the solar calibration of Asplund et al. (2009). The same result 12 + log (O/H) = 7.88 ± 0.36 is obtained using the Te direct method with the prescriptions of Pagel et al. (1992), Izotov et al. (1994), and Thuan et al. (1995).
This oxygen abundance is in agreement with the value of Thuan et al. (1996) who derived 12 + log (O/H) = 8.0 with a CLOUDY two-zone model of Mrk 996. It is, however, considerably less (by a factor of 3) than the lower limit of 12 + log (O/H) ~ 8.37 obtained by James et al. (2009) for the broad-line region, based on an assumed electron temperature of 10 000 K. Our value of the oxygen abundance is more reliable since the [O iii] λ4363 line intensity, and hence the electron temperature, was determined directly in the low-density region outside the nucleus.
7.5.2. Nitrogen abundances
The derived nitrogen abundance for the low-density region is log (N/O) = −1.53 ± 0.15, in good agreement with the value of − 1.43 obtained by James et al. (2009). It is typical of values derived for BCDs (Izotov et al. 2006).
However, the nuclear region is nitrogen enhanced by a factor of ~20, with log (N/O) = −0.15 ± 0.1. In this case, we assumed a two-density model in nebular, with Ne(low) = 450 cm-3, Ne(high) = 106 cm-3, Te(low) = 104 K and Te(high) = 4 × 104 K. Te(high) is derived from the extinction corrected ratio of [O iii] broad-line fluxes assuming Ne(high). Our high N/O in the broad-line region is in agreement with that obtained by Thuan et al. (1996) from CLOUDY modeling (model 2), and with the value of − 0.13 obtained by James et al. (2009). This nitrogen enhancement is probably due to local pollution from WR stars. Similar cases for a nitrogen enhancement have been observed, for example, in the central region of the nearby dwarf starburst galaxy NGC 5253 by Monreal-Ibero et al. (2012) and by Westmoquette et al. (2013), and for the very metal-deficient (12 + log (O/H) = 7.64) luminous (MB = −18.1 mag) BCD HS 0837+4717 by Pustilnik et al. (2004). Brinchmann et al. (2008), in turn, have noted an elevated N/O for galaxies with WR features in their optical spectrum from SDSS survey. López-Sánchez & Esteban (2010) have also detected a high N/O ratio in objects showing strong WR features (HCG 31 AC, UM 420, IRAS 0828+2816, III Zw 107, ESO 566-8, and NGC 5253). They claim that the ejecta of the WR stars may be the origin of the N enrichment in these galaxies. However, as pointed out by Izotov et al. (2006), this high N/O cannot be caused by WR nitrogen-enriched ejecta with a number density Ne similar to that of the ambient gas, but only by considerably denser ejecta since the emissivity of the [N ii] lines is proportional to  .
.
8. Summary and conclusions
The galaxy Mrk 996 is an extraordinary blue compact dwarf galaxy with a dense unresolved nucleus (<160 pc) and a central density of ~106 cm-3. The dense nucleus is surrounded by a lower density star-forming region, with a density of ~102 cm-3. We present here integral field spectroscopy obtained with GEMINI-SOUTH/GMOS/IFU which allows us to study in 2D the physical conditions, ionization structures, and kinematic properties of these two regions, as well as their relationship.
We have made an extensive comparison with the results of the previous similar IFU work by James et al. (2009) on Mrk 996. Our results fully agree with theirs on the spatial variation of the physical properties and detected internal structures of Mrk 996. However, our quantitative results differ somewhat in the number of massive stars present in the star forming nucleus, and in the determination of the chemical abundances. The first disagreement may be partly due to absolute calibration differences. Their fluxes are a factor of ~5 brighter than our simulated VIMOS aperture. We believe our reduction and calibration procedures to be correct as they have been double-checked independently by us using different standard stars. The red cube and blue data cubes were derived from observations of different nights and the calibrations agreed, without the need for averaging the data. Other external checks have also shown consistency. More importantly, we have made a more precise determination of oxygen abundance in the low-density gas by directly detecting the narrow line of [O iii]λ4363 outside the nucleus. This detection was confirmed, independently, by the use of a new innovative method of data cube analysis.
We have thus obtained the following results:
-
1)
The integrated spectrum shows four kinematically distinctsystems of emission lines, with line-widths decreasing outwardsfrom the center. The first system shows both broad and narrowlines, originating from the nuclear region. The broad compo-nent is probably associated with the circumnuclear envelopesaround WR stars, while the narrow component is probablyrelated to the circumnuclear envelopes around O stars. The sec-ond system comes from the innermost and densest part of thestar-forming region. It consists of the peculiar emission of the[O iii]λ4363 line which is broad (σ ~ 200 km s-1)and blueshifted by 60 km s-1 relativeto the narrow Hβ line. The third system consistsof the permitted hydrogen and helium lines, and of the auro-ral [N ii] line. These also showlarge widths, similar to those in the second system, but are lessblueshifted (~20 km s-1). They are likely to originate inregions farther away from the center than the second line system.The fourth system consists only of narrow lines of hydrogen,helium, doubly ionized ions, and of forbidden lines of neutral andsingly ionized species. These all have the same radial velocities asthe narrow Hβ emission line.
-
2)
Most of the observed physical conditions and kinematics of the nucleus of Mrk 996 appear to be related to the presence of a WR stellar population, as inferred by the presence of the blue and red bump spectral features. We estimate, from the integrated spectrum as well as from the spatially resolved maps of these features, that the nuclear region of Mrk 996 contains ~473 WNL and ~98 WCE stars, with N(WR)/N/(O + WR) = 0.19, at the high end for WR galaxies.
-
3)
The monochromatic emission maps and the line ratio, velocity, and dispersion maps of the nuclear region suggest an isotropic ionized gas outflow from the center (<160 pc), superposed on an underlying rotation pattern. This outflow is probably associated with the ejecta from the WR stellar population. The narrow (σ ~ 45 km s-1) and broad (σ ~ 200 km s-1) lines from the nucleus are supersonic. The [O iii]λ 4363 and [N ii]λ 5755 lines show peculiar kinematics, suggestive of outflow motions from the nucleus, or multiplicity due to a patchy ISM.
-
4)
We have also performed a PCA tomography analysis that corroborates, in a completely independent manner, the kinematic picture outlined above for Mrk 996: an outflow from the inner region, associated with winds from WR stars, superposed on an underlying rotation pattern, affecting the motions of low-density clouds. This recently developed statistical method for handling data cubes has also resulted in the independent detection of the narrow component of the [O iii]λ 4363 line, not seen previously in integrated spectra. This detection allows a reliable and direct measurement of the chemical abundances in the region outside the nucleus.
-
5)
We obtain an oxygen abundance 12 + log (O/H) = 7.90 ± 0.30 (~0.2 Z⊙) for the low-density narrow-line region around the nucleus, in agreement with the abundance derived by Thuan et al. (1996), but considerably less than the lower limit of 12 + logO/H = 8.37 derived by James et al. (2009) for the broad-line region, based on an assumed electron temperature. The N/O ratio in the low-density region is typical of BCDs. However, as discussed by previous investigators, there is a nitrogen enhancement by a factor of ~20 in the nuclear region, probably due to nitrogen-enriched WR ejecta, but also to enhanced nitrogen line emission in a high-density environment. The presence of a large number of WR stars in the nucleus of this dwarf starburst galaxy greatly affecting its local kinematics is somewhat unexpected because of its sub-solar oxygen abundances. If we take the results of stellar population models at face value (see, e.g., Cerviño & Mas-Hesse 1994), this implies that we are witnessing a very short phase of the evolution of the starburst in Mrk 996.
-
6)
Finally, we have used a method recently proposed by Steiner et al. (2009a) to map low- and high-density regions in Mrk 996. By performing surface photometry on the resulting high-density image, we have obtained an upper limit of ~1
 6 (~160 pc) for the diameter of the nuclear region. This region is where the broad lines originate. The emission line ratios in the BPT diagnostic diagram appear to indicate ionization from UV radiation of massive stars alone. The presence of harder ionizing radiation, as implied by the presence of the [O iv] λ25.9 μm emission-line in its MIR spectrum (Thuan et al. 2008), is most likely due to fast radiative shocks propagating in a dense ISM. This is in agreement with the Chandra X-ray study of Mrk 996 by Georgakakis et al. (2011) who rule out an AGN, but also favor shocks as the ionization source for the [O iv] λ25.9 μm emission. We intend to investigate this issue further with new integral field observations in the near-IR with adaptive optics. This will allow us to set more stringent upper limits to the size of the broad-line emitting region, and also to study additional physical properties of the nebular emission in this wavelength range including possible H2 emission that probe the warm molecular gas in the shells around the photo-dissociation regions.
6 (~160 pc) for the diameter of the nuclear region. This region is where the broad lines originate. The emission line ratios in the BPT diagnostic diagram appear to indicate ionization from UV radiation of massive stars alone. The presence of harder ionizing radiation, as implied by the presence of the [O iv] λ25.9 μm emission-line in its MIR spectrum (Thuan et al. 2008), is most likely due to fast radiative shocks propagating in a dense ISM. This is in agreement with the Chandra X-ray study of Mrk 996 by Georgakakis et al. (2011) who rule out an AGN, but also favor shocks as the ionization source for the [O iv] λ25.9 μm emission. We intend to investigate this issue further with new integral field observations in the near-IR with adaptive optics. This will allow us to set more stringent upper limits to the size of the broad-line emitting region, and also to study additional physical properties of the nebular emission in this wavelength range including possible H2 emission that probe the warm molecular gas in the shells around the photo-dissociation regions.
The advent of Integral Field Units has allowed spatially resolved spectroscopy, with the simultaneous acquisition of a complete set of spectra covering a spatially resolved field of view. Despite this great instrumental advance, the superior and abundant data that are obtained with IFUs are still mostly analyzed with the traditional techniques of 1D slit spectroscopy. Although these traditional methods are useful for a first look at the data, they do not fully exploit the wealth of information given by integral field spectroscopy. In some cases, they may not even be the proper tools to use, particularly when assumptions on boundaries of regions need to be made, or other structure-dependent physical equilibria need to be assumed. We have attempted to apply a few new techniques to the data in this paper, and they have yielded useful results. More new methodologies for analysis are required, and we will apply them as they are devised.
Acknowledgments
E.T. acknowledges the US Gemini Fellowship by AURA that supported his visit to the Astronomy Department of the University of Virginia where most of this work was carried out. T.X.T. is grateful for the hospitality of the Institut d’Astrophysique de Paris. We thank Roberto Cid Fernandes, Linda J. Smith, Mark Whittle, and François Cuisinier (in memorium) for reading the manuscript and providing fruitful comments. We are also indebted to Joao Steiner and Tiago Ricci for their comprehensive help with the application and interpretation of our PCA tomography results. We are specially thankful to the referee for his/her careful analysis of this manuscript and criticisms and suggestions that greatly improved the presentation of our results.
References
- Allington-Smith, J., Graham, M., Content, R., et al. 2002, PASP, 114, 892 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Baldwin, J. A., Phillips, M. M., & Terlevich, R. 1981, PASP, 93, 5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baldwin, J. A., Spinrad, H., & Terlevich, R. 1982, MNRAS, 198, 535 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, S. C., Turner, J. L., Langland-Shula, L. E., et al. 2002, AJ, 124, 2516 [NASA ADS] [CrossRef] [Google Scholar]
- Bordalo, V., Plana, H., & Telles, E. 2006, ApJ, 696, 1668 [Google Scholar]
- Bosch, G., Terlevich, E., & Terlevich, R. 2002, MNRAS, 329, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Brinchmann, J., Kunth, D., & Durret, F. 2008, A&A, 485, 657 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cerviño, M., & Mas-Hesse, J. M. 1994, A&A, 284, 749 [NASA ADS] [Google Scholar]
- De Robertis, M. M., Dufour, R. J., & Hunt, R. W. 1987, J. Roy. Astron. Soc. Canada, 81, 195 [Google Scholar]
- Filippenko, A. F. 1982, PASP, 94, 715 [NASA ADS] [CrossRef] [Google Scholar]
- Georgakakis, A., Tsamis, Y. G., James, B. L., & Aloisi, A. 2011, MNRAS, 413, 1729 [NASA ADS] [CrossRef] [Google Scholar]
- Gil de Paz, A., Madore, B. F., & Pevunova, O. 2003, ApJS, 147, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Groves, B. A., Heckman, T. M., & Kauffmann, G. 2006, MNRAS, 371, 1559 [NASA ADS] [CrossRef] [Google Scholar]
- Guseva, N. G., Izotov, Y. I., & Thuan, T. X. 2000, ApJ, 531, 776 [NASA ADS] [CrossRef] [Google Scholar]
- Hair J. F. Jr, Anderson R. E., Tatham R. L., & Black W. C. 1998, Multivariate Data Analysis, 5th edn. (Upper Saddle River, NJ: Prentice Hall) [Google Scholar]
- Hook, I., Jorgensen, I., Allington-Smith, J. R., et al. 2004, PASP, 116, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., & Thuan, T. X. 2007, ApJ, 665, 1115 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., Thuan, T. X., & Lipovetsky, V. A. 1994, ApJ, 435, 647 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., Stasińska, G., Meynet, G., Guseva, N. G., & Thuan, T. X. 2006, A&A, 448, 955 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Izotov, Y. I., Thuan, T. X., & Stasińska, G. 2007, ApJ, 662, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., Guseva, N. G., Fricke, K. J., et al. 2010, A&A, 517, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- James, B. L., Tsamis, Y. G., Barlow, M. J., et al. 2009, MNRAS, 398, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Lagos, P., Telles, E., Muñoz-Tuñón, C., et al. 2009, AJ, 137, 5068 [NASA ADS] [CrossRef] [Google Scholar]
- Lagos, P., Telles, E., Nigoche Netro, A., & Carrasco, E. R. 2012, MNRAS, 427, 740 [NASA ADS] [CrossRef] [Google Scholar]
- Loose, H.-H., & Thuan, T. X. 1985, in Star-Forming Dwarf Galaxies and Related Objects, eds. D. Kunth, T. X. Thuan, & J. T. T. Van (Gif-sur-Yvette: Éditions Frontières), 73 [Google Scholar]
- López-Sánchez, Á. R., & Esteban, C. 2010, A&A, 517, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Monreal-Ibero, A., Walsh, J. R., & Vílchez, J. M. 2012, A&A, 544, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Osterbrock, D. E., & Ferland, G. J. 2006, Astrophysics of gaseous nebulae and active galactic nuclei, 2nd. edn. (Sausalito, CA: University Science Books) [Google Scholar]
- Pagel, B. E. J., Simonson, E. A., Terlevich, R. J., & Edmunds, M. G. 1992, MNRAS, 255, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Porter, R. L., Bauman, R. P., Ferland, G. J., & MacAdam, K. B. 2005, ApJ, 622, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Peimbert, M., Luridiana, V., & Peimbert, A. 2007, ApJ, 666, 636 [NASA ADS] [CrossRef] [Google Scholar]
- Pustilnik, S., Kniazev, A., Pramskij, A., et al. 2004, A&A, 419, 469 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ricci, T. V., Steiner, J. E., & Menezes, R. B. 2011, ApJ, 734, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Riffel, R., Riffel, R. A., Ferrari, F., & Storchi-Bergmann, T. 2011, MNRAS, 416, 493 [NASA ADS] [Google Scholar]
- Robbins, R. R. 1968, ApJ, 151, 511 [NASA ADS] [CrossRef] [Google Scholar]
- Sanmartim, D., Storchi-Bergmann, T., & Brotherton, M. S. 2013, MNRAS, 428, 867 [NASA ADS] [CrossRef] [Google Scholar]
- Schaerer, D., & Vacca, W. D. W. 1998, ApJ, 497, 618 [NASA ADS] [CrossRef] [Google Scholar]
- Schnorr Müller, A., Storchi-Bergmann, T., Riffel, R. A., et al. 2011, MNRAS, 413, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Stasińska, G., & Izotov, Y. I. 2001, A&A, 378, 817 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stasińska, G., Cid Fernandes, R., Mateus, A., Sodré, L., & Asari, N. V. 2006, MNRAS, 371, 972 [NASA ADS] [CrossRef] [Google Scholar]
- Steiner, J.E., Menezes, R.B., Ricci, T. V., & Oliveira, A. S. 2009a, MNRAS, 396, 788 [NASA ADS] [CrossRef] [Google Scholar]
- Steiner, J. E., Menezes, R. B., Ricci, T. V., & Oliveira, A. S. 2009b, MNRAS, 395, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Steiner, J. E., Menezes, R. B., Ricci, T. V., & de Oliveira, A. S. 2010, in Co-Evolution of Central Black Holes and Galaxies, eds. B. M. Peterson, R. S. Somerville, & T. Storchi-Bergmann, IAU Symp. (Cambridge: Cambridge Univ. Press), 267, 85 [Google Scholar]
- Steiner, J. E., Menezes, R. B., & Amorim, D. 2013, MNRAS, 431, 2789 [NASA ADS] [CrossRef] [Google Scholar]
- Telles, E., Melnick, J., & Terlevich, R. 1997, MNRAS, 288, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Thuan, T. X., Izotov, Y. I., & Lipovetsky, V. A. 1995, ApJ, 445, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Thuan, T. X., Izotov, Y. I., & Lipovetsky, V. A. 1996, ApJ, 463, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Thuan, T. X., Lipovetsky, V. A., Martin, J.-M., & Pustilnik, S. A. 1999, A&AS, 139, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thuan, T. X., Hunt, L. K., & Izotov, Y. I. 2008, ApJ, 689, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Westmoquette, M. S., James, B., Monreal-Ibero, A., & Walsh, J. R. 2013, A&A, 550, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Emission line parameters derived from the integrated spectrum within a 1 6 aperture.
6 aperture.
Emission line parameters derived from the outer spectrum within a 2 7 × 4
7 × 4 4 excluding the inner circle with 1
4 excluding the inner circle with 1 3 radius.
3 radius.
All Figures
 |
Fig. 1 The GMOS 3 |
| In the text | |
 |
Fig. 2 Integrated GMOS spectrum of the nucleus of Mrk 996 within a 1 |
| In the text | |
 |
Fig. 3 Example of the deblend fitting procedure with the Hα line. Upper panel: the integrated profile of the Hα line as in Fig. 2 (black solid line). The red-dotted line shows the resulting fit to the broad component. The blue-dashed line shows the resulting fit to the narrow component. The integrated fluxes in the broad and narrow components in Table 3 are derived in this manner. Lower panel: residuals to the fit. |
| In the text | |
 |
Fig. 4 Radial velocity maps. Left: map of the narrow component of the Hα line. This map is representative of all other narrow-line maps (e.g., narrow [O iii] λ5007, [O i] λ6300, [S ii] λ6717). Right: map of the He i λ7065 line. This map is representative of other broad-line maps (e.g., [O iii] λ4363, broad Hα). Contours are the monochromatic intensity of the corresponding emission-line from decreasing intensity intervals of 2 × 10-17 erg cm2 s-1 in peak intensity for Hα and 10-18 erg cm2 s-1 for He i. Only pixels above 3σ of the noise are shown for He i. In both panels, north is up and east is to the left. |
| In the text | |
 |
Fig. 5 Velocity dispersion maps. Left: map of the narrow component of the Hα line, representative of all other narrow-line maps (narrow [O iii] λ5007, [O i] λ6300, [S ii] λ6717). Right: map of the He i λ7065 line, representative of all other broad-line maps ([O iii] λ4363, broad Hα). The contours and orientation are the same as in Fig. 4. |
| In the text | |
 |
Fig. 6 The peculiar kinematics of the [O iii] λ4363 line (upper panels) and of [N ii]λ5755 (lower panels). Contours are the monochromatic intensity of the corresponding emission-line from decreasing intensity intervals of 10-18 erg cm2 s-1in peak intensity. Pixels within the contours are 3σ above noise. North is up and east is left. |
| In the text | |
 |
Fig. 7 Maps of low (left) and high (right) electron density emission. The orientation is the same as in Fig. 4. |
| In the text | |
 |
Fig. 8 Tomogram (left) and eingeinvector (E1) in red cube (5700–7200 Å). Bottom right: the spectrum from the original data cube; upper right: the extracted spectrum from the reconstructed data cube, using the PCA tomography results (eigenvector 1 and tomogram 1) (see Steiner et al. 2009b). |
| In the text | |
 |
Fig. 9 Tomogram (left) and eingeinvector (E2) in red cube 5700–7200 Å (right). The eigenvector shown in the lower-right panel is a zoom in a shorter wavelength range for a better visualization of the features of interest. |
| In the text | |
 |
Fig. 10 Tomogram (left) and eingeinvector (E3) in blue cube 4300–5100 Å (right). The eigenvector shown in the lower-right panel is a zoom in a shorter wavelength range for a better visualization of the features of interest. |
| In the text | |
 |
Fig. 11 Left: logarithmic extinction coefficient map derived from the Balmer decrement using integrated line profiles (broad + narrow components). Pixels with high noise at the border were masked out. Right: Hβ equivalent width map (per pixel in Å). The orientation is the same as in Fig. 4. |
| In the text | |
 |
Fig. 12 Map of the [S ii] λ6717/[S ii] λ6731 ratio. The orientation is the same as in Fig. 4. |
| In the text | |
 |
Fig. 13 Excitation maps: BPT diagram of narrow emission line ratios. Left: log ([O iii] λ5007/Hβ). Middle: log ([N ii] λ6584/Hα). Right: log ([S ii] λ6717,6731/Hα). The orientation is the same as in Fig. 4. |
| In the text | |
 |
Fig. 14 Maps of Wolf-Rayet spectral features. Left: blue bump (without the [Fe iii] emission). Right: red bump. The fluxes in the bumps are given in units of 10-16 erg s-1 cm-2. The orientation is the same as in Fig. 4. |
| In the text | |
 |
Fig. 15 Spatially narrow-line region spectrum (lower red spectrum) displayed with the integrated spectrum of the nuclear region (upper black spectrum). |
| In the text | |
 |
Fig. 16 Comparison of the measured line fluxes in the integrated spectrum of the outer region outside the nucleus (Table 5) with the fluxes measured in the narrow components of the integrated spectrum of the nucleus of Mrk 996 (Table 3). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


