| Issue |
A&A
Volume 560, December 2013
|
|
|---|---|---|
| Article Number | A29 | |
| Number of page(s) | 16 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201321986 | |
| Published online | 03 December 2013 | |
The VLT-FLAMES Tarantula Survey⋆,⋆⋆
XII. Rotational velocities of the single O-type stars
1 Astronomical Institute Anton Pannekoek, Amsterdam University, Science Park 904, 1098 XH Amsterdam, The Netherlands
e-mail: o.h.ramirezagudelo@uva.nl
2 Instituto de Astrofísica de Canarias, C/ vía Láctea s/n, 38200 La Laguna, Tenerife, Spain
3 Departamento de Astrofísica, Universidad de La Laguna, Avda. Astrofísico Francisco Sánchez s/n, 38071 La Laguna, Tenerife, Spain
4 Space Telescope Science Institute, 3700 San Martin Drive, Baltimore MD 21218, USA
5 Instituut voor Sterrenkunde, Universiteit Leuven, Celestijnenlaan 200 D, 3001 Leuven, Belgium
6 Observatories of the Carnegie Institution for Science, 813 Santa Barbara St, Pasadena CA 91101, USA
7 Cahill Center for Astrophysics, California Institute of Technology, Pasadena CA 91125, USA
8 Astrophysics Research Centre, School of Mathematics and Physics, Queen’s University of Belfast, Belfast BT7 1NN, UK
9 Armagh Observatory, College Hill, Armagh BT61 9DG, Northern Ireland, UK
10 UK Astronomy Technology Centre, Royal Observatory Edinburgh, Blackford Hill, Edinburgh EH9 3HJ, UK
11 Argelander-Institut für Astronomie, Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
12 European Space Astronomy Centre (ESAC), Camino bajo del Castillo s/n, Urbanizacion Villafranca del Castillo, Villanueva de la Cañada, E-28692 Madrid, Spain
13 Instituto de Astrofísica de Andalucía-CSIC, Glorieta de la Astronomía s/n, 18008 Granada, Spain
14 Institute of Astronomy with NAO, Bulgarian Academy of Science, PO Box 136, 4700 Smoljan, Bulgaria
15 Centro de Astrobiología (CSIC-INTA), Ctra. de Torrejón a Ajalvir km-4, 28850 Torrejón de Ardoz, Madrid, Spain
16 Universitäts-Sternwarte München, Scheinerstrasse 1, 81679 München, Germany
Received: 29 May 2013
Accepted: 10 September 2013
Context. The 30 Doradus (30 Dor) region of the Large Magellanic Cloud, also known as the Tarantula nebula, is the nearest starburst region. It contains the richest population of massive stars in the Local Group, and it is thus the best possible laboratory to investigate open questions on the formation and evolution of massive stars.
Aims. Using ground-based multi-object optical spectroscopy obtained in the framework of the VLT-FLAMES Tarantula Survey (VFTS), we aim to establish the (projected) rotational velocity distribution for a sample of 216 presumably single O-type stars in 30 Dor. The sample is large enough to obtain statistically significant information and to search for variations among subpopulations – in terms of spectral type, luminosity class, and spatial location – in the field of view.
Methods. We measured projected rotational velocities, νesini, by means of a Fourier transform method and a profile fitting method applied to a set of isolated spectral lines. We also used an iterative deconvolution procedure to infer the probability density, P(νe), of the equatorial rotational velocity, νe.
Results. The distribution of νesini shows a two-component structure: a peak around 80 kms-1 and a high-velocity tail extending up to ~600 kms-1. This structure is also present in the inferred distribution P(νe) with around 80% of the sample having 0 < νe ≤ 300 kms-1 and the other 20% distributed in the high-velocity region. The presence of the low-velocity peak is consistent with what has been found in other studies for late O- and early B-type stars.
Conclusions. Most of the stars in our sample rotate with a rate less than 20% of their break-up velocity. For the bulk of the sample, mass loss in a stellar wind and/or envelope expansion is not efficient enough to significantly spin down these stars within the first few Myr of evolution. If massive-star formation results in stars rotating at birth with a large portion of their break-up velocities, an alternative braking mechanism, possibly magnetic fields, is thus required to explain the present-day rotational properties of the O-type stars in 30 Dor. The presence of a sizeable population of fast rotators is compatible with recent population synthesis computations that investigate the influence of binary evolution on the rotation rate of massive stars. Even though we have excluded stars that show significant radial velocity variations, our sample may have remained contaminated by post-interaction binary products. That the high-velocity tail may be populated primarily (and perhaps exclusively) by post-binary interaction products has important implications for the evolutionary origin of systems that produce gamma-ray bursts.
Key words: stars: early-type / stars: rotation / line: profiles / Magellanic Clouds / galaxies: star clusters: individual: 30 Doradus
Full Tables 3 and 4 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/560/A29
© ESO, 2013
1. Introduction
The distribution of stellar rotation rates at birth is a “fingerprint” of the formation process of a population of stars. For massive stars the rotational distribution is especially interesting because so little is known about how these stars form (e.g., Zinnecker & Yorke 2007). Considerations of angular momentum conservation during the gravitational collapse of a molecular cloud suggest an “angular momentum problem”; i.e., it appears difficult for the forming stars – whether they be of low- or high-mass – not to rotate near critical velocities. However, very few massive O-type stars are known to be extreme rotators.
If massive stars form through disk accretion, in a similar way to low-mass stars, their initial spin rates are likely to be controlled by gravitational torques (Lin et al. 2011). Only massive stars that have low accretion rates, long disk lifetimes, weak magnetic coupling with the disk, and/or surface magnetic fields that are significantly stronger than what current observational estimates suggest, may have their initial spin regulated by magnetic torques (Rosen et al. 2012). Perhaps in these cases, intrinsic slow rotators can be formed.
The initial rotation rate is also one of the main properties affecting the evolution of a massive star. For instance, rotation induces internal mixing and prolongs the main-sequence life time (see Maeder & Meynet 2000; Brott et al. 2011a; Ekström et al. 2012). A very high initial rotation rate may cause rotational distortion and gravity darkening (Collins 1963; Collins & Harrington 1966) and may even lead to homogeneous evolution (Maeder 1980; Brott et al. 2011a,b). In low-metallicity environments it has been suggested that this type of evolution leads to gamma-ray bursts (Yoon & Langer 2005; Woosley & Heger 2006).
With the above science topics in mind, considerable effort has been invested in establishing the full distribution of equatorial rotational velocities (νe) of massive stars. Spectroscopic studies provide projected rotational velocities (νesini, where i is the inclination angle of the stellar rotation axis with respect to the line-of-sight). Large populations are thus preferred in order to confidently deconvolve the observed distribution and obtain a true νe distribution (Penny 1996; Huang & Gies 2006; Hunter et al. 2008; Penny & Gies 2009; Huang et al. 2010; Dufton et al. 2013). Obviously, the current values of spin rates do not necessarily reflect initial values. Stellar expansion and/or angular momentum loss via stellar winds are proposed as mechanisms that spin down stars as time passes. Both these mechanisms, however, seem rather ineffective for the bulk of the massive stars. Internal redistribution of angular momentum effectively prevents the spin down of the surface layers as the star evolves to larger main-sequence radii and mass loss only seems effective for stars more massive than 40 M⊙ at birth (Brott et al. 2011a,b; Vink et al. 2010, 2011).
Since the intrinsic multiplicity fraction of massive stars at birth seems very high (Sana et al. 2012), it is also important to consider the effects of binary evolution on the rotational properties. Interestingly enough, binary interaction quite often occurs early on in the evolution of these systems, with up to 40% of all stars born as O-type stars experiencing mass transfer before leaving the main sequence (Sana et al. 2012). Using the intrinsic binary properties of Galactic O-type stars (Sana et al. 2012), de Mink et al. (2013) show that binary interaction strongly affects spin rates, producing a ‘high-velocity tail’ in the νesini distribution through angular momentum transfer processes. Though studies of O-type star populations often try to select samples from which the known binaries have been removed, de Mink et al. (in prep.) show that such samples likely remain strongly contaminated by (unidentified) binary interaction products. Whether the results of de Mink et al. are consistent with all rapidly (νe > 200 − 300 kms-1) spinning O-type stars being spun-up binary products is an intriguing question. A positive answer may imply that the proposed homogeneous single-star channel to gamma-ray-bursts mentioned above does not occur in nature.
The VLT-FLAMES Tarantula Survey (VFTS) is a multi-epoch spectroscopic campaign targeting over 800 massive O and early-B stars across the 30 Doradus (30 Dor) region in the Large Magellanic Cloud (LMC), including targets in the OB clusters NGC 2070 and NGC 2060. The distance to 30 Dor is well constrained (Gibson 2000), and its foreground extinction is relatively low (see Evans et al. 2011, hereafter Paper I). The large massive-star population is ideal for studying the rotational velocity distribution. The low metal content of the LMC is in this sense even beneficial, because for such an environment the tail of the νesini distribution produced by binary effects is expected to be more extended and pronounced (de Mink et al. 2013).
The dense core cluster of the Tarantula nebula, Radcliffe 136 (R136), has a likely age of 1–2 Myr (de Koter et al. 1998; Massey & Hunter 1998), but may actually be a composite of two sub-clusters (Sabbi et al. 2012), with a third population that is a few million years older nearby (Selman et al. 1999). The very central regions were excluded from the VFTS because of crowding issues. A series of distinct populations, with varying ages reaching up to ~25 Myr can be distinguished in the Tarantula field (Walborn & Blades 1997), suggesting that 30 Dor has been continuously forming massive stars over the past 25 Myr, although probably with a variable formation rate.
The key questions we want to address in this study are: How are the rotational velocities of O-type stars in 30 Dor distributed? Which fraction of the stars are slow rotators? Does the distribution have a high-velocity tail? If present, is the distribution of rapid rotators suggestive of a contribution of unidentified binaries? The layout of the paper is as follows. Section 2 describes the selection of our sample. The methodology and the results from different diagnostic lines are described in Sect. 3. Section 4 presents the νesini and νe distributions. The results are discussed in Sect. 5 and our conclusions are summarized (Sect. 6).
2. Sample
The VFTS project and the data have been described in Paper I. Here, we focus on the presumably single O-type stars that have been observed using the Medusa fibers. The total Medusa sample contains 332 O-type objects. Sana et al. (2013, hereafter Paper VIII have identified spectroscopic binaries from multi-epoch radial velocity (RV) measurements: 172 O-type stars show no significant RV variations and are presumably single; 116 objects show significant RV variations with a peak-to-peak amplitude (ΔRV) higher than 20 kms-1 and are considered binaries. The remaining 44 objects show low-amplitude significant RV variations (ΔRV ≤ 20 kms-1 ). The latter variations may be the result of photospheric activity (pulsations and wind variability) or indicate a spectroscopic binary system. In Paper VIII, we estimated that photospheric variations and genuine binaries contribute to the low-amplitude RV variation sample in roughly equal portions. To avoid biasing our analysis against supergiants, which are expected to show spectroscopic variability (see e.g., Simón-Díaz et al. 2010), we include these 44 low-amplitude RV variable objects in our sample, reaching thus a total sample size of 216 O-type stars.
Because of the limited number of observing epochs, a subset of stars in our RV-constant sample are expected to be undetected binaries. Given the VFTS binary detection probability among O-type stars (of ≈0.7, Paper VIII), one estimates that this may be the case for up to about 25% of our single-star sample. Undetected binaries are primarily wide and/or low-mass companions (see Sect. 3 in Paper VIII). Tidal interactions are thus expected to be negligible for these systems so that the measurement of the rotational velocity of the main component should be mostly unaffected by the binary status.
 |
Fig. 1 Spectral type (SpT) distribution of the O-type stars in our sample, binned per spectral subtype. Different colors indicate different luminosity classes (LC), see legend. |
The spectral classifications of the O-type stars in the VFTS will be presented in Walborn et al. (in prep.). Figure 1 shows the spectral type (SpT) and luminosity-class (LC) distribution for our sample, which is dominated by O9-O9.7 stars (52% of the sample size) and by dwarfs and subgiants (LC V-IV). As indicated in Fig. 1, a luminosity classification is missing for 22 stars, i.e. about 10% of our sample. For seven stars the precise spectral type has not been established either due to the poor signal-to-noise ratio (S/N) or heavy nebular contamination. These seven stars have been excluded from Fig. 1 but are still incorporated in our analysis.
The spatial distribution of our sample is shown in Fig. 2. The field of view is dominated by the central cluster NGC 2070. A circle of radius 2.4′ (or 37 pc) around the cluster center contains 105 stars from our sample: 62 are of LC V-IV, 15 are LC III and 28 are LC II-I. A second concentration of 45 O-type stars is found in a similar sized region around the NGC 2060 cluster, located about 6′ to the southwest of NGC 2070. NGC 2060 is somewhat older than NGC 2070 (Walborn & Blades 1997). Accordingly, it contains a larger fraction of LC II-I stars (23%) than NGC 2070 (9%). The remaining stars, throughout the paper referred to as the stars outside clusters, are spread throughout the field of view. These may originate in either NGC 2070 or 2060, but may also have formed in other star-forming events in the 30 Dor region at large.
 |
Fig. 2 Spatial distribution of the presumably single O-type stars as a function of the LC. The circles define regions within 2.4’ of NGC 2070 (central circle) and NGC 2060 (SW circle). Colors have the same meaning as in Fig. 1 (only available in the online version). |
3. Measuring the projected rotational velocity
3.1. Methodology
The projected rotational velocity (νesini) of stars can be measured directly from the broadening of their spectral lines (Carroll 1933; Gray 1976). Commonly used methods for OB-type stars include direct measurement of the full width at half maximum (FWHM; e.g., Slettebak et al. 1975; Herrero et al. 1992; Abt et al. 2002), cross-correlation of the observed spectrum against a template spectrum (e.g., Penny 1996; Howarth et al. 1997), and comparison with synthetic lines calculated from model atmospheres (e.g. Mokiem et al. 2006). In this study we use a Fourier transform (FT) method and a line profile fitting method which we refer to as the goodness of fit (GOF) method. Both methods are applied to a set of suitable spectral lines present in the VFTS Medusa LR02 and LR03 spectra (see Sect. 3.2). A comparison of the measurements obtained from both methods allows us to verify the internal consistency of the derived values.
The FT method is explained in Gray (1976). It has been systematically applied to OB-type stars by Ebbets (1979) and Simón-Díaz & Herrero (2007). In summary, the first minimum of the Fourier spectrum uniquely identifies the value of νesini. One advantage of the FT method is that the derived νesini value is in principle not strongly affected by the presence of photospheric velocity fields, such as macro-turbulent motions1. However, the method encounters difficulties in case of strong nebular contamination, poor S/N, weak lines, or when the rotational broadening contribution is close to the intrinsic broadening of the line.
Overview of the diagnostic lines used to derive the projected rotational velocity.
The GOF method (e.g., Ryans et al. 2002; Simón-Díaz et al. 2010) adjusts a synthetic line profile to the observed profile using a least-square fit, taking the intrinsic, instrumental, rotational, and macro-turbulent broadening contributions into account through successive convolutions. In this study we neglect the intrinsic width of the spectral lines, effectively adopting a delta function for the intrinsic profile. The latter is then convolved with an instrumental (Gaussian) function that preserves the equivalent width (EW). For the rotational and macro-turbulent profiles, we follow the description given by Gray (1976). The rotational profile assumes a linear limb darkening law. We finally use a radial-tangential (RT) model parametrized with the quantity ΘRT as an appropriate representation of the macro-turbulent profile.
3.2. Diagnostic lines
In general, different diagnostic lines do not provide the same accuracy in the νesini measurements. Metallic lines do not suffer from strong Stark broadening nor from nebular contamination and hence are best for obtaining νesini estimates. Si iiiλ4552 is the only suitable metal line in our data set for these purposes. Unfortunately, it is only present in 6% of the sample and restricted to late spectral subtypes. Next in line in terms of reliability are nebular free or weakly contaminated He i lines, notably He iλ4713, 4922, 4387, and 4471. By using the neutral helium lines we can study an additional 54% of the sample (see Table 1).
The remaining sample of stars (31%) suffers from strong nebular contamination, features only weak He i lines or – for the earliest spectral subtypes – does not show these lines at all. In those cases, amounting to 26% of our sample, we relied on He iiλ4541. Finally, 14 stars2 present strong nebular contamination in He i, weak He ii lines and no Si iii line. We have estimated νesini for these sources by comparing rotationally broadened synthetic line profiles calculated using FASTWIND (Puls et al. 2005) to the wings of He i and He ii lines. Though FASTWIND does not take macro-turbulent broadening into account, it does, at least, allow us to derive upper limits on νesini for this small subset of stars.
The assumption of a delta function for the intrinsic profile ignores a possible contribution from Stark broadening (more relevant for He i and He ii lines). Aware of that, we scrutinized the reliability of these lines for νesini determinations in Sect. 3.4. For practical purposes we refer to the group of stars for which the Si iiiλ4552 and/or nebular free He i lines can be used as Group A and the remaining sample as Group B. Group A thus identifies the stars for which the highest quality diagnostic lines are available, while Group B has diagnostics of a lower quality.
 |
Fig. 3 Spatial distribution of our sample in the 30 Dor field of view. Different colors identify the different groups listed in Table 1 and are identified in the legend. |
 |
Fig. 4 Diagnostic lines used as a function of the SpT of the stars in our sample. |
 |
Fig. 5 Example of the GOF and FT measurement methods applied to the He iλ4713 line of VFTS 280 (top row, high S/N) and VFTS 163 (bottom row, poor S/N), to illustrate two different data qualities. Left-hand column: line profile (black) and its GOF solution (red). Right-hand column: Fourier transform of the observed spectrum (black) and of the best fit GOF profile (red). The dashed lines indicate the position of the FT first minimum. |
The resolving power of the VFTS Medusa LR02 and LR03 is ~0.6 Å (Paper I), corresponding to 40 kms-1. We have adopted this value as our resolution limit, so that when a νesini measurement is below 40 kms-1, the corresponding star is systematically assigned to the 0–40 kms-1 bin (see Sect. 4) without any further indication of the specific νesini value.
Figure 3 shows the spatial distribution of stars below the resolution limit and of stars in Groups A and B. Group A stars are spread out within the two clusters and show a lower fraction in the field of view. Group B stars are mainly concentrated in NGC 2070. There are two reasons that can explain this difference. First, part of the NGC 2070 cluster lies behind a filament of nebular gas, therefore contamination is stronger. Second, NGC 2070 is younger and, pro rata, contains more hot early O-type stars that show neither Si iii nor He i lines in their spectra.
Figure 4 shows the spectral lines used for νesini measurements as a function of SpT. For late SpT, measurements are mostly obtained from He i, while He iiλ4541 is increasingly used for earlier SpT. Stars with νesini below the resolution limit and stars featuring the Si iiiλ4552 line are almost exclusively late O-type stars. All stars showing Si iii also display at least one suitable He i line. The accuracy of, and the systematics between, νesini measurements obtained from both methods and for the different lines are discussed in the next sections.
3.3. Comparison of results from FT and GOF methods
An example of FT and GOF νesini measurements for the He iλ4713 line is presented in Fig. 5 for two different data qualities. In the upper panel the derived νesini from the FT and the GOF methods are in agreement. In the lower panel, the noise affects the FT, resulting in an erroneous νesini value, while the correct νesini value is associated with the shallow FT minimum at ~200 kms-1. The combined investigation of results from FT and GOF methods thus helps identify the more ambiguous cases that must be explored in more detail.
The upper panel in Fig. 6 compares νesini values obtained from applying the FT and GOF methods to the He iλ4713 line. This plot includes all stars in our sample in which the He iλ4713 line is detected and the νesini (FT) measurements are above the resolution limit (116 stars). In addition to the full set of good quality measurements, different symbols are used to highlight various cases: (i) strong nebular contamination; (ii) low S/N (<60) and/or a comparatively weak diagnostic line (EW ≤ 50 mÅ); (iii) ambiguous first minimum in Fourier space (this is, for example, the case for VFTS163 in Fig. 5); and (iv) a central depth of the absorption-line profile that is smaller than three times the noise level. These explain all but 14 deviating points, which correspond to cases in which νesini (GOF) is below the resolution limit and νesini (FT) > νesini (GOF). This behavior is expected when the rotational broadening contribution to the line profile is similar to the intrinsic broadening and the S/N is not sufficiently high. In this situation the FT of the line may result in a spurious first zero, which is moved to higher values of νesini compared to the FT’s true first zero (see, e.g., Simón-Díaz & Herrero 2007). In these specific cases νesini (FT) measurements must be considered as upper limits for the actual projected rotational velocity. Save for one instance, these cases occur when νesini ≤ 80 kms-1.
 |
Fig. 6 Comparison of νesini values obtained from the FT and GOF methods for He iλ4713. Upper panel: different symbols indicate different data qualities, identified in the legend. Lower panel: same as above after discarding the lower quality data. Information on the LC and SpT of the targets is provided by the symbol shapes and colors (see legend). In both panels, the dotted lines indicates the 1:1 relation. The dashed lines show the ± 20 kms-1 or ± 20%, whichever is the largest, around the 1:1 relation. |
Once the poorer quality measurements resulting from cases (i) to (iv) are left aside, the νesini measurements for the 76 stars left in our comparison show strong agreement between FT and GOF estimates over the full range of velocities, save for νesini measurements close to the spectral resolution limit (Fig. 6, bottom panel). Similar conclusions about the high degree of agreement between FT and GOF estimates can be drawn for the other He i lines and from Si iiiλ4552. From now on the analysis is presented but excluding poor-quality measurements.
The situation is, however, less clear for measurements based on He iiλ4541 (Fig. 7, 101 stars). Above 150 kms-1, the FT and GOF measurements agree to within 20%. A significant dispersion is, however, observed at lower velocities, with FT resulting in systematically higher νesini values than GOF. The origin of the observed systematics is discussed further in Sect. 3.4.2.
 |
Fig. 7 Comparison of the νesini measurements from the FT and GOF methods for He iiλ4541. Information on the LC and SpT of the targets is provided by the symbol shapes and colors. Lines have the same meaning as in Fig. 6. |
3.4. Comparison of results from the different diagnostic lines
In this section we compare the νesini measurements obtained from different diagnostic lines (Table 3). Figures 8 to 10 show different cases of these comparisons, and Table 2 summarizes the degree of agreement between the lines that have been investigated. Only νesini measurements that fulfill the quality criteria outlined in Sect. 3.3 are considered.
3.4.1. Si III λ4552 and He I lines
Figure 8 compares the νesini values obtained from Si iiiλ4552 and He iλ4713 for 12 stars. Measurements from both lines agree within ±20% or ±20 kms-1, whichever is the largest, in over 90% of the cases. A similar degree of agreement is observed between FT measurements of He iλ4713 and He iλ4922 (Fig. 9): 53 of the 58 stars displaying both lines again agree within ±20% or ±20 kms-1, hence about 91% of the sample. We conclude that the comparison between νesini measurements obtained from Si iii and from different He i lines (Figs. 8, 9 and Table 2) reveals no systematic differences. This justifies the grouping of all the measurements from stars in Group A, irrespective of the diagnostic line from which they have been obtained.
 |
Fig. 8 Comparison of νesini values from the FT method for He iλ4713 and Si iiiλ4552. Information on the LC and SpT of the targets is provided by the symbol shapes and colors. Lines have the same meaning as in Fig. 6. |
 |
Fig. 9 Comparison of νesini obtained from the FT method for He iλ4922 and He iλ4713. Information on the LC and SpT of the targets is provided by the symbol shapes and colors. Lines have the same meaning as in Fig. 6. |
Comparison between different diagnostic lines.
Measured values of νesini (in kms-1) for every star and diagnostic line.
3.4.2. He II λ4541
As discussed in Sect. 3.3, the FT and GOF measurements obtained from the He iiλ4541 line show general agreement well within the 20% for νesini ≥ 150 kms-1 (Fig. 7). However, the larger dispersion and systematics observed below 150 kms-1 cast some doubts on the reliability of the He iiλ4541 measurements for slow rotators. In this section we explore this issue further by comparing the He iiλ4541 rotational velocities with those obtained from He i lines for those stars in Group A that display both He i and He ii lines. This comparison will allow us to decide which of our two methodologies provides the more reliable νesini information for Group B stars.
 |
Fig. 10 Comparison of νesini measurements from He iλ4713 and He iiλ4541. Upper panel: both diagnostic lines analyzed using the FT method. Lower panel: He iiλ4541 analyzed using the GOF and He iλ4713 using the FT. Information on the LC and SpT of the targets is provided by the symbol shapes and colors. Lines have the same meaning as in Fig. 6. |
Figure 10 (upper panel) compares νesini measured from He iiλ4541 and from He iλ4713 using the FT method. In the low-velocity domain (νesini < 150 kms-1), FT values from He iiλ4541 are systematically larger by about 30 kms-1, on average, with a dispersion of about 23 kms-1 compared to He i FT measurements. In this domain, the contribution of Stark broadening to the He iiλ4541 line causes the power of the first lobe of the FT to diminish. As a consequence, the first zero is easily hidden within the white noise if the S/N is not high enough. The method then returns νesini values corresponding to the first FT zero that peaks out of the noise. This artificially moves the measurement to higher νesini values.
As illustrated in the lower panel of Fig. 10, the impact of the Stark broadening on our νesini measurements is partially mitigated by using the GOF rather than the FT method for He iiλ4541. Although large deviations still occur in some cases, the average systematic difference in the measurements between He i and He ii drops off to 3 kms-1, which is negligible in comparison with our expected accuracy. Using the GOF instead of the FT for He ii measurements thus allows to avoid a systematic bias in the measurements, leaving the derived νesini values only affected by random, though relatively large, uncertainties.
In the high-velocity domain (νesini > 250 kms-1), a systematically lower νesini is obtained from He iiλ4541 than from He iλ4713. The good agreement found between FT and GOF estimates for He iiλ4541 in this νesini domain suggests that the difference is real and not related to a methodological bias. Fast rotation produces equatorial stretching of stars, which in turn induces a nonuniform surface gravity and temperature distribution (von Zeipel 1924). In the particular case of fast-rotating O-type stars, this means that the poles are hotter than the equator. As a consequence, photospheric regions closer to the pole (resp. equator) will contribute more to the formation of He ii (resp. He i) lines. Projected rotational velocities derived from He ii lines are thus expected to be lower than those from HeI lines, as observed in Fig. 10.
3.5. Measurement uncertainties
The methods that we have adopted to estimate νesini do unfortunately not provide measurement errors. We have estimated the typical accuracy of our measurements by examining the dispersions observed between measurements based on independent lines. We outline here the main conclusions. At low rotational velocities, absolute uncertainties provide a more sensible estimate of the true measurement error. At high rotational velocity, however, uncertainties are better expressed in relative terms.
For Group A stars, the root mean square (rms) dispersion between measurements from the different He i and Si iii lines amounts to about 10 kms-1 for projected rotational velocities below 100 kms-1 (see Figs. 8, 9 and Table 2). It is of the order of 10% or better above 100 kms-1. For Group B stars, the rms dispersion in the lower panel of the same figure indicates uncertainties not exceeding 30 kms-1 below νesini = 200 kms-1, and not exceeding 10% above 200 kms-1 (see lower panel Fig. 10).
As pointed out in the previous section, our He ii measurements may underestimate the true rotational velocity of the stars for νesini ≥ 250 kms-1. The five stars in Fig. 10 for which this is relevant indicate that the effect is probably in the range of 15% to 20%. Similarly, gravity darkening may cause our measurements to underestimate the true νesini at high rotational velocity (see also the discussion in Dufton et al. 2013, hereafter Paper X). Though both effects are not negligible, it will not affect our conclusion on the presence of a well-populated high-velocity tail in the rotational velocity distribution. Correcting these values would even strengthen that outcome.
As a last point, we note that most of the comparisons performed in this section concern mid- and late-O stars. The He i lines in early-O stars (O2-O5) are too weak to provide reliable νesini measurements, depriving us of an anchor point to test the quality of He ii-based νesini measurements. In Appendix A we compare νesini measurements obtained from He iiλ4541 with those obtained from N vλ4604 for a small set of stars. We find that above 80 kms-1, He ii and N v agree to within 10%. This adds confidence in the quality of νesini measurements for early-type Group B stars in that regime. The quality of the He ii-based νesini of early-O stars with νesini~ < 80 kms-1 cannot be investigated further with the current data set, and we adopt a formal uncertainty of 30 kms-1 for these 15 stars.
3.6. Strategy for obtaining νe sin i estimates
Based on the analysis presented in Sects. 3.3 and 3.4, we have adopted the following strategy to obtain the final νesini measurements (see Table 4) for the full sample of 216 O-type stars:
-
For those stars in Group A with FT measurementsbelow 40 kms-1, we adopt an upperlimit of 40 kms-1, and include them in the 0–40 bin ofthe νesini histograms (see Sect. 4).
-
For those stars in Group A with FT measurements above 40 kms-1, we compute an unweighted average of the individual values obtained from the available He i and Si iii lines (see Table 3).
-
For all stars in Group B where the He iiλ4541 diagnostic line is available, we adopt the GOF measurement obtained from that line. If the obtained value is below 40 kms-1, we consider the object below our resolution limit and assign it to the lowest velocity bin in our histograms.
-
For the remaining 14 stars for which the above diagnostics cannot be applied, we use the wings of the lines and compare them to synthetic spectra as described in Sect. 3.2.
While the GOF measurements of νesini based on He ii lines are good enough for the purposes of this study, individual values must be handled with care because the measurements have a large dispersion. In particular, some of the Group B stars included in the first three bins of the νesini distributions presented in the next sections may move between adjacent bins due to sizeable uncertainties. Because we verified earlier that there are no systematic effects, the larger uncertainties for some stars in Group B do not affect the overall distributions presented in this paper.
Averaged νesini measurements and adopted uncertainties.
4. The νe sin i distribution
In this section, we construct and investigate the νesini distributions of the overall O-type star population within 30 Dor, as well as within subpopulations of stars in our sample. We approximate the probability density function (pdf) using histograms with a bin size of 40 kms-1. Such a bin size is consistent with our resolution limit (see Sect. 2) and is large enough to mitigate the effect of measurement uncertainties on the appearence of the histograms. Figure 11 shows the overall νesini distribution. It is dominated by a clear peak at fairly low νesini and a well-populated high-velocity tail that extends continuously to 500 kms-1. With a measured νesini of 609 and 610 kms-1, VFTS 285 (Walborn et al. 2012) and VFTS 102 (Dufton et al. 2011) complete the projected rotational distributions at extreme rotation rates.
In the following sections, we analyze the νesini distribution as a function of spatial location, LC and SpT. We use Kuiper tests (KP, Kuiper 1960) to search for significant differences between the considered subpopulations. Results are reported in Table 5. Specifically, KP tests allow us to test the null hypothesis that two observed distributions are randomly drawn from the same parent population. Compared to the more widely used Kolmogorov-Smirnov test (KS, Kolmogorov 1933), the KP test has the advantage of being similarly sensitive to differences in the tails and around the median of the distributions, while the KS test is known to be less sensitive if differences are located in the tails of the distribution. To support our discussion of the outcomes of the KP tests, we also show the cumulative distribution functions (cdf) because they provide a more direct view of the location of the differences between the distributions.
 |
Fig. 11 Histogram of the projected rotational velocities of our sample of 216 O-type stars in 30 Dor. |
Kuiper test (KP) statistics for different sets of the O-type stars (Cols. 1 and 2).
4.1. Spatial variations
Figure 12 shows the νesini distributions for stars in the NGC 2070 and NGC 2060 clusters and for stars outside these two clusters. Qualitatively, all three distributions are similar with a peak in the low-velocity region and a high-velocity tail. The distributions for stars in the two clusters are statistically compatible. A KP test, however, indicates that the νesini distribution of stars outside the clusters shows differences with the NGC 2070 and NGC 2060 distributions, at the 9% and 3% significance levels, respectively. For NGC 2070 the difference manifests itself in the high-velocity regime, the fraction of rapid rotators being larger outside of the clusters. For NGC 2060 both the low- and high-velocity region contribute to the significance of the differences detected by the KP test.
The difference in age between the two clusters, hence in the evolutionary stage of their O-type star population, does not seem to have strongly affected the νesini distribution of NGC 2060 compared to the younger NGC 2070. This suggests that standard evolutionary effects, such as spin down through wind mass loss and/or envelope expansion are modest. The presence of a larger fraction of fast rotators outside clusters may, however, be linked to binary evolution if the field is relatively overpopulated with post-interaction objects. Binary interaction is indeed expected to produce rapidly rotating stars either through mass and angular momentum transfer to the secondary star during Roche lobe overflow or through the merging of the two components (de Mink et al. 2013). A relative overpopulation of the field can be obtained in two ways. Some of these binary products may have outlived their coeval single star counterparts thanks to the rejuvenation effects resulting from the interaction process. Alternatively, post-interaction systems may have been ejected from their natal cluster when the primary experienced its supernova explosion. The correlation between rapid spin and high radial velocity of the field stars identified in the VFTS O-type star sample (Sana et al., in prep.) is an argument in favor of the latter scenario. This will be the topic of a separate investigation within the VFTS series of papers.
Qualitatively, the origin of the lower number of slow rotators within NGC 2060 remains unclear. It may be related to the specific evolutionary stage of most of the stars in the clusters or reveal differences in the initial νesini distribution. That dwarfs and subgiants (LC V-IV) and bright giants and supergiants (LC II-I) have very similar distributions at low velocities (Fig. 13) tends to rule out differences in the evolutionary stage of the two clusters as a straightforward explanation.
 |
Fig. 12 Cumulative (upper panel) and frequency (lower panel, with Poisson error bars) distributions of the projected rotational velocities of the O-type stars for three spatially selected groups. |
 |
Fig. 13 Cumulative (upper panel) and frequency (lower panel, with Poisson error bars) distributions of the projected rotational velocities of the O-type stars for three different LC categories. |
 |
Fig. 14 Cumulative (upper panel) and frequency (lower panel, with Poisson error bars) distributions of the projected rotational velocities of the O-type stars for three different spectral type categories. |
4.2. Luminosity class
Figure 13 shows the νesini distributions for three luminosity groups: V-IV (119 stars), III (38 stars), and II-I (33 stars). There are 26 stars in our sample with no LC classification available, so we only used 190 stars. KP tests do not reveal statistically significant differences between the distributions of giants (LC III) and bright giants and supergiants (LC II-I). Both distributions are, however, statistically different from those of the dwarfs and subgiants (LC V-IV), this latter group dominating the extreme of the high-velocity tail (νesini ≥ 450 kms-1).
The difference in the high-velocity regime between the V-IV class and the other classes can be explained from evolutionary considerations. Following Weidner & Vink (2010), some 18% of our total sample presents masses above 40 M⊙ (see Sect. 5.2). The bulk of our O-type star sample consists thus of main sequence stars initially less massive than about 40 M⊙. For such stars the loss of angular momentum as a result of mass loss in a stellar wind is quite limited, therefore this is not expected to be an efficient mechanism for spin down (see Vink et al. 2010; Brott et al. 2011a). As the O-type stars evolve away from the zero-age main sequence their radii expand and one may naively expect to observe a spin down of the surface layers for more evolved stars. The spin down with increasing radius is, however, prevented by a simultaneous contraction of the stellar core and the efficient transport of angular momentum from the core to the envelope (Ekström et al. 2008; Brott et al. 2011a).
The critical rotation rate of a star, which is the maximum surface velocity above which the centrifugal force exceeds gravity, is, however, mostly defined by its size. Dwarfs are more compact than supergiants by about a factor two to three (Martins et al. 2005), which corresponds to break-up velocities a factor up to  higher. Break-up velocities for dwarfs and supergiants typical of our sample are around 700 and 400 kms-1, respectively (de Mink et al. 2013). These estimates match the maximum rotational velocities observed in Fig. 13 well. It also explains the absence of very rapid rotators among supergiants: such stars simply cannot rotate faster than about 400 kms-1.
higher. Break-up velocities for dwarfs and supergiants typical of our sample are around 700 and 400 kms-1, respectively (de Mink et al. 2013). These estimates match the maximum rotational velocities observed in Fig. 13 well. It also explains the absence of very rapid rotators among supergiants: such stars simply cannot rotate faster than about 400 kms-1.
The low-velocity region shows a lower frequency of giants compared to the other LCs. Although the cause of this is unclear, possible explanations include different parent populations, different effects of the macroturbulent velocity field, and/or low number statistics. Further investigations with higher resolution data are needed to search for the origin of the observed paucity of giants with νesini< 120 kms-1.
4.3. Spectral type
Figure 14 shows the νesini distributions for the different spectral type categories. There are seven stars with no SpT available, so we only consider 209 stars here. Though once again the overall appearance of the distributions seems similar, the early-type group (O2-5) does not contain stars that rotate faster than 300 kms-1, while the later SpT groups show a more extended high-velocity tail. Indeed a KP test indicates that the O2-5 rotation rates are statistically different from the νesini distribution of the later types. The true maximum rotation rate of O2-5 stars could be slightly higher than the observed 300 kms-1, since He iiλ4541 is the only rotational velocity diagnostic for the early-O stars and systematically underestimates νesini by 15% to 20% compared to measurements based on HeI lines (see Sect. 3.4.2). Even taking this into consideration does not make the early-O stars spin as fast as the later-type stars.
The peak of the velocity distribution is also at somewhat higher νesini for the earlier type stars compared to the later types. The fraction of earlier type stars in the first bin (below our resolution limit) increases when progressing to later groups of spectral subtypes. This trend continues in the B-star domain as shown in Paper X. Because of the limitation of the current data set, it is difficult to decide whether this trend traces a real effect or results from a measurement artifact. We discuss both options below.
In Sect. 3.4.2 we showed that there is a significant dispersion for νesini (He ii) with respect to νesini (He i) measurements for νesini< 150 kms-1. This comparison is only done for mid-O stars, since a similar comparison cannot be performed for stars earlier than O6. If broadening due to the linear Stark effect and as a result of macroturbulent velocity fields is stronger among early-O-type stars (see, e.g., Fig. 1 in Simón-Díaz et al. 2013, for the case of Galactic O-type stars) and if our method cannot distinguish between rotation and extra broadening for early-O stars, as well as for mid- and late-O stars, the rotation rates of the earliest types may be somewhat overestimated. It is, however, unclear why the trend should continue for late O- and early B-type stars.
If the signal is real, it suggests either that more massive stars cannot be spun down as efficiently as lower mass stars or that an additional line broadening mechanism exists whose strength correlates with spectral type. Such a mechanism remains to be identified. A similar conclusion is reached by Markova et al. (in prep.) and Simón-Díaz et al. (in prep.) using high-resolution data of Galactic samples of O-type stars.
The absence of a high-velocity tail among early O-type stars may also be related to binary evolution effects (see Sect. 5.3). During a mass-transfer event, the secondary less massive star accretes mass and angular momentum from the primary star. As a result secondaries are efficiently spun up to break-up velocities. Because the masses of primary stars are higher than those of secondaries, and the distribution of the mass ratio (q = M2/M1) favors relatively lower mass companions (fq ∝ q-1 in the VFTS field; Paper VIII), the secondaries in the O+O binaries in 30 Dor will be mid- and late-O stars much more frequently than early-O stars. A population of unidentified post-interacting binary products in our sample could explain the strong preference for mid- or late-type stars in the high-velocity tail of Fig. 14. Alternatively, because they have the strongest winds, the earliest O-type stars may already have experienced a larger spin down due to mass loss compared to later spectral sub-type stars. However, current evolutionary models do not predict this effect to be sufficient, unless of course the adopted mass-loss recipes have underestimated the true mass-loss rates of these more extreme objects.
4.4. Comparison with earlier studies
Penny & Gies (2009) used FUSE UV observations with a spectral resolving power of about 20 000 and a cross-correlation method to measure νesini in a sample of 258 stars in the Galaxy (97 stars in total), LMC (106), and SMC (55). The cross-correlation method measures the overall broadening of the line and does not allow distinguishing between rotation and macro-turbulence. The method is, however, versatile in that it allows double-lined spectroscopic binaries to be identified3. For all three metallicity environments, the authors report a lack of very slowly rotating stars (i.e., νesini ≤ 50 kms-1), which they interpret as the signature of additional-broadening due to macro-turbulent motions.
Penny & Gies (2009) also divided their total sample into relatively unevolved (V-IV) and evolved (II-I) stars, omitting LC III stars. For their Galactic sample, the unevolved and evolved samples were statistically different for νesini < 200 kms-1. The authors interpret this as the result of a stronger photospheric macro-turbulence of the evolved stars. For the LMC and SMC stars, such behavior was not observed, suggesting that macro-turbulence depends on metallicity . Similar comparisons at high projected rotational velocities (i.e. >200 kms-1) revealed no significant statistical difference between the unevolved and evolved objects.
The slowly rotating dwarfs in the three metallicity environments showed statistical differences, but no clear trend could be identified, while the more rapidly rotating dwarfs (>200 kms-1) showed compatible distributions. For the evolved low νesini stars, a trend could be identified: the higher the metallicity the smaller the fraction of slow rotators. This too is consistent with a metallicity dependence of macro-turbulent effects, in that such effects seem more prominent for higher metal content. The rapidly spinning evolved objects did not show a clear trend, though the SMC environment appears to be somewhat richer in these objects.
Huang & Gies (2006) used moderate resolution spectra to study projected rotational velocities of 496 presumably single OB stars ( ΔRV ≤ 30 kms-1). Their sample stars belong to 19 different open clusters in the Galaxy and span an age of 7–73 Myr. By using different diagnostic lines, such as He iλ4026, 4387, 4471, and Mg iiλ4481, they fit νesini using TLUSTY-SYNSPEC stellar atmospheres (Hubeny & Lanz 1995). They find that the νesini distribution of B-type field stars contains a larger fraction of slow rotators than the B-type stars in clusters. Their high-velocity tail extends up to 350 kms-1 and 400 kms-1, respectively. They finally suggests that some of these rapid rotators may have been spun up through mass transfer in close binary systems.
As a part of the VFTS project, Paper X studied a sample of around 300 stars spanning SpT from O9.5 to B3, excluding supergiants. In addition to the set of diagnostic lines used here, Paper X also made use of He iλ4026, Mg iiλ4481, C iiλ4267, and O iiλ4661. As in the present work, the FT method was used to estimate the νesini for stars that do not show significant radial velocity variations. Because of uncertainties in the initial crude VFTS classification, 47 stars, predominantly O9.5 and O9.7 stars, were analyzed both in Paper X and in the present paper. The agreement in νesini in the overlapping set of stars between our and their analysis is excellent (see Appendix B). The νesini distribution and the deconvolved νe distribution of the B-type stars in VFTS show a distinct bimodal structure with 25% of the sample having νe < 100 kms-1 (see Paper X). The components of the bimodal structure do not correlate with different episodes of star formation nor with different locations in the field of view.
 |
Fig. 15 Comparison of the cumulative distributions of projected rotational velocities of our work (VFTS-O sample – purple), Penny & Gies (blue), Huang & Gies (green), and the VFTS-B sample of Dufton et al. (2013) (red). |
Figure 15 compares our νesini cumulative distribution of the O-type stars in 30 Dor with those from the studies summarized above. For Penny & Gies, we only show the LMC sample (106 stars). From the total sample of Huang & Gies, Fig. 15 presents a subsample of 216 stars spanning SpT from O9.5 to B1.5 (see Fig. 4 of their work). Their higher spectral resolution allowed them to extract lower νesini values than is possible for our data set (i.e. νesini ≤ 40 kms-1, see Sect. 3.2). Finally, the VFTS B-type star distribution excludes the 47 late-O stars in common with the present work, to preserve the independence of the two samples.
The KP tests indicate that the Penny & Gies and VFTS B-star distributions are statistically different, with a confidence level better than 1%, while the Huang & Gies distribution marginally agrees with our O-star distribution (p ~ 11%). That Penny & Gies do not correct for macro-turbulence is a straightforward explanation for the absence of slow rotators in their sample. The other three distributions agree well with respect to the fraction of extremely slow rotators. The fraction of VFTS O- and B-stars below our νesini resolution limit (see Sect. 3.6), for instance, is roughly similar.
The distribution of νesini of the Penny & Gies sample peaks at the same projected rotational velocity as in our distribution. The lack of stars spinning faster than 300 kms-1 in their sample is intriguing, but may result from a selection effect. Indeed the FUSE archives may not be representative of the population of fast rotators in the LMC, as individual observing programs may have focused on stars most suitable for their respective science aims, possibly excluding fast rotators as these are notoriously difficult to analyze.
The similarities between the O-star distribution in 30 Dor and the distribution of late-O and early-B Galactic stars of Huang & Gies suggests a limited influence of metallicity. This is consistent with our expectation that stellar winds do not play a significant role in shaping the rotational velocity distributions in both samples, because they are dominated by stars less massive than 40 M⊙.
The differences with the VFTS B-star sample are striking and lack a straightforward explanation. The B-type stars show a bimodal population of very slow rotators and fast rotators, with few stars rotating at rates that are typical of the low-velocity peak seen in the VFTS O-type stars. We return to this issue in Sect. 5.
 |
Fig. 16 Observed νesini and Lucy-deconvolved νe distributions. The dot-dashed line shows the estimates, after 4 iterations in the Lucy-deconvolution, of the probability density function for the projected rotational velocity distribution. The solid line shows the probability density function of the actual rotational velocities. |
4.5. Analytical representation of the νe distribution
The size of our sample is large enough to investigate the distribution of intrinsic rotational velocities. By assuming that the rotation axes are randomly distributed, we infer the probability density function of the rotational velocity distribution P(νe) from that of νesini. We adopt the iterative procedure of Lucy (1974), as applied in Paper X for the B-type stars in the VFTS, to estimate the pdf of the projected rotational velocity P(νesini) and of the corresponding deprojected pdf velocity P(νe). As expected, P(νe) moves to higher velocities compared to P(νesini) due to the effect of inclination. At νe ≥ 300 kms-1, P(νe) presents small scale fluctuations that probably result from small numbers in the observed distribution. The two extremely fast rotators at νesini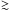 600 kms-1 are excluded from the deconvolution for numerical stability reasons.
600 kms-1 are excluded from the deconvolution for numerical stability reasons.
We can approximate the deconvolved rotational velocity distribution well by an analytical function with two components. We use a gamma distribution for the low-velocity peak and a normal distribution to model the high-velocity contribution: 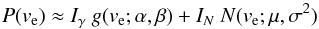 (1)where
(1)where
![\begin{eqnarray} &&g(x; \alpha,\beta) = \frac{\beta^\alpha}{\Gamma(\alpha)} x^{\alpha-1} {\rm e}^{- \beta x},\\[3mm] &&N\left(x; \mu, \sigma^2\right) = \frac{1}{\sqrt{2 \pi} \sigma } {\rm e}^{-(x-\mu)^2 / 2 \sigma^2 }, \end{eqnarray}](/articles/aa/full_html/2013/12/aa21986-13/aa21986-13-eq44.png) and Iγ and IN are the relative contributions of both distributions to P(ve). The best representation, shown in Fig. 17, is obtained for
and Iγ and IN are the relative contributions of both distributions to P(ve). The best representation, shown in Fig. 17, is obtained for ![\begin{eqnarray} P(v_\mathrm{e}) & \approx & 0.43\, g \left(\alpha=4.82,\beta=1/25 \right) \nonumber \\[3mm] && + ~ 0.67\, N \left(\mu=205~\kms, \sigma^2= \left(190~\kms \right)^2 \right). \label{eq: analytic} \end{eqnarray}](/articles/aa/full_html/2013/12/aa21986-13/aa21986-13-eq48.png) (4)The function is normalized to 0.99 to allow for including of an additional 1% component to represent the two extremely fast rotators in our sample. One should note that the reliability of the fit function is limited by the sample size at extreme rotational velocities. This analytical representation of the intrinsic rotational velocity distribution may be valuable in stellar population synthesis models that account for rotational velocity distributions.
(4)The function is normalized to 0.99 to allow for including of an additional 1% component to represent the two extremely fast rotators in our sample. One should note that the reliability of the fit function is limited by the sample size at extreme rotational velocities. This analytical representation of the intrinsic rotational velocity distribution may be valuable in stellar population synthesis models that account for rotational velocity distributions.
5. Discussion
The most distinctive feature of the νesini and νe distributions of the O-type stars in 30 Dor is its two-component structure: a low-velocity peak and an extended high-velocity tail. In this section, we consider possible physical mechanisms that may be responsible for the global shape of our νe distribution. We start, however, by assessing the projected spin rates νesini relative to the critical spin rates.
5.1. νe sin i relative to the critical rotation rate
To estimate the critical rotation rate, νcrit, the sample is divided into three groups with LC V-IV, III, and II-I. Stellar masses (M), luminosities (L), and radii (R) are then obtained from the SpT calibration for the representative LC (V, III, or I) from the spectral subtype calibration for rotating LMC stars by Weidner & Vink (2010). We approximate 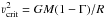 by correcting the mass for the effect of radiation pressure on free electrons with an Eddington factor Γ. Around 50% of our sample stars are found in the low-velocity peak with νesini between 50 and 150 kms-1, implying rotation rates less than 20% of the critical rotation rate νcrit. Figure 18 confirms the general behavior found in Sect. 4.3 that earlier O-type stars in our sample lack extremely fast rotators relative to later spectral subtypes, either in absolute νesini or as a fraction of νcrit.
by correcting the mass for the effect of radiation pressure on free electrons with an Eddington factor Γ. Around 50% of our sample stars are found in the low-velocity peak with νesini between 50 and 150 kms-1, implying rotation rates less than 20% of the critical rotation rate νcrit. Figure 18 confirms the general behavior found in Sect. 4.3 that earlier O-type stars in our sample lack extremely fast rotators relative to later spectral subtypes, either in absolute νesini or as a fraction of νcrit.
5.2. The low-velocity peak
The low-velocity peak contains the large majority of the stars in our sample. The origin of this peak may be related to the formation or early evolution of these stars. Massive stars inherit their angular momentum from their parental cloud that contains more than enough angular momentum to spin up the protostar to critical rotation (see Larson 2010). Interestingly, Lin et al. (2011) find that gravitational torques prohibit a star from rotating above ~50% of its break-up speed during formation. Magnetic coupling between the massive protostar and its accretion disk is expected to be insufficient in spinning down the star further (Rosen et al. 2012). As pointed out earlier, stellar winds and (single-star) evolution are also not effective in reducing the rotation rate during most of the main sequence phase, save for objects initially more massive than 40 M⊙. An additional braking mechanism is thus needed.
 |
Fig. 18 Projected rotational velocity normalized to critical velocity, νesini/ vcrit, vs. spectral subtype for our sample stars with known spectral types. Critical velocities are estimated using the SpT calibration by Weidner & Vink (2010). See legend for the information on the luminosity class. Stars indicated in the legend as “upper limits” refer to stars with νesini ≤ 40 kms-1. |
Meynet et al. (2011) and Potter et al. (2012) have explored stellar evolution models for magnetic main sequence stars. Based on a model for magnetic braking of ud-Doula & Owocki (2002), they both predict that a massive star rotates at only a modest fraction of its break-up velocity if it has a surface magnetic field strength on the order of 2 kG. Most O-type stars in the Milky Way have no measured magnetic field, and the majority of the few known magnetic O-type star have a magnetic field strength of several hundred G to a few kG (Donati & Landstreet 2009; Grunhut et al. 2012). If magnetic braking is indeed the mechanism that slows down the stars after their birth, most of the spin down has to occur within the first Myr, after which the strength of the stellar magnetic field has to decrease below the detection limit of the current surveys.
Within the context of a main-sequence magnetic braking scenario, the absence of a large population of very slow rotators (νesini< 40 kms-1) in our sample may indicate that either magnetic fields disappear before being able to fully spin down the star or that the generation of the magnetic field itself is related to the high rotational velocity. The analysis of spin rates for the early-B stars in the VFTS field (Paper X) shows a bimodal distribution with a low-velocity component that peaks at lower velocities relative to that for the O-stars. If this difference is connected to magnetic braking it may indicate that magnetic fields are initially stronger and/or more efficient in spinning down early-B stars.
5.3. The high-velocity tail
Although most of the stars must spin down quickly after their formation to produce the low-velocity peak (see Sect. 5.2), it is possible that some very young stars – potentially rotating faster than average – are still present in our sample. Figure 18 shows that the later spectral subtypes contain a pro rata higher percentage of fast-rotating stars, almost reaching the critical speed. The compatible rotational distributions of the stars in NGC 2060 and the younger NGC 2070 (see Sect. 4.1) and the fact that star formation has very likely stopped in NGC 2060, however, argue against newborn stars being a suitable explanation for the high-velocity tail.
The presence of a high-velocity tail is, however, predicted by recent population synthesis computations that study the influence of binary evolution on the projected rotation rate of massive stars (de Mink et al. 2013). Those simulations can create a population of stars with high rotational rates through binary interaction. Such a population is composed of mergers and of secondary stars that have been spun up by mass transfer. In a second paper, de Mink et al. (in prep.) also argue that most post-interaction binary products cannot be identified by RV investigations and will thus contaminate our “single-star” sample. Interestingly, we find that the fraction of fast rotators (νe> 300 kms-1) observed in the 30 Dor O-type star population (19% of our “single-star” sample, hence ~11% of the whole VFTS O-type star population) is the same order of magnitude as the numerical predictions by de Mink et al. Dedicated simulations that take the star formation history of 30 Dor into account are, however, desirable for further investigating this scenario. Sana et al. (2013; Paper VIII) report that the measured O-type star binary fraction in 30 Dor (51%) is apparently lower than this fraction measured in young nearby Milky Way clusters (69%; Sana et al. 2012). The assumption that most of the stars in our high rotational-velocity tail are post-binary interaction products could potentially conciliate these two measurements. The pronounced high-velocity component in the νesini distribution of the early-B stars in the VFTS (Paper X) may also be in line with a post-binary nature, as secondaries more often are of spectral type B than O.
If our interpretation of the high-velocity tail as resulting from binary interaction is correct, it suggests that the low-velocity part of our distribution is a cleaner original single-star sample. As, discussed by de Mink et al. (2013), the contamination of the high-velocity end of the distribution by unresolved binary products complicates, and may even invalidate, surface abundance analysis that aims to test or calibrate rotational mixing theories, since such surface enrichment may also be the result of mass transfer or mixing in merger products.
5.4. The single and binary channels for long-duration gamma-ray bursts
The nature of the high-velocity tail of the distribution of rotation rates as discussed in Sect. 5.3 has important implications for the evolutionary origin of systems that produce long-duration gamma-ray bursts (LGRBs). In both the collapsar model (Woosley 1993) and the millisecond-magnetar model (Lyutikov & Blackman 2001), the Wolf-Rayet progenitor system of a stellar explosion producing a long (at least two-second) burst of gamma rays is required to have a rapidly spinning core (see, e.g., Langer 2012). Most, perhaps all (Niino 2011), of such gamma-ray bursts occur in regions of their host galaxies that have a low-metal content (Fruchter et al. 2006; Modjaz et al. 2008; Gräfener & Hamann 2008). Two channels leading up to a GRB have been proposed. First, a close interacting binary system may lead to the late production and spin-up of a Wolf-Rayet star (Izzard et al. 2004; Fryer & Heger 2005; Podsiadlowski et al. 2010; Tout et al. 2011). With only limited time left before the supernova explosion, the stellar wind of the Wolf-Rayet is not able to remove sufficient angular momentum to prevent a gamma-ray burst, especially not at low-metallicity where the outflow is less dense (Vink & de Koter 2005). Second, an LGRB may occur for a single star that rotates so fast that mixing processes cause the interior to become quasi-chemically homogeneous and the star as a whole to remain compact (Yoon & Langer 2005; Woosley & Heger 2006). Since such a system develops Wolf-Rayet characteristics early on, a low-metallicity environment is required to avoid wind-induced spin down.
The single-star LGRB progenitors need O-type star descendants that at birth spin faster than ~300–400 kms-1 and are more massive than about 20 M⊙ (Brott et al. 2011a). Mokiem et al. (2006) identified presumably-single candidate objects for such evolution, a result that actually spurred the above-mentioned groups to put forward the possibility of a single-star channel. If indeed the high-end tail of the velocity distribution is dominated by, or is exclusively due to, post-interaction binaries and mergers, the relative importance of the single-star channel is reduced. Indeed, if the high-end tail is exclusively composed of binary products, then the existence of the single-star GRB channel may be challenged altogether.
6. Conclusions
We have estimated projected rotational velocities for the presumably single O-type stars in the VFTS sample (216 stars). We find that the most distinctive feature of the νesini distribution of O stars in 30 Dor is a two-component structure: a low-velocity peak at ~80 kms-1 and a high-velocity tail extending up to ~600 kms-1. The presence of the low-velocity peak is consistent with previous LMC surveys, but we conclusively find a considerable population of rapidly spinning stars (νe> 300 kms-1 for 20% of the sample). The homogeneity and size of the sample also allows us to study the νesini distribution as a function of spatial distribution, luminosity class, and spectral type.
Based on expectations of star formation and single-star evolution, most of the stars seem to have to spin down shortly after their formation, from critical or half-critical rotation rates to a much smaller fraction of their break-up velocity. For the bulk of O stars, angular momentum loss in a stellar wind is insufficient and another mechanism should act to efficiently spin down the stars; magnetic fields being prime candidates.
The presence of a well populated high-velocity tail is compatible with expectations from binary evolution, and it qualitatively agrees with recent population synthesis predictions (de Mink et al. 2013). The nature of the high-velocity tail of the distribution has an important implication for the evolutionary origin of systems that produce long-duration gamma-ray bursts. If the objects in the high-velocity tail were predominantly products of binary interaction and mergers, a scenario for long-duration GRB production without a preferred metallicity (range) for the progenitor systems would be implied, unless binarity itself presents a metallicity dependence in LGRB progenitor production. If the high-velocity tail is dominated by single stars after all, a low-metallicity environment seems required for LGRBs.
For evolved (B-type) supergiants macro-turbulent broadening may be caused by non-radial gravity-mode pulsations. For a subset of these pulsators the νesini values derived using the FT method may be offset by 10–30 kms-1 (Aerts et al. 2009).
In those cases Penny & Gies (2009) provide νesini values for both the primary and the secondary stars.
Acknowledgments
S.d.M. acknowledges support by NASA through an Einstein Fellowship grant, PF3-140105, and a Hubble Fellowship grant, HST-HF-51270.01-A, awarded by the STScI operated by AURA under contract NAS5-26555. JMA acknowledges support from the Spanish Government Ministerio de Educación y Ciencia through grants AYA2010-15081 and AYA2010-17631 and the Consejería de Educación of the Junta de Andalucía through grant P08- TIC-4075. SS-D and AH acknowledge financial support from the Spanish Ministry of Economy and Competitiveness (MINECO) under the grants AYA2010-21697-C05-04, Consolider-Ingenio 2010 CSD2006-00070, and Severo Ochoa SEV-2011-0187, and by the Canary Islands Government under grant PID2010119. FN ackowledges support by the Spanish MINECO under grants AYA2010-21697-C05-01 and FIS2012-39162-C06-01.
References
- Abt, H. A., Levato, H., & Grosso, M. 2002, ApJ, 573, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Aerts, C., Puls, J., Godart, M., & Dupret, M.-A. 2009, A&A, 508, 409 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brott, I., de Mink, S. E., Cantiello, M., et al. 2011a, A&A, 530, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brott, I., Evans, C. J., Hunter, I., et al. 2011b, A&A, 530, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carroll, J. A. 1933, MNRAS, 93, 478 [NASA ADS] [CrossRef] [Google Scholar]
- Collins, G. W. II 1963, ApJ, 138, 1134 [NASA ADS] [CrossRef] [Google Scholar]
- Collins, G. W. II, & Harrington, J. P. 1966, ApJ, 146, 152 [NASA ADS] [CrossRef] [Google Scholar]
- de Koter, A., Heap, S. R., & Hubeny, I. 1998, ApJ, 509, 879 [NASA ADS] [CrossRef] [Google Scholar]
- de Mink, S. E., Langer, N., Izzard, R. G., Sana, H., & de Koter, A. 2013, ApJ, 764, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J.-F., & Landstreet, J. D. 2009, ARA&A, 47, 333 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Dufton, P. L., Dunstall, P. R., Evans, C. J., et al. 2011, ApJ, 743, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Dufton, P. L., Langer, N., Dunstall, P. R., et al. 2013, A&A, 550, A109 (Paper X) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ebbets, D. 1979, ApJ, 227, 510 [NASA ADS] [CrossRef] [Google Scholar]
- Ekström, S., Meynet, G., Maeder, A., & Barblan, F. 2008, A&A, 478, 467 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ekström, S., Georgy, C., Eggenberger, P., et al. 2012, A&A, 537, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evans, C. J., Taylor, W. D., Hénault-Brunet, V., et al. 2011, A&A, 530, A108 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fruchter, A. S., Levan, A. J., Strolger, L., et al. 2006, Nature, 441, 463 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Fryer, C. L., & Heger, A. 2005, ApJ, 623, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Gibson, B. K. 2000, Mem. Soc. Astron. Italiana, 71, 693 [Google Scholar]
- Gräfener, G., & Hamann, W.-R. 2008, A&A, 482, 945 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gray, D. 1976, The Observation and Analysis of Stellar Photospheres, third edn. (Cambridge University Press) [Google Scholar]
- Grunhut, J. H., Wade, G. A., & MiMeS Collaboration 2012, in AIP Conf. Ser. 1429, eds. J. L. Hoffman, J. Bjorkman, & B. Whitney, 67 [Google Scholar]
- Herrero, A., Kudritzki, R. P., Vilchez, J. M., et al. 1992, A&A, 261, 209 [NASA ADS] [Google Scholar]
- Howarth, I. D., Siebert, K. W., Hussain, G. A. J., & Prinja, R. K. 1997, MNRAS, 284, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, W., & Gies, D. R. 2006, ApJ, 648, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, W., Gies, D. R., & McSwain, M. V. 2010, ApJ, 722, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Hubeny, I., & Lanz, T. 1995, ApJ, 439, 875 [Google Scholar]
- Hunter, I., Lennon, D. J., Dufton, P. L., et al. 2008, A&A, 479, 541 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Izzard, R. G., Ramirez-Ruiz, E., & Tout, C. A. 2004, MNRAS, 348, 1215 [NASA ADS] [CrossRef] [Google Scholar]
- Kolmogorov, A. 1933, Gior. Ist. Ital. Attuari, 4, 83 [Google Scholar]
- Kuiper, N. H. 1960, Proceedings of the Koninklijke Nederlandse Akademie Van Wetenshappen, 63, 38 [Google Scholar]
- Langer, N. 2012, ARA&A, 50, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B. 2010, Rep. Prog. Phys., 73, 014901 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, M.-K., Krumholz, M. R., & Kratter, K. M. 2011, MNRAS, 416, 580 [NASA ADS] [Google Scholar]
- Lucy, L. B. 1974, AJ, 79, 745 [NASA ADS] [CrossRef] [Google Scholar]
- Lyutikov, M., & Blackman, E. G. 2001, MNRAS, 321, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A. 1980, A&A, 92, 101 [NASA ADS] [Google Scholar]
- Maeder, A., & Meynet, G. 2000, A&A, 361, 159 [NASA ADS] [Google Scholar]
- Martins, F., Schaerer, D., & Hillier, D. J. 2005, A&A, 436, 1049 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massey, P., & Hunter, D. A. 1998, ApJ, 493, 180 [NASA ADS] [CrossRef] [Google Scholar]
- Meynet, G., Eggenberger, P., & Maeder, A. 2011, A&A, 525, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Modjaz, M., Kewley, L., Kirshner, R. P., et al. 2008, AJ, 135, 1136 [NASA ADS] [CrossRef] [Google Scholar]
- Mokiem, M. R., de Koter, A., Evans, C. J., et al. 2006, A&A, 456, 1131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Niino, Y. 2011, MNRAS, 417, 567 [NASA ADS] [CrossRef] [Google Scholar]
- Penny, L. R. 1996, ApJ, 463, 737 [NASA ADS] [CrossRef] [Google Scholar]
- Penny, L. R., & Gies, D. R. 2009, ApJ, 700, 844 [NASA ADS] [CrossRef] [Google Scholar]
- Podsiadlowski, P., Ivanova, N., Justham, S., & Rappaport, S. 2010, MNRAS, 406, 840 [NASA ADS] [Google Scholar]
- Potter, A. T., Chitre, S. M., & Tout, C. A. 2012, MNRAS, 424, 2358 [NASA ADS] [CrossRef] [Google Scholar]
- Puls, J., Urbaneja, M. A., Venero, R., et al. 2005, A&A, 435, 669 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rosen, A. L., Krumholz, M. R., & Ramirez-Ruiz, E. 2012, ApJ, 748, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Ryans, R. S. I., Dufton, P. L., Rolleston, W. R. J., et al. 2002, MNRAS, 336, 577 [NASA ADS] [CrossRef] [Google Scholar]
- Sabbi, E., Lennon, D. J., Gieles, M., et al. 2012, ApJ, 754, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Sana, H., de Mink, S. E., de Koter, A., et al. 2012, Science, 337, 444 [Google Scholar]
- Sana, H., de Koter, A., de Mink, S. E., et al. 2013, A&A, 550, A107 (Paper VIII) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Selman, F., Melnick, J., Bosch, G., & Terlevich, R. 1999, A&A, 347, 532 [NASA ADS] [Google Scholar]
- Simón-Díaz, S., & Herrero, A. 2007, A&A, 468, 1063 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simón-Díaz, S., Herrero, A., Uytterhoeven, K., et al. 2010, ApJ, 720, L174 [NASA ADS] [CrossRef] [Google Scholar]
- Simón-Díaz, S., Castro, N., Herrero, A., et al. 2013, in Four decades of research on massive stars, eds. L. Drissen, C. Rubert, N. St-Louis, & A. F. J. Moffat, ASP Conf. Ser., 465, 19 [Google Scholar]
- Slettebak, A., Collins, G. W. II, Parkinson, T. D., Boyce, P. B., & White, N. M. 1975, ApJS, 29, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Tout, C. A., Wickramasinghe, D. T., Lau, H. H.-B., Pringle, J. E., & Ferrario, L. 2011, MNRAS, 410, 2458 [NASA ADS] [CrossRef] [Google Scholar]
- ud-Doula, A., & Owocki, S. P. 2002, ApJ, 576, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Vink, J. S., & de Koter, A. 2005, A&A, 442, 587 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vink, J. S., Brott, I., Gräfener, G., et al. 2010, A&A, 512, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vink, J. S., Muijres, L. E., Anthonisse, B., et al. 2011, A&A, 531, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- von Zeipel, H. 1924, MNRAS, 84, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Walborn, N. R., & Blades, J. C. 1997, ApJS, 112, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Walborn, N. R., Sana, H., Taylor, W. D., Simón-Díaz, S., & Evans, C. J. 2012, in Proceedings of a Scientific Meeting in Honor of Anthony F. J. Moffat, eds. L. Drissen, C. Rubert, N. St-Louis, & A. F. J. Moffat, ASP Conf. Ser., 465, 490 [Google Scholar]
- Weidner, C., & Vink, J. S. 2010, A&A, 524, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woosley, S. E. 1993, in Compton gamma-ray observatory, eds. M. Friedlander, N. Gehrels, & D. J. Macomb, AIP Conf. Proc., 280, 995 [Google Scholar]
- Woosley, S. E., & Heger, A. 2006, ApJ, 637, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Yoon, S.-C., & Langer, N. 2005, A&A, 443, 643 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zinnecker, H., & Yorke, H. W. 2007, ARA&A, 45, 481 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: N v λ4604 line
Though the N v line is not widely used to obtain νesini, the line is affected little by Stark broadening and may thus provide an alternative anchor point for He ii-based measurements. Since N vλ4604 is intrinsically strong, it may be partly formed in the stellar outflow. It can thus only be used for νesini determination if the wind is weak and the line is of photospheric origin; i.e., it should be symmetric.
 |
Fig. A.1 Comparison of the νesini measurements for He iiλ4541 and N vλ4604. Information on the LC of the targets is provided by the symbol shapes. The dashed lines show the ± 10 kms-1 and/or ± 10%, whichever is the largest, around the 1:1 relation. |
Eight stars in our sample (VFTS 016, 072, 267, 506, 518, 566, 599, 621) show both N vλ4604 and He iiλ4541.VFTS 180 was discarded due to its asymmetric profile. Figure A.1 compares the νesini measurements obtained, for this subsample, from both diagnostic lines. Save for one target, all measurements agree within ±10 kms-1 or ±10% of the 1:1 relation. The comparison lacks stars with low projected spin rates. The sole case for which the comparison is poor has the lowest spin rate when using the N v diagnostic. On the basis of one case, we cannot conclude whether this indicates a systematic effect at low νesini or whether it is the result of the relatively large dispersion of spin rate measurements based on He ii at modest rotational velocities (see Sect. 3.4.2).
Appendix B: Comparison with overlapping sample of the O and B-type stars in the VFTS
Rotational velocities for the single B-type stars in the Tarantula Survey have been presented in Paper X. There the FT technique was also used, but a different set of lines was applied reflecting the different temperature range. Owing to uncertainties in the preliminary spectral classification, 47 late-O and early-B stars were included in both data sets.
Figure B.1 compares both νesini measurements. We find that there are no significant systematic differences between the two sets of measurements. Despite two outliers (VFTS 412 and 594 at about ~180 kms-1), the overall comparison presents an excellent agreement, with an rms dispersion of about 10% of the 1:1 relation.
 |
Fig. B.1 Comparison of the νesini measurements of the overlapping late O-type sample in Dufton et al. (2013) and this study. Information on the LC of the targets is provided by the symbol shapes. The dashed and dotted lines have the same meaning as in Fig. 6. |
All Tables
Overview of the diagnostic lines used to derive the projected rotational velocity.
Kuiper test (KP) statistics for different sets of the O-type stars (Cols. 1 and 2).
All Figures
 |
Fig. 1 Spectral type (SpT) distribution of the O-type stars in our sample, binned per spectral subtype. Different colors indicate different luminosity classes (LC), see legend. |
| In the text | |
 |
Fig. 2 Spatial distribution of the presumably single O-type stars as a function of the LC. The circles define regions within 2.4’ of NGC 2070 (central circle) and NGC 2060 (SW circle). Colors have the same meaning as in Fig. 1 (only available in the online version). |
| In the text | |
 |
Fig. 3 Spatial distribution of our sample in the 30 Dor field of view. Different colors identify the different groups listed in Table 1 and are identified in the legend. |
| In the text | |
 |
Fig. 4 Diagnostic lines used as a function of the SpT of the stars in our sample. |
| In the text | |
 |
Fig. 5 Example of the GOF and FT measurement methods applied to the He iλ4713 line of VFTS 280 (top row, high S/N) and VFTS 163 (bottom row, poor S/N), to illustrate two different data qualities. Left-hand column: line profile (black) and its GOF solution (red). Right-hand column: Fourier transform of the observed spectrum (black) and of the best fit GOF profile (red). The dashed lines indicate the position of the FT first minimum. |
| In the text | |
 |
Fig. 6 Comparison of νesini values obtained from the FT and GOF methods for He iλ4713. Upper panel: different symbols indicate different data qualities, identified in the legend. Lower panel: same as above after discarding the lower quality data. Information on the LC and SpT of the targets is provided by the symbol shapes and colors (see legend). In both panels, the dotted lines indicates the 1:1 relation. The dashed lines show the ± 20 kms-1 or ± 20%, whichever is the largest, around the 1:1 relation. |
| In the text | |
 |
Fig. 7 Comparison of the νesini measurements from the FT and GOF methods for He iiλ4541. Information on the LC and SpT of the targets is provided by the symbol shapes and colors. Lines have the same meaning as in Fig. 6. |
| In the text | |
 |
Fig. 8 Comparison of νesini values from the FT method for He iλ4713 and Si iiiλ4552. Information on the LC and SpT of the targets is provided by the symbol shapes and colors. Lines have the same meaning as in Fig. 6. |
| In the text | |
 |
Fig. 9 Comparison of νesini obtained from the FT method for He iλ4922 and He iλ4713. Information on the LC and SpT of the targets is provided by the symbol shapes and colors. Lines have the same meaning as in Fig. 6. |
| In the text | |
 |
Fig. 10 Comparison of νesini measurements from He iλ4713 and He iiλ4541. Upper panel: both diagnostic lines analyzed using the FT method. Lower panel: He iiλ4541 analyzed using the GOF and He iλ4713 using the FT. Information on the LC and SpT of the targets is provided by the symbol shapes and colors. Lines have the same meaning as in Fig. 6. |
| In the text | |
 |
Fig. 11 Histogram of the projected rotational velocities of our sample of 216 O-type stars in 30 Dor. |
| In the text | |
 |
Fig. 12 Cumulative (upper panel) and frequency (lower panel, with Poisson error bars) distributions of the projected rotational velocities of the O-type stars for three spatially selected groups. |
| In the text | |
 |
Fig. 13 Cumulative (upper panel) and frequency (lower panel, with Poisson error bars) distributions of the projected rotational velocities of the O-type stars for three different LC categories. |
| In the text | |
 |
Fig. 14 Cumulative (upper panel) and frequency (lower panel, with Poisson error bars) distributions of the projected rotational velocities of the O-type stars for three different spectral type categories. |
| In the text | |
 |
Fig. 15 Comparison of the cumulative distributions of projected rotational velocities of our work (VFTS-O sample – purple), Penny & Gies (blue), Huang & Gies (green), and the VFTS-B sample of Dufton et al. (2013) (red). |
| In the text | |
 |
Fig. 16 Observed νesini and Lucy-deconvolved νe distributions. The dot-dashed line shows the estimates, after 4 iterations in the Lucy-deconvolution, of the probability density function for the projected rotational velocity distribution. The solid line shows the probability density function of the actual rotational velocities. |
| In the text | |
 |
Fig. 17 Analytical representation of the deconvolved rotational velocity distribution (Eq. (4)). |
| In the text | |
 |
Fig. 18 Projected rotational velocity normalized to critical velocity, νesini/ vcrit, vs. spectral subtype for our sample stars with known spectral types. Critical velocities are estimated using the SpT calibration by Weidner & Vink (2010). See legend for the information on the luminosity class. Stars indicated in the legend as “upper limits” refer to stars with νesini ≤ 40 kms-1. |
| In the text | |
 |
Fig. A.1 Comparison of the νesini measurements for He iiλ4541 and N vλ4604. Information on the LC of the targets is provided by the symbol shapes. The dashed lines show the ± 10 kms-1 and/or ± 10%, whichever is the largest, around the 1:1 relation. |
| In the text | |
 |
Fig. B.1 Comparison of the νesini measurements of the overlapping late O-type sample in Dufton et al. (2013) and this study. Information on the LC of the targets is provided by the symbol shapes. The dashed and dotted lines have the same meaning as in Fig. 6. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


