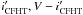| Issue |
A&A
Volume 560, December 2013
|
|
|---|---|---|
| Article Number | A13 | |
| Number of page(s) | 25 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201321508 | |
| Published online | 28 November 2013 | |
The Monitor Project: stellar rotation at 13 Myr
I. A photometric monitoring survey of the young open cluster h Persei⋆,⋆⋆,⋆⋆⋆
1
UJF-Grenoble 1 / CNRS-INSU, Institut de Planétologie et d’Astrophysique de
Grenoble (IPAG) UMR 5274,
38041
Grenoble,
France
e-mail:
estelle.moraux@obs.ujf-grenoble.fr
2
Crimean Astrophysical Observatory, p/o Nauchny, 98409
Crimea,
Ukraine
3
Harvard-Smithsonian Center for Astrophysics, 60 Garden Street,
Cambridge
MA
02138,
USA
4
Ulugh Bek Astronomical Institute of the Uzbek Academy of Sciences,
Astronomicheskaya
33, 700052
Tashkent,
Uzbekistan
5
Byurakan Astrophysical Observatory, 0213
Aragatsotn reg.,
Armenia
6
Istituto Nazionale di Astrofisica, Osservatorio Astronomico di
Torino, Strada Osservatorio 20, 10025
Pino Torinese,
Italy
7
Institute of Astronomy, University of Cambridge,
Madingley Road,
Cambridge
CB3 0HA,
UK
8
Astrophysics, Denys Wilkinson Building, University of Oxford,
Oxford
OX1 3RH,
UK
Received:
19
March
2013
Accepted:
18
June
2013
Aims. We aim at constraining the angular momentum evolution of low-mass stars by measuring their rotation rates when they begin to evolve freely towards the zero-age main sequence (ZAMS), i.e., after the disk accretion phase has stopped.
Methods. We conducted a multisite photometric monitoring of the young open cluster h Persei, which has an age of ~13 Myr. The observations were done in the I-band using four different telescopes, and the variability study is sensitive to periods from less than 0.2 day to 20 days.
Results. Rotation periods are derived for 586 candidate cluster members over the mass range 0.4 ≤ M/M⊙ ≤ 1.4. The rotation period distribution indicates a slightly higher fraction of fast rotators for the lower mass objects, although the lower and upper envelopes of the rotation period distribution, located respectively at ~0.2–0.3 d and ~10 d, are remarkably flat over the whole mass range. We combine this period distribution with previous results obtained in younger and older clusters to model the angular momentum evolution of low mass stars during the pre-main sequence (PMS) phase.
Conclusions. The h Per cluster provides the first statistically robust estimate of the rotational period distribution of solar-type and lower mass stars at the end of the PMS accretion phase (≥10 Myr). The results are consistent with models that assume significant core-envelope decoupling during the angular momentum evolution to the ZAMS.
Key words: stars: rotation / stars: low-mass / open clusters and associations: individual: h Per
Based on observations made with telescopes at the Maidanak Observatory, at the Crimean Astrophysical Observatory, at the Byurakan Observatory, and with MegaPrime/MegaCam on the Canada-France-Hawaii Telescope (CFHT).
Appendix A is available in electronic form at http://www.aanda.org
The list of periodic objects including periods and photometric measurements (Table 2) is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/560/A13
© ESO, 2013
1. Introduction
The angular momentum evolution of low-mass stars is best characterized by measuring the rotation rates of coeval populations at well-defined evolutionary stages. Star-forming regions and young open clusters offer such an opportunity for the pre-main sequence (PMS) and main sequence (MS) evolutionary phases, as they harbor rich stellar populations of known age. Thus, in recent years, thousands of rotational periods have been derived for low-mass stars and brown dwarfs in these environments, covering an age range from 1 Myr to 1 Gyr. A compilation of these efforts was provided by Irwin & Bouvier (2009) and rotational distributions at additional age steps have been further documented since then (e.g., Hartman et al. 2010; Littlefair et al. 2010; Meibom et al. 2011; Affer et al. 2013). These results yield prime observational constraints for the developement of stellar angular momentum models (e.g., Gallet & Bouvier 2013). Yet, a major deficiency on the time sampling provided by these studies concerns the end of the PMS evolution, between 5 Myr (Irwin et al. 2008a) and 40 Myr (Irwin et al. 2008b), which remains poorly documented (Messina et al. 2010, 2011). The goal of the study presented in this paper is to remedy the lack of statistically robust rotational distributions in this age range by measuring the rotational periods of hundreds of low-mass members of the young open cluster h Per at an age of about 13 Myr (Mayne & Naylor 2008).
Journal of the observations.
H Per, also known as NGC 869, is the westernmost of the Perseus double cluster with χ Per (or NGC 884), separated by about 30′. Visible to the naked eye and probably known since antiquity, this region was first cataloged by Hipparchus as a patch of light in the Perseus constellation in ~130 B.C. Its true nature, however, was only discovered in 1780, well after the invention of the telescope, when Sir William Herschel recognized h and χ Persei as two separate stellar clusters. Since early 1900, it has been the target of extensive photometric surveys using photographic plates (e.g., van Maanen 1911; Oosterhoff 1937) and spectroscopic studies (e.g., Trumpler 1926; Bidelman 1943; Schild 1965), leading to some controversy about the distances and relative ages of h and χ Per. More recent studies (e.g., Keller et al. 2001; Capilla & Fabregat 2002; Slesnick et al. 2002; Uribe et al. 2002; Bragg & Kenyon 2005; Mayne et al. 2007; Currie et al. 2010) are now converging to similar properties for both clusters, with a distance modulus of ~11.8, an extinction E(B − V) ~ 0.54, and an age of ~13 Myr (Mayne & Naylor 2008). H Per is about 30% more populous than χ Per with at least ~3000 stars within its 10’ center and has an estimated mass of ~4700 M⊙ (Currie et al. 2010).
The age of h Per probes a critical phase for angular momentum evolution models. By that age, the disk accretion process has ceased and the stars begin to freely evolve towards the zero-age main sequence (ZAMS). Hence, deriving the rotational distribution of low-mass stars in this cluster allows us to characterize the angular momentum properties of stars at the end of the accretion phase, when they have finally acquired their total mass and their angular momentum evolution is not affected any more by the interaction with the circumstellar disk. The distribution of rotation rates at this age also provides the initial conditions for further evolution to the ZAMS and onto the MS.
The paper is organized as follows. In the next section we describe the observations and explain briefly how the light curves were produced for selected possible candidate members. In Sect. 3, we present the method we used to measure rotational periods and discuss possible biases and contamination before giving our results. A general discussion on the angular momentum PMS evolution follows in Sect. 4, and Sect. 5 summarizes our conclusions.
2. Observations and light curve production of possible cluster members
Within the framework of the Monitor Project (Aigrain et al. 2007), we conducted a multisite photometric monitoring of h Persei during the fall
2008 using four different telescopes: the 3.6 m Canada-France-Hawaii Telescope (CFHT), the
1.5 m telescope in Maidanak (Uzbekistan), the 2.6 m Shajn Telescope (ZTSh) at the Crimean
Astrophysical Observatory (CrAO, Ukraine), and the 2.6 m telescope of Byurakan Observatory
(Armenia). The total amount of time spent monitoring the cluster was ~110 h, spread over
two months from Sep. 5 to Oct. 27, 2008. The observations were done in the
I-band, and the individual exposure times were adapted to reach the
equivalent of  , with a
signal-to-noise ratio larger than or equal to ten at each telescope. The details of the
observations performed at each telescope are described below. Table 1 provides a summary of all the observations, Fig. 1 represents the various field of views, and Fig. 2 shows the sampling rate of the light curves.
, with a
signal-to-noise ratio larger than or equal to ten at each telescope. The details of the
observations performed at each telescope are described below. Table 1 provides a summary of all the observations, Fig. 1 represents the various field of views, and Fig. 2 shows the sampling rate of the light curves.
 |
Fig. 1 Pointings of the various instruments used for this monitoring campaign: CFHT/MegaCam (red square), Maidanak (cyan square), CrAO, Byurakan (white circle). The field of view observed in the optical by Currie et al. (2010; blue rectangles) and in the near-infrared with CFHT/WIRCam by Cardoso et al. (in prep.; yellow square) are also shown. Their photometry is used to assess membership (see Sect. 2.3). |
 |
Fig. 2 Temporal sampling of photometric measurements obtained at Mt. Maidanak (black open circles), CFHT (blue crosses), CrAO (red dots), and Byurakan (green triangles) observatories. |
2.1. Instrumentation and observing strategy
At CFHT, the observations were performed in the  filter with the 1
deg × 1 deg MegaCam CCD mosaic (Boulade et al. 2003)
over two runs (runID: 08BF06, P.I. E. Moraux and runID: 08BH17, P.I. B. Reipurth).
Observing blocks of ~2 h were obtained over ten nights from Oct. 1–7 and on Oct. 21, 26,
27, 2008, yielding a total observing time of 23 h. In total, 698 individual exposure times
of 75 s as well as 55 short exposures of 20 s were obtained. The observing conditions were
photometric and obtained during dark or grey time. The seeing was between 0.6 and 1
arcsec. One of the longest observing nights included continuous measurements over more
than 6 h (0.25 d), which proved very useful to distinguish between long and short period
aliases in the period search analysis (cf. Sect. 3.1).
filter with the 1
deg × 1 deg MegaCam CCD mosaic (Boulade et al. 2003)
over two runs (runID: 08BF06, P.I. E. Moraux and runID: 08BH17, P.I. B. Reipurth).
Observing blocks of ~2 h were obtained over ten nights from Oct. 1–7 and on Oct. 21, 26,
27, 2008, yielding a total observing time of 23 h. In total, 698 individual exposure times
of 75 s as well as 55 short exposures of 20 s were obtained. The observing conditions were
photometric and obtained during dark or grey time. The seeing was between 0.6 and 1
arcsec. One of the longest observing nights included continuous measurements over more
than 6 h (0.25 d), which proved very useful to distinguish between long and short period
aliases in the period search analysis (cf. Sect. 3.1).
 |
Fig. 3 Plot of rms scatter per data point measured over the CFHT and Maidanak dataset as a
function of |
At Maidanak, the observations were obtained in the IMaid-band filter using the SI 600 Series 4k × 4k CCD camera at the 1.5 m AZT-22 telescope. The field of view (FOV) of the camera is 18′ × 18′. The images are round and good up to 15 arcmin from the center but there is a small comatic aberration at the edge of the FOV. The individual exposure time was 300 s. A total of 42.3 observing hours (corresponding to 402 individual frames) divided into blocks of ~3 h were obtained over three different periods (Sep. 5–9, Sep. 25–Oct. 7, and Oct. 25–26). Only the first two periods benefited from good weather conditions, and the data obtained during the third period were not used in our analysis.
At CrAO, the observations were carried out in the ICrAO photometric band, using a FLI PL-1001E CCD camera at the prime focus of the 2.6-m Shajn Telescope (ZTSh). The pixel size of the 1024 × 1024 size CCD matrix KAF-1001E is 0.5 arcsec and the field of view is 8.4′ × 8.4′. The cluster was imaged during seven nights on Sep. 8, 10, 11, 15, 16 and Oct. 16, 19, 2008. The exposure time for each frame was 120 s, and the total time of observations was about 33 h, corresponding to ~5 h per night. This yielded a total of 992 images. As weather conditions on September 15–16 were bad, we have excluded these two nights from the subsequent analysis.
At Byurakan, the observations were done at the prime focus of the 2.6m telescope with the ByuFOSC-2 camera, equipped with 2058 × 2063 pix Loral CCD matrix. This equipment provides a scale of 0.5 arcsec/pix and a full view of 17′ × 17′. However, due to the absence of correcting optics, the nondistorted FOV is reduced to about 9′ × 9′. Images were taken through the IByur-band filter with an exposure time of 120 s. The seeing was about 2 arcsec during the observations performed over 5 nights on Oct. 6, 7, 8, 10, and 19, and the observing blocks were 2 hours long, except on Oct. 19, when it was 4 h long, yielding a total of 142 images.
2.2. Light curve production
Data processing and light curve production were performed for each dataset separately, following the procedure described in Irwin et al. (2007a). Briefly, a master frame was created by stacking the images taken in the best seeing conditions before using the source detection software. The resulting master catalog containing the positions of the detected objects was then used to perform aperture photometry on all the individual images. For each frame, the difference between each source magnitude and its median (calculated across all frames) was measured to compute the frame offset and correct for seeing variation. A 2D fit of the residual map was then subsequently removed to account for varying differential atmospheric extinction across each frame. Light curves were extracted for ~219 000, ~8000, ~2000, and ~3000 objects from the CFHT, Maidanak, CrAO, and Byurakan images.
For the CFHT dataset, the achieved photometric precision for each data point is very
good: it is better than 2 mmag for the brightest objects
( ), with a scatter <1 per
cent up to
), with a scatter <1 per
cent up to 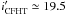 (see Fig. 3). The detection limit on a single frame corresponding to a
signal-to-noise ratio of five is reached at
(see Fig. 3). The detection limit on a single frame corresponding to a
signal-to-noise ratio of five is reached at 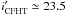 . The photometric precision for
the Maidanak data is also very good, although not as deep. For the CrAO and Byurakan
photometry, however, the rms scatter never gets better than 5 mmag, even for the brightest
objects.
. The photometric precision for
the Maidanak data is also very good, although not as deep. For the CrAO and Byurakan
photometry, however, the rms scatter never gets better than 5 mmag, even for the brightest
objects.
For each possible cluster member (see next section for a description of the selection), a
quality check of each data point was performed before combining the light curves of the
four different sites. If the magnitude was brighter than
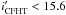 (
( ) for the long (short)
exposures of the CFHT images or
) for the long (short)
exposures of the CFHT images or  for
the other data, we considered it as saturated (see Fig. 3). If the aperture contained bad pixels, if the frame seeing was extremely bad,
or if the frame offset was very large (typically if it falls in the worst 5% of the
distribution in both cases), the data point was qualified as bad. We also marked all the
objects located more than 550 pixels (or 4.6 arcmin) away from the center of Byurakan
images due to strong distortion. Finally, we used a sigma clipping to identify all the
data points for which the magnitude is more than three sigma away from the average
magnitude of the ten closest data points. In all cases, a flag was added to the data
point, and we kept only those with a flag 0 for our analysis.
for
the other data, we considered it as saturated (see Fig. 3). If the aperture contained bad pixels, if the frame seeing was extremely bad,
or if the frame offset was very large (typically if it falls in the worst 5% of the
distribution in both cases), the data point was qualified as bad. We also marked all the
objects located more than 550 pixels (or 4.6 arcmin) away from the center of Byurakan
images due to strong distortion. Finally, we used a sigma clipping to identify all the
data points for which the magnitude is more than three sigma away from the average
magnitude of the ten closest data points. In all cases, a flag was added to the data
point, and we kept only those with a flag 0 for our analysis.
For each object, we then computed the median magnitude of each light curve using only the good data points. We normalized the obtained value to the CFHT median taken as a reference by applying an offset, and we combined the light curves. No color term was applied. However, for the period search described in Sect. 4, we used only the data from CFHT and Maidanak because photometric precision is best for these two datasets. The data from CrAO and Byurakan observatory were used a posteriori to check the goodness of the period found.
2.3. Possible cluster member selection
We first built a master catalog by cross-correlating all the sources detected in any of
the monitoring images described above, i.e., from either CFHT, Maidanak, CrAO or the
Byurakan Observatory. Since the FOV and the image quality was better for the CFHT and
Maidanak datasets, we decided to focus on the objects that were detected at least in one
of these two. The cross-correlation was done by coordinates with TOPCAT (Taylor 2005) using a matching radius of 2 arcsec. This leads
to a catalog with 219 642 sources with  –24.
–24.
We then cross-correlated our master catalog with data from the literature (Slesnick et al. 2002; Uribe et al. 2002; Mayne et al. 2007; Currie et al. 2007a,b,c, 2008 and 2010) to get as much photometric and/or spectroscopic information for each source. In particular, we used the V and IC magnitude from Currie et al. (2010) as the observed FOV is very similar to our MegaCam pointing (see Fig. 1). We also used YJHK CFHT/WIRCam data (Cardoso et al., in prep.) as well as Chandra X-ray data (Argiroffi, priv. comm.). Again, the matching radius was set to 2 arcsec, except for the X-ray data for which we used 2.5 arcsec.
 |
Fig. 4
|
Using all the available photometric data we built color-magnitude diagrams (CMDs). Since
the cluster sequence is clearly visible in all the CMDs, we defined an empirical sequence
to assess membership. As an example, we can see in Fig. 4 the selection that we made in 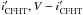 . The two solid
lines represent the custer sequence shifted in colors by ± 0.1 mag plus the amount of the
photometric error, and by –0.75 mag in
. The two solid
lines represent the custer sequence shifted in colors by ± 0.1 mag plus the amount of the
photometric error, and by –0.75 mag in 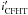 for the upper
envelope to take into account binaries. All the objects located between the two lines were
selected as candidate members. We performed the same selection on all the available CMDs.
An object was eventually considered as a possible cluster member if its optical
for the upper
envelope to take into account binaries. All the objects located between the two lines were
selected as candidate members. We performed the same selection on all the available CMDs.
An object was eventually considered as a possible cluster member if its optical
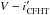 color and/or
near-infrared WIRCam colors (J − H,
J − K and H − K)
were consistent with membership. Alternatively, if these colors were not available (no
detection), but the object was detected in Hα (Currie et al. 2007c) or in X-ray (Currie et al. 2009, and C. Argiroffi, priv. comm.), or was classified as possible
member by Currie et al. (2010; membership flag ≥1)
or Uribe et al. (2002) based on proper motion, we
kept it as a cluster candidate. We ended up with a rather conservative final catalog of
19 224 sources selected as possible members over the whole FOV. Based on their photometric
colors, 45 710 objects were rejected, and 154 708 objects were classified as “unknown”
since we did not have any membership information (objects detected only in one filter,
usually with MegaCam at CFHT since its FOV is larger than any other h Per survey that has
been performed so far).
color and/or
near-infrared WIRCam colors (J − H,
J − K and H − K)
were consistent with membership. Alternatively, if these colors were not available (no
detection), but the object was detected in Hα (Currie et al. 2007c) or in X-ray (Currie et al. 2009, and C. Argiroffi, priv. comm.), or was classified as possible
member by Currie et al. (2010; membership flag ≥1)
or Uribe et al. (2002) based on proper motion, we
kept it as a cluster candidate. We ended up with a rather conservative final catalog of
19 224 sources selected as possible members over the whole FOV. Based on their photometric
colors, 45 710 objects were rejected, and 154 708 objects were classified as “unknown”
since we did not have any membership information (objects detected only in one filter,
usually with MegaCam at CFHT since its FOV is larger than any other h Per survey that has
been performed so far).
To estimate the level of contamination by field objects in our photometric selection, we
used the Besançon Galactic model (Robin et al. 2003). We performed the same analysis on our data and on the synthetic catalog to
which photometric noise had been added. In both cases the considered FOV was restricted to
the WIRCam pointing and we used only two CMDs (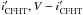 and
and
 ) for
the selection. This only provides us with an upper limit of the contamination as we
actually used more colors for the final photometric selection. However, this is sufficient
for our purpose, especially as these two colors are the most constraining for membership
selection. Overall, we found a contamination level of 14% after selection on both
) for
the selection. This only provides us with an upper limit of the contamination as we
actually used more colors for the final photometric selection. However, this is sufficient
for our purpose, especially as these two colors are the most constraining for membership
selection. Overall, we found a contamination level of 14% after selection on both
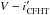 and
and
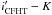 colors
(26% if only
colors
(26% if only 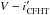 is used, 34%
if only
is used, 34%
if only 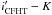 ) in the
magnitude range
) in the
magnitude range 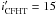 –21.
The contamination per magnitude bin is given in Fig. 5. It is interesting to note that the selection drops to zero for the faintest
objects. This is due to the fact that the cluster members are much redder than the
galactic population in the chosen CMDs for
–21.
The contamination per magnitude bin is given in Fig. 5. It is interesting to note that the selection drops to zero for the faintest
objects. This is due to the fact that the cluster members are much redder than the
galactic population in the chosen CMDs for 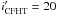 –21 (see Fig. 4). There is therefore no contamination by field stars in
this magnitude range (but by galaxies). For brighter magnitudes, however, the
contamination gets larger, especially when the cluster sequence joins the dwarf locus.
–21 (see Fig. 4). There is therefore no contamination by field stars in
this magnitude range (but by galaxies). For brighter magnitudes, however, the
contamination gets larger, especially when the cluster sequence joins the dwarf locus.
 |
Fig. 5 Photometric contamination level per magnitude bin using the Besançon Galactic model
after selection in both |
For the rest of the paper, we restricted our study to the possible members with
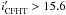 (16 381 objects) to avoid
saturation on the CFHT long exposures (the time sampling on the short exposures being too
low). Following the work from Cardoso et al. (in prep.), we converted the
(16 381 objects) to avoid
saturation on the CFHT long exposures (the time sampling on the short exposures being too
low). Following the work from Cardoso et al. (in prep.), we converted the
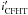 magnitude of
each candidate member into mass using the mass-magnitude relationship from Siess model at
13 Myr (Siess et al. 2000).
magnitude of
each candidate member into mass using the mass-magnitude relationship from Siess model at
13 Myr (Siess et al. 2000).
3. Period measurement analysis
3.1. Period search
To take the best benefit of our sampling, we performed the period search on objects
detected in both CFHT and Maidanak images, i.e., with light curves containing more than
800 measurements (and up to 986). This allowed us to be sensitive to both short and long
periods and to avoid confusion between harmonics as much as possible. The CFHT and
Maidanak measurements were spread over 51 nights, from JD 2 454 716 to JD 2 454 767, with
two large observing gaps from JD 2 454 720 to JD 2 454 735 and from JD 2 454 748 to
JD 2 454 761. The sampling rate is graphically shown in Fig. 2. Photometry obtained at other sites is of lower quality and was only used a
posteriori to confirm the measured periods. Of the 16 381 h Per photometric candidate
members located within the CFHT FOV with 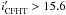 , only 2287 were detected in
both CFHT and Maidanak data. We thus restricted our period analysis to these sources.
, only 2287 were detected in
both CFHT and Maidanak data. We thus restricted our period analysis to these sources.
Periodic signals were searched in the light curves using three methods: Lomb-Scargle periodogram (Scargle 1982; Horne & Baliunas 1986), CLEAN discrete Fourier transform (CLN DFT, Roberts et al. 1987) and string-length minimization (Dworetsky 1983). In all cases, we probed a range of frequency from 0.05 to 5.0 d-1 (i.e., periods from 0.2 to 20 days). The lower frequency limit is about twice the frequency resolution, δf ≃ 1/T, where T is the total time span of the observations. The higher frequency limit was set somewhat arbitrarily to reduce computation time, though we are sensitive to much shorter periods (fmax ≃ δt-1 ≃ 20 d-1, see below). The frequency range was explored by step of 0.001 d-1. At every sampled frequency, the power of the periodogram and of the CLEAN DFT, as well as the string-length were computed. For each light curve, we thus derive three possible periods corresponding to the highest peaks in the periodogram and CLN DFT, as well as to the shortest string-length in the phase diagram.
The power of the highest peak recorded in the periodogram of each of the 2287 light curves is plotted as a function of frequency in Fig. 6. A clear accumulation of peaks occurs at frequencies around 0.5 and 1 d-1. These peaks correspond to spurious periods resulting from the nightly sampling rate. We therefore removed all periods lying in the frequency ranges 0.48–0.51 and 0.95–1.03 d-1. This left us with 1761 possibly periodic h Per candidate members. As the investigated light curves have nearly the same number of measurements and a similar temporal sampling, the highest peak power also corresponds to the lowest false alarm probability (FAP, cf. Scargle 1982).
We derived FAP levels from a control sample (discussed in more detail in Sect. 3.3) of 1307 field stars, i.e., photometric
non-members spanning a similar magnitude and color ranges in the
( ) color-magnitude as
h Per photometric candidate members. The light curves of these 1307 field stars also have
a temporal sampling similar to those of the h Per candidate members under analysis. The
cumulative distribution of the power of the highest peak in the periodograms of the field
stars provides an estimate of the FAP, i.e., the probability that a given peak power
merely results from statistical noise. After removal of spurious peaks at frequencies
around 0.5 and 1.0 d-1 (see above), we are left with 890 field stars, from
which we derive a FAP level of 0.01 for a peak power of 116 and FAP of 0.05 for a peak
power of 72. These FAPs are illustrated in Fig. 6. As
discussed by Littlefair et al. (2010), this
approach is more accurate than analytical estimates of the FAP and/or FAP derived from
Monte Carlo simulations.
) color-magnitude as
h Per photometric candidate members. The light curves of these 1307 field stars also have
a temporal sampling similar to those of the h Per candidate members under analysis. The
cumulative distribution of the power of the highest peak in the periodograms of the field
stars provides an estimate of the FAP, i.e., the probability that a given peak power
merely results from statistical noise. After removal of spurious peaks at frequencies
around 0.5 and 1.0 d-1 (see above), we are left with 890 field stars, from
which we derive a FAP level of 0.01 for a peak power of 116 and FAP of 0.05 for a peak
power of 72. These FAPs are illustrated in Fig. 6. As
discussed by Littlefair et al. (2010), this
approach is more accurate than analytical estimates of the FAP and/or FAP derived from
Monte Carlo simulations.
Of the 1761 h Per candidates under analysis, we retained 872 with a FAP level less than 0.05 (604 with a FAP < 0.01) as being possibly periodic1. Their light curves were phase folded, with period estimates derived from the periodogram, CLN DFT, and string-length methods. In most cases, the periodogram and CLN DFT returned similar results. Whenever the three methods yielded different estimates, we relied visually on the phase diagrams to decide on the best period, if any. CLN DFT method proved very reliable to detect the periods of sinusoidal-like light curves, while string-length was found sometimes, though rarely, superior for more complex signals (e.g., double-spotted light curves, cf. HPer-195, -243, -431). The FAP analysis is not fully reliable on its own (cf. Littlefair et al. 2010) and must be complemented by eye-inspection of the phased light curves to remove interlopers. A significant fraction of the selected possibly periodic candidate members did not show any convincing phased light curves, and we rejected 283 candidates as being nonperiodic. Among them, 90 had a FAP less than 0.01, while the others (193) had a FAP between 0.01 and up to 0.05. We considered that their phased light curves did not show periodic modulation by surface spots for one of the following reasons: unconvincing periods close to 0.5 d or 1 d (about 50% of the rejected light curves have periods in the range 0.4–0.6 d or 0.8–1.2 d); presence of superimposed low and high frequency modulations, presumably frequency aliases, which do not allow us to reliably assess the true period; discontinuous photometric jumps in the phased light curves and/or systematic offsets between Maidanak and CFHT data; significant discrepancies between CFHT and Maidanak phased light curves; single flares or dips dominating the photometric amplitude.
To test the effect of the chosen FAP level, we defined two samples based on two different FAP cuts at 0.01 and 0.05, containing respectively 514 and 586 periodic objects after eye examination. We then compared their period distributions for the four mass bins discussed in Sect. 3.5. The KS probability that both distributions are drawn from the same population is larger than 99.99% for the three higher mass bins and is equal to 82.36% for the lower mass bin (04–0.6 M⊙), indicating that there is no significative difference between the two samples. Because choosing one or the other cut in FAP level would thus not affect the results of the paper, we decided to use the less selective threshold (FAP < 0.05). It allowed us to select all the clear periodic variables, which was in line with the previous Monitor studies from Irwin et al. (2007b, 2008a,b, 2009).
 |
Fig. 6 Distribution of the power of the highest periodogram peak shown as a function of frequency for 2287 h Per photometric candidate members analyzed for periodicity. Spurious periods occurring at frequencies around 0.5 and 1.0 d-1 (shown as blue crosses) were discarded. The FAP levels computed from a control sample of nonperiodic field stars are indicated. The 586 h Per candidate members that were eventually considered as periodic are encircled (red). |
We ended with a sample of 586 periodic h Per candidate members, with a spectral type
spanning a range from ~F0 to M6. It is interesting to note that we measured a rotation
period for about 50 F stars, which is of the same order as the number of such periodic
stars found by Saesen et al. (2010), who
investigated the variability of bright stars in χ Per in a similar FOV.
Table 2 (available online at the CDS) lists the periods and photometric amplitudes of all
the periodic objects. The rms error on each period can be computed as
δP = δν × P2, where
δν = 0.0145 d-1 is the average sigma of the Gaussian fit to
the highest peak in the CLN DFT. The amplitude of variability was derived from a
sinusoidal fit to the light curves using FAMOUS2. The
phased light curves of the 586 periodic variables are shown in appendix, Fig. A.1. In some
cases, especially for objects with short periods, the phased light curve provides clear
evidence for phase and/or amplitude variations over the time span of the observations,
indicative of spot evolution and/or surface differential rotation over a timescale of
weeks (see, e.g., HPer-208, 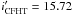 as an extreme case).
as an extreme case).
We note that some periods reported here are shorter than 0.2d, the lower limit of our period search range. This is because visual inspection of some phase diagrams clearly indicated that we had detected a lower frequency harmonic of the true period. In such a case, the period search analysis was repeated with a lower limit of 0.05d. This yielded five objects with clear photometric periods shorter than 0.2d, with the two shortest ones amounting to only 0.0662 d (1.59 h) and 0.0982 d (2.36 h), as illustrated in Fig. 7. The spectral type (F1 ± 2.5 according to Currie et al. 2010), mass (~1.4 M⊙), and low photometric amplitude (~0.008 mag) of HPer-215 suggests δ-Scuti type pulsations rather than rotational modulation (Saesen et al. 2010; Chang et al. 2013). However, the red colors (V − IC ~ 4.5; Mayne et al. 2007) of HPer-513, indicative of a spectral type ~M6, put this object far from expected pulsational instability strips at the age of the cluster (Rodríguez-López et al. 2012; Baran et al. 2011; Palla & Baraffe 2005). The shape of the phased light curve is somewhat suggestive of a contact binary (Nefs et al. 2012) with Porb = 0.19654 d.
 |
Fig. 7 Light curves of the 2 h Per candidate members with the shortest photometric periods are shown in the top panels (red: CFHT, black: Maidanak), their frequency spectrum in the middle panels (black: periodogram, red: CLEAN DFT), and their phased light curves in the bottom panels (red: CFHT, black: Maidanak). Left: HPer-215 with a period of 0.06626 d; Right: HPer-513 with a period of 0.09827 d. |
The period analysis above was performed on the combined Maidanak and CFHT datasets. The CrAO and Byurakan datasets, which were of lower quality and with a sparser, though complementary, temporal sampling, were used to visually confirm the results. In most cases, whenever the signal-to-noise ratio of the latter datasets was high enough, the additional measurements adjusted consistently, albeit with a much increased scatter, onto the phased light curve. They provided further support to the reported periods.
3.2. Period detection, completeness and reliability
 |
Fig. 8 Period detection completeness and reliability for sinusoidal signals with amplitudes from 0.002 to 0.02 mag (black histograms) and from 0.01 to 0.02 mag (red dashed histograms). The period detection completeness is shown as a function of period in panel a), photometric amplitude in panel b), and stellar magnitude in panel c). The reliability of the recovered periods is shown in panel d). Reliable periods are defined as those within 10% of the input periods (shown as a function of input period). Contaminating periods are those that differ from the input period by more than 10% (shown as a function of detected period). The lower left and right panels show the estimated periods as a function of the input periods on a linear scale and on log scale, respectively. Periods recovered with a FAP ≤ 0.01 are shown by large (black) triangles, while those with 0.01 < FAP ≤ 0.05 are shown by small (red) circles. The straight lines show the locus of equal periods and factor of 2 harmonics, and the curves show the location of 1 d period aliases. |
We describe here Monte Carlo simulations that we ran on synthetic light curves to
estimate the robustness and completeness of the period search analysis presented in the
previous section. To build synthetic light curves, we first selected photometric cluster
nonmembers in the CMD, i.e., objects running below the lower envelope of the cluster
sequence, over the range 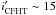 –21 mag. We further selected a
subset of these nonmembers, whose photometric light curves had an rms dispersion lower
than the median photometric error at a given brightness. Of this subset, we retained only
those with light curves having at least 800 measurements from CFHT and Maidanak, thus
yielding a sampling rate similar to those of the h Per members analyzed above. This
procedure resulted in a sample of 1065 light curves for non- (or low-)variable field
stars.
–21 mag. We further selected a
subset of these nonmembers, whose photometric light curves had an rms dispersion lower
than the median photometric error at a given brightness. Of this subset, we retained only
those with light curves having at least 800 measurements from CFHT and Maidanak, thus
yielding a sampling rate similar to those of the h Per members analyzed above. This
procedure resulted in a sample of 1065 light curves for non- (or low-)variable field
stars.
To these light curves we then added a sinusoidal signal, with a log-uniform distribution of periods in the range 0.2–20 d and of amplitudes from 0.002 to 0.02 mag, and random phases. The resulting light curves were subjected to exactly the same period search analysis as described above for the candidate members. After removing spurious periodogram peaks at frequencies around 0.5 and 1.0 d-1, thus leaving 941 synthetic light curves, we retained 592 objects with a FAP less than 0.05 and vizualized their phased light curves. We rejected 50 additional objects based on the large scatter in their phased light curves. We were thus left with 542 periodic object from this subsample, i.e., a global detection rate of 542/1065 = 51%.
Comparing the detected periods to the input periods thus allows us to estimate the period
detection rate as a function of period, amplitude, and brightness, and to assess the
sensitivity of the method to aliases and harmonics. We note that the production of
synthetic periodic light curves has been done by one of the authors, and the search for
periods has been performed by another two authors who ignored the input parameters so as
not to bias the results.The results are shown in Fig. 8. The completeness plot, i.e., the number of detected periods divided by the
number of input periods in a given period bin, indicates that the period detection rate is
relatively uniform over the 0.2–20 d range (Fig. 8,
panel a). Figure 8 (panel b) also indicates that the
period detection rate is quite sensitive to the input amplitude, increasing from about 20%
for amplitudes of 0.002 mag to nearly 80% for amplitudes of 0.02 mag. A sinusoidal fit to
the light curves with detected periods recovers the input amplitudes to within 1.1 mmag
rms. The period detection rate is equally sensitive to the stellar magnitude (Fig. 8, panel c), decreasing from ~80% at
 .5 to a mere 5% at
.5 to a mere 5% at
 5, where the photometric noise
becomes comparable to the injected amplitudes (see Fig. 3). We should stress, however, that for the large surface spots expected for
low-mass stars at the age of h Per, the photometric amplitudes are likely to be larger
than ~0.01 mag, thus alleviating the issue of photometric noise for faint members.
5, where the photometric noise
becomes comparable to the injected amplitudes (see Fig. 3). We should stress, however, that for the large surface spots expected for
low-mass stars at the age of h Per, the photometric amplitudes are likely to be larger
than ~0.01 mag, thus alleviating the issue of photometric noise for faint members.
It is quite noticeable that a large fraction (490/542 = 90%) of the recovered periods agree with the input ones to better than 10% (cf. Fig. 8, panel d). The contamination of the recovered period distribution by incorrect periods is generally small (≤10%), except in the period range around 1 day and from 5 to 11 days. The excess of periods around 1 d mainly results from aliases of longer input periods (7–17 d), while the excess of periods in the range 5–11 d arises partly from harmonics of longer input periods (12–20 d) (cf. Fig. 8, lower panels). This illustrates the fact that the sampling of the light curves is not optimal for the detection of long periods, mostly due to a large gap of about 20 nights in the observing window between the Maidanak and CFHT datasets (cf. Fig. 2). Finally, we note that detected periods with a FAP ≤ 0.01 have a recovery rate of 95%, while those with 0.01 < FAP ≤ 0.05 have a recovery rate of 74% (cf. Fig. 8, lower panels).
The simulations we ran include very small amplitudes and long periods, none of which may be characteristic of such young stars as the 13 Myr-old h Per members. Therefore, the actual period detection rate for h Per members is likely to be significantly larger than what these simulations suggest. To illustrate this, restricting the completeness analysis to input light curves with amplitudes larger than 0.01 mag raises the period detection rate from 51% to 71% and brings the recovery rate to 90% or more for all periods smaller than 10 d. Indeed, what is most important here is not so much to reach a high completeness level but rather to be able to measure reliable periods in an unbiased way over the whole period range between 0.2 d and at least 10 d. The Monte Carlo simulations presented here suggest that the combination of Maidanak and CFHT datasets allows us to derive such a relatively robust and largely unbiased rotational period distribution for h Per members over this period range.
3.3. Rotational contamination by field stars
 |
Fig. 9 Distribution of 40 periods detected in a sample of 1347 field stars shown as a
function of |
The sample of 2287 h Per photometric candidate members we selected for period analysis
includes a fraction of contaminating field stars, as estimated above (cf. Sect. 2.3). To investigate the pollution of the h Per
rotational distribution by unrelated periodic field stars, we selected a control sample of
photometric nonmembers. Among the 45 710 photometric nonmembers, 3169 have at least 800
data points from CFHT and Maidanak in their combined light curve. Of these, 1347 have been
selected in the  CMD as lying in a
locus parallel to the cluster sequence, either above its upper envelope up to 0.7 mag
redder or below the lower envelope down to –0.7 mag bluer. The control sample thus
encompasses a similar magnitude and color range as the sample of h Per photometric
candidate members. We then applied to the control sample the same period analysis as we
did for the photometric members. Sorting the results by decreasing periodogram peak power,
we vizualized the phased light curves to decide on periodic and nonperiodic objects. Over
1347 objects, we retained 40 objects as being periodic. The remaining 1307 nonperiodic
field objects were used to estimate the FAP levels discussed above (cf. Sects. 3.1, 3.2).
CMD as lying in a
locus parallel to the cluster sequence, either above its upper envelope up to 0.7 mag
redder or below the lower envelope down to –0.7 mag bluer. The control sample thus
encompasses a similar magnitude and color range as the sample of h Per photometric
candidate members. We then applied to the control sample the same period analysis as we
did for the photometric members. Sorting the results by decreasing periodogram peak power,
we vizualized the phased light curves to decide on periodic and nonperiodic objects. Over
1347 objects, we retained 40 objects as being periodic. The remaining 1307 nonperiodic
field objects were used to estimate the FAP levels discussed above (cf. Sects. 3.1, 3.2).
The distribution of periods for the control sample is shown in Fig. 9. Periods typically range from 0.4 to 12d over the brightness range 16–21 mag. The shortest periods (P ≤ 1 d) we detect in the control sample probably relate to synchronized field binaries and the longer periods of a few days may pertain to the young stellar population of the galactic field (cf., e.g., Briceno et al. 1997). In any case, the period detection rate is very low for field stars, amounting to a mere 40/1347 = 3%. The photometric contamination of the sample of 2287 h Per candidates by field stars is estimated to be 18.7% (cf. Sect. 2.3), i.e., about 428 field stars are included in this sample of candidate members. We expect to detect a period for 3% of the contaminants, yielding 13 periodic field stars. We thus estimate the contamination of the h Per rotational period distribution by field stars to 13/586, i.e., 2.2% over the mass range 0.3–1.6 M⊙. Furthermore, since the period distribution we obtain for field stars appears relatively uniform in the range 1–13 days, this low level of contamination is unlikely to introduce any significant bias in the period distribution of h Per candidate members. We notice, however, an apparent excess of field stars with periods shorter than 1 d, presumably short period binaries.
3.4. Rotational bias due to synchronized binaries
As synchronized binaries are expected to have a different angular momentum evolution than
detached systems and single stars, we investigated how the former may impact on the period
distribution we derive for h Per candidate members. To this aim, we first identified
photometric binaries in our sample of 2287 h Per candidate members from their location in
the  CMD. In
this diagram, the binary sequence is fairly well separated from the single star sequence
and we defined the empirical boundary as follows:
CMD. In
this diagram, the binary sequence is fairly well separated from the single star sequence
and we defined the empirical boundary as follows: 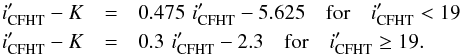 391
objects are redder than this limit and have been classified as binaries.
391
objects are redder than this limit and have been classified as binaries.
 |
Fig. 10 Top panel: distribution of periods as a function of stellar mass for h Per photometric binary candidates (red circles) and for h Per candidate members lying on the cluster’s single-star photometric sequence (blue crosses). Bottom panels: cumulative distribution of periods for photometric binaries and single stars in two mass ranges (left: M ≥ 1.2 M⊙; right: M < 1.2 M⊙). In the two mass bins, there is a clear excess of short period binaries compared to short period single stars (see text). |
Among the 586 periodic h Per candidate members, 142 are identified as photometric binaries. The distribution of periods as a function of mass is shown in Fig. 10 for the subsamples of photometric binaries and of single stars. There is a clear excess of short period binary systems over the whole mass range from 0.3 to 1.5 M⊙, which is particularly conspicuous in the mass range above 1.2 M⊙. The cumulative period distribution of single and binary stars is shown in Fig. 10 in two mass bins on either side of 1.2 M⊙. A KS test indicates that the probability for the binary and single-star period distributions to be drawn from the same distribution is 9 × 10-6 in the higher mass bin and 6 × 10-3 in the lower mass one. Clearly, the excess of short period binaries strongly skews the overall rotational distribution of the h Per candidate members.
Indeed, when removing rapid rotators with P < 1 d from the period distribution, a KS test on the remaining single and binary period distributions indicate they are the same with a probability of 0.77 in the higher mass bin and 0.58 in the lower mass one. This suggests that, unlike synchronized binaries that have a specific rotational evolution due to tidal effects, the components (or at least the primary) of wider binary systems appear to undergo a similar angular momentum evolution as single stars. A similar result was reported for binaries in the Pleiades cluster (Bouvier et al. 1997).
To avoid the bias introduced by synchronized binaries, we thus removed the 79 photometric binaries detected with P < 1 d from the sample of 586 periodic h Per candidate members. Since the period distribution of wider binary systems appears to be statistically similar to that of single stars, we kept them for the following analysis. This left us a sample of 508 h Per candidate members with measured periods over the mass range from 0.3 to 1.5 M⊙, which we could use to investigate stellar rotation at 13 Myr and angular momentum evolution prior to the arrival on the MS.
3.5. Period distribution
The period distribution of h Per candidate members is shown as a function of mass in Fig. 11. It extends widely from ~0.2 to ~12 days at all masses, from ~0.3 to ~1.4 M⊙, and its lower and upper envelopes do not show any clear dependence on mass. We have divided our sample of periodic objects to four mass bins, centered on 0.5, 0.75, 1.0, and 1.25 M⊙, respectively, and plot their distributions in Fig. 12. In each mass bin, most of the periods lie in the range 2–10 d, with a tail of slower rotators extending up to about 20 days and a peak of fast rotators, with periods less than 1 d. This peak is particularly conspicuous at the lowest masses and becomes weaker in the highest mass bin. The fraction of objects rotating faster than two days is 47 ± 8%, 31 ± 6%, 35 ± 7%, and 34 ± 5% from the lowest to the highest mass bin. On a log scale, the period distributions in each mass bin appear somewhat bimodal, especially at low masses again, with a primary peak around 8–10 days and a secondary peak at a fraction of a day. Such bimodal period distributions, albeit on a linear period scale, have previously been reported for young stars in the ONC at 1 Myr, with peaks at 7–9 days and 1–2 days (e.g., Herbst et al. 2001).
 |
Fig. 11 Periods detected for 508 h Per photometric candidate members (excluding
synchronized binaries with period ≤1 d) are shown as a function of stellar mass.
Periods are plotted on a linear scale in the upper panel and on a
log scale in the lower one. On the top panel, the
upper x-axis scale corresponds to
|
 |
Fig. 12 Histograms of the periods of h Per candidate members in four mass bins. From bottom to top: 0.4–0.6 M⊙, 0.6–0.9 M⊙, 0.9–1.1 M⊙, and 1.1–1.4 M⊙. The mass bins contain 90, 123, 103, and 152 periodic h Per candidate members, respectively. The histograms are shown on a linear scale on the left panels and on a logarithmic scale on the right panels. |
 |
Fig. 13 Photometric amplitudes derived from a sinusoidal fit to the periodic light curves
shown as a function of |
KS tests were run to compare the period distribution of each mass bin to the next (i.e., 0.4–0.6 M⊙ vs. 0.6–0.9 M⊙, 0.6–0.9 M⊙ vs. 0.9–1.1 M⊙, and 0.9–1.1 M⊙ vs. 1.1–1.4 M⊙). The probability that the distributions are drawn from the same overall parental distribution is 0.04, 0.17, and 0.33, respectively. Hence, while the period distribution does not seem to depend on mass at an age of 13 Myr above 0.6 M⊙, there is an indication that the 0.4–0.6 M⊙ mass objects rotate faster on average. This is in agreement with the finding of previous studies indicating a larger fraction of fast rotators among the lowest mass stars (e.g., Herbst et al. 2001; Irwin et al. 2007b, 2008a,b).
The photometric amplitudes of the 508 periodic h Per candidate members are plotted as a
function of 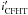 -band
magnitude and period in Fig. 13. The lower envelope
of the photometric amplitude is seen to increase with
-band
magnitude and period in Fig. 13. The lower envelope
of the photometric amplitude is seen to increase with
 -band
magnitude. This trend clearly points to an observational bias, as it is increasingly
difficult to detect lower amplitude variables among fainter objects (cf. Fig. 3). The upper envelope of the photometric amplitude,
however, also appears to increase towards fainter, i.e., lower mass, objects. This
suggests that lower mass stars either have a larger fractional coverage by stellar spots
or that the spot distribution at their surface is more asymmetric than in higher mass
stars, thus leading to a larger contrast along the rotational cycle. No correlation is
found betweeen photometric amplitude and rotational period in Fig. 13. A KS test on photometric amplitudes for stars with periods shorter
and longer than 1 d returns a probability of 0.06 of being drawn from the same
distribution. Hence, a weak trend, if any, might be present with median values of 0.034
and 0.029 mag for the photometric amplitudes of fast and slow rotators, respectively.
Taken together, these results suggest that the origin of increasing maximum photometric
amplitude towards lower mass stars at 13 Myr is not primarily linked to rotation but more
likely related to the internal structure of the PMS objects and possibly to the extent of
their convective zones.
-band
magnitude. This trend clearly points to an observational bias, as it is increasingly
difficult to detect lower amplitude variables among fainter objects (cf. Fig. 3). The upper envelope of the photometric amplitude,
however, also appears to increase towards fainter, i.e., lower mass, objects. This
suggests that lower mass stars either have a larger fractional coverage by stellar spots
or that the spot distribution at their surface is more asymmetric than in higher mass
stars, thus leading to a larger contrast along the rotational cycle. No correlation is
found betweeen photometric amplitude and rotational period in Fig. 13. A KS test on photometric amplitudes for stars with periods shorter
and longer than 1 d returns a probability of 0.06 of being drawn from the same
distribution. Hence, a weak trend, if any, might be present with median values of 0.034
and 0.029 mag for the photometric amplitudes of fast and slow rotators, respectively.
Taken together, these results suggest that the origin of increasing maximum photometric
amplitude towards lower mass stars at 13 Myr is not primarily linked to rotation but more
likely related to the internal structure of the PMS objects and possibly to the extent of
their convective zones.
4. Discussion
4.1. Angular momentum distribution at 13 Myr
At 13 Myr, the accretion process has terminated and the stars are no longer magnetically coupled to their disk (Currie et al. 2007a; Fedele et al. 2010). Measurements of rotational periods in the h Per cluster thus provide the initial angular momentum distribution of freely evolving stars. We computed the specific angular momentum of the 508 stars with known rotational periods assuming uniform rotation, i.e., J/M = I Ω/M, where the stellar moment of inertia I is derived at each mass from Baraffe et al. (1998) 13 Myr models and Ω = 2π/Prot. The resulting distribution of specific stellar angular momenta at 13 Myr is shown as a function of mass in Fig. 14. A large dispersion is observed between log (J/M) ~ 15.7–17.5, with a weak trend for increasing J/M with mass. The lower value of the specific angular momentum of solar-mass stars at 13 Myr ((J/M)min ~ 1016 cm2 s-1) is still about an order of magnitude larger than that of the present-day Sun (J/M = 9.2 × 1014 cm2 s-1, Pinto et al. 2011).
Rebull (2001) and Herbst & Mundt (2005) reported the distribution of specific angular momenta for low-mass stars in the Orion nebula cluster (ONC) and its flanking fields at an age of ~1 Myr. They both find a large dispersion of J/M, with a range of log (J/M) ~ 16.0–17.7 and a peak at log (J/M) ~ 16.5 in Rebull (2001)3, and a range of log (J/M) ~ 16.2–17.5 with a peak at log (J/M) ~ 16.5 in Herbst & Mundt (2005)4. The scatter in J/M in both studies (1.7 and 1.3 dex, respectively) is roughly similar to what we derive (1.8 dex) for the J/M distribution of h Per low-mass members at 13 Myr. However, the peak of the J/M distribution for h Per members (log (J/M) ~ 16.2) appears to be slighty shifted towards lower values. The decrease of the specific angular momentum of low-mass stars between ~1 and 13 Myr presumably reflects angular momentum loss due to the star-disk interaction during the early PMS (Rebull et al. 2004).
 |
Fig. 14 Specific angular momentum (cm2 s-1) of 508 periodic h Per candidate members shown as a function of mass in the upper panel. The ratio of their angular velocity to the break-up velocity (ωcrit = (GM)1/2R−3/2) is shown as a function of mass in the lower panel. |
Figure 14 also shows the ratio of angular velocity to critical velocity, ω/ωcrit as a function of mass for the 508 periodic h Per candidate members. For a few stars (including HPer-215 and HPer-513; see Sect. 3.1), this ratio exceeds unity, suggesting that the photometric period could reflect either pulsation or orbital motion instead of rotation. The distribution is strongly peaked at ω ≤ 0.1ωcrit, with a median value of 0.048 and a tail extending up to ω ~ 0.5ωcrit. Of the 508 periodic members, 492 (97%) have ω ≤ 0.5ωcrit. No evidence for a mass dependence is found, except perhaps at masses larger than 1.1 M⊙, where the lower envelope of the ω/ωcrit distribution may slightly increase. The range and shape of the ω/ωcrit distribution we derive for low-mass stars at 13 Myr is qualitatively similar to that reported for similar stars in the ONC cluster at an age of 1 Myr (Stassun et al. 2001). When projected to the ZAMS assuming no angular momentum loss, i.e., ω/ωcrit ∝ I-1R1.5, the ω/ωcrit ratio increases by a factor of 1.4 to 2.3 over the mass range 0.4–1.4 M⊙. The projected distribution on the ZAMS has a median value of ω/ωcrit ~ 0.1, and 80 stars (16%) have ω > 0.5ωcrit, including 15 stars with ω/ωcrit ≥ 1. This suggests that some angular momentum loss must occur during the late PMS evolution, an issue to which we return in the next section.
4.2. Angular momentum evolution to the ZAMS
The derivation of hundreds of rotational periods for low-mass stars in the 13 Myr-old h Per cluster provides a new time step to investigate PMS angular momentum evolution. This time step, which was not previously covered by other cluster studies (e.g., Irwin & Bouvier 2009; Messina et al. 2010, 2011), is particularly interesting as it marks the end of the PMS disk accretion process. Disk accretion is thought to be largely terminated by 10 Myr (Kennedy & Kenyon 2009; Fedele et al. 2010), leaving at most a few per cent of stars still actively accreting from their disk in h Per (Currie et al. 2007c). The “disk-locking process” by which stars are prevented from spinning up during their early PMS evolution is therefore over for most of the h Per low-mass population. These stars are thus expected to freely spin up as they contract towards the ZAMS, which they eventually reach at an age of 22, 33, 66, and 100 Myr for a mass of 1.2, 1.0, 0.7, and 0.5 M⊙, respectively. The rotational distribution of h Per members is thus particularly suited to investigate stellar spin-up at the end of PMS evolution and on the approach to the ZAMS.
 |
Fig. 15 Period versus mass distributions for clusters with an age ranging from 4 to 150 Myr. The clusters’ name and age are given in each panel. Red dotted lines are drawn at periods of 0.2 and 10 days to guide the eye. References: Cep OB3b: Littlefair et al. (2010); NGC 2362: Irwin et al. (2008a); NGC 2547: Irwin et al. (2008b); Pleiades: Hartman et al. (2010); M 50: Irwin et al. (2009); NGC 2516: Irwin et al. (2007b); M35: Meibom et al. (2009). |
Figure 15 compares the rotational distribution of h Per members with those of solar-type and lower mass members of various open clusters over the age range from 5 to 150 Myr. At all ages, a significant scatter is seen in the rotational period distributions, which cannot be accounted for by observational errors but reflects a true dispersion of rotation rates during the PMS. In these period-mass plots, both early-PMS and ZAMS clusters exhibit some similarities with h Per but also striking differences. The upper envelope of the period distribution, located at ~10 days in h Per, does not appear to evolve much between 5 and 40 Myr over the mass range from 0.4 to 0.9 M⊙. This suggests that at least a fraction of slow rotators are prevented from spinning up over this timescale. By the age of the Pleiades (125 Myr), the upper envelope of the distribution has decreased towards faster rotation for masses larger than 0.7 M⊙. A significant fraction of lower mass stars, even at this age, still exhibits long periods, suggesting that the pre-ZAMS spin-up is more efficient for solar-mass than for low-mass stars.
In contrast, the lower envelope of the period distribution exhibits quite a drastic evolution from 5 Myr to the ZAMS. In h Per, the lower envelope appears rather flat over the mass range 0.4–1.1 M⊙ at a period of ~0.2–0.3 d. In younger clusters, the minimum period seems to strongly depend on mass, ranging from ~0.4–0.5 d at 0.4–0.6 M⊙ to 1.0 d or more for solar-type stars. This provides good evidence for PMS spin-up for the fast rotators between 5 and 13 Myr. While the mass sampling and period statistics are unfortunately sparser in NGC 2547, its 40 Myr-old rotational distribution does not show any clear evolution for the fastest rotators between 13 and 40 Myr over the mass range 0.4–0.8 M⊙. From 13 to 130 Myr, however, the fastest rotators in the 0.8–1.1 M⊙ mass range have been spun down, presumably upon their arrival on the ZAMS, while lower mass stars down to 0.4 M⊙ still exhibit the same maximum rotation rate of ~0.3 d. The most striking difference between the 13 Myr-old h Per cluster and ZAMS clusters at an age of 125–150 Myr is the lack of mass dependency in the rotational distribution of the former, while the latter exhibit a narrow rotation-mass relationship for masses larger than about 0.7 M⊙. Indeed, the largest scatter of rotation rates over the investigated mass range is observed for the 13 Myr-old h Per cluster, which is at the end of the PMS accretion phase. This result supports the role of disk accretion in establishing the initial dispersion of stellar angular momentum in low-mass stars (Bouvier et al. 1993; Rebull et al. 2004).
 |
Fig. 16 Histograms of period distributions in three mass bins for clusters with an age ranging from 4 to 150 Myr. The clusters’ name and age are given in each panel. Left: 0.4–0.6 M⊙, Middle: 0.6–0.9 M⊙, Right: 0.9–1.1 M⊙. The number of stars in each mass bin is indicated in the lower left corner of the panels. |
Stellar moment of inertia (I/I⊙).
A more detailed comparison of the rotational distributions at four time steps between the early PMS and the ZAMS is provided in Fig. 16 for three mass bins centered at 0.5, 0.75, and 1.0 M⊙, respectively. We do not consider here stars in the mass range 1.1–1.4 M⊙ as their rotational period distributions are still missing for most young open clusters. To improve statistics and smooth out any dependence of rotation on environment (cf. Littlefair et al. 2010), the two 4–5 Myr clusters have been merged, as have been the four clusters in the age range 125–150 Myr. The temporal evolution of these distributions can now be compared to the expected PMS spin-up in the absence of angular momentum loss. Table 4.2 lists the evolution of the stellar moment of inertia resulting from the star’s contraction and the development of a radiative core. In all three mass bins considered here, the reduction of the moment of inertia would translate into a spin-up by a factor of ~2 from 5 to 13 Myr, and by a factor of ~2.5 from 13 to 40 Myr. The observed distributions do suggest some PMS spin-up between 5 and 13 Myr in all mass bins, with the bulk of fast rotators (P < 2 d) shifting towards shorter periods, as expected from the evolution of the stellar structure. The evolution of the fast rotators is less clear from 13 to 40 Myr. This is partly due to the small statistics affecting the distribution of NGC 2547 in the 0.4–0.6 M⊙ mass range, although in the better sampled 0.6–0.9 M⊙ range, little evolution is observed for fast rotators, contrary to model expectations. Unfortunately, no data exist for NGC 2547 solar-type stars and only a few rotational periods have been published in the 0.9–1.1 M⊙ range (Messina et al. 2011). Slow rotators (P ≥ 2 d) as a whole do not appear to spin up as much as fast ones. In the 0.6–0.9 M⊙ range, the peak of the slow rotator distribution varies from ~7.5 d at 5 Myr, to ~6.5 d at 13 Myr, and to ~5.5d at 40 Myr, i.e., much less than the reduction of the stellar moment of inertia would imply. Similar conclusions are reached for the other mass bins. Clearly, some angular momentum loss must occur in at least a fraction of slow rotators over the 5–40 Myr age range to compensate for the spin-up due to contraction.
Angular momentum model parameters.
While the rotational distributions of fast and slow rotators provide some clues to the angular momentum evolution of PMS stars, the complete distributions have to be modeled to understand the processes at play. We therefore computed angular momentum evolution models starting from the observed 5 Myr rotational distributions as initial conditions and evolved them at ages of 13, 40, and 130 Myr to compare with observations. The models assume all stars are released from their disk at 5 Myr and therefore do not include any “disk-locking” process after this age. Angular momentum loss due to stellar winds are included in the way described in Irwin & Bouvier (2009). Core-envelope decoupling is also included in the model through the introduction of a coupling timescale τc over which angular momentum is exchanged between the radiative core and the convective envelope (Allain 1998). Previous modeling efforts suggest that τc is significantly shorter for rapid rotators than for slow ones (Bouvier 1997; Irwin et al. 2007b; Bouvier 2008; Irwin & Bouvier 2009; Denissenkov et al. 2010; Spada et al. 2011). We illustrate here three classes of models: solid-body rotation models (τc = 1 Myr), decoupled models with a constant coupling timescale (τc = 50–100 Myr), and a velocity-dependent coupling model with τc = τc0 (ω/ω⊙)-1 Myr and τc0 = 100–500 Myr. The other parameters of the models, namely, the angular momentum loss scaling and saturation velocity (see Irwin & Bouvier 2009) are summarized in Table 4. Owing to the observed scatter of rotation rates among field stars (Harrison et al. 2012), the models are required to reproduce the angular velocity of the Sun to within 30% for solar-type stars, and up to a factor of 2 lower rotation rates for lower mass stars. In addition, the solar-mass models must comply with heliosismology results, which indicate no residual excess rotation in the radiative core of solar-mass stars by the age of the Sun (Thompson et al. 2003). Stellar evolution models for 0.5, 0.8, and 1.0 M⊙ stars are taken from Baraffe et al. (1998).
The results for solar-mass stars are shown in Fig. 17, where the initial period distribution at 5 Myr is projected forward in time using the three models to ages of 13 and 130 Myr and then compared to the observed distributions at those ages. It is seen that, starting from 5 Myr, the projected distributions at 13 Myr do not depend much of the assumed model. This is because the radiative core only recently developed at this stage and the amount of core-envelope decoupling hardly impacts on the early PMS rotational evolution. Indeed, the projected distributions at 13 Myr encompass the full range of rotational periods observed for solar-mass stars in the h Per cluster. These results support the hypothesis that most of the disk-locking process is over in solar-mass stars by 5–10 Myr (Rebull et al. 2004), which is consistent with current estimates of disk lifetimes (Fedele et al. 2010). Once on the ZAMS, however, significant differences occur between the models. Solid-body rotation models successfully reproduce the fastest ZAMS rotators but fail to account for the bulk of slow rotators in Pleiades-like clusters. On the opposite, distributions projected with fully decoupled models do yield a population of ZAMS slow rotators but do not exhibit the observed tail of fast rotators. Only the ω-dependent τc model (τc = 100 (ω/ω⊙)-1 Myr) simultaneously accounts for both the peak of slow rotators and the high-velocity tail observed in ZAMS clusters. This confirms the need for a core-envelope coupling timescale that depends upon the rotation rate. As discussed in Bouvier (2008), the different PMS rotational history of slow and fast rotators may leave imprints in the properties of field stars once their angular velocities have converged on the MS, such as an increased Li dispersion (e.g., Pasquini et al. 1997).
 |
Fig. 17 Initial distribution of periods at 5 Myr (top panels) for 0.9–1.1 M⊙ stars projected to 13 Myr (middle panels) and 130 Myr (bottom panels) using three models: strong core-envelope coupling (τc = 1 Myr, left panels), weak core-envelope coupling (τc = 100 Myr, middle panels), and a velocity-dependent coupling timescale (τc = 100 (ω/ω⊙)-1 Myr, right panels). The observed distributions are shown as black shaded histograms, the projected ones as red bar histograms. |
We ran a similar analysis for stars in the mass bin 0.6–0.9 M⊙. The results are shown in Fig. 18 and the model parameters are listed in Table 4. Starting from the 5 Myr period distribution, a short coupling timescale between the core and the envelope (τc = 1 Myr) is required to yield fast rotators on the ZAMS, while a much longer coupling timescale (τc = 50 Myr) is needed to account for the slow rotators. The best results are obtained for the solar-mass stars by assuming a rotation-dependent coupling timescale. Figure 18 shows that a model assuming τc = 500 (ω/ω⊙)-1 Myr provides a reasonable description of the observed angular momentum evolution of 0.6–0.9 M⊙ stars from 5 to 130 Myr. A small fraction of ZAMS stars in this mass range, however, have rotational periods longer than ten days and up to ~20 days, which are not accounted for by the model. Assuming these slow rotators result from an extended disk-locking period during the PMS, this suggests that disk lifetimes may exceed 5 Myr for about 7% of stars in this mass range. This result would be consistent with current estimates of accretion disk lifetimes (Fedele et al. 2010).
 |
Fig. 18 Initial distribution of periods at 5 Myr (top panels) for 0.6–0.9 M⊙ stars is projected to 13 and 130 Myr (top to bottom panels) using three models: strong core-envelope coupling (τc = 1 Myr, left panels), weak core-envelope coupling (τc = 50 Myr, middle panels), and a velocity-dependent coupling timescale (τc = 500 (ω/ω⊙)-1 Myr, right panels). The observed distributions are shown as black shaded histograms, the projected ones as red bar histograms. |
 |
Fig. 19 Initial distribution of periods at 5 Myr (top panels) for 0.4–0.6 M⊙ stars projected to 13 and 130 Myr (top to bottom panels) using three models: strong core-envelope coupling (τc = 1 Myr, left panels), weak core-envelope coupling (τc = 50 Myr, middle panels), and a velocity-dependent coupling timescale (τc = 500 (ω/ω⊙)-1 Myr, right panels). The observed distributions are shown as black shaded histograms, the projected ones as red bar histograms. |
Finally, model simulations were run for the lowest mass bin, 0.4–0.6 M⊙. The results are shown in Fig. 19. While a short coupling timescale (τc = 1 Myr) clearly fails to reproduce slow rotators in this mass range on the ZAMS, the observed evolution of the rotational period distributions can be reproduced by assuming either a longer coupling timescale (τc = 50 Myr) for all stars or a rotation-dependent core-envelope coupling (τc = 500 (ω/ω⊙)-1 Myr). This is because, as the convective envelope thickens in the lowest mass bin, surface rotation becomes less sensitive to varying coupling timescales. As in the 0.6–0.9 M⊙ bin, a small fraction (6%) of low-mass stars have rotational periods in excess of ten days on the ZAMS, which may indicate a prolonged star-disk coupling during the early PMS, up to 10 Myr. Alternatively, we cannot exclude that some of these slow rotators, which mostly arise from the M50 cluster study by Irwin et al. (2009), may be slowly rotating field star contaminants.
Applying quantitative statistical analysis, such as two-sided KS tests, indicates that the formal agreement between the observed and model projected rotational distributions is poor. This may result both from shortcomings of the models and from uncertainties in the observed rotational distributions. As for the models, we considered the accretion process to be fully completed by 5 Myr. As discussed above, assuming instead that a small fraction of PMS stars have disk lifetimes in excess of 5 Myr would increase the fraction of slow rotators on the ZAMS and bring the observed and projected distribution in better agreement. The observed distribution themselves may suffer various biases. We have shown in Sect. 3.4 that short-period synchronized binaries significantly impact on the h Per rotational distribution and consequently removed them from the analysis. To our knowledge, synchronized binaries have not been identified and similarly discarded in other studies. Field contaminants in the photometric samples may also affect the rotational distributions by increasing the fraction of slow rotators, with long-period field stars being uncorrectly classified as cluster members. Finally, environmental conditions may play a role in shaping the initial distribution of angular momenta (e.g., Clarke & Bouvier 2000; Littlefair et al. 2010). Such intrinsic cluster-to-cluster differences would undermine a detailed comparison between observed and projected distributions. Given these numerous sources of uncertainty, we believe it is premature to attempt to reproduce the detailed shape of the observed rotational distributions. Instead, we merely aimed here at a qualitative agreement between the observed and modeled distributions by trying to best account for the range of observed rotational periods as a function of age.
5. Conclusions
We have presented the results of an extensive photometric monitoring campaign in the 13 Myr open cluster h Per to look for variability in the I-band. Thanks to the combination of CFHT/MegaCam and Maidanak data, the study is sensitive to periodic variations on timescales of less than 0.2 day to 20 days. A selection of candidate members using empirical isochrones in various CMDs in the optical and the near-infrared found 2287 candidates in the Maidanak camera FOV (18′ × 18′). The field contamination is estimated to be around 18%, according to the Besançon Galactic model.
The light curves of the candidate cluster members were searched for periodic modulations due to stellar rotation, giving 586 detections over the mass range 0.4 ≤ M/M⊙ ≤ 1.4. This provides a statistically large sample with uniform completeness of rotational periods for low mass stars at 13 Myr, a time step that was not covered by previous cluster studies. This age is particularly important to understand the angular momentum evolution prior to the ZAMS since it corresponds to the time when most of the stars have dissipated their disk and start to freely spin up as they contract towards the ZAMS.
The rotation period distribution exhibits a wide dispersion, with most of the measured periods in the range ~0.3 to ~9 days and a few slow rotators around 15 days. We found that photometric binaries skew the distribution towards short periods, especially in the mass range above 1.2 M⊙. We suggest that this is due to the presence of synchronized binaries that have a specific rotational evolution due to tidal fields and should therefore be removed to investigate the angular momentum evolution of single stars. The distribution of the remaining 508 rotational periods (excluding the photometric binaries with a period P < 1 d) does not show any clear dependence on mass. In particular, the upper and lower envelopes (corresponding respectively to slow and fast rotators) is remarkably flat over the whole mass range.
Comparing the rotational period distribution of h Per members to those of low mass stars in other young clusters allowed us to model the angular momentum evolution of low-mass stars during the PMS up to the ZAMS. Models suggest that core-envelope decoupling occurs on a timescale inversely proportional to surface rotation. Furthermore, models indicate that less than 10% of stars may remain coupled to their disk beyond 5 Myr in order to reproduce the spin evolution to the ZAMS, in agreement with current estimates of disk lifetimes.
Online material
Appendix A: Phased light curves of the 586 periodic h Per candidate members
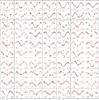 |
Fig. A.1 Phased light curves of periodic h Per candidate members (red dots: CFHT, black dots: Maidanak). The object number is given in each panel (top) as well as the period (in days, bottom left) and amplitude (in magnitude, bottom right). The light curves are ordered by decreasing periodogram peak power. |
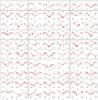 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
Based on the frequency mapping FAMOUS, by F. Mignard, OCA/CNRS, ftp://ftp.obs-nice.fr/pub/mignard/Famous
Rebull (2001) computed angular momenta using I = k2MR2 and assuming a gyration factor k2 of 2/5, which corresponds to a solid-body rotating sphere of uniform density. However, for their sample of fully convective stars, the correct gyration factor is 0.205 (polytrope n = 1.5, Horedt 2004). We therefore reduced Rebull’s J/M value by a factor of 2 to compare with ours.
Herbst & Mundt (2005) computed the specific angular momentum of the surface shell of ONC stars and used a gyration factor k2 ~ 2/3. Here we calculated J/M for the whole star and used k2 = 0.205, assuming that the star is fully convective and rotates as a solid body, and neglecting rotational distortion. To compare Herbst & Mundt (2005) results with our study, we therefore reduced their specific angular momentum values by a factor 3.3. This is valid for all stars but the most rapid rotators.
Acknowledgments
The authors thank B. Reipurth for giving us access to his CFHT data; K. Zwintz for the pulsation analysis of the two fast rotators; A. Scholz for useful discussion about fast rotation from synchronized binaries; F. Mignard for help with the FAMOUS program; and A. Robin for the use of the Besançon Galactic Model. We are also grateful to the CFHT QSO team for service observing and to J.-C. Cuillandre for the pre-reduction of CFHT data. This work has been supported by the EGIDE ECONET 1886YF program and by bilateral programs with the Academy of Science in Armenia and Ukraine. J. Bouvier and E. Moraux acknowledge funding from the Agence Nationale de la Recherche grants ANR-2011-Blanc-SIMI5-6-020-01 “Toupies: Towards understanding the spin evolution of stars” (http://ipag.osug.fr/Anr_Toupies/) and ANR-2010-JCJC-0501-1 “DESC: Dynamical Evolution of Stellar Clusters” (http://ipag.osug.fr/~emoraux/DESC) respectively.
References
- Affer, L., Micela, G., Favata, F., Flaccomio, E., & Bouvier, J. 2013, MNRAS, 430, 1433 [NASA ADS] [CrossRef] [Google Scholar]
- Aigrain, S., Hodgkin, S., Irwin, J., et al. 2007, MNRAS, 375, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Allain, S. 1998, A&A, 333, 629 [NASA ADS] [Google Scholar]
- Baraffe, I., Chabrier, G., Allard, F., & Hauschildt, P. H. 1998, A&A, 337, 403 [NASA ADS] [Google Scholar]
- Baran, A. S., Winiarski, M., Krzesiński, J., et al. 2011, Acta Astron., 61, 37 [NASA ADS] [Google Scholar]
- Bidelman, W. P. 1943, ApJ, 98, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Boulade, O., Charlot, X., Abbon, P., et al. 2003, Proc. SPIE, 4841, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Bouvier, J. 1997, Mem. Soc. Astron. Italiana, 68, 881 [Google Scholar]
- Bouvier, J. 2008, A&A, 489, L53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouvier, J., Cabrit, S., Fernandez, M., Martin, E. L., & Matthews, J. M. 1993, A&A, 272, 176 [NASA ADS] [Google Scholar]
- Bouvier, J., Rigaut, F., & Nadeau, D. 1997, A&A, 323, 139 [NASA ADS] [Google Scholar]
- Bragg, A. E., & Kenyon, S. J. 2005, AJ, 130, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Briceno, C., Hartmann, L. W., Stauffer, J. R., et al. 1997, AJ, 113, 740 [NASA ADS] [CrossRef] [Google Scholar]
- Capilla, G., & Fabregat, J. 2002, A&A, 394, 479 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chang, S.-W., Protopapas, P., Kim, D.-W., & Byun, Y.-I. 2013, AJ, 145, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Clarke, C. J., & Bouvier, J. 2000, MNRAS, 319, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Currie, T., Balog, Z., Kenyon, S. J., et al. 2007a, ApJ, 659, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Currie, T., Kenyon, S. J., Rieke, G., Balog, Z., & Bromley, B. C. 2007b, ApJ, 663, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Currie, T., Kenyon, S. J., Balog, Z., Bragg, A., & Tokarz, S. 2007c, ApJ, 669, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Currie, T., Kenyon, S. J., Balog, Z., et al. 2008, ApJ, 672, 558 [Google Scholar]
- Currie, T., Evans, N. R., Spitzbart, B. D., et al. 2009, AJ, 137, 3210 [NASA ADS] [CrossRef] [Google Scholar]
- Currie, T., Hernandez, J., Irwin, J., et al. 2010, ApJS, 186, 191 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Denissenkov, P. A. 2010, ApJ, 719, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Dworetsky, M. M. 1983, MNRAS, 203, 917 [NASA ADS] [Google Scholar]
- Fedele, D., van den Ancker, M. E., Henning, T., Jayawardhana, R., & Oliveira, J. M. 2010, A&A, 510, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallet, F., & Bouvier, J. 2013, A&A, 556, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harrison, T. E., Coughlin, J. L., Ule, N. M., & López-Morales, M. 2012, AJ, 143, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Hartman, J. D., Bakos, G. Á., Kovács, G., & Noyes, R. W. 2010, MNRAS, 408, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Herbst, W., & Mundt, R. 2005, ApJ, 633, 967 [NASA ADS] [CrossRef] [Google Scholar]
- Herbst, W., Bailer-Jones, C. A. L., & Mundt, R. 2001, ApJ, 554, L197 [NASA ADS] [CrossRef] [Google Scholar]
- Horedt, G. P. 2004, Astrophys. Space Sci. Lib., 306 [Google Scholar]
- Horne, J. H., & Baliunas, S. L. 1986, ApJ, 302, 757 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, J., & Bouvier, J. 2009, IAU Symp., 258, 363 [NASA ADS] [Google Scholar]
- Irwin, J., Irwin, M., Aigrain, S., et al. 2007a, MNRAS, 375, 1449 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, J., Hodgkin, S., Aigrain, S., et al. 2007b, MNRAS, 377, 741 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, J., Hodgkin, S., Aigrain, S., et al. 2008a, MNRAS, 384, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, J., Hodgkin, S., Aigrain, S., et al. 2008b, MNRAS, 383, 1588 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, J., Aigrain, S., Bouvier, J., et al. 2009, MNRAS, 392, 1456 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Keller, S. C., Grebel, E. K., Miller, G. J., & Yoss, K. M. 2001, AJ, 122, 248 [NASA ADS] [CrossRef] [Google Scholar]
- Kennedy, G. M., & Kenyon, S. J. 2009, ApJ, 695, 1210 [NASA ADS] [CrossRef] [Google Scholar]
- Littlefair, S. P., Naylor, T., Mayne, N. J., Saunders, E. S., & Jeffries, R. D. 2010, MNRAS, 403, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Mayne, N. J., & Naylor, T. 2008, MNRAS, 386, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Mayne, N. J., Naylor, T., Littlefair, S. P., Saunders, E. S., & Jeffries, R. D. 2007, MNRAS, 375, 1220 [NASA ADS] [CrossRef] [Google Scholar]
- Meibom, S., Mathieu, R. D., & Stassun, K. G. 2009, ApJ, 695, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Meibom, S., Barnes, S. A., Latham, D. W., et al. 2011, ApJ, 733, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Messina, S., Desidera, S., Turatto, M., Lanzafame, A. C., & Guinan, E. F. 2010, A&A, 520, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Messina, S., Desidera, S., Lanzafame, A. C., Turatto, M., & Guinan, E. F. 2011, A&A, 532, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nefs, S. V., Birkby, J. L., Snellen, I. A. G., et al. 2012, MNRAS, 425, 950 [NASA ADS] [CrossRef] [Google Scholar]
- Oosterhoff, P. T. 1937, Annalen van de Sterrewacht te Leiden, 17, A1 [Google Scholar]
- Palla, F., & Baraffe, I. 2005, A&A, 432, L57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pasquini, L., Randich, S., & Pallavicini, R. 1997, A&A, 325, 535 [NASA ADS] [Google Scholar]
- Pinto, R. F., Brun, A. S., Jouve, L., & Grappin, R. 2011, ApJ, 737, 72 [Google Scholar]
- Rebull, L. M. 2001, AJ, 121, 1676 [NASA ADS] [CrossRef] [Google Scholar]
- Rebull, L. M., Wolff, S. C., & Strom, S. E. 2004, AJ, 127, 1029 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, D. H., Lehar, J., & Dreher, J. W. 1987, AJ, 93, 968 [NASA ADS] [CrossRef] [Google Scholar]
- Robin, A. C., Reylé, C., Derrière, S., & Picaud, S. 2003, A&A, 409, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rodríguez-López, C., MacDonald, J., & Moya, A. 2012, MNRAS, 419, L44 [NASA ADS] [CrossRef] [Google Scholar]
- Saesen, S., Carrier, F., Pigulski, A., et al. 2010, A&A, 515, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scargle, J. D. 1982, ApJ, 263, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Schild, R. E. 1965, ApJ, 142, 979 [NASA ADS] [CrossRef] [Google Scholar]
- Siess, L., Dufour, E., & Forestini, M. 2000, A&A, 358, 593 [NASA ADS] [Google Scholar]
- Slesnick, C. L., Hillenbrand, L. A., & Massey, P. 2002, ApJ, 576, 880 [NASA ADS] [CrossRef] [Google Scholar]
- Spada, F., Lanzafame, A. C., Lanza, A. F., Messina, S., & Collier Cameron, A. 2011, MNRAS, 416, 447 [NASA ADS] [Google Scholar]
- Stassun, K. G., Mathieu, R. D., Vrba, F. J., Mazeh, T., & Henden, A. 2001, AJ, 121, 1003 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, M. B. 2005, in Astronomical Data Analysis Software and Systems XIV, eds. P. Stopbell, M. Britto, & R. Ebert, ASP Conf. Ser., 347, 29 [Google Scholar]
- Thompson, M. J., Christensen-Dalsgaard, J., Miesch, M. S., & Toomre, J. 2003, ARA&A, 41, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Trumpler, R. J. 1926, PASP, 38, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Uribe, A., García-Varela, J.-A., Sabogal-Martínez, B.-E., Higuera G., M. A., & Brieva, E. 2002, PASP, 114, 233 [NASA ADS] [CrossRef] [Google Scholar]
- van Maanen, A. 1911, Recherches Astronomiques de l’Observatoire d’Utrecht, 5, 1 [NASA ADS] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Pointings of the various instruments used for this monitoring campaign: CFHT/MegaCam (red square), Maidanak (cyan square), CrAO, Byurakan (white circle). The field of view observed in the optical by Currie et al. (2010; blue rectangles) and in the near-infrared with CFHT/WIRCam by Cardoso et al. (in prep.; yellow square) are also shown. Their photometry is used to assess membership (see Sect. 2.3). |
| In the text | |
 |
Fig. 2 Temporal sampling of photometric measurements obtained at Mt. Maidanak (black open circles), CFHT (blue crosses), CrAO (red dots), and Byurakan (green triangles) observatories. |
| In the text | |
 |
Fig. 3 Plot of rms scatter per data point measured over the CFHT and Maidanak dataset as a
function of |
| In the text | |
 |
Fig. 4
|
| In the text | |
 |
Fig. 5 Photometric contamination level per magnitude bin using the Besançon Galactic model
after selection in both |
| In the text | |
 |
Fig. 6 Distribution of the power of the highest periodogram peak shown as a function of frequency for 2287 h Per photometric candidate members analyzed for periodicity. Spurious periods occurring at frequencies around 0.5 and 1.0 d-1 (shown as blue crosses) were discarded. The FAP levels computed from a control sample of nonperiodic field stars are indicated. The 586 h Per candidate members that were eventually considered as periodic are encircled (red). |
| In the text | |
 |
Fig. 7 Light curves of the 2 h Per candidate members with the shortest photometric periods are shown in the top panels (red: CFHT, black: Maidanak), their frequency spectrum in the middle panels (black: periodogram, red: CLEAN DFT), and their phased light curves in the bottom panels (red: CFHT, black: Maidanak). Left: HPer-215 with a period of 0.06626 d; Right: HPer-513 with a period of 0.09827 d. |
| In the text | |
 |
Fig. 8 Period detection completeness and reliability for sinusoidal signals with amplitudes from 0.002 to 0.02 mag (black histograms) and from 0.01 to 0.02 mag (red dashed histograms). The period detection completeness is shown as a function of period in panel a), photometric amplitude in panel b), and stellar magnitude in panel c). The reliability of the recovered periods is shown in panel d). Reliable periods are defined as those within 10% of the input periods (shown as a function of input period). Contaminating periods are those that differ from the input period by more than 10% (shown as a function of detected period). The lower left and right panels show the estimated periods as a function of the input periods on a linear scale and on log scale, respectively. Periods recovered with a FAP ≤ 0.01 are shown by large (black) triangles, while those with 0.01 < FAP ≤ 0.05 are shown by small (red) circles. The straight lines show the locus of equal periods and factor of 2 harmonics, and the curves show the location of 1 d period aliases. |
| In the text | |
 |
Fig. 9 Distribution of 40 periods detected in a sample of 1347 field stars shown as a
function of |
| In the text | |
 |
Fig. 10 Top panel: distribution of periods as a function of stellar mass for h Per photometric binary candidates (red circles) and for h Per candidate members lying on the cluster’s single-star photometric sequence (blue crosses). Bottom panels: cumulative distribution of periods for photometric binaries and single stars in two mass ranges (left: M ≥ 1.2 M⊙; right: M < 1.2 M⊙). In the two mass bins, there is a clear excess of short period binaries compared to short period single stars (see text). |
| In the text | |
 |
Fig. 11 Periods detected for 508 h Per photometric candidate members (excluding
synchronized binaries with period ≤1 d) are shown as a function of stellar mass.
Periods are plotted on a linear scale in the upper panel and on a
log scale in the lower one. On the top panel, the
upper x-axis scale corresponds to
|
| In the text | |
 |
Fig. 12 Histograms of the periods of h Per candidate members in four mass bins. From bottom to top: 0.4–0.6 M⊙, 0.6–0.9 M⊙, 0.9–1.1 M⊙, and 1.1–1.4 M⊙. The mass bins contain 90, 123, 103, and 152 periodic h Per candidate members, respectively. The histograms are shown on a linear scale on the left panels and on a logarithmic scale on the right panels. |
| In the text | |
 |
Fig. 13 Photometric amplitudes derived from a sinusoidal fit to the periodic light curves
shown as a function of |
| In the text | |
 |
Fig. 14 Specific angular momentum (cm2 s-1) of 508 periodic h Per candidate members shown as a function of mass in the upper panel. The ratio of their angular velocity to the break-up velocity (ωcrit = (GM)1/2R−3/2) is shown as a function of mass in the lower panel. |
| In the text | |
 |
Fig. 15 Period versus mass distributions for clusters with an age ranging from 4 to 150 Myr. The clusters’ name and age are given in each panel. Red dotted lines are drawn at periods of 0.2 and 10 days to guide the eye. References: Cep OB3b: Littlefair et al. (2010); NGC 2362: Irwin et al. (2008a); NGC 2547: Irwin et al. (2008b); Pleiades: Hartman et al. (2010); M 50: Irwin et al. (2009); NGC 2516: Irwin et al. (2007b); M35: Meibom et al. (2009). |
| In the text | |
 |
Fig. 16 Histograms of period distributions in three mass bins for clusters with an age ranging from 4 to 150 Myr. The clusters’ name and age are given in each panel. Left: 0.4–0.6 M⊙, Middle: 0.6–0.9 M⊙, Right: 0.9–1.1 M⊙. The number of stars in each mass bin is indicated in the lower left corner of the panels. |
| In the text | |
 |
Fig. 17 Initial distribution of periods at 5 Myr (top panels) for 0.9–1.1 M⊙ stars projected to 13 Myr (middle panels) and 130 Myr (bottom panels) using three models: strong core-envelope coupling (τc = 1 Myr, left panels), weak core-envelope coupling (τc = 100 Myr, middle panels), and a velocity-dependent coupling timescale (τc = 100 (ω/ω⊙)-1 Myr, right panels). The observed distributions are shown as black shaded histograms, the projected ones as red bar histograms. |
| In the text | |
 |
Fig. 18 Initial distribution of periods at 5 Myr (top panels) for 0.6–0.9 M⊙ stars is projected to 13 and 130 Myr (top to bottom panels) using three models: strong core-envelope coupling (τc = 1 Myr, left panels), weak core-envelope coupling (τc = 50 Myr, middle panels), and a velocity-dependent coupling timescale (τc = 500 (ω/ω⊙)-1 Myr, right panels). The observed distributions are shown as black shaded histograms, the projected ones as red bar histograms. |
| In the text | |
 |
Fig. 19 Initial distribution of periods at 5 Myr (top panels) for 0.4–0.6 M⊙ stars projected to 13 and 130 Myr (top to bottom panels) using three models: strong core-envelope coupling (τc = 1 Myr, left panels), weak core-envelope coupling (τc = 50 Myr, middle panels), and a velocity-dependent coupling timescale (τc = 500 (ω/ω⊙)-1 Myr, right panels). The observed distributions are shown as black shaded histograms, the projected ones as red bar histograms. |
| In the text | |
 |
Fig. A.1 Phased light curves of periodic h Per candidate members (red dots: CFHT, black dots: Maidanak). The object number is given in each panel (top) as well as the period (in days, bottom left) and amplitude (in magnitude, bottom right). The light curves are ordered by decreasing periodogram peak power. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.