| Issue |
A&A
Volume 560, December 2013
|
|
|---|---|---|
| Article Number | A44 | |
| Number of page(s) | 29 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201321109 | |
| Published online | 05 December 2013 | |
Chemical abundances in LMC stellar populations
II. The bar sample⋆,⋆⋆,⋆⋆⋆
1 Observatoire de la Côte d’Azur, CNRS UMR 7293, BP4229, 06304 Nice Cedex 4, France
e-mail: Mathieu.Van-der-Swaelmen@oca.eu; Vanessa.Hill@oca.eu
2 European Southern Observatory, Karl Schwarzschild Str. 2, 85748 Garching b. München, Germany
e-mail: fprimas@eso.org
3 School of Mathematics & Physics, University of Tasmania, Private Bag 37, Hobart, 7001 Tasmania, Australia
e-mail: andrew.cole@utas.edu.au
Received: 15 January 2013
Accepted: 27 March 2013
Aims. This paper compares the chemical evolution of the Large Magellanic Cloud (LMC) to that of the Milky Way (MW) and investigates the relation between the bar and the inner disc of the LMC in the context of the formation of the bar.
Methods. We obtained high-resolution and mid signal-to-noise ratio spectra with FLAMES/GIRAFFE at ESO/VLT and performed a detailed chemical analysis of 106 and 58 LMC field red giant stars (mostly older than 1 Gyr), located in the bar and the disc of the LMC respectively. To validate our stellar parameter determinations and abundance measurement procedures, we performed thorough tests using the well-known mildly metal-poor Milky-Way thick disc giant Arcturus (HD 124897, α Boo). We measured elemental abundances for O, Mg, Si, Ca, Ti (α-elements), Na (light odd element), Sc, V, Cr, Co, Ni, Cu (iron-peak elements), Y, Zr, Ba, La, and Eu (s- and r-elements).
Results. We find that the α-element ratios [Mg/Fe] and [O/Fe] are lower in the LMC than in the MW while the LMC has similar [Si/Fe], [Ca/Fe], and [Ti/Fe] to the MW. As for the heavy elements, [Ba,La/Eu] exhibit a strong increase with increasing metallicity starting from [Fe/H] ≈ -0.8 dex, and the LMC has lower [Y + Zr/Ba + La] ratios than the MW. Cu is almost constant over all metallicities and about 0.5 dex lower in the LMC than in the MW. The LMC bar and inner disc exhibit differences in their [α/ Fe] (slightly larger scatter for the bar in the metallicity range [−1, −0.5]), their Eu (the bar trend is above the disc trend for [Fe/H] ≥ -0.5 dex), their Y and Zr, their Na and their V (offset between the bar and the disc distributions).
Conclusions. Our results show that the chemical history of the LMC experienced a strong contribution from type Ia supernovae as well as a strong s-process enrichment from metal-poor AGB winds. Massive stars made a smaller contribution to the chemical enrichment compared to the MW. The observed differences between the bar and the disc speak in favour of an episode of enhanced star formation a few Gyr ago, occurring in the central parts of the LMC and leading to the formation of the bar. This is in agreement with recently derived star formation histories.
Key words: stars: abundances / Magellanic Clouds / galaxies: abundances / galaxies: evolution
Full Tables 3, 5, 7, 9, 11 and abundances tables for the LMC bar and disc samples are only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/560/A44
Table 11 is also available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
Despite decades of intensive observational and theoretical work, we are still far from a complete and clear understanding of the nearby universe, the MW and its neighbours. Among the satellites of the MW, the Small Magellanic Cloud (SMC) and the LMC are of particular interest since they form the closest example of galaxies in gravitational and hydrodynamical interaction, and therefore constitute a unique laboratory to study the effect of tides and matter exchange on the chemical evolution and star formation history (SFH) of a galaxy.
The LMC is an almost face-on, gas-rich galaxy with regions of active stellar formation located at a distance of 50 kpc (Alves 2004). It has a mass of 1010 M⊙ (van der Marel et al. 2002), intermediate between massive spirals and dwarf galaxies. Because of its bar-like feature embedded in a disc and its single spiral arm, the LMC is classified as a Barred Magellanic Spiral (SBm; de Vaucouleurs & Freeman 1972). The young population exhibits an irregular morphology, likely the stigmata of a very recent interaction with the SMC, while the old and intermediate-age populations are located within a regular disc and a prominent and luminous off-centre bar. However, the morphology of the LMC is not well understood. For instance, the globular cluster (GC) population of the LMC is intriguing since no object of age between 3 and 10 Gyr is found (e.g. Da Costa 1991; Rich et al. 2001); this age gap is not observed in the SMC GC population. We still do not know the origin and the true nature of the asymmetric bar-like structure: is it a dynamical bar driven by disc instabilities like the one found at the centre of the MW or is it a new stellar population? In addition, distance measurements based on Red Clump stars or RR Lyrae variables located in the LMC bar suggest that the bar is about 5 kpc above the disc plane (Haschke et al. 2012a). This feature is also puzzling and difficult to understand: is it a deformation of the LMC disc due to gravitational interaction with the SMC? Another interesting feature is that the bar is off-centre: the centroids of the bar and the disc differ (van der Marel 2001). Zaritsky (2004) showed that these features can be explained by a triaxial stellar bulge embedded in a highly obscuring thin disc: unfortunately, this solution is not completely satisfactory since it requires a strong reddening (or a very inclined disc which has equivalent effect). If this were the case, one would then have to understand the origin of such a stellar bulge (driven by a dynamical instability in the past or similar to early-type bulges?). The Magellanic Bridge, made of gas and stars, connects the LMC and the SMC and is the site of matter exchange between the two Clouds.
Numerous authors (e.g. Besla et al. 2007; Bekki & Chiba 2005; Bekki 2009) have tried to self-consistently reproduce the large- and small-scale structure of the LMC (asymmetric off-centre bar, GC age gap, Magellanic Bridge...) in their dynamical models, taking the interaction with the SMC and/or with the MW into account. However, because of uncertainties on the proper motions (Kallivayalil et al. 2006b,a), we still do not know whether the {LMC+SMC} system is performing its first passage about the MW, or whether the two Magellanic Clouds formed as separate entities and became gravitationally bound later on; a variety of dynamical models have therefore been proposed. For instance, Besla et al. (2012) tested two first infall models: at the beginning, the MC are a binary pair, evolving in isolation until their first passage close to the MW. Their model 2 reproduces most of the morphological and dynamical features. In particular, Besla et al. (2012) explains the asymmetric off-centre bar: as the LMC disc is bar unstable, the bar is present from the beginning; it becomes asymmetric off-centre due to a close encounter of the LMC and SMC a few Myr ago. On the other hand, Smecker-Hane et al. (2002) derived the SFHs for field stars located in the LMC bar and the inner part of the disc from deep colour-magnitude diagram (CMD). They show that the SFH of the bar and the inner disc were similar at old epochs (between 7 and 14 Gyr); but while the SFR of the inner disc has remained rather constant, the bar experienced a dramatic increase SFR between 4 to 6 Gyr ago. Thus, the SFH supports the scenario of a new burst of stellar formation at the centre of the LMC, which could lead to the appearance of the bar-like structure.
Kinematic and chemical tagging of stellar populations is a powerful tool to help reconstruct the past history of a given galactic environment. Pompéia et al. (2008) provided for the first time a detailed chemical analysis of a large sample of LMC red giant branch (RGB) stars located in the LMC disc, ~2 degrees south of the LMC bar, hereafter the inner disc. Lapenna et al. (2012) measured the [α/Fe] of 89 stars in a field close to the LMC GC NGC 1786, some 3 ° north-west of the bar. The present work aims at bringing new light on the nature of the bar: to this end, we provide a detailed chemical tagging of a large sample of LMC bar RGB stars and compare the elemental trends to the reanalysed trends of the inner disc. Section 2 describes the sample selection and the data reduction. Sections 3 and 4 explain the stellar parameter and abundance measurement methods. Section 5 provides the results and their interpretation. Section 6 summarises the main results of this work.
2. Observations and data reduction
2.1. Sample selection
Cole et al. (2005) observed 373 RGB stars in the field of the LMC bar and derived radial velocities and metallicities from low-resolution infrared Ca ii triplet spectra. We used their metallicity distribution to select 113 RGB stars (the maximum number we could accommodate in a single multi-object fibre configuration of FLAMES) belonging to the LMC bar, taking care to sample as evenly as possible the whole metallicity range from [Fe/H] CaT =−1.69 dex to [Fe/H] CaT = 0.14 dex. Because metal-poor stars ([Fe/H] ≤ -1.0 dex) are rare, a random selection would not provide many metal-poor stars; hence this metallicity pre-selection is a necessary precaution to trace the early epochs of the LMC history (represented in the low-metallicity tail of the distribution). Figure 1 shows the location of the 373 stars from Cole et al. (2005) and our 113 targets on a I, (V − I) CMD and the metallicity distribution function of these two samples. We obtained high resolution spectra of our 113 stars at ESO/VLT with the FLAMES/GIRAFFE multifibre spectrograph (Pasquini et al. 2002). In order to measure numerous elemental abundances, we used three setups HR11 (λcentral = 572.8 nm, Rλcentral ≃ 24 200), HR13 (λcentral = 627.3 nm, Rλcentral ≃ 22 500) and HR14 (λcentral = 651.5 nm, Rλcentral ≃ 17 740)1, covering a total of ≈1000 Å. The spectra thus cover lines belonging to the α (Ca, O, Mg, Ti, Si), iron-peak (Sc, V, Cr, Co, Ni, Cu), s-process and r-process elements (Ba, La, Zr, Y, Eu). Thanks to the MEDUSA mode of the GIRAFFE spectrograph up to 135 objects can be observed simultaneously in a single exposure. For our purposes, around 10 to 20 fibres were allocated to sky positions and the other remaining fibres were devoted to the observation of LMC bar stars. In addition, three hot (O-B type) stars in the LMC were allocated to fibres, to allow an accurate correction for telluric absorption lines.
 |
Fig. 1 Colour–magnitude diagram (left panel) and metallicity distribution (right panel) of Cole et al. (2005) RGB sample (green) and our selected RGB stars (red). V and I magnitudes are from the OGLE catalogue Udalski et al. (1997, 2000); Szymanski (2005) for the samples of Cole et al. (2005) and the present paper, while black dots in the CMD are photometric data from Zaritsky et al. (2004) catalogue. Metallicities in the right panel are those derived from the infrared Ca ii triplet index by Cole et al. (2005). |
2.2. Data reduction
We carried out the data reduction with the help of the ESO GIRAFFE pipeline (built upon the Geneva GIRAFFE pipeline described in Blecha et al. 2000), part of the esorex framework2. The reduction steps include the bias and dark current correction, wavelength calibration (using a Th-Ar lamp), spectrum extraction and flat fielding. As the pipeline does not support sky subtraction nor radial velocity correction, we carried out those operations separately.
Sky subtraction.
We visually ranked the sky spectra according to their quality and discarded those showing the lowest signal-to-noise ratio (S/N) or spectral contamination like jumps in flux due to scattered light (stellar light, CCD glow, simultaneous calibration lamp) or a CCD defect. After this quality selection, we ended up with a handful of sky spectra (at least five to eight) in most cases. The selected sky spectra were averaged with k-σ clipping rejection and the resulting master-sky was subtracted from each stellar spectrum (see Fig. 2). This procedure was repeated for each observation of the 113 bar stars and for each setup.
 |
Fig. 2 Top panel: example of raw spectrum (blue) for star 05244301-6943412 and the corresponding master-sky (black) we used to obtain the sky-subtracted spectrum (red). In the red spectrum sky emission lines have been correctly removed. A cosmic ray remains at ~ 6290 Å. Bottom panel: the sky-subtracted spectrum of 05244301-6943412 before (red) and after (blue) the correction for the telluric lines. The spectrum of the fast rotator is plotted in black to show the position of telluric features. The green spectrum is the co-added spectrum: the σ-clipping has removed the remaining cosmic rays and the signal-to-noise ratio is clearly improved compared to the single exposure. All spectra are plotted in the same scale, except for the fast rotator spectrum (it has been scaled for legibility). |
Correction of telluric absorption band around 6300 Å.
Among the two oxygen lines (at 6300 Å and 6363 Å) that are available in the optical wavelength range, the first is the strongest line and is more appropriate for abundance measurements. Unfortunately, it is in a region contaminated by atmospheric spectral features (from 6270 Å to 6330 Å). To measure abundance reliably, it is mandatory to correct for the telluric lines. Three hot stars were observed simultaneously to our science targets for that purpose: 05235121-6934233, 05235885-6952357, 05242945-6937236. We inspected the spectra of the three stars. As the star 05235885-6952357 showed the broadest stellar spectral features (highest rotation) and the highest S/N, we used its spectrum for a telluric correction: in the wavelength region [6270 Å,6330 Å], we divided our individual stellar spectra by the hot star spectrum. We checked that no discontinuities were introduced (see Fig. 2).
Radial velocity measurements and correction.
We obtained multiple observations of the same star in a given setup: 10 exposures with HR11, 5 exposures with HR13 and 4 exposures with HR14, which represents a total of more than 2000 spectra. Table 1 lists the observations, the dates and the total exposure times. We wrote a cross-correlation routine using our own Gaussian masks (continuum with discrete Gaussian absorption profiles centred at the position of particular stellar lines) to perform the radial velocity measurement. In order to build Gaussian masks resembling our spectra in terms of stellar parameters (temperature, gravity, metallicity, microturbulent velocity) and spectral resolution, we used a set of our LMC spectra: in each spectrum, we selected a high number (≥30) of strong spectral features (iron, calcium... lines), fitted them with a Gaussian profile, computed an average absorption line profile, and then built a mask for each setup. The cross-correlation routine returned the radial velocity in the Earth frame; to correct it for the Earth motion and obtain the barycentric velocity υrad, we used the MIDAS task barycor. Using a k-σ clipping rejection (over the radial velocity) allowed us to point out suspicious spectra requiring a special investigation, and we discarded them if justified (e.g. low S/N leading to a poor determination of the radial velocity). For instance, in the setup HR14, for the star 05231321-6946382, we measured four radial velocities: 270.2 km s-1, 270.3 km s-1, 270.5 km s-1 and 275.4 km s-1; based on the above procedure, we flagged the observation leading to a velocity of 275.4 km s-1. As the poor S/N (~2) explains the disagreement, we discarded this observation. We only excluded a few spectra with this test. Figure 3 shows an example of a cross-correlation function and the parabolic fit used to determine the radial velocity.
For each setup, the exposures, the total exposure times and the observation dates are given.
 |
Fig. 3 Left panel: example of cross-correlation function (black line) and its Gaussian fit (red thick line). Right panel: zoom in on the maximum of the cross-correlation function and its parabolic fit (red thick line). We first used a Gaussian fit to locate the position of the maximum and then defined a smaller velocity range (Gaussian fit FWHM) and computed the cross-correlation function over a finer grid to improve the determination of the radial velocity. |
Stars showing a disagreement in their mean radial velocities from one setup to another.
Radial velocities of LMC bar stars. 2MASS identifiers, υrad, σ(υrad), number of independent measurements and S/N for each setup, final mean υrad and its error.
In order to detect any systematic effect (from one setup to the other) or possible variations of the radial velocity, we computed a mean barycentric radial velocity for each star in each setup. For a given setup s, we used the Ns estimates to compute the mean radial velocity vrad,s. As the setup HR11 provides the highest number of exposures, the standard deviation of the radial velocity distribution is better defined in this setup; we therefore employed it to estimate the precision of a single velocity measurement by computing the mean of the standard deviations over the sample, finding a value of 0.6 km s-1. For each setup s, we compute the standard error of the mean radial velocity per setup vrad,s as 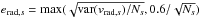 . We performed a T-test to compare vrad,HR11, vrad,HR13, and vrad,HR14, taken two by two:
. We performed a T-test to compare vrad,HR11, vrad,HR13, and vrad,HR14, taken two by two:
-
H0: the two mean radial velocities are equal
-
H1: they are different; significance level: 1%
-
hypothesis of equal variance.
For 103 stars (91% of the sample), we conclude that the three mean radial velocities are equal at the significance level of 1%. For those stars, the radial velocity measurements in the various setups are remarkably similar (rms in parenthesis): ⟨vrad,HR11 − vrad,HR13⟩ = −0.1 km s-1 (0.6 km s-1), ⟨vrad,HR11 − vrad,HR14⟩ = 0.3 km s-1 (0.7 km s-1) and ⟨vrad,HR13 − vrad,HR14⟩ = 0.4 km s-1 (0.3 km s-1). For the 10 stars reported in Table 2 however, at least one of the three T-tests failed. We remark that for all reported cases, the radial velocities measured for HR13 and HR14 agree rather well, while the radial velocity measured for HR11 is discrepant with the two others. The stars 05240482-6948280, 05254540-6940531, and 05224448-6954402 show the most dramatic disagreement with differences of about 8, 17, 18 km s-1 (respectively) between HR11 and HR13 or between HR11 and HR14. The mean epoch and time span of the observations for each setup are given in the last columns of the Table 2: the observations in HR13 and HR14 were run at similar epochs (for HR13, more than two months separate the first and the last observation, which explains the large values of standard deviations observed for this setup for stars with a variable υrad) while those in HR11 were carried out two years later. The discrepancies between setups for those stars therefore reveal a true radial velocity variation, most probably due to an internal stellar variability or a binary system. Figure 4 displays the radial velocity curves for the five stars with the most extreme variations. The period of variation seems to be large, which is expected for giant stars.
 |
Fig. 4 Radial velocity curves for six stars. The relative radial velocities vrad,s − ⟨vrad,s⟩ determined for each exposure are plotted as a function of MJD for five stars where the T-test failed and we suspect a variability in the radial velocity. The curves were shifted for legibility (the dashed line represents the offset). The bottom curve (star 05223082-6944147) is a star with no radial velocity variability and shown here for reference. In red: HR11, in green: HR13, in blue: HR14 (for HR13 data and HR14 data obtained at the same epoch, the green crosses are below the blue ones). Error bars are smaller than the symbols (≤ 1 km s-1). |
Table 3 provides the weighted mean radial velocity defined by ⟨υrad⟩ = ∑ sωsvrad,s, where the sum is over the three setups s and ωs = (erad,s2)-1/ ∑ s(erad,s2)-1, together with the associated error defined by 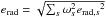 . The typical error on the final radial velocity is ~0.16 km s-1. Figure 5 shows the distribution of the radial velocities in the LMC bar; the mean of the ⟨υrad⟩ distribution is 261 km s-1 and the standard deviation of the distribution is 25 km s-1, in good agreement with values reported in Cole et al. (2005) (257 km s-1, σ =24.7 km s-1).
. The typical error on the final radial velocity is ~0.16 km s-1. Figure 5 shows the distribution of the radial velocities in the LMC bar; the mean of the ⟨υrad⟩ distribution is 261 km s-1 and the standard deviation of the distribution is 25 km s-1, in good agreement with values reported in Cole et al. (2005) (257 km s-1, σ =24.7 km s-1).
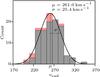 |
Fig. 5 Distribution of the radial velocities of the LMC bar stars. The histogram overplotted in red denotes the stars for which we suspect a radial velocity variability. The mean and the standard deviation of the distribution are respectively 261 km s-1 and 25 km s-1. A Gaussian curve (μ;σ) is plotted over the histogram. |
Values of S/N corresponding to the qualifiers high (best 10% of the sample), median, and low (worst 10% of the sample).
Co-addition and S/Nratio.
To compute the S/Nratio, we used the error spectrum produced by the ESO GIRAFFE pipeline, so that the S/Nratio at pixel i is given by SNRi = fluxi/ errori (actually, this estimator of the S/Nratio underestimates the S/Nratio because the errors are overestimated in the GIRAFFE pipeline; but it is still a good index to compare the quality of a spectrum to another). Before co-adding multiple exposures, we selected the spectra according to their median S/Nratio, requiring it to be higher than ~3. Some observations were taken with the old FLAMES CCD, affected by the so-called glow (polluting light in one corner of the CCD); when necessary, we removed the part of the spectrum altered by this extra source of light. Some observations were obtained with the simultaneous calibration (simcal) lamp turned on: the light of a Th-Ar lamp feeds 5 MEDUSA fibres and allows for small corrections to the wavelength calibration. However, some well-known strong emission lines of the Th-Ar gas leak and contaminate the stellar light of the ~5 science fibres adjacent to a given simcal fibre; we removed these wavelength regions when needed. Once all exposures of the same star were in the same velocity frame, we averaged them with k-σ clipping rejection (over the fluxes at a given wavelength) to clean for cosmic rays and increase S/Nratio. We ended up with a typical final S/Nratio of around 25 for HR11, 40 for HR13 and 48 for HR14. Table 4 lists the typical lowest, median and highest values of S/Nratio as well as an empirically corrected S/Nratio (see Sect. 2.3).
2.3. Arcturus as a benchmark star
To control any systematic effect that could hamper the comparison of our derived abundances to literature measurements, we have tested and applied our methods to the well-known mildly metal-poor Milky-Way thick disc giant Arcturus (HD 124 897, α Boo). Indeed, well-known stars such as the Sun, or the giant stars μLeo or Arcturus are often chosen (e.g., Ramírez et al. 2009; Meléndez et al. 2009; Lecureur et al. 2007; Worley et al. 2009; Alves-Brito et al. 2010) as reference stars for differential analysis, since the literature is broad and provides a good knowledge of their stellar parameters and atmospheric chemical composition (from independent and less model-dependent methods). Arcturus, with Teff = 4286 K, log g = 1.66 and [Fe/H] = -0.52 dex (Ramírez & Allende Prieto 2011, and see references therein), is very similar to the stars of our LMC sample, hence the choice of this star as a benchmark for our sample.
We sliced the Hinkle et al. (2000) spectral atlas of Arcturus (high resolution R ~ 150 000, high S/N~1000) into three pieces to simulate an HR11 (550 nm to 589 nm), an HR13 (609 nm to 641 nm) and an HR14 (629 nm to 671 nm) spectrum. We then degraded the resolution (according to the setup, see Sect. 2.1) and sampling of these spectra to reach a best quality spectrum for each setup (referred to as {low-resolution, low sampling, ∞S/N} in the following). We finally added Gaussian noise according to the typical noise encountered in our LMC sample for each setup, to match four assumptions of S/Nratio: an ∞S/N, which is the original quality of the Hinkle et al. (2000) atlas; a high S/N, which corresponds to the median of the ninth decile of the S/Nratio distribution (the best 10% of the sample); a median S/N, which corresponds to the ~median of the S/Nratio distribution; a low S/N, which corresponds to the median of the first decile of the S/Nratio distribution (the worst 10% of the sample).
As mentioned in Sect. 2.2, the S/Nratio computed from the GIRAFFE pipeline products (as the ratio of the flux over its propagated error) is not accurate and likely underestimated. In order to empirically find a correspondence between the measured S/N and the genuine S/N, we employed the automated tool DAOSPEC (Stetson & Pancino 2008), designed to measure equivalent width (EW): when it performs this task, the software splits the input spectrum S into a fitted continuum component Cf and a fitted line component Lf and returns a number σresidual called “relative flux dispersion in residual spectrum”, which is the dispersion (expressed in percentage) of | Si − (Cfi + Lfi) | /Cfi (where i is the pixel index). Therefore, σresidual depends on the S/Nratio with an observed dependence as shown in Fig. 6. For each setup and S/Nratio regime (low, median or high) observed in our LMC spectra, we investigated various values of σnoise2 until the σresidual matched the targeted S/Nratio. Table 4 gives for each setup, the values of S/Nratio (measured and corrected values) corresponding to the qualifiers high, median, and low.
Photometry and Cat metallicity of LMC bar stars. 2MASS identifiers, V, 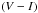 ,
, 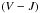 ,
, 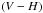 and
and 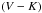 (Udalski et al. 1997, 2000; Szymanski 2005) and [Fe/H] CaT (Cole et al. 2005).
(Udalski et al. 1997, 2000; Szymanski 2005) and [Fe/H] CaT (Cole et al. 2005).
Mean difference between the four photometric scales and standard deviation.
 |
Fig. 6 σresidual vs. S/N. Black solid line: we measured σresidual of the Arcturus HR13 spectrum for different values of artificially added noise σnoise2 = (S/N)-2. Red dots: LMC HR13 spectra. For Arcturus with artificial noise, σresidual ≃ 2 when S/N ≃ 55 while for our LMC spectra, σresidual ≃ 2 when S/N ≃ 40. |
Thus we added a Gaussian noise (with zero-mean and variance σnoise2 = (S/N∗)-2) to the three {low-resolution, low sampling, ∞S/N} spectra according to S/Nratio values listed in Table 4. We drew 101 realisations for each high, median and low S/Nratio version of the Arcturus spectra. In the following, we will employ the single ∞S/N, the 101 high S/N, the 101 median S/N, and the 101 low S/N spectra when we determine the stellar parameters (Sect. 3) and when we measure the chemical abundances (Sect. 4).
3. Stellar parameters
To derive the stellar parameters of our LMC stars (the temperature Tphot, the gravity log g, the overall metallicity [M/H] and the microturbulent velocity ξmicro), we used a combination of photometric and spectroscopic methods. We used our set of Arcturus spectra to assess our iterative procedure and estimate the errors on [M/H] and ξmicro.
3.1. Photometric temperature Tphot
For our stars, visible (V and I magnitude, from the OGLE catalogue, Udalski et al. 1997, 2000; Szymanski 2005) and infrared (J, H and K magnitude, from the 2MASS catalogue Skrutskie et al. 2006) photometry is available. Table 5 gives the V magnitude, the four colour indices we used and the CaT metallicity index for our LMC bar stars. We used the Ramírez & Meléndez (2005a,b) photometric calibrations for giants (the calibrations are functions of the colour index and the [Fe/H]; they are available for our photometric systems, so no conversion of magnitude from one photometric system to another is needed) to compute four scales of photometric temperatures, using the de-reddened  ,
, 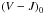 ,
, 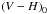 and
and 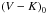 colour indices. Table 6 shows that the agreement between the four photometric temperature scales is very good with a mean difference always smaller than 100 K (in absolute value), therefore we simply averaged the four estimates to derive our final Tphot.
colour indices. Table 6 shows that the agreement between the four photometric temperature scales is very good with a mean difference always smaller than 100 K (in absolute value), therefore we simply averaged the four estimates to derive our final Tphot.
The photometric calibrations are subject to, at least, four sources of uncertainty: the dispersion σcalib of the calibration relation itself, the uncertainty σcolour of the two magnitudes combined to form the colour index, the uncertainty σ(E(B − V)) of the reddening E(B − V), and the uncertainty σ( [Fe/H] ) of the [Fe/H] ratio. The dispersion of the calibration relations can be taken from Ramírez & Meléndez (2005b, their Table 3); they are smaller than 50 K and account for less than 20 K in the error on the final temperature (for the colour indices we used in this study). The errors on the magnitudes were taken from the OGLE and 2MASS catalogues. The typical error is of the order of 0.05 mag, and the error on the colour index translates in a typical error of ~35 K on the final mean Tphot. We used the Ca ii triplet (CaT) metallicity from Cole et al. (2005) as the initial estimator of the [Fe/H] ratio. Although the CaT metallicity is not a very precise estimator of [Fe/H] (mean error of ~0.20 dex), the calibrations are not very sensitive to this parameter (typical error of <5 K on the final mean Tphot). For the reddening, we used E(B − V) = 0.14 mag and a conservative error σ(E(B − V)) = 0.07 mag (see Sect. 3.5). It results in a typical error on the final mean Tphot of the order of 130 K. Among the four sources of uncertainty denoted above, the reddening is the least constrained quantity and accounts for most of the final error on the final mean temperature. After propagating all the errors, we end up with a typical error on the mean photometric temperature Tphot of about 150 K.
Stellar parameters of LMC bar stars. 2MASS identifiers, Tphot, log g, [M/H], ξmicro, [Fe i/ H], [Fe ii/ H].
3.2. Surface gravity log g
The surface gravities log g were derived using the Bayesian estimation algorithm of stellar parameters of da Silva et al. (2006), based on evolutionary tracks3. The required input parameters (and their associated errors) are: the effective temperature, [Fe/H], the dereddened V magnitude V0, and the parallax πLMC. We assumed a constant SFR and an initial mass function from Chabrier (2001). We used the photometric temperature as the effective temperature, and the CaT metallicity index as an initial guess of [Fe/H]. The V magnitude was taken from the OGLE catalogue, and was dereddened using the reddening value defined above. The parallax of the LMC was set to (20 ± 1) × 10-6 arcsec which corresponds to a distance modulus of (18.5 ± 0.1) mag (Alves 2004). The typical error on log g returned by the method is of the order of 0.16 dex.
3.3. Overall metallicity [M/H] and microturbulent velocity ξmicro
The overall metallicity and the microturbulent velocity were derived simultaneously by requiring that different Fe i lines of different EW give the same iron abundance [Fe i/ H]. We used the automated tool DAOSPEC (Stetson & Pancino 2008) to measure the EW and their associated error, and we used the grid of OSMARCS model atmospheres4 (Gustafsson et al. 2008) together with the spectrum synthesis code turbospectrum (turbospectrum is described in Alvarez & Plez 1998 and has been improved along the years by B. Plez) to convert the EW into abundances. Since our stars are giants, atmosphere models and radiative transfer were both in spherical geometry. We built the atmosphere model for a given set of stellar parameters by interpolation onto the OSMARCS grid with the interpolation routine written by Masseron (2006).
The iterative procedure is as follows:
-
1.
for a given set of stellar parameters{ Tphot,log g, ξmicro, [M/H] }, abundances of around 45 Fe i lines are derived from their EW;
-
2.
the mean [Fe i/ H] is computed and compared to the input metallicity; if |⟨[Fe i/ H] ⟩ − [M/H] | > 0.01 dex, then the global metallicity is updated ([M/H] ← ⟨ [Fe i/ H]⟩) and we go back to step 1. If the convergence is not reached after 10 iterations, we release the previous criterion and increase the threshold by 0.01 dex;
-
3.
the linear regression of [Fe i/ H] vs. EW′ is made, where EW′ is the reduced equivalent width (log EW/λ). As previously noted, the errors on the EW are given by DAOSPEC and are turned into errors on [Fe i/ H] abundances by turbospectrum. There is no analytical solution to the problem of linear regression with errors on both coordinates, so various recipes exist to answer this question. In our case, the errors of the EW (explanatory variable) and the abundances (dependent variable) are correlated because we used the former to derive the latter. In order to handle the errors on both coordinates as properly as possible, we used a linear regression algorithm based on bootstrapping, as it turns out that the low statistics (number of Fe i lines) dominate the uncertainty on the slope of the regression.
This procedure is repeated for each value of ξmicro in the range { 1.0,1.1,...,2.5 } (km s-1). We then selected the set of parameters which gives a minimum slope, smaller than its error (in absolute value). The estimate of the error on the metallicity [M/H] and the microturbulent velocity ξmicro is not a straightforward task and a method is proposed in Sect. 3.4.
Table 7 gives the final stellar parameters for our LMC bar stars. For the stars 05223316-6951389, 05225632-6942269, 05225980-6954368, 05224240-6940567, 05232554-6943388, 05244301-6943412, 05253235-6943137, the procedure did not converge towards a satisfactory solution. Figure 7 (left panel) shows the location of the LMC bar stars in the Hertzsprung-Russel diagram.
 |
Fig. 7 Location of the LMC bar (left panel) and disc (right panel) stars in the Hertzsprung-Russel diagram. Legend: blue: -2 dex ≤ [Fe i/ H] ≤ -1.3 dex, cyan: -1.3 dex ≤ [Fe i/ H] ≤ -1.0 dex, green: -1.0 dex ≤ [Fe i/ H] ≤ -0.8 dex, yellow: -0.8 dex ≤ [Fe i/ H] ≤ -0.6 dex, magenta: -0.6 dex ≤ [Fe i/ H] ≤ -0.4 dex, red: -0.4 dex ≤ [Fe i/ H] ≤ 0.0 dex. |
3.4. Arcturus
Our set of Arcturus spectra served as a test of our iterative procedure giving the overall metallicity [M/H] and the microturbulent velocity ξmicro. To this end, we used the effective temperature and the gravity published by Ramírez & Allende Prieto (2011): Teff = 4286 K (spectral energy distribution fitting) and log g = 1.66 (isochrone fitting). These were kept constant while we applied the iterative procedure described in Sect. 3.3 on the 101 realisations of high, median and low S/N version of the Arcturus spectra. Table 8 gives the mean [M/H], [Fe i/ H], [Fe ii/ H] and ξmicro and the standard deviation around the mean; results for the ∞S/N are also given for reference. As could be anticipated, results differ according to the S/N, but the differences are mild: the lower the S/Nratio, the higher the metallicity (or [Fe i/ H], or [Fe ii/ H]), the higher the difference Δ = [Fe i/ H] − [Fe ii/ H], and the lower the microturbulent velocity. We note that the standard deviation around the mean value increases when the S/Nratio decreases, which is again an expected behaviour. Our procedure tends to lead to lower metallicities and higher microturbulent velocity than the reference values in the literature (in fact, in our procedure, the bias in [Fe i/ H] varies linearly with the bias in ξmicro), although this effect is paradoxically alleviated at the median and low S/N of our LMC sample: Worley et al. (2009) found [Fe i/ H] = -0.6 dex and ξmicro = 1.5 km s-1; Ramírez & Allende Prieto (2011) found [Fe i/ H] = -0.52 dex and ξmicro = 1.74 km s-1.
Mean and standard deviation of the distribution of [M/H], [Fe i/ H], [Fe ii/ H] and ξmicro for the 101 realisations of high, median and low S/N version of the Arcturus spectra.
Standard deviations reported in Table 8 can also be used as an estimator of the (random) error on the determined metallicity and microturbulent velocity in the LMC sample, due to the (random) error on the EW measurements (itself originating in the noise present in the stellar spectra). In the following, we will keep the conservative estimates: σ( [M/H] ) = 0.1 dex and σ(ξmicro) = 0.15 km s-1.
 |
Fig. 8 First and second rows: distribution of a given quantity for our LMC stars assuming E(B − V) = 0.06 mag and E(B − V) = 0.14 mag respectively. Third row: distribution of a given quantity for the 101 median S/N Arcturus spectra. First column: distributions of the slopes ([Fe i/ H]|log (EW/λ)) (spectroscopic criterion used to derive ξmicro). Second column: distributions of the slopes ([Fe i/ H]|χex) (excitation equilibrium). Third column: distribution of the difference Δ(Fe) = [Fe i/ H] − [Fe ii/ H] (ionisation equilibrium). Fourth column: distribution of the sample standard deviation of [Fe i/ H]. |
Stellar parameters of LMC disc stars.
3.5. Choice of the reddening
The mapping of the reddening in the LMC has been a longstanding issue, and depending on the targeted stars and the technique used, different reddenings are derived. Zaritsky et al. (2004) published a reddening map of the LMC based on a colour decomposition. We estimated the reddening for our LMC bar field from their catalogue5. As all of our stars were not studied by Zaritsky et al. (2004) and as individual reddening values are reported to be too uncertain, we extracted all of the Zaritsky et al. (2004) stars located in our field of view (4287 extracted stars for a search radius of 12 ′), and computed a median value of the extinction AV: AV = 0.44 mag, hence a median reddening E(B − V) = AV/ 3.24 ≈ 0.14 mag (Cardelli et al. 1989). This value of reddening is similar to what was found by Udalski et al. (1999) from Red Clump (RC) stars (comparison of the observed and the theoretical RC colour): E(B − V) ≃ 0.13 mag in the bar region. Haschke et al. (2012b) have derived optical reddening maps using two different techniques: RC stars and RR Lyrae (comparison of the apparent and intrinsic colour, the latter being computed from the period and metallicity). They found similar results with the two techniques and their reddening map gives E(B − V) ≃ 0.06 mag and σ(E(B − V)) = 0.05 mag for our bar field. They found good agreement with other works from Subramaniam (2005, RC stars) and Pejcha & Stanek (2009, RR Lyrae). Based on these variations for the reddening in our region, we decided to use a conservative error of 50%, σ(E(B − V)) = 0.07 mag to propagate the errors on our stellar parameters (see Sect. 3), which covers the range of possible reddenings in this field.
To further investigate the most probable reddening for our field, we tested two possible values: E(B − V) = 0.06 mag and E(B − V) = 0.14 mag. The choice of reddening has a strong effect on the photometric temperature scale, a moderate effect on the microturbulent velocity (comparable to the typical error on the parameter), and a small effect on the gravity and overall metallicity (lower than the typical error): ⟨Tphot [E(B − V) = 0.14] − Tphot [E(B − V) = 0.06] ⟩ = 140 K, with a rms of 40 K; ⟨log g [E(B − V) = 0.14] − log g [E(B − V) = 0.06] ⟩ = 0.03, with a rms of 0.07; ⟨[M/H] [E(B − V) = 0.14] − [M/H] [E(B − V) = 0.06] ⟩ = -0.02 dex, with a rms of 0.12 dex; ⟨ξmicro [E(B − V) = 0.14] − ξmicro [E(B − V) = 0.06] ⟩ = 0.17 km s-1, with a rms of 0.13 km s-1. Figure 8 shows the results of the determination of the stellar parameters for the LMC bar stars (first row: E(B − V) = 0.06 mag; second row: E(B − V) = 0.14 mag) and for the median S/N Arcturus spectra (third row). The choice of reddening has a small effect on the distribution of the slopes ([Fe i/ H]|log (EW/λ)) (first column): for E(B − V) = 0.06 mag and 0.14 mag respectively, the medians are −0.008 dex and −0.017 dex, the semi-interquartile ranges are 0.037 dex and 0.030 dex respectively. We note however that the distribution is narrower when the reddening is higher. Similarly, the effect on the distribution of the slopes ([Fe i/ H]|χex) (excitation equilibrium, second column) is also small: the medians are similar in both cases and close to zero (≃-0.023 dex eV-1), but the distribution is narrower when the reddening is higher: the semi-interquartile ranges are 0.023 dex eV-1 and 0.020 dex eV-1 for E(B − V) = 0.06 mag and 0.14 mag respectively. Whatever the assumed reddening, we see that our photometric scales do not deviate dramatically from excitation equilibrium and that the higher reddening value seems to slightly improve the general trends. The largest effect is observed for the ionisation equilibrium: changing the reddening will shift the distribution of the difference Δ(Fe) = [Fe i/ H] − [Fe ii/ H] (ionisation equilibrium, third column). Indeed, the medians are −0.12 dex (over-ionisation) and 0.06 dex (under-ionisation) for E(B − V) = 0.06 mag and 0.14 mag respectively, with similar semi-interquartile ranges of 0.12 dex and 0.11 dex respectively. The last column of Fig. 8 shows that the reddening (thus the temperature) has a small effect on the distribution of the standard deviations of Fe i abundances (though the situation improves slightly for E(B − V) = 0.14 mag: smaller median, less prominent tail in the distribution). Therefore, the change in reddening has negligible effect on the agreement of Fe i lines (when the pipeline has converged). As the high reddening tends to slightly improve the determination of parameters (distribution of slopes are narrower, the departure from the ionisation equilibrium is reduced), we decided to adopt this value.
We checked that results obtained for the 101 median S/N Arcturus spectra share the same properties: the distribution of the slopes ([Fe i/ H]|log (EW/λ)) is centred around zero; the excitation equilibrium is not exactly fulfilled (the median of the distribution is −0.024 dex eV-1, similar to the median of our LMC sample), and we found a small over-ionisation (the median of Δ(Fe) is −0.05 dex).
3.6. Re-analysis of Pompéia et al. (2008) sample
In the following, we will compare our results for the LMC bar to the results for the LMC inner disc published by Pompéia et al. (2008). Pompéia et al. (2008) chemically analysed 59 LMC RGB field stars located in the LMC inner disc, 2° south of the bar. Similar to ours, their spectroscopic data were obtained with FLAMES/GIRAFFE in three setups HR11, HR13 and HR14 (they used an older version of the setup definition, where the resolution was slightly higher than what we used for the bar, at the cost of a slightly smaller wavelength coverage). Therefore, the wavelength coverage, the resolution and the S/N of the Pompéia et al. (2008) sample and ours are nearly identical. In order to remove systematic effects due to differences in the analysis procedures, we re-analysed the 59 stars of the inner disc field and derived a new set of stellar parameters, assuming a reddening E(B − V) = 0.12 mag (computed from Zaritsky et al. (2004) catalogue as for the bar). We found a good agreement, within the error bars, between our newly derived stellar parameters and those of Pompéia et al. (2008): ⟨Tspec,Pompeia − Tphot⟩ = −25 K (rms = 65 K); ⟨log gspec,Pompeia − log g⟩ = −0.13 (rms = 0.14); ⟨[Fe i/ H] Pompeia − [Fe i/ H] ⟩ = -0.06 dex (rms = 0.15 dex); ⟨[Fe ii/ H] Pompeia − [Fe ii/ H] ⟩ = -0.11 dex (rms = 0.17 dex); ⟨ξmicro,Pompeia − ξmicro⟩ = 0.05 km s-1 (rms = 0.22 km s-1). It is remarkable to find such a good agreement between physical quantities (temperature, gravity) derived by different methods (photometry/spectroscopy, isochrone/spectroscopy respectively).
Table 9 gives the final stellar parameters for the LMC disc stars. Compared to Pompéia et al. (2008), our procedure did not converge towards a satisfactory solution for the star 0758. Figure 7 (right panel) shows the location of the LMC disc stars in the Hertzsprung-Russel diagram. In Sect. 4.4, we will use our new set of stellar parameters to re-derive the abundances for the inner disc stars.
3.7. [Fe/H]CaT vs. [Fe/H]spectro
Figure 9 compares for both bar and inner disc fields the [Fe i/ H] ratio derived from high-resolution spectroscopy to the metallicity derived from the infrared Ca ii triplet (CaT) index. The typical error bar on [Fe/H] CaT is 0.1–0.2 dex (Cole et al. 2005), and the typical error bar on [Fe/H] spectro is 0.11 dex (quadratic sum of the typical random and systematic errors on the mean Fe abundance). We see a rather good agreement, within the errors, between the two indices up to [Fe/H] CaT ≈ -0.5 dex; then, for higher [Fe/H] CaT, we have [Fe/H] CaT ≥ [Fe/H] spectro. A possible explanation is that for metal-rich stars the continuum placement in the CaT region becomes difficult and leads to poor abundance determinations. A possible contribution to the discrepancy could also be due to the presence of stars in the 0.8–1.2Gyr age range in the field samples, where the Red Clump magnitude is changing very quickly and few calibrators of the CaT method are available. Based on the trends in the Padova stellar isochrones and with reference to the empirical data in Cole et al. (2004) there might be a bias of order +0.1 dex in the CaT abundances for stars aged ~1 Gyr. Good agreement between CaT metallicities (e.g., Grocholski et al. 2006; Olszewski et al. 1991) and spectroscopic abundances (e.g., Mucciarelli et al. 2008) has been seen for LMC GC with [Fe/H] = −0.4 ± 0.1 and ages around ~2 Gyr. Very few to no LMC GC with abundances [Fe/H] > −0.3 are known, so we have no direct tests of the correspondence between the two methods for LMC stars. For the remainder of this paper we take the spectroscopic [Fe i/ H] to be the true metallicity.
In the metal-poor range, one LMC bar star (05232680-6953109) and four LMC disc stars (0606, 0633, 0699, 1105) have very discrepant [Fe/H] CaT and [Fe/H] spectro (| Δ | ≥ 0.4 dex). Except for disc star 0606, we could not find any anomaly in the stellar parameters determination or the abundance measurements. Star 0606 with [Fe/H] = -2.07 dex has normal α-ratios ([Ca/Fe] = 0.39 dex) but overabundant s- and r-ratios ([Ba/Fe] = 0.57 dex, [La/Fe] = 0.51 dex). This is in agreement with Pompéia et al. (2008) who found [Fe/H] = -1.74 dex, [Ca/Fe] = 0.13 dex (our LMC disc Ca ratios are +0.1 dex higher in the mean, see Sect. 4), [Ba/Fe] = 0.80 dex, [La/Fe] = 0.30 dex. The high fraction of s-process elements in this star could be the sign that it is part of a binary system (the s-process elements would have been transferred from a former AGB companion).
 |
Fig. 9 Comparison of [Fe/H] CaT and [Fe/H] spectro. Δ( [Fe/H] ) = [Fe/H] CaT − [Fe/H] spectro vs. [Fe/H] CaT. Legend: black filled circles: LMC bar; blue open pentagons: LMC disc. |
4. Abundance analysis
4.1. Abundance measurements
Methods.
We used both equivalent widths and fitting of absorption profiles to measure elemental abundances. As mentioned in Sect. 3.3, we used DAOSPEC to measure the EW. We converted EW into abundances, and computed synthetic spectra with turbospectrum (in spherical geometry, with LTE spherical radiative transfer) together with the grid of OSMARCS spherical model atmospheres.
The fitting of absorption profiles consists of computing a grid of theoretical spectra by varying the abundance of an element, and searching the grid for the best fit to an observed absorption line of the element. We set up the following procedure:
-
1.
For a given absorption line ℒ of an element X, with a central wavelength λ0, we define a small wavelength interval I in which the profile fitting is performed. The interval is defined by the compromise between three contradictory requirements: covering as many pixels as possible, avoiding neighbouring lines and including continuum on both sides of the line. The typical width of the wavelength interval considered ranges from 3 to 5 Å.
-
2.
We compute a grid of theoretical spectra by varying the abundance ratio [X/Fe]6 with turbospectrum, from −1 dex up to 1 dex, by increments of 0.1 dex. We compute the spectra over a wavelength range centred on λ0 and convolve them with a Gaussian profile to take the combined effects of rotation, macroturbulence, and instrumental response into account.
-
3.
We normalise the theoretical spectra and the observed spectrum in the same way and then compute the quantity:
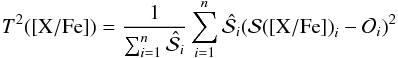 where i is the pixel index, n is the number of pixel in the interval I,
where i is the pixel index, n is the number of pixel in the interval I, 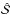 is the (normalised) theoretical spectrum without the element X,
is the (normalised) theoretical spectrum without the element X, 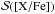 is the (normalised) theoretical spectrum for a given value of [X/Fe], and
is the (normalised) theoretical spectrum for a given value of [X/Fe], and 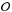 is the (normalised) observed spectrum.
is the (normalised) observed spectrum. 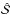 allows the weighting of each pixel by its contamination: if the flux at pixel i is only due to the absorption by the element X, then
allows the weighting of each pixel by its contamination: if the flux at pixel i is only due to the absorption by the element X, then 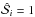 ; if the flux at pixel i is the result of the absorption by the element X and by one or more other chemical entities, then
; if the flux at pixel i is the result of the absorption by the element X and by one or more other chemical entities, then 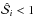 . Therefore, the more contaminated, the less it counts in T2( [X/Fe]).
. Therefore, the more contaminated, the less it counts in T2( [X/Fe]). -
4.
T2 is (generally) a convex function of [X/Fe]; the position of the minimum
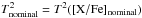 gives us the best-fit abundance [X/Fe] nominal. T2( [X/Fe]) is not a genuine χ2 since we do not divide the quadratic difference
gives us the best-fit abundance [X/Fe] nominal. T2( [X/Fe]) is not a genuine χ2 since we do not divide the quadratic difference 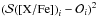 by the error at pixel i (the errors returned by the pipeline do not take the correlation into account) but we can still use it to find the best fit.
by the error at pixel i (the errors returned by the pipeline do not take the correlation into account) but we can still use it to find the best fit. -
5.
The last step aims at accepting or rejecting the solution. Once again, as T2( [X/Fe]) is not a genuine χ2, we cannot apply usual statistics theorems, and for instance, we cannot check the goodness of fit. Therefore, to decide whether the solution has to be rejected, we checked the shape of the T2 curve according to simple geometric criteria. Indeed, the shape of the T2 curve is not accidental and reveals the curve of growth of the measured line. For instance, a saturated line is likely to produce a very open curve; a weak line is likely to produce a curve with a well defined minimum, but with a left branch that becomes flat for the smallest abundance; the mismatch between the synthetic and observed spectrum will influence the value of
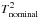 . So it is easier to work with the normalised T2 given by
. So it is easier to work with the normalised T2 given by 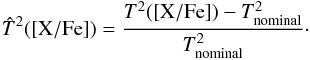 Non-detection: as we cover a broad abundance range ([X/Fe] varies from −1 to +1 dex), we expect (in general) a strong variation of T2 over this interval. A flat T2 curve (or at least, if the curve has a completely flat left branch) is the symptom of a non-detection of the line. If the line is very weak, then the profile of the absorption line will slightly change from one abundance point of the grid to the next, at least as long as [X/Fe] is small (say
Non-detection: as we cover a broad abundance range ([X/Fe] varies from −1 to +1 dex), we expect (in general) a strong variation of T2 over this interval. A flat T2 curve (or at least, if the curve has a completely flat left branch) is the symptom of a non-detection of the line. If the line is very weak, then the profile of the absorption line will slightly change from one abundance point of the grid to the next, at least as long as [X/Fe] is small (say 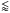 –0.3 dex). Therefore,
–0.3 dex). Therefore,  , thus T2( [X/Fe] ) ≈ cst. For larger abundances, the line appears in the synthesis and T2 (or
, thus T2( [X/Fe] ) ≈ cst. For larger abundances, the line appears in the synthesis and T2 (or  ) steeply increases. We can detect a flat left (right) branch with this criterion:
) steeply increases. We can detect a flat left (right) branch with this criterion: 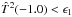 (
(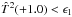 , respectively). We empirically fixed ϵ1 to 4.0. In other words, we require T2 to be five times as high as
, respectively). We empirically fixed ϵ1 to 4.0. In other words, we require T2 to be five times as high as 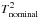 at the grid border for the solution to be meaningful. It may happen that the nominal abundance is close to the grid edge; thus the left (right) branch will not be complete and the solution will be mistakenly rejected. In such cases, we checked the local symmetry of the
at the grid border for the solution to be meaningful. It may happen that the nominal abundance is close to the grid edge; thus the left (right) branch will not be complete and the solution will be mistakenly rejected. In such cases, we checked the local symmetry of the 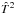 curve around the nominal abundance. If the curve is non-symmetric, the solution is rejected. In the mean, the rejection rate is of about ten lines/star; the rejection is minimum for stars with a metallicity between −1 and −0.5 dex and tends to be higher for metallicities lower than −1.0 dex or larger than −0.5 dex.
curve around the nominal abundance. If the curve is non-symmetric, the solution is rejected. In the mean, the rejection rate is of about ten lines/star; the rejection is minimum for stars with a metallicity between −1 and −0.5 dex and tends to be higher for metallicities lower than −1.0 dex or larger than −0.5 dex.
We used the EW or the fitting of absorption profile depending on the line: if the number of lines was high (≥5), we preferred the EW; if only few lines were available or if a blend was present or if the element has a hyperfine structure (hfs), we preferred the fitting of absorption profile.
List of elements.
Because of our broad wavelength coverage, we are in position to measure elemental abundances for 18 elements (the method used, equivalent width (EW) or spectrum synthesis (SS), and the number of available lines are given in parenthesis): O i (SS, 1), Mg i (SS, 3), Si i (EW, 3), Ca i (EW, 13), Ti i (EW, 8), Ti ii (EW, 3), Na i (SS, 4), Sc ii (SS, 6), V i (SS, 12), Cr i (SS, 4), Co i (SS, 3), Ni i (EW, 7), Cu i (SS, 1), Y i (SS, 1), Zr i (SS, 4), Ba ii (SS, 2), La ii (SS, 3), Eu ii (SS, 2). We compiled the atomic line lists from the line database VALD7 (Kupka et al. 1999, 2000); for the measured lines, we used the log gf quoted in Pompéia et al. (2008). We took the hyperfine structure (hfs) for Sc ii into account (Wiese et al. 1966: 5640 Å, 5667 Å, 5669 Å, 6245 Å; Martin et al. 1988: 5657 Å, 6604 Å), V i (Martin et al. 1988: 6119 Å, 6135 Å, 6150 Å, 6199 Å, 6224 Å, 6274 Å, 6285 Å, 6292 Å, 6357 Å, 6452 Å, 6531 Å; Kurucz 1988: 6224 Å), Co i (Fuhr et al. 1988: 5647.240 Å, 6117.000 Å, 6282.600 Å), Cu i (Bielski 1975: 5782.127 Å), Ba ii (Rutten 1978: 6496.912 Å; no hfs data for 6141.713 Å), La ii (Lawler et al. 2001a: 6262.287 Å, 6390.477 Å; no hfs data for 6320.430 Å), and Eu ii (Lawler et al. 2001b: 6437.640 Å, 6645.064 Å). We extracted the hfs data from the Kurucz database8 (Kurucz 1995) for Sc, V, Co, and Cu; we computed the hyperfine splitting for Ba, La and Eu using the published hyperfine constants. As our stars are cool (Tphot ~ 4500 K), molecules in the stellar atmospheres produce absorption bands in the stellar spectra: we included the molecular line lists of 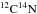 ,
, 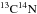 (Plez, priv. comm.) and TiO (Plez 1998) in the spectrum synthesis. We consider the solar composition from Grevesse & Sauval (1998). For all our LMC stars, we fixed the carbon and nitrogen abundances: [C/Fe] = -0.65 dex and [N/Fe] = 0.3 dex (values derived from Smith et al. 2002). Knowing [C/Fe] and [N/Fe] is necessary for the CN and CO equilibria. The CO equilibrium has an effect on the derived O abundance. If we assume [C/Fe] = 0. and [N/Fe] = 0. instead of [C/Fe] = −0.65 and [N/Fe] = + 0.3, then in the mean, [O/Fe] is increased by 0.09 dex (rms of the difference = 0.04 dex). However, we estimated [C/Fe] and [N/Fe] ratios from measurements in LMC RGB stars (Smith et al. 2002), i.e. stars in the same evolutionary stage as ours. Therefore, we do not expect an error of 0.3 or 0.6 dex on [C/Fe] and [N/Fe] respectively, and the corresponding systematic error on [O/Fe] should be much lower than 0.1 dex. The CN equilibrium plays a role in modelling CN lines and some CN lines contribute to blends. For instance, the Ba line at 6496 Å is blended with CN lines. However, the assumption on [C/Fe] and [N/Fe] has a marginal effect on Ba measurements.
(Plez, priv. comm.) and TiO (Plez 1998) in the spectrum synthesis. We consider the solar composition from Grevesse & Sauval (1998). For all our LMC stars, we fixed the carbon and nitrogen abundances: [C/Fe] = -0.65 dex and [N/Fe] = 0.3 dex (values derived from Smith et al. 2002). Knowing [C/Fe] and [N/Fe] is necessary for the CN and CO equilibria. The CO equilibrium has an effect on the derived O abundance. If we assume [C/Fe] = 0. and [N/Fe] = 0. instead of [C/Fe] = −0.65 and [N/Fe] = + 0.3, then in the mean, [O/Fe] is increased by 0.09 dex (rms of the difference = 0.04 dex). However, we estimated [C/Fe] and [N/Fe] ratios from measurements in LMC RGB stars (Smith et al. 2002), i.e. stars in the same evolutionary stage as ours. Therefore, we do not expect an error of 0.3 or 0.6 dex on [C/Fe] and [N/Fe] respectively, and the corresponding systematic error on [O/Fe] should be much lower than 0.1 dex. The CN equilibrium plays a role in modelling CN lines and some CN lines contribute to blends. For instance, the Ba line at 6496 Å is blended with CN lines. However, the assumption on [C/Fe] and [N/Fe] has a marginal effect on Ba measurements.
Calibration of the line lists.
When a line of interest is blended with one arising from another chemical species (atom or molecule), the abundance measurement becomes more difficult. This is most problematic if the absorption profile of the contaminant is poorly predicted (lack of accurate experimental quantum data or reliable theoretical predictions), as is the case for the CN lines. We therefore calibrated a number of CN lines that contaminate crucial lines of Eu, La, Y, Ba, and Zr using Arcturus.
4.2. Arcturus
Hereafter, we will derive the abundances for Arcturus so that it will provide the zeropoint of our abundance scale. In order to have a unique Arcturus atmosphere model for any S/N hypothesis, we chose as stellar parameters Teff = 4286 K, log g = 1.66, [M/H] = -0.65 dex and ξmicro = 1.8 km s-1: the former two are from Ramírez & Allende Prieto (2011) while we determined the latter two in Sect. 3.4 (median S/Nratio hypothesis).
We followed the same procedure described above to derive the abundances from our Arcturus spectra. For the high, median, and low S/N hypotheses, we computed a mean abundance and dispersion (over the 101 realisations) for each individual line of a given element, and then we computed the final mean abundance ratio (over the Nlines) following the procedure described in Sect. 4.3. The error on the individual line abundance (dispersion over the 101 realisations) was propagated when we computed the final mean abundance. We did the same for the ∞S/Nhypothesis (except for the averaging over the realisations); as we have only one realisation for this S/N hypothesis, we used the standard error of the mean as an error estimator (hence the lack of error bar when only one line was used). Table 10 gives the results for the ∞, high, median and low S/N version of the Arcturus spectra as well as the abundance ratios (and their errors) published by Ramírez & Allende Prieto (2011) and Worley et al. (2009).
Elemental abundances, and errors for our ∞, high, median, and low S/N versions of the Arcturus spectra as well as abundance ratios (and their errors) published by Ramírez & Allende Prieto (2011) and Worley et al. (2009).
Chemical differences appeared for two elements: calcium and vanadium. When we first computed [Ca/Fe], we obtained ≈−0.12 dex which is not the expected ratio for a disc star and is very different from the Ramírez & Allende Prieto (2011) and Worley et al. (2009) ratios. The log gf we used had been taken from the NIST9 database and used in Pompéia et al. (2008). We tested two other sets of log gf: the Kurucz log gf gave also ≈−0.12 dex (the Kurucz and the NIST log gf of our Ca i lines are almost equal); the VALD log gf gave ≈0.05 dex, which is closer to the quoted [Ca/Fe]. We decided to keep the VALD log gf (Drozdowski et al. 1988; Smith & Raggett 1981; Smith 1981, 1988) in order to alleviate the disagreement. Vanadium has a hyperfine structure: when we take into account the hfs, [V/Fe] ≈ 0.01 dex, while without the hfs, [V/Fe] ≈ 0.23 dex. The latter value is closer to the value that Ramírez & Allende Prieto (2011) seemingly derived without taking the hyperfine splitting for V into account (we have five V i lines in common). So the hfs seems to explain the disagreement. In the following, we will derive the V ratios with the hfs.
Except for V, our derived elemental ratios are in good agreement within the errors with Ramírez & Allende Prieto (2011) or Worley et al. (2009) and are perfectly understandable if we consider all the possible differences between our study and theirs (stellar parameters, atomic data, method to derive the abundances). We refer the reader to Lebzelter et al. (2012) who offer a broad analysis of the effects of models, input data and procedures on the derived stellar parameters and chemical composition; for instance, differences of up to ~0.3 dex are observed for [Ca/Fe] between the different works.
In our determinations, we note that, in general, when S/N decreases, [X/Fe] slightly decreases (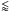 0.05 dex) and the error increases. The generally good agreement for Arcturus between our results and the literature makes us confident of the detailed chemical analysis of our LMC sample. There is no strong bias and we are able to compare directly the abundance trends of the LMC to those of the MW, at all S/Nratios.
0.05 dex) and the error increases. The generally good agreement for Arcturus between our results and the literature makes us confident of the detailed chemical analysis of our LMC sample. There is no strong bias and we are able to compare directly the abundance trends of the LMC to those of the MW, at all S/Nratios.
4.3. Final elemental abundances
Computation of the mean abundance.
As shown in the previous section, for a number of elements, two lines or more are available in the full spectral coverage, and we measured all of them whenever possible.
To combine the abundances from multiple lines, we distinguished three different cases to compute the quantity ⟨[X/Fe]⟩. If Nlines = 1, then the final elemental abundance is simply equal to the single measurement. If 2 ≤ Nlines< 5, then we computed the simple mean of the Nlines measurements. If Nlines ≥ 5, then we applied a 3σ-clipping to remove discrepant measurement, and computed the simple mean of the remaining measurements. The complete abundance table for our LMC bar stars is available at CDS and provides the reader with all abundance ratios and their corresponding random and systematic errors.
Cleaning of the line lists.
We used Arcturus and our LMC stars to study the behaviour of each absorption line. It helped us to identify discrepant lines which were then removed from the abundance analysis. In the end, we discarded a few lines for Ca i (5601 Å, 6162 Å, 6572 Å), Cr i (6362 Å), Co i (6117 Å), Na i (5682 Å), Ni i (6314 Å), Sc ii (5657 Å, 6245 Å), Si i (5665 Å), V i (6119 Å, 6199 Å, 6357 Å, 6452 Å) and Zr i (6140 Å) and updated the computation of the mean abundances accordingly. We decided to keep in our abundance analysis the Ba line at 6141.713 Å (resp. the La line at 6320.430 Å) for which no hfs data is available since we noted a good agreement with the other Ba (resp. La) line, with a difference of 0.2 dex for Ba (resp. 0.1 dex for La) in the mean (over the whole sample) between the line with and without hfs. Table 11 gives the final line list.
4.4. Re-analysis of Pompéia et al. (2008) sample
To derive the abundances for the LMC disc stars, we used the same EW and the same reduced spectra that were used by Pompéia et al. (2008). The differences between their work and ours lie in the stellar parameters and the methods to derive and compute the final abundances. Table 12 gives a comparison of our new abundances for the LMC disc stars and those published in Pompéia et al. (2008). For most of the elements, the agreement between our abundance ratios and those from Pompéia et al. (2008) is good, with a mean difference less than ≈0.15 dex, i.e. of the order of the error. Thus, it is reasonable to attribute the observed differences to the differences in the stellar parameters, and in the measurement of the individual abundances and their combination. For six elements, Mg i, Na i, Sc ii, V i, Y i, and Zr i, the differences are larger. Those elements, as well as Ca i, are discussed below:
-
Mg i: Pompéiaet al. (2008)used the Mg i line at5711 Å while we used in ad-dition two other lines (6318 Åand 6319 Å). If wehad used only the line at 5711 Å, then⟨[Mg/Fe] us − [Mg/Fe] P08⟩ = -0.09 dex (rms = 0.12 dex), instead of −0.22 dex.
Table 12Comparison of our new abundances for the LMC disc stars and those published in Pompéia et al. (2008): mean m and rms s of the distribution of [X/Fe] us − [X/Fe] P08.
-
Ca i: we recall that we changed the log gf of the Ca i lines (see Sect. 4.2). Consequently, all the abundances are shifted by about 0.2 dex. With the old log gf, ⟨[Ca/Fe] us − [Ca/Fe] P08⟩ = -0.08 dex; with the new log gf, ⟨[Ca/Fe] us − [Ca/Fe] P08⟩ = + 0.09 dex.
-
Na i: Pompéia et al. (2008) used four lines and derived the individual abundances from EW while we used only three lines after having discarded the Na i line at 5862 Å (that we found systematically discrepant) and derived the individual abundances from SS. If we had used all four lines, then ⟨[Na/Fe] us − [Na/Fe] P08⟩ = +0.03 dex (rms = 0.18 dex).
-
Sc ii: Pompéia et al. (2008) used only the Sc ii line at 5657 Å instead of four lines and took the hfs into account when deriving the abundance. If we limit ourselves to the line at 5657 Å, then ⟨[Sc/Fe] us − [Sc/Fe] P08⟩ = +0.05 dex (rms = 0.11 dex).
-
V i: as explained in Sect. 4.2, we took the hfs into account in the abundance measurement, while Pompéia et al. (2008) did not. This explains the disagreement.
-
Y i, Zr i: for Y i we used the same line and the same method (fitting of line profile) to derive the abundance as Pompéia et al. (2008) did. For Zr i, Pompéia et al. (2008) used the Zr i line at 6134 Å while we used three lines. But if we restrict the analysis to the same line, we still have ⟨[Zr/Fe] us − [Zr/Fe] P08⟩ = +0.46 dex (rms = 0.21 dex). For those two elements, the lines are weak and difficult to measure. Therefore, the abundance measurement is likely less robust and more sensitive to the method (e.g. the wavelength range where the synthesis is compared to the data, the continuum placement).
In addition, we derived the Eu abundances for the LMC disc stars. The wavelength coverage of Pompéia et al. (2008)’s spectra is not exactly the same as ours since the setup HR14 they used was different. Consequently, the Eu ii line at 6645 Å is not available; but the Eu ii line at 6437 Å is present. Although this line is weaker than the other, we could use it successfully for most of the LMC disc stars. The complete abundance table for our LMC disc stars is available at CDS and provides the reader with all abundance ratios and their corresponding random and systematic errors.
4.5. Error budget
Four main sources of uncertainty exist: uncertainties on the atomic data describing the measured lines, uncertainties due to the modelling of the absorption line, uncertainties on the abundance measurement (for both EW or SS, due to the noise in the fluxes, the continuum placement, the profile integration or profile fitting, and if the line is blended, the hypothesis on the contaminant abundance), and uncertainties on the stellar parameters.
Abundance measurement.
DAOSPEC provides us with an error on the EW, which is obtained during the least-square fit of the line. As mentioned in Stetson & Pancino (2008), this error is not a genuine 1σ confidence interval (e.g., the correlation between the pixels is not taken into account). We checked it using our Arcturus spectra and the set of Fe i lines (51 lines measured which cover a broad range of line strengths and wavelengths). For each S/N hypothesis and for each Fe i line, we computed the sample standard deviation s [EW] of the EW distribution, as well as the mean m [edao(EW)] of the error returned by DAOSPEC . s [EW] is a good estimator of the error on the EW since it encompasses the effect of the noise in the fluxes and the continuum placement. Figure 10 shows the comparison of m [edao(EW)] and s [EW]. There is a fairly good agreement between the two: the mean of (s [EW] − m [edao(EW)]) is −0.18 mÅ, −0.54 mÅ, −0.76 mÅ for the low, median and high S/N respectively; when the Monte-Carlo simulation predicts large errors, DAOSPEC does also; the error decreases when the S/Nratio increases. In the mean, DAOSPEC tends to mildly overestimate the error bar, especially when the S/Nratio gets better. So it is reasonable to use the error computed by DAOSPEC.
Another pitfall is the conversion of the error on the EW into an error on the abundance. Indeed, when we feed turbospectrum with the pair (EW,edao(EW)), it computes the abundances corresponding to EW, and EW ± edao(EW) and often provides asymmetric (right and left) errors. This is not a priori a proper way to find the error on the abundance since the relationship between [X/Fe] ± e( [X/Fe]) and EW ± edao(EW) is not known. We performed similar tests for the abundances as we did for EW in the previous paragraph. For each S/N hypothesis and for each Fe i line, we computed the sample standard deviation s [[Fe/H]] of the [Fe/H] distribution, as well as the mean m [eturbo( [Fe/H])] of the error returned by turbospectrum . Figure 10 shows the comparison of m [eturbo( [Fe/H])] and s [[Fe/H]]. We obtain a similar pattern for the abundances as for the EW: the agreement is fairly good but the errors tend to be mildly overestimated when the S/Nratio increases (though the effect is <0.05 dex at high S/N). Here again, we consider it safe to keep the error returned by turbospectrum (i.e., the mean of the right and left errors).
 |
Fig. 10 Left panel: m [edao(EW)] vs. s [EW]. Right panel: m [eturbo( [Fe/H])] vs. s [[Fe/H]]. Red dots: low S/N; green dots: median S/N; blue dots: high S/N. |
Unfortunately, for the lines measured by absorption line fitting, we cannot use classical theorems to derive an error on the abundance measurement. Indeed, T2 is not a random variable which follows a χ2 distribution since we do not divide each term of the quadratic sum by the error on the flux at pixel i (the GIRAFFE pipeline certainly provides an error for each pixel but it is overestimated and correlated, see Sect. 2.2) and the  are correlated due to the interpolation or rebinning performed during the data reduction. One way to get an estimator of the 1σ error is to do Monte-Carlo simulations. We used the Arcturus spectra to estimate the error eArcturus( [X/Fe]) on each single line (by computing the standard deviation of the abundance distribution) and to assign the error to the LMC stars depending on the S/Nratio category in which they fall.
are correlated due to the interpolation or rebinning performed during the data reduction. One way to get an estimator of the 1σ error is to do Monte-Carlo simulations. We used the Arcturus spectra to estimate the error eArcturus( [X/Fe]) on each single line (by computing the standard deviation of the abundance distribution) and to assign the error to the LMC stars depending on the S/Nratio category in which they fall.
For a given element X, we propagated the errors on the individual lines eturbo( [X/Fe]) or eArcturus( [X/Fe]), which gave us eprop( ⟨ [X/Fe]⟩).
Atomic data and line modelling.
Our capacity to model an absorption line correctly, and thus to measure the abundances accurately, depends on the quality of the atomic data describing the radiative transitions but also on our understanding of the underlying physics. Line lists are often a compilation of various sources aiming at giving the best parameters for a given line, and therefore, the precision of these parameters (among which log gf holds the main role) varies from line to line. The resulting synthetic spectrum is model-dependent (systematic error due to the choice of the grid of model atmospheres, the assumptions on the thermodynamic equilibrium, the atom models) and data-dependent (random error due to the log gf provided by the line lists). The sample dispersion s [[X/Fe]] of the individual abundances about the mean can be used to estimate the combination of these effects (if enough lines are available to estimate it). We derived conservative errors as follows:
To assess our method of error estimation, we compared the standard error of the mean to the propagated error for Ca, Ni, Sc and V. We recall that for these elements, we have enough lines to compute a meaningful variance, and that we derived Ca and Ni abundances from EW and Sc and V abundances from SS. We found a median difference of ~0.02 dex: thus, this check validates the use of eturbo( [X/Fe]) or eArcturus( [X/Fe]) for the individual measurements.
Stellar parameters.
The error eparams on chemical abundances due to the adopted stellar parameters is a thorny question. The four stellar parameters are mutually dependent and changing one of them will imply a change of the others (see McWilliam et al. 1995; Johnson et al. 2006, for a discussion on covariance terms). When the propagation of error is not straightforward, a usual practise is to perturb the explanatory variable (input) by ± its error and to look at the corresponding shift of the dependent variable (output). For the abundances, it would come down to repetition of this procedure for each parameter, keeping the other three constant. The pitfall is to work with a set of parameters that do not satisfactorily describe the atmosphere of the star under study. For instance, when the temperature is changed by, say, 150 K, and { log g, [M/H] ,ξmicro } nominal (which were found for the nominal temperature) are kept, it is likely that the spectroscopic criterion used to find ξmicro does not hold anymore and therefore the determination of abundances from strong lines will not be correct. We followed the prescription from Cayrel et al. (2004): as Tphot has the major effect on the abundance determination, we change it by ± its error and determine the three other stellar parameters corresponding to this new temperature { log g, [M/H] ,ξmicro } ± σ(Tphot); we derive the chemical abundances corresponding to this perturbed solution and compare them to those given by the nominal solution. The final systematic error on [A/B] due to errors on effective temperature is then given by: 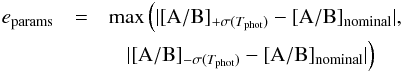 and the total error by:
and the total error by: 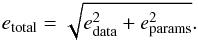 Table 13 gives the typical (i.e. the mean over the sample) edata and eparams (given as [A/B] + σ(Tphot) − [A/B] nominal and [A/B] − σ(Tphot) − [A/B] nominal) for different elemental ratios for our LMC bar stars. In the vast majority of cases, the errors due to stellar parameters dominate over the random measurement errors. Both these sources of error are plotted in Figs. 11–20.
Table 13 gives the typical (i.e. the mean over the sample) edata and eparams (given as [A/B] + σ(Tphot) − [A/B] nominal and [A/B] − σ(Tphot) − [A/B] nominal) for different elemental ratios for our LMC bar stars. In the vast majority of cases, the errors due to stellar parameters dominate over the random measurement errors. Both these sources of error are plotted in Figs. 11–20.
Typical edata and eparams, given as [A/B] − σ(Tphot) − [A/B] nominal and [A/B] + σ(Tphot) − [A/B] nominal, for different elemental ratios for our LMC bar stars.
5. Results and discussion
In this section, we present the results for the key elements: O, Mg, Si, Ca, Ti (α-elements), Na (light odd element), Sc, V, Cr, Co, Ni, Cu (iron-peak elements), Y, Zr, Ba, La and Eu (s- and r-elements). We compare our results for the LMC field stars (bar and inner disc) to LMC GC stars (Johnson et al. 2006; Mucciarelli et al. 2008, 2010), and to the MW stellar populations (thin and thick disc: Bensby et al. 2005; Reddy et al. 2003, 2006; halo: Fulbright 2000; Stephens & Boesgaard 2002; Reddy et al. 2006; Eu and La ratios: Simmerer et al. 2004; Brewer & Carney 2006; O ratios of halo stars: Carretta et al. 2000). Our results for Arcturus are plotted as well to check our abundance scale (Arcturus) versus the literature abundance scales (the MW thick disc compilation).
5.1. α-elements
Figures 11 and 12 show the abundance trends for [O/Fe], [Mg/Fe], [Si/Fe], [Ca/Fe] and [Ti/Fe]. O, Mg, Si, Ca and Ti belong to the α-elements and are used to track the epoch when type II supernovae (SNII) drove the chemical evolution of the galaxy. Indeed, α-elements are formed by successive α captures occurring in the interiors of massive stars, released to the intestellar medium (ISM) by SNII explosions (Burbidge et al. 1957). As iron-peak elements are also processed in massive stars, it results in a constant [α/ Fe] ratio. When type Ia supernovae (SNIa) start to dominate the chemical enrichment and release huge amount of iron-peak elements (Timmes et al. 2003), [α/ Fe] decreases (SNIa efficiently produce iron-peak elements without producing α-elements).
The bottom panel of Fig. 11 shows [α/ Fe] = [O + Mg/2Fe] for the LMC and the MW (when O, Mg ratios were available, we computed [α/ Fe] the same way for the MW). We clearly see that compared to the MW, the LMC exhibits deficient [α/ Fe] for [Fe/H] ≥ -1.3 dex. Those low [α/ Fe] ratios can be explained by a higher contribution of type Ia supernova (SNIa) to the chemical enrichment of the LMC, compared to the MW (e.g. Pagel & Tautvaisiene 1998).
 |
Fig. 11 First row: [O i/ Fe i] vs. [Fe i/ H]. Second row: [Mg i/ Fe i] vs. [Fe i/ H]. Third row: [O i + Mg i/ 2Fe i] vs. [Fe i/ H]. Legend: black filled circles: LMC bar (this work); blue open pentagons: LMC inner disc (this work); green asterisk: Arcturus (this work, data for median S/Nratio); red downward triangle: LMC GC (Johnson et al. 2006; Mucciarelli et al. 2008, 2010); black tiny dots: MW thin and thick disc (Bensby et al. 2005; Reddy et al. 2003, 2006), halo (Fulbright 2000; Stephens & Boesgaard 2002; Reddy et al. 2006), and additional MW data for O from Carretta et al. (2000). Typical random (left) and systematic (right) error bars on both coordinates are provided for our LMC samples. |
 |
Fig. 12 First row: [Si i/ Fe i] vs. [Fe i/ H]. Second row: [Ca i/ Fe i] vs. [Fe i/ H]. Third row: [Ti ii/ Fe i] vs. [Fe i/ H]. Legend: same as Fig. 11. |
 |
Fig. 14 First row: [Ba ii/ Fe i] vs. [Fe i/ H]. Second row: [Ba ii/ Eu ii] vs. [Fe i/ H]. Third row: [La ii/ Fe i] vs. [Fe i/ H]. Fourth row: [La ii/ Eu ii] vs. [Fe i/ H]. Legend: same legend as Fig. 11; additional MW data for Eu and La from Simmerer et al. (2004); Brewer & Carney (2006); horizontal blue dashed line: [Bar/ Eur] = -0.69 dex and [Lar/ Eur] = -0.4 dex (Arlandini et al. 1999); horizontal blue dotted line: [Bar/ Eur] = -0.82 dex and [Lar/ Eur] = -0.59 dex (Sneden et al. 2008). |
 |
Fig. 15 First row: [Y i/ Fe i] vs. [Fe i/ H]. Second row: [Zr i/ Fe i] vs. [Fe i/ H]. Legend: same as Fig. 11. |
 |
Fig. 19 First row: [V i/ Fe i] vs. [Fe i/ H]. Second row: [Cr i/ Fe i] vs. [Fe i/ H]. Third row: [Co i/ Fe i] vs. [Fe i/ H]. Fourth row: [Ni i/ Fe i] vs. [Fe i/ H]. Legend: same as Fig. 11. |
The comparison of the LMC trends to those of the MW shows that the α-elements can be divided in two groups: on one hand, O and Mg, and on the other hand, Si, Ca and Ti. Indeed, the LMC distributions of O and Mg (Fig. 11) are below those of the MW at all metallicities (except for the very most metal-poor stars), while the LMC distribution of Si, Ca and Ti (Fig. 12) completely or partially overlap the MW distributions. Although O, Mg, Si, Ca and Ti are all α-elements, their production efficiency depends on the mass of the type II supernova (SNII) progenitor: while O and Mg are predicted to be mainly produced in very massive SNII progenitors (Woosley & Weaver 1995), Si, Ca and Ti are predicted to be produced in intermediate mass SNII and, in smaller quantity, by SNIa (Tsujimoto et al. 1995; Thielemann et al. 2002). The discrepancy between Galactic and LMC trends for O and Mg is not an artifact of the abundance analysis: for instance, for a 1 dex metallicity bin centred around Arcturus, we have ⟨[O/Fe] LMCBar⟩ = 0.1 dex, ⟨[O/Fe] MWDiscs⟩ = 0.47 dex, [O/Fe] Arcturus = 0.44 dex, hence Δ(MW − LMC) ≈ Δ(Arcturus − LMC) (the same is true for Mg). Therefore, it suggests that the LMC formed high-mass stars less efficiently than the MW.
Our two fields do not exhibit strong differences in their α trends: for O, Mg, Si and Ti, the trends of the bar and the disc overlap at all metallicities. On the other hand, we observe a larger scatter for the bar [α/ Fe] for -0.8 dex ≤ [Fe/H] ≤ -0.4 dex: over this range of metallicities, rms( [α/ Fe] ) = 0.08 dex for the bar, rms( [α/ Fe] ) = 0.05 dex for the disc. According to the age–metallicity relation (Cole et al. 2005), this metallicity range corresponds to ages between 2 Gyr to 6 Gyr ago, thus the suspected epoch of the bar formation. The slight increase of the scatter between the two fields can be understood in the scenario where a new population is formed. Indeed, if the bar is the result of a new population formation, sustained by gas inflow, then the number of massive stars will increase and they will release significant amounts of freshly formed α-elements into the ISM. We should then expect an increase of [α/ Fe] a few Myr after the start of the star burst (Gilmore & Wyse 1991; Tsujimoto et al. 1995; Pagel & Tautvaisiene 1998). In fact, this increase would be too small to be clearly identifiable in our data because of uncertainties in both [Fe/H] and [α/ Fe], but a larger scatter should appear instead of a distinctive bump in the trend. So, if the observed scatter is true, then it supports the scenario of a new stellar population instead of a dynamically-driven bar.
Unlike the MW, the plateau corresponding to the SNII-dominated regime is not clearly visible in the LMC field star distribution. Two possibilities can lead to this: either there is a plateau but it appears at a much lower metallicity, which means that the chemical evolution has been very slow compared to the MW (when the SNIa start to explode in the LMC, the metallicity has reached a lower value than in the MW). Or there is no plateau, which Bekki & Tsujimoto (2012, their Fig. 2) explain by prompt SNIa, for which the onset of SNIa occurs as soon as 100Myr after the formation of the progenitors. Since the lowest metallicity of our samples is only ≈−1.6 dex, we cannot draw firm conclusions about the presence or absence of a plateau in the LMC. However, LMC GCs can also be used to infer the [α/Fe] in the metal-poor regime. Except for O (for which metal-poor LMC GC stars exhibit chemical anomalies due to self-enrichment), there is a good agreement between LMC GC and LMC field stars at both low (-1.5 dex ≤ [Fe/H] ≤ -1.2 dex) and high (-0.5 dex ≤ [Fe/H] ≤ -0.2 dex) metallicity. The metal-poor LMC GC populate the metallicity range [− 2, − 1.2] and line up along a MW-like plateau at low metallicity (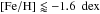 ). Furthermore, Haschke et al. (2012c) also find that extremely metal-poor RR-Lyrae stars in the LMC populate a plateau similar to that of the MW.
). Furthermore, Haschke et al. (2012c) also find that extremely metal-poor RR-Lyrae stars in the LMC populate a plateau similar to that of the MW.
Let us note that Bekki & Tsujimoto (2012) also used prompt SNIa in their models to reproduce the LMC trends of Mg and Ca (based on abundances of LMC field stars and GC stars) and conclude that prompt SNIa have influenced the chemical evolution of the LMC. We remark that to fully explain the low LMC [Ca/Fe], Bekki & Tsujimoto (2012) had to invoke galactic winds which remove Ca more efficiently than the others α-elements, but this may not be necessary with our revised abundances (they used abundance measurements from Pompéia et al. 2008 and our revised abundances are ≈0.1 dex higher).
Finally, we note that Lapenna et al. (2012) have measured O, Mg and Si for 89 stars in a field in the LMC disc (around the GC NGC 1786, some 3 degrees north-west of the bar centre) and found similar trends as ours.
5.2. Heavy elements
Figures 13 to 16 present the elemental distributions for the heavy elements Eu, Y, Zr, Ba, La. Unlike the elements lighter than iron, the heavy elements are produced by neutron captures through s- and r-processes. The naming of the two nucleosynthetic channels refers to the neutron flow: the slow-process (s-process) refers to neutron captures where only a few neutron captures happen before a radioactive β-decay (τcapture>τdecay with τcapture the timescale of a neutron capture event and τdecay the timescale of β-decay) while the rapid-process (r-process) refers to processes where numerous neutron captures occur before a radioactive β-decay (τcapture<τdecay). While it is known that the envelopes of asymptotic giant branch (AGB) stars are the place of the s-process (e.g., Busso et al. 1999), there is no consensus as to where the r-process is made, except that it should be linked to massive stars. The more promising candidates (providing the needed high neutron fluxes) are SNII (Wasserburg et al. 1996), but neutron stars (Freiburghaus et al. 1999) also enter the lists (Qian 2012). Unlike Y, Zr, Ba, and La which can be mainly produced by the s-process (more than 60% in the solar system) with a minor contribution from the r-process (e.g., ≈85% of the solar Ba was produced by the s-process Burris et al. 2000; Sneden et al. 2008), Eu is often considered as a pure r-process element (the r-process contribution to the solar Eu is of 94% according to Arlandini et al. 1999 and 97% according to Sneden et al. 2008).
Europium.
In Fig. 13, we see that the LMC bar and disc Eu distributions agree very well: they both exhibit a constant [Eu/Fe] ≈ 0.5 dex for [Fe/H] ≤ -0.8 dex, then a decreasing trend with increasing metallicity. While for the metal-poor stars the abundance ratios of the LMC and the MW halo overlap, it is clear that for [Fe/H] ≥ -1 dex the LMC trend is above that of MW. This enhancement for metal-rich stars is not an artifact of our analysis since Arcturus has the expected Eu abundance (i.e. it falls on top of the MW thick disc). This is in fact a chemical anomaly already noticed in LMC supergiant stars (Russell & Bessell 1989; Hill et al. 1995) and LMC GC stars (Mucciarelli et al. 2008; Colucci et al. 2012) and its origin still remains unclear. Different mechanisms can help in maintaining a high Eu ratio in late stages of the chemical evolution: (1) new star bursts will form a high number of massive stars which will, in turn, inject fresh Eu in the ISM; (2) another source of r-processed Eu; (3) a stronger contribution of s-processed Eu. Explanation (1) is not supported by the star formation history (SFH) of our two LMC fields (Smecker-Hane et al. 2002): although recent star bursts (about 5 Gyr ago and less than 1 Gyr ago) are expected in the bar, they are not expected in the inner disc; so it cannot explain the high ratios observed in both fields. Moreover, they would produce similar α enhancements, which are not observed. But it can explain the small difference between the LMC bar and disc observed for the most metal-rich stars (above −0.5 dex). Indeed, while the disc [Eu/Fe] still decreases and reaches lower values than the bar, the bar [Eu/Fe] seems to remain constant ([Eu/Fe] ≈ 0.4 dex). (2) or (3) are more likely to explain the differences between the LMC and the MW. The contribution of the s-process to the solar system Eu is estimated to be a few percent (3% according to Sneden et al. 2008) and therefore, it is dubious that the s-process could be responsible for the Eu enhancement. However, in the MW, a particular class of metal-poor stars – carbon enhanced metal-poor (CEMP) stars – exhibits carbon enhancements, understood as the result of a binary interaction with a (now deceased) AGB companion. In addition, CEMP stars are called CEMP-s (respectively CEMP-r/s) stars when they also have s enhancements (respectively r and s enhancements). Several scenarios have been proposed to explain the origin of, e.g., Ba and Eu enhancements in CEMP-r/s stars but they all invoke both s- and r-processes: three mass-transfers in a binary system (see Cohen et al. 2003); two successive mass accretions from a 8–10 M⊙ companion (see Wanajo et al. 2006); pre-r enrichment followed by s-material accretion (see Bisterzo et al. 2012). But Masseron et al. (2010) found a correlation between [Pb/Ba,La,Ce,] and [N/H], and interpreted it as evidence of the operation of the 22Ne(α,n)25Mg chain in the CEMP-r/s companion. As this chain is associated with high neutron density, Masseron et al. (2010) claimed that the Eu enhancement observed today in CEMP-r/s stars is due to the production of Eu via the s-process in the deceased AGB companion, i.e. they invoke a unique site to explain both s- and r-enhancements. In addition, in their study of CEMP-s and CEMP-r/s stars, Allen et al. (2012) found a correlation between [Ba/Fe] and [Eu/Fe] and that [Eu/Fe] is coupled to the degree of C over-abundance, i.e. Eu was produced by the former AGB companion. Consequently, Allen et al. (2012) claim that Ba and Eu have the same origin in CEMP-r/s, i.e. they are produced by the s-process occurring during the AGB phase of the more massive star of a binary system. In essence, the CEMP-r/s stars would be stars polluted by metal-poor AGB with significant Eu production. Thus, those new results and the dominant role played by AGB stars in the chemical evolution of the LMC (see below) support explanation (3).
Barium and lanthanum.
While the MW has constant solar [Ba/Fe] and [La/Fe] ratios (with a weak increase towards high metallicities), both LMC fields exhibit a dramatic increase of [Ba/Fe] and [La/Fe] with increasing metallicity (first and third panels of Fig. 14): the LMC distributions agree with MW halo trends, i.e. for [Fe/H] ≤ -1.0 dex, and are above the MW elsewhere. The bar and disc field distributions overlap for both Ba and La. Ba has the strongest increase, starting from solar value at [Fe/H] = -1.5 dex and reaching 0.8 dex for [Fe/H] ≥ -0.3 dex. La, on the other hand, remains approximately constant from [Fe/H] ≈ -0.7 dex ([La/Fe] ≈ 0.5 dex for the LMC bar and ≈0.4 dex for the LMC disc). Furthermore, there is an excellent match between the LMC field and GC populations. This indicates that the production of Ba and La has been much more efficient in the LMC than in the MW.
To identify the process responsible for this high production, we examine [Ba/Eu] and [La/Eu] in the second and fourth panels of Fig. 14. We see that for LMC GC and field metal-poor stars (from −2.0 dex to -0.8 dex), [Ba,La/Eu] is constant and compatible (within uncertainties) with a pure r-process source (Arlandini et al. 1999: [Bar/ Eur] = -0.69 dex and [Lar/ Eur] = -0.4 dex; Sneden et al. 2008: [Bar/ Eur] = -0.82 dex and [Lar/ Eur] = -0.59 dex). On the other hand, for [Fe/H] ≥ -0.8 dex, the increase of the LMC [Ba,La/Eu] is interpreted as the rise of a new source of Ba and La, i.e. the s-process. The MW exhibits similar patterns (constant ratio at low metallicity, then an increase) but two differences exist with the LMC: first, the increase of [Ba,La/Eu] starts at lower metallicity in the LMC ([Fe/H] ≈ -0.8 dex) than in the MW ([Fe/H] ≈ -0.4 dex), reflecting the slower metal-enrichment in the LMC; secondly, while for the MW, [Ba/Eu] reaches a solar value, for the LMC, [Ba/Eu] reaches a much higher value ([Ba/Eu] ≈ 0.4 dex). This suggests that the production of Ba and La by the s-process has been much more efficient in the LMC than in the MW, and indicates that AGB stars played a stronger role in the chemical enrichment of the LMC compared to the MW.
Yttrium and zirconium.
For [Fe/H] ≤ -1 dex, the LMC bar and disc seem to have a solar Zr ratio (Fig. 15) and a solar Y ratio (at least for the disc field; we do not have enough data points for the bar field). For [Fe/H] > -1 dex, the two LMC fields have a flat Y and Zr distribution with a large scatter but the LMC disc and bar exhibit a different mean behaviour in their Y and Zr trends: in the mean, the bar has higher [Y/Fe] and [Zr/Fe] than the disc (bar: ⟨[Y/Fe] ⟩ = 0.31 dex, ⟨[Zr/Fe] ⟩ = 0.19 dex; disc: ⟨[Y/Fe] ⟩ = -0.04 dex, ⟨[Zr/Fe] ⟩ = -0.08 dex). We checked for possible systematic effects explaining the differences but found none (same kind of stars, same instrument and observing setups, similar data reduction procedure, same procedures to derive stellar parameters and abundances). In particular, we checked whether one of the three Zr lines used could be responsible for the difference. In the mean, each line gives higher Zr abundances for the bar than for the disc: for the bar, ⟨[Zr/Fe] ⟩ = 0.22 dex, 0.20 dex and 0.14 dex; for the disc, ⟨[Zr/Fe] ⟩ = -0.04 dex, 0.0 dex, and −0.14 dex (respectively for the lines at 6127 Å, 6134 Å and 6143 Å). We also looked for possible correlations between the derived abundances and the stellar parameters and found for both fields a clear correlation between [Y,Zr/Fe] and Teff or ξmicro, i.e. increasing abundance ratio with increasing temperature or microturbulence velocity. LMC GC stars of Mucciarelli et al. (2008, 2010) follow the same correlation as ours, and since they have lower temperature than our stars, they have Y and Zr abundances lower than ours. Furthermore, our two samples do not have the same temperature coverage (3900 K to 5200 K for the bar, 3800 K to 4600 K for the inner disc). But if we select only stars in the temperature range [4000,4400], the dispersion slightly decreases in each field, but the two fields remain significantly different: ⟨[Y/Fe] ⟩ = 0.25 dex, ⟨[Zr/Fe] ⟩ = 0.15 dex for the bar, and ⟨[Y/Fe] ⟩ = 0.0 dex, ⟨[Zr/Fe] ⟩ = -0.07 dex for the disc. The typical random error (due to pixel noise) on the final Y or Zr abundances are respectively 0.08 dex and 0.04 dex while the typical systematic error (due to errors on effective temperature) are 0.4 dex and 0.29 dex respectively. Thus, errors can explain the observed scatter but cannot explain the offset between our two LMC populations.
Such a discrepancy is not seen for Ba and La for which the distributions of our two LMC fields agree rather well. Interestingly, Y and Zr belong to the first peak of the s-process, while Ba and La on the other hand belong to the second peak (the positions of the peaks correspond to magic numbers for nuclear stability). The observed differences may be an effect of the metallicity of the AGB stars producing the s-elements because the second peak is favoured when metal-poor AGB stars dominate the chemical enrichment (e.g., Straniero et al. 1997; Gallino et al. 1998; Cristallo et al. 2011). This suggests that AGB stars were more metal-poor in the disc than in the bar of the LMC. We note that the metal-rich LMC GC have [Y/Fe] and [Zr/Fe] clearly lower than those of the LMC bar, and probably similar to the LMC inner disc, which is understandable since their projected locations lie in the LMC disc. Thus, the differences observed between the LMC bar and disc for Y and Zr for 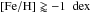 speak in favour of a different chemical evolution path: unlike the disc, the bar experienced a recent episode of stellar formation (a few Gyrs ago) which generated metal-rich AGB that explain the present Y an Zr ratios.
speak in favour of a different chemical evolution path: unlike the disc, the bar experienced a recent episode of stellar formation (a few Gyrs ago) which generated metal-rich AGB that explain the present Y an Zr ratios.
Figure 16 shows [Y + Zr/Ba + La]. We recall that Y and Zr are light-s (ls) elements, while Ba and La are heavy-s elements (hs). Thus the ratio [ls/hs] tracks the relative importance of metal-poor and metal-rich AGB. For 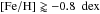 , we know from above that the s-process dominates the chemical enrichment. We remark that the LMC trend is below that of the MW, which suggests that the AGB stars which dominated the LMC enrichment were more metal-poor than those of the MW. While the bar distribution is flat, the disc distribution seems to slightly decrease with increasing metallicity. Colucci et al. (2012) also found a decrease of [Y/Ba] in intermediate-age clusters. This could be a mass effect (in the LMC, metal-poor low-mass AGB stars still contribute significantly to the enrichment) but only a consistent chemical evolution modelling can confirm this explanation. We remark that the match between LMC GC and our LMC fields is again excellent.
, we know from above that the s-process dominates the chemical enrichment. We remark that the LMC trend is below that of the MW, which suggests that the AGB stars which dominated the LMC enrichment were more metal-poor than those of the MW. While the bar distribution is flat, the disc distribution seems to slightly decrease with increasing metallicity. Colucci et al. (2012) also found a decrease of [Y/Ba] in intermediate-age clusters. This could be a mass effect (in the LMC, metal-poor low-mass AGB stars still contribute significantly to the enrichment) but only a consistent chemical evolution modelling can confirm this explanation. We remark that the match between LMC GC and our LMC fields is again excellent.
5.3. Sodium and iron-peak elements
Figures 17 to 19 show the elemental distributions of Na and iron-peak elements Sc, V, Cr, Co and Ni.
Sodium.
In Fig. 17, for stars whose metallicity is below −1.1 dex, we see that the LMC bar and disc [Na/Fe] agree rather well within uncertainties (bar: ⟨[Na/Fe] ⟩ = -0.28 dex; disc: ⟨[Na/Fe] ⟩ = -0.37 dex) and they overlap the MW halo distribution. On the other hand, for [Fe/H] ≥ -1.1 dex, the two LMC distributions become different. The bar [Na/Fe] seems to increase with increasing metallicity and reaches solar values (⟨[Na/Fe] ⟩ = -0.13 dex, rms = 0.17 dex), thus overlapping the Galactic trends. On the other hand, the disc [Na/Fe] remains sub-solar with a flat distribution (⟨[Na/Fe] ⟩ = -0.35 dex, rms = 0.13 dex). Both fields exhibit a large scatter in this metallicity regime: although only five bar stars and four disc stars are observed for [Fe/H] ≤ -1.1 dex, we can guess that the scatter is smaller than for [Fe/H] ≥ -1.1 dex (if the scatter were the same, it would be unlikely to have five or four measures concentrated within 0.2 dex). None of the three Na lines used is responsible for the difference; in the mean, each line gives higher Na abundances for the bar than for the disc: for the bar, ⟨[Na/Fe] ⟩ = -0.11 dex, −0.15 dex and 0.12 dex; for the disc, ⟨[Na/Fe] ⟩ = -0.31 dex, −0.35 dex, and −0.36 dex (respectively for the lines at 5688 Å, 6154 Å and 6160 Å). As for Y and Zr, there is a correlation between [Na/Fe] and Teff and again, if we select only the stars in the temperature range [4000,4400], the dispersion slightly decreases but we still see the different mean behaviour. We note that there is excellent agreement at both low and high metallicity between the LMC GC and our LMC fields. As for Y and Zr, the typical random and systematic error on the final Na abundance are 0.04 dex and 0.14 dex respectively, and can explain the scatter but not the offset between the two fields.
The production of Na is still uncertain and is thought to occur in high-mass SNII (Woosley & Weaver 1995) and AGB stars (Goriely & Mowlavi 2000; Cristallo et al. 2006; Bisterzo et al. 2010). Issues on the abundance measurement have been reported, e.g. in Pasquini et al. (2004) where the authors find a disagreement between Na abundances of giant and dwarf stars belonging to the same cluster. Different explanations are quoted to explain these issues: departure from local thermodynamic equilibrium, surface Na abundances modified by the first dredge-up or uncertainties on atomic data (Smiljanic 2012). It is therefore difficult to understand the LMC trends relative to those of the MW (most of the MW abundances were measured in dwarf stars) but comparing the two LMC fields is still valid. The discrepancy between the LMC bar and disc fields tells us that the production of Na has been more efficient in the bar than in the disc: it could be the result of the star burst that gave birth to the new population in the central parts of the LMC.
Scandium.
Figure 18 shows the LMC bar and disc Sc distributions. The bar and disc have similar [Sc/Fe]. They overlap the MW halo but are below the MW discs. As noticed for the MW (Nissen et al. 2000; Reddy et al. 2003, 2006), Sc in the LMC behaves approximately like Ca or Ti: small scatter at all metallicities; [Sc/Fe] decreases with increasing metallicity; the distribution for the most metal-poor stars ([Fe/H] ≤ -1 dex) is compatible with a plateau (especially for the bar); the amplitude of the decrease between the metal-poor edge and the metal-rich edge is of 0.2 dex. Prochaska & McWilliam (2000) claimed that the α-like pattern of Sc could be due to poor hfs data but Reddy et al. (2003, 2006) used weak Sc ii lines in dwarf stars for which the hfs has little effect on the derived abundances. For our giant stars, the hfs must be taken into account since Sc ii lines are strengthened; and we see that Arcturus [Sc/Fe] lies on the top of the thick disc distribution, as expected.
Other iron-peak elements.
Figure 19 presents the abundance distributions of V, Cr, Co and Ni. Although they all belong to the iron-peak and are mainly produced by SNIa, these elements exhibit different patterns. The abundance distributions of V, Cr and Co are characterised by a rather large scatter, V being the most dramatic case. Cr and Co have flat distributions overlapping those of the MW for both LMC fields while Ni is sub-solar at all metallicities for both LMC fields.
On the other hand, for V, the bar and disc distributions agree only for [Fe/H] ≤ -1.1 dex. For [Fe/H] ≥ -1.1 dex, in the mean, the bar has higher [V/Fe] than the disc (bar: ⟨[V/Fe] ⟩ = -0.11 dex; disc: ⟨[V/Fe] ⟩ = -0.30 dex ). Among the iron-peak elements, V is the one with the highest number of measured lines (7 lines, most of the time) but it exhibits the largest scatter, which should in principle be a sign that the scatter is astrophysical. As for Na, the disagreement between the two LMC fields appears to reach −1 dex. We performed similar sanity checks for V as we did for Y, Zr and Na, and found a correlation between the derived abundance and the temperature; but a selection on temperature leaves the discrepancy unchanged. The typical random and systematic error respectively 0.04 dex and 0.29 dex and can explain the scatter but not the offset between the two fields.
5.4. Copper
Figure 20 shows the abundance trends of Cu. While the LMC bar and disc ratios match those of the MW for [Fe/H] ≤ -1.1 dex, the LMC ratios are significantly lower than those of the MW for higher metallicities: ⟨[Cu/Fe] ⟩ = -0.56 dex for the bar and ⟨[Cu/Fe] ⟩ = -0.64 dex for the disc. Since we found the expected value for Arcturus, the observed deficiency for Cu is not an artifact of our abundance analysis. The origin of Cu is still heavily debated since Cu is thought to have both primary and secondary production: Romano & Matteucci (2007) see the origin of Cu in neutron captures occurring in massive stars dying as SNII (primary production), Travaglio et al. (2004) invoke a minor contribution from s-process in AGB (secondary production) and Mishenina et al. (2002) consider the thermonuclear nucleosynthesis in SNIa as the main source (secondary production). We saw in Sect. 5.1 that a stronger contribution of SNIa is needed to explain the low α ratios and in Sect. 5.2, that a stronger contribution of AGB is needed to explain the high Ba and La ratios. In addition, Pignatari et al. (2010) found that more than half of the solar copper is produced through weak s-process occurring in massive stars (25 M⊙). Therefore, SNIa and AGB stars cannot be the main site of Cu production in the LMC and the hypothesis of massive stars being the main source of Cu seems to be more plausible: Cu in the LMC has mainly a primary origin. As with the α elements O and Mg, our results for Cu support the scenario of a chemical enrichment dominated by intermediate mass AGB stars and SNIa, with a smaller contribution from very massive stars (compared to the MW).
6. Summary and conclusions
To compare the chemical history of the LMC to that of the MW and disentangle the chemical evolution of the LMC bar and disc, we performed a detailed chemical analysis of LMC giant stars using high-resolution spectra obtained at ESO/VLT. Our sample was made up of 106 newly observed stars in a field centred on the LMC bar, plus 58 stars observed by Pompéia et al. (2008) in an inner disc field ~2° south of the bar. We took great care to insure the homogeneity of the two samples, and furthermore used the local thick disc giant Arcturus to insure a proper comparison to Milky Way samples. Our main findings can be summarised as follows:
-
The two samples cover the metallicity range[Fe/H] from −1.5 to −0.1 dex, covering the full LMC disc metallicity distribution (Cole et al. 2005; Carrera et al. 2008), albeit leaving out the most metal-poor (and less numerous) tail of the distribution despite our deliberate overpopulation of this tail in the target selection. 80% of the sample is contained between −1.1 and −0.4 dex. As this sample is metallicity-biased, it cannot be used for metallicity distribution studies.
-
In the metallicity range covered by both types of objects, the LMC field and GC elemental abundances exhibit an excellent agreement for all elements (except for O and Na at low metallicity; the low-metallicity clusters have experienced self-enrichment, creating anti-correlated O-Na star to star variations).
-
The α-element ratios [Mg/Fe] and [O/Fe] are lower in the LMC than in the MW suggesting a smaller contribution of massive stars (with respect to SNIa) in the LMC, or a slower enrichment. The presence of a plateau for [α/ Fe] is not convincingly probed by our sample due to a lack of metal-poor members, although the most metal-poor GC do seem to lie on a plateau. [Ba,La/Eu] exhibit a strong increase from [Fe/H] ≈ -0.8 dex with increasing metallicity, showing that the chemical enrichment of the LMC has been slower than that of the MW, and that the neutron-capture elements were dominated by the s-process, mainly occurring in AGB stars. The LMC has lower [Y + Zr/Ba + La] ratios than the MW indicating that these AGBs were more metal-poor in the LMC.
-
Eu does not follow the expected trend which could be an indication of an efficient s-production of this element, despite the usually assumed almost pure r-process origin of this element. This finding is supported by the recent work by Allen et al. (2012) who advocate a strong s-process contribution to Eu in a certain category of extremely metal-poor carbon and s-process enhanced stars (the so-called sr-stars).
-
Cu is almost constant over the metallicity range and about 0.5 dex lower in the LMC than in the MW showing that in the LMC Cu has mainly a primary origin (through weak s-process in massive stars).
-
The LMC bar and disc exhibit subtle differences in their [α/ Fe] (slightly larger scatter for the bar in the metallicity range [− 1, − 0.5]), their [Eu/Fe] (the bar trend is above the disc trend for [Fe/H] ≥ -0.5 dex, their Y and Zr, their Na and their V (offset between the bar and the disc distributions). These differences are possibly related to the formation of a new stellar population in the central part of the LMC: the resulting new generation of massive stars will inject freshly synthesised α-elements (hence the increased scatter observed in the bar) and Eu (hence the higher [Eu/Fe] ratios in the bar) and the new generation of metal-rich AGB stars will produce Na, Y and Zr (hence the offset). These findings strengthen a scenario where the LMC bar is not a mere dynamically driven (or interaction driven) overdensity, but implied a fresh episode of star formation. This scenario also supported by the SFH derived in the bar, that highlights an increased star formation 2–5 Gyr ago, with no clear counterparts in other locations in the LMC disc (Smecker-Hane et al. 2002). More globally, Harris & Zaritsky (2009) have established a map of SFHs across the whole LMC and find again that the dominant star formation episode that occurred some 5 Gyr is more pronounced in the bar than anywhere else in the LMC. Even younger bursts of star formation seem to follow the bar morphology, around 500 and 100 Myr ago. Gallart et al. (2008), although their sample does not include the bar per se, also highlight that the younger populations in the LMC are found closer to the centre together with a positive age-gradient of the youngest star formation episode towards the outskirts. All these findings regarding the SFH of the LMC bar and disc strengthen a scenario where the bar is the strongest manifestation of the higher recent star formation activity in the central parts of the LMC.
Online material
Line list.
For technical details see http://www.eso.org/sci/facilities/paranal/instruments/flames/doc/VLT-MAN-ESO-13700-2994_v86.0.pdf
Pipeline available at http://www.eso.org/projects/dfs/dfs-shared/web/vlt/vlt-instrument-pipelines.html
Web interface at http://stev.oapd.inaf.it/cgi-bin/param
Models available at http://marcs.astro.uu.se/
Online LMC reddening estimator at http://djuma.as.arizona.edu/~dennis/lmcext.html
Acknowledgments
M. Van der Swaelmen thanks ESO and the CNRS for funding his Ph.D. work. We thank Bertrand Plez for his program to compute hyperfine structure. DAOSPEC has been written by P. B. Stetson for the Dominion Astrophysical Observatory of the Herzberg Institute of Astrophysics, National Research Council, Canada. This research has made use of NASA’s Astrophysics Data System Bibliographic Services, of the VALD and Kurucz databases. M. Van der Swaelmen and V. Hill are thankful for the support from the French Programme National Galaxies (INSU) which allowed this research to be carried out. We would like to pay a special tribute to our collaborator and friend Luciana Pompeia who passed away much too soon. She was a key person early in this LMC project and we have special thoughts towards her family, friends and colleagues.
References
- Allen, D. M., Ryan, S. G., Rossi, S., Beers, T. C., & Tsangarides, S. A. 2012, A&A, 548, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alvarez, R., & Plez, B. 1998, A&A, 330, 1109 [NASA ADS] [Google Scholar]
- Alves, D. R. 2004, New Astron., 48, 659 [Google Scholar]
- Alves-Brito, A., Meléndez, J., Asplund, M., Ramírez, I., & Yong, D. 2010, A&A, 513, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arlandini, C., Käppeler, F., Wisshak, K., et al. 1999, ApJ, 525, 886 [NASA ADS] [CrossRef] [Google Scholar]
- Bekki, K. 2009, MNRAS, 393, L60 [NASA ADS] [CrossRef] [Google Scholar]
- Bekki, K., & Chiba, M. 2005, MNRAS, 356, 680 [NASA ADS] [CrossRef] [Google Scholar]
- Bekki, K., & Tsujimoto, T. 2012, ApJ, 761, 180 [NASA ADS] [CrossRef] [Google Scholar]
- Bensby, T., Feltzing, S., Lundström, I., & Ilyin, I. 2005, A&A, 433, 185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Besla, G., Kallivayalil, N., Hernquist, L., et al. 2007, ApJ, 668, 949 [NASA ADS] [CrossRef] [Google Scholar]
- Besla, G., Kallivayalil, N., Hernquist, L., et al. 2012, MNRAS, 421, 2109 [NASA ADS] [CrossRef] [Google Scholar]
- Bielski, A. 1975, J. Quant. Spectr. Rad. Transf., 15, 463 [Google Scholar]
- Biemont, E., Baudoux, M., Kurucz, R. L., Ansbacher, W., & Pinnington, E. H. 1991, A&A, 249, 539 [NASA ADS] [Google Scholar]
- Bisterzo, S., Gallino, R., Straniero, O., Cristallo, S., & Käppeler, F. 2010, MNRAS, 404, 1529 [NASA ADS] [Google Scholar]
- Bisterzo, S., Gallino, R., Straniero, O., Cristallo, S., & Käppeler, F. 2012, MNRAS, 422, 849 [NASA ADS] [CrossRef] [Google Scholar]
- Blecha, A., Cayatte, V., North, P., Royer, F., & Simond, G. 2000, in Proc. SPIE 4008, eds. M. Iye, & A. F. Moorwood, 467 [Google Scholar]
- Brewer, M.-M., & Carney, B. W. 2006, AJ, 131, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Burbidge, E. M., Burbidge, G. R., Fowler, W. A., & Hoyle, F. 1957, Rev. Mod. Phys., 29, 547 [NASA ADS] [CrossRef] [Google Scholar]
- Burris, D. L., Pilachowski, C. A., Armandroff, T. E., et al. 2000, ApJ, 544, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Busso, M., Gallino, R., & Wasserburg, G. J. 1999, ARA&A, 37, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Carretta, E., Gratton, R. G., & Sneden, C. 2000, A&A, 356, 238 [NASA ADS] [Google Scholar]
- Carrera, R., Gallart, C., Hardy, E., Aparicio, A., & Zinn, R. 2008, AJ, 135, 836 [NASA ADS] [CrossRef] [Google Scholar]
- Cayrel, R., Depagne, E., Spite, M., et al. 2004, A&A, 416, 1117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chabrier, G. 2001, ApJ, 554, 1274 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, J. G., Christlieb, N., Qian, Y.-Z., & Wasserburg, G. J. 2003, ApJ, 588, 1082 [NASA ADS] [CrossRef] [Google Scholar]
- Cole, A. A., Smecker-Hane, T. A., Tolstoy, E., Bosler, T. L., & Gallagher, J. S. 2004, MNRAS, 347, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Cole, A. A.,Tolstoy, E.,Gallagher, J. S., III, & Smecker-Hane, T. A. 2005, AJ, 129, 1465 [NASA ADS] [CrossRef] [Google Scholar]
- Colucci, J. E., Bernstein, R. A., Cameron, S. A., & McWilliam, A. 2012, ApJ, 746, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Cristallo, S., Gallino, R., Straniero, O., Piersanti, L., & Domınguez, I. 2006, Mem. Soc. Astron. It., 77, 774 [Google Scholar]
- Cristallo, S., Piersanti, L., Straniero, O., et al. 2011, ApJS, 197, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Da Costa, G. S. 1991, in The Magellanic Clouds, eds. R. Haynes, & D. Milne, IAU Symp., 148, 183 [Google Scholar]
- da Silva, L., Girardi, L., Pasquini, L., et al. 2006, A&A, 458, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Vaucouleurs, G., & Freeman, K. C. 1972, Vistas Astron., 14, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Drozdowski, R., Ignaciuk, M., Kwela, J., & Heldt, J. 1988, Z. Phys., 21, 2827 [Google Scholar]
- Freiburghaus, C., Rosswog, S., & Thielemann, F.-K. 1999, ApJ, 525, L121 [Google Scholar]
- Fuhr, J. R., Martin, G. A., & Wiese, W. L. 1988, J. Phys. Chem. Ref. Data, 17 [Google Scholar]
- Fulbright, J. P. 2000, AJ, 120, 1841 [NASA ADS] [CrossRef] [Google Scholar]
- Gallart, C., Stetson, P. B., Meschin, I. P., Pont, F., & Hardy, E. 2008, ApJ, 682, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Gallino, R., Arlandini, C., Busso, M., et al. 1998, ApJ, 497, 388 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gilmore, G., & Wyse, R. F. G. 1991, ApJ, 367, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Goriely, S., & Mowlavi, N. 2000, A&A, 362, 599 [NASA ADS] [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Grocholski, A. J., Cole, A. A., Sarajedini, A., Geisler, D., & Smith, V. V. 2006, AJ, 132, 1630 [NASA ADS] [CrossRef] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harris, J., & Zaritsky, D. 2009, AJ, 138, 1243 [NASA ADS] [CrossRef] [Google Scholar]
- Haschke, R., Grebel, E. K., & Duffau, S. 2012a, AJ, 144, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Haschke, R., Grebel, E. K., Duffau, S., & Jin, S. 2012b, AJ, 143, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Haschke, R., Grebel, E. K., Frebel, A., et al. 2012c, AJ, 144, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Hill, V., Andrievsky, S., & Spite, M. 1995, A&A, 293, 347 [NASA ADS] [Google Scholar]
- Hinkle, K., Wallace, L., Valenti, J., & Harmer, D. 2000, Visible and Near Infrared Atlas of the Arcturus Spectrum 3727–9300 Å (San Francisco: ASP) [Google Scholar]
- Johnson, J. A., Ivans, I. I., & Stetson, P. B. 2006, ApJ, 640, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Kallivayalil, N., van der Marel, R. P., & Alcock, C. 2006a, ApJ, 652, 1213 [NASA ADS] [CrossRef] [Google Scholar]
- Kallivayalil, N., van der Marel, R. P., Alcock, C., et al. 2006b, ApJ, 638, 772 [NASA ADS] [CrossRef] [Google Scholar]
- Kupka, F., Piskunov, N., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Kupka, F. G., Ryabchikova, T. A., Piskunov, N. E., Stempels, H. C., & Weiss, W. W. 2000, Baltic Astron., 9, 590 [Google Scholar]
- Kurucz, R. L. 1988, in Trans. IAU XXB, ed. D. McNally (Dordrecht: Kluwer), 168 [Google Scholar]
- Kurucz, R. L. 1995, in Astrophysical Applications of Powerful New Databases, eds. S. J. Adelman, & W. L. Wiese, ASP Conf. Ser., 78, 205 [Google Scholar]
- Lapenna, E., Mucciarelli, A., Origlia, L., & Ferraro, F. R. 2012, ApJ, 761, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Lawler, J. E., Bonvallet, G., & Sneden, C. 2001a, ApJ, 556, 452 [NASA ADS] [CrossRef] [Google Scholar]
- Lawler, J. E., Wickliffe, M. E., den Hartog, E. A., & Sneden, C. 2001b, ApJ, 563, 1075 [CrossRef] [Google Scholar]
- Lebzelter, T., Heiter, U., Abia, C., et al. 2012, A&A, 547, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lecureur, A., Hill, V., Zoccali, M., et al. 2007, A&A, 465, 799 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martin, G. A., Fuhr, J. R., & Wiese, W. L. 1988, Atomic transition probabilities. Scandium through Manganese (New York: AIP) [Google Scholar]
- Masseron, T. 2009, P.h.D. Thesis [Google Scholar]
- Masseron, T., Johnson, J. A., Plez, B., et al. 2010, A&A, 509, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McWilliam, A., Preston, G. W., Sneden, C., & Searle, L. 1995, AJ, 109, 2757 [NASA ADS] [CrossRef] [Google Scholar]
- Meléndez, J., Asplund, M., Gustafsson, B., & Yong, D. 2009, ApJ, 704, L66 [NASA ADS] [CrossRef] [Google Scholar]
- Mishenina, T. V., Kovtyukh, V. V., Soubiran, C., Travaglio, C., & Busso, M. 2002, A&A, 396, 189 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mucciarelli, A., Carretta, E., Origlia, L., & Ferraro, F. R. 2008, AJ, 136, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Mucciarelli, A., Origlia, L., & Ferraro, F. R. 2010, ApJ, 717, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Nave, G., Johansson, S., Learner, R. C. M., Thorne, A. P., & Brault, J. W. 1994, APJS, 94, 221 [Google Scholar]
- Nissen, P. E., Chen, Y. Q., Schuster, W. J., & Zhao, G. 2000, A&A, 353, 722 [NASA ADS] [Google Scholar]
- Olszewski, E. W., Schommer, R. A., Suntzeff, N. B., & Harris, H. C. 1991, AJ, 101, 515 [NASA ADS] [CrossRef] [Google Scholar]
- Pagel, B. E. J., & Tautvaisiene, G. 1998, MNRAS, 299, 535 [NASA ADS] [CrossRef] [Google Scholar]
- Pasquini, L., Avila, G., Blecha, A., et al. 2002, The Messenger, 110, 1 [NASA ADS] [Google Scholar]
- Pasquini, L., Randich, S., Zoccali, M., et al. 2004, A&A, 424, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pejcha, O., & Stanek, K. Z. 2009, ApJ, 704, 1730 [NASA ADS] [CrossRef] [Google Scholar]
- Pignatari, M., Gallino, R., Heil, M., et al. 2010, ApJ, 710, 1557 [NASA ADS] [CrossRef] [Google Scholar]
- Plez, B. 1998, A&A, 337, 495 [NASA ADS] [Google Scholar]
- Pompéia, L., Hill, V., Spite, M., et al. 2008, A&A, 480, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prochaska, J. X., & McWilliam, A. 2000, ApJ, 537, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Qian, Y.-Z. 2012, AIP Conf. Proc., 1484, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez, I., & Allen de Prieto, C. 2011, ApJ, 743, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez, I., & Meléndez, J. 2005a, ApJ, 626, 446 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Ramírez, I., & Meléndez, J. 2005b, ApJ, 626, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez, I., Meléndez, J., & Asplund, M. 2009, A&A, 508, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reddy, B. E.,Tomkin, J.,Lambert, D. L., & Allen de Prieto, C. 2003, MNRAS, 340, 304 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, B. E., Lambert, D. L., & Allen de Prieto, C. 2006, MNRAS, 367, 1329 [NASA ADS] [CrossRef] [Google Scholar]
- Rich, R. M., Shara, M. M., & Zurek, D. 2001, AJ, 122, 842 [NASA ADS] [CrossRef] [Google Scholar]
- Romano, D., & Matteucci, F. 2007, MNRAS, 378, L59 [NASA ADS] [Google Scholar]
- Russell, S. C., & Bessell, M. S. 1989, ApJS, 70, 865 [NASA ADS] [CrossRef] [Google Scholar]
- Rutten, R. J. 1978, Sol. Phys., 56, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Shetrone, M., Venn, K. A., Tolstoy, E., et al. 2003, AJ, 125, 684 [NASA ADS] [CrossRef] [Google Scholar]
- Simmerer, J., Sneden, C., Cowan, J. J., et al. 2004, ApJ, 617, 1091 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Smecker-Hane, T. A., Cole, A. A., Gallagher, J. S., III, & Stetson, P. B. 2002, ApJ, 566, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Smiljanic, R. 2012, MNRAS, 422, 1562 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, G. 1981, A&A, 103, 351 [NASA ADS] [Google Scholar]
- Smith, G. 1988, J. Phys. B Atom. Mol. Phys., 21, 2827 [CrossRef] [Google Scholar]
- Smith, G., & Raggett, D. S. J. 1981, J. Phys. B Atom. Mol. Phys., 14, 4015 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, V. V., Suntzeff, N. B., Cunha, K., et al. 2000, AJ, 119, 1239 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, V. V., Hinkle, K. H., Cunha, K., et al. 2002, AJ, 124, 3241 [NASA ADS] [CrossRef] [Google Scholar]
- Sneden, C., Cowan, J. J., & Gallino, R. 2008, ARA&A, 46, 241 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stephens, A., & Boesgaard, A. M. 2002, AJ, 123, 1647 [NASA ADS] [CrossRef] [Google Scholar]
- Stetson, P. B., & Pancino, E. 2008, PASP, 120, 1332 [Google Scholar]
- Straniero, O., Chieffi, A., Limongi, M., et al. 1997, ApJ, 478, 332 [NASA ADS] [CrossRef] [Google Scholar]
- Subramaniam, A. 2005, A&A, 430, 421 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Szymanski, M. K. 2005, Acta Astron., 55, 43 [NASA ADS] [Google Scholar]
- Thielemann, F.-K., Argast, D., Brachwitz, F., et al. 2002, Ap&SS, 281, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Timmes, F. X., Brown, E. F., & Truran, J. W. 2003, ApJ, 590, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Travaglio, C., Gallino, R., Arnone, E., et al. 2004, ApJ, 601, 864 [NASA ADS] [CrossRef] [Google Scholar]
- Tsujimoto, T., Nomoto, K., Yoshii, Y., et al. 1995, MNRAS, 277, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Udalski, A., Kubiak, M., & Szymanski, M. 1997, Acta Astron., 47, 319 [NASA ADS] [Google Scholar]
- Udalski, A., Soszynski, I., Szymanski, M., et al. 1999, Acta Astron., 49, 223 [Google Scholar]
- Udalski, A., Szymanski, M., Kubiak, M., et al. 2000, Acta Astron., 50, 307 [Google Scholar]
- van der Marel, R. P. 2001, AJ, 122, 1827 [NASA ADS] [CrossRef] [Google Scholar]
- van der Marel, R. P., Alves, D. R., Hardy, E., & Suntzeff, N. B. 2002, AJ, 124, 2639 [NASA ADS] [CrossRef] [Google Scholar]
- Wanajo, S., Nomoto, K., Iwamoto, N., Ishimaru, Y., & Beers, T. C. 2006, ApJ, 636, 842 [NASA ADS] [CrossRef] [Google Scholar]
- Wasserburg, G. J., Busso, M., & Gallino, R. 1996, ApJ, 466, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Wiese, W. L., Smith, M. W., & Glennon, B. M. 1966, Atomic transition probabilities, Vol.: Hydrogen through Neon. A critical data compilation (Washington DC: US Dept of Commerce) [Google Scholar]
- Woosley, S. E., & Weaver, T. A. 1995, ApJS, 101, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Worley, C. C., Cottrell, P. L., Freeman, K. C., & Wylie-de Boer, E. C. 2009, MNRAS, 400, 1039 [NASA ADS] [CrossRef] [Google Scholar]
- Zaritsky, D. 2004, ApJ, 614, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Zaritsky, D., Harris, J., Thompson, I. B., & Grebel, E. K. 2004, AJ, 128, 1606 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
For each setup, the exposures, the total exposure times and the observation dates are given.
Stars showing a disagreement in their mean radial velocities from one setup to another.
Radial velocities of LMC bar stars. 2MASS identifiers, υrad, σ(υrad), number of independent measurements and S/N for each setup, final mean υrad and its error.
Values of S/N corresponding to the qualifiers high (best 10% of the sample), median, and low (worst 10% of the sample).
Photometry and Cat metallicity of LMC bar stars. 2MASS identifiers, V, 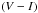 ,
, 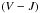 ,
, 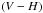 and
and 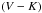 (Udalski et al. 1997, 2000; Szymanski 2005) and [Fe/H] CaT (Cole et al. 2005).
(Udalski et al. 1997, 2000; Szymanski 2005) and [Fe/H] CaT (Cole et al. 2005).
Stellar parameters of LMC bar stars. 2MASS identifiers, Tphot, log g, [M/H], ξmicro, [Fe i/ H], [Fe ii/ H].
Mean and standard deviation of the distribution of [M/H], [Fe i/ H], [Fe ii/ H] and ξmicro for the 101 realisations of high, median and low S/N version of the Arcturus spectra.
Elemental abundances, and errors for our ∞, high, median, and low S/N versions of the Arcturus spectra as well as abundance ratios (and their errors) published by Ramírez & Allende Prieto (2011) and Worley et al. (2009).
Comparison of our new abundances for the LMC disc stars and those published in Pompéia et al. (2008): mean m and rms s of the distribution of [X/Fe] us − [X/Fe] P08.
Typical edata and eparams, given as [A/B] − σ(Tphot) − [A/B] nominal and [A/B] + σ(Tphot) − [A/B] nominal, for different elemental ratios for our LMC bar stars.
All Figures
 |
Fig. 1 Colour–magnitude diagram (left panel) and metallicity distribution (right panel) of Cole et al. (2005) RGB sample (green) and our selected RGB stars (red). V and I magnitudes are from the OGLE catalogue Udalski et al. (1997, 2000); Szymanski (2005) for the samples of Cole et al. (2005) and the present paper, while black dots in the CMD are photometric data from Zaritsky et al. (2004) catalogue. Metallicities in the right panel are those derived from the infrared Ca ii triplet index by Cole et al. (2005). |
| In the text | |
 |
Fig. 2 Top panel: example of raw spectrum (blue) for star 05244301-6943412 and the corresponding master-sky (black) we used to obtain the sky-subtracted spectrum (red). In the red spectrum sky emission lines have been correctly removed. A cosmic ray remains at ~ 6290 Å. Bottom panel: the sky-subtracted spectrum of 05244301-6943412 before (red) and after (blue) the correction for the telluric lines. The spectrum of the fast rotator is plotted in black to show the position of telluric features. The green spectrum is the co-added spectrum: the σ-clipping has removed the remaining cosmic rays and the signal-to-noise ratio is clearly improved compared to the single exposure. All spectra are plotted in the same scale, except for the fast rotator spectrum (it has been scaled for legibility). |
| In the text | |
 |
Fig. 3 Left panel: example of cross-correlation function (black line) and its Gaussian fit (red thick line). Right panel: zoom in on the maximum of the cross-correlation function and its parabolic fit (red thick line). We first used a Gaussian fit to locate the position of the maximum and then defined a smaller velocity range (Gaussian fit FWHM) and computed the cross-correlation function over a finer grid to improve the determination of the radial velocity. |
| In the text | |
 |
Fig. 4 Radial velocity curves for six stars. The relative radial velocities vrad,s − ⟨vrad,s⟩ determined for each exposure are plotted as a function of MJD for five stars where the T-test failed and we suspect a variability in the radial velocity. The curves were shifted for legibility (the dashed line represents the offset). The bottom curve (star 05223082-6944147) is a star with no radial velocity variability and shown here for reference. In red: HR11, in green: HR13, in blue: HR14 (for HR13 data and HR14 data obtained at the same epoch, the green crosses are below the blue ones). Error bars are smaller than the symbols (≤ 1 km s-1). |
| In the text | |
 |
Fig. 5 Distribution of the radial velocities of the LMC bar stars. The histogram overplotted in red denotes the stars for which we suspect a radial velocity variability. The mean and the standard deviation of the distribution are respectively 261 km s-1 and 25 km s-1. A Gaussian curve (μ;σ) is plotted over the histogram. |
| In the text | |
 |
Fig. 6 σresidual vs. S/N. Black solid line: we measured σresidual of the Arcturus HR13 spectrum for different values of artificially added noise σnoise2 = (S/N)-2. Red dots: LMC HR13 spectra. For Arcturus with artificial noise, σresidual ≃ 2 when S/N ≃ 55 while for our LMC spectra, σresidual ≃ 2 when S/N ≃ 40. |
| In the text | |
 |
Fig. 7 Location of the LMC bar (left panel) and disc (right panel) stars in the Hertzsprung-Russel diagram. Legend: blue: -2 dex ≤ [Fe i/ H] ≤ -1.3 dex, cyan: -1.3 dex ≤ [Fe i/ H] ≤ -1.0 dex, green: -1.0 dex ≤ [Fe i/ H] ≤ -0.8 dex, yellow: -0.8 dex ≤ [Fe i/ H] ≤ -0.6 dex, magenta: -0.6 dex ≤ [Fe i/ H] ≤ -0.4 dex, red: -0.4 dex ≤ [Fe i/ H] ≤ 0.0 dex. |
| In the text | |
 |
Fig. 8 First and second rows: distribution of a given quantity for our LMC stars assuming E(B − V) = 0.06 mag and E(B − V) = 0.14 mag respectively. Third row: distribution of a given quantity for the 101 median S/N Arcturus spectra. First column: distributions of the slopes ([Fe i/ H]|log (EW/λ)) (spectroscopic criterion used to derive ξmicro). Second column: distributions of the slopes ([Fe i/ H]|χex) (excitation equilibrium). Third column: distribution of the difference Δ(Fe) = [Fe i/ H] − [Fe ii/ H] (ionisation equilibrium). Fourth column: distribution of the sample standard deviation of [Fe i/ H]. |
| In the text | |
 |
Fig. 9 Comparison of [Fe/H] CaT and [Fe/H] spectro. Δ( [Fe/H] ) = [Fe/H] CaT − [Fe/H] spectro vs. [Fe/H] CaT. Legend: black filled circles: LMC bar; blue open pentagons: LMC disc. |
| In the text | |
 |
Fig. 10 Left panel: m [edao(EW)] vs. s [EW]. Right panel: m [eturbo( [Fe/H])] vs. s [[Fe/H]]. Red dots: low S/N; green dots: median S/N; blue dots: high S/N. |
| In the text | |
 |
Fig. 11 First row: [O i/ Fe i] vs. [Fe i/ H]. Second row: [Mg i/ Fe i] vs. [Fe i/ H]. Third row: [O i + Mg i/ 2Fe i] vs. [Fe i/ H]. Legend: black filled circles: LMC bar (this work); blue open pentagons: LMC inner disc (this work); green asterisk: Arcturus (this work, data for median S/Nratio); red downward triangle: LMC GC (Johnson et al. 2006; Mucciarelli et al. 2008, 2010); black tiny dots: MW thin and thick disc (Bensby et al. 2005; Reddy et al. 2003, 2006), halo (Fulbright 2000; Stephens & Boesgaard 2002; Reddy et al. 2006), and additional MW data for O from Carretta et al. (2000). Typical random (left) and systematic (right) error bars on both coordinates are provided for our LMC samples. |
| In the text | |
 |
Fig. 12 First row: [Si i/ Fe i] vs. [Fe i/ H]. Second row: [Ca i/ Fe i] vs. [Fe i/ H]. Third row: [Ti ii/ Fe i] vs. [Fe i/ H]. Legend: same as Fig. 11. |
| In the text | |
 |
Fig. 13 [Eu ii/ Fe i] vs. [Fe i/ H]. Legend: same as Fig. 11. |
| In the text | |
 |
Fig. 14 First row: [Ba ii/ Fe i] vs. [Fe i/ H]. Second row: [Ba ii/ Eu ii] vs. [Fe i/ H]. Third row: [La ii/ Fe i] vs. [Fe i/ H]. Fourth row: [La ii/ Eu ii] vs. [Fe i/ H]. Legend: same legend as Fig. 11; additional MW data for Eu and La from Simmerer et al. (2004); Brewer & Carney (2006); horizontal blue dashed line: [Bar/ Eur] = -0.69 dex and [Lar/ Eur] = -0.4 dex (Arlandini et al. 1999); horizontal blue dotted line: [Bar/ Eur] = -0.82 dex and [Lar/ Eur] = -0.59 dex (Sneden et al. 2008). |
| In the text | |
 |
Fig. 15 First row: [Y i/ Fe i] vs. [Fe i/ H]. Second row: [Zr i/ Fe i] vs. [Fe i/ H]. Legend: same as Fig. 11. |
| In the text | |
 |
Fig. 16 [Y i + Zr i/ Ba ii + La ii] vs. [Fe i/ H]. Legend: same as Fig. 11. |
| In the text | |
 |
Fig. 17 [Na i/ Fe i] vs. [Fe i/ H]. Legend: same as Fig. 11. |
| In the text | |
 |
Fig. 18 [Sc ii/ Fe i] vs. [Fe i/ H]. Legend: same as Fig. 11. |
| In the text | |
 |
Fig. 19 First row: [V i/ Fe i] vs. [Fe i/ H]. Second row: [Cr i/ Fe i] vs. [Fe i/ H]. Third row: [Co i/ Fe i] vs. [Fe i/ H]. Fourth row: [Ni i/ Fe i] vs. [Fe i/ H]. Legend: same as Fig. 11. |
| In the text | |
 |
Fig. 20 [Cu i/ Fe i] vs. [Fe i/ H]. Legend: same as Fig. 11. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



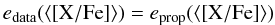
![$$e_{\mathrm{data}}(\langle \abratio{X}{Fe} \rangle) = \max \left( \frac{s[\abratio{X}{Fe}]}{\sqrt{N_{\mathrm{lines}}}}, e_{\mathrm{prop}}(\langle \abratio{X}{Fe} \rangle) \right).$$](/articles/aa/full_html/2013/12/aa21109-13/aa21109-13-eq441.png)