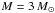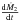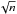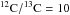| Issue |
A&A
Volume 559, November 2013
|
|
|---|---|---|
| Article Number | A66 | |
| Number of page(s) | 13 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201322420 | |
| Published online | 15 November 2013 | |
A nova re-accretion model for J-type carbon stars ⋆
Argelander-Institut für Astronomie, Auf dem Hügel 71, 53121
Bonn, Germany
e-mail: sutirtha@astro.uni-bonn.de
Received:
1
August
2013
Accepted:
3
October
2013
The J-type carbon (J)-stars constitute 10–15% of the observed carbon stars in both our
Galaxy and the Large Magellanic Cloud (LMC). They are characterized by strong
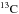 absorption bands with low
12C/13C ratios along with other chemical signatures peculiar for
typical carbon stars, e.g. a lack of s-process enhancement. Most of the J-stars are dimmer
than the N-type carbon stars some of which, by hot-bottom burning, make
absorption bands with low
12C/13C ratios along with other chemical signatures peculiar for
typical carbon stars, e.g. a lack of s-process enhancement. Most of the J-stars are dimmer
than the N-type carbon stars some of which, by hot-bottom burning, make
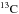 only in a narrow range of masses. We
investigate a binary-star formation channel for J-stars involving re-accretion of
carbon-rich nova ejecta on main-sequence companions to low-mass carbon-oxygen
white-dwarfs. The subsequent evolution of the companion stars in such systems is studied
with a rapid binary evolutionary code to predict chemical signatures of nova pollution in
systems which merge into giant single stars. A detailed population synthesis study is
performed to estimate the number of these mergers and compare their properties with
observed J-stars. Our results predict that such nova polluted mergers evolve with low
luminosities as well as low 12C/13C ratios like the majority of
observed J-stars (e.g. in the LMC) but cannot account for the observed fraction of J-stars
in existing surveys of carbon stars.
only in a narrow range of masses. We
investigate a binary-star formation channel for J-stars involving re-accretion of
carbon-rich nova ejecta on main-sequence companions to low-mass carbon-oxygen
white-dwarfs. The subsequent evolution of the companion stars in such systems is studied
with a rapid binary evolutionary code to predict chemical signatures of nova pollution in
systems which merge into giant single stars. A detailed population synthesis study is
performed to estimate the number of these mergers and compare their properties with
observed J-stars. Our results predict that such nova polluted mergers evolve with low
luminosities as well as low 12C/13C ratios like the majority of
observed J-stars (e.g. in the LMC) but cannot account for the observed fraction of J-stars
in existing surveys of carbon stars.
Key words: stars: carbon / stars: chemically peculiar / novae, cataclysmic variables / white dwarfs / stars: abundances / stars: statistics
Appendices A and B are available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
Stars spend about 90% of their lifetime on the main sequence, during which they convert
hydrogen (H) to helium (He) in their cores by the pp-chain or the CNO-cycle. Following core
hydrogen exhaustion they leave the main sequence and depending on their mass, many proceed
to advanced stages of nuclear burning. In low and intermediate-mass stars
( ), the triple-α reaction
acts as a source of energy after depletion of internal hydrogen and produces carbon during
their He-burning phase of evolution. When these stars ascend the asymptotic giant branch
(AGB), the products of He-burning (mainly
), the triple-α reaction
acts as a source of energy after depletion of internal hydrogen and produces carbon during
their He-burning phase of evolution. When these stars ascend the asymptotic giant branch
(AGB), the products of He-burning (mainly 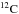 ) along with s-process elements formed
through neutron captures are mixed into the convective envelope during the thermally pulsing
(TP) phase and brought to the stellar surface by third dredge-up (TDU). This AGB scenario
explains the origin of the majority of all carbon (C)-stars (characterized by surface
C/O > 1 by number) – the N-type stars (Iben & Renzini
1983). However, spectral classification of C-stars reveals other peculiar scenarios
of carbon enrichment especially in binaries (Wallerstein
& Knapp 1998). Mass transfer from a carbon-rich AGB primary star can pollute
its binary companion with enough carbon to turn it into a dwarf carbon star which explains
the origin of the CH and Ba-stars (Jorissen et al.
1998). In this work, we investigate a binary model that aims to explain the origin
of possibly the least understood class among all C-stars – the J-type (J)-stars – whose
evolutionary origin has remained a mystery for decades.
) along with s-process elements formed
through neutron captures are mixed into the convective envelope during the thermally pulsing
(TP) phase and brought to the stellar surface by third dredge-up (TDU). This AGB scenario
explains the origin of the majority of all carbon (C)-stars (characterized by surface
C/O > 1 by number) – the N-type stars (Iben & Renzini
1983). However, spectral classification of C-stars reveals other peculiar scenarios
of carbon enrichment especially in binaries (Wallerstein
& Knapp 1998). Mass transfer from a carbon-rich AGB primary star can pollute
its binary companion with enough carbon to turn it into a dwarf carbon star which explains
the origin of the CH and Ba-stars (Jorissen et al.
1998). In this work, we investigate a binary model that aims to explain the origin
of possibly the least understood class among all C-stars – the J-type (J)-stars – whose
evolutionary origin has remained a mystery for decades.
1.1. J-stars
The J-stars are a class of red-giant C-stars that are characterized by strong
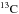 bands (Bouigue 1954) and low
bands (Bouigue 1954) and low 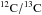 ratios (Ohnaka & Tsuji 1999), and constitute a significant fraction (10−15%) of all
carbon stars in our Galaxy (Abia & Isern 2000)
and the Large Magellanic Cloud (LMC; Morgan et al.
2003). AGB models of C-stars cannot explain most of the chemical peculiarities
associated with J-stars e.g. no s-process overabundance and Li enhancements (Hatzidimitriou et al. 2003). Moreover, their
luminosities and variability classes indicate that they are less evolved objects than the
N-type C-stars (Abia & Isern 2000). However, the
presence of high luminosity J-stars in our Galaxy (e.g. WZ Cas) suggests the existence of
at least two types of J-stars, with different formation scenarios. Moreover, an intriguing
sub-class of J-stars known as silicate carbon stars, characterized by oxygen-rich
circumstellar material possibly stored in a circumbinary disk (Lloyd Evans 1991), points to a binary origin for this peculiar class of
C-stars (e.g. BM-Gem; Ohnaka et al. 2008; Izumiura et al. 2008). A recent study exploring
white-dwarf (WD) red-giant (RG) binary mergers in the context of the R-type C-stars, has
found a possible evolutionary channel for J-stars (Zhang
& Jeffery 2013). We investigate another binary scenario considering chemical
pollution of main-sequence (MS) companions to WDs in classical novae explosions and study
their long-term evolutionary outcome in context of peculiarities associated with J-stars.
ratios (Ohnaka & Tsuji 1999), and constitute a significant fraction (10−15%) of all
carbon stars in our Galaxy (Abia & Isern 2000)
and the Large Magellanic Cloud (LMC; Morgan et al.
2003). AGB models of C-stars cannot explain most of the chemical peculiarities
associated with J-stars e.g. no s-process overabundance and Li enhancements (Hatzidimitriou et al. 2003). Moreover, their
luminosities and variability classes indicate that they are less evolved objects than the
N-type C-stars (Abia & Isern 2000). However, the
presence of high luminosity J-stars in our Galaxy (e.g. WZ Cas) suggests the existence of
at least two types of J-stars, with different formation scenarios. Moreover, an intriguing
sub-class of J-stars known as silicate carbon stars, characterized by oxygen-rich
circumstellar material possibly stored in a circumbinary disk (Lloyd Evans 1991), points to a binary origin for this peculiar class of
C-stars (e.g. BM-Gem; Ohnaka et al. 2008; Izumiura et al. 2008). A recent study exploring
white-dwarf (WD) red-giant (RG) binary mergers in the context of the R-type C-stars, has
found a possible evolutionary channel for J-stars (Zhang
& Jeffery 2013). We investigate another binary scenario considering chemical
pollution of main-sequence (MS) companions to WDs in classical novae explosions and study
their long-term evolutionary outcome in context of peculiarities associated with J-stars.
1.2. 13C enhancement scenarios
The triple-α process operating in cores of AGB stars makes
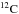 which is subsequently brought to their
surface during dredge up thus forming a C-star. The synthesis of
which is subsequently brought to their
surface during dredge up thus forming a C-star. The synthesis of
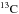 requires a further proton capture on
requires a further proton capture on
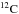 that can only occur in regions with
conditions suitable for operation of the CNO cycle. The β-unstable
isotope
that can only occur in regions with
conditions suitable for operation of the CNO cycle. The β-unstable
isotope 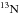 produced in CN cycle by
produced in CN cycle by
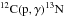 decays to
decays to
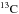 which when transported to the stellar
surface leads to low
which when transported to the stellar
surface leads to low 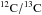 ratios characteristic of J-stars. Such
processes occur during the evolutionary stages of both single and binary stellar systems
as described next.
ratios characteristic of J-stars. Such
processes occur during the evolutionary stages of both single and binary stellar systems
as described next.
1.2.1. Single stars
It is not easy to construct a model of an AGB star with the peculiar properties of
J-stars. AGB star models predict low 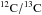 ratios for masses
ratios for masses
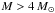 if temperatures at the base of the
convective envelope are sufficiently high for hot bottom burning (HBB, Boothroyd et al. 1995). However, the CN-cycle
operating under such conditions destroys
if temperatures at the base of the
convective envelope are sufficiently high for hot bottom burning (HBB, Boothroyd et al. 1995). However, the CN-cycle
operating under such conditions destroys 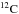 and consequently lowers the C/O ratio in
the envelope to below 1 making the star O-rich. Only narrow ranges of masses and
mass-loss rates lead to short phases (~0.1 Myr) on the AGB with both C/O > 1
and 12C/13C < 10 corresponding to J-stars. Moreover, TDU in the
TPAGB phase also enriches of the envelope with s-process elements that are synthesized
in the inter-pulse period when
and consequently lowers the C/O ratio in
the envelope to below 1 making the star O-rich. Only narrow ranges of masses and
mass-loss rates lead to short phases (~0.1 Myr) on the AGB with both C/O > 1
and 12C/13C < 10 corresponding to J-stars. Moreover, TDU in the
TPAGB phase also enriches of the envelope with s-process elements that are synthesized
in the inter-pulse period when 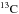 formed in the intershell region acts as
a neutron source via the 13C(α,n)16O reaction
(Straniero et al. 1995). However, observational
studies of J-stars show that abundances of s-process elements with respect to iron for
most of them are nearly solar (e.g. Utsumi 1985).
Later works also conclude that mean heavy element abundance among the J-stars in their
sample is compatible with no enrichment (Abia & Isern
2000).
formed in the intershell region acts as
a neutron source via the 13C(α,n)16O reaction
(Straniero et al. 1995). However, observational
studies of J-stars show that abundances of s-process elements with respect to iron for
most of them are nearly solar (e.g. Utsumi 1985).
Later works also conclude that mean heavy element abundance among the J-stars in their
sample is compatible with no enrichment (Abia & Isern
2000).
Statistically the narrow range of masses for which the HBB AGB models predict such chemical features cannot account for the observed fraction of J-stars among C-stars . Luminosity estimates from carbon-star surveys in the LMC also suggest that the HBB AGB models cannot explain the dimmer (MBol > −5) majority of J-stars (Hatzidimitriou et al. 2003).
1.2.2. Binary systems
While the HBB AGB scenario explains qualitatively the luminous J stars, a different
chain of events seems to be responsible for the anomalous features observed in the
majority of J-stars. Some other classes of C-stars also show traits common with J-stars
e.g. the R and CH stars which also show low 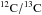 ratios (Vanture 1992) and are associated with binary formation scenarios (e.g. Izzard et al. 2007). Moreover observations of
silicate carbon stars which constitute about 10% of J-stars (Lloyd Evans 1991), provide further evidence of a link with binarity
(Lambert et al. 1990). Chemical pollution in
mass-transfer phases in binary systems during a nova-phase (Stehle & Ritter 1999) can result in peculiar surface abundances
for the secondary star in a semi-detached state (Marks
et al. 1997). Such pollution in nova systems presents a case of particular
interest in the context of the observed
ratios (Vanture 1992) and are associated with binary formation scenarios (e.g. Izzard et al. 2007). Moreover observations of
silicate carbon stars which constitute about 10% of J-stars (Lloyd Evans 1991), provide further evidence of a link with binarity
(Lambert et al. 1990). Chemical pollution in
mass-transfer phases in binary systems during a nova-phase (Stehle & Ritter 1999) can result in peculiar surface abundances
for the secondary star in a semi-detached state (Marks
et al. 1997). Such pollution in nova systems presents a case of particular
interest in the context of the observed 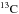 enhancements in J-stars.
enhancements in J-stars.
1.3. Classical novae
Novae are thermonuclear explosions in close binaries of the cataclysmic variable (CV)
type (Warner 1995) with a WD accreting
hydrogen-rich matter from a companion star undergoing Roche lobe overflow (RLOF). Among
them, classical novae involve RLOF from a MS star to a WD (CO or ONe) in a close binary
system resulting from a preceding common envelope (CE) phase (Paczynski 1976). At low accretion rates (below
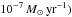 , hydrogen is compressed to degenerate
conditions until ignition occurs, which leads to a thermonuclear runaway (TNR). Explosive
hydrogen burning synthesizes some short-lived β-unstable nuclei (e.g.
, hydrogen is compressed to degenerate
conditions until ignition occurs, which leads to a thermonuclear runaway (TNR). Explosive
hydrogen burning synthesizes some short-lived β-unstable nuclei (e.g.
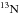 ,
, 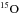 ) which are transported by convection to
the cooler outer envelope where isotopes like
) which are transported by convection to
the cooler outer envelope where isotopes like 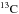 are produced from subsequent
β-decays. These decays release sufficient energy which causes an
explosive outburst in the outer shells of the WD accompanied by mass ejection with typical
velocities 102−103 km s-1 (Gehrz et al. 1998).
are produced from subsequent
β-decays. These decays release sufficient energy which causes an
explosive outburst in the outer shells of the WD accompanied by mass ejection with typical
velocities 102−103 km s-1 (Gehrz et al. 1998).
The energetics of the eruption, including the speed and mass of the ejecta, as well as
the ejecta composition, are determined by the mass of the underlying WD,
MWD, and the mass accretion rate, Ṁ. In
classical novae, Ṁ typically ranges between
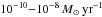 (Nomoto et
al. 2007). For
(Nomoto et
al. 2007). For 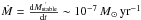 , the accreted material can burn steadily
resulting in growth of the WD mass possibly up to the Chandrasekhar limit leading to a
Type Ia supernova (Whelan & Iben 1973; Wheeler 1992; Hachisu
et al. 1996).
, the accreted material can burn steadily
resulting in growth of the WD mass possibly up to the Chandrasekhar limit leading to a
Type Ia supernova (Whelan & Iben 1973; Wheeler 1992; Hachisu
et al. 1996).
1.4. Nova nucleosynthesis
Observations of nova ejecta often show C, N and O overabundances with respect to solar indicating that there is some mixing between the core and the accreted envelope (Gehrz et al. 1998). The mixing between the accreted envelope and the underlying WD is a necessary condition both to power the explosion and to interpret the extra-solar metallicities observed in nova ejecta (Hernanz et al. 2001). Even though the exact mechanism and the extent of this mixing remain unclear, the WD core composition plays a crucial role in the subsequent nucleosynthesis making it essential to distinguish between novae occurring on CO and ONe WDs (Glasner et al. 2012) .
1.4.1. 13C production in novae
The synthesis of 13C in novae is initiated through
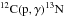 when the temperature at the base of the
accreted material on the WD surface reaches about 107K as required for the
cold CNO cycle to operate. The fate of 13C is determined by the competition
between destruction via
when the temperature at the base of the
accreted material on the WD surface reaches about 107K as required for the
cold CNO cycle to operate. The fate of 13C is determined by the competition
between destruction via 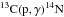 which operates near the burning shell,
and production by means of
which operates near the burning shell,
and production by means of  in the outer, cooler layers of the
envelope where a fraction of
in the outer, cooler layers of the
envelope where a fraction of 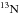 is carried to via convection just above
the burning shell. The Jose & Hernanz (1998)
nova models show much higher overproduction of 13C for CO novae as compared
to ONe novae. This is expected primarily because of the higher initial
is carried to via convection just above
the burning shell. The Jose & Hernanz (1998)
nova models show much higher overproduction of 13C for CO novae as compared
to ONe novae. This is expected primarily because of the higher initial
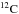 content of CO WDs, and the operation of
the hot CNO cycle when
content of CO WDs, and the operation of
the hot CNO cycle when 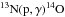 is faster than
is faster than
 (at base temperatures
>108 K) in more massive ONe WDs.
(at base temperatures
>108 K) in more massive ONe WDs.
All of these model calculations assume a uniform WD composition without explicitly
taking into account predictions from detailed evolutionary calculations. The nova ejecta
composition depends critically on the initial composition of the WD material mixed with
the accreted matter during explosion, and the predicted yields could well show larger
enhancements of heavier (CNO) elements if outer layers of the underlying WD has a
non-uniform composition (e.g. C:O = 50:50 for a CO nova). This could also account for
the wide range of C/O observed in nova ejecta (Gehrz et
al. 1998). José et al. (2004) refer to a
0.6 M⊙ CO WD model with initial C:O = 60:40 that gives
ejecta with C/O > 1. Such a case is of particular interest in context of carbon
(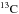 in particular) pollution in nova
explosions due to re-accretion of ejecta from the WD on its companion, and is considered
in a systematic approach as detailed in the following section.
in particular) pollution in nova
explosions due to re-accretion of ejecta from the WD on its companion, and is considered
in a systematic approach as detailed in the following section.
2. Method
This section outlines the nova re-accretion model we use to investigate pollution in MS companions to WDs (WD-companions hereafter) in nova binaries. The input physics and assumptions used in binary_c/nucsyn – our population nucleosynthesis code based on the BSE code of Hurley et al. (2002), extended to include various nucleosynthesis algorithms (Izzard et al. 2004, 2006, 2009) – are also described.
2.1. Nova re-accretion model
We use a simple geometric prescription to estimate the fraction of ejected mass
re-accreted by the WD-companion (secondary) during the nova-outbursts following the
approach used to study chemical pollution of the secondary during novae by Scott et al. (1994). Though nova shells are often
observed to be asymmetric, this is most likely caused by the interaction of the expanding
shells with the secondary star (Warner 1995).
Hence, in order to estimate the amount of ejected material that is accreted back on the
surface of the secondary, it is justifiable to assume a spherically symmetric outburst
with a geometric factor for the fraction of the nova-ejecta intercepted by the secondary,
 (1)which is the ratio of the cross-sectional
area of the secondary star of radius
(1)which is the ratio of the cross-sectional
area of the secondary star of radius 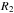 to the area of a sphere of radius equal to
the binary separation a. The mass of material re-accreted by the
secondary star is thus given by,
to the area of a sphere of radius equal to
the binary separation a. The mass of material re-accreted by the
secondary star is thus given by, 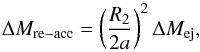 (2)where ΔMej is the
mass ejected during the outburst. During the nova (semi-detached) phase when the secondary
overfills its Roche lobe, R2 is approximately the Roche lobe
radius RL,2, and hence Eq. (1) gives the fraction fnova as a analytic
function of the mass ratio.
(2)where ΔMej is the
mass ejected during the outburst. During the nova (semi-detached) phase when the secondary
overfills its Roche lobe, R2 is approximately the Roche lobe
radius RL,2, and hence Eq. (1) gives the fraction fnova as a analytic
function of the mass ratio.
Equation (2) provides an upper estimate for the amount of material re-accreted, assuming all of the nova ejecta intercepted by the secondary sticks on to its surface. Detailed (3D) hydrodynamical studies also predict significant re-accretion of the ejecta in nova explosions on the surface of the WD companion (Campbell et al. 2010) and justify our simple choice for the prescription for re-accretion also used in previous works investigating similar effects of nova pollution (e.g. Marks et al. 1997).
2.2. Nova input physics
During novae, we assume that all but a small fraction ϵ = 0.001 of the accreted material is ejected in the explosion so that the WD does not grow significantly (Epelstain et al. 2007). Jose & Hernanz (1998) yields are used for the composition of the ejecta of classical novae with WD masses in the range of 0.8−1.35 M⊙ including both CO & ONe WD models, along with an additional 0.6 M⊙ CO-WD explosion model provided by Jose (priv. comm.).
 |
Fig. 1 Mass fractions of carbon and oxygen in the core of a TPAGB star with initial
|
All the CO-WD nova models assume a uniform composition C:O = 50:50 as initial input for the nucleosynthesis calculations in the explosion. However, a low mass CO-WD is expected to be carbon-rich (C/O > 1) in its outer layers that are mixed into the accreted envelope during the nova explosion (cf. Fig. 1). To account for this, an enhanced C/O ~ 2 is adopted for the ejecta composition of this 0.6 M⊙ CO-WD model. This choice is well within the observed range of ejecta compositions for classical novae as listed in the compilation of Gehrz et al. (1998), with even higher C/O for the ejecta of CO-novae e.g. V842 Cen with a estimated C/O ~ 5 (Andrea et al. 1994).
2.2.1. Common envelope prescription
The evolution of all CV systems, including those that go through a nova phase,
necessarily involves a CE phase which shrinks the orbital separation allowing a
subsequent semi-detached phase of mass-transfer from the secondary (e.g. a MS star for
classical novae). Hence, the CE phase plays an important role in determining which
binary systems go through a nova phase after the envelope is ejected. We treat the CE
phase using the α-formalism of Paczynski (1976) assuming that the orbital energy release during the inspiral
is transferred to the envelope with an efficiency αCE, and
can expand and eject at least some of the envelope (Hurley et al. 2002). The envelope binding energy is parametrized as,
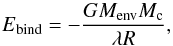 (3)where
Menv, Mc and
R are the envelope mass, core mass and radius of the star and
λ is a measure of central condensation of the star that is calculated
from detailed stellar models (Dewi & Tauris
2000). The choice of the parameter αCE is critical
for any population synthesis study involving nova binaries (Nelson et al. 2004). It is most probably not a constant (Davis et al. 2012) though population synthesis models
usually assume a constant
(3)where
Menv, Mc and
R are the envelope mass, core mass and radius of the star and
λ is a measure of central condensation of the star that is calculated
from detailed stellar models (Dewi & Tauris
2000). The choice of the parameter αCE is critical
for any population synthesis study involving nova binaries (Nelson et al. 2004). It is most probably not a constant (Davis et al. 2012) though population synthesis models
usually assume a constant 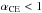 . Our systematic approach to constrain
αCE for nova systems, as outlined in Appendix A, involves
estimating the expected rate of novae in our Galaxy (Z = 0.02) in order
to compare with existing observational constraints on the Galactic nova rate (Shafter 2002). Based on the results of our
calculations (cf. Table A.1) we adopt a constant
αCE = 0.2 for our population synthesis work which is also
consistent with recent observational studies of post-CE binaries constraining
αCE (Zorotovic et al.
2010; De Marco et al. 2011), and briefly
discuss the systematic effect of this choice on our population synthesis predictions.
. Our systematic approach to constrain
αCE for nova systems, as outlined in Appendix A, involves
estimating the expected rate of novae in our Galaxy (Z = 0.02) in order
to compare with existing observational constraints on the Galactic nova rate (Shafter 2002). Based on the results of our
calculations (cf. Table A.1) we adopt a constant
αCE = 0.2 for our population synthesis work which is also
consistent with recent observational studies of post-CE binaries constraining
αCE (Zorotovic et al.
2010; De Marco et al. 2011), and briefly
discuss the systematic effect of this choice on our population synthesis predictions.
2.3. binary_c/nucsyn
To investigate the re-accretion of nova ejecta by WD-companions according to the
prescription described in Sect. 2.1, the
binary_c/nucsyn code is used to evolve grids of binaries at
metallicities Z = 0.008and0.02 for a range of initial primary
(M1) and secondary (M2) masses
with M1 > M2, and initial
separations (a) which give nova systems within a Hubble time (13.7 Gyr).
The following limits are therefore chosen for M1,
M2 and a,
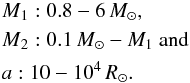 (4)
(4)
2.3.1. Initial distributions
The initial distributions of binary parameters M1,
M2 and a are given by the functions
Ψ(lnM1), Φ(lnM2) and
χ(lna) with, 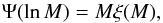 (5)where
ξ(M) is the initial mass function (IMF) of Kroupa et al. (1993). The distribution Φ for
M2 is chosen to be flat in the mass ratio
q = M2/M1 and
the separation distribution χ is taken to be flat in
log a, to facilitate comparison with previous works of Politano et al. (2010), Nelson et al. (2004).
(5)where
ξ(M) is the initial mass function (IMF) of Kroupa et al. (1993). The distribution Φ for
M2 is chosen to be flat in the mass ratio
q = M2/M1 and
the separation distribution χ is taken to be flat in
log a, to facilitate comparison with previous works of Politano et al. (2010), Nelson et al. (2004).
2.3.2. Binary fraction
We assume a constant binary fraction 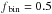 which corresponds to an equal number of
single and binary systems in our stellar population (Duquennoy & Mayor 1991).
which corresponds to an equal number of
single and binary systems in our stellar population (Duquennoy & Mayor 1991).
2.3.3. Binary grid
With the above choices for initial binary parameters, a logarithmic grid is set up in
M1 − M2 − a
space for all binary stars and in M (initial mass with same choice of
distribution and range as M1) for single stars. The grid is
split into n stars per dimension such that each star represents the
centre of a logarithmic grid-cell of size δV where, 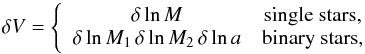 (6)with
(6)with 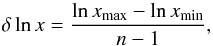 (7)where x represents
M, M1, M2 or
a and xmin and
xmax are the grid limits. The probability for the
ith model in the grid is given by,
(7)where x represents
M, M1, M2 or
a and xmin and
xmax are the grid limits. The probability for the
ith model in the grid is given by, 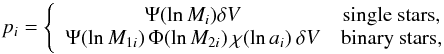 (8)where
(8)where
 (9)over the entire range of parameter space
i.e. over masses (e.g. over M for single stars) and separations. Hence
for binaries,
(9)over the entire range of parameter space
i.e. over masses (e.g. over M for single stars) and separations. Hence
for binaries, 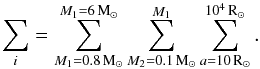 (10)
(10)
2.3.4. Population synthesis
The re-accretion model as outlined in Sect. 2.1
is applied to grids of binary models at a fixed metallicities Z = 0.02
(solar) and 0.008 (LMC). The initial abundances are chosen to be solar-scaled based on
the values of Anders & Grevesse (1989). The
number of stars of a certain type (e.g. a C or J-star) is counted by calculating the
probability of the existence of the stellar system (single or binary) given by Eq.
(8) and the time it spends in the
evolutionary phase of interest Δti from,
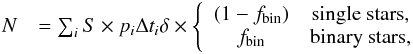 (11)where δ = 1 if the star is
in the phase of interest (and zero otherwise), the binary fraction
fbin = 0.5 = 1 − fbin and
S = 7.086 yr-1 is the (constant) star formation rate
obtained following the prescription of Hurley et al.
(2002). Thus, for C-stars, δ = 1 if C/O > 1, and if in
addition
(11)where δ = 1 if the star is
in the phase of interest (and zero otherwise), the binary fraction
fbin = 0.5 = 1 − fbin and
S = 7.086 yr-1 is the (constant) star formation rate
obtained following the prescription of Hurley et al.
(2002). Thus, for C-stars, δ = 1 if C/O > 1, and if in
addition 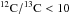 , they also classify as J-stars. Also, C
and J-stars are only counted as giants (stellar types GB, EAGB, TPAGB; Hurley et al. 2002) to compare with the statistics
from observational surveys since luminosity estimates indicate that the stars are all
giants. The number of J-type stars (NJ) is then calculated
according to Eq. (11), along with the
total number of C-stars (NC) to predict the ratio
NJ/NC giving the frequency of
J-stars among C-stars.
, they also classify as J-stars. Also, C
and J-stars are only counted as giants (stellar types GB, EAGB, TPAGB; Hurley et al. 2002) to compare with the statistics
from observational surveys since luminosity estimates indicate that the stars are all
giants. The number of J-type stars (NJ) is then calculated
according to Eq. (11), along with the
total number of C-stars (NC) to predict the ratio
NJ/NC giving the frequency of
J-stars among C-stars.
3. Results
The evolution of nova binaries that are of interest in the re-accretion scenario for J-stars is presented in this section followed by an estimate for the number fraction of such nova-polluted C-stars expected to evolve as J-stars.
Initial binary parameters M1, M2 and a for typical post-nova merger progenitors with for Z = 0.008, αCE = 0.2.
3.1. Evolution of WD-companions in nova binaries
The orbital evolution of binary systems that emerge from a first CE phase as a WD-MS
binary depends on the mass ratio qdonor (Pylyser & Savonije 1988) given by,
 (12)where Mdonor is
the mass of the WD-companion. Assuming conservative mass-transfer, the orbital separation
decreases during the nova phase if qdonor > 1, and
Mdonor decreases until
qdonor < 1. Thereafter, the orbit widens and the ultimate
fate of such a system is a detached state with Mdonor being
too low to evolve up to the giant branch within a Hubble time. Hence such systems are not
interesting as progenitors for nova-polluted J-stars.
(12)where Mdonor is
the mass of the WD-companion. Assuming conservative mass-transfer, the orbital separation
decreases during the nova phase if qdonor > 1, and
Mdonor decreases until
qdonor < 1. Thereafter, the orbit widens and the ultimate
fate of such a system is a detached state with Mdonor being
too low to evolve up to the giant branch within a Hubble time. Hence such systems are not
interesting as progenitors for nova-polluted J-stars.
3.1.1. Post-nova mergers as J-stars
The ultimate fate of systems which keep qdonor > 1 during the nova phase depends critically on the rate of mass-transfer, Ṁ. The systems in Table 1 represent typical cases in which the binary eventually merges into a giant single star that satisfies the adopted criteria for J-stars (Sect. 2.3.4). Such post-nova mergers classify into two distinct binary evolutionary channels depending on the evolution of mass-transfer during the nova phase:
-
1.
Coalescence (COAL): if the nova phase continues withṀ < 10-7 M⊙ yr-1 until the WD companion (donor) becomes a low-mass (Mdonor ≃ 0.7 M⊙) MS star, mass-transfer to the WD becomes dynamically unstable as the donor (MS) star becomes deeply convective and qdonor (>1) also exceeds the critical mass-ratio qcrit for stable RLOF (Hurley et al. 2002). All the material is accreted and swells up to form a giant envelope around the WD which becomes the core of a merged giant (TPAGB) star. If re-accretion of nova-ejecta pollutes the WD-companion such that its surface C/O > 1 and 12C/13C < 10, the coalesced (AGB) star classifies as a J-star. Such a typical system is labeled as COAL-A in Table 1 in which the merged star is a 1.2 M⊙ TPAGB star with a CO core mass ~0.6 M⊙ and hence has a lower luminosity L ~ 103 L⊙ (⇒MBol > −4) compared to typical AGB C(N)-stars with L ~104 L⊙ (⇒MBol < −4) and M ≳ 2 M⊙. . However, following the nova-phase, if the WD-companion has surface C/O < 1 but 12C/13C < 10, the merger can subsequently evolve on the AGB with C/O > 1 because of TDU until its 12C/13C > 10, and classify as a J-star. A typical example is labeled as COAL-B in Table 1 with a higher luminosity (MBol < −4) as compared to the COAL-A system depending on their evolutionary phases on the AGB when they classify as J-stars. Figure 2 illustrates the differences in evolution of these two typical COAL systems through the nova-phase followed by the AGB phase of the nova-polluted merger that evolves into a J-star.
-
2.
Common envelope (CE): for suitable initial parameters (M1, M2, a), e.g. systems CE-A/B of Table 1, RLOF proceeds at the thermal rate of the WD-companion when it evolves as a Hertzsprung Gap (HG) star with a radiative or thin convective envelope. When the thermal rate is less than 10-7 M⊙ yr-1, the nova phase continues until the WD-companion becomes a giant (GB) when mass-transfer is dynamically unstable and leads to a (second) CE phase. Consequently the system merges and the CO-WD becomes the core surrounded by a He-shell (core of the giant donor) resembling an EAGB star whose surface abundances are determined primarily by the donor star which suffers from nova-pollution. A typical case is labelled as CE-A in Table 1 with the merged EAGB star having both C/O > 1 and 12C/13C < 10. If the thermal rate exceeds
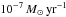 during the RLOF-phase, steady
H-burning on the surface of the accreting WD ends the nova phase. Thereafter, the
orbit continues to shrink leading to runaway mass transfer until the material
accreted onto the WD swells up to form a giant star and the system also merges in
a (second) CE-phase. Such an example is the CE-B case of Table 1 for which the CE merger outcome ascends the
AGB with 12C/13C < 10 owing to previous nova-pollution
until it becomes a C-star when C/O > 1 because of TDU. Thus it classifies as a
J-star only for a brief phase (~105 yr) of its TPAGB until
12C/13C > 10 because 12C is brought to the
surface by TDU. The evolution of this system is shown in Fig. 3 for the nova phase preceding the CE, and the AGB phase of the
merged star that becomes a J-star on the EAGB for the CE-A system but requires TDU
on the TPAGB for the CE-B system.
during the RLOF-phase, steady
H-burning on the surface of the accreting WD ends the nova phase. Thereafter, the
orbit continues to shrink leading to runaway mass transfer until the material
accreted onto the WD swells up to form a giant star and the system also merges in
a (second) CE-phase. Such an example is the CE-B case of Table 1 for which the CE merger outcome ascends the
AGB with 12C/13C < 10 owing to previous nova-pollution
until it becomes a C-star when C/O > 1 because of TDU. Thus it classifies as a
J-star only for a brief phase (~105 yr) of its TPAGB until
12C/13C > 10 because 12C is brought to the
surface by TDU. The evolution of this system is shown in Fig. 3 for the nova phase preceding the CE, and the AGB phase of the
merged star that becomes a J-star on the EAGB for the CE-A system but requires TDU
on the TPAGB for the CE-B system.
Thus, the nova re-accretion scenario predicts mergers that evolve as J-stars with very low 12C/13C (<4) ratios and luminosities L ~ 103 L⊙ (⇒MBol > −4) unlike typical AGB C-stars undergoing HBB with low 12C/13C. Post-nova merger systems like COAL-A and CE-A are C-rich from the re-accretion of nova-ejecta and thus classify as J-stars even without TDU. On the other hand, cases COAL-B and CE-B which emerge as post-nova mergers necessarily require TDU to have C/O > 1 and thus behave as more luminous J-stars on the TPAGB.
 |
Fig. 2 Evolution of COAL type systems of Table 1.
For each system i.e. COAL-A (Fig. A) and COAL-B (Fig. B), the top
and bottom panels on the left show
masses and evolutionary stages of both the primary (WD) and the secondary stars
during the nova phase when the mass-transfer rate
( |
 |
Fig. 3 Evolution of CE type systems of Table 1. Refer to Fig. 2 caption for description of evolutionary stages shown. The CE-A merger exhibits properties of a J-star on the EAGB unlike the COAL-B merger which has C/O > 1 only during TDU and hence has a short phase on the TPAGB (marked by the dotted lines) when it classifies as a J-star. |
3.1.2. Initial binary parameters for post-nova mergers
Figure 4 shows the range of initial binary
parameters (M1vs.M2,
M1vs.a) for the post-nova merger s that
evolve to become J-stars. The COAL mergers that classify as J-stars mostly originate
from binary systems with WD masses close to 0.6 M⊙ for
M1 < 3 M⊙. CE mergers
mostly originate from systems with 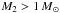 which involve thermal-timescale
mass-transfer (mostly on the HG) during RLOF.
which involve thermal-timescale
mass-transfer (mostly on the HG) during RLOF.
 |
Fig. 4 Range of initial primary mass M1, initial secondary mass M2 and initial separation a for nova-merger cases (COAL/CE) that form J-stars. |
3.2. J-stars from Case-B RLOF mergers
Unlike nova progenitor systems that emerge as a WD-MS binary following a CE phase, depending on their initial separation binaries also merge in the CE phase because of unstable mass transfer from a primary star on the GB to a MS secondary (Case-B RLOF). This is illustrated in Fig. 5 which distinguishes the evolutionary channel for these systems from the post-nova mergers (COAL/CE) as described in Sect. 3.1.1. The merged (GB) star has a lower helium core mass than expected for a single star of the same total mass at the beginning of the GB. The typical evolution of such an object on the TPAGB is shown in Fig. B.1 (cf. Appendix B), along with a single star model of similar total mass, which illustrates the difference in evolutionary time-scales for the two cases. As a result, they contribute significantly to the number of stars that classify as C and J-stars in our population synthesis calculations as described next.
 |
Fig. 5 Binary evolutionary channels which lead to mergers with properties of J-stars from re-accretion of nova-ejecta followed by COAL and CE mergers or HBB in AGB-phases of GB-MS (Case-B RLOF) mergers. The different stellar evolutionary phases are marked (with colours) as – blue: MS star, red: giant-envelope/CE, golden: He-core/WD, black: CO-core/WD, orange: nova-polluted star (MS/HG). |
3.3. Population synthesis
With the method outlined in Sect. 2.3.4, a binary grid of resolution 100 × 50 × 100 in M1 − M2 − a space is evolved for Z = 0.008 and 0.02, αCE = 0.2 and fbin = 0.5 to estimate the total number of J-stars expected from the instances of nova-pollution as described in Sect. 3.1.1, as well as from HBB in both single and binary AGB stars.
3.3.1. Observational selection effects
Our population synthesis is performed considering possible selection effects in
observations from existing surveys for J-stars. For instance in the LMC survey of Morgan et al. (2003), the J,
H, K magnitudes for all J-stars lead to bolometric
magnitudes MBol < −2.8 derived using the relation (as
adopted in Hatzidimitriou et al. 2003),
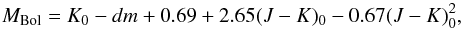 (13)with a distance modulus
dm = 18.45 for the LMC (Westerlund
1997), a K-band absorption
AK = 0.02 (Wood et al. 1983) along with mean reddening
E(J − K) = 0.07 (Costa & Frogel 1996) to find the de-redenned
colours denoted by
K0 = K − AK
and
(J − K)0 = (J − K) − E(J − K).
We use this as a low-luminosity cut-off in our estimates for the number of C
(NC) and J (NJ) stars.
(13)with a distance modulus
dm = 18.45 for the LMC (Westerlund
1997), a K-band absorption
AK = 0.02 (Wood et al. 1983) along with mean reddening
E(J − K) = 0.07 (Costa & Frogel 1996) to find the de-redenned
colours denoted by
K0 = K − AK
and
(J − K)0 = (J − K) − E(J − K).
We use this as a low-luminosity cut-off in our estimates for the number of C
(NC) and J (NJ) stars.
3.3.2. NJ/NC ratio
The number of stars of interest (i.e. NJ, NC) is calculated as described in Sect. 2.3.4 for all systems both in our single and binary grids for metallicities Z = 0.008 (LMC) and 0.02 (solar). The resulting NJ/NC ratio are presented in Table 2, with the binary J-stars separated (in columns) according to their evolutionary origin i.e. post-nova merger or HBB. Furthermore, the difference in the values of the ratios between the upper and lower rows in each of these two columns occurs from counting Case-B RLOF mergers (as described in Sect. 3.2) which have considerably longer HBB-AGB phases compared to single AGB stars of same total mass (cf. Appendix B) and classify as J-stars. However, the total NJ/NC ratio considering all single (HBB) and binary (merger) J-stars is still below the observed fraction (10−15%) for both Z = 0.008 and 0.02.
NJ/NC ratios for single (Col I) and binary (Col II) stars.
3.3.3. Luminosity function for LMC J-stars
The J-star luminosity function (JSLF) is constructed with the NJ/NC ratio binned in MBol intervals of 0.5 mag (Fig. 6). In order to compare with observations, Eq. (13) is used to derive the bolometric magnitudes of all the 156 LMC J-stars of Morgan et al. (2003).
 |
Fig. 6 Luminosity function of LMC J-stars (JSLF). The histograms binned in
MBol intervals of 0.5 mag show expected number
fraction
(NJ/NC)
of J-stars among C-stars for HBB (single) stars and binary mergers (post-nova or
Case-B RLOF) – compared with the JSLF constructed for the LMC J-stars of Morgan et al. (2003) with Poisson
|
 |
Fig. 7 Luminosity function of LMC J-stars (JSLF). Number fraction (NJ/NC) of J-stars among C-stars for post-nova mergers and HBB-stars excluding Case-B RLOF binary mergers is shown with observed J-stars from the sample of Morgan et al. (2003) binned in MBol intervals of 0.5 mag. The total NJ/NC ratio is ~2% for the nova-polluted mergers – lower than the total NJ/NC in Fig. 6 (~5%) and the observed fraction (~10%) of the stars in the sample of Morgan et al. (2003). |
 |
Fig. 8 Distributions of |
Figure 6 shows that the post-nova merger channel produces J-stars that are dimmer (with MBol > −5) but much rarer compared to the HBB stars (with MBol < −6). In contrast, the distribution constructed from the observed sample of Morgan et al. (2003) has the majority of J-stars dimmer than MBol = −6. However, most of the J-stars with MBol < −6 result from Case-B RLOF whose post-merger evolution on the (TP)AGB is different compared to single (AGB) stars of similar masses (cf. Fig. B.1). The JSLF for the post-nova mergers is shown separately in Fig. 7 along with that of single and binary HBB-AGB stars excluding the Case-B RLOF mergers. It has closer resemblance to the JSLF of the stars from Morgan et al. (2003), with a higher fraction of low-luminosity J-stars as observed in the Morgan et al. (2003) survey, though the predicted NJ/NC is still lower and well below the observed fraction for the dimmer (MBol > −6) J-stars in the LMC.
3.3.4. Number distributions
The number distributions for masses (M) and
12C/13C ratios of LMC (Z = 0.008) J-stars are
shown in Fig. 8, excluding the HBB Case-B RLOF
mergers (as described in Sect. 3.2). The post-nova
mergers have 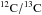 ratios lower than 4, and low masses
(<2 M⊙) unlike the HBB stars, since majority of the
post-nova mergers owe their C-enhancement to the re-accretion of C-rich nova ejecta from
a low-mass (~0.6 M⊙) CO-WD and can evolve as J-stars
without TDU on the AGB. The
ratios lower than 4, and low masses
(<2 M⊙) unlike the HBB stars, since majority of the
post-nova mergers owe their C-enhancement to the re-accretion of C-rich nova ejecta from
a low-mass (~0.6 M⊙) CO-WD and can evolve as J-stars
without TDU on the AGB. The 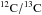 ratios remain low on the AGB for such
systems e.g. COAL-A (cf. Table 1) whereas for
HBB-stars (>2 M⊙) the
ratios remain low on the AGB for such
systems e.g. COAL-A (cf. Table 1) whereas for
HBB-stars (>2 M⊙) the
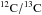 ratios increase during TDU when they
become C(J)-stars.
ratios increase during TDU when they
become C(J)-stars.
4. Discussion
The binary scenario for the origin of J-stars explored in this work illustrates the need for detailed evolutionary studies in several aspects of both single and binary star evolution. The nucleosynthesis associated both with nova explosions for low-mass CO-WDs as well the treatment of HBB during AGB evolution, particularly in context of binary mergers, require detailed models that account for the evolutionary history of the associated binary system. Particularly, detailed evolutionary calculations of RG-MS (Case-B RLOF) mergers are required to determine their evolutionary time-scales and nucleosynthesis (especially the phase with HBB) on the AGB.
In the context of post-nova mergers that can exhibit properties associated with J-stars, other chemical peculiarities e.g. the O-isotopic ratios, N-enhancements, Li-enrichment, s-process abundances etc., need to be investigated and compared with observations (e.g. Hedrosa et al. 2013). To quantitatively predict these isotopic ratios for the J-stars expected from the nova-pollution scenario, a detailed low-mass CO-WD nova model is required providing ejecta composition for initial C:O ratio different from a uniform one (50:50) as used in existing models of CO-WD explosions. Also, chemical pollution of the secondary (donor) star during the nova phase with carbon rich ejecta should influence the subsequent nova explosions when RLOF from the nova-polluted donor transfers some of the material from its surface back to the WD. However, investigating such an effect requires nova models with varying accretion compositions which is beyond the scope of the present study.
The systematic uncertainties associated with our prediction for the NJ/NC ratio for the post-nova merger channel (without HBB stars) include our choice of the CE ejection efficiency parameter αCE. The post-CE separations for the WD-MS nova progenitor systems increase with αCE which prevents RLOF from the WD-companion during its MS/HG phase of evolution and a subsequent nova phase for the binary. We adopt a constant αCE = 0.2 based on our estimate for the Galactic nova rate (refer Appendix A) which is constrained by observations (Shafter 2002). With regard to other assumptions in our modelling of nova systems, the use of a nearly constant WD mass in the nova phase is justifiable within the usual range of classical novae mass transfer rates (Ṁ ~ 10-10−10-8 M⊙ yr-1) based on detailed models which investigate the ratio of mass ejected to that accreted in outbursts for the entire range of MWD (Yaron et al. 2005). We also use a constant binary fraction fbin = 0.5 in our population synthesis since the post-nova mergers that classify as J-stars evolve from low-mass WD-MS systems and in view of existing observations estimating the binary fraction for this range (~1 M⊙) of stellar masses (Duchêne & Kraus 2013).
5. Conclusions
This work investigates the effect of chemical pollution of WD companions in nova binaries
because of re-accretion of nova ejecta and their subsequent evolution with observed
properties of J-stars. The re-accretion model (Sect. 2.1) is applied to a population of binary systems using the population
nucleosynthesis code binary_c/nucsyn to predict the properties of post-nova
systems that evolve as giant stars having both C/O > 1 and
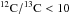 – properties characteristic to J-stars. We
identify systems which merge (COAL or CE) as a result of unstable (dynamical or thermal)
mass-transfer following a nova phase during which the material ejected from the WD pollutes
its companion with enough carbon (including
– properties characteristic to J-stars. We
identify systems which merge (COAL or CE) as a result of unstable (dynamical or thermal)
mass-transfer following a nova phase during which the material ejected from the WD pollutes
its companion with enough carbon (including 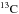 ) to have
) to have
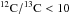 .
.
The post-nova mergers evolve as AGB J-stars with a low-mass WD as its core and the
companion absorbed into its envelope. Such low mass (<2 M⊙)
AGB stars have low 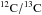 and are dimmer than
MBol = −5, resembling observed J-stars in the LMC that cannot
otherwise be explained with single star (HBB) models. However, our population synthesis
study shows that this channel together with HBB (single or binary) stars cannot account for
the observed fraction of J-stars among C-stars in the LMC and our Galaxy. It indicates that
other channels for the origin of J-stars need to be taken into account in future studies
aiming to explain the observed frequency of J-stars. The GB-MS (Case B RLOF) mergers that
possibly behave differently from normal (single) AGB stars are of particular interest and
detailed evolutionary calculations are necessary to determine their evolutionary
time-scales. Other binary scenarios such as HeWD-giant mergers (Zhang & Jeffery 2013) should also be investigated in a population
synthesis framework to explain the observed fraction of J-stars among C-stars. Such
scenarios could also lead to possible evolutionary connections with other classes of C-stars
e.g. CEMP-no stars which show chemical peculiarities common to J-stars at much lower
metallicities associated with the Galactic halo.
and are dimmer than
MBol = −5, resembling observed J-stars in the LMC that cannot
otherwise be explained with single star (HBB) models. However, our population synthesis
study shows that this channel together with HBB (single or binary) stars cannot account for
the observed fraction of J-stars among C-stars in the LMC and our Galaxy. It indicates that
other channels for the origin of J-stars need to be taken into account in future studies
aiming to explain the observed frequency of J-stars. The GB-MS (Case B RLOF) mergers that
possibly behave differently from normal (single) AGB stars are of particular interest and
detailed evolutionary calculations are necessary to determine their evolutionary
time-scales. Other binary scenarios such as HeWD-giant mergers (Zhang & Jeffery 2013) should also be investigated in a population
synthesis framework to explain the observed fraction of J-stars among C-stars. Such
scenarios could also lead to possible evolutionary connections with other classes of C-stars
e.g. CEMP-no stars which show chemical peculiarities common to J-stars at much lower
metallicities associated with the Galactic halo.
Online material
Appendix A: Constraining CE ejection efficiency
Our choice of the CE ejection efficiency parameter αCE is
based on the following population synthesis estimate for the Galactic nova rate (per
year) which is constrained by observations (Shafter
2002). In the population synthesis algorithm for counting novae, the total
frequency (νtot) of nova-explosions (per year) for
Z = 0.02 and a constant star formation rate,
S = 7.086 yr-1 (following the prescription of Hurley et al. 2002), is estimated from, 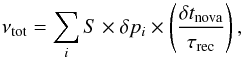 (A.1)with the nova recurrence time
(A.1)with the nova recurrence time
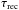 for a binary system calculated for every
timestep δtnova of its evolution in a nova-phase from,
for a binary system calculated for every
timestep δtnova of its evolution in a nova-phase from,
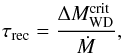 (A.2)using the expression of Yungelson et al. (1995) for the critical ignition
mass
(A.2)using the expression of Yungelson et al. (1995) for the critical ignition
mass 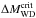 ,
,
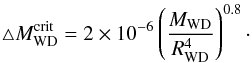 (A.3)The WD radius
RWD is determined according to the formula of Nauenberg (1972),
(A.3)The WD radius
RWD is determined according to the formula of Nauenberg (1972),
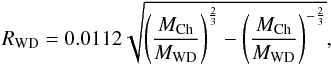 (A.4)where
MCh = 1.43 M⊙ is the Chandrasekhar mass.
(A.4)where
MCh = 1.43 M⊙ is the Chandrasekhar mass.
Appendix A.1: Galactic nova rate
With the above prescription, the total rate of novae in the Galaxy
(Z = 0.02) is calculated using binary_c/nucsyn as,
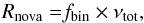 (A.5)assuming a constant binary fraction
fbin = 0.5 (Duquennoy
& Mayor 1991). As shown in Table A.1, our estimate of the Galactic nova rate is consistent with existing
estimates of 30 ± 10 yr-1 (Shafter
2002) within a factor of ~2–3, being closer to the observed rate for
values of αCE < 0.5, and decreasing with higher values
of αCE.
(A.5)assuming a constant binary fraction
fbin = 0.5 (Duquennoy
& Mayor 1991). As shown in Table A.1, our estimate of the Galactic nova rate is consistent with existing
estimates of 30 ± 10 yr-1 (Shafter
2002) within a factor of ~2–3, being closer to the observed rate for
values of αCE < 0.5, and decreasing with higher values
of αCE.
 |
Fig. A.1 Histograms of predicted Galactic nova rate as function of WD mass, MWD per 0.1 M⊙ bin, for αCE = 0.2 (upper panel) and 0.5 (lower panel). The total rate of novae in the Galaxy Rnova is the sum of the contributions from all MWD bins. |
Figure A.1 further illustrates the sensitivity of the nova rate to the choice of αCE. The nova rate decreases sharply at higher WD masses and for more efficient CE ejection. This is expected because the final separation after the CE phase increases with αCE, so that for a higher αCE, the post-CE binary is too wide for the secondary to evolve to fill its Roche lobe. Because of shorter recurrence times for massive WDs which lead to more frequent outbursts, the total nova rate drops sharply with increasing αCE (0.2to0.5). Nelson et al. (2004) also find an increase in the nova rate by a factor of ~2–3 for lower CE ejection efficiency. For αCE < 0.2, the nova rate decreases as more systems merge following the CE phase that leads to the WD-MS binary.
Appendix A.2: Additional tests for nova binaries
The fraction, α, of binary systems hosting WDs that lead to novae is
also estimated as, 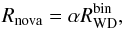 (A.6)where
(A.6)where
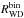 is the birth rate of WDs in binary
systems. Also, the frequency averaged WD mass (⟨MWD⟩ in
M⊙) is calculated for different choices of
αCE (<1). As shown in Table A.1, our estimates for this fraction α (defined by
Eq. (A.6)) is close to the value of
0.02 used by Romano & Matteucci (2005) to
match the observed nucleosynthesis yields for Galactic novae. The averaged (by nova
frequency) WD mass ⟨MWD⟩ is also in agreement with the
values in the range of 0.8−1.1 M⊙ as obtained by Nelson et al. (2004).
is the birth rate of WDs in binary
systems. Also, the frequency averaged WD mass (⟨MWD⟩ in
M⊙) is calculated for different choices of
αCE (<1). As shown in Table A.1, our estimates for this fraction α (defined by
Eq. (A.6)) is close to the value of
0.02 used by Romano & Matteucci (2005) to
match the observed nucleosynthesis yields for Galactic novae. The averaged (by nova
frequency) WD mass ⟨MWD⟩ is also in agreement with the
values in the range of 0.8−1.1 M⊙ as obtained by Nelson et al. (2004).
Appendix B: HBB J-stars: single stars vs. binary mergers
If mass ratio q exceeds a critical value
qcrit (as defined in Hurley et al. 2002), RLOF from a GB star to a lower mass MS companion is
dynamically unstable and mass transfer leads to a CE phase in which the system can merge
depending on the initial separation. For such a Case-B RLOF merger, the MS star is
absorbed into the envelope and the core-mass of the merger is determined by the core of
the GB donor star at the onset of the CE phase. Consequently, following the CE phase,
the merged star has a lower core mass on the GB compared to a single star of same total
mass. Because the core mass at the base of the AGB phase in our synthetic models depends
on the core mass at the base of the GB (Hurley et al.
2002), such mergers ascend the AGB with lower core masses than single AGB stars
of similar total masses. Consequently they live longer on the AGB and, for total masses
higher than about 4 M⊙ for which HBB occurs along with
TDU, we predict such mergers also behave as J-stars for a longer phase on the AGB as
compared to single HBB AGB stars. Figure B.1 shows
an example of the J-star phase for such a binary merger that lasts for about 1 Myr
compared to the much shorter span of about 0.1 Myr for an equivalent single star. The
binary system initially consists of a 3.1 M⊙ primary star
which overflows its Roche lobe on the GB with a core mass of
0.45 M⊙ that subsequently forms the core of the merged
star following a CE phase with the 1.3 M⊙ (MS) secondary
absorbed into the giant envelope. Thus, the merger core (and envelope) mass is
significantly different from a single star of similar total mass, and consequently the
core mass can only grow to 0.47 M⊙ at the end of the GB –
significantly lower than the expected core mass
(~0.73 M⊙) of a corresponding single star. This in
turn leads to a lower core mass at the start of the TPAGB for the binary merger and
consequently it evolves for a longer phase with TDU because of which its surface C/O
exceeds 1, and HBB that decreases the isotopic ratios of
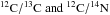 on the stellar surface classifying it as
a J-star.
on the stellar surface classifying it as
a J-star.
 |
Fig. B.1 Evolutionary properties on the TPAGB for a single star (upper
panel) and a GB-MS (Case-B RLOF) binary merger (lower
panel) of similar total mass. The core mass
Mc and surface C/O are plotted on the left scale,
along with surface isotopic ratios, |
Acknowledgments
We acknowledge the anonymous referee for useful comments and interesting suggestions for further studies. SS thanks K. Ohnaka for sharing his observational expertise throughout the course of this work and for his valuable comments to improve the manuscript. Special thanks also go to J. Jose and R.J. Stancliffe for providing their models for this work. S.S. received the financial support from the Bonn-Cologne Graduate School for Physics and Astronomy and the Bonn International Graduate School and is a member of the International Max Planck Research School for Astronomy and Astrophysics at the Universities of Bonn and Cologne. R.G.I. and H.H.B.L. thank the Alexander von Humboldt foundation for funding their positions in Bonn.
References
- Abia, C., & Isern, J. 2000, ApJ, 536, 438 [NASA ADS] [CrossRef] [Google Scholar]
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Andrea, J., Drechsel, H., & Starrfield, S. 1994, A&A, 291, 869 [NASA ADS] [Google Scholar]
- Boothroyd, A. I., Sackmann, I.-J., & Wasserburg, G. J. 1995, ApJ, 442, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Bouigue, R. 1954, Annales d’Astrophysique, 17, 104 [Google Scholar]
- Campbell, S., Jose, J., Cabezon, R., & García-Berro, E. 2010, in 11th Symposium on Nuclei in the Cosmos, PoS(NIC XI)203 [Google Scholar]
- Costa, E., & Frogel, J. A. 1996, AJ, 112, 2607 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, P. J., Kolb, U., & Knigge, C. 2012, MNRAS, 419, 287 [NASA ADS] [CrossRef] [Google Scholar]
- De Marco, O., Passy, J.-C., Moe, M., et al. 2011, MNRAS, 411, 2277 [NASA ADS] [CrossRef] [Google Scholar]
- Dewi, J. D. M., & Tauris, T. M. 2000, A&A, 360, 1043 [NASA ADS] [Google Scholar]
- Duchêne, G., & Kraus, A. 2013, ARA&A, 51, 269 [Google Scholar]
- Duquennoy, A., & Mayor, M. 1991, A&A, 248, 485 [NASA ADS] [Google Scholar]
- Epelstain, N., Yaron, O., Kovetz, A., & Prialnik, D. 2007, MNRAS, 374, 1449 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrz, R. D., Truran, J. W., Williams, R. E., & Starrfield, S. 1998, PASP, 110, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Glasner, S. A., Livne, E., & Truran, J. W. 2012, MNRAS, 427, 2411 [NASA ADS] [CrossRef] [Google Scholar]
- Hachisu, I., Kato, M., & Nomoto, K. 1996, ApJ, 470, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Hatzidimitriou, D., Morgan, D. H., Cannon, R. D., & Croke, B. F. W. 2003, MNRAS, 341, 1290 [NASA ADS] [CrossRef] [Google Scholar]
- Hedrosa, R. P., Abia, C., Busso, M., et al. 2013, ApJ, 768, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Hernanz, M., José, J., & Coc, A. 2001, in Cosmic evolution, eds. E. Vangioni-Flam, R. Ferlet, & M. Lemoine, 149 [Google Scholar]
- Hurley, J. R., Tout, C. A., & Pols, O. R. 2002, MNRAS, 329, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, I., & Renzini, A. 1983, ARA&A, 21, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Izumiura, H., Noguchi, K., Aoki, W., et al. 2008, ApJ, 682, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Izzard, R. G., Tout, C. A., Karakas, A. I., & Pols, O. R. 2004, MNRAS, 350, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Izzard, R. G., Dray, L. M., Karakas, A. I., Lugaro, M., & Tout, C. A. 2006, A&A, 460, 565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Izzard, R. G., Jeffery, C. S., & Lattanzio, J. 2007, A&A, 470, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Izzard, R. G., Glebbeek, E., Stancliffe, R. J., & Pols, O. R. 2009, A&A, 508, 1359 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jorissen, A., Van Eck, S., Mayor, M., & Udry, S. 1998, A&A, 332, 877 [NASA ADS] [Google Scholar]
- Jose, J., & Hernanz, M. 1998, ApJ, 494, 680 [NASA ADS] [CrossRef] [Google Scholar]
- José, J., Hernanz, M., Amari, S., Lodders, K., & Zinner, E. 2004, ApJ, 612, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P., Tout, C., & Gilmore, G. 1993, MNRAS, 262, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Lambert, D. L., Smith, V. V., & Hinkle, K. H. 1990, AJ, 99, 1612 [NASA ADS] [CrossRef] [Google Scholar]
- Lloyd Evans, T. 1991, MNRAS, 249, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Marks, P. B., Sarna, M. J., & Prialnik, D. 1997, MNRAS, 290, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Morgan, D. H., Cannon, R. D., Hatzidimitriou, D., & Croke, B. F. W. 2003, MNRAS, 341, 534 [NASA ADS] [CrossRef] [Google Scholar]
- Nauenberg, M. 1972, ApJ, 175, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, L. A., MacCannell, K. A., & Dubeau, E. 2004, ApJ, 602, 938 [NASA ADS] [CrossRef] [Google Scholar]
- Nomoto, K., Saio, H., Kato, M., & Hachisu, I. 2007, ApJ, 663, 1269 [NASA ADS] [CrossRef] [Google Scholar]
- Ohnaka, K., & Tsuji, T. 1999, A&A, 345, 233 [NASA ADS] [Google Scholar]
- Ohnaka, K., Izumiura, H., Leinert, C., et al. 2008, A&A, 490, 173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paczynski, B. 1976, in Structure and Evolution of Close Binary Systems, eds. P. Eggleton, S. Mitton, & J. Whelan, IAU Symp., 73, 75 [Google Scholar]
- Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Politano, M., van der Sluys, M., Taam, R. E., & Willems, B. 2010, ApJ, 720, 1752 [NASA ADS] [CrossRef] [Google Scholar]
- Pylyser, E., & Savonije, G. J. 1988, A&A, 191, 57 [NASA ADS] [Google Scholar]
- Romano, D., & Matteucci, F. 2005, Nucl. Phys. A, 758, 328 [NASA ADS] [CrossRef] [Google Scholar]
- Scott, A. D., Rawlings, J. M. C., Krautter, J., & Evans, A. 1994, MNRAS, 268, 749 [NASA ADS] [Google Scholar]
- Shafter, A. W. 2002, in Classical Nova Explosions, eds. M. Hernanz, & J. José, AIP Conf. Ser., 637, 462 [Google Scholar]
- Stehle, R., & Ritter, H. 1999, MNRAS, 309, 245 [Google Scholar]
- Straniero, O., Gallino, R., Busso, M., et al. 1995, ApJ, 440, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Utsumi, K. 1985, in Cool Stars with Excesses of Heavy Elements, eds. M. Jaschek & P. C. Keenan, Astrophys. Space Sci. Lib., 114, 243 [Google Scholar]
- Vanture, A. D. 1992, AJ, 103, 2035 [NASA ADS] [CrossRef] [Google Scholar]
- Wallerstein, G., & Knapp, G. R. 1998, ARA&A, 36, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Warner, B. 1995, Cataclysmic variable stars., 28 [Google Scholar]
- Westerlund, B. E. 1997, The Magellanic Clouds (Cambridge: Cambridge Univ. Press) [Google Scholar]
- Wheeler, J. C. 1992, in Evolutionary Processes in Interacting Binary Stars, eds. Y. Kondo, R. Sistero, & R. S. Polidan, IAU Symp., 151, 225 [Google Scholar]
- Whelan, J., & Iben, J. I. 1973, ApJ, 186, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Wood, P. R., Bessell, M. S., & Fox, M. W. 1983, ApJ, 272, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Yaron, O., Prialnik, D., Shara, M. M., & Kovetz, A. 2005, ApJ, 623, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Yungelson, L., Livio, M., Tutukov, A., & Kenyon, S. J. 1995, ApJ, 447, 656 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, X., & Jeffery, C. S. 2013, MNRAS, 430, 2113 [NASA ADS] [CrossRef] [Google Scholar]
- Zorotovic, M., Schreiber, M. R., Gänsicke, B. T., & Nebot Gómez-Morán, A. 2010, A&A, 520, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Initial binary parameters M1, M2 and a for typical post-nova merger progenitors with for Z = 0.008, αCE = 0.2.
All Figures
 |
Fig. 1 Mass fractions of carbon and oxygen in the core of a TPAGB star with initial
|
| In the text | |
 |
Fig. 2 Evolution of COAL type systems of Table 1.
For each system i.e. COAL-A (Fig. A) and COAL-B (Fig. B), the top
and bottom panels on the left show
masses and evolutionary stages of both the primary (WD) and the secondary stars
during the nova phase when the mass-transfer rate
( |
| In the text | |
 |
Fig. 3 Evolution of CE type systems of Table 1. Refer to Fig. 2 caption for description of evolutionary stages shown. The CE-A merger exhibits properties of a J-star on the EAGB unlike the COAL-B merger which has C/O > 1 only during TDU and hence has a short phase on the TPAGB (marked by the dotted lines) when it classifies as a J-star. |
| In the text | |
 |
Fig. 4 Range of initial primary mass M1, initial secondary mass M2 and initial separation a for nova-merger cases (COAL/CE) that form J-stars. |
| In the text | |
 |
Fig. 5 Binary evolutionary channels which lead to mergers with properties of J-stars from re-accretion of nova-ejecta followed by COAL and CE mergers or HBB in AGB-phases of GB-MS (Case-B RLOF) mergers. The different stellar evolutionary phases are marked (with colours) as – blue: MS star, red: giant-envelope/CE, golden: He-core/WD, black: CO-core/WD, orange: nova-polluted star (MS/HG). |
| In the text | |
 |
Fig. 6 Luminosity function of LMC J-stars (JSLF). The histograms binned in
MBol intervals of 0.5 mag show expected number
fraction
(NJ/NC)
of J-stars among C-stars for HBB (single) stars and binary mergers (post-nova or
Case-B RLOF) – compared with the JSLF constructed for the LMC J-stars of Morgan et al. (2003) with Poisson
|
| In the text | |
 |
Fig. 7 Luminosity function of LMC J-stars (JSLF). Number fraction (NJ/NC) of J-stars among C-stars for post-nova mergers and HBB-stars excluding Case-B RLOF binary mergers is shown with observed J-stars from the sample of Morgan et al. (2003) binned in MBol intervals of 0.5 mag. The total NJ/NC ratio is ~2% for the nova-polluted mergers – lower than the total NJ/NC in Fig. 6 (~5%) and the observed fraction (~10%) of the stars in the sample of Morgan et al. (2003). |
| In the text | |
 |
Fig. 8 Distributions of |
| In the text | |
 |
Fig. A.1 Histograms of predicted Galactic nova rate as function of WD mass, MWD per 0.1 M⊙ bin, for αCE = 0.2 (upper panel) and 0.5 (lower panel). The total rate of novae in the Galaxy Rnova is the sum of the contributions from all MWD bins. |
| In the text | |
 |
Fig. B.1 Evolutionary properties on the TPAGB for a single star (upper
panel) and a GB-MS (Case-B RLOF) binary merger (lower
panel) of similar total mass. The core mass
Mc and surface C/O are plotted on the left scale,
along with surface isotopic ratios, |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.