© ESO, 2013

1. Introduction

The intracluster medium (ICM) plays central role in the evolution of baryons in the universe. The ICM is the hot plasma filling the gravitational potential of galaxy clusters, the largest virialized structures in the universe. Since most of the cluster baryons reside in the ICM (~85 percent), this gaseous medium represents the crucible out of which essential astrophysical structures condense. It is often assumed that the ICM settles in hydrostatic equilibrium after the initial cosmological collapse in the potential well of the cluster. However, the ICM plasma is a remarkably dynamic entity, continuously perturbed by mergers, feedback processes (active galactic nuclei – AGN, supernovae – SNe), galaxy motions, and cosmological accretion, all shaping a chaotic and turbulent atmosphere.

Current X-ray observations have in general hard time detecting surface brightness (SB_x) fluctuations, due to the significant level of Poisson noise dominating on small scales (several tens kpc for nearby clusters) and projection smearing effects. This has lead, throughout the past decades, to the common assumption that the ICM is a static entity, both in theoretical and observational work. Only in recent time, few observational investigations have started to focus on the perturbations in the ICM, thanks to deep Chandra or XMM-Newton data. Schuecker et al. (2004) found that at least ~10 percent of the total ICM pressure in Coma hot cluster is in turbulent form. The spectrum of pressure fluctuations, in the range 40−90 kpc, appears to be described by a Kolmogorov slope. Very recently, Churazov et al. (2012, and in prep.) have analyzed very deep observations of Coma (650 × 650 kpc; Sect. 2.1). The characteristic amplitude of the relative density fluctuations reaches 5−10 percent, from small (30 kpc) to large scales (500 kpc), again resembling the Kolmogorov trend. Sanders & Fabian (2012) also studied density/pressure perturbations in a cool-core cluster, AWM7, finding an amplitude of ~4 percent, with a large-scale spectrum shallower than Kolmogorov.

Cosmological simulations (e.g. Norman & Bryan 1999; Dolag et al. 2005; Nagai et al. 2007, 2013; Lau et al. 2009; Vazza et al. 2009, 2011; Borgani & Kravtsov 2011) indicate that subsonic chaotic motions are ubiquitous, with turbulent pressure support in the range 5−30 percent, from relaxed to merging clusters. On the other hand, large-scale simulations have severe difficulty in studying the details of perturbations, due to the limited resolution, the adaptive mesh (AMR) derefinement, or the smoothed particle hydrodynamics viscosity. From a theoretical point of view, little attention has thus been paid to studying the role of density perturbations, and in particular the associated power spectrum, down to kpc scale. In idealized periodic boxes, Kim & Ryu (2005) showed that isothermal turbulence produce a Kolmogorov spectrum, progressively flattening with increasing Mach number. Even in the presence of weak magnetic fields, the power spectrum seems to retain the Kolmogorov slope, at least in ideal magnetohydrodynamics (MHD) simulations (Kowal et al. 2007). In multiphase flows (e.g. the interstellar medium – ISM), thermal instability generate a more complex nonlinear dynamics, inducing high small-scale density perturbations, still increasing with M (Kissmann et al. 2008; Gazol & Kim 2010).

In the current work, we intend to carefully study the power spectrum (or better, the characteristic amplitude) of 3D density fluctuations, driven by turbulent motions (Sect. 2.3) in a real galaxy cluster, Coma (Sect. 2.1). This run will set the reference model. We pay particular attention in modeling a realistic hot ICM plasma, as tracking both electrons and ions (2T; Sect. 2.5), and avoiding restrictive assumptions on the equation of state (e.g. isothermality). Ideal hydrodynamics is however not enough to study a consistent evolution of an astrophysical plasma as the ICM. The very high temperatures (~10⁸ K), combined with the low electron densities (~10^-3 cm^-3), warn that thermal conduction may have a profound impact in shaping density inhomogeneities (Sect. 2.4).

The electron thermal conductivity of the ICM is a highly debated topic in astrophysics, and currently poorly (or not) constrained. In the standard picture of a uniformly magnetized plasma, classic Spitzer conduction (Sect. 2.4) is suppressed perpendicular to the B-field lines (by a factor f ≲ 10^-12), due to electron scattering limited by the Larmor radius. However, turbulent plasmas develop tangled magnetic fields with a chaotic topology. According to Rechester & Rosenbluth (1978) and Chandran & Cowley (1998), after ~30 times a random walk of the B-field coherence length l_B, an electron in the ICM could be fully isotropized, leading to an effective isotropic suppression f ~ 10^-2−10^-3, still a substantially stifled conductive flux. Narayan & Medvedev (2001) and Chandran & Maron (2004) further argued that, in a turbulent plasma, field lines can be chaotically tangled even on scales <l_B, possibly restoring the effective conductivity up to f ~ 0.1 − 0.4 (the Spitzer value).

Past investigations have mainly focused on the role of conduction in balancing radiative losses. In order to prevent the cooling catastrophe, the level of thermal conduction requires to be substantial, f ≳ 0.1, or even impossible for several observed clusters, f > 1 (Kim & Fabbiano 2003; Zakamska & Narayan 2003; Voigt & Fabian 2004). Simulations also confirm the inefficiency of conduction (Dolag et al. 2004; Parrish et al. 2009), requiring other heating mechanisms, as AGN feedback (Churazov et al. 2000, 2001; Ruszkowski & Begelman 2002; Brighenti & Mathews 2003; Gaspari et al. 2011a,b, 2012a, 2013a) or turbulent mixing (Ruszkowski & Oh 2010, 2011). Overall, observations lean towards highly suppressed conduction (f ≲ 10^-3), given the ubiquitous presence of cool cores, along with sharp temperature gradients linked to cold fronts (Ettori & Fabian 2000; Roediger et al. 2013; ZuHone et al. 2013), X-ray cavities, or cold filaments (Forman et al. 2007; Sanders et al. 2013). However, these constraints do not provide the effective isotropic conductivity in the bulk of the ICM; in fact, the magnetic field lines tend to naturally align perpendicular to the temperature gradient in a turbulent medium (Komarov et al. 2013), hence strongly preventing the heat exchange between sharp fronts.

Scope of this work is to provide, for the first time, a global constrain on the conductive and turbulent state of the ICM, instead of relying on local features. This will be possible exploiting the power spectrum of density perturbations. After setting the physical and numerical framework (Sect. 2), we proceed step by step with controlled experiments (Sect. 3), assessing first the role of turbulence (weak, moderate, strong), and then, gradually increasing the effective thermal conductivity. The three features of the power spectrum unveil each a crucial aspect of the ICM state. The normalization results to be linearly related to the turbulent Mach number. The slope of the spectrum steepens from Kolmogorov to Burgers trend, with rising conductivity. The decay/cutoff of the spectrum is provided by a key recurrent threshold, t_cond/t_turb ≲ 100 (Sect. 3). In Sect. 4, we discuss important properties of the models, and provide a simple model to assess the effective conductivity and turbulence. We apply the prescription to new very deep observations of Coma cluster, constraining the actual state of the hot ICM. The results are summarized in Sect. 5. In the Appendices, we compare different methods to calculate the spectrum, and analytically study the β-profile in Fourier space. The increasing quality of future X-ray data will provide a big opportunity to exploit and perfect this new modeling, and hopefully to lead to high-precision measurements of the ICM (“ICMology”).

2. Physics and numerics

2.1. Initial conditions: Coma galaxy cluster

Hot galaxy clusters are optimal systems to study the effects of thermal conduction and turbulence, due to the fairly low ICM densities and the substantial level of dynamical activity. The archetypal non-cool-core system is Coma cluster (Abell 1656). Given its proximity, brightness and flat X-ray core, it is ideal to study density perturbations. Churazov et al. (2012) retrieved the characteristic amplitude of density fluctuations in Coma from deep XMM and Chandra observations, finding significant values up to 10 percent, while resolving scales of tens kpc.

In this study, we adopt Coma cluster as fiducial astrophysical laboratory, setting the density and temperature profile according to the most recent XMM observations (Fig. 1). An excellent fit to the radial electron density distribution is given by a single β-model profile: ${\mathit{n}}_{\mathrm{e}}\mathrm{=}{\mathit{n}}_{\mathrm{e}\mathit{,}\mathrm{0}}{\left[\mathrm{1}\mathrm{+}{\left(\frac{\mathit{r}}{{\mathit{r}}_{\mathrm{c}}}\right)}^{\mathrm{2}}\right]}^{\mathrm{-}\mathrm{3}\mathit{\beta }\mathit{/}\mathrm{2}}\mathit{,}$(1)with central density n_e,0 = 3.9 × 10^-3 cm^-3, core radius r_c = 272 kpc, and β = 0.75. In Appendix B, we discuss the properties of the β-profile in Fourier space. The gas temperature is roughly isothermal in the core, declining at large radii as observed for the majority of clusters (e.g. Vikhlinin et al. 2006): $\mathit{T}\mathrm{=}{\mathit{T}}_{\mathrm{0}}\hspace{0.17em}{\left[\mathrm{1}\mathrm{+}{\left(\frac{\mathit{r}}{{\mathit{r}}_{\mathrm{t}}}\right)}^{\mathrm{2}}\right]}^{-0.45}\mathit{,}$(2)where T₀ = 8.5 keV and r_t = 1.3 Mpc. The electron and ion temperature (Sect. 2.5) are initially in equilibrium. The combined property of high temperature and low density sets a perfect environment to study the role of conduction, since the thermal diffusivity is ∝${\mathit{T}}_{\mathrm{e}}^{\mathrm{5}\mathit{/}\mathrm{2}}\mathit{/}{\mathit{n}}_{\mathrm{e}}$ (Sect. 2.4). In addition, radiative cooling is ineffective, t_cool ~ 2.5   t_H. The simulated system is initialized in hydrostatic equilibrium. The gas temperature and density allow to retrieve the gravitational acceleration (dominated by dark matter). The resulting potential is appropriate for a massive cluster in the ΛCDM universe, with virial mass M_vir ~ 10¹⁵M_⊙ and r_vir ~ 2.9 Mpc (r₅₀₀ ~ 1.4 Mpc).

Since deep observations of density perturbations reach at most 0.5   r₅₀₀ (Fig. 1), we adopt a 3D box with a diagonal of ~2.4 Mpc. As turbulence is volume filling and since we are interested in the power spectrum, the best numerical approach is to use a fixed grid, without adaptive refinement. In fact, there is no trivial AMR criterium to apply due to the uniformly chaotic dynamics. Moreover, when the cube is de-refined by more than 50 percent, we found that that the density spectrum has a significant decrease in power towards the small scales (producing a mock diffusivity), by over a factor of 2. Based on these tests, we warn that using large-scale (cosmological) simulations will numerically steepen the slope of power spectra (density, velocity, etc.), as also shown by Vazza et al. (2009). Albeit computationally challenging, we thus run all the models with fixed grid and high resolution of 512³ (considering the implemented physics). We tested also 256³ runs, finding a very similar evolution and spectrum, though with double dissipation scale. The simulations are thus in the convergence limit.

The resolution is Δx  ~   2.6 kpc, i.e. roughly on the scale of the (unmagnetized) plasma mean free path. Going below this scale would formally require a kinetic approach. This also means that numerical viscosity is on the scale of the physical Spitzer viscosity, further corroborating the use of such resolution (Sect. 2.6). The total evolution time is typically ≳2 eddy turnover times, roughly the statistical steady state after the turbulent cascade. Boundary zones have Dirichlet condition, with value given by the large-scale radial profile. Inflow is prohibited, in order to avoid any spurious wave altering the dynamics inside the domain.

2.2. Hydrodynamics

We use a modified version of the grid code FLASH4 (Fryxell et al. 2000) in order to integrate the 3D equations of hydrodynamics for a 2 temperature (electron-ion; Sect. 2.5) plasma, with the addition of turbulence (Sect. 2.3) and electron thermal conduction (Sect. 2.4):

$\begin{array}{ccc}& & \frac{\mathit{\partial \rho }}{\mathit{\partial t}}\mathrm{+}\mathrm{\nabla }\mathrm{·}\left(\mathit{\rho }{v}\right)\mathrm{=}\mathrm{0}\\ & & \frac{\mathit{\partial \rho }{v}}{\mathit{\partial t}}\mathrm{+}{\nabla }\mathrm{·}\left(\mathit{\rho }{v}\mathrm{\otimes }{v}\right)\mathrm{+}{\nabla }\mathit{P}\mathrm{=}\mathit{\rho }{g}\hspace{0.17em}\mathrm{+}\mathit{\rho }{{a}}_{\mathrm{stir}}\\ & & \frac{\mathit{\partial \rho }{\mathit{e}}_{\mathrm{i}}}{\mathit{\partial t}}\mathrm{+}\mathrm{\nabla }\mathrm{·}\left(\mathit{\rho }{\mathit{e}}_{\mathrm{i}}\hspace{0.17em}{v}\right)\mathrm{+}{\mathit{P}}_{\mathrm{i}}\mathrm{\nabla }\mathrm{·}{v}\mathrm{=}\mathit{\rho }{\mathrm{\mathscr{H}}}_{\mathrm{i}\mathrm{-}\mathrm{e}}\\ & & \frac{\mathit{\partial \rho }{\mathit{e}}_{\mathrm{e}}}{\mathit{\partial t}}\mathrm{+}\mathrm{\nabla }\mathrm{·}\left(\mathit{\rho }{\mathit{e}}_{\mathrm{e}}\hspace{0.17em}{v}\right)\mathrm{+}{\mathit{P}}_{\mathrm{e}}\mathrm{\nabla }\mathrm{·}{v}\mathrm{=}\mathit{\rho }{\mathrm{\mathscr{H}}}_{\mathrm{e}\mathrm{-}\mathrm{i}}\mathrm{-}\mathrm{\nabla }\mathrm{·}{{F}}_{\mathrm{cond}}\\ & & {\mathit{P}}_{\mathrm{tot}}\mathrm{=}\left(\mathit{\gamma }\mathrm{-}\mathrm{1}\right)\hspace{0.17em}\mathit{\rho }\mathrm{(}{\mathit{e}}_{\mathrm{i}}\mathrm{+}{\mathit{e}}_{\mathrm{e}}\mathrm{)}\end{array}$where ρ is the gas density, v the velocity, e_i and e_e the specific internal energy of ions and electrons, P_tot the total pressure (ions and electrons), γ = 5/3 the adiabatic index. The mean atomic weight of electrons and ions is μ_i ≃ 1.32, μ_e ≃ 1.16, providing a total gas μ ≃ 0.62, appropriate for a totally ionized plasma with ~25% He in mass. The atomic weight determines also the specific (isochoric) heat capacity, c_V = k_B/ [(γ − 1)   μm_p]. For numerical consistency, the total energy (e_tot = e_i + e_e + v²/2) equation, in conservative form, is also integrated.

In order to integrate the hyperbolic part of the hydrodynamics equations, we use a robust third order reconstruction scheme (piecewise parabolic method) in the framework of the unsplit flux formulation with hybrid Riemann solver (Lee & Deane 2009). Albeit computationally expensive, this setup keeps at minimum the numerical diffusivity. We tested different Riemann solvers (e.g. HLLC, Roe), characteristic slope limiters (Min-Mod, Van Leer, Toro), and other parameters (e.g. Courant number, interpolation order). They give comparable results, although we note that lower order reconstruction schemes (e.g. MUSCL) are more diffusive and thus truncate the turbulent cascade on roughly two times larger scale.

2.3. Turbulence driving

Continuous injection of turbulence is modeled with a spectral forcing scheme that generates statistically stationary velocity fields (Eswaran & Pope 1988; Fisher et al. 2008; Gaspari et al. 2013b). This scheme is based on an Ornstein-Uhlenbeck (OU) random process, analogous to Brownian motion in a viscous medium. The driven acceleration field is time-correlated, with zero mean and constant root mean square, an important feature for modeling realistic driving forces. In the OU process, the value of the gas acceleration at previous timestep aⁿ decays by an exponential damping factor f = exp( −    Δt/τ_d), where τ_d is the correlation time. Simultaneously, a new Gaussian-distributed acceleration with variance ${\mathit{\sigma }}_{\mathit{a}}^{\mathrm{2}}\mathrm{=}{\mathit{ϵ}}^{\mathrm{\ast }}\mathit{/}{\mathit{\tau }}_{\mathrm{d}}$ is added as ${\mathit{a}}_{\mathrm{stir}}^{\mathit{n}\hspace{0.17em}\mathrm{+}\hspace{0.17em}\mathrm{1}}\mathrm{=}\mathit{f}\hspace{0.17em}{\mathit{a}}_{\mathrm{stir}}^{\mathit{n}}\mathrm{+}{\mathit{\sigma }}_{\mathit{a}}\hspace{0.17em}\sqrt{\mathrm{1}\mathrm{-}{\mathit{f}}^{\mathrm{2}}}{\mathit{G}}^{\mathit{n}}\mathit{,}$(8)where Gⁿ is the Gaussian random variable, ϵ^∗ is the specific energy input rate, and ${\mathit{a}}_{\mathrm{stir}}^{\mathit{n}\mathrm{+}\mathrm{1}}$ is the updated acceleration. The six amplitudes of the acceleration (3 real and 3 imaginary) are evolved in Fourier space and then directly converted to physical space. In this approach, turbulence can be driven by stirring the gas on large scales and letting it cascade to smaller scales. This is an efficient approach as the alternative would involve executing fast Fourier transforms (FFTs) for the entire range of scales, where the vast majority of modes would have small amplitudes. Since ICM turbulence is always subsonic, we impose a divergence-free condition on acceleration, through a Helmholtz decomposition in Fourier space.

The physical quantity of interest is the resultant 3D turbulent velocity dispersion, σ_v, which drives the ICM dynamics. The driving of turbulence is intentionally kept simple as our goal is not to consider any specific stirring source, but to keep the calculation fairly general. For example, the (combined) sources of turbulence may be major or minor mergers, galaxy motions, AGN feedback or supernovae. Observations (Schuecker et al. 2004; Churazov et al. 2008; de Plaa et al. 2012; Sanders & Fabian 2013) and simulations (Norman & Bryan 1999; Lau et al. 2009; Vazza et al. 2009, 2011; Gaspari et al. 2012b; Borgani & Kravtsov 2011 for a review) show that ICM turbulent energies are in the range few −30 percent of the thermal energy, from very relaxed to merging clusters.

We test therefore three regimes of ICM turbulence, weak (M ~ 0.25), mild (M ~ 0.5), and strong (M ~ 0.75), corresponding to a ratio of turbulent to thermal energy of 3.5, 14 and 31 percent (E_turb ≃ 0.56   M²E_th). This is achieved by adjusting the energy per mode¹ϵ^∗ and correlation time τ_d (ϵ^∗ ~ 5 × 10^-5 − 10^-3 cm² s^-3 and 200 Myr, respectively). As long as different choices of these parameters result in the same velocity dispersion, the dynamics of the flow remains unaffected. We stir the gas only on large scales, with typical injection peak L ~ 600 kpc (in the last set of runs L′ ~ 300 kpc), letting turbulence to naturally cascade. This allows us to exploit the entire dynamic range of our box (512³) and to better appreciate the effect of conduction, without being strongly affected by numerical diffusion. Notice that in few t_eddy, large-scale turbulence is not able to eject a substantial amount of mass outside the box. Since turbulence is kept subsonic, dissipational heating, which is proportional to ${\mathit{\sigma }}_{\mathit{v}}^{\mathrm{3}}\mathit{/}\mathit{L}$, is also secondary. Turbulent diffusion can instead effectively flatten the global entropy gradient, especially in the non-conductive runs. We are nevertheless interested in the relative variations of δρ/ρ, removing the underlying profile.

The characteristic time of turbulence is defined by the eddy turnover time at a given physical scale l (e.g. Fig. 8, magenta line). Extrapolating from the injection scale via the Kolmogorov scaling, σ_v = σ_v,inj   (l/L)^1/3, yields ${\mathit{t}}_{\mathrm{turb}}\mathrm{=}\frac{\mathit{l}}{{\mathit{\sigma }}_{\mathit{v}}}\mathrm{~}\frac{{\mathit{L}}^{\mathrm{1}\mathit{/}\mathrm{3}}}{{\mathit{\sigma }}_{\mathit{v,}\mathrm{inj}}}\hspace{0.17em}{\mathit{l}}^{\mathrm{2}\mathit{/}\mathrm{3}}\mathit{.}$(9)Finally, we note turbulence can be expressed as a diffusion process acting on entropy on sufficiently large scales, ≳l, albeit the equations are intrinsically hyperbolic. We define the effective turbulent diffusivity as ${\mathit{D}}_{\mathrm{turb}}\mathrm{=}{\mathit{c}}_{\mathrm{t}}\hspace{0.17em}{\mathit{\sigma }}_{\mathit{v}}\hspace{0.17em}\mathit{l}\mathit{.}$(10)The transport of heat due to turbulent diffusion can be written as ${\nabla }\mathrm{·}{{F}}_{\mathrm{mix}}\mathrm{=}\mathrm{-}{\nabla }\mathrm{·}\mathrm{\left(}{\mathit{D}}_{\mathrm{turb}}\mathit{\rho T}{\nabla }\mathit{s}\mathrm{\right)}\mathit{,}$(11)where s = c_Vln(P/ρ^γ) is the entropy. We remark that turbulence diffuses entropy, while seeding perturbations in density and temperature. In our analysis and discussion, we assume a diffusion constant c_t = 1, but in real plasmas this uncertain value could be much lower (Dennis & Chandran 2005, and references therein).

2.4. Thermal conduction

In ionized plasmas such as the ICM, electrons conduct internal energy with a heating rate per unit volume given by ${\nabla }\mathrm{·}{{F}}_{\mathrm{cond}}\mathrm{=}\mathrm{-}\hspace{0.17em}{\nabla }\mathrm{·}\mathrm{(}\mathit{\kappa }\hspace{0.17em}{\nabla }{\mathit{T}}_{\mathrm{e}}\mathrm{)}\mathit{.}$(12)The thermal conductivity can be written as (Spitzer 1962; Cowie & McKee 1977) $\mathit{k}\mathrm{\simeq }\mathit{f}\hspace{0.17em}\hspace{0.17em}\frac{\mathrm{1.84}\mathrm{\times }{\mathrm{10}}^{-5}\hspace{0.17em}{\mathit{T}}_{\mathrm{e}}^{\mathrm{5}\mathit{/}\mathrm{2}}}{\ln {\mathrm{\Lambda }}_{\mathrm{ei}}}\mathrm{[}\mathrm{erg}\hspace{0.17em}{\mathrm{s}}^{-1}\hspace{0.17em}{\mathrm{K}}^{-1}\hspace{0.17em}\mathrm{c}{\mathrm{m}}^{-1}\mathrm{]}\mathit{,}$(13)where lnΛ_ei = 37.8 + ln [(T_e/10⁸  K)   (n_e/10^-3  cm^-3)^− 1/2] is the Coulomb logarithm (the ratio of the largest to smallest impact parameter; e.g. Voigt & Fabian 2004), and f is the magnetic suppression factor (Sect. 2.4.1). 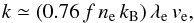The previous conductivity derives from the more significant expression $\mathit{k}\mathrm{\simeq }\mathrm{(}\mathrm{0.76}\hspace{0.17em}\mathit{f}\hspace{0.17em}{\mathit{n}}_{\mathrm{e}}\hspace{0.17em}{\mathit{k}}_{\mathrm{B}}\mathrm{)}\hspace{0.17em}{\mathit{\lambda }}_{\mathrm{e}}\hspace{0.17em}{\mathit{v}}_{\mathrm{e}}\mathit{,}$(14)which points out that the characteristic length scale and speed of conduction is the electron mean free path ${\mathit{\lambda }}_{\mathrm{e}}\mathrm{\approx }{\mathrm{10}}^{\mathrm{4}}{\mathit{T}}_{\mathrm{e}}^{\mathrm{2}}\mathit{/}{\mathit{n}}_{\mathrm{e}}$ and the electron thermal speed v_e = (3k_BT_e/m_e)^1/2, respectively. Another important quantity is the isochoric diffusivity (cm² s^-1), defined as D_Sp = κ/c_V,e   ρ = κ/1.5   n_e   k_B ≃ 0.5   v_eλ_e.

2.4.1. Magnetic field suppression

The intracluster plasma is likely magnetized. Although the ICM magnetic field (few μG) appears dynamically unimportant compared to the thermal pressure, electrons and ions are anchored to the B-field lines. The gyroradius or Larmor radius is many orders of magnitude lower than the Coulomb mean free path, hence the charged particles can diffuse only along the B-field lines. On the other hand, a real atmosphere is always characterized by some degree of chaotic motions (e.g. AGN/supernovae feedback, sloshing, mergers, galaxy motions). Ruszkowski & Oh (2010) showed through 3D MHD simulations that very weak subsonic turbulence always induces a tangled magnetic field with small coherence length (l_B ≲ 10 kpc; Fig. 2). Faraday rotation measures also indicate small l_B (e.g. Kim et al. 1990). Therefore, on scales larger than the B-field coherence length, the average suppression due to anisotropic conduction can be parametrized with the so-called f factor, as in our study. If l_B is instead very large (as in the idealized case of a parallel topology), this prescription is less accurate: parallel and perpendicular conductivity should be studied separately. The spectral analysis should be nevertheless not strongly affected by localized features (as fronts and filaments), weighing more volume-filling properties; Fourier spectra provide thus the conductivity in the bulk of the ICM.

High-resolution MHD² simulations are required to assess the role of anisotropic conduction and will be tackled in a future work. Assuming a sufficiently tangled field, f is geometrically expected to be ⟨ cos²θ ⟩  ≈ 1/3 (θ is the angle between the B field and the T gradient), as confirmed by turbulent MHD runs (Ruszkowski & Oh 2010). Microscopic effects and plasma instabilities can severely suppress the conductive flux down to f ~ 10^-3 (Rechester & Rosenbluth 1978; Chandran & Cowley 1998), although Narayan & Medvedev (2001) argue that in a highly tangled and chaotic field conduction may be restored to f ~ 0.2 (Sect. 1). Considering these uncertainties, we test a wide range of f values, ranging from the strongly to weakly suppressed regime, f ~ 10^-3 − 1.

From an observational point of view, deep data (e.g. Markevitch & Vikhlinin 2007) show sharp contact discontinuities in the ICM, leading to the conclusion that conduction is severely suppressed, f ~ 10^-3 (Ettori & Fabian 2000). However, these estimates focus only on local features. Simulations of sloshing motions (e.g. ZuHone et al. 2013) show that the magnetic field tends to remain perpendicular to the temperature gradient (a natural outcome of the frozen-in property; Komarov et al. 2013), with a strong suppression across the front. It is still unknown what is the effective global conductivity of the turbulent ICM (and hence global heat diffusion), which we aim to constrain with our spectral method, comparing simulated and observed density perturbations (Sect. 4.3).

2.4.2. Saturation

Since the conductive flux depends also on the temperature gradient, electrons may conduct heat much faster than their thermal velocity in an unphysical way. This happens whenever the temperature scale height is smaller than the electron mean free path, l_T ≡ T/ | ∇T |  ≲ λ_e. In this regime, the conductive flux saturates at a value given by (Cowie & McKee 1977; Balbus & McKee 1982) ${{F}}_{\mathrm{sat}}\mathrm{=}\mathrm{-}\hspace{0.17em}\mathit{\alpha }\hspace{0.17em}{\mathit{n}}_{\mathrm{e}}{\mathit{k}}_{\mathrm{B}}{\mathit{T}}_{\mathrm{e}}\hspace{0.17em}{\mathit{v}}_{\mathrm{e}}\hspace{0.17em}\mathrm{sgn}\mathrm{\left(}{\nabla }\mathit{T}\mathrm{\right)}\mathit{,}$(15)where α is an uncertainty factor representing microscopic processes in the magnetized plasma (as instabilities). Following the indication of Balbus (1986) based on plasma experiments, we set α ~ 0.1, although the exact value has no great impact on the dynamics. Saturation changes the nature of the equations, from parabolic to hyperbolic, yet we can define an effective diffusivity of the form D_sat =  | ∇T/F_sat |. Numerically, saturation is implemented via a smooth flux limiter on the diffusion coefficient: ${\mathit{D}}_{\mathrm{cond}}\mathrm{=}\mathrm{(}{\mathit{D}}_{\mathrm{Sp}}^{-2}\mathrm{+}{\mathit{D}}_{\mathrm{sat}}^{-2}{\mathrm{)}}^{\mathrm{-}\mathrm{1}\mathit{/}\mathrm{2}}$. We tested other types of limiters, as harmonic or min/max, without finding relevant differences. Saturation is only relevant in the unsuppressed regime, with typically less than 10 percent of zones saturated, while negligible for f ≲ 0.1 models.

The final diffusivity is important to determine the characteristic timescale of conduction (see Fig. 8, black line): ${\mathit{t}}_{\mathrm{cond}}\mathrm{=}\frac{{\mathit{l}}^{\mathrm{2}}}{{\mathit{D}}_{\mathrm{cond}}}\mathrm{·}$(16)In order to integrate the diffusion equation, we initially used an explicit flux-based scheme. However, the computational time becomes prohibitive since it is strongly limited by Eq. (16), allowing to integrate only few 100 Myr. It is thus essential to adopt the (unsplit) implicit solver, allowing for a fast yet accurate execution. The solver efficiently uses the HYPRE linear algebra package to solve the diffusion equation linked to electron thermal conduction (cf. FLASH4 guide for the validation tests). The associated boundaries are set in outflow or zero-gradient mode.

2.5. 2T plasma: electron–ion equilibration

In astrophysical simulations, it is widely assumed that the plasma has one single temperature, T_e ≈ T_i. However, this approximation is only good for a relatively cold medium. For hot clusters, especially non-cool-core systems, the ion–electron equilibration time due to Coulomb collisions can be t_ei ≳ 50 Myr. Since conduction operates on the Myr scale and only on electrons, it is important to follow the evolution of both the electron and ion temperature (or internal energy; Eqs. (5), (6)). The heat exchange rate (erg s^-1) between ions and electrons is given by ${\mathrm{\mathscr{H}}}_{\mathrm{i}\mathrm{-}\mathrm{e}}\mathrm{=}\frac{{\mathit{c}}_{\mathit{V,}\mathrm{e}}}{{\mathit{t}}_{\mathrm{ei}}}\mathrm{(}{\mathit{T}}_{\mathrm{e}}\mathrm{-}{\mathit{T}}_{\mathrm{i}}\mathrm{)}\mathit{,}{\mathrm{\mathscr{H}}}_{\mathrm{e}\mathrm{-}\mathrm{i}}\mathrm{=}\frac{{\mathit{c}}_{\mathit{V,}\mathrm{e}}}{{\mathit{t}}_{\mathrm{ei}}}\mathrm{(}{\mathit{T}}_{\mathrm{i}}\mathrm{-}{\mathit{T}}_{\mathrm{e}}\mathrm{)}\mathit{,}$(17)where we choose the widely used Spitzer electron–ion equilibration time for a fully ionized plasma (Huba 2009): ${\mathit{t}}_{\mathrm{ei}}\mathrm{=}\frac{\mathrm{3}\hspace{0.17em}{\mathit{k}}_{\mathrm{B}}^{\mathrm{3}\mathit{/}\mathrm{2}}}{\mathrm{8}\sqrt{\mathrm{2}\mathit{\pi }}\hspace{0.17em}{\mathit{e}}^{\mathrm{4}}}\hspace{0.17em}\frac{\mathrm{(}{\mathit{m}}_{\mathrm{i}}{\mathit{T}}_{\mathrm{e}}\mathrm{+}{\mathit{m}}_{\mathrm{e}}{\mathit{T}}_{\mathrm{i}}{\mathrm{)}}^{\mathrm{3}\mathit{/}\mathrm{2}}}{\mathrm{(}{\mathit{m}}_{\mathrm{e}}{\mathit{m}}_{\mathrm{i}}{\mathrm{)}}^{\mathrm{1}\mathit{/}\mathrm{2}}\hspace{0.17em}{\mathit{n}}_{\mathrm{i}}\hspace{0.17em}\ln {\mathrm{\Lambda }}_{\mathrm{ei}}}\mathrm{·}$(18)The equilibration time is dominated by ∝(m_iT_e)^3/2. Therefore, in systems with characteristic temperature ≲6 keV (and dense cores), the equilibration time is comparable or less than the unsuppressed conduction timescale (∝T^− 5/2), even on few kpc, t_ei ≲ 1 Myr. Neglecting equilibration in the strongly conductive runs, the ions would be forced to be quickly isothermal, inducing spurious features. In the more realistic evolution, turbulent motions displace the ions before having time to fully equilibrate with electrons, leading to a gentler equilibration. To our knowledge, this is the first attempt to study ICM turbulence and conduction with a two-temperature (2T) simulation, in analogy with high-energy physics studies.

2.6. Viscosity

Viscosity may in principle not be neglected when conduction operates, since both transport processes are intimately connected on the microscopic scale, and both altered by B-field instabilities and topology. In the present work, we do not implement a direct physical viscosity, yet we point out two important arguments. Since viscosity is the transport of momentum due to ions, while the conductive flux is associated with electrons, viscous stresses are slower by at least 1−2 orders of magnitude compared with conduction (thermal v_i ≃ v_e/43), and should have a secondary role in damping density perturbations (see also Sect. 3). Further, we choose numerical resolution to be on the scale of the ion mean free path (λ_i ≃ λ_e); the flow velocity is also comparable to the characteristic velocity of viscosity. This implies that numerical diffusivity approximately reflects Spitzer viscous diffusion (∝λ_i   v_i) – the unsuppressed dynamic viscosity in Coma is 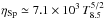${\mathit{\eta }}_{\mathrm{Sp}}\mathrm{\simeq }\mathrm{7.1}\mathrm{\times }{\mathrm{10}}^{\mathrm{3}}\hspace{0.17em}{\mathit{T}}_{\mathrm{8.5}}^{\mathrm{5}\mathit{/}\mathrm{2}}$ g cm^-1 s^-1 (cf. Reynolds et al. 2005). For example, the non-conductive spectrum in Fig. 2 indicates that the typical Reynolds number at injection is Re_L ≃ (L/λ_T)² ~ 500, where the Taylor scale λ_T marks the incipit of dissipation. Comparing the simulated Taylor scale with the Spitzer value, λ_T ≃ (ν_Sp   L/σ_v)^1/2 ~ 80 kpc (ν_Sp = η_Sp/ρ), we see that the grid acts as an effective viscosity with f_η ~ 1/4. In future, we will test the effects of a varying and anisotropic physical viscosity.

2.7. Power spectrum of density perturbations

To study density perturbations, we adopt the characteristic amplitude, instead of the power spectrum P(k) (or energy spectrum E(k)), defined as $\mathit{A}\mathrm{\left(}\mathit{k}\mathrm{\right)}\mathrm{\equiv }\sqrt{\mathit{P}\mathrm{\left(}\mathit{k}\mathrm{\right)}\hspace{0.17em}\mathrm{4}\mathit{\pi }{\mathit{k}}^{\mathrm{3}}}\mathrm{=}\sqrt{\mathit{E}\mathrm{\left(}\mathit{k}\mathrm{\right)}\hspace{0.17em}\mathit{k}}\mathit{,}$(19)where $\mathit{k}\mathrm{=}\sqrt{{\mathit{k}}_{\mathit{x}}^{\mathrm{2}}\mathrm{+}{\mathit{k}}_{\mathit{y}}^{\mathrm{2}}\mathrm{+}{\mathit{k}}_{\mathit{z}}^{\mathrm{2}}}$ (we typically use l = 1/k in kpc units). The characteristic amplitude is insightful, since the units are the same of the variable in real space. Since we are interested in the relative perturbations of density, δ ≡ δρ/ρ, A(k)_δ represents the typical level of fluctuations at a given scale k. The peak of A(k)_δ provides a good and simple estimate for the total amount of perturbations; the exact total variance can be computed integrating P(k)   4πk²dk over the whole range of scales (the difference may reach a factor of 1.4, depending on the power slope).

We retrieve the relative density perturbations δ, dividing ρ by the background profile, δ = ρ/ρ_b − 1. For each snapshot, we execute a best-fitting routine to compute the new underlying β-profile (e.g. strong turbulent diffusion can lower the central density by a factor of 2 over few Gyr), minimizing the deviation between the data and the model. We note that the β-profile removal affects only the spectrum on very large scales. In principle, A(k)_δ could be studied even without removing the background, since perturbations start to dominate on large k (see Appendix B). The power spectrum of δ is finally computed with the “Mexican Hat” filtering (Arévalo et al. 2012) instead of performing Fourier transforms, which can lead to spurious features due to the non-periodicity of the box (see Appendix A).

3. Results

We now describe the results of the simulated models, reminding that the main goal of the present investigation is to understand the role of turbulence and conduction in shaping the power spectrum of density perturbations, A(k)_δ (Sect. 2.7; we defer to future work the study of other statistics, as PDFs and structure functions). We are interested in the characteristic level of δρ/ρ perturbations, the slope of the spectrum, as well as any evident decline (or cutoff). Table 1 summarizes the key retrieved properties and serves as a guide for the analysis of A(k)_δ.

A key quantity for describing the evolution of perturbations is the ratio of the conduction and turbulence timescale (Eqs. (9) and (16)), which normalized to reference values of the unsuppressed conductive run results to be $\frac{{\mathit{t}}_{\mathrm{cond}}}{{\mathit{t}}_{\mathrm{turb}}}\mathrm{\simeq }\hspace{0.17em}\hspace{0.17em}\mathrm{1}\hspace{0.17em}{\mathit{l}}_{\mathrm{550}}^{\mathrm{4}\mathit{/}\mathrm{3}}\left[\frac{{\mathit{\sigma }}_{\mathit{v,}\mathrm{370}}\hspace{0.17em}\hspace{0.17em}{\mathit{n}}_{\mathrm{e}\mathit{,}\mathrm{0.004}}}{{\mathit{L}}_{\mathrm{650}}^{\mathrm{1}\mathit{/}\mathrm{3}}\hspace{0.17em}\hspace{0.17em}{\mathit{f}}_{\mathrm{1}}\hspace{0.17em}\hspace{0.17em}{\mathit{T}}_{\mathrm{e}\mathit{,}\mathrm{8}}^{\mathrm{5}\mathit{/}\mathrm{2}}}\right]\mathrm{·}$(20)We do not consider saturated conduction for this estimate, since the temperature gradient is not steep for the majority of the zones (the interpolated D_cond shall be used in this case for higher accuracy; Sect. 2.4). This key timescale ratio can be also seen as the Prandtl number applied to turbulence, instead of to the kinematic viscosity, which we define as ${\mathit{P}}_{\mathrm{t}}\mathrm{\equiv }\frac{{\mathit{D}}_{\mathrm{turb}}}{{\mathit{D}}_{\mathrm{cond}}}\mathrm{=}\frac{{\mathit{l}}^{\mathrm{2}}\mathit{/}{\mathit{D}}_{\mathrm{cond}}}{{\mathit{l}}^{\mathrm{2}}\mathit{/}{\mathit{D}}_{\mathrm{turb}}}\mathrm{=}\frac{{\mathit{t}}_{\mathrm{cond}}}{{\mathit{t}}_{\mathrm{turb}}}\mathit{,}$(21)where the thermal and turbulent diffusivities are provided in Sects. 2.3, 2.4. The reference value is usually taken at the injection scale, l = L. Remarkably, the qualitative evolution of a very complex nonlinear dynamics can be approximately predicted via the dominant timescale ratio (or dimensionless number; see discussion in Sect. 4.1). For instance, different values of f and M can lead to the same P_t, hence to a similar qualitative dynamics and power spectrum of density perturbations (cf. Sects. 3.2 and 3.4).

3.1. Weak turbulence: M ~ 0.25

The first set of models implements a low level of stirring, with average mass-weighted 3D Mach number M  ~   0.25 (~370  km  s^-1). Observations and simulations suggest in fact that turbulence in the ICM typically remains subsonic (Nagai et al. 2007, 2013; Vazza et al. 2011; Gaspari et al. 2012b; Sanders & Fabian 2013). The turbulent energy is ~3.5 percent of the total thermal energy, E_turb ≃ 0.5   γ(γ − 1)   M²E_th ≃ 0.56   M²E_th. Dissipational heating is thus negligible. In the current models, t_eddy = L/σ_v ~ 1.6 Gyr. We always analyze the system as soon as it establishes statistical steady state, i.e. after ~2   t_eddy.

In the purely hydrodynamic run (f = 0, i.e. no conduction or P_t → ∞) the driven stirring motions generate a turbulent cascade in the δρ/ρ power spectrum analogous to that of the turbulent velocities. The characteristic amplitude shows the typical injection peak at low k (l ~ 600 kpc), followed by the inertial range and the final steepening due to dissipation (Fig. 2, black line). The characteristic level of perturbations, given by the maximum of A(k)_δ, is 6.5 percent (6.7 percent using FFTs). An important result is that the inertial range of the density perturbations is remarkably similar to the Kolmogorov slope, A(k)_δ ∝ k^− 1/3 (or E(k) ∝ k^− 5/3), slightly flattening towards the injection scale. Stratification has overall a secondary impact on δ (Sect. 4.1). Dissipation via numerical viscosity (mimicking Spitzer viscosity; Sect. 2.6) becomes substantial below 6 resolution elements. Notice that current observations are limited to scales ≳30 kpc due to Poisson noise and projection (Fig. 9), which are well resolved by the current runs. The dynamics is driven by key hydrodynamical instabilities, as Kelvin-Helmholtz (K-H) and Rayleigh-Taylor (R-T), inducing the characteristic rolls, curls, and edges in both δ (Fig. 3) and SB_x maps (Fig. 4, top).

Overdense and underdense regions are associated with a mixture of isobaric and adiabatic perturbations, which we analyze in Sect. 4.2. With weak stirring the former dominates, while strong turbulence enhances the adiabatic mode (analogous to pressure waves). Unlike in the strongly conductive runs, the entropy gradient becomes progressively shallower, inducing a lower central density (30 percent) and higher temperature (10 percent). The transport of heat due to turbulent diffusion is ∝D_turb∇s (Eq. (11)). Therefore, turbulence seeds perturbations in density and temperature, while diffusing entropy. Conduction diffuses instead temperature and density fluctuations.

In the next experiment, we enable electron thermal conduction. We start analyzing the unmagnetized case (f = 1), though even in the unsuppressed regime, conduction can be limited by the saturated flux (Sect. 2.4). The overall dynamics and A(k)_δ is however not affected by saturation; the fraction of saturated zones is less than 10 percent (becoming ≲1 in the f = 0.1 run). The discrepancy between the purely turbulent and the conductive run is evident in the density perturbations (Fig. 2, red line), allowing to put critical constraints on the physical properties of the ICM. Three are the key modifications imparted by conduction. First, density perturbations are significantly damped over the whole range, by a factor of 4 on small scales to a factor of 2 on large scales, where the peak of perturbations reaches 3.5 percent. Second, the slope after the injection hump is considerably steeper than Kolmogorov, following a Burgers-like³ spectrum k^− 1/2 (E(k) ∝ k^-2). Third, there is no evident cutoff, meaning that conduction efficiently operates on all scales, while turbulence is not able to consistently regenerate perturbations. Considering the dimensionless turbulent Prandtl number (Eq. (21)), at the injection scale P_t ~ 1 (Fig. 8). Albeit thermal diffusion is a small-scale process (P_t ∝ l), it is ubiquitous and quick enough to efficiently stifle the full turbulent cascade in the whole cluster. The spectrum does not sharply decline to zero value, since turbulent regeneration is continuous. This is in analogy with the observed radio spectra, where relativistic electrons are regenerated by turbulence, preventing a dramatic cutoff.

The δρ/ρ maps of the strongly conductive runs (Fig. 3, bottom) clearly show the absence of significant density perturbations, especially on small scales. Since turbulent diffusion is severely inhibited, the cluster strongly retains the initial spherical symmetry and radial profiles, as indicated by the X-ray surface brightness map in Fig. 4 (bottom row). Only the electron temperature is able to become quickly isothermal both locally and globally; due to the non-negligible ion–electron equilibration delay, ~50 Myr (Sect. 2.5), the ion temperature has instead difficulty in becoming fully isothermal as T_e. The discrepancy is in the range (T_e − T_i)/T_i ~ 1 − 15 percent, from the inner to external radial shells (in particular beyond r_c, where the decreasing densities increase the lagging; cf. Sect. 4.1). In the opposite regime, the purely turbulent run shows numerous filaments and depressions in density. In the SB_x image (top row), the perturbations are partially veiled by the line of sight integration; the ideal location to observe perturbations is at r ≳ r_c (see Appendix B).

We apply now a suppression factor of 10 on thermal conduction. The regime f ~ 0.1 − 0.3 is widely adopted in astrophysical studies (e.g. Narayan & Medvedev 2001; Voigt & Fabian 2004; Dennis & Chandran 2005; Ruszkowski & Oh 2010, 2011; see Sect. 2.4.1). As shown in Fig. 2, the characteristic amplitude is similar to the unsuppressed case. This is a key result, telling us that density perturbations are suppressed regardless of commonly adopted suppression factors (f ≳ 0.1). Observations could hence put strong limits on the suppression f, based on the steepness and/or normalization of A(k)_δ spectrum (Sect. 4). Compared with f = 1 model, the density fluctuations increase by a factor of 0.3 on large scales, while small perturbations have similar power. The absence of a dramatic decline is mainly due to the fact that on small scales the sound crossing time becomes greater than the conduction time (e.g. Fig. 8), hence the tiny bubbles do not have time to find a new pressure equilibrium. Besides global diffusion, strong conduction can thus promote minor stirring motions on small scales, preventing an abrupt decay of A(k)_δ. In this run, the spectrum slope in the inertial regime is steep, A(k)_δ ∝ k^− 2/3, significantly different from the no-conduction run. Radial profiles and SB_x maps (Fig. 4, bottom) are very similar to the f = 1 model, retaining their initial spherical morphology. The P_t number is roughly 10 at the injection scale. Albeit turbulent regeneration starts to be more effective on large scales, the key P_t threshold appears to be an order of magnitude higher, as shown by the next model.

We suppress further the conductive flux by f = 10^-2, a value advocated by several plasma physics theories (e.g. Rechester & Rosenbluth 1978; Chandran & Cowley 1998). The Prandtl number is 100 at the injection scale: turbulence can now restore part of the perturbations, though only near L (the normalization rises again to ~6 percent). This marked discrepancy between large and small scales induces a remarkably steep slope, A(k)_δ ∝ k^− 4/5 (E(k) ∝ k^-2.5), which should emerge in observed data in a clear way, if f ~ 10^-2 is the conductive regime of the ICM. The δρ/ρ map (Fig. 3, third panel) visualizes well the regeneration of turbulent eddies on large scales, while the small-scale flow remains considerably smooth, as corroborated by the SB_x map (Fig. 4, third row). Since this model shows a clear cutoff, it represents the cleanest case to retrieve the key threshold for the suppression of density perturbations, which we find to be P_t    ~ 100. This is not a strict demarcation line, but rather a transition layer.

Only when conduction is substantially suppressed, f = 10^-3 (the typically lowest suppression factor adopted in theories), the turbulent cascade is significantly restored, generating the same peak and density spectrum down to ~L/2. Since thermal diffusion is too week, Kelvin-Helmholtz rolls and Rayleigh-Taylor instabilities can develop again over a large range, defining the entire flow dynamics (Fig. 3) and perturbing the X-ray surface brightness (Fig. 4, second row). Turbulent diffusion is able to efficiently mix the entropy profile, again lowering/increasing the central density/temperature (the discrepancy between T_e and T_i is now ≲1 percent; Sect. 4.1). Conduction can affect only the scales smaller than 100 kpc, creating a gentle exponential decrease in the logarithmic A(k)_δ. The suppression of δ reaches a factor of 2 near 30 kpc. Notice how conduction still dominates the diffusivity, overcoming (numerical) viscosity. When turbulent regeneration is efficient, it is not trivial to define an exact cutoff. Nevertheless, the threshold P_t    ~ 100 (l ~ 100 kpc) appears a robust criterium: at that scale we see the beginning of a substantial decay of the density spectrum (changing slope to k^− 1/2).

3.2. Mild turbulence: M ~ 0.5

We now increase the level of turbulent motions by a factor of two, M ~ 0.5 (σ_v ~ 750 km s^-1). Turbulent energy is thus ~14 percent of the thermal energy, still within the range retrieved by ICM observations and cosmological simulations. The characteristic eddy turnover time is t_eddy ~ 0.8 Gyr.

Figure 5 shows that the overall behavior of A(k)_δ is similar to the previous set of models, with differences laying in the details. The purely turbulent case (f = 0) forms the usual injection peak, with maximum at ~12 percent (Table 1), i.e. two times that of the previous run with half the turbulent velocity. Therefore, we infer that δρ/ρ ∝ M, or more precisely δρ/ρ ≃ 1/4  M (with l = L; the 0.25 factor is likely related to γ – see Sect. 4.1). This is a key result that will be further corroborated by the runs with stronger turbulence and smaller injection scale. In the non-conductive runs, the direct relation between the density and velocity power spectrum holds also on intermediate scales.

The inertial range of A(k)_δ in the purely turbulent run is slightly shallower than the Kolmogorov spectrum (∝k^− 1/5; cf. Kim & Ryu 2005). The decrease due to viscous dissipation occurs again within 15−20 kpc, while it is dominated by thermal diffusion in all the conductive runs. Given the significant level of turbulent diffusion, the entropy profile flattens twice more rapidly, doubling its central value to 700 keV cm² in less than 2 Gyr (the best-fit profile has almost twice lower normalization, with 20 percent larger core radius). Turbulent dissipational heating still plays a secondary role, since the temperature at large radii is increased by just 15 percent (its timescale is ~4   t_eddy; Gaspari et al. 2013b). Overall, it is remarkable that the density perturbations follow in a fairly strict way the Kolmogorov velocities, even in the presence of a stratified atmosphere.

We proceed testing thermal conduction, starting from the highest suppression factor. As before, when f = 10^-3, a gentle exponential cutoff develops. The Prandtl number is ~2000 at the injection scale (twice the previous models, P_t ∝ M), signaling that turbulent regeneration is extremely efficient, as highlighted by the filamentary SB_x image (Fig. 4, second column). The dynamics is dominated by K-H and R-T instabilities. We see a significant decline in density perturbations only at l ≲ 60 kpc, i.e. P_t ~ 100. This threshold appears again a robust indicator for the suppression of density inhomogeneities. When P_t < 100, the slope steepens from nearly Kolmogorov to Burgers spectrum (A(k)_δ ∝ k^− 1/2). The threshold and spectrum slope are independent of L (see Sect. 3.4), since shaped by the specific physical parameters of the plasma conductivity.

The effects of conduction can be best appreciated when f = 10^-2. Using the key threshold P_t ~ 100, we predict a sharp decline around ~330 kpc, and indeed we see the k^− 1/2 spectrum appearing on this large scale. The suppression of δ on small scales is a factor of 3, while near the injection scale turbulent regeneration is unhindered (A(k)_δ ~ 11 percent). The SB_x maps also reveal that only the large filaments, edges, and rolls are retained. Assuming a deep exposure, X-ray imaging will thus help to assess the role of conduction and turbulence in the ICM.

Restoring the conductive flux to strong levels (f ~ 0.1 − 1, i.e. P_t ~ 20 − 2 at L) promotes a global suppression of δ, by a factor of ~2−3, from large to small scales (Fig. 5, red lines; the maxima of A(k)_δ show less separation compared with the models with weak turbulence). The slope is slightly shallower than Burgers spectrum, A(k) ∝ k^− 4/9 (although turbulence has now twice more strength). As in Sect. 3.1, strong conduction can drive small-scale stirring, due to the fast conduction timescale relative to the gas/ion sound speed (Fig. 8). These models confirm that when P_t ≲ 20 (f ≳ 0.1) the density perturbations are strongly suppressed, producing a similar A(k)_δ and smooth/spherical SB_x maps (Fig. 4), regardless of the exact suppression factor.

A relevant result, which will be dissected in future work, is that conduction does not dramatically alter the power spectrum of the velocity field (nearly Kolmogorov), both in slope and normalization. Therefore, the quoted M or velocity dispersion (roughly v(k) at the injection scale) does not change between simulations with different suppression f.

3.3. Strong turbulence: M ~ 0.75

In the next experiments, we test the case with strong (still subsonic) turbulence, with three times higher turbulent velocities compared with the reference model (Sect. 3.1), M ~ 0.75 (σ_v ~ 1100 km s^-1). Statistical steady state is reached fast, since t_eddy ~ 0.5 Gyr. The turbulent energy is ~0.31 the thermal energy. Approaching the transonic regime becomes progressively unrealistic: it has been shown both in observations and cosmological simulations that the turbulent pressure support in the ICM should remain in the range few −30 percent (e.g. Churazov et al. 2008; Lau et al. 2009; Vazza et al. 2009, 2011), the upper envelope defined by unrelaxed systems. Dissipational heating also starts to be relevant (∝M²) increasing the overall temperature by ≳30 percent, though we are now interested in the relative variations.

The current set of simulations corroborates the previous key findings. According to our modeling, δρ/ρ ≃ 1/4   M, we predict a characteristic level of density perturbations of 18.75 percent (for the weakly conductive models, f < 0.1). Measuring the normalization of the A(k)_δ peak (f < 0.1), we retrieve a value of 18.8 percent (Table 1), an excellent match. Albeit the evolution is strongly chaotic and nonlinear, it is remarkable that we can convert the Mach number and density perturbations in a linear and simple way. In fact, the normalization of A(k)_δ is 2.9 (1.6) times that of the models with weak (mild) turbulence. Therefore, we expect real clusters to show density perturbations in the same range of the observed (low) Mach numbers. This could also explain why clusters do not show exaggerated clumpiness.

The other features of the density power spectrum, i.e. the slope and decay (Fig. 6), follow the analysis described in the previous two sections. We summarize the key points. The A(k)_δ slope of the f = 0 run is again slightly shallower than k^− 1/3, although not shallower than the M ~ 0.5 model, indicating that the Kolmogorov spectrum is indeed the “saturated” regime, at least for subsonic turbulence⁴. Enabling conduction leads to the steeping of the characteristic amplitude towards the k^− 1/2 regime, with the clearest manifestation in the f = 10^-2 case, where turbulence is able to regenerate perturbations near L (notice the short formation of the gentle exponential decline), while small scales are substantially damped. In the strong conductive regime (f ≳ 0.1) conduction inhibits the perturbations up to a factor of ~2. There is no drastic decline at small scales (A(k)_δ ∝ k^− 4/9) since conduction also promotes minor stirring, albeit the increased gas sound speed/entropy (due to turbulent heating and diffusion) alleviates this process. The commonly adopted suppression factors f ≥ 0.1 do not have a diverse impact on the density perturbations, which are damped over the whole range.

The turbulent Prandtl number is increased by a factor of 3 compared with the reference run, P_t ~ 3−3000 (f ~ 1−10^-3) at the injection scale. This translates in a less marked – though not globally different – suppression between the purely turbulent and conductive case. More important, P_t ~ 100 corresponds to ~45 and 240 kpc for the f = 10^-3  and  10^-2 model, respectively (in the f ≳ 0.1 runs, the transition is well over L). Indeed, the substantial decline occurs around these scales. This threshold is thus a robust criterium to estimate the impact of conduction in a realistic cluster atmosphere.

The surface brightness maps (Fig. 4, third column) highlight the substantial level of perturbations, which are now clearly manifest even in the cluster core (especially when f ≳ 10^-2). Such a configuration could be easily spotted in X-ray images even by eye inspection. Notice how in the weakly suppressed runs, the K-H and R-T instabilities translate into extended filaments and curved edges/fronts in X-ray brightness. The strong conductive flux instead smears out most of these features, preventing the ICM to depart from its spherical and smooth hydrostatic shape. This might be seen as an effective equation of state with a lower adiabatic index, implying a less reactive pressure during thermodynamic transformations (P ∝ ρ versus P ∝ ρ^5/3). Remarkably, the gas velocities remain ~1000 km s^-1 on large scales, with the v(k) spectrum not much affected by conduction (an in-depth comparison will be presented in a companion work).

3.4. Small injection scale: M ~ 0.25, L/2

The final set of simulations includes testing turbulence and conduction diminishing the injection scale. To carry on a proper comparison, we set the new injection scale as L′ = L/2 ~ 300 kpc, but maintaining the turbulent Mach number of the reference run, M ~ 0.25 (via the scaling σ_v ~ (N   L′   ϵ^∗)^1/3; Sect. 2.3). The characteristic eddy turnover time is t_eddy ~ 0.8 Gyr, i.e. the same characteristic timescale of the previous models with M ~ 0.5 but larger injection scale (Sect. 3.2). The typical turbulent energy is 3.5 percent of E_th (as in Sect. 3.1).

The key result is that the overall A(k)_δ spectra are analogous to the models with M ~ 0.5 (Fig. 7). The characteristic Prandtl numbers, at the respective injection scales, are in fact the same. The major differences are twofold. First, the current spectra are truncated exactly at the smaller injection scale L′. Second, the normalization is defined only by the characteristic Mach number (and not P_t). In fact, using our previous A(k)_δ modeling and rescaling it with the new injection scale, we estimate A(k)_δ,max ≃ 1/4   M   (L′/L)^1/5 ≃ 0.054. The measured peak in the simulated run is 5.3 percent (Table 1), confirming well the prediction. Notice that the A(k)_δ,max fit is very weakly dependent on the injection scale, implying that the linear conversion between δ and M is fairly general (see Sect. 4.1).

Similar to previous M ~ 0.5 models, the strongly conductive runs (f ≳ 0.1) show density perturbations damped by a factor of 2−3, from large to small scales. The A(k)_δ slope follows also the previous trends, slightly shallower than Kolmogorov in the f = 0 run (∝k^− 1/5; higher D_turb means faster δ regeneration), while steepening towards the Burgers-like spectrum for the conductive runs. Using the threshold P_t ~ 100, we retrieve the region where A(k)_δ substantially decays. Interestingly, the estimated cutoff for the f = 10^-2 run is slightly larger than the injection scale (~330 kpc) and indeed we see the decrease in normalization (by 10 percent), instead of a progressive decline from the f = 0 baseline. In the f = 10^-3 run, the threshold is still below 100 kpc, allowing the exponential cutoff to partially develop, although entering quickly the regime of substantial suppression on few tens kpc. The hydrodynamics is similar to the M ~ 0.5 models, with K-T and R-T instabilities producing filaments and edges in SB_x (if f < 0.1), but now with maximum size ~100 kpc. On the other hand, strong conduction has the ability to preserve the smooth and spherical shape of the galaxy cluster (cf. last row in Fig. 4).

4. Discussion

We now explain and discuss the key features of the models, and then constrain ICM conduction and turbulence in real Coma cluster through density perturbations.

4.1. Dominant timescales and simple predictions

The qualitative evolution of a dynamical system can be described via the timescale ratio of the physical processes involved, i.e. via characteristic dimensionless numbers. Let us consider as reference Fig. 8, showing the typical timescales for M ~ 0.25 and strong conduction (f = 1) run, within the core radius. The first key quantity is the (turbulent) Mach number, M = t_cs/t_turb (<1), which we found to be linearly related to the relative density perturbations δ. The scaling may be justified by simple physical arguments (see also Zhuravleva et al. 2013, and in prep.). Perturbations tend to settle back towards shells of similar entropy. Assuming an isobaric blob, its entropy varies as K ∝ ρ^− γ ∝ (1 + δ)^− γ – for an isothermal blob K ∝ (1 + δ)^1 − γ. Since the cluster entropy typically scales with the radius, the displacement is directly linked to the density contrast, Δr/r_init ≈ ΔK/K_init = 1 − (1 + δ)^− γ ≈ γ   δ. In a stratified medium, the balancing force is F ∝ g   δ, again directly related to the displacement. Since the specific kinetic energy is v² ∝ F   Δr ∝ (Δr)², we infer that M ∝ Δr ∝ δ, with the normalization shaped by the effective γ and the K(r) slope. In the limiting case of negligible buoyancy, density may be instead roughly treated as a passive scalar. In the classic theory of Obukhov & Corrsin (Warhaft 2000 for a review), the spectrum of passive scalars is expected to be directly related to v(k). The scaling δ ∝ M is thus fairly general.

The second key quantity is the conduction timescale (Fig. 8), which is typically the shortest one (≲50 Myr). The black line shows that conduction dominates the dynamics over the whole range of scales, even in the saturated regime (upper black line). Increasing the level of suppression (f ≪ 1) induces the crossover of the conduction and turbulence (magenta) timescale. The predicted threshold for the turbulent regeneration of perturbations is P_t ≡ t_cond/t_turb ~ 100. If P_t ~ 100 occurs within the injection scale, the normalization of the spectrum does not decrease, and a decay appears on intermediate scales (Table 1). In this work, we used a turbulent diffusion coefficient c_t = 1, yet the actual value could be as low as 0.1−0.01 (Kim & Fabbiano 2003; Dennis & Chandran 2005), rescaling the threshold to P_t ~ 1.

Other timescales, linked to the relevant physics, are involved in the complex dynamics, although inducing secondary effects. The Brunt-Väisälä timescale tracks the impact of the restoring buoyant forces along the radial direction: t_BV =  [γ   (r/g)   (d   lnK/d   lnr)^-1] ^1/2. Buoyancy is thus defined by gravity g and the slope of the entropy profile⁵. Within the core radius, ∇K is very shallow (and gravity roughly constant), hence t_BV > t_turb, or Froude number Fr > 1 (Fig. 8, yellow line), implying that the ICM is approaching neutral buoyancy and turbulent motions can easily retain isotropy. On large scales, the entropy profile follows the self-similar slope ∝r, as most clusters, but it is balanced by the decreasing gravity: buoyancy can again not efficiently inhibit radial motions. Substantially weaker stirring may progressively force the chaotic flow to follow tangential streamlines (Fr ≪ 1). Notice that the buoyancy timescale is essentially the free-fall time, within a factor of a few: t_ff = (2r/g)^1/2. The ratio of the free-fall time and the gas sound-crossing time (red line) is always >1, i.e. the cluster is in global hydrostatic equilibrium. As seen in Fig. 8, in the strongly conductive runs (f ≳ 0.1) the sound-crossing time may slightly fall below the conduction time, approaching the small scales. Albeit saturation prevents electrons to conduct faster than their thermal speed, t_cs/t_cond ≲ 1 warns that small fluctuations do not have time to re-adjust via pressure equilibrium. Progressively stronger conduction is thus not able to completely stifle A_δ at large k.

The electron-ion equilibration introduces another relevant timescale (Fig. 8, cyan). On small scales, t_e − i is usually larger than t_cond and comparable to the eddy turnover time. This means that the proton temperature can not become as quickly isothermal as T_e (lagging by 50−100 Myr), a feature aggravated by the continuously chaotic ambient. The discrepancy resides in the range 1−15 percent, from the inner to outer radial bins (for model M ~ 0.25, f = 1), decreasing to a maximum of 10, 3, and 1 percent, for f = 10^-1,10^-2, and 10^-3, respectively. Higher Mach number linearly increases the maximum discrepancy (occurring at r > r_c, where the medium is more rarefied). The estimate of | T_e − T_i | /T_i can be used to properly constrain the turbulent velocities from the observed spectral lines (e.g. Inogamov & Sunyaev 2003). In order to remove thermal line broadening (∝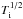${\mathit{T}}_{\mathrm{i}}^{\mathrm{1}\mathit{/}\mathrm{2}}$), it is assumed T_i = T_e, hence an effectively lower ion temperature would imply higher turbulent σ_v.

4.2. Modes of perturbations: isobaric, isothermal, isentropic

It would be tempting to characterize chaotic fluctuations with a single mode, as adiabatic (isentropic), isobaric, or isothermal. As experiment, we set up the cube with pure isobaric fluctuations (fixing Kolmogorov spectrum). The hydro run develops the turbulent cascade, preserving the isobaric fluctuations, which gradually decay in few t_eddy due to no forcing. However, as soon as conduction is enabled, the mode of perturbations suddenly change from isobaric to isothermal/adiabatic. The result is the generation of acoustic oscillations and, strikingly, a density power spectrum similar to that of the cosmic microwave background (CMB; Planck Collaboration 2013), although the two processes are inherently different – CMB evolution is driven by (compressive) gravity. The spectra observed in clusters do not present such an imprint, meaning that the actual type of fluctuations is a mixture of desynchronized modes between the adiabatic and isobaric extremes⁶.

We analyze our models to understand the correlation between relative density (δ_ρ) and temperature fluctuations (δ_T = T_e/T_b − 1, where T_b is the underlying radial profile). The correlation is positive for adiabatic fluctuations (δ_ρ/δ_T = γ − 1; constant entropy), while negative for the isobaric mode (δ_ρ/δ_T =  −1); the isothermal mode is the intermediate regime (δ_ρ/δ_T = ∞). Analyzing the linear regression coefficient of the δ_T-δ_ρ diagram (512³ points) is not much meaningful, since there is too high dispersion. We use thus Pearson coefficient⁷ to assess the degree of positive and negative linear correlation. In the no-conduction run with M ~ 0.25, the correlation is r_P ≃  − 0.86, implying that weak turbulence prefers isobaric fluctuations (adiabatic sound waves are negligible). Since stirring is subsonic, the fluctuations can not deviate much from hydrostatic equilibrium. When conduction is enabled, though partially suppressed, the scatter in the phase diagram progressively increases: fluctuations start filling also the adiabatic region, showing r_p =  −0.82, − 0.78, − 0.65, for the runs with f = 10^-3,10^-2,10^-1, respectively. With full Spitzer conduction (f = 1), the correlation drops to r_p =  −0.30: the perturbations are now almost equally isobaric and adiabatic.

Increasing the strength of stirring (M ~ 0.75), rises the level of turbulent mixing, leading to shallower entropy gradients. In fact, even in the hydro run, the adiabatic and isobaric modes are balanced (r_P ≃  − 0.20). Conduction tries to push the correlation towards the isothermal regime, albeit there is no clear preference in the mixture of perturbations (r_P ~  − 0.1; f = 1 run). Smaller injection scales also induce a more efficient turbulent cascade, promoting mixing and leading to higher adiabatic fluctuations (the latter are also enhanced in supersonic⁸ turbulence). Overall, we suggest to exploit the correlation between δ_T and δ_ρ to assess the dominant physics in the ICM.

4.3. Comparison with real Coma cluster

In order to constrain the transport properties in the bulk of the ICM, we take as exemplary case Coma cluster, due to the availability of new deep observations (~500 ks; Churazov et al., in prep.). We refer to Churazov et al. (2012) for the extraction method of A_δ, accounting for Poisson noise, point sources, and deprojection. The hot ICM, as in Coma, is best suited for this analysis, due to the potential strong conductivity and negligible cooling or AGN heating. In cold, dense systems (T_vir < 5 keV) conduction is at least 100−1000 times weaker, thus its impact is expected to be marginal (Dolag et al. 2004; Smith et al. 2013), even if unsuppressed, and very difficult to isolate (the analysis of other systems will be provided in a subsequent work).

The previous simulations provided a clear picture of the interplay between conduction and turbulence in the hot ICM. We can thus formulate a simple, general model linking conduction and turbulence to the level of density fluctuations at a given physical scale l (=k^-1): $\mathit{\delta }\mathrm{\left(}\mathit{l}\mathrm{\right)}\mathrm{\simeq }\left[\mathrm{0.25}\hspace{0.17em}\mathit{M}\hspace{0.17em}{\mathrm{(}{\mathit{L}}_{\mathrm{inj}}\mathit{/}{{\mathit{L}}_{\mathrm{500}}}^{\mathrm{)}}}^{{\mathit{\alpha }}_{\mathrm{h}}}\right]\mathrm{(}\mathit{l}\mathit{/}{\mathit{L}}_{\mathrm{inj}}{\mathrm{)}}^{{\mathit{\alpha }}_{\mathrm{c}}}\mathit{.}$(22)The term in brackets represents the normalization of δ which must be rescaled to the current injection scale L_inj, using the slope given by the purely hydrodynamic cascade, α_h (≈0.2−0.3; Table 1). As shown before, the characteristic spectrum slope α_c is dictated by the level of conduction, and can be much steeper than α_h (α_c ≳ 0.45, for f ≳ 10^-2). A steep slope combined with globally smooth residual/SB_x maps indicates that the normalization should be reduced by 1.3−2, due to very strong conductivity (f ≳ 0.1; Table 1). This prescription is sufficient to assess the physical state of the hot ICM. For a more precise modeling, we suggest to insert two (exponential) cutoffs linked to the injection, exp[− ⁽l/a₁L^)η₁], and dissipation scale, exp[− (a₂Δx/l)^η₂]; typical parameters fitting our simulated spectra are η₁ = 4, η₂ = 3/2, a₁ = 2, a₂ = 3.

In Fig. 9, we present the characteristic amplitude of density perturbations observed in real Coma cluster (within statistical uncertainties; cyan envelope), compared with the prediction based on our modeling (black line). It is clear that the observed spectrum is shallow. A power-law with slope α_c ≃ 0.36, slightly steeper than Kolmogorov (0.33), fits well the inertial range of the spectrum. Coma observations of pressure perturbations further corroborate this trend (Schuecker et al. 2004). Any plasma with significant conduction would produce instead a steeper spectrum. We can therefore exclude a strong or mild conductive state of the ICM, f ≥ 10^-2. The inertial range develops unimpeded down to tens kpc, indicating that turbulent regeneration is substantial and that the Prandtl number at the injection scale is high (P_t ≳ 2000). The fact that we do not see a sharp cutoff, but only a gentle decay, indicates that the suppression factor is very low, f ≃ 10^-3, although not f = 0 (the non-conductive cascade would be significantly higher below 60 kpc; P_t ~ 100). In addition, the observed δ map (Churazov et al. 2012) is not smooth, revealing a variegated morphology of local features, reminiscent of Fig. 3 (top two panels). The relation between the velocity and density spectrum can finally break any ambiguity of the proper regime (Gaspari et al., in prep.).

As reviewed in Sects. 1 and 2.4.1, the level of suppression in turbulent plasmas is a matter of debate. It strongly depends on the topology of magnetic field lines and the relation between the electrons mean free path and the field correlation length, l_B (e.g. Rechester & Rosenbluth 1978; Chandran & Cowley 1998; Malyshkin & Kulsrud 2001; Narayan & Medvedev 2001; Chandran & Maron 2004). For example, the latter authors suggested a suppression f ~ 0.1 if λ_e ≪ l_B, while in the opposite regime magnetic mirrors can further suppress heat transport. On top of this, kinetic plasma instabilities can substantially lower f. If the field is more ordered, the conductivity across the field can be heavily suppressed, f ≪ 1, as found by observational and theoretical analyses of sharp features in the ICM, e.g. cold fronts (Ettori & Fabian 2000; Roediger et al. 2013; ZuHone et al. 2013) and linear filaments (Forman et al. 2007; Sanders et al. 2013). Interestingly, the low value of f could explain the survival of positive T gradients in the center of many clusters since z ~ 1.2 (McDonald et al. 2013). It is also clear that such a low conductivity can not provide sufficient heating for quenching radiative cooling, leaving AGN feedback as the main solution for the cooling flow problem (Sect. 1).

The A_δ(k) peak, i.e. the normalization, is ≃10 percent, which can be achieved by a level of turbulence with M ≃ 0.45. The ratio of turbulent to thermal energy is thus 11 percent, concordant with observations and cosmological simulations of clusters (Sect. 2.3). The spectrum suggests an injection scale ~250 kpc, similar to the estimated impact parameter of merging clusters (Sarazin 2002).

We warn that the observed low frequencies have significant uncertainty, due to the stochastic nature of perturbations and modeling errors, as the deprojection and the underlying profile removal. For instance, Churazov et al. (2012) tested asymmetric models, finding that non-sphericity can vary the deprojected amplitude above 300 kpc up to a factor of 2, while smaller scales remain unaffected. The current simulations also do not model mergers or external accretion. Density inhomogeneities due to the substructures in the potential and accreted filaments may come on top of the large-scale perturbations directly related to the turbulent cascade (Churazov et al. 2012; Sanders et al. 2013). Multiple injection scales may also flatten the spectrum, although they require fine-tuning to be masked as a single spectral profile. While the turbulent cascade can be formed by a variety of drivers, its appearance, modeled in the present work, is nevertheless expected to be largely universal. It is no coincidence that the cascade in cosmological simulations is nearly Kolmogorov (e.g. Vazza et al. 2011), similar to our hydro runs. We remark that strong conduction would be clear in the spectrum, regardless of the above-mentioned mechanisms, uniquely stifling the cascade.

On very small scales, the observed spectrum is limited by Poisson noise, overcoming the fluctuations below ~30 kpc. The range 30−300 kpc is yet sufficient to determine the state of the ICM, since the effects of diffusion would clearly emerge within this range (Sect. 3). A steep slope can indeed not be produced by changing M or L_inj, but only increasing f. The SB_x map can further clarify the proper regime. Notice that if the precise L_inj is larger, the estimate of M should not vary significantly, since the more extended cascade provides a higher A_δ(k) peak. With even deeper data, the A_δ(k) slope could be traced down to smaller scales, further constraining the role of conduction (notice that low resolution smoothens the δ field). Future deeper X-ray observations might further improve these values, perhaps combining several clusters, and providing a high-precision spectrum of ICM perturbations.

In passing, we note that the δ prescription (Eq. (22)) can be very useful for those (subgrid) simulations, semi-analytic or analytic works, which intend to model, ab initio and in a simple way, the interplay of conduction, turbulence, and inhomogeneities in the ICM. For instance, the above equation can be used either to set the level of density (and T; Sect. 4.2) perturbations from the Mach number (particularly useful for clumpiness studies), or to impose the effective Mach number from the amplitude of density fluctuations. The current method can be readily applied to other areas of astrophysics, as the interstellar or intergalactic medium. Interestingly, also the ISM shows a nearly Kolmogorov slope over five orders of magnitude (Armstrong et al. 1995), though steepening in dwarf galaxies (Dutta et al. 2009); conduction seems thus substantially suppressed in different astrophysical atmospheres.

5. Conclusions

Using 3D high-resolution hydrodynamic simulations, we thoroughly tested the physics of thermal conduction (f = 0 → 1) and turbulence (M = 0.25 → 0.75) in the hot ICM, tracking both electrons and ions (|T_e − T_i | /T_i ≲ 0.15). We showed how to exploit the power spectrum of the relative gas density perturbations δ = δρ/ρ (normalization, slope, decay), in order to accurately constrain the effective conductive and turbulent state of the ICM. We chose Coma cluster as reference laboratory. The main results are as follows.

• The normalization of the characteristic amplitude spectrum, $\mathit{A}\mathrm{(}\mathit{k}{\mathrm{)}}_{\mathit{\delta }}\mathrm{=}\sqrt{\mathit{P}\mathrm{(}\mathit{k}{\mathrm{)}}_{\mathit{\delta }}\hspace{0.17em}\mathrm{4}\mathit{\pi }{\mathit{k}}^{\mathrm{3}}}\mathrm{=}\sqrt{\mathit{E}\mathrm{(}\mathit{k}{\mathrm{)}}_{\mathit{\delta }}\hspace{0.17em}\mathit{k}}$, determines the strength of turbulence, and vice versa. The peak amplitude is linearly related to the average 3D Mach number as A(k)_δ,max = c   M, where c ≃ 0.25 for injection scale L_inj ≃ 500 kpc. In the hydro run, the spectrum of δ tracks that of velocities even on intermediate scales. After rescaling, the steady spectra are remarkably similar despite different M or L_inj, allowing to build a general theory of ICM perturbations.

• The slope of A_δ(k) determines the level of diffusion dominated by conduction. In a non-conductive ICM (f = 0), subsonic stirring motions generate a nearly Kolmogorov cascade, E_δ(k) ∝ k^− 5/3. Similar to velocities, the inertial range of density perturbations peaks at the injection scale, and decays below 10 kpc due to “viscous” dissipation. Increasing the level of conduction, with magnetic suppression f = 10^-3 → 1, progressively steepens the spectrum slope towards the Burgers-like regime (E_δ(k) ∝ k^-2; Table 1), a feature that would be manifest in observations. The velocity spectrum is not much affected by conduction. Even with f = 1, the δ amplitude does not drop to zero, since strong conduction also promotes fluctuations. The A_δ(k) slope is only weakly dependent on M, becoming slightly shallower above M ≳    0.5.

• The dominant dimensionless number or timescale ratio, shaping the flow dynamic similarity (Sect. 4.1), is the turbulent Prandtl number: P_t = D_turb/D_cond = t_cond/t_turb. The threshold P_t ≲ 100 approximately indicates where A_δ(k) has a significant decay due to diffusion. The transition is very gentle for strong suppression of conduction, f ≲ 10^-3, becoming a sharp decay – though not a cutoff – in the opposite regime. If P_t ~ 100 occurs above the injection scale, density perturbations are inhibited over the whole range of scales, inducing a decrease in normalization up to a factor of ~2 (on small scales the suppression can reach a factor of 4). This state occurs only with strong conductivity, f ≥ 0.1 and would be pinpointed by the SB_x or residual δ images, in which K-H/R-T rolls and filaments are washed out, preserving the smooth and spherical shape of the cluster.

• Realistic perturbations, in a stratified system, are characterized by a mixture of modes, shaped by the dominant physics. Weak turbulence drives higher isobaric perturbations (δ_ρ/δ_T =  −1); strong turbulence enhances the adiabatic modes (δ_ρ/δ_T = γ − 1), while increasing conduction forces both modes towards the intermediate isothermal regime. Although density statistics is much better constrained by observations, unveiling temperature perturbations could substantially advance our knowledge of the ICM physics.

• Based on our experiments, we provided a general analytic model to constrain density perturbations, conduction, and turbulence in the bulk of the ICM: δ(l) ≃  [0.25   M   (L_inj/L₅₀₀)^α_h] (l/L_inj)^α_c (see Sect. 4.3). We apply it to new very deep Chandra observations of Coma. The observed A_δ(k) spectrum is best consistent with strongly suppressed conduction, f ≃ 10^-3, and mild subsonic turbulence, M ≃ 0.45 (L_inj ~ 250 kpc). The latter (E_turb ≃ 0.11   E_th) is in agreement with cosmological simulations of clusters formation and line-broadening observations. The low conductivity corroborates the survival of local sharp features (cold fronts, filaments, bubbles), and indicates that cooling flows may not be balanced by conduction, leaving AGN feedback as the main driver of heating.

The increasing quality and sample size of future X-ray data will provide a key opportunity to exploit this new spectral modeling, and hopefully to open the path to high-precision physics of the ICM, as has been done for the CMB.

Online material

Appendix A: Mexican Hat versus FFT spectrum

Since the data cube is non periodic, computing the power spectrum via FFTs is in principle inconsistent. As a consequence, the unresolved large scale power can leak into the available frequency range, distorting the spectrum. We use thus a modified Δ-variance method, known as “Mexican Hat” filtering (MH; cf. Arévalo et al. 2012). For each spatial scale σ, the method consists of three steps:

• 1.

  the real-space cube C is convolved with two Gaussian filters having slightly different smoothing lengths: ${\mathit{\sigma }}_{\mathrm{1}}\mathrm{=}\mathit{\sigma }\mathit{/}\sqrt{\mathrm{1}\mathrm{+}\mathit{ϵ}}$ and ${\mathit{\sigma }}_{\mathrm{2}}\mathrm{=}\mathit{\sigma }\sqrt{\mathrm{1}\mathrm{+}\mathit{ϵ}}$, where ϵ ≪ 1;

• 2.

  the difference of the two cubes is computed, resulting in a cube dominated by the fluctuations at scales ≈σ (the difference of two Gaussian filters is simply the Mexican Hat filter, F(x) ∝ ϵ    [1 − x²/σ²]    exp [ − x²/2σ²], characterized by a positive core and negative wings);

• 3.

  the variance V_σ of the previous cube is calculated and recast into the estimate of the power, knowing that $\begin{array}{ccc}{\mathit{V}}_{\mathit{\sigma }}\mathrm{=}\mathrm{\int }\mathrm{(}\mathit{C}\mathrm{\ast }\mathit{F}{\mathrm{)}}^{\mathrm{2}}{\mathrm{d}}^{\mathrm{3}}\mathit{x}\mathrm{=}\mathrm{\int }{\mathit{P}}_{\mathit{k}}\hspace{0.17em}{\left|\mathit{F̂}\mathit{k}\right|}^{\mathrm{2}}{\mathrm{d}}^{\mathrm{3}}\mathit{k}\mathrm{\propto }{\mathit{P}}_{\mathit{\sigma }}\hspace{0.17em}{\mathit{k}}^{\mathrm{3}}\mathit{.}& & \end{array}$

We refer to Arévalo et al. (2012) – Appendix A – for the technical procedure and normalization. In order to handle the non-periodicity of the cube, we use a “mask” which is 1 inside and 0 outside the domain. The big advantage of the MH is that it avoids any leakage of power linked to the non-periodicity of the data; the drawback is that it can not capture very sharp features in the power spectrum, due to the smoothening over Δk ~ k.

In Fig. A.1, we show the comparison between the MH and FFT spectrum, for the run with M ~ 0.5 and f ~ 10^-2. In our study, there is no dramatic difference between the two methods. The slope in the inertial range is almost identical. At very small scales, the FFT spectrum produces a characteristic hook, in part due to the numerical noise near the maximum resolution, but also due to the contamination of jumps at the non-periodic boundaries. The MH spectrum shows instead a gentle decline. In the opposite regime, the MH filter tends to smooth the scales greater than the injection scale, while the FFT spectrum shows a steeper decrease. The FFT peak is slightly higher, typically by 2−3 percent, likely affected by the non-periodic box. Progressively trimming the box increases the relative normalization of the FFT spectrum, even by 20 percent, while distorting the low-frequency slope; the MH spectrum is instead unaltered.

Appendix B: β-profile in Fourier space

We present here the analytic conversion of the β-profile to Fourier space, and its interplay with a power-law noise. Using the notation $\mathit{f̂}\mathrm{\left(}\mathit{k}\mathrm{\right)}\mathrm{=}{{}^{\mathrm{\int }}}_{\mathrm{-}\mathrm{\infty }}^{\mathrm{\infty }}\mathit{f}\mathrm{\left(}\mathit{x}\mathrm{\right)}\hspace{0.17em}\exp \mathrm{\left[}\mathrm{i}\mathit{kx}\mathrm{\right]}\hspace{0.17em}\mathrm{d}\mathit{x}\mathit{/}\sqrt{\mathrm{2}\mathit{\pi }}$, the Fourier transform of the β-profile (Eq. (1)) results to be $\mathit{n̂}\mathit{\beta }\mathrm{\left(}\mathit{k}\mathrm{\right)}\mathrm{=}{\mathit{n}}_{\mathrm{0}}\hspace{0.17em}\frac{{\mathrm{2}}^{\mathrm{1}\mathrm{-}\mathit{\xi }}{\mathit{r}}_{\mathrm{c}}^{\mathit{\xi }\mathrm{+}\mathrm{1}\mathit{/}\mathrm{2}}\mathrm{\left|}\mathit{k}{\mathrm{|}}^{\mathit{\xi }\mathrm{-}\mathrm{1}\mathit{/}\mathrm{2}}{\mathit{K}}_{\mathrm{1}\mathit{/}\mathrm{2}\mathrm{-}\mathit{\xi }}\mathrm{\right[}\mathrm{\left|}\mathit{k}\mathrm{\right|}\hspace{0.17em}{\mathit{r}}_{\mathrm{c}}\mathrm{]}}{\mathrm{\Gamma }\mathrm{\left[}\mathit{\xi }\mathrm{\right]}}\mathit{,}$(B.1)where ξ ≡ 3β/2, K_1/2 − ξ is a modified Bessel function of the second kind, and Γ is the Gamma function. The (1D) power spectrum is as usual retrieved as . Assuming β = 2/3 ≃ 0.66 (a typical value for galaxy clusters), the power spectrum of the β-profile reduces to $\mathit{P}\mathrm{\left(}\mathit{n̂}\mathit{\beta }\mathrm{\right)}\mathrm{=}\left(\frac{\mathit{\pi }}{\mathrm{2}}{\mathit{r}}_{\mathrm{c}}^{\mathrm{2}}\right)\hspace{0.17em}\exp \mathrm{[}\mathrm{-}\hspace{0.17em}\mathrm{2}\hspace{0.17em}\mathrm{|}\mathit{k}\mathrm{|}\hspace{0.17em}{\mathit{r}}_{\mathrm{c}}\mathrm{]}\mathit{.}$(B.2)The previous equation strikes for its simplicity, and can be readily used in semi-analytic studies. Changing β in the range 0.5−1 does not significantly alter P(k), hence Eq. (B.2) is an excellent approximation for the majority of clusters (Fig. B.1, red line). A remarkable feature is that the transition from real to Fourier space does not dramatically deform the profile, in tight analogy with Gaussian functions (∝exp [ − k²]). The spectrum is dominated by the power on large scales, with the core radius playing a crucial role; a progressively rising r_c leads to an increase in both the normalization and steepness of the spectrum.

For our study, it is useful to analyze the superposition of the β-profile and a power-law Kolmogorov noise (with 1D power ∝k^− 5/3), n_p = n_β   (1 + δ). Using the convolution theorem, the power spectrum of the perturbed density profile is given by . The cross terms cancel out since the

δ field is random and the phases are uncorrelated. In Fig. B.1, we show three power spectra: β-profile (red), noise with ~10 percent relative amplitude (blue), and the superposition of both (black). Beyond the core radius (k ≳ 0.05), the noise clearly starts to dominate. It is thus not essential to remove the underlying profile or large-scale coherent structures, in order to unveil density perturbations, especially with substantial turbulence.

---

Acknowledgments

The FLASH code was in part developed by the DOE NNSA-ASC OASCR Flash center at the University of Chicago. We acknowledge the MPA, RZG, and CLS center for the availability of high-performance computing resources. M.G. is grateful for the financial support provided by the Max Planck Fellowship. E.C. acknowledges support by the Research Program OFN-17 of the Division of Physics, Russian Academy of Science. We thank R. Sunyaev, A. Schekochihin, F. Vazza, and the anonymous referee for helpful comments.

References

All Tables

All Figures