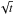| Issue |
A&A
Volume 559, November 2013
|
|
|---|---|---|
| Article Number | A33 | |
| Number of page(s) | 18 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201322278 | |
| Published online | 31 October 2013 | |
Warm ice giant GJ 3470b
I. A flat transmission spectrum indicates a hazy, low-methane, and/or metal-rich atmosphere⋆
1 Max-Planck Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
e-mail: ianc@mpia.de
2 Lowell Observatory, 1400 West Mars Hill Road, Flagstaff, AZ 86001, USA
3 Department of Physics & Astronomy, University of California Los Angeles, Los Angeles, CA 90095, USA
4 Institute for Astronomy, University of Hawaii, 2680 Woodlawn Drive, Honolulu, HI 96822, USA
Received: 14 July 2013
Accepted: 29 August 2013
We report our spectroscopic investigation of the transiting ice giant GJ 3470b’s atmospheric transmission, and the first results of extrasolar planet observations from the new Keck/MOSFIRE spectrograph. We measure a planet/star radius ratio of 0.0789+0.0021-0.0019 in a bandpass from 2.09–2.36 μm and in six narrower bands across this wavelength range. When combined with existing broadband photometry, these measurements rule out cloud-free atmospheres in chemical equilibrium assuming either solar abundances (5.4σ confidence) or a moderate level of metal enrichment (50× solar abundances, 3.8σ), confirming previous results that such models are not representative for cool, low-mass, externally irradiated extrasolar planets. Current measurements are consistent with a flat transmission spectrum, which suggests that the atmosphere is explained by high-altitude clouds and haze, disequilibrium chemistry, unexpected abundance patterns, or the atmosphere is extremely metal-rich (≳200 × solar). Because GJ 3470b’s low bulk density sets an upper limit on the planet’s atmospheric enrichment of ≲300 × solar, the atmospheric mean molecular weight must be ≲9. Thus, if the atmosphere is cloud-free its spectral features should be detectable with future observations. Transit observations at shorter wavelengths will provide the best opportunity to discriminate between plausible scenarios. We obtained optical spectroscopy with the GMOS spectrograph, but these observations exhibit large systematic uncertainties owing to thin, persistent cirrus conditions. Finally, we also provide the first detailed look at the steps necessary for well-calibrated MOSFIRE observations, and provide advice for future observations with this instrument.
Key words: techniques: spectroscopic / techniques: photometric / planets and satellites: atmospheres / stars: individual: GJ 3470 / eclipses
Light curves are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/559/A33
© ESO, 2013
1. Introduction
1.1. Sub-Jovian planets are common
Planets with masses similar to Uranus and Neptune are a plausible link between gaseous Jupiter-class giants and rocky terrestrial-class planets, and are often defined by their failure to capture gas from the protoplanetary nebula and become fully fledged gas giants. Yet their presence and properties, by virtue of that very same lack of a natural explanation, offer crucial information about how planets form and possibly move during the evolution of planetary systems.
Scenarios to explain the origins of hot Jupiters by migration predicted that Neptune-mass planets would be scarce at short periods, because of the fine tuning required to avoid the rapid accretion of gas from the nebula while also using the gas to migrate inwards (Ida & Lin 2008; Mordasini et al. 2009). Yet radial velocity searches have uncovered many planets which fall into this class (Howard et al. 2010; Mayor et al. 2011). Thus, in-depth study of these enigmatic planets could potentially shed new light on the nature of what now appears to one of the more common class of planetary system.
GJ 3470b transit parameters (2.09–2.36 μm).
Although hot Neptunes are not expected from the most commonly adopted migration models, several other possibilities have been discussed. Tidal capture has been proposed as an explanation for hot Jupiters (Rasio & Ford 1996; Fabrycky & Tremaine 2007; Nagasawa et al. 2008; Naoz et al. 2011) and could potentially produce low mass planets, but the effectiveness of this process depends strongly on the poorly constrained efficiency of tidal dissipation in such planets (e.g., Kennedy & Kenyon 2008; Barnes et al. 2009). Migration of several low-mass planets in a resonant chain may help to slow the migration and prevent the planets from being swallowed by the star (Terquem & Papaloizou 2007; Ogihara & Ida 2009; Ida & Lin 2010). Neptune-mass planets may also represent the accretion-starved analogues of Jupiter-class planets that assemble in situ (Hansen & Murray 2012), although this likely requires a substantial inventory of solid material to assemble a sufficiently large core mass.
All of these scenarios imply different histories and compositions for the resulting planets, and this can potentially be probed by an in depth study of the planetary atmosphere and composition. Measurements of bulk properties such as planetary radii and masses provide insight into planetary interior structures and compositions. This approach is powerful, but for planets with Uranus-like bulk properties it long been known that degeneracies exist and the interior structure and composition cannot be uniquely inferred (e.g., Wildt 1947; Miner 1990, and references therein). The same limitation apply to extrasolar planets (e.g., Adams et al. 2008; Figueira et al. 2009; Nettelmann et al. 2011). A complementary technique is to observe a planet’s atmosphere (whether by transits, occultations, phase curves, in-situ probes, etc.), thereby constraining the atmosphere’s structure and chemical composition and (we hope) inferring something about the planet’s interior composition. Among other goals, such measurements should provide clues about the planet’s formation history which are encoded in their bulk and atmospheric properties (e.g., Öberg et al. 2011; Fortney et al. 2013).
1.2. Atmospheric characterization of short-period exoplanets
Since the first detection of an exoplanet’s atmosphere (Charbonneau et al. 2002) numerous hot Jupiters have been studied via the emission or transmission of their atmospheres. This has led to robust detections of numerous atomic species and molecules (Charbonneau et al. 2002; Barman 2007), high-altitude hazes (Pont et al. 2008, 2013; Lecavelier Des Etangs et al. 2008), and a diverse range of atmospheric circulation patterns (Knutson et al. 2007; Crossfield et al. 2010) and albedos (Rowe et al. 2008; Demory et al. 2011). These discoveries continue to fuel an ongoing revolution in the field of externally irradiated planetary atmospheres. However, despite the greater frequency with which smaller, lower-mass planets occur most are not amenable to such followup observations: their transit depths, temperatures, and/or host star apparent fluxes are typically too low.
To date only two planets of roughly Neptune size or smaller have been subjected to detailed scrutiny: GJ 1214b and GJ 436b. The small, cool planet GJ 1214b has one of the most complete transmission spectra of any extrasolar planet (Bean et al. 2011; Berta et al. 2012, and references therein), but these measurements are consistent with a flat, featureless spectrum. GJ 1214b’s bulk properties likely require a substantial volatile envelope, but this envelope’s composition is unknown (Nettelmann et al. 2011; Rogers & Seager 2010). The ensemble of current data indicates that the planet’s atmosphere is either shrouded in an opaque haze or it is composed predominately of heavy molecules such as H2O (Howe & Burrows 2012; Morley et al. 2013; Benneke & Seager 2013).
Photometry of the hotter, more massive GJ 436b has been more revealing: the planet’s substantial H2 envelope (Adams et al. 2008; Figueira et al. 2009) is significantly depleted in CH4 and enhanced in CO when compared to equilibrium conditions and solar composition (Stevenson et al. 2010; Knutson et al. 2011). These results suggest that the planet’s atmosphere is metal-rich compared to its host star, and may exhibit strong internal diffusion that brings CO up into the observable photosphere and/or significant photochemistry (Line et al. 2011; Madhusudhan et al. 2011). Recent investigations of very high metallicity atmospheres (>100 × solar) indicate that such compositions can also explain observations of GJ 436b (Fortney et al. 2013; Moses et al. 2013). However, to date no reliable spectroscopy has been obtained for GJ 436b (but see Pont et al. 2009; Gibson et al. 2011).
1.3. Introducing GJ 3470b
The recently discovered planet GJ 3470b presents another excellent target for atmospheric characterization of a relatively small and cool object via transmission spectroscopy. The planet was discovered by radial velocity measurements and subsequently seen to transit (Bonfils et al. 2012); subsequent observations demonstrate that the planet is larger and of slightly lower mass than Uranus, with radius 4−5 R⊕ and mass 14 M⊕ (Demory et al. 2013; Fukui et al. 2013; Biddle et al., in prep.). The planet orbits an early M star whose mass and radius are roughly half that of the Sun, and which may be slightly metal-rich (Demory et al. 2013; Pineda et al. 2013; Biddle et al., in prep.). The stellar flux varies by ~1% in R band (Biddle et al., in prep.), which will be important for future work but is not significant for our relatively poor final precision. We summarize the stellar and planetary parameters used in this study in Table 1.
Compared to previously studied planets, GJ 3470b’s mass and equilibrium temperature (600–800 K) lie between those of GJ 1214b and GJ 436b, and GJ 3470b is the largest of these three planets. According to interior models, GJ 3470b must have a H2 envelope that is ~10% the mass of the planet (Fortney et al. 2007; Rogers & Seager 2010; Valencia 2011; Demory et al. 2013; Fukui et al. 2013). Thus GJ 3470b, like GJ 436b, likely has a H2 envelope over a denser central core containing a large large ice (H2O, CH4, NH3) complement.
If GJ 3470b has a clear atmosphere it presents an attractive target for transmission spectroscopy owing to the planet’s large atmospheric scale height, transit depth and duration, and host star apparent magnitude (Miller-Ricci et al. 2009). In this case the high-altitude opacity structure should be detectable as a variation of transit depth with wavelength: i.e., the planet would appear larger at wavelengths of high opacity. A marginal detection of this effect in broadband photometry has already been reported by Fukui et al. (2013).
However, optically thick clouds or haze can obscure atmospheric features during transit and produce a flat transmission spectrum, and haze has been invoked for several relatively cool (sub-1200 K) transiting planets (Knutson et al. 2011; Benneke & Seager 2012; Pont et al. 2013; Gibson et al. 2013; Morley et al. 2013). The most well-studied case is that of HD 189733b, in which the optically thick haze first seen at visible wavelengths (Pont et al. 2008; Lecavelier Des Etangs et al. 2008) appears to extend at least into the near-infrared (Sing et al. 2009). Though the composition of any such haze in these planets’ atmospheres remains unknown, if present a haze would substantially modify the emission and transmission spectra by increasing the atmospheric opacity and thereby raising the altitude of the effective photosphere and obscuring signatures at deeper altitudes (Pont et al. 2013). Clouds have been invoked to explain a range of observed characteristics of brown dwarf atmospheres and self-luminous exoplanets (Barman et al. 2011; Witte et al. 2011; Marley et al. 2012). As yet few such studies have been undertaken for short-period exoplanets (Zahnle et al. 2009; Morley et al. 2013; Parmentier et al. 2013); the conditions under which such hazes may form in these objects’ atmospheres (like their interior compositions) remains unknown.
1.4. Paper overview
We have undertaken a campaign of transit photometry and spectroscopy to probe the physical parameters of the GJ 3470 system and the atmospheric composition of GJ 3470b. Paper II (Biddle et al., in prep.) will discuss an analysis of new transit photometry which dramatically improves the system parameters. In this work, we discuss our optical and near-infrared (NIR) transmission spectroscopy obtained during two transits of GJ 3470b, which provides evidence for a flat transmission spectrum. In Sect. 2 we describe our observations and initial data calibration. In Sect. 3 we describe our approach to modeling light curves, accounting for limb darkening, and estimating our final measurement uncertainties. In Sect. 4 we present our atmospheric models of GJ 3470b’s atmosphere, which leads to our primary results: we rule out a solar-abundance atmosphere in chemical equilibrium, and find that more metal-enriched atmospheres are also disfavored. In Sect. 5 we discuss the implications of these results in the broader context of atmospheric characterization of cool, low-mass planets, and conclude in Sect. 6. Finally, in Appendix A we present guidelines for improved calibration of observations with the Keck Observatory’s new MOSFIRE instrument.
2. Data acquisition and calibration
2.1. Keck/MOSFIRE
2.1.1. Observations
We observed GJ 3470 on UT 2013-04-08 with the Keck I telescope using the new MOSFIRE multi-object spectrograph (McLean et al. 2008, 2010, 2012; Kulas et al. 2012). MOSFIRE is a near-infrared multi-object spectrograph located on a rotatable mount at the Keck I Cassegrain focus. The instrument provides spectral resolution of roughly 3500 (with a slit width of 0.7″) for targets over a field of view of roughly 6′ × 6′; a single photometric band is covered at each instrument setting. We have learned a considerable amount about how best to obtain high-precision spectrophotometric light curves with this instrument; we present the finer points of this discussion in Appendix A.
In total we obtained 401 K-band frames during 257 min and over an airmass range of 1.00−2.3. Because of GJ 3470’s bright infrared flux (KS = 7.99; Skrutskie et al. 2006), we used exposures of 5.82 s duration with 2 coadds; each coadd used four non-destructive reads to “sample up the ramp” during the integration. We attempted to save all non-destructive reads from the detector (Bean et al.2011 discuss why this is desirable), but the instrument electronics were unable to keep up with our high data rate and we were forced to abandon this strategy.
We obtained simultaneous spectroscopy of GJ 3470, TYC 1363-2087-1, and the fainter star 2MASS 07591321+1524069. Figure 1 shows the raw spectra of the first two stars. We discuss all objects’ spectral characteristics in Sect. 2.3, but we use only the first two objects in our MOSFIRE analysis. We used wide (10″) slits to ensure that the spectrograph captures essentially all stellar flux, regardless of guiding errors or changes in seeing. We nodded the telescope along the slit axis (see Sect. A.2). Our spectra cover wavelengths from 1.96−2.39 μm for both GJ 3470 and our primary comparison star, and we achieved signal-to-noise ratio (S/N) of roughly 80−120 column-1 frame-1.
 |
Fig. 1 GMOS (top) and MOSFIRE (bottom) spectra of exoplanet host star GJ 3470 (black) and simultaneously-observed comparison star TYC 1363-2087-1 (gray). The former is a main-sequence M dwarf, while the latter is a rather hotter giant. The short black bars in the top panel indicate the locations of the gaps between the GMOS CCDs. |
 |
Fig. 2 Instrumental trends for spectroscopic observations of GJ 3470. Left: GMOS. The effects of intermittent cirrus are apparent in the raw stellar flux; this also increases the scatter in the relative light curve. Right: MOSFIRE. Some parameters appear double-valued because data were taken while alternating between two nod positions on the slit. The data shown here are available as an electronic supplement to this article. |
We acquired GJ 3470 just as transit began. When observations were scheduled the planet’s ephemeris was still poorly known, so transit began shortly after sunset; in addition, technical issues further delayed the start of observations. A subset of instrumental parameters during our observations is shown in Fig. 2. Instrumental seeing (w, measured by fitting a Gaussian profile along the spatial direction of GJ 3470’s spectrum in each raw frame) varied from full width at half maximum (FWHM) values of 0.5−1.3″. Spectral motions along the dispersion and spatial axes were roughly 3 pixels each and mainly dominated by a gradual trend attributable to differential atmospheric refraction owing to the use of an optical-wavelength guider. A software upgrade under development should correct for this differential refraction.
The stellar traces moved in the spatial direction (y) by about 3 pixels (excluding a brief 4-pixel jump and subsequent recovery) during the observations. All of w, x (movement in the dispersion direction), and y exhibit rapid changes near mid-transit, which introduces a change in the measured fluxes which is not wholly removed when dividing by the comparison star’s flux. This abrupt event occurs close in time to a discontinuity in the secondary and telescope focus positions. Telescope staff currently have no explanation for this effect. As we describe below we attempt to account for this effect in our light curve fits using these parameters as decorrelation variables. Future MOSFIRE observations of GJ 3470 may achieve better stability by correcting for the refractive effects described above, and by defocusing the telescope to decrease the sensitivity to instrumental flexure and to allow longer integration times.
2.1.2. Calibration
We calibrate the MOSFIRE data using our own set of Python and PyRAF routines1; many of the initial steps are similar to those previously employed in calibration of Subaru/MOIRCS imaging data (Crossfield et al. 2012). These routines construct two master flat frames by median-stacking individual frames taken with 0.7″ slits while the dome lamps were on and off. The difference of the two frames produces the master, unnormalized dome flat frame. To remove the gross signatures of instrumental throughput and the lamp spectrum, we divide the spectral region from each slit by a one-dimensional median-filtered spectral profile; we also divide by the median spatial profile to remove the effects of MOSFIRE’s nonuniform slit widths as discussed in Appendix A. The resulting master flat frame approximately captures the pixel-to-pixel sensitivity variations in the MOSFIRE detector.
Our calibration routines next divide each raw science frame by the resulting flat frame. We then correct the frames for the infrared array detector’s intrinsic nonlinearity on a pixel-by-pixel basis, using the approach of Vacca et al. (2004); we compute the necessary nonlinearity coefficients from a large set of flat frames generously provided to us by Dr. K. Kulas. Next we flag all isolated pixels that differ from their neighbors by ≳10 × the deviations expected from photon and read noise, and replace these presumably bad pixels with the median of their four nearest good neighbors. The final step is to subtract the thermal and sky background from each frame. For each pixel in a given frame, we fit a linear trend in time to the same pixel in the preceding and succeeding frames (which are taken at the opposite nod position), interpolate to the time of the frame of interest, and subtract the interpolated value.
Wavelength calibration is provided by a set of frames using the same 0.7″ slits used for the flat frames and taken with Ne and Ar arc lamps illuminating the dome interior. We extract the line emission spectra from the master arc frame, and use the standard IRAF task ecidentify to mark known lines and fit low-order polynomials of pixel number versus wavelength. We find that a cubic function adequately fits the wavelength solution for all targets; the best-fit coefficients vary somewhat across the detector but the mean solution is λ(x)/μm = λ0 + (2.1953 × 10-4)x + (2.68 × 10-9)x2 + (7.6 × 10-13)x3, where λ0 is the wavelength offset for each star and x is the pixel number. The fit residuals have RMS values of roughly 0.1 Å, with maximum excursions of 0.4 Å occurring near the ends of some spectra; the effective size of the stars on the detector varies with seeing but is approximately 13 Å. Considering the very wide spectral bandpasses we employ below, this level of calibration is probably adequate for our purposes. As a final step, we compare the wavelength-calibrated spectra to a model telluric absorption spectrum to correct for any offsets (as would be caused by slightly mis-centering a star in our wide slits). The median MOSFIRE spectrum of GJ 3470 and our comparison star are shown in Fig. 1.
2.2. Gemini-North/GMOS optical spectroscopy
2.2.1. Observations
We observed GJ 3470 on UT 2013-03-29 with the GMOS multi-object optical spectrograph (Hook et al. 2004) at Gemini North. This instrument (and its twin at Gemini South) has already been used for transmission spectroscopy of several systems (Gibson et al. 2013; Stevenson et al. 2013). As at Keck, the combination of uncertainty in GJ 3470b’s ephemeris and technical problems caused our observations to begin just as transit ingress started. We observed using integration times of 100 s, and read out only a subset of the detector pixels to reduce overheads. In this way we obtained 135 frames during 252 min and covering an airmass range of 1.01−1.72.
We observed in the red optical using the RG610 filter and R600 grating, which gives a spectral resolution of 3700 for a 0.5″ slit. Again, we used 10″ slits and TYC 1363-2087-1 as our sole telluric calibrator; raw spectra of these stars are shown in Fig. 1. Throughout the night we observed through thin cirrus, which introduced relatively large-amplitude (but largely wavelength-independent) variations in our final time series data. GJ 3470b’s transit is clearly visible in the wavelength-integrated relative light curve shown (along with other, generally stable, instrumental trends) in Fig. 2.
2.2.2. Calibration
To calibrate the raw GMOS frames we first bias-subtract them and apply a flat-field correction. The flat frames were taken with a mask otherwise identical to our science mask, but with 0.7″ slits. For wavelength calibration we acquired CuAr arc lamp frames with this same mask, and we determine wavelength solutions in the same manner as for MOSFIRE.
GMOS spectra are dispersed across three independent CCD detectors, which exhibit slight misalignments. We therefore perform independent wavelength calibration and spectral extraction for each detector. Our final light curve analysis (described below) explicitly ignores data taken near the detector gaps.
2.3. Comparison stars
The object TYC 1363-2087-1 serves as our primary telluric calibrator for both the infrared and optical analyses. This star has Ks = 8.05 and lies 2.9′ northeast of GJ 3470; the latter’s photometric colors are rather redder. A comparison of the two stars’ spectra show that TYC 1363-2087-1 is a giant or subgiant with Teff greater than that of GJ 3470. The comparison star exhibits stronger absorption at Brackett γ, in the CO bandheads at λ > 2.29 μm, and in the ~ 0.86 μm Ca II triplet, and it shows weaker absorption at the 0.82 μm and 2.206 μm Na I doublets, Ca I 2.263 μm triplet, and red-optical TiO bandheads (Kleinmann & Hall 1986; Rayner et al. 2009).
We also obtained infrared and optical spectroscopy of 2MASS 07591321+1524069; this red object’s CO bandhead, Na, and Ca absorption are all shallower than for GJ 3470, so it may be a main sequence star. However, it is much fainter (I = 13.4,KS = 11.9) than our primary comparison star and so its light curves are too noisy to be of further use in our analysis.
2.4. Spectral extraction and final calibration steps
We use the standard IRAF task apall to extract spectra from our calibrated data frames and we explore a wide range of extraction parameters: background and target aperture sizes, and polynomial orders used for tracing the spectral traces and for fitting residual sky background. We employed this approach in two parallel ways: in one the extraction aperture is constant for all data frames, whereas in the other the extraction aperture for each frame varies linearly with the spatial FWHM of the spectral trace in each frame. The optimal extraction parameters are those values which minimize the RMS of the best-fit residuals in light curve fits to several wavelength channels.
In our initial extraction parameter surveys, we find that the approach with variable extraction aperture size typically gives slightly lower residual RMS values. The parameters which minimize the residual dispersion in our MOSFIRE analysis uses extraction apertures with a total width of (2 × FWHM + 16) pixels, surrounded by an 8 pixel buffer and then a background aperture 45 pixels wide, traced with a fifth-order polynomial and including a linear trend in the background estimation and subtraction. For the GMOS analysis we find the best results using an extraction aperture 20 pixels wide, with a 6 pixel buffer on each side flanked by 24 pixels of background aperture, tracing the spectra on each chip with a third-order polynomial and assuming a constant sky background across the region of interest.
After extraction, the final step in all cases is to cross-correlate each star’s spectra with the median of all extracted spectra to measure any spectral shift in the dispersion direction, and then shift each spectrum to a common wavelength scale using sub-pixel interpolation. We convert each frame’s timestamps in the raw FITS file headers into the BJDTDB time system using the online interface of Eastman et al. (2010).
3. Light curve analysis
Before describing our approach to fitting the wavelength-integrated and spectroscopic light curves, we first discuss how we treat stellar limb darkening (Sect. 3.1), model fitting and parameter uncertainty estimation (Sect. 3.2), model selection (Sect. 3.3), and the details of fitting the wavelength-integrated (Sect. 3.4) and spectroscopic (Sect. 3.5) light curves. Finally, in Sect. 3.6 we investigate systematic errors using a set of injection and recovery tests.
3.1. Limb darkening
A proper treatment of limb darkening is essential for an accurate retrieval of light curve parameters. A common practice is to use model stellar atmospheres to help constrain limb-darkening parameters (e.g., Bean et al. 2010; Berta et al. 2012). To this end, we investigate two approaches which give consistent results.
In both cases, we perform fits for each individual wavelength channels of the model atmosphere; the results are averaged together after weighting the fits by the mean observed spectrum of GJ 3470. In agreement with previous studies (Diaz-Cordoves & Gimenez 1992; van Hamme 1993), we find that a root-square darkening relation – of the form 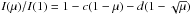 – represents the stellar models better than a quadratic relation. Our data are not of sufficient precision to justify the use of the full four-parameter functional form, while the use of a linear law gives higher residual RMS values (though the ultimate results of this latter analysis are consistent with our final results). The limb-darkening priors used in our analysis are listed in Table 2.
– represents the stellar models better than a quadratic relation. Our data are not of sufficient precision to justify the use of the full four-parameter functional form, while the use of a linear law gives higher residual RMS values (though the ultimate results of this latter analysis are consistent with our final results). The limb-darkening priors used in our analysis are listed in Table 2.
Stellar limb-darkening coefficients were calculated by fitting monochromatic intensities from a spherically symmetric PHOENIX stellar atmosphere model (following Hauschildt et al. 1999) customized for GJ 3470. A stellar temperature of 3500 K, a surface gravity equal to 105 cm s-2, and solar abundances were adopted for the final analysis. These stellar parameters were motivated by previously published values (Demory et al. 2013) and a desire to closely match optical to infrared broad-band photometry for this star. We then fit the root-square limb-darkening relation to the high-resolution output of this model. This is the approach used for the results we present below.
By adjusting the stellar parameters (log 10g, Teff, and [Fe/H]) to generate several new models, then re-fitting, we obtain estimates of how the uncertainties in the stellar parameters influence our uncertainties in the limb-darkening values. We compute the covariance matrix of c and d, and use this with optimal model’s parameters to impose a two-dimensional Gaussian prior in the fitting process. This approach makes full use of our insight into the expected correlations between multiple limb-darkening parameters. Because different models can give different limb-darkening profiles (especially for cooler stars), we multiply the covariance matrix by 4 to account for systematic uncertainties in the stellar atmosphere models.
We also investigated the use of Kurucz model atmospheres (Kurucz 1979) for estimating limb-darkening coefficients. We draw a large number of values of Teff and log g from Gaussian distributions described by the parameters in Table 1; we use the set of models with [Fe/H] = 0.2, appropriate for GJ 3470’s metallicity (Demory et al. 2013; Pineda et al. 2013; Biddle et al., in prep.). For each draw we interpolate the four nearest models and compute the desired limb-darkening coefficients. The mean and covariance matrix of the distribution are then applied as described above. Using this second set of models gives a transmission spectrum consistent with our primary result.
3.2. Light curve analysis: parameter fitting and statistical uncertainties
We model the light curves using the standard Mandel & Agol (2002) equations, with a root-square limb darkening law and the “small-planet” approximation (to speed computation time). We fit to the data using a model of form  (1)where F(t) is the final model at time t, f is the transit light curve, p is a polynomial function of t, and the si are the state vectors with coefficients ki used for additional decorrelation (see Sect. 3.3). Our model parameters are the transit time TT, RP/R∗, R∗/a, P, i, c, d, the ki, and the coefficients of p (variables not otherwise defined here have their usual meaning). In all our analyses, we impose a Gaussian prior on the orbital period P, with mean and standard deviation 3.336665 ± 0.000008 d (Biddle et al., in prep.). Our final results are insensitive to small changes in P; for example, our conclusions do not change significantly if we instead take P from the work of Demory et al. (2013).
(1)where F(t) is the final model at time t, f is the transit light curve, p is a polynomial function of t, and the si are the state vectors with coefficients ki used for additional decorrelation (see Sect. 3.3). Our model parameters are the transit time TT, RP/R∗, R∗/a, P, i, c, d, the ki, and the coefficients of p (variables not otherwise defined here have their usual meaning). In all our analyses, we impose a Gaussian prior on the orbital period P, with mean and standard deviation 3.336665 ± 0.000008 d (Biddle et al., in prep.). Our final results are insensitive to small changes in P; for example, our conclusions do not change significantly if we instead take P from the work of Demory et al. (2013).
Function optimization is accomplished using optimize.fmin, the SciPy implementation of the downhill simplex algorithm. After an initial fit, data points whose absolute residuals exceed 10σd are flagged as outliers, where σd is the width of the symmetric interval enclosing 68.3% of the data points. We then perform a weighted fit in which the data points are given equal weights, such that the total χ2 equals the number of valid (i.e., non-outlier) points. Data points whose absolute residuals exceed 5σd are set to zero weight and the process repeats; typically only a single iteration is required and only a small number of data points (3−4) are de-weighted.
 |
Fig. 3 Noise analysis of the residuals to the spectrophotometric light curves shown in Figs. 6 and 7 for data from GMOS (left) and MOSFIRE (right). Top: decrease in RMS of binned residuals with increasing binned size. The solid curves correspond to the individual wavelength channels, and the dashed line shows the 1/ |
We explore the likelihood distributions of our parameters of interest using the affine-invariant Markov chain Monte Carlo (MCMC) sampler emcee (Foreman-Mackey et al. 2013). This tool computes parameter distributions using many (in our case, several hundred) independent Markov Chains; its affine-invariance means that the algorithm is unaffected by the parameter correlations that plague transit light curve fitting. The software therefore requires little fine-tuning. We verify by eye that the resulting chains are well-mixed by examining the evolution of their χ2 values. In each fit, we take as our final parameter estimates the resulting best-fit parameters from the optimizer.
In the highly multidimensional parameter spaces we explore, we find that optimizers easily become stuck in local likelihood maxima. To guard against this eventuality, after each 20% segment of every MCMC run we re-apply the function optimization described above using using the most recent parameters from 12 of the chains. If any of the resulting fits have a higher likelihood than our previous best fit, we update the weights on the data points, re-initialize the MCMC sampler, and begin the procedure all over again. This approach affords us some assurance that the sampler and optimizer do not become trapped in local minima in χ2 space.
In our experience, correlated noise is present in (at least) all ground-based infrared observations of exoplanet transits and occultations. The χ2 statistic implicitly assume statistically independent measurements, i.e. an absence of correlated effects, so relying on this parameter (or the related BIC; see below) can result in underestimated parameter uncertainties. We employ three techniques to investigate the level of any correlated noise in the data. The first technique is the now-standard examination of how the residuals to the best-fit model bin down over larger and larger time intervals. We employ the β-statistic approach of Winn et al. (2008) to inflate our initial uncertainties (estimated as the lower and upper values corresponding to the 15.87% and 84.13% percentiles of each parameters’ distribution) based on the level of correlated noise on the timescale of transit ingress. To prevent the result being influenced by small-scale structure, we compute ⟨ βT12 ⟩, which we define as the mean of the β values from half to twice the ingress timescale. This approach estimates our statistical uncertainties; we employ a separate injection-and-recovery approach (described in Sect. 3.6) to estimate our systematic uncertainties. We eschew the use of the common residual-permutation bootstrap (or prayer-bead) analysis. As has been noted elsewhere, bootstrap techniques can be poorly suited to sampling the entirety of a posterior distribution (Line et al. 2013).
Following Gibson et al. (2012), we also always inspect the discrete autocorrelation of the residuals and the power spectral density of the residuals. Correlated noise induces large-scale structure in the autocorrelation, and induces generally stronger peaks in the power spectrum. These indications are more qualitative than quantitative, but still give us greater confidence in our ability to ascertain whether any correlated noise is present. We plot all of these metrics for all spectrophotometric light curves in Fig. 3.
3.3. Model selection
In the analysis of transit light curves, several techniques have been used to address the issue of model selection, including Gaussian Processes (Gibson et al. 2012) and statistical Information Criterion (Liddle 2007; Stevenson et al. 2010). At least as often a single parametric model is assumed, but there is no guarantee as to the accuracy of model parameters and uncertainties so derived. We use the Bayesian Information Criterion (BIC = χ2 + klnn when fitting n measurements with a k-dimensional model; Schwarz 1978), which penalizes models that use too many parameters.
In our case, the extra parameters are the additional observables shown in Fig. 2 that we use as the si in our analysis. We fit our model function to the white-light (wavelength-integrated) light curve using many different combinations of these state vectors and compute the BIC for each model. If one naively follows the standard practice of rescaling our measurement weights to give χ2 = n, then a zero-parameter model will always minimize the BIC. Instead, we follow our former approach (Crossfield et al. 2012) and rescale our measurement weights based on an initial, baseline fit. For both MOSFIRE and GMOS analyses, our baseline model is the product of the standard light curve relation and a quadratic function in time. We then compare the BIC resulting from more complicated models to the BIC from this model.
3.4. White light curve analysis
We test various combinations of state vectors on our MOSFIRE data, and in Table 3 list the resulting values in χ2 and BIC, the ⟨ βT12 ⟩ values, and the standard deviation of the baseline-normalized residuals (SDNR). Our best BIC-minimizing models listed in Table 3 all produce results consistent within the reported uncertainties, so our precise choice of model does not affect our ultimate conclusions.
MOSFIRE wavelength-integrated (2.09–2.36 μm) model fits.
Note that the use of BIC as a model selection tool is probably not the optimal choice, because it ignores the correlated noise present in the data. An ideal metric would penalize greater model complexity, per-point residuals, and models whose residuals exhibit a greater level of internal correlation. A more rigorous approach to these matters will eventually be necessary if the exquisitely precise measurements planned with JWST are to be reliable (e.g., Deming et al. 2009; Kaltenegger & Traub 2009).
For the GMOS data, the scatter in the relative light curve (see Fig. 2) is much greater than would be expected from photon noise considerations. This increased scatter is likely the result of the thin cirrus layer present throughout the night, and to a large degree it affects all wavelength channels equally. Because the noise level is clearly very high (and the noise does not correlate well with other observables), we adopt an essentially differential approach for these data. For the wavelength-integrated analysis we use a quadratic trend in time with no other state vectors. We then use the residuals to this fit as the single state vector for analyzing the spectroscopic light curves (as described in the next section). Such self-calibration can artificially reduce the noise level in each wavelength channel. We therefore inflate all GMOS spectroscopic-channel uncertainties by  , where v is the number of spectroscopic channels used.
, where v is the number of spectroscopic channels used.
 |
Fig. 4 Injection-and-recovery results for K-band MOSFIRE data. The light curves shows simulated transits that have been injected into real data and re-fit as described in Sect. 3.6; they are plotted here after removal of overall trends and state vectors. The dotted line shows the wavelength-independent injected value of 7.0%. The thick solid lines and points shows the best-fit recovered transit parameters; the error bars derive from the MCMC analyses and have been inflated by ⟨ βT14 ⟩ as discussed in Sect. 3.2. The dashed lines indicates the weighted means for each test. In both cases the recovered spectra are consistent with a constant value, and the systematic offsets are <2σ. |
3.5. Spectroscopic analysis
After selecting the state vectors to use in decorrelating our photometry (x for MOSFIRE, and the white-light residuals for GMOS), we perform an analysis of light curves constructed by splitting our stellar spectra of target and comparison star into several bins. For both optical and NIR analyses we choose to use six bins to strike a balance between our final uncertainties and retaining some moderate spectral resolution.
The spectroscopic analysis proceeds as follows. First, in succession we perform an initial fit to each channel’s light curve using the parameters from the white-light analysis as an initial guess (but without using any state vectors). The fit residuals are again used to set the per-point weights; points with zero weight in the white-light analysis are also de-weighted in the per-channel analysis, and any additional points more than 5σ discrepant are also de-weighted; these steps repeat 1−2 times, until convergence.
Next, we compute a linear least-squares fit of the state vectors to the residuals obtained. We combine the least-squares parameters with the other parameters previously determined as a guess for a full fit to the channel’s light curve; again, we de-weight outliers and reset the weights so that χ2 equals the number of data points. As described previously, we then conduct an MCMC analysis of the channel and interrupt the MCMC process several times during its run to test for new and improved parameter sets. These steps are repeated for each of the spectroscopic channels that are to be analyzed.
Now the real analysis begins: we analyze all spectroscopic light curves in a single optimization and MCMC run. We use the weights calculated previously for each channel, and use the best-fit parameters from the individual fits as an initial guess. A single value controls each of the physical and achromatic parameters (a/R∗, TT, P, and i) for all of the light curves, but c, d, and Rp/R∗ are allowed to take different values in each channel and the si and coefficients of p take on independent values in each nod position. With N channels we have 7N + 4 free parameters for the GMOS analysis and 11N + 4 for MOSFIRE. As before we then fit this large number of parameters to the data, conduct an MCMC analysis, and check several times for parameter combinations that improve the quality of the fit. We then estimate statistical parameter uncertainties as described in Sect. 3.2.
3.6. Injection and recovery tests
To best understand the accuracy and precision of our analysis, we conduct a series of tests in which we attempt to recover signals of known amplitude which we inject into the residual data. Such injection tests are commonly used to determine the performance of high-contrast imaging programs (e.g., Nielsen & Close 2010), planet surveys using radial velocity (e.g., Wittenmyer et al. 2011) and transit (e.g., Petigura et al. 2013) methods, and exoplanet spectroscopy (Crossfield et al. 2011; Crouzet et al. 2012; Deming et al. 2013). We insert artificial signals into the observed data, then re-analyze the synthetic data sets using our standard techniques. Any differences between the artificial signals’ recovered parameters and the known input values provide a quantitative measure of how our analysis methods and the data’s noise properties affect the parameters retrieved from the non-injected analysis.
We implement the injection and recovery scheme as follows. First, we take the extracted spectra and conduct the analysis described in the preceding sections. We then remove the best-fit transit signature from each wavelength channel (to provide sufficient coverage outside of transit) while leaving all trends and systematic effects unaltered. To the extent that removing the best-fit transit signature inevitably reduces the noise level of the remaining data, the accuracy estimated from our approach is overly optimistic; however, this is likely to be a minor effect.
We next inject a simulated transit light curve computed by taking P, a/R∗, i, and the limb darkening coefficients from the current channel’s best-fit parameters; RP/R∗ and TT are each set to the same values across all channels. TT in particular is chosen to be offset by at least T14/2 from its nominal location to avoid re-fitting data sets which are essentially identical; in practice this means our relatively short data sets limit us to ~2 such independent tests (i.e., signals injected halfway through the data and at the end of the data). Because the signals are injected into the absolute (not relative) spectrophotometry our approach also automatically injects a signal into the white-light (wavelength-integrated) light curve. We then run the analysis process described in the preceding sections on the new, synthetic data set and compare the results to the input parameters. The primary difference between our approach and residual permutation analysis is that we are examining how the overall character of the measured transmission spectrum is affected by systematic effects and correlated noise, whereas residual permutation is typically used as an estimate of the noise properties of an individual light curve, independent of other wavelength channels.
GJ 3470b transmission spectrum.
We show the result of the MOSFIRE injection-and-recovery tests in Fig. 4. Both recovered spectra are flat (reduced  when compared to a flat spectrum) and show systematic offsets between the mean injected signal (RP/R∗ = 0.07) and the recovered values of <2σ. We note that the recovered spectra both exhibit similar shapes, with extrema near 2.25−2.30 μm. Although this shape is correlated with the limb-darkening priors applied in our analysis, we recover a spectrum with the same shape even when imposing no limb-darkening prior. In addition, GJ 3470b’s true recovered K-band transmission spectrum (shown in Fig. 8) does not exhibit this shape. We estimate our MOSFIRE systematic uncertainties to be σRP/R∗ = 0.03 (absolute) and 0.16% (relative), where the former is computed by taking the weighted mean of the computed offsets and the latter by the root quadrature mean of the RMS from the recovered spectra; both values are lower than the per-channel uncertainties presented in Table 4. All these encouraging factors lead us to conclude that at our current level of precision, our MOSFIRE spectrum is not significantly affected by systematic sources of error. However, future observations with better pre- and post-transit coverage should reach higher precision and these tests should be repeated then.
when compared to a flat spectrum) and show systematic offsets between the mean injected signal (RP/R∗ = 0.07) and the recovered values of <2σ. We note that the recovered spectra both exhibit similar shapes, with extrema near 2.25−2.30 μm. Although this shape is correlated with the limb-darkening priors applied in our analysis, we recover a spectrum with the same shape even when imposing no limb-darkening prior. In addition, GJ 3470b’s true recovered K-band transmission spectrum (shown in Fig. 8) does not exhibit this shape. We estimate our MOSFIRE systematic uncertainties to be σRP/R∗ = 0.03 (absolute) and 0.16% (relative), where the former is computed by taking the weighted mean of the computed offsets and the latter by the root quadrature mean of the RMS from the recovered spectra; both values are lower than the per-channel uncertainties presented in Table 4. All these encouraging factors lead us to conclude that at our current level of precision, our MOSFIRE spectrum is not significantly affected by systematic sources of error. However, future observations with better pre- and post-transit coverage should reach higher precision and these tests should be repeated then.
The GMOS injection-test results are shown in Fig. 5. As with MOSFIRE, the injected signal has RP/R∗ = 0.070. When the signal is injected into the middle of the data set, the resulting spectrum is quite flat (σRp/R∗ = 0.13% and reduced  ). However, when we inject a signal at the end of the observations, the recovered spectrum is worse (σRp/R∗ = 0.16%, reduced
). However, when we inject a signal at the end of the observations, the recovered spectrum is worse (σRp/R∗ = 0.16%, reduced  ). With so few wavelength bins this
). With so few wavelength bins this 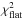 value could occur by chance in 14% of cases, but it is still troubling. The systematic offsets between the injected signal and the mean recovered value are quite large, confirming our hypothesis that the differential analysis used here is not sensitive to the absolute transit depth. We estimate systematic uncertainties of 0.75% (absolute) and 0.14% (relative) for the GMOS data. Most troubling, the shape and amplitude of the spectrum recovered from the observed (non-injected) GMOS data is quite similar to that of the spectra recovered from the injection tests: a slope below 0.90 μm with a local extremum near that wavelength. We therefore conclude that the GMOS data is likely to be contaminated by systematic errors induced by the variable cloud conditions that prevailed when during these observations.
value could occur by chance in 14% of cases, but it is still troubling. The systematic offsets between the injected signal and the mean recovered value are quite large, confirming our hypothesis that the differential analysis used here is not sensitive to the absolute transit depth. We estimate systematic uncertainties of 0.75% (absolute) and 0.14% (relative) for the GMOS data. Most troubling, the shape and amplitude of the spectrum recovered from the observed (non-injected) GMOS data is quite similar to that of the spectra recovered from the injection tests: a slope below 0.90 μm with a local extremum near that wavelength. We therefore conclude that the GMOS data is likely to be contaminated by systematic errors induced by the variable cloud conditions that prevailed when during these observations.
 |
Fig. 5 Injection-and-recovery results showing simulated light curves and results for optical GMOS data. Sub-figures and symbols are the same as Fig. 4. Because we analyze the GMOS data in a differential fashion (Sect. 3.4) these data are insensitive to the absolute transit depth. In addition, the retrieved spectrum in the bottom sub-figure exhibits considerable systematic errors and the systematics in the top sub-figure (though weaker) are similar in shape to the results of the true (non-injected) GMOS analysis shown in Fig. 8. |
3.7. Transit analysis: results
3.7.1. MOSFIRE K band analysis
We restrict the range of our MOSFIRE data to 2.09−2.36 μm because data outside this range show increasingly strong systematic errors in the spectroscopic analysis; this effect could be due to a slight mismatch in wavelength calibration and correlations with telescope pointing and instrumental seeing.
Using this bandpass, the results from our MOSFIRE white-light (wavelength-integrated) are listed in Table 1. Our best-fit orbital parameters (i and a/R∗) are consistent with those presented previously (Demory et al. 2013; Fukui et al. 2013) and we find 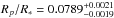 , which is <1.5σ discrepant from all previously reported values for GJ 3470b.
, which is <1.5σ discrepant from all previously reported values for GJ 3470b.
3.7.2. Retrieved transmission spectrum
The MOSFIRE light curves, best-fit models, and residuals to the fits are shown in Fig. 6 and the model parameters are listed in Table 4. The residual scatter in these fits is 2−3× greater than predicted by Poisson statistics. We find that we come closer to the photon noise limit in regions free of telluric OH line emission, consistent with previous analyses (Bean et al. 2011).
 |
Fig. 6 MOSFIRE transit light curves: a) raw spectrophotometric data showing the systematic offsets between the two nod positions, and best-fit models; b) normalized and corrected measurements and models; c) residuals; d) final transmission spectrum after scaling error bars by ⟨ βT12 ⟩. The data shown in panel a) are available as an electronic supplement to this article. |
Because GMOS uses three CCDs, there are slight gaps (corresponding to light lost between the CCDs) in our optical analysis; we split each detector into two, giving six wavelength channels. Because of our differential (self-calibrating) approach our GMOS transit depths are precisely determined relative to the determined white-light transit depth, but their absolute accuracy is limited to the accuracy of the low S/N parameters from the noisy wavelength-integrated light curve. The GMOS light curves, best-fit models, and residuals to the fits are shown in Fig. 7. As discussed in Sect. 3.6, the GMOS observations were contaminated by cirrus-induced systematic effects and we do not consider these data further.
 |
Fig. 7 GMOS transit light curves: a) raw spectrophotometric data showing the common-mode flux variations, and best-fit models; b) normalized and corrected measurements and models; c) residuals multiplied by 3; d) final transmission spectrum after scaling error bars by ⟨ βT12 ⟩. Because we analyze the GMOS data in a differential fashion (Sect. 3.4) these data are insensitive to the absolute transit depth. Further, as shown in Fig. 5 these measurements are likely affected by systematic errors. |
 |
Fig. 8 Transmission spectrum of GJ 3470b. Colored points with error bars are our MOSFIRE measurements; black points are the measurements of Fukui et al. (2013) and Demory et al. (2013). The solid lines show the model transmission spectra described in Sect. 5. The ensemble of measurements rule out equilibrium-chemistry models with solar composition (blue) and 50× solar abundances (green) at 5.4σ and 3.8σ, respectively. A methane-depleted atmosphere (pink), a very highly enriched atmosphere (200× solar, light blue), and a simple flat spectrum suggestive of high-altitude haze (dashed) all remain plausible. These scenarios are discussed in Sect. 5. The dotted lines at bottom show the filter profiles (from Fukui et al. (2013), 2MASS, and Spitzer/IRAC) used to compute the band-integrated model points (shown as colored open circles). |
4. Atmospheric models and observations
4.1. Model parameters and spectra
To interpret our observations, we present the first model transmission spectra calculated specifically for GJ 3470b. These models include cloud-free PHOENIX models in chemical equilibrium with 1×, 50 ×, and 200 × solar abundances, and an otherwise identical set of models with the abundance of carbon set to zero (to simulate an atmosphere in severe chemical disequilibrium or with a low C/O ratio, as has been investigated for GJ 436b; Line et al. 2011; Madhusudhan & Seager 2011). We motivate our choice of 200× solar as an upper limit in Sect. 5.3. All models are calculated following the steps outlined by Barman (2007), with the only exceptions being the use of more recent CH4 line data (Sromovsky et al. 2012; Bailey et al. 2011) and new collision-induced opacities (Richard et al. 2012). We plot the temperature-pressure profiles and vertical abundance profiles of several molecular species in Fig. 9. Note that these models do not include the effect of photochemistry or disequilibrium processes, which can significantly affect atmospheric abundances in planets orbiting M stars (e.g., Line et al. 2011; Moses et al. 2013).
 |
Fig. 9 Atmospheric parameters for our equilibrium-chemistry models assuming solar abundances of heavy elements (solid), 50× solar (dashed), and 200× solar (dotted). The panels show as a function of altitude: a) the effective planetary radii, b) the temperature-pressure profiles, and c) the abundances of several molecular species. We discuss these models in Sect.4, and show the model transmission spectra derived from them in Fig. 8. |
The equilibrium chemistry changes significantly across the metallicity range considered. With solar abundances ratios CH4 is the most abundance C-bearing molecule by far. As the abundances of heavy elements are increased, the abundances of O-bearing species increases more quickly than that of CH4 (because the solar C/O ratio <1). Thus in the 200× solar model, CO2 is more common than both CO and CH4 throughout most of the atmosphere. H2O remains the most abundant molecule (after H2) in all models at pressures ≲0.1 mbar. The main effects of increased metallicity in the model spectra, shown in Fig. 8, are therefore: a reduction in CH4 features throughout the infrared spectrum; the steadily strengthening CO2 opacity feature at 4.3 μm; lower amplitudes for features throughout the spectrum owing to the greater mean molecular weight and smaller scale height. The C-free models have H2O mole fractions of roughly 6.4 × 10-4,0.031, and 0.12, and these values are very nearly constant with altitude.
4.2. Comparing models to data
Figure 8 shows these model transmission spectra and the observations of GJ 3470b. The figure also presents the predicted transit depths in several photometric bandpasses (computed by weighting the models with the stellar flux incident in each bandpass).
With our new MOSFIRE measurements, transit observations of GJ 3470b currently comprise eleven measurements: our six spectroscopic points and the previous five photometric measurements (Fukui et al. 2013; Demory et al. 2013, we neglect the discovery transit measurements of Bonfils et al. 2013 owing to the poor quality of those data). We cannot discriminate between our models on the basis of the MOSFIRE data alone, but using all available data we compute the χ2 statistic for each of the atmospheric models presented above. We tune each model only inasmuch as we add a constant value to match the weighted mean of all measurements. Table 5 shows the resulting χ2 values and the probability P(χ2) of each χ2 value occurring by chance.
Goodness of fit for atmospheric models.
Of all models tested, the lowest χ2 results from a planetary radius that is constant with wavelength: i.e., a flat transmission spectrum. Such a model gives χ2 = 15.1, indicating that it is reasonably consistent with the data. The C-free models have χ2 ≲ 20; worse than the flat case, but close enough that we cannot distinguish between these cases.
Finally, the two lower-metallicity models provide the worst fits: the 50× solar abundance and solar models give χ2 = 34.4 and 52.8. Thus, the data disfavor these models at confidence levels of 3.8σ and 5.4σ, respectively, when considering the ensemble of all data.
5. Interpreting A flat transmission spectrum
The transmission spectrum of GJ 3470b is flat within current measurement uncertainties. Such a result admits of several interpretations. Below we discuss several possibilities. The planet could have no (or a negligible) atmosphere (Sect. 5.1); some or all of the observations to date could suffer from undetected systematic errors (Sect. 5.2); or the planet’s atmosphere could be: dominated by molecules heavier than H2 (Sect. 5.3); hydrogen-dominated but with less methane than expected (Sect. 5.4); or enshrouded in optically thick clouds or haze (Sect. 5.5).
5.1. No or negligible atmosphere?
If GJ 3470b had only a tenuous atmosphere, or no atmosphere whatsoever, its radius would naturally appear nearly constant across the wavelengths probed. However, models of planetary interiors predict that a planet with GJ 3470b’s observed mass and radius should consist of ≳10% hydrogen by mass (Fortney et al. 2007; Adams et al. 2008; Figueira et al. 2009; Valencia 2011); whether primordial or outgassed, such a massive atmosphere clearly indicates that a substantial planetary atmosphere is preferred for this planet.
5.2. Measurement errors?
Early transit photometry of GJ 1214b showed a transit significantly deeper in K band than at optical and Spitzer/IRAC wavelengths, a result which was interpreted as evidence for a H2-dominated atmosphere depleted in CH4 and/or with a low carbon content (Croll et al. 2011; Crossfield et al. 2011); a new, independent K band photometric data set is consistent with this early result (de Mooij et al. 2012). However, K band transit spectroscopy of GJ 1214b shows a transit shallower than the photometrically-derived values (Bean et al. 2011). The discrepancy has not yet been resolved, despite the significant implications for the composition of GJ 1214b’s atmosphere. The controversy highlights the need for multiple and independent transit analyses when retrieval of atmospheric parameters is desired. In a similar manner, future observations of GJ 3470b may reveal a discrepancy in one or more of the transit observations we consider here.
We verified that a flat transmission still fits better than other models, even when we impose no priors whatsoever on the stellar limb darkening. Our results change only slightly if we perturb the prior imposed on P, or if we impose priors on i and a/R∗ using results from previous analyses (Demory et al. 2013). Thus, the MOSFIRE transit measurements appear robust.
Our own optical-wavelength transit light curve analysis (Biddle et al., in prep.) gives a transit depth consistent with previous measurements (Fukui et al. 2013). GJ 3470’s 1% R band variability (Biddle et al., in prep.) should not induce significant systematic offsets between transits measured at different epochs, considering the measurement uncertainties available. We note that previous analyses of GJ 3470b’s transit light curves did not report the magnitude of correlated noise on their measurement uncertainties (Demory et al. 2013; Fukui et al. 2013), so additional analyses and observations clearly warranted2. At present, we see no cause to mistrust the data in hand.
5.3. An atmosphere with high mean molecular weight
Atmospheres which contain a large percentage of molecules heavier than H2 will have smaller scale heights, an effect which reduces the amplitude of spectral features seen in transmission (e.g., Miller-Ricci et al. 2009). For example, GJ 1214b’s mostly-flat transmission spectrum has been interpreted as evidence for an atmosphere with a large H2O component (Bean et al. 2011; Berta et al. 2012; Howe & Burrows 2012; Benneke & Seager 2013). Our 200× solar abundance model shows spectral features somewhat smaller in amplitude than those of our solar-abundance model (Fig. 8) because of the former’s higher mean molecular weight; this high-metallicity model is consistent with the existing data.
It has been suggested that the formation of low-mass, low-density planets by core accretion could lead to extremely high atmospheric enrichment in heavier elements (>100 × solar; Fortney et al. 2013). GJ 3470’s supersolar metallicity (Demory et al. 2013; Pineda et al. 2013; Biddle et al., in prep.) lends further support to the idea that GJ 3470b’s atmosphere could be metal-rich3, perhaps more so than those of solar system ice giants.
In particular, a variety of theoretical models predict that planets with GJ 3470b’s mass would form with high envelope metallicities. Population synthesis models of planet migration predict envelope metallicities of Z = 0.6 − 0.9, corresponding to atmospheric mean molecular weights of roughly 5−12 (assuming H2O is the dominant heavy molecule; Fortney et al. 2013). Models of in situ accretion (Hansen & Murray 2012) predict global metallicities of Z = 0.3 − 0.6, prior to envelope evaporation. However, the bulk properties of GJ 3470b constrain the metallicity of the atmosphere to be not much above 300 × solar abundances (μ = 9). We arrive at this estimate by assuming: GJ 3470b’s bulk composition is 10% H/He by mass (Demory et al. 2013), the planet’s heavy-element content is composed solely of H2O, any metals not in the core are distributed evenly throughout the atmosphere, and the planet’s radius does not change when metals are moved from the core to the envelope. These assumptions may not all hold, but the point remains that GJ 3470b’s low bulk density sets an upper limit to the planet’s total metal content. If we further assume that the planet formed via gas accretion onto a solid core of roughly 5 M⊕, the planet’s atmospheric abundances must be ≲200 × the solar level.
As Table 5 and Fig. 8 show, such a high enrichment is consistent with the data. Even higher metallicities (up to 10 000 × solar) have been recently proposed to explain observations of GJ 436b’s atmosphere (Moses et al. 2013). If low-mass planets like GJ 3470b and GJ 436b can indeed form with such highly metal-enriched atmospheres (Fortney et al. 2013), then GJ 3470b’s lower density and consequent tighter constraints on envelope metallicity may make this system a more attractive target for transmission spectroscopy than GJ 436b. For now, a metal-enriched (~200−300× solar), high-mean molecular weight atmosphere seems a plausible explanation for GJ 3470b.
5.4. Methane-poor atmosphere
Methane is a strong opacity source at 2.1−2.4 μm and is predicted to be the dominant C-bearing molecule at temperatures of 600−800 K. In chemical equilibrium, a solar composition atmospheres at these temperatures has a CH4 mixing ratio of >10-4 for pressures P = 1 − 1000 mbar and >10-3 for a 30 × solar metallicity atmosphere. At all but the upper end of this temperature range, CO is predicted to be less abundant than CH4. Indeed, our lower-metallicity models of GJ 3470b’s atmosphere predict CH4 to be more dominant than CO at pressures <0.01 mbar (Fig. 9).
However, we see no evidence for the large differential ([4.5] – K) transit depth expected for an atmosphere with strong CH4 absorption (e.g., Miller-Ricci & Fortney 2010; Crossfield et al. 2011). This indicates that CH4 opacity does not contribute significantly to the transmission spectrum. Such a scenario can be explained by intrinsically low C abundances (Madhusudhan 2012), by disequilibrium processes such as photochemistry and eddy diffusion, or by a highly metal-enriched atmosphere (which will tend to favor CO and CO2 over CH4, as shown in Figs. 8 and 9 ).
The situation appears similar to that of GJ 436b, which is only slightly warmer than GJ 3470b and also shows no evidence for the predicted CH4 absorption in transmission or emission on the basis of Spitzer photometry at >3 μm (Stevenson et al. 2010; Knutson et al. 2011). These observations of GJ 436b have been attributed to a high-metallicity (≳10 × solar) atmosphere with internal diffusion and perhaps photochemistry also playing a role (Line et al. 2011; Madhusudhan & Seager 2011; Moses et al. 2013). Strong parallels also exist between these atmospheric properties and those of Uranus and Neptune (Lunine 1993), though to date models cannot explain the extreme level of disequilibrium chemistry inferred in GJ 436b’s atmosphere. Nonetheless, some combination of low C/O and/or chemical disequilibrium by a combination of convection and/or diffusion & photochemistry could explain GJ 3470b’s current transmission spectrum.
5.5. Hazy or cloud-covered atmosphere
The best-fitting model transmission spectrum is a constant value from 0.5–5.0 μm, indicating that currently no spectral features are detected in GJ 3470b’s atmosphere. A flat transmission spectrum is also a simple approximation for an atmosphere largely or partially obscured by optically thick clouds or hazes (e.g., Crossfield et al. 2011; Berta et al. 2012). The presence of significant hazes and/or clouds has been predicted to be a ubiquitous feature of externally irradiated exoplanet atmospheres (Fortney 2005; Fortney et al. 2013). Indeed, such atmospheres have been invoked to explain observations of cool, low-mass planets such as GJ 1214b (Howe & Burrows 2012; Morley et al. 2013) and of hotter, more massive planets such as hot Jupiter HD 189733b (Pont et al. 2013). The hypothesis is that either condensate clouds (analogous to those found in brown dwarf atmospheres; e.g., Woitke & Helling 2004; Freytag et al. 2010) or photochemical hazes (similar to those found in Solar System gas giant atmospheres; e.g., Pilcher 1977; Pollack et al. 1987) could form stable layers at high altitudes where they would significantly alter the character of the planet’s transmission and emission spectra.
Condensate clouds have received considerable attention owing to their importance in brown dwarf atmospheres, but hazes in cooler (<1000 K), externally-irradiated exoplanet atmospheres have not undergone much study. However, the recent excellent study undertaken by Morley et al. (2013) indicates that physically motivated models can explain the approximately flat transmission spectrum of GJ 1214b: either clouds in a high-metallicity atmosphere or hydrocarbon haze composed of sub-μm sized particles. Our model atmosphere parameters shown in Fig. 9 are only slightly cooler than those used by Morley et al. (2013), suggesting that their results are applicable to GJ 3470b. This similarity indicates that GJ 3470b’s flat transmission spectrum could be explained by either condensate clouds or hazes produced by hydrocarbon photolysis.
6. Conclusions and future work
6.1. Conclusions
Our observations provide the best constraints to date on the atmosphere of the cool, sub-Neptune mass ice giant GJ 3470b. The high S/N possible for GJ 3470b will lead to this planet becoming a touchstone object that will strongly influence our understanding of cool, low-mass planetary atmospheres. The transmission spectroscopy presented here represents the first step toward that goal. Our K band spectroscopy, combined with optical and Spitzer photometry, allows us to rule out a solar-abundance atmosphere in chemical equilibrium and without clouds or hazes with 5.4σ confidence (Fig. 8). A similar model with 50× solar abundances is also disfavored, albeit with lower confidence (3.8σ).
However, the precise nature of GJ 3470b’s atmosphere remains uncertain because the ensemble of measurements are reasonably well fit by a single value of Rp/R∗, independent of wavelength; i.e., the transmission spectrum is flat. After considering many possible explanations (Sect. 5), we conclude that GJ 3470b’s atmosphere is either depleted in CH4 relative to equilibrium expectations and solar abundances (as has been previously claimed for the hotter and more massive GJ 436b; Sect. 5.4), is enshrouded in an optically thick cloud or haze layer (as suggested for the smaller, cooler GJ 1214b; Sect. 5.5), or is highly enriched in metals (as suggested for both GJ 436b and GJ 1214b; Sect. 5.3). We note that these explanations are not mutually exclusive: for example, the atmosphere could have a high metallicity and also host clouds or haze, while a metal-rich atmosphere would naturally result in low levels of CH4.
We have presented the first exoplanetary results obtained with the new MOSFIRE instrument, and present detailed discussion of some of MOSFIRE’s idiosyncrasies (Appendix A). The precision of our MOSFIRE data are limited by having little pre-transit coverage, but our injection and recovery tests (Sect. 3.6) indicate that our MOSFIRE results are not significantly affected by systematic sources of error. Intermittent cirrus interferes with our optical spectroscopy observations, and our analysis indicates that these measurements are probably contaminated by cloud-induced systematic errors. This indicates that the self-calibration technique adopted in several analyses (Gibson et al. 2013; Stevenson et al. 2013) gives inconsistent results in the limit of very large systematic variations. Those analyses did not attempt transit injection and recovery tests, but we strongly urge future researchers to do so in order to empirically and convincingly determine the amplitude of systematic errors.
6.2. Future work
Further observations of GJ 3470b at optical and infrared wavelengths are clearly warranted. Further transit photometry with Warm Spitzer and from ground-based facilities will be of great use in refining the planet’s orbital and bulk physical properties (Biddle et al., in prep.). Such observations might help to characterize the planet’s broadband transmission spectrum: e.g., 3.6 μm observations could provide an independent confirmation of CH4 depletion and sufficiently precise 4.5 μm observations could constrain the high abundances of CO2 predicted for high-metallicity atmospheres (see Fig. 8). Caution is warranted in light of troubling inconsistencies in similar transit photometry of GJ 436b (Beaulieu et al. 2010; Knutson et al. 2011), and it remains to be seen whether GJ 3470’s stellar variability will permit a meaningful comparison of transit photometry taken at different epochs.
In this most pessimistic case, transit spectroscopy and simultaneous multiband photometry would be the only way to reveal the nature of GJ 3470b’s atmosphere. Additional H and K band transit spectroscopy would confirm our nondetection of CH4. Transmission spectroscopy at 0.5−0.8 μm and at J and Y bands seems best suited to discriminate between the different plausible atmospheric scenarios (see Fig. 8). Optical observations could provide strong constraints on the presence of any optically thick clouds or hazes; in the absence of such phenomena, the absorption signatures of H2O could be descried in the red optical and shorter-wavelength observations could measure the atmosphere’s Rayleigh slope and thereby independently constrain the mean molecular weight of the planet’s atmosphere.
Detection of clouds or haze could suggest a high albedo that would decrease the received stellar energy input and increase the level of internal heating necessary to explain the planet’s luminosity. Further RV observations, or ideally occultation timing measurements, would place better limits on the level of any tidal heating. Currently, detection of GJ 3470b’s occultations is only feasible with Warm Spitzer; such measurements would allow a direct comparison with measurements of GJ 436b’s dayside emission and would provide a strong, independent test of the relative abundances of CH4 and CO in GJ 3470b’s atmosphere. The degree of similarity between GJ 436b’s and GJ 3470b’s atmospheres, both in terms of carbon-species chemistry and/or optical hazes, will be an important benchmark test for the next generation of atmospheric models4.
Most these routines are available from the primary author’s website, currently at http://www.mpia-hd.mpg.de/homes/ianc/.
B.-O. Demory informs us that their analysis estimated that correlated noise was a <10% effect in their data using the β approach of Winn et al. (2008).
Simultaneously with this report, an analysis of optical transit photometry of GJ 3470b was released that also suggests a hazy atmosphere (Nascimbeni et al. 2013). Further infrared measurements are still necessary to constrain GJ 3470b’s atmospheric chemistry and abundances.
Acknowledgments
We thank P. Cubillos and Dr. J. Harrington for in-depth discussions about the finer points of light-curve fitting and systematic uncertainties, Dr. H. Knutson for discussions of GJ 436b and its transmission spectrum, Dr. M. Kassis, J. Aycock, Dr. P. Hirst, and B. Walp for their assistance in obtaining our MOSFIRE and GMOS observations, and Drs. I. McLean and K. Kulas for useful discussions regarding the MOSFIRE instrument. This material is based upon work supported by NASA Origins of Solar Systems under Grant No. NNX10AH31G awarded to T.B.
References
- Adams, E. R., Seager, S., & Elkins-Tanton, L. 2008, ApJ, 673, 1160 [NASA ADS] [CrossRef] [Google Scholar]
- Bailey, J., Ahlsved, L., & Meadows, V. S. 2011, Icarus, 213, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Barman, T. 2007, ApJ, 661, L191 [NASA ADS] [CrossRef] [Google Scholar]
- Barman, T. S., Macintosh, B., Konopacky, Q. M., & Marois, C. 2011, ApJ, 733, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, R., Jackson, B., Raymond, S. N., West, A. A., & Greenberg, R. 2009, ApJ, 695, 1006 [NASA ADS] [CrossRef] [Google Scholar]
- Bean, J. L., Miller-Ricci Kempton, E., & Homeier, D. 2010, Nature, 468, 669 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bean, J. L., Désert, J.-M., Kabath, P., et al. 2011, ApJ, 743, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Beaulieu, J. P., Kipping, D. M., Batista, V., et al. 2010, MNRAS, 409, 963 [NASA ADS] [CrossRef] [Google Scholar]
- Benneke, B., & Seager, S. 2012, ApJ, 753, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Benneke, B., & Seager, S. 2013, ApJ, submitted [arXiv:1306.6325] [Google Scholar]
- Berta, Z. K., Charbonneau, D., Désert, J.-M., et al. 2012, ApJ, 747, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Bonfils, X., Gillon, M., Udry, S., et al. 2012, A&A, 546, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charbonneau, D., Brown, T. M., Noyes, R. W., & Gilliland, R. L. 2002, ApJ, 568, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Croll, B., Albert, L., Jayawardhana, R., et al. 2011, ApJ, 736, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Crossfield, I. J. M., Hansen, B. M. S., Harrington, J., et al. 2010, ApJ, 723, 1436 [NASA ADS] [CrossRef] [Google Scholar]
- Crossfield, I. J. M., Barman, T., & Hansen, B. M. S. 2011, ApJ, 736, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Crossfield, I. J. M., Barman, T., Hansen, B. M. S., Tanaka, I., & Kodama, T. 2012, ApJ, 760, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Crouzet, N., McCullough, P. R., Burke, C., & Long, D. 2012, ApJ, 761, 7 [NASA ADS] [CrossRef] [Google Scholar]
- de Mooij, E. J. W., Brogi, M., de Kok, R. J., et al. 2012, A&A, 538, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deming, D., Seager, S., Winn, J., et al. 2009, PASP, 121, 952 [NASA ADS] [CrossRef] [Google Scholar]
- Deming, D., Wilkins, A., McCullough, P., et al. 2013, ApJ, 774, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Demory, B.-O., Seager, S., Madhusudhan, N., et al. 2011, ApJ, 735, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Demory, B.-O., Torres, G., Neves, V., et al. 2013, ApJ, 768, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Diaz-Cordoves, J., & Gimenez, A. 1992, A&A, 259, 227 [NASA ADS] [Google Scholar]
- Eastman, J., Siverd, R., & Gaudi, B. S. 2010, PASP, 122, 935 [NASA ADS] [CrossRef] [Google Scholar]
- Fabrycky, D., & Tremaine, S. 2007, ApJ, 669, 1298 [NASA ADS] [CrossRef] [Google Scholar]
- Figueira, P., Pont, F., Mordasini, C., et al. 2009, A&A, 493, 671 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Fortney, J. J. 2005, MNRAS, 364, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Fortney, J. J., Marley, M. S., & Barnes, J. W. 2007, ApJ, 659, 1661 [NASA ADS] [CrossRef] [Google Scholar]
- Fortney, J. J., Mordasini, C., Nettelmann, N., et al., 2013, ApJ, 775, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Freytag, B., Allard, F., Ludwig, H.-G., Homeier, D., & Steffen, M. 2010, A&A, 513, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fukui, A., Narita, N., Kurosaki, K., et al. 2013, ApJ, 770, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Gibson, N. P., Pont, F., & Aigrain, S. 2011, MNRAS, 411, 2199 [NASA ADS] [CrossRef] [Google Scholar]
- Gibson, N. P., Aigrain, S., Roberts, S., et al. 2012, MNRAS, 419, 2683 [NASA ADS] [CrossRef] [Google Scholar]
- Gibson, N. P., Aigrain, S., Barstow, J. K., et al. 2013, MNRAS, 428, 3680 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, B. M. S., & Murray, N. 2012, ApJ, 751, 158 [Google Scholar]
- Hauschildt, P. H., Allard, F., & Baron, E. 1999, ApJ, 512, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Hook, I. M., Jørgensen, I., Allington-Smith, J. R., et al. 2004, PASP, 116, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Howard, A. W., Marcy, G. W., Johnson, J. A., et al. 2010, Science, 330, 653 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Howe, A. R., & Burrows, A. S. 2012, ApJ, 756, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Ida, S., & Lin, D. N. C. 2008, ApJ, 673, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Ida, S., & Lin, D. N. C. 2010, ApJ, 719, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Kaltenegger, L., & Traub, W. A. 2009, ApJ, 698, 519 [NASA ADS] [CrossRef] [Google Scholar]
- Kennedy, G. M., & Kenyon, S. J. 2008, ApJ, 682, 1264 [NASA ADS] [CrossRef] [Google Scholar]
- Kleinmann, S. G., & Hall, D. N. B. 1986, ApJS, 62, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Knutson, H. A., Charbonneau, D., Allen, L. E., et al. 2007, Nature, 447, 183 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Knutson, H. A., Madhusudhan, N., & Cowan, N. B. 2011, ApJ, 735, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Kulas, K. R., McLean, I. S., & Steidel, C. C. 2012, in SPIE Conf. Ser., 8453 [Google Scholar]
- Kurucz, R. L. 1979, ApJS, 40, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Lecavelier Des Etangs, A., Pont, F., Vidal-Madjar, A., & Sing, D. 2008, A&A, 481, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Liddle, A. R. 2007, MNRAS, 377, L74 [NASA ADS] [Google Scholar]
- Line, M. R., Vasisht, G., Chen, P., Angerhausen, D., & Yung, Y. L. 2011, ApJ, 738, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Line, M. R., Wolf, A., Zhang, X., et al. 2013, ApJ, 775, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Lunine, J. I. 1993, ARA&A, 31, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Madhusudhan, N. 2012, ApJ, 758, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Madhusudhan, N., & Seager, S. 2011, ApJ, 729, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Madhusudhan, N., Harrington, J., Stevenson, K. B., et al. 2011, Nature, 469, 64 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Mandel, K., & Agol, E. 2002, ApJ, 580, L171 [NASA ADS] [CrossRef] [Google Scholar]
- Marley, M. S., Saumon, D., Cushing, M., et al. 2012, ApJ, 754, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Marmier, M., Lovis, C. et al. 2011, A&A, submitted [arXiv:1109.2497] [Google Scholar]
- McLean, I. S., Steidel, C. C., Matthews, K., Epps, H., & Adkins, S. M. 2008, in SPIE Conf. Ser., 7014 [Google Scholar]
- McLean, I. S., Steidel, C. C., Epps, H., et al. 2010, in SPIE Conf. Ser., 7735 [Google Scholar]
- McLean, I. S., Smith, E. C., Bechlin, E. E., et al. 2012, in SPIE Conf. Ser., 8446, 19 [Google Scholar]
- Miller-Ricci, E., & Fortney, J. J. 2010, ApJ, 716, L74 [NASA ADS] [CrossRef] [Google Scholar]
- Miller-Ricci, E., Seager, S., & Sasselov, D. 2009, ApJ, 690, 1056 [NASA ADS] [CrossRef] [Google Scholar]
- Miner, E. D. 1990, Uranus – The planet, rings and satellites [Google Scholar]
- Mordasini, C., Alibert, Y., & Benz, W. 2009, A&A, 501, 1139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morley, C. V., Fortney, J. J., Kempton, E. M.-R., et al. 2013, ApJ, 775, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Moses, J. I., Line, M. R., Visscher, C., et al. 2013, ApJ, submitted [arXiv:1306.5178] [Google Scholar]
- Nagasawa, M., Ida, S., & Bessho, T. 2008, ApJ, 678, 498 [NASA ADS] [CrossRef] [Google Scholar]
- Naoz, S., Farr, W. M., Lithwick, Y., Rasio, F. A., & Teyssandier, J. 2011, Nature, 473, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Nascimbeni, V., Piotto, G., Pagano, I., et al. 2013, A&A, accepted [arXiv:1308.6765] [Google Scholar]
- Nettelmann, N., Fortney, J. J., Kramm, U., & Redmer, R. 2011, ApJ, 733, 2 [Google Scholar]
- Nielsen, E. L., & Close, L. M. 2010, ApJ, 717, 878 [NASA ADS] [CrossRef] [Google Scholar]
- Öberg, K. I., Murray-Clay, R., & Bergin, E. A. 2011, ApJ, 743, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Ogihara, M., & Ida, S. 2009, ApJ, 699, 824 [NASA ADS] [CrossRef] [Google Scholar]
- Parmentier, V., Showman, A. P., & Lian, Y. 2013, A&A, 558, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petigura, E. A., Marcy, G. W., & Howard, A. W. 2013, ApJ, 770, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Pilcher, C. B. 1977, ApJ, 214, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Pineda, J. S., Bottom, M., & Johnson, J. A. 2013, ApJ, 767, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Pollack, J. B., Rages, K., Pope, S. K., Tomasko, M. G., & Romani, P. N. 1987, J. Geophys. Res., 92, 15037 [NASA ADS] [CrossRef] [Google Scholar]
- Pont, F., Knutson, H., Gilliland, R. L., Moutou, C., & Charbonneau, D. 2008, MNRAS, 385, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Pont, F., Gilliland, R. L., Knutson, H., Holman, M., & Charbonneau, D. 2009, MNRAS, 393, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Pont, F., Sing, D. K., Gibson, N. P., et al. 2013, MNRAS, 432, 2917 [NASA ADS] [CrossRef] [Google Scholar]
- Rasio, F. A., & Ford, E. B. 1996, Science, 274, 954 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Rayner, J. T., Cushing, M. C., & Vacca, W. D. 2009, ApJS, 185, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Richard, C., Gordon, I. E., Rothman, L. S., et al. 2012, J. Quant. Spec. Radiat. Transf., 113, 1276 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, L. A., & Seager, S. 2010, ApJ, 716, 1208 [NASA ADS] [CrossRef] [Google Scholar]
- Rowe, J. F., Matthews, J. M., Seager, S., et al. 2008, ApJ, 689, 1345 [NASA ADS] [CrossRef] [Google Scholar]
- Schwarz, G. 1978, Ann. Stat., 6, 461 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Sing, D. K., Désert, J., Lecavelier Des Etangs, A., et al. 2009, A&A, 505, 891 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Sromovsky, L. A., Fry, P. M., Boudon, V., Campargue, A., & Nikitin, A. 2012, Icarus, 218, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Stevenson, K. B., Harrington, J., Nymeyer, S., et al. 2010, Nature, 464, 1161 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Stevenson, K. B., Bean, J. L., Seifahrt, A., et al. 2013, ApJ, submitted [arXiv:1305.1670] [Google Scholar]
- Terquem, C., & Papaloizou, J. C. B. 2007, ApJ, 654, 1110 [NASA ADS] [CrossRef] [Google Scholar]
- Vacca, W. D., Cushing, M. C., & Rayner, J. T. 2004, PASP, 116, 352 [NASA ADS] [CrossRef] [Google Scholar]
- Valencia, D. 2011, in IAU Symp., eds. A. Sozzetti, M. G. Lattanzi, & A. P. Boss, 276, 181 [Google Scholar]
- van Hamme, W. 1993, AJ, 106, 2096 [NASA ADS] [CrossRef] [Google Scholar]
- Wildt, R. 1947, MNRAS, 107, 84 [NASA ADS] [Google Scholar]
- Winn, J. N., Henry, G. W., Torres, G., & Holman, M. J. 2008, ApJ, 675, 1531 [NASA ADS] [CrossRef] [Google Scholar]
- Witte, S., Helling, C., Barman, T., Heidrich, N., & Hauschildt, P. H. 2011, A&A, 529, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wittenmyer, R. A., Tinney, C. G., & Butler, R. P. 2011, ApJ, 738, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Woitke, P., & Helling, C. 2004, A&A, 414, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zahnle, K., Marley, M. S., & Fortney, J. J. 2009 [arXiv:0911.0728] [Google Scholar]
Appendix A: A closer Look at MOSFIRE
MOSFIRE was designed to obtain high-quality NIR spectroscopy and photometry of relatively faint objects; extragalactic and, to a lesser extent, brown dwarf science helped to define the instrument’s capabilities. The study of transiting exoplanets (or other high-precision measurements of bright sources) did not drive instrument requirements; nonetheless the instrument still works quite well for this purpose so long as certain important steps are followed.
Appendix A.1: Nonuniform and non-repeatable slit widths
For several reasons, MOSFIRE’s spectroscopic flat frames have more structure than past users of milled masks may expect. First, MOSFIRE has no internal flat-field calibration source and so flat frames are acquired by pointing at the telescope dome. Thus telluric absorption lines are imprinted on the initial flat frames. To the extent that a particular wavelength remains matched to the identical pixel throughout the night, this effect is unimportant because it will divide out. However, any motion of the target in the dispersion direction (whether because of uncorrected flexure, pointing wander in our large slits, or from other sources) may induce systematic, wavelength- and spectral-motion-dependent flux offsets into the final spectra.
A more complicated effect results from MOSFIRE’s use of a custom cryogenic configurable slit unit (CSU) rather than milled masks. The CSU allows rapid reconfiguration of mask designs (see McLean et al. 2010, 2012). The CSU consists of 46 pairs of actuated bars, which move across the focal plane to create either 46 slits (each 7″ wide) or a smaller number of longer slits. The slit-facing end of each bar is equipped with an infrared-black knife edge.
Each bar’s motion is repeatable to roughly 0.02″ on the sky (McLean et al. 2012), a value which corresponds to roughly 3% of the width of a typical 0.7″-wide slit (such as we used to obtain our flat field frames). Thus any movement of the CSU bars between science and flat field observations induce variations in the line profile of several percent. These variations manifest themselves as horizontal banding in the images, with each band corresponding to one of the 46 CSU bar pairs. To avoid deleterious effects, we recommend obtaining dome flats for a given mask immediately before or after that mask’s science observations.
Furthermore, the slits produced by the CSU exhibit nonuniformities in width, which we hypothesize result from slight misalignments and imperfections of the knife edges at the end of each CSU slit bar. We have not investigated the repeatability of this second effect, but estimate its amplitude to again be several percent. If calibration files taken with one slit mask are used to calibrate a second mask (as in our case, where high flux levels prevented us from taking flat and arc frames with our 10″-wide slits), the flat frame must be normalized in the spatial direction (in addition to the standard normalization in the spectral direction). We merely divide each detector column by the median of all detector columns, but other approaches may prove more effective.
Observe calibrations frames immediately before or after science frames for a given mask design. Otherwise, avoid placing a star near the border between two CSU bars.
Appendix A.2: Fringing
Our experience shows significant fringing in wide-slit MOSFIRE spectra taken in the vicinity of telluric OH emission lines. In K band the fringes reach a maximum (slit-width-dependent) amplitude of roughly 4 ADU s-1 arcsec-1; in general the amplitude, spatial frequency, orientation, and phase of these fringes all vary both spatially and temporally. We have observed similar effects in similar observations taken with Subaru/MOIRCS, and we hypothesize that a similar phenomenon of lower amplitude could explain the worse-than-expected performance of Bean et al. (2011)’s spectrophotometric light curve obtained with Magellan/MMIRS in the H band (where OH emission is particularly strong). MOIRCS instrument scientist Dr. I. Tanaka informs us that his instrument’s fringing was eliminated by replacing MOIRCS’ standard plane-parallel filters with wedged substrates. This success suggests a possible mitigation strategy for MOSFIRE.
These fringes cause severe difficulties in extracting high-quality spectra and high-precision time series data when observing in the fixed-position “staring” mode that has become common in infrared photometry and spectroscopy of transiting exoplanets (e.g., Croll et al. 2011; Bean et al. 2011). We explored a number of strategies to remove the fringes. Sinusoidal and wavelet fitting fail because the fringe parameters vary and cannot be accurately measured at the most important location: within the region of high stellar flux. Scaling and shifting a template sky frame, or related techniques using principal component analysis, also fail, both because the fringe pattern evolves over time and because of rapid and non-correlated variations in the sky emission spectrum at different wavelengths.
We therefore conclude that nodding the telescope along the slit axis, and subtracting frames obtained at nearby times, is the optimal MOSFIRE observing strategy whenever smooth, well-behaved background levels are desired. So long as the nod cadence is less than a few minutes, telluric emission remains relatively unchanged and the fringing emission is well-subtracted. Nod subtraction also helps mitigate the slit width nonuniformities discussed above, because any residual signature of this effect will largely subtract out. The primary disadvantage is the S/N penalty incurred because the background flux effectively doubles for the standard Poisson calculations. Despite this, for bright targets the classically computed S/N expected from MOSFIRE spectroscopy still exceeds that expected from 8 m-class telescopes even in the absence of nodding.
All Tables
All Figures
 |
Fig. 1 GMOS (top) and MOSFIRE (bottom) spectra of exoplanet host star GJ 3470 (black) and simultaneously-observed comparison star TYC 1363-2087-1 (gray). The former is a main-sequence M dwarf, while the latter is a rather hotter giant. The short black bars in the top panel indicate the locations of the gaps between the GMOS CCDs. |
| In the text | |
 |
Fig. 2 Instrumental trends for spectroscopic observations of GJ 3470. Left: GMOS. The effects of intermittent cirrus are apparent in the raw stellar flux; this also increases the scatter in the relative light curve. Right: MOSFIRE. Some parameters appear double-valued because data were taken while alternating between two nod positions on the slit. The data shown here are available as an electronic supplement to this article. |
| In the text | |
 |
Fig. 3 Noise analysis of the residuals to the spectrophotometric light curves shown in Figs. 6 and 7 for data from GMOS (left) and MOSFIRE (right). Top: decrease in RMS of binned residuals with increasing binned size. The solid curves correspond to the individual wavelength channels, and the dashed line shows the 1/ |
| In the text | |
 |
Fig. 4 Injection-and-recovery results for K-band MOSFIRE data. The light curves shows simulated transits that have been injected into real data and re-fit as described in Sect. 3.6; they are plotted here after removal of overall trends and state vectors. The dotted line shows the wavelength-independent injected value of 7.0%. The thick solid lines and points shows the best-fit recovered transit parameters; the error bars derive from the MCMC analyses and have been inflated by ⟨ βT14 ⟩ as discussed in Sect. 3.2. The dashed lines indicates the weighted means for each test. In both cases the recovered spectra are consistent with a constant value, and the systematic offsets are <2σ. |
| In the text | |
 |
Fig. 5 Injection-and-recovery results showing simulated light curves and results for optical GMOS data. Sub-figures and symbols are the same as Fig. 4. Because we analyze the GMOS data in a differential fashion (Sect. 3.4) these data are insensitive to the absolute transit depth. In addition, the retrieved spectrum in the bottom sub-figure exhibits considerable systematic errors and the systematics in the top sub-figure (though weaker) are similar in shape to the results of the true (non-injected) GMOS analysis shown in Fig. 8. |
| In the text | |
 |
Fig. 6 MOSFIRE transit light curves: a) raw spectrophotometric data showing the systematic offsets between the two nod positions, and best-fit models; b) normalized and corrected measurements and models; c) residuals; d) final transmission spectrum after scaling error bars by ⟨ βT12 ⟩. The data shown in panel a) are available as an electronic supplement to this article. |
| In the text | |
 |
Fig. 7 GMOS transit light curves: a) raw spectrophotometric data showing the common-mode flux variations, and best-fit models; b) normalized and corrected measurements and models; c) residuals multiplied by 3; d) final transmission spectrum after scaling error bars by ⟨ βT12 ⟩. Because we analyze the GMOS data in a differential fashion (Sect. 3.4) these data are insensitive to the absolute transit depth. Further, as shown in Fig. 5 these measurements are likely affected by systematic errors. |
| In the text | |
 |
Fig. 8 Transmission spectrum of GJ 3470b. Colored points with error bars are our MOSFIRE measurements; black points are the measurements of Fukui et al. (2013) and Demory et al. (2013). The solid lines show the model transmission spectra described in Sect. 5. The ensemble of measurements rule out equilibrium-chemistry models with solar composition (blue) and 50× solar abundances (green) at 5.4σ and 3.8σ, respectively. A methane-depleted atmosphere (pink), a very highly enriched atmosphere (200× solar, light blue), and a simple flat spectrum suggestive of high-altitude haze (dashed) all remain plausible. These scenarios are discussed in Sect. 5. The dotted lines at bottom show the filter profiles (from Fukui et al. (2013), 2MASS, and Spitzer/IRAC) used to compute the band-integrated model points (shown as colored open circles). |
| In the text | |
 |
Fig. 9 Atmospheric parameters for our equilibrium-chemistry models assuming solar abundances of heavy elements (solid), 50× solar (dashed), and 200× solar (dotted). The panels show as a function of altitude: a) the effective planetary radii, b) the temperature-pressure profiles, and c) the abundances of several molecular species. We discuss these models in Sect.4, and show the model transmission spectra derived from them in Fig. 8. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.