| Issue |
A&A
Volume 559, November 2013
|
|
|---|---|---|
| Article Number | A112 | |
| Number of page(s) | 9 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201322007 | |
| Published online | 22 November 2013 | |
Weak-lensing detection of intracluster filaments with ground-based data
1 Zentrum für Astronomie der Universität Heidelberg, Institut für Theoretische Astrophysik, Philosophenweg 12, 69120 Heidelberg, Germany
e-mail: maturi@uni-heidelberg.de
2 Jet Propulsion Laboratory, California Institute of Technology, 4800 Oak Grove Drive, MS 169-237, Pasadena, CA 91109, USA
e-mail: jmerten@caltech.edu
Received: 1 June 2013
Accepted: 13 September 2013
According to the current standard model of cosmology, matter in the Universe arranges itself along a network of filamentary structure. These filaments connect the main nodes of this so-called “cosmic web”, which are clusters of galaxies. Although its large-scale distribution is clearly characterized by numerical simulations, constraining the dark-matter content of the cosmic web in reality turns out to be difficult. The natural method of choice is gravitational lensing. However, the direct detection and mapping of the elusive filament signal is challenging and in this work we present two methods that are specifically tailored to achieve this task. A linear matched filter aims at detecting the smooth mass-component of filaments and is optimized to perform a shear decomposition that follows the anisotropic component of the lensing signal. Filaments clearly inherit this property due to their morphology. At the same time, the contamination arising from the central massive cluster is controlled in a natural way. The filament 1σ detection is of about κ ~ 0.01 − 0.005 according to the filter’s template width and length, enabling the detection of structures beyond reach with other approaches. The second, complementary method seeks to detect the clumpy component of filaments. The detection is determined by the number density of subclump identifications in an area enclosing the potential filament, as was found within the observed field with the filter approach. We tested both methods against mocked observations based on realistic N-body simulations of filamentary structure and proved the feasibility of detecting filaments with ground-based data.
Key words: methods: numerical / galaxies: clusters: general / cosmology: observations / large-scale structure of Universe / dark matter
© ESO, 2013
1. Introduction
N-body numerical simulations (e.g. Springel et al. 2005) predict the existence of dark-matter halos, which contribute the knots within a network of filamentary structure. This peculiar arrangement of matter is frequently called the cosmic web. The appearance of these filaments holds important information on the underlying cosmology and structure formation history and constitutes an important tool for investigating the main mechanisms of cosmic structure formation, along with and confirmed by other observables (Klypin & Shandarin 1983; White et al. 1987; Colberg et al. 2005; Aragón-Calvo et al. 2010; Bond et al. 2010; Fedeli et al. 2011). The first observational evidence of such structures came from spectroscopic surveys like the 2dF Galaxy Redshift Survey (see Colless et al. 2001, and references in them), but these data do not return direct information on the matter density distribution. A mass-to-light ratio in filaments, which might be scale dependent, must be assumed or estimated from independent observations. Thus, it is important to find other means to evaluate physical properties of filaments, especially when it comes to the distribution and total amount of dark matter therein. The use of gravitational lensing is, in principle, the most direct and elegant way to do so. Cosmic shear surveys are already providing good constraints on cosmological models by looking at the shear-shear correlation function (e.g. Kilbinger et al. 2013; Schrabback et al. 2010). Even if these surveys perform well in estimating the global properties of the linear matter power spectrum, they are still failing in retrieving a complete picture of the cosmic web, although the path has been outlined by the dark-matter map of the COSMOS field (Massey et al. 2007), studies of the surroundings of SCL2243-0935 and MACS J0717.5+3745 (Schirmer et al. 2011; Jauzac et al. 2012), and recent results in the CFHTLenS (Van Waerbeke et al. 2013).
The difficulties in getting direct measures from weak gravitational lensing are due to the very weak deflection field, which, so far, could be measured statistically over very large portions of the sky, but not filament by filament in the field. But exactly this information is most important for studying the relation between galaxy clusters and intracluster filaments. However, promising progress has been made in detecting filaments between subclumps in merging clusters of galaxies. Recent examples can be found in the super-cluster Abell 222/223 (Dietrich et al. 2012) and the possible gas bridge connecting pairs of clusters, as detected with cosmic microwave background observations (Planck Collaboration 2013).
Different weak-lensing methods for detecting filaments have been proposed in the literature and are mostly based on a circular aperture mass or on its second momenta (Dietrich et al. 2005; Mead et al. 2010; Schirmer et al. 2011). These local lensing estimates are somewhat limited in their sensitivity and so far have been applied to tight pairs of clusters only, where the signal is expected to be higher, but at the cost of a strong degeneracy with the signal induced by the main halos. In this paper we overcome this limitation by providing a method that uses all first-order lensing information coming from filaments as a whole and which provides stronger signals, even with ground-based data. We study a specific case where a massive cluster is situated at the terminal end of such a filamentary structure, which is standard scenario, as suggested by N-body numerical simulations. We show that our general approach is favorable for controlling the strong cluster signal in a natural way and is able to highlight the structure of interest, the intracluster filament, and in general all matter anisotropies surrounding the central cluster. Since this method is sensitive to the smooth distribution of the dark matter only, we propose an additional approach to exploit complementary information: the overdensity of dark-matter clumps expected to align with the cosmic web. These two different approaches should be used together since, on the one hand, intracluster filaments could be seen as composed of a continuous distribution of matter, and on the other hand as an ensemble of single dark-matter halos.
We structure our work as follows: in Sect. 2 we summarize the main properties of intracluster filaments relevant for weak lensing, followed by Sect. 3, which presents the weak-lensing technique to infer their properties. In Sect. 4 we test the method against numerical simulations. The complementary approach to incorporate weak-lensing peak counts for filament detection is outlined in Sect. 5. In Sect. 6 we draw our conclusions.
2. Lensing from intracluster filaments
All observables of a cosmic structure related to gravitational lensing can be derived through the so-called lensing potential 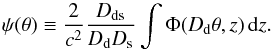 (1)It characterizes the properties of intervening lenses between a given population of background sources and the observer, and with a width along the line-of-sight that is negligible compared to the large angular distances involved (thin-lens approximation). Here, Φ defines the Newtonian potential of this matter distribution, θ = { θ1,θ2 } defines angular positions in the plane of the sky, c is the speed of light, and Dds, Dd and Ds are the lens-source, observer-lens and observer-source angular diameter distances, respectively. In this work we study only very weak potentials, therefore we considered first-order lensing quantities such as the scalar convergence κ and the complex shear γ = γ1 + iγ2, which for any lensing potential ψ are
(1)It characterizes the properties of intervening lenses between a given population of background sources and the observer, and with a width along the line-of-sight that is negligible compared to the large angular distances involved (thin-lens approximation). Here, Φ defines the Newtonian potential of this matter distribution, θ = { θ1,θ2 } defines angular positions in the plane of the sky, c is the speed of light, and Dds, Dd and Ds are the lens-source, observer-lens and observer-source angular diameter distances, respectively. In this work we study only very weak potentials, therefore we considered first-order lensing quantities such as the scalar convergence κ and the complex shear γ = γ1 + iγ2, which for any lensing potential ψ are 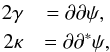 (2)with the complex lensing operator
(2)with the complex lensing operator 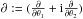 (see Bartelmann & Schneider 2001; Schneider & Er 2008; Bartelmann 2010). The main lensing observable is the complex reduced shear g = γ/(1 + κ), but we can safely approximate g with γ since for filaments the approximation κ ≪ 1 holds with very high accuracy. In any case, all equations presented in this study can be used with the reduced shear instead of the shear whenever necessary.
(see Bartelmann & Schneider 2001; Schneider & Er 2008; Bartelmann 2010). The main lensing observable is the complex reduced shear g = γ/(1 + κ), but we can safely approximate g with γ since for filaments the approximation κ ≪ 1 holds with very high accuracy. In any case, all equations presented in this study can be used with the reduced shear instead of the shear whenever necessary.
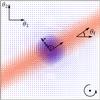 |
Fig. 1 Schematic sketch of our mock filament and cluster setup. The background whisker plot shows the shear fields of the filament (red) and the NFW halo (blue). Note that the length of the filament whiskers is enhanced by a factor of 15 with respect to the halo ones for clarity. The global coordinate system θ, the filament’s orientation θf, and the distance from the filament center along an axis perpendicular to its extension h are also clearly marked. The 3D orientation of the coordinate frame is right-handed. In our analysis we treat the two sides of the filament as independent so that we can access all possible geometrical configurations. The figure shows the most simple configuration however, which is an identical orientation angle for the two sides of the filament with respect to the main halo. |
 |
Fig. 2 Shear pattern induced by an ensemble of 4, 8, 16, and 32 NFW halos forming an elongated structure that resembles an intracluster filament located at z = 0.55. The haloes have random masses ranging from 0 to a fixed upper limit of 1015 M⊙/h, 5 × 1014 M⊙/h, 2.5 × 1014 M⊙/h and 1.25 × 1014 M⊙/h, respectively, to keep the total mass of the structure in different panels fixed. The shear sampling is analoguous to the one typical for weak-lensing observations with a source number density of ns = 15 arcmin-2. These toy models illustrate the two regimes in the shear pattern caused by elongated structures, i.e. an alignment tangential to the center of the structure at large radii and the alignment orthogonal to the filament’s major axis. The two regimes are separated by an area of vanishing shear. |
Once the general lensing quantities are defined, it is straightforward to quantify the intracluster filaments by means of a simple mass model which is shown in Fig. 1. For simplicity, we assumed that the filaments to lie on the plane of the sky, to have a finite width but an infinite length, and that their matter distribution is not varying along their major axis so that, for symmetry reasons, the gravitational potential is constant along this direction. Hence, the shear is aligned orthogonally to the filament, that is γ1 = −κ and γ2 = 0, assuming that the filament falls on the respective Cartesian axis defined by the plane of the sky θ. Generalizing for arbitrary filament directions θf and distances h to its major axis, we have ![\begin{equation} \label{eq:gamma} \gamma=-\kappa(h) \left[\cos(2\theta_{\rm f})-{\rm i} \sin(2\theta_{\rm f})\right] . \end{equation}](/articles/aa/full_html/2013/11/aa22007-13/aa22007-13-eq34.png) (3)As mentioned before, we assumed that the convergence is varying only orthogonally to the filament direction and, following Colberg et al. (2005) and Mead et al. (2010), we assumed a convergence profile for the filament
(3)As mentioned before, we assumed that the convergence is varying only orthogonally to the filament direction and, following Colberg et al. (2005) and Mead et al. (2010), we assumed a convergence profile for the filament 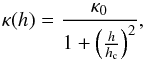 (4)where κ0 is the filament’s maximum convergence, and hc a scale radius representing its typical width (compare Fig. 1). Note that this profile requires a truncation at large radii to avoid divergencies. However, this truncation is just a technicality and does not represent a fundamental limitation of the method discussed in Sect. 3. Other profiles are certainly possible, but they could not differ too much from what we adopted since our model is based on constraints imposed by N-body numerical simulations (Colberg et al. 2005). Moreover, not a higher level of detail in defining the template is necessary to describe the shear behavior of filaments.
(4)where κ0 is the filament’s maximum convergence, and hc a scale radius representing its typical width (compare Fig. 1). Note that this profile requires a truncation at large radii to avoid divergencies. However, this truncation is just a technicality and does not represent a fundamental limitation of the method discussed in Sect. 3. Other profiles are certainly possible, but they could not differ too much from what we adopted since our model is based on constraints imposed by N-body numerical simulations (Colberg et al. 2005). Moreover, not a higher level of detail in defining the template is necessary to describe the shear behavior of filaments.
 |
Fig. 3 Numerical simulation of a cluster-filament configuration. Left panel: shear amplitude map centered on a massive galaxy cluster surrounded by filamentary structures.The circles enclose the area in which we measure the lensing signal for the filament detection. Right panel: whisker visualization of the shear pattern of the same simulation. The shear of the central part of the main cluster was removed for clarity. |
To give a better understanding of this peculiar shear pattern, we plot in Fig. 2 four different structures located at z = 0.55 and composed of an ensemble of 4, 8, 16, and 32 halos, respectively, all described by a Navarro-Frank-White (NFW) density profile (Navarro et al. 1997; Bartelmann 1996). Their masses are randomly chosen, ranging from 0 to a fixed upper limit of 1015 M⊙/h, 5 × 1014 M⊙/h, 2.5 × 1014 M⊙/h, and 1.25 × 1014 M⊙/h, respectively, to keep the same total mass for all panels. In the limit of an infinite number of haloes the structure would resemble a continuous structure. All halos belonging to each structure are aligned along the respective field’s diagonal and are equally spaced by 0.5 arcmin so that the object length grows linearly with the number of halos. The shear is sampled such that it resembles typical weak-lensing observations with a source number density of ns = 15 arcmin-2. This specific representation of a filament illustrates how the shear pattern caused by elongated structures can be split into two regimes, one at large scales where the shear is aligned almost tangentially with respect to the structure barycenter (this feature is not present in the model where the filament has an infinite length in the plane of the sky), and one in the vicinity of the bar/filament where the shear is displaced orthogonally with respect to the structure elongation. An extreme example of the latter case in the strong-lensing regime is given by the straight arc visible in the highly elongated cluster ACT-CL J0102-4915 (Zitrin et al. 2013), which finds its full explanation in the structure layout we present here. Note how the shear vanishes at the boundary between these two regimes because of the symmetry properties of this structure. Clearly, the approximations discussed in this section hold very well, justifying their use in describing the main properties of intracluster filaments, which are in return used for the actual filament detection.
A realistic case of the expected signal is plotted in Fig. 3, which shows the convergence (left panel) and shear pattern (right panel) of an N-body numerical simulation carried out with GADGET-2 (Springel 2005; Springel et al. 2001), which contain a central massive, merging galaxy cluster together with an extended filamentary structure. The simulation is based on a flat ΛCDM model with a present matter density parameter Ωm = 0.3, a present baryon density parameter Ωb = 0.04, a Hubble parameter h = 0.7, and a power spectrum normalization corresponding to σ8 = 0.9. The number of gas and DM particles enclosed in the simulation box of (50 × 50 × 70) Mpc, was 1.4 × 107 and 1.7 × 107, respectively. Their masses were set to mgas = 2.43 × 108 M⊙ and mDM = 1.61 × 109 M⊙. The Plummer-equivalent gravitational softening was set to ϵpl = 7 kpc comoving from z = 2 to 0, while it was taken to be fixed in physical units at higher redshifts (for more details on the simulation see Dolag et al. 2006). The shear pattern known from Fig. 2 is clearly visible also in this realistic case, where four main filaments depart from the central cluster. Note how in this case the filaments are aligned such as to create a cross-like structure with two non-orthogonal arms. This configuration, with two connected filaments symmetrically extending from two opposite sides of the central cluster, is quite common and constitutes one third of all cases of aligned filamentary structures in cosmological simulations (Colberg et al. 2005). Nevertheless, we treated the two sides of the filament as independent, so that we are able to access all possible geometrical configurations.
3. Intracluster filament detection
The very weak shear signal expected for filaments (e.g. Dolag et al. 2006) clearly poses the challenge in detecting and quantifying the dark-matter properties of these structures. This is mainly due to observational noise, large-scale structure (LSS) contamination (defined as the population of all filaments along the line-of-sight except for the one under investigation) and the massive galaxy clusters expected to be located along their major axes. To overcome these difficulties, we endeavored to fully exploit the peculiar morphological properties of the setup and the large area covered by filaments. Hence, we aimed at using global lensing properties as data input instead of measuring local quantities.
Specific filament configurations with respect to the surrounding galaxy clusters have to be identified and considered since, if favorable, they might provide the crucial piece of information to help in detecting and quantifying the dark-matter content. Therefore we restricted our search to a specific configuration that is still general enough to be applied to the majority of the observable cases. We focused our attention on the case in which a large galaxy cluster is located at the terminal end of a straight filament. This is a very general case (Colberg et al. 2005), where the cluster helps to define a physical coordinate frame and has symmetry properties, as we below show, which greatly enhances the separation of the cluster and filament components.
3.1. Shear decomposition for filaments
The shear signal of intracluster filaments is aligned with their major axis as discussed in Sect. 2 and shown in Figs. 1–3. It is thus convenient to decompose the shear into a tangential and a cross-component relative to the filament direction, ![\begin{equation} \label{eq:decompose} \gamma_{\rm q} = -\left[ \gamma_1\cos(2\alpha_{\rm q}) + \gamma_2\sin(2\alpha_{\rm q}) \right] , \end{equation}](/articles/aa/full_html/2013/11/aa22007-13/aa22007-13-eq58.png) (5)where γq stands for the tangential or cross-shear components with αt = θf − π/2 and αx = θf − π/4, respectively (see Fig. 1 for visual orientation). If we now use the filament model defined by Eqs. (3) and (4), we obtain
(5)where γq stands for the tangential or cross-shear components with αt = θf − π/2 and αx = θf − π/4, respectively (see Fig. 1 for visual orientation). If we now use the filament model defined by Eqs. (3) and (4), we obtain 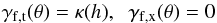 (6)where, in radial coordinates, h = rcos(θ − θf). The same decomposition has to be applied to all contributing matter components including the central cluster, for which
(6)where, in radial coordinates, h = rcos(θ − θf). The same decomposition has to be applied to all contributing matter components including the central cluster, for which 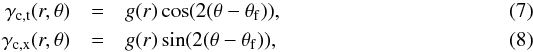 and where g(r) is the cluster’s reduced shear radial profile, which we assumed to follow an NFW profile. Note that, in contrast to the filament itself, for the central part of the cluster the approximation γ ≪ 1 is not valid and the reduced shear has to be used.
and where g(r) is the cluster’s reduced shear radial profile, which we assumed to follow an NFW profile. Note that, in contrast to the filament itself, for the central part of the cluster the approximation γ ≪ 1 is not valid and the reduced shear has to be used.
To perform this decomposition, the filament direction θf must be known in advance. We explain below how the input lensing data can be directly used to infer this information. For the moment and simplicity of the argument, we assumed to have perfect knowledge of θf.
3.2. Optimal filter
From now on, we use the decomposition scheme described in Sect. 3.1 together with a filtering approach directly applicable to input weak-lensing catalogs that contain galaxy ellipticities. We follow the recipe proposed by Maturi et al. (2005), which is based on physically motivated quantities such as the expected filament shear profile, the cosmic shear power spectrum, and the survey properties. This method avoids of using polynomial or Gaussian weight functions for which the parameters have to be determined empirically with the help of expensive numerical simulations and which generally do not ensure optimized results with respect to the signal-to-noise ratio (Maturi et al. 2007; Pace et al. 2007). This is a linear matched filter, typically applied under the assumption of circular symmetry and in close analogy to the aperture mass (Fahlman et al. 1994; Schneider 1996). However, in this work, we considered the filament geometry, which is far from being circular. In addition to this optimal filter, we show that the adopted decomposition provides a natural way for controlling the central cluster contribution.
To obtain the filter function, we based its derivation on a data model, d, tailored to our case 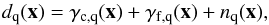 (9)where γc,q and γf,q are the cluster (isotropic) and filament (anisotropic) signals already discussed above and n is the random noise, contribution given by the LSS contamination, shot noise and intrinsic ellipticity of the galaxies. Again, q stands for the tangential or cross shear components, t and x, respectively. The noise component, n, can be modeled as an isotropic Gaussian random field with zero mean so that it is fully described by its power spectrum P(k): ⟨n(k)n(k′)⟩ = (2π)2δ(k − k′)P(k). According to Eq. (4), the filament signal is linear in amplitude, κ0. Therefore, it is convenient to define a linear estimator that in its most general form is given by
(9)where γc,q and γf,q are the cluster (isotropic) and filament (anisotropic) signals already discussed above and n is the random noise, contribution given by the LSS contamination, shot noise and intrinsic ellipticity of the galaxies. Again, q stands for the tangential or cross shear components, t and x, respectively. The noise component, n, can be modeled as an isotropic Gaussian random field with zero mean so that it is fully described by its power spectrum P(k): ⟨n(k)n(k′)⟩ = (2π)2δ(k − k′)P(k). According to Eq. (4), the filament signal is linear in amplitude, κ0. Therefore, it is convenient to define a linear estimator that in its most general form is given by  (10)with an outcome variance
(10)with an outcome variance 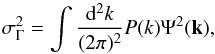 (11)conveniently derived in the Fourier space.
(11)conveniently derived in the Fourier space.
 |
Fig. 4 Optimal matched filter in real space for a filament template extending in the range limit of 0 < r < 10 arcmin. The filter was rotated around the cross in the middle, in order to investigate all angles. |
 |
Fig. 5 Optimal matched linear filter for filament detection. Top panel: variance for filaments at redshift z = 0.55. For a given survey with intrinsic ellipticity scatter of σϵ = 0.4, different core radii hc and different galaxy number densities n are plotted. Continuous lines refer to a filter with length L = 10, arcmin while dashed lines refer to L = 20 arcmin. Bottom panel: expected filter response for a filament located at z = 0.55, with a major axis position angle of θ = 30 degrees, a maximum convergence of κ0 = 0.02, and a scale radius of hc = 0.25 Mpc/h. The filter was truncated with an inner cutoff of 2.5 arcmin and two different outer cutoffs of 5 arcmin and 10 arcmin. |
The optimal filter function, Ψ, is derived through a constrained minimization where the variance of the measure has to be minimal, that is 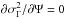 , while returning unbiased results with respect to κ0, that is ⟨κ0⟩ = Γt(0) and reads
, while returning unbiased results with respect to κ0, that is ⟨κ0⟩ = Γt(0) and reads 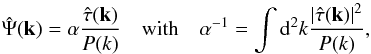 (12)where
(12)where 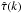 is the Fourier transform of the expected filament tangential shear, expressed as γf,t(x) = κ0τ(x). P(k) = Pg(k) + PLSS(k) is the noise power spectrum including the linearly evolved LSS through PLSS, as well as the source shot noise and intrinsic ellipticity
is the Fourier transform of the expected filament tangential shear, expressed as γf,t(x) = κ0τ(x). P(k) = Pg(k) + PLSS(k) is the noise power spectrum including the linearly evolved LSS through PLSS, as well as the source shot noise and intrinsic ellipticity 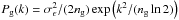 , given their angular number density ng and the intrinsic ellipticity dispersion σϵ (Maturi et al. 2005). The exponential in the Pg term accounts for the average background source separation that limits the angular resolution achievable by the filter and in general by any method. A visual impression of the filter shape in real space can be found in Fig. 4 for the case in which the filament template extends in the range limit of 0 < r < 10 arcmin. One of the filter ends is centered on the small cross in the middle of the reference frame so that the filter can be rotated around this point to scan all possible angles.
, given their angular number density ng and the intrinsic ellipticity dispersion σϵ (Maturi et al. 2005). The exponential in the Pg term accounts for the average background source separation that limits the angular resolution achievable by the filter and in general by any method. A visual impression of the filter shape in real space can be found in Fig. 4 for the case in which the filament template extends in the range limit of 0 < r < 10 arcmin. One of the filter ends is centered on the small cross in the middle of the reference frame so that the filter can be rotated around this point to scan all possible angles.
In the top panel of Fig. 5 we evaluate the noise variance for different filament widths, lengths, and general survey properties. In this example we considered a structure located at z = 0.55 and for the noise contribution expressed by the LSS power spectrum we adopted a ΛCDM model with a matter overdensity, a cosmological constant, and an Hubble expansion rate of Ωm = 0.3, Λ = 0.7 and h = 0.7, respectively. We furthermore assumed the sources to be placed at redshift z = 1.0, we fixed their intrinsic ellipticity to σϵ = 0.4, and truncated the filter length to 20 arcmin, that is ~ 5.5 Mpc/h at this redshift, a common value for current wide-field ground-based imagers, to avoid possible misleading features given by a square field of view. The variance decreases for a larger template width hc because more sources are involved in the estimate which reduces the shot noise and intrinsic ellipticity scatter. Note that the variance does not change with the square root of n because of the LSS component, which is constant for any survey.
3.3. Natural way of controlling the central cluster contribution
The applied filtering scheme is explicitly designed to maximize the filament’s contribution to the signal-to-noise ratio with respect to the stochastic noise, but it can also take into account, albeit not explicitly, the central cluster contamination in our case is another source of noise. On the one hand, by taking advantage of the filter’s linearity, we inserted Eq. (9) into Eq. (10) so that we are left with the following three distinct components where: 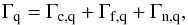 (13)where Γn,q is a Gaussian random quantity, characterized by Eq. (11). On the other hand, the shear decomposition scheme described in Eq. (5) allowed us to separate the anisotropic signal component given by the filament from the isotropic one associated to the central cluster. In fact, the filter is asymmetric due to the highly elongated template τ, describing the filament shape and therefore, the outcome of applying the filter to a given filament configuration strongly depends on its orientation θf. Hence, it is necessary to scan the filter through all possible orientation angles.
(13)where Γn,q is a Gaussian random quantity, characterized by Eq. (11). On the other hand, the shear decomposition scheme described in Eq. (5) allowed us to separate the anisotropic signal component given by the filament from the isotropic one associated to the central cluster. In fact, the filter is asymmetric due to the highly elongated template τ, describing the filament shape and therefore, the outcome of applying the filter to a given filament configuration strongly depends on its orientation θf. Hence, it is necessary to scan the filter through all possible orientation angles.
As a natural choice, the center of the reference frame was placed on a massive galaxy cluster because it marks the center around which we expect to find filamentary structures departing from its center. Once the filter was centered within the reference frame, we scanned all angles in a standard right-handed Cartesian system; see Fig. 1. By doing so, the measured tangential components of the filament as a function of the spanned angle θ have a maximum, Γf,t(θ = θf) = κ0, while the cross component is zero, Γf,x(θ = θf) = 0. This is shown in the bottom panel of Fig. 5, where we plot the expected filter response for filament located at z = 0.55, with a major axis position angle of θ = 30 degrees, a maximum convergence of κ0 = 0.02, and a scale radius of hc = 0.25 Mpc/h (typical values derived from numerical simulations, see Colberg et al. 2005; Mead et al. 2010). This signature indicates the filament orientation and a direct estimate of the filament convergence κ0. This behavior is a distinctive indicator to separate the filament’s signal components in contrast to the contribution from the main central halo, Γc,t(θ) ≈ const. and Γc,x(θ) ≈ 0, which are nearly constant (nearly because clusters are just approximately circularly symmetric) for all angles θ. With this approach we maximized the filament’s signal-to-noise ratio with respect to the survey properties by using the Maturi et al. (2005) optimal filter and controlled the cluster signal, which turns out to be nearly constant for any angle θ. A spurious oscillatory behavior resulting from the cluster may be due to a possible cluster ellipticity, but if this is the case, it is always possible to mask a circularly symmetric area centered on the cluster to reduce its significance. An alternative, and perhaps more conservative, way to approach the interpretation of the outcome signal is to simply consider its isotropic and anisotropic components regardless of their association to the filament or the central cluster, given the fact that these two are physically tightly related, and constitute a single system.
 |
Fig. 6 Optimal matched linear filter applied to realistic data. Left panel: the filter response on a mock catalog based on the N-body numerical simulation without noise and as a function of scanning angle. Each line represents the result for three different radial cutoffs. Right panel: this case considers the noise given by a finite source number density of ns = 15 arcmin-2 and an intrinsic ellipticity rms of σg = 0.4. The red line represents the expected theoretical signal (the same as in the left panel), the blue line the filter outcome for noisy data, and the dashed blue lines its ~ 1σ upper and lower uncertainty. The most significant filamentary structure (at α ~ 70 deg) has been recovered at the ~ 4σ level, all others are detected with a lower significance. |
Summarizing, the strategy leads to the final, simple check-list for filament detection:
-
1.
Define the reference coordinates with respect to a massive galaxy cluster.
-
2.
Apply the optimal filter described in Eq. (12) to the tailored shear components of the input data (Eq. (5)) and sample all position angles.
-
3.
All anisotropic signal components will be picked up as oscillations and maxima. If a straight, intracluster filament is detectable, a relatively sharp maximum is expected in the tangential component, Γt, in coincidence with the filament major axis direction.
4. Testing the filter on a realistic N-body numerical simulation
To test our novel filtering approach, we realized a mock catalog of galaxies lensed by the halos and filamentary structures present in the N-body numerical simulation described in Sect. 2. The contribution of LSS was neglected for the source catalog construction, but its power spectrum was used in the filter definition. Throughout the following analysis, we present a case study for a system at redshift z = 0.55 and an intrinsic ellipticity dispersion of σϵ = 0.4. The chosen source number density of n = 15 arcmin-2 and a field of view of (50 × 50) arcmin are typical values for ground-based observations of a cluster field. In this case, we applied an external circular truncation to the filament template with an exponential drop to avoid artifacts given by the square field of view. The filter was renormalized accordingly to preserve its unbiased properties presented in the previous sections.
Since we are dealing with discrete sources, it is necessary to approximate Eqs. (10) and (11) by summing over the galaxy ellipticities, which are an estimator of the shear ![\begin{eqnarray} \Gamma_{\rm q}(\theta) &=& \frac{1}{n}\sum_i \epsilon_{\rm iq}\Psi(\vec{x};\theta) , \\[-1mm] \sigma^2_{\rm \Gamma_q}(\theta) &=& \frac{1}{2n^2}\sum_i |\epsilon_{\rm iq}|^2\Psi^2(\vec{x};\theta) . \end{eqnarray}](/articles/aa/full_html/2013/11/aa22007-13/aa22007-13-eq125.png) Here ϵiq denotes the tangential or cross-component of the i-th galaxy ellipticity relative to the shortest line connecting its location to the filament major axis, see Eq. (5).
Here ϵiq denotes the tangential or cross-component of the i-th galaxy ellipticity relative to the shortest line connecting its location to the filament major axis, see Eq. (5).
The results of the filter applied to this mock simulation with and without the intrinsic ellipticity noise of the background galaxies and for different radius cut-offs are shown in the left and right panels of Fig. 6, respectively. We implemented a filter template with a scale radius of hc = 0.25 Mpc/h, a total length of L = 10 arcmin, and an inner truncation of 2.5 arcmin to avoid the central cluster contamination. These radial cut-offs are shown in Fig. 3. The expected behavior, that is a signal peak conform with the position angles (PA) of the filamentary structures around the central cluster at θ ≈ 70 and θ ≈ 260 degrees, is seen with a significance of ~ 4σ and ~ 1σ, respectively. The two smaller elongated structures at θ ≈ 0 and θ ≈ 190 degrees are also picked up by the filter at a 2σ level, showing its sensitivity. We note that the expected theoretical rms including the LSS contamination for this case is σΓ = 0.015, as derived by Eq. (11). In this realistic case, the ellipticity of the central cluster plays a role in the signal as well since the filter is sensitive to all anisotropic contributions. Even if the cluster elongation is physically correlated to a filament, both in direction and amplitude as seen in N-body numerical simulations, we aimed to minimize its contribution by applying a circular mask of 2.5 arcmin in radius centered on the main cluster. We did this because our target was the filament alone, even though its tight connection to the central cluster would be physically motivated and in fact the study of the signal anisotropy around clusters would be a sensible question to answer with this method. Another representation of this result is given in Fig. 7, where we performed a Fourier analysis of the filter outcome to highlight the most important scales involved.
 |
Fig. 7 Signal power resulting from a Fourier analysis of the filter applied to the N-body numerical simulation. Red bars represent results without intrinsic ellipticity noise of galaxies, blue bars take it into account. |
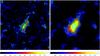 |
Fig. 8 Weak-lensing analysis of the N-body numerical simulation (Dolag et al. 2006) performed with the isotropic, optimal matched filter described in Maturi et al. (2005). The filter was optimized to detect NFW dark-matter halos with masses of 5 × 1013 M⊙/h (left panel) and 1 × 1015 M⊙/h (right panel). The isocontours start from S ! N = 2 in steps of ΔS ! N = 1. The main halo and its ellipticity are clearly visible in the center of the field, as are the additional small substructures in the field. |
If a single, massive filamentary structure can be detected at a 4σ level, the characterization of an anisotropic component around clusters can be carried out in a statistical sense and over a large number of clusters. One obvious way is stacking, but this would lead to biased results toward higher filter responses. A more promising approach is to count the maxima of the signal response instead, in analogy to the shear peak that count statistics, allowing an unbiased estimate which is representative of the filament population in the vicinity of clusters. Moreover, this would allow one to separate the actual signal from the contribution of matter distributed along the line of sight, which is uncorrelated to the investigated structures.
5. Alternative method based on peak counts
We have shown that a relatively continuous and smooth distribution of matter, organized in a filamentary structure, can be detected down to κ0 ~ 0.01 − 0.005. This number assumes a source number density of n = 15 arcmin-2 and an intrinsic background source ellipticity dispersion of σϵ = 0.4, which are typical values for ground-based observations. Although the suggested method seems to be sensitive to intracluster filaments even with ground-based observations, we suggest an additional, complementary approach to search for filamentary structures. This different technique is based on shear peak-counts (Maturi et al. 2010; Dietrich & Hartlap 2010; Maturi et al. 2011; Marian et al. 2013) and is motivated by N-body numerical simulations, which predict an overdensity of collapsed substructures along these filaments that could be directly correlated with other observables such as optical cluster detection methods (see e.g. Bellagamba et al. 2011). Using this method together with the proposed filtering approach poses the interesting task of comparing the ratio of the dark matter distributed in the smooth filament component, composed of an ensemble of numerous halos of galaxy/group size, and in the distinct clumps, of more massive halos, along its major axes.
To detect collapsed structures, we again applied the recipe described by Maturi et al. (2005) but in its original form, which is an aperture mass filter designed to maximize the signal-to-noise ratio of the lensing signal arising from dark-matter halos. It takes into account the general survey properties and LSS. We tuned this filter to search for NFW (sub-) structures with a mass of m = 5 × 1013 M⊙/h that are located at the main cluster’s redshift. Different masses and redshifts could be used, but we focused our search on relatively small halos that are more likely to belong to filaments. If smaller masses, that is scales, are used as input template for the filter, its optimization criteria will prevent from acting on excessively small angular scales. This is to keep the source shot noise and intrinsic ellipticity minimal.
We applied this isotropic filter to the mock catalog derived from the previous N-body numerical simulation. We show the signal-to-noise ratio map in Fig. 8, together with the results for the same filter but tuned to detect halos with M = 1015M⊙, for comparison. The isocontours represent signal-to-noise ratios higher than S/N = 2 in steps of ΔS/N = 1. The most significant structures are aligned along an axis centered on the main cluster and with an inclination of ~ 60 degrees, showing a clear correlation of collapsed structures with the filament. Other minor structures are also visible in the field of view. To quantify the significance of this correlation, we evaluated the number density of detections made in a rectangular area centered on the larger filament detected in Sect. 4, that is the one pointing in the θ = 60 degrees direction. This rectangular area excluded the central cluster within a distance of r = 2.5 arcmin and its width was set to 7 arcmin, a typical value found in N-body numerical simulations (see e.g. Aragón-Calvo et al. 2010; Bond et al. 2010; Fedeli et al. 2011; Colberg et al. 2005, for details). The other smaller structures are not detectable with other commonly used weak-lensing techniques. The resulting overdensity contrast with respect to the rest of the field, defined as the remaining area, is f = 2.66 ± 0.63.
6. Conclusions
We investigated the possibility of detecting straight filaments centered on a single massive cluster with actual ground-based weak-lensing data. In this lensing approach we solely focused on the dark-matter content and on filaments that depart radially from a massive cluster. We choose this specific filament/cluster configuration because it represents the large majority of cases (Colberg et al. 2005) and because it has convenient geometrical properties that help their detection through weak lensing. We demonstrated this last aspect by analyzing a mock catalog of galaxy ellipticities based on an N-body numerical simulation containing a massive galaxy cluster with connecting filamentary structures.
For this purpose, and in particular for the detection of the smooth component of the filament’s matter distribution, we adapted the Maturi et al. (2005) optimal matched filter and modified it to serve our specific case. We used a template tailored to the elongated signal of straight filaments, together with a peculiar shear decomposition that splits the shear into two components, one orthogonal and one perpendicular to a given direction chosen such as to verify the presence of a filament in the field of interest. In fact, the shear of a filamentary structure was aligned orthogonally to its major axis, thereby defining the signal we were looking for. We demonstrated that this decomposition is optimal in maximizing the filament’s signal when combined with the optimal filter and allows its clear separation from the central cluster isotropic contribution. This separation of components derives from the fact that the filter signal for the cluster is nearly constant for all PAs, because it is isotropic, while it has an angular dependence for all anisotropic signal contributions such as those produced by filaments. In particular, the signal peaks when the filter is aligned with a filament. Note that the adopted decomposition is substantially different from the one commonly used, implicitly or explicitly, in typical weak-lensing mass reconstructions or object detection, and great care has to be taken when comparing and interpreting different approaches. With our proposed method, the minimum convergence detectable in the filament’s smooth component, at 1σ level, lies in the range 0.005 < κ0 < 0.02, depending on the filter’s template width and length. This performance is clearly superior to other means of filament detection.
We stress that the filter is sensitive to all anisotropic signal components such as a possible central cluster ellipticity, which would be degenerate in the presence of a filament. This is not a problem because, since the filter can be used in different ways depending on the question asked. In particular: (1) By using all data, such that the overall system anisotropic component (cluster ellipticity plus filament) will be measured. One would expect the two components add constructively since they are physically correlated; (2) by masking out a circular area centered on the main central cluster such that the filament’s convergence alone is measured; (3) by running the filter twice: The first time only on an area centered on the cluster, the second time only on the rest of the field. The last option is of particular interest because it allows one to quantify the correlation between the cluster ellipticity and the presence or the absence of a filament, together with their respective alignment.
In addition, we presented a simple method based on weak-lensing peak counts. These substructure halos are expected to be more abundant along the filament in the rest of the field, contributing to the individual identification of filaments. This second method was also tested on the N-body numerical simulation containing straight filamentary structures. This approach
complements the previous one and helps to obtain a better picture of the amount of dark matter contained both in the filament’s, smooth and collapsed component.
Despite the simplicity of the proposed two methods, we have proven that they are efficient in detecting the dark-matter content of intracluster filaments in mock observations. This statement holds for ground-based data quality parameters, defining new possibilities in the study of structure formation and cosmology via weak gravitational lensing.
Acknowledgments
We are grateful to Klaus Dolag for providing us the N-body numerical simulation used in this work and to Massimo Meneghetti for his help in extracting its lensing properties. This work was supported by the Transregional Collaborative Research Centre TRR 33 (M.M.). This research was carried out in part at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with NASA.
References
- Aragón-Calvo, M. A., van de Weygaert, R., & Jones, B. J. T. 2010, MNRAS, 408, 2163 [NASA ADS] [CrossRef] [Google Scholar]
- Bartelmann, M. 1996, A&A, 313, 697 [NASA ADS] [Google Scholar]
- Bartelmann, M. 2010, Class. Quant. Gravity, 27, 233001 [NASA ADS] [CrossRef] [Google Scholar]
- Bartelmann, M., & Schneider, P. 2001, Phys. Rep., 340, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Bellagamba, F., Maturi, M., Hamana, T., et al. 2011, MNRAS, 413, 1145 [NASA ADS] [CrossRef] [Google Scholar]
- Bond, N. A., Strauss, M. A., & Cen, R. 2010, MNRAS, 406, 1609 [NASA ADS] [Google Scholar]
- Colberg, J. M., Krughoff, K. S., & Connolly, A. J. 2005, MNRAS, 359, 272 [NASA ADS] [CrossRef] [Google Scholar]
- Colless, M., Dalton, G., Maddox, S., et al. 2001, MNRAS, 328, 1039 [NASA ADS] [CrossRef] [Google Scholar]
- Dietrich, J. P., & Hartlap, J. 2010, MNRAS, 402, 1049 [NASA ADS] [CrossRef] [Google Scholar]
- Dietrich, J. P., Schneider, P., Clowe, D., Romano-Díaz, E., & Kerp, J. 2005, A&A, 440, 453 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dietrich, J. P., Werner, N., Clowe, D., et al. 2012, Nature, 487, 202 [Google Scholar]
- Dolag, K., Meneghetti, M., Moscardini, L., Rasia, E., & Bonaldi, A. 2006, MNRAS, 370, 656 [NASA ADS] [Google Scholar]
- Fahlman, G., Kaiser, N., Squires, G., & Woods, D. 1994, ApJ, 437, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Fedeli, C., Pace, F., Moscardini, L., Grossi, M., & Dolag, K. 2011, MNRAS, 416, 3098 [NASA ADS] [CrossRef] [Google Scholar]
- Jauzac, M., Jullo, E., Kneib, J.-P., et al. 2012, MNRAS, 426, 3369 [Google Scholar]
- Kilbinger, M., Fu, L., Heymans, C., et al. 2013, MNRAS, 430, 2200 [NASA ADS] [CrossRef] [Google Scholar]
- Klypin, A. A., & Shandarin, S. F. 1983, MNRAS, 204, 891 [NASA ADS] [Google Scholar]
- Marian, L., Smith, R. E., Hilbert, S., & Schneider, P. 2013, MNRAS, 432, 1338 [NASA ADS] [CrossRef] [Google Scholar]
- Massey, R., Rhodes, J., Ellis, R., et al. 2007, Nature, 445, 286 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Maturi, M., Meneghetti, M., Bartelmann, M., Dolag, K., & Moscardini, L. 2005, A&A, 442, 851 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maturi, M., Schirmer, M., Meneghetti, M., Bartelmann, M., & Moscardini, L. 2007, A&A, 462, 473 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maturi, M., Angrick, C., Pace, F., & Bartelmann, M. 2010, A&A, 519, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maturi, M., Fedeli, C., & Moscardini, L. 2011, MNRAS, 416, 2527 [NASA ADS] [CrossRef] [Google Scholar]
- Mead, J. M. G., King, L. J., & McCarthy, I. G. 2010, MNRAS, 401, 2257 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Pace, F., Maturi, M., Meneghetti, M., et al. 2007, A&A, 471, 731 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2013, A&A, 550, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schirmer, M., Hildebrandt, H., Kuijken, K., & Erben, T. 2011, A&A, 532, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, P. 1996, MNRAS, 283, 837 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, P., & Er, X. 2008, A&A, 485, 363 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schrabback, T., Hartlap, J., Joachimi, B., et al. 2010, A&A, 516, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Springel, V. 2005, MNRAS, 364, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., Yoshida, N., & White, S. D. M. 2001, New A, 6, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., White, S. D. M., Jenkins, A., et al. 2005, Nature, 435, 629 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Van Waerbeke, L., Benjamin, J., Erben, T., et al. 2013, MNRAS, 433, 3373 [Google Scholar]
- White, S. D. M., Frenk, C. S., Davis, M., & Efstathiou, G. 1987, ApJ, 313, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Zitrin, A., Menanteau, F., Hughes, J. P., et al. 2013, ApJ, 770, L15 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Schematic sketch of our mock filament and cluster setup. The background whisker plot shows the shear fields of the filament (red) and the NFW halo (blue). Note that the length of the filament whiskers is enhanced by a factor of 15 with respect to the halo ones for clarity. The global coordinate system θ, the filament’s orientation θf, and the distance from the filament center along an axis perpendicular to its extension h are also clearly marked. The 3D orientation of the coordinate frame is right-handed. In our analysis we treat the two sides of the filament as independent so that we can access all possible geometrical configurations. The figure shows the most simple configuration however, which is an identical orientation angle for the two sides of the filament with respect to the main halo. |
| In the text | |
 |
Fig. 2 Shear pattern induced by an ensemble of 4, 8, 16, and 32 NFW halos forming an elongated structure that resembles an intracluster filament located at z = 0.55. The haloes have random masses ranging from 0 to a fixed upper limit of 1015 M⊙/h, 5 × 1014 M⊙/h, 2.5 × 1014 M⊙/h and 1.25 × 1014 M⊙/h, respectively, to keep the total mass of the structure in different panels fixed. The shear sampling is analoguous to the one typical for weak-lensing observations with a source number density of ns = 15 arcmin-2. These toy models illustrate the two regimes in the shear pattern caused by elongated structures, i.e. an alignment tangential to the center of the structure at large radii and the alignment orthogonal to the filament’s major axis. The two regimes are separated by an area of vanishing shear. |
| In the text | |
 |
Fig. 3 Numerical simulation of a cluster-filament configuration. Left panel: shear amplitude map centered on a massive galaxy cluster surrounded by filamentary structures.The circles enclose the area in which we measure the lensing signal for the filament detection. Right panel: whisker visualization of the shear pattern of the same simulation. The shear of the central part of the main cluster was removed for clarity. |
| In the text | |
 |
Fig. 4 Optimal matched filter in real space for a filament template extending in the range limit of 0 < r < 10 arcmin. The filter was rotated around the cross in the middle, in order to investigate all angles. |
| In the text | |
 |
Fig. 5 Optimal matched linear filter for filament detection. Top panel: variance for filaments at redshift z = 0.55. For a given survey with intrinsic ellipticity scatter of σϵ = 0.4, different core radii hc and different galaxy number densities n are plotted. Continuous lines refer to a filter with length L = 10, arcmin while dashed lines refer to L = 20 arcmin. Bottom panel: expected filter response for a filament located at z = 0.55, with a major axis position angle of θ = 30 degrees, a maximum convergence of κ0 = 0.02, and a scale radius of hc = 0.25 Mpc/h. The filter was truncated with an inner cutoff of 2.5 arcmin and two different outer cutoffs of 5 arcmin and 10 arcmin. |
| In the text | |
 |
Fig. 6 Optimal matched linear filter applied to realistic data. Left panel: the filter response on a mock catalog based on the N-body numerical simulation without noise and as a function of scanning angle. Each line represents the result for three different radial cutoffs. Right panel: this case considers the noise given by a finite source number density of ns = 15 arcmin-2 and an intrinsic ellipticity rms of σg = 0.4. The red line represents the expected theoretical signal (the same as in the left panel), the blue line the filter outcome for noisy data, and the dashed blue lines its ~ 1σ upper and lower uncertainty. The most significant filamentary structure (at α ~ 70 deg) has been recovered at the ~ 4σ level, all others are detected with a lower significance. |
| In the text | |
 |
Fig. 7 Signal power resulting from a Fourier analysis of the filter applied to the N-body numerical simulation. Red bars represent results without intrinsic ellipticity noise of galaxies, blue bars take it into account. |
| In the text | |
 |
Fig. 8 Weak-lensing analysis of the N-body numerical simulation (Dolag et al. 2006) performed with the isotropic, optimal matched filter described in Maturi et al. (2005). The filter was optimized to detect NFW dark-matter halos with masses of 5 × 1013 M⊙/h (left panel) and 1 × 1015 M⊙/h (right panel). The isocontours start from S ! N = 2 in steps of ΔS ! N = 1. The main halo and its ellipticity are clearly visible in the center of the field, as are the additional small substructures in the field. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


