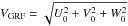EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 559 (November 2013) A&A, 559 (2013) A12 Full HTML
Free Access
Issue
A&A
Volume 559, November 2013
Article Number A12
Number of page(s) 14
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201221012
Published online 29 October 2013

© ESO, 2013

1. Introduction

Hypervelocity stars (HVSs) are stars that have space velocities higher than the Galactic escape velocity. According to Hills (1988), HVSs are a natural consequence of the presence of a massive black hole in the Galactic center. The first HVS was discovered by Brown et al. (2005): SDSS J090745.0+024507, a late B-type main-sequence star at a distance of ~110 kpc in the Galactic halo with a radial velocity (RV) of 853±12 km s-1. Following this discovery, several other HVSs and HVS candidates, the majority of them early-type main-sequence stars, were also found in subsequent surveys using the photometric filters of the Sloan Digital Sky Survey (SDSS) combined with spectroscopic observations (Brown et al. 2009). Further main-sequence HVSs were found by Li et al. (2012) using data from SDSS. These authors found other main-sequence HVSs stars, all of them metal-poor F stars. The star US 708 was the first evolved object found to be an HVS (Hirsch et al. 2005). The blue horizontal branch star SDSS J153935.67+023909.8, which is the first Population II HVS, with VGRF ~ 700 km s-1, became one of the fastest known halo stars (Przybilla et al. 2010). The discovery that US 708 is an HVS triggered a project to search for these kinds of objects using SDSS, and Tillich et al. (2011) successfully found ten additional new subdwarf HVS candidates.

Kinematic studies of HVSs have been mainly performed solely on their RVs. This is because proper motions can be measured only for a few HVSs (Tillich et al. 2009, 2011). Therefore only stars with very high RVs are considered as potential HVSs. However, as we show in this work, a star does not need to have an extreme RV such as those quoted in Table 1 of Brown et al. (2009a), to be considered an HVS.

The metal-poor red horizontal branch (RHB) star CD-41°15048 with a RV of 229 km s-1 and a large proper motion is another HVS candidate depending on the adopted Galactic potential. We will see that CD-41°15048 travels with the Galactocentric Reference Frame velocity (GRF)1, VGRF = 583 km s-1, which is higher than the local escape velocity according to the Galactic potential of Allen & Santillan (1991) but lower than local escape velocity according to the Galactic gravitational potential of Ortega et al. (2002). We also investigate in this work the kinematic behavior of the RHB star HD 214362 and show that this star has a highly eccentric orbit and passes quite close to the Galactic center.

2. Observations

The high-resolution spectra of CD-41°15048 and HD 214362 analyzed in this work the were obtained with FEROS, the Fiber-fed extended range optical spectrograph (Kaufer et al. 1999), at the 2.2 m ESO telescope at La Silla (Chile) on the night of September 6, 2007 and August 26, 2007. The FEROS spectral resolving power is R = 48   000, corresponding to 2.2 pixels of 15   μm, and the wavelength coverage goes from 3800 Å to 9200 Å. The nominal signal-to-noise ratio (S/N) was evaluated by measuring the rms flux fluctuation in selected continuum windows, and the typical value was S/N = 100 − 150 after one exposure of 1200 s. The spectra were reduced with the MIDAS pipeline reduction package, which consists of the following standard steps: CCD bias correction, flatfielding, spectrum extraction, wavelength calibration, correction of barycenter velocity, and spectrum rectification. Figure 1 shows the spectra of both stars in the 6110−6150 Å region.

thumbnail Fig. 1

Spectra of CD-41°15048 (top) and HD 214362 (bottom). Absorption lines due to the transitions of Ca i 6122.23, Fe i 6137.70, and Ba ii 6141.73 are also shown. Dashed lines represent their rest wavelengths. The spectral lines are shifted towards the red by about 4.6 Å  for CD-41°15048 due to a RV of 228.9 ± 0.6 km s-1. For HD 214362, the absorption lines are shifted towards the blue by about 2.0 Å  due to a RV of −92.4 ± 0.7 km s-1.

3. Analysis and results

3.1. Line selection, equivalent width measurements, and oscillator strengths

The atomic absorption lines selected in the present study are basically the same as those used in the previous study devoted to the analysis of photospheric abundances of the candidate hypervelopcity CH star CD-62°1346 (Pereira et al. 2012, hereafter Paper I). Table 1 shows the Fe i and Fe ii lines employed in the analysis, the lower excitation potentials χ(eV) of the transitions, the log gf values and the measured equivalent widths Wλ. The log gf values for the Fe i and Fe ii lines given in Table 1 were taken from Cohen et al. (2004) and Lambert et al. (1996).

3.2. Determination of the atmospheric parameters

The determination of stellar atmospheric parameters such as effective temperature (Teff), surface gravity (log g), microturbulence (ξ), and metallicity ([Fe/H]) (we use the notation [X/H] = log (NX/NH)⋆ − log (NX/NH)⊙) were determined using the local thermodynamic equilibrium (LTE) model atmospheres of Kurucz (1993) and the spectral analysis code moog (Sneden 1973). The atmospheric parameters with their respective uncertainties were obtained in the same way as we did in Paper I. The adopted atmospheric parameters are given in Table 2. Table 2 also provides atmospheric parameter determinations derived in previous studies. Typical uncertainties of σ(Teff) =  ± 120 K, σ(log g) =  ± 0.2 dex, and σ(ξ) =  ± 0.3 km s-1 were found.

Spectroscopic gravities of low-metallicity giants derived from ionization balance are generally lower than photometric gravities derived from stellar parallaxes or evolutionary models (Mashonkina et al. 2011; Ruchti et al. 2013; Serenelli et al. 2012). According to the recent work of Ruchti et al. (2013), the non-local thermodynamic equilibium (NLTE) correction to the spectroscopic gravity is about +0.4 dex. Besides the metallicity and surface gravity, the NLTE corrections depend on the effective temperature. In a thorough study of RHB stars in the globular cluster M15, with even lower metallicity ([Fe/H] < −2.0) than CD-41°15048, Preston et al. (2006) derived corrections to spectroscopic gravities (Δlog g = log gphot − log gspec) and showed that the Δlog g value increases strongly with the decrease of the effective temperature, achieves values of about +0.4 for RHB stars with Teff below ~5130 K, and essentially disappears for hotter stars. The explanation for this temperature behavior of the log g correction in RHB stars is given in For & Sneden (2010). They point out that in the line-forming region of RHB stars the electron pressure rises sharply with Teff, increasing by a factor of more than 30 from the coolest RHB stars of M 15 (Teff = 5000 K) to the warmest Teff = 6250 K ones.

The range of effective temperatures and surface gravities of RHB stars in M15 cover well the corresponding values of CD-41°15048 and HD 214362 analyzed in our work. In its analytical form, the relation Δlog g vs. Teff used in the paper of For & Sneden (2010) is

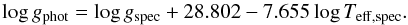loggphot=loggspec+28.802−7.655logTeff,spec.$$ \log g_{\rm phot} = \log g_{\rm spec} + 28.802 -7.655\log T_{\rm eff,spec}. $$Using this relation, we obtained Δlog g =  + 0.1 for CD-41°15048. Therefore in the present work we consider two possible corrections for the gravity of CD-41°15048, as given in For & Sneden (2010) and Ruchti et al. (2013), and draw the conclusions taking into account both corrections. We note that adopting an NLTE correction of +0.4 results in log g    =    2.3. In this case, the distance to the star would be 0.7 kpc and the star will not escape in any of the adopted Galactic potentials (Sects. 4.2.1 and 4.3).

For the star HD 214362, which has an even higher effective temperature, the correction to the log gspec disappears, and hence no correction was applied. In fact, we see that for HD 214362, the distance obtained based on the spectroscopic gravity (640 pc, Sect. 4.2.2) is inside the range of the distances given by the Hipparcos parallax, which is between 240 and 730 pc.

Table 2

Atmospheric parameters of CD-41°15048 and HD 214362.

Having determined the temperatures and gravities of CD-41°15048 and HD 214362, we are in a position to obtain their masses using horizontal branch tracks in the Teff − log g plane. Because the atmospheres of the metal-poor stars are overabundant in the α-elements, we have used the evolutionary tracks computed by Pietrinferni et al. (2006) with [α/Fe] = +0.4. Figure 2 displays the evolutionary tracks for several stellar masses in the Teff − log g plane at a metallicity of Z = 0.0003. The positions of CD-41°15048 and HD 214362 in this plane are also shown. For CD-41°15048 we found two possible masses, depending on the adopted gravity (calculated with corrections of +0.1 and +0.4 dex), 0.57   M⊙ or 0.68   M⊙. For HD 214362, the mass is 0.60   M⊙.

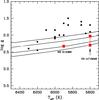thumbnail Fig. 2

Location of CD-41°15048 and HD 214362 in the log (Teff,log g) plane (red squares). We also show the α-enhanced horizontal branch tracks from Pietrinferni et al. (2006) at metallicity Z = 0.0003 and Y    =    0.245 for stellar masses, from top to bottom, 0.55, 0.57, 0.60, and 0.68   M⊙. Black squares represent the positions of some RHB stars analyzed by For & Sneden (2010). For CD-41°15048 we show two possible gravities after correction.

3.3. Abundance analysis and uncertainties

The abundances of chemical elements with their respective uncertainties were determined in the same way as in Paper I. The current version of the line-synthesis code moog (Sneden 1973) was used to carry out the calculations. Table 3 shows the atomic lines used to derive the abundances of the elements. We also provide the reference for the log gf values (fifth column) used in the abundance determination.

The barium abundance was derived using the Ba ii lines at λ4554.0, λ4934.1, λ5853,7, and λ6141.7 Å. The line data that include hyperfine splitting were taken from McWilliam (1998). The cobalt abundance was derived using the Co i line at λ4121.33 Å, where the hyperfine splitting was taken from McWilliam et al. (1995). The europium abundance was found using the line of Eu ii at λ4129.72 Å, and the hyperfine splitting was taken from Mucciarelli et al. (2008). The derived abundances are given in Table 4. The adopted abundances for the elements analyzed in this work were normalized to the solar abundances of Grevesse & Sauval (1998). For the solar iron abundance, we adopted log ε(Fe) = 7.52.

The abundance uncertainties owing to errors in the stellar atmospheric parameters Teff, log g, and ξ were estimated by varying these parameters by their standard errors and then computing the changes incurred in the element abundances. The abundance uncertainties owing to errors in the equivalent width measurements were computed from the expression provided by Cayrel (1988). The errors in the equivalent widths are essentially set by the signal-to-noise ratio and by the resolution of the spectra. In our case, having R ≈ 50   000 and a typical S/N of 150, the expected uncertainties in the equivalent widths are about 2−3 mÅ. The results of these calculations are displayed in Cols. 2 to 5 of Table 5.

Table 4

Abundance in the log ε(H) = 12.0 scale and in the notation [X/Fe].

4. Discussion

4.1. Abundances

Below we discuss the abundance pattern of CD-41°15048 and HD 214362 by comparing them with previous studies done for some halo population stars and also with other RHB stars. Figures 3−5 show the abundance ratios [X/Fe] versus metallicity of the elements analyzed in this work.

In metal-poor stars, the aluminum abundance was investigated by Fulbright (2000), Carretta et al. (2002), and Cohen et al. (2004), to mention just a few studies. Between [Fe/H] =  −1.0 and − 3.0, the [Al/Fe] ratio decreases from ≈+0.4 to ≈−0.8. In metal-poor RHB stars, aluminum is underabundant, ⟨[Al/Fe]⟩  ≈  −0.6 (For & Sneden 2010). Our value of ≈−0.5 for the [Al/Fe] ratio for the stars CD-41°15048 and HD 214362 follows the trend observed in the metal-poor stars.

The mean α-element abundances as given by ([Mg/Fe]+ [Si/Fe]+[Ca/Fe]+[Ti/Fe])/4 for CD-41°15048 and HD 214362 are, respectively, 0.36 ± 0.10 and 0.45 ± 0.05, similar for stars at this metallicity (Carretta et al. 2002; Stephens & Boesgaard 2002; Roederer 2009). For the RHB stars studied by For & Sneden (2010), the authors obtained a mean value of +0.3 for the same ratio, having a metallicity between −3.0 and −1.0.

The iron-group elements (Cr, Co, Ni, and Zn) abundances are expected to follow the iron abundance. Chromium does, indeed, and the [Cr/Fe] ratio is basically zero for both stars. Cobalt is slightly underabundant in CD-41°15048 but follows the iron abundance in HD 214362. For stars with [Fe/H] < −1.0, the [Ni/Fe] ratio starts to show a scatter around the mean [Ni/Fe] = 0.0 (Roederer 2009) larger than for stars with higher metallicity. Both RHB stars analyzed in this work have [Ni/Fe] ratios similar to those derived by Fullbright (2000), Gratton & Sneden (1991), and For & Sneden (2010).

For [Fe/H] > −1.0, the [Zn/Fe] ratio is also close to zero (Reddy et al. 2006). From the work of Cayrel et al. (2004) and Lai et al. (2008), it can be seen that the [Zn/Fe] ratio increases for metallicities down to [Fe/H] < −2.0. Between − 2.0   <  [Fe/H]  <  − 1.0, the [Zn/Fe] ratio has a value around ≈+0.2, which is consistent with values found for the stars analyzed in this work.

Similar to the α-elements and the iron-peak elements, the elements with atomic numbers Z > 30 investigated in this work generally also follow a typical trend seen in halo stars. For HD 214362, we found log ε (La/Eu) = 0.52 ± 0.19 in agreement with the value of 0.34 obtained by Simmerer et al. (2004). Relative to field stars in the Galaxy at similar metallicities, we did not detect any overabundances of these elements in both stars analyzed in this work. Our [X/Fe] ratios for the heavier elements are also in agreement with those obtained by For & Sneden (2010) for RHB stars.

4.2. Distance determinations

4.2.1. CD-41°15048

The relation between the star distance to the Sun r and the temperature, gravity, mass, V magnitude, and interstellar absorption (AV) is given by 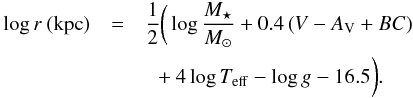logr(kpc)=12(logM⋆M⊙+0.4(V−AV+BC)  +4logTeff−logg−16.5).\begin{eqnarray} \log r\: ({\rm kpc}) & = & \frac{1}{2}\bigg(\log \frac{M_{\star}}{M_{\odot}} + 0.4\left(V-A_{\rm V}+BC\right) \nonumber \\ & & {{\,}\atop{\,}} + 4\log T_{\rm eff} - \log g - 16.5\bigg). \end{eqnarray}(1)For the derived temperature and the visual magnitude, V = 10.2 2, Eq. (1) can be written as 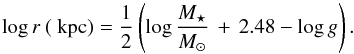logr(kpc)=12(logM⋆M⊙ + 2.48−logg).\begin{equation} \log r\: ({\rm~kpc}) = \frac{1}{2}\left(\log \frac{M_{\star}}{M_{\odot}}\,+\, 2.48- \log g\right). \end{equation}(2)In these calculations, we used Mbol ⊙ =  + 4.74 (Bessel 1998) and BC = 0.19 (Alonso et al. 1999). The interstellar absorption was estimated from the relation between the equivalent width of the Na D2 interstellar line and the color excess E(B − V) given in Munari & Zwitter (1997). For the equivalent width of 38 mÅ, we found a color excess of 0.01. Finally, we obtain a distance r = 1.3 ± 0.3 kpc for the value of log g = 2.0, after applying a correction of +0.1 dex discussed in Sect. 3.2 and for a mass of M∗    =    0.57   M⊙. For the value of log g = 2.3, after applying a correction of +0.4 dex, and a mass of M∗    =    0.68   M⊙ we obtain a distance r = 0.7 ± 0.2 kpc. Based on the distance and interstellar absorption, we estimated the absolute visual magnitude as MV =  −0.4 ± 0.5 and MV = 0.9 ± 0.6 for the above determined distances. These possible values for the absolute magnitudes are in the range of the MV values of other RHB stars (e.g. the MV − log Teff diagram of Simmerer et al. 2004).

There is no previous distance determination for CD-41°15048. The Hipparcos parallax for this star is very uncertain, π   (mas) = 0.2 ± 1.8 (van Leeuwen 2007).

4.2.2. HD 214362

For the derived temperature and visual magnitude V = 9.1 of HD 214362, Eq. (1) can be written as 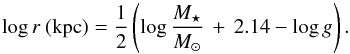logr(kpc)=12(logM⋆M⊙ + 2.14−logg).\begin{equation} \log r\: ({\rm kpc}) = \frac{1}{2}\left(\log \frac{M_{\star}}{M_{\odot}}\,+\, 2.14- \log g\right). \end{equation}(3)We also used the bolometric correction BC = 0.15 by Alonso et al. (1999). As for CD-41°15048, the interstellar absorption was estimated from the relation between the equivalent width of the Na D2 interstellar line and the color excess. For the equivalent width of 88 mÅ, we found a color excess of 0.02. Finally, for the value of log g = 2.3 and a mass of M∗ = 0.6   M⊙, we obtain a distance of r = 644 ± 150 pc or π   (mas) = 1.55 ± 0.37, in good agreement with the distance given by Hipparcos (van Leeuwen 2007) (π   (mas) = 2.79 ± 1.42), within the considered errors.

From our determined distance, we find that the absolute visual magnitude of HD 214362 is MV = 0.03 ± 0.50. This value is smaller than the one (MV    =    0.6) obtained by Simmerer et al. (2004). This is probably because Simmerer et al. (2004) derived a gravity higher by about +0.3 dex than our value. A higher log g value implies a smaller distance (they obtained 490 pc) and hence a higher value for the absolute visual magnitude.

4.3. Kinematics

At the distances derived in the previous section and with the RVs obtained from the spectroscopic data, we calculated the heliocentric space velocity components for the stars analyzed in this work. Table 6 shows the results. We followed the same procedure as in Paper I. A Galactocentric solar distance of 8.5 kpc and a local standard of rest (LSR) rotation velocity relative to the GRF of 220 km s-1 was adopted in our calculations. For CD-41°15048, we computed the space velocities considering the distances of 1.3 and 0.7 kpc. In our computations, U is positive away from the Galactic center (l = 0°,b = 0°), V is positive in the direction of the Galactic rotation (l = 90°,b = 0°), and W is positive toward the North Galactic Pole (b = 90°). The star escape velocity (vesc) was computed using two Galactic gravitational potential models: Allen & Santillan (1991) and Ortega et al. (2002). The star escape velocity obtained from the Galactic potential is compared with the velocity (VGRF) computed from the Galactocentric velocity components of the star.

The distances were calculated using Eq. (1), taking into consideration the temperature and gravity already determined. Bolometric corrections derived by Alonso et al. (1999) were also employed. Interstellar absorption was considered using the results from the literature and was not higher than AV = 0.3. Proper motions were taken from Hipparcos catalogue (van Leeuwen 2007). We adopted M∗ = 0.6   M⊙ for all the stars. We also included in Table 6 other RHB stars with proper motions greater than 100 mas yr-1.

In the next subsections, we discuss our results for the two stars analyzed in this work and the most relevant results for the other RHB stars.

Table 6

Atmospheric parameters (effective temperature and surface gravity), distance, radial velocity (RV), proper motions, Galactocentric velocity components (U0,   V0, W0), Galactocentric reference frame velocity (VGRF), and escape velocity (vesc) in different Galactic potentials for some RHB stars.

4.3.1. CD-41°15048 and HD 214362

Table 6 shows that if CD-41°15048 is at a distance of 700 pc it will be a bound object in any Galactic potential considered by us. However, for a distance of 1.3 kpc, this star may be an unbound object in the Galactic potential of Allen & Santillan (1991) but not in the Galactic potential of Ortega et al. (2002). In Fig. 6 we show the distribution probability of the Galactic reference frame velocities for CD-41°15048 for a distance of 1.3 kpc. We took into consideration the error in the RV, distance, and proper motions. Changing these three parameters with their respective errors, we applied a Monte Carlo method to obtain the distribution of space velocity components and then to obtain the Galactocentric reference frame velocities (VGRF). Finally, the calculated area under the curve, which is lower-limited either by the Galactic potential of Allen & Santillan (solid vertical line) or by the Galactic potential of Ortega et al. (2002) (dashed vertical line), gives the probability of CD-41°15048 being bound or unbound. For the Galactic potential of Allen & Santillan (1991), CD-41°15048 has a 78% probability of being unbound to the Galaxy. However, according to the Galactic potential of Ortega et al. (2002), the star is bound to the Galaxy and has only a 9% probability of being unbound. As far as HD 214362 is concerned, it is a bound star in any of the Galactic potentials considered.

thumbnail Fig. 6

Probability distribution of the Galactic reference frame velocities for CD-41°15048. The solid vertical line represents the Galactic escape velocity according to the Galactic potential of Allen & Santillan (1991), and the dashed vertical line represents the Galactic escape velocities according to the Galactic potential of Ortega et al. (2002), as given in Table 6.

4.3.2. Red horizontal branch stars analyzed with data taken from the literature: BD+09°3223 and HD 184266

Among the other RHB stars with spectroscopic data taken from the literature, two stars, BD+09°3223 (for a distance of 1.5 kpc) and HD 184266, have the highest negative values of the V0, thus indicating retrograde motion. They also have the highest values for the Galactocentric reference frame velocity. BD+09°3223 has a Galactocentric reference frame velocity (VGRF) that is very close to the escape velocity according to the Galactic potential of Ortega et al. (2002). However, it is an unbound star according to the Galactic potential of Allen & Santillan (1991), with an escape velocity of 544 km s-1. The other RHB star, HD 184266, does not leave the Galaxy according to the Galactic potential of Ortega et al. (2002). However, according to the Galactic potential of Allen & Santillan (1991), with an escape velocity of 540 km s-1, it almost does it. BD+09°3223, for a distance of 1.5 kpc, has an 83% probability of being unbound to the Galaxy according to the Galactic potential of Allen & Santillan (1991) and a 35% probability of being unbound to the Galaxy according to the Galactic potential of Ortega et al. (2002). All these findings show that CD-41°15048 and BD+09°3223 are the first hypervelocity RHB candidate stars. This adds those objects to the group of hypervelocity B stars first identified by Brown et al. (2005) and joins them to the other small group of hypervelocity cool stars, CD-62°1346 and HD 5223 (Paper I).

4.4. The orbits of CD-41°15048, HD 214362, and BD+09°3223 in the Galaxy

We also studied the dynamical orbital evolution in the Galaxy of the two RHB stars analyzed in this work and one star from the literature, BD+09°3223. We computed their orbits integrating back and forward for the two potentials considered in this work for the time interval from −2.0 to +2.0 Gyr. We integrated in time, beginning with the present distance or initial XYZ positions relative to the Sun and with current spatial velocities (UVW). As we have already mention, CD-41°15048 being at the distance of 0.7 kpc, is a bound object in any Galactic potential considered. So we show the orbits of this star for a distance of 1.3 pc. Figures 7 to 12 show the past and future orbits by considering the distance given in Table 6. The 6D position vector of the stars in the Galaxy is given by the space velocity components and their heliocentric coordinates. The velocities are given in Table 6. The Galactocentric coordinates for the three stars for which we show the orbits are X = 7.88 kpc, Y = 0.05 kpc, and Z = 1.13 kpc for CD-41°15048 (for an adopted distance of 1.3 kpc), X = 8.23 kpc, Y =  −0.18 kpc, and Z =  −0.53 kpc for HD 214362, and X = 7.38 kpc, Y =  −0.52 kpc, and Z = 0.87 kpc for BD+09°3223, at a distance of 1.5 kpc.

CD-41°15048 has an orbit that goes quite high from the Galactic plane, reaching up to Z ~ 150 kpc, while the whole trajectory, from −2.0 Gyr to 2.0 Gyr, extends from (X,Y) = ( − 55,425) to (X,Y) = ( − 190, − 400). HD 214362 has a highly eccentric orbit (e = 0.95) and is almost unbound to the Galaxy, traveling up to 50 kpc from the Galactic plane. The orbit goes up to almost 70 kpc from the Galactic disk (in the X-axis, see Fig. 9), 80 kpc from the Galactic plane. Also, due to its high eccentricity, it passes very close to the Galactic center, at a distance of 2 kpc from it. Finally, there exists the possibility that HD 214362 could have been accelerated in the region of the Galactic bulge.

thumbnail Fig. 7

Trajectory of CD-41°15048 according to the Galactic potentials of Ortega et al. (2002) (solid line) and according to the Galactic potential of Allen & Santillan (1991) (dashed line) in the XY plane. We show the whole trajectory from −2.0 Gyr to 2.0 Gyr in time for the Galactic potential of Ortega et al. (2002) while for the trajectory according to the Galactic potential of Allen & Santillan (1991) we show only a part of it from −0.5 Gyr to +0.5 Gyr. The present position is labeled with “X”.

thumbnail Fig. 9

Same as in Fig. 7, but for HD 214362 in the XY plane. For the Galactic potential of Ortega et al. (2002), the trajectory calculated from −2.0 Gyr to +2.0 Gyr starts and ends close to (X,Y) = (0,0). For the Galactic potential of Allen & Santillian (1991), we also show the beginning and the end of the trajectory. The present position is labeled with “X”.

Figures 11 and 12 also show the past and future orbit of BD+09°3223 computed for both different Galactic potentials. As we have already shown, BD+09°3223 is a star bound to the Galaxy according to the Galactic potential of Ortega et al. (2002) and an unbound star according to the Galactic potential of Allen & Santillan (1991). Since some globular clusters have a high population of RHB stars, it is also probable that BD+09°3223 and CD-41°15048 could have been ejected from one of these systems. Alternatively, they could have an extragalactic origin and were captured by the Milky Way after a tidal disruption of a nearby satellite galaxy; in that case they do not belong to the Galaxy since their velocities VGRF exceed the Galaxy escape velocity.

We have also verified how the uncertainty in the heliocentric distance and velocity propagates with time during the orbit integrations. We applied the same Monte Carlo procedure used in Sect. 4.3 to generate different initial orbits, taking into account the errors in distance and RV. Then each orbit was integrated backwards and forwards for ± 2 Gyr using the Allen & Santillan (1991) potential, and we recorded the minimum Galactocentric distance and the corresponding time of closest approach to the Galactic center. In the case of HD 214362, the orbits registered a close approach to the Galactic center at 2.9 ± 0.1 kpc around 13.8 ± 0.6 Myr (Fig. 13). But the closest approach at 1.7 ± 0.5 kpc occurred only for the bounded orbits about 1.2 ± 0.4 Gyr in the past (Fig. 14). Moreover, bounded orbits will have another closest approach at 1.5 ± 0.5 kpc around 1.2 ± 0.4 Gyr in the future.

The approaches of the orbits of CD-41°15048 to the Galactic center are at a distance of 7.8 ± 1.9 kpc, about 3 Myr in the future. Bounded orbits of this star repeated such a close approach around 1.5 ± 0.2 Gyr in the past. The case of BD+09°3223 is very similar, with a closest approach to the Galactic center at 4.3 ± 0.2 kpc, about 11 Myr in the future, and another passage at 3.7 ± 0.1 kpc, about 1.6 Gyr in the past, for the bounded orbits. Our results seem to contradict the idea of a close passage through the Galactic center as the origin of the hypervelocity of these three stars.

thumbnail Fig. 13

Distribution of the closest approaches to the Galactic center for HD 214362 at t ~ 14 Myr in the past.

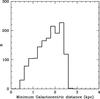thumbnail Fig. 14

Distribution of the closest approaches to the Galactic center for HD 214362 (t = 1.2 Gyr).

5. Conclusions

The results of our abundance and kinematical analysis employing high-resolution optical spectra of the two RHB stars CD-41°15048 and HD 214362 can be summarized as follows:

  • 1.

    CD-41°15048 is a metal-poor star ([Fe/H] = −1.98), with Teff = 5600 K and log gspec = 1.9. We discussed the non-LTE corrections to the spectroscopic gravity and derive the log g value of 2.0 or 2.3 after the correction considered in Sect. 3.2. It is also a RHB star, as can be deduced from its position on the (Teff, log g) diagram. CD-41°15048 and HD 214362 have abundances similar to other RHB stars previously analyzed (Simmerer et al. 2004; For & Sneden 2010).

  • 2.

    If we accept a distance of 1.3 kpc, the extreme retrograde motion of CD-41°15048 (V0    =     −546      km   s-1) would suggest that it has an extragalactic origin and was captured by the Milky Way. However, the high α-element abundances, which are typical of halo stars of this metallicity, do not support this suggestion. Nissen & Schuster (2010) showed that dwarf halo stars can be distinguished according to their [α/Fe] ratios. Those with high [α/Fe] ratios would belong to the halo population, and those with low [α/Fe] ratios may have been captured from nearby galaxies. HD 214362 has a VGRF close to the Galaxy escape velocity, making it marginally bound according to the adopted mass and hence the distance.

  • 3.

    Among other RHB stars, we found that BD+09°3223 can be bound or unbound to the Galaxy, according to the Galactic potential considered.

  • 4.

    Tidal disruption of a satellite galaxy or ejection from a globular cluster are good suggestions to explain the kinematical properties of CD-41°15048. However, the high α-element content of this star may provide a better explanation of the origin of this star. Since HD 214362 passes very close to the Galactic center, we cannot exclude the possibility that it has been influenced by a slingshot mechanism due to mass concentration in that region as well as the stars investigated by Tillich et al. (2011).

  • 5.

    CD-41°15048 is another evolved star, in addition to the CH stars CD-62°1346 and HD 5223 (Paper I), to join the restricted group of HVSs, which formerly consisted of B-type stars only. CD-41°15048 does not have an extreme RV, as usually seen among the B-type HVSs. However, the combination of its RV of 228.9 ± 0.6 km s-1 and its high proper motion for a distance of 1.3 kpc makes this star another candidate for an HVS.

  • 6.

    The calculations of the 3D dynamical orbits seem to contradict the idea that a passage of a star very close to the Galactic center is the only possible origin of the HVSs.

Online material

thumbnail Fig. 3

Abundance ratios [X/Fe] for aluminum and α-elements versus [Fe/H]. The data were taken from Luck & Heiter (2007) (black crosses); Reddy et al. (2006) (green crosses); Fulbright (2000) (red crosses); Gratton & Sneden (1991), and For & Sneden (2011) (blue crosses). CD-41°15048 and HD 214362 are represented by black squares.

thumbnail Fig. 4

Abundance ratios [X/Fe] for the iron group elements versus [Fe/H]. Symbols have the same meaning as in Fig. 3.

thumbnail Fig. 5

Abundance ratios [X/Fe] for the heavy elements. Symbols have the same meaning as in Fig. 3, except for zirconium and lanthanum. For zirconium we used the results of Edvardsson et al. (1993) (black crosses), and for lanthanum we used the results of Mishenina et al. (2006) (black crosses).

thumbnail Fig. 8

Same as in Fig. 7, but in the YZ plane.

thumbnail Fig. 10

Same as in Fig. 9, but in the YZ plane.

thumbnail Fig. 11

Same as in Fig. 7, but for BD+09°3223 in the XY plane. The present position is labeled with “X”.

thumbnail Fig. 12

Same as in Fig. 11, but in the YZ plane.

Table 1

Observed Fe i and Fe ii lines.

Table 3

Other lines studied.

Table 5

Abundance uncertainties for CD-41°15048.

1

VGRF is the velocity of a star in the Galactocentric reference frame and is defined as VGRF=U02+V02+W02\hbox{$V_{\rm GRF}=\sqrt{U_{0}^2+V_{0}^2 +W_{0}^2}$}, where U0, V0, and W0 are the star Galactocentric velocity components.

Acknowledgments

N.A.D. acknowledges the support of PCI/MCTI grant under the Project 311.868/2011-8. N.A.D. also acknowledges support of the Saint Petersburg State University, Russia, under the Project 6.38.73.2011.

References

  1. Allen, C., & Santillan, A. 1991, Rev. Mex. Astron. Astrofis., 22, 255 [NASA ADS] [Google Scholar]
  2. Alonso, A., Arribas, S., & Martínez-Roger, C. 1999, A&A, 140, 261 [Google Scholar]
  3. Aoki, W., Honda, S., Beers, T. C., et al. 2007, ApJ, 660, 474 [Google Scholar]
  4. Beers, T. C., Chiba, M., Yoshii, Y., et al. 2000, AJ, 119, 2866 [NASA ADS] [CrossRef] [Google Scholar]
  5. Behr, B. B. 2003, ApJS, 149, 101 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bessell, M. S., Castelli, F., & Plez, B. 1998, A&A, 333, 231 [NASA ADS] [Google Scholar]
  7. Biemont, E., & Godefroid, M. 1980, A&A, 84, 361 [NASA ADS] [Google Scholar]
  8. Brown, W. R., Geller, M. J., Kenyon, S. J., & Kurtz, M. J. 2005, ApJ, 622, L33 [NASA ADS] [CrossRef] [Google Scholar]
  9. Brown, W. R., & Geller, M. J., Kenyon, S. J., & Bromley, B. C. 2009a, ApJ, 690, L69 [NASA ADS] [CrossRef] [Google Scholar]
  10. Brown, W. R., Geller, M. J., & Kenyon, S. J. 2009b, ApJ, 690, 1639 [NASA ADS] [CrossRef] [Google Scholar]
  11. Carney, B. W., Latham, D. W., Stefanik, R. P., Laird, J. B., & Morse, J. A. 2003, AJ, 125, 293 [NASA ADS] [CrossRef] [Google Scholar]
  12. Carretta, E., Gratton, R., Cohen, J. G., Beers, T. C., & Christlieb, N. 2002, AJ, 124, 481 [NASA ADS] [CrossRef] [Google Scholar]
  13. Cayrel, R. 1988, Data Analysis, in The Impact of Very High S/N Spectroscopy on Stellar Physics, eds. G. Cayrel de Strobel, & M. Spite (Dordrecht: Kluwer), 345 [Google Scholar]
  14. Cayrel, R., Depagne, E., Spite, M., et al. 2004, A&A, 416, 1117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Chen, Y. Q., Zhao, G., Nissen, P. E., Bai, G. S., & Qiu, H. M. 2003, ApJ, 591, 925 [NASA ADS] [CrossRef] [Google Scholar]
  16. Cohen, J. G., Christlieb, N., McWilliam, A., et al. 2004, ApJ, 612, 1107 [NASA ADS] [CrossRef] [Google Scholar]
  17. Cohen, J. G., McWilliam, A., Shectman, S., et al. 2006, AJ, 132, 137 [NASA ADS] [CrossRef] [Google Scholar]
  18. Depagne, E., Hill, V., Spite, M., et al. 2002, A&A, 390, 187 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Drake, J. J., & Smith, G. 1991, MNRAS, 250, 89 [NASA ADS] [Google Scholar]
  20. Edvardsson, B., Andersen, J., Gustafsson, B., et al. 1993, A&A, 275, 101 [NASA ADS] [Google Scholar]
  21. For, Bi-Q., & Sneden, C. 2010, AJ, 140, 1694 [NASA ADS] [CrossRef] [Google Scholar]
  22. Fulbright, J. P. 2000, AJ, 120, 1841 [NASA ADS] [CrossRef] [Google Scholar]
  23. Gratton, R. G., & Sneden, C. 1988, A&A, 204, 193 [NASA ADS] [Google Scholar]
  24. Gratton, R. G., & Sneden, C. 1991, A&A, 241, 501 [NASA ADS] [Google Scholar]
  25. Grevesse, N., & Sauval, A. J. 1998, SSRv, 85, 161 [Google Scholar]
  26. Hills, J. G. 1988, Nature, 331, 687 [Google Scholar]
  27. Hirsch, H. A., Herber, U., O’Toole, S. J., & Bresolin, F. 2005, A&A, 444, L61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Johnson, J. A., Ivans, I. I., & Stetson, P. B. 2006, ApJ, 640, 801 [NASA ADS] [CrossRef] [Google Scholar]
  29. Kaufer, A., Stahl, O., Tubbesing, S., et al. 1999, The Messenger, 95, 8 [Google Scholar]
  30. Kurucz, R. L. 1993, CD-ROM 13, Atlas9 Stellar Atmosphere Programs and 2 km s-1 Grid (Cambridge: Smithsonian Astrophys. Obs) [Google Scholar]
  31. Lai, D. K., Bolte, M., Johnson, J. A., et al. 2008, ApJ, 681, 1524 [NASA ADS] [CrossRef] [Google Scholar]
  32. Lambert, D. L., Heath, J. E., Lemke, M., & Drake, J. 1996, ApJS, 103, 183 [NASA ADS] [CrossRef] [Google Scholar]
  33. Li, Y., Luo, A., Zhao, G., et al. 2012, ApJ, 744, L24 [NASA ADS] [CrossRef] [Google Scholar]
  34. Luck, R. E., & Heiter, U. 2007, AJ, 133, 2464 [NASA ADS] [CrossRef] [Google Scholar]
  35. Martin, W. C., Fuhr, J. R., Kelleher, D. E., et al. 2002, NIST Atomic Spectra Database Version 2.0, NIST Standard Reference Database, National Institute of Standards and Technology, Gaithersburg Maryland [Google Scholar]
  36. Mashonkina, L., Gehren, T., Shi, J.-R., Korn, A. J., & Grupp, F. 2011, A&A, 528, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. McWilliam, A. 1998, AJ, 115, 1640 [NASA ADS] [CrossRef] [Google Scholar]
  38. McWilliam, A., Preston, G. W., Sneden, C., & Searle, L. 1995, AJ, 109, 275 [Google Scholar]
  39. Mishenina, T. V., Bienaymé, O., Gorbaneva, T. I., et al. 2006, A&A, 456, 1109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Mucciarelli, A., Caffau, E., Freytag, B., Ludwig, H.-G., & Bonifacio, P. 2008, A&A, 484, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Munari, U., & Zwitter, T. 1997, A&A, 318, 269 [NASA ADS] [Google Scholar]
  42. Nissen, P. E., & Schuster, W. J. 2010, A&A, 511, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Norris, J., Bessell, M. S., & Pickles, A. J. 1985, ApJS, 58, 463 [NASA ADS] [CrossRef] [Google Scholar]
  44. Ortega, V. G., de la Reza, R., Jilinski, E., & Bazzanella, B. 2002, ApJ, 575, L75 [NASA ADS] [CrossRef] [Google Scholar]
  45. Pereira, C. B., Jilinski, E., Drake, N. A., et al. 2012, A&A, 543, A58 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2006, ApJ, 642, 797 [NASA ADS] [CrossRef] [Google Scholar]
  47. Preston, G. W., Sneden, C., Thompson, I. B., Shectman, S. A., & Burley, G. S. 2006, AJ, 132, 85 [NASA ADS] [CrossRef] [Google Scholar]
  48. Przybilla, N., Tillich, A., Heber, U., & Scholz, R. D. 2010, ApJ, 718, 37 [NASA ADS] [CrossRef] [Google Scholar]
  49. Reddy, B. E., Bakker, E. J., & Hrivnak, B. J. 1999, ApJ, 524, 831 [NASA ADS] [CrossRef] [Google Scholar]
  50. Reddy, B. E., Tomkin, J., Lambert, D. L., & Allen de Prieto, C. 2003, MNRAS, 340, 304 [NASA ADS] [CrossRef] [Google Scholar]
  51. Reddy, B. E., Lambert, D. L., & Allen de Prieto, C. 2006, MNRAS, 367, 1329 [NASA ADS] [CrossRef] [Google Scholar]
  52. Roederer, I. U., 2009, AJ, 137, 272 [NASA ADS] [CrossRef] [Google Scholar]
  53. Ruchti, G. R., Fulbright, J. P., Wyse, R. F. G., et al. 2011, ApJ, 737, 9 [NASA ADS] [CrossRef] [Google Scholar]
  54. Ruchti, G. R., Bergemann, M., Serenelli, A., Casagrande, L., & Lind, K. 2013, MNRAS, 429, 126 [NASA ADS] [CrossRef] [Google Scholar]
  55. Serenelli, A. M., Bergemann, M., Ruchti, G. R., & Casafrande, L. 2013, MNRAS, 429, 3645 [NASA ADS] [CrossRef] [Google Scholar]
  56. Simmerer, J., Sneden, C., Cowan, J. J., et al. 2004, ApJ, 617, 1091 [NASA ADS] [CrossRef] [Google Scholar]
  57. Smalley, B., Smith, K. C., Wonnacott, D., & Allen, C. S. 1996, MNRAS, 278, 688 [NASA ADS] [CrossRef] [Google Scholar]
  58. Smith, G., Edvardsson, B., & Frisk, U. 1986, A&A, 165, 126 [NASA ADS] [Google Scholar]
  59. Sneden, C. 1973, Ph.D. Thesis, Univ. of Texas [Google Scholar]
  60. Sneden, C., McWilliam, A., Preston, G. W., & Cowan, J. J. 1996, ApJ, 467, 819 [NASA ADS] [CrossRef] [Google Scholar]
  61. Stephens, A., & Boesgaard, A. M. 2002, AJ, 123, 1647. [NASA ADS] [CrossRef] [Google Scholar]
  62. Tillich, A., Przybilla, N., Scholz, R.-D., & Heber, U. 2009, A&A, 507, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Tillich, A., Heber, U., Geier, S., et al. 2011, A&A, 527, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. van Leeuwen, F. 2007, in Hipparcos, the New Reduction of the Raw Data, Astrophys. Space Sci. Libr., 350 [Google Scholar]
  65. van Winckel, H., & Reyniers, M., 2000, A&A, 354, 135 [NASA ADS] [Google Scholar]
  66. Venn, K. 1993, ApJ, 414, 316 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 2

Atmospheric parameters of CD-41°15048 and HD 214362.

In the text
Table 4

Abundance in the log ε(H) = 12.0 scale and in the notation [X/Fe].

In the text
Table 6

Atmospheric parameters (effective temperature and surface gravity), distance, radial velocity (RV), proper motions, Galactocentric velocity components (U0,   V0, W0), Galactocentric reference frame velocity (VGRF), and escape velocity (vesc) in different Galactic potentials for some RHB stars.

In the text
Table 1

Observed Fe i and Fe ii lines.

In the text
Table 3

Other lines studied.

In the text
Table 5

Abundance uncertainties for CD-41°15048.

In the text

All Figures

thumbnail Fig. 1

Spectra of CD-41°15048 (top) and HD 214362 (bottom). Absorption lines due to the transitions of Ca i 6122.23, Fe i 6137.70, and Ba ii 6141.73 are also shown. Dashed lines represent their rest wavelengths. The spectral lines are shifted towards the red by about 4.6 Å  for CD-41°15048 due to a RV of 228.9 ± 0.6 km s-1. For HD 214362, the absorption lines are shifted towards the blue by about 2.0 Å  due to a RV of −92.4 ± 0.7 km s-1.
In the text
thumbnail Fig. 2

Location of CD-41°15048 and HD 214362 in the log (Teff,log g) plane (red squares). We also show the α-enhanced horizontal branch tracks from Pietrinferni et al. (2006) at metallicity Z = 0.0003 and Y    =    0.245 for stellar masses, from top to bottom, 0.55, 0.57, 0.60, and 0.68   M⊙. Black squares represent the positions of some RHB stars analyzed by For & Sneden (2010). For CD-41°15048 we show two possible gravities after correction.
In the text
thumbnail Fig. 6

Probability distribution of the Galactic reference frame velocities for CD-41°15048. The solid vertical line represents the Galactic escape velocity according to the Galactic potential of Allen & Santillan (1991), and the dashed vertical line represents the Galactic escape velocities according to the Galactic potential of Ortega et al. (2002), as given in Table 6.
In the text
thumbnail Fig. 7

Trajectory of CD-41°15048 according to the Galactic potentials of Ortega et al. (2002) (solid line) and according to the Galactic potential of Allen & Santillan (1991) (dashed line) in the XY plane. We show the whole trajectory from −2.0 Gyr to 2.0 Gyr in time for the Galactic potential of Ortega et al. (2002) while for the trajectory according to the Galactic potential of Allen & Santillan (1991) we show only a part of it from −0.5 Gyr to +0.5 Gyr. The present position is labeled with “X”.
In the text
thumbnail Fig. 9

Same as in Fig. 7, but for HD 214362 in the XY plane. For the Galactic potential of Ortega et al. (2002), the trajectory calculated from −2.0 Gyr to +2.0 Gyr starts and ends close to (X,Y) = (0,0). For the Galactic potential of Allen & Santillian (1991), we also show the beginning and the end of the trajectory. The present position is labeled with “X”.
In the text
thumbnail Fig. 13

Distribution of the closest approaches to the Galactic center for HD 214362 at t ~ 14 Myr in the past.
In the text
thumbnail Fig. 14

Distribution of the closest approaches to the Galactic center for HD 214362 (t = 1.2 Gyr).
In the text
thumbnail Fig. 3

Abundance ratios [X/Fe] for aluminum and α-elements versus [Fe/H]. The data were taken from Luck & Heiter (2007) (black crosses); Reddy et al. (2006) (green crosses); Fulbright (2000) (red crosses); Gratton & Sneden (1991), and For & Sneden (2011) (blue crosses). CD-41°15048 and HD 214362 are represented by black squares.
In the text
thumbnail Fig. 4

Abundance ratios [X/Fe] for the iron group elements versus [Fe/H]. Symbols have the same meaning as in Fig. 3.
In the text
thumbnail Fig. 5

Abundance ratios [X/Fe] for the heavy elements. Symbols have the same meaning as in Fig. 3, except for zirconium and lanthanum. For zirconium we used the results of Edvardsson et al. (1993) (black crosses), and for lanthanum we used the results of Mishenina et al. (2006) (black crosses).
In the text
thumbnail Fig. 8

Same as in Fig. 7, but in the YZ plane.
In the text
thumbnail Fig. 10

Same as in Fig. 9, but in the YZ plane.
In the text
thumbnail Fig. 11

Same as in Fig. 7, but for BD+09°3223 in the XY plane. The present position is labeled with “X”.
In the text
thumbnail Fig. 12

Same as in Fig. 11, but in the YZ plane.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.