| Issue |
A&A
Volume 558, October 2013
|
|
|---|---|---|
| Article Number | A12 | |
| Number of page(s) | 17 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201322004 | |
| Published online | 26 September 2013 | |
Particle-physics constraints from the globular cluster M5: neutrino dipole moments ⋆
1 Pontificia Universidad Católica de Chile, Departamento de Astronomía y Astrofísica, Av. Vicuña Mackenna 4860, 782-0436 Macul, Santiago, Chile
e-mail: nviaux@astro.puc.cl
2 Pontificia Universidad Católica de Chile, Centro de Astroingeniería, Av. Vicuña Mackena 4860, 782-0436 Macul, Santiago, Chile
3 The Milky Way Millennium Nucleus, Av. Vicuña Mackenna 4860, 782-0436 Macul, Santiago, Chile
4 National Research Council, 5071 West Saanich Road, Victoria, BC V9E 2E7, Canada
5 Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), Föhringer Ring 6, 80805 München, Germany
6 Arnold Sommerfeld Center, Ludwig-Maximilians-University, Theresienstr. 37, 80333 München, Germany
7 Universidade Federal do Rio Grande do Norte, Depto. de Física, 59072-970 Natal, RN, Brazil
8 Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 85748 Garching, Germany
Received: 31 May 2013
Accepted: 19 August 2013
Stellar evolution is modified if energy is lost in a “dark channel” similar to neutrino emission. Comparing modified stellar evolution sequences with observations provides some of the most restrictive limits on axions and other hypothetical low-mass particles and on non-standard neutrino properties. In particular, a putative neutrino magnetic dipole moment μν enhances the plasmon decay process, postpones helium ignition in low-mass stars, and therefore extends the red giant branch (RGB) in globular clusters (GCs). The brightness of the tip of the RGB (TRGB) remains the most sensitive probe for μν and we revisit this argument from a modern perspective. Based on a large set of archival observations, we provide high-precision photometry for the Galactic GC M5 (NGC 5904) and carefully determine its TRGB position. On the theoretical side, we add the extra plasmon decay rate brought about by μν to the Princeton-Goddard-PUC (PGPUC) stellar evolution code. Different sources of uncertainty are critically examined. The main source of systematic uncertainty is the bolometric correction and the main statistical uncertainty derives from the distance modulus based on main-sequence fitting. (Other measures of distance, e.g., the brightness of RR Lyrae stars, are influenced by the energy loss that we wish to constrain.) The statistical uncertainty of the TRGB position relative to the brightest RGB star is less important because the RGB is well populated. We infer an absolute I-band brightness of MI = −4.17 ± 0.13 mag for the TRGB compared with the theoretical prediction of − 3.99 ± 0.07 mag, in reasonable agreement with each other. A significant brightness increase caused by neutrino dipole moments is constrained such that μν < 2.6 × 10-12 μB (68% CL), where μB ≡ e/2me is the Bohr magneton, and μν < 4.5 × 10-12 μB (95% CL). In these results, statistical and systematic errors have been combined in quadrature.
Key words: globular clusters: general / globular clusters: individual: M5 / stars: evolution / stars: interiors / neutrinos / Hertzsprung-Russell and C-M diagrams
The photometric catalog is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/558/A12
© ESO, 2013
1. Introduction
Stellar evolution theory is one of the best established and most successful theories in the history of astrophysics. Indeed, the level of agreement between the predictions of canonical stellar evolution models and observations of globular clusters (GCs), in particular their color–magnitude diagrams (CMDs), is remarkable (e.g., VandenBerg 2000; Marín-Franch et al. 2009). However, this excellent level of agreement can be spoiled if we complement standard evolution with effects caused by physics beyond the standard model, such as new weakly interacting particles. As such, GCs can be considered as one of the largest available laboratories for particle physics studies (Raffelt 1996).
The inclusion of a new energy-loss channel implies that the effective rate of local energy production of the star, ϵ = ϵnuc + ϵgrav − ϵν, will decrease according to ϵ = ϵnuc + ϵgrav − ϵν − ϵx, where ϵx is the effective rate of local energy production in the new channel. Due to the additional cooling, a red giant branch (RGB) star will be more luminous, and have a more massive degenerate He core, at the onset of helium ignition, than would be the case otherwise, thus giving rise to a brighter RGB tip (e.g., Sweigart & Gross 1978; Raffelt & Weiss 1992). The more massive He core also implies that the horizontal branch (HB) level will be more luminous (e.g., Sweigart & Gross1976; Raffelt1990; Raffelt1996; Catelan et al.1996).
Neutrino emission becomes more efficient as stars evolve. On the main sequence (core H-burning), neutrinos are primarily emitted by nuclear reactions of the proton-proton chain and CNO cycle. In advanced evolutionary phases, thermal processes dominate, notably plasmon decay, Compton processes, pair annihilation and bremsstrahlung. In low-mass stars, near the tip of the RGB (TRGB), temperatures and densities around 108 K and 106 g cm-3, respectively, are reached in the degenerate helium core (e.g., Cassisi et al. 2007; Catelan 2009). Under these conditions, plasmon decay 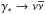 is the most important neutrino loss mechanism. It will be enhanced if neutrinos have hypothetical direct electromagnetic interactions caused by milli-charges or dipole moments (Bernstein et al. 1963). Such enhanced neutrino losses are particularly large when the plasma frequency is large and thus especially important during the RGB, asymptotic giant branch (AGB), and white dwarf (WD) phases.
is the most important neutrino loss mechanism. It will be enhanced if neutrinos have hypothetical direct electromagnetic interactions caused by milli-charges or dipole moments (Bernstein et al. 1963). Such enhanced neutrino losses are particularly large when the plasma frequency is large and thus especially important during the RGB, asymptotic giant branch (AGB), and white dwarf (WD) phases.
One particularly sensitive observable to constrain enhanced energy losses is the brightness of the TRGB in GCs (Raffelt1990; Raffelt & Weiss1992; Catelan et al.1996). Together with other observables such as the HB brightness in several galactic GCs, it was found that the core mass at He ignition should not exceed its standard value by about 0.025 M⊙ or 5% of its standard value, which in turn means that the full plasmon decay rate should not exceed its standard value (Haft et al. 1994) by more than a factor of 3. These results translate into a limit on the neutrino dipole moment of about μν < 3 × 10-12 μB, where μB ≡ e/(2me) is the Bohr magneton, much more stringent than corresponding laboratory limits (Beringer et al.2012). Similar arguments have been used to constrain novel energy losses by other novel low-mass particles, including axions, milli-charged particles, Kaluza-Klein gravitons and others (for a review see Raffelt 1999).
Most of these tests of novel particle physics have not benefited from the newly available, exquisite CMDs that have become available only recently, both based on ground- and space-based observations (e.g., Bergbusch & Stetson 2009; King et al. 2012). These previous tests were also performed before the revolution in opacity tables and equations of state (EOS) of the mid-1990 s and therefore relied on older tables (Sweigart 1973; Cox & Stewart 1970; Hubbard & Lampe 1969). In addition, the analysis of systematic and statistical errors was not detailed enough to assign a clear quantitative confidence level to the derived constraints, making it difficult to compare with laboratory results.
The main goal of our work is accordingly to use state-of-the-art astronomical observations and stellar evolution codes, in order to obtain new constraints on novel properties of particle physics, with a more objective assessment of the confidence level on the derived constraints. Our main result, a new limit on μν, will be similar to previous astrophysical limits if the latter are interpreted as 1σ constraints. However, our new result is based on homogeneous observations of a single GC and based on a detailed error budget.
To achieve this goal, we first provide in Sect. 2 a new CMD for the GC selected for this study, namely M5 (NGC 5904), based on archival observations. We then briefly describe the stellar evolution code used in our theoretical calculations (Sect. 3). The errors due to observational and theoretical sources are discussed in Sects. 4 and 5. In Sect. 6 we compare observations with theoretical models to set constraints on μν. Our conclusions are drawn in Sect. 7. In future papers, we plan to extend our analysis to other GCs and consider other particle properties, notably those of the hypothetical axion.
2. Observational framework
2.1. Cluster selection
In principle, each of the fully resolved and well-populated Milky Way GCs could be useful for our study. However, to derive the most meaningful particle-physics constraints, we impose stringent criteria on the properties of the selected GC, providing us with clean CMDs and straightforward interpretation of the results. First, we require that the cluster be sufficiently massive, with an absolute magnitude satisfying MV < − 8.0 mag, so as to ensure a sufficiently well-populated CMD1. Second, we restrict the amount of foreground reddening to a maximum of E(B − V) = 0.1 mag, which also helps reduce the possibility of significant differential reddening towards the cluster. Third, we make sure that the cluster metallicity is neither too high nor too low, leading to a fairly uniformly populated HB, thus avoiding GCs with extremely red or blue HB morphologies. Fourth, candidates must be sufficiently close that deep, high-quality photometric data are available. Last but not least, we avoid GCs for which there is strong evidence of multiple CMD sequences, and in particular, those for which the level of internal variation in the He abundance has been suggested to be high (Gratton et al. 2010). Note that the TRGB is unaffected from the O-Na anomaly that is present in GCs (Salaris et al. 2006).
This leaves us with a much reduced set of GCs, with M5 at the top of our list. This is a well-studied, fairly massive cluster, with MV = −8.81 mag, a moderate metallicity of [Fe/H] = −1.29, and a foreground reddening of only E(B − V) = 0.03 mag. The distance modulus of the cluster is (Layden et al. 2005)  (1)which corresponds to a modest distance of 7.5 kpc from the Sun. The cluster distance to the Galactic center is about 6.2 kpc2.
(1)which corresponds to a modest distance of 7.5 kpc from the Sun. The cluster distance to the Galactic center is about 6.2 kpc2.
Most importantly for our purposes, the recent, detailed spectroscopic and photometric study by Gratton et al. (2013) reveals no evidence for a significant internal spread in the He abundance, except perhaps for the component of the cluster that falls on the extreme blue end of its HB – which, according to the analysis by Gratton et al. (2010), could be enhanced in He by a maximum of ΔY ≈ 0.03. This is to be compared with much higher levels of He enhancement suggested for other GCs, such as NGC 2808 and ω Centauri = NGC 5139, which may reach ΔY ≈ 0.14 (e.g., King et al. 2012; Milone et al. 2012, and references therein).
Accordingly, we will focus on M5, and in future extend our study to other GCs in the reduced sample just described.
2.2. Data acquisition and photometry
We have carried out crowded-field, point-spread function (PSF) photometry for M5 using the DAOPHOT II/ALLFRAME suite of programs (Stetson 1987, 1994). For this purpose we have amassed an extensive database comprised of data sets obtained from many different sources, including public archives. This effort represents a continuation of previous similar work that was carried out for other GCs (see Stetson 2009, for a review and references).
The current corpus of observations for M5 consists of 2840 CCD images obtained during 40 observing runs on 12 telescopes over a span of 27 years. Details of the observations are provided in Table 1. The measurements were contained in 147 separate data sets, each of which was individually transformed to the photometric system of Landolt (1992) as described elsewhere (e.g., Stetson 2000, 2005). In the case of the M5 observations, 114 of the data sets were reduced in photometric (all-sky) mode, while the remaining 33 were reduced in non-photometric (local) mode.
NGC 5904 observations.
It should be noted that detectors of different projected areas were directed at various pointings in the cluster. Furthermore, each of the Optical Imager Galileo on Telescopio Nazionale Galileo and the SOAR Optical Imager on the Southern Astrophysical Research telescope consists of a pair of non-overlapping CCDs; the Wide Field Camera on the Isaac Newton Telescope contains four detectors; and the Wide Field Imager on the Max Planck Gesellschaft/European Southern Observatory telescope contains eight (“Multiplex” column in Table 1). As a result, no individual star appeared in all the images. In fact, the greatest number of independent observations for any star was 34 in the U band, 77 in B, 134 in V, 35 in R, and 128 in I.
Figure 1a shows the derived CMD which is clearly contaminated with field stars. We remove the field component with a statistical decontamination, using the method described in Gallart et al. (2003). The cleaned CMD is shown in Fig. 1b.
 |
Fig. 1 Color–magnitude diagram of M5. Left: original. Right: after field star decontamination. |
Details and uncertainties regarding the calibration and the possibility of saturation close to the TRGB will be discussed further in Sect. 4.
2.3. Finding the TRGB
2.3.1. RGB and AGB stars in M5
One of our main points of interest is the TRGB. For Milky Way GCs it is not trivial to identify this point in the CMD because the evolution close to the TRGB is fast, and accordingly this region of the CMD is thinly populated. The brightest RGB star, apart from small photometric errors, provides a lower limit to the brightness of the TRGB. Therefore, one task is to identify the brightest RGB star in M5. Moreover, we need to estimate the likely brightness difference Δtip = I1 − ITRGB between the TRGB (ITRGB) and the brightest star (I1) in the I-band, or rather, the probability distribution for Δtip in view of the overall RGB population.
In order to evaluate this statistical distribution we first show, in Fig. 2, the upper CMD for M5. The RGB and AGB are well separated and we assign nominal membership to one of these branches based on the distance of a given star from the RGB. As a first possibility to describe the locus of the RGB we have tried an isochrone which here is identical to the evolutionary track of a star with our benchmark parameters (see the solid line in Fig. 2. However, it does not provide a good fit near the TRGB. We prefer to use a simple empirical fit function of the form ![\begin{equation} \label{eq:RGBfit} I=I_0+3.83\,[1.95 - (V-I)]^{2.5} \end{equation}](/articles/aa/full_html/2013/10/aa22004-13/aa22004-13-eq35.png) (2)shown as a solid line. We use I0 = I1 − 0.04 mag = 10.289 mag where I1 = 10.329 mag refers to the brightest star.
(2)shown as a solid line. We use I0 = I1 − 0.04 mag = 10.289 mag where I1 = 10.329 mag refers to the brightest star.
 |
Fig. 2 Upper part of the CMD for M5. Nominal identification of RGB and AGB stars as explained in the text. Solid line: RGB track with initial parameters described in Sect. 3.2. Dashed line: Nominal RGB according to the fit function of Eq. (2). |
The crest value I0 of our fit function is 0.04 mag brighter than the brightest star and a reasonable first estimate for ITRGB. Therefore, we think of I0 as our provisional TRGB and study the distribution of stars relative to this reference point. We cut the CMD at 2.5 mag below I0, safely away from the HB and the RGB bump, yet including as many as 136 stars. Had we used the brightest star as a reference point, a 2.5 mag interval would have reached 0.04 mag dimmer, including 5 more stars. In other words, our somewhat arbitrary choice of reference point has only a minor impact on the overall statistics.
We next determine the distance Δ of every star in our remaining ensemble relative to our reference line. In Fig. 3 we show the star distribution as a function of Δ. Note that the horizontal scale in Fig. 3 (in magnitudes) is strongly expanded relative to the vertical scale, i.e., the RGB is almost vertical. In this sense, Δ is essentially the color difference to the reference line, except near the TRGB, where this line becomes almost horizontal.
Our reference line tracks the RGB very well indeed and the AGB and RGB are well separated. Stars with Δ < −0.04 are almost certainly on the AGB whereas those with −0.02 < Δ are almost certainly on the RGB. In addition, there are six stars almost lined up at Δ = −0.03 (dashed line) where the association with one of the branches is not obvious. We use the dashed line as a formal separation – in this way these six stars are equally divided. With this choice, we find NRGB = 95 and NAGB = 41.
 |
Fig. 3 Distance Δ from our RGB reference line of Eq. (2) and distribution of stars as a function of Δ. |
 |
Fig. 4 Top: luminosity functions of RGB (filled histogram) and AGB. Thick black line: expectation from evolutionary speed. Dashed lines: fit to data. Bottom: cumulative luminosity function for RGB stars (in blue) and AGB stars (in red) and fit functions for each case. |
Next we show the I-brightness distribution of our RGB and AGB stars in Fig. 4. From an evolutionary RGB track (described in Sect. 3.2) we can predict this distribution from the evolutionary speed (dI/dt)-1 shown as a black thick solid line in the upper panel. The evolution accelerates as the star ascends the RGB, corresponding to fewer bright stars. Just before reaching the TRGB, the brightness increase slows down, reaches a peak, and then quickly drops. Therefore, (dI/dt)-1 has a cusp at the TRGB.
In our brightness range, and ignoring this cusp, the theoretical distribution is rather well represented by a function of the form ![\begin{equation} \label{eq:distributionfit} \frac{{\rm d}N_{\rm RGB}}{{\rm d}I}=N_{\rm RGB}\,\left[a + b\,(I-I_0)^2\right], \end{equation}](/articles/aa/full_html/2013/10/aa22004-13/aa22004-13-eq46.png) (3)shown as a dashed line. The corresponding cumulative distribution looks even more similar to the one from the numerical evolution speed. The requirement that the distribution is normalized to the total number of stars in our 2.5 mag brightness interval relates the coefficients as b = 12 (2 − 5a)/125 and numerically we find a = 0.177 and b = 0.107.
(3)shown as a dashed line. The corresponding cumulative distribution looks even more similar to the one from the numerical evolution speed. The requirement that the distribution is normalized to the total number of stars in our 2.5 mag brightness interval relates the coefficients as b = 12 (2 − 5a)/125 and numerically we find a = 0.177 and b = 0.107.
For the AGB, we do not have a good theoretical prediction because the evolution is strongly affected by mass loss. A function of the form of Eq. (3) with a = 0.0787 and b = 0.154 is a reasonable fit (Fig. 4). Our overall number of AGB stars is roughly half of the RGB, but the AGB stars die out more quickly toward the TRGB. In the 1 mag brightest interval we have 5 AGB stars (including two that might be questionable) and 23 RGB stars, i.e., the random chance that a star in the top brightness range is an AGB star is roughly 18%. This approximate fraction also derives from our fit parameters a and the total number of stars as aAGBNAGB/(aAGBNAGB + aRGBNRGB) = 16%.
2.3.2. TRGB relative to brightest star
In order to derive a probability distribution for ΔTRGB = I1 − Itip we have used the results of the previous section and have performed Monte Carlo simulations of the star distribution in the I-band. We use 95 RGB stars in our 2.5 mag fiducial interval, following on average the theoretical distribution, i.e., the thick black line in Fig. 4. The observed distribution in M5 agrees very well with this expectation, i.e., it looks like a typical random realization of the expected distribution.
In Fig. 5 we show the Δtip distribution from a large number of Monte Carlo realizations. It is well approximated by an exponential plus a cusp, reflecting the cusp of (dI/dt)-1 near the TRGB. A good analytic representation, normalized to unity, is 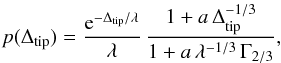 (4)where Γ2/3 ≈ 1.3541 is the Gamma function at argument 2/3, λ = 0.068 mag represents the exponential decline, and a = 2.30 mag1/3 the cusp contribution.
(4)where Γ2/3 ≈ 1.3541 is the Gamma function at argument 2/3, λ = 0.068 mag represents the exponential decline, and a = 2.30 mag1/3 the cusp contribution.
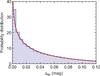 |
Fig. 5 Probability distribution for Δtip = I1 − ITRGB between the TRGB and the brightest star. The histogram is from a Monte Carlo simulation, the red line is the analytic representation of Eq. (4). |
Additional neutrino cooling caused by μν shifts the TRGB to brighter values and in this way changes the expected brightness distribution relative to the TRGB. Repeating our exercise with evolutionary tracks for the relevant range of μν values, we find only small modifications of the implied parameters λ and a. Likewise, we have repeated this exercise for other BC prescriptions and also find only a small influence.
We conclude that in M5, almost independently of μν and the BC used (see Sect. 5), the TRGB is within 0.05 mag (68% CL), and within 0.16 mag (95% CL) of the brightest star. Moreover, the average value and rms variance are 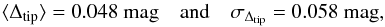 (5)respectively. Note that the distribution is very asymmetric and σtip is the formal rms variance, not a Gaussian error.
(5)respectively. Note that the distribution is very asymmetric and σtip is the formal rms variance, not a Gaussian error.
2.3.3. Identifying the brightest RGB star in M5
What remains is to identify the brightest RGB star in M5. Our selection based on color suggests that the brightest stars are on the RGB, although our empirical track was somewhat constructed in this way. Based on distance from the isochrone (solid line in Fig. 2), however, would put even more of the brightest stars on the RGB. Still, this assignment may not be entirely trustworthy. Of course, the paucity of AGB stars alone tells us that it is extremely unlikely that the brightest stars are all on the AGB. Another possibility for discrimination is based on chemical abundance variation. In Table 2 we list the identification of the three brightest stars by different authors.
Evolutionary state for the brightest stars in M5.
All evidence points to the brightest star in M5 being on the RGB. If this were not the case after all, we should use the second or third brightest star. The TRGB would then be found dimmer by 0.034 or 0.091 mag, allowing for less novel particle emission. Therefore, assuming the brightest star to be on the RGB is conservative for the purpose of deriving particle-physics limits.
Madore & Freedman (1995) tested four possible observational problems (photometric errors, crowding, contamination by field stars, and population size) that can affect the empirical determination of the TRGB in globular clusters and nearby galaxies. Specifically, using bins of 0.1 mag, there is claimed that, in order to have a precision of 0.1 mag, are required a signal-to-noise ratio greater than 5, a crowding with 25% in the first three magnitudes, no more than 20 field stars per bin, and a minimum of 100 stars in the brightest bin. Even though these are good tests, observations and decontamination techniques have had huge improvements during the last two decades that CMD of GCs show narrow stellar populations (Sandquist & Bolte 2004). In particular, using present-day observations is possible to define the minimum luminosity of the TRGB with high precision if the identification of the brightest RGB stars is done thoroughly, as is the goal of Sect. 2.3.2.
3. Theoretical framework
3.1. Neutrino emission rate
Throughout this paper we use the Princeton-Goddard-PUC (PGPUC; Valcarce et al. 2012) code in our evolutionary calculations. Our benchmark tracks do not implement mass loss on the RGB. The dominant neutrino emission process on the RGB evolution is plasmon decay for which PGPUC uses the analytic approximation formulas of Haft et al. (1994).
To incorporate μν effects, we follow the procedure prescribed by Raffelt & Weiss (1992), i.e., we scale the standard plasmon emission rate by the prescription given in their Eqs. (9) and (10). The discussion of standard and nonstandard plasma emission rates of Haft et al. (1994) reveals that the error introduced by this simple prescription can be around 10% for the relevant conditions and is therefore not crucial for deriving bounds on μν.
3.2. Modified stellar models
To show the effects of different μν values, we compute evolutionary tracks with an initial mass of M = 0.82 M⊙, Y = 0.245, Z = 0.00136, and [α/Fe] = + 0.30 for the range μν = (0–9) × 10-12 μB. The initial parameters (M, Y, Z, and [α/Fe]) were chosen according to the following criteria:
-
For the metallicity we adopt[Fe/H] = −1.33 ± 0.02 dex, from Carretta et al. (2009, see also Koch & McWilliam 2010. With an abundance of the α-capture elements given by [α/Fe] = + 0.30 (Lai et al. 2011), this gives a global metallicity value of Z = 0.00136 for M53.
-
The He abundance was selected assuming that M5 is sufficiently metal-poor that no significant He enhancement took place before the formation of its stars. Thus a He abundance close to the primordial nucleosynthesis value (e.g., Izotov et al. 2007 ; Steigman 2007 , 2012 ) is applicable, as indeed favored by detailed CMD studies of Galactic GCs (e.g., Salaris et al. 2004 ).
-
The mass of the star at the TRGB (M = 0.82 M⊙) corresponds to what is expected for the adopted chemical composition and an age similar to the age of the Universe, currently estimated at 13.8 Gyr (Komatsu et al. 2011).
Figure 6 shows our evolutionary tracks close to the TRGB, where the μν effects become important. For our later comparison with observational data, we transform the relative luminosity L/L⊙ into I-band absolute brightness using the bolometric corrections of Worthey & Lee (2011). The results, presented in Fig. 7, can be expressed in terms of a simple analytic fit formula, 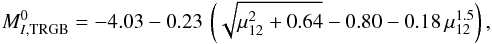 (6)where μ12 = μν/10-12 μB.
(6)where μ12 = μν/10-12 μB.
 |
Fig. 6 PGPUC evolutionary tracks around the TRGB for the indicated values of μν, where μ12 = μν/10-12 μB. |
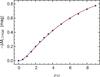 |
Fig. 7 I-band brightness increase of the TRGB corresponding to the modified tracks shown in Fig. 6. We also show the analytic approximation formula of Eq. (6). |
As explained in the earlier literature (Raffelt1990, Raffelt & Weiss1992, Catelan et al.1996), the dominant effect of increased neutrino losses on the upper RGB is to allow the degenerate He core to grow to a somewhat larger mass. In this sense the effects of novel energy losses can be expressed in terms of the core mass at He ignition which, in turn, determines the brightness at the TRGB. We here prefer to discuss our results directly in terms of μν, but for comparison we provide the core-mass increase in terms of an analytic fit formula ![\begin{equation} \label{eq:coremass} \Delta M_{\rm core}=0.023\,M_\odot\, \left[\sqrt{\mu_{12}^2+1.05^2}-1.05-0.16\,\mu_{12}^{1.5}\right]\,. \end{equation}](/articles/aa/full_html/2013/10/aa22004-13/aa22004-13-eq80.png) (7)This result is very similar to Eq. (11) of Raffelt & Weiss (1992) in spite of the slightly different input parameters, EOS, and opacity tables used.
(7)This result is very similar to Eq. (11) of Raffelt & Weiss (1992) in spite of the slightly different input parameters, EOS, and opacity tables used.
4. Observational uncertainties
4.1. Cluster distance
As a next step we examine observational uncertainties affecting our results and begin with the cluster distance. According to Table 4 in Coppola et al. (2011), previous distance determinations for M5 fall in the range 14.32 ≤ (m − M)0 ≤ 14.67. A weighted mean over the results compiled in their Table 4, but including also their own distance determination, gives for the cluster a distance modulus of (m − M)0 = 14.43 ± 0.02 mag. However, several of these distances are based on HB and RR Lyrae stars, whose properties also depend on the presence of additional cooling in their RGB progenitors. Therefore, to avoid circular reasoning, we rely only on the distance determinations which do not depend on evolved distance indicators which may be affected by the cooling process which we want to constrain, as is the case with HB, RR Lyrae, and WD stars.
We thus adopted the distance modulus Eq. (1) derived via main-sequence fitting by Layden et al. (2005). This result and corresponding error 0.11 already take into account interstellar extinction. This distance modulus is in excellent agreement with the weighted mean value derived above, on the basis of different distance indicators.
To check if the adopted distance modulus is consistent with our model calculations, in Fig. 8 we overplot a ZAHB locus, computed with PGPUC for the adopted chemical composition and age, on the HB region of the M5 CMD, under different assumptions for the distance modulus. We can see that the adopted distance modulus does appear to provide a reasonable approximation to the lower envelope of the observed HB distribution.
 |
Fig. 8 PGPUC ZAHB loci for different assumptions on the distance modulus overplotted on the HB region of M5. Variable stars from the Clement et al. (2001) catalog are plotted in yellow. |
4.2. Photometric calibration
Stetson (2005) has revised the photometric calibration of the standard fields that are used to calibrate our M5 photometry. In particular, this author performs a comparison with Landolt’s (1992) standard fields, finding that the difference between Landolt’s system and the adopted calibration is not larger than 0.02 mag in the I-band (see Fig. 1 of Stetson 2005).
4.3. Saturation
In Stetson et al. (2003), the image-quality index χ is defined, which shows us the level of agreement between the perceived brightness profile for an object and the model PSF for the frame where this object is measured. Reliable stars should have χ ≈ 1, while significantly larger values of χ indicate nonstellar objects or profiles corrupted by image defects.
This paper also defines the sharp index, which is a first-order estimate of the intrinsic angular radius of a resolved source. For reliable stars, sharp should be around zero.
In Fig. 9 we plot sharp and χ vs. the I-band magnitude for our M5 photometry. The three brightest stars are shown as red triangles. They are reliable based on these arguments. In particular, if saturation were present we would have expected large values for sharp and χ, but this is not seen in our data.
 |
Fig. 9 Sharp (upper panel) and χ (lower panel). Red triangles: three brightest stars. |
If saturation were present, we might also expect large errors in the derived I-band magnitudes. In Fig. 10 we plot these errors vs. the I magnitudes themselves. Again the three brightest stars are shown as red triangles. Their errors are all less than 0.0064 mag. Since the sharp, χ and σ(I) values for the three brightest stars are all small, these stars appear not to be saturated and can accordingly be safely used in our study.
 |
Fig. 10 Photometric error σ(I). Red triangles: three brightest stars. Inset: zoom around the brightest stars. The vertical plume of points at I ≈ 14.5 mag consists of the RR Lyrae variables. |
On the other hand, we have also examined the individual I-band magnitude measurements for each of these brightest stars, and found that the rms deviation of one measurement is, in each case, around 0.05 mag. This is larger than the observational scatter for stars that are a few magnitudes fainter, as is reflected in the increase in σ for magnitudes brighter than I ≈ 12 in Fig. 10. An increase in photometric uncertainties for the very brightest stars is commonly seen in DAOPHOT reductions, and may be due to incipient saturation: when individual pixels in a star image approach or exceed the known saturation level of the detector, the software attempts to estimate the star’s brightness by fitting the model PSF only to unsaturated pixels in the flanks and wings of the stellar profile. Since these magnitude estimates are based on fewer pixels, and on pixels that are less sensitive to brightness than the central pixels of fainter stars, these brightness determinations are noisier than those obtained for fainter stars. In the case of the three brightest giants in M5, we find that the measured magnitudes, while noisy, are not correlated with telescope aperture or exposure time. We infer that the DAOPHOT software’s treatment of incipient saturation – while subject to greater noise – is not significantly biased in these particular images. There are enough independent measurements of the I-band magnitudes for each star that, despite the increased observation-to-observation dispersion, the standard error of the mean magnitude is still estimated to be well under 0.01 mag in each case.
 |
Fig. 11 Radial distance (in arcmin) vs. I-magnitude for different kinds of errors in V − I. Red triangles: three brightest stars. |
4.4. Completeness and crowding
Incompleteness is unlikely at the bright CMD levels that we are considering in this study. However, to help us confirm that incompleteness can be safely ignored, in Fig. 11 we plot the radial distance in arcminutes (between the center of M5 and each star) versus the I-band magnitude for different ranges of photometric errors. As an upper limit for photometric errors in color we set 0.05 < σ(V − I) < 0.1, since for higher errors the photometry cannot be considered reliable. This range is plotted as blue points. They can be taken as defining a reference locus beyond which our photometric catalog can be considered incomplete. Consistent with expectations, this reference locus is flat at large distances from the cluster center, but moves towards brighter magnitudes as one approaches the core. Stars much brighter than this reference locus can be considered effectively complete at that radius. Stars near the reference locus can be considered more than normally unreliable and probably incomplete, whereas stars much fainter than the reference locus are impossible to measure at that radius. Our catalog is virtually 100% complete down to the HB level (where the RR Lyraes are) all the way to the center of the cluster. Outside of r = 3–4 arcmin, the catalog is virtually complete to I = 21 mag. As expected, the brightest stars in our sample, marked as red triangles in Fig. 11, are much brighter than the level at which incompleteness kicks in. We thus conclude that our TRGB measurements are not affected by incompleteness.
On the other hand, and again as can be seen in Fig. 11, the three brightest red giants in M5 fall quite close to the cluster center (recall that M5’s half-light radius is 1.77 arcmin; Harris 1996,2010 update), and can thus be plausibly affected by crowding. To look further into this possibility, we have examined images from the Hubble Space Telescope’s Advanced Camera for Surveys (HST/ACS) archives. Looking at the three brightest stars in a stacked HST/ACS Wide-Field Camera image, we see no stars that are both within one or two arcseconds and within approximately five magnitudes of the stars in question. Therefore, we do not expect contamination in excess of one per cent or so, which is essentially negligible for our purposes.
4.5. Differential reddening
The amount of foreground reddening in the direction of M5 is quite low, and a large amount of differential reddening that could change the relative position of stars in the CMD and lead to wrong identifications of RGB/AGB stars, is therefore unlikely. To see if differential reddening is present in M5 at a level that might affect our measurements, in Fig. 12 we divide the observed cluster field in four parts, producing separate CMDs for each quadrant as shown in Fig. 13, color–coded according to Fig. 12. Overplotting the CMD for all four quadrants with our empirical RGB fit of Eq. (2) in Fig. 13 reveals that the same fiducial line properly describes all four quadrants. In addition, the giant branches are narrow, consistent with the photometric errors. We thus conclude that no significant amount of differential reddening is present in the direction of the cluster.
 |
Fig. 12 Differential reddening test. Here we show the four different quadrants of the cluster that were selected to produce the CMDs shown in Fig. 13. Black triangles denote the position of the three brightest cluster stars, with their sizes proportional to their apparent brightness. |
To further verify this conclusion, we have examined the COBE/DIRBE dust maps provided by Schlegel et al. (1998). Within a circle of 5 arcmin radius centered on M5, the minimum and maximum values of E(B − V) estimated from 100-micron dust emission are 0.0359 and 0.0398 mag, respectively – again confirming the lack of significant differential extinction across the face of the cluster.
 |
Fig. 13 Color–magnitude diagrams for the different quadrants shown in Fig. 12 with the same color coding. The black line in all panels corresponds to the empirical RGB fit of Eq. (2). |
4.6. Summary
The observational TRGB brightness is that of the brightest star I1 given in Table 2, shifted by the estimated average brightness difference between TRGB and brightest star ⟨ Δtip ⟩ of Eq. (5), and corrected with the distance modulus of Eq. (1), i.e.,  . The error of I1 is σI = 0.023, which is ± 0.0057 mag added in quadrature with the error of the calibration of the photometry ± 0.02 mag (Sect. 4.2). Saturation, completeness, and crowding combined likely contribute less than ± 0.01 mag to σI (Sects. 4.3 and 4.4). The statistical error of the estimation of the TRGB relative to I1 is σΔtip = 0.058. The largest error, σm − M = 0.11, is that of the distance modulus. Overall we thus find
. The error of I1 is σI = 0.023, which is ± 0.0057 mag added in quadrature with the error of the calibration of the photometry ± 0.02 mag (Sect. 4.2). Saturation, completeness, and crowding combined likely contribute less than ± 0.01 mag to σI (Sects. 4.3 and 4.4). The statistical error of the estimation of the TRGB relative to I1 is σΔtip = 0.058. The largest error, σm − M = 0.11, is that of the distance modulus. Overall we thus find 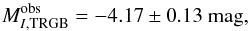 (8)where we have added the errors in quadrature. Note that this is appropriate even though the quantity Δtip has a very asymmetric distribution because, after convolution with the broad Gaussian distance error distribution, we again have essentially a Gaussian with a shifted mean and variance obtained by adding the variances of the convolved distributions.
(8)where we have added the errors in quadrature. Note that this is appropriate even though the quantity Δtip has a very asymmetric distribution because, after convolution with the broad Gaussian distance error distribution, we again have essentially a Gaussian with a shifted mean and variance obtained by adding the variances of the convolved distributions.
5. Theoretical uncertainties
We next address uncertainties that affect the predicted TRGB I-band absolute magnitude MI,TRGB. Our benchmark model parameters were described in Sect. 3. We use the bolometric correction (BC) of Worthey & Lee (2011) which cover the range log g < 0, which is not the case for most other BC prescriptions. Moreover, Worthey & Lee (2011) provide error estimates that we can use in our assessment and, within this error estimate, agree with other BC prescriptions.
 |
Fig. 14 Evolutionary tracks in the MI, V − I plane are shown for different: a) Mass values, b)Y values, c)Z values, d) [α/Fe] ratios. The insets at the lower-right corner of each panel show zoom-ins around the TRGB position (note the different scales used in the different insets). |
5.1. Selected mass
As mentioned in Sect. 3, we have selected an RGB mass of 0.82 M⊙, as appropriate for the adopted chemical composition and an age of about 13.8 Gyr. Uncertainties in GC ages remain significant. For instance, Dotter et al. (2010) estimate for M5, on the basis of HST/ACS images, an age of 12.25 ± 0.75 Gyr. However, changing the age by ± 1 Gyr changes the mass of the star at the TRGB by only about ± 0.015 M⊙. Here we evaluate the level of uncertainty in MI,TRGB brought about by a generous uncertainty in age of 1.5 Gyr. Selecting masses of 0.80 M⊙ and 0.85 M⊙ (see Fig. 14a), we obtain 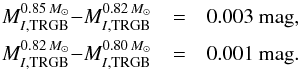 We conclude that uncertainties in the age, and thus in the RGB mass, affect MI,TRGB at the level of about ± 0.002 mag only.
We conclude that uncertainties in the age, and thus in the RGB mass, affect MI,TRGB at the level of about ± 0.002 mag only.
5.2. Helium abundance
The He abundance Y is uncertain for several reasons, including statistical and systematic errors in the primordial He abundance Yp (e.g., Aver et al. 2010, and references therein) and the He enrichment parameter ΔY/ΔZ (e.g., Valcarce et al. 2012, and references therein). The primordial He abundance is most strongly constrained by studies of extragalactic H ii regions. Based on several recent such studies (e.g., Izotov et al. 2007; Izotov & Thuan 2010; Aver et al. 2010), we estimate a range of uncertainty in the primordial He abundance of 0.230 < Yp < 0.260. At the relevant metallicity Z, the error arising from uncertainties in ΔY/ΔZ is negligible in comparison. The impact of variations in Y at this level upon the TRGB position is shown in Fig. 14b. We conclude that MI,TRGB changes by about ± 0.010 mag for a change in Y by ± 0.015.
5.3. Iron abundance
As explained in Sect. 3, we have adopted an iron abundance with respect to the Sun [Fe/H] = −1.33 ± 0.02 dex, from Carretta et al. (2009). The level of uncertainty in the cluster’s [Fe/H] value was critically evaluated by Koch & McWilliam (2010), who recommended a value [Fe/H] = −1.33 ± 0.02(stat.) ± 0.03(syst.) dex. Indeed, the increased error bar appears to better accomodate other recent [Fe/H] determinations, including Lai et al. (2011) and Saviane et al. (2012). Assuming [α/Fe] = + 0.3 (see Sect. 5.4), the error associated to the iron abundance σ[Fe/H] = ± 0.036 dex translates into an error in the global metallicity of σZ = ± 0.00011. However, the uncertainty in the solar metallicity proper (see Catelan 2013, for a review and references) also adds up to the budget, leading to a final uncertainty estimate in Z of ± 0.00035. The impact of variations in Z at this level upon the TRGB position is shown in Fig. 14c. This leads to a change in MI,TRGB of + 0.070 mag, which, perhaps somewhat surprisingly, is positive for both the higher and lower Z values, possibly due to the substantial curvature of the TRGB in the CMD.
5.4. [α/Fe] ratio
As explained in Sect. 3, we have adopted an α-element-to-iron enhancement ratio of [α/Fe] = + 0.3 (for fixed [Fe/H] this therefore increases the value of Z of the models), based on Lai et al. (2011). Based on this latter study, one can estimate a reasonable uncertainty in this ratio of about ± 0.1, ignoring the oxygen determinations during to their large associated errors. Figure 14d shows a comparison between evolutionary tracks with different [α/Fe] values covering this range. An increment in [α/Fe] implies a fainter TRGB, as found by Cassisi et al. (2004). We finally estimate a 1σ error in MI,TRGB of ∓0.0044 mag.
 |
Fig. 15 As in Fig. 14, but for different: a)αMLT values, b) treatment of diffusion, c) boundary conditions, d)κr values. |
5.5. Mixing-length parameter, overshooting and diffusion
In spite of its limitations (e.g., Ludwig & Kučinskas 2012), we have adopted the mixing-length theory (MLT) as described in Valcarce et al. (2012). In other words, following the usual procedure, the mixing-length parameter αMLT of convection theory has been fixed to reproduce the present-day solar parameters, allowing for a quite satisfactory match of the CMDs of GCs over a wide range of metallicities (e.g., Freytag & Salaris 1999; Palmieri et al. 2002; Ferraro et al. 2006; VandenBerg et al. 2008; Cassisi 2012, and references therein). From such studies, an uncertainty of ± 0.1 in αMLT (for a given evolutionary code) appears reasonable (see Salaris et al. 2002).
In addition, an uncertainty due the calibration of αMLT is needed. In Valcarce et al. (2012), αMLT was calibrated without atomic diffusion, but it is known that the sound-speed profile of the Sun agrees better with helioseismological data if one includes atomic diffusion (see Sect. 5 of Pietrinferni et al. 2004). The difference between αMLT calibrated with and without diffusion is approximately 0.1 from the GARSTEC stellar evolution code (Weiss & Schlattl 2008) and S. Cassisi (priv. comm.).
We finally adopt an uncertainty of ± 0.2. Note that such changes in αMLT also affect the amount of He that is dredged up as a consequence of the first dredge up episode. The tracks computed for different αMLT values (Fig. 15a) reveal that an uncertainty of ± 0.2 in αMLT changes MI,TRGB by ∓ 0.056 mag.
According to Ludwig & Kučinskas (2012), overshooting needs to be included to bring MLT models into agreement with 3D simulations of the outer layers of RGB stars. In this sense, overshooting had previously also been suggested as a means to reconcile predicted and observed positions of the RGB luminosity function “bump” (see Salaris et al. 2002, for a review and references to early work and also Cassisi2012, for a more recent review). Typically, overshooting is modeled, as an extension of the MLT formalism, by extending the formal boundary of the convective zone by a fraction (typically around 20–25%; e.g., VandenBerg et al. 2006; Cassisi et al. 2011, and references therein) of the local pressure scale height. In this way, it can be anticipated that uncertainties in the treatment of overshooting will play a minor role, compared with the uncertainty in αMLT proper, as far as the TRGB position goes. We accordingly ignore overshooting as a separate source of uncertainty.
Atomic diffusion can also be a source of uncertainty for MI,TRGB. Compared with the case without diffusion, evolutionary tracks of low-mass stars which take into account fully efficient atomic diffusion include the following: lower envelope He abundances (by ~0.01, after the main sequence); changes in the detailed stellar evolution path close to the main-sequence turnoff point (Salaris et al. 2002); and an increment in the He core mass (by ~0.004 M⊙, at the TRGB). These effects cannot be studied separately. Unfortunately, PGPUC does not yet include atomic diffusion, and so it is not possible for us to study this question. Therefore, we have obtained evolutionary tracks with and without diffusion from the GARSTEC stellar evolution code (Weiss & Schlattl 2008) using our stellar parameters. These tracks (Fig. 15b) imply that diffusion changes MI,TRGB by − 0.0123 mag. Since diffusion is partly compensated by turbulence, which is not included in the GARSTEC calculations, the likely level of change brought about by the inclusion of diffusion is around − 0.0062 mag in MI,TRGB.
 |
Fig. 16 As in Fig. 14, but for different: a)κc values, b) neutrino emissivities, c) screening factors, d) mass loss parameters. |
5.6. Boundary conditions
Different treatments of surface boundary conditions will naturally change the location of the TRGB (see, e.g., Salaris et al.2002; VandenBerg et al.2008). In this sense, PGPUC uses the T(τ) relation given in Eq. (1) of Valcarce et al. (2012). Figure 7 of Tanner et al. (2012) shows that different prescriptions for the treatment of the outer regions of a red giant may change the resulting T(τ) relation by approximately ± 5%. In Fig. 15c we show the impact of such a change, after recalibrating the solar model accordingly. We conclude that such an uncertainty leads to an MI,TRGB uncertainty of ∓ 0.0068 mag.
5.7. Radiative opacities
Under non-degenerate conditions, radiative transfer is the prime mechanism of energy transfer. But as the luminosity of the TRGB is regulated mainly by the degenerate He core, one expects that uncertainties in the radiative opacities κrad are not of primary importance for the evolution close to the TRGB. The current best estimates of uncertainties in κrad tend to fall around the 5% level, but there have been suggestions, raised primarily in the framework of the so-called “solar abundance problem”, that the uncertainties in κrad may be higher, possibly reaching up to 20–30% at some points in the stellar interior (see Catelan2013 for a recent review and references).
To evaluate the impact of κrad uncertainties, we have changed κrad by ± 10% and recalibrated the solar model accordingly, resulting in a MI,TRGB change by only ∓ 0.00025 mag (Fig. 15d). As suspected, uncertainties in κrad are negligible for the predicted TRGB position.
5.8. Conductive opacities
Energy transport, in the degenerate conditions characterizing the He cores of RGB stars, occurs primarily by electron conduction. Accordingly, the conductive opacity κcond plays a crucial role in the determination of the He core mass at the TRGB (e.g., CFP96; Cassisi et al. 2007; Catelan 2009). It is difficult to evaluate the current level of uncertainty in κcond, because this uncertainty is expected to be both temperature- and density-dependent. Recently, Valle et al. (2013) adopted a level of 5% uncertainty as a reasonable average uncertainty in their RGB models. According to A. Potekhin (2012, priv. comm.), an uncertainty of ± 10% should provide a reasonable estimate of the remaining uncertainties in this key physical ingredient. We have accordingly computed additional RGB tracks in which we changed κcond by ± 10%, again recalibrating the solar model accordingly, as shown in Fig. 16a. The corresponding uncertainty in MI,TRGB is ± 0.016 mag.
5.9. Nuclear reaction rates
Uncertainties in the main thermonuclear reactions rates considered in PGPUC may affect the TRGB position. The main reactions of hydrogen burning via the proton-proton chain are 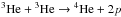 ,
, 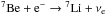 and
and 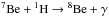 . For the CNO cycle, the reaction considered is 14N(p,γ)15O. It is the slowest reaction in the CN cycle, sets the pace for the operation of the cycle in equilibrium, and hence is the most important one for our purposes. For helium burning, the reactions considered are 4He(αα,γ)12C and 12C(α,γ)16O. Each of these reactions are assumed to operate in chemical equilibrium.
. For the CNO cycle, the reaction considered is 14N(p,γ)15O. It is the slowest reaction in the CN cycle, sets the pace for the operation of the cycle in equilibrium, and hence is the most important one for our purposes. For helium burning, the reactions considered are 4He(αα,γ)12C and 12C(α,γ)16O. Each of these reactions are assumed to operate in chemical equilibrium.
In Table 3 we present the changes in MI,TRGB that are brought about by uncertainties in the different nuclear reaction rates, after recalibrating the solar model as needed in each case. The latter uncertainty levels are adopted directly from the original sources of the nuclear reaction rates used in PGPUC, and are similar, for instance, to those adopted in Valle et al. (2013), and also of the same order of magnitude as estimated by Adelberger et al. (2011). We note from Table 3 that the triple-α reaction is the one that impacts TRGB the most. In summary, our calculations allow us to estimate a global uncertainty in MI,TRGB at the level of ± 0.019 mag, as a consequence of uncertainties in the relevant nuclear reaction rates.
MI,TRGB uncertainties caused by nuclear reaction rates.
5.10. Screening of the nuclear reactions
In addition to the nuclear reaction rates proper, the corresponding screening corrections must also be taken into account. These corrections have been discussed for a long time, and have included electrostatic screening (Salpeter 1954) and dynamical screening (e.g., Shaviv & Shaviv 2000). In this sense, while the recent experimental results of Anderegg et al. (2010) are claimed to “fully corroborate” the validity of the Salpeter results, the results of recent dynamic screening calculations (Mussack & Däppen 2011, and references therein) provide a rather different perspective, not being able to confirm the significant enhancements in the nuclear reaction rates over their unscreened values that are predicted in the static regime.
From a practical perspective, it is useful to note that Weiss et al. (2001) have implemented different screening factors in a solar model, using the Grevesse & Sauval (1998) abundances for the Sun, concluding that a deviation of the screening factor by ± 10% is strongly discrepant with the solar sound speed profile estimated with helioseismology. Recently, new and highly sophisticated estimations of the solar abundances have become available (e.g., Asplund et al. 2005, 2009; Caffau et al. 2011), but these new abundances further increase the differences between theoretical estimations and helioseismological measurements of the solar sound speed profile. Several hypotheses have been suggested to solve this “solar abundance problem” (see, e.g., Catelan 2013, for a recent review and references). In Weiss (2008), it was pointed out that an increase of the screening factor by 10–15% over the static values can recover the agreement with the seismic sound speed profile in the envelope, when the Asplund et al. (2005) chemical composition is used. However, in the center of the Sun such an increase in the screening factor makes the sound speed profile deviate significantly from the helioseismological values (see also Goupil et al. 2011). Taking these considerations into account, here we conservatively adopt an uncertainty of ± 20% in the screening factors. Tracks computed with an enhancement factor β in the range 80–120% over the reference (static) case are shown in Fig. 16c, where the corresponding solar models were also recalibrated as required. The associated uncertainty in MI,TRGB is ± 0.011 mag.
5.11. Neutrino emission
The neutrino emission rate used in PGPUC is described in Haft et al. (1994), where an analytic expression for the plasma neutrino emission rates is provided (based mosltly on the work of Braaten & Segel 1993), which is likely correct at the ± 5% level (see Valle et al. 2013, for a recent discussion and additional references). On the upper RGB, neutrino emission is the most important energy-loss mechanism from the center of the star. Therefore, any change in this formulation will have a direct impact on the predicted level of the TRGB. Changing the neutrino emission rates by ± 5%, we find that MI,TRGB is changed by ∓ 0.013 mag (Fig. 16b).
5.12. Mass loss
It is well known (e.g., Castellani & Castellani 1993; D’Cruz et al. 1996; Soker et al. 2001) that the position of the TRGB will change depending on the amount of mass loss, with stars “peeling off” from the RGB locus at a lower luminosity with increasing mass loss (see also Fig. 16d). However, the TRGB position is expected to be dominated by RGB stars that undergo the least amount of mass loss, since these are expected to be brighter than their mass-losing counterparts. This is why we originally adopted as reference case the evolutionary tracks computed without mass loss. At any point in the life of the cluster, however, and due to small-number statistics, the stars closest to the TRGB may actually be the more strongly mass-losing giants that may be present in the cluster.
 |
Fig. 17 Comparison between the observed M5 CMD locus and PGPUC ZAHB predictions. The blue star symbols indicate the approximate locations of ZAHB stars with the indicated mass values, corresponding to overall RGB mass loss amounts of 0.19–0.28 M⊙. |
Therefore, to evaluate the impact of mass loss, we need to constrain the range in total mass loss that may be present among M5’s RGB stars. Judging from Fig. 17, where we overplot a zero-age HB (ZAHB) locus obtained for the adopted chemical composition and age with the observed CMD, the minimum masses reached by this cluster’s HB stars are around 0.54 M⊙, which implies an upper limit for the overall RGB mass loss of about 0.82 − 0.54 = 0.28 M⊙, compared with an average value of order 0.82 − 0.63 = 0.19 M⊙ (a mass of 0.63 M⊙ corresponding roughly to the mid point of the HB, as seen in Fig. 17) and a minimum amount of mass loss of order 0.82 − 0.70 = 0.12 M⊙, corresponding to the reddest stars along the ZAHB. Taking these constraints into account, and using the PGPUC code with the Schröder & Cuntz (2005, 2007) mass loss formalism, we find that for the minimum observed mass loss of 0.12 M⊙ the value of MI,TRGB is shifted by + 0.022 mag, whereas for the maximum of 0.28 M⊙ it is shifted by + 0.024 mag. However, MI,TRGB does not depend linearly on mass loss, presenting a maximum at 0.22 M⊙ where MI,TRGB = 0.035 mag (see Fig. 16d). We thus conclude that the uncertainty due to mass loss falls in the range 0.022–0.035 mag.
5.13. Equation of state (EOS)
Different kinds of EOS exist in the literature that can be implemented in stellar evolution codes. PGPUC uses FreeEOS (Irwin 2007, see Table 2 of Valcarce et al.2012), while other codes use other prescriptions. To test impact on the TRGB we select different EOS and compare with FreeEOS. This study was performed with the GARSTEC stellar evolution code (Weiss & Schlattl 2008) because in PGPUC only two EOS have been implemented, whereas in GARSTEC we can choose between eight different versions:
-
1.
MHD (Mihalas et al. 1988).
-
2.
OPAL 2001 (Rogers & Nayfonov 2002).
-
3.
OPAL 2001–MHD (OPAL extended when needed with MHD).
-
4.
OPAL 2005 (Rogers, unpublished).
-
5.
OPAL 1996 (Rogers et al. 1996).
-
6.
SAHA-degeneracy (Kippenhahn et al. 2013).
- 7.
-
8.
FreeEOS.
Figure 18 shows the impact of these different EOS prescriptions and the change in MI,TRGB. Other stellar parameters were held fixed at our benchmark values and the same physical input of PGPUC was used with the exception of the T − τ relation. We infer an MI,TRGB uncertainty of −0.0045/+0.0242 mag.
 |
Fig. 18 Color–magnitude diagrams for different EOS based on GARSTEC. Inset: numbers mark the TRGB for the respective EOS cases. The steps in the inset are due to limited number of digits in model output. |
5.14. Color transformations and bolometric corrections
Different approaches can be followed to obtain the BCs and color transformations that are needed to translate luminosities and temperatures given by stellar evolution codes to observational quantities. One may use purely theoretical model atmospheres, re-calibrated model atmospheres, or empirical transformations (see, e.g, Salaris et al. 2002). Naturally, each of these routes possesses its own uncertainties, and it is beyond the scope of this paper to perform a critical evaluation of this complex subject. Nonetheless, one may obtain a sense of the uncertainties involved by comparing the prescriptions provided by different authors. Figure 19 compares the predicted CMD loci, adopting the prescriptions of Castelli & Kurucz (2004), VandenBerg & Clem (2003), Girardi et al. (2002), and Worthey & Lee (2011)4. We see that the differences in predicted TRGB color are larger than those in the TRGB magnitude. As to the latter, the main discrepancies are between the formulations of Worthey & Lee (2011) and Girardi et al. (2002).
As an error estimate caused by the BC we adopt the uncertainties provided explicitly by Worthey & Lee (2011). For the TRGB magnitude, these are significantly larger than the spread between the results of the different formulations shown in Fig. 19. In this sense, using the error estimate of Worthey & Lee (2011) is conservative.
Note that the error of the predicted MI,TRGB value depends strongly on μν because the effective temperature of the TRGB decreases for higher μν values (see Fig. 6), thus implying greater errors in the BC (see Table 2 of Worthey & Lee2011). The uncertainties extracted from Worthey & Lee (2011) for the relevant range of μν are well represented by 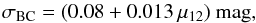 (9)where again μ12 = μν/10-12 μB. Note that this adopted error is more likely to be seen as an estimated maximum error and not a 1-σ uncertainty.
(9)where again μ12 = μν/10-12 μB. Note that this adopted error is more likely to be seen as an estimated maximum error and not a 1-σ uncertainty.
 |
Fig. 19 As in Fig. 14, but for different prescriptions for the color transformations and bolometric corrections. |
5.15. Comparison with other stellar evolution codes
In Fig. 3 of Valcarce et al. (2012), a comparison between PGPUC and other stellar evolution codes is made, as far as predicted CMD positions are concerned. This figure implies that PGPUC reaches the TRGB with a luminosity that is lower than predicted by other codes. Our discussion of different EOS cases in Sect. 5.13, calculated with GARSTEC, reveals that for identical input parameters and the same EOS, PGPUC finds MI,TRGB about 0.05 mag dimmer than GARSTEC. It would be too difficult to isolate the impact of the numerical algorithms and different input physics adopted by the different authors upon this result, but the reliability of the numerical approach adopted in the PGPUC code was discussed at some length by Sweigart (1994). Rather than associating a formal “error bar” stemming from this comparison, we simply emphasize that the μν constraints obtained using PGPUC are less stringent (more conservative) than those that would have been derived using most other evolutionary codes.
Error budget in theoretically predicted 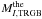 .
.
5.16. Summary
The sources of theoretical error are summarized in Table 4, except for the BC, given in Eq. (9). All of these uncertainties are systematic (not statistical) and constitute our best estimates of the maximum error. The associated probability distributions are in most cases completely unknown, so we make the simplest possible choice and use top-hat, flat probability distributions in the ranges shown in Table 4. The convolution of all these distributions is well represented by a Gaussian with mean and standard deviation  The shift of the mean is due to the fact that the error ranges are not symmetric (and we have chosen flat probabilities). Otherwise our procedure corresponds to adding systematic errors in quadrature as recommended, for example, by Barlow et al. (2002).
The shift of the mean is due to the fact that the error ranges are not symmetric (and we have chosen flat probabilities). Otherwise our procedure corresponds to adding systematic errors in quadrature as recommended, for example, by Barlow et al. (2002).
One important contribution to the shift comes from mass-loss. Our theoretical prediction 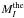 of Eq. (6) was computed setting zero mass-loss, but we have seen that mass-loss falls in the range 0.12–0.28 M⊙. Since
of Eq. (6) was computed setting zero mass-loss, but we have seen that mass-loss falls in the range 0.12–0.28 M⊙. Since 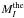 increases with the mass loss (the TRGB becomes dimmer) our best estimate has to be shifted accordingly (to 0.2 M⊙, which corresponds to 0.03 mag for MI,TRGB). For a single top-hat distribution, the standard deviation is
increases with the mass loss (the TRGB becomes dimmer) our best estimate has to be shifted accordingly (to 0.2 M⊙, which corresponds to 0.03 mag for MI,TRGB). For a single top-hat distribution, the standard deviation is 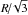 where R is the half-width. The standard deviation of the convolution, σthe, is well represented by
where R is the half-width. The standard deviation of the convolution, σthe, is well represented by 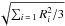 as it corresponds to the convolution of a sum of uncorrelated errors. This completes our estimate of theoretical uncertainties.
as it corresponds to the convolution of a sum of uncorrelated errors. This completes our estimate of theoretical uncertainties.
6. Comparing observational and theoretical results
After all ingredients are complete, we can now compare the predicted and observed I-band absolute brightness of the TRGB in M5. For the empirical TRGB brightness we have found the value of Eq. (8). This result is to be compared with the predicted value, Eq. (6), corrected for mass-loss and other non-symmetric systematics according to Eq. (10), i.e., 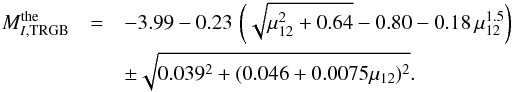 (12)In the absence of neutrino dipole moment (μ12 = 0), this corresponds to
(12)In the absence of neutrino dipole moment (μ12 = 0), this corresponds to 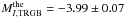 .
.
Let us now discuss the implications of a non-zero neutrino dipole moment. Figure 20 shows the predicted and observed values for MI,TRGB (with 1σ errors) as a function of μ12. In order to compare them, we combine the observational and theoretical errors in quadrature. The most robust information we can extract from our study are upper limits on μ12. Integrating the combined probability distribution from μ12 = 0 to the limiting value, we obtain the following upper limits, 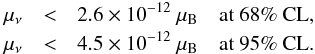 (13)In Fig. 20 we see a small disagreement at μν = 0, which naively suggests a best fit value of μ12 ~ 2. This small discrepancy can be blamed entirely on the distance uncertainty, and implies that we obtain a relatively poor limit. A more precise future distance determination will lead either to a much improved limit or reveal significant deviations from standard stellar evolution theory.
(13)In Fig. 20 we see a small disagreement at μν = 0, which naively suggests a best fit value of μ12 ~ 2. This small discrepancy can be blamed entirely on the distance uncertainty, and implies that we obtain a relatively poor limit. A more precise future distance determination will lead either to a much improved limit or reveal significant deviations from standard stellar evolution theory.
 |
Fig. 20 Absolute TRGB I-band magnitude inferred from observations and predicted by our calculations, both with 1σ error bands. |
7. Conclusions
We have derived the new astrophysical constraints on neutrino dipole moments μν shown in Eq. (13). We have used precise observations of the GC M5, carefully determined its TRGB position, compared against theoretical predictions for different μν values, and most importantly have taken into detailed account the different sources of error affecting both the empirical and theoretical TRGB position.
Our 68% CL limit is almost identical with the constraints found in the earlier literature by similar methods (Raffelt1990, Raffelt & Weiss1992, Catelan et al.1996), although it is not possible to associate a formal confidence limit to the older results. In this sense, our new result is more robust because it is based on state-of-the-art astronomical data, evolutionary calculations using up-to-date input physics, and a careful analysis of the several different error sources affecting the TRGB position, both observational and theoretical.
The paucity of stars on the upper RGB is not our main source of error, yet repeating our analysis for additional GCs should allow us to improve our limits and check for overall consistency in other cases. The systematic errors associated with the theoretical prediction is dominated by the uncertainty of the BC, followed by the mixing-length theory and uncertain mass loss. A better understanding of the BC uncertainty, in particular, would strongly help to improve our results. The main observational error, as well as the largest single source of uncertainty, derives from the distance modulus which should be improved in future by the results of the GAIA mission. Depending on the distance found and the remaining errors, a significant improvement of our results could be obtained.
The stellar energy-loss limit remains the most restrictive constraint on μν (valid for only neutrinos with masses below the keV range). The most restrictive laboratory limit uses the  flux from reactors and studies the electron recoil spectrum upon
flux from reactors and studies the electron recoil spectrum upon  scattering, leading to the constraint
scattering, leading to the constraint 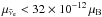 (90% CL) on neutrino magnetic or transition moments that are connected to
(90% CL) on neutrino magnetic or transition moments that are connected to  (Beda et al. 2010). This quantity is different from our μν which effectively sums over all direct and transition moments between all flavors and therefore is more general. It also applies to transition moments between ordinary active and putative sterile neutrinos, provided the latter are light enough to be emitted from the degenerate helium core near the TRGB, i.e., the mass is safely below the relevant plasma frequency of about 10–20 keV.
(Beda et al. 2010). This quantity is different from our μν which effectively sums over all direct and transition moments between all flavors and therefore is more general. It also applies to transition moments between ordinary active and putative sterile neutrinos, provided the latter are light enough to be emitted from the degenerate helium core near the TRGB, i.e., the mass is safely below the relevant plasma frequency of about 10–20 keV.
Neutrino dipole moments also lead to radiative neutrino decays of the form ν2 → ν1 + γ, allowing one to derive constraints on μν from the absence of anomalous photon fluxes in connection with astrophysical neutrino fluxes. However, neutrino oscillation experiments now tell us that the mass differences between ordinary active neutrinos are very small, suppressing radiative decays by phase-space effects, so that the stellar energy loss argument is more constraining (Raffelt 1998).
Since our 1σ limit is similar to previously stated GC bounds on μν, we expect that other previous constraints, for example on the axion-electron interaction, remain valid if interpreted as 1σ limits. We will study other cases more explicitly in a forthcoming paper.
GCs remain powerful particle-physics laboratories. It is timely to put such results on a firmer observational basis and understand more deeply the associated uncertainties and errors.
Unless otherwise noted, GC parameters are adopted from the Feb. 2010 version of the Harris (1996) catalog.
M5 actually appears to be an outer-halo GC that spends much of its time at distances larger than ~50 kpc, but which just happens to lie close to its perigalacticon at this point in time (Cudworth 1997, and references therein).
For instance, according to Salaris et al. (1993), the global metallicity can be computed as [M/H] = [Fe/H] + log (0.638 fα + 0.362), where fα = 10[α/Fe]. In our case, we use the metallicity calculator that is available in the PGPUC Online webpage, http://www2.astro.puc.cl/pgpuc/FeHcalculator.php
Here we adopt Mbol, ⊙ = 4.7554 ± 0.0004 mag, following http://www.pas.rochester.edu/~emamajek/sun.txt
Acknowledgments
The authors are grateful to S. Cassisi for useful discussions and for kindly providing unpublished evolutionary tracks computed using BaSTI. Support for N.V. and M.C. is provided by the Chilean Ministry for the Economy, Development, and Tourism’s Programa Iniciativa Científica Milenio through grant P07-021-F, awarded to The Milky Way Millennium Nucleus; by Proyecto Fondecyt Regular #1110326; by the BASAL Center for Astrophysics and Associated Technologies (PFB-06); and by Proyecto Anillo ACT-86. Support for N.V. is also provided by MECESUP Project No. PUC0609 (Chile). G.R. acknowledges partial support by the Deutsche Forschungsgemeinschaft through grant No. EXC 153 and by the European Union through the Initial Training Network “Invisibles”, grant No. PITN-GA-2011-28944. J.R. acknowledges support by the Alexander von Humboldt Foundation.
References
- Adelberger, E. G., García, A., Robertson, R. G. H., et al. 2011, Rev. Mod. Phys., 83, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Anderegg, F., Driscoll, C. F., Dubin, D. H. E., & O’Neil, T. M. 2010, Phys. Plasmas, 17, 055702 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, eds. T. G. Barnes, III, & F. N. Bash, ASP Conf. Ser., 336, 25 [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Aver, E., Olive, K. A., & Skillman, E. D. 2010, J. Cosmology Astropart. Phys., 5, 3 [Google Scholar]
- Barlow, R., Cahn, R., Cowan, G., et al. 2002, BABAR Analysis Document, 318, 1 [Google Scholar]
- Beda, A. G., Brudanin, V. B., Egorov, V. G., et al. 2010, Phys. Part. Nucl. Lett., 7, 406 [CrossRef] [Google Scholar]
- Bergbusch, P. A., & Stetson, P. B. 2009, AJ, 138, 1455 [NASA ADS] [CrossRef] [Google Scholar]
- Beringer, J., et al. 2012, Phys. Rev., D86, 010001 [Google Scholar]
- Bernstein, J., Ruderman, M., & Feinberg, G. 1963, Phys. Rev., 132, 1227 [NASA ADS] [CrossRef] [Google Scholar]
- Braaten, E., & Segel, D. 1993, Phys. Rev. D, 48, 1478 [NASA ADS] [CrossRef] [Google Scholar]
- Caffau, E., Ludwig, H.-G., Steffen, M., Freytag, B., & Bonifacio, P. 2011, Sol. Phys., 268, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R., D’Orazi, V., & Lucatello, S. 2009, A&A, 508, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cassisi, S. 2012, in Uncertainties and Systematics in Stellar Evolution Models of Red Giant Stars, eds. A. Miglio, J. Montalbán, & A. Noels, 57 [Google Scholar]
- Cassisi, S., Salaris, M., Castelli, F., & Pietrinferni, A. 2004, ApJ, 616, 498 [NASA ADS] [CrossRef] [Google Scholar]
- Cassisi, S., Potekhin, A. Y., Pietrinferni, A., Catelan, M., & Salaris, M. 2007, ApJ, 661, 1094 [NASA ADS] [CrossRef] [Google Scholar]
- Cassisi, S., Marín-Franch, A., Salaris, M., et al. 2011, A&A, 527, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castellani, M., & Castellani, V. 1993, ApJ, 407, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Castelli, F., & Kurucz, R. L. 2004 [arXiv:astro-ph/0405087] [Google Scholar]
- Catelan, M. 2009, Ap&SS, 320, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Catelan, M. 2013, in Eur. Phys. J. Web Conf., 43, 1001 [Google Scholar]
- Catelan, M., de Freitas Pacheco, J. A., & Horvath, J. E. 1996, ApJ, 461, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Clement, C. M., Muzzin, A., Dufton, Q., et al. 2001, AJ, 122, 2587 [NASA ADS] [CrossRef] [Google Scholar]
- Coppola, G., Dall’Ora, M., Ripepi, V., et al. 2011, MNRAS, 416, 1056 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, A. N., & Stewart, J. N. 1970, ApJS, 19, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Cudworth, K. M. 1997, in Proper Motions and Galactic Astronomy, ed. R. M. Humphreys, ASP Conf. Ser., 127, 91 [Google Scholar]
- D’Cruz, N. L., Dorman, B., Rood, R. T., & O’Connell, R. W. 1996, ApJ, 466, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Dotter, A., Sarajedini, A., Anderson, J., et al. 2010, ApJ, 708, 698 [NASA ADS] [CrossRef] [Google Scholar]
- Ferraro, F. R., Valenti, E., Straniero, O., & Origlia, L. 2006, ApJ, 642, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Freytag, B., & Salaris, M. 1999, ApJ, 513, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Gallart, C., Zoccali, M., Bertelli, G., et al. 2003, AJ, 125, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Girardi, L., Bertelli, G., Bressan, A., et al. 2002, A&A, 391, 195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goupil, M. J., Lebreton, Y., Marques, J. P., Samadi, R., & Baudin, F. 2011, J. Phys. Conf. Ser., 271, 012031 [Google Scholar]
- Gratton, R. G., Carretta, E., Bragaglia, A., Lucatello, S., & D’Orazi, V. 2010, A&A, 517, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gratton, R. G., Lucatello, S., Sollima, A., et al. 2013, A&A, 549, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Haft, M., Raffelt, G., & Weiss, A. 1994, ApJ, 425, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, W. E. 1996, AJ, 112, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- Hubbard, W. B., & Lampe, M. 1969, ApJS, 18, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, A. W. 2007, http://freeeos.sourceforge.net/ [Google Scholar]
- Ivans, I. I., Kraft, R. P., Sneden, C., et al. 2001, AJ, 122, 1438 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., & Thuan, T. X. 2010, ApJ, 710, L67 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Izotov, Y. I., Thuan, T. X., & Stasińska, G. 2007, ApJ, 662, 15 [NASA ADS] [CrossRef] [Google Scholar]
- King, I. R., Bedin, L. R., Cassisi, S., et al. 2012, AJ, 144, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Kippenhahn, R., Weigert, A., & Weiss, A. 2013, Stellar Structure and Evolution, Astron. Astrophys. Lib. (Berlin: Springer) [Google Scholar]
- Koch, A., & McWilliam, A. 2010, AJ, 139, 2289 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E., Smith, K. M., Dunkley, J., et al. 2011, ApJS, 192, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Lai, D. K., Smith, G. H., Bolte, M., et al. 2011, AJ, 141, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Landolt, A. U. 1992, AJ, 104, 340 [NASA ADS] [CrossRef] [Google Scholar]
- Layden, A. C., Sarajedini, A., von Hippel, T., & Cool, A. M. 2005, ApJ, 632, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Ludwig, H.-G., & Kučinskas, A. 2012, A&A, 547, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Madore, B. F., & Freedman, W. L. 1995, AJ, 109, 1645 [NASA ADS] [CrossRef] [Google Scholar]
- Marín-Franch, A., Aparicio, A., Piotto, G., et al. 2009, ApJ, 694, 1498 [NASA ADS] [CrossRef] [Google Scholar]
- Mihalas, D., Dappen, W., & Hummer, D. G. 1988, ApJ, 331, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Milone, A. P., Piotto, G., Bedin, L. R., et al. 2012, A&A, 537, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mussack, K., & Däppen, W. 2011, ApJ, 729, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Palmieri, R., Piotto, G., Saviane, I., Girardi, L., & Castellani, V. 2002, A&A, 392, 115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2004, ApJ, 612, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Raffelt, G. G. 1990, ApJ, 365, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Raffelt, G. G. 1996, Stars as Laboratories for Fundamental Physics: The Astrophysics of Neutrinos, Axions, and other Weakly Interacting Particles (Chicago, IL: Univ. Chicago Press) [Google Scholar]
- Raffelt, G. G. 1998, Phys. Rev. Lett., 81, 4020 [NASA ADS] [CrossRef] [Google Scholar]
- Raffelt, G. G. 1999, Ann. Rev. Nucl. Part. Sci., 49, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Raffelt, G., & Weiss, A. 1992, A&A, 264, 536 [NASA ADS] [Google Scholar]
- Rogers, F. J., & Nayfonov, A. 2002, ApJ, 576, 1064 [Google Scholar]
- Rogers, F. J., Swenson, F. J., & Iglesias, C. A. 1996, ApJ, 456, 902 [NASA ADS] [CrossRef] [Google Scholar]
- Salaris, M., Chieffi, A., & Straniero, O. 1993, ApJ, 414, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Salaris, M., Cassisi, S., & Weiss, A. 2002, PASP, 114, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Salaris, M., Riello, M., Cassisi, S., & Piotto, G. 2004, A&A, 420, 911 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salaris, M., Weiss, A., Ferguson, J. W., & Fusilier, D. J. 2006, ApJ, 645, 1131 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. E. 1954, Aust. J. Phys., 7, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Sandquist, E. L., & Bolte, M. 2004, ApJ, 611, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Saviane, I., da Costa, G. S., Held, E. V., et al. 2012, A&A, 540, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Schröder, K.-P., & Cuntz, M. 2005, ApJ, 630, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Schröder, K.-P., & Cuntz, M. 2007, A&A, 465, 593 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shaviv, G., & Shaviv, N. J. 2000, ApJ, 529, 1054 [NASA ADS] [CrossRef] [Google Scholar]
- Soker, N., Catelan, M., Rood, R. T., & Harpaz, A. 2001, ApJ, 563, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Steigman, G. 2007, Ann. Rev. Nucl. Part. Sci., 57, 463 [Google Scholar]
- Steigman, G. 2012, in Adv. High Energy Phys., 268321, DOI: 10.1155/2012/268321 [Google Scholar]
- Stetson, P. B. 1987, PASP, 99, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Stetson, P. B. 1994, PASP, 106, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Stetson, P. B. 2000, PASP, 112, 925 [NASA ADS] [CrossRef] [Google Scholar]
- Stetson, P. B. 2005, PASP, 117, 563 [CrossRef] [Google Scholar]
- Stetson, P. B. 2009, in IAU Symp. 258, eds. E. E. Mamajek, D. R. Soderblom, & R. F. G. Wyse, 197 [Google Scholar]
- Stetson, P. B., Bruntt, H., & Grundahl, F. 2003, PASP, 115, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Sweigart, A. V. 1973, A&A, 24, 459 [NASA ADS] [Google Scholar]
- Sweigart, A. V. 1994, ApJ, 426, 612 [NASA ADS] [CrossRef] [Google Scholar]
- Sweigart, A. V., & Gross, P. G. 1976, ApJS, 32, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Sweigart, A. V., & Gross, P. G. 1978, ApJS, 36, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Tanner, J. D., Basu, S., & Demarque, P. 2012, ApJ, 759, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Valcarce, A. A. R., Catelan, M., & Sweigart, A. V. 2012, A&A, 547, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valle, G., Dell’Omodarme, M., Prada Moroni, P. G., & Degl’Innocenti, S. 2013, A&A, 549, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- VandenBerg, D. A. 2000, ApJS, 129, 315 [NASA ADS] [CrossRef] [Google Scholar]
- VandenBerg, D. A., & Clem, J. L. 2003, AJ, 126, 778 [NASA ADS] [CrossRef] [Google Scholar]
- VandenBerg, D. A., Bergbusch, P. A., & Dowler, P. D. 2006, ApJS, 162, 375 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- VandenBerg, D. A., Edvardsson, B., Eriksson, K., & Gustafsson, B. 2008, ApJ, 675, 746 [NASA ADS] [CrossRef] [Google Scholar]
- Weiss, A. 1999, Habilitation thesis, University of Munich [Google Scholar]
- Weiss, A. 2008, Phys. Scr. T, 133, 014025 [NASA ADS] [CrossRef] [Google Scholar]
- Weiss, A., & Schlattl, H. 2008, Ap&SS, 316, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Weiss, A., Flaskamp, M., & Tsytovich, V. N. 2001, A&A, 371, 1123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Worthey, G., & Lee, H.-C. 2011, ApJS, 193, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Color–magnitude diagram of M5. Left: original. Right: after field star decontamination. |
| In the text | |
 |
Fig. 2 Upper part of the CMD for M5. Nominal identification of RGB and AGB stars as explained in the text. Solid line: RGB track with initial parameters described in Sect. 3.2. Dashed line: Nominal RGB according to the fit function of Eq. (2). |
| In the text | |
 |
Fig. 3 Distance Δ from our RGB reference line of Eq. (2) and distribution of stars as a function of Δ. |
| In the text | |
 |
Fig. 4 Top: luminosity functions of RGB (filled histogram) and AGB. Thick black line: expectation from evolutionary speed. Dashed lines: fit to data. Bottom: cumulative luminosity function for RGB stars (in blue) and AGB stars (in red) and fit functions for each case. |
| In the text | |
 |
Fig. 5 Probability distribution for Δtip = I1 − ITRGB between the TRGB and the brightest star. The histogram is from a Monte Carlo simulation, the red line is the analytic representation of Eq. (4). |
| In the text | |
 |
Fig. 6 PGPUC evolutionary tracks around the TRGB for the indicated values of μν, where μ12 = μν/10-12 μB. |
| In the text | |
 |
Fig. 7 I-band brightness increase of the TRGB corresponding to the modified tracks shown in Fig. 6. We also show the analytic approximation formula of Eq. (6). |
| In the text | |
 |
Fig. 8 PGPUC ZAHB loci for different assumptions on the distance modulus overplotted on the HB region of M5. Variable stars from the Clement et al. (2001) catalog are plotted in yellow. |
| In the text | |
 |
Fig. 9 Sharp (upper panel) and χ (lower panel). Red triangles: three brightest stars. |
| In the text | |
 |
Fig. 10 Photometric error σ(I). Red triangles: three brightest stars. Inset: zoom around the brightest stars. The vertical plume of points at I ≈ 14.5 mag consists of the RR Lyrae variables. |
| In the text | |
 |
Fig. 11 Radial distance (in arcmin) vs. I-magnitude for different kinds of errors in V − I. Red triangles: three brightest stars. |
| In the text | |
 |
Fig. 12 Differential reddening test. Here we show the four different quadrants of the cluster that were selected to produce the CMDs shown in Fig. 13. Black triangles denote the position of the three brightest cluster stars, with their sizes proportional to their apparent brightness. |
| In the text | |
 |
Fig. 13 Color–magnitude diagrams for the different quadrants shown in Fig. 12 with the same color coding. The black line in all panels corresponds to the empirical RGB fit of Eq. (2). |
| In the text | |
 |
Fig. 14 Evolutionary tracks in the MI, V − I plane are shown for different: a) Mass values, b)Y values, c)Z values, d) [α/Fe] ratios. The insets at the lower-right corner of each panel show zoom-ins around the TRGB position (note the different scales used in the different insets). |
| In the text | |
 |
Fig. 15 As in Fig. 14, but for different: a)αMLT values, b) treatment of diffusion, c) boundary conditions, d)κr values. |
| In the text | |
 |
Fig. 16 As in Fig. 14, but for different: a)κc values, b) neutrino emissivities, c) screening factors, d) mass loss parameters. |
| In the text | |
 |
Fig. 17 Comparison between the observed M5 CMD locus and PGPUC ZAHB predictions. The blue star symbols indicate the approximate locations of ZAHB stars with the indicated mass values, corresponding to overall RGB mass loss amounts of 0.19–0.28 M⊙. |
| In the text | |
 |
Fig. 18 Color–magnitude diagrams for different EOS based on GARSTEC. Inset: numbers mark the TRGB for the respective EOS cases. The steps in the inset are due to limited number of digits in model output. |
| In the text | |
 |
Fig. 19 As in Fig. 14, but for different prescriptions for the color transformations and bolometric corrections. |
| In the text | |
 |
Fig. 20 Absolute TRGB I-band magnitude inferred from observations and predicted by our calculations, both with 1σ error bands. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


