EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 558 (October 2013) A&A, 558 (2013) A59 Full HTML
Free Access
Issue
A&A
Volume 558, October 2013
Article Number A59
Number of page(s) 9
Section Cosmology (including clusters of galaxies)
DOI https://doi.org/10.1051/0004-6361/201321949
Published online 04 October 2013

© ESO, 2013

1. Introduction

Supermassive black holes (SMBHs) with more than 109 M⊙ have been observed at z > 6 (Fan et al. 2001, 2003, 2004, 2006), and recently even at z = 7.085 (Mortlock et al. 2011). While theoretical considerations indicate a variety of potential pathways, including direct collapse to a black hole, collapse to a supermassive star, collapse of stellar clusters or clusters of black holes (Rees 1984; Haiman 2006; Volonteri & Bellovary 2012), substantial efforts have been made to assess the validity of such scenarios.

1.1. Black hole formation scenarios

As the most straightforward possibility, one could imagine these SMBHs to originate from remnants of the first stars, which were proposed to be very massive with 100−1000 M⊙ (Abel et al. 2002; Bromm & Larson 2004). Stellar evolution calculations by Heger & Woosley (2002) indeed show that black holes may form for stellar masses between 10−30 M⊙, or 100−300 M⊙, thus yielding the seeds for further growth to SMBHs.

New calculations following the evolution of primordial star formation beyond the first core, however, show that fragmentation can occur efficiently (Stacy et al. 2010, 2012; Turk et al. 2009; Clark et al. 2011; Greif et al. 2011; Smith et al. 2011). While the effect of the accretion luminosity on the protostellar core seems to be minor (Smith et al. 2011, 2012), UV feedback during the main sequence phase appears to set the upper limit to the stellar mass to 50−100 M⊙ (Hosokawa et al. 2011, 2012b; Susa 2013). Even if very massive stars could form, the resulting HII region is likely to inhibit accretion for at least 108 yrs (Milosavljević et al. 2009a,b). An additional problem has been identified by Whalen & Fryer (2012), who showed that black holes resulting from such stars would be born with strong dynamical kicks, implying that they should readily be expelled from the halo.

On the other hand, dense stellar clusters may form at high redshift in the presence of trace amounts of dust (Schneider et al. 2003, 2008, 2012a,b; Omukai et al. 2005, 2012; Clark et al. 2008; Dopcke et al. 2011, 2013; Klessen et al. 2012). The relativistic instability of such clusters has been explored in a semi-analytic framework by Devecchi & Volonteri (2009) and Devecchi et al. (2010, 2012), finding characteristic black hole masses of up to ~3000 M⊙. The latter is already substantially higher than the masses of the first stars, though it may still be difficult to obtain masses as high as 109 M⊙ at z = 7. In the presence of a significant black hole spin, which will be rapidly obtained in the presence of efficient accretion, one typically expects an additional growth by about four orders of magnitude, thus requiring seed masses on the order of 105 M⊙ (Shapiro 2005).

The formation of such massive seeds has been considered in the context of the direct collapse model, where gas in a 107–108 M⊙ halo is expected to collapse without fragmentation into a single central object (Koushiappas et al. 2004; Begelman et al. 2006; Lodato & Natarajan 2006; Spaans & Silk 2006; Volonteri et al. 2008; Begelman & Shlosman 2009). In order to avoid fragmentation, molecular hydrogen needs to be efficiently dissociated, requiring a strong ambient UV field (Omukai 2001; Bromm & Loeb 2003; Shang et al. 2010; Schleicher et al. 2010; Latif et al. 2011; Van Borm & Spaans 2013). Such radiation backgrounds may have been provided by nearby starburst galaxies, which may indeed occur frequently enough to explain the observed abundance of SMBHs at z ~ 6 (Dijkstra et al. 2008; Agarwal et al. 2012). As an alternative, Inayoshi & Omukai (2012) suggested that black hole formation may occur in the presence of strong shocks, leading to collisional dissociation of molecular hydrogen.

Using numerical simulations, Wise et al. (2008) have modeled the gravitational collapse of massive primordial halos cooling via atomic hydrogen, reporting an isothermal density profile and angular momentum transport via bar-like instabilities during the formation of the first core. Regan & Haehnelt (2009) presented the first study following the evolution beyond the first core, and modeling the formation of self-gravitating disks on parsec-scales. While these studies employed a typical resolution of 16 cells per Jeans length, it was recently demonstrated that turbulent structures can only be resolved with a resolution of at least 32 cells per Jeans length, preferably more (Sur et al. 2010; Federrath et al. 2011; Turk et al. 2012). In a set of high-resolution simulations following the formation of the first core, Latif et al. (2013a,b) found extended turbulent structures in the center of massive primordial halos, but no signs of simple disks or bar-like instabilities. Disks do, however, form at later stages of the evolution, with masses of ~1000 M⊙ on scales of 30 AU, and characteristic accretion rates of ~1 M⊙ yr-1 (Latif et al. 2013c). As a result, very massive central objects may indeed form in rather short cosmic times. The dynamics at early times have also been explored by Choi et al. (2013), finding a somewhat different result including the formation of toroidal structures on scales of several parsec. It is, however, not fully clear to which extent the latter is a result of the simplified initial conditions employed in their calculation. To provide more quantitative predictions regarding the conditions where black holes may form, Prieto et al. (2013) explored the correlations of the baryon spin with the spin of the dark matter, showing that the resulting correlation is, however, weak, and that the baryon properties cannot be naively extrapolated from the dark matter.In a similar study, de Souza et al. (2013) report that the dynamical properties of the dark matter halo may leave an imprint on the resulting stellar mass.

1.2. Quasi-stars vs. supermassive stars

While the accumulation of high masses seems feasible from a hydrodynamical point of view, the resulting object is still considerably more uncertain. As a first step, we expect the formation of a massive protostar, as the gas becomes optically thick at high densities (Omukai & Palla 2001, 2003; Hosokawa et al. 2012a). It is, however, unclear how these objects are going to evolve, and whether they will form a supermassive star or a quasi-star.

In the present context, we define a supermassive main sequence star as a conventional star with very high mass (M = 103−106 M⊙) (see also Shapiro & Teukolsky 1986), which predominantly generates its energy via nuclear burning. A quasi-star refers to an object with mass similar to that of a supermassive star, but whose central core has collapsed into a black hole (Begelman et al. 2006; Begelman 2010). The progenitors of both types of objects are rapidly accreting high-mass protostars, and we aim to explore in this paper under which conditions they evolve into a quasi-star or a supermassive main-sequence star.

To explore the evolution of such protostars, Hosokawa et al. (2012a) recently followed the evolution of rapidly accreting protostars, showing that they expand as cool supergiants, thus inhibiting the feedback from accretion luminosity and potentially allowing accretion to proceed for very long times. Hosokawa et al. also found that nuclear burning starts at stellar masses of about ~50 M⊙, and is maintained until the end of their calculation at 103 M⊙. Therefore, their model indicates no transition toward a quasi-star at least during the evolutionary phase considered. It is, however, important to assess how long this phase of efficient accretion can be maintained, and under which conditions a transition to a supermassive main-sequence star can be expected, which can potentially influence the accretion flow via radiative feedback (Omukai & Inutsuka 2002; Johnson et al. 2011, 2012). While the majority of such supermassive stars directly collapses into a black hole (Fryer & Heger 2011), a small mass window exists around 55 000 M⊙ where violent supernova explosions of up to 1055 erg may occur (Johnson et al. 2013).

Following a different approach, Begelman et al. (2006) and Begelman (2010) have proposed the formation of a black hole in the interior of rapidly accreting objects, leading to quasi-stars as the progenitors of SMBHs. Begelman et al. (2006) argued that for quasi-stars with 104–105 M⊙, the typical accretion timescale is considerably shorter than the timescale for nuclear burning, and as a result, the latter may not be able to stop the collapse of the central core. A potential advantage of such a configuration is that the accretion onto the central object is not limited by the Eddington accretion rate of the black hole, but by the Eddington accretion rate of the more massive quasi-star (Begelman et al. 2008). Begelman (2010) considers objects with more than 106 M⊙, which first evolve toward the main sequence as a supermassive star, but then form a black hole after an extended phase of nuclear burning. Ball et al. (2011) followed the evolution of black holes in a quasi-star employing the Cambridge STARS stellar evolution package (Eggleton 1971; Pols et al. 1995), finding that the black hole may efficiently accrete 10% of the stellar mass before hydrostatic equilibrium breaks down. They also report that the results are sensitive to the boundary condition in the interior. The contraction of an embedded isothermal core in a stellar envelope was further explored by Ball et al. (2012) in the framework of the Schönberg-Chandrasekhar limit.

While the models for the quasi-stars typically employed a Thomson-scattering opacity, Hosokawa et al. (2012a) reported that H− rather than Thomson scattering dominates the opacity in the protostellar atmosphere. They find luminosities close to the Eddington luminosity, 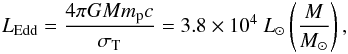LEdd=4πGMmpcσT=3.8×104L⊙(MM⊙),\begin{eqnarray} L_{\rm Edd}=\frac{4 \pi G M m_{\rm p} c}{\sigma_{\rm T}}=3.8\times10^4~L_\odot \left( \frac{M}{M_\odot} \right),\label{LEddstar} \end{eqnarray}(1)where G is the gravitational constant, mp the proton mass, c the speed of light, σT the Thomson scattering cross section and M the mass of the star. The temperatures in the atmosphere are rather cool, ~5000 K, as the protostars are on the Hayashi track. 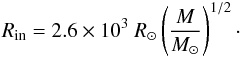As a result, the characteristic radii evolve asRin=2.6×103R⊙(MM⊙)1/2·\begin{eqnarray} R_{\rm in}=2.6\times10^3~R_\odot\left( \frac{M}{M_\odot} \right)^{1/2}\cdot\label{Rint} \end{eqnarray}(2)The protostars are thus considerably more extended and show an increasing stellar radius as a function of mass, while the models of Begelman et al. (2006) indicate a constant radius as a function of stellar mass. Begelman (2010) consider a mass-dependent stellar radius, which is, however, still more compact due to the assumption of Thomson scattering opacities.

The difference between these scenarios may, however, turn out to be highly relevant, as the stellar radius regulates the temperature on the surface, and thus the strength of protostellar feedback. In fact, the behavior reported by Hosokawa et al. 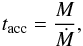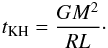(2012a) is well-known (Omukai & Palla 2001, 2003) in cases where the accretion timescale, tacc=MṀ,\begin{eqnarray} t_{\rm acc}=\frac{M}{\dot{M}}, \end{eqnarray}(3)is much smaller than the Kelvin-Helmholtz timescale, tKH=GM2RL·\begin{eqnarray} t_{\rm KH}=\frac{GM^2}{R L}\cdot \end{eqnarray}(4)However, Hosokawa et al. (2012a) report that this behavior extends into the regime where tKH < tacc, i.e. where Kelvin-Helmholtz contraction is faster than mass growth via accretion. The physical mechanism which allows this phase to continue will be discussed in detail in Sect. 2. 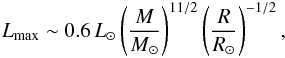Taking the maximum luminosity of the star Lmax~0.6 L⊙(MM⊙)11/2(RR⊙)−1/2,\begin{eqnarray} L_{\max}\sim0.6\,L_\odot \left( \frac{M}{M_\odot} \right)^{11/2}\left( \frac{R}{R_\odot} \right)^{-1/2}, \end{eqnarray}(5)which assumes Kramers’ opacity κ ∝ ρT-3.5 (Hayashi et al. 1962) and an initial radius as given in Eq. 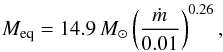(2), they show that both timescales are equal at protostellar masses of Meq=14.9 M⊙(ṁ0.01)0.26,\begin{eqnarray} M_{\rm eq}=14.9\,M_\odot\left( \frac{\dot{m}}{0.01} \right)^{0.26}, \end{eqnarray}(6)where we parametrized the accretion rate as Ṁ ≡ ṁ M⊙ yr-1. On the other hand, the accreting star remains on the Hayashi track up to stellar masses of 1000 M⊙, the highest mass reached in the calculation of Hosokawa et al. (2012a). The extended envelope locked at Teff ~ 5000 K allows efficient accretion with only moderate feedback for a longer period.

In this paper, we aim to assess how long this efficient accretion phase can be maintained beyond M ~ 1000 M⊙ without strong feedback from the protostar. In addition, we will discuss the potential impact of nuclear burning for the evolution of the accreting objects, and the conditions under which a quasi-star as opposed to a supermassive star may form. For this purpose, we explore the interplay of mass accretion and Kelvin-Helmholtz contraction in Sect. 2. We calculate the impact of nuclear burning in Sect. 3. A final discussion of our results is provided in Sect. 4. The impact of additional processes such as deuterium shell burning and hydrogen burning via the pp-chain is assessed in the Appendix.

2. The interplay of mass accretion and Kelvin-Helmholtz contraction

In the following, we will sketch why the protostar may maintain large envelopes even if the Kelvin-Helmholtz timescale becomes shorter than the timescale for accretion. For this purpose, we consider mass shells of enclosed mass M, located at radii R(M,t). A mass shell M forms at the time M/Ṁ, with an initial radius as given by Eq. (2). 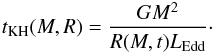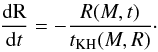The radii of these mass shells evolve on their Kelvin-Helmholtz timescale, given as tKH(M,R)=GM2R(M,t)LEdd·\begin{eqnarray} t_{\rm KH}(M,R)=\frac{GM^2}{R(M,t) L_{\rm Edd}}\cdot \label{tkh} \end{eqnarray}(7)As a result, we have dRdt=−R(M,t)tKH(M,R)·\begin{eqnarray} \frac{\rm dR}{{\rm d}t}=-\frac{R(M,t)}{t_{\rm KH}(M,R)}\cdot \end{eqnarray}(8)The equation is integrated between the initial radius Rin when the mass shell forms, given in (2), corresponding to the time tin(M) = M/Ṁ, to the current radius R at time t. 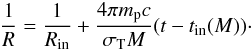The integration yields 1R=1Rin+4πmpcσTM(t−tin(M))·\begin{eqnarray} \frac{1}{R}=\frac{1}{R_{\rm in}}+\frac{4\pi m_{\rm p} c}{\sigma_{\rm T} M}(t-t_{\rm in}(M))\cdot\label{shell} \end{eqnarray}(9)Inserting the initial radius as given in Eq. (2) and expressing the result in astrophysical units, we obtain 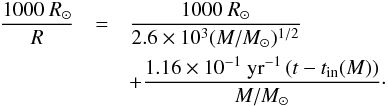1000R⊙R=1000R⊙2.6×103(M/M⊙)1/2\begin{eqnarray} \frac{1000~R_\odot}{R}&=&\frac{1000~R_\odot}{2.6\times10^3(M/M_\odot)^{1/2}}\nonumber\\ &&+\frac{1.16\times10^{-1}\ \mathrm{yr}^{-1}\left(t-t_{\rm in}(M)\right)}{M/M_\odot}\cdot\label{evR} \end{eqnarray}(10)The first term on the right-hand side thus dominates right after the formation of a mass shell and determines its initial radius, while the second term describes its evolution due to Kelvin-Helmholtz contraction. It is remarkable that at late times, the second term dominates and the evolution of the radii appears to be independent of their initial position. This can be understood, as our expression for the Kelvin-Helmholtz timescale, Eq. (7), scales with the inverse radius of the mass shell. As a result, the evolution slows down during the contraction, implying that the Kelvin-Helmholtz timescale may increase significantly in the interior. An example for the resulting structure in a 105 M⊙ star is given in Fig. 1, including both the regime where the first and the second term of the equation dominate.

thumbnail Fig. 1

Enclosed mass as a function of radius in the protostar calculated from Eq. (10), assuming a total stellar mass of 105 M⊙ and mass accretion rates ṁ = 0.1,1.,10. The current time t is calculated as t = (M/M⊙)/ṁ. For a given mass shell, higher accretion rates imply larger radii, as the star had less time to contract.

We now aim to estimate when a given mass shell reaches the densities of nuclear burning, which we take as ρnuc ~ 1 g cm-3 (Hosokawa et al. 2012a). We obtain a radius of nuclear burning, which is given as 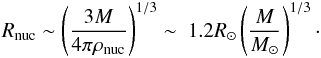Rnuc~(3M4πρnuc)1/3~1.2R⊙(MM⊙)1/3·\begin{eqnarray} R_{\rm nuc}\sim\left( \frac{3M}{4\pi\rho_{\rm nuc}} \right)^{1/3}\sim\ 1.2R_\odot\left(\frac{M}{M_\odot}\right)^{1/3}\cdot\label{Rnuc} \end{eqnarray}(11)We note that the above provides only a rough estimate of the radius of the nuclear core. If the latter were more compact, the timescale for a given mass scale to reach nuclear burning would become even longer, implying that more mass could be accreted during that time. A comparison with Eq. (2) shows that this radius always remains smaller than the radius of the star by at least a factor of 1000, and in fact increases more gradually with stellar mass. A given mass shell M will only reach nuclear densities on timescales much longer than the initial Kelvin-Helmholtz timescale tKH, which increases as R-1. We can thus determine the time when nuclear densities are reached by equating (11) with the second term in (10). 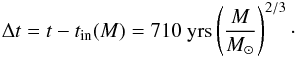As a result, we obtainΔt=t−tin(M)=710yrs(MM⊙)2/3·\begin{eqnarray} \Delta t=t-t_{\rm in}(M)=710\ \mathrm{yrs}\left( \frac{M}{M_\odot} \right)^{2/3}\cdot\label{Deltat} \end{eqnarray}(12)During the time interval Δt, the star will accrete an additional mass ΔM = ṀΔt. 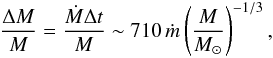Considering a given mass shell, we can calculate the ratio ΔMM=ṀΔtM~710 ṁ(MM⊙)−1/3,\begin{eqnarray} \frac{\Delta M}{M}=\frac{\dot{M}\Delta t }{M}\sim710\,\dot{m}\left( \frac{M}{M_\odot} \right)^{-1/3}, \end{eqnarray}(13)which describes how much additional mass is accreted before the shell reaches nuclear densities. 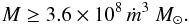The ratio drops below 1 only for protostellar masses of M≥3.6×108 ṁ3M⊙.\begin{eqnarray} M\geq3.6\times10^8\,\dot{m}^3~M_\odot.\label{Mmax} \end{eqnarray}(14)While for typical accretion rates of ṁ ~ 10-3, this happens already at mass scales of order unity, this transition occurs only at substantially higher masses above 1000 M⊙ for ṁ > 10-2. While a given shell evolves toward nuclear densities, the amount of additional mass that is accreted is thus substantially higher than the mass in that shell. From Eq. (12), we can further derive the mass in the nuclear core in the limit that t ≫ tin(M). 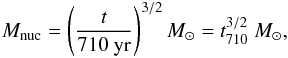We obtainMnuc=(t710yr)3/2M⊙=t7103/2M⊙,\begin{eqnarray} M_{\rm nuc}=\left( \frac{t}{710\ \mathrm{yr}} \right)^{3/2}M_\odot=t_{710}^{3/2}~M_\odot,\label{Mnuc} \end{eqnarray}(15)where we defined t710 = t/(710 yr). As we neglected the term M/Ṁ in Eq. (12), we note that the derivation here implicitly assumes a sufficient mass supply to the protostar in order to feed the core. Clearly, this approximation will break down at the mass scale derived in (14). At that point, the protostellar mass may become approximately constant, and we expect a transition toward supermassive main sequence stars.

From this model, we already obtain a set of relevant conclusions concerning the evolution of the protostar. In particular, if the accretion rate is high, a substantial amount of additional matter is accreted before a given shell reaches nuclear densities. As a result, the evolution of the protostar is dominated not by the interior shells, but by the additional matter which is accreted during the contraction. This behavior will only change when the timescale of accretion becomes comparable to the timescale on which the outer mass shell is able to reach nuclear densities. As we show here, the latter is significantly larger than the Kelvin-Helmholtz timescale of the star, and scales as 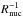Rnuc-1\hbox{$R_{\rm nuc}^{-1}$}. The transition occurs when a critical mass scale of 3.6 × 108ṁ3 M⊙ is reached, implying a transition toward a supermassive main sequence star. We note that the transition may even occur earlier if ṁ decreases with time.

3. The nuclear evolution

In this section, we will assess the potential role of nuclear burning. For this purpose, we show that the transition to the CNO-cycle rapidly occurs and regulates the production of helium in the nuclear core. We will then calculate under which conditions the fuel in the nuclear core will be exhausted while the protostar maintains its extended envelope. The latter implies the potential formation of a black hole in the interior, thus a transition into a quasi-star.

3.1. Importance of the CNO-cycle

While the pp-cycle will dominate in the very beginning (see appendix), we show here that the transition to the CNO-cycle rapidly occurs as a result of helium burning via the triple-α process. Following Padmanabhan (2000), the energy production rate via triple-α is given as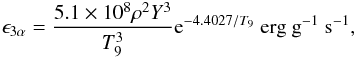ϵ3α=5.1×108ρ2Y3T93e−4.4027/T9ergg-1s-1,\begin{eqnarray} \epsilon_{3\alpha}=\frac{5.1\times10^8\rho^2Y^3}{T_9^3}{\rm e}^{-4.4027/T_9}\mathrm{\ erg\ g}^{-1}\mathrm{\ s}^{-1}, \end{eqnarray}(16)where Y ~ 0.25 denotes the mass fraction of helium and T9 denotes the gas temperature in units of 109 K. It is straightforward to check that the energy production rate changes by several orders of magnitude for temperature changes on the order of 10%. As shown by Hosokawa et al. (2012a), the highest temperatures with T9 ~ 0.15 are expected in the center of the nuclear core, which has an enhanced nuclear density of 10 g cm-3. With a volume filling factor ϵfill ~ 0.01−0.1, the contribution of that region to helium burning is significant due to the steep temperature dependence. For the following estimates, we will assume that efficient mixing occurs throughout the nuclear core, implying that the heavy elements produced in the central region will be available throughout the core. On the other hand, if mixing is inefficient, nuclear burning via the CNO cycle will dominate even more in the central region due to its higher metallicity.

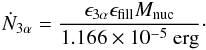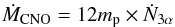Noting that the energy released by a single triple-α reaction corresponds to 1.166 × 10-5 erg,the number of heavy elements produced per unit time is given asṄ3α=ϵ3αϵfillMnuc1.166×10-5erg·\begin{eqnarray} \dot N_{3\alpha}=\frac{\epsilon_{3\alpha}\epsilon_{\rm fill} M_{\rm nuc}}{1.166\times 10^{-5}~{\rm erg}}\cdot \end{eqnarray}(17)The CNO mass in the core thus evolves as ṀCNO=12mp×Ṅ3α\begin{eqnarray} \dot M_{\rm CNO} = 12 m_{\rm p} \times \dot N_{3\alpha} \end{eqnarray}(18)and an integration yieldsMCNO=7.1×10-17ϵfill t7105/2 M⊙.\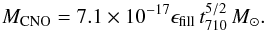begin{eqnarray} M_{\mathrm{CNO}}=7.1\times10^{-17}\epsilon_{\rm fill}\,t_{710}^{5/2}\,M_\odot. 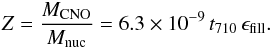\end{eqnarray}(19)Assuming efficient mixing, the resulting metallicity in the nuclear core is then Z=MCNOMnuc=6.3×10-9 t710 ϵfill.\begin{eqnarray} Z=\frac{M_{\mathrm{CNO}}}{M_{\rm nuc}}=6.3\times10^{-9}\,t_{710}\,\epsilon_{\rm fill}.\label{Zprod} \end{eqnarray}(20)We recall that the energy production rate in the CNO cycle is given as (Padmanabhan 2000)ϵCNO=4.4×1025ρXZT92/3e−15.228/T91/3ergg-1s-1.\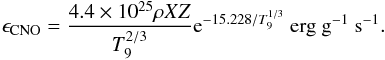begin{eqnarray} \epsilon_{\mathrm{CNO}}=\frac{4.4\times10^{25}\rho X Z}{T_9^{2/3}}{\rm e}^{-15.228/T_9^{1/3}}\mathrm{\ erg\ g}^{-1}\mathrm{\ s}^{-1}. \end{eqnarray}(21)Since the energy production rate depends sensitively on the temperature, we expect its contribution in the innermost core to be dominant. For the temperature T9 = 0.15, it is straightforward to show that energy production via the CNO cycle becomes comparable to the pp cycle for a metallicity of Zc = 2 × 10-12. A comparison with Eq. 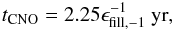(20) shows that the CNO cycle thus dominates after a short time of tCNO=2.25ϵfill,−1-1yr,\begin{eqnarray} t_{\mathrm{CNO}}=2.25\epsilon_{\rm fill,-1}^{-1}~\mathrm{yr}, \end{eqnarray}(22)where we introduced ϵfill = 0.1ϵfill, −1. We note here that this timescale is probably not accurate, as our assumptions in Sect. 2 (in particular concerning the Eddington luminosity) only become valid at later times. Nevertheless, this result implies that the CNO cycle can be expected to be relevant early on, and thus needs to be considered. As the production of elements becomes increasingly efficient at late times, we expect that the expression (20) will yield a reasonable estimate in the period of interest.

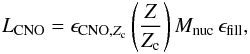With the above assumptions, the CNO luminosity due to nuclear burning is given as LCNO=ϵCNO,Zc(ZZc)Mnuc ϵfill,\begin{eqnarray} L_{\mathrm{\mathrm{CNO}}}=\epsilon_{\mathrm{CNO},Z_{\rm c}}\left(\frac{Z}{Z_{\rm c}}\right)M_{\rm nuc}\,\epsilon_{\rm fill}, \end{eqnarray}(23)where ϵCNO,Zc denotes the energy production rate via the CNO cycle evaluated at the critical metallicity Zc. 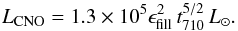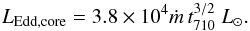Inserting (20), we obtainLCNO=1.3×105ϵfill2 t7105/2 L⊙.\begin{eqnarray} L_{\mathrm{CNO}}=1.3\times10^5 \epsilon_{\rm fill}^2 \,t_{710}^{5/2}\,L_\odot.\label{EqCNO} \end{eqnarray}(24)The Eddington luminosity of the nuclear core is given asLEdd,core=3.8×104ṁ t7103/2L⊙.\begin{eqnarray} L_{{\mathrm{Edd,core}}}=3.8\times10^4\dot{m}\,t_{710}^{3/2}~L_\odot.\label{EqCore} \end{eqnarray}(25)The ratio of these luminosities to the Eddington luminosity of the star is given in Fig. 2. Even here, the luminosity produced by nuclear burning approaches the Eddington luminosity of the star only around stellar masses of 108 M⊙, implying no relevant impact on the stellar evolution during the earlier stages. 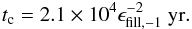A comparison of these expressions yields the timescale tc=2.1×104ϵfill,−1-2yr.\begin{eqnarray} t_{\rm c}=2.1\times10^4\epsilon_{\rm fill,-1}^{-2}~\mathrm{yr}. \end{eqnarray}(26)For ϵfill, −1 ~ 1, as indicated by Hosokawa et al. (2012a) for ṁ = 0.1, the CNO luminosity would exceed the Eddington luminosity of the core after ~2 × 104 yr, shortly after the end of their simulations. However, when the Eddington luminosity is reached, one would expect an expansion of the nuclear core, implying lower densities and an adiabatically decreasing temperature. Due to this thermostat, it is likely that the core will adjust to a state maintaining its Eddington luminosity.

thumbnail Fig. 2

Ratio of nuclear luminosity provided via the CNO-cycle over the Eddington luminosity of the star as a function of protostellar mass for different mass accretion rates. The CNO luminosity is calculated here as the minimum of the estimate in Eq. (24) and the Eddington luminosity of the nuclear core in Eq. (25). At high protostellar masses, one can clearly recognize the transition to the regime where nuclear burning is limited by the Eddington luminosity of the core. Higher accretion rates imply that less time was available for contraction, thus reducing the nuclear luminosities.

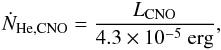We will now demonstrate that the nuclear core is not converted to helium before the critical timescale tc after which the core radiates at its Eddington luminosity. 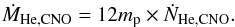We consider the production of helium by the CNO process, given as ṄHe,CNO=LCNO4.3×10-5erg,\begin{eqnarray} \dot{N}_{\mathrm{He,CNO}}=\frac{L_{\mathrm{CNO}}}{4.3\times10^{-5}\mathrm{\ erg}}, \end{eqnarray}(27)and the helium mass production rateṀHe,CNO=12mp×ṄHe,CNO.\begin{eqnarray} \dot{M}_{\mathrm{He,CNO}}=12m_{\rm p}\times\dot{N}_{\mathrm{He,CNO}}. 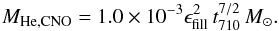\end{eqnarray}(28)An integration yields MHe,CNO=1.0×10-3ϵfill2 t7107/2 M⊙.\begin{eqnarray} M_{\mathrm{He,CNO}}=1.0\times10^{-3}\epsilon_{\rm fill}^2\,t_{710}^{7/2}\,M_\odot. 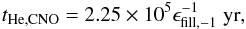\end{eqnarray}(29)A comparison with the mass of the core indicates that they become comparable at tHe,CNO=2.25×105ϵfill,−1-1yr,\begin{eqnarray} t_{\mathrm{He,CNO}}=2.25\times10^5\epsilon_{\rm fill,-1}^{-1}\mathrm{\ yr}, \end{eqnarray}(30)implying that a pure helium core will only be formed once the nuclear luminosity is equal to the Eddington luminosity of the core.

3.2. Formation of a helium core

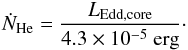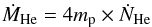We will now calculate the helium production rate under the assumption that the formation of a helium core occurs once the nuclear luminosity equals the Eddington luminosity of the core. 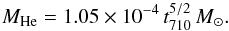Thus, ṄHe=LEdd,core4.3×10-5erg·\begin{eqnarray} \dot{N}_{\rm He}=\frac{L_{\mathrm{Edd,core}}}{4.3\times10^{-5}~\mathrm{erg}}\cdot \end{eqnarray}(31)The helium mass production rate is thus given asṀHe=4mp×ṄHe\begin{eqnarray} \dot{M}_{\rm He}=4m_{\rm p}\times\dot{N}_{\rm He} \end{eqnarray}(32)and an integration yieldsMHe=1.05×10-4 t7105/2 M⊙.\begin{eqnarray} M_{\rm He}=1.05\times10^{-4}\,t_{710}^{5/2}\,M_\odot .\label{coreHe} \end{eqnarray}(33)Equating Eq. (33) with Eq. (15), we find that the nuclear core becomes a pure helium core after tf ≃ 6.8 × 106 yr. We note that at this point, the mass of the nuclear core is given as Mf ≃ 9.4 × 105 M⊙. In order to illustrate how the latter translates into total stellar masses, the ratio of helium mass to total mass in the core is displayed in Fig. 3 for different accretion rates, showing that the hydrogen fuel is indeed exhausted for stellar masses of 3 × 105−3 × 107 M⊙ depending on the accretion rate. After that point, the burning of heavier elements will occur, but only last for a short period. As the mass of the core is considerably higher than the Chandrasekhar mass scale and the Tolman-Oppenheimer-Volkoff mass scale, the core may collapse and form a black hole within the star, a so-called quasi-star, as proposed by Begelman et al. (2006) and Begelman (2010). The interior black hole may then continue accreting from the stellar envelope, while the accretion rate of the quasi-star will only be limited by the Eddington rate corresponding to the total mass of the configuration. 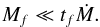The derivation of tf and Mf, however, implicitly assumes that enough mass has been accreted in order to build up the core, requiring that Mf≪tfṀ.\begin{eqnarray} M_f\ll t_f \dot{M}. \end{eqnarray}(34)To form a quasi-star, we thus require an accretion rate of Ṁ ≫ Mf/tf, i.e. 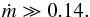ṁ≫0.14.\begin{eqnarray} \dot{m}\gg 0.14. \end{eqnarray}(35)For lower accretion rates, we expect that the extended envelope of the star cannot be maintained at late times, implying that the star will contract and form a supermassive main sequence star. During this period, both the stellar mass and the mass in the nuclear core will be approximately constant, implying a characteristic hydrogen burning timescale of 2 × 106 yr. For stellar masses above 300 M⊙, these are expected to collapse to massive black holes (Fryer et al. 2001; Fryer & Heger 2011).

thumbnail Fig. 3

Fraction of helium in the nuclear core, corresponding to the amount of exhausted fuel for nuclear burning, as a function of protostellar mass for different accretion rates. Higher accretion rates imply less time for protostellar contraction. As a result, nuclear densities are reached later, implying less time for nuclear burning.

4. Discussion and outlook

To investigate the interplay of accretion and Kelvin-Helmholtz-contraction of the protostar, we have presented an analytical model following the evolution of the mass shells from the extended envelope down to nuclear densities. Based on this model, we are able to explain the fundamental result by Hosokawa et al. (2012a) that the accreting protostar keeps its extended envelope beyond the adiabatic accretion phase. The reason is that the timescale on which a given mass shell may reach nuclear densities is much longer than the Kelvin-Helmholtz timescale of the star, as the protostellar radius is considerably larger than the radius of the nuclear core. Instead of the Kelvin-Helmholtz timescale evaluated at the protostellar radius, the relevant timescale is thus the Kelvin-Helmholtz timescale at the expected core radius after contraction, providing an appropriate estimate of the evolutionary timescale. As a consequence, rapidly accreting protostars are expected to keep their extended envelopes until stellar masses of 3.6 × 108 ṁ3 M⊙. At this point, the accretion timescale becomes longer than the Kelvin-Helmholtz timescale in the stellar interior, implying that the star will subsequently contract toward the main sequence. Then, we expect it to follow the typical evolution of a supermassive star as sketched by Shapiro & Teukolsky (1986).

We further assessed the impact of nuclear burning for the evolution of these stars. While deuterium burning will never be relevant during the protostellar evolution, hydrogen burning via the pp-cycle could potentially affect the stellar evolution after 1015 years, which is, however, practically irrelevant. Due to the efficient metal production via the triple-α process, a transition to the CNO cycle is expected early on. The energy production by the CNO cycle is considerably more efficient, implying that the core can radiate at its Eddington luminosity. As a result, a helium core forms after 7 × 106 yr. The expected mass of the core is then 106 M⊙, which provides an upper limit on the initial mass of the interior black hole. Therefore, if the available gas reservoir is sufficient to maintain accretion rates ṁ ≫ 0.14 until this point, the central core may collapse during the protostellar evolution phase, and the object becomes a quasi-star. Alternatively, the protostar will evolve toward the main sequence to become a supermassive star. Such an object is then expected to collapse into a SMBH at the end of its lifetime (Fryer & Heger 2011). A summary of our results regarding the evolution of rapidly accreting protostars is given in Table 1.

Table 1

Pathways to the formation of main-sequence supermassive stars and quasi-stars depending on the critical mass scale Mcr(ṁ) = 3.6 × 108 ṁ3 M⊙ and the accretion rate ṁ in solar masses per year.

Our results have been derived based on a comparison of the mass accumulated by accretion with the characteristic mass scale where we expect a pure helium core. This mass scale is based on the reasonable assumption that the luminosity of the core is given by its Eddington luminosity, in agreement with the numerical results by Hosokawa et al. (2012a). Uncertainties are, however, present, as our calculation for the evolution of the core mass assumes that the luminosity of each mass shell is given by the Eddington luminosity. Following Hosokawa et al. (2012a), the latter is a good but not precise approximation. Further corrections can be expected in particular when approaching nuclear densities, when feedback from nuclear burning becomes significant.We further note that in the regime where deviations from the hydrostatic equilibrium are significant, as during the collapse of the nuclear core or during the accretion onto the protostellar envelope, it is conceivable that the luminosity released from the gravitational potential may locally exceed the Eddington luminosity if the accretion rate is high enough. Due to the momentum of the flow, we, however, expect that such accretion rates could still overcome the radiative feedback and effectively trap the photons in the optically thick material. We further note that Dotan & Shaviv (2012) propose a scenario where porosity induced by instabilities may lead to super-Eddington luminosities.

The results obtained differ from the scenario proposed by Begelman et al. (2006) and Begelman (2010), as we make use of new results on the protostellar evolution that were obtained in the recent study by Hosokawa et al. (2012a). In particular, we note that Begelman et al. (2006) still assumed a time-independent radius of the quasi-stars, and both Begelman et al. (2006) and Begelman (2010) adopted Thomson scattering as the only opacity source. However, Hosokawa et al. (2012a) have shown that H− may significantly contribute to the opacity in the atmosphere. By considering the timescale required for a given mass shell to reach nuclear densities, we further have shown here that the star may remain on the Hayashi track for a much longer period than expected before. The latter gives rise to considerable differences in the stellar evolution, and allows for significant amounts of accretion while feedback is weak.

Additional effects could be introduced as a result of rotation, which was not included in this model. We thus expect our results to provide an order of magnitude estimate for the critical accretion rate, which may be determined more accurately employing stellar evolution calculations, but also a more realistic model for the time-dependent accretion rate. We also note here that Hosokawa et al. (2012a) reported a slight dependence of their results on the employed boundary conditions for the protostar. While their main calculations adopted shock boundary conditions, they also explored the effect of lower-entropy accretion provided by photospheric boundary conditions. In that case, a slightly higher accretion rate of 0.3 M⊙ yr-1 appears to be required to maintain the extended envelopes, but the overall evolution remains very similar.

For comparison, we note that recent simulations by Latif et al. (2013c) reported accretion rates of ~1 M⊙ yr-1 in halos with ~107 M⊙. Adopting a constant accretion rate, the transition to a supermassive main sequence star would occur at a stellar mass of 3.6 × 108 M⊙. As the nuclear fuel is, however, exhausted earlier, a central black hole may form before this transition, giving rise to an evolution as sketched by Ball et al. (2011). Due to the limited gas reservoir, and as here the halo mass is in fact comparable to the mass scale of the corresponding quasi-star, it seems likely that the accretion rate will substantially decrease at late times, implying that the transition toward the supermassive star should occur at an earlier stage which is then determined by the time evolution of the accretion rate, and that supermassive stars with 104−105 M⊙ might be the most generic outcome of the collapse. More massive objects appear to be possible at least in principle, if a larger gas reservoir is available in more massive dark matter halos.

In order to assess the potential influence of rotation, we estimated the amount of rotational support in the central 103 M⊙ clumps reported by Latif et al. (2013c), which varied between 5−20% in different simulations. With densities of ~10-10 g cm-3, these are still orders of magnitudes below the characteristic densities within the protostar, such that we cannot yet draw strong conclusions regarding the final amount of rotational energy. However, we note that Stacy et al. (2012) reported a significant amount of rotation in primordial protostars based on numerical simulations of Greif et al. (2012), and a quite similar case can be expected here. As recently shown by Reisswig et al. (2013), the latter may have a substantial impact on the collapse of supermassive stars, implying the potential formation of a black hole binary and a subsequent merger, accompanied with efficient emission of gravitational waves. The latter provides a potential pathway of probing black hole formation scenarios with LISA1. In a narrow mass range around ~55 000 M⊙, one may further expect the occurence of highly energetic supernovae with energies up to 1044 erg, which can be potentially detected with JWST2 (Johnson et al. 2013).

Returning to the fate of supermassive stars, their evolution in the presence of UV feedback was assessed by Omukai & Inutsuka (2002) and Johnson et al. (2012) in the case of spherical symmetry. These authors find that UV feedback is unable to stop accretion for rates above ~0.1 M⊙ yr-1. As a result, the expected stellar mass is 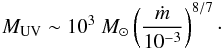MUV~103M⊙(ṁ10-3)8/7·\begin{eqnarray} M_{\rm UV}\sim10^3~M_\odot\left( \frac{\dot{m}}{10^{-3}} \right)^{8/7}\cdot \end{eqnarray}(36)For accretion rates of ~0.1 M⊙ yr-1, our results exceed this value, as the protostars remain on the Hayashi track up to a mass of ~3 × 105 M⊙, making feedback inefficient. Therefore, taking protostellar evolution into account favors the formation of more massive objects. In all cases, a critical question concerns the time evolution of the accretion rate, since the transition to supermassive stars is regulated by the accretion rate at late times. While this paper provides a first assessment for the case of constant accretion rates and spherical symmetry, the potential implications of time-dependent accretion rates need to be addressed in more detail in the future, along with the implications of rotation during protostellar evolution.

1

LISA webpage: http://lisa.nasa.gov/

2

JWST webpage: http://www.jwst.nasa.gov/

Acknowledgments

D.R.G.S. and M.L. thank for funding from the Deutsche Forschungsgemeinschaft (DFG) via the SFB 963/1 “Astrophysical flow instabilities and turbulence” (project A12). DRGS further acknowledges financial support via the Schwerpunktprogramm SPP 1573 “Physics of the Interstellar Medium” under grant SCHL 1964/1-1.We thank the anonymous referee for valuable comments that helped to improve our manuscript.

References

  1. Abel, T., Bryan, G. L., & Norman, M. L. 2002, Science, 295, 93 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  2. Agarwal, B., Khochfar, S., Johnson, J. L., et al. 2012, MNRAS, 425, 2854 [NASA ADS] [CrossRef] [Google Scholar]
  3. Ball, W. H., Tout, C. A., Żytkow, A. N., & Eldridge, J. J. 2011, MNRAS, 414, 2751 [NASA ADS] [CrossRef] [Google Scholar]
  4. Ball, W. H., Tout, C. A., & Żytkow, A. N. 2012, MNRAS, 421, 2713 [NASA ADS] [CrossRef] [Google Scholar]
  5. Begelman, M. C. 2010, MNRAS, 402, 673 [NASA ADS] [CrossRef] [Google Scholar]
  6. Begelman, M. C., & Shlosman, I. 2009, ApJ, 702, L5 [NASA ADS] [CrossRef] [Google Scholar]
  7. Begelman, M. C., Volonteri, M., & Rees, M. J. 2006, MNRAS, 370, 289 [NASA ADS] [CrossRef] [Google Scholar]
  8. Begelman, M. C., Rossi, E. M., & Armitage, P. J. 2008, MNRAS, 387, 1649 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bromm, V., & Loeb, A. 2003, ApJ, 596, 34 [NASA ADS] [CrossRef] [Google Scholar]
  10. Bromm, V., & Larson, R. B. 2004, ARA&A, 42, 79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Choi, J.-H., Shlosman, I., & Begelman, M. C. 2013, ApJ, 774, 149 [NASA ADS] [CrossRef] [Google Scholar]
  12. Clark, P. C., Glover, S. C. O., & Klessen, R. S. 2008, ApJ, 672, 757 [NASA ADS] [CrossRef] [Google Scholar]
  13. Clark, P. C., Glover, S. C. O., Smith, R. J., et al. 2011, Science, 331, 1040 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  14. de Souza, R. S., Ciardi, B., Maio, U., & Ferrara, A. 2013, MNRAS, 428, 2109 [NASA ADS] [CrossRef] [Google Scholar]
  15. Devecchi, B., & Volonteri, M. 2009, ApJ, 694, 302 [NASA ADS] [CrossRef] [Google Scholar]
  16. Devecchi, B., Volonteri, M., Colpi, M., & Haardt, F. 2010, MNRAS, 409, 1057 [NASA ADS] [CrossRef] [Google Scholar]
  17. Devecchi, B., Volonteri, M., Rossi, E. M., Colpi, M., & Portegies Zwart, S. 2012, MNRAS, 421, 1465 [NASA ADS] [CrossRef] [Google Scholar]
  18. Dijkstra, M., Haiman, Z., Mesinger, A., & Wyithe, J. S. B. 2008, MNRAS, 391, 1961 [NASA ADS] [CrossRef] [Google Scholar]
  19. Dopcke, G., Glover, S. C. O., Clark, P. C., & Klessen, R. S. 2011, ApJ, 729, L3 [NASA ADS] [CrossRef] [Google Scholar]
  20. Dopcke, G., Glover, S. C. O., Clark, P. C., & Klessen, R. S. 2013, ApJ, 766, 103 [NASA ADS] [CrossRef] [Google Scholar]
  21. Dotan, C., & Shaviv, N. J. 2012, MNRAS, 427, 3071 [NASA ADS] [CrossRef] [Google Scholar]
  22. Eggleton, P. P. 1971, MNRAS, 151, 351 [NASA ADS] [CrossRef] [Google Scholar]
  23. Fan, X., Naraynan, V. K., Lupton, R. H., et al. 2001, AJ, 122, 2833 [NASA ADS] [CrossRef] [Google Scholar]
  24. Fan, X., Strauss, M. A., Schneider, D. P., et al. 2003, AJ, 125, 1649 [NASA ADS] [CrossRef] [Google Scholar]
  25. Fan, X., Hennawi, J. F., Richards, G. T., et al. 2004, AJ, 128, 515 [NASA ADS] [CrossRef] [Google Scholar]
  26. Fan, X., Strauss, M. A., Richards, G. T., et al. 2006, AJ, 131, 1203 [NASA ADS] [CrossRef] [Google Scholar]
  27. Federrath, C., Sur, S., Schleicher, D. R. G., Banerjee, R., & Klessen, R. S. 2011, ApJ, 731, 62 [NASA ADS] [CrossRef] [Google Scholar]
  28. Fryer, C. L., & Heger, A. 2011, Astron. Nachr., 332, 408 [NASA ADS] [CrossRef] [Google Scholar]
  29. Fryer, C. L., Woosley, S. E., & Heger, A. 2001, ApJ, 550, 372 [NASA ADS] [CrossRef] [Google Scholar]
  30. Greif, T. H., Springel, V., White, S. D. M., et al. 2011, ApJ, 737, 75 [NASA ADS] [CrossRef] [Google Scholar]
  31. Greif, T. H., Bromm, V., Clark, P. C., et al. 2012, MNRAS, 424, 399 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  32. Haiman, Z. 2006, New Astron. Rev., 50, 672 [NASA ADS] [CrossRef] [Google Scholar]
  33. Hayashi, C., Hōshi, R., & Sugimoto, D. 1962, Progr. Theoret. Phys. Suppl., 22, 1 [Google Scholar]
  34. Heger, A., & Woosley, S. E. 2002, ApJ, 567, 532 [NASA ADS] [CrossRef] [Google Scholar]
  35. Hosokawa, T., & Omukai, K. 2009, ApJ, 703, 1810 [NASA ADS] [CrossRef] [Google Scholar]
  36. Hosokawa, T., Omukai, K., Yoshida, N., & Yorke, H. W. 2011, Science, 334, 1250 [Google Scholar]
  37. Hosokawa, T., Omukai, K., & Yorke, H. W. 2012a, ApJ, 756, 93 [Google Scholar]
  38. Hosokawa, T., Yoshida, N., Omukai, K., & Yorke, H. W. 2012b, ApJ, 760, L37 [NASA ADS] [CrossRef] [Google Scholar]
  39. Inayoshi, K., & Omukai, K. 2012, MNRAS, 422, 2539 [NASA ADS] [CrossRef] [Google Scholar]
  40. Johnson, J. L., Khochfar, S., Greif, T. H., & Durier, F. 2011, MNRAS, 410, 919 [NASA ADS] [CrossRef] [Google Scholar]
  41. Johnson, J. L., Whalen, D. J., Fryer, C. L., & Li, H. 2012, ApJ, 750, 66 [NASA ADS] [CrossRef] [Google Scholar]
  42. Johnson, J. L., Whalen, D. J., Even, W., et al. 2013, ApJ, submitted [arXiv:1304.4601] [Google Scholar]
  43. Klessen, R. S., Glover, S. C. O., & Clark, P. C. 2012, MNRAS, 421, 3217 [NASA ADS] [CrossRef] [Google Scholar]
  44. Koushiappas, S. M., Bullock, J. S., & Dekel, A. 2004, MNRAS, 354, 292 [NASA ADS] [CrossRef] [Google Scholar]
  45. Latif, M. A., Schleicher, D. R. G., Spaans, M., & Zaroubi, S. 2011, A&A, 532, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Latif, M. A., Schleicher, D. R. G., Schmidt, W., & Niemeyer, J. 2013a, MNRAS, 430, 588 [NASA ADS] [CrossRef] [Google Scholar]
  47. Latif, M. A., Schleicher, D. R. G., Schmidt, W., & Niemeyer, J. 2013b, MNRAS, 432, 668 [NASA ADS] [CrossRef] [Google Scholar]
  48. Latif, M. A., Schleicher, D. R. G., Schmidt, W., & Niemeyer, J. 2013c, MNRAS, 433, 1607 [NASA ADS] [CrossRef] [Google Scholar]
  49. Lodato, G., & Natarajan, P. 2006, MNRAS, 371, 1813 [NASA ADS] [CrossRef] [Google Scholar]
  50. Milosavljević, M., Bromm, V., Couch, S. M., & Oh, S. P. 2009a, ApJ, 698, 766 [NASA ADS] [CrossRef] [Google Scholar]
  51. Milosavljević, M., Couch, S. M., & Bromm, V. 2009b, ApJ, 696, L146 [NASA ADS] [CrossRef] [Google Scholar]
  52. Mortlock, D. J., Warren, S. J., Venemans, B. P., et al. 2011, Nature, 474, 616 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  53. Omukai, K. 2001, ApJ, 546, 635 [NASA ADS] [CrossRef] [Google Scholar]
  54. Omukai, K. 2012, PASJ, 64, 114 [NASA ADS] [Google Scholar]
  55. Omukai, K., & Inutsuka, S.-I. 2002, MNRAS, 332, 59 [NASA ADS] [CrossRef] [Google Scholar]
  56. Omukai, K., & Palla, F. 2001, ApJ, 561, L55 [NASA ADS] [CrossRef] [Google Scholar]
  57. Omukai, K., & Palla, F. 2003, ApJ, 589, 677 [NASA ADS] [CrossRef] [Google Scholar]
  58. Omukai, K., Tsuribe, T., Schneider, R., & Ferrara, A. 2005, ApJ, 626, 627 [NASA ADS] [CrossRef] [Google Scholar]
  59. Omukai, K., Schneider, R., & Haiman, Z. 2008, ApJ, 686, 801 [NASA ADS] [CrossRef] [Google Scholar]
  60. Padmanabhan, T. 2000, Theoretical Astrophysics – Vol. 1, Astrophys. Proc. (Cambridge University Press) [Google Scholar]
  61. Pols, O. R., Tout, C. A., Eggleton, P. P., & Han, Z. 1995, MNRAS, 274, 964 [NASA ADS] [CrossRef] [Google Scholar]
  62. Prieto, J., Jimenez, R., & Haiman, Z. 2013 [arXiv:1301.5567] [Google Scholar]
  63. Rees, M. J. 1984, ARA&A, 22, 471 [NASA ADS] [CrossRef] [Google Scholar]
  64. Regan, J. A., & Haehnelt, M. G. 2009, MNRAS, 396, 343 [NASA ADS] [CrossRef] [Google Scholar]
  65. Reisswig, C., Ott, C. D., Abdikamalov, E., et al. 2013 [arXiv:1304.7787] [Google Scholar]
  66. Schleicher, D. R. G., Spaans, M., & Glover, S. C. O. 2010, ApJ, 712, L69 [NASA ADS] [CrossRef] [Google Scholar]
  67. Schneider, R., Ferrara, A., Salvaterra, R., Omukai, K., & Bromm, V. 2003, Nature, 422, 869 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  68. Schneider, R., Omukai, K., Bianchi, S., & Valiante, R. 2012a, MNRAS, 419, 1566 [NASA ADS] [CrossRef] [Google Scholar]
  69. Schneider, R., Omukai, K., Limongi, M., et al. 2012b, MNRAS, 423, L60 [NASA ADS] [CrossRef] [Google Scholar]
  70. Shang, C., Bryan, G. L., & Haiman, Z. 2010, MNRAS, 402, 1249 [NASA ADS] [CrossRef] [Google Scholar]
  71. Shapiro, S. L. 2005, ApJ, 620, 59 [NASA ADS] [CrossRef] [Google Scholar]
  72. Shapiro, S. L., & Teukolsky, S. A. 1986, Black Holes, White Dwarfs and Neutron Stars: The Physics of Compact Objects [Google Scholar]
  73. Smith, R. J., Glover, S. C. O., Clark, P. C., Greif, T., & Klessen, R. S. 2011, MNRAS, 414, 3633 [NASA ADS] [CrossRef] [Google Scholar]
  74. Smith, R. J., Hosokawa, T., Omukai, K., Glover, S. C. O., & Klessen, R. S. 2012, MNRAS, 424, 457 [NASA ADS] [CrossRef] [Google Scholar]
  75. Spaans, M., & Silk, J. 2006, ApJ, 652, 902 [NASA ADS] [CrossRef] [Google Scholar]
  76. Stacy, A., Greif, T. H., & Bromm, V. 2010, MNRAS, 403, 45 [NASA ADS] [CrossRef] [Google Scholar]
  77. Stacy, A., Greif, T. H., & Bromm, V. 2012, MNRAS, 422, 290 [NASA ADS] [CrossRef] [Google Scholar]
  78. Sur, S., Schleicher, D. R. G., Banerjee, R., Federrath, C., & Klessen, R. S. 2010, ApJ, 721, L134 [NASA ADS] [CrossRef] [Google Scholar]
  79. Susa, H. 2013, ApJ, 773, 185 [NASA ADS] [CrossRef] [Google Scholar]
  80. Turk, M. J., Abel, T., & O’Shea, B. 2009, Science, 325, 601 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  81. Turk, M. J., Oishi, J. S., Abel, T., & Bryan, G. L. 2012, ApJ, 745, 154 [NASA ADS] [CrossRef] [Google Scholar]
  82. Van Borm, C., & Spaans, M. 2013, A&A, 553, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  83. Volonteri, M., & Bellovary, J. 2012, Rep. Progr. Phys., 75, 124901 [Google Scholar]
  84. Volonteri, M., Lodato, G., & Natarajan, P. 2008, MNRAS, 383, 1079 [NASA ADS] [CrossRef] [Google Scholar]
  85. Whalen, D. J., & Fryer, C. L. 2012, ApJ, 756, L19 [NASA ADS] [CrossRef] [Google Scholar]
  86. Wise, J. H., Turk, M. J., & Abel, T. 2008, ApJ, 682, 745 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Additional nuclear processes

In Sect. 3.1, we have shown that the transition to the CNO cycle rapidly occurs, implying that the latter will regulate the formation of a helium core as discussed in Sect. 3.2. However, additional nuclear processes are expected to simultaneously occur, which we discuss here for completeness. In the two sub-sections below, we assess the role of deuterium shell burning as well as the impact of hydrogen burning via the pp-chain during the stellar evolution, showing that these processes will only have a minor impact on the stellar evolution.

Appendix A.1: Deuterium burning

As reported by Hosokawa & Omukai (2009), deuterium shell burning may occur even before nuclear burning starts in the core. The luminosity from deuterium shell burning is given as LD=1.5×105L⊙(ṁ0.1)([D/H]2.5×10-5),\appendix \setcounter{section}{1} \begin{eqnarray} L_D=1.5\times10^5~L_\odot \left( \frac{\dot{m}}{0.1} \right)\left( \frac{[\mathrm{D/H}]}{2.5\times10^{-5}} \right), \end{eqnarray}(A.1)where [D/H] denotes the deuterium abundance relative to hydrogen. For an accretion rate of ṁ = 0.1, Hosokawa et al. (2012a) demonstrated that deuterium shell burning starts only at protostellar masses of ~80 M⊙, and presumably even higher masses in case of higher accretion rates. A comparison with the Eddington accretion rate in Eq. (1) thus shows that the luminosity from deuterium shell burning will never become dominant in this mass range, but in fact becomes increasingly less relevant for higher masses.

It is also clear that deuterium shell burning is not going to occur close to the outer surface. While the characteristic temperature for a given mass shell scales as T ∝ GM/R, we note that, from Eq. (10), GM/R ∝ t = M/Ṁ at times t ≫ M/Ṁ. In this regime, the central temperature is almost spatially constant, consistent with the results of Hosokawa et al. (2012a), but already considerably larger than the deuterium burning temperature of ~106 K. Deuterium burning will thus occur when the first term in Eq. (10) is still relevant. From Fig. 1, it is evident that the radius of the shells changes considerably in that regime, while the mass in the shells is almost unchanged. Adopting a scaling relation of T ∝ GM/R with almost constant M implies that the radius has to change by 2–3 orders of magnitude for the atmospheric temperature of 5000 K to increase to a value above 106 K. We therefore expect that the radius of deuterium burning will correspond to a fixed fraction of the protostellar radius as long as the protostar maintains its bloated envelope. From a comparison with Hosokawa et al. (2012a) at a stellar mass of 1000 M⊙, we obtain the normalization of this relation to be 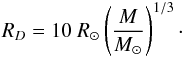RD=10R⊙(MM⊙)1/3·\appendix \setcounter{section}{1} \begin{eqnarray} R_{D}=10~R_\odot \left( \frac{M}{M_\odot} \right)^{1/3}\cdot \end{eqnarray}(A.2)As long as the protostar remains on the Hayashi track, the deuterium burning shell will not be able to move toward the atmosphere, and, therefore, it does not have an impact on the evolution of the protostar.

Appendix A.2: The pp-cycle

We consider first the energy production in the nuclear core via the pp-cycle, as the composition of the star is initially primordial. As shown by Hosokawa et al. (2012a), the typical temperature in the core is ~108 K, and the nuclear density ~1 g cm-3. We adopt here the expression of Padmanabhan (2000) for the energy production rate, noting that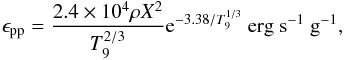ϵpp=2.4×104ρX2T92/3e−3.38/T91/3ergs-1g-1,\appendix \setcounter{section}{1} \begin{eqnarray} \epsilon_{\rm pp}=\frac{2.4\times 10^4\rho X^2}{T_9^{2/3}}{\rm e}^{-3.38/T_9^{1/3}}\mathrm{\ erg\ s}^{-1}\mathrm{\ g}^{-1}, \end{eqnarray}(A.3)where T9 denotes the temperature in units of 109 K and X ~ 0.75 the mass fraction of hydrogen. While the pp-cycle considered here has only a moderate temperature dependence, we note that the CNO cycle scales as T20 around temperatures of 106 K, and the triple-α process as T40 around temperatures of 108 K. For the latter cases, we will thus need to take into account the higher temperatures within the center of the core, as they substantially contribute to the energy production via nuclear burning. Now, with ρnuc ~ 1 g cm-3 and T9 = 0.1, we have ϵpp = 43 erg g-1 s-1. 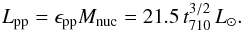The luminosity provided by the pp-cycle is then given as Lpp=ϵppMnuc=21.5 t7103/2 L⊙.\appendix \setcounter{section}{1} \begin{eqnarray} L_{\rm pp}=\epsilon_{\rm pp}M_{\rm nuc}=21.5\, t_{710}^{3/2}\, L_\odot. 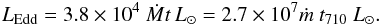\label{EqLpp} \end{eqnarray}(A.4)For comparison, the Eddington luminosity of the protostar is given as LEdd=3.8×104Ṁt L⊙=2.7×107ṁt710L⊙.\appendix \setcounter{section}{1} \begin{eqnarray} L_{\rm Edd}=3.8\times10^4~\dot{M} t\,L_\odot=2.7\times10^7\dot{m}~t_{710}~L_\odot . \label{EqLEdd} \end{eqnarray}(A.5)The ratio of these luminosities is given in Fig. A.1, showing that it remains considerably smaller than unity for stellar masses up to 108 M⊙. Equating the two expressions, we find that the luminosity resulting from the pp-burning is relevant only at very late times tpp = 1.1 × 1015 yr.

thumbnail Fig. A.1

Ratio of nuclear luminosity provided via the pp-cycle (Eq. (A.4)) over the Eddington luminosity of the star (Eq. (A.5)) as a function of protostellar mass for different mass accretion rates. Higher accretion rates imply that less time was available for contraction, thus reducing the nuclear luminosities.

For practical accretion rates of ṁ = 10-3−10 and protostellar masses between 103−108 M⊙, the contribution from the pp-chain will never be relevant, and can thus be neglected for the overall evolution of the stars.

We now estimate the amount of helium produced in the core. 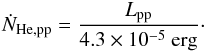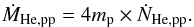During one fusion event, an average energy of 4.3 × 10-5 erg is released, implying a helium production rate of ṄHe,pp=Lpp4.3×10-5erg·\appendix \setcounter{section}{1} \begin{eqnarray} \dot{N}_{\mathrm{He,pp}}=\frac{L_{\rm pp}}{4.3\times10^{-5}\mathrm{\ erg}}\cdot \end{eqnarray}(A.6)The helium mass in the core thus evolves asṀHe,pp=4mp×ṄHe,pp.\appendix \setcounter{section}{1} \begin{eqnarray} \dot{M}_{\mathrm{He,pp}}=4m_{\rm p}\times\dot{N}_{\rm He,pp}. 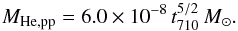\end{eqnarray}(A.7)An integration yields MHe,pp=6.0×10-8 t7105/2 M⊙.\appendix \setcounter{section}{1} \begin{eqnarray} M_{\mathrm{He,pp}}=6.0\times10^{-8}\,t_{710}^{5/2}\,M_\odot. \end{eqnarray}(A.8)Equating the resulting mass with the total mass in the core, a helium core can be expected after a time of 1.2 × 1010 yr. In summary, when only the pp-cycle is considered, nuclear burning is rather inefficient, and never going to have a significant impact on the evolution of the star.

All Tables

Table 1

Pathways to the formation of main-sequence supermassive stars and quasi-stars depending on the critical mass scale Mcr(ṁ) = 3.6 × 108 ṁ3 M⊙ and the accretion rate ṁ in solar masses per year.

In the text

All Figures

thumbnail Fig. 1

Enclosed mass as a function of radius in the protostar calculated from Eq. (10), assuming a total stellar mass of 105 M⊙ and mass accretion rates ṁ = 0.1,1.,10. The current time t is calculated as t = (M/M⊙)/ṁ. For a given mass shell, higher accretion rates imply larger radii, as the star had less time to contract.

In the text
thumbnail Fig. 2

Ratio of nuclear luminosity provided via the CNO-cycle over the Eddington luminosity of the star as a function of protostellar mass for different mass accretion rates. The CNO luminosity is calculated here as the minimum of the estimate in Eq. (24) and the Eddington luminosity of the nuclear core in Eq. (25). At high protostellar masses, one can clearly recognize the transition to the regime where nuclear burning is limited by the Eddington luminosity of the core. Higher accretion rates imply that less time was available for contraction, thus reducing the nuclear luminosities.
In the text
thumbnail Fig. 3

Fraction of helium in the nuclear core, corresponding to the amount of exhausted fuel for nuclear burning, as a function of protostellar mass for different accretion rates. Higher accretion rates imply less time for protostellar contraction. As a result, nuclear densities are reached later, implying less time for nuclear burning.

In the text
thumbnail Fig. A.1

Ratio of nuclear luminosity provided via the pp-cycle (Eq. (A.4)) over the Eddington luminosity of the star (Eq. (A.5)) as a function of protostellar mass for different mass accretion rates. Higher accretion rates imply that less time was available for contraction, thus reducing the nuclear luminosities.

In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.