| Issue |
A&A
Volume 558, October 2013
|
|
|---|---|---|
| Article Number | A76 | |
| Number of page(s) | 11 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201321916 | |
| Published online | 07 October 2013 | |
Solar flares and focused energy transport by MHD waves
1
Division of MathematicsUniversity of Dundee,
Nethergate,
Dundee
DD1 4HN,
UK
e-mail:
arussell@maths.dundee.ac.uk
2
SUPA, School of Physics and Astronomy, University of Glasgow,
University Avenue, Glasgow, G12
8QQ, UK
e-mail:
d.stackhouse.1@research.gla.ac.uk
Received:
17
May
2013
Accepted:
8
August
2013
Context. Transport of flare energy from the corona to the chromosphere has traditionally been assigned to electron beams; however, interest has recently been renewed in magnetohydrodynamic (MHD) waves as a complementary or alternative mechanism.
Aims. We determine whether, and under what conditions, MHD waves deliver spatially localised energy to the chromosphere, as required if MHD waves are to contribute to emission from flare ribbons and kernels. This paper also highlights several properties of MHD waves that are relevant to solar flares and demonstrates their application to the flare problem.
Methods. Transport is investigated using a magnetic arcade model and 2.5D MHD simulations. Different wave polarisations are considered and the effect of fine structuring transverse to the magnetic field is also examined. Ray tracing provides additional insight into the evolution of waveguided fast waves.
Results. Alfvén waves are very effective at delivering energy fluxes to small areas of chromosphere, localisation being enhanced by magnetic field convergence and phase mixing. Fast waves, in the absence of fine coronal structure, are more suited to powering emission from diffuse rather than compact sources; however, fast waves can be strongly localised by coronal waveguides, in which case focused energy is best transported to the chromosphere when waveguides are directly excited by the energy release.
Conclusions. MHD waves pass an important test for inclusion in future flare models.
Key words: Sun: flares / Sun: corona / magnetohydrodynamics (MHD) / waves
© ESO, 2013
1. Introduction
During a solar flare, up to 1025J of energy is released in the corona and transported to the underlying chromosphere where the majority of flare radiative emissions are formed in UV and white light (Hudson 2011). Traditionally, this energy transport has been attributed to beams of electrons travelling at semi-relativistic speeds, a major strength of this hypothesis being that it is reasonably successful at explaining the basic features of chromospheric hard X-ray (HXR) emission (de Jager 1964; Arnoldy et al. 1968; Brown 1971; Hudson 1972). Nonetheless, other energy transport mechanisms may also function during flares, with magnetohydrodynamic (MHD) waves being of particular interest (Emslie & Sturrock 1982; Fletcher & Hudson 2008). Since chromospheric flare emission includes compact sources, such as flare ribbons and kernels (Fletcher et al. 2011), an ability to deliver spatially localised energy fluxes to the chromosphere is an important constraint on flare energy transport processes. The potential of MHD waves to deliver such focused energy and the conditions that favour spatial localisation are the subjects of this paper.
A reappraisal of energy transport during flares is motivated by developments in several quarters. Firstly, flare models relying solely on electron beams appear to face a number of theoretical difficulties. These have been described in detail elsewhere (e.g. Brown et al. 1990, 2009; Fletcher & Hudson 2008), but briefly, one of the central issues is that the energy flux required to power flare emissions seems to require electron number fluxes in excess of what can be supplied by a coronal accelerator, in turn requiring an effective “resupply” mechanism. This is compounded by the small area of the HXR footpoint sources determined by RHESSI observations, which implies electron beam densities in the corona high enough for the beams to be unstable, especially in the presence of a return current (Brown & Melrose 1977; Fletcher 2005; Zharkova & Gordovskyy 2005; Krucker et al. 2011). Solutions to these problems are currently being sought within the framework of coronal electron beams, but they could also be resolved if some portion of the flare energy is transported to the chromosphere by other means. For example, if this energy were later used to accelerate chromospheric electrons (Fletcher & Hudson 2008) or to re-accelerate energetic electrons in the chromosphere that had previously precipitated from the corona (Brown et al. 2009), then the electron number problem could be disposed of. Alternatively, since MHD waves are capable of transporting energy to the chromosphere and heating it by ion-neutral friction (Emslie & Sturrock 1982; Russell & Fletcher 2013), they could also contribute directly to flare radiative emissions, thus reducing the energy flux that must be provided by electron beams.
Direct evidence that electron beams are not the only form of energy transport acting during solar flares is provided by observations of rapid changes to both the line-of-sight and horizontal magnetic field at the photosphere around the time of the flare impulsive phase (Wang et al. 1992, 1994, 2012; Sudol & Harvey 2005; Wang & Liu 2010; Petrie & Sudol 2010; Su et al. 2011; Cliver et al. 2012; Johnstone et al. 2012). These represent significant perturbations to the magnetic field deep in the solar atmosphere that are presumably driven by rearrangement of coronal magnetic field and must therefore be communicated over tens of Mm, transporting energy as Alfvénic Poynting flux in the process. Interestingly, Sudol & Harvey (2005) and Johnstone et al. (2012) have shown that magnetic field changes spatially coincide with and temporally lag UV emission in the chromosphere. While they may be separate consequences of a common driver that just happen to be co-located, there may also be a more direct connection – e.g., are changes in photospheric magnetic field a signature of MHD waves that also deposit energy in the chromosphere, contributing to UV emissions?
Waves and Poynting flux are also receiving renewed attention in reconnection theory, where studies by Longcope & Priest (2007), Birn et al. (2009), Kigure et al. (2010), and Longcope & Tarr (2012) have highlighted their role carrying signals and energy away from the reconnection site into the surrounding medium. These aspects are particularly apparent if reconnection is time-dependent, conditions are low-beta, waves are allowed to freely propagate away from the reconnection site without being reflected by artificial boundaries, and resistivity is small or localised to the reconnection site so that waves are not artificially overdamped. Under these conditions, all of which apply to the Sun, Poynting flux or waves can be the dominant form of outgoing energy flux. As discussed by Fletcher & Hudson (2008) and Russell & Fletcher (2013), the Poynting flux carried by even small amplitude MHD waves in solar active regions can be of the order required to power the radiative emissions of a flare, so it is interesting to ask the general question of what happens to the waves produced by magnetic reconnection and the energy they carry.
Since the late 1990s, high-cadence and high-resolution observations of the corona and chromosphere have shown that MHD waves are a ubiquitous feature of the solar atmosphere (e.g. reviews by Nakariakov & Verwichte 2005; De Moortel & Nakariakov 2012; Mathioudakis et al. 2012, and references therein) and the flux of upgoing waves in the quiet Sun is considered by McIntosh et al. (2011), among others, to be large enough to be of interest for coronal heating and acceleration of the solar wind. Observations have also shown that eruptive events such as flares and coronal mass ejections (CMEs) produce compressive waves (Moreton & Ramsey 1960; Moreton 1960; Moses et al. 1997; Thompson et al. 1998, 1999), which can excite loop oscillations at considerable distance away from the energy release (Aschwanden et al. 1999; Nakariakov et al. 1999), sometimes trigger other eruptions (Mullan 1975; Schrijver & Title 2011) and can explain type II radio bursts where local conditions produce strong shocks (Uchida 1960, 1974). At present, the idea that downgoing waves may play a role during flares is considered more novel, although some progress in this field has been made by Emslie & Sturrock (1982), Melrose (1992), Wheatland & Melrose (1994), Liu et al. (2006), Fletcher & Hudson (2008), Stasiewicz & Ekeberg (2008), Birn et al. (2009), McClements & Fletcher (2009), Haerendel (2009, 2012), Bian et al. (2010), Bian & Kontar (2011), Tsiklauri (2012) and Russell & Fletcher (2013). Downgoing waves are also thought to play an important role in Alfvénic auroras that is in some ways analogous (Stasiewicz et al. 2000; Chaston et al. 2002, 2007; Semeter et al. 2005; Keiling 2009; Watt & Rankin 2010).
The ability of MHD waves to deliver flare energy to spatially confined regions of the lower solar atmosphere, as required to contribute to emissions from ribbons and kernels, has not been investigated in detail and is the subject of this paper. We emphasise that waves must be able to provide such focused energy transport if they are to play a substantial role in powering flare radiative emissions. Most discussion of this point to date has appealed in general terms to the fact that pure Alfvén waves (with properties obtained, for example, by analysis of plane waves in a uniform medium) transport energy parallel to the magnetic field. In the real corona, wave energy is likely to be partitioned between fast magnetoacoustic and Alfvén waves, conditions are highly nonuniform and magnetic field is curved, therefore, a fuller treatment is needed.
The study of most relevance to this paper is an MHD simulation of 3D reconnection by Birn et al. (2009), that showed fragmentation of a 3D coronal current sheet creates tightly focused spots of intense Poynting flux above the chromosphere. This result demonstrates that localised Poynting fluxes of interest to flares can form and do not rely on idealised conditions. The authors did not, however, examine the wave properties that govern how these energy fluxes are established or evolve. Separately, significant work has gone into modelling coronal waves in active regions to improve understanding of observed coronal oscillations (e.g. Ofman & Thompson 2002; Terradas & Ofman 2004; Brady & Arber 2005; Ofman 2005, 2007; Díaz et al. 2006; Verwichte et al. 2006; McLaughlin & Hood 2006; McLaughlin & Ofman 2008; Pascoe et al. 2009; De Moortel & Pascoe 2009; Schmidt & Ofman 2010), but little attention has been given to focused transport as relevant to flares. This paper seeks to bridge the gap between the sub-disciplines of flare physics and MHD waves by investigating whether, and under what conditions, MHD waves can deliver spatially localised energy fluxes to the chromosphere, and by highlighting for the flare community the wave concepts applicable to this problem.
2. Methods
2.1. Arcade model
In this paper, MHD waves are studied as perturbations to a 2D potential equilibrium
magnetic field, Be, defined by 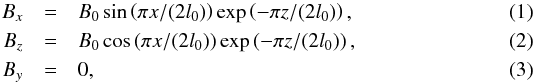 where
z is the vertical direction, y is the horizontal
direction that we assume invariant, and x is the horizontal direction
that completes the system. These components prescribe an arcade structure with half-width
l0, which is shown by the arrows in Fig. 1. Magnetic field strength,
|Be| = B0exp(−πz/(2l0)),
is a function of z only and decays exponentially with a scale height of
2l0/π. Fourier
(harmonic) modes of oscillation for this magnetic field and hydrostatic density have
previously been obtained by Oliver et al. (1993).
where
z is the vertical direction, y is the horizontal
direction that we assume invariant, and x is the horizontal direction
that completes the system. These components prescribe an arcade structure with half-width
l0, which is shown by the arrows in Fig. 1. Magnetic field strength,
|Be| = B0exp(−πz/(2l0)),
is a function of z only and decays exponentially with a scale height of
2l0/π. Fourier
(harmonic) modes of oscillation for this magnetic field and hydrostatic density have
previously been obtained by Oliver et al. (1993).
The magnetic field prescribed above is presumably much simpler than the complex, non-potential fields that are likely to exist in a 3D flaring active region, nonetheless, it closely resembles magnetic structures formed in the vicinity of a polarity inversion line, which may be directly involved in solar flares (e.g. Schrijver 2007), and also the magnetic field shown by Birn et al. (2009) below their simulated reconnection region. All three magnetic fields share a common topology in which a region of positive photospheric flux is connected to a region of negative photospheric flux by the coronal field. Similar configurations are found as subdomains of more complex magnetic fields produced by multiple photospheric sources, which suggests that our model may be also viewed as a “building block” for understanding wave behaviour in more general magnetic fields.
Other important features shared by our model and more realistic magnetic fields include magnetic field curvature in the corona and expansion of magnetic flux tubes with height, both of which can influence energy transport by MHD waves. Fine structuring of the magnetic field, which we do not model, produces spatial structuring of the Alfvén speed and could therefore be important for wave propagation in the real solar atmosphere, especially during solar flares. The effects of fine magnetic structuring will be similar to those caused by fine density structuring since both act through the Alfvén speed, and the latter is examined in detail. The arcade model thus demonstrates the properties of MHD waves that are most relevant to focused energy transport in solar flares, and it does so more clearly than do more complex models in which these details can be obscured.
A more accurate approximation to the magnetic field near a polarity inversion line might be a sheared arcade, modelled by setting By to a uniform (non-zero) value (i.e. adding a guide field), in which case the 2.5D magnetic field remains in potential equilibrium with ∇·B = 0. The impact that this change would have on our results is discussed in Sect. 2.2. We proceed with By = 0 primarily because it aids clear and detailed interpretation that complements numerical demonstrations of the evolution of more realistic non-equilibrium magnetic fields as already performed by, e.g., Birn et al. (2009).
Mass density is described using hydrostatic equilibrium. For an isothermal, fully ionised
plasma, this gives 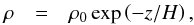 (4)where
H = 2kBT/(mig)
is the density scale height. Taking the coronal temperature as 1 MK and
mi as the proton mass gives
H = 60Mm.
(4)where
H = 2kBT/(mig)
is the density scale height. Taking the coronal temperature as 1 MK and
mi as the proton mass gives
H = 60Mm.
For investigation of wave trapping and waveguiding caused by fine structuring of the Alfvén speed, density is allowed to vary transverse to the equilibrium magnetic field. This is done by specifying a region bounded by two magnetic field lines and changing the internal density to a multiple of the external density at the same z (the density scale height is the same inside these loops as outside, but the value of ρ0 is different). This creates an overdense loop (equivalently, a region of low Alfvén speed), with curvature and expansion defined by the equilibrium magnetic field, and discontinuities in Alfvén speed at the loop’s edges.
Simulations are arranged so that l0 = H.
Therefore the Alfvén speed, 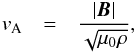 (5)becomes
(5)becomes
 (6)and
decreases with increasing height.
(6)and
decreases with increasing height.
2.2. Governing equations for linear perturbations
For this investigation, we consider small amplitude perturbations with the magnetic field perturbation much less than the background field strength and velocities much less than the background Alfvén speed. This allows us to solve the linearised MHD equations, which are simpler than their non-linear counterparts but retain the essential elements of transport and are more straightforward to interpret. Given the large energy release of a solar flare it seems likely that flare-generated waves are non-linear, at least at some point in their evolution for large flares, and it is therefore desirable that non-linear effects such as wave steepening, non-linear coupling and cascades to small scales are explored in future work. For the present study, however, a linear study offers significant progress on the question of focused flare energy transport by MHD waves.
Non-ideal effects such as resistivity, viscosity and Hall effects are neglected because the length scales in our simulation are much larger than the dissipative and dispersive length scales at which they become important. We also neglect the forces of thermal pressure gradients and gravity in favour of magnetic forces. These assumptions are reasonable because the present study is restricted to a coronal domain where the plasma beta, β, is much less than unity (equivalently, the Alfvén speed is much larger than the sound speed) and the length scale of perturbations is much less than H/β. (We do not investigate what happens to wave energy that enters the chromosphere and the magnetic field does not contain null points.) Neglecting thermal pressure excludes slow magnetoacoustic waves from our analysis.
The governing equations are therefore the linear momentum equation and the induction
equation derived from ideal Ohm’s law. Writing v and
b for the velocity and magnetic field perturbations,
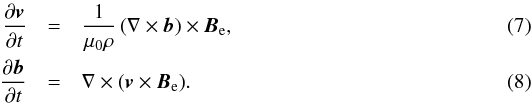 For
this investigation, the components of these equations are separated into two decoupled
sets, each corresponding to a different polarisation, by setting
By = 0 and assuming that perturbations
are invariant in the y direction.
For
this investigation, the components of these equations are separated into two decoupled
sets, each corresponding to a different polarisation, by setting
By = 0 and assuming that perturbations
are invariant in the y direction.
Components of v and b in the
invariant y-direction are governed by:  These
transport energy along the magnetic field and not across it, acting through magnetic
tension force with no compression of the magnetic field (since
∇·v = ∂vy/∂y = 0).
This polarisation is a pure (decoupled) Alfvén wave and we shall refer it as the Alfvén
wave.
These
transport energy along the magnetic field and not across it, acting through magnetic
tension force with no compression of the magnetic field (since
∇·v = ∂vy/∂y = 0).
This polarisation is a pure (decoupled) Alfvén wave and we shall refer it as the Alfvén
wave.
Components of v and b in the
x-z plane (the plane of the equilibrium magnetic
field) form a second set of equations: 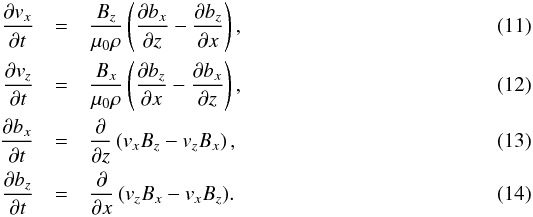 Energy
is again transported along the magnetic field by magnetic tension, however it can also be
transported across the magnetic field by magnetic pressure (since
∇·v ≠ 0 in general). The resulting wave can travel in
all directions and does so at the Alfvén speed. This is a zero beta fast wave and shall be
referred to simply as the fast wave.
Energy
is again transported along the magnetic field by magnetic tension, however it can also be
transported across the magnetic field by magnetic pressure (since
∇·v ≠ 0 in general). The resulting wave can travel in
all directions and does so at the Alfvén speed. This is a zero beta fast wave and shall be
referred to simply as the fast wave.
If a guide field is added to the magnetic arcade model to form a sheared arcade, then
additional terms proportional to By enter
Eqs. (10), (11) and (12), coupling
the two sets. In such a case, a pure Alfvén mode cannot exist because the invariant
direction is nowhere perpendicular to the magnetic field and hence displacements
perpendicular to the magnetic field cause compression and rarefaction. Instead waves are
of a mixed type. Nonetheless, if By is small
compared to 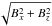 ,
then coupling will have only a small effect during the time a wave travels from the site
of the coronal energy release to the chromosphere, and the main conclusions will be
similar to those found in the By = 0 case.
,
then coupling will have only a small effect during the time a wave travels from the site
of the coronal energy release to the chromosphere, and the main conclusions will be
similar to those found in the By = 0 case.
The two sets of governing equations also become coupled if perturbations are allowed to vary in the y-direction, because gradients ∂vy/∂y cause compression and rarefaction, and magnetic pressure gradients caused by flows in x and z drive flows in y. If perturbations have normal mode structure in y with wave number ky, then the coupling terms are proportional to ky. Coupling becomes unimportant during the times of interest if perturbations are sufficiently elongated in y, i.e. vary over a sufficiently greater distance in the y direction than in the x-y plane, in which case perturbations are said to be “quasi-2D” and evolution is well-approximated by the 2D model.
The purpose of this paper is to illustrate the ability of MHD waves to deliver spatially concentrated energy to the chromosphere, and to collect and discuss wave concepts relevant to solar flare energy transport. The relative simplicity of a model with By = 0 and invariance in y strongly supports these goals and, as noted above, similar conclusions are expected for a broader class of models in which fast and Alfvén waves are weakly coupled. For strongly sheared magnetic arcades or fully 3D perturbations, coupling between fast and Alfvén waves may substantially change the outcomes, for example by rapidly transferring energy from one to the other. Such cases are not investigated here, however it is expected that the properties of decoupled or weakly-coupled waves will be a useful reference when interpreting even strongly coupled situations.
2.3. Energy densities
The topic of this paper is energy transport, so it is frequently useful to refer to
energy density. The assumption of linear perturbations leads to consideration of both
first and second order energy densities. The first order energy density represents changes
in magnetic energy due to compression or rarefaction of the equilibrium magnetic field by
the fast wave, and is given by  (15)This
is positive where the fast wave compresses Be and
negative where the wave rarefies Be. The second
order energy density is always positive and can be thought of as the “self-energy” of wave
perturbations, thus,
(15)This
is positive where the fast wave compresses Be and
negative where the wave rarefies Be. The second
order energy density is always positive and can be thought of as the “self-energy” of wave
perturbations, thus, 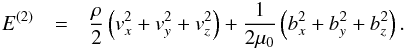 (16)
(16)
2.4. MHD simulations
Equations (9) to (14) were solved numerically in dimensionless form, with time in Alfvén crossing times, τA = l0/vA0, where vA0 is the Alfvén speed at z = 0. Spatial derivatives were approximated using second order finite differences, and variables were advanced in time using a fourth order Runge-Kutta scheme (e.g. Press et al. 2007). The resulting code conserves first order energy, second order energy and momentum to a high degree (i.e. subject to the usual, negligible, numerical dissipation) and has been tested against known behaviours such as fast and Alfvén waves in a uniform medium.
Boundaries are open at x = 0 (left) and z = l0 (top), line-tied (v = 0) at z = 0 (bottom), and symmetry-based at x = l0 (right). Open boundaries were implemented by solving one-sided versions of the governing equations that explicitly exclude incoming waves, obtained using the method described by Thompson (1987). The bottom boundary represents the top of the chromosphere. Here, line-tying implies zero transmission of energy, whereas in the real Sun some fraction of the wave energy reaching this boundary will enter the chromosphere (e.g. Russell & Fletcher 2013). Delivery of energy to the bottom boundary is therefore interpreted as delivery of energy to the chromosphere.
Waves were excited by specifying an initial velocity perturbation perpendicular to the
magnetic field, with magnitude 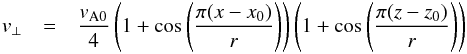 (17)where
(x0,z0) is the
centre of the disturbance and r is its radius. This is intended to
represent a localised injection of energy, as might be produced by a burst of reconnection
during a solar flare. (We do not attempt to model an actual reconnection event, the
purpose of this paper being to investigate later evolution of MHD waves.) Unless otherwise
stated, simulations use x0 = l0,
z0 = 0.5l0 and
r = 0.1l0.
(17)where
(x0,z0) is the
centre of the disturbance and r is its radius. This is intended to
represent a localised injection of energy, as might be produced by a burst of reconnection
during a solar flare. (We do not attempt to model an actual reconnection event, the
purpose of this paper being to investigate later evolution of MHD waves.) Unless otherwise
stated, simulations use x0 = l0,
z0 = 0.5l0 and
r = 0.1l0.
The direction of the initial perturbation determines which wave is excited: a velocity in the y-direction excites the Alfvén wave while a velocity in the x-z plane excites the fast wave. No accompanying magnetic field perturbation is specified, so the velocity perturbation describes a superposition of two counterpropagating waves. In the Alfvén wave case, one wave propagates to the left while its mirror image propagates to the right, thereby satisfying the symmetry conditions at x = l0. In the fast wave case, the initial condition corresponds to one wave front propagating radially outwards and another propagating inwards, but the latter soon passes through itself to become an outgoing wave that follows behind the former.
In terms of energy densities, Eq. (15) shows that E(1) is initially zero everywhere (thus its volume integral over a closed system is always zero) and Eq. (16) shows that changing the direction of the velocity perturbation (to excite Alfvén or fast waves) leaves E(2) unchanged. Governing equations are linear, so a driver of scaled velocity amplitude ϵvA0 will behave exactly as in the case shown, but with velocity and magnetic field perturbations and first order energy density scaled by ϵ, and second order energy density scaled by ϵ2.
2.5. Ray tracing
MHD simulations are complemented by ray tracing, which indicates the path taken by waves as they refract and reflect in a non-uniform medium. The direction of a ray is parallel to the wave vector, k, and the travel time along many rays can reveal the location of phase-fronts at a given time.
In a continuous medium, zero-beta fast waves refract with:
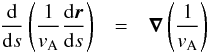 (18)where
ds is a differential path length along a ray and
r is the position vector of the ray (e.g. Smith et al. 1980, and references therein).
(18)where
ds is a differential path length along a ray and
r is the position vector of the ray (e.g. Smith et al. 1980, and references therein).
At discontinuous interfaces, like those in our simple model of an overdense loop,
zero-beta fast waves reflect with the angle of reflection,
θr, equal to the angle of incidence,
θi. The angle of transmission is determined
by Snell’s law, which states 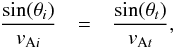 (19)where
vAi
(vAt) is the Alfvén speed on the incident
(transmitted) side of the interface. Equation (19) is valid for
θi < θc
where
(19)where
vAi
(vAt) is the Alfvén speed on the incident
(transmitted) side of the interface. Equation (19) is valid for
θi < θc
where  (20)is
a critical angle of incidence that exists for
vAi < vAt.
If
vAi < vAt
so that θc is defined and if
θi > θc,
then the incident wave is totally reflected at the interface. Thus, the most efficient
wave trapping and waveguiding occurs inside structures with a low Alfvén speed compared to
their surroundings, for example in overdense loops, in which case waves that graze the
boundary do not transmit energy to the environment.
(20)is
a critical angle of incidence that exists for
vAi < vAt.
If
vAi < vAt
so that θc is defined and if
θi > θc,
then the incident wave is totally reflected at the interface. Thus, the most efficient
wave trapping and waveguiding occurs inside structures with a low Alfvén speed compared to
their surroundings, for example in overdense loops, in which case waves that graze the
boundary do not transmit energy to the environment.
3. Results
3.1. Alfvén waves
 |
Fig. 1 Evolution of the Alfvén wave in a magnetic arcade, shown through second order energy density at times a) t/τA = 0, b) t/τA = 0.5, c) t/τA = 1.25 and d) t/τA = 1.79. Black arrows show the direction and strength of the equilibrium magnetic field. |
 |
Fig. 2 Energy delivered to bottom boundary by Alfvén wave, as a function of time and location. Dashed horizontal lines mark the magnetic footpoints of the initial energy injection. |
The first simulation examines transport by Alfvén waves. The initial condition and three later snapshots are shown in Fig. 1, with panels (a) through (d) corresponding to t/τA = 0 (initial condition), t/τA = 0.5 (wave propagating downwards), t/τA = 1.25 (wave reflecting at chromospheric boundary) and t/τA = 1.79 (reflected wave propagating upwards). Colour contours represent second order energy density and black arrows indicate the direction and strength of the equilibrium magnetic field. First order energy density is zero everywhere at all times because the decoupled Alfvén wave does not compress the magnetic field.
Evolution of Alfvén waves is characterised by transport along the magnetic field and panel 1(c) shows Alfvén wave energy arriving at a very concentrated location on the chromospheric boundary at t/τA = 1.25. Note also that all of the energy injected into the Alfvén wave is at some time incident on the bottom boundary. Arrival of energy at the bottom boundary is examined further in Fig. 2, which plots E(2) at z = 0 as a function of x and t. This immediately confirms that Alfvén waves are very good at delivering focused energy to the chromosphere.
Looking more closely at Figs. 1 and 2, the Alfvén wave arrives at the chromosphere with a much shorter length scale than is imposed in the corona by the initial condition. Quantifying these scales from E(2) as twice the full width at half maximum, energy is injected with a horizontal length scale of 0.146l0 and arrives at the bottom boundary with a horizontal length scale of 0.043l0. Thus, the horizontal length scale has reduced by a factor of 3.4 during the transit from loop apex to chromospheric boundary. This spatial localisation has two contributing causes.
The first cause is that magnetic field converges towards the chromosphere, thus, as the Alfvén wave propagates along the field, it is forced into a smaller area. In this simulation, energy is initially injected onto field lines spanning z/l0 ∈ (0.4,0.6) on x/l0 = 1, which map to x/l0 ∈ (0.255,0.358) at z = 0, therefore, magnetic convergence accounts for shortening by a factor 1.9. To confirm this, the magnetic footpoints have been marked in Fig. 2 as dashed horizontal lines and energy is clearly restricted to the region between them. It is also clear, however, that field convergence is not solely responsible for the concentration of energy, since energy is only ever present at the boundary across a small range in x within the magnetic footpoints.
The other process at work is phase mixing (Pridmore-Brown 1966; Burghes et al. 1969; Tataronis & Grossmann 1973; Hasegawa & Chen 1974; Heyvaerts & Priest 1983). Returning to Fig. 1 and comparing panels (a), (b) and (d), over time, the region of perturbed energy density (wave packet) becomes longer parallel to the magnetic field and shorter across it. The physical explanation is that the wave travel time from the loop apex to the chromosphere varies between field lines: inner loops are shorter and, by Eq. (6), Alfvén waves travel more quickly along them, therefore, the wave packet becomes distorted as Alfvén waves on inside, faster “tracks” race ahead. The resulting difference in arrival time is responsible for the slope seen in Fig. 2. Moreover, Alfvén waves forming the centre of the wave packet are incident at the chromospheric boundary at t/τA = 1.25, but at this time the Alfvén waves forming the rightmost part have already departed and those forming the leftmost part have yet to arrive, thereby narrowing the wave packet transverse to the field while it is simultaneously elongated along it. (A similar analysis can be applied at any time on a cut passing through the centre of the wave packet and transverse to the field, showing the continuous effect of phase mixing.)
Unlike focusing due to magnetic field convergence, which is reversed when Alfvén waves return to regions of lower field strength, shortening of length scales by phase mixing can continue over many orders of magnitude (until scales are small enough to make microphysics or instabilities significant). Hence, if coronal Alfvén waves are incident on the chromosphere multiple times, which they will be if trapped on closed field lines, their horizontal length scale on later incidences will be even smaller than for the first incidence. Referring to previous studies of the length scale produced by phase mixing (e.g. Mann et al. 1995; Russell & Wright 2010) we also note for the reader that phase mixing gives a transverse length scale λ⊥ ∝ 1/t and proceeds most rapidly in the presence of strong Alfvén speed gradients.
Placing these results in the context of solar flares, we conclude that Alfvén waves, aided by magnetic field convergence and phase mixing, have an excellent ability to deliver focused energy to the lower solar atmosphere, as required to contribute to emission from flare ribbons or kernels, or to produce localised changes in the photospheric magnetic field during flares.
 |
Fig. 3 Evolution of the fast wave in a magnetic arcade. Panels a) to d) show first order energy density. Panels e) to h) show second order energy density. |
3.2. Fast waves
The next simulation investigates fast waves when the Alfvén speed is slowly varying. Dynamics are presented in Fig. 3, with panels (a) to (d) showing snapshots of E(1) and panels (e) to (h) showing E(2). The location and size of the initial velocity perturbation are the same as for the perturbation used to launch the Alfvén wave in Sect. 3.1, but this time the initial velocity is directed downwards.
Evolution of fast waves is characterised by propagation in all directions away from the source. Inspecting Fig. 3 at t/τA = 0.5 (panels (a) and (e)), the fast wave forms a pair of rings around its point of origin. In E(2) (panel (e)), each ring is continuous, showing that energy has been transported in all directions. Asymmetry is also apparent: wave fronts have travelled further in downward directions than upward directions, owing to the z-dependence of vA (if vA were uniform then the rings would be perfect circles). Related to this, when fast waves propagate into decreasing (increasing) wave speed, i.e. upwards (downwards) in this simulation, the trailing edge of the wave catches up on (falls further behind) the leading edge, thereby narrowing (widening) the wave front and concentrating (diluting) energy density. Looking at E(1) (panel (a)), below the source the fast wave first compresses the magnetic field (E(1) > 0), which then rebounds and becomes rarefied (E(1) < 0), returning to E(1) = 0 when the wave front passes. A reversed sequence occurs above the source. Spatial variation of E(1) shows the narrowing and widening of wave fronts with changes in vA that were seen in E(2), however, variation of E(1) also reflects the relative importance of magnetic pressure in transmitting the fast wave in different directions: where the wave propagates transverse to the background magnetic field, it causes the greatest changes in E(1) and hence magnetic pressure; where it propagates parallel to the background field, magnetic pressure forces are negligible, magnetic tension instead providing the restoring force.
Shortly after t/τA = 0.5, part of the fast wave meets the chromospheric boundary, directly under the source and with a horizontal length scale significantly longer than that initially injected. Examining the remaining panels of Fig. 3, the intersection between the wave front and the chromosphere sweeps outward over time, while the incident wave is reflected to form an upgoing wave. A significant fraction of the injected energy never reaches the chromosphere because it is transported upwards or is refracted away from higher Alfvén speed near the chromosphere. Energy arrival at the bottom boundary is examined further in Fig. 4, which plots E(1) (panel (a)) and E(2) (panel (b)) at z = 0 as a function of x and t. These confirm that energy is delivered with a large scale, first arriving below the injection and then spreading outwards. This style of transport is much more suited to helping power diffuse emission from flaring regions (e.g. widespread brightening of plage) rather than compact emission (e.g. ribbons and kernels).
At late times (panels (d) and (h) of Fig. 3) the fast wave forms a dome that expands sideways and upwards. Although the focus of this paper is transport of flare energy to the lower solar atmosphere, it is worth noting the connection between these wave fronts and flare- or CME-excited fronts in the chromosphere and corona. Shortly after Moreton waves were discovered in Hα (Moreton & Ramsey 1960; Moreton 1960), Uchida (1968) proposed an interpretation as the intersection of a coronal fast wave with the chromosphere, similar to that in our simulation. Uchida (1960, 1974) also pointed out that if a coronal fast wave is launched with sufficient amplitude and enters part of the corona where the Alfvén speed is low, then it forms a strong shock that accelerates electrons, in turn exciting plasma waves that convert into escaping radio waves. Type II radio bursts (Wild & McCready 1950; Wild 1950) are thought to be the result of this process and may therefore be considered as evidence of coronal fast waves. Coronal fast waves have also been sought in extreme ultraviolet images, with “EIT waves” initially interpreted as the coronal counterpart of Moreton waves (Moses et al. 1997; Thompson et al. 1998, 1999). The properties of EIT waves, however, do not always fit well with a fast wave explanation – objections listed by Wills-Davey et al. (2007) include that in many cases EIT waves appear too slow to be fast waves – and an alternative explanation is that many EIT “waves” are non-wave phenomena driven by CMEs (e.g. Chen et al. 2002). The resolution may be that when the most prominent EIT front is CME driven, high-cadence observations with TRACE and SDO/AIA reveal a faster, sharper wave front ahead of it that does correspond to a fast wave (Harra & Sterling 2003; Chen & Wu 2011; Asai et al. 2012). Thus, coronal fast waves like those in the far-field of our simulation are observed in the solar atmosphere, and since Fig. 4 shows substantially more fast wave energy is incident on the chromosphere at the flare site than in the far-field, it is plausible such fast waves could also influence the flare emission.
 |
Fig. 4 Energy delivered to bottom boundary by fast wave in arcade model with hydrostatic density, shown as function of time and location. Part a) shows first order energy density. Part b) shows second order energy density. |
 |
Fig. 5 Evolution of the fast wave excited inside an overdense loop (density contrast of ten). Panels a) to d) show first order energy density, panels e) to h) show second order energy density and magenta lines mark the edges of the loop. |
3.3. Waveguided fast waves
Based on Sect. 3.2, it first appears that fast waves are a poor candidate for focused energy transport, however, the behaviour of fast waves changes dramatically if we recognise that the corona is structured transverse to the magnetic field.
Figure 5 shows how the fast wave evolves if energy
is injected inside a loop that is denser than its surroundings, akin to directly exciting
the loop and producing a wave related to the fast kink mode (Edwin & Roberts 1983). Edges of the loop are marked in Fig.
5 as magenta lines and the density contrast between
the loop and its environment is ten. Since structuring acts through
vA, the same results would be obtained if density were
unstructured but there was a weak field region between the magenta lines (corresponding
magnetic field contrast 1/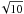 ).
The initial velocity driver used in this simulation is the same as used in Sect. 3.2 but the ten-fold increase in density at the location
of the driver gives a corresponding increase in energy density.
).
The initial velocity driver used in this simulation is the same as used in Sect. 3.2 but the ten-fold increase in density at the location
of the driver gives a corresponding increase in energy density.
Panels (a) to (d) of Fig. 5 show snapshots of E(1), panels (e) to (h) show E(2). It is clear from these that a substantial fraction of the fast wave energy is trapped inside the loop and that the loop directs this energy to a localised part of the chromospheric boundary where the horizontal length scale of the wave is the width of the loop (panels (c) and (g)). Delivery of focused energy to the chromosphere is confirmed by Fig. 6, in which the arrival of energy inside the loop at t/τA = 4.2 is particularly prominent. Figures 5c, 5g and 6 also show that concentrated energy extends a little way into the exterior region, which is because trapped waves are evanescent in the exterior region rather than zero.
The most important conclusion is that fast waves, not only Alfvén waves, are capable of delivering focused energy to the chromosphere, provided transverse structuring creates coronal waveguides. We also note that, although the most significant delivery of energy to the bottom boundary is concentrated within the waveguide footpoint, leakage does allow some fast wave energy to reach the boundary underneath the loop, where it may have broader, less intense effects than in the waveguide footpoint.
 |
Fig. 6 Energy delivered to bottom boundary by fast wave excited inside an overdense loop. Part a) shows first order energy density. Part b) shows second order energy density. Horizontal dashed lines mark the footpoints of the overdense loop. |
 |
Fig. 7 Evolution of the fast wave excited above an overdense loop (density contrast of ten). Panels a) to d) show first order energy density, panels e) to h) show second order energy density and magenta lines mark the edges of the loop. |
A companion simulation is also presented in which the source of the fast wave is positioned above the waveguide (initial perturbation centred on x = l0, z = 0.8l0; less energy is injected than in Sect. 3.2 since v⊥ is otherwise fixed and ρ decreases with height). Snapshots are shown in Fig. 7 and energy densities delivered to the chromospheric boundary are shown in Fig. 8. In this case, no significant energy is delivered to the waveguide footpoint, and the evolution instead takes the following course. First (Figs. 7a and e), the fast wave spreads in all directions from the source as was seen in Sect. 3.2. When the downgoing wave meets the top of the loop, part is reflected to form an upgoing wave front. The transmitted part is refracted on entering the loop, losing curvature and turning its direction of propagation more directly across the loop. The transmitted wave reaches the far side of the loop shortly before t/τA = 1.8 (panels (b) and (f)), where it divides again into reflected and transmitted parts. The transmitted wave that exits below the loop gains curvature through refraction at the change in vA and then travels to the chromospheric boundary, delivering the maximum energy densities seen in Fig. 8 across a wide area under the loop. Over time, repeated transmissions and reflections form complicated small-scale patterns of wave energy within the loop, but this energy is concentrated at the loop apex and away from the chromospheric boundary (panels (c), (d), (g) and (h)).
It is interesting that waveguided fast waves can be so successful at delivering focused energy to the chromosphere if a waveguide is directly excited (i.e. fast wave launched inside it, Figs. 5 and 6), but poor when the fast wave is initially launched above it (Figs. 7 and 8). This is investigated further using a ray tracing analysis.
Panels (a), (b) and (c) of Fig. 9 show the trajectories of waves launched from the centre of the loop at different initial angles (0.75π, π and 1.25π respectively, measured anti-clockwise from the x-direction). Rays refract due to changes in vA and when they meet the edge of the loop the reflected ray is followed. For a straight waveguide with parallel sides, rays would bounce down the waveguide to infinity, however, because our model loop converges and is curved, rays can be mirrored before they reach the chromospheric boundary. This mirroring means that rays launched across the waveguide remain near the apex of the loop (panels (a) and (c)), while rays launched along the waveguide reach the chromosphere (panel (b)). Rays launched from the centre of the loop reach the chromosphere if their initial angle lies between 0.13π and − 0.04π, or between 0.87π and 1.04π: these ranges are visualised in Fig. 9d as the combined cyan and red segments. Some rays are always totally reflected at the loop edge and therefore retain their associated wave energy, while others leak energy into the loop’s surroundings by partial transmission. The initial ray angles yielding non-leaky waves are a subset of those that reach the chromosphere and are represented in Fig. 9d as the red segments (in this case angles between 0.07π and 0.005π or 0.93π and 1.005π). Figures 9e and f show similar visualisations for sources at the top of the loop (panel (e)) and a point on the upper boundary not on the central axis.
 |
Fig. 8 Energy delivered to bottom boundary by fast wave excited above an overdense loop. Part a) shows first order energy density. Part b) shows second order energy density. Horizontal dashed lines mark the footpoints of the overdense loop. |
 |
Fig. 9 Ray tracing analysis tracking reflections inside an overdense loop. Parts a), b) and c) show trajectories of waves launched from the centre of the loop with initial angles of 0.75π, π and 1.25π (measured anti-clockwise from the x-direction). Parts d), e) and f) show the initial ray angles for which waves emanating from the centre of the loop (x0 = l0, z0 = 0.512l0, panel d)), top of the loop (x0 = l0, z0 = 0.611l0, panel e)), and a point on the upper boundary not on the central axis (x0 = 0.7l0, z0 = 0.537l0, panel f)) reach the chromosphere (cyan and red segments) and the subset of rays perfectly trapped by total internal reflection (red segments only). Source locations used in d) to f) are indicated by the magenta circles in panel c). |
Relating the ray tracing analysis to our MHD simulations, the first waveguide simulation was initiated with an initial disturbance inside the loop that was composed of wave vectors pointing in all directions. Those within a critical range, roughly aligned along the loop, reach the chromosphere and a significant fraction of these are perfectly trapped, keeping energy inside the loop and successfully guiding it to the loop footpoint. Waves that are not perfectly trapped leak from the loop into the environment, reducing the maximum energy density inside the loop until only the trapped components remain (note reduction in colour axis in Fig. 5). In the second waveguide simulation (initial disturbance above the loop), wave fronts refract as they enter the loop, thus, wave vectors are seeded at the top edge of the loop pointing roughly across the loop. None of their angles fall within the critical range, therefore they mirror before reaching the chromospheric footpoint of the loop.
We conclude that waveguided fast waves can be very effective at delivering focused flare energy to the chromosphere, however, magnetic curvature and convergence can act to restrict waves to near to the loop apex, and transport to the chromosphere is therefore most effective when the waveguide is directly excited by an energy release.
4. Discussion
This paper has demonstrated delivery of spatially focused energy to the chromosphere by Alfvén and fast-magnetoacoustic waves, and highlighted the processes responsible for localisation. This represents an important theoretical test for the inclusion of MHD waves in flare models, because spatially focused transport is required for MHD waves to contribute to emission from flare ribbons and kernels. Had the opposite conclusion been reached, the viability of MHD waves to usefully contribute to the brightest chromospheric flare emission would have been in serious doubt.
Alfvén waves by their nature transport energy along the magnetic field, and they access length scales less then the injection scale via phase mixing and concentration by converging magnetic field. They are therefore very effective at delivering energy to small areas of chromosphere. Fast waves, in the absence of fine coronal structure, are more suited to powering emission from diffuse rather than compact sources, however, they can be strongly localised by coronal waveguides, in which case focused energy is best transported to the chromosphere when waveguides are directly excited by the energy release. For waveguides that are indirectly excited, fast wave energy remains close to the loop apex, which we have explained in terms of magnetic convergence and curvature using a ray tracing analysis. Transverse structure in the corona is therefore very important for the delivery of wave energy to the chromosphere, with the length scale of focused fast waves determined by the footpoint size of the waveguide.
Observational studies of radio and HXR emission from flares show a spectrum of time scales from milliseconds to tens of minutes, from which it has been suggested that flares are composed of elementary flare bursts having durations in the range 1−25 s (van Beek et al. 1974; de Jager & de Jonge 1978), and energy release fragments in the range 50−1000 ms (Kiplinger et al. 1983; Benz 1985, 1986; Machado et al. 1993), with longer time scales attributable to pileup of shorter events. In this context, the driver in our simulations represents the injection of a fundamental element by the energy release, from which a general picture of wave transport is obtained by considering many such bursts with varying durations, superimposed in a chain lasting up to several minutes. In the linear regime, the waves produced by multiple injections of energy are simply superimposed, therefore, Alfvén waves and waveguided fast waves will deliver a stream of focused energy to the chromosphere if the corona is repeatedly driven. It must be noted, however, that MHD waves produced by large solar flares are likely to be non-linear, at least at some point in their evolution, in which case a wave front passing through another may experience a change in Alfvén speed due to the other wave, and the evolution will no longer be a simple linear superposition. Non-linear evolution therefore warrants further study, and this matter will be returned to later in this discussion.
Connecting the present paper with previous works, MHD simulations of 3D reconnection by Birn et al. (2009) have already shown that bursty reconnection produces focused spots of Poynting flux on the chromospheric boundary. These were located near the separatrices of the reconnecting arcade, within the domain of closed magnetic flux, and were associated with “the break-up of an initially extended, quasi 2D, reconnection line (separator) into smaller, spatially more localised, reconnection sites”. The authors of that study did not investigate the processes responsible for focused transport, but the present paper shows that the properties of Alfvén and fast waves, concentration by magnetic field convergence, phase mixing and waveguiding are likely to be responsible. From the shape of the strongest concentrations of Poynting flux seen by Birn et al. (2009), they seem more likely to correspond to waveguided fast waves than plane Alfvén waves, although torsional Alfvén waves, and plane Alfvén waves coupled to fast waves are not ruled out. The dominant type of “Alfvénic” wave in these regions could be determined with much greater confidence by inspecting the local variation of Alfvén speed close to energy concentrations and the patterns of magnetic field and velocity perturbations associated with the waves, but these data were not published by Birn et al. (2009). If waveguiding is responsible for concentration of energy, then the waveguides may be established in response to bursty reconnection by magnetic field becoming locally weaker in some regions while it is concentrated in others.
Our study also complements research by Russell & Fletcher (2013) that examined transmission of waves from the corona to the chromosphere and heating by ion-neutral friction. They studied Alfvénic waves in 1D two-fluid models (plasma plus neutrals) using semiempirical models of the preflare solar atmosphere, and found that energy transmission from the corona to the chromosphere can exceed 20% for wave periods of 1 s or less, with a significant fraction of this being converted to heat in the mid- and upper-chromosphere by ion-neutral friction (37%–100% of it for subsecond wave periods). The present work demonstrates that MHD waves can deliver energy to spatially focused locations, while the study by Russell & Fletcher (2013) shows a significant fraction of this can enter the chromosphere and be converted to heat, potentially contributing to flare radiative emissions. The waves in our study, especially unguided fast waves, also deliver energy to broader regions, so MHD wave transport should be able to contribute the more diffuse chromospheric flare emissions such as plage brightening as well as the more compact emissions such as from ribbons and kernels.
In addition, it has been suggested by Fletcher & Hudson (2008) that waves in the chromosphere may cascade to small wavelengths at which parallel electric fields are produced, and these wave fields may accelerate electrons (see also Brown et al. 2009). If this were to occur, our study suggests the delivery of focused wave energy could concentrate the wave-particle interactions to spatially localised regions, as required to produce HXR kernels.
This paper has so far concentrated on transport to the chromosphere, but a successful flare model must also accelerate electrons in the corona to explain coronal radio and HXR emissions. If electrons are accelerated by reconnection parallel electric fields, then they have to pass through the reconnection site itself, which is likely to be very small for typical coronal conditions. One possible solution proposed by Miller et al. (1996) is that electrons could be accelerated in a much larger volume by fast wave turbulence driven by reconnection outflows (see also Larosa & Moore 1993; Yan et al. 2008). Returning to our Fig. 7, when the fast wave was injected above a waveguide, multiple transmissions and reflections led to the formation of complicated small-scale patterns of wave energy within the waveguide, particularly near the loop apex. These patterns are consistent with an early stage leading to turbulence – if energy was repeatedly injected, later wave fronts would be distorted when passing through smaller-scale waves, establishing a nonlinear cascade to small scales where electrons can be accelerated. It is interesting that our study suggests waveguides as locations where fast wave turbulence (and hence coronal electron acceleration) may be preferentially located.
Our final comment on the present work is that transverse structuring of the coronal Alfvén speed is clearly of great importance when evaluating the role of MHD waves in solar flares. This is perhaps unsurprising, given the emphasis of transverse structure in magnetoseismology (e.g. Edwin & Roberts 1983). For flares, our study suggests that waveguides directly excited by the energy release are most important for transporting wave energy to the chromosphere. Assuming that energy is injected into waveguides as they pass through a reconnection site, one expects focused wave energy to be delivered to the chromosphere close to magnetic separatrices or quasi-separatrix layers, and this is consistent with the spatial relationship observed between flare ribbons, kernels and magnetic topology deduced from magnetic extrapolations (Gorbachev & Somov 1989; Mandrini et al. 1991; Demoulin et al. 1993, 1997). Meanwhile, fast waves that are not injected into a waveguide are likely to contribute to more widespread emissions such as plage brightening, while indirectly excited waveguides may become preferential locations for acceleration of coronal electrons by fast wave turbulence.
Flare models incorporating waves are, in many ways, at an early stage of development compared to models that assume only coronal electron beams. Although important work has been done to make the case for including waves and to examine particular aspects of the problem, significant future work is required to piece these together, fill in theoretical gaps and propose the observational tests that will conclusively determine the true significance of waves in flares.
Arriving at a complete and rigorous physical model is a long term goal, however some shorter-term objectives are readily set. Building on the results presented in this paper, it would be worthwhile to conduct a similar study including non-linear effects, aiming to confirm the extension of our linear results to the non-linear regime, and to investigate the locations where MHD turbulence preferentially develops and the manner in which it does so. At that stage, it would also be interesting to consider a continually driven problem in addition to the initial value problem considered here. Other limitations of the present work include that energy was injected “by hand” and the model employed a background magnetic field that was 2D and in equilibrium, neither of which applies to solar flares. These choices gave clarity to our interpretation, and the results can be compared to the 3D study by Birn et al. (2009) in which the energy release was produced self-consistently by magnetic reconnection. Nonetheless, future studies that include bursty reconnection as a driver (and therefore non-equilibrium “background” magnetic field) offer opportunities to investigate how waveguides are created and the effects of finite waveguide lifetimes. 3D studies also have potential to clarify the types of waves involved in transport and the importance of wave coupling. Our final desire for the near future is to bridge the gap between the present 2.5D study of coronal waves and the 1D study by Russell & Fletcher (2013) of Alfvénic waves propagating from the corona to the chromosphere, to produce an integrated study of wave transport and damping across both the coronal and chromospheric domains.
Acknowledgments
AJBR was supported by a Royal Commission for the Exhibition of 1851 Research Fellowship while this work was undertaken, and acknowledges STFC consolidated grant ST/K000993/1 for present support. D.J.S. is supported by an STFC studentship through consolidated grant ST/J501049/1. We sincerely thank Lyndsay Fletcher and Hugh Hudson for valuable discussions contributing to this work and an anonymous reviewer for suggestions that improved the paper.
References
- Arnoldy, R. L., Kane, S. R., & Winckler, J. R. 1968, ApJ, 151, 711 [NASA ADS] [CrossRef] [Google Scholar]
- Asai, A., Ishii, T. T., Isobe, H., et al. 2012, ApJ, 745, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., Fletcher, L., Schrijver, C. J., & Alexander, D. 1999, ApJ, 520, 880 [NASA ADS] [CrossRef] [Google Scholar]
- Benz, A. O. 1985, Sol. Phys., 96, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Benz, A. O. 1986, Sol. Phys., 104, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Bian, N. H., & Kontar, E. P. 2011, A&A, 527, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bian, N. H., Kontar, E. P., & Brown, J. C. 2010, A&A, 519, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Birn, J., Fletcher, L., Hesse, M., & Neukirch, T. 2009, ApJ, 695, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Brady, C. S., & Arber, T. D. 2005, A&A, 438, 733 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, J. C. 1971, Sol. Phys., 18, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. C., & Melrose, D. B. 1977, Sol. Phys., 52, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. C., Karlicky, M., MacKinnon, A. L., & van den Oord, G. H. J. 1990, ApJS, 73, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. C., Turkmani, R., Kontar, E. P., MacKinnon, A. L., & Vlahos, L. 2009, A&A, 508, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burghes, D. N., Kendall, P. C., & Sweet, P. A. 1969, MNRAS, 143, 9 [NASA ADS] [Google Scholar]
- Chaston, C. C., Bonnell, J. W., Peticolas, L. M., et al. 2002, Geophys. Res. Lett., 29, 110000 [CrossRef] [Google Scholar]
- Chaston, C. C., Carlson, C. W., McFadden, J. P., Ergun, R. E., & Strangeway, R. J. 2007, Geophys. Res. Lett., 34, 7101 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, P. F., & Wu, Y. 2011, ApJ, 732, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, P. F., Wu, S. T., Shibata, K., & Fang, C. 2002, ApJ, 572, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Cliver, E. W., Petrie, G. J. D., & Ling, A. G. 2012, ApJ, 756, 144 [NASA ADS] [CrossRef] [Google Scholar]
- de Jager, C. 1964, in Astronomical Observations From Space Vehicles, ed. J. C. Seinberg [Google Scholar]
- de Jager, C., & de Jonge, G. 1978, Sol. Phys., 58, 127 [NASA ADS] [CrossRef] [Google Scholar]
- De Moortel, I., & Nakariakov, V. M. 2012, Roy. Soc. London Philos. Trans. Ser. A, 370, 3193 [Google Scholar]
- De Moortel, I., & Pascoe, D. J. 2009, ApJ, 699, L72 [NASA ADS] [CrossRef] [Google Scholar]
- Demoulin, P., van Driel-Gesztelyi, L., Schmieder, B., et al. 1993, A&A, 271, 292 [NASA ADS] [Google Scholar]
- Demoulin, P., Bagala, L. G., Mandrini, C. H., Henoux, J. C., & Rovira, M. G. 1997, A&A, 325, 305 [NASA ADS] [Google Scholar]
- Díaz, A. J., Zaqarashvili, T., & Roberts, B. 2006, A&A, 455, 709 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Edwin, P. M., & Roberts, B. 1983, Sol. Phys., 88, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Emslie, A. G., & Sturrock, P. A. 1982, Sol. Phys., 80, 99 [Google Scholar]
- Fletcher, L. 2005, Space Sci. Rev., 121, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Fletcher, L., & Hudson, H. S. 2008, ApJ, 675, 1645 [NASA ADS] [CrossRef] [Google Scholar]
- Fletcher, L., Dennis, B. R., Hudson, H. S., et al. 2011, Space Sci. Rev., 159, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Gorbachev, V. S., & Somov, B. V. 1989, SvA, 33, 57 [Google Scholar]
- Haerendel, G. 2009, ApJ, 707, 903 [NASA ADS] [CrossRef] [Google Scholar]
- Haerendel, G. 2012, ApJ, 749, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Harra, L. K., & Sterling, A. C. 2003, ApJ, 587, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Hasegawa, A., & Chen, L. 1974, Phys. Rev. Lett., 32, 454 [NASA ADS] [CrossRef] [Google Scholar]
- Heyvaerts, J., & Priest, E. R. 1983, A&A, 117, 220 [NASA ADS] [Google Scholar]
- Hudson, H. S. 1972, Sol. Phys., 24, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Hudson, H. S. 2011, Space Sci. Rev., 158, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Johnstone, B. M., Petrie, G. J. D., & Sudol, J. J. 2012, ApJ, 760, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Keiling, A. 2009, Space Sci. Rev., 142, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Kigure, H., Takahashi, K., Shibata, K., Yokoyama, T., & Nozawa, S. 2010, PASJ, 62, 993 [NASA ADS] [Google Scholar]
- Kiplinger, A. L., Dennis, B. R., Frost, K. J., Orwig, L. E., & Emslie, A. G. 1983, ApJ, 265, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Krucker, S., Hudson, H. S., Jeffrey, N. L. S., et al. 2011, ApJ, 739, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Larosa, T. N., & Moore, R. L. 1993, ApJ, 418, 912 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, W., Liu, S., Jiang, Y. W., & Petrosian, V. 2006, ApJ, 649, 1124 [Google Scholar]
- Longcope, D. W., & Priest, E. R. 2007, Phys. Plasmas, 14, 122905 [NASA ADS] [CrossRef] [Google Scholar]
- Longcope, D. W., & Tarr, L. 2012, ApJ, 756, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Machado, M. E., Ong, K. K., Emslie, A. G., et al. 1993, Adv. Space Res., 13, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Mandrini, C. H., Demoulin, P., Henoux, J. C., & Machado, M. E. 1991, A&A, 250, 541 [NASA ADS] [Google Scholar]
- Mann, I. R., Wright, A. N., & Cally, P. S. 1995, J. Geophys. Res., 100, 19441 [NASA ADS] [CrossRef] [Google Scholar]
- Mathioudakis, M., Jess, D. B., & Erdélyi, R. 2012, Space Sci. Rev., 94 [Google Scholar]
- McClements, K. G., & Fletcher, L. 2009, ApJ, 693, 1494 [NASA ADS] [CrossRef] [Google Scholar]
- McIntosh, S. W., de Pontieu, B., Carlsson, M., et al. 2011, Nature, 475, 477 [NASA ADS] [CrossRef] [Google Scholar]
- McLaughlin, J. A., & Hood, A. W. 2006, A&A, 452, 603 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McLaughlin, J. A., & Ofman, L. 2008, ApJ, 682, 1338 [NASA ADS] [CrossRef] [Google Scholar]
- Melrose, D. B. 1992, ApJ, 387, 403 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, J. A., Larosa, T. N., & Moore, R. L. 1996, ApJ, 461, 445 [NASA ADS] [CrossRef] [Google Scholar]
- Moreton, G. E. 1960, AJ, 65, 494 [Google Scholar]
- Moreton, G. E., & Ramsey, H. E. 1960, PASP, 72, 357 [Google Scholar]
- Moses, D., Clette, F., Delaboudinière, J.-P., et al. 1997, Sol. Phys., 175, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Mullan, D. J. 1975, A&A, 40, 41 [NASA ADS] [Google Scholar]
- Nakariakov, V. M., & Verwichte, E. 2005, Liv. Rev. Sol. Phys., 2, 3 [Google Scholar]
- Nakariakov, V. M., Ofman, L., Deluca, E. E., Roberts, B., & Davila, J. M. 1999, Science, 285, 862 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ofman, L. 2005, Adv. Space Res., 36, 1572 [NASA ADS] [CrossRef] [Google Scholar]
- Ofman, L. 2007, ApJ, 655, 1134 [NASA ADS] [CrossRef] [Google Scholar]
- Ofman, L., & Thompson, B. J. 2002, ApJ, 574, 440 [NASA ADS] [CrossRef] [Google Scholar]
- Oliver, R., Ballester, J. L., Hood, A. W., & Priest, E. R. 1993, A&A, 273, 647 [NASA ADS] [Google Scholar]
- Pascoe, D. J., de Moortel, I., & McLaughlin, J. A. 2009, A&A, 505, 319 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petrie, G. J. D., & Sudol, J. J. 2010, ApJ, 724, 1218 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 2007, Numerical Recipes 3rd Edition: The Art of Scientific Computing, 3rd edn. (Cambridge University Press) [Google Scholar]
- Pridmore-Brown, D. C. 1966, Phys. Fluids, 9, 1290 [NASA ADS] [CrossRef] [Google Scholar]
- Russell, A. J. B., & Fletcher, L. 2013, ApJ, accepted [Google Scholar]
- Russell, A. J. B., & Wright, A. N. 2010, A&A, 511, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schmidt, J. M., & Ofman, L. 2010, ApJ, 713, 1008 [NASA ADS] [CrossRef] [Google Scholar]
- Schrijver, C. J. 2007, ApJ, 655, L117 [Google Scholar]
- Schrijver, C. J., & Title, A. M. 2011, J. Geophys. Res. (Space Phys.), 116, 4108 [Google Scholar]
- Semeter, J., Heinselman, C. J., Sivjee, G. G., Frey, H. U., & Bonnell, J. W. 2005, J. Geophys. Res. (Space Physics), 110, 11310 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, A., Goldberg, M., & Liu, E. 1980, Ultrasonic Imaging, 2, 291 [Google Scholar]
- Stasiewicz, K., & Ekeberg, J. 2008, ApJ, 680, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Stasiewicz, K., Bellan, P., Chaston, C., et al. 2000, Space Sci. Rev., 92, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Su, J. T., Jing, J., Wang, H. M., et al. 2011, ApJ, 733, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Sudol, J. J., & Harvey, J. W. 2005, ApJ, 635, 647 [NASA ADS] [CrossRef] [Google Scholar]
- Tataronis, J., & Grossmann, W. 1973, Zeitschrift Phys., 261, 203 [Google Scholar]
- Terradas, J., & Ofman, L. 2004, in SOHO 13 Waves, Oscillations and Small-Scale Transients Events in the Solar Atmosphere: Joint View from SOHO and TRACE, ed. H. Lacoste, ESA SP, 547, 469 [NASA ADS] [Google Scholar]
- Thompson, K. W. 1987, J. Comput. Phys., 68, 1 [Google Scholar]
- Thompson, B. J., Plunkett, S. P., Gurman, J. B., et al. 1998, Geophys. Res. Lett., 25, 2465 [Google Scholar]
- Thompson, B. J., Gurman, J. B., Neupert, W. M., et al. 1999, ApJ, 517, L151 [NASA ADS] [CrossRef] [Google Scholar]
- Tsiklauri, D. 2012, Phys. Plasmas, 19, 082903 [NASA ADS] [CrossRef] [Google Scholar]
- Uchida, Y. 1960, PASJ, 12, 376 [NASA ADS] [Google Scholar]
- Uchida, Y. 1968, Sol. Phys., 4, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Uchida, Y. 1974, Sol. Phys., 39, 431 [NASA ADS] [CrossRef] [Google Scholar]
- van Beek, H. F., de Feiter, L. D., & de Jager, C. 1974, in Space Research XIV, eds. M. J. Rycroft, & R. D. Reasenberg (Berlin: Verlag), 447 [Google Scholar]
- Verwichte, E., Foullon, C., & Nakariakov, V. M. 2006, A&A, 446, 1139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, H., & Liu, C. 2010, ApJ, 716, L195 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, H., Varsik, J., Zirin, H., et al. 1992, Sol. Phys., 142, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, H., Ewell, Jr., M. W., Zirin, H., & Ai, G. 1994, ApJ, 424, 436 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, S., Liu, C., Liu, R., et al. 2012, ApJ, 745, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Watt, C. E. J., & Rankin, R. 2010, J. Geophys. Res. (Space Phys.), 115, 7224 [NASA ADS] [CrossRef] [Google Scholar]
- Wheatland, M. S., & Melrose, D. B. 1994, PASA, 11, 25 [NASA ADS] [Google Scholar]
- Wild, J. P. 1950, Aust. J. Sci. Res. A Phys. Sci., 3, 399 [NASA ADS] [Google Scholar]
- Wild, J. P., & McCready, L. L. 1950, Aust. J. Sci. Res. A Phys. Sci., 3, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Wills-Davey, M. J., DeForest, C. E., & Stenflo, J. O. 2007, ApJ, 664, 556 [Google Scholar]
- Yan, H., Lazarian, A., & Petrosian, V. 2008, ApJ, 684, 1461 [NASA ADS] [CrossRef] [Google Scholar]
- Zharkova, V. V., & Gordovskyy, M. 2005, A&A, 432, 1033 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 Evolution of the Alfvén wave in a magnetic arcade, shown through second order energy density at times a) t/τA = 0, b) t/τA = 0.5, c) t/τA = 1.25 and d) t/τA = 1.79. Black arrows show the direction and strength of the equilibrium magnetic field. |
| In the text | |
 |
Fig. 2 Energy delivered to bottom boundary by Alfvén wave, as a function of time and location. Dashed horizontal lines mark the magnetic footpoints of the initial energy injection. |
| In the text | |
 |
Fig. 3 Evolution of the fast wave in a magnetic arcade. Panels a) to d) show first order energy density. Panels e) to h) show second order energy density. |
| In the text | |
 |
Fig. 4 Energy delivered to bottom boundary by fast wave in arcade model with hydrostatic density, shown as function of time and location. Part a) shows first order energy density. Part b) shows second order energy density. |
| In the text | |
 |
Fig. 5 Evolution of the fast wave excited inside an overdense loop (density contrast of ten). Panels a) to d) show first order energy density, panels e) to h) show second order energy density and magenta lines mark the edges of the loop. |
| In the text | |
 |
Fig. 6 Energy delivered to bottom boundary by fast wave excited inside an overdense loop. Part a) shows first order energy density. Part b) shows second order energy density. Horizontal dashed lines mark the footpoints of the overdense loop. |
| In the text | |
 |
Fig. 7 Evolution of the fast wave excited above an overdense loop (density contrast of ten). Panels a) to d) show first order energy density, panels e) to h) show second order energy density and magenta lines mark the edges of the loop. |
| In the text | |
 |
Fig. 8 Energy delivered to bottom boundary by fast wave excited above an overdense loop. Part a) shows first order energy density. Part b) shows second order energy density. Horizontal dashed lines mark the footpoints of the overdense loop. |
| In the text | |
 |
Fig. 9 Ray tracing analysis tracking reflections inside an overdense loop. Parts a), b) and c) show trajectories of waves launched from the centre of the loop with initial angles of 0.75π, π and 1.25π (measured anti-clockwise from the x-direction). Parts d), e) and f) show the initial ray angles for which waves emanating from the centre of the loop (x0 = l0, z0 = 0.512l0, panel d)), top of the loop (x0 = l0, z0 = 0.611l0, panel e)), and a point on the upper boundary not on the central axis (x0 = 0.7l0, z0 = 0.537l0, panel f)) reach the chromosphere (cyan and red segments) and the subset of rays perfectly trapped by total internal reflection (red segments only). Source locations used in d) to f) are indicated by the magenta circles in panel c). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


