| Issue |
A&A
Volume 558, October 2013
|
|
|---|---|---|
| Article Number | A112 | |
| Number of page(s) | 8 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201321898 | |
| Published online | 14 October 2013 | |
Laboratory rotational spectra of the dimethyl ether 13C-isotopologues up to 1.5 THz⋆
1
I. Physikalisches Institut, Universität zu Köln,
Zülpicher Str. 77, 50937
Köln, Germany
e-mail: koerber@ph1.uni-koeln.de
2
Centre for Star and Planet Formation, Natural History Museum of
Denmark, Øster Voldgade
5-7, 1350
Copenhagen,
Denmark
3
Centre for Star and Planet Formation, Niels Bohr
Institute, Juliane Mariesvej
30, 2100
Copenhagen Ø.,
Denmark
4
Institut für Anorganische Chemie, Universität zu
Köln, Greinstr. 6,
50939
Köln,
Germany
Received:
15
May
2013
Accepted:
29
August
2013
Context. Dimethyl ether is found in high abundance in the interstellar medium. Owing to its strong and dense spectrum throughout the entire microwave and terahertz regime, it contributes to the spectral confusion in astronomical line surveys. The great sensitivity of new observatories like ALMA enhances the need for reliable spectroscopic data, especially for isotopic species of abundant molecules. In addition, the study of the interstellar 12C/13C isotopic ratio can be used as a tracer of the formation process of a molecular species, and thus it gives insight into the chemical evolution of the observed region.
Aims. The interpretation of astronomical observations depends on the knowledge of accurate rest frequencies and intensities. The objective of this work is to provide spectroscopic data for the two 13C-isotopologues of dimethyl ether in the vibrational ground state.
Methods. High-resolution rotational-torsional spectra of 12CH3O13CH3 and (13CH3)2O have been measured in the laboratory covering frequencies up to 1.5 THz. The analysis is based on an effective rotational Hamiltonian for molecules with two large-amplitude motions.
Results. Predictions of the complete ground state rotational spectrum of dimethyl ether-13C1 and -13C2 up to 2 THz are presented with accuracies better than 1 MHz. Based on the laboratory work, transitions of 12CH3O13CH3 dimethyl ether have been detected for the first time in a large submillimeter line survey of the high-mass star forming region G327.3-0.6 performed with the APEX telescope.
Key words: molecular data / methods: laboratory / ISM: molecules / ISM: abundances / astrochemistry
Full Tables 5 and 6 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/558/A112
© ESO, 2013
1. Introduction
Dimethyl ether (DME) is an asymmetric top molecule with a relatively strong permanent dipole moment of μ = 1.302(10) D (Blukis et al. 1963). Its rotational spectrum is complicated by large-amplitude internal motion of both methyl groups interacting with the overall rotation of the molecule. This causes a splitting of each rotational level into torsional substates. Therefore DME exhibits a strong and dense spectrum throughout the entire microwave and terahertz regime that is relevant for astronomical observations. In addition, DME is known to be a prominent molecule in star forming regions that contributes to spectral line confusion in line surveys of these regions. First interstellar detection of DME was in the Orion nebula as reported by Snyder et al. (1974). Identification of DME in spectra of numerous high-mass star forming regions followed (e.g., Sutton et al. 1995; Nummelin et al. 1998, 2000). DME is detected as well in low-mass star forming regions (e.g., Cazaux et al. 2003; Jørgensen et al. 2005; Bacmann et al. 2012; Persson et al. 2012). The latest generation of telescopes like the Atacama Large Millimeter Array (ALMA) enhance the need for accurate prediction of transition frequencies in the terahertz region. Owing to the increased sensitivity of these observing facilities predictions are also required for isotopologues and vibrationally excited states of prominent molecules like DME.
Despite its abundance in star forming regions, the interstellar formation process of DME
(CH3OCH3) has remained unclear up to now. Peeters et al. (2006) concluded that gas-phase synthesis via
self-methylation of methanol (CH3OH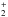 + CH3OH →
CH3OCH
+ CH3OH →
CH3OCH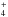 + H2O) is the most efficient
formation route for DME. Current gas-grain models (e.g., Garrod & Herbst 2006) assume that the surface reaction CH3 +
CH3O → CH3OCH3 is the most likely surface formation route
in warm dense regions. They predict strong variations in the DME abundance during the
evolutionary stage of a protostar with strong coupling of gas-phase and grain-surface
chemistry (Garrod et al. 2008). However, the utility
of DME as a “chemical clock” for the post-evaporation phase lies in the assumption that it
is only formed from methanol (Peeters et al. 2006).
Extensive modeling of the CH3OCH3 emission in the high-mass star
forming region G327.3-0.6 (Bisschop et al. 2013)
suggests that the gas-phase formation mechanism is dominant, but that a fraction greater
than 5% of DME is likely formed on the surfaces of icy grains.
+ H2O) is the most efficient
formation route for DME. Current gas-grain models (e.g., Garrod & Herbst 2006) assume that the surface reaction CH3 +
CH3O → CH3OCH3 is the most likely surface formation route
in warm dense regions. They predict strong variations in the DME abundance during the
evolutionary stage of a protostar with strong coupling of gas-phase and grain-surface
chemistry (Garrod et al. 2008). However, the utility
of DME as a “chemical clock” for the post-evaporation phase lies in the assumption that it
is only formed from methanol (Peeters et al. 2006).
Extensive modeling of the CH3OCH3 emission in the high-mass star
forming region G327.3-0.6 (Bisschop et al. 2013)
suggests that the gas-phase formation mechanism is dominant, but that a fraction greater
than 5% of DME is likely formed on the surfaces of icy grains.
A more direct method of testing grain-surface formation of molecules has been proposed by Charnley et al. (2004) and is called “posterior isotopic labelling”. The ion-molecule process 13C+ + 12CO → 13CO + 12C+ with an exothermicity of 35 K is found to efficiently incorporate 13C into CO at the expense of 12C (Langer et al. 1984). This process is only efficient at 10 K. Therefore the atoms and molecules that accrete on cold grains and can participate in surface reactions to form complex molecules will be selectively fractionated in 13C. If atom addition reactions to solid CO and HCO are the origin of organic molecules detected in hot molecular cores, these molecules should possess the same 12C/13C ratio as their parent molecules. Wirström et al. (2011) investigated the 12C/13C ratio of CO and methanol in various sources, and their results are consistent with the formation of methanol from hydrogenation of CO on grain surfaces. Further studies on 13C-isotopologues of larger organic molecules like DME enable us to test astrochemical models and can provide important constraints on their evolutionary cycle.
Several laboratory studies of DME’s main isotopologue (12CH3)2O have been performed over the past 50 years. Myers & Wilson (1960) applied group theory to derive symmetry properties, selection rules and spin statistical weights. In 1963Blukis et al. recorded a few transitions of six isotopic species of DME to determine its structure and dipole moment. The potential barrier height to internal rotation was obtained by Durig et al. (1976) by measuring microwave transitions of the main isotopologue, as well as two deuterated forms of DME. First predictions for radio astronomy were provided by Lovas et al. (1979) in their review of all previous laboratory studies and new measurements of the vibrational ground state, which were later enhanced by Neustock et al. (1990). The most comprehensive work on the vibrational ground state of DME’s main isotopologue was published by Groner et al. (1998), which was further expanded to higher frequencies by Endres et al. (2009). This work makes accurate predictions of the rotational spectrum possible up to 2.5 THz. The two lowest vibrationally excited states, ν11 = 1 and ν15 = 1, have also been studied by Endres et al. (in prep.), enabling a first astronomical detection of vibrationally excited DME by Bisschop et al. (2013). However, only very little is known about the 13C-isotopologues of DME. Niide & Hayashi (2003) report some transition frequencies of DME-13C1 (12CH3O13CH3) below 50 GHz with maximum rotational quantum number J = 8. For DME-13C2 ((13CH3)2O), so far no rotational spectroscopic data are available.
The objective of the study reported in this paper is to provide accurate predictions of the rotational-torsional spectrum of both 13C-isotopologues of DME up to terahertz frequencies to enable the astronomical detection of these species and in this way make it possible to study their abundances for astrochemical modeling. The paper is structured as follows. In Sect. 2 we present the symmetry properties of the dimethyl ether 13C-isotopologues and summarize the theoretical approach to model their rotational spectra. Details on the experimental setup are given in Sect. 3. Using this setup, laboratory rotational spectra of 12CH3O13CH3 and (13CH3)2O were recorded. Details on the experimental dataset and their analysis are given in Sect. 4. In Sect. 5 we conclude the laboratory analysis and discuss the implications for the astronomical detection of 13C-isotopologues of dimethyl ether. Predictions based on the laboratory analysis have already led to a first detection of 12CH3O13CH3 in the interstellar medium, which is also introduced in Sect. 5.
2. Theoretical model
DME is an asymmetric rotor close to the limiting case of a prolate symmetric top (Ray’s parameter κ = −0.92). The permanent dipole moment of μ = 1.302(10) D lies parallel to the b principal inertial axis in the plane of symmetry. The two 13C-isotopologues differ in their symmetry properties: Due to the identical methyl groups in (13CH3)2O, this molecule has the same symmetry as the main isotopologue (12CH3)2O. In the rigid rotor approximation both molecules belong to the C2v point group. DME-13C1, 12CH3O13CH3, does not have an axis of rotational symmetry, because its methyl groups are not equivalent. The point group symmetry of this isotopologue is Cs. However, the two methyl groups in DME perform large amplitude internal motions around the C-O bond with a barrier to internal rotation of 900 to 950 cm-1 (Durig et al. 1976; Groner & Durig 1977; Lutz & Dreizler 1978; Neustock et al. 1990; Niide & Hayashi 2004). The non-zero tunneling probability between the nine equivalent configurations of the molecule means that DME cannot be described as a rigid rotor. When taking the torsional motion into account, the symmetry of (13CH3)2O is given by the molecular symmetry group G36 (Longuet-Higgins 1963), whereas the symmetry of 12CH3O13CH3 is described by the molecular symmetry group G18 (Bunker 1965). Each rotational energy level splits up into torsional substates, which are labeled by (00), (10), (01), (11), and (1-1)1,2 rather than using the symmetry labels of the molecular symmetry group. In this labeling scheme, the notation for both isotopologues is equivalent, which avoids confusion. Pure rotational transitions only occur within each torsional substate. Owing to the equivalent methyl tops in (13CH3)2O, the (10) and (01) states are degenerate and each rotational transition splits up into four torsional components3 (00), (01), (11), and (1-1) with spin statistical weights 36, 64, 20, 16 for ee − oo transitions and 28, 64, 12, 16 for eo − oe transitions, respectively4. The rotational transitions of 12CH3O13CH3 split up into five components5 (00), (01), (10), (11), and (1-1). The spin statistical weight factors are 32, 32, 32, 16, and 16. Because of the interaction between the overall rotation and the torsional motion of the molecule, the torsional splitting of the ground state rotational levels is a function of the rotational quantum numbers J and K. The size of the splitting between the torsional substates (00), (01), and (11) is typically several megahertz, but the splitting between the substates (01) and (10), as well as (11) and (1-1), is significantly smaller and usually just a few kilohertz. Thus in Doppler limited measurements the splitting of transitions between these substates is not resolved in most cases. Usually a characteristic triplet is measured in the laboratory for rotational transitions of both DME isotopologues with the most intense torsional component (10)/(01) located between the two equally intense components (00) and (11)/(1-1).
To model the rotational-torsional levels of DME the effective rotational Hamiltonian ERHAM proposed by Groner was used. Details on the model are given in Groner (1997, 2012). In the following, only the very basic ideas are summarized. In the ERHAM approach, the basis for the wavefunctions is set up as products of the symmetric rotor eigenfunctions |JKM⟩ and internal motion basis functions |νσ1(K)σ2(−K)⟩. The quantum number ν characterizes the set of vibrational states, and σ1, σ2 are the symmetry numbers labeling the torsional substates. The internal motion basis functions |νσ1(K)σ2(−K)⟩ are derived from the solutions |νσ1(K1)σ2(K2)⟩ of the torsional Hamiltonian HI in the ρ-axis system, where K1,2 are the projections of the overall angular momentum J onto the ρ1,2-axes of the molecule. In the ERHAM approach, these solutions are not calculated explicitly. Groner makes use of their periodicity, and the internal motion basis functions are expressed in terms of localized functions with their spatial probability distribution localized in one of the nine minima of the potential. As a result, the matrix elements of the Hamiltonian become Fourier series whose coefficients are integrals of the localized functions. The benefit of this expansion is that every vibrational state ν is described by an individual set of Fourier coefficients without knowledge of the potential function. If the barrier to torsion is sufficiently high, the Fourier expansion quickly converges, which reduces the number of fitting parameters of this effective Hamiltonian significantly.
Spectroscopic parameters for 12CH3O13CH3 and (13CH3)2O in the vibrational ground state.
The effective Hamiltonian is finally given by 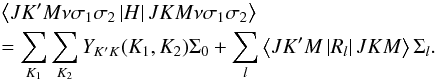 (1)The first term describes the matrix elements of
the torsional energy, expressed as a two-dimensional Fourier series Σ0. The
matrix
YK′K(K1,K2)
depends on the polar angles β1,2 of the vectors
ρ1,2 to the principal inertial axes. It transforms the basis
of the ρ-axis system to the principal axis system of the rotational
operators. The second term of Eq. (1)
contains the matrix elements of the rotational operators
Rl in A-reduction multiplied by a
two-dimensional Fourier series Σl. The Fourier series are given
by
(1)The first term describes the matrix elements of
the torsional energy, expressed as a two-dimensional Fourier series Σ0. The
matrix
YK′K(K1,K2)
depends on the polar angles β1,2 of the vectors
ρ1,2 to the principal inertial axes. It transforms the basis
of the ρ-axis system to the principal axis system of the rotational
operators. The second term of Eq. (1)
contains the matrix elements of the rotational operators
Rl in A-reduction multiplied by a
two-dimensional Fourier series Σl. The Fourier series are given
by ![\begin{eqnarray} \Sigma_0=\epsilon_{00} &+& 2\sum_{q>0}\bigg[ \epsilon_{qq}\cos\alpha'_{qq}+\epsilon_{q-q}\cos\alpha'_{q-q}\\ \nonumber &+&\sum_{q'=-q+1}^{q-1}(\epsilon_{qq'}\cos\alpha'_{qq'}+ \epsilon_{q'q}\cos\alpha'_{q'q})\bigg] \end{eqnarray}](/articles/aa/full_html/2013/10/aa21898-13/aa21898-13-eq90.png) (2)with
(2)with
![\begin{equation} \alpha'_{qq'}=\tfrac{2\pi}{3}[q(\sigma_1-\rho K_1)+q'(\sigma_2-\rho K_2)] \end{equation}](/articles/aa/full_html/2013/10/aa21898-13/aa21898-13-eq91.png) (3)and
(3)and
![\begin{eqnarray} \Sigma_l=T^{(\kappa)}_{l00}&+&2\sum_{q>0}\bigg[ T^{(\kappa)}_{lqq}\cos\alpha_{qq}+T^{(\kappa)}_{lq-q}\cos\alpha_{q-q} \\ \nonumber &+& \sum_{q'=-q+1}^{q-1}(T^{(\kappa)}_{lqq'}\cos\alpha_{qq'}+ T^{(\kappa)}_{lq'q}\cos\alpha_{q'q})\bigg] \end{eqnarray}](/articles/aa/full_html/2013/10/aa21898-13/aa21898-13-eq92.png) (4)with
κ = K − K′ and
(4)with
κ = K − K′ and
![\begin{equation} \alpha_{qq'}=\tfrac{\pi}{3}[q(2\sigma_1-\rho(K+K'))+q'(2\sigma_2+\rho(K+K'))]. \end{equation}](/articles/aa/full_html/2013/10/aa21898-13/aa21898-13-eq94.png) (5)Together with the internal motion parameter
ρ and the polar angle β, the coefficients
ϵqq′ and
(5)Together with the internal motion parameter
ρ and the polar angle β, the coefficients
ϵqq′ and
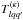 of these Fourier series are the
spectroscopic parameters. The Fourier coefficients with
q = q′ = 0 are the parameters describing the overall
rotation (equivalent to the rotational parameters of molecules without torsional motion) and
Fourier coefficients with q > 0 or q′ > 0 arise from
the interaction between internal and overall rotation. For equivalent internal rotors like
in the case of (13CH3)2O the Fourier coefficients with
qq′ are equal to those with
q′q, which simplifies the equations given above and
further reduces the number of parameters needed to describe the molecule.
of these Fourier series are the
spectroscopic parameters. The Fourier coefficients with
q = q′ = 0 are the parameters describing the overall
rotation (equivalent to the rotational parameters of molecules without torsional motion) and
Fourier coefficients with q > 0 or q′ > 0 arise from
the interaction between internal and overall rotation. For equivalent internal rotors like
in the case of (13CH3)2O the Fourier coefficients with
qq′ are equal to those with
q′q, which simplifies the equations given above and
further reduces the number of parameters needed to describe the molecule.
Characterization of the different datasets used in the analysis of 12CH3O13CH3.
Characterization of the different datasets used in the analysis of (13CH3)2O.
The parameters of the effective Hamiltonian shortly introduced in this section (a detailed derivation is given in Groner 1997, 2012) were fitted to the experimental data in a least-squares analysis described in Sect. 4. A list of the parameters introduced to model the spectrum of the DME 13C-isotopologues in the present investigation is given in Table 1.
3. Experimental details
Torsion-rotation spectra of DME-13C1 and -13C2 were recorded in Cologne in the millimeter and submillimeter regimes. Several broadband scans were performed which cover the available frequency regions (see Tables 2 and 3) above 300 GHz completely. In addition, especially for the frequency regions below 300 GHz, numerous single scans were performed to measure spectra of single transitions with optimized signal-to-noise ratios. For frequencies up to 70 GHz, a commercial synthesizer was used as radiation source, and for frequencies up to 120 GHz, the synthesizer output was multiplied by a tripler. In both cases the signal was detected by a Schottky diode at room temperature. We used a single-pass absorption cell of 5 m length. For frequencies between 300 and 840 GHz, a combination of synthesizer and multiplier chain was used to produce high-power signals around 100 GHz, which were further multiplied by a superlattice device (for details on superlattice multipliers see Endres et al. 2007). Superlattice multipliers produce odd harmonics of the input frequency with the output power decreasing with each higher harmonic by about an order of magnitude. Transitions of DME in the frequency regimes of the 3rd, the 5th, and the 7th harmonic of the input frequency were assigned. To facilitate identification of spectra belonging to the 5th and the 7th harmonic, the spectra were measured three times using different dichroic filters to attenuate the radiation of the lower harmonics. The design and operation of dichroic filters is described in detail by Winnewisser et al. (1998). Higher frequencies up to 1.5 THz were accessed by combining the synthesizer with a multiplier chain producing the 108th harmonic of the input frequency. The setups for frequencies above 300 GHz used an InSb hot electron bolometer for detection and an absorption cell of 3 m length. To assure a frequency stability of the radiation sources of Δν/ν = 10-11, the synthesizer was locked to a reference signal of a rubidium atomic clock. For better signal-to-noise ratios, all spectra were recorded with 2f-source modulation technique. The measurements were performed at room temperature with typical gas pressures between 15 and 50 μbar.
The sample of 13C-DME was synthesized by slowly heating equal parts of 12C- and 13C-methanol with sulfuric acid. The evolving DME gas was condensed into a vacuum flask. The sample contained all possible carbon isotopic configurations (12CH3)2O, 12CH3O13CH3, and (13CH3)2O with proportion 1:2:1. In case of (13CH3)2O a pure sample was also synthesized from 13C-methanol, which was used for the scans of single transitions. 13C-methanol (at. 99%)6 was used for the synthesis of DME without further purification.
4. Measured laboratory spectrum and analysis
A total of 1510 new lines were measured for 12CH3O13CH3 and assigned to 4474 transitions. Energy levels including J = 60 and Ka = 25 were accessed. Previously published frequencies from Niide & Hayashi (2003) were included in the analysis for transitions up to 34 GHz with an uncertainty of 50 kHz. A number of 24 transitions between 35 and 48 GHz were remeasured with our spectrometer, and the new frequencies with lower uncertainty were added to the dataset. Deviations to the experimental frequencies given by Niide & Hayashi were between 10 kHz (experimental uncertainty) and 300 kHz. In the case of (13CH3)2O, 1435 lines were measured and assigned to 3055 transitions including energy levels with J = 60 and Ka = 20. Assignments of this isotopologue in broad frequency scans were slightly complicated by the lower abundance of (13CH3)2O in the sample resulting in a lower signal-to-noise ratio compared to corresponding transitions of 12CH3O13CH3. Details on the different datasets used in the analysis are given in Table 2 for 12CH3O13CH3 and Table 3 for (13CH3)2O. The analysis for both isotopologues includes a large number of Q- and R-branch transitions, as well as some P-branch and ΔKa = 3 transitions. To visualize and facilitate the assignments the AABS package by Kisiel was used. A brief description of the program package is given in Kisiel et al. (2005). The assignment of transitions was guided by predicted line positions and the intensity pattern that is in most cases characteristic. The predictions were improved iteratively during the assignments. Lines were not included in the analysis if the line profile and intensity were not reproduced well enough owing to a complicated structure or unknown blended transitions. The largest complications were due to level crossings affecting the order of nearly degenerate asymmetry levels with the same Ka. For some transitions, it was not possible to clearly define the asymmetric rotor labeling of the involved states since the Ka-doublets were degenerate, and the labels frequently shifted due to numerical noise (see Groner 2012). These transitions are marked with an asterisk in the linelists, available at the CDS, given as supplementary material to this paper. However, thanks to the degeneracy of the energy levels, the transition frequencies are not affected by this.
 |
Fig. 1 Rotational transition JKa,Kc = 143,11−134,10 in the ground state of DME-13C1 at 60 GHz. The torsional splitting into the five substates (00), (10), (01), (11), and (1-1) is fully resolved. The spin statistical weights are denoted beneath each peak and are reflected by the relative intensities of the measured lines. |
In the lower frequency ranges, the line widths are small enough to completely resolve the torsional splitting into five substates (00), (01), (10), (11), and (1-1) in the case of DME-13C1 (four substates (00), (01), (11), and (1-1) in the case of DME-13C2 with two equivalent rotors). More than 250 transitions with at least partially resolved torsional splitting were recorded that access energy levels with J = 52 and Ka = 8. Pure rotational transitions only occur within a specific torsional substate. In most cases a characteristic pattern of three lines is observed for both isotopologues with blending of the substates (01) and (10), as well as (11) and (1-1). Transitions with completely resolved torsional splitting are shown in Fig. 1 for 12CH3O13CH3 and in Fig. 2 for (13CH3)2O. The spin statistical weights given in the figures are reflected well in the relative intensities of the lines recorded. These transitions provide valuable information on the torsional splitting of energy levels, because at higher frequencies the Doppler width of lines usually becomes too large to resolve the splitting. Therefore the dataset includes a large number of blended transitions. In the least-squares fit, the assigned frequency for a blended transition is weighted with its relative intensity compared to the other components of the spectral line. The intensities were taken from predictions using a dipole moment of μ = 1.302 D. Although systematic errors associated with improper intensity predictions cannot be fully excluded and could result in incorrect description of the torsional splitting, comparison of simulated and measured spectra indicates no obvious problems. As an example, Fig. 3 shows the torsional splitting for Q-branch transitions with Ka = 6−5 and Kc = J − Ka + 1. The experimental values agree nicely with the calculated transition frequencies within the given experimental uncertainties.
 |
Fig. 2 Rotational transition JKa,Kc = 143,11−134,10 in the ground state of DME-13C2 at 53 GHz. The torsional splitting into the four substates (00), (01), (11), and (1-1) is fully resolved. The spin statistical weights are denoted beneath each peak and are reflected by the relative intensities of the measured lines. |
 |
Fig. 3 Torsional splitting of Q-branch transitions with Ka = 6−5 and Kc = J − Ka + 1 in the vibrational ground state of DME-13C1. The solid lines connect predicted transitions belonging to the same torsional substate. Experimental data are shown as errorbars. The splitting displayed is the difference between the transition frequency observed or predicted and the frequency derived if all tunneling parameters are neglected. |
 |
Fig. 4 Detail of the APEX line survey towards the hot core G327.3-0.6. The observed spectrum is depicted in black, and the model for 12CH3O13CH3 is overplotted in red. The general model including transitions of all previously identified molecules is given in blue. The spectroscopic assignment of transitions of DME-13C1 is given in the upper left of each individual panel. The asymmetry splitting and the torsional splitting of transitions is not resolved in these lines, except for the first panel, in which the torsional splitting into three components is indicated. |
The least-squares analysis of all assigned transitions was performed using the computer program ERHAM (Groner 1997) based on the effective Hamiltonian given in Sect. 2. As starting values for the fitting procedure, the values published for the main isotopologue by Endres et al. (2009) were taken. Just the rotational constants A, B, C, and the quartic centrifugal distortion parameters ΔJ, ΔJK, ΔK, δJ, and δK were scaled to account for the effect of isotopic substitution on the moments of inertia. To find the best parameter set for the model to fit the assigned experimental transition frequencies, at first only transitions with low K values were fitted with an appropriate set of parameters. Successively, the range of K values in the fit was increased, and additional parameters were included to reproduce the assigned transitions within their experimental uncertainties. The spectroscopic parameters for 12CH3O13CH3 and (13CH3)2O obtained from this analysis are given in Table 1. Only Fourier parameters with q,q′ = 0 and q,q′ = 1 were needed to describe the spectrum. In case of 12CH3O13CH3 Fourier parameters with qq′ and q′q occur due to the two non-equivalent rotors. However, it was not possible to fit most of these parameters independently. For this reason, parameters with q′q were set to the same value as the corresponding parameter with qq′. It is expected that the difference between the values of these parameters should be very small because the two rotors in 12CH3O13CH3 are very similar given that the two different carbon isotopes are located almost on the axes of internal rotation. When including new parameters in the fit, several possible coefficients were tested, and those were kept that have the largest effect on the reduced standard deviation of the fit. A discussion of the differences in the spectroscopic parameters for all three carbon isotopologues of DME is given in detail in the Ph.D.-Thesis by Koerber (2012).
 |
Fig. 5 Rotational diagram for CH3O13CH3 corrected for the optical depth. The data has been corrected for the dust optical depth, as well as the modeled line emission from other species. The filled squares (■) represent transitions detected with SHeFI in the 230, 290, and 345 GHz windows, and the open triangles (△) indicate CHAMP+ data. The solid line shows the fit to the combined SHeFI and CHAMP+ data, the dotted lines the fit to the main isotopologue by Bisschop et al. (2013) corrected for a 12C/13C ratio of 20 and 30, and the dashed lines a 12C/13C ratio of 10 and 40. |
5. Conclusion and discussion
New laboratory data on DME-13C1 and -13C2 were recorded from 34 GHz up to 1.5 THz. For 12CH3O13CH3, the existing data by Niide & Hayashi (2003) were substantially extended, and for (13CH3)2O the first rotational spectroscopic data are presented. Transitions involving energy levels up to J = 60 and Ka = 25 (Ka = 20, respectively) were analyzed and fitted to experimental uncertainty using the ERHAM effective rotational Hamiltonian for molecules with two large-amplitude motions.
Based on the laboratory analysis reported in this paper, transitions of DME-13C1 were detected in interstellar space for the first time as part of a large unbiased line-survey toward the chemically rich, high-mass hot core G327.3-0.6 (Bisschop et al., in prep.) performed with the APEX telescope (Güsten et al. 2006). The resulting bandwidth was 1.9 GHz covered per setting in the 230, 290, and 345 GHz frequency windows, and 2.8 GHz at 690 and 810 GHz. For more details on the observations, see Bisschop et al. (2013) and references therein.
Resulting best fit for the myXCLASS model.
Excerpt from the experimental transition frequencies of 12CH3O13CH3.
Excerpt from the experimental transition frequencies of (13CH3)2O.
In this survey, more than 100 previously unassigned emission lines correspond to rotational transitions of 12CH3O13CH3. An example of four transitions at frequencies around 300 GHz and 600 GHz, respectively, is given in Fig. 4. In Fig. 5 the Boltzmann diagram is shown for the 41 unblended features detected for CH3O13CH3, and the fits for the main isotopologue are overplotted for different ratios. This comparison shows that the abundance ratio for the 12C/13C dimethyl ether isotopologues lies between 20 and 30. The intensities of the blended transitions are consistent with our expectations based on the unblended transitions in combination with the other species contributing to these line blends.
The model for the CH3O13CH3 emission has been determined with the myXCLASS program7 (Comito et al. 2005). The program assumes the source to be isothermal and line shapes to be Gaussian. The CH3O13CH3 transitions were best fit with the same two-component model as for its main isotopologue, but with a lower abundance by a factor of ~25. The source size (θ), rotational temperature (Trot), source averaged column density (NT), and linewidth (ΔV) are given in Table 4. The source sizes were assumed to be the same as for the main isotopologue, since none of the CH3O13CH3 transitions were found to be optically thick, and the source size could thus not be determined independently.
The 12C/13C abundance ratio for DME in this interstellar source of about 25 ± 5 indicates the gas-phase formation route to be dominant for DME. Both carbon atoms are equivalent in DME, and thus its 12C/13C abundance ratio is expected to be less than that of, say, methanol (which is around 50) if gas-phase processes are significant for the formation of DME. A detailed analysis will be given in an upcoming paper by Bisschop et al. (in prep.).
The laboratory analysis enables us to predict the complete ground state rotational spectra of DME-13C1 and -13C2 up to 2 THz. For transitions not exceeding the range of quantum numbers covered by the laboratory analysis presented in this paper, the accuracy is expected to be better than 1 MHz. In astronomical sources the main isotopologue of DME in its vibrational ground state has been detected at various rotational temperatures; e.g., in Orion KL rotational temperatures of 89 K (Schilke et al. 1997) and 360 K (Schilke et al. 2001) were reported. For an intermediate rotational temperature of 200 K, the most intense transitions for the 13C-isotopologues are found between 750 GHz and 900 GHz with quantum numbers J and Ka in the range of 10−13. Therefore the data presented here for the two 13C-isotopologues of DME offer a very reliable basis for astronomical applications and makes an interstellar detection of these isotopologues possible in other line-rich hot core sources. The range of predictions and their accuracy also fulfill the requirements for ALMA with its exceptional sensitivity and spatial resolution, which will also be able to probe weaker transitions. With ALMA it may even be possible to detect transitions of DME-13C2. Transitions within excited vibrational states of DME-13C1 will also play a role in the ALMA spectra, since at 200 K a fraction of about 15% and 11% of the molecules is excited to the two lowest torsional states. Therefore we will further extend our laboratory studies of the 13C-isotopologues of DME to torsional excited states. The list of measured frequencies of the laboratory study presented here is given as supplementary material of this paper lodged at the CDS. Tables 5 and 6 show a preview of the data stored at the CDS. Predictions are available through the Cologne Database for Molecular Spectroscopy (CDMS8, Müller et al. 2001, 2005), together with the values of the partition function for different temperatures.
In the commonly used notation referring to the 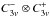 group introduced by Myers & Wilson (1960), the torsional states of
(13CH3)2O are labeled (00)= AA, (01) =
EE, (11) = AE, and (1-1) = EA (see
also Dreizler 1961b).
group introduced by Myers & Wilson (1960), the torsional states of
(13CH3)2O are labeled (00)= AA, (01) =
EE, (11) = AE, and (1-1) = EA (see
also Dreizler 1961b).
Alternatively, the torsional levels for
12CH3O13CH3 are labeled with (00) =
AA, (01) = AE, (10) = EA, (11) =
EE, and (1-1) = EE′ using the
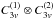 group (see Dreizler 1961a; Ohashi et al. 2004).
group (see Dreizler 1961a; Ohashi et al. 2004).
Acknowledgments
We thank the Deutsche Forschungsgemeinschaft (DFG) for financial support through research grants “Molecular Complexity”, contract no. SCHL341/10-1, and the Collaborative Research Council 956, sub-project B3.
References
- Bacmann, A., Taquet, V., Faure, A., Kahane, C., & Ceccarelli, C. 2012, A&A, 541, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bisschop, S. E., Schilke, P., Wyrowski, F., et al. 2013, A&A, 552, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blukis, U., Myers, R. J., & Kasai, P. H. 1963, J. Chem. Phys., 38, 2753 [NASA ADS] [CrossRef] [Google Scholar]
- Bunker, P. R. 1965, Mol. Phys., 9, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Cazaux, S., Tielens, A. G. G. M., Checcarelli, C., et al. 2003, ApJ, 593, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Charnley, S. B., Ehrenfreund, P., Millar, T. J., et al. 2004, MNRAS, 347, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Comito, C., Schilke, P., Philips, T. G., et al. 2005, ApJS, 156, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Dreizler, H. 1961a, Z. Naturforsch. A, 16, 1354 [NASA ADS] [Google Scholar]
- Dreizler, H. 1961b, Z. Naturforsch. A, 16, 477 [NASA ADS] [Google Scholar]
- Durig, J. R., Li, Y. S., & Groner, P. 1976, J. Mol. Spectrosc., 62, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Endres, C. P., Lewen, F., Giesen, T. F., et al. 2007, Rev. Sci. Instr., 78, 043106 [Google Scholar]
- Endres, C. P., Drouin, B. J., Pearson, J. C., et al. 2009, A&A, 504, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garrod, R. T., & Herbst, E. 2006, A&A, 457, 927 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garrod, R. T., Widicus Weaver, S. L., & Herbst, E. 2008, ApJ, 682, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Groner, P. 1997, J. Chem. Phys., 107, 4483 [NASA ADS] [CrossRef] [Google Scholar]
- Groner, P. 2012, J. Mol. Spectrosc., 278, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Groner, P., & Durig, J. R. 1977, J. Chem. Phys., 66, 1856 [NASA ADS] [CrossRef] [Google Scholar]
- Groner, P., Albert, S., Herbst, E., & De Lucia, F. C. 1998, ApJ, 500, 1059 [NASA ADS] [CrossRef] [Google Scholar]
- Güsten, R., Nyman, L. A., Schilke, P., et al. 2006, A&A, 454, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jørgensen, J. K., Bourke, T. L., Myers, P. C., et al. 2005, ApJ, 632, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Kisiel, Z., Pszczolkowski, L., Medvedev, I. R., et al. 2005, J. Mol. Spectrosc., 233, 231 [Google Scholar]
- Koerber, M. 2012, Ph.D. Thesis, Universität zu Köln [Google Scholar]
- Langer, W. D., Graedel, T. E., Frerking, M. A., & Armentrout, P. B. 1984, ApJ, 277, 581 [NASA ADS] [CrossRef] [Google Scholar]
- Longuet-Higgins, H. C. 1963, Mol. Phys., 6, 445 [NASA ADS] [CrossRef] [Google Scholar]
- Lovas, F. J., Lutz, H., & Dreizler, H. 1979, J. Phys. Chem. Ref. Data, 8, 1051 [NASA ADS] [CrossRef] [Google Scholar]
- Lutz, H., & Dreizler, H. 1978, Z. Naturforsch. A: Phys. Sci, 33, 1498 [NASA ADS] [Google Scholar]
- Müller, H. S. P., Thorwirth, S., Roth, D. A., & Winnewisser, G. 2001, A&A, 370, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Myers, R. J., & Wilson, Jr., E. B. 1960, J. Chem. Phys., 33, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Neustock, W., Guarnieri, A., Demaison, J., & Wlodarczak, G. 1990, Z. Naturforsch. A: Phys. Sci., 45, 702 [Google Scholar]
- Niide, Y., & Hayashi, M. 2003, J. Mol. Spectrosc., 220, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Niide, Y., & Hayashi, M. 2004, J. Mol. Spectrosc., 223, 152 [Google Scholar]
- Nummelin, A., Bergman, P., Hjalmarson, A., et al. 1998, ApJS, 117, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Nummelin, A., Bergman, P., Hjalmarson, A., et al. 2000, ApJS, 128, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Ohashi, N., Hougen, J. T., Suenram, R. D., et al. 2004, J. Mol. Spectrosc., 227, 28 [Google Scholar]
- Peeters, Z., Rodgers, S. D., Charnley, S. B., et al. 2006, A&A, 445, 197 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Persson, M. V., Jørgensen, J. K., & van Dishoeck, E. F. 2012, A&A, 541, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schilke, P., Groesbeck, T. D., Blake, G. A., & Phillips, T. G. 1997, ApJS, 108, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Schilke, P., Benford, D. J., Hunter, T. R., Lis, D. C., & Phillips, T. G. 2001, ApJS, 132, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Snyder, L. E., Buhl, D., Schwartz, P. R., et al. 1974, ApJ, 191, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Sutton, E. C., Peng, R., Danchi, W. C., et al. 1995, ApJS, 97, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Winnewisser, C., Lewen, F., & Helm, H. 1998, Appl. Phys. A, 66, 593 [NASA ADS] [CrossRef] [Google Scholar]
- Wirström, E. S., Geppert, W. D., Hjalmarson, A., et al. 2011, A&A, 533, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Spectroscopic parameters for 12CH3O13CH3 and (13CH3)2O in the vibrational ground state.
All Figures
 |
Fig. 1 Rotational transition JKa,Kc = 143,11−134,10 in the ground state of DME-13C1 at 60 GHz. The torsional splitting into the five substates (00), (10), (01), (11), and (1-1) is fully resolved. The spin statistical weights are denoted beneath each peak and are reflected by the relative intensities of the measured lines. |
| In the text | |
 |
Fig. 2 Rotational transition JKa,Kc = 143,11−134,10 in the ground state of DME-13C2 at 53 GHz. The torsional splitting into the four substates (00), (01), (11), and (1-1) is fully resolved. The spin statistical weights are denoted beneath each peak and are reflected by the relative intensities of the measured lines. |
| In the text | |
 |
Fig. 3 Torsional splitting of Q-branch transitions with Ka = 6−5 and Kc = J − Ka + 1 in the vibrational ground state of DME-13C1. The solid lines connect predicted transitions belonging to the same torsional substate. Experimental data are shown as errorbars. The splitting displayed is the difference between the transition frequency observed or predicted and the frequency derived if all tunneling parameters are neglected. |
| In the text | |
 |
Fig. 4 Detail of the APEX line survey towards the hot core G327.3-0.6. The observed spectrum is depicted in black, and the model for 12CH3O13CH3 is overplotted in red. The general model including transitions of all previously identified molecules is given in blue. The spectroscopic assignment of transitions of DME-13C1 is given in the upper left of each individual panel. The asymmetry splitting and the torsional splitting of transitions is not resolved in these lines, except for the first panel, in which the torsional splitting into three components is indicated. |
| In the text | |
 |
Fig. 5 Rotational diagram for CH3O13CH3 corrected for the optical depth. The data has been corrected for the dust optical depth, as well as the modeled line emission from other species. The filled squares (■) represent transitions detected with SHeFI in the 230, 290, and 345 GHz windows, and the open triangles (△) indicate CHAMP+ data. The solid line shows the fit to the combined SHeFI and CHAMP+ data, the dotted lines the fit to the main isotopologue by Bisschop et al. (2013) corrected for a 12C/13C ratio of 20 and 30, and the dashed lines a 12C/13C ratio of 10 and 40. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


