| Issue |
A&A
Volume 558, October 2013
|
|
|---|---|---|
| Article Number | A27 | |
| Number of page(s) | 5 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201321565 | |
| Published online | 27 September 2013 | |
Research Note
Nonisothermal filaments in equilibrium
1 Institute of Astrophysics, Vienna University, Türkenschanzstrasse 17, 1180 Vienna, Austria
e-mail: simone.recchi@univie.ac.at
2 MEMOTEF, Sapienza University of Rome, via del Castro Laurenziano 9, 00161 Rome, Italy
Received: 25 March 2013
Accepted: 22 August 2013
Context. The physical properties of the so-called Ostriker isothermal filament have been classically used as a benchmark to interpret the stability of the filaments observed in nearby clouds. However, recent continuum studies have shown that the internal structure of the filaments depart from the isothermality, typically exhibiting radially increasing temperature gradients.
Aims. The presence of internal temperature gradients within filaments suggests that the equilibrium configuration of these objects should be therefore revisited. The main goal of this work is to theoretically explore how the equilibrium structure of a filament changes in a nonisothermal configuration.
Methods. We solve the hydrostatic equilibrium equation by assuming temperature gradients similar to those derived from observations.
Results. We obtain a new set of equilibrium solutions for nonisothermal filaments with both linear and asymptotically constant temperature gradients. For sufficiently large internal temperature gradients, our results show that a nonisothermal filament could present significantly larger masses per unit length and shallower density profiles than the isothermal filament without collapsing by its own gravity.
Conclusions. We conclude that filaments can reach an equilibrium configuration under nonisothermal conditions. Detailed studies of both the internal mass distribution and temperature gradients within filaments are then needed to judge the physical state of filaments.
Key words: stars: formation / ISM: clouds / ISM: kinematics and dynamics / ISM: structure
© ESO, 2013
1. Introduction
Although the observations of filaments within molecular clouds have been reported for decades (e.g. Schneider & Elmegreen 1979), their presence has been recognized only recently as an unique characteristic of the star-formation process. The latest Herschel results have revealed the direct connection between the filaments, dense cores, and stars in all kinds of environments along the Milky Way, ranging from low-mass and nearby clouds (André et al. 2010) to the most distant and high-mass star-forming regions (Molinari et al. 2010). As a consequence, characterizing the physical properties of these filaments has been revealed as key to our understanding of the origin of the stars within molecular clouds.
Classically, filaments have been interpreted, assuming that (i) they are isothermal; (ii) they are isolated; (iii) they can be modeled as cylindrical structures with infinite length; and (iv) that their support against gravity comes solely from thermal pressure. However, observational evidence is mounting that none of the above hypotheses can be considered strictly valid: (i) Recent continuum observations of filaments in different clouds have shown that the dust temperature gradually decreases toward the main axis of these structures (e.g. Stepnik et al. 2003; Palmeirim et al. 2013); (ii) filaments are typically found forming intricate networks (e.g. hub-filament associations, Myers 2009) or even compact bundles of small-scale filaments (Hacar et al. 2013); (iii) filaments with aspect ratios of ~4−5 are not uncommon (Hacar & Tafalla 2011), and (iv) millimeter line studies show that the molecular emission arising from the filaments exhibit superthermal linewidths, suggesting that the nonthermal motions could play a non-negligible role in their stability (e.g. Arzoumanian et al. 2013). The inclusion of any of these characteristics could drastically change the interpretation of the physical state of the filaments. It is then clear that the equilibrium properties of the filaments should be revisited.
In this paper, we concentrate on the theoretical study of nonisothermal filaments. The main aim of this work is to show how the equilibrium structure of a filament changes if the hypothesis of isothermality is relaxed. In a companion paper (Recchi et al., in prep.), we investigate the stability and structure of nonisolated filaments. In a future paper we will investigate the effect of nonthermal pressure support within the filament.
2. Isothermal filaments
Starting from the seminal paper of Chandrasekhar & Fermi (1953), the stability of isothermal filaments has been studied by a number of authors. Stodólkiewicz (1963) and Ostriker (1964) first demonstrated that the radial profile of an isothermal filament in hydrostatic equilibrium can be described by ![\begin{equation} \rho_{\rm eq}(r)=\rho_{\rm c}\left[1+\left(\frac{r}{H}\right)^2\right]^{-2} \mbox{ with } H=\sqrt{\frac{2c_{\rm s}^2}{\pi G \rho_{\rm c}}}, \label{eq:equil} \end{equation}](/articles/aa/full_html/2013/10/aa21565-13/aa21565-13-eq7.png) (1)where r is the radial distance from the axis, ρc is the central density (i.e., the density at the axis), and cs is the isothermal sound speed (i.e.
(1)where r is the radial distance from the axis, ρc is the central density (i.e., the density at the axis), and cs is the isothermal sound speed (i.e. 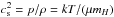 ). The mass per unit length (or linear mass) of this isothermal cylinder, known as the Ostriker filament, is given by
). The mass per unit length (or linear mass) of this isothermal cylinder, known as the Ostriker filament, is given by 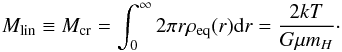 (2)Assuming a μ = 2.3 as a typical mean molecular weight in molecular clouds and a temperature typical of the interstellar medium of T = 10 K, the linear mass of an isothermal cylinder in equilibrium is then 16.6 M⊙ pc-1. In filaments with larger linear masses, equilibrium between pressure and self-gravity cannot be established. Under these conditions, self-gravity prevails, and the cylinder is destined to collapse into a spindle (e.g. Inutsuka & Miyama 1992).
(2)Assuming a μ = 2.3 as a typical mean molecular weight in molecular clouds and a temperature typical of the interstellar medium of T = 10 K, the linear mass of an isothermal cylinder in equilibrium is then 16.6 M⊙ pc-1. In filaments with larger linear masses, equilibrium between pressure and self-gravity cannot be established. Under these conditions, self-gravity prevails, and the cylinder is destined to collapse into a spindle (e.g. Inutsuka & Miyama 1992).
3. Equilibrium solutions for nonisothermal filaments
In parallel to the isothermal analysis, Ostriker (1964) also developed the theory of stability for nonisothermal cylinders. He considered a generic polytropic equation of state (EOS) P = Knρ1 + 1/n (n corresponds to 1/(γ − 1), where γ is the ratio of specific heats). By combining the equation of hydrostatic equilibrium ∇P = ρ∇V (where V is the gravitational potential) and the Poisson’s equation ∇2V = −4πGρ, he found the equation Kn(n + 1)∇2ρ1/n = −4πGρ. With the change of variables ![\hbox{$r=a\xi \equiv \left[\frac{(n+1)K_n}{4\pi G \rho_{\rm c}^{1-1/n}}\right]^{1/2}\xi$}](/articles/aa/full_html/2013/10/aa21565-13/aa21565-13-eq25.png) and σ = (ρ/ρc)1/n (originally defined as θ by Ostriker), the resulting equation is simply
and σ = (ρ/ρc)1/n (originally defined as θ by Ostriker), the resulting equation is simply 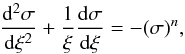 (3)which is subject to the initial conditions σ(0) = 1 and σ′(0) = 0. Equation (3) has real solutions only if n ≥ −1, or equivalently if γ ≥ 0 (but see Viala & Horedt 1974 for the case n < −1). These solutions include the isothermal solution when n = + ∞ (and γ = 1). Under these conditions, both the linear mass and the radius of the filament in equilibrium reach a finite value (see Ostriker 1964 for a discussion).
(3)which is subject to the initial conditions σ(0) = 1 and σ′(0) = 0. Equation (3) has real solutions only if n ≥ −1, or equivalently if γ ≥ 0 (but see Viala & Horedt 1974 for the case n < −1). These solutions include the isothermal solution when n = + ∞ (and γ = 1). Under these conditions, both the linear mass and the radius of the filament in equilibrium reach a finite value (see Ostriker 1964 for a discussion).
Nowadays, detailed observations of the dust emission in filaments offer us the unique opportunity to directly estimate their radial temperature profile (see Stepnik et al. 2003 for L1506 using PRONAOS; Nutter et al. 2008 for TMC-1 using SCUBA, and, more recently; Arzoumanian et al. 2011 for IC 5146 or Palmeirim et al. 2013 for B211 using Herschel). In contrast to the temperature profiles expected for filaments in equilibrium with polytropic EOS, the dust temperature gradients observed in nearby molecular filaments show that it is radially increasing (e.g. Stepnik et al. 2003; Palmeirim et al. 2013), probably due to the radiation field incident on the exterior of the filament complex. It is important to remark that it is impossible to obtain radially increasing temperature profiles by solving Eq. (3) for n > −1. In fact, T ∝ ρ1/n, hence T ∝ σ. For n > 0, both ρ and σ (hence T) decrease outwards. For n = 0, corresponding to ρ = const., the well-known solution is 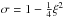 (decreasing outwards). It is easy to verify numerically that σ and T still decrease outwards for −1 < n < 0, whereas ρ increases outwards because ρ ∝ σn. The same result has been obtained by Viala & Horedt (1974; see their Tables 11−13). It is also interesting to remark that values of γ < 1 are expected for polytropic filaments in gravitational collapse, according to simulations (Kawachi & Hanawa 1998). As a result, the observation of these temperature profiles has been interpreted as a signature of instability.
(decreasing outwards). It is easy to verify numerically that σ and T still decrease outwards for −1 < n < 0, whereas ρ increases outwards because ρ ∝ σn. The same result has been obtained by Viala & Horedt (1974; see their Tables 11−13). It is also interesting to remark that values of γ < 1 are expected for polytropic filaments in gravitational collapse, according to simulations (Kawachi & Hanawa 1998). As a result, the observation of these temperature profiles has been interpreted as a signature of instability.
To take the observationally-based result of radially increasing temperature gradients into account, we must thus adopt a different approach. We assume that the gas temperature profile T(r) is known and we recover the corresponding equilibrium density profile. We still use the hydrostatic equilibrium relation ∇P = gρ, reminding, however, that now both T and ρ vary with radius (we still assume μ to be constant). The resulting (integro-differential) equation is 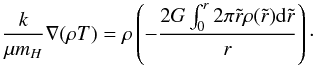 (4)Here, we define ρ = θρc, T = τT0 and r = Hx, where ρc, and T0 are the density and the temperature at the filament axis, respectively, and H is given by Eq. (1) with T = T0. The resulting normalized equation is
(4)Here, we define ρ = θρc, T = τT0 and r = Hx, where ρc, and T0 are the density and the temperature at the filament axis, respectively, and H is given by Eq. (1) with T = T0. The resulting normalized equation is 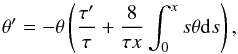 (5)where primes indicate differentiation with respect to x. This equation is subject to the initial condition θ(0) = 1 (i.e., ρ(x = 0) = ρc). This equation can be manipulated as follows: Differentiate it with respect to x, and use Eq. (5) to get rid of the integral. The resulting second-order ODE is
(5)where primes indicate differentiation with respect to x. This equation is subject to the initial condition θ(0) = 1 (i.e., ρ(x = 0) = ρc). This equation can be manipulated as follows: Differentiate it with respect to x, and use Eq. (5) to get rid of the integral. The resulting second-order ODE is 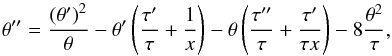 (6)where it is easy to see that the isothermal Ostriker solution θi = [1 + x2]-2 (i.e., the normalized version of Eq. (1)) satisfies the above ODE if τ = 1 (i.e. T(x) = T0). This form of the equation is more convenient than the Lane-Emden equation (Eq. (3)) for the problem at hand. It is also important to note that the above equation is subject to the initial conditions θ(0) = 1 and θ′(0) = −τ′(0). This initial condition is because the value of the pressure gradient at the axis must be zero (see below). The consequence of this initial condition is relevant: if the temperature profiles have positive gradients at the axis (as it appears from the observations), the density profiles must have negative gradients. That is, they must show central cusps.
(6)where it is easy to see that the isothermal Ostriker solution θi = [1 + x2]-2 (i.e., the normalized version of Eq. (1)) satisfies the above ODE if τ = 1 (i.e. T(x) = T0). This form of the equation is more convenient than the Lane-Emden equation (Eq. (3)) for the problem at hand. It is also important to note that the above equation is subject to the initial conditions θ(0) = 1 and θ′(0) = −τ′(0). This initial condition is because the value of the pressure gradient at the axis must be zero (see below). The consequence of this initial condition is relevant: if the temperature profiles have positive gradients at the axis (as it appears from the observations), the density profiles must have negative gradients. That is, they must show central cusps.
 |
Fig. 1 Normalized density profiles θ = ρ/ρc (left panel) and values of α (right panel; see Sect. 3.1 for the definition of α) as a function of x = r/H for models with temperature profiles as described by Eq. (8) for different normalized temperature gradients A. The reference isothermal profile is also plotted in both panels. |
Another way to manipulate Eq. (4) is the following: Call η the pressure, normalized to the central value (i.e. η = P/P0). The obtained integro-differential equation for η is 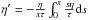 . Manipulating this equation exactly as done for Eq. (5), the following differential equation can be found:
. Manipulating this equation exactly as done for Eq. (5), the following differential equation can be found: 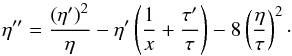 (7)The initial conditions are η(0) = 1 and η′(0) = 0. This second initial condition is derived from the equation of hydrostatic equilibrium ∇P = gρ, if we assume g(0) = 0. Given a temperature profile τ(x), the density profile for a nonisothermal filament in equilibrium θ(x) can be then derived solving Eqs. (6) or (7).
(7)The initial conditions are η(0) = 1 and η′(0) = 0. This second initial condition is derived from the equation of hydrostatic equilibrium ∇P = gρ, if we assume g(0) = 0. Given a temperature profile τ(x), the density profile for a nonisothermal filament in equilibrium θ(x) can be then derived solving Eqs. (6) or (7).
3.1. Filaments with linear temperature gradients
It is instructive to consider a simplified case, where the temperature linearly increases with radius as follows: 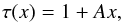 (8)where A is the normalized temperature gradient in units of the normalized radius x. This linear increase in the temperature closely resembles the observations summarized at the beginning of this section, at least for radii sufficiently close to the axis. We have numerically solved Eq. (6) for different values of A. We have also solved Eq. (7) and verified that the two solutions are identical. This is a useful check of the consistency of our solution. The resulting density profiles θ(x) are shown in Fig. 1 (left panel). We can notice from this figure that the density profile tends, as expected, to the isothermal profile θi = [1 + x2]-2 for A → 0. Within the range of normalized temperature gradients considered here (i.e., 0.01 ≤ A ≤ 0.5), the equilibrium configuration derived from Eq. (6) closely resembles the Ostriker profile at short radii (at least sufficiently close to the axis; i.e. x < 2). In contrast, the derived density profiles clearly depart from the equilibrium solution for an isothermal filament at larger radii under the presence of temperature gradients with A ≥ 0.1. Indeed, if A = 0.5 the density profile for an nonisothermal filament in equilibrium can be more than one order of magnitude higher than the expected value in the isothermal case at x ≥ 6.
(8)where A is the normalized temperature gradient in units of the normalized radius x. This linear increase in the temperature closely resembles the observations summarized at the beginning of this section, at least for radii sufficiently close to the axis. We have numerically solved Eq. (6) for different values of A. We have also solved Eq. (7) and verified that the two solutions are identical. This is a useful check of the consistency of our solution. The resulting density profiles θ(x) are shown in Fig. 1 (left panel). We can notice from this figure that the density profile tends, as expected, to the isothermal profile θi = [1 + x2]-2 for A → 0. Within the range of normalized temperature gradients considered here (i.e., 0.01 ≤ A ≤ 0.5), the equilibrium configuration derived from Eq. (6) closely resembles the Ostriker profile at short radii (at least sufficiently close to the axis; i.e. x < 2). In contrast, the derived density profiles clearly depart from the equilibrium solution for an isothermal filament at larger radii under the presence of temperature gradients with A ≥ 0.1. Indeed, if A = 0.5 the density profile for an nonisothermal filament in equilibrium can be more than one order of magnitude higher than the expected value in the isothermal case at x ≥ 6.
To better characterize the density profile, we consider the quantity 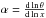 . If the density profile can be approximated by a power law, α clearly represents the exponent. The functions α(x) for the different density profiles discussed above as a function of the normalized radius x are plotted in Fig. 1 (right panel). For the isothermal profile θi(x) it is easy to see that
. If the density profile can be approximated by a power law, α clearly represents the exponent. The functions α(x) for the different density profiles discussed above as a function of the normalized radius x are plotted in Fig. 1 (right panel). For the isothermal profile θi(x) it is easy to see that 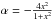 , with α tending to −4 for x → ∞. Compared to the Ostriker solution, the equilibrium configuration for a nonisothermal filament with A > 0 presents, therefore, shallower profiles at large radii. Particularly for 0.1 ≤ A ≤ 0.5, the filaments tend to present slopes with − 3 ≲ α ≲ − 2 for normalized radii within 4 < x < 10.
, with α tending to −4 for x → ∞. Compared to the Ostriker solution, the equilibrium configuration for a nonisothermal filament with A > 0 presents, therefore, shallower profiles at large radii. Particularly for 0.1 ≤ A ≤ 0.5, the filaments tend to present slopes with − 3 ≲ α ≲ − 2 for normalized radii within 4 < x < 10.
The presence of density profiles shallower than the Ostriker solution has important implications in the linear mass that can be supported by these nonisothermal filaments. As can be seen in Fig. 1, α tends to increase at large values of x. Indeed, it is possible to show (see Appendix A) that α must asymptotically tend to a value αlim ∈ ] −2, −1 [. This implies also that the normalized linear mass 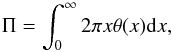 (9)diverges. This can be explained because the temperature tends to infinity for x → ∞, so the increasingly large thermal pressure at large radii must be counterbalanced by an increasingly large gravity. As a consequence, the linear mass for a nonisothermal filament in equilibrium presenting a linear temperature gradient can be arbitrarily large. To avoid the divergence of the linear mass, a filament described by a temperature profile as in Eq. (8) has to be necessarily pressure-truncated at some radius.
(9)diverges. This can be explained because the temperature tends to infinity for x → ∞, so the increasingly large thermal pressure at large radii must be counterbalanced by an increasingly large gravity. As a consequence, the linear mass for a nonisothermal filament in equilibrium presenting a linear temperature gradient can be arbitrarily large. To avoid the divergence of the linear mass, a filament described by a temperature profile as in Eq. (8) has to be necessarily pressure-truncated at some radius.
Finally, we notice that the properties of the nonisothermal filaments that are derived above resemble the equilibrium configuration found in turbulent dominated filaments. Gehman et al. (1996) demonstrated that an isothermal filament with a radially increasing turbulent pressure presents a shallower density profile and larger linear mass than the equivalent Ostriker-like filament at the same temperature. Compared to the nonisothermal configuration, in these models the increasing gravitational energy is balanced by a pressure generated from the radial increase of the nonthermal motions, while the filament is always thermally supported in our case.
3.2. Filaments presenting asymptotically constant temperature gradients
It is also useful to look for a temperature profile resembling Eq. (8) for small values of x but tending to a finite value for x → ∞. These kinds of profiles are similar to those found in the observations, where the temperature flattens out for large radii (typically at radii ~0.4−0.5 pc; see Stepnik et al. 2003; Palmeirim et al. 2013). A function with such properties could be 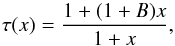 (10)where τ(x) tends to (1 + B) for x → ∞. The density profiles and the slopes α(x) for this temperature profile are shown in Fig. 2. As can be seen in the figure, the density profiles obtained for filaments described by Eq. (10) are closer to the isothermal profile when compared to the linear case if B is small (i.e. B ≲ 0.2), while they only become significantly different to the Ostriker profile at large radii under the presence of large gradients (i.e., with B ~ 0.5). Additionally for all the B values, the slopes of the density profiles decrease monotonically, with values of α < − 3.5 for normalized radii x > 8.
(10)where τ(x) tends to (1 + B) for x → ∞. The density profiles and the slopes α(x) for this temperature profile are shown in Fig. 2. As can be seen in the figure, the density profiles obtained for filaments described by Eq. (10) are closer to the isothermal profile when compared to the linear case if B is small (i.e. B ≲ 0.2), while they only become significantly different to the Ostriker profile at large radii under the presence of large gradients (i.e., with B ~ 0.5). Additionally for all the B values, the slopes of the density profiles decrease monotonically, with values of α < − 3.5 for normalized radii x > 8.
For those nonisothermal filaments in equilibrium with a temperature structure described by Eq. (10), it is possible to show (see again Appendix A) that α must be smaller than − 2. In contrast to the linear case, this implies also that the integral in Eq. (9) defining the linear mass is converging.
In this sense, we have also numerically calculated the relation between both the linear mass Π and the half-mass radius x1/2 (the radius within which the mass is 0.5Π) of a filament described by Eq. (10) as a function of B, comparing them with the equivalent values for the linear mass (which turns out to be equal to π) and the half-mass radius (=1) for the Ostriker filament. Our results show that these two quantities can be well approximated by the following quadratic fits
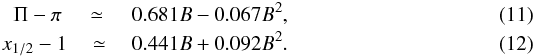 We can thus see that a nonisothermal filament (with temperature increasing outwards but tending to a constant value) can sustain again more mass than an isothermal Ostriker-like filament without being gravitationally unstable. However, the differences in the linear mass between these two models in this case are not very large (typically of less than 20−30%).
We can thus see that a nonisothermal filament (with temperature increasing outwards but tending to a constant value) can sustain again more mass than an isothermal Ostriker-like filament without being gravitationally unstable. However, the differences in the linear mass between these two models in this case are not very large (typically of less than 20−30%).
4. Conclusions
The steep radial profile, which is typically ∝r-4, and the characteristic mass per unit length with 16.6 M⊙ pc-1 at 10 K of the the isothermal Ostriker filament have been used to define the equilibrium state of the filaments within molecular clouds. As shown in Sect. 3, the nonisothermal nature of the filaments introduce an additional support for the stability of these objects compared to their isothermal counterparts. Indeed, these results illustrate how the nonisothermal filaments could present larger linear masses and shallower radial profiles than the Ostriker-like filaments without being necessary unstable, where these differences increase under the presence of large temperature gradients.
Available observations suggest shallow dust temperature gradients. For instance, the temperature gradient of the filament B211/3 derived by Palmeirim et al. (2013) indicates A ≃ 0.022. However, dust and gas temperatures are not likely to be well coupled in filaments. This happens for densities larger than ~3 × 104 cm-3 (Galli et al. 2002). The derived central density in B211/3 is ~4.5 × 104 cm-3 (Palmeirim et al. 2013, see their footnote 2); thus, dust and gas temperatures are probably very similar close to the axis. They decouple at some distance from the axis with cosmic rays ionization playing a role in heating up the gas. It is thus reasonable to expect gas temperature profiles that are steeper than what dust measurements indicate. This analytic work illustrates how only dedicated and combined studies of both the mass distribution and thermal structure within these objects (in addition to simulations) can be then used to determine the physical state of filaments in molecular clouds.
Acknowledgments
This publication is supported by the Austrian Science Fund (FWF). Useful suggestions from an anonymous referee and from the Editor, M. Walmsley, are acknowledged.
References
- André, P., Men’shchikov, A., Bontemps, S., et al. 2010, A&A, 518, L102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arzoumanian, D., André, P., Didelon, P., et al. 2011, A&A, 529, L6 [Google Scholar]
- Arzoumanian, D., André, P., Peretto, N., & Konyves, V. 2013, A&A, 553, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chandrasekhar, S., & Fermi, E. 1953, ApJ, 118, 116 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Gehman, C. S., Adams, F. C., Fatuzzo, M., & Watkins, R. 1996, ApJ, 457, 718 [NASA ADS] [CrossRef] [Google Scholar]
- Galli, D., Walmsley, M., & Gonçalves, J. 2002, A&A, 394, 275 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hacar, A., & Tafalla, M. 2011, A&A, 533, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hacar, A., Tafalla, M., Kauffmann, J., & Kovacs, A. 2013, A&A, 554, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Inutsuka, S.-I., & Miyama, S. M. 1992, ApJ, 388, 392 [NASA ADS] [CrossRef] [Google Scholar]
- Kawachi, T., & Hanawa, T. 1998, PASJ, 50, 577 [NASA ADS] [CrossRef] [Google Scholar]
- Molinari, S., Swinyard, B., Bally, J., et al. 2010, A&A, 518, L100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Myers, P. C. 2009, ApJ, 700, 1609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakamura, F. 1998, ApJ, 507, L165 [NASA ADS] [CrossRef] [Google Scholar]
- Nutter, D., Kirk, J. M., Stamatellos, D., & Ward-Thompson, D. 2008, MNRAS, 384, 755 [NASA ADS] [CrossRef] [Google Scholar]
- Ostriker, J. 1964, ApJ, 140, 1056 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Palmeirim, P., André, P., Kirk, J., et al. 2013, A&A, 550, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, S., & Elmegreen, B. G. 1979, ApJS, 41, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Stepnik, B., Abergel, A., Bernard, J.-P., et al. 2003, A&A, 398, 551 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stodólkiewicz, J. S. 1963, Acta Astron., 13, 30 [NASA ADS] [Google Scholar]
- Viala, Y., & Horedt, G. P. 1974, A&AS, 16, 173 [NASA ADS] [Google Scholar]
Appendix A: The asymptotic slope of the density profile
In this appendix, we study the asymptotic behavior of the density profile θ(x). A similar problem has been previously discussed in Ostriker (1964) and Gehman et al. (1996) for filaments in equilibrium ruled by different EOS. In this case, we aim to investigate the asymptotic behavior of the normalized radial profile (θ) and linear mass (Π) of a nonisothermal filament in equilibrium with a temperature structure described by Eqs. (8) or (10).
Let us first assume a temperature profile like Eq. (8). As explained in Sect. 3, if we assume a power law dependence θ ~ xα, then 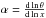 . From Eq. (8), we transform Eq. (5) to calculate the quantity
. From Eq. (8), we transform Eq. (5) to calculate the quantity 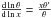 . Assuming that θ(x) can be well approximated by a power law only for x > x∗, one then obtains
. Assuming that θ(x) can be well approximated by a power law only for x > x∗, one then obtains 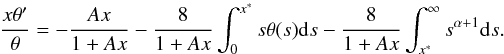 (A.1)For x → ∞, the left hand side tends to α; the first term on the right hand side tends to − 1; the second tends to 0, and the third is proportional to xα − 1 if α ≠ − 2 and to
(A.1)For x → ∞, the left hand side tends to α; the first term on the right hand side tends to − 1; the second tends to 0, and the third is proportional to xα − 1 if α ≠ − 2 and to  if α = −2. We see now that α cannot be larger than − 1; otherwise, the right hand side diverges. It cannot also be smaller than (or equal to) − 2, since α would tend to − 1 in this case. This would contradict the assumption that α ≤ − 2. A more careful analysis, based on the assumption that θ(x) = xα + R(x), where R(x) is a small residual function, leads to the conclusion that α ∈ ] − 2, − 1 [. Consequently, the integral Π = ∫2πxθ(x)dx is divergent.
if α = −2. We see now that α cannot be larger than − 1; otherwise, the right hand side diverges. It cannot also be smaller than (or equal to) − 2, since α would tend to − 1 in this case. This would contradict the assumption that α ≤ − 2. A more careful analysis, based on the assumption that θ(x) = xα + R(x), where R(x) is a small residual function, leads to the conclusion that α ∈ ] − 2, − 1 [. Consequently, the integral Π = ∫2πxθ(x)dx is divergent.
We employ now the temperature profile from Eq. (10). From it, Eq. (5) then becomes ![\appendix \setcounter{section}{1} \begin{equation} \frac{\theta^\prime}{\theta}\!=\!-\frac{B}{(1\!+\!x)[1+(B+1)x]} - \frac{8(1+x)}{x[1+(B+1)x]}\int_0^x \!\!s \theta(s){\rm d}s. \label{eq:thetadynamics} \end{equation}](/articles/aa/full_html/2013/10/aa21565-13/aa21565-13-eq136.png) (A.2)Proceeding as before, it is easy to see that
(A.2)Proceeding as before, it is easy to see that 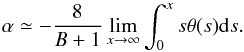 (A.3)We define now I as
(A.3)We define now I as 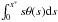 . It is easy to obtain
. It is easy to obtain 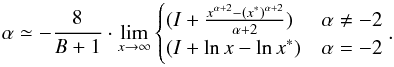 (A.4)The case α = −2 can be immediately ruled out because, the right hand side of (A.4) explodes to − ∞ for x → ∞, and analogously we cannot accept values of α larger than − 2. Hence, we conclude that α < − 2 necessarily. This range of values for α is particularly relevant in that it implies finite masses. In fact, the integral
(A.4)The case α = −2 can be immediately ruled out because, the right hand side of (A.4) explodes to − ∞ for x → ∞, and analogously we cannot accept values of α larger than − 2. Hence, we conclude that α < − 2 necessarily. This range of values for α is particularly relevant in that it implies finite masses. In fact, the integral 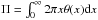 does not diverge in this case.
does not diverge in this case.
All Figures
 |
Fig. 1 Normalized density profiles θ = ρ/ρc (left panel) and values of α (right panel; see Sect. 3.1 for the definition of α) as a function of x = r/H for models with temperature profiles as described by Eq. (8) for different normalized temperature gradients A. The reference isothermal profile is also plotted in both panels. |
| In the text | |
 |
Fig. 2 As Fig. 1 but for models with temperature profiles as described by Eq. (10). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


